Estimating optimal shared-parameter dynamic regimens with application to a multistage depression clinical trial

Summary

A dynamic treatment regimen consists of decision rules that recommend how to individualize treatment to patients based on available treatment and covariate history. In many scientific domains, these decision rules are shared across stages of intervention. As an illustrative example, we discuss STAR*D, a multistage randomized clinical trial for treating major depression. Estimating these shared decision rules often amounts to estimating parameters indexing the decision rules that are shared across stages. In this paper, we propose a novel simultaneous estimation procedure for the shared parameters based on Q-learning. We provide an extensive simulation study to illustrate the merit of the proposed method over simple competitors, in terms of the treatment allocation matching of the procedure with the “oracle” procedure, defined as the one that makes treatment recommendations based on the true parameter values as opposed to their estimates. We also look at bias and mean squared error of the individual parameter-estimates as secondary metrics. Finally, we analyze the STAR*D data using the proposed method.

1. Introduction

Dynamic treatment regimens (DTRs) offer an operationalized framework for developing individually tailored multistage treatments (Murphy, 2003; Robins, 2004; Chakraborty and Moodie, 2013). Precisely, a DTR is a sequence of decision rules, where each decision rule takes a patient's treatment and covariate history up to that stage as inputs, and outputs one or more treatment recommendations. An important research goal in the DTR arena is to construct an optimal data-driven DTR in a well-defined sense (e.g., optimal mean outcome).

A less-understood class of DTRs is the one with shared decision rules across stages. It is plausible in many scientific domains to have decision rules that are common to more than one stage of treatment, e.g., when the decision rule at each stage is believed to be the same function of one or more time-varying covariate(s); some specific examples follow. Patients with major depression are given medication in episodes when an appropriate depression score, e.g., quick inventory of depressive symptomatology (Rush et al., 2003), rises above a threshold. In the treatment of schizophrenia, treatment is switched when the reduction in the positive and negative syndrome scale is below a threshold (Shortreed and Moodie, 2012). For treating HIV infection, highly active antiretroviral therapy is initiated when the patient's CD4 T-cell count falls below a threshold (Cain et al., 2010). In all these examples, the threshold for initiating or changing treatment does not vary with the duration of illness or the length of time already on treatment; in other words, the threshold is shared across stages. More generally, the decision rules are often formulated in terms of linear functions of two or more time-varying covariates, in which case the concept of a common threshold generalizes to a few parameters that appear as coefficients of a linear combination determining the common decision rule. For example, suppose X₁ and X₂ are two time-varying covariates, and there are two possible treatment options at each of J stages, coded 1 and −1. Then a shared-parameter DTR can be specified by the common rule: d_j,ψ(x_1j, x_2j) = sign (ψ₀ + ψ₁ x_1j + ψ₂ x_2j), j = 1,…, J, where ψ = (ψ₀, ψ₁, ψ₂) is the vector of shared parameters, and sign (u) = 1 if u > 0 and −1 otherwise. Here and throughout, we use upper case letters to denote random variables, and lower case letters to denote corresponding realized values.

Estimating an optimal DTR, with or without shared decision rules, is a problem of multistage decision making. Q-learning (Murphy, 2005; Nahum-Shani et al., 2012) is a popular method for estimating optimal DTRs. In its various implementations to date, Q-learning is a recursive estimation procedure that moves backward through stages, and thus is not suitable for the shared-parameter problem as such. Semiparametric methods such as iterative minimization of regrets (IMOR) (Murphy, 2003) and simultaneous g-estimation (Robins, 2004) can, in principle, handle the shared-parameter problem; however IMOR was found to be numerically unstable in a relatively simple data analysis (Rosthoj et al., 2006), and very little is known about the empirical performance of simultaneous g-estimation (see Moodie and Richardson, 2010, for further discussion). More recently, Zhao et al. (2015) proposed a machine learning based method called simultaneous outcome weighted learning (SOWL) that too can handle the shared-parameter problem. However, it is a complex method that requires minimizing a multi-dimensional hinge loss (generalization of the loss function used in support vector machines); furthermore, the authors report some numerical instability when more than two stages of decision-making are involved (Zhao et al., 2015, p. 594). IMOR, g-estimation and SOWL share a common feature: they are all conceptually very difficult for practitioners to understand and implement. This relative scarcity of practically appealing methods to estimate shared-parameter DTRs led us to devise a simple yet novel Q-learning based simultaneous estimation procedure – we call this method Q-shared.

The current article is partly motivated by our intention to estimate the optimal DTR for treating major depression, based on data from the Sequenced Treatment Alternatives to Relieve Depression (STAR*D) trial (Rush et al., 2004), which was a multistage randomized trial designed to assess the comparative effectiveness of different treatment regimens for outpatients with nonpsychotic major depressive disorder. In this study, there were four main levels (denoted 1, 2, 3, 4) and one supplementary level attached to level 2 (denoted 2A). Severity of depression was assessed using the clinician-rated and self-reported versions of the 16-item Quick Inventory of Depressive Symptomatology (QIDS) scores (Rush et al., 2003). At the end of each level, treatment success was assessed in terms of “remission”, defined as a total clinician-rated QIDS score ≤ 5. At level 1, all the patients were treated with citalopram (CIT); no randomization was involved. Those without remission or experiencing medication intolerance (non-responders) after level 1 were eligible to be randomized to one of several treatment options at level 2, which we classify as either mono therapy or combination therapy. A subgroup of level-2 patients were eligible to receive additional treatments at level 2A. Non-responders at level 2 (and level 2A, if applicable) continued to level 3 and were randomized to mono therapy vs. combination therapy options. Similarly, non-responders at level 3 moved to level 4 and were randomized to mono therapy vs. combination therapy options. Patients achieving a satisfactory response at any level entered a naturalistic follow-up phase, in which by research protocol they did not receive any new treatment but were supposed to maintain the successful treatment. The actual treatment options at various levels are described in Section A.7 of the Web Supplement. The categorization of treatments as mono therapy or combination therapy is clinically justifiable because at any level the combination therapy can be viewed as a more intensive treatment path compared to mono therapy, with potentially higher chance of success but also higher risk of side-effects. Our goal is to find out, based on STAR*D data, whether it is better to treat a patient with a mono therapy or a combination therapy, based on his/her treatment and covariate history, over three stages of intervention.

The contributions of the current article can be summarized as follows. First, to the best of our knowledge, this article is the first thorough and focussed attempt to shed light on the problem of shared-parameter DTRs in a practically appealing way. In this article, we propose and show the merit of a novel Q-learning based simultaneous estimation procedure, which is substantially more user-friendly than existing methods. Second, we consider a novel analysis of the STAR*D data. While previous analyses of STAR*D data in the DTR literature typically considered only two stages (e.g., Chakraborty et al., 2013), we look at all three stages of randomization in a Q-learning framework with parameter sharing.

The remainder of this article is organized as follows. In Section 2, we introduce the novel Q-shared approach for estimating shared-parameter DTRs, followed by a thorough simulation study to show the finite-sample performance of this method in Section 3. We present the analysis of the STAR*D data using the Q-shared method in Section 4. Finally we conclude with a discussion in Section 5. Additional materials are deferred to the Web Supplement.

2. Estimation of DTRs with Shared Parameters

We consider studies with J stages, in which longitudinal data on a single patient are given by the trajectory (O₁, A₁,…,O_J, A_J, O_J+1), where O_j denotes the covariates measured prior to treatment at the beginning of the j-th stage and A_j is the treatment assigned at the j-th stage subsequent to observing O_j, for j = 1,…, J, and finally O_J+1 is the observation at the end of stage J (end of study). There are two possible treatments at each stage, coded −1 and 1, and randomly assigned with known randomization probabilities. For notational convenience, define the “history” at each stage as: H_j = (O₁, A₁,…, O_j) for j = 1,…, J + 1. Finally, the primary outcome is defined as a known function of the entire history, say Y = g(H_J+1); see Eqn. (2) for an example. A DTR is a vector of decision rules, (d₁,…, d_J), with d_j(H_j) ∈ 𝒜_j, where 𝒜_j is the space of treatments at the j-th stage (j = 1,…, J).

Following Murphy (2005), define the objective functions called Q-functions as: Q_J(H_J, A_J) = E[Y|H_J, A_J] and Q_j(H_j, A_j) = E[max_aj+1 Q_j+1(H_j+1, a_j+1)|H_j, A_j], for j = J–1,…, 1. The optimal DTR, using dynamic programming, is given by d_j(h_j) = arg max_aj Q_j(h_j, a_j), ∀_j. In practice, the Q-functions often need to be estimated from data on n patients; in the simplest case, they are estimated via linear regression using working models $Q_j(H_j,A_j;{\beta }_j,{\psi }_j)={\beta }_j^T{H}_{j0}+({\psi }_j^T{H}_{j1})A_j$, where H_j0 and H_j1 are possibly different features of H_j (both H_j0 and H_j1 include intercept-like terms). Accordingly, $d_j(h_j)=arg{arg}_{a_j}{Q}_j(h_j,a_j;{\beta }_j,{\psi }_j)=\mathit{\text{sign}}({\psi }_j^T{H}_{j1})$, which are often estimated by standard, recursive Q-learning; see Section A.1 of the Web Supplement for details. To distinguish it from the Q-shared method to be proposed next, we shall refer to the standard, recursive Q-learning as Q-unshared.

Now we consider the setting where the decision rule parameters are shared across stages, i.e., ψ₁ = … = ψ_J = ψ, but the nuisance parameters β_js are left unshared. Assuming correctly specified models, one can write Q_j = E[Y_j(θ_j+1)|H_j, A_j] for 1 ≤ j < J, where $Y_j({\theta }_{j+1})={\beta }_{j+1}^T{H}_{j+1,0}+|{\psi }_{j+1}^T{H}_{j+1,1}|$ is the population-level stage-j pseudo-outcome. Then one can write J regression equations Q_j = Z_jθ_j, with ${\theta }_j^T=({\beta }_j^T,{\psi }^T)$ and ${\mathbf{Z}}_j=(H_{j0}^T,H_{j1}^T{A}_j)$, for j = 1,…, J. Partitioning the design matrices Z_j according to the partitions of θ_j, and combining the data from all J stages, we can write the following regression equation:

$$\left(\begin{array}{c}Y\\ Y_{J-1}({\theta }_J)\\ ⋮\\ Y_1({\theta }_2)\end{array}\right)=\left(\begin{array}{ccccc}{\mathbf{Z}}_J^{({\beta }_J)}& \mathbf{0}& \cdots & \mathbf{0}& {\mathbf{Z}}_J^{(\psi )}\\ \mathbf{0}& {\mathbf{Z}}_{J-1}^{({\beta }_{J-1})}& \cdots & \mathbf{0}& {\mathbf{Z}}_{J-1}^{(\psi )}\\ ⋮& ⋮& & ⋮& ⋮\\ \mathbf{0}& \mathbf{0}& \cdots & {\mathbf{Z}}_1^{({\beta }_1)}& {\mathbf{Z}}_1^{(\psi )}\end{array}\right)\left(\begin{array}{c}{\beta }_J\\ {\beta }_{J-1}\\ ⋮\\ {\beta }_1\\ \psi \end{array}\right)+\epsilon \text{or},Y^{\ast }(\theta )=\mathbf{Z}\theta +\epsilon ,$$ (1)

where ${\theta }^T=({\beta }_J^T,\dots ,{\beta }_1^T,{\psi }^T)$ and ε is the associated error term. From Eqn. (1), θ seems to be estimable by minimizing J(θ) = ‖Y*(θ) – Zθ‖². But direct minimization is problematic because: (i) Y*(θ) is defined in terms of the unknown parameters θ; and (ii) some of the parameters are shared. Hence no closed-form solution is available; instead, an iterative procedure needs to be employed.

Note that settings where all the components of θ_j are shared (not considered here) are analogous to stationary Markov decision processes with function approximations considered in the reinforcement learning literature (Sutton and Barto, 1998); in those settings, J(θ) can be identified with the (approximate) squared Bellman error (see, e.g. Gordon, 1999). It is well-known that due to the non-smooth maximization operation used in defining the pseudo-outcomes, algorithms directly geared towards minimizing the squared Bellman error can be unstable and may not even converge to the true solution, particularly when a “small” (e.g., linear) approximation space for Q-functions is used (Sutton and Barto, 1998; Antos et al., 2008). While our current shared-parameter DTR setting is not exactly the same as the one discussed above, it is close enough to experience some of the problems of direct minimization of J(θ) (we verified this in our preliminary numerical investigation). Hence to tackle this challenge in a relatively simple fashion, we proceed by proposing an estimating equation involving the Bellman residual, (Y*(θ) – Zθ), instead of minimizing its squared L₂-norm, J(θ). The proposed estimating equation is: S_θ(Z) × (Y*(θ) – Zθ) = 0, where S_θ(Z) is an appropriate “score” function. For simplicity, we take $S_{\theta }(\mathbf{Z})=\frac{\partial }{\partial \theta }({(\mathbf{Z}\theta )}^T)={\mathbf{Z}}^T$. While the proposed estimating equation is still non-linear in θ and needs an iterative approach to solve, it leads to much higher numerical stability. We propose the following iterative algorithm.

Q-shared Algorithm

1. Set initial value of θ (either estimate from data, or otherwise guess); denote it as ${\widehat{\theta }}^{(0)}={({\widehat{\beta }}_J^{{(0)}^T},\dots ,{\widehat{\beta }}_1^{{(0)}^T},{\widehat{\psi }}^{{(0)}^T})}^T$.

2. At the (k + 1)th iteration, k = 0, 1, 2,…:

   1. Construct the vector Y*(θ̂^(k)).
   2. Solve the estimating equation Z^T(Y*(θ̂^(k)) – Zθ) = 0 for θ to obtain θ̂^(k+1).

3. Repeat steps (2a) – (2b) until convergence, i.e. until ‖θ̂^(k+1) – θ̂^(k)‖ < ε, for a pre-specified value ε, for some k.

A Few Possible Choices of Initial Values

Below we list five possible choices of initial values, which is not meant to be exhaustive. The first four choices require the user to first estimate θ_j via Q-unshared (see Section A.1 of the Web Supplement); call the resulting initial estimates ${\widehat{\theta }}_j^{(0)}$, j = J,…, 1. Note that for the shared parameters ψ, J distinct estimates, say ${\widehat{\psi }}_j^{(0)}$, j = 1,…, J, are obtained. To combine them into a single estimate, define ${\widehat{\psi }}^{(0)}=f({\widehat{\psi }}_J^{(0)},\dots ,{\widehat{\psi }}_1^{(0)})$, for a known function f. Hence define ${\widehat{\theta }}^{(0)}={({\widehat{\beta }}_J^{{(0)}^T},\dots ,{\widehat{\beta }}_1^{{(0)}^T},{\widehat{\psi }}^{{(0)}^T})}^T$. The last choice does not require any initial estimation; it simply sets all parameters to be zero. The list of choices follows.

1. Simple Average: ${\widehat{\theta }}^{(\mathit{\text{SA}})}={({\widehat{\beta }}_J^{{(0)}^T},\dots ,{\widehat{\beta }}_1^{{(0)}^T},{\widehat{\psi }}^{{(SA)}^T})}^T$, where ${\widehat{\psi }}^{(\mathit{\text{SA}})}=\frac{1}{J}{\sum }_{j=1}^J{\widehat{\psi }}_j^{(0)}$;

2. Inverse Variance Weighted Average: ${\widehat{\theta }}^{(\mathit{\text{IVWA}})}={({\widehat{\beta }}_J^{{(0)}^T},\dots ,{\widehat{\beta }}_1^{{(0)}^T},{\widehat{\psi }}^{{(\mathit{\text{IVWA}})}^T})}^T$, where ${\widehat{\psi }}^{(\mathit{\text{IVWA}})}=({\sum }_{j=1}^J\frac{{\widehat{\psi }}_j^{(0)}}{{\widehat{\sigma }}_j^2})/({\sum }_{j=1}^J\frac{1}{{\widehat{\sigma }}_j^2})$ and ${\widehat{\sigma }}_j^2$ is the estimated large-sample variance of ${\widehat{\psi }}_j^{(0)}$, j = 1,…, J;

3. Maximum: ${\widehat{\theta }}^{(\mathit{MAX})}={({\widehat{\beta }}_J^{{(0)}^T},\dots ,{\widehat{\beta }}_1^{{(0)}^T},{\widehat{\psi }}^{{(\mathit{MAX})}^T})}^T$, where ${\widehat{\psi }}^{(\mathit{MAX})}=max\{{\widehat{\psi }}_1^{(0)},\dots ,{\widehat{\psi }}_J^{(0)}\}$;

4. Minimum: ${\widehat{\theta }}^{(\mathit{MIN})}={({\widehat{\beta }}_J^{{(0)}^T},\dots ,{\widehat{\beta }}_1^{{(0)}^T},{\widehat{\psi }}^{{(\mathit{MIN})}^T})}^T$, where ${\widehat{\psi }}^{(\mathit{MIN})}=min\{{\widehat{\psi }}_1^{(0)},\dots ,{\widehat{\psi }}_J^{(0)}\}$;

5. All Zeroes: θ̂^(ZERO) = (0^T,…, 0^T, 0^T)^T.

For ease of reference, we call the five resulting versions of the Q-shared method Q-shared.SA, Q-shared.IVWA, Q-shared.MAX, Q-shared.MIN and Q-shared.ZERO, respectively.

3. Simulation Study

In this section, we consider a simulation study with two goals. The first goal is to investigate the finite-sample performance of the proposed Q-shared method in comparison with standard recursive Q-learning (Q-unshared); we hypothesize that Q-shared will perform better in general. To provide a more complete perspective, we also consider two secondary competitors: (1) Q-learning with simple averaging (Q-SA); and (2) Q-learning with inverse variance weighted averaging (Q-IVWA). These methods respectively estimate θ̂^(SA) and θ̂^(IVWA),which are two choices of initial values used by Q-shared, but do not enter the iterative algorithm thereafter. The IVWA approach was previously considered by Robins (2004, p.33) in the g-estimation context. We view Q-SA and Q-IVWA as two very simple yet sensible ways to deal with the shared-parameter problem, and clearly they lie in between Q-unshared and Q-shared in the spectrum of methods for estimating the shared parameters. The second goal of the simulation study is to assess the robustness of the Q-shared method to the choice of initial values, and for this we implement the five versions of this method listed in Section 2.

As primary metric for comparison, we consider a treatment allocation matching between the regimen resulting from a candidate method and an “oracle” regimen; this simple but intuitive metric will allow us to gauge how far a DTR estimated by a candidate method is from the oracle DTR that utilizes the true underlying parameter values. More specifically, suppose the Q-models are correctly specified. Then the oracle regimen would be d^ψ that would know the true parameter values ψ and would allocate the best treatments accordingly. Any estimation method would result in an estimated regimen d^ψ̂. Then a measure of the quality of d^ψ̂ at stage j would be the probability of allocation matching with the oracle at stage j, defined as $M_j=P[d_j^{\widehat{\psi }}(H_j)=d_j^{\psi }(H_j)]$, where P is the probability distribution of H_j. Note that M_j can be estimated by corresponding sample proportion and expressed as a percentage. To avoid the “optimism” of in-sample estimates, we estimate the M_js based on a separate Monte Carlo evaluation data set of the same size and drawn from the same distribution as the training data set. Finally, we combine all the stage-specific allocation matchings by weighted averaging into a single metric, $M=\frac{{\sum }_{j=1}^J{n}_j{M}_j}{{\sum }_{j=1}^J{n}_j}$, where n_js are the number of patients at stage j = 1,…, J. This weighting is important because different stages can have very different number of subjects. In addition, we compute the overall allocation matching over all the stages, M̃ = P[d^ψ̂ = d^ψ]. We also compute bias and mean squared error (MSE) of the estimates of the individual shared parameters as secondary metrics.

3.1 Simulation Design

In designing this study, we follow the STAR*D trial closely. There are three stages of this study, and only a fraction of the subjects (non-responders) move from stage j to (j + 1) of the trial (j = 1, 2), while the rest (responders) move to the follow-up phase and thus exit the main study. Let R₁ and R₂ denote the response indicators (1 = response, 0 = non-response) at the end of stages 1 and 2 respectively; here we generate them from Bernoulli distributions with success rates τ₁ and τ₂ respectively, and set τ₁ = 0.38 and τ₂ = 0.18, as in STAR*D. In the primary simulation study, the stage 1 sample size is taken as 300, reflective of the typical size of a sequentially randomized trial. To illustrate the effect of sample size, we also consider a secondary study with sample size 1200, comparable to that of STAR*D; this second study is deferred to the Web Supplement (Section A.5). The Monte Carlo simulation size is 1000.

We consider randomized binary treatments, e.g. $P[A_j=1]=P[A_j=-1]=\frac{1}{2}$, j = 1, 2, 3. The binary covariates are generated as $P[O_1=1]=P[O_1=-1]=\frac{1}{2}$, P[O₂ = 1|O₁, A₁] = 1 – P[O₂ = −1|O₁, A₁] = expit(δ₂₁O₁ + δ₂₂A₁), and P[O₃ = 1|O₁, A₁, O₂, A₂] = 1 – P[O₃ = −1|O₁, A₁, O₂, A₂] = expit(δ₃₁O₂+δ₃₂A₂+ δ₃₃A₁A₂), where expit(x) = exp(x)/(1+ exp(x)). We generate the stage-specific outcomes as: Y₁ = γ₁ + γ₂O₁ + γ₃A₁ + γ₄O₁A₁ + ε₁, $Y_2=Y_1+\frac{3}{2}[{\gamma }_5{O}_2+{\gamma }_6{A}_2+{\gamma }_7{O}_2{A}_2+{\gamma }_8{A}_1{A}_2]+{\epsilon }_2$, and Y₃ = Y₂ + 3[γ₉O₃ + γ₁₀A₃ + γ₁₁O₃A₃ + γ₁₂A₂A₃ + γ₁₃A₁A₂A₃]+ε₃, where ε₁, ε₂, ε₃ ∼ N(0,1) are the associated error terms. Finally, the individual Y_js are combined to define the final primary outcome Y using Eqn. (2). The specific form of Y_js considered above make the primary outcome for the subjects who move all the way till the third stage of the study (i.e., those with R₁ = R₂ = 0) equal to a standard linear regression model as follows: Y = γ₁ + γ₂O₁ + γ₃A₁ + γ₄O₁ A₁ + γ₅O₂ + γ₆A₂ + γ₇O₂A₂ + γ₈A₁A₂ + γ₉O₃ + γ₁₀A₃ + γ₁₁O₃A₃ + γ₁₂A₂A₃ + γ₁₃A₁A₂A₃ + ε, where $\epsilon =\frac{1}{3}({\epsilon }_1+{\epsilon }_2+{\epsilon }_3)$. The parameters γ₁,…, γ₁₃, and δ₂₁, δ₂₂, δ₃₁, δ₃₂, δ₃₃, in conjunction with the response rates τ₁ and τ₂, completely specify the generative model. For the purpose of analysis, we specify the following Q-models (note that Q₃ is correctly specified for Y):

$$\begin{array}{c}{Q}_3={\beta }_{30}+{\beta }_{31}{O}_1+{\beta }_{32}{A}_1+{\beta }_{33}{O}_1{A}_1+{\beta }_{34}{O}_2+{\beta }_{35}{A}_2+{\beta }_{36}{O}_2{A}_2+{\beta }_{37}{A}_1{A}_2+{\beta }_{38}{O}_3+({\psi }_0+{\psi }_1{O}_3+{\psi }_2{A}_2+{\psi }_3{A}_1{A}_2)A_3,\\ Q_2={\beta }_{20}+{\beta }_{21}{O}_1+{\beta }_{22}{A}_1+{\beta }_{23}{O}_1{A}_1+{\beta }_{24}{O}_2+({\psi }_0+{\psi }_1{O}_2+{\psi }_2{A}_1)A_2,\\ Q_1={\beta }_{10}+{\beta }_{11}{O}_1+({\psi }_0+{\psi }_1{O}_1)A_1.\end{array}$$

Clearly, ψ₀ and ψ₁ are the shared parameters of interest. The optimal DTR is given by the decision rule: d_j(H_j) = sign(ψ₀ + ψ₁O_j + ψ₂A_j–1 + ψ₃A_j–2A_j–1), j = 1, 2, 3, where, for convenience, we define the fake variables A₀ ≡ 0 and A₋₁ ≡ 0. In this light, ψ₂ and ψ₃ too can be viewed as shared parameters; however data from all stages do not provide information towards their estimation. The relationships between the generative model parameters (γs) and the analysis model parameters (ψs) are derived in Section A.3 of the Web Supplement. By varying the generative model parameters, we construct seven example scenarios reflecting varying degrees of nonregularity expressed in terms of p₃ = P[ψ^TH₃₁ = 0] and p₂ = P[ψ^TH₂₁ = 0] (see Section A.2 of the Web Supplement for details); these examples allow us to capture the performance of the methods over a broad region of interest in the moderately high-dimensional parameter space. We report the values of ψ₀, p₃ and p₂ in Table 1; see Table 1 of the Web Supplement for a complete description of the examples.

Table 1.

Bias of ψ₀ and Allocation Matching with the Oracle (%) for Sample Size 300. The metrics $M={\sum }_{j=1}^J{n}_{j}P[d_j^{\widehat{\psi }}(H_j)=d_j^{\psi }(H_j)]/{\sum }_{j=1}^J{n}_j$ and M̃ = P[d^ψ̂ = d^ψ] denote weighted average matching and all-stage matching, respectively.

Ex	(ψ0, P3, P2)	Method	Bias (ψ0)	Allocation Matching
				M (%)	M (%)
		Q-Unshared	-	56.62	35.36
		Q-SA	0.0179	59.23	44.72
		Q-IVWA	0.0232	59.56	45.96
1	(0.01, 0, 0)	Q-Shared.SA	0.0158	58.78	43.47
		Q-Shared.IVWA	0.0154	59.08	43.74
		Q-Shared.MAX	0.0156	59.23	43.90
		Q-Shared.MIN	0.0154	59.14	43.80
		Q-Shared.ZERO	0.0154	59.13	43.80
		Q-Unshared	-	61.97	45.20
		Q-SA	0.0145	67.24	58.11
		Q-IVWA	0.0152	61.21	52.15
2	(-0.05, 0.5, 0.5)	Q-Shared.SA	-0.0062	75.64	67.21
		Q-Shared.IVWA	-0.0063	75.57	67.11
		Q-Shared.MAX	-0.0061	75.52	67.15
		Q-Shared.MIN	-0.0063	75.64	67.20
		Q-Shared.ZERO	-0.0063	75.60	67.17
		Q-Unshared	-	57.84	33.33
		Q-SA	-0.0159	67.12	51.89
		Q-IVWA	-0.0489	53.47	38.46
3	(0.05, 0.5, 0)	Q-Shared.SA	-0.0134	67.42	51.45
		Q-Shared.IVWA	-0.0132	67.86	51.91
		Q-Shared.MAX	-0.0129	67.96	52.07
		Q-Shared.MIN	-0.0132	67.82	51.88
		Q-Shared.ZERO	-0.0132	67.83	51.94
		Q-Unshared	-	58.51	34.97
		Q-SA	-0.0147	67.65	52.80
		Q-IVWA	-0.0467	53.83	38.98
4	(0.05, 0, 0)	Q-Shared.SA	-0.0119	69.53	54.13
		Q-Shared.IVWA	-0.0119	69.25	54.17
		Q-Shared.MAX	-0.0117	69.30	54.27
		Q-Shared.MIN	-0.0120	69.23	54.21
		Q-Shared.ZERO	-0.0119	69.17	54.21
		Q-Unshared	-	76.96	62.35
		Q-SA	-0.0160	85.84	79.58
		Q-IVWA	-0.0172	76.43	68.21
5	(0.1, 0.25, 0)	Q-Shared.SA	0.0196	93.06	88.56
		Q-Shared.IVWA	0.0199	93.29	88.96
		Q-Shared.MAX	0.0201	93.38	89.08
		Q-Shared.MIN	0.0199	93.27	88.97
		Q-Shared.ZERO	0.0199	93.29	88.95
		Q-Unshared	-	73.09	57.40
		Q-SA	-0.0228	81.14	73.33
		Q-IVWA	-0.0374	69.58	61.30
6	(0.1, 0.25, 0.25)	Q-Shared.SA	0.0046	87.12	80.52
		Q-Shared.IVWA	0.0063	90.32	85.12
		Q-Shared.MAX	0.0064	90.46	85.30
		Q-Shared.MIN	0.0063	90.43	85.25
		Q-Shared.ZERO	0.0063	90.46	85.25
		Q-Unshared	-	73.61	53.19
		Q-SA	0.0159	83.52	72.18
		Q-IVWA	0.0382	70.70	58.76
7	(-0.1, 0, 0)	Q-Shared.SA	-0.0055	89.26	79.65
		Q-Shared.IVWA	-0.0053	88.55	78.75
		Q-Shared.MAX	-0.0052	88.60	78.80
		Q-Shared.MIN	-0.0053	88.62	78.77
		Q-Shared.ZERO	-0.0052	88.65	78.81

3.2 Simulation Results

The allocation matching figures, as well as the bias of ψ₀ (which is the leading shared parameter in the decision rule) are presented in Table 1. Bias and MSE of all the shared parameters (ψ₀, ψ₁, ψ₂ and ψ₃) are presented in Table 2 (Section A.4) of the Web Supplement.

Table 2.

Number of patients showing response and non-response at each level.

Level	Stage	Dropouts among Previous-stage Non-responders	Total Patients on Treatment	Responders	Non-responders
1	-	-	4008	1394	2614
2	1	1394	1220	463	757
3	2	449	308	55	253
4	3	168	85	-	-

In Ex 1, the bias of ψ₀ is substantial (> 100%) across all the methods, and none of the methods do very well in terms of allocation, with the weighted average matching (M) varying between 56% and 60%, and the all-stage matching (M̃) varying between 35% and 46%. In Ex 2, for ψ₀, the averaged methods (Q-SA and Q-IVWA) and the five versions of the Q-shared method have bias of opposite signs. But the amount of bias as a percentage of the true value of ψ₀ is much smaller for Q-shared. This translates to a moderately high allocation matching for all the versions of Q-shared (M ≈ 76%, M̃ ≈ 67%), which dominates the performance of Q-unshared and the two averaged methods (M ≈ 61–67%, M ≈ 45–58%). In Ex 3, the bias is particularly severe in case of Q-IVWA, resulting in poor allocation matching (M ≈ 53%, M̃ ≈ 38%), comparable to that of Q-unshared (M ≈ 58%, M̃ ≈ 33%). On the other hand, Q-SA and all five versions of Q-shared perform comparably (M ≈ 67%, M̃ ≈ 52%). Ex 4 is quite similar in underlying parameter setting to Ex 3 (see Table 1 of the Web Supplement), and hence the methods perform similarly as in Ex 3; specifically, Q-unshared and Q-IVWA continue to perform poorly in terms of allocation compared to the rest. In Ex 5, for ψ₀, the averaged methods have bias of opposite sign compared to Q-shared, but the amount of bias as a percentage of the true ψ₀ is not too large for any method. Q-shared (M ≈ 93%, M̃ ∼ 89%) dominates Q-SA (M ≈ 86%, M̃ ≈ 80%), which in turn dominates Q-unshared and Q-IVWA (M ≈ 76%, M̃ ≈ 62–68%). In Ex 6, the bias for ψ₀ is smaller when estimated by Q-shared, which translates to an improved performance (M ≈ 87–90%, M̃ ≈ 82–85%) over Q-SA (M ≈ 81%, M̃ ≈ 73%); the other two methods lag further behind (M ≈ 69–73%, M̃ ≈ 57–61%). Finally in Ex 7, the same trend of dominance across methods continues, with Q-shared doing the best (M ≈ 89%, M̃ ≈ 79%). Overall, the five versions of Q-shared perform the best, with Q-SA in second place. The inverse variance weighted averaging does not work well in general; this is due to poor estimation of the variance in finite samples using large-sample approximations (see Robins, 2004, pp. 33-34). Results for the larger sample size (n = 1200) are presented in Section A.4 of the Web Supplement. Qualitative behavior of the methods is similar, but the allocation performance improves for all the methods, as expected with a larger sample size.

There are a few key findings that merit further discussion. First, across all the seven examples, the five versions of the proposed Q-shared method perform almost identically in terms of bias and allocation matching, speaking for its robustness to the choice of initial values. Second, the version of the Q-shared method that initially sets all the parameter values to zero (Q-shared.ZERO) does not even require an initial run of standard Q-learning (Q-unshared) to supply the initial values. This may increase the appeal of the method to some practitioners. Third, the estimation of ψ₀ seems to have the primary impact on allocation matching; the rest of the shared parameters seem to have little effect (see Table 2 of Web Supplement). This is not surprising, because ψ₀ corresponds to the “main effect” of treatment A_j at stage j, whereas ψ₁, ψ₂ and ψ₃ represent various interactions. Fourth, in Ex 5, the magnitude of bias of ψ₀ is higher for Q-shared compared to the two averaged methods, and yet Q-shared performs better in terms of allocation. While this seems odd at first, careful thinking reveals a viable explanation. Note that in this example, for Q-shared, the bias of ψ₀ has the same sign as that of true ψ₀. This matching of signs moves the estimated value of the contrast function ${\psi }^{T}H=\frac{1}{2}[Q(H,A=+1;\beta ,\psi )-Q(H,A=-1;\beta ,\psi )]$ (whose sign determines the treatment allocation) away from the “decision boundary” of 0, thereby improving the allocation performance. On the other hand, for the two averaged methods, the bias of ψ₀ has the opposite sign as that of the true ψ₀, which moves the estimated value of ψ^TH closer to the decision boundary of 0, thus affecting its allocation performance. The same phenomenon also happens in Examples 2, 6 and 7, but the biases of the Q-shared method in these examples are not larger in magnitude than the averaged methods, and so the better performance of Q-shared does not strike the reader as an oddity. Furthermore, in all examples except the first, the bias of ψ₀ for both Q-SA and Q-IVWA have the opposite sign as that of the true ψ₀, explaining why these methods generally perform poorly compared to Q-shared. In summary, it might be reasonable to say that in allocation problems like the present one, a quantity like “signed bias” (bias × sign of the true parameter) may be a good indicator of the allocation matching with the oracle; in these problems, bias in the direction away from the decision boundary actually helps the allocation performance. The above phenomenon is analogous to classification, where “large margin classifiers” (e.g., support vector machines) perform well because they tend to move the “margin” away from the decision boundary. In the context of DTRs, the contrast function ψ^TH plays the role of the margin.

4. Analysis of STAR*D Data

The objective of the current analysis is to estimate the optimal three-stage, shared-parameter DTR for treating major depressive disorder, based on STAR*D data. Since the level 1 of STAR*D involves only a single treatment option (CIT) given to everyone, we consider data from this level as part of the baseline information rather than as a separate stage of treatment. Also, for the purpose of the current analysis, we combine levels 2 and 2A into a single level; this implies that any patient who went into level 2A is deemed to have received combination therapy in the combined level 2+2A. Thus, we rename level 2+2A as stage 1, level 3 as stage 2, and level 4 as stage 3. A simplified schematic of the study design is given in Figure 1.

Figure 1.

A schematic of the treatment assignment algorithm in the STAR*D study. An “R” within a circle denotes randomization.

STAR*D enrolled a total of 4041 patients. After omitting a few entries due to gross missingness and other inconsistencies, there were 4008 patients at level 1. Response and non-response along with the number of patients treated at each level are presented in Table 2.

Since at each stage the outcome data are available only for the previous-stage non-responders, we define, following Chakraborty et al. (2013), the overall outcome for every subject as

$$Y=R_1{Y}_1+(1-R_1)R_2\left(\frac{Y_1+Y_2}{2}\right)+(1-R_1)(1-R_2)\left(\frac{Y_1+Y_2+Y_3}{3}\right),$$ (2)

where Y₁, Y₂ and Y₃ are the –QIDS scores (clinician-rated) at the end of stages 1, 2 and 3 respectively, and R_j is the response indicator (1 = response, 0 = non-response) at the end of stage j (j = 1,2). Since a lower QIDS score reflects a better patient outcome, we take –QIDS in the definition of Y so that its maximization corresponds to better patient outcome. The primary outcome defined in (2) represents the average end-of-stage outcome of a subject during the stages s/he has been in the trial. Next, we consider the initial (clinician-rated) QIDS score at the beginning of a stage (QIDS.start), slope of the QIDS score over the previous stage (QIDS.slope), a binary version of side effect intensity from the previous stage (side.effect = 0 for low and 1 for high) and previous stage treatment type (mono therapy or combination therapy) as the covariates (and tailoring variables). Treatment A_j (j = 1, 2, 3) is coded 1 for mono therapy and −1 for combination therapy. QIDS.slope is defined as the difference between the end-of-stage and initial QIDS scores, divided by the number of weeks in between. We use the following models for the Q-functions:

$$\begin{array}{c}{Q}_3(H_3,A_3)={\beta }_{03}+{\beta }_{13}\times \text{QIDS}.{\text{start}}_3+{\beta }_{23}\times \text{QIDS}.{\text{slope}}_3+{\beta }_{33}\times \text{side}.{\text{effect}}_3+{\beta }_{43}\times A_2+({\psi }_0+{\psi }_1\times \text{QIDS}.{\text{start}}_3+{\psi }_2\times \text{QIDS}.{\text{slope}}_3+{\psi }_3\times \text{side}.{\text{effect}}_3+{\psi }_4\times A_2)\times A_3.\\ Q_2(H_2,A_2)={\beta }_{02}+{\beta }_{12}\times \text{QIDS}.{\text{start}}_2+{\beta }_{22}\times \text{QIDS}.{\text{slope}}_2+{\beta }_{32}\times \text{side}.{\text{effect}}_2+{\beta }_{42}\times A_1+({\psi }_0+{\psi }_1\times \text{QIDS}.{\text{start}}_3+{\psi }_2\times \text{QIDS}.{\text{slope}}_2+{\psi }_3\times \text{side}.{\text{effect}}_2+{\psi }_4\times A_1)\times A_2.\\ Q_1(H_1,A_1)={\beta }_{01}+{\beta }_{11}\times \text{QIDS}.{\text{start}}_1+{\beta }_{21}\times \text{QIDS}.{\text{slope}}_1+({\psi }_0+{\psi }_1\times \text{QIDS}.{\text{start}}_1+{\psi }_2\times \text{QIDS}.{\text{slope}}_1)\times A_1.\end{array}$$

Note that the stage-1 Q-model does not include side.effect and previous level treatment as covariates; this is a deliberate step to avoid singularity (prior treatment for everyone at stage 1 is CIT, and side effect from CIT is nil for almost all patients). According to the above Q-models, the optimal DTR is given by the following three decision rules: d₃(H₃) = sign(ψ₀ + ψ₁ × QIDS.start₃ + ψ₂ × QIDS.slope₃ + ψ₃ × side.effect₃ + ψ₄ × A₂), d₂(H₂) = sign(ψ₀ + ψ₁ × QIDS.start₂ + ψ₂ × QIDS.slope₂ + ψ₃ × side.effect₂ + ψ₄ × A₁), and d₁(H₁) = sign(ψ₀ + ψ₁ × QIDS.start₁ + ψ₂ × QIDS.slope₁). We apply the Q-shared method to estimate (d₁, d₂, d₃). We use the following pseudo-outcomes for stages 2 and 1:

$$\begin{array}{c}{Y}_2({\theta }_3)=R_1{Y}_1+(1-R_1)R_2\left(\frac{Y_1+Y_2}{2}\right)+(1-R_1)(1-R_2)\times \underset{a_3}{max}{Q}_3(H_3,a_3),\\ Y_1({\theta }_2)=R_1{Y}_1+(1-R_1)\times \underset{a_2}{max}{Q}_2(H_2,a_2).\end{array}$$

To avoid any selection bias resulting from drop-outs, we employ inverse probability weighting. At the end of stages 1 and 2, the probabilities of moving to the next stage are estimated using logistic regression with covariates side.effect, QIDS.slope, QIDS.end and treatment, and the inverse of these probabilities are used as weights in the corresponding Q-regressions. For greater stability, we use a truncation scheme where weights above the 99th percentile of the distribution are replaced by the 99th percentile (Xiao et al., 2013). We apply the m-out-of-n bootstrap based on 1000 replications (Chakraborty et al., 2013), detailed in the Web Supplement (Section A.5), to compute the confidence intervals (CIs) of the parameter estimates. Since the contrast function ψ^TH plays a key role in DTR analysis, we also study pointwise CI of ψ^TH for various values of the treatment and covariate history.

4.1 Results

Before running the shared-parameter analysis, it is worthwhile to look at stage-specific estimates of the shared parameters based on the Q-unshared method. These estimates, their bootstrap standard errors, and the R² values are presented in Table 6 of the Web Supplement. High values of adjusted-R² (> 98% for stage 3, > 95% for stage 2, > 81% for stage 1) indicate strong goodness of fit of the linear Q-models.

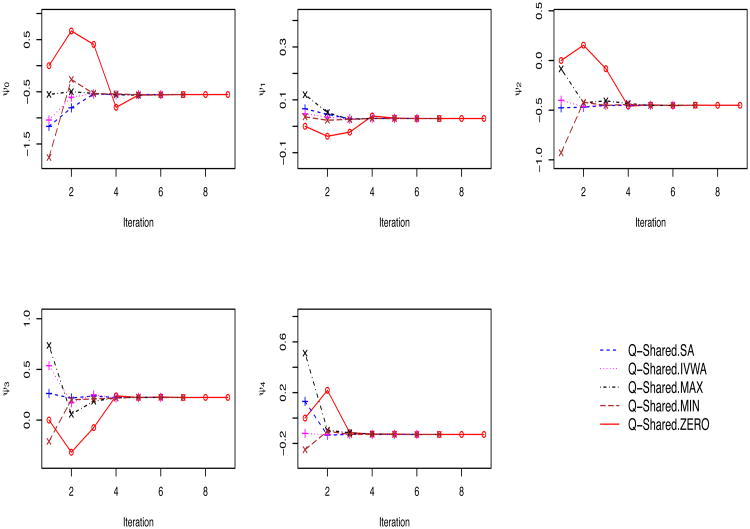
Next, we apply all five versions of Q-shared to estimate the ψs. All five versions produce identical parameter-estimates and the corresponding bootstrap confidence intervals up to third decimal point, reflecting the robustness of the method to the choice of initial values, which is consistent with our findings in the simulation study. Results are presented in Table 3. Furthermore, Figure 2 shows the convergence patterns of the individual shared parameters ψ₀,…, ψ₄ for the five versions of Q-shared. While all five versions converged to the same solution, they reached the solution at varying speed: Q-shared.SA and Q-shared.IVWA converged in 6 iterations, Q-shared.MAX and Q-shared.MIN in 7 iterations, and finally Q-shared.ZERO in 9 iterations; this pattern of speed of convergence is unsurprising.

Table 3.

Estimated values of the shared parameters via the Q-shared method, along with their 95% m-out-of-n bootstrap confidence intervals.

Shared Parameter	Estimate	Bootstrap CI
ψ0	−0.554	(−1.399, 0.164)
ψ1	0.029	(−0.028, 0.095)
ψ2	−0.450	(−0.890, −0.046)
ψ3	0.224	(−0.559, 0.773)
ψ4	−0.129	(−0.453, 0.157)

Figure 2.

Convergence patterns of ψ₀, ψ₁, ψ₂, ψ₃ and ψ₄ for the five versions of the Q-shared method (corresponding to five initial values) in the STAR*D study.

Among the shared parameters, the only significant one is ψ₂, which has a negative estimate. The corresponding tailoring variable, QIDS.slope, represents the rate of change in QIDS over the previous stage. Thus, a negative ψ₂ means that if QIDS.slope is positive and large, indicating a patient's worsening of depressive symptoms, and all other covariates remain constant, then in order to maximize the primary outcome, the estimated optimal DTR would recommend the more aggressive combination therapy. Recommending aggressive treatment to rapidly worsening patients by the estimated DTR is well-aligned with clinical judgement.

4.2 Inference for the Contrast Function, ψ^TH

Note that ψ^TH_j = ψ₀ + ψ₁ × QIDS.start_j + ψ₂ × QIDS.slope_j + ψ₃ × side.effect_j + ψ₄ × A_j–1, where QIDS.start and QIDS.slope are two continuous covariates, but side.effect and previous treatment are binary. For fixed values of the binary covariates, one can plot the “point estimate” of the contrast function, ψ̂^TH, as a function of QIDS.start and QIDS.slope in a 3-D plot; it would be a 2-D plane. Likewise, one can also plot the pointwise lower and upper confidence planes, ${\widehat{\psi }}_{\text{lower}}^{T}H$ and ${\widehat{\psi }}_{\text{upper}}^{T}H$, where ψ̂_lower and ψ̂_upper represent the lower and upper confidence bounds of ψ, respectively.

Figure 3a shows such a 3-D plot of the contrast function along with its lower and upper confidence bounds based on the Q-shared.SA method, corresponding to side.effect = 0 and previous treatment = −1 (fixed). In this figure, the range of QIDS.start is taken as [0, 26] and that of QIDS.slope is taken as [−10, 4], based on the observed STAR*D data. We have also included the 0-plane for reference. Our interest lies in the region of the (QIDS.start, QIDS.slope)-plane where both the lower and upper confidence planes are on the same side of the 0-plane; for the points in this region, the contrast function becomes significant, meaning one treatment is significantly better than the other.

Figure 3.

Confidence planes for the contrast functions and resulting regions of varying recommended optimal treatments in the (QIDS.start, QIDS.slope) plane, for subjects who have experienced low side effect intensity (0) and were treated with combination therapy (−1) at the previous stage, based on the Q-shared method for estimation and m-out-of-n bootstrap for inference.

Next, note that for (side.effect, previous treatment) = (0, −1), the estimated contrast function, ψ̂^TH = −0.554+0.029 × QIDS.start − 0.450×QIDS.slope+0.224× 0–0.129×(−1) = 0.029 × QIDS.start − 0.450 × QIDS.slope − 0.425. Equating this expression to 0, we obtain the line where the above plane intersects with the 0-plane as: 0.029 × QIDS.start − 0.450 × QIDS.slope = 0.425. Similarly, we find the lines of intersection between the 0-plane and the lower and upper confidence planes, respectively, as: −0.028 × QIDS.start − 0.890 × QIDS.slope = 0.946 and 0.095 × QIDS.start − 0.046 × QIDS.slope = −0.007.

Figure 3b shows the 0-plane along with lines where different planes (e.g., estimated contrast function, lower confidence plane and upper confidence plane) intersect with it, for the same setting as in figure 3a. The sky-blue region represents the covariate profiles for which all the three planes of interest are above the 0-plane, recommending mono therapy (1) to the corresponding patients. The interpretation is, whenever QIDS.slope is large negative (approximately −1 or less), indicating that the patient has been improving lately in terms of depressive symptoms, the estimated DTR recommends the less aggressive mono therapy, irrespective of the current depression level (QIDS.start). On the other hand, the patients whose covariate profiles lie in the green region are recommended combination therapy (−1), since all the three planes of interest are below the 0-plane. This region represents patients whose current depression level is relatively mild (QIDS.start is less than 3 or so), but their symptoms have been worsening over the previous stage (QIDS.slope is mostly positive); the estimated DTR recommends more aggressive combination therapy to this vulnerable group. Finally, the white region denotes patients who are already severely depressed (high QIDS.start) and whose symptoms have also been worsening over the previous stage (positive QIDS.slope). For this group of patients, there is no significant difference between mono therapy and combination therapy, likely because both are equally ineffective. In this case, the estimated DTR does not recommend one treatment or the other, leaving it to the clinician to make a subjective judgement call, or to consider treatments outside STAR*D.

To summarize, for patients with a history of receiving combination therapy and experiencing low side effects, the estimated optimal DTR suggests, “At any stage, if a patient's QIDS.slope ≤ −1, give monotherapy; otherwise, if QIDS.start < 3 and QIDS.slope > 0, give combination therapy; else, use clinical judgement or consider treatments outside STAR*D”.

5. Discussion

Sharing of parameters in DTR analysis, in our view, is a choice about the type of DTR of scientific and clinical interest to the scientist, rather than a statistical modeling assumption to be made by a data analyst; such sharing is appropriate when there are underlying clinical or biological reasons behind making that assumption. Trying to formally test this assumption may be misleading due to potentially high small-sample bias present in stage-specific Q-learning estimates (see Robins, 2004, pp. 33-34, for a discussion in the context of g-estimation). In this paper, we have proposed a novel simultaneous estimation method called Q-shared that directly accounts for sharing of parameters. Interestingly, Q-shared can be viewed as a Q-learning analog of simultaneous g-estimation; we have established an analytical connection between these two methods (see Web Supplement, Section A.2).

We have compared Q-shared with existing methods through extensive simulations, in which Q-shared has emerged as the overall winner in terms of allocation matching with the oracle. An interesting finding is that bias of the parameters in the direction away from the decision boundary improves the allocation matching. This property is analogous to the “large margin” behavior of classifiers like support vector machines.

We have empirically illustrated the convergence of Q-shared for five different choices of the initial values in case of STAR*D data (see Figure 2). However, due to the use of linear models, its convergence to the true solution cannot be theoretically guaranteed; this is consistent with the findings of Robins (2004) in the context of simultaneous g-estimation. Various approaches to circumvent the convergence problem have been studied in the reinforcement learning literature. For example, Ernst et al. (2005) considered fitted value iteration with regression trees, the underlying approximation class being much larger than a linear model. Lagoudakis and Parr (2003) considered a least squared fixed-point approximation approach instead of directly minimizing the squared Bellman error. Antos et al. (2008) used a modified version of the squared Bellman error as the objective function. For all of these more sophisticated methods, interpretability of the resulting decision rules can be greatly compromised, and hence not practically appealing. More recently, Lizotte (2011) guaranteed convergence of a fitted value iteration algorithm with linear models by imposing additional restrictions on the model space. A modification of this approach could potentially be suitable in the DTR context; we did not pursue this direction since interpretation is still less straightforward compared to Q-shared. Nonetheless, this may be an interesting avenue for future research.

Last but not least, even though in principle the proposed Q-shared method should be extendable to more than three stages, a thorough evaluation of its empirical performance and assessment of its computational burden in a setting with a large number of stages would be worth investigating in future. In particular, this may become appealing in settings like electronic medical records or mobile health intervention studies.