A 16-channel combined loop-dipole transceiver array for 7 Tesla body MRI

Abstract

Purpose

To develop a 16-channel transceive body imaging array at 7.0T with improved transmit, receive and SAR performance by combining both loop and dipole elements and utilizing their respective and complementary near and far field characteristics.

Methods

A 16-channel RF coil array consisting of eight loop-dipole blocks (16LD) was designed and constructed. Transmit and receive performance was quantitatively investigated in phantom and human model simulations, and experiments on five healthy volunteers inside the prostate. Comparisons were made with 16-channel microstrip-line (16ML) and 10-channel fractionated dipole antenna (10DA) arrays. The 16LD was used to acquire anatomic and functional images of the prostate, kidneys and heart.

Results

The 16LD provided >14% improvements in SNR, peak B₁⁺, B₁⁺ transmit and SAR efficiencies over the 16ML and 10DA in simulations inside the prostate. Experimentally, the 16LD had >20% higher SNR and B₁⁺ transmit efficiency compared to other arrays, and achieved up to 51.8% higher peak B₁⁺ compared to 10DA.

Conclusion

Combining loop and dipole elements provided a body imaging array with high channel count and density while limiting inter-element coupling. The 16LD improved both near and far field performance compared to existing 7.0T body arrays and provided high quality MRI of the prostate kidneys and heart.

Introduction

Ultrahigh field (UHF, B₀≥7T) MRI of the human body is challenging due to reduced wavelengths in tissue resulting in electro-magnetic (EM) field interferences, causing B₁⁺ field inhomogeneities, reduced RF penetration and reduced transmit efficiency (1-5). To overcome some of these challenges, multi-channel local transmit coil arrays have been developed consisting of loop coils (6-8), microstrip line elements (9-11) and dipole antennas (12-15).

Using dipole antennae is becoming increasingly popular at UHF and in deep tissue targets, as linear (i.e. electric dipole-like) current patterns are recognized as being favorable when considering ultimate signal-to-noise ratio (SNR) (16). Several coil arrays have been successfully used in body imaging applications by using different implementations of dipole antenna designs (12-15). Current designs rely on element separation to maintain adequate decoupling performance; a requirement that limits the number of elements that can be placed around the body in a single row (i.e. 8-12 elements). Arrays with higher numbers of elements can improve transmit performance by providing more degrees of freedom for shimming algorithms and can also provide a means to deliver higher peak power in systems with the available hardware (17). Especially in UHF applications where demanding high peak B₁⁺ acquisitions are needed and/or where deeply situated or large tissue targets are pursued, utilizing the full capabilities of the MR transmit hardware has utmost importance.

The current distribution of a dipole antenna is symmetric along its long axis, whereas a loop coil demonstrates an anti-symmetric current distribution (18). Due to these distinct current distribution patterns, a dipole antenna and a loop element can be decoupled from each other by carefully aligning the two elements along their center longitudinal axes. Combining electric dipoles with loop coils have been proposed by Eryaman et al. in simulation studies (19,20) to reduce local SAR in 7T head and spine imaging. Head coil arrays consisting of 8 loops and 8 dipoles on receive have improved the SNR at the central locations of the head compared to loop-only array designs (21,22). Voogt et al. constructed a 7T body imaging array with 8 fractionated dipole antenna transceivers along with 16 loop receivers and demonstrated improved SNR inside the prostate when both dipole and loop elements were used on reception (23). Despite these developments, the combined use of dipole and loop elements simultaneously as transceivers has not been experimentally investigated to date. As dipole antennae generally have better transmit and receive performance at greater depths and loop elements at shallower depths, combining both element structures as transceivers in an RF coil array promises increased performance beyond that of SNR.

The goal of this work is to develop a 16-channel transceiver array by combining 8 loop and 8 dipole elements (16LD) taking advantage of a system with 16-channel transmit hardware. Combining loop and dipole elements is anticipated to improve the SNR, B₁⁺ transmit and SAR efficiencies in order to alleviate the B₁ related challenges encountered in body imaging at 7T. The performance of the proposed 16LD design is investigated and benchmarked against an existing 16-channel microstrip line transceiver array (16ML) (10) and a 10-channel version of the fractionated dipole antenna array (10DA) (12) using both numerical simulations and experiments inside the prostate of subjects with varying body sizes. Finally, the 16LD is used to acquire anatomic MRI of the prostate, kidney and heart at 7T on healthy subjects.

Methods

Design of combined loop-dipole (LD) block

The 16-channel loop-dipole transceiver array (16LD) consisted of 8 identical loop-dipole building blocks (LD), with each block containing a dipole antenna and a rectangular loop coil (Figure 1.a). The dipole element was a replica of the original fractionated dipole antenna design by Raaijmakers et al. (12). The size of the loop was 8-by-18cm with 6mm wide conductors. The loop conductors were broken at six locations for the placement of distributed tuning capacitors. The dipole and loop elements were etched on separate 1.35mm thick FR4 printed circuit boards, and fixed value non-magnetic ceramic chip capacitors were used to tune and match the elements. Both elements were fed using lattice balun networks (24) to reduce common mode currents and cable interactions.

Figure 1.

(a) Positioning of the dipole and loop element conductors, (b) physical implementation of a LD block and (c) fabric housing containing four LD blocks are shown.

The loop was mounted between 3.18mm and 6.35mm thick thermoplastic polyetherimide blocks (ULTEM™ 1000 resin, Sabic Global, Pittsfield, MA). The dipole was mounted on top of the 6.35mm thick block on the opposite side from the load. The loop and dipole were aligned and centered along their long axes. Precise relative placement of the two elements was crucial to achieve acceptable decoupling performance within a single block. A photograph of an LD block is shown in Figure 1.b.

Numerical analysis of a single LD block

The transmit performance of an LD block was investigated numerically using SEMCAD X software (Version 14.8, Schmid & Partner Engineering AG, Zürich, Switzerland). A geometrically and electrically correct model of the block was created and placed 1cm away from the surface of a 30×20×40cm³ rectangular phantom with a relative permittivity ε_r=34 and electrical conductivity σ=0.4 S/m, which represent the average human tissue properties at 300MHz (25). The conductors of the elements inside the block were meshed at ≤1mm, while the rest of the model was meshed at ≤2mm. Both elements were driven with 50Ω voltage sources where the reflection parameters at the ports (S₁₁) were matched to better than -15dB at 297.2MHz. EM-field distributions were calculated using the finite-difference time-domain (FDTD) solver in the SEMCAD software and exported into Matlab (Mathworks, Inc., Natick, MA) for analysis. Peak voxel-wise SAR per unit power (SAR_peak/P), B₁⁺ transmit efficiency ( ${\mathrm{B}}_1^{+}/\sqrt{\mathrm{P}}$) and B₁⁺ SAR efficiency ( ${\mathrm{B}}_1^{+}/\sqrt{{\text{SAR}}_{\text{peak}}}$) were calculated for the dipole-only, loop-only and dipole-loop combined. B₁⁺ distributions were averaged inside 8cm³ cubes centered at 2, 4, 6 and 8cm depths inside the phantom aligned with the center of the LD block. The combined simulations were computed for a variety of relative phase settings between the LD block elements by adding the EM-field distributions of each element at equal forward input power at different phase shifts (range: 1-360°, 1° increments). Furthermore, SAR and B₁⁺ distributions of the combination with loop power attenuated with respect to the dipole power by 0 to 10dB in 0.5dB increments were calculated at a constant relative phase difference determined by B₁⁺ shimming for efficiency at a depth 6cm inside the phantom (26).

16-channel loop-dipole array (16LD) design

The 16LD was assembled using a total of eight LD blocks, four anterior and four posterior. Two housings made of vinyl fabric each contained the four LD blocks on a given side (i.e. anterior or posterior). Within each housing, a constant separation of 3.5cm between the edges of neighboring blocks was maintained with a center to center distance of ∼11.5cm. Flexibility of the housing was essential in conforming the elements to subjects with differing body sizes, shapes and at different locations on the body to maintain performance by providing designed loading conditions for this fixed tune and match coil.

Numerical analysis of the 16LD: Pelvis

For prostate simulations, the 16LD was modeled around the pelvis by placing four LD blocks on the anterior and four on the posterior side of an anatomically correct human model (Duke from Virtual Family (27)). The blocks were placed 1cm off the surface of the skin and centered on the prostate along the z-dimension. All the elements were terminated using 50Ω voltage source ports and were tuned and matched to at least an S₁₁ of -15dB at 297.2MHz. The gradient shield and whole body of the Duke model were included in the simulations. EM-field distributions of each coil element (8 loop, 8 dipole) were computed with an FDTD solver in SEMCAD using variable meshing resolutions (≤1mm for all conductors and ≤2mm for all tissues) and were imported to Matlab for analysis.

In order to evaluate the full performance of the 16LD, both amplitude and phase shimming was explored with the goal of maximizing B₁⁺ transmit efficiency ( ${\mathrm{B}}_1^{+}/\sqrt{{\mathrm{P}}_{\text{coil}}}$)and B₁⁺ SAR efficiency ( ${\mathrm{B}}_1^{+}/\sqrt{{\text{SAR}}_{\text{peak}10\mathrm{g}}}$) inside the prostate. Peak 10g-averaged SAR, B₁⁺ transmit efficiency inside the prostate normalized to unit total coil power and B₁⁺ SAR efficiency normalized to peak 10g SAR were computed by first re-gridding the EM-field distributions onto a 2mm uniform grid using nearest-neighbor interpolation and then using the 10g-averaged SAR Q-matrices formed with a modified version of the N-gram averaging algorithm provided by Carluccio et al (28). Virtual observation points (VOP) were determined using the 10g averaged SAR Q-matrix in order to accelerate the shim-dependent peak local SAR calculations (29,30).

In contrast to the above simulations which investigated all combination of phase and amplitude shimming, simulations to mimic experimental studies in the prostate were performed with phase-only shimming (26). In order to explore the tradeoffs in B₁⁺ and SAR performance of the different resonance structures even without amplitude shimming, relative power levels between the dipole and loop elements were simulated. While the relative power used to drive the different elements do not impact phase-based efficiency shimming, they do affect the quantitative performance metrics including peak 10g SAR, B₁⁺ transmit efficiency and peak B₁⁺ inside the prostate. Specifically, the loops were simulated with equal power, no power at all and with attenuations levels from 1 to 10 dB in 1 dB increments with respect to the dipoles. The time averaged power (TAP) limits yielding 20 W/kg peak local 10g averaged SAR were determined from these 13 excitation scenarios and were used to ensure RF safety in compliance with IEC guidelines (31) when performing in vivo prostate studies. Peak B₁⁺ was calculated taking into account the specific hardware configuration at the study site including the number of transmit channels, maximum available power from the power amplifiers, and cable and hardware losses up to the coil.

Receive performance of the 16LD was investigated by calculating the SNR and geometry factor (g-factor) maps from simulation. SNR inside the prostate was computed by taking the normalized magnitude summation of the B₁^- of individual coil elements ( $\text{SNR}~\frac{{\sum }_{\mathrm{n}=1}^{16}|{\mathrm{B}}_{1,\mathrm{n}}^{-}|}{\sqrt{{\mathrm{P}}_{\text{coil}}}}$). G-factor maps for accelerations of 1-6 in left-right (L-R) and 1-2 in anterior-posterior (A-P) directions were calculated using Musaik RF Array Designer toolbox (Schmid & Partner Engineering AG, Zürich, Switzerland).

Numerical analysis of the 16LD: Kidney & Heart

Due to larger size and more complex geometries of the kidneys and heart compared to the prostate, optimizing for B₁⁺ efficiency is frequently insufficient for these targets. In order to address this issue, tradeoff solutions between homogeneity and efficiency are generally used when B₁⁺ shimming (32). Therefore, anatomy specific safe power limits for the 16LD were determined using the worst-case 10g-averaged SAR from phase-only shim solutions for the kidney and heart when driving all elements with equal power. To accomplish this, the 16LD was modeled around the torso of the Duke model centered at the level of the kidneys and the heart. VOPs were determined from the 10g-average SAR Q-matrices using the same methods described above, and TAP limits were calculated yielding 20 W/kg peak local SAR with the worst-case phase-only shimming at each imaging location.

Experimental Methods

In vivo imaging was performed on 6 healthy volunteers with the 16LD after providing informed written consent to participate in an institutionally approved protocol on a whole-body Magnetom 7 Tesla scanner (Siemens Healthcare, Erlangen, Germany). The system is equipped with sixteen 1kW power amplifiers managed through a separate phase and gain controller (Communications Power Corporation, Hauppauge, NY) and a custom built power monitoring system (33). The elements of the 16LD were connected to a 16-channel transmit/receive box (Virtumed LLC, Minneapolis MN) using RG-400 type co-axial cables.

For prostate studies, 5 individuals were imaged with body mass indices (BMIs) ranging from 21.3 to 29.7kg/m² (mean: 25.6kg/m²) and with anterior-posterior (AP) pelvic dimensions ranging between 17.2 and 23.8cm (mean: 20.8cm). Subject-dependent RF shimming was performed to maximize B₁⁺ fields inside the prostate (i.e. phase-only shimming) (26). B₁⁺ maps were calculated from data acquired with the actual flip angle technique (34) (TR₁/TR₂/TE: 20/120/3ms, FA=50°, acquisition-matrix: 128×128×24, voxel-size: 2.7×2.7×5mm³). Transmit performance was evaluated in terms of B₁⁺ normalized to unit total coil power and peak B₁⁺. SNR was calculated by acquiring a fully relaxed gradient echo sequence (TR/TE: 10s/3.1ms, FA=90°, voxel-size: 2.7×1.4×3mm³) and a noise scan using the methods of Edelstein et al. (35). Post-processing of the acquired data was performed in Matlab where prostate regions were drawn manually slice-by-slice to quantify B₁⁺ transmit efficiency, peak B₁⁺ and SNR of the 16LD.

Parallel imaging performance of the 16LD was investigated by computing g-factors (36) on SNR acquisitions performed in a torso-sized phantom. The g-factors corresponding to reduction factors (R) of 1 to 6 fold in the left-right (LR) and 1 to 2 fold in the anterior-posterior (AP) directions were calculated. The phantom itself and an additional validation study to demonstrate correspondence between simulations and experiments are described in the Appendix.

For renal and cardiac imaging, B₁⁺ shimming was performed with different optimization goals. For the kidney, phase-only shimming optimized for field homogeneity with a targeted RF efficiency of 50% was used (32). For cardiac imaging a single static shim setting optimized for B₁⁺ homogeneity over the entire heart was employed.

Anatomic and functional MRI acquisitions

For all prostate studies, T2-weighted images were obtained using a turbo spin-echo (TSE) sequence (TR/TE: 6000/74ms, FOV: 220×220mm², voxel-size: 0.5×0.5×3mm³, 13 slices, duration: 3m 43s).

Anatomic images of the kidneys were acquired with an interleaved multi-slice, fat-suppressed gradient echo (GRE) sequence (TR/TE: 120/2.8ms, FOV: 350×350mm², acquisition voxel-size: 1.2×0.8×5mm³, GRAPPA R=2, 32 slices, duration: 23s). For visualizing the vessels, a sequentially acquired multi-2D, fat-suppressed GRE sequence was performed (TR/TE: 4.5/1.9ms, FOV: 270×360mm², acquisition voxel-size: 1.4×1.1×3mm³, duration: 18s).

Cardiac functional imaging consisted of cine acquisitions obtained during a single breath-hold with a 2D retrospectively ECG-gated GRE sequences (FOV: 277×339mm², acquisition voxel-size: 1.4×1.1×4mm³, GRAPPA R=2, duration: 14s). Short-axis, long-axis and straight-coronal views of the heart were acquired with flow compensation using the following acquisition parameters (TR/TE: 66/2.8ms). The four-chamber view was acquired without flow compensating gradients (TR/TE: 50/1.8ms).

Coil Comparisons

The 16LD was compared against two existing transceiver body arrays which have been previously characterized, including a 16-channel microstrip line array (16ML) (10) and a 10-channel version of the fractionated dipole antenna array (10DA) (MR Coils B.V., Drunen, The Netherlands) (12). These comparisons, including both simulation and experimental results, were performed in the pelvis with the prostate as the target anatomy. Simulations for the two arrays followed the same methods described above with the exception that the 16ML was positioned 1.5cm from the body in contrast to the 1cm gap for the 16LD and 10DA. The in vivo results of the 16ML and 10DA used for comparison were reproduced from a previous study which involved 5 healthy male volunteers with BMIs and AP dimensions covering a similar range as the current study.

Results

Numerical analysis of the LD block

Numerically computed magnitude and vector distributions of the E-fields for the dipole-only, loop-only and dipole-loop combined excitations on a coronal slice at a depth of 2cm inside the block are shown in Supporting Figure S1. The SAR is proportional to the magnitude of the E-field squared. The directions of the dipole-only E-field vectors were uniform across the coronal slice, however the loop-only E-fields had a rotational symmetry. The E-field distribution of the dipole-only excitation was highest underneath the feed point of the antenna between the poles, whereas that same location had zero E-field for the loop-only simulation. Meanwhile, the E-field distributions of the loop-only excitation were highest underneath the mid-point of the long-axis of the loop conductors. The E-field hotspot of the combined excitation shifted along the –x direction where the fields from the two simulations constructively interfere. The impact of changing the relative phases of the dipole and loop on the B₁⁺ and SAR distribution inside the phantom during combined excitation can be visualized in Supporting Video S1 (available online). The magnitude and location of the SAR hot-spot changes when changing the relative transmit phases of the two elements. Peak voxel-wise SAR, B₁⁺ transmit efficiency and B₁⁺ SAR efficiency for the dipole-only, loop-only and dipole-loop combined are shown when both elements are driven at the same power and when the relative phase between the two elements in the block are varied (Figure 2.a-c). Coincidentally, peak voxel-wise SAR of the loop and dipole elements were identical. Depending on the phase difference between the dipole and loop elements, the combined excitation yielded from a -31% to +17% peak SAR per unit power compared to dipole-only and loop-only excitations. Using the loop and dipole in combination with an efficiency B₁⁺ shim, a transmit efficiency gain of 26% and 62% was realized over the dipole-only and loop-only, respectively, at the expense of a 13% increase in peak SAR (Figure 2). Since the B₁⁺ transmit efficiency gain was higher than the increase in SAR, the SAR efficiency of the combined excitation increased by 21% and 55% compared to dipole-only and loop-only excitations, respectively (Figure 2). This evaluation was performed by averaging over the 8 cm³ regions inside the phantom model.

Figure 2.

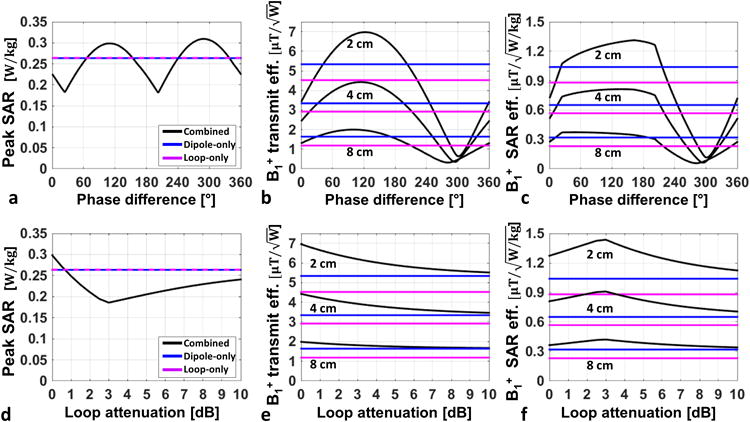
Loop-dipole block simulations of (a, d) peak voxel-wise SAR, (b, e) B₁⁺ transmit efficiency (c, f) B₁⁺ SAR efficiency are shown for dipole-only (blue), loop-only (purple) and loop-dipole combined (black) excitations. Plots in the top row show the impact of changing the relative phase of loop-dipole combined excitation. Plots in the bottom row investigate the impact of attenuating the loop excitation power compared to dipole in the loop-dipole B₁⁺ efficiency phase optimized combined excitation.

The impact of changing the relative excitation amplitudes between the dipole and loop on the B₁⁺ and SAR distributions during simultaneous excitation are shown animated in Supporting Video S2 (available online). Peak SAR, B₁⁺ transmit efficiency and B₁⁺ SAR efficiency for the dipole-only, loop-only and combined simulations are plotted in Figure 2.d-f. The combined simulations provided up to a 30% reduction in peak SAR resulting in up to 35% and 73% higher B₁⁺ SAR efficiency compared to dipole-only and loop-only excitations, respectively. The highest B₁⁺ transmit efficiency was achieved when the dipole and loop excitation power levels were the same (i.e. ‘phase-only’ shimming), and the highest B₁⁺ SAR efficiency was achieved when the loop excitation was 3dB lower than the dipole excitation.

Numerical analysis of the 16LD

A numerically computed S-parameter matrix of the 16LD when placed around the Duke model is shown in Figure 3, with matrix indices of 1 to 8 showing the dipole elements and 9 to 16 showing the loop elements. Reflection parameters of the channels were less than -16.5dB (mean: -21.5dB). Coupling between the loop and dipole elements in the same LD block was less than -17.4dB (mean: -22.6dB), showing that the symmetrical placement of the loop and dipole elements was sufficient to decouple these elements. The highest amount of coupling occurred between neighboring loop elements (mean, max: -12.2dB, -9.9dB) while average coupling between the neighboring dipole elements was -15.9dB (max: -14.4dB). Finally, the amount of coupling between neighboring dipole and loop elements were on average -13.8dB (max: -12.7dB). A simulated scattering matrix indicated an adequate decoupling performance between the elements of the 16LD array without the use of capacitive and/or inductive decoupling networks.

Figure 3.

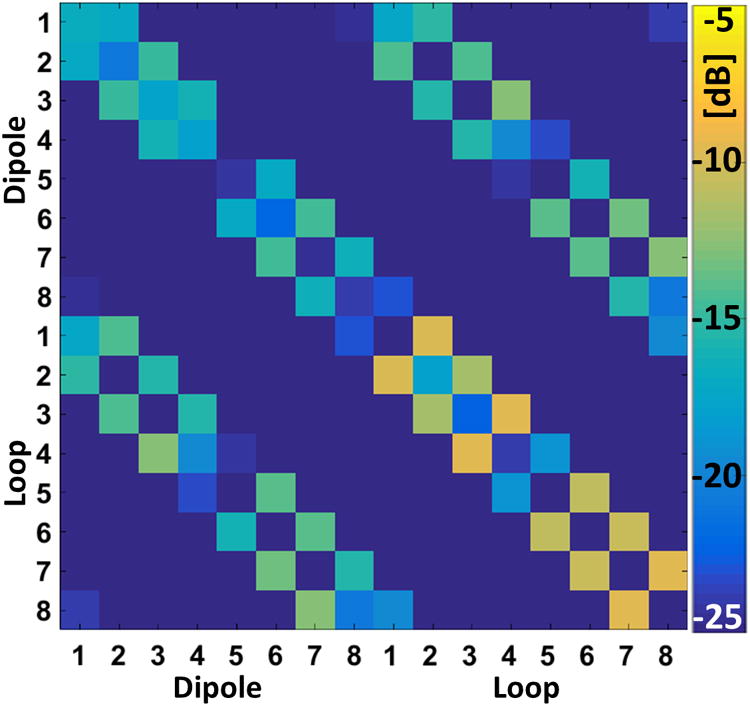
Magnitude of the numerically computed scattering parameter matrix of the 16LD on the Duke model is shown.

Transmit performance metrics of the 16LD, 16ML and 10DA with both amplitude and phase shimming targeting either maximum B₁⁺ transmit efficiency or B₁⁺ SAR efficiency in the prostate are listed in Table 1. Under these conditions the 16LD provided 13.7% and 18.3% higher B₁⁺ transmit efficiency, 9.2% and 26.5% higher B₁⁺ SAR efficiency over the 16ML and 10DA, respectively.

Table 1.

Numerically computed peak 10g SAR, B₁⁺ transmit and B₁⁺ SAR efficiencies of 16LD, 16ML and 10DA are listed for amplitude-phase shimming maximizing the B₁⁺ transmit efficiency and B₁⁺ SAR efficiency.

Shim Target ➔	B1+ transmit efficiency			B1+ SAR efficiency
Coil	$\frac{{\text{SAR}}_{10\mathrm{g}}}{{\mathrm{P}}_{\text{coil}}}$	B1+ transmit efficiency	B1+ SAR efficiency	$\frac{{\text{SAR}}_{10\mathrm{g}}}{{\mathrm{P}}_{\text{coil}}}$	B1+ transmit efficiency	B1+ SAR efficiency
	[W/kg]	$[\frac{\mathrm{\mu }\mathrm{T}}{\sqrt{\mathrm{W}}}]$	$[\frac{\mathrm{\mu }\mathrm{T}}{\sqrt{\mathrm{W}/\text{kg}}}]$	[W/kg]	$[\frac{\mathrm{\mu }\mathrm{T}}{\sqrt{\mathrm{W}}}]$	$[\frac{\mathrm{\mu }\mathrm{T}}{\sqrt{\mathrm{W}/\text{kg}}}]$
16LD – All channels	0.400	0.291	0.460	0.122	0.237	0.678
16LD – Loop-only (8ch)	0.460	0.195	0.288	0.136	0.161	0.436
16LD – Dipole-only (8ch)	0.365	0.225	0.372	0.143	0.197	0.520
16ML	0.391	0.256	0.410	0.077	0.172	0.621
10DA	0.401	0.246	0.388	0.142	0.202	0.536

Numerically computed transmit performance metrics of the 16LD with phase-only B₁⁺ efficiency shim settings at various relative power levels between all loop and dipole elements are listed in Table 2. The metrics include peak 10g averaged SAR, TAP limits, B₁⁺ transmit efficiency, B₁⁺ SAR efficiency and peak B₁⁺. Dipole-only and loop-only 8-channel excitations show that the dipole elements are more efficient than loop elements in this configuration. Two particular excitation schemes are printed in bold face type in Table 1. The first is when the maximum peak power was applied to all channels generating the highest peak B₁⁺ of 23.3μT in simulation. The second is when the loops were attenuated by 7dB relative to the dipoles which provided high B₁⁺ transmit and SAR efficiencies compared to the other scenarios. These two excitation schemes were employed in vivo.

Table 2.

Numerically computed peak 10g SAR per unit total coil power with phase-only prostate peak B₁⁺ efficiency shim solution inside Duke of the 16LD, 16ML and 10DA are listed along with time average power (TAP) limits for RF safety. Transmit performance of the 16LD is investigated using dipole-loop combined excitation with loop excitation power equal to or less than the dipole excitation power level, as well as dipole-only and loop-only 8 channel excitation schemes. B₁⁺ transmit and SAR efficiencies, and peak B₁⁺ inside the prostate of Duke using the hardware settings at the study site are shown for 16LD, 16ML and 10DA. Simulated SNR of the arrays inside the prostate are listed along the last column.

Coil	Excitation scheme	$\frac{{\text{SAR}}_{10\mathrm{g}}}{{\mathrm{P}}_{\text{coil}}}$	TAP limit [W]			B1+ transmit efficiency	B1+ SAR efficiency	Peak B1+	SNR
			total	per channel
		[W/kg]		Dipole	Loop	$[\frac{\mathrm{\mu }\mathrm{T}}{\sqrt{\mathrm{W}}}]$	$[\frac{\mathrm{\mu }\mathrm{T}}{\sqrt{\mathrm{W}/\text{kg}}}]$	[μT]	[a.u]
16LD	Dipole + Loop	0.269	74.4	4.65	4.65	0.258	0.497	23.3	3.017
	Dipole + Loop(-1dB)	0.266	75.1	5.23	4.16	0.259	0.502	22.2
	Dipole + Loop(-2dB)	0.263	76.2	5.84	3.68	0.260	0.506	21.2
	Dipole + Loop(-3dB)	0.258	77.5	6.45	3.24	0.259	0.510	20.3
	Dipole + Loop(-4dB)	0.253	79.1	7.07	2.81	0.258	0.513	19.5
	Dipole + Loop(-5dB)	0.247	80.9	7.68	2.43	0.256	0.515	18.8
	Dipole + Loop(-6dB)	0.241	82.9	8.28	2.08	0.254	0.517	18.2
	Dipole + Loop(-7dB)	0.236	84.9	8.85	1.77	0.251	0.518	17.6
	Dipole + Loop(-8dB)	0.230	87.1	9.40	1.49	0.249	0.519	17.1
	Dipole + Loop(-9dB)	0.224	89.3	9.91	1.25	0.246	0.519	16.7
	Dipole + Loop(-10dB)	0.219	91.4	10.39	1.04	0.243	0.519	16.3
	Dipole-only (8 ch)	0.222	90.1	11.27	0.00	0.204	0.433	13.0
	Loop-only (8 ch)	0.356	56.3	0.00	7.03	0.165	0.277	10.6
16ML		0.250	80.1	5.01		0.225	0.451	20.4	2.522
10DA		0.265	75.5	7.55		0.217	0.421	15.5	2.394

Simulated transmit performance metrics of the 16ML and 10DA with prostate B₁⁺ efficiency phase-only shim settings are also listed in Table 2 for comparison with the 16LD. B₁⁺ transmit efficiency of the 16LD was more than 15% higher than both the 16ML and 10DA. Compared to the 16ML and 10DA, the B₁⁺ SAR efficiency of the 16LD was 15.1% and 23.2% higher and the peak B₁⁺ was 14.2% and 50.3% higher, respectively.

The numerically computed SNR distributions of the 16LD, 16ML and 10DA are shown in Supporting Figure S2 and the mean SNR inside the prostate are listed in Table 2. The SNR of the 16LD from simulation was 19.6% and 26.0% higher than 16ML and 10DA, respectively. The 16LD outperformed both 16ML and 10DA in terms of B₁⁺ transmit efficiency, B₁⁺ SAR efficiency, and SNR by at least 15% in simulations on the Duke model.

Safety limits for kidney and heart imaging

Worst-case 10g-averaged local SAR normalized to unit total coil power for phase-only shim solutions were 0.452W/kg for the kidney and 0.529W/kg for the heart. Resulting TAP limits for safe operation were determined to be 2.76 and 2.36 W per channel for the kidney and heart, respectively.

Experimental results of the 16LD

The B₁⁺ transmit efficiency and SNR distributions along an axial slice intersecting the prostate of a subject with a BMI = 26.9kg/m² are shown in Supporting Figure S3. Experimentally measured B₁⁺ transmit efficiency, peak B₁⁺ and SNR of the 16LD inside the prostate are listed in Table 3 in comparison to the 16ML and 10DA. Compared to the 16ML and 10DA, the 16LD had on average, 29.1% and 20.0% higher B₁⁺ transmit efficiency, 29.1% and 51.8% higher peak B₁⁺, and 26.9% and 20.4% higher SNR, respectively.

Table 3.

Mean values and standard deviations of the experimentally acquired B₁⁺ transmit efficiency, peak B₁⁺ and SNR of the 16LD, 16ML and 10DA inside the prostate of healthy subjects are listed along with the BMI and pelvic AP dimensions of the subjects.

Coil	BMI	Pelvic AP dimension	B1+ transmit efficiency	Peak B1+	SNR
	kg/m2	cm	$\frac{\mathrm{\mu }\mathrm{T}}{\sqrt{\mathrm{W}}}$	μT	${10}^4\sqrt{\text{Hz}}/\text{ml}$
16LD	25.6 ± 3.2	20.8 ± 2.5	0.221 ± 0.042	20.0 ± 3.8	7.21 ± 1.07
16ML	26.1 ± 3.6	20.4 ± 2.3	0.171 ± 0.034	15.5 ± 3.1	5.68 ± 1.45
10DA	26.1 ± 3.6	20.4 ± 2.3	0.184 ± 0.013	13.2 ± 0.9	5.99 ± 0.61

Average g-factors of the 16LD in a 4cm² square region mimicking the size and location of the prostate inside the torso sized phantom are listed in Table 4. The additional SNR penalty due to parallel imaging was on average less than 20% if the reduction factor was equal to or smaller than 6.

Table 4.

G-factor values of the 16LD computed using numerical simulations on Duke and experimental acquisitions on torso phantom are listed for acceleration factors of 1 and 2 along AP and 1 to 6 along LR dimensions.

			Reduction in L-R dimension
			1	2	3	4	5	6
Simulated (Duke)	Reduction in A-P dimension	1	1.00±0.00	1.02±0.02	1.04±0.01	1.06±0.03	1.28±0.03	1.65±0.05
		2	1.07±0.07	1.09±0.08	1.14±0.07	1.24±0.13	1.49±0.16	2.03±0.27
Experimental (Phantom)		1	1.00±0.00	1.00±0.00	1.03±0.01	1.05±0.03	1.04±0.02	1.15±0.05
		2	1.11±0.06	1.13±0.07	1.17±0.08	1.24±0.10	1.27±0.13	1.47±0.20

MRI anatomic and functional studies

Representative axial and coronal T2-weighted TSE images of the prostate from two of the 5 healthy subjects imaged as part of this study are shown in Figure 4.

Figure 4.

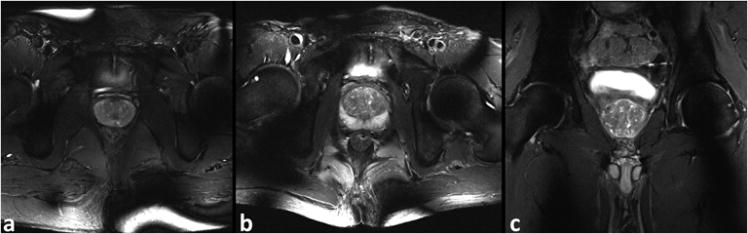
(a-b) Axial and (c) coronal T2-weighted TSE images of the prostate at 0.5×0.5 mm² in-plane resolution acquired on two different subjects (part a, BMI = 27.9 kg/m²; part b-c, BMI = 22.3 kg/m²).

Anatomic MRI of the kidneys along coronal and axial slices are shown in Figure 5. A 25mm thin slab maximum intensity projection (MIP) of the multi-slice GRE acquisition is shown in Figure 5c at the level of the renal arteries.

Figure 5.

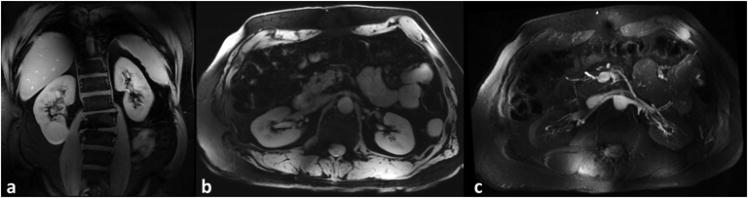
(a) Coronal and (b) axial fat suppressed T1-weighted GRE images of the kidney acquired on a subject with BMI = 26.9 kg/m². (c) 25mm MIP of a multi-slice 2D imaging series at the level of the renal arteries.

Single frames of four chamber, short axis, straight coronal through the left ventricular outflow tract and two chamber long axis cines of the heart are shown in Figure 6 while an animated cine series are provided in Supporting Video S3. Fine structures such as the heart valves and the left coronary artery can be observed in parts a and c, respectively.

Figure 6.

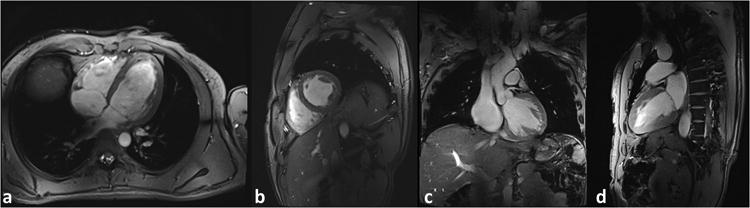
Single frames from cine series of (a) four chamber, (b) short-axis, (c) straight-coronal and (d) two-chamber views. The coronal view (c) shows the aortic root and the left proximal coronary artery. Data are from a male subject with a BMI of 25.3 kg/m². (image voxel-size: 1.18×1.18×4mm³). Animated cine series of these acquisitions are provided in Supporting Video S3 (available online).

Discussion

We have developed and investigated a 16-channel transceiver array (16LD) consisting of 8 identical building blocks each containing a fractionated dipole antenna (12) and a symmetrically placed rectangular loop element for body imaging at 7T. Currently, arrays consisting of dipole antennae rely on physical separation between neighboring elements to minimize coupling (12,15), which limits the number of elements that can be placed around the body without diminishing the decoupling performance. Combining loop and dipole elements increased the element density and channel count without compromising the decoupling achieved by maintaining the distance between adjacent elements. Another advantage of combining loop and dipole elements stems from their inherent transmit and receive characteristics. Loop elements generally have better transmit and receive performance at shallower depths compared to dipoles (18). On the other hand, dipole antenna elements can improve transmit and receive performance at greater depths compared to conventional loop coils and microstrip line elements at 7T (18,37). Therefore, combining loop and dipole elements in the 16LD allowed the advantages of each to be utilized to increase overall performance not only on receive, but also on transmit, the latter of which is uniquely explored in this work. On receive, this performance can be seen in Supporting Figure S2, where the 16LD demonstrates significantly higher SNR around the periphery of the pelvis as well as higher SNR inside the prostate compared to the 16ML and 10DA in simulations. Meanwhile, both B₁⁺ transmit and SAR efficiencies improve with the 16LD as a result of the complementary electromagnetic field distributions of the two resonant structures.

The B₁⁺ transmit efficiency metric relates to the B₁⁺ levels that can be achieved at a target location, which has great implications on the successful implementation of a pulse sequence. If the desired B₁⁺ cannot be achieved, this may lead to poor image quality and altered image contrast. The B₁⁺ SAR efficiency metric has direct implications on the scan duration of a particular pulse sequence which is constrained by power deposition limits. A coil with a higher B₁⁺ SAR efficiency can reduce or remove restrictions on sequence timing, and/or shorten scan durations.

Combining dipole and loop elements in an UHF imaging array by simultaneously receiving the MR signal from both structures were shown to improve the SNR in the head (21,22) and inside the prostate (23). In a simulation study, Eryaman et al. demonstrated that the addition of dipole elements in the so-called “dark-mode” could reduce the local SAR of a loop array for spine imaging (20). However until our study, the B₁⁺ excitation and SAR performance of a combined dipole-loop array had not been experimentally investigated as a means to address the major challenges facing body imaging application at UHF.

In the design of the 16LD, loop widths of 8cm were chosen to provide adequate circumferential coverage around the body using 8 blocks, while simultaneously maintaining sufficient decoupling between neighboring loop elements without the need for additional decoupling strategies (38,39). In larger subjects, individual LD blocks could be placed further apart from each other in order to reduce the amount of coupling between neighboring elements, and/or more blocks can be included. The fabric housing was used to maintain a similar loading condition between different subjects by helping to keep the elements in close contact to the body across their length when imaging the various anatomical targets. It was found that inter-subject loading variations did not result in significant tuning and matching variations on the subjects included in this study. This is an important point as elements of the 16LD were tuned and matched using fixed value lumped elements. Subject dependent manual tuning and matching may still improve the performance of the array at the expense of increased preparation time and design complexity. It is worth noting that if the LD blocks cannot lay flat against the surface of the body along a significant portion of their length due to certain body geometries, loading variations may result in shifts in the tuning frequency and may reduce coil performance. Automated tuning and matching approaches may help to achieve optimum array performance on different subjects without extending the preparation time prior to imaging (40).

While imaging acquisitions were not specifically optimized for use with this coil and available SNR, the in vivo studies of the prostate, kidneys and heart demonstrate the potential of the 16LD to obtain high quality data even when imaging larger anatomic targets. The improved SNR of the 16LD enabled in-plane voxel-sizes of 0.5×0.5mm² inside the prostate of all subjects with acceptable SNR, approaching the resolutions obtained at 3T using external surface arrays combined with endo-rectal coils (41). The kidney images show the ability to provide high SNR in the periphery and in the descending aorta positioned at the center of the body with relatively even contrast through the axial and coronal cross-sections. The cardiac scans demonstrate excellent contrast and SNR at the posterior of the heart in all three main views using a single RF shim solution optimized for homogeneity. In these acquisitions phase-only static B₁⁺ shimming provided adequate field homogeneity and transmit efficiency, however use of parallel transmission RF pulses (42-45) and RF optimized excitation schemes could further improve the excitation homogeneity and image quality which will be investigated in future studies.

A limitation of this study is that the 16LD was simulated on only one human model (Duke with BMI: 23.1kg/m²) with a limited number of shim settings while it is known that B₁⁺ and SAR distributions depend on the subject, coil placement and applied shim. Modelling of the 16LD on human models with different genders, body sizes and shapes, and at different imaging locations and investigating a variety of shim solutions may be necessary to fully investigate its performance and to assess the safe operating limits especially when employing more complex RF shimming strategies. Quantitative analysis of the 16LD and its comparison to the 16ML and 10DA was performed on the prostate due to its relatively small size and deep central location inside the pelvis. However, the 16LD is being used to image a variety of anatomies inside the body including kidneys and heart where more in depth evaluations of performance is warranted.

Conclusion

We have developed a 16-channel transceiver array (16LD) consisting of 8 dipole antennae and 8 rectangular loop coils. Combining loop and dipole elements maintained both the higher transmit and receive performance of the loop elements at shallower depths and the improved performance of the dipole elements at greater depths. Furthermore, the loop-dipole combination increased channel count and density beyond what can be currently achieved when using dipole elements alone. The 16LD outperformed a 16-channel microstrip line (10) and a 10-channel fractionated dipole antenna (12) arrays in both simulations and experiments in terms of transmit and receive performance inside the prostate. MRI of the prostate, kidneys and the heart were acquired using the 16LD on healthy subjects showing the potential of this RF coil design to successfully image targets throughout the torso and pelvis at 7T.

Acronyms

UHF

ultrahigh field (B₀ ≥ 7 Tesla)

SAR

Specific Absorption Rate

SNR

signal to noise ratio

EM

electro-magnetic

RF

radio-frequency

LD

loop-dipole

16LD

16-channel combined loop dipole transceiver array

16ML

16-channel microstrip line transceiver array

10DA

10-channel fractionated dipole antenna array

BMI

body-mass index

Appendix

To assess the accuracy of numerical simulations, the B₁⁺ transmit efficiency of the LD block was investigated both numerically and experimentally on a torso-sized phantom (ε=77.8, σ=0.82 S/m) (46) using the FDTD solver of SEMCAD. B₁⁺ transmit efficiency was measured experimentally on the torso sized phantom filled with a saline solution (4.5 g/l NaCl, 1 g/l CuSO₄) giving the permittivity and conductivity used in the simulation. The MRI system and methods used for measuring the B₁⁺ transmit efficiency are described in the ‘MRI experiments’ section.

Numerically computed and experimentally calculated B₁⁺ distributions of a LD block with dipole-only, loop-only and dipole-loop B₁⁺ efficiency optimized combined excitations are shown in Supporting Figure S4 (top row: simulations, bottom row: experiments). Simulation and experimental results are in close agreement.

To evaluate the accuracy of the 16LD numerical model, B₁⁺ distributions of the 16LD on the torso phantom were simulated and experimentally measured using the same configuration. Phase-only B₁⁺ efficiency shimming inside a 4 cm² region mimicking the size and location of the prostate was performed (26). B₁⁺ distributions for dipole-only, loop-only, dipole-loop combined at equal power and dipole-loop combined with loop excitation power attenuated by 7dB were calculated both numerically and experimentally. Flip angle maps were acquired using the methods detailed above and scaled to yield B₁⁺ distributions in μT.

Numerically computed and experimentally calculated B₁⁺ distributions of the 16LD with dipole-only, loop-only, dipole-loop combined excitation where the loop excitation power is either attenuated by 7 dB or at equal power compared to the dipole are shown in Supporting Figure S5 (top row: simulations, bottom row: experiments). Simulated B₁⁺ transmit efficiency distributions demonstrate good agreement with the experimental results.