Methods for 2D and 3D Endobronchial Ultrasound Image Segmentation

Abstract

Endobronchial ultrasound (EBUS) is now commonly used for cancer-staging bronchoscopy. Unfortunately, EBUS is challenging to use and interpreting EBUS video sequences is difficult. Other ultrasound imaging domains, hampered by related difficulties, have benefited from computer-based image-segmentation methods. Yet, so far, no such methods have been proposed for EBUS. We propose image-segmentation methods for 2D EBUS frames and 3D EBUS sequences. Our 2D method adapts the fast-marching level-set process, anisotropic diffusion, and region growing to the problem of segmenting 2D EBUS frames. Our 3D method builds upon the 2D method while also incorporating the geodesic level-set process for segmenting EBUS sequences. Tests with lung-cancer patient data showed that the methods ran fully automatically for nearly 80% of test cases. For the remaining cases, the only user-interaction required was the selection of a seed point. When compared to ground-truth segmentations, the 2D method achieved an overall Dice index = 90.0%±4.9%, while the 3D method achieved an overall Dice index = 83.9±6.0%. In addition, the computation time (2D, 0.070 sec/frame; 3D, 0.088 sec/frame) was two orders of magnitude faster than interactive contour definition. Finally, we demonstrate the potential of the methods for EBUS localization in a multimodal image-guided bronchoscopy system.

I. INTRODUCTION

As part of the lung-cancer staging process, a physician performs bronchoscopy to collect a tissue sample of suspect diagnostic regions of interest (ROIs) [1]. Guided by live endobronchial video, the physician navigates the bronchoscope through the patient’s airways toward an ROI. When the physician reaches the airway closest to the ROI, the localization phase of bronchoscopy begins, whereby the physician refines the bronchoscope’s position for final tissue biopsy.

Unfortunately, most ROIs, be they lymph nodes or nodules, lie outside the airways, implying they are invisible to the bronchoscope. This forces the physician to “guess” at appropriate airway-wall puncture sites, resulting in missed biopsies and low yield. In addition, a videobronchoscope’s lack of extraluminal guidance information risks patient safety: nearby major vessels could be accidentally punctured by poorly selected biopsy sites. To address these issues, endobronchial ultrasound (EBUS) now exists that provides in vivo visualization of extraluminal anatomical structures [1]–[3].

State-of-the-art dual-mode bronchoscopes integrate a video-bronchoscope and a convex-probe EBUS into one device to provide both endobronchial video and fan-shaped EBUS imagery [2], [3]. With such a device, the physician uses endobronchial video for bronchoscopic navigation and later invokes EBUS for localization. To enable visualization of extraluminal anatomy, the EBUS device provides an EBUS video stream, where each frame represents a 2D B-mode gray-scale image of the scanned anatomy [4]. During localization, the physician sweeps the EBUS probe along the interior airway-wall surface near the ROI and examines the EBUS video stream. The physician continues the sweep until the EBUS presents a satisfactory confirming view of the ROI. In this way, the physician gains a mental impression of the relevant 3D local extraluminal anatomy. To complete the examination, the physician makes an ROI diameter measurement, if desired, and performs the indicated biopsy.

EBUS has become a standard procedure for cancer-staging bronchoscopy [1]. Studies have shown that EBUS-guided tissue biopsy is more accurate in predicting central-chest lymph node status than CT or positron emission tomography (PET) [5]. Unfortunately, EBUS is challenging to use, as procedural success depends on a physician’s dexterity, training, and procedure frequency [6]. Executing a suitable EBUS sweep trajectory for localizing an ROI poses a complex 3D problem. Furthermore, mentally inferring 3D information from a sequence of 2D EBUS images is very difficult. In reality, the physician essentially discards the EBUS video stream and makes decisions based only on discrete 2D frames; the physician does not have the benefit of a true 3D presentation.

Computer-based methods for segmenting EBUS images could help alleviate these issues. Such methods would enable more straightforward ROI measurements than the current interactive approach. They would also assist in integrating the 3D information present in the video stream. Lastly, they could serve as a major aid in enabling live image-based procedure guidance. Unfortunately, little research has been conducted to date in devising 2D or 3D image-analysis methods for endobronchial ultrasound [7]–[10].

Nakamura et al. applied interactive 2D analysis of EBUS images using a general-purpose image-processing toolbox [7]. Nguyen et al. performed simple MATLAB-based texture analysis of manually segmented EBUS frames [8]. Fiz et al. applied computer-based fractal analysis to 2D EBUS images, but did not consider image segmentation [9]. Finally, Andreassen et al. considered the reconstruction of 3D image volumes for EBUS sequences collected from cadavers, but relied upon tedious manual interaction to segment the individual 2D images [10]. Thus, no automatic or semi-automatic computer-based methods currently exist for segmenting 2D EBUS images or sequences of EBUS images. We propose image-segmentation methods for 2D EBUS images and 3D EBUS sequences. We also demonstrate their applicability in an image-guided bronchoscopy system.

The issues highlighted above for EBUS are reminiscent of the well-known issues arising in interpreting image sequences encountered in other ultrasound imaging domains, such as echocardiography, angiography, obstetrics, et al. [11]. This has spurred much progress in these domains in devising methods for segmenting 2D images and 3D image sequences [12]–[14]. Given the dearth of research in EBUS image analysis, we derived inspiration from these efforts for our work.

Before continuing, we summarize the requirements for segmentation methods in the EBUS domain. First, a method must be able to segment ROIs having variable sizes and shapes; at times, the ROIs may appear incomplete within the EBUS probe’s limited fan-shaped field of view. Second, we require robustness to high noise and resilience to uncertain probe contact in the air/tissue medium. Third, the method must be usable during a live (real-time) procedure; this requires a computationally efficient method that entails little or no user interaction (fully automatic or semi-automatic). Section II elaborates further on these requirements.

Regarding previous ultrasound segmentation research, early intravascular-ultrasound work drew upon traditional methods such as edge enhancement/detection and active contour analysis [15], [16]. Unfortunately, we have verified that such methods are ill-suited to EBUS images, which suffer significantly from wide shape and size variations, partially arising from the EBUS probe’s sometimes uncertain contact with the air/tissue medium [17], [18]. Related to this point, intravascular ultrasound probes operate in a blood/tissue medium that arguably depicts vessels with relatively well-defined elliptical region borders. Also, other ultrasound imaging domains, such as echocardiography, breast and liver cancer, and obstetrics, draw upon external probes that maintain relatively consistent contact with the tissue interface.

Regarding fully automatic ultrasound segmentation methods, Haas et al. proposed a method for segmenting ultrasound images based on a Markov-process model applicable to 2D and 3D sequences [19]. Unfortunately, the authors recommended applying the method off-line, because of its computation time. Other methods have been shown to run in real-time, yet require some form of prior shape knowledge or force ROIs to fit a predetermined shape model [20], [21].

More recent ultrasound image-segmentation research has drawn upon the versatile level-set paradigm [12]–[14], [22]–[27]. Level sets offer a framework for combining region- and gradient-based information into a flexible contour propagation process [28]. To gain the benefits of the level-set method while also being computationally efficient, a few ultrasound applications employed the common variant referred to as the fast-marching method [22], [23]. Other applications, especially those considering 3D sequences, employed the more elaborate geodesic level-set approach [24]–[26]. Also, given the high-noise and relatively simple form of ultrasound images, a few applications supplemented the level-set method with some form of anisotropic diffusion and/or multi-scale pyramidal analysis [25], [26]. A notable issue with all of these methods, including those of the early research, is that they require some form of user interaction to initialize, be it an initial contour or interactively selected seed points [15], [16], [20]–[27].

As Section II describes, our proposed 2D segmentation method adapts the fast-marching technique, anisotropic diffusion, and pyramidal decomposition to the problem of segmenting 2D EBUS frames. Our 3D method builds upon the 2D method while incorporating the geodesic level-set method to the problem of segmenting 3D EBUS sequences. Section III provides validation results using data from lung-cancer patients. The results show the efficacy and computational efficiency of the methods. Detailed parameter-sensitivity tests, given in the on-line supplement, further demonstrate method robustness. As our long-term goal is to incorporate computer-based EBUS analysis into the cancer-staging work flow, Section III also illustrates the potential of the computer-based EBUS analysis methods during image-guided bronchoscopy. Finally, Section IV offers concluding comments.

II. METHODS

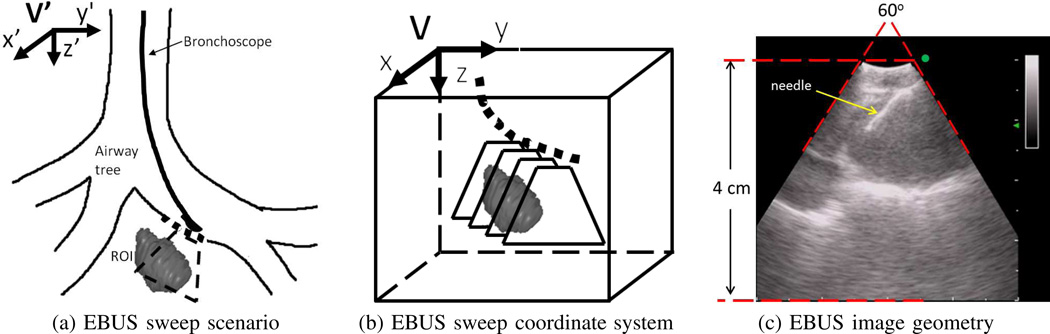
Fig. 1 illustrates the EBUS data-acquisition process and associated 3D coordinate systems. The EBUS probe sweeps a short linear trajectory along the airway-tree’s interior surface. This results in a 2D sequence of EBUS frames I_l (x, y), l = 1, 2, …, N,, where the sequence sweeps out a 3D subvolume V situated about a target ROI. Each 2D image I_l, with 3D image space coordinates (x, y, z), maps into the World space V′ with coordinates (x′, y′, z′).

Fig. 1.

EBUS data-acquisition scenario. (a) Schematic lay-out of EBUS sweep of a trajectory (dotted line) along an airway. Fan-shaped region indicates 2D sub-plane scanned by EBUS. (b) 3D local coordinate system for subvolume V bounding the 3D region swept by EBUS. (c) Image geometry for a convex-probe EBUS device [3]; the top curved portion represents the EBUS probe’s contact region within the airways. In this example, a biopsy needle is visible in the view. (station 4R lymph node, case I).

EBUS devices employ a fan beam, similar to that encountered for imaging the liver and heart [22], [24]–[26]. The resulting images consist of 300 × 300 pixels, where a non-zero fan-shaped 60° sector Ω corresponds to the EBUS probe’s scan region (Fig. 1c) [3]. As the EBUS scan spans a range of 4 cm over the y-axis, I_l ’s pixel resolution Δx = Δy = 0.133̄ mm. Within this context, we have two goals: 1) segment individual 2D EBUS frames I_l; and 2) perform 3D segmentation of an ROI over an entire sequence I_l, l = 1, 2, …, N.

In standard practice, the physician sweeps the device so that a target ROI appears centered in the EBUS frame and situated ≈1–2 cm from the airway surface. Being “centered” implies that a biopsy needle inserted through the bronchoscope’s needle entry port is able to pierce the ROI (Fig. 1c).

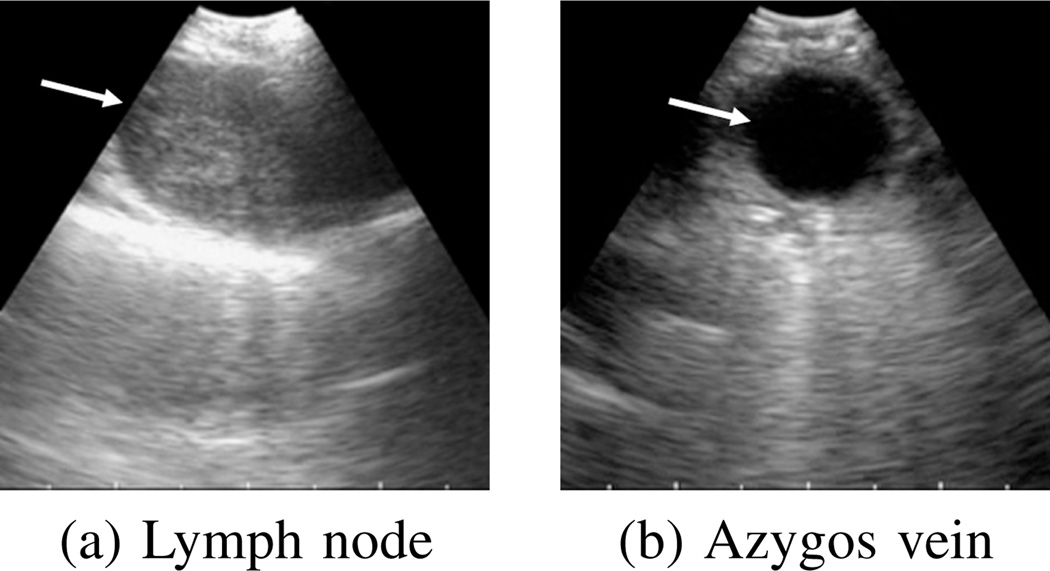
Lymph nodes and nodules usually appear as hypoechoic regions surrounded by hyperechoic boundaries (Fig. 2). Blood has low echogenicity and absorbs more ultrasonic energy than its surroundings. Hence, these structures appear as dark homogeneous regions surrounded by bright borders, and the EBUS segmentation problem entails a search for connected clusters of pixels whose intensities are lower than their neighbors.

Fig. 2.

Example 2D EBUS images. Arrows indicate ROIs. (a) station 4R Lymph node (case I). (b) Azygos vein (case G).

Three factors adversely affect the ultrasonic signal’s transmission [4]. First, as the signal propagates through tissue, its energy becomes progressively attenuated. Second, the EBUS probe often does not maintain proper contact with the airway wall; i.e., air intervenes between the probe/wall interface. As air strongly reflects ultrasonic energy, it greatly reduces the effective propagation depth of the transmitted signal. Finally, a saline-filled balloon, commonly used to improve EBUS contact, sometimes contains air. Overall, these factors limit EBUS’s practical range to < 4 cm, reducing the confidence of image findings further from the EBUS transducer. Thus, regions far from the transducer tend to have less certain boundaries and contrast, making them difficult to discern.

In addition, two other EBUS limitations impact a region’s form in an image. First, the wave interference phenomenon known as “speckle” degrades the image such that the noise level and contrast vary depending on local signal strength [29], [30]. Second, while ultrasound-wave reflections highlight region borders in an EBUS image, the reflected values depend on the incident angle between the ultrasonic signal transmission and the medium interface. This orientation dependence results in missing border components. Overall, EBUS images have a granular appearance corrupted by drop-outs.

Our segmentation methods, discussed below, strive to mitigate these limitations by enabling robust ROI definition.

A. 2D EBUS Segmentation

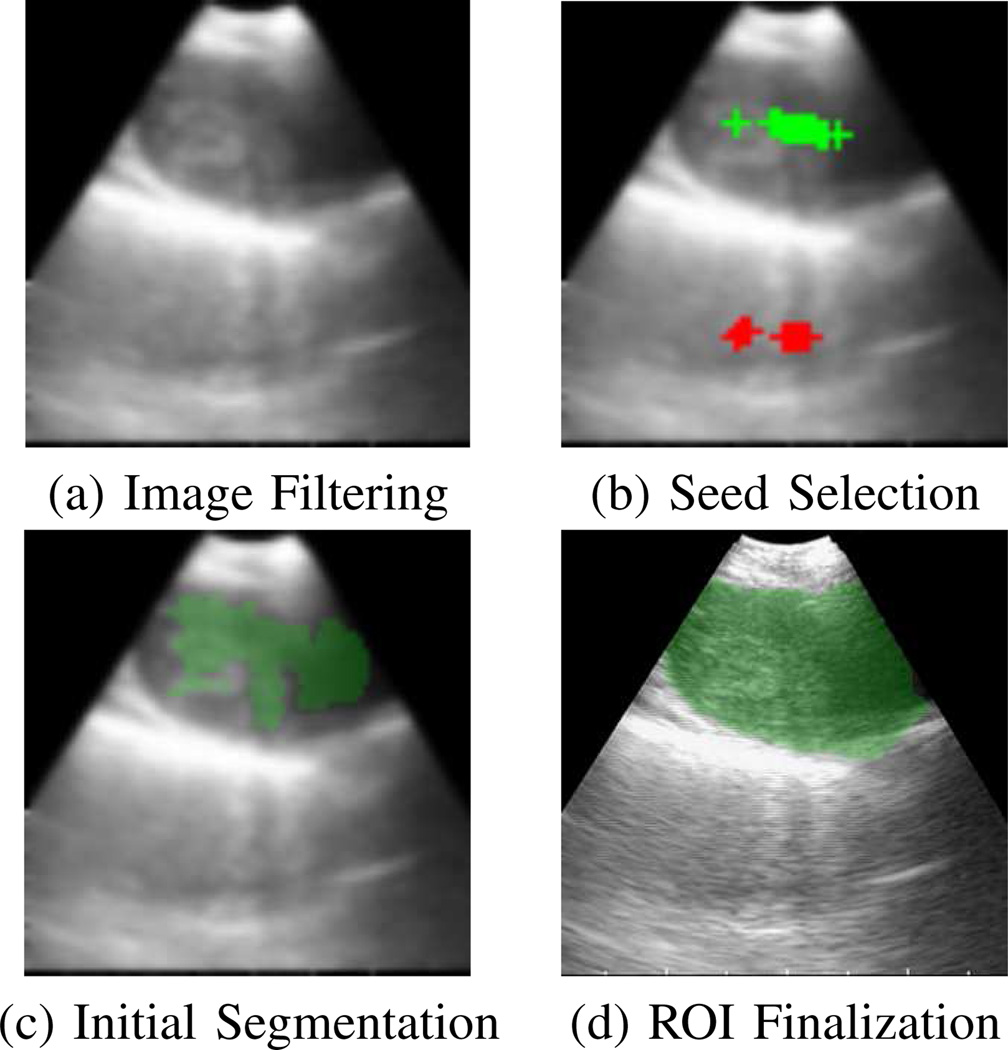
2D EBUS segmentation accepts a single 2D EBUS frame I as input, where we drop the subscript “l” for convenience. In principle, the method extracts all large isolated dark regions depicted in I, where at least one region appears approximately situated near the middle of I. The basic method has four steps:

1. Image Filtering: Using a combination of anisotropic diffusion and pyramidal decomposition, reduce noise and sharpen image borders.

2. Seed Selection: Select seed points for candidate ROIs, where selected seeds lie within a central needle-accessible subregion of the EBUS scan region Ω.

3. Initial ROI Segmentation: Drawing upon the selected seeds, perform a level-set-based segmentation on the filtered image to arrive at initial ROI definitions.

4. ROI Finalization: Finalize ROI shapes.

The subsections below give details for each of these steps.

1) Image Filtering

To improve the efficacy of subsequent segmentation operations, we begin by filtering input EBUS image I. Our approach draws upon past research, which showed that a combination of anisotropic diffusion and pyramidal decomposition effectively reduces speckle noise in ultrasound images while also preserving and sharpening region borders [25], [26], [29], [30]. An additional benefit of pyramidal decomposition is that the computation time of subsequent segmentation steps is greatly reduced.

Letting I^k denote the pyramidal decomposition of image I at level k, our approach initializes the 0^th pyramid level by setting k = 0 and I^k = I. Next, the following operations are run:

1. Apply adaptive anisotropic diffusion to I^k.

2. Decimate image I^k via the operation

   $$I^{k+1}=I^k\downarrow 2$$ (1)

   to create the next pyramid level, where (1) downsamples I^k by a factor of two in both the x and y dimensions.

Anisotropic diffusion is based on the well-known relation

$$\frac{\partial I(x,y)}{\partial t}=\text{div }[c(|\nabla I|)\nabla I]$$ (2)

where I is the input image, t is a scale-space parameter with larger t corresponding to a coarser scale, “div” denotes the divergence operator, ∇I corresponds to the gradient of I, |∇I| equals gradient magnitude, and c(·) is the conduction coefficient [31]. Drawing upon Steen’s suggestion, we let

$$c(|\nabla I|)=\{\begin{array}{cc}{e}^{-\frac{{|\nabla I|}^2}{2{\hat{\sigma }}^2}},\hfill & \text{if }|\nabla I|\le \hat{\sigma }\hfill \\ \frac{e^{-\frac{\hat{\sigma }}{2}}}{|\nabla I|},\hfill & \text{otherwise},\hfill \end{array}$$ (3)

where gradient-threshold parameter σ̂ is calculated via

$$\hat{\sigma }(x,y)={\sigma }_n{ŝ}^{\frac{1}{2}}(x,y),$$ (4)

and

$$ŝ(x,y)=\frac{-{\sigma }_n^2}{2}+\sqrt{\frac{{\sigma }_n^4}{4}+s(x,y)}$$ (5)

is a local maximum likelihood estimate of the image signal at (x, y), σ_n corresponds to the level of image detail to preserve, and s(x, y) equals the average value of I(x, y) in a 3 × 3 neighborhood about (x, y) [29]. Equations (3–5) constitute an approach that locally adapts to the noise level about each pixel (x, y). In this way, the diffusion process can preserve edges of differing strength depending on the strength of the local signal. Unlike Steen, who preset σ_n to a fixed value, we estimate σ_n via the robust median absolute-deviation estimator [30].

We employ a standard implementation of iterative relation (2), using the mean-absolute error as a stopping criterion [30], [31]. In addition, we iterate the two-stage filtering method twice, given I² as the final output. For simplicity, we will refer to this image as I in the discussion to follow. Fig. 3a illustrates Image Filtering.

Fig. 3.

2D EBUS segmentation method applied to station 4R lymph node of Fig. 2a. (a) Output after image filtering. (b) Result after seed selection; green and red crosses mark true- and false-positive seeds, respectively. (c) Initial segmentation of ROI (green). (d) Finalized ROI segmentation (green).

2) Seed Selection

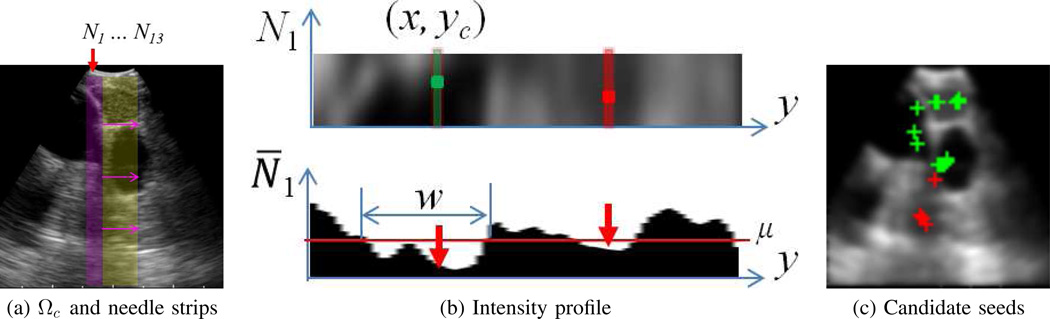
Seed Selection examines the filtered image to isolate a set of ROI seed pixels S = {s₁, s₂, …, s_M}. It draws upon the premise that the physician centers target ROIs in the EBUS image so that a biopsy needle can successfully puncture the ROI. Based on this premise, Seed Selection searches a rectangular central region situated just beyond the EBUS probe’s transducer and locates isolated dark regions that can be pierced by a biopsy needle. To perform the search, a thin vertical strip approximating a biopsy needle’s shape pans across the central region to locate candidate dark-region cross-sections, which in turn results in selected seed points.

For the EBUS scenario, filtered image I consists of 75 × 75 pixels, with pixel resolution Δx = Δy = 0.533̄ mm. The EBUS probe’s fan-shaped scan region Ω emanates from the image’s top center. Because the contact region of the EBUS transducer/balloon assembly produces an uninformative zone demarcated by bright hemispherical lines, the image’s informational portion begins at y = 5 (Fig. 1c). Thus, we define the 17 × 70 (0.90 cm × 3.7 cm) region just below this point as the central region Ω_c, where 17 pixels corresponds to the width of the EBUS probe’s top contact region in I (Fig. 4a). Each valid ROI R must intersect Ω_c; i.e., we must be able to locate at least one seed s_m ∈ Ω_c such that s_m ∈ R.

Fig. 4.

Seed Selection example (case G). (a) Configuration of the needle strip N_j panning across the image’s central region Ω_c (yellow). N₁ (magenta) is the left-most vertical strip, with succeeding strips shift to the right one column at a time. (b) Localization of candidate seeds for N₁. Top view shows 5 × 70 array of image data defining N₁ (turned sideways for easier viewing). Bottom view depicts the corresponding average intensity profile N̅₁. Two low-intensity valleys exist, having widths 20 and 11 pixels; each valley gives in a candidate seed. (c) Depiction of candidate seeds. Per the SVM analysis, 13 seeds (green crosses) were deemed to be true seeds, while 4 were rejected as false positives (red crosses).

Continuing, define the vertical needle strip N_j having dimensions 5 × 70 pixels (0.26 cm × 3.7 cm), in line with the 0.18 cm diameter of a standard 22-gauge TBNA needle. This strip will be panned across central region Ω_c one column at a time, implying 13 distinct strip positions, N_j, j = 1, 2, …, 13, fit within Ω_c (Fig. 4a). Thus, R must intersect at least one of these strip positions, which in turn implies that R intersects Ω_c. That is, there must be at least one N_j such that we can locate at least one seed s_m ∈ N_j and s_m ∈ R. In general a prospective ROI could result in multiple seeds being selected across > 1 strip positions.

Given this set up, Seed Selection proceeds as follows. First, we calculate the mean intensity value μ of pixels constituting the central EBUS scan region Ω_c. Next, for each N_j, j = 1, 2, …, 13:

1. Compute the average strip intensity profile (Fig. 4b)

   $${\overline{N}}_j(y)=\frac{1}{5}\sum _{x=1}^5{N}_j(x,y)$$

2. Search profile N̅_j for connected low-intensity valleys of points having width w > W, where a low-intensity point y satisfies N̅_j (y) < μ.

3. For each valley, derive its valley centroid y_c. Next, locate pixel (x, y_c) in strip N_j having minimum intensity value. (x, y_c) denotes a candidate seed point s_m for this valley. Retain the valley’s width w and centroid y_c in a feature vector f_m = [y_c w]^T characterizing s_m.

4. Apply a support-vector machine (SVM) classifier to determine the validity of each candidate seed s_m by evaluating cost

   $$C({\mathbf{s}}_m)=\sum _{{\mathbf{v}}_n\in V}({\alpha }_n({\mathbf{f}}_m·{\mathbf{v}}_n)+b),$$

   where “·” denotes vector dot product, b is a bias term, and (v_n, α_n), n = 1, 2, …, 16, denote the n^th support vector and associated weight for the 16 support vectors we use to define the SVM classifier [32]. If C(s_m) > 0, then seed s_m is retained as a valid seed in S (Fig. 4c).

Fig. 3b gives an example of Seed Selection.

Threshold W determines the method’s sensitivity to detecting dark ROI valleys. Overly small values produce false-positive seeds, especially within small shadow-artifact regions. We chose W = 5 in line with the width of the needle strips.

To train the SVM, we used the 2D EBUS images pertaining to 20 consecutive ROIs from cases F through I of the 52-ROI database described in Section III-A. These ROIs span the variety of structures observed in EBUS, including lymph nodes, vessels, and nodules [18]. To each of the images, we applied Image Filtering (Section II-A1) and steps 1–3 of the Seed Selection process. This resulted in 271 potential candidate seeds and associated feature vectors. By manually examining these candidate seed locations in the EBUS images, we marked 222 candidates as valid seeds. The remaining 49 seeds were designated as false positives. Next, we used these data to produce a classifier defined by 16 support vectors and associated weights, using a standard SVM implementation [33]. The resulting classifier gave a true positive valid-seed rate of 96% (213/222), while rejecting 100% of false-positive seeds.

EBUS procedure conventions (Section II-B) dictate that an EBUS sweep focus attention on a truly valid ROI. Thus, the central-region Ω_c does not need to completely cover an ROI to enable seed selection, and it obviously does not take into account image data to the left and right of Ω_c. “ROIs” completely outside Ω_c are either too small to be significant or too distant from the EBUS device’s needle port to enable satisfactory biopsy.

As Section III demonstrates, Seed Selection finds seeds automatically for roughly 80% of proper ROIs. For 2D EBUS frames where Seed Selection fails to identify a seed, the user can interactively select a seed, as done previously in other ultrasound imaging domains [22], [27]. For our work, we provide a graphical user interface, whereby the user specifies a seed by performing a simple mouse click within the ROI depicted in the currently displayed EBUS frame. This operation is simpler than what the physician currently performs when making live EBUS-based ROI diameter measurements.

3) Initial ROI Segmentation

Given filtered image I and seed set S, a level-set-based technique defines an initial region segmentation R. The level-set paradigm offers greater flexibility than deformable-contour analysis in that it readily incorporates local and global region shape/intensity characteristics [24], [28]. Furthermore, the paradigm is robust to initialization, since it smoothly handles region topological changes; e.g., regions evolving from separate seeds can merge into one ROI. The level-set paradigm is especially suitable for ultrasonic images, in that it can robustly segment ROIs exhibiting varying shape/intensity properties and missing boundary components.

For 2D segmentation, the level-set methodology introduces a hypersurface function ϕ(x, y, t), which embeds the (x, y)-space ROI contour C as the zero-valued level set of this function [28]. In particular, let C(t) represent the contour’s propagating front evolving over t consisting of all pixels (x, y) such that ϕ(x, y, t) = 0; or, stated equivalently,

$$\varphi (\mathbf{C}(t),t)=0\text{ for all }t.$$ (6)

The general level-set evolving equation is given by

$$\frac{\partial \varphi (x,y,t)}{\partial t}+F(x,y,t)|\nabla \varphi (x,y,t)|=0$$ (7)

with appropriate initial conditions for ϕ(·, ·, 0), where F is the so-called speed function. As t advances, ϕ(x, y, t) evolves. Because ϕ covers the entire image and, hence, includes ROI front C(t) per (6), it automatically handles topological changes to C(t) as t advances. Various local and global factors influencing the segmentation process are readily incorporated into F, including: 1) image features, such as intensity and gradient; and 2) front features, which depend upon the shape and position of the evolving front.

Numerical implementation involves: 1) discretizing (7) or its equivalent into an iterative process; and 2) choosing speed function F and initial conditions. For 2D EBUS segmentation, we apply the computationally efficient fast-marching method [22], [23]. Instead of solving the general level-set equation (7) for ϕ, the fast-marching method solves the Eikonal equation, a special case of (7) given by

$$|\nabla T(x,y)|F(x,y)=1.$$ (8)

(8) uses the observation that pixel distance ∝ speed × arrival time, where T is an arrival time function. Our level-set-based method expands the seed set S into set R ∈ I, where

$$\mathbf{R}(x,y)=\{\begin{array}{cc}1,\hfill & \text{if pixel }(x,y)\in \mathbf{R}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (9)

T models the evolution of ROI fronts C, where T (x, y) equals the “time” that C(t) crosses pixel (x, y) in image I. Because contour front C always expands during the process — or, equivalently, R grows outward from the seeds, T is a monotonically increasing function. For our application, we construct F by first computing the image gradient

$$G(x,y)=\nabla I(x,y).$$

We then apply a sigmoid filter

$$Ĝ(x,y)={[1+e^{-\frac{|G(x,y)|-d}{a}}]}^{-1}$$ (10)

to highlight a selected range in G(x, y) [27]. Finally,

$$F(x,y)=e^{-hĜ(x,y)}.$$ (11)

In (10–11), parameters a and d denote the width and center of the desired gradient window, while h controls how fast F varies. We default these parameters to a = 25.5, d = 76.5, and h = 5. Overall, F ≈ 1.0 for pixels having low gradient magnitude and is near zero for pixels having high gradient magnitude. Thus, as (8) iterates, the evolving C(t) swiftly propagates through smooth, homogenous regions, while slowly moving, or stopping, near region boundaries. For our problem, we apply the well-known upwind approximation [28]

$$\text{max }{[D^{-x}T(x,y),-D^{+x}T(x,y),0]}^2+\text{max }{[D^{-y}T(x,y),-D^{+y}T(x,y),0]}^2=\frac{1}{F{(x,y)}^2}$$ (12)

to iteratively solve (8), where

$$D^{\pm x}T(x,y)=\pm T(x\pm 1,y)\mp T(x,y)$$ (13)

$$D^{\pm y}T(x,y)=\pm T(x,y\pm 1)\mp T(x,y).$$

Algorithm 1 incorporates (9–13) into a region-segmentation algorithm. The algorithm first initializes F, T, and R for all image pixels. In addition, seed set S begins a min-heap data structure ℒ, where the minimum arrival-time pixel always lies at the top of the heap. Next, the main while loop invokes an evolution process, whereby the ROI contour front marches across the image resulting in pixels being progressively added to R. The while loop terminates when ℒ is empty.

Algorithm 1 draws inspiration for the concepts of alive pixels, old/current arrival times T_o/T_c, and the adaptive arrival-time threshold T_R from [22], [28]. It represents a specially tailored form of fast-marching image segmentation for EBUS, where our procedure for handling boundary pixels is new in that it guards against leakage through boundary gaps, which could result in excessive region growth. It also employs the modified speed function (10–11), better suited to EBUS images. Fig. 3c illustrates Initial ROI Segmentation.

4) ROI Finalization

Because the fast-marching method constructs ROIs based on gradient information, it extracts a significant portion of ROI pixels situated in homogeneous locations. Nevertheless, image noise, which is well-known to greatly affect image-gradient values, limits ROI completeness. ROI Finalization performs complementary region growing based on intensity information to identify pixels missing from ROIs. Starting with filtered image I and initial segmentation R, ROI Finalization proceeds as follows:

1. Identify connected components in R. These correspond to distinct ROIs R_i, i = 1, 2, …, requiring finalization.

   Algorithm 1.

   Initial ROI Segmentation

   1:	Inputs: seed set S, filtered image I
   2:	// Initialize data structures
   3:	for all p ∈ I do
   4:	Compute F (p) using (10–11)
   5:	if p ∈ S then
   6:	T (p) = 0, R(p) = 1
   7:	else
   8:	T (p) = ∞, R(p) = 0
   9:	S → ℒ // Begin the heap
   10:	Tc = To = 0
   11:	while ℒ ≠ ∅ do
   12:	// Make heap’s top pixel, which has min T (p), alive
   13:	pop(ℒ) → p, Alive(p) = TRUE
   14:	Tc = T (p), ΔR = 0
   15:	// Locate pixels constituting R
   16:	if Tc − To ≥ 2 then
   17:	TR = To + 1
   18:	for all q ∈ I such that R(q) ≠ 1 do
   19:	if T (q) ≤ TR then
   20:	R(q) = 1
   21:	exit
   22:	else if Tc − To ≥ 1 then
   23:	TR = Tc
   24:	for all q ∈ I such that R(q) ≠ 1 do
   25:	if T (q) ≤ TR then
   26:	R(q) = 1, ΔR = ΔR + 1
   27:	if ΔR ≤ Δmin then
   28:	exit // Avoid potential ROI leakage
   29:	else
   30:	To = Tc
   31:	// Check 4-neighbors of p
   32:	for all q ∈ 𝒩(p) such that ¬Alive(q) do
   33:	Compute T (q) using (eq:FastMarching) // Update arrival time
   34:	if q ∉ ℒ then
   35:	q → ℒ // Add to heap
   36:	heap-sort(ℒ) // Resort the heap
   37:	fill-holes(R) → R // Fill holes in final output
   38:	return R

2. For each ROI R_i, i = 1, 2, …, do the following:

   1. Compute R_i ’s mean μ_i and variance ${\sigma }_i^2$.
   2. Add neighbor (x, y) to R_i if

      $$\left|\frac{I(x,y)-{\mu }_i}{{\sigma }_i}\right|\le {\delta }_{\text{min}}.$$ (14)

3. If the total number of pixels added to all regions is ≤ R_min, stop the process. Otherwise, iterate step 2.

Test (14) assumes that pixels (x, y) constituting R_i abide by normal distribution $N({\mu }_i,{\sigma }_i^2)$ [25] and

$$\text{Prob }\left\{\right|\frac{I(x,y)-{\mu }_i}{{\sigma }_i}|\le {\delta }_{\text{min}}\}=Q_{\text{min}}.$$ (15)

Such pixels nominally belong to the same distribution as R_i. For our implementation, we used the default Q_min = 0.95, which immediately sets δ_min = 1.96 in (14–15). We also set R_min = 3%. Fig. 3d illustrates a finalized segmentation.

B. 3D EBUS Segmentation

Referring to the Fig. 1 scenario, the physician sweeps a volume in accordance with three EBUS procedural conventions:

1. The sweep focuses on one ROI R.

2. The device moves slowly along the sweep trajectory.

3. The device maintains contact with the airway wall so that R remains continuously visible.

More specifically, the physician invokes EBUS when the bronchoscope reaches a pre-designated ROI such as a lymph node (typical long-axis length ≥ 1 cm). The sweep generally spans ≈ 2 cm and takes 1–2 sec to complete. Therefore, given a 30 frames/sec video rate, individual frames I_l are typically spaced < 1 mm apart. Hence, R’s shape clearly changes incrementally between consecutive frames; i.e.,

$${\mathbf{R}}_l\approx {\mathbf{R}}_{l-1},$$ (16)

where R_l represents the 2D cross-section of R on frame I_l. Lastly, if the EBUS breaks contact with the airway wall, then the resulting frames are unlikely to provide useful data.

We now present a method for segmenting R across an entire sweep sequence. Exploiting condition (16), our method uses a previous frame’s segmentation R_l−1 to initialize an adjacent frame’s segmentation R_l. Next, a geodesic level-set process refines this estimate. Finally, as with the 2D method, the segmentation is finalized. The method then iterates this process for succeeding frames. More specifically, for EBUS sequence I_l, l = 1, 2, …, N, the method involves the following steps:

1. For I₁, apply 2D segmentation to produce R₁.

2. For I_l, l = 2, 3, …, N,

   1. Filter and decimate I_l.
   2. Initialize ROI contour

      $$\mathbf{C}=\partial {\mathbf{R}}_{l-1},$$

      where ∂R_l−1 signifies the boundary of R_l−1.
   3. Using C, apply a geodesic level-set process to I_l to evolve R_l.
   4. Perform ROI finalization on R_l.
   5. If R_l ≠ ∅, continue iteration. Otherwise, terminate, as frame I_l does not contain R, implying that the ROI is no longer visible in the sequence.

2D segmentation uses the complete method of Section II-A. The image filtering/decimation and ROI-finalization steps employ the methods of Sections II-A1 and II-A4, respectively.

The geodesic level-set process of step 2c entails the core of the method. The process solves the general level-set equation (7) and draws upon a more sophisticated speed function than (11). In particular, a special case of (8) with F(x, y) = 1 for (x, y) is first solved; i.e.,

$$|\nabla \hat{T}(x,y)|=1,$$ (17)

where T̂(x, y) is simply equal to the shortest Euclidean distance between pixel (x, y) and the given initial estimate C, and T̂(C) = 0 [28]. Next, initial conditions for ϕ are set as a signed distance function [26]:

$$\varphi (x,y,0)=\{\begin{array}{cc}\hfill -\hat{T}(x,y),& \text{if }{\mathbf{R}}_{l-1}(x,y)=1\hfill \\ \hfill \hat{T}(x,y),& \text{otherwise}\hfill \end{array}$$ (18)

Continuing, the speed function is given by

$$\hat{F}(x,y,t)=F(x,y)(1-\epsilon \kappa (x,y,t))+\eta \nabla F(x,y)·\left(\frac{\nabla \varphi (x,y,t)}{|\nabla \varphi (x,y,t)|}\right),$$ (19)

where F is the function (11) and ε and η are parameters. Because the F(x, y) term only allows for expansion in one direction, previous researchers omitted this term in F̂ to avoid potential contour leakage over large boundary gaps in ultrasound images [24]. Our method, however, includes F(x, y) to better enable supplemental contour evolution toward high-gradient boundaries. By adjusting ε, the method limits contour overgrowth through small boundary gaps, commonly seen in EBUS images. Quantity κ, which denotes the curvature of ϕ, is a geometric term that regularizes the propagating level-set front’s smoothness, where [28]

$$\kappa (x,y,t)=\text{div }\left(\frac{\nabla \varphi (x,y,t)}{|\nabla \varphi (x,y,t)|}\right)=\frac{{\varphi }_{xx}{\varphi }_y^2-2{\varphi }_x{\varphi }_y{\varphi }_{xy}+{\varphi }_{yy}{\varphi }_x^2}{{({\varphi }_x^2+{\varphi }_y^2)}^{\frac{3}{2}}}.$$ (20)

Also, the η-dependent component of (19) is a stabilizing advection term that attracts the level-set front toward region boundaries. Finally, combining (7) and (19) gives

$$\frac{\partial \varphi (x,y,t)}{\partial t}+F(x,y)(1-\epsilon \kappa (x,y,t))|\nabla \varphi (x,y,t)|-\eta \nabla F(x,y)·\nabla \varphi (x,y,t)=0,$$ (21)

which represents our tailored form of the geodesic level-set equation for EBUS segmentation.

For digital implementation, we discretize and solve (21) iteratively using the finite forward-difference scheme

$$\varphi (x,y,t+1)=\varphi (x,y,t)+\tau \{(\epsilon \kappa (x,y,t)-1)F(x,y){[{(D^{0x}\varphi (x,y,t))}^2{(D^{0y}\varphi (x,y,t))}^2]}^{\frac{1}{2}}-\eta [\text{max}(D^{0x}F(x,y),0)D^{-x}\varphi (x,y,t)+\text{min}(D^{0x}F(x,y),0)D^{+x}\varphi (x,y,t)+\text{max}(D^{0y}F(x,y),0)D^{-y}\varphi (x,y,t)+\text{min}(D^{0y}F(x,y),0)D^{+y}\varphi (x,y,t)]\},$$ (22)

where τ is a parameter, D^±x and D^±y are given by (13) and the D^0x and D^0y terms and ϕ_x, ϕ_xx, etc., constituting κ are digitized similarly [18], [28].¹

Therefore, given I_l and C from steps 2ab, the geodesic level-set process (step 2c) runs as follows:

1. Initialize ϕ(·, ·, 0) using (17) and (18).

2. For t = 0, 1, …,

   1. ∀(x, y) ∈ I_l, update ϕ(x, y, t) using (20) and (22).
   2. If ℰ_t > ℰ_min, continue iterating. Otherwise, terminate the process.
3. Define the segmented region via

   $${\mathbf{R}}_l(x,y)=\{\begin{array}{cc}1,\hfill & \text{if }\varphi (x,y,t)\le 0\hfill \\ 0.\hfill & \text{otherwise}\hfill \end{array}$$

   ℰ_t is the root-mean-squared difference of the evolving contour front between consecutive iterations, where only pixels neighboring a contour pixel are considered in ℰ_t. In our implementation, we default ε = 8 and η = 10 in (19), τ = 0.1 in (22), and ℰ_min = 0.02.

Fig. 5 depicts an application of the complete 3D EBUS segmentation method over a 40-frame EBUS sequence. It is important to realize that the fast-marching method is not applicable here, since fast marching requires the initial contour to either monotonically increase or decrease from one frame to the next. This is clearly not the case here, as a region’s 2D shape can clearly expand or shrink from one frame to the next. The geodesic level-set method is, of course, more complex than the fast-marching method. Nevertheless, condition (16) typically ensures that initial contour C provides a good starting estimate for R_l+1, resulting in a minimal computational penalty for running the method.

Fig. 5.

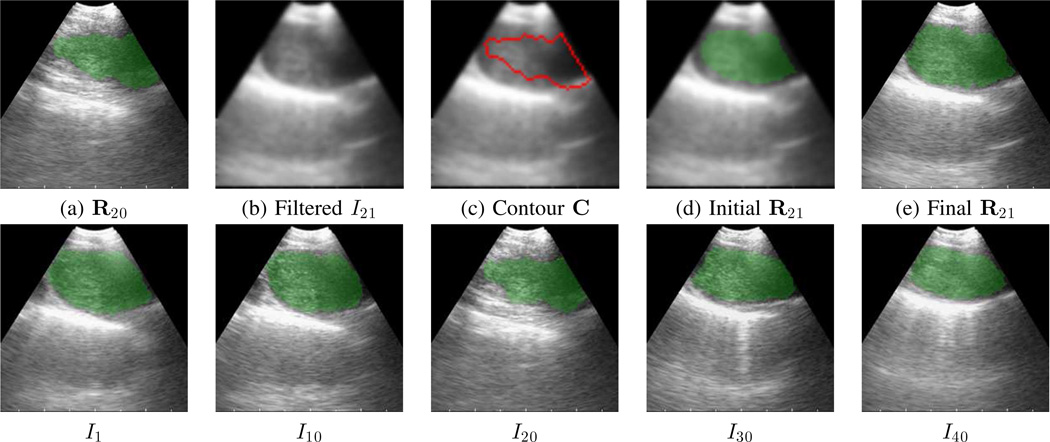
3D EBUS segmentation method applied to a 40-frame sequence depicting a 4R lymph node (case L, sequence 1). Top row (a–e) focus on calculations for frame I₂₁. (a) Previous segmentation result R₂₀ (green) superimposed on frame I₂₀. (b) Filtered version of I₂₁. (c) Initial ROI contour C (red) superimposed on I₂₁. (d) ROI R₂₁ (green) after geodesic level-set analysis. (e) Final segmentation R₂₁ (green). Bottom row depicts five sample frames for the complete segmentation across the sequence.

We point out that it is possible to apply the 2D method of Section II-A to every sequence frame on a frame-by-frame basis. Unfortunately, since automatic seed selection is likely to fail for some sequence frame, this naive approach works poorly in general and we do not recommend it [18].

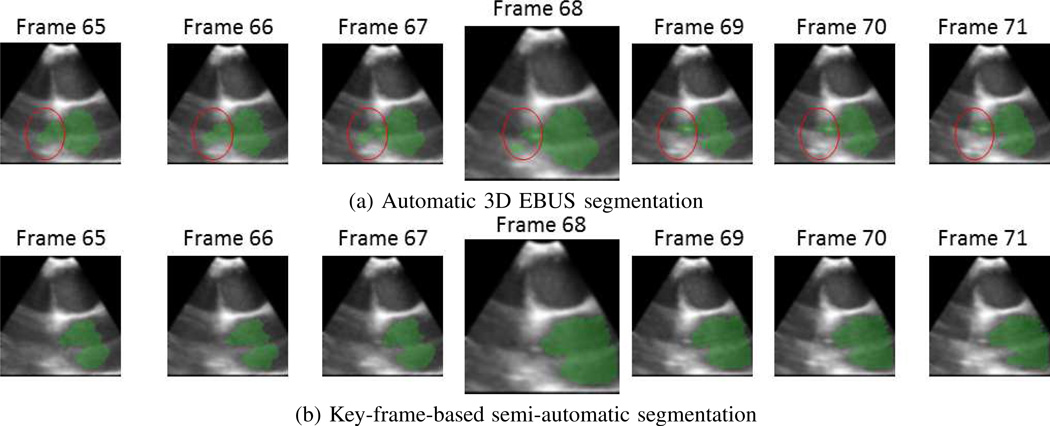
On the other hand, the automatic 3D segmentation method can diverge toward incorrect 2D segmentations (either excessively shrinking or expanding), but this is easily corrected by applying a key-frame-based method. Briefly, the system automatically identifies a frame I_l in the segmented EBUS video stream in which the number of segmented ROIs changes from the preceding frame I_l−1. The user then interactively repeats the 2D method on the given frame. Finally, the automatic 3D method restarts M frames preceding this key frame (frame I_l−M) to process the remainder of the sequence. Section III-B illustrates this method, with more detail given in [18].

III. RESULTS

We tested the proposed segmentation methods using data from 13 lung-cancer patients. For all procedures, the physician used a standard Olympus BF-UC180F linear ultrasound bronchoscope (6.9 mm distal-end diameter; 10 MHz transducer) [3]. This device gives both endobronchial video and B-mode endobronchial ultrasound imagery. To evaluate method performance, we used the following well-known evaluation metrics [14]:

$$\text{Dice}(\mathbf{R},\mathbf{G})=\frac{2|\mathbf{R}\cap \mathbf{G}|}{|\mathbf{R}|+|\mathbf{G}|},\hspace{0.17em}\mathrm{F}\mathrm{D}\mathrm{R}(\mathbf{R},\mathbf{G})=1-\frac{|\mathbf{R}\cap \mathbf{G}|}{|\mathbf{R}|},$$

where FDR is the false discovery rate (measure of segmentation leakage), and R and G are the segmented and ground-truth versions of an ROI. Below, we give test results for the 2D and 3D methods and conclude with an application of our methods in a complete bronchoscopy guidance system. The on-line supplement provides additional results and sensitivity analysis for the proposed segmentation methods.

A. 2D EBUS Segmentation Tests

During a conventional EBUS ROI localization sweep, the physician first examines the resulting EBUS video stream and then picks a representative 2D EBUS frame to verify the ROI and make measurements. In keeping with this procedure, we selected representative EBUS test frames for 52 ROIs from the 13 patient studies. These included 24 lymph nodes, 26 central-chest blood vessels, and 2 suspect cancer masses.

Before testing method performance, we first established ground-truth segmentation results. To do this, an experienced EBUS technician employed the semi-automatic live wire to define ground-truth contours for all ROIs. The live wire is a popular semi-automatic contour-definition method that enables substantially more reproducible segmentation results than manual region tracing [34], [35].

We next benchmarked ground-truth reproducibility. For the test, two experienced EBUS technicians (includes the technician who established the original ground truth for all ROIs) and a novice EBUS user segmented four ROIs drawn from 4 human cases, spanning a range of region complexity and noise level. Each technician performed three trials of the segmentation task, spaced over a period of three weeks to reduce memory. During each trial, a technician followed the conventional EBUS protocol: 1) examine the EBUS video for an ROI; 2) based on the video observation, segment the selected 2D frame using the live wire. We next pooled these results by computing the intra-observer and inter-observer reproducibilities given by

$$\text{Intra}-\text{observer}({\mathbf{R}}_i,O_j,{𝒯}_l,{𝒯}_m)=\text{Dice}({\mathbf{B}}_{{\mathbf{R}}_i,O_j,{𝒯}_l},{\mathbf{B}}_{{\mathbf{R}}_i,O_j,{𝒯}_m}),l\ne m$$

$$\text{Intra}-\text{observer}({\mathbf{R}}_i,O_j,O_k,{𝒯}_l,{𝒯}_m)=\text{Dice}({\mathbf{B}}_{{\mathbf{R}}_i,O_j,{𝒯}_l},{\mathbf{B}}_{{\mathbf{R}}_i,O_k,{𝒯}_m}),j\ne k$$

where B_{Ri, Oj, 𝒯l} denotes the segmentation of R_i by observer (technician) O_j on trial 𝒯_l [34], [35]. Overall, the intraobserver/inter-observer reproducibilities had ranges [89.5%, 97.0%] and [87.1%, 96.9%], respectively, with a typical standard deviation per ROI equal to a few percent. The mean interaction time to segment a 2D frame was 16 sec, excluding video preview. These benchmark results help establish the maximally attainable performance for 2D EBUS segmentation.

As a first test of method performance, we measured the sensitivity of the 2D method to parameter variations using a subset of typical ROIs. For each test, we varied one parameter in one of the four steps constituting the 2D EBUS segmentation method and fixed all other parameters to default values. The on-line supplement details these tests, with [18] giving complete results. We highlight the findings of these tests below.

• The mean Dice index of segmented ROIs improved from 81.1%±12.7% (no filtering) to 88.3%±4.5% with filtering. Without filtering, high noise and uncertain boundary segments result in excessive segmentation leakage and/or under-segmentation. Also, other tests varying the number of pyramid levels showed that three levels produced the best results.

• In a test where a user interactively varied seed location such that the user cooperated and placed the seeds in “sensible” locations (i.e., near the middle of the ROI), we found that the subsequent steps (Initial ROI Segmentation and ROI Finalization) were robust to seed-location variations and provided reproducible segmentations. In particular, segmentations varied <1% on average when the seed positions were varied. Automatic seed selection gave an aggregate Dice index = 89.1%±5.2% versus 86.2%±6.2% when using interactively selected seeds. The automatic method often gives > 1 seed per ROI, which might account for the slightly better performance. The discussion below associated with Table II discusses the efficacy of automatic seed selection.

• Little bias appears to arise from the data used to train the SVM for Seed Selection. For the 20 ROIs used to train the SVM, the Dice index of segmentation performance was 90.2%±5.9%, as opposed to 90.0%±4.9% for the complete 52-ROI set. We also performed a separate 2D segmentation test for the 32 ROIs not used in training the SVM; we achieved a Dice index = 89.7±4.3 for this test.

• Parameters d and Δ_min in the fast-marching process of Initial ROI Segmentation could be varied significantly with respect to our chosen defaults without greatly degrading performance. Parameter d could safely be varied over the range [66.5, 101.5], while Δ_min gave similar acceptable results for the range [5%, 10%].

• Regarding ROI Finalization, parameter R_min enabled effective operation over the range [3%, 15%]. Q_min required a value in the vicinity of the default 0.95; low values could overly limit region growth, while a high value could result in excessive leakage.

Because leakage can be severe in EBUS segmentation, our strategy for picking parameters tended toward conservative segmentations. In addition, ROI Finalization proved to be an important step to fill in undersegmented ROIs arising after Initial ROI Segmentation. Specifically, we noted that the Dice metric increased from 72.7±9.4 after Initial ROI Segmentation to 86.9±6.4 after ROI Finalization. Finally, as pointed out in Section III-C, we have successfully applied the method in a live guidance scenario in an ongoing prospective patient study.

TABLE II.

2D EBUS segmentation results. “No.” denotes the number of ROIs per case. “Auto” indicates the number of ROIs processed fully automatically. Evaluation metrics are listed as a [min, max] range over all ROIs for each case. The last six rows give aggregate results over various subsets of cases.

Case	No.	Auto	Dice	FDR
A	2	2	[84.5, 92.2]	[4.1, 10.9]
B	2	2	[89.4, 91.5]	[1.4, 1.6]
C	1	1	94.8	1.7
D	2	1	[84.1, 91.4]	[3.6, 13.1]
E	1	0	85.1	11.9
F	3	3	[82.1, 94.4]	[0.6, 0.6]
G	4	4	[78.5, 94.0]	[0.0, 7.6]
H	12	8	[74.6, 95.3]	[0.1, 6.9]
I	6	6	[85.2, 96.8]	[0.6, 1.9]
J	5	4	[82.7, 94.6]	[0.0, 3.3]
K	3	2	[89.7, 93.4]	[3.7, 11.5]
L	8	8	[81.4, 92.4]	[1.1, 8.8]
M	3	0	[91.7, 95.9]	[0.9, 2.2]
overall	52		90.0±4.9 [74.6, 96.8]	3.4±3.5 [0.0, 13.1]
automatic	41		90.0±4.5 [78.5, 96.8]	3.1±3.1 [0.0, 10.9]
semi-automatic	11		90.2±6.3 [74.6, 95.9]	4.7±4.7 [0.1, 13.1]

Table I breaks down the computation time for the method, based on tests done with three representative EBUS frames. We performed 10 runs for each frame to benchmark computation time. All code was implemented in Visual C++ and run on a Dell Precision T5500 workstation (dual 2.8 GHz 6-core Xeon processors, 24 GB RAM, an NVidia Quadro 4000 graphics card with 2 GB of dedicated memory). In Seed Selection, we used OpenMP to process all strip positions N_j in parallel. For ROI Finalization, we broke out separate measures for region growing and image upsampling, which involves restoring the image to its original size and filling region holes. Image Filtering and ROI Finalization consume the large majority of computation time. Per the table, the method operated extremely efficiently.

TABLE I.

Computation time of 2D EBUS segmentation method.

Method Step	Time (msec)
1. Image Filtering	36.73
2. Seed Selection	0.06
3. Initial ROI Segmentation	0.91
4. ROI Finalization
a. Region Growing	4.94
b. Upsample	27.05
TOTAL	69.69

Table II summarizes the 2D EBUS segmentation results for the 52-ROI test set, while Fig. 3 gives a segmentation example. 41/52 ROIs (79%) were segmented effectively using the fully automatic method with a Dice index mean±SD equal to 90.0±4.5.

The remaining 11/52 ROIs (21%) were judged not to provide satisfactory automatic segmentations (Dice index mean±SD = 28.7±28.9, range [0.0, 78.6]). For all of these ROIs, automatic seed selection failed to select correct seeds, necessitating the need for interactive seed selection. In particular, for 4 ROIs, no automatic seeds were selected and, hence, no region was segmented. For 5 ROIs, the automatically selected seeds were both correct and incorrect, which resulted in corrupted segmentations. Finally, for 2 large diffuse ROIs, the automatic seeds were poorly located, resulting in unsatisfactory segmentations. Our empirical observations indicate that the following attributes characterize an ROI that our method fails to segment fully automatically: a) it is relatively far from the transducer; b) its appearance is heterogeneous and/or it contains calcifications; or c) no clear boundary exists between the ROI and an adjacent artifact “region.” After running the semi-automatic method for these 11 problematic ROIs, wherein the user interactively selected a seed at a sensible location. the resulting segmentations had an aggregate Dice index mean±SD equal to 90.2±6.3, a performance essentially identical to that for the 41 automatically segmented ROIs.

B. 3D EBUS Segmentation Tests

For 3D segmentation tests, we selected 14 EBUS sequences from 7 patients. 8 sequences focused on a lymph node, while the remaining sequences focused on a blood vessel (aorta, pulmonary artery, or azygos vein). In keeping with standard EBUS protocol, each sequence began with the desired ROI appearing in the first frame. To benchmark segmentation accuracy, we also constructed ground-truth segmentations for all sequences, wherein an expert EBUS technician used the live wire to interactively segment individual sequence frames.

We again begin with a parameter sensitivity test, as done for the 2D method. See the on-line supplement and [18] for details on these tests. Below are highlights of these tests; note that all parameters arise in the geodesic level-set process.

• Parameter τ could be varied widely over the range [0.0, 0.25], but anomalous results did occur for large values. Hence, the default τ = 0.10 proved satisfactory.

• The range [5, 12] proved to be acceptable for ε (default ε = 8). Low values resulted in excessive leakage, while high values prematurely terminated the segmentation process.

• η enabled robust operation over the range [0.0, 20.0] (default: η = 10.0). Nullifying η, however, removes the advection term in F̂, a condition we do not recommend.

• ℰ_min could be successfully varied over the wide range [0.001, 0.064] (default: ℰ_min = 0.02). Low values could prematurely terminate the segmentation process, while high values enabled excessive leakage.

As we did for 2D EBUS segmentation, we again adopted a conservative strategy in selecting method parameters, favoring under-segmentation to over-segmentation (and potential severe leakage). We also note that the 3D method’s computation time averaged ≈ 0.088 sec/frame, per Tables III–IV.

TABLE III.

Segmentation performance — EBUS sequences segmented fully automatically. “No.” denotes sequence number, “N” denotes the number of sequence frames, and “Time” gives the computation time to segment a sequence in sec. Evaluation metrics are calculated over all sequence frames, with mean±SD giving per-frame values. The last two rows give aggregate results over the 9 sequences.

Case	No.	N	Time	Dice	FDR
F	1	36	3.7	74.6±8.4	1.0±1.7
G	1	50	4.3	83.2±1.3	7.9±5.4
H	1	52	4.4	86.6±2.9	4.1±1.3
I	1	40	3.7	90.0±5.8	7.5±5.3
	3	49	4.3	81.4±7.1	1.5±3.5
	5	75	6.0	89.3±2.1	0.9±1.8
J	1	61	5.7	75.4±7.7	0.9±1.2
K	1	54	3.7	90.9±2.0	3.0±1.4
L	3	85	9.4	83.7±8.8	1.5±2.3
		Mean±SD:		83.9±6.0	3.1±2.8
		Range:		[74.6, 90.9]	[0.9, 7.9]

TABLE IV.

Segmentation performance — sequences not successfully segmented automatically. For each sequence, the first row gives automatic-method results (labeled “auto”). The second row presents results using the semi-automatic key-frame-based method; numbers in the “Key Frame” column denote the frame(s) I_l interactively selected as a key frame(s) for restarting the segmentation method. The last four rows give aggregate results over the 5 sequences.

Case	No.	N	Time	Key Frame	Dice	FDR
F	2	233	26.8	auto	83.5±9.1	11.1±14.5
			54.7	207	89.6±6.0	4.8±8.2
I	2	49	4.9	auto	81.0±6.7	12.1±9.7
			10.9	14	81.7±6.0	9.7±3.3
	4	75	6.0	auto	76.9±6.6	4.0±3.8
			15.5	68	77.3±9.4	3.6±3.2
L	1	53	6.3	auto	80.7±15.9	17.0±24.5
			13.4	35	88.9±5.4	0.8±1.8
	2	38	4.1	auto	62.2±17.7	27.0±19.0
			8.7	9, 26	85.0±4.9	3.1±3.3
			automatic		76.8±7.6 [62.2, 83.5]	14.2±7.6 [4.0, 27.0]
			semi-automatic		84.5±4.6 [77.3, 89.6]	4.4±2.9 [0.8, 9.7]

Tables III and IV next give segmentation results, while Figs. 5 and 6 depict successful segmentation examples. Overall, automatic 3D segmentation was more conservative relative to the ground truth than automatic 2D segmentation (3D segmentation Dice index = 83.9±6.0 versus 2D segmentation Dice index = 90.0±4.5). On the other hand, our conservative parameter choices appropriately resulted in a similarly low FDR (segmentation leakage) for both 3D and 2D segmentation (3D, FDR= 3.1±2.8; 2D, 3.1±3.1). Most importantly, the method successfully extracted the ROI over an entire sequence or a large portion of a sequence for all 14 test sequences.

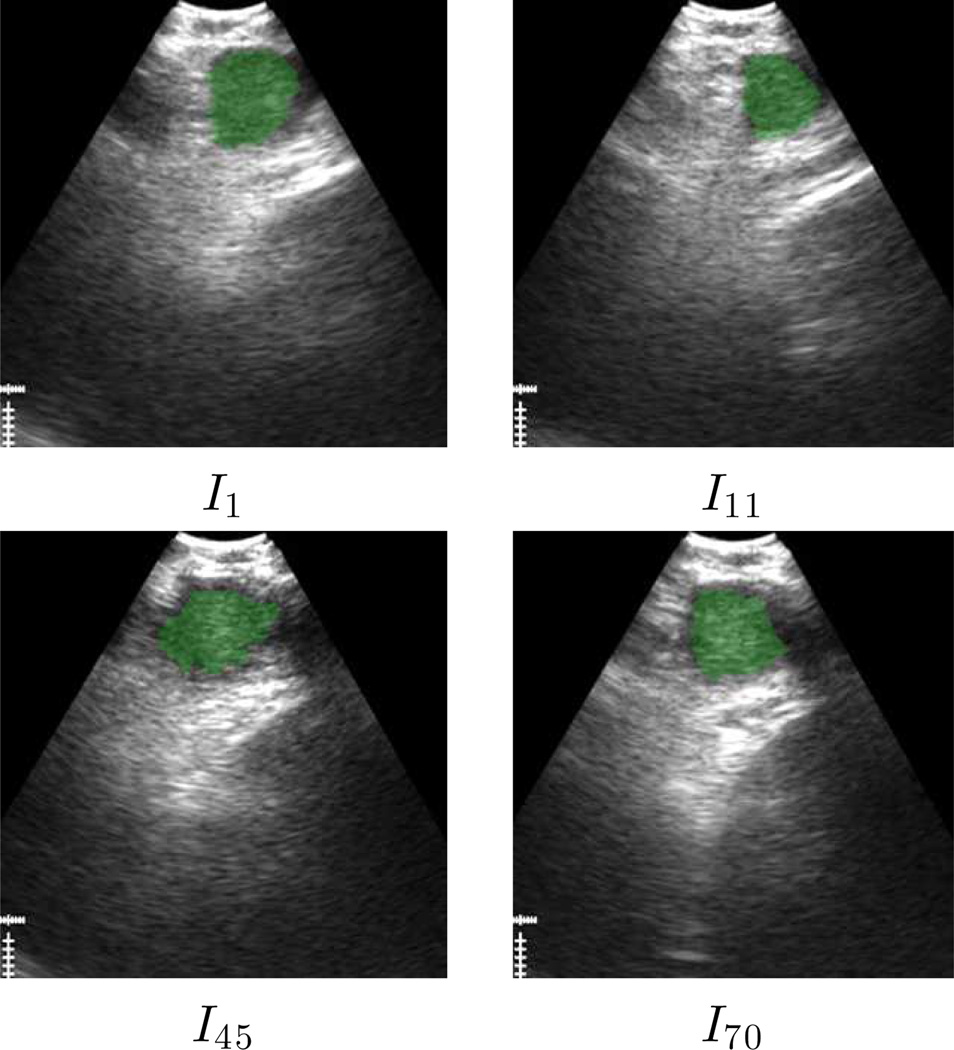
Fig. 6.

3D EBUS segmentation example for a station 7 lymph node (case L, sequence 3). Segmented ROI appears in green.

For 9/14 sequences, the ROI was successfully segmented on every frame (Table III). For the 5 remaining sequences (Table IV), automatic segmentation resulted in 3D segmentations characterized by a seemingly viable Dice index = 76.8±7.6 (range, [62.2, 83.5]). A closer examination of these sequences, however, revealed that the evolving ROI segmentation either started to leak excessively, causing oversegmentation of subsequent frames, or disappeared altogether. Hence, corrective action was required to successfully segment these sequences over their entire extent. (We point out in passing that for 2 of these sequences, segmentation proceeded correctly for approximately the first 90% of sequence frames, while for the remaining 3 sequences, 3D segmentation succeeded fully automatically for many frames at the beginning of a sequence.) We note that these failures arose for the following reasons: a) the EBUS probe appeared not to maintain proper contact for the complete sequence; or b) the ROI exhibits— possibly over several consecutive frames — the characteristics highlighted earlier for automatic 2D-method failures.

For these 5 sequences, we applied the semi-automatic key-frame-based method highlighted in Section II-B, as illustrated by Fig. 7. Per Table IV, this semi-automatic approach resulted in a Dice index = 84.5±4.6, comparable to that achieved for the 9 automatically segmented sequences (M = 3 for the results).

Fig. 7.

Semi-automatic method for correcting errors in fully automatic 3D EBUS segmentation (sequence 4, case I). (a) Since the aorta depicts incomplete boundaries in some frames, automatic segmentation gradually results in leakage (red circle) being introduced and the ROI breaking apart into multiple parts. (b) By interactively selecting frame 68 and restarting the automatic segmentation process three frames earlier, a correct segmentation results.

C. Application to Image-Guided Bronchoscopy

Image-guided bronchoscopy systems have become an integral part of lung-cancer management [36], [37]. Such systems draw upon a patient’s chest computed-tomography (CT) scan to offer enhanced graphics-based navigation guidance during bronchoscopy [37]. Recently, a few clinical studies employed EBUS in concert with an image-guided bronchoscopy system, but these studies used EBUS “decoupled” from the guidance system [38], [39]. Related to this point, no existing guidance system incorporates automated 2D/3D EBUS analysis or provides specialized guidance suitable for EBUS localization.

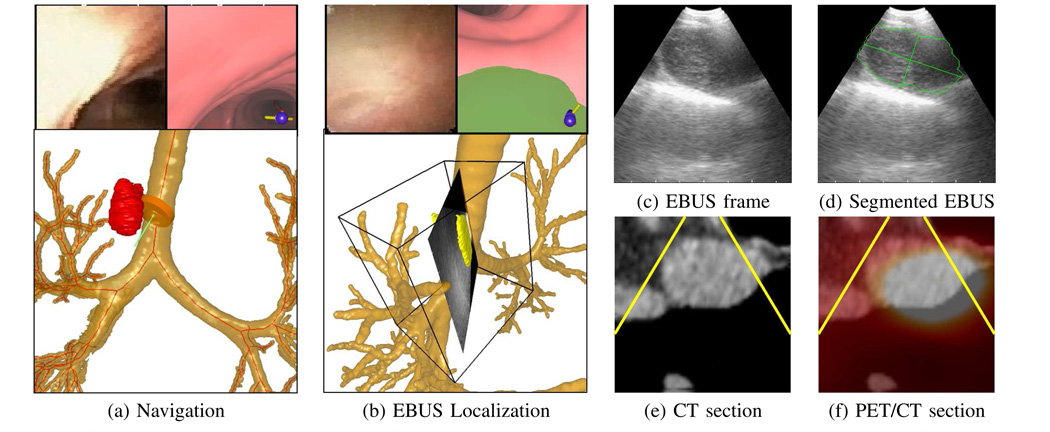
Our group has been striving to fill these gaps by developing a new multimodal image-guided bronchoscopy system [40]. Fig. 8 illustrates some of the system’s capability for the lymph node of Fig. 1c. The physician first identified the node as PET avid, and hence suspicious, on the patient’s co-registered whole-body PET/CT study. Using the whole-body PET/CT study and a complementary high-resolution chest CT study, a procedure plan, consisting of an optimal airway route leading to the suspect node and image-based ROI information, was then computed to help guide subsequent bronchoscopy.

Fig. 8.

Multimodal image-guided bronchoscopy system applied to a station 4R lymph node (case I). (a) System view during navigation. Top left: bronchoscopic video; top right: registered CT-based VB view; bottom: CT-based rendered airway tree, ROI (red), and bronchoscope location (orange can + green needle). All views are synchronized to the same 3D viewpoint. (b) System view during EBUS localization. Top: bronchoscopic video and CT-based VB view (green structure is the extraluminal node); bottom: rendered airway tree and fused 2D EBUS frame at current 3D location, 3D segmented node (yellow), and a parallelepiped delimiting the EBUS sweep region’s subvolume V. Parts (c–f) depict 2D views during localization synchronized to the same 3D viewpoint as the EBUS frame depicted in (b). (c) EBUS frame. (d) EBUS frame with segmented ROI (green) and ROI major and minor axes (major axis = 23 mm, minor axis = 12 mm). (e) CT oblique section clearly showing lymph node; yellow lines delimit the 2D fan-shaped region scanned by EBUS at the same viewpoint. (f) Fused PET/CT oblique section; white area highlights the overlapping ROI region in CT and PET.

During bronchoscopy, the guidance system first facilitated bronchoscopic navigation toward the suspect node, as done with standard guidance systems. As shown in Fig. 8a, a global 3D airway-tree rendering indicates that the bronchoscope had reached a location appropriate for beginning EBUS localization. Next, during localization, the system gave an oblique CT section registered to the EBUS position. As shown in Fig. 8e, the CT section clearly indicates that the current EBUS position will intersect the ROI. This helps assert that the physician should sweep the EBUS about this location to get in vivo confirmation of the node. This sweep resulted in a 40-frame sequence about the node. Figs. 8d–f show a segmentation of the node on one EBUS section and co-registered oblique CT and fused PET/CT sections at this same location, while Fig. 8b shows a 3D EBUS segmentation and reconstruction of the node mapped and fused into 3D CT (World) space. As discussed in [17], [18], the segmented sequence in space V was mapped into World space V′ to facilitate proper 3D reconstruction via a pixel nearest-neighbor (PNN) approach. A tissue biopsy of this site, as illustrated by Fig. 1c, revealed that the node was malignant. References [41], [42] provide further results for this multimodal system in an ongoing patient study.

IV. CONCLUSION

To the best of our knowledge, our methods are the first to be proposed for the computer-based segmentation of 2D EBUS frames and 3D EBUS sequences. The methods proved to be robust to speckle noise and to situations where ROIs are only delineated by partially distinguishable boundaries. They also give the physician an objective reproducible means for understanding 2D and 3D ROI structure, thereby reducing the subjective interpretation of conventional EBUS video streams.

The 2D method offers a new combination of anisotropic diffusion, pyramidal decomposition, ROI seed selection, level-set analysis, and region growing, suitable for EBUS image segmentation. The automatic seed-selection technique is new, while the front-end filtering/decomposition operations are tailored to our EBUS scenario. Our level-set-based approach for initially defining the ROI (Algorithm 1) makes two significant departures from previously proposed fast-marching level-set-based ultrasound-segmentation methods [22], [23]. First, it modifies the conventional fast-marching method to enable cautious expansion of an ROI to avoid segmentation leakage through region-boundary gaps. Second, it considers the entire ROI in a computationally efficient process, as opposed to drawing only on the ROI’s outer contour [22] or using a computationally intense probabilistic approach [23]. In addition, the final region growing operation helps complete the ROI cautiously defined by the fast-marching process. In this way, we judiciously draw upon the respective strengths of the two segmentation approaches. The method’s computation time (0.070 sec/frame) was > 2 orders of magnitude faster than interactive contour definition via the “rapid” live wire (16 sec/frame).

79% of ROIs were segmented fully automatically with a mean Dice metric = 90.0% relative to ground truth. 21% were segmented semi-automatically with mean Dice metric = 90.2%, where the semi-automatic method was essentially identical the the automatic method with the addition of interactive ROI seed selection. These results compared favorably to those found in a ground-truth observer study, which drew upon interactive contour definition (inter-observer variability range = [89.5%, 97.0%]). Also, parameter sensitivity tests given in the on-line supplement asserted method robustness.

The 3D segmentation method builds upon on our 2D method to give an approach that proves to be computationally efficient over an entire sequence. A major innovation of the method is the geodesic level-set process used to compute initial ROI segmentations. The process modifies the method of [24] by using an augmented speed function that better enables the process to evolve an ROI. The process also adapts robustly to the limitations encountered in using EBUS throughout an input sequence. The results were again encouraging, with a slightly more modest correlation to ground-truth segmentations relative to single-frame segmentation (mean Dice metric = 83.9%) and good robustness to parameter variations. The computation time was similar to that observed for the 2D method (0.088 sec/frame). The automatic method successfully segmented a major portion of all test sequences, with a semi-automatic key-framed-based approach improving anomalous cases.

Our results are, of course, biased by the ROIs selected in the patient studies. We, however, did accept cases as they became available per our IRB protocol’s patient-selection criteria. Hence, our results are unbiased from this standpoint. A major motivation of our work is the acknowledged difficulty physicians have in using EBUS and in interpreting EBUS imagery. Related to this need, we have integrated our methods into an image-guided system for live EBUS-based ROI localization during cancer-staging bronchoscopy [41], [42].

Further study could attempt to address the difficulty that arises when the EBUS temporarily loses contact with the airway wall, resulting in image obscuration. As another open area, radial-probe EBUS, which is inserted into the bronchoscope’s working channel, can image ROIs in the lung periphery [5], [38]. But since radial-probe EBUS is decoupled from the bronchoscope, it has also proven to be difficult to use. Computer-based analysis could help improve the utility of these devices.