Lung cancer—a fractal viewpoint

Abstract

Fractals are mathematical constructs that show self-similarity over a range of scales and non-integer (fractal) dimensions. Owing to these properties, fractal geometry can be used to efficiently estimate the geometrical complexity, and the irregularity of shapes and patterns observed in lung tumour growth (over space or time), whereas the use of traditional Euclidean geometry in such calculations is more challenging. The application of fractal analysis in biomedical imaging and time series has shown considerable promise for measuring processes as varied as heart and respiratory rates, neuronal cell characterization, and vascular development. Despite the advantages of fractal mathematics and numerous studies demonstrating its applicability to lung cancer research, many researchers and clinicians remain unaware of its potential. Therefore, this Review aims to introduce the fundamental basis of fractals and to illustrate how analysis of fractal dimension (FD) and associated measurements, such as lacunarity (texture) can be performed. We describe the fractal nature of the lung and explain why this organ is particularly suited to fractal analysis. Studies that have used fractal analyses to quantify changes in nuclear and chromatin FD in primary and metastatic tumour cells, and clinical imaging studies that correlated changes in the FD of tumours on CT and/or PET images with tumour growth and treatment responses are reviewed. Moreover, the potential use of these techniques in the diagnosis and therapeutic management of lung cancer are discussed.

Introduction

Despite advances in diagnosis and therapy, lung cancer remains the number one cause of cancer-related mortality in the USA; in 2015, the estimated number of newly diagnosed lung cancer cases is expected to reach 221,200, with the number of deaths cause by lung cancer predicted to reach 158,040—accounting for 27% of all cancer-related deaths.¹ At diagnosis, the majority (57%) of patients with lung cancer have locally advanced or metastatic disease, and thus a very poor prognosis.¹ Indeed, the estimated overall 5-year survival rate for patients with lung cancer is only 17%.¹ Although the incidence of this disease has decreased slightly in recent years, more than 400,000 patients are currently living with lung cancer in the USA alone, and lung cancer continues to account for more cancer-related deaths than the next three most common cancer types combined (breast, colon, and prostate cancer).^1,2 The development of more-effective diagnosis, treatment, and surveillance tools, therefore, remains a critical and immediate goal for lung cancer research.

The alterations in lung structure that define the appearance of lung cancer in medical images are more readily perceived than measured. For example, lung nodules are most often characterized by size alone, despite the intricately detailed information present in images, especially CT scans. Use of classic, integer dimension (1D, 2D, 3D, and so on) Euclidean geometry, which is routinely used in computer graphics and medical image analysis, can distinguish gross differences in geometry (volume, density, and so on); however, information that is hidden in the complexity of the structure under examination (such as texture and statistical properties of shape) can often be missed. Images of the lung obtained at different magnifications exhibit self-similarity, thus, they are amenable to characterization and measurement using fractal geometry—fractals are mathematical constructs that can have non-integer (fractal) dimensions and efficiently capture structural features that repeat over a range of scales. The purpose of this Review is to introduce fractals and illustrate the potential of fractal analysis for imaging in patients with lung cancer, with regard to analysis of CT scans as well as histological slides. The potential benefits of using fractals to quantify characteristics of lung cancer lesions and measure response to therapy are explained.

Understanding fractals

In biology we are often presented with complex and irregular shapes, such as cell membranes, vascular and neuronal networks, and tumours (Figure 1a,b). The characterization of these structures using simple geometrical quantities, such as length or volume (which, although useful, do not fully characterize the complexity of the shape), can be challenging. Tumour volume is typically used as a measure of tumour burden, and can provide clinically useful information; however, this measure is not ideal, and volume estimates can be unreliable for smaller tumours or those with unfavourable anatomical features, such as high structural complexity and irregular borders.³ Fractal geometry is a mathematical concept that can be used to quantify structures that are poorly represented by conventional Euclidean geometry and might, therefore, be a useful additional parameter in classifying biological structures. Fractals are characterized by three properties: firstly, self-similarity, whereby any small piece of the object is an exact replica of the whole; secondly, scaling—fractals appear the same over multiple scales (for example, at the microscopic and macroscopic levels), a property often referred to as ‘scale invariance’; thirdly, they have a fractional (non-integer) dimension.⁴

Figure 1.

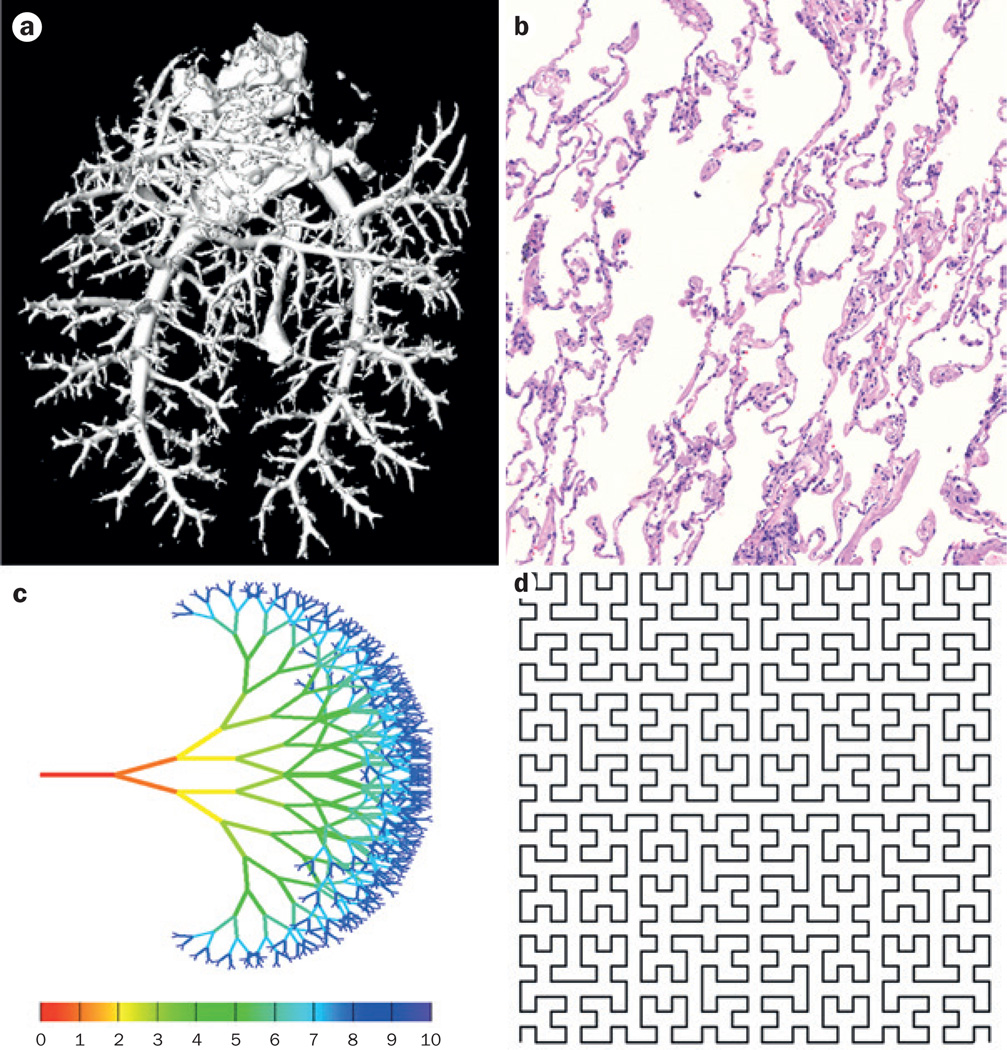
Examples of biological and mathematical fractal patterns. Biological fractals may be statistically self-similar over a limited range of scales, known as a scaling window. a | Rat pulmonary arterial vasculature, imaged via contrast-enhanced CT angiography, which is an example of a biological fractal. b | Normal lung tissue specimen stained with haematoxylin and eosin, which also has fractal properties, and thus is amenable to fractal-dimension analysis. In comparison with biological fractals, mathematical fractals can be infinitely self-similar, examples are fractal trees and the Hilbert curve. c | A fractal tree, showing the first 10 iterations of symmetrical branching. d | The Hilbert curve, a continuous space filling fractal curve with a fractal dimension of 2—a non-fractal curve has a dimension of 1. The first 5 iterations of the Hilbert curve are shown here.

In the strict mathematical context, fractal geometry applies to structures with recursive patterns, such as iterative branching structures or the Hilbert curve (Figure 1c,d).⁵ True fractals are limited to mathematically generated curves, such as the Koch curve or Sierpinski gasket, which are infinitely self-similar.⁶ Natural fractal objects differ from archetypical mathematical fractals in two important ways. Firstly, they exhibit fractal properties, such as self-similarity, only within a limited (finite) range of scales, referred to as the ‘scaling window’. This scaling window is usually between 1–3 orders of magnitude. Secondly, they can be fractal in a quantitative statistical sense, rather than a strict geometrical sense. An object is statistically self-similar if “a statistical property of every small piece of an object is not significantly different from the same statistical property measured on the whole object”.^4,7 This definition of a fractal can be applied to a wide variety of natural and biological objects, as well as related temporal series. For example coastlines, clouds, mountain ranges, stock-market price, and heart-rate fluctuations all exhibit statistical self-similarity.⁴

Fractal dimension

A fundamental feature of fractals is that their measured metrics (such as length, area, and volume) change depending on the scale of the unit used for measurement. Benoit Mandelbrot,⁸ who developed this concept and coined the term ‘fractal’, gave the measurement of Britain’s coastline as a now classic example. Mandelbrot stated that when measuring a complex irregular curved shape, the outcome of the measurement is dependent on the scale of the units used. In other words, if one were to measure the coast in steps of 1 km in length, for example, and then repeat the process with steps that are 1 m in length, one would obtain considerably different coastal lengths. This disparity arises because using smaller units reveals more of the complexity and detail of the object—that is, the line measured follows a more curvilinear course and thus increases the length measured. As such, a fractal structure has no fixed length, but rather its length is dependent on the scale at which it is considered.

Fractal dimension (FD) is a non-integer value that describes the intrinsic shape of an object; it relates to the relationship between the measured metric and the scale used. In Euclidean geometry, a line has a dimension of 1, a plane has a dimension of 2, and a cube a dimension of 3—lines, planes and cubes are examples of 1D, 2D, and 3D objects, respectively. A fractal, however, can have a dimension between those values, such as 1.50 or 2.33—a fractional spatial dimension. FD represents a quantitative characteristic to describe morphological complexity, and provides information on the self-similarity properties of the shape. For temporal series, FD analysis can be used to quantify short-range and long-range complexity within the data set. When plotting the values of any chosen measure over time, a curve is generated. Simple smooth curves, such as a straight line, a sine wave, or an exponential, are by definition 1D. As the time-series fluctuations become increasingly complex, with many more short-range details, the trace of the data will become rougher, filling more, and more of the (2D) page on which it is plotted. Consequently, the FD will increase above one and towards two for a very complex, plane-filling curve. Thus, a small FD can be interpreted as denoting a lack of complexity and the presence of long-range variations only, whereas a large FD indicates an abundance of short-term variation.⁹

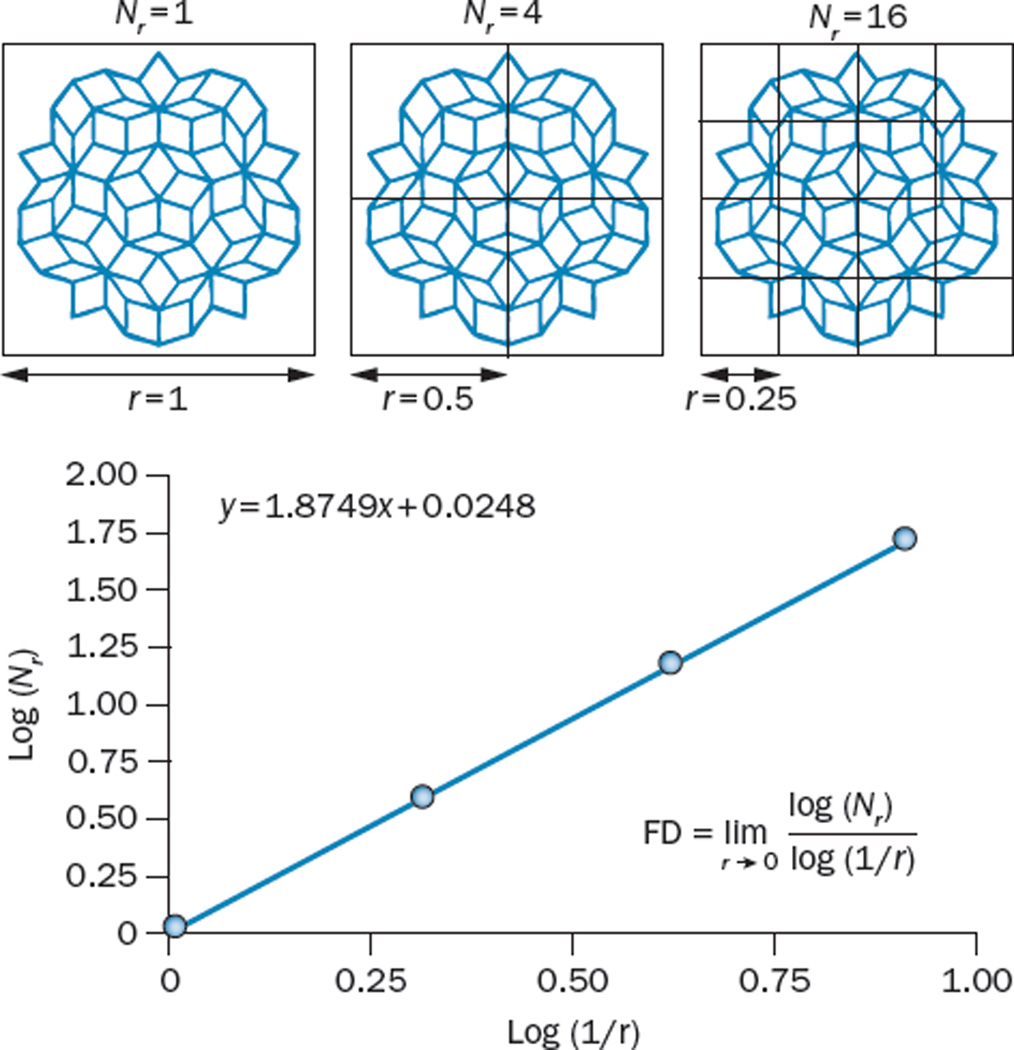
Several methods have been developed to estimate the FD of an object, with the aim of optimizing computation time, or in search of better precision. However, most approaches follow the same basic premise: measure the particular characteristic of an object at different length scales, plot these points (characteristic versus scale), and fit a least-squares regression line. The slope of the resulting line will be an estimate of the FD of the object.¹⁰ Herein, we limit our description to the box-counting method, which calculates the Minkowski–Boulignad dimension.¹¹ This method is one of the most-commonly used and is easily understood. Furthermore, other methods for calculating FD, such as the grid method, are based on the box-counting method. In the box-counting method a set of boxes of a defined size (r), that is, a grid, is placed over the object to be measured, and the number of boxes in that grid (N_r) that are needed to completely cover the shape is counted. This process is then repeated using grids comprising boxes of a different size. The log of N_r is then plotted against the log 1/r, and the slope of the resulting line is the FD (Figure 2). More-complete descriptions of the box-counting and other methods of calculating FD (including the grid, mass-radius, dilation, and power-spectrum methods) have been described elsewhere.^10,12–17 Several software packages are available that offer the ability to calculate FD (Box 1).

Figure 2.

The box-counting method of calculating FD. Box counting is among the most commonly used methods to calculate the FD of shapes, such as the one presented in this figure. Firstly, the number of boxes (N_r), each of different side lengths (r), that are needed to cover the shape is counted. In this example, for a box size of r = 1, one box is sufficient to cover the shape. For r = ½, four boxes are required, and for r = ¼, 16 boxes are needed; 48 boxes would be sufficient if r = ⅛ (not shown). In practice this procedure is repeated for several values of r. Next, log(N_r) is plotted against log(1/r) and fitted to a straight line. The slope of the fit gives an estimated measure of FD. In this instance, this calculation returns an FD of 1.874. Abbreviation: FD, fractal dimension.

Box 1. Fractal image processing software.

Many open-source software packages, which are freely available, enable the computation of fractal geometrical properties from images and the synthesis of fractal patterns. Additionally, modules in some commercially available Picture Archiving and Communication Systems (PACS) and medical image-processing workstations support calculation of fractal properties. Some of the best-known free software modules for fractal image processing include:

• ▪ImageJ⁵²
• ▪FracLac plugin for ImageJ⁵³
• ▪FracLab⁸⁹
• ▪Fractalyse⁹⁰
• ▪Ultra Fractal 5⁹¹
• ▪FDim⁹²
• ▪3DFD⁸⁷

Of note, FD is not a unique descriptor of the complexity of a shape or object. In fact, shapes that look very different can have the same or a similar FD. FD should, therefore, be considered alongside other parameters and not in isolation. Another useful parameter to examine in this context is ‘lacunarity’.

Lacunarity

Lacunarity is a geometric measurement used to describe the ‘texture’ or distribution and size of gaps within an object or image—that is, the way in which the object fills space.¹⁸ This property can also be thought of as a measure of rotational (or translational) invariance, and can be used to describe both fractal and nonfractal images.^13,15 Images or patterns with high heterogeneity are more rotationally variant (they appear different if rotated) and have higher lacunarity in comparison to those with low heterogeneity (Figure 3). Similarly to FD, lacunarity can also be calculated using box-counting methods. However, in this setting, the variation in number of pixels occupied per box at different scales (pixel density) is measured, rather than variation in the number of boxes covering the shape.¹³ A number of other methods for calculating lacunarity exist, which are beyond the scope of this Review, and more in-depth details and discussion on lacunarity can be found elsewhere.^18–20

Figure 3.

Lacunarity. Lacunarity is a measure of the texture or distribution of gaps within an image. It can be helpful to think of lacunarity as an indicator of rotational invariance. The images on the right are 90° rotations of the images on the left. a | This image has a low lacunarity (Λ = 0.343), and is relatively unaffected by rotation—the rotated image appears the same as the original. b | The image in the middle row has a higher lacunarity than the image in the top row (Λ = 0.520), and is more affected by rotation owing to greater heterogeneity in the image. Thus, the rotated image appears slightly different to the original image. c | The image in the lower row has the highest lacunarity (Λ = 0.644)—it is most affected by rotation and has the highest heterogeneity. In this case the rotated image appears very different to the original image.

Fractal nature of the normal lung

The macroscopic lung

One of the most well-known examples of a biological fractal is the lung, which was identified as a fractal by Mandelbrot himself.⁴ The fractal design and structure of the lung play a large part in determining its functional capacity as a gas-exchanger.²¹ Two key elements necessary for optimum lung function are a very large surface area and a very thin tissue barrier—the surface area of the lung is estimated to be similar to that of a tennis court and yet it fits into the limited space of the chest cavity.²¹ Lung morphogenesis is an iterative process that begins with the bifurcation of the developing trachea into the left and right lung buds. Following a sequential branching pattern, the lung buds grow and divide to form a fractal space-filling, tree-like architecture with 23-generations of branching.^21–23 Similarly, the pulmonary vasculature develops alongside the airways (Figure 1a), and the gas-exchange surfaces are formed on the peripheral generations of the branching system. Through this developmental pathway, the packing of a large surface area into a very limited space is achieved, along with the coordinated branching and interface of the airway and vascular systems.^21,24 The lung can be further divided into the conducting airways (bronchi and bronchioles), which comprise the first 10–16 generations of branching, followed by the gas-exchanging portion (bronchioles, alveolar ducts, and alveolar sacs), also referred to as the acinus, which is composed of nine generations of branches. The acinus has a slightly different branching structure to the conducting region of the lung and its architecture is elegantly described by the Hilbert curve fractal (Figure 1d).²⁵

The fractal nature of the lung branching system confers error or fault tolerance to the lung. In his examination of error tolerance in fractal systems, and the lung in particular, Bruce West^26,27 reported that a classic scaling model (dichotomous branching system with one constant scaling fraction) of the lung would propagate an error in an exponential fashion (presumably leading to a serious malformation and dysfunction), whereas the fractal branching model (multiple scales) was essentially unresponsive to error. Thus, the fractal nature of the lung probably ensures that development of this organ is robust and can adapt more easily to genetic alterations or other insults that affect its architecture while preserving its overall morphology and function. Fractal branching is, therefore, a fundamental and crucial feature of lung development.

The fractal branching pattern of the lung also regulates recruitment of the terminal airspaces from a previously unventilated compartment during inhalation. Suki et al.^28,29 reported that airway inflation in the lung proceeds in a manner in which ‘avalanches’ of airway openings are seen; the terminal airway or alveolar spaces open in bursts rather than all at once and opening of one space can initiate the opening of other peripheral spaces.^28,29 These avalanches are regulated in part by discontinuities in airway resistance along the fractal branching tree, which in turn are regulated by airflow resistance and airway elasticity.^28,29 This model also dictates that both the magnitude and timing of pressure changes at the airway entrance (inhalation) are critical in determining the extent of avalanche propagation and, hence, alveolar recruitment/inflation.^28,29 Changes in airway structure or elasticity, as occurs in many lung pathologies, including asthma, emphysema, and lung cancer, disrupt the avalanche process leading to decreased alveolar recruitment and declines in lung function.³⁰ In an autopsy study of airway remodelling in asthma, Boser et al.³¹ reported that airway ‘pruning’ could be detected based on subtle changes in the FD of the lung airways, which was calculated using 2D digital images of negative-pressure silicone-rubber casts. These changes in FD were apparent before any obvious changes in the lung structure that could be visualized on 3D casts.³¹ FD analysis has also been applied to CT images of the lung and can be useful to detect early pathological changes, and this approach is discussed further in the following sections.

The microscopic lung

Fractal patterns are also observed on a cellular and subcellular level in the lungs and other tissues. The alveolar surface, including the cell membranes of individual cells, can be considered fractal; if these structures are examined at increasing magnification, increasing levels of detail and complexity can be observed.³² The same concept can also be applied to the membranes of subcellular organelles, such as those of the mitochondria, nucleus, and endoplasmic reticulum.^33,34

In addition, the organization and packing of chromatin within the cell nucleus (both DNA and associated proteins) has been revealed to be fractal.^35,36 The ‘fractal globule’ model of polymer collapse, whereby polymer condensation results in a dense but completely unknotted globule owing to topological constraints that prevent one region of the chain from passing across another was first proposed by Grosberg et al.³⁷ as a model for chromatin organization in 1988. The chromatin fractal globule model essentially considers chromatin as a polymer. According to this model, the chromatin collapse begins with the formation of increasing numbers of small crumples, leading to the formation of a thicker ‘polymer-of-crumples’, which in turn forms large crumples. Grosberg et al.³⁷ postulated that the resulting ‘globule’, with its hierarchy of crumples, formed a self-similar fractal structure. Evidence reported by Bancaud et al. and Liberman-Aiden et al.^35,36 support the fractal globule model of chromatin packing, and indicates that this model allows for the dynamic folding and unfolding of any genomic location, to enable active gene transcription, for example, while preserving dense chromatin packing elsewhere. Thus, alterations in the FD could be suggestive of modifications in chromatin packing and might be of prognostic or diagnostic importance in multiple cancer pathologies, as is discussed in the ‘Pathology’ section of this Review.³⁸ Of note, bright-light and confocal microscopy images of nuclei can be quickly and easily used to measure the FD of chromatin and/or the nucleus.³⁸

Fractals and lung genetics

We have described how fractal geometry can be applied to the analysis of the complex shapes and anatomy of the lung, from whole-organ to subcellular scales. However, this geometrical framework has also shown potential for the analysis of biological complexities beyond the physical aspects of the lung. For example, the information stored in the genome and the temporal properties of lung function are amenable to analyses based on fractals.

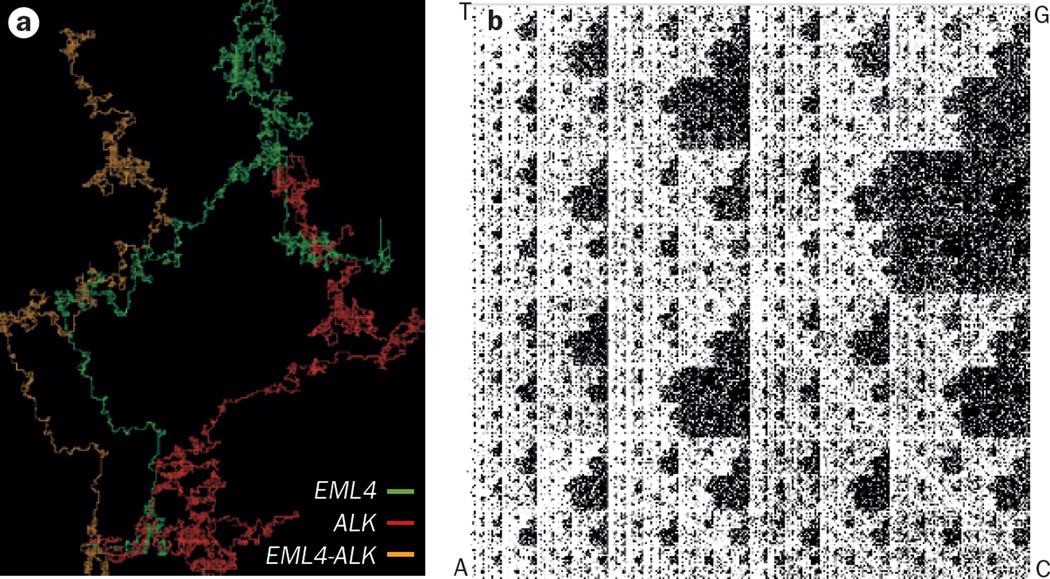
The fractal nature of DNA sequences can be explored in silico using simple ‘DNA walks’ or ‘chaos game’ representations. A DNA walk is a vectorial representation of the DNA sequence.^39,40 Using this technique, the two pairs of complementary DNA nucleotides (A–T and G–C) can be used to transform the DNA sequence into a 2D trajectory; starting at the origin, the walk is moved by one unit/position for each sequential base, up for ‘A’, down for ‘T’, right for G and left for C, to produce a trace. The technique can be applied quickly to any length of DNA sequence, from single genes to entire genomes. A DNA walk can reveal patterns, such as palindromes, repeats, GC skew, translocations and gene duplications, and initially revealed the fractal nature of DNA by uncovering long-range correlations in nucleotide sequences.^40,41 We have provided a comparison of the DNA walk trajectories for the ALK and EML4 genes, and an EML4–ALK fusion-protein gene relevant to lung cancer (Figure 4a).

Figure 4.

Fractal analysis of DNA sequences. Nucleotide sequences of DNA exhibit fractal properties including self-similarity, which can be illustrated in silico using DNA walks or chaos games. In the DNA walk approach, the nucleotide sequence is represented vectorially, with the two pairs of complementary DNA nucleotide pairs (A–T and G–C) translated into a 2D trajectory, starting at the origin and moving progressively in directions dictated by the sequence of nucleotides in the gene—up one unit for ‘A’, down one unit for ‘T’, right for ‘G’, and left for ‘C’. a | Image illustrating the DNA walks of the EML4 (green), ALK (red) genes, and EML4–ALK fusion gene (orange), revealing differences in the fractal properties of each of these DNA sequences. b | Chaos game representation of chromosome 2. In the chaos game representation each corner of a square is assigned a DNA base (either A, C, G, or T). Starting at the centre of the square, we moved half the distance towards the corner corresponding to the first base in the DNA sequence and plotted this point, and then moved half the distance from that point towards the corner corresponding to the second base, again plotting a point at the location arrived at. This process was repeated for each base in the DNA sequence of chromosome 2. The resulting pattern is a fractal. Supplementary Video 2 shows how the fractal pattern of the DNA chaos game repeats as we zoom in on the image, illustrating a defining feature of a fractal: self-similarity over a range of scales.

Fractal DNA sequences can also be displayed by means of a chaos game representation.⁴² In a chaos game, a fractal image is generated using a series of random points within a confined space. The chaos game can be played as follows: label the corners of a triangle with the numbers 1–6, assigning two numbers to each corner; starting at a random point within the triangle, roll a die and move halfway from the starting point towards the corner labelled with the number rolled; repeat this process, rolling the die and moving half way from the current position to the new number, for multiple iterations. After sufficient iterations, the ensemble of points visited during the game forms a fractal image, in this case the Sierpinski gasket (Supplementary Video 1). The chaos game can be thought of as an iterative mapping function—the same operation is repeated using the outcome of one iteration as the input for the next operation. In a DNA chaos game, performed within a square with each of the corners assigned to one of the four DNA bases, the DNA sequence (nonrandom) is used, instead of random numbers, to dictate the movements and construct a fractal pattern. Figure 4b illustrates a chaos game representation for the DNA sequence of chromosome 2 (Supplementary Video 2 highlights the self-similarity of the chromosome 2 chaos game fractal when the image is examined over a range of scales). The first report of a DNA chaos game representation was published in 1990,⁴² although it might only be now, in the era of ‘big data’, that the full potential of iterative mapping, as a computationally efficient, alignment-free sequence comparison and analysis tool, can be exploited. Indeed, iterative mapping functions are now used in many sequence analysis and genomic reconstruction algothrims.⁴³ These programmes can improve the quality of draft genome assemblies while reducing the time and computing memory needed.⁴⁴

Fractal analysis of lung physiology

Along with its structural features, some functional aspects of the lung also exhibit fractal properties. For example, breathing or respiratory rate variability (BRV or RRV), follows a nonrandom fractal pattern that shows long-range correlations over time.^45,46 The FD of BRV increases with age, indicating that the breathing rate becomes more complex. The identification of fractal patterns in breathing rate, together with an increased understanding of how the fractal structure of the lung regulates alveolar inflation, has led to alterations in the use of mechanical ventilation apparatus. Programming a mechanical ventilator with a fractal or biologically variable breathing pattern has been shown to increase arterial oxygenation and enhances respiratory sinus arrhythmia.^46,47 In a study of respiratory variation during mechanical ventilation, Gutierrez et al.⁴⁸ reported that patients who had the lowest RRV during ventilation support had the highest mortality. Similarly, Seely and colleagues⁴⁹ reported that altered BRVs are associated with extubation failure in patients undergoing mechanical ventilation. Not all of these studies used fractal analyses per se; however, their results imply that the fractal properties of breathing/respiration rates are not accidental. Furthermore, a change in the FD of BRV might explain differences in the efficiency of the entire respiratory system, and could potentially be predictive of respiratory complications or failure. However, the clinical relevance of fractal alterations in breathing and respiration rates specific to lung cancer remains to be determined.

Fractal alterations in lung cancer

We have highlighted how fractals can describe multiple aspects of the lung: morphology, physiology, and genetics. In the following sections we review some examples of the application of fractal geometry to characterization of the cancerous lung.

Pathology

As discussed, fractals can be used to describe the complex anatomy and cellular characteristics of the normal lung. The gross morphological changes caused by tumour growth should, therefore, have a substantial impact on the FD of the lung tissue (Figure 5). To date, we have seen only limited reports in the literature examining the relationship between FD of lung tumour histopathology images and tumour type. However, FD has been used to differentiate between adenocarcinoma and squamous-cell carcinoma (SCC) of the lung.⁵⁰ In this study, images of microarrays of formalin-fixed paraffin-embedded (FFPE) tissues stained with fluorescent anti-pan-cytokeratin antibodies were digitally processed to extract the outlines of epithelial structures, and the FD for each image was then calculated using the box-counting method.⁵⁰ Adenocarcinoma specimens (n = 88) were found to have a statistically significantly lower FD than SCC samples (n = 64) (1.702 versus 1.780; P = 1.179 × 10⁻⁸).⁵⁰ Furthermore, the authors found a positive correlation between survival durations and FD. This correlation was not statistically significant; however, the authors noted that not enough time had passed for their sample population to reach the median survival duration.⁵⁰ These results suggest that tissue FD might be a useful biomarker in the histological classification of lung cancer subtypes and that it might even be a possible indicator of prognosis.

Figure 5.

Fractal analysis of lung cancer histology. Representative haematoxylin and eosin stained tissue slides for normal lung and four common lung cancer histologies (adenocarcinoma, large-cell carcinoma, small-cell carcinoma and a lepidic-type adenocarcinoma; n = 1 for each histological subtype) were scanned and the images were then converted to 8-bit greyscale using ImageJ.⁵² The box-counting FD (D_B) and lacunarity (Λ) of specimens of normal lung tissue and four different histological variants of lung tumours were calculated using FracLac.⁵³ See Supplementary Figure 1 of a pictorial representation of the methodological approach. Six regions of each specimen were selected at random and analysed; images a–e are representative of the regions analysed for each subtype. The D_B and Λ for each individual region were as follows: a | normal lung: D_B = 1.7117; Λ = 0.0299. b | Adenocarcinoma: D_B = 1.7435; Λ = 0.0083. c | Lepidic-type adenocarcinoma: D_B = 1.7715; Λ = 0.0042. d | Large-cell carcinoma: D_B = 1.7488; Λ = 0.0051. e | Small-cell lung cancer: D_B= 1.7615; Λ= 0.0045. In each image, the scale bar depicts 500 µm). f | Plot of individual values of FD (D_B) against lacunarity (Λ) for each region sampled (n = 6 for each histological subtype). As FD is not a unique identifier (different shapes can have similar FD), lacunarity can be used to help differentiate these shapes. Abbreviation: FD, fractal dimension.

Another interesting and potentially powerful application of FD analysis in pathology was reported by Vasiljevic et al.⁵¹ In a large-scale study of bone metastasis (comprising 1,050 patients), this group attempted to identify the primary cancer type (lung, renal, or breast) based on a multifractal classification of cells from haematoxylin and eosin (H&E)-stained slides.⁵¹ Multifractal structures represent a further level of complexity compared with (mono)fractals—they are not well described by a single FD but rather by a whole spectrum of FDs. One instance in which multifractality can arise is a scenario in which the FD of an object varies with x–y position (that is, across subregions of the region assessed). For example, one might obtain a different FD when considering the nucleus of a cell, its mitochondria, and its membrane. Using the ImageJ⁵² plugin FracLac,⁵³ Vasiljevic and colleagues calculated a number of multifractal parameters, including the maximal generalized FD and the maximal multifractal spectrum for each intensity-thresholded image, and then rated the fractal parameters for accuracy, sensitivity, specificity, and precision.⁵¹ The accuracy of classification for each parameter in all three groups of primary tumour types was >73%;⁵¹ sensitivity, specificity, and precision were greater than 60%, 76%, and 59%, respectively, for each parameter.⁵¹ These results indicate that a multifractal analysis of metastatic lesions might be useful in determining the site of the primary tumour in patients with cancer of unknown primary (CUP).

Alterations in chromatin or nuclear FD have been detected in cancer cells, compared with normal tissues, and could potentially prove to be useful diagnostic and prognostic indicators. These differences should not come as a surprise, as alterations in higher-order chromatin structure are associated with changes in gene-expression profiles that occur in all cancers and even pre-malignant cells.^54,55 Indeed, the first papers reporting studies that examined changes in chromatin FD in cancer appeared in the early 1990s.⁵⁶ An attractive feature of FD analysis of chromatin is that the approach can be readily applied to tissue or cells stained with common histological stains, such as H&E. No additional tissue processing is needed, which also enables the retrospective analysis of banked slides. A review by Metze,³⁸ who has published numerous papers on chromatin FD analysis, outlines the potential diagnostic applications of this approach in cancer. Although no dedicated studies on chromatin FD alterations in lung cancer have been reported to date, this approach has been applied to numerous other cancer types. For instance, a study by Streba et al.⁵⁷ examined differences in nuclear and vascular FD between primary hepatocellular carcinomas and liver metastases from other tumour types, including adenocarcinoma of the lung. Binary images were generated from haematoxylin-stained tumour slides and these images were analysed using ImageJ and FracLac.⁵⁷ Although this study was limited to one sample for each tumour type, the authors reported statistically significant differences in nuclear and vascular FD between different tumour types, and between the tumour and surrounding normal tissues.⁵⁷ Used in this way, the authors suggest FD analysis could be a useful diagnostic tool to differentiate between primary hepatic tumours and liver metastases, including hepatic metastases derived from adenocarcinoma of the lung. However, much larger studies are needed to confirm the usefulness of FD in pathology.

For the purposes of this Review, we performed a limited analysis of FD and lacunarity on histological samples from different lung tumour types (Figure 5). We selected six areas at random within each FFPE tumour section (one specimen for each tumour type); images were converted to greyscale and the selected regions were analysed using FracLac (see Supplementary Figure 1).⁵³ We found that the FD of all the assessed lung cancer histological subtypes was increased, to various degrees, compared with normal lung tissue, whereas lacunarity is considerably decreased. Of note, the values for the six regions of each cancer subtype showed marked clustering, although whether this similarity in FD and lacunarity would extend to different specimens of the same histological subtype remains unclear. Nevertheless, these findings suggest that this type of image analysis, together with chromatin, cellular, and radiological analyses, could be useful in the clinical diagnosis and classification of patients with lung cancer.

Radiological imaging

Numerous genetic alterations associated with lung cancer have been identified that might contribute to the development of specific types of lung cancer, patterns of metastasis, drug resistance, or disease recurrence.⁵⁸ One characteristic common to all lung cancers is the alteration of the normal lung morphology. These morphological abnormalities can be clearly observed in histological samples and radiographic images (Figures 5 and 6), and implementation of FD analysis to detect clinically relevant changes during lung cancer development and treatment is already beginning to be considered in radiology.^59–62 Noise in an image can reduce its diagnostic utility, by obscuring or masking some tumour characteristics (such as texture and fine structure). This loss of detail might hinder correct identification of tumour subtype or accurate staging. An advantage of FD calculation is that it is relatively immune to the effects of noise in an image. Al-Kadi⁶³ compared the effects of noise in CT images on FD and other commonly used texture measurements, including model-based methods (gaussian Markov random fields), statistical-based methods, (co-occurrence matrices, run-length matrices, autocovariance function) and wavelet-based methods (Gabor filters, wavelet packet transform). He reported that FD and wavelet packet transform calculations were least susceptible to noise and also gave the best characterization of lung tissue.⁶³ For FD, this advantage is due to the fact that the calculation encompasses multiple scales, at which the effects of noise are not similar and, therefore, are minimized.

Figure 6.

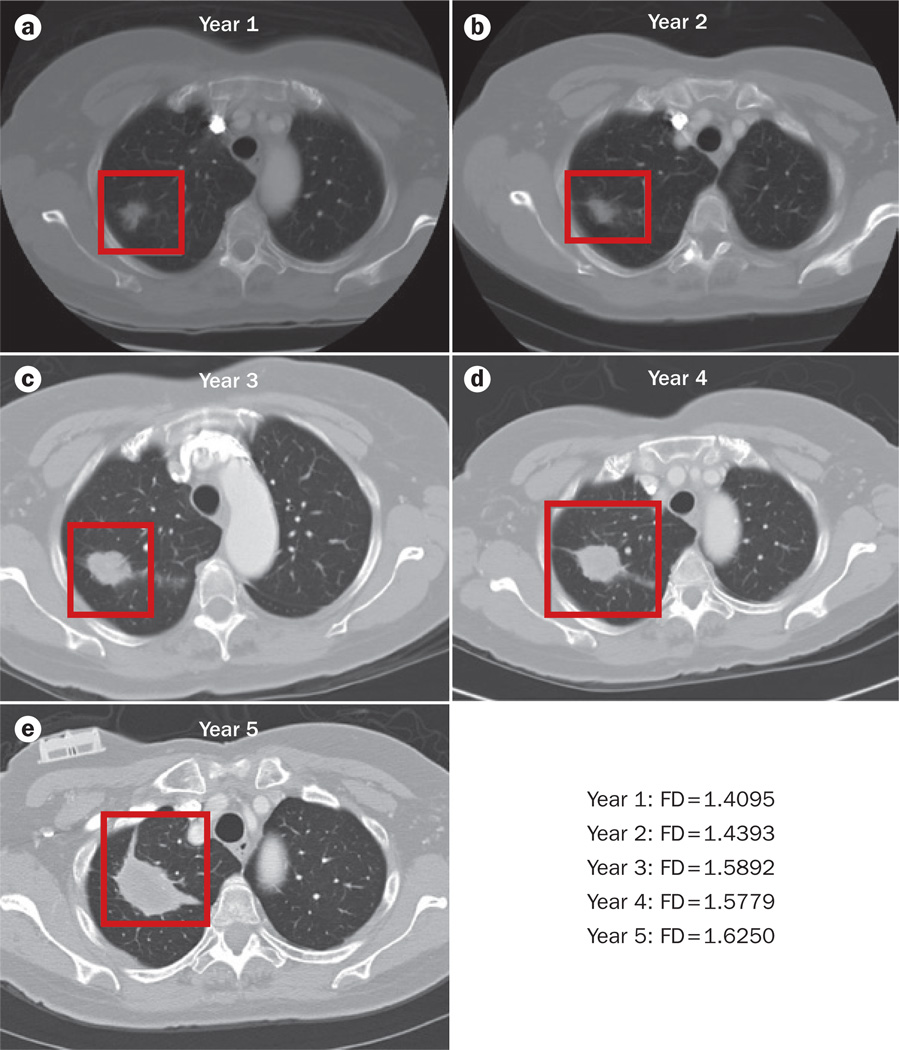
Lung cancer progression and fractal dimension. Sequential CT images of a patient diagnosed with stage I adenocarcinoma of the lung who declined treatment and showed progressive tumour growth over 5 years were subjected to fractal analysis; contrast-enhanced CT scans were obtained at yearly intervals over this 5-year period (parts a–e). These images were loaded in Image J (Version 1.49),⁵² converted to 8-bit, and binarized; the background was set to white. The region of interest containing the tumour was defined manually. The FD of the tumour outline was then determined using the ImageJ plugin FracLac (Version 2015Febb4135).⁵³ Using the batch-processing mode of this software, we applied the box-counting method to the binary images at 12 different grid positions. The box sizes within the grids used ranged from a minimum of 2 × 2 pixels and increased until they reached a maximum size of 45% of the selected image area. The estimated FD was calculated for each grid position from the regression line of a log–log plot of intensity versus box size—the FD given is the average of these estimated FDs. See Supplementary Figure 2 for a pictorial representation of the methodology used. The data derived from these calculations showed that the FD of the tumour–stroma interface increased from a | 1.4095 in year 1 to e | 1.6250 in year 5. This might indicate increased invasion of the tumour into the surrounding stroma. Abbreviation: FD, fractal dimension.

Miwa and colleagues⁶² have shown that FD analysis of ¹⁸F-fluorodeoxyglucose (FDG) uptake imaged by PET can be useful for differential diagnosis of malignant and benign pulmonary nodules. They reported that heterogeneity of FDG uptake in the nodules, reported as density-FD (d-FD; a quantitative measure of intra-lesion heterogeneity of FDG uptake, with higher values indicating greater heterogeneity), was significantly lower in malignant non-small-cell lung cancer (NSCLC) than benign (inflammatory) nodules (P <0.05).⁶² Miwa and co-workers⁶² hypothesized that the higher d-FD of the benign inflammatory nodules reflected the metabolically more-varied components (bronchial tissue, inflammatory cells, vascular cells, and the stroma, for example) of benign nodules compared with the relatively homogeneous malignant tissue. Furthermore, the researchers reported that, although the greater diagnostic accuracy of d-FD compared with maximum standardized uptake value (SUV_max) was not statistically significant, d-FD was not dependent on tumour size (whereas SUV_max was correlated with lesion size).⁶² This finding indicates that d-FD might provide unique information about the tumour, which could potentially be of diagnostic utility.

Dimitrakopoulou-Strauss et al.⁶⁴ argue that FD analysis performed on time–activity curves might be more suitable than spatial-based calculations (such as SUV) for kinetic analysis of FDG-PET data. In a feasibility study by this group, temporal FD analysis was included as a possible predictor of survival of patients with NSCLC (n = 14) following chemotherapy.⁶⁴ In this study, dynamic FDG-PET studies were performed before the initiation of chemotherapy and again after the first cycle, and the FD of tumour FDG time–activity curves was calculated independently for each voxel, thus yielding a FD parametric image.⁶⁴ The pre-chemotherapy and post-chemotherapy FD parametric images were compared and were found to be statistically different (P = 0.05); however, the results did not help to classify the patients with respect to survival durations.^64,65

Kido et al.⁶⁰ applied FD analysis to thin-section CT images of bronchioalveolar carcinoma (BAC) and non-BAC tumours to examine differences in the internal texture of the carcinoma and the peripheral (lung–carcinoma interface) texture. 3D density surfaces were constructed based on CT data for selected regions of interest (internal areas of the tumour and the tumour–stroma interface) and were characterized by FD analysis.⁶⁰ The researchers concluded that FD-based analysis could differentiate between small, localized BACs (n = 30) with good prognosis from non-BAC tumours (n = 40), which have a poorer prognosis.⁶⁰ BACs had higher FD values, indicating greater structural complexity calculated by either the internal or peripheral texture analysis.⁶⁰ Indeed, the authors concluded that the higher FD of BACs was attributable to the high level of aerogenous components, which resulted in a greater variability in the CT data, thus creating more texture in the 3D density surface. Similarly, a study by Al-Kadi and Watson⁶⁶ assessed whether aggressive and nonaggressive lung tumours could be classified using fractal analysis of contrast-enhanced CT-image time series. The study demonstrated that the FD of lung-tumour tissue was higher than that of normal lung tissue, and that tumour FD was strongly correlated with FDG-PET SUVs.⁶⁶ The study also reported that more-aggressive tumours (stages III–IV) had a higher FD compared with nonaggressive tumours (stage I), and the accuracy of distinguishing between advanced-stage and early-stage tumours based on FD analysis was 83.3%.⁶⁶ However, these conclusions were based on evaluation of data from a limited number of patients, and require confirmation in a larger-scale study. The researchers also observed that, independently of tumour stage, higher FD corresponded to lower lacunarity, which the authors hypothesized could reflect the increased homogeneity of these tumours. The implications of lower lacunarity on contrast-enhanced CT images have not been investigated and its relationship to tumour heterogeneity remains to be confirmed. However, this property could be another indicator of tumour vascularization or differentiation. In future studies, correlating radiological imaging data with histopathlogical examination would be useful to address this issue.

To explore the clinical potential of fractal-based analysis for ourselves, we performed an FD analysis of a time series of CT images from a patient diagnosed with stage I adenocarcinoma of the lung who declined treatment using FracLac (Supplementary Figure 2).⁵³ The CT images illustrate the natural progression of the tumour over time (Figure 6). We measured the FD of the tumour–stroma interface and found it increased over time from 1.4095 to 1.625. In addition, we calculated the FD of pretreatment and post-treatment CT images for a patient diagnosed with ALK-positive stage IV adenocarcinoma of the lung who responded to an ALK-targeted therapy (Figure 7); we used a method of FD analysis similar to that reported by Hayano et al.^59,67 to detected differences in the FD of tumours in patients with hepatocellular carcinoma before and after treatment with one cycle of either sunitinib or bevacizumab. The FD of the lung tumour on contrast-enhanced CT images decreased from 1.1237 before treatment to 1.0597 post-treatment—a change of 0.064 following treatment in this patient. By comparison, the FD of the patient’s other unaffected lung showed only a minor change of FD of 0.016 (1.0556 before treatment to 1.0396 post-treatment). These results suggest that further investigation of the use of FD as a predictive indicator of therapeutic response or progression is warranted.

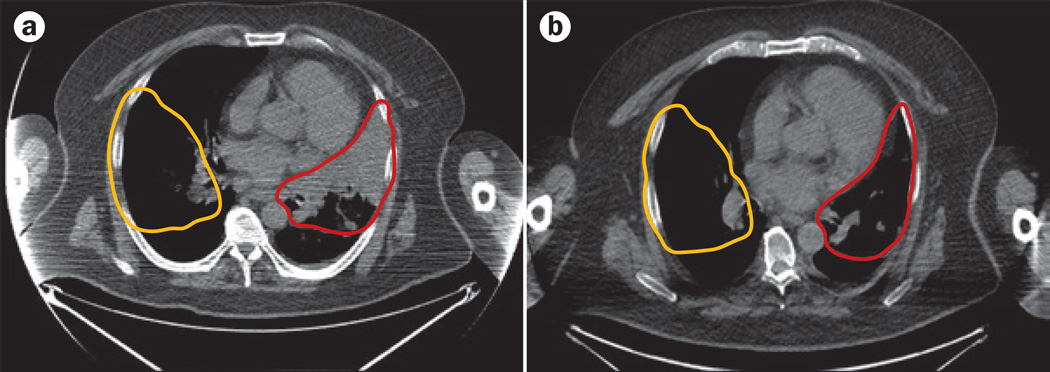
Figure 7.

Treatment response and FD. CT images of a patient diagnosed with ALK-positive stage IV adenocarcinoma of the lung who responded to an ALK-targeted therapy were analysed to assess changes in FD of the lungs. The FDs of the tumour area in the right lung (red outline) and an area corresponding to the unaffected left lung (yellow outline) were calculated using a | pretreatment and b | post-treatment CT images. The ROI containing the tumour (or the unaffected lung) was defined manually. The ImageJ plugin FracLac (Version 2015Febb4135),⁵³ was used to perform box-counting greyscale differential FD analysis on the ROI, using 12 different grid positions with box sizes ranging from a minimum of 2 × 2 pixels and increased until they reached a maximum size of 45% of the ROI. A box-counting greyscale differential analysis returns an intensity FD based on the difference in pixel intensity in each box. The FD is the average of the estimated FD calculated for each grid position from the regression line of a log–log plot of box number versus box size. The FD of the pretreatment tumour area was 1.1237 and decreased by 0.064 to 1.0597 in the post-treatment image. By contrast, the FD of the unaffected lung showed only a relatively minor change in FD from 1.0556 before treatment to 1.0396 post-treatment—a change of 0.016. Abbreviations: FD, fractal dimension; ROI, region of interest.

Future directions

We have outlined a number of examples of instances in which FD has been used to characterize lung cancer. Perhaps one of the most-exciting uses of fractal analysis is its application to clinical radiological imaging. FD might be useful in predicting and assessing therapeutic response, as reported by Hayano et al.^59,67 Importantly, using fractal analysis, this group was able to detect a change in FD before any detectable change in overall tumour size or volume.^59,67 FD alterations soon after initiation of treatment could have critical clinical implications as a potential early indicator of therapeutic response. We believe there is a solid rationale for the addition of FD to the list of parameters (such as tumour volume and SUV_max) routinely considered when examining CT and PET images, because this measure can provide additional useful information that might improve clinical decision-making.

The majority of reports in the literature of the application of fractal analysis to tumour histopathology have focused on detecting changes in the vascularization of tumour samples. Fractal analysis is often used to study neovascularization changes associated with diabetic retinopathy,^68–70 and similar techniques are now being applied to quantify tumour vascularity.^71–76 In their study of retinopathy, Lee et al.⁶⁹ demonstrated that FD is sensitive to new vessel formation, but is relatively insensitive to image preprocessing and vessel thickness per se, thereby making it eminently suitable to measure neovascularization-associated changes in tissues. Several reports have emerged in which vascular FD calculated from histological samples has been used to assign tumour stage in head and neck, and brain cancers.^71–76 These publications suggest that fractal analysis of lung cancer vascular networks could prove useful in detecting early changes due to tumour growth and angiogenesis, and in assessing tumour perfusion.

In cases of limited sample availability, fractal analyses of nuclei or chromatin might have utility, as a small number of cells can be sufficient to determine the phenotype by FD analysis compared with traditional pathology methods. In a study that used May–Grünwald–Giemsa-stained bone-marrow slides to determine the fractal characteristics of multiple myeloma, Ferro et al.⁷⁷ reported that 30–40 cells was sufficient to calculate the mean FD (using the Minkowski-Bouligand box-counting method; Figure 2) of the nuclei in a sample. Thus, this method could aid in the identification of tumour-positive samples in which cell numbers are limited, such as fine-needle aspirates.

In 2014, Al-Kadi⁷⁶ proposed a computer-aided decision-support system for analysis of histopathological images of brain tumours. This analysis method first decomposes the image into wavelet packets, each representing different length-scales. Wavelet decomposition is a mathematical representation akin to the more-common Fourier transform: in the latter, the ‘signal’ is decomposed in terms of sines and cosines of different spatial frequencies (length-scales); in the former, wavelets are used instead. Wavelets are more-generalized oscillatory functions, that can form a complete orthonormal set (packet), and can be used to represent data. Fractal analysis can then be used to choose a set of packets that best denotes the distinguishing features of the image. The result of a Fourier transform of an image is itself an image, but in Fourier space, also known as k-space. In a similar manner, wavelet decomposition of images produces further images, with each wavelet packet producing a different image. These second generation images are then analysed using fractal geometry to determine which packet more completely and accurately describes the original medical image. This approach highlights how the fractal analysis framework can be applied not only to raw or minimally processed images, but also to higher-order datasets derived from them. Furthermore, this method enables the use of colour images in the analysis, removing the need for binary images and preserving more information on tissue texture. This approach could be readily applied to assessments of lung tumour histopathology samples in the future. Indeed, on the basis of these reports relating to multiple cancer types, the application of fractal analysis in lung cancer histopathology has the potential to provide clinically relevant information on multiple aspects of cancer, including vascularization, malignancy, and even patient prognosis.

However, FD analysis is not limited to determination of cell and tumour types; it can be useful in characterizing cellular behaviours in vitro, such as migration, apoptosis, and differentiation. These measurements might be useful for the characterization of lung cancer cell lines. For example, Pasqualato et al.⁷⁸ reported that the FD of the cell membrane profile of colon cancer cells increased as the cells started to migrate in a wound healing assay (at 0–3 h time points) and then decreased again at 24 h when they had closed the wound. Changes in membrane FD might, therefore, be indicative of the migratory potential or activity of cells. Induction of apoptosis can also cause changes in nuclear and cellular FD and lacunarity before detection of other classic markers of apoptosis, such as DNA fragmentation or membrane damage.⁷⁹ Such changes could be used to screen for toxicity or resistance to drug treatments in vitro. FD analysis of F-actin has been used to detect cytoskeletal changes in response to shear and mechanical stress, silencing of the gene encoding Rho-GDP dissociation inhibitor α (Rho-GDIα; a factor involved in the regulation of small GTPase function, particularly in the context of F-actin dynamics), or stimulation of cell differentiation.^80–83 These examples indicate the usefulness of FD analysis in basic research, and similar evaluations could be readily applied to lung cancer cell lines to monitor invasiveness and/or metastatic potential, drug cytotoxicity, and epithelial–mesenchymal transition.

Challenges of fractal analysis

Fractal analysis of clinical and biological images has the potential to become a powerful and useful tool; however, a number of issues remain to be resolved. It should be underscored that many of these limitations are, in general, common to all computer-aided image-analysis techniques. Principal among these issues is a lack of standardization. As discussed, numerous algorithms have been developed for FD calculation, each of which can give slightly discordant results depending on the image analysed. Therefore, it is important that researchers note which method they have used for their calculations. Furthermore, users can often be confronted with a ‘black box’ scenario: they might possess limited knowledge of the inner workings of the algorithms. This lack of technical expertise means that the user might not fully appreciate how sensitive the analysis tools are to the input data. Factors that affect the quality of the input data include region of interest (ROI)-selection accuracy, image resolution, signal-to-noise ratio, and image bit depth. For instance, the resolution of the image is important, as it could limit the fractal scaling window. Image preparation or processing techniques can also introduce some variation into the results. Ideally, tools for fractal analysis should be provided with guidance and tutorials, including examples that highlight these sensitivity issues.

Of note, many of the current FD-analysis tools are limited to assessment of binary images. This means that, in many cases, information contained within the image is lost during the binarization process, and the use of different binarization algorithms could introduce further variation to the results. The development of tools capable of analysing binary, greyscale, or colour images, such as that reported by Al-Kadi,⁷⁶ will increase the applicability and, probably, the sensitivity of fractal analysis.

Some attempts have been made to develop standardized protocols for FD analysis, but a great deal of variation remains in the techniques being used.⁸⁴ The use of reference or calibration images, similar to the Brodatz images used in digital imaging for texture classification,^85,86 would be extremely useful to researchers and developers, and could enable better calibration of and comparison between image-analysis tools and datasets.

For histological analyses, variation in the processing of the samples themselves (fixation methods, sectioning, and staining) can affect the tissue and is another common problem facing image analysis. These sample artefacts could be subtle enough as to be imperceptible by simple microscopic observation, but could, nevertheless, compound more-sensitive fractal analyses. Careful sample handling and preparation is, therefore, needed to ensure the preservation of tissue and cellular morphology, and to minimize sample-handling artefacts.

Current fractal analysis tools are also largely restricted to evaluation of 2D images. Fractal analysis of clinical images in 3D will probably be even more informative and useful than the current 2D-based approaches. Although some tools for the analysis of 3D images have been developed, many are not readily accessible or require some computer-programming knowledge. A web-based tool, 3DFD, has been developed for 3D analysis of brain MRI images (Box 1).⁸⁷ The 3DFD online interface allows users to upload their own images for analysis, and the programme uses a box-counting methodology to calculate the FD. 3DFD is an excellent example of a user-friendly fractal analysis tool. The development of similarly user-friendly, widely available tools for the analysis of lung CT or PET images would surely prove invaluable. Vakoc et al.⁸⁸ have used 3D intravital microscopy in mice and FD analysis to detect differences between the normal and tumour vasculatures in the brain in vivo. Eventually, similar studies in patients with lung cancer could provide information that aids drug development and clinical decision-making.

Conclusions

Lung cancer is a heterogeneous disease entity that can be classified into many histological and molecular subtypes. Clinically, lung cancer can be highly aggressive in terms of primary tumour growth and metastasis to the lymph nodes and other organs. New tools are required to obtain a better understanding of the biology of lung cancer development, progression, and molecular heterogeneity. Fractal-based analyses are versatile and sensitive tools that have many potential applications in lung cancer research. Substantial effort is needed to increase the utility of fractal analysis, but already a number of examples of its use in other cancer types have been presented. Importantly, FD calculations can be applied at multiple levels, ranging from DNA-sequence analysis to assessment of cellular, tissue, and whole-organ images. The development of web-based and ImageJ-based software packages (Box 1), have brought fractal analysis within the reach of scientists and clinicians with an interest in quantitative image analysis. The examples presented herein serve only to highlight the potential of fractal analysis, and certainly do not represent an exhaustive illustration of the possible uses of this approach. Indeed, we hope to promote, and look forward to, the development of many more applications of fractal analysis in investigations of the unique anatomy and biology of the lung, and lung cancer.

Key points.

• ▪Cancer-related structural alterations in lung tissue and individual cells can often be readily observed, but can be difficult to quantify using conventional metrics, such as length or volume
• ▪Fractals are mathematical constructs that appear infinitely self-similar over a range of scales
• ▪Many biological entities, including the lung, can be considered as fractals within a limited scaling range known as a ‘scaling window’
• ▪A fractal dimension (FD) is a non-integer value that relates how the detail and complexity of an object changes with scale
• ▪FD can be used to quantify complex shapes and patterns in a range of clinical and biological images, including those illustrating DNA, cellular architectural, histopathological, and radiological features
• ▪Fractal dimension can detect subtle changes in images and could potentially provide clinically useful information relating to tumour type, stage, and response to therapy