Genetic variation in fitness within a clonal population of a plant RNA virus

Abstract

A long-standing observation in evolutionary virology is that RNA virus populations are highly polymorphic, composed by a mixture of genotypes whose abundances in the population depend on complex interaction between fitness differences, mutational coupling and genetic drift. It was shown long ago, though in cell cultures, that most of these genotypes had lower fitness than the population they belong, an observation that explained why single-virion passages turned on Muller’s ratchet while very large population passages resulted in fitness increases in novel environments. Here we report the results of an experiment specifically designed to evaluate in vivo the fitness differences among the subclonal components of a clonal population of the plant RNA virus tobacco etch potyvirus (TEV). Over 100 individual biological subclones from a TEV clonal population well adapted to the natural tobacco host were obtained by infectivity assays on a local lesion host. The replicative fitness of these subclones was then evaluated during infection of tobacco relative to the fitness of large random samples taken from the starting clonal population. Fitness was evaluated at increasing number of days post-inoculation. We found that at early days, the average fitness of subclones was significantly lower than the fitness of the clonal population, thus confirming previous observations that most subclones contained deleterious mutations. However, as the number of days of viral replication increases, population size expands exponentially, more beneficial and compensatory mutations are produced, and selection becomes more effective in optimizing fitness, the differences between subclones and the population disappeared.

1. Introduction

RNA viruses are obligate intracellular parasites found infecting all life forms, except perhaps the ciliates. The reason for this evolutionary success steams from a combination of the high mutation (Sanjuán et al. 2010) and recombination (Simon-Loriere and Holmes 2011) rates of their error-prone RNA-dependent RNA polymerases (RdRp), very short generation times and potentially huge population sizes (Wasik and Turner 2013). The combination of these three factors results in highly polymorphic and evolvable mutant swarms that respond very efficiently to environmental perturbations. However, an excessive mutational load is a double-edge sword (Elena and Sanjuán 2005; Belshaw et al. 2007). Although it allows for rapid exploration of genotypic spaces in situations of environmental stress, the drawbacks come with the generation of large amounts of deleterious mutations and inviable genotypes that may jeopardize the viability of small populations in which purifying selection may not be efficient (Gabriel, Lynch, and Bürger 1993). Indeed, it has been widely observed with many RNA viruses that when viral populations are submitted to consecutive transmission bottlenecks of size one, without subsequent population expansions, viral fitness declines in a process compatible with the onset of the Muller’s ratchet (e.g. Chao 1990; Duarte et al. 1992; Clarke et al. 1993; Escarmís et al. 1996; Yuste et al. 1999; De la Iglesia and Elena 2007). On the other hand, large population passages in a new environment always result in fitness increases (e.g. Clarke et al. 1993; Novella et al. 1995, 1999). The role of genetic variability and minority variants in the collective behavior of viral populations as a whole has been well established (Duarte et al. 1994; Cuevas, Moya, and Sanjuán 2005; Schulte and Andino 2014; Bordería et al. 2015; Combe et al. 2015) and is in the origin of phenomena such as evolvability (Burch and Chao 2000; Ciota et al. 2007, 2012) or the memory to past environmental constraints (Ruiz-Jarabo et al. 2000) experienced by the viral mutant swarms.

In a hallmark study, Duarte et al. (1994) characterized the distribution of fitness for individual genomes isolated from a clonal population of vesicular stomatitis rhabdovirus (VSV). They found that the majority of genomes produced during replication of this VSV clone contained deleterious mutations, being the average fitness of clones significantly lower than the fitness of the entire population (Elena, Codoñer, and Sanjuán 2003). Later on, using again VSV, Cuevas, Moya, and Sanjuán (2005) found that the main driver of the fitness differences between individual clones was their ability to complete infection cycles rather than viral yield per cell or differences in adsorption and cell-to-cell transmission rates. However, one may argue that these studies suffer the weakness of being done in cell cultures, which represents a highly artificial environment that lacks the inherent complexity (morphological, physiological, and in defense responses) of real multicellular eukaryotic hosts. To explore whether these observations hold in the context of the infection of a real host, we have performed experiments conceptually identical to those reported by Duarte et al. (1994) but using the plant pathosystem formed by Tobacco etch virus (TEV, genus Potyvirus, family Potyviridae) and its natural host, tobacco.

TEV is a prototypical example of a picorna-like virus; it is a very well-characterized plant RNA virus that has become a model system for studying plant RNA virus evolution in recent years (reviewed in Elena et al. 2008, 2011). TEV genome is composed by ca. 9.5 kb single-strand RNA molecule of positive polarity that contains a large open reading frame (ORF), whose product is a polyprotein that self-processes into ten mature peptides, plus a second small ORF in the +2 reading frame that encodes for an additional peptide (Revers and García 2015). TEV infects numerous plant species, though most of its natural hosts are restricted to the family Solanaceae (Shukla, Ward, and Brunt 1994). The usual symptoms in solanaceous plants include stunting and mottling, necrotic etching, and leaf malformation (Shukla, Ward, and Brunt 1994).

In short, we generated a clonal TEV population by inoculating a single tobacco plant with infectious TEV RNA generated by in vitro transcription. Next, 164 individual biological subclones were isolated from this clonal population using a lesion-forming assay in leafs of quinoa, which is equivalent to the well-known plaque-forming assay in monolayers of susceptible cells with solid overlay agar. It is important to mention that some subclones may actually correspond to the same genotype, as the probability of resampling the same genotype depends ultimately on its population frequency. The fitness of biological subclones and of random samples of the clonal population was evaluated in parallel at increasing numbers of days post-inoculation (dpi) in tobacco plants. The fitness of subclones relative to that of the clonal population was compared.

2. Methods

2.1. Preparation of the starting TEV clonal population

The infectious clone pMTEV (Bedoya and Daròs 2010) contains a full-length cDNA of TEV and a 44 nt long poly-T tail followed by a unique BglII restriction site. After linearization with BglII, the plasmid was transcribed with SP6 mMESSAGE mMACHINE kit (Ambion) following the manufacturer’s instructions. RNA integrity and quantity were assessed by gel electrophoresis. The RNA transcript was mixed with a 1:10 volume of inoculation buffer (0.5 M K₂HPO₄, 100 mg/ml Carborundum). Five µL containing 5 µg of 5′ capped infectious RNA were inoculated by rubbing the third true leaf of twenty-five 4-weeks old Nicotiana tabacum (L.) var Xanthi NN plants (Carrasco et al. 2007a). Inoculations were done in a single experimental block and all plants were at similar growth stages. Afterwards, plants were maintained in a Biosafety Level-2 greenhouse at 25°C under a 16-h light and 8-h dark photoperiod. Eight dpi, after symptoms appeared, virus-infected leafs and apexes of twenty-five plants were collected in plastic bags (after removing the inoculated leaf). The whole tissue collected was mixed, frozen in liquid nitrogen, ground with mortar and pestle, and aliquoted (100 mg each). These aliquots of TEV-infected tissue were stored at −80°C.

2.2. Isolation of biological subclones, infection of tobacco plants with individual subclones, and samples from the clonal population

Supplementary Figure S1 shows a schematic representation of the experimental protocol followed to isolate subclonal components and random samples from the clonal population. Isolation of subclonal components of the TEV clonal population was done by the dilution-inoculation assay method on the local-lesion host Chenopodium quinoa Willd (Kleczkowski 1950; De la Iglesia and Elena 2007). First, 100 mg of TEV-infected tobacco tissue were ground with mortar and pestle in 1 ml of K₂HPO₄ buffer. Second, nine fully developed leafs from each one of four different 4-week-old C. quinoa plants were inoculated by rubbing with 10 µl of undiluted, 10- and 100-fold diluted grounded tissue stock; three leafs of each dilution were inoculated to minimize plant effects (Kleczkowski 1950) and 100 mg/ml Carborundum was added to facilitate inoculation. Two additional leafs were mock-inoculated with 0.5 M inoculation buffer. Nine dpi, clearly isolated local lesions were collected individually, immediately frozen with liquid nitrogen, ground in 1.5 ml tubes with pestles and kept in liquid nitrogen until the moment of inoculating tobacco plants. At the time of inoculation, 20 µl of inoculation buffer were added to each tube, mixed thoroughly and inoculated in tobaccos, as explained above. In parallel, a number of aliquots from the stock clonal population were processed in the same way and used to inoculate tobacco plants. The full inoculation experiment was divided into four blocks, each block containing a number of inoculations with subclones and a number of inoculations with samples from the clonal population. All infected tobacco plants showed clear symptoms 4–6 dpi. Viral load of infected plants was evaluated after 5 (fifty-two plants infected with subclones and seventeen infected with the population), 7 (five and three plants), 9 (seven and three plants), and 12 (100 and 25 plants) dpi as described below.

2.3. RNA extraction from infected tobacco plants and quantification of viral load

Total RNA was extracted from 100 mg of fresh tissue of mock-inoculated and virus-infected systemic leaves of tobacco using InviTrap Spin Plant RNA Mini Kit (Stratec Molecular) and the concentration was adjusted to 100 ng/µl. Quantification of viral load was measured by absolute RT-qPCR using standard curves. Standard curves were constructed using ten serial dilutions of the ancestral TEV RNA produced as described earlier and diluted in total plant RNA obtained from healthy tobacco plants, treated like all other plants on the experiment. RT-qPCR reactions were performed in 20 µl volume using One Step SYBR PrimeScript RT-PCR Kit II (Perfect Real Time) (TaKaRa) following the manufacturer’s instructions. The forward (q-TEV-F 5′-TTGGTCTTGATGGCAACGTG-3′) and reverse (q-TEV-R 5′-TGTGCCGTTCAGTGTCTTCCT-3′) primers were chosen to amplify a 71 nt fragment in the 3′ end of TEV genome and would only quantify complete genomes but not partial incomplete amplicons (Lalić et al. 2011). Amplifications were performed in ninety-six-well plates, each plate containing twenty samples from plants infected with subclones, five samples from plants infected with the clonal population and the RNA samples necessary to built the standard curve. Three technical replicates per infected plant were done. Amplifications were done using the StepOne Plus RT-PCR (Applied Biosystems), according to the following thermal profile: RT phase consisted of 5 min at 42°C and 10 s at 95°C; PCR phase consisted of forty cycles of 5 s at 95°C and 34 s at 60°C; final phase consisted of 15 s at 95°C, 1 min at 60°C and 15 s at 95°C. Quantification results were examined using StepOne software version 2.2.2 (Applied Biosystems).

2.4. Fitness

Viral loads at time t dpi, V_t, obtained by RT-qPCR were transformed into Malthusian growth parameters using the expression $m= \frac{1}{t}\text{ln}{V}_t$. Since we are interested in evaluating the performance of subclonal components relative to random samples from the clonal population, the relative fitness of subclone i in the sample taken t dpi was computed as $W_{it}=e^{m_{it}-m_t^{\text{pop}}}$, where $m_t^{\text{pop}}$ is the average Malthusian growth parameter estimated for the population samples taken t dpi.

2.5. Statistical analyses

We believe it is important to highlight at this point that differences among subclones are biologically meaningful, since each subclone potentially corresponds to a different genomic sequence (although the probability of some subclones may share the same genomic sequence would ultimately depend on their abundance in the clonal population), whereas differences among large samples taken from the entire clonal population are mostly statistically meaningful and evaluate our ability to reproducibly estimate fitness for a large population.

Prior to any further statistical analyses, relative fitness data were checked for violations of the assumptions of normality and homoscedasticity of variances. We found that data were not normally distributed (one-sample Kolmogorov-Smirnov test: D = 0.201, P < 0.001) nor variances were homogeneous among groups (Levene test: F_139,496 = 21.520, P < 0.001). Therefore, we opted for a generalized linear model (GLM) approach for data analysis. The model incorporated three random factors: the source of inoculum used to infect the tobacco plant (S; i.e. a subclone or a random sample from the population), the biological replicate (R; i.e. the individual subclone or the sample from the population) which is nested within S, and the dpi at which samples were taken, T, which is treated as a covariable. The model equation reads

$$W_{ijkl}=\mu + S_i+R{\left(S\right)}_{ij}+T_k+{\left(S\times T\right)}_{ij}+{\xi }_{ijkl},$$

where $\mu$ is the grand mean value and ξ_ijkl is the error associated with individual measure l (estimated from the technical replicates of the RT-qPCR reaction). A Normal distribution and an identity link function were assumed (based on the minimal Bayes information criterion). The statistical significance of each factor was evaluated using a likelihood ratio test (LRT) that asymptotically follows a χ² distribution. The magnitude of the different factors included in the model was evaluated using the ${\eta }_P^2$ statistic that represents the proportion of total variability attributable to a given factor. Conventionally, values ${\eta }_P^2$ < 0.05 are considered as small, 0.5 ≤ ${\eta }_P^2$ < 0.15 as medium and ${\eta }_P^2$ ≥ 0.15 as large effects. The partition of total variance among the different factors was done by maximum likelihood.

All statistical tests were performed using IBM SPSS software version 22. Otherwise indicated, all confidence intervals reported represent ±1 SEM.

3. Results

3.1. Statistical modeling of fitness data and analysis of variance

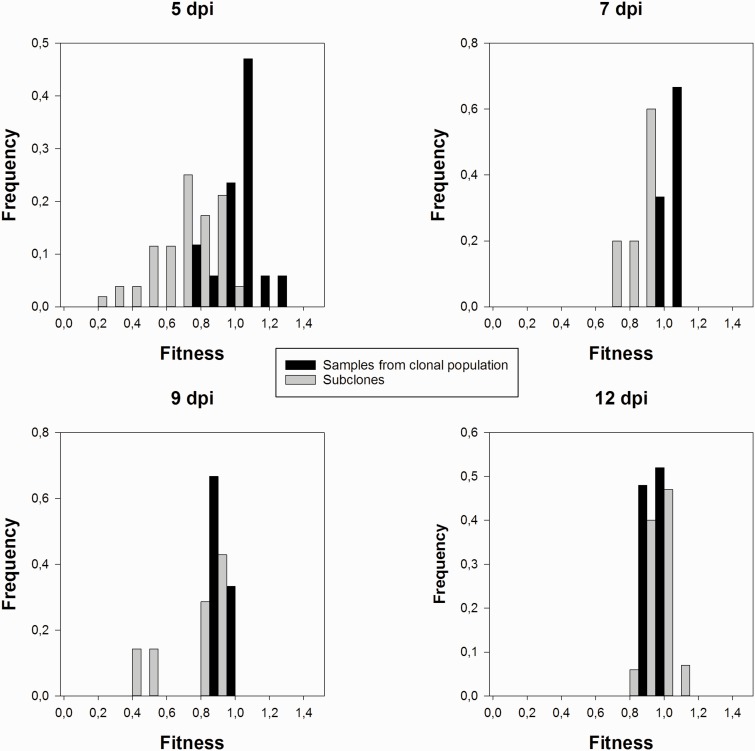
Figure 1 shows the distribution of relative fitness values estimated for individual subclones and for large samples randomly taken from the original clonal population at increasing numbers of dpi. These fitness data were fitted to the statistical linear model described in the ‘Methods’ section by means of GLM techniques. Table 1 summarizes the results of the model fitting and the significance tests for all factors involved in the model. First, these analyses show that overall highly significant differences exist between fitness of the subclonal components and the repeated measures obtained for the entire clonal population (second row in Table 1). Indeed, the grand mean relative fitness for subclones is 0.870 ± 0.003, whereas the grand mean relative fitness estimated for the entire clonal population is 1.001 ± 0.006. This result suggests that the fitness of the whole clonal population can not be predicted simply by averaging the fitness of the individual subclones that compose it. Second, a significant time effect exists (third row in Table 1) and, more interestingly, time affects the magnitude of differences between subclones and the population samples in a different manner (fourth row in Table 1): while the estimates of fitness for the clonal population does not change with time, the fitness of the subclones increases with the number of dpi. This effect will be addressed more specifically in Sections 3.2 and 3.3 below.

Figure 1.

Distribution of relative fitness values at different sampling times post-inoculation (dpi) for individual subclones (gray bars) and random samples from the entire clonal population (black bars).

Table 1.

GLM analysis of the relative fitness data.

Effect	LRT	d.f.	P	${\mathit{\eta }}_{\mathit{P}}^2$	1 − βa
Intercept ($\mu$)	1,218.534	1	<0.001	0.872	0.163
Sample type (S)	386.746	1	<0.001	0.340	1
dpi (T)	275.726	1	<0.001	0.352	1
Slopes (S×T)	285.508	1	<0.001	0.362	1
Replicates (R(S))	626.917	138	<0.001	0.627	1

^aStatistical power of the corresponding test.

Third, significant differences exist among relative fitness of the biological replicates within each group (fifth row in Table 1), that is, between subclones and/or between samples from the entire population. What causes such differences? To address this question, we computed the maximum likelihood estimates for the genetic component of variance for relative fitness among subclones and among the different samples from the clonal population at different dpi. In the case of subclones, the genetic contribution to the observed fitness differences ranged between (3.240 ± 0.051) × 10⁻² at 5 dpi and (3.086 ± 0.031)×10⁻³ at 12 dpi, suggesting that genetic differences among subclones are large shortly after inoculation but are being erased at longer times as the newly generated populations accumulate more and more genetic variants that make them more genetically homogeneous in terms of fitness (ca. one order of magnitude less diverse). In a sharply contrasting pattern, the genetic contribution to the fitness differences observed among independent samples of the entire clonal population rank from 0 at 5 and 7 dpi to (4.090 ± 0.178) × 10⁻⁴ at 12 dpi, suggesting that population samples were really homogeneous right after inoculation, as expected, but start slowly diverging as they accumulate genetic variants in an independent manner during the progress of single infections.

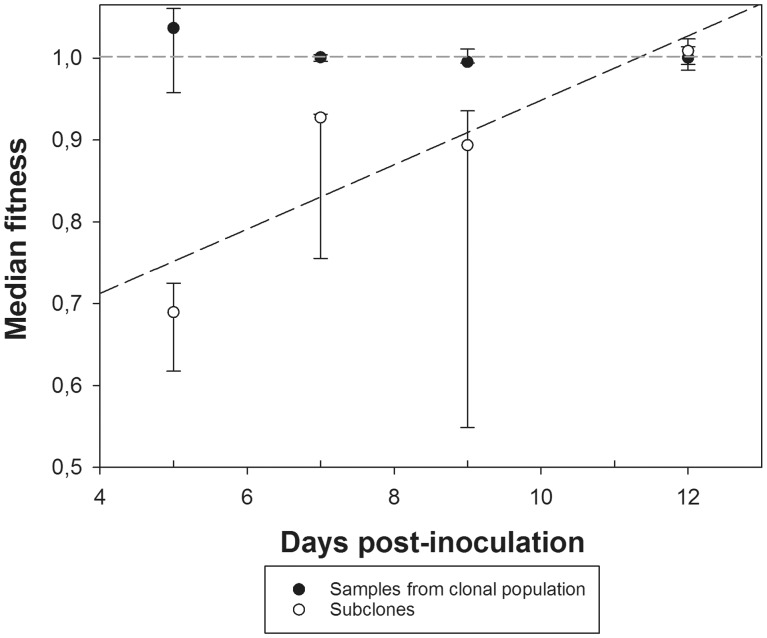
3.2. The average fitness of subclones does not predict the fitness of the whole clonal population at early time points

Figure 2 illustrates the effect of the duration of infection on the differences in relative fitness between the average subclone and the whole clonal population. Let’s pay attention now to the earliest time point evaluated, 5 dpi. The distribution of relative fitness values estimated from the whole clonal population is symmetrical (g₁ = −0.337 ± 0.550; t₁₆ = 0.613, P = 0.548) and mesokurtic (g₂ = 1.360 ± 1.063; t₁₆ = 1.279, P = 0.220), as expected for a Normal distribution. The distribution is centered around a mean relative fitness value of 1.036 ± 0.030. In contrast, the distribution of fitness values among subclones is moderately yet significantly left-skewed (g₁ = −0.778 ± 0.330; t₅₁ = 2.358, P = 0.022), that is, the fitness of most subclones is below the mean value, although the distribution is still mesokurtic (g₂ = 0.252 ± 0.650; t₅₁ = 0.388, P = 0.700), that is, most values lie near the center of the distribution rather than in the tails. The mean relative fitness of a randomly chosen subclone was 0.689 ± 0.025. Therefore, the average fitness of subclones 5 dpi is 33.49% smaller than the expected fitness of the entire clonal population after the same number of dpi, representing a highly significant difference in centrality (Mann-Whitney’ test: U = 38, P < 0.001) and shape (two-samples Kolmogorov-Smirnov test: D = 0.825, P < 0.001) between both distributions. The observed negative difference in mean fitness indicates that mutations making subclones differ from each other were deleterious on average.

Figure 2.

Evolution of median fitness for subclones and large samples taken from the whole clonal population. Error bars represent 95% confidence intervals of the median obtained using the bootstrap resampling method (1,000 pseudosamples).

We have tested whether the differences between subclones and samples from the clonal population remained significant at intermediate time points (7 and 9 dpi) despite the smaller sample sizes, as suggested by the non-overlapping 95% confidence intervals of the median shown in Figure 2. Seven dpi the distribution of fitness among subclones has a mean value of 0.886 ± 0.034, which is significantly smaller than the average fitness estimated for independent samples of the clonal population, 1.000 ± 0.002 (Mann-Whitney’ test: U = 0, one-tailed P = 0.018; Kolmogorov-Smirnov test: D = 1, P = 0.047). After 9 dpi, both samples remain different both in centrality parameters (Mann-Whitney’ test: U = 0, one-tailed P = 0.009), with mean values of 0.794 ± 0.077 and 1.000 ± 0.006 for subclones and samples from the clonal population, respectively, and in shape (Kolmogorov-Smirnov test: D = 1, P = 0.030).

3.3. Differences in fitness between subclones and the population disappear after long periods of replication

As shown in Table 1 and discussed in Section 3.1, the duration of infection had a significant effect on relative fitness that depended in magnitude on whether it was measured for the entire clonal population or for individual subclones. Figure 2 clearly shows that the large and significant differences observed at early times post-inoculation disappears at the latest times of infection (12 dpi). The distribution of relative fitness values for independent samples taken from the whole clonal population remains symmetrical (g₁ = 0.079 ± 0.464; t₂₄ = 0.170, P = 0.866) and mesokurtic (g₂ = −0.862 ± 0.902; t₂₄ = 0.956, P = 0.349), again, as expected for a Normal distribution of values taken from the same population. The distribution is centered around a mean value of 1.000 ± 0.005. Twelve dpi, the distribution of relative fitness values for the subclones was also symmetrical (g₁ = −0.126 ± 0.241; t₉₉ = 0.523, P = 0.602) and mesokurtic (g₂ = −0.260 ± 0.478; t₉₉ = 0.544, P = 0.588), with a mean value of 1.009 ± 0.006. No significant differences exist between these two distributions neither in centrality nor in shape (Mann-Whitney’ test: U = 1,089, P = 0.320; two-samples Kolmogorov-Smirnov test: D = 0.300, P = 0.055). Therefore, we conclude that the initially diverse subclones have compensated their deleterious mutational load and converged towards the average relative fitness of the clonal population from which they were isolated.

4. Discussion

Two decades ago, Duarte et al. (1994) described for the first time great phenotypic heterogeneity among subclonal components of a clonal population of VSV. This variability among individual genomes, that were naïvely expected to be clonal, was an unavoidable consequence of the error-prone replication of RNA viruses, with mutation rates that usually are within the range of 0.1–1 mutations per genome (Sanjuán et al. 2010). Furthermore, since the vast majority of random mutations had a negative effect on viral fitness, the average fitness of the subclonal components was significantly lower than the fitness of the population as a whole. Here, we have extended these observations to a plant RNA virus, the potyvirus TEV, and in a fully realistic biological situation, the infection of plants of the natural host tobacco, in contrast to the highly artificial and over-simplistic cell culture environment used by Duarte et al. (1994). Shortly after infection, our results fully reproduced those from Duarte et al. (1994): we have observed highly significant differences among subclones and the clonal population from which they were isolated, being the subclones less fit than the population. Furthermore, we have also observed a great amount of genetic variance for fitness among subclones, indicative of different mutations being fixed on each subclone. Beyond what was described in the VSV work, here we have found that after long periods of infection, the genetic differences among subclones were erased. Again, the error-prone replication of these clones resulted in mutant swarms upon which positive selection operated to bring the average fitness of these newly created mutant swarms back to the same value of the ancestral population in the natural host.

Some readers might be concerned about the possible effect of isolating subclonal components in a host, C. quinoa, different from the actual host in which fitness effects were evaluated, N. tabacum. We have previously shown that host switching in TEV occurs with concomitant changes in fitness (Agudelo-Romero, De la Iglesia, and Elena 2008; Bedhomme, Lafforgue, and Elena 2012; Hillung et al. 2014). However, this to happen needs of very large effective population sizes so beneficial mutations improving fitness in the new host can be generated, survive drift, and increase frequency in the population until reaching fixation. The severe bottlenecks imposed during the local lesion assays in the quinoa leafs makes adaptation to this host highly unlikely and thus the initial fitness differences observed short times after infection of tobaccos are most likely due to the deleterious nature of standing variation in the clonal population rather than to the emergence of mutations beneficial in quinoa and of negative pleiotropic effects in tobacco.

Transmission bottlenecks are common during the infection of individual plant hosts mediated by insect vectors or by direct contact (Moury, Fabré, and Senoussi 2007; Betancourt et al. 2008; Sacristán et al. 2011), during cell-to-cell spread within the inoculated leaf (Miyashita and Kishino 2010; Tromas et al. 2014), during systemic movement via the phloem and subsequent colonization of distal tissues (Hall et al. 2001a,b; Sacristán et al. 2003; French and Stenger 2005; González-Jara et al. 2009; Ali and Roossinck 2010; Gutiérrez et al. 2010, 2012, 2015; Tromas et al. 2014), and even during vertical seed transmission (Fabré et al. 2014). In all these cases, bottlenecks are strong and the number of transmitted genomes varies within the range of units or tens (Zwart and Elena 2015). These strong bottlenecks minimize the efficiency of purifying selection to remove deleterious alleles, which are constantly produced during error-prone genomic RNA replication, and result in the onset of Muller’s ratchet. Muller’s ratchet has been amply described operating in RNA virus populations under the appropriate demographic conditions (Chao 1990; Duarte et al. 1992; Clarke et al. 1993; Yuste et al. 1999), including plant viruses (De la Iglesia and Elena 2007). The rate at which the ratchet clicks accelerates in a feed-back process known as mutational meltdown (Lynch and Gabriel 1990; Gabriel, Lynch, and Bürger 1993; Lynch et al. 1993): the higher the mutational load, the less viable individuals in the population and, hence, the smaller the effective population size and the stronger the bottleneck. Despite the pervasive presence of bottlenecks during plant infections, plant RNA viruses do not extinguish themselves. Why? Our observation that compensatory evolution takes place as soon as the subclones regenerate a new mutant swarm, and evolve back to the fitness of the original population, are relevant to answer this question. The longer the duration of the infection, the more chances for the mutant swarm to contain the right combination of compensatory mutations or reversion mutants that are quickly and efficiently selected for, resulting in fitness recoveries within the host. Indeed, it was shown for the chikungunya alphavirus that this recovery from the deleterious effect of fixed mutations was strongly dependent on the fidelity of viral replicases RdRps (Coffey et al. 2011): while wildtype viruses created highly evolvable and virulent mutant swarms, viruses having a high-fidelity RdRp were unable of recovering fitness as they produced more homogeneous mutant swarms (Coffey et al. 2011).

Two considerations must be made in the context of the operation of Muller’s ratchet in finite viral populations. First, the distribution of fitness differences among subclonal components represents a biased sample from the real underlying distribution of mutational fitness effects associated to single point mutations for TEV on its natural host (Carrasco, De la Iglesia, and Elena 2007b). Although real distributions incorporate a substantial fraction of lethal mutations for TEV (Carrasco, De la Iglesia, and Elena 2007b) and VSV (Sanjuán, Moya, and Elena 2004a), the sample generated in this study only contains viable genotypes, that is, those able of generating a visible local lesion in quinoa leafs. This problem was also evident in Duarte et al. (1994) study with VSV. The existence of lethal alleles within a mutant swarm further reduces its effective population size, as lethal genotypes cannot contribute to the next generation, thus eventually accelerating Muller’s ratchet. Second, the subclonal components may contain more than one mutation, and likely the newly created mutant swarms will contain genotypes carrying more than one mutation. If mutations interact epistatically, especially if they do so in a synergistic manner, and mutational effects are all identical, the speed of the ratchet will halt (Kondrashov 1994). However, if mutational effects follow some continuous distribution, the ratchet will operate regardless the way mutations interact (Butcher 1995). As already mentioned, mutational effects are variable for TEV and VSV, while epistasis among mutations has been shown to be predominantly of antagonistic type for these two viruses (Sanjuán, Moya, and Elena 2004b; Lalić and Elena 2012), thus keeping the field open for the ratchet to operate.

A final consideration to avoid misconceptions. As we have discussed, Muller’s ratchet is expected to operate only in small viral populations wherein selection is relaxed and drift plays a major role. This has not to be confused with lethal mutagenesis, a completely different phenomenon. Lethal mutagenesis in viral populations is a deterministic process that is independent of population size and only depends on extra-high mutation rate and on the number of replication-competent offspring per parent being small (Bull, Sanjuán, and Wilke 2007). The potential effectiveness of lethal mutagenesis as an antiviral therapy is beyond this study.

Data availability

Data are available through LabArchives doi: 10.6070/H4BV7DN9.

Supplementary data

Supplementary data are available at Virus Evolution online.

Funding

This work was supported by grants BFU2012-30805 from the Spanish Ministry of Economy and Competitiveness (MINECO), PROMETEOII/2014/021 from Generalitat Valenciana and the EvoEvo project (ICT610427) from the European Commission seventh Framework Program to S.F.E. H.C. was supported by predoctoral contract BES2013-065595 from MINECO.