Radiobiology of hypofractionated stereotactic radiotherapy: what are the optimal fractionation schedules?

Abstract

In hypofractionated stereotactic radiotherapy (SRT), high doses per fraction are usually used and the dose delivery pattern is different from that of conventional radiation. The daily dose is usually given intermittently over a longer time compared with conventional radiotherapy. During prolonged radiation delivery, sublethal damage repair takes place, leading to the decreased effect of radiation. In in vivo tumors, however, this decrease in effect may be counterbalanced by rapid reoxygenation. Another issue related to hypofractionated SRT is the mathematical model for dose evaluation and conversion. The linear–quadratic (LQ) model and biologically effective dose (BED) have been suggested to be incorrect when used for hypofractionation. The LQ model overestimates the effect of high fractional doses of radiation. BED is particularly incorrect when used for tumor responses in vivo, since it does not take reoxygenation into account. Correction of the errors, estimated at 5–20%, associated with the use of BED is necessary when it is used for SRT. High fractional doses have been reported to exhibit effects against tumor vasculature and enhance host immunity, leading to increased antitumor effects. This may be an interesting topic that should be further investigated. Radioresistance of hypoxic tumor cells is more problematic in hypofractionated SRT, so trials of hypoxia-targeted agents are encouraged in the future. In this review, the radiobiological characteristics of hypofractionated SRT are summarized, and based on the considerations, we would like to recommend 60 Gy in eight fractions delivered three times a week for lung tumors larger than 2 cm in diameter.

INTRODUCTION

Stereotactic radiation therapy (SRT) is now widely employed as a definitive treatment for various tumors, including those of the brain, lung and liver. While SRT has a definite advantage in dose distribution, it differs from conventional radiotherapy from a radiobiological standpoint. First, SRT is usually delivered with a hypofractionated schedule employing high doses per fraction. The effects of single high doses can be different from conventionally used lower doses in several aspects. Second, each treatment session takes a longer time than in conventional radiotherapy, often with many intermissions between the delivery of beams from different directions. Third, the effects of single high doses may be difficult to predict from the linear–quadratic (LQ) model that is very useful for conventional radiotherapy [1, 2]. These radiobiological issues have been investigated by several groups, and various aspects have been clarified.

In this review, we summarize the results of radiobiological studies of the issues regarding the prolonged beam delivery time, the effect of high doses per fraction, evaluation of different fractionation schedules, and conversion of radiation doses using mathematical models. We also review the clinical data regarding these issues, and based on the biological and clinical implications, we propose fractionation schedules that we believe are optimal for SRT. Parts of the contents of this article have been published previously [3], so we will briefly summarize them, updating where necessary. 

BIOLOGICAL EFFECTS OF INTERMITTENT RADIATION DELIVERY

Sublethal radiation damage repair during intermittent radiation in vitro

Our laboratory studies regarding the biological effects of intermittent irradiation have been published previously [4–7], so they are briefly summarized below. In the first study, the effects of fractionated doses delivered at intervals of a few minutes were evaluated in EMT6 and SCCVII cells [4]. In experiments where 8 Gy was given in 2 fractions, sublethal radiation damage repair (SLDR) was observed when the interval was 2 or 3 min or longer. In the next experiment, where 8 Gy was given in 5 fractions at intervals of 1–5 min, significant SLDR was observed when the interval was 2 min or longer in both cell lines. When the interval was 5 min, 8 Gy in 5 fractions corresponded to 7.38 Gy in a single fraction in EMT6 cells and 7.29 Gy in SCCVII cells. It was thus concluded that dose-modifying factors of 1.08–1.1 need to be considered when the total irradiation time is ∼25 min.

Effects of intermittent irradiation on murine tumors and rapid reoxygenation in vivo

Using subcutaneously transplanted 1-cm-diameter EMT6 and SCCVII tumors, the effects of 20 Gy in 2, 5 or 10 fractions delivered at various intervals were investigated [6]. Tumor cell survival was determined using an in vivo – in vitro assay. Contrary to the in vitro data, no decrease in radiation effects was observed by placing intervals between fractions; instead, by placing intervals of up to 15 min between fractions, the general trend was that the effect became stronger. Similar results were obtained in 10-fraction experiments. It was speculated that SLDR in vivo might be counterbalanced or even outweighed by other phenomena such as reoxygenation.

Therefore, reoxygenation at 0–15 min after single 13-Gy irradiation in SCCVII tumors was investigated using a paired survival curve assay [7]. The hypoxic fraction was 100% at 0 and 2.5 min after the end of the 13-Gy irradiation, but at 5 min it fell to 67% (95% confidence interval, 41–93%). Thus, reoxygenation was observed at 5 min after irradiation. It was suggested that rapid reoxygenation could compensate for SLDR in vivo. However, it was noted in a growth delay assay of SCCVII tumors that, when reoxygenation was restricted, intermittent radiation decreased the radiation effects in vivo due to SLDR.

Other laboratory studies on the biological effects of intermittent irradiation

Several other in vitro studies have indicated the decreased biological effects of intermittent irradiation, as reviewed in our previous publication [3]. Briefly, in an experiment using U-87MG cells, the effect of radiation was decreased with prolongation of the treatment time, and a correction factor of 0.02–0.03 Gy/min was proposed when a total dose of 6–18 Gy was given [8]. This indicates that when the treatment time is prolonged by 30 min, 8 Gy would correspond to 7.1–7.4 Gy delivered continuously, giving dose-modifying factors of 1.08–1.13. In another study investigating the correlation between the magnitude of the loss of effect due to a prolonged treatment time and the α/β ratio in three cell lines, the dose deficit to bring cell survival to the same level was 4.1 Gy in one line, but it was 24.9 and 31.1 Gy in the other two lines, when their results were projected to a 30-fraction treatment [9]. The dose deficit did not relate to the α/β ratio of the three cell lines. In two hepatoma cell lines, however, a significant decrease in cell survival due to prolonged fraction delivery was observed in one line with an α/β ratio of 3.1 Gy, but not in another with an α/β ratio of 7.4 Gy [10]. Therefore, the relationship with the α/β ratio remains unclear and requires further investigation.

Two other in vivo studies have been published since our studies. When C57BL mice bearing Lewis lung cancer were irradiated under conditions of limited reoxygenation, intermittent radiation delivery led to a significant reduction in the biological effects [11]. Another study also showed a similar result [12], but more in vivo investigations appear to be warranted in the near future. Our study suggests that SLDR in vivo can be counterbalanced by reoxygenation. In tumors that reoxygenate rapidly, adverse effects of prolonging the radiation delivery time may be absent or negligible. However, little is known about reoxygenation in human tumors, so this issue is also an important topic to be investigated in the future to elucidate the effect of intermittent or prolonged radiation delivery in clinical practice.

APPLICABILITY OF THE LQ MODEL TO HYPOFRACTIONATED SRT

Current controversy

To compare different fractionation schedules, the LQ formalism (n₂d₂/n₁d₁ = (1 + d₁/[α/β])/(1 + d₂/[α/β]), where d₁ and d₂ are fractional doses and n₁ and n₂ are fraction numbers) and the biologically effective dose (BED) derived from the LQ model (BED = D(1 + d/[α/β]), where D is the total dose and d is the fractional dose) are often used because of their convenience and simplicity [2]. Although it has been suggested that BED is not applicable to higher daily doses or smaller fraction numbers [1, 2], many clinicians have used BED to convert hypofractionated doses to single doses and to evaluate their SRT doses. To further complicate the issue, some investigators claim that the LQ model is applicable to SRT [13, 14]. The support for the latter group is somewhat limited in that the existing clinical data do not significantly deviate from those expected from LQ model calculations, and their data do not necessarily indicate that the LQ model fits best to the high-dose data. Since clinical data usually contain large errors, experimental evaluation of the reliability of the LQ model in single-fraction and hypofractionated radiation schedules would appear to be important.

Cell survival data for the reliability of the LQ model at high doses per fraction

The theoretical basis behind the LQ model not being applicable with high doses per fraction is that dose–survival curves for cultured cells cannot be fitted well by the LQ model in high-dose ranges. The LQ model, with which the cell survival curve continues to bend at high doses, does not seem to fit the actual curves in the high-dose range. Joiner and Bentzen [2] stated that extrapolation by the LQ model beyond 5–6 Gy per fraction is likely to lack clinically useful precision. In a study investigating the compatibility of the LQ model for dose–survival curves of four cell lines, the LQ model did not fit the curves at high dose ranges that were >7.5–13 Gy, depending on the cell line [15].

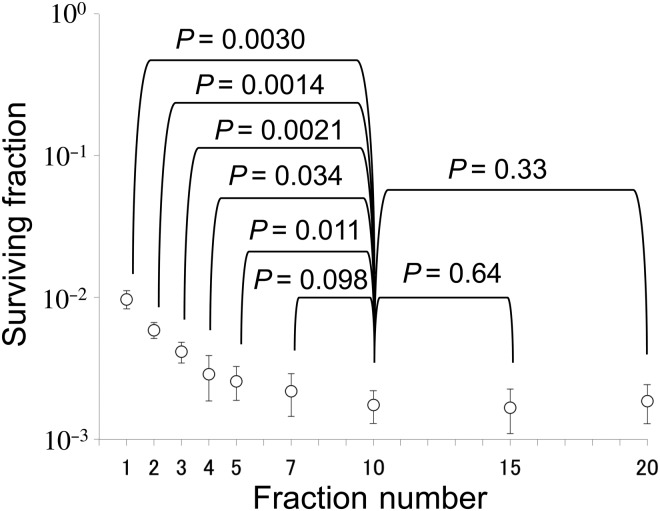
We investigated the applicability of the BED in EMT6 cells [16]. The α/β ratio of the cells determined from single-dose experiments was 3.18 Gy, and the BED3.18 for 20 Gy in 10 fractions was calculated to be 32.6 Gy. Fractional doses yielding the same BED3.18 were calculated for 1-, 2-, 3-, 4-, 5-, 7-, 15- and 20-fraction irradiation using LQ formalism, and then irradiation with these schedules was actually given. The effects of 7-, 15- and 20-fraction irradiation with BED3.18 of 32.6 Gy were similar to those of the 10-fraction irradiation, while the effects of 1- to 5-fraction irradiation were lower (Fig. 1). Thus, the LQ model was considered applicable to 7- to 20-fraction irradiation or doses per fraction of 2.57 Gy or smaller in this cell line.

Fig. 1.

Surviving fractions of EMT6 single cells after single or fractionated irradiation with a BED of 32.6 Gy for an α/β ratio of 3.18 Gy. Bars represent standard deviations. If the BED concept is correct, cell survival should be at the same level, irrespective of the fraction number. Reproduced from reference 16 with permission from the publisher.

Our group also investigated the reliability of LQ formalism in converting hypofractionated doses (in 2–5 fractions) to single doses in cultured cells, spheroids, and murine tumors; the equivalent single doses for the hypofractionated doses calculated by LQ formalism were apparently lower than the equivalent single doses actually measured [17, 18]. LQ formalism underestimated the effect of fractionated irradiation. The magnitudes of errors were 6–19% for 2- or 3-fraction schedules in V79 and EMT6 single cells, 18–30% for 2- to 5-fraction schedules in V79 spheroids, and 21–42% for 2- to 5-fraction schedules in EMT6 tumors. The large discrepancy between single cells and in vivo tumors seemed to be largely due to reoxygenation during interfraction intervals in the hypofractionated groups. These studies indicated that LQ formalism is inadequate for the conversion of hypofractionated doses to single doses.

Total dose versus BED10 for prediction of the antitumor effects of SRT

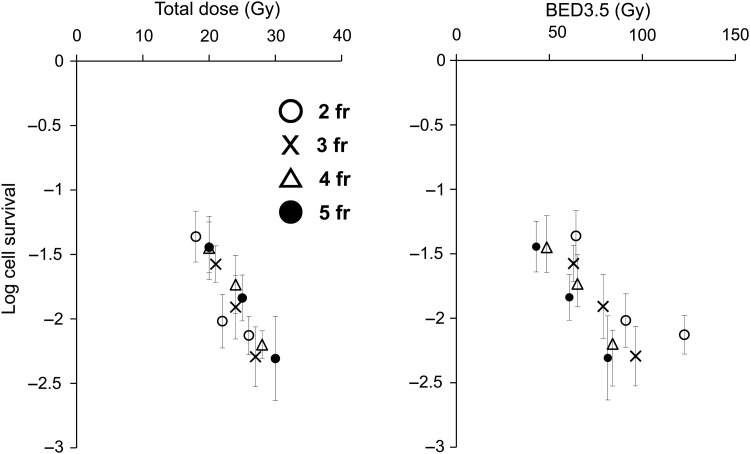
To further evaluate the appropriateness of the BED concept in hypofractionated SRT, we compared 2- to 5-fraction irradiation schedules simultaneously in the EMT6 tumors in Balb/mice [18]. Total doses of 18–30 Gy were given in 2–5 fractions to the tumor-bearing mice at 4-h intervals, and tumor cell survival was assessed with an in vivo – in vitro assay. Cell surviving fractions were plotted against the total dose and BED3.5. In the in vitro cell survival determination conducted along with the in vivo experiment, the α/β ratio of the cell line was 3.5 Gy, so BED3.5 was adopted as a substitute for ‘BED10’, often used clinically to represent the tumor response. As shown in Fig. 2, respective cell surviving fractions appeared to almost lie on a line when cell survival was plotted against the total radiation doses. However, the cell survival curves for respective fractions (actually not shown in the figure) appeared to shift downwards by increasing the fraction number when cell survival was plotted against BED3.5; if the BED concept was correct, the respective cell survival curves would overlap on this figure. Thus, it seems that BED is inadequate for use in SRT, especially for the tumor response. The total dose reflected the actual effect (tumor cell survival) more accurately than BED in this experiment. The calculated BED tended to become larger than expected from the actual effects when the fraction number decreased. Thus, BED tended to overestimate the actual effects with increasing fractional doses.

Fig. 2.

Surviving fractions of EMT6 cells in vivo after 2-fraction (open circle), 3-fraction (cross), 4-fraction (open triangle), or 5-fraction (closed circle) irradiation plotted against the total radiation dose and BED3.5. Bars represent SE. Reproduced from reference 18 with permission from the publisher.

There are similar clinical data showing that the total dose more precisely predicts clinical effects than BED10 in SRT for lung tumors. Aoki et al. [19] conducted a clinical study investigating various fractionation regimens. Table 1 summarizes their results. They investigated 4- to 10-fraction regimens employing 6–12 Gy per fraction. BED10 varied with the regimens, but the total doses were in the range of 50–56 Gy. In the group receiving 54 Gy in 9 fractions, the proportion of tumors >3 cm was significantly higher than in the other groups. The 10-fraction regimen is the most recently studied, so follow-up data appear immature. When 4–8-fraction regimens were compared, the local control rates were similar, despite the difference in BED10. The total dose was in a much narrower range (50–56 Gy), and this result may indicate that the total dose is more important in hypofractionated SRT than BED10. This result agrees with our experimental data, and can be interpreted as showing that reoxygenation plays a very important role.

Table 1.

Local control rates after stereotactic body radiotherapy with various fractionation schedules for localized lung tumors

Dose (Gy)/fraction	Total dose (Gy)	BED10 (Gy)	3-year local control (%)
6 × 9	54	86.4	90
7 × 8	56	95.2	95
8 × 7	56	100.8	95
9 × 6	54	102.6	95
10 × 5	50	100	100

Each group consists of 20 patients. Data from Aoki et al. [19]. Permission was obtained from the authors.

Normal tissue response data for the LQ model reliability at high doses per fraction

The reliability of the LQ model can also be evaluated based on normal tissue data. Classic radiobiology studies regarding this issue were reviewed in detail in our previous publication [3]. Briefly, the isoeffect curves for a number of normal tissues were investigated by Fowler et al. [20]; most of them were linear in the dose range of 1–8 Gy, suggesting that the LQ model is adequate in this range of doses per fraction. However, the curves were not linear above the dose range. In another study [14], the isoeffect curves for the rat spinal cord response, mouse skin reaction, and murine intestinal damage could be visually fitted with straight lines in the range between 0 and 25 Gy, so the LQ model appeared applicable throughout this dose range. However, statistical validation of the linearity was not performed. Later, the data for various normal tissues were analyzed in more detail [21], and the LQ formula appeared to closely fit the curve for the late reaction of the mouse spinal cord for fractions up to ∼10 Gy. However, the data for cervical vascular damage did not fit the LQ model but fitted the linear–quadratic–linear (LQL) model. Fowler et al. [22] suggested that for certain epithelial tissues, the LQ model might be applicable up to 23 Gy per fraction.

These observations are somewhat contradictory, but the discrepancy may be partly explained by the α/β ratio for the normal tissue responses. The applicability of the LQ model may not simply depend on the absolute dose per fraction; for a tissue with a large α/β ratio, its applicability may be extended to a higher dose region. This is the case with epithelial tissues that usually have an α/β ratio of ∼10 Gy. Since the α/β ratio represents the dose at which cell killing from linear (α) and quadratic (β) components of the LQ formula is equal, the LQ model holds around the dose level of the α/β ratio. However, with an increase in the dose, the β-cell killing component dominates in the LQ model, from which actual cell-survival data have been shown to deviate. This deviation appears to become evident in the dose range of over 2-fold the α/β ratio [15]. From these considerations, it is considered that the model is applicable up to a radiation dose ∼2-fold the α/β ratio.

More recently, radiation pneumonitis data were analyzed in patients undergoing lung SRT [23]. Various fractionation schedules were employed ranging from 35 Gy in 4 fractions to 60 Gy in 8 fractions. They tried to correlate the mean lung dose with the occurrence of radiation pneumonitis, and found that the data were best fitted by the LQ model with an α/β ratio of 3 Gy. Although the prescribed dose per fraction was 7.5–12 Gy, the mean lung dose per fraction is usually much lower, so it is not surprising that the LQ model fitted their mean lung dose data.

Other models offering an alternative to the LQ model

Since it is becoming clearer that LQ formalism is not adequate for SRT, other models have been proposed. They were reviewed in our previous publication [3]. Briefly, the models include the universal survival curve model [24], the LQL model [25] (or modified LQ model [26]), and the generalized LQ (gLQ) model [27]. The universal survival curve model combines the LQ model for low doses and the classic multitarget model [28] for high doses beyond a single transition dose (DT), so the concept is relatively simple. The equations for the LQL model are more complex, but cell survival curves extend nearly linearly in the high-dose range, as compared with the LQ model [25]. Therefore, the applicability of the universal survival curve model and the LQL model to the high-dose region may be similar. The gLQ model takes SLDR and the conversion of sublethal damage to lethal damage during irradiation into account; the model is designed to cover any dose delivery pattern. All of these newer models seem to fit better than the LQ model in the high-dose range. We also evaluated how the LQ and other models fitted experimental data. In an in vitro study, the classic multitarget model and the repairable–conditionally repairable model tended to fit better than the LQ model at high doses [29]. In the near future, it will be desirable for an optimal model to be established for clinical use in hypofractionated SRT. However, it should be noted that these models are generally applicable to the normal tissue response, especially late damage, and not to tumors, since none of these models takes the reoxygenation phenomenon, cell cycle effects, host immune effects, or effects on vascular/stromal elements into account. In future studies, models that incorporate these factors, especially reoxygenation should be developed.

Use of the LQ model in hypofractionated SRT

At the present time, there is no adequate dose-conversion model for SRT, and the LQ model calculation is considered to overestimate the effect of high doses. In using the LQ model, we would propose increasing doses of a smaller fraction number calculated from a larger fraction number by 5–20%. For example, when a 3-fraction schedule is converted to a single dose using the LQ model, the single dose that is actually equivalent should be higher than calculated, so the calculated single dose should be increased by ∼15%. This rough estimation is likely to be relatively valid in the absence of reoxygenation (i.e. for normal tissue responses); for tumor responses, the calculated doses should be further increased.

PHENOMENA INFLUENCING EFFECTS OF HIGH DOSES PER FRACTION

Vascular damage at high doses and secondary cell killing

Several investigators reported that high fractional doses of radiation have biological effects greater than predicted by direct tumor cell killing [30]. Park et al. [31] suggested that radiation doses of 10 Gy or higher induce vascular damage, leading to indirect tumor cell death. In an older study, it was shown that clonogenic fractions of Walker 256 rat tumors fell during the first 4 days after irradiation, and this observation was suggested to be due to vascular damage [32]. Although this is an interesting hypothesis, the data to support it are still fragmentary. In contrast, other data showed no evidence of the increased cell killing as a function of time after 10 or 20 Gy irradiation in a rat model of rhabdomyosarcoma [33]. Thus, more experimental evidence is necessary if we are to suggest that this potential mechanism plays a role in the sensitivity of tumors to high-dose-per-fraction radiotherapy.

Enhanced antitumor immunity after tumor irradiation

In metastatic melanoma patients, SRT of a tumor was reported to contribute to the immunologic rejection of a metastatic lesion at a distant site [34]. Since data have only been reported for two patients, it remains unclear whether this phenomenon occurs only at high doses per fraction and whether tumors other than melanoma might show this effect. Other preclinical data also suggest that radiation enhances the antigenicity of tumors [35–37]. It has been reported that this effect is greater for fractionated irradiation than for single doses [38]. In that study, the radiation schedules tested were similar to those employed in SBRT: 20 Gy × 1, 8 Gy × 3, and 6 Gy × 5 fractions in consecutive days. Among the schedules, the fractionated 8 Gy was the most effective, with the 6 Gy intermediate and 20 Gy the least effective. Another preclinical study reported a similar enhancement of antitumor immunity by local tumor irradiation, but in that study, a single 20 Gy dose had a greater effect than 5 Gy × 4 over 2 weeks [39]. More information is needed to determine the best doses per fraction and timing of the radiation regimen to optimize this effect. It is of major importance to discover how general the phenomena of enhanced antitumor immunity by high-dose-per-fraction radiotherapy is across the spectrum of tumors undergoing radiation therapy.

IMPORTANCE OF TUMOR HYPOXIA AND REOXYGENATION

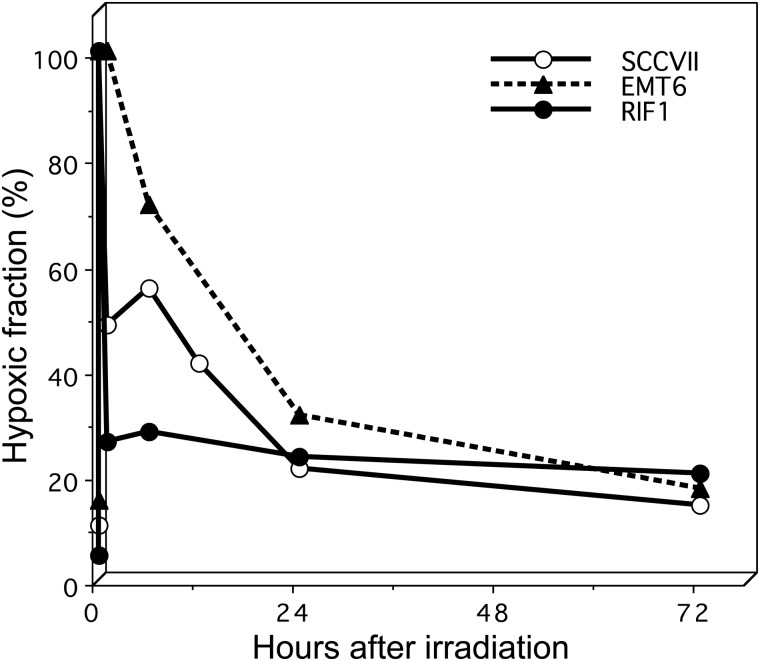
It is now well recognized that most human tumors, except for very small ones, have radioresistant hypoxic cells. The negative influence of hypoxic cells against local tumor control is apparently greater in hypofractionated SRT and the greatest in single-fraction treatment. During fractionation, however, surviving hypoxic tumor cells reoxygenate and become more sensitive to subsequent irradiation. Figure 3 shows the changes in hypoxic fractions after single high-dose (13–15 Gy) irradiation in three 1-cm murine tumors [40]. These data were obtained without using anesthesia or the physical restraint of mice, both of which markedly influence the hypoxic fraction of tumors [41]. In all three tumors, the hypoxic fractions at 24 h after irradiation were significantly lower than those immediately after irradiation, so reoxygenation was clearly seen. In EMT6 tumors, reoxygenation was relatively slow, and it took more than 24 h for the hypoxic fraction to return to the pre-irradiation level. In the other tumors too, the hypoxic fractions tended to decrease further after 24 h. Taking these results into consideration, we think a 24-hour interval between fractions of SRT may not be optimal, and longer intervals may allow more reoxygenation to occur. Therefore, we use interfraction intervals of at least 72 h in 4-fraction SRT for lung cancers [42].

Fig. 3.

Changes in the hypoxic fraction after single high-dose (13 or 15 Gy) irradiation in three murine tumors. Drawn from reference 39 with permission from the authors.

Reoxygenation is a very important phenomenon that should be fully utilized in hypofractionated SRT. Thus, we propose the concept of the ‘reoxygenation utilization rate’ in fractionated radiotherapy (Table 2). In 1-fraction SRT, the very favorable phenomenon of reoxygenation cannot be utilized. In 2-fraction treatment, reoxygenation can be utilized after the first fraction but not for the second fraction. So, the reoxygenation utilization rate is 50%. With an increase in the fraction number, this utilization rate goes up to 75% for 4-fraction treatment, 83% for 6-fraction treatment, and 87.5% for 8-fraction treatment. In 30-fraction treatment, this rate is 97%, so the authors think that 6–8-fraction treatment may be reasonably sufficient to utilize the reoxygenation phenomenon. In future SRT studies, this fact should be taken into account in planning the optimal fractionation schedule.

Table 2.

Reoxygenation utilization rate in fractionated radiotherapy

Fraction number	Utilization rate (%)
1	0
2	50
3	67
4	75
5	80
6	83
8	87.5
10	90
20	95
30	97

Reoxygenation utilization rate (%) = (Fraction number – 1)/(Fraction number) × 100.

In view of the greater negative influence of hypoxic tumor cells in SRT, treatment strategies against hypoxic cells are more important than in conventional radiotherapy. Hypoxic cell radiosensitizers are not very efficient when combined with conventional radiotherapy, but they may have a greater chance of success when combined with SRT. When 2-nitroimidazole sensitizers were combined with intraoperative radiotherapy where a single dose of 20 Gy or higher was employed, a cure was achieved for several patients with unresectable non-metastatic pancreatic cancer [43, 44]. Various nitroazole radiosensitizers are available [45] and attempts at using one of them in combination with SRT is encouraged. Other agents that exert specific effects against hypoxic cells also deserve attention. With the aid of hypoxia-targeting strategies, SRT is expected to further develop as an alternative to surgery for many tumors.

CONCLUSION: PROPOSAL OF ADEQUATE SRT SCHEDULES

Taking all issues stated above into consideration, we propose hypofractionated SRT schedules that we think are optimal for Stage I non–small cell lung cancer. Important points are: (i) to more efficiently utilize the reoxygenation phenomenon, a 6- to 8-fraction is better than a 4-fraction schedule; (ii) reoxygenation may not be complete within 24 h, so interfraction intervals of 48–72 h may be better than 24-h intervals; and (iii) the LQ model overestimates the effects of high doses per fraction, so this should be taken into account when considering optimal doses using the LQ model.

So far, standard SRT doses for lung cancer have been 48 Gy in 4 fractions in Japan. We now use 50 Gy in 4 fractions. Small tumors (<2 cm) may be efficiently treated with this protocol, but for larger tumors, we propose 60 or 64 Gy in 8 fractions delivered every other day. If calculated by LQ formalism with an assumption of an α/β ratio of 10 Gy, 60 Gy in 8 fractions corresponds to 48 Gy in 4 fractions. If an α/β ratio of 3 Gy is assumed, 60 Gy in 8 fractions may have weaker effects (against late-responding normal tissues) than 48 Gy in 4 fractions according to the LQ formalism. However, considering the overestimation of the effects of high fractional doses by the LQ model and reoxygenation between fractions, 60 Gy in 8 fractions may be more effective against tumors than 48 Gy in 4 fractions, while the late normal tissue responses may not be so different. With the refinement of fractionation protocols, we expect that the outcomes for patients treated with SRT will further improve, and SRT will become one of the standard treatments, comparable with surgery for many cancers.

FUNDING

Funding to pay the open access publication charge for this article was provided by the Japanese Ministry of Education, Culture, Sports, Science and Technology.