Abstract
This report is an analysis of the structure of the compound biological effectiveness (CBE) factor. The value of the CBE factor previously reported was revalued for the central nervous system, skin and lung. To describe the structure, the following terms are introduced: the vascular CBE (v-CBE), intraluminal CBE (il-CBE), extraluminal CBE (el-CBE) and non-vascular CBE (nv-CBE) factors and the geometric biological factor (GBF), i.e. the contributions that are derived from the total dose to the vasculature, each dose to vasculature from the intraluminal side and the extraluminal side, the dose to the non-vascular tissue and the factor to calculate el-CBE from il-CBE, respectively. The el-CBE factor element was also introduced to relate il-CBE to el-CBE factors. A CBE factor of 0.36 for disodium mercaptoundecahydrododecaborate (BSH) for the CNS was independent of the 10B level in the blood; however, that for p-Boron-L-phenylalanine (BPA) increased with the 10B level ratio of the normal tissue to the blood (N/B). The CBE factor was expressed as follows: factor = 0.32 + N/B × 1.65. The factor of 0.32 at 0 of N/B was close to the CBE factor for BSH. GBFs had similar values, between BSH and BPA, 1.39 and 1.52, respectively. The structure of the CBE factor for BPA to the lung was also elucidated based on this idea. The factor is described as follows: CBE factor = 0.32 + N/B × 1.80. By this elucidation of the structure of the CBE factor, it is expected that basic and clinical research into boron neutron capture therapy will progress.
Keywords: CBE factor, BPA, BSH, radiation myelopathy, dermal necrosis, radiation pneumonitis
INTRODUCTION
Boron neutron capture therapy (BNCT) is one of high linear-energy-transfer (LET) particle radiotherapies. The 10B nucleus efficiently captures thermal neutrons with energy of <0.5 eV and emits two particles following the reaction: 10B(n,α)7Li. The cross-section of this reaction is ∼2000 times larger than that of the nitrogen–neutron reaction, 14N(n,p)14C, which has the largest cross-section among the elements composing human tissue. Moreover, track ranges of these particles are extremely short, ∼9 μm and 4 μm, respectively, for the α particle and the 7Li nucleus. Because they deposit all their kinetic energy in short ranges, the particles are high-LET radiations. Their track ranges are also shorter than the diameters of general cells. Therefore, if a 10B atom accumulates selectively in a tumor cell, it would be destroyed by the irradiation of neutrons.
BNCT has been tried for treating X-ray refractory cancers for various reasons. Since no effective alternative treatments exist, recurrent cases of glioblastoma have been regarded as good target cancers from the first stage of clinical development [1, 2]. BNCT for malignant melanoma has also been tried, based upon the X-ray–resistant nature of the melanoma cell [3].
BNCT is an attractive treatment; however, it is difficult for general radiation oncologists to understand and the research into BNCT is still limited to small groups. The major reason is the difficulty of dose assessment to the tumors and also to normal tissues. This is because the area in which the α particle and 7Li nucleus deliver their doses is roughly localized to the 10B-accumulated cells. In general, the microdistribution of 10B compounds in a tumor is not uniform because they are distributing through tumor vasculature, and accumulation depends on the biological natures or states of tumor cells [4–6]. This heterogeneous distribution occurs also in normal tissue because the normal tissue consists of various kinds of cells and structures with different characters with respect to the status of proliferation and/or transportation of chemicals [7–11].
In radiotherapy, the maximum dose given to a lesion is generally limited by the late damage to the surrounding normal tissue. In high-LET radiotherapy, the dose concept of Gy-Eq, in which relative biological effectiveness (RBE) is simply multiplied by the absorbed physical dose, is generally used. RBE is determined by comparing the doses of X-rays and high-LET radiation concerned to give an equal biological effect. In BNCT, because of the heterogeneous microdistribution of 10B compound in the tissue, the radiation dose is heterogeneously delivered to the cells as described above. In addition to this, the cell populations involved in the radiation effect, especially in late damage, are indefinite. Therefore, it is impossible to determine the RBE of BNCT as easily and accurately as is usual for high-LET radiation beams for external radiotherapy.
To solve this problem, a very clever and smart concept was proposed by Morris et al. in 1994 [12]—the compound biological effectiveness (CBE) factor. The calculation formula is as follows and looks very similar to that of the usual RBE. Effective dose 50 (ED50) is the dose to induce a prescribed level of radiation injury in 50% of the test animals.
| (1) |
The main difference between the RBE and the CBE factor calculation is in the absorbed radiation dose. In the determination of the RBE, the actual radiation dose to the tissue is applied. However, in the determination of the CBE factor, the radiation dose is calculated by assuming that the 10B compound is distributed uniformly throughout the tissue at a level equal to that in the blood. The CBE factor calculation is based on this assumed dose. This CBE concept is very convenient for the clinical practice of BNCT. The 10B level in the blood and the neutron fluence to the tissue can be easily measured or estimated during neutron irradiation. Thus, the radiation oncologist can calculate the biologically X-ray–equivalent tissue dose by multiplying the CBE factor by the assumed physical dose and taking into consideration the tolerance of normal tissue to BNCT. However, the RBE and the CBE factor can change markedly with compound, tissue or the combination of both [12–17]. For these reasons, the factors are determined by animal experiments for each combination of compound and tissue. This requires a lot of labor, time and research expense. In order to reduce the laborious work of determining CBE factors, and consequently to advance clinical BNCT, the reported data were reanalyzed to reveal the structure of the CBE factor.
MATERIALS AND METHODS
The adjustment of the CBE factor for disodium mercaptoundecahydrododecaborate for the central nervous system by the corrected RBE of the neutron beam itself
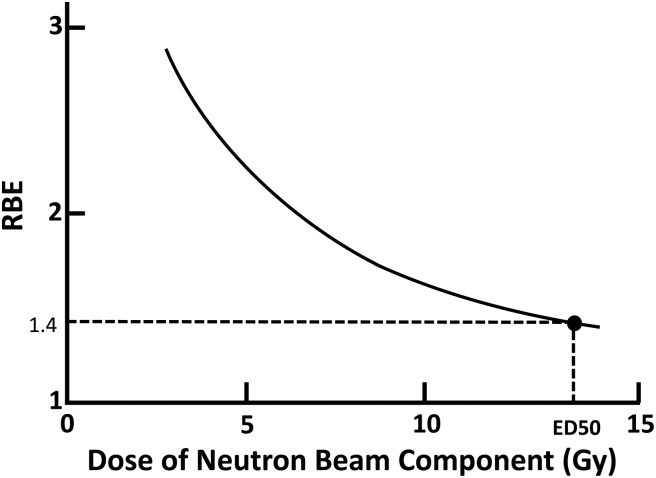
The RBE of the neutron beam itself is determined through the comparison of the ED50s of the X-ray and the neutron beams at an initial step. Thereafter, an experiment using the neutron beam combined with the 10B compound is performed to obtain a dose–effect curve. By analyzing the dose–effect curve, the CBE factor for the 10B compound is calculated. Morris et al. reported CBE factors for disodium mercaptoundecahydrododecaborate (BSH: Na2B12H11SH) and p-Boron-L-phenylalanine (BPA: C9H12BNO4) determined using radiation myelopathy as an endpoint [15, 17]. In 1997, his group reported the important observation that the RBE of the Brookhaven Medical Research Reactor (BMRR) neutron beam varied with neutron dose itself. Therefore, the CBE factors determined using a fixed RBE were not accurate [18]. They reassessed the CBE factors for BPA taking into account the variation in the RBE of the neutron beam according to dose (Table 1). However, the CBE factors were not reassessed for BSH (Table 2). In this study, the RBE was reassessed using the RBE versus neutron dose relation curve that was applied to adjust the CBE factors for BPA (Fig. 1). Subsequently, the CBE factors for BSH previously reported in 1996 by Morris et al. were adjusted.
Table 1.
ED50, Neutron component, 10B(n,α)7Li component, RBE and CBE factors for radiation myelopathy following X-ray or neutron irradiation with or without BPA
| Beam+BPA 10B Level (ppm) |
ED50 Total Dose (Gy) |
Neutron Beam Component (Gy) |
10B(n, α)7Li component (Gy) |
Original RBE or original CBE factor of 10B(n, α)7Li component computed using original RBE | Adjusted RBE of Neutron Beam | Adjusted CBE of 10B(n, α)7Li component |
aN/B of 10B level |
|---|---|---|---|---|---|---|---|
| 93 | 25.0 ± 0.6 | 3.4 ± 0.7 | 21.6 ± 0.5 | 0.66 ± 0.07 | 2.57 | 0.48 | 0.1 |
| 42 | 17.5 ± 0.7 | 4.6 ± 0.9 | 12.9 ± 0.6 | 0.97 ± 0.11 | 2.25 | 0.67 | 0.2 |
| 19 | 13.8 ± 0.6 | 7.0 ± 0.5 | 6.8 ± 0.2 | 1.34 ± 0.13 | 1.86 | 0.88 | 0.33 |
| 12 | 13.8 ± 0.5 | 8.9 ± 0.4 | 4.9 ± 0.7 | 1.33 ± 0.16 | 1.67 | 0.85 | 0.33 |
| 0 | 13.6 ± 0.4 | 13.6 ± 0.4 | 0 |
19.0 ± 0.2/13.6 ± 0.4
= 1.40 ± 0.04 |
19.0 ± 0.2/13.6 ± 0.4
= 1.40 ± 0.04 |
||
| X-rays | 19.0 ± 0.2 | 0 | 0 |
Table 2.
ED50, Neutron component, 10B(n,α)7Li component, RBE and CBE factors for myelopathy following X-ray and neutron irradiation with or without BSH
| BSH dose (mg/kg) |
ED50 Total Dose (Gy) |
Neutron Beam Component (Gy) |
10B(n, α)7Li component (Gy) |
Original RBE or original CBE factor of 10B(n, α)7Li component computed using original RBE |
aAdjusted RBE of Neutron Beam |
aAdjusted CBE of 10B(n, α)7Li component computed using adjusted RBE |
|---|---|---|---|---|---|---|
| 190 | 32.4 ± 1.9 | 3.6 ± 0.2 | 28.8 ± 1.92 | 0.49 ± 0.03 | 2.50 | 0.35 |
| 140 | 28.4 ± 0.6 | 4.1 ± 0.1 | 24.3 ± 0.6 | 0.55 ± 0.02 | 2.36 | 0.38 |
| 80 | 27.2 ± 0.9 | 5.2 ± 0.2 | 22.0 ± 0.9 | 0.53 ± 0.03 | 2.13 | 0.36 |
| 40 | 24.9 ± 1.2 | 7.3 ± 0.2 | 17.6 ± 1.2 | 0.50 ± 0.04 | 1.80 | 0.33 |
| 20 | 20.7 ± 1.9 | 9.2 ± 0.2 | 11.5 ± 1.9 | 0.53 ± 0.10 | 1.62 | 0.36 |
| 0 | 13.6 ± 0.4 | 13.6 ± 0.4 | 0 |
19.0 ± 0.2/13.6 ± 0.4
= 1.40 ± 0.04 |
19.0 ± 0.2/13.6 ± 0.4
= 1.40 ± 0.04 |
|
| X-rays | 19.0 ± 0.2 | 0 | 0 |
Original average Adjusted average
CBE= 0.52 ± 0.02 CBE= 0.36 ± 0.02.
aBy using the data in Table 1, the author has constructed the dose vs RBE relation curve for the neutron beam (Fig. 1), and adjusted the RBE according to the dose. Then, CBE factors were also adjusted using the adjusted RBE. The values written in italics are the data reported in the original tables in reference [17].
Fig. 1.
Dose vs RBE of BMRR neutron beam. The author constructed the curve using the data in Table 1. The original data have been reported in the literature [18].
Analysis of the relationship between the CBE factor for BPA to the central nervous system and N (normal tissue)/B (blood) of the 10B level
Morris et al. noted that the CBE factor, using radiation myelitis as an endpoint, varied with the BPA dose administered. Furthermore, it was also recognized that the BPA dose influenced the N/B of the 10B level [18]. Their data reported are in Table 1. However, Morris et al. did not analyze the data further. In the present study, their data on the CBE factor for BPA have been reanalyzed, especially with respect to the quantitative relation between the CBE factor and the N/B for the 10B level.
Analysis of the structure of the CBE factor for BSH and BPA to the central nervous system
A healthy blood–brain barrier inhibits penetration of BSH into the central nervous system (CNS) [7, 8]. Consequently, the CBE factor for BSH to the spinal cord is considered to be derived from the radiation dose irradiated to the vasculature from the intraluminal side. BPA, however, can penetrate the blood–brain barrier and enter the CNS, and the vasculature receives radiation from both sides; the non-vascular tissue also receives radiation. Taking into account these differences in radiation dose deposition, the CBE factors for BSH and BPA were compared and the structure of the CBE factor was elucidated quantitatively.
The structure of the CBE factor and its components were applied to the understanding of late damage to the skin and lung
The precedent radiation pathology study [19] revealed that radiation injury of the vasculature is the cause of late reaction of the skin (dermal necrosis). In the lung, it is thought that radiation pneumonitis is induced via two pathways [20]: damage to an alveolar type II cell initiating the first process, and damage to an endothelial cell prompting the second. These pathways interact with each other to stimulate the differentiation of progenitor fibroblast cells into fibroblasts, which eventually generates collagen, through the aid of macrophages and cytokines. So, whether the late effect (caused by different mechanisms) to these two organs could be explained by the structure of the CBE factor was investigated.
RESULTS
Adjustment of CBE factors for BSH to the CNS by the corrected RBE of the neutron beam itself
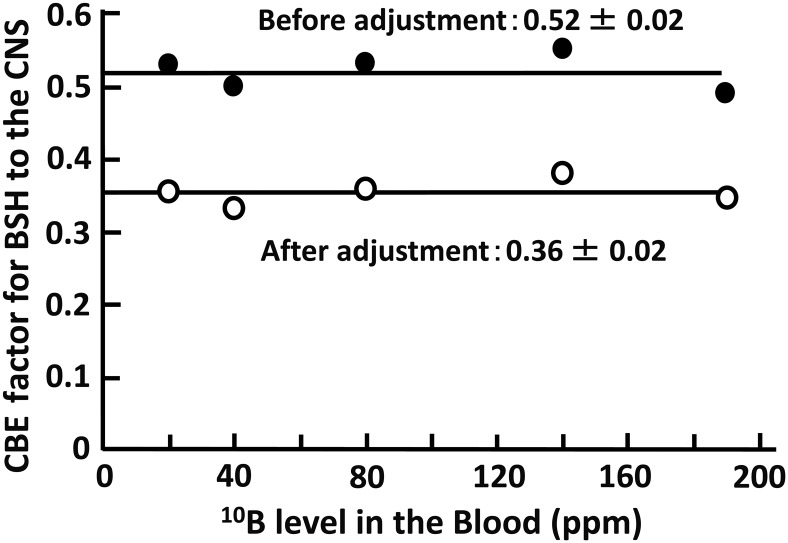
Using the relation between the neutron beam dose and the RBE in Fig. 1, the RBE for each neutron dose reported in the literature by Morris et al. was reevaluated. In their paper, a fixed value for the RBE of 1.40 was applied in calculating the CBE factor for BSH; however, the RBE increased from 1.62 to 2.50 with decrease in the neutron dose from 13.6 Gy to 3.6 Gy after reevaluation. By using these corrected neutron RBEs, the CBE factor for BSH was recalculated using Formula 1. The original CBE factor before recalculation ranged around 0.52, but it ranged around 0.36 after recalculation (Table 2). The relationship between the CBE factor and the 10B level in the blood is presented in Fig. 2, both before and after recalculation. The factors were stable and independent of the 10B level in the blood.
Fig. 2.
CBE factor for BSH to the CNS vs 10B level in the blood (ppm).
Analysis of the relationship between the CBE factor for BPA to the CNS and the N/B of the 10B level
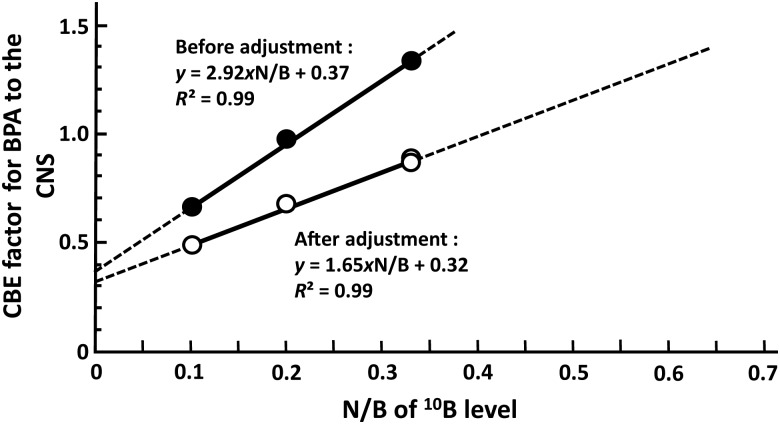
The values for the CBE factor were plotted as a function of N/B for the 10B level. The data reported in the literature were applied as the ratio at each 10B level in the blood [18]. Four data points were precisely on the straight line, and the CBE factor increased with N/B of the 10B level (Fig. 3). At 0 for the N/B of 10B level, which doesn't exist in actual BPA administration, CBE factors of 0.37 and 0.32 were predicted for the value before and after adjustment using the corrected RBE, respectively. After adjustment, the CBE factor for BPA to the CNS late damage is described by the following formula:
| (2) |
Fig. 3.
The correlation between the CBE factor for BPA to the CNS and the N/B of the 10B level before and after the adjustment of the RBE of the neutron beam.
Elucidation of the structure of the CBE factors for BSH and BPA to the CNS
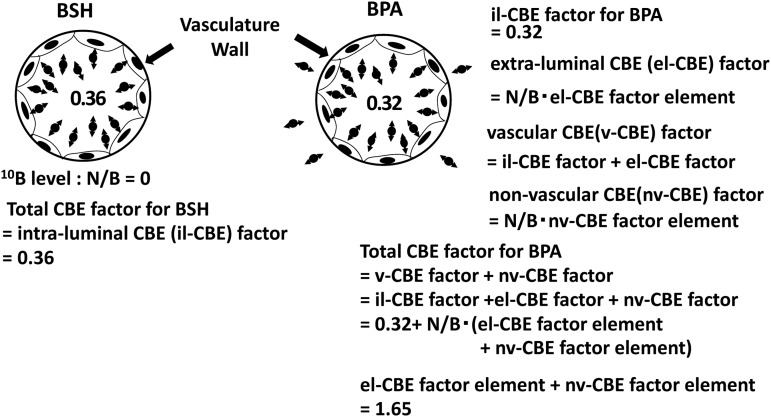
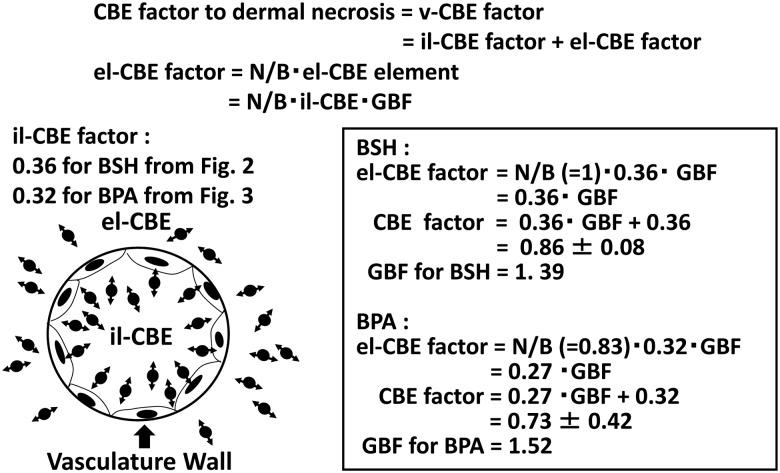
In BSH–BNCT the vasculature of the normal CNS is irradiated only from the intraluminal side. Therefore, 0.36 in Fig. 2 can be defined as an intraluminal CBE (il-CBE) factor for BSH. This value is very close to 0.32 of the il-CBE factor that BPA has at the virtual condition. BSH and BPA have very different biological characteristics from each other, but this indicates they have very similar il-CBE factors.
BPA penetrates normal CNS tissue; thus the vasculature receives radiation from the extraluminal side. This contribution can be named the extraluminal CBE (el-CBE) factor. The vascular CBE (v-CBE) factor consists of the il-CBE and the el-CBE factors. Furthermore, it is also necessary to consider the contribution of the injury induced in non-vascular structures. This component of the CBE factor can be called the non-vascular CBE (nv-CBE) factor. It is obvious that el- and nv-CBE factors are dictated by the N/B of the 10B level. Thus, the el-CBE and nv-CBE factors are defined as the products of N/B and of each element of the el- and nv-CBE factors.
This thought process is described in the following formulas and Fig. 4:
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
Fig. 4.
The dissolution of the CBE factors for BSH and BPA to each component: il-CBE, el-CBE and nv-CBE and their elements.
The value of (el-CBE factor element + nv-CBE factor element) was calculated to be 1.65 using Formula 2 and Formula 7.
The structure of the CBE factor and its components were applied to interpretation of late damage to the skin and lung
It is thought that injury to a capillary is the cause of dermal necrosis, a form of the late damage associated with BNCT [12]. This would mean that the CBE factors for BSH and BPA to the dermal necrosis, 0.86 ± 0.08 and 0.73 ± 0.42 respectively, can be regarded as the v-CBE factor for each compound, as introduced above. From this, the quantitative relationship between the il- and el-CBE factors, which are components of the v-CBE factor, was analyzed using the above values in a subsequent step.
10B existing in extraluminal tissue delivers a larger radiation dose to the vasculature than that delivered by intraluminal 10B, even when the 10B level in the extraluminal tissue is equal to that in the blood (N/B = 1). The ratio between these two radiation doses obviously varies depending on the vascular diameter. Furthermore, since the LETs of an α-particle and a 7Li nucleus change throughout their extremely short track ranges, this means that these particles cause biological injury of varying degree to the vasculature depending on the location of the nuclear reaction. For this geometric and biological complexity of action, the term ‘geometric biological factor’ (GBF) was introduced (Fig. 5). The GBF is defined as the ratio of the biological radiation dose delivered from both sides of the vasculature wall when the 10B level in the extraluminal tissue is equal to that in the blood (N/B = 1).
Fig. 5.
The introduction of GBF to correlate el-CBE factor with il-CBE factor.
Consequently, the mutual relationship between the il-CBE factor, el-CBE factor and el-CBE factor element can be written as follows:
| (8) |
By using the CBE factors for BSH and BPA to the dermal necrosis (0.86 ± 0.08 and 0.73 ± 0.42, respectively), GBFs for BSH and BPA were calculated. N/B of the 10B level for BSH and BPA reported in the literature were also used for the calculation [12], and the GBFs for BSH and BPA were 1.39 and 1.52, respectively.
The GBF for BPA was applied to analysis of CBE factor for late damage to the lung. Values of 1.1 for the N/B of 10B level and 2.3 for the CBE factor were reported in the literature concerned [21, 22]. Using these values, 0.32 of il-CBE factor and 1.52 of GBF for BPA, the elements of el-CBE factor and nv-CBE factor were calculated as follows using Formulas 3–6 and 8:
DISCUSSION
The data on CBE factors for BSH and BPA for radiation myelopathy was analyzed and the figures were compared. As a result of the analysis, the CBE factor for BSH was found not to be influenced by the 10B level in the blood, but was constant (Table 2 and Fig. 2). Morris et al. noted this characteristic of BSH [17]. By theoretical calculation, Kitao et al. estimated that the vascular wall received 6–7 Gy during one application of BNCT, i.e. one-third to one-fifth of the 10B(n,α)7Li dose to the blood assuming the wall thickness was 1 μm and the outer diameter of the vasculature was 20 μm [23]. However, when large RBEs of the particles are considered, the CBE factor is too small compared with the estimated physical dose to the vascular wall.
The CBE factor for BPA was precisely dictated by the N/B of the 10B level and the value in its virtual state, i.e.10B is existing only in the blood, and it is close to the CBE factor for BSH after the adjusting for the corrected RBE of the neutron beam (Fig. 2 vs Fig. 3). From this analysis, the il-CBE factor, which is derived from the 10B level in the blood, could be extracted from the CBE factor. In comparison, the il-CBE factor for BSH was only a little larger than that of BPA in its virtual state. The 10B level of BSH in the blood plasma is a little higher than that of BPA, even if their 10B levels in the blood are equal; this is because BSH is relatively difficult take up into the cells [24]. The difference between the 10B levels in the plasma (P) is confirmed by the measurement of BNCT patients' blood samples. The P/Bs for the 10B level were 1.27 ± 0.12 and 1.57 ± 0.12 for BPA and BSH, respectively (unpublished data). This means that the vascular endothelium was exposed to 10B at a higher level in the plasma in the case of BSH compared with BPA. This difference between the two boron compounds may be able to explain the difference in the il-CBE factors for BSH and BPA qualitatively. Though the 10B levels in the plasma were different, the radiation doses were calculated from the 10B levels in the blood rather than the plasma, and both radiation doses were equal. Consequently, the il-CBE factor for BSH was higher than that for BPA.
Injury to vasculature is thought to be the cause of dermal necrosis, a late adverse effect of the skin. This has been fairly well established by pathological and radiobiological studies on X-ray–irradiated tissues. The CBE factors for BPA and BSH for dermal necrosis were very similar; this finding also supports the idea that injury to the vasculature is a primary cause of radiation necrosis of the skin [12]. Using the above idea and the CBE factors reported, the el-CBE factor and the el-CBE factor element could be extracted from the structure of the CBE factor. It was necessary to introduce the term ‘GBF’, which relates the el-CBE factor to the il-CBE factor. The GBFs for BSH and BPA were also similar (1.39 vs 1.52). These values were obtained assuming that the dermal necrosis was completely attributable to vascular injury, and that the il-CBE and el-CBE factors were independent of the kinds of tissues; however, the degree of contribution of vascular injury to late damage varies with the organs. Therefore, it is impossible to completely eliminate the possibility of interfusion of a part of nv-CBE factor into GBF.
In the analysis of late damage to the lung, there was a residue after subtracting il-CBE and el-CBE from the total CBE factor. It was possible to explain the CBE factor by including the nv-CBE factor. This supports the two biological processes established by pathological and radiobiological studies of late damage of X-rays to the lung [20]. The nv-CBE factor for BPA was 1.44—very close to the CBE factor (1.4) assessed no later than 110 days after BNCT [22]. This agreement seems unlikely to be due to coincidence. Further investigation of this finding is necessary. When the same analysis was performed on the CBE factor for BPA for damage to the CNS, the nv-CBE factor element was 1.16, which was a little smaller than that for damage to the lung (=1.31). This difference means that non-vascular injury contributes to late damage to the lung more than it does in late damage to the CNS.
The CBE factor was able to be divided into vascular and non-vascular components, and investigation of the precise microdistribution of 10B in tissues has been possible by a simple and rapid method [25]. This method also enables estimation of the microdistribution of 10B(n,α)7Li dose in tissues. Therefore, by using these methods, the CBE factors for some organs may be determined fairly precisely without animal experiments, especially for organs in which vascular injury induces the late damage. For example, it is thought that late radiation damage to the liver presents as veno-occlusive disease (VOD), characterized by central vein thrombosis whereby occlusion of the centrilobular veins causes atrophy and loss of the surrounding hepatocytes [26]. Thus, the primary cause of the late radiation damage to the liver is vascular injury, so the CBE factor for BPA was extrapolated from the N/B of the 10B level in the liver after BPA administration. The values of 1.09 or 1.47 were applied to the calculation as the N/B of 10B level in the liver [22, 27]. Thus, a CBE factor of 0.85 or 1.04 could be estimated for the late damage to the liver without animal experimentation. In the case of BSH, a CBE factor of 1.00 can be obtained using 1.27 as the N/B of the 10B level for calculation [27]. A pioneering clinical trial of BNCT for patients with multiple liver metastases was performed by following a procedure reported from Italy [28]. The liver was totally extracted from the patient after BPA administration, transported and irradiated with neutrons at a research reactor site. Thereafter, the liver was returned to the patient. Throughout the clinical course, the late adverse effect did not appear. The CBE factor of ∼1.0 for BPA to the liver predicted in this paper is smaller than the value for late damage to the brain that is usually used in clinical BNCT to the malignant glioma, as described later. When the clinical outcomes of BNCT to liver tumors and brain tumors are considered together, the CBE factor predicted by the method in this paper seems reliable.
BNCT for malignant brain tumors has been tried by many groups. However, there are many values for CBE factors for CNS damage reported in the literature and researchers often waver in the choice of an optimum value. In Japan, researchers in KURRI and their collaborators are irradiating neutrons while continuously infusing with BPA to maintain the 10B level in the blood. The N/B of the 10B level was estimated to be between 0.6 and 0.7, based upon the data by 18F-BPA PET studies on animals and patients [29, 30]. When this ratio was applied to the calculation of the CBE factor, it ranged from 1.31 to 1.48. Therefore, the value in clinical use was confirmed to be rational [31]. It is well known (from PET examination of patients) that the T/B and N/B of the 18F-BPA level do not change concurrently with time after 18F-BPA injection. An accumulation of 18F-BPA in a tumor reaches a plateau rapidly. However, the level of 18F-BPA gradually increases with time in the normal brain, in spite of a decline in the 18F-BPA level in the blood [30, 32]. In other words, CBE factors for a normal brain are changing with time. When a change of CBE factor with the N/B of the 10B level is considered, the best timing of neutron irradiation should be selected to give the highest dose ratio between the tumor and the normal CNS. Thus, the best timing for neutron irradiation should be incorporated in future sophisticated treatment planning for BNCT. The formula for predicting the CBE factor may also be useful when seeking to reduce the N/B of the 10B level in order to decrease the effect on the normal brain [33].
CONCLUSION
The structure of the CBE factor was revealed by analyzing experimental data previously reported in the literature. The results reported here should be useful in enabling prediction of CBE factors fairly precisely, without the need for animal experiments for every organ. Thus, basic and clinical research into BNCT can be expected to accelerate.
FUNDING
This research was partly supported by a Grant-in-Aid for challenging Exploratory Research Number 14513884 to Koji Ono from the Japan Society for the Promotion of Science. Funding to pay the Open Access publication charges for this article was provided by the ICRR2015.
ACKNOWLEDGEMENTS
The contents of this paper were presented at ICRR-2015 in Kyoto.
REFERENCES
- 1.Farre LE, Sweet WH, Robertson JS et al. Neutron capture therapy with boron in the treatment of glioblastoma multiforme. Am J Roentgenol Radium Ther Nucl Med 1954;71:279–93. [PubMed] [Google Scholar]
- 2.Hatanaka H, Sano K, A revised boron-neutron capture therapy for malignant brain tumours. I. Experience on terminally ill patients after Co-60 radiotherapy. Z Neurol 1973;204:309–92. [DOI] [PubMed] [Google Scholar]
- 3.Mishima Y, Honda C, Ichihashi M et al. Treatment of malignant melanoma by single thermal neutron capture therapy with melanoma-seeking 10B-compound. The Lancet 1989;334:388–9. [DOI] [PubMed] [Google Scholar]
- 4.Smith DR, Chandra S, Coderre JA et al. Ion microscopy imaging of 10B from p-boronophenylalanine in a brain tumor model for boron neutron capture therapy. Cancer Res 1996;56:4302–6. [PubMed] [Google Scholar]
- 5.Ono K, Masunaga S, Kinashi Y et al. Radiobiological evidence suggesting heterogeneous microdistribution of boron compound in tumors: its relation to quiescent cell population and tumor cure in neutron capture therapy. Int J Radiat Oncol Biol Phys 1996;34:1081–6. [DOI] [PubMed] [Google Scholar]
- 6.Yokoyama K, Miyatake S, Kajimoto Y et al. Analysis of boron distribution in vivo for boron neutron capture therapy using two different boron compounds by secondary ion mass spectrometry. Radiat Res 2007;167:102–9. [DOI] [PubMed] [Google Scholar]
- 7.Abe M, Amano K, Kitamura K et al. Boron distribution analysis by alpha-autoradiography. J Nucl Med 1986;27:677–84. [PubMed] [Google Scholar]
- 8.Takagaki M, Oda Y, Miyatake S et al. Boron neutron capture therapy: preliminary study of BNCT with sodium borocaptate (Na2B12H11SH). J Neurooncol 1997;35:177–85. [DOI] [PubMed] [Google Scholar]
- 9.Morris GM, Smith DR, Patel H et al. Boron microlocalization in oral mucosa tissue: implications of boron neutron capture therapy. Br J Cancer 2000;82:1764–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Suzuki M, Masunaga S, Kinashi Y et al. The effects of boron neutron capture therapy on liver tumors and normal hepatocytes in mice. Jpn J Cancer Res 2000;91:1058–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kigar WS, Micca PL, Morris GM. Boron microquantification in oral mucosa and skin following administration of neutron capture therapy agent. Radiat Protect Dosimetry 2002;99:409–12. [DOI] [PubMed] [Google Scholar]
- 12.Morris GM, Coderre JA, Hopewell JW et al. Response of rat skin to boron neutron capture therapy with p-boronophenylalanine or borocaptate sodium. Radiother Oncol 1994;32:144–53. [DOI] [PubMed] [Google Scholar]
- 13.Hiratsuka J, Fukuda H, Kobayashi T et al. The relative biological effectiveness of 10B-neutron capture therapy for early skin reaction in the hamster. Radiat Res 1991;128:186–91. [PubMed] [Google Scholar]
- 14.Gavin PR, Huiskamp R, Wheeler FJ et al. Large animal normal tissue tolerance using an epithermal neutron beam and borocaptate sodium. Strahlenther Onkol 1993;169:48–56. [PubMed] [Google Scholar]
- 15.Morris GM, Coderre JA, Hopewell JW et al. Response of the central nervous system to boron neutron capture irradiation: evaluation using rat spinal cord model. Radiother Oncol 1994;32:249–55. [DOI] [PubMed] [Google Scholar]
- 16.Fukuda H, Hiratsuka J, Honda C et al. Boron neutron capture therapy of malignant melanoma using 10B-paraboronophenylalanine with special reference to evaluation of radiation dose and damage to the normal skin. Radiat Res 1994;38:435–42. [PubMed] [Google Scholar]
- 17.Morris GM, Coderre JA, Hopewe11 JW et al. Boron neutron capture irradiation of the rat spinal cord: effects of variable doses of borocaptate sodium. Radiother Oncol 1996;39:253–59. [DOI] [PubMed] [Google Scholar]
- 18.Morris GM, Coderre JA, Micca PL et al. Central nervous system tolerance to boron neutron capture therapy with p-boronophenylalanine. Br J Cancer 1997;76:1623–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dorr W. Pathogenesis of normal-tissue side-effects. In: Joiner M, Kogel A (eds). Basic Clinical Radiobiology 4th edn. London: Hodder Arnold, 2009, 178. [Google Scholar]
- 20.Dorr W. Pathogenesis of normal-tissue side-effects. In: Joiner M, Kogel A (eds). Basic Clinical Radiobiology 4th edn. London: Hodder Arnold, 2009, 184–5. [Google Scholar]
- 21.Kiger JL, Kiger WS, Patel H et al. Effects of boron neutron capture irradiation on the normal lung of rats. Appl Radiat Isot 2004;61:969–73. [DOI] [PubMed] [Google Scholar]
- 22.Kiger JL, Kiger WS, Riley KJ et al. Functional and histological changes in rat lung after boron neutron capture therapy. Radiat Res 2008;170:60–9. [DOI] [PubMed] [Google Scholar]
- 23.Kitao H. A method for calculating the absorbed dose near interface from 10B(n,α)7Li reaction. Radiat Res 1975;61:304–15. [PubMed] [Google Scholar]
- 24.Ono K, Kinashi Y, Masunaga S et al. Electroporation increases the effect of borocaptate (10B-BSH) in neutron capture therapy. Int J Radiat Oncol Biol Phys 1998;42:823–6. [DOI] [PubMed] [Google Scholar]
- 25.Tanaka H, Sakurai Y, Suzuki M et al. Development of a simple and rapid method of precisely identifying the position of 10B atoms in tissue: an improvement in standard alpha autoradiography. J Radiat Res 2014;55:373–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dorr W. Pathogenesis of normal-tissue side-effects. In: Joiner M, Kogel A (eds). Basic Clinical Radiobiology 4th edn. London: Hodder Arnold, 2009, 184. [Google Scholar]
- 27.Wittig A, Malago M, Collette L et al. Uptake of two 10B-compounds in liver metastases of colorectal adenocarcinoma for extracorporeal irradiation with boron neutron capture therapy (EORTC trial 11001). Int J Cancer 2008;122:1164–71. [DOI] [PubMed] [Google Scholar]
- 28.Zonta A, Pinelli T, Prati U et al. Extra-corporeal liver BNCT for the treatment of diffuse metastases: what was learned and what is still to be learned. Appl Radiat Isot 2009;67 (7–8 Suppl):S67–75. [DOI] [PubMed] [Google Scholar]
- 29.Hanaoka K, Watabe T, Naka S et al. FBPA PET in boron neutron capture therapy for cancer: prediction of 10B concentration in the tumor and normal tissue in a rat xenograft model. EJNMMI Res 2014;4:70–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Koivunoro H, Hippeläinen E, Auterinen I et al. Biokinetic analysis of tissue boron (10B) concentrations of glioma patients treated with BNCT in Finland. Appl Radiat Isot 2015;106:189–94. [DOI] [PubMed] [Google Scholar]
- 31.Tanaka H, Sakurai Y, Suzuki M et al. Characteristics comparison between a cyclotron-based neutron source and KUR-HWNIF for boron neutron capture therapy. Nucl Inst Meth Phys Res B 2009;267:1970–7. [Google Scholar]
- 32.Imahori Y, Ueda S, Ohmori Y et al. Fluorine-18-labeled fluoroboronophenylalanine PET in patients with glioma. J Nucl Med 1998;39:325–33. [PubMed] [Google Scholar]
- 33.Watanabe T, Tanaka H, Fukutani S et al. L-phenylalanine preloading reduces the 10B(n, α)7Li dose to the normal brain by inhibiting the uptake of boronophenylalanine in boron neutron capture therapy for brain tumours. Cancer Lett 2016;370:27–32. [DOI] [PubMed] [Google Scholar]