Thrombotic risk stratification using computational modeling in patients with coronary artery aneurysms following Kawasaki disease

Abstract

Kawasaki disease (KD) is the leading cause of acquired heart disease in children and can result in life-threatening coronary artery aneurysms in up to 25 % of patients. These aneurysms put patients at risk of thrombus formation, myocardial infarction, and sudden death. Clinicians must therefore decide which patients should be treated with anticoagulant medication, and/or surgical or percutaneous intervention. Current recommendations regarding initiation of anticoagulant therapy are based on anatomy alone with historical data suggesting that patients with aneurysms ≥8 mm are at greatest risk of thrombosis. Given the multitude of variables that influence thrombus formation, we postulated that hemodynamic data derived from patient-specific simulations would more accurately predict risk of thrombosis than maximum diameter alone. Patient-specific blood flow simulations were performed on five KD patients with aneurysms and one KD patient with normal coronary arteries. Key hemodynamic and geometric parameters, including wall shear stress, particle residence time, and shape indices, were extracted from the models and simulations and compared with clinical outcomes. Preliminary fluid structure interaction simulations with radial expansion were performed, revealing modest differences in wall shear stress compared to the rigid wall case. Simulations provide compelling evidence that hemodynamic parameters may be a more accurate predictor of thrombotic risk than aneurysm diameter alone and motivate the need for follow-up studies with a larger cohort. These results suggest that a clinical index incorporating hemodynamic information be used in the future to select patients for anticoagulant therapy.

1 Introduction

Kawasaki disease (KD) is a self-limited vasculitis and the leading cause of acquired heart disease in children, with more than 5,000 cases diagnosed each year in the USA (Holman et al. 2010). The disease is more common in Japan with an incidence of 240 cases per 100,000 children <5 years (Nakamura et al. 2012). Up to 25 % of untreated children with KD develop coronary artery aneurysms, putting them at risk for coronary artery thrombosis and subsequent myocardial ischemia, infarction, and sudden death (Kato et al. 1996). While the incidence of aneurysms can be reduced to 5 % by treatment with intravenous immunoglobulin within 10 days of fever onset, delays and missed diagnoses are common, leading to a missed treatment window in many patients (Newburger et al. 1991; Wilder et al. 2007).

Long-term management of KD patients with aneurysms is challenging due to a lack of data to guide treatment decisions, which could include antiplatelet therapy, systemic anticoagulation, percutaneous coronary artery interventions such as stenting or rotational ablation, and coronary artery bypass surgery (Newburger et al. 2004). Medical management decisions for KD patients with aneurysms are currently based on anatomy alone, with a diameter of at least 8 mm as the arbitrary cutoff for the initiation of systemic anticoagulation therapy, although this practice is based only on historical outcomes data (Suda et al. 2011; Sugahara et al. 2008). Clinicians are thus often faced with a difficult decision to treat otherwise normal healthy patients with aggressive anticoagulation therapy or to treat with antiplatelet therapy alone and accept the risk of possible myocardial infarction (Tsuda et al. 2011).

Coronary aneurysm shape varies greatly among patients and can be saccular, fusiform, or have a string-of-pearls appearance. While aneurysms can be imaged to obtain detailed anatomical information, there are currently no available clinical tools to predict the risk of coronary artery thrombosis or myocardial infarction. Imaging flow in the coronary arteries noninvasively using phase-contrast magnetic resonance imaging (MRI) is possible, but technically challenging because the coronary arteries are small and mobile, with maximum displacements in the distal right and left coronary arteries of about 16 and 10 mm, respectively (Hundley et al. 1996; Johnson et al. 2004). Computed tomography (CT) angiography can now be performed with relatively low radiation doses to noninvasively image coronary artery anatomy (Earls et al. 2008), but provides no direct hemodynamic information. Limited flow information can be obtained invasively through cardiac catheterization, but this is typically limited to global flow and pressure waveforms. It is therefore desirable to obtain the missing hemodynamic information through the use of patient-specific simulations.

Simulations can provide critical hemodynamic information linked to thrombotic risk, including wall shear stress (WSS), wall shear stress gradients (WSSG), particle residence time (PRT), particle residence time gradient (PTRg), and oscillatory shear index (OSI), which are difficult or impossible to obtain from standard imaging modalities. Simulations have been used extensively in other clinical applications, including congenital heart disease (Marsden et al. 2010), abdominal aortic aneurysms (Les et al. 2010), cerebral aneurysms (Cebral et al. 2005), surgery optimization (Yang et al. 2010), and coronary artery bypass grafts (Sankaran and Marsden 2010; Sankaran et al. 2012), and there is growing interest in the use of simulations as a diagnostic tool in the coronary arteries (Min et al. 2012).

However, prior application to KD is limited to a single-case study performed by our group in which a virtual normal model was used as the patient’s own control (Sengupta et al. 2012). That study demonstrated that custom downstream coronary boundary conditions, along with a lumped parameter heart model (Kim et al. 2009; Kim et al. 2010), effectively captured the physiologic coronary circulation. Further, it was shown that the presence of aneurysms did not produce significant changes in the global flow and pressure waveforms. However, order of magnitude changes in local hemodynamic quantities, including WSS, WSSG, OSI, and PRT were observed. Our study was the first to reveal and quantify the severely abnormal hemodynamic conditions, with large temporal and spatial variations, in a KD patient with aneurysms.

In contrast to other types of aneurysms (abdominal, cerebral), which are commonly treated with covered stents, coils, or surgery to prevent or delay rupture, the primary clinical decision in KD is typically whether or not to treat with systemic anticoagulation medication. Aneurysms caused by KD typically do not grow after the initial acute phase of the disease and do not post a risk of rupture. Instead, the primary clinical concern is formation of occlusive thrombus leading to myocardial infarction.

In the present study, we applied patient-specific modeling to a cohort of five KD patients with aneurysms and one KD patient with normal coronary arteries. This work incorporates recent advances in simulation technology, including lumped parameter boundary conditions (Lagana et al. 2002), increasing anatomical realism, particle tracking (Shadden and Taylor 2008), and non-discrete residence time computations (Esmaily-Moghadam et al. 2013). In addition, we also make a direct comparison between simulations with rigid and deformable walls to quantify the resulting differences in wall shear stress (WSS) (Figueroa et al. 2006). We calculated key hemodynamic quantities that are postulated to be surrogates for thrombotic risk and, for the first time in studies of KD, compared these with patient outcomes, including incidence of thrombosis and myocardial infarction. We also compared conditions among aneurysms of different shapes from more saccular to more fusiform. This comparison uncovered surprising and nonintuitive relationships between aneurysm diameter, the currently accepted standard for treatment decisions, and hemodynamic quantities linked to thrombus formation. Our results show that large anatomical differences, even in aneurysms with the same maximum diameter, can lead to drastically different hemodynamic conditions, and likely different thrombotic risk. These data suggest that patient-specific computational analysis based on CT imaging could be used to construct a clinical index to risk-stratify patients if confirmed in follow-up studies with significantly larger patient cohorts.

2 Methods

2.1 Subject data

Six KD patients were modeled in this pilot study, of whom five had coronary aneurysms (A–E) and one (F) did not, and served as the control. A brief clinical history was collected for all patients (Table 1), and clinical data used for simulations were obtained at or near the time of the performance of the computed tomography angiogram (CTA) that was used for the patient-specific modeling (Table 3). Patient-specific geometry was obtained from clinically indicated CT angiograms, with patient A–D and F imaged at UCSD (CT750 HD 64-slice CT scanner, GE Medical, Milwaukee, WI), and patient E imaged at Sechenov First Moscow State University (Aquilion ONE 320 slice CT scanner, Toshiba, Tokyo, Japan). This study was approved by the Institutional Review Board at UCSD and First Moscow State University, and written subject consent or assent and parental consent were obtained as appropriate for the imaging and simulation studies.

Table 1.

Summary of clinical data for patients A–F, including serial imaging findings, timing of thrombosis and other adverse events, and clinical interventions

Patient ID	Year and age  at KD  diagnosis	Ethnicity	Imaging studies  (*used for  modeling)	Clinical findings	Medical therapy	Percutaneous  intervention	Surgery
A	1999, age 3	Caucasian	January, 2006	Large aneurysms in right  and left CA. Small regions  of mural calcification.	IVIG and  methylprednisolone on  the 7[th] day of illness.  Warfarin + aspirin, then  dabigatran + aspirin	None	None
			August, 2007* (age 8)	Increased mural  calcification
			February, 2010	Progressive calcification  and laminated  non-occlusive LAD  thrombus
B	2010, age 16	Chinese	March, 2010* (age 16)	Aneurysms in both right  and left CA. No  observable thrombosis or  calcification	IVIG on the 11[th]  day of illness.  warfarin and  aspirin	Cardiac catheteri- zation	CABG
			June, 2011	Thrombosis of both CA.
C	1956, KD- compat- ible illness, age 7	Chinese	November, 2010*, (age 61)	Calcification in both right  and left CA, MI with  RCA thrombosis at age 33	Warfarin and aspirin	Angioplasty age 33	None
D	No known KD diagnosis	Vietnamese	July, 2010* (age 28)	Aneurysms in right and left  CA, MI at age 22 with  acute thrombotic  occlusion in the RCA.  Calcification in LCA	Warfarin and aspirin	Angioplasty age 22	None
E	2009, age 3	Caucasian	September, 2010	Aneurysm in the left CA.  No observable thrombosis  or calcification	Warfarin and aspirin.	Cardiac  catheterization	None
			April, 2011* (age 5)	No observable thrombosis  or calcification
F	1986, age 11 months	Asian-Filipino	April, 2010* (age 24)	No observable thrombosis  or calcification	None	None	None

Table 3.

Clinical data used for tuning boundary conditions in models of patients A–F

Patient ID	Blood pressure (mmHg)	Cardiac output (L/min)	Stroke volume (mL)	Heart rate (bpm)	Body surface area (m2)
A	105/52	3.4	58.00	59	1.16
B	108/67	4.9	83.20	59	1.79
C	140/82	5.5	91.67	60	2.10
D	96/57	5.2	112.80	46	1.97
E	90/55	4.3	41.00	105	0.76
F	123/81	3.8	90.47	42	1.70

2.2 3D anatomical models

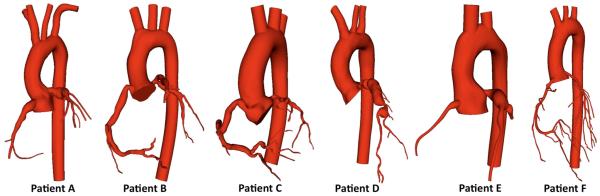
Patient-specific 3D anatomical models were constructed from the CT image data using a customized version of the open source SimVascular software package following our previous work (Sengupta et al. 2012). Three steps were used to reconstruct 3D geometric models from the CTA: (i) creation of centerline paths for vessels of interest, (ii) segmentation of the vessel lumen through a combination of pixel intensity thresholding and level set methods, and (iii) lofting the segmentations to construct a final 3D model. Anatomy in the models included all left and right coronary artery branches resolved in the image data, the ascending and descending aorta, and the subclavian arteries. Figure 1 shows the reconstructed models for all patients. Patient D had an occluded right coronary artery, and the RCA was excluded from the model as no contrast filling was observed in the CT image data. An unstructured finite element mesh was constructed for each patient-specific model using the commercial software Meshsim (Symmetrix, Inc, Clifton Park, NY). We employed mesh adaptation with Hessian-based error estimators with an average mesh size of approximately 0.2 mm to ensure mesh convergence (Sahni et al. 2006), and resulting meshes had on average over 3.5 million elements. Mesh adaptation was essential for obtaining sufficient resolution in the coronary arteries because of the size disparity between different vessels in the model.

Fig. 1.

Patient-specific models constructed from CT image data for KD patients with aneurysms (A–B) and without aneurysms (F). Patient D had a fully occluded RCA that was not modeled

2.3 Simulation methods

Blood flow simulations were performed with a custom finite element Navier–Stokes solver. The flow solver uses the second-order accurate generalized alpha method for time discretization, and spatial stabilization is achieved utilizing a streamline-upwind Petrov Galerkin (SUPG) method, enabling the use of linear finite elements (Whiting and Jansen 2001), blood is modeled as a Newtonian fluid with density 1.06 g/cc and a dynamic viscosity of 0.04 dynes/cm², and walls are assumed to be rigid, though capacitance elements in each of the outlets capture the global effect of wall compliance. Simulations were run for 6 cardiac cycles, after which the cycle-to-cycle pressure variations were less than 1 %. The required simulation time for each model was approximately 26 h using 60 parallel CPU cores of a CentOS 5.2 Linux-based cluster (AMD Opteron 2378, 2.4 ghz QuadCore). Additional backflow stabilization terms acting only during the periods of flow reversal were used to prevent simulation divergence due to backflow (Moghadam et al. 2011).

2.4 Boundary conditions

The choice of boundary conditions is critical in hemodynamics simulations, particularly for coronary arteries since pressure and flow waveforms are out of phase due to changing resistance during cardiac contraction. In addition, measuring coronary flow directly with phase-contrast MRI remains an area of active research, so patient-specific flow waveforms cannot be readily obtained for use as coronary inflow boundary conditions.

To properly model coronary physiology, specialized lumped parameter boundary conditions were applied at the outlets of the coronary arteries, following the work of Kim et al Kim et al. (2010) using the coupled multidomain method (Vignon-Clementel et al. 2006), as applied previously by our group in a case study of KD (Sengupta et al. 2012). The coronary outlet models were coupled to a lumped parameter heart model consisting of resistors, inductors, diodes, and time-varying elastance functions to model viscous losses, inertia, contraction of the myocardial muscles, and the valves. The heart model was used offline to solve for the myocardial pressure, which was imposed in the lumped parameter coronary model to drive changes in vascular resistance with cardiac contraction. The boundary condition parameter values were tuned to match patient-specific clinical data (Table 3), as in our previous work. In all models, the coronary resistances were tuned such that total coronary flow was approximately 4 % of the total cardiac output, and the right/left flow split was approximately 40 %/60 % of the total coronary flow (Johnson et al. 2008). Resistances of the individual coronary outlets were weighted to be inversely proportional to their outlet area. Capacitance values were chosen to match previously reported ratios for the coronary arteries (Kim et al. 2010; Burattini et al. 1985). Parameter values were iteratively tuned by running successive simulations until the target patient blood pressure, the assumed flow splits in the coronary arteries, and the target ratio between the systolic and diastolic peak in the coronary flow waveform were obtained (Marcus et al. 1999.) The resulting models successfully captured typical physiologic flow features of the coronary circulation reported previously in the literature, with maximum flow during diastole and minimum flow during systole.

At the aortic inflow face, a volumetric flow waveform (i.e. Dirichlet boundary condition) was applied. For patients C and D, the aortic flow waveform was obtained from phase-contrast MRI measurements and directly imposed on the inflow face. For all other patients, a typical aortic waveform was scaled to match the cardiac output from echocardiography and heart rate of the patient. At all other outlets, i.e., the abdominal aorta and subclavian vessels, Windkessel RCR boundary conditions were applied (Vignon-Clementel et al. 2010). Resistances were estimated as the ratio of mean pressure to mean flow, using patient blood pressure as a target value. The relative resistance values at different outlets, as well as ratios of proximal to distal resistances and capacitance values were tuned to match patient-specific blood pressures and literature data as in our previous work (Les et al. 2010).

2.5 Particle residence time

PRT was quantified using Lagrangian particle tracking. Mass less particles were released in the proximal region of each coronary vessel and tracked over multiple cardiac cycles (Sengupta et al. 2012). The particles were advected by the flow until approximately all particles were flushed from the computational domain, requiring as many as 12 cardiac cycles. Particles were assumed to be massless, and effects of diffusion were neglected owing to the short residence time of the particles in the computational domain. The advection scheme used a Runge–Kutta–Fehlberg time-integration algorithm with a maximum error tolerance of 10⁵ and a linear interpolation of the velocity data in space and time.

Approximately 15 million massless particles were released uniformly at the inlet of the coronary arteries at the start of every cardiac cycle. We confirmed that final results were not sensitive to the seeding density and rate and the integration error tolerance.

As a measure of blood flow stagnation and recirculation, two quantities were calculated. First, we computed the percentage of particles remaining in the coronary vasculature after one, five and ten cardiac cycles. Second, we computed the total number of cardiac cycles required for all particles to completely wash out of the coronary vessels. Increased values of these two parameters indicate high recirculation time and flow stagnation, which is hypothesized to be linked to a higher risk of thrombosis (Fraser et al. 2012).

An additional measure of residence time was computed for one patient using a recently developed non-discrete method (Esmaily-Moghadam et al. 2013). An advection diffusion equation with a nonzero source term was solved as a post-processing step on the simulated velocity field of patient B, allowing for computation of residence time in an Eulerian framework. This method avoids certain issues with discrete methods, including mesh dependency, and the large number of particles required for adequate resolution, and enables computation of the spatial distribution. The residence time, which is a scalar field, represents the total time a parcel of fluid has been inside the computational domain. By computing the gradient of residence time (PRTg) in this work, we removed the dependence of the spatial distribution of PRT on the distance of a parcel of fluid from the inflow of the computational domain. The streamwise component of the PRTg vector is identical to the definition of local residence time (RTx) in our prior work, while the normal component represents the changes in fluid entrapment moving across different layers of the flow. While the streamwise component is large in lower velocity regions, the normal component is dominant in regions of recirculation. In this study, we report the 2-norm of the PRTg vector, hence combining the contribution of both components into a single scalar field. This allowed for identification of “hot spots” of high residence time gradient that can be compared with regions of developing thrombus.

2.6 Geometric parameters and aneurysm shape index

Three geometric parameters were determined from the patient-specific models. The first was the maximum aneurysm diameter. The second was an aneurysm shape index, which we defined to classify aneurysm geometries on a continuous scale from saccular to fusiform. A representative aneurysm length was defined as the ratio of aneurysmal volume to maximum aneurysmal area. The aneurysm volume included all regions in the coronary arteries in which the diameter was greater than a Z-score value of zero. The aneurysm shape index was then defined as the nondimensional ratio of the aneurysm length to the maximum aneurysmal diameter. A high shape index indicates a more fusiform shape, while low shape index value indicates a more saccular shape. The third, aneurysm sphericity (Ψ), was defined using the following equation:

$$\Psi =\frac{{\pi }^{\frac{1}{3}}{\left(6V\right)}^{\frac{2}{3}}}{A}$$ (7)

where V is the aneurysm volume and A is the surface area. Low aneurysm sphericity indicates a more fusiform shape while higher aneurysm sphericity indicates a more saccular shape, where Ψ = 1 is a perfect sphere.

2.7 Hemodynamic parameters

Additional hemodynamic parameters, including WSS, WSSG, and OSI, were post-processed from the simulated velocity and pressure fields. WSS is a measure of force exerted on the vessel wall by the flow field. OSI is an indicator of the directionality of flow (Ku et al. 1985), with a minimum value of 0 corresponding to unidirectional traction and a maximum value of 0.5 corresponding to zero mean traction with equal time spent in both directions. WSSG quantifies the spatial variations in hemodynamic forces on the vessel wall (Lei et al. 1997). These quantities have been experimentally linked to thrombosis, with low WSS, high OSI, and high WSSG generally thought to correspond to increased risk (Passerini et al. 2004; Sriramarao et al. 1996; Kroll et al. 1996; Hwang et al. 2003).

2.8 Fluid–solid interaction

A deformable wall simulation was performed on a model of the aneurysmal portion of the left coronary artery of patient A with one inlet and one outlet. Inflow boundary conditions were extracted from the full model simulation of patient A. A time-varying resistance was prescribed at the outlet boundary. The resistance waveform was derived using the pressure and flow waveforms from the full model simulation of patient A. Identical boundary conditions were used for rigid and deformable wall simulations.

The deformability of the wall was incorporated using a coupled momentum method which adopts a variational approach with a fixed fluid mesh with nonzero fluid velocities at the fluid–solid interface, and a linearized kinematics membrane formulation for the solid domain (Figueroa et al. 2006). A linear elastic isotropic model (enhanced with transverse shear) was used to model vessel wall deformation assuming small (<10 %) strains. This assumption is justified by experimental evidence showing that vessel wall constitutive behavior can be reasonably assumed as linear within the physiologic range of pressures (Zhou and Fung 1997). The vessel wall thickness and Young’s modulus were set to 0.8 mm and 4 × 10⁶ dynes/cm², respectively, which are in the range reported in prior studies (Lu et al. 2004; Holzapfel et al. 2005) and correspond to the linear section of previous experimentally reported stress—stretch curves. Poisson’s ratio was 0.5, and the wall density was 1.0 g/cm³. For the deformable wall simulation, we simulated 12,000 time steps using a 0.5 ms time step size. Data from the final cardiac cycle were used for analysis, after periodicity was achieved.

2.9 Statistical analysis

The nonparametric Mann–Whitney U test was used to determine statistical significance among the parameters investigated, with p values < 0.5 considered to be statistically significant. We report p values only for statistically significant quantities, and all others may be assumed insignificant.

3 Results

3.1 Flow and pressure waveforms

The simulated coronary flow waveforms confirmed that the lumped parameter boundary conditions captured the expected physiologic features. The flow waveforms of both the LAD and RCA peaked during diastole, when coronary resistance is at minimum. Simulated aortic pressure wave-forms matched the clinical systolic and diastolic blood pressure data for all patients and shape agreed with clinical observation.

3.2 Hemodynamic parameters

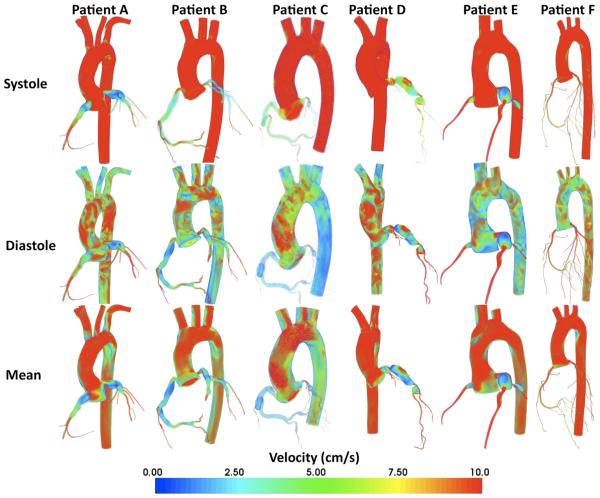
Aneurysmal velocities were persistently low during diastole for most patients, with some patients demonstrating low velocities throughout the entire cardiac cycle (Fig. 2). The presence of the aneurysms in patients A–E caused substantial flow stagnation and recirculation, with persistently lower velocities compared to control patient F.

Fig. 2.

Volume-rendered velocity magnitude for all patients during systole (top), diastole (middle), and time averaged (lower). As shown in the simulation of the normal arterial tree, velocity was maximal during diastole (red). Sluggish or stagnant flow was demonstrated in many of the aneurysms (blue)

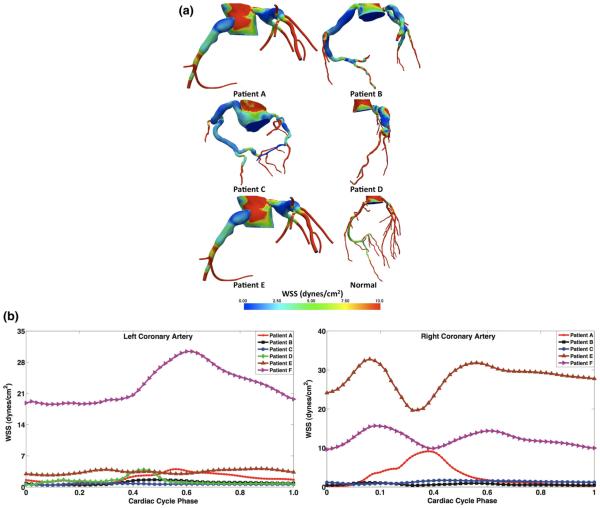
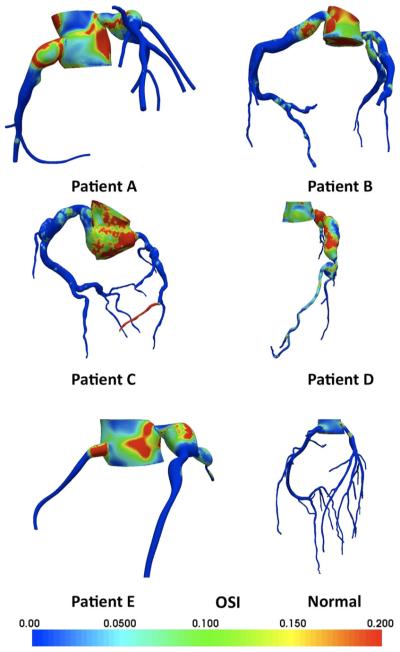
The mean WSS was an order of magnitude lower in the aneurysmal regions of the arteries in patients A–E compared to vessels with no aneurysms (patient F and the RCA of patient E) (Fig. 3a) with some variability in waveform shape (Fig. 3b). Distal to the aneurysms, where coronary artery diameters return to normal, the WSS also returned to the normal range, verifying that the aneurysms cause only localized disturbances in hemodynamics. Aneurysms were associated with higher than normal values of OSI (Fig. 4). Distal to the aneurysms, as well as in the normal vessels, OSI values were near zero, indicating that the flow was unidirectional.

Fig. 3.

a Mean wall shear stress from simulation in all patient-specific models, showing lower values in aneurysmal regions, and large variation among patients. b Wall shear stress versus time in the LCA (left) and RCA (right) for one cardiac cycle in all models shows order of magnitude lower values in aneurysmal regions compared to normal

Fig. 4.

Oscillatory shear index in all patient models, showing increased OSI in aneurysmal regions compared to normal

3.3 Comparison of hemodynamic data and clinical outcomes

Hemodynamic and geometric quantities were extracted from simulation results during post-processing and compared to patient outcomes (Table 2). The location and extent of thrombosis were evaluated for each aneurysmal vessel from each subject. Thrombosis was considered to be present if there was any evidence of thrombosis (either occlusive or non-occlusive) visible in the CT study. Patients B and C developed occlusive thrombosis, while patients A and D developed laminated non-occlusive thrombus in the vessel wall region visible on the CT scan. Thrombosis in patients A, B, and D was found in follow-up CT studies performed after the scan used for the modeling. Thrombosis in patient C occurred prior to the modeling study, but was treated by percutaneous intervention, presumably leaving the geometry unaltered. The timing of these events is listed in Table 1.

Table 2.

Hemodynamic and geometric parameters for KD patients A–F, with corresponding clinical outcomes

Patient ID	Vessel	Geometric Parameters			Hemodynamic Parameters								Thrombosis (yes/no)
		Max diameter (cm)	ASI	ψ	Mean WSS at max diameter (dynes/cm2)	Mean WSS (dynes/cm2)	Mean WSSG (dynes/ cm2)	Mean OSI	Percent of particles after			Number of cycles parti- cles recircu- late
									1 Cardiac cycle	5 Cardiac cycles	10 Cardiac cycles
A	LAD	1.14	1.38	0.83	2.75	3.2	20.12	0.079	32	0	0	4	+
A	LCX	0.64	1.27	0.75	2.47	4.53	17.01	0.009	18	0	0	3	−
A	RCA	1.08	1.38	0.77	3.45	4.05	18.50	0.075	28	0	0	5	−
B	LAD	0.95	4.93	0.68	1.65	2.22	8.53	0.029	82	51	0	10	+
B	LCX	0.7	5.35	0.56	1.13	3.18	24.33	0.016	75	41	0	8	+
B	RCA	1.03	6	0.51	0.92	2.8	24.00	0.028	98	63	16	12	+
C	LAD	0.87	1.58	0.48	1.33	7.86	56.00	0.007	71	10	0	6	+
C	RCA	0.96	9.86	0.48	1.85	3.09	18.24	0.017	82	17	0	7	−
D	LAD	1.18	6.09	0.61	1.43	6.72	54.20	0.14	79	16	0	7	+
E	LAD	1.03	1.25	0.88	3.5	6.6	60.83	0.070	49	0	0	3	−
E	LCX	0.44	2.34	1.11	4.72	10.21	112.00	0.045	20	0	0	2	−
E	RCA	0.16	−	−	−	28.07	85.833	0.029	5	0	0	1	−
Normal	LAD	0.35	−	−	−	20.2	63.25	0.010	9	0	0	1.2	−
Normal	RCA	0.32	−	−	−	14.35	51.7	0.000	14	0	0	1	−

Hemodynamic parameters included the WSS at the maximum diameter, averaged WSS in the aneurysms, percent of particles remaining after 1,5, and 10 cardiac cycles, and the number of cardiac cycles required for all particles to wash out of the model. Geometric parameters were maximum diameter, aneurysm shape index, and aneurysm sphericity. A total of 6 patients with 14 coronary artery segments were studied (Table 2). The LCX was evaluated separately only for patients who had aneurysms in that vessel (A, B, and E). Occurrence of thrombus is marked with a “+” and indicates any evidence of thrombosis observed by CT

Aneurysmal arteries (N = 11) had significantly lower WSS than normal arteries (N = 3) (4.9 for aneurysmal vs. 20.9 for normal, p < 0.01). Aneurysmal arteries also required significantly more cardiac cycles for particles to exit the domain (6.1 for aneurysmal vs. 1.1 for normal, p < 0.01). Aneurysmal arteries had lower WSS gradients (37.6 for aneurysmal vs. 67 for normal) and higher OSI (0.047 for aneurysmal vs. 0.01 for normal). Velocity fields also showed regions of stagnant flow that persisted throughout the cardiac cycle in aneurysmal regions, which were not observed in normal arteries.

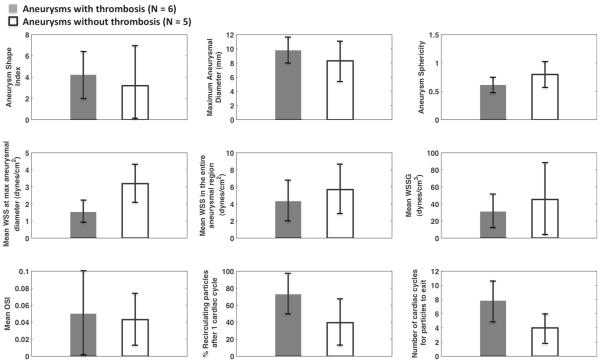
We next compared geometric and hemodynamic parameters between aneurysmal vessels in the thrombosed and non-thrombosed groups (Fig. 5). Aneurysms with thrombosis required almost twice as many cardiac cycles (mean 7.8±2.8 vs. 4.0 ± 2.0) for particles to exit the aneurysm domain in simulation and had 108 % lower mean WSS (1.5 ± 0.64 compared to 3.2 ± 1.1dynes/cm²) at maximum diameter compared to aneurysms without thrombosis. WSS was also 32 % lower for the thrombosis group when measured over the entire aneurysm. Mean WSSG was 45 % lower, while mean OSI was 67 % higher in the entire aneurysm of the thrombosis group. Thrombosed vessels had a 30 % lower sphericity index than non-thrombosed vessels, and a 24 % higher aneurysm shape index, suggesting that aneurysms of a more fusiform geometry confer a higher risk of thrombosis. The differences in mean values between the thrombosed versus non-thrombosed groups were not statistically significant.

Fig. 5.

Comparison of hemodynamic parameters between aneurysmal arteries with (n = 6) and without (n = 5) thrombus. Vessels were considered to have thrombosis if there was any evidence of thrombus (occlusive or non-occlusive) observed in by CT. None of these differences were statistically significant

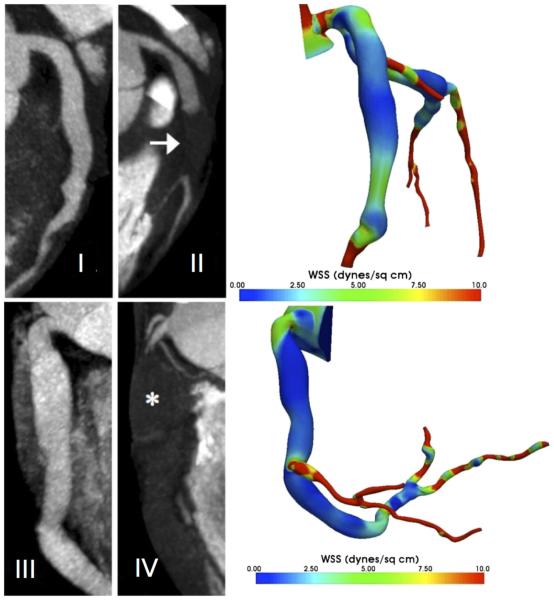
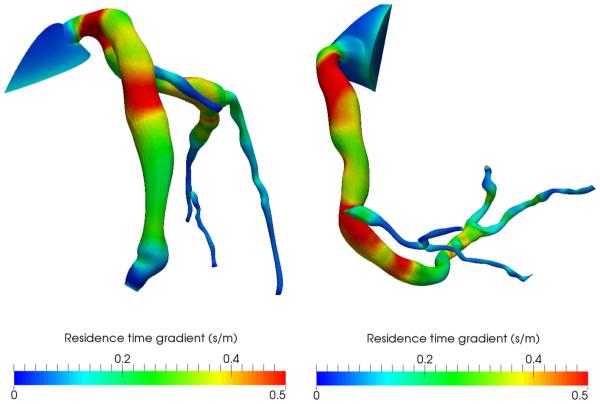
Following our initial simulations, patient B became symptomatic and developed thrombus in both left and right coronary arteries as documented by CT imaging. The locations of thrombus formation corresponded to regions of lowest WSS in simulations in both the left and right coronaries (Fig. 6). Patient B had the highest particle recirculation times and the lowest value of WSS in the RCA among all patients in the cohort (Table 2). We also compared the spatial distribution of residence time gradient (PRTg) with locations of thrombus formation in patient B, revealing “hot spots” of high PRTg in regions of subsequent thrombus formation (Fig. 7). This patient subsequently underwent coronary bypass surgery for ischemia due to progressive stenosis secondary to thrombus formation.

Fig. 6.

Left CT angiograms of the LAD (I, II) and RCA (III, IV) on a subject with a history of KD performed acutely (I, III) and 1 year after KD onset (II, IV), showing the interval development of thrombosis of the mid-LAD (arr ow, II) and nearly the entire RCA (ast er i sk, IV); Right simulation results for the same patient showing areas of lowest WSS in the corresponding regions of thrombosis

Fig. 7.

Spatial distribution of particle residence time gradient (PRTg) magnitude in the right coronary (right) and left coronary (left) arteries of patient B. Regions of high PRTg correspond well to regions of subsequent thrombus formation, revealing regions of prolonged residence time that were possible locations of thrombus initiation

3.4 Fluid–solid interaction

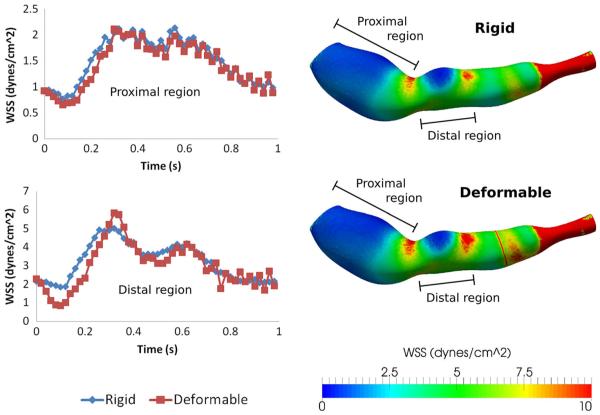
Comparing the WSS between the rigid and deformable simulations in the left coronary artery of patient A, we found differences of 8.5 and 16.3 % (averaged across the cardiac cycle) in the proximal and distal sections of the aneurysm, respectively. The deformable simulation on average exhibited lower WSS than the rigid simulation. The finding that the incorporation of vessel deformation affects WSS in the proximal regions more significantly than in the distal regions is consistent with previous literature (Zeng et al. 2008). These results are summarized in Fig. 8, showing both qualitative and quantitative comparisons of WSS between the rigid and deformable simulations.

Fig. 8.

Left comparison of WSS versus time with rigid and deformable walls for proximal and distal regions of the left coronary aneurysm from patient A. Differences in WSS average 8 % in the proximal regions, and 16 % in the distal region. Right contours of WSS in rigid (top) and deformable (bottom) at peak flow, revealing modest differences in spatial patterns

4 Discussion

Patient-specific modeling allows for computation of spatial and temporal variations in hemodynamic quantities that cannot be readily obtained through conventional clinical imaging modalities. Using computational modeling, we showed that the presence of aneurysms in the coronary arteries of KD patients leads to severely abnormal flow conditions, including low WSS and high PRT that appear to be linked to increased risk of thrombosis. This study, together with our prior work (Sengupta et al. 2012), is the first to apply patient-specific modeling to compare flow conditions in a cohort of KD patients using realistic aneurysm geometries. In agreement with our previous study, we identified significant order of magnitude differences between aneurysmal and normal coronary flow conditions.

This study suggests several surprising relationships between flow conditions, aneurysm geometry, and clinical outcomes. First, simulations confirmed that flow conditions are markedly different among patients, even among those with similar aneurysm diameters. This may call into question the current clinical practice of using a single diameter measurement to determine thrombotic risk and the need for anticoagulant medication, and motivates the need for future studies with larger cohorts to validate these findings.

Second, our results suggest that hemodynamic parameters, or a combination of hemodynamic and geometric parameters, may better predict thrombotic risk than maximum aneurysm diameter alone. When comparing differences between the thrombosis and non-thrombosis groups, the maximum diameter had the smallest percentage difference (15 %) between the two groups of all the parameters examined. The largest percentage differences between the two groups were in WSS and the number of cardiac cycles required for particles to exit the simulation domain. Though we have not yet achieved statistical significance, these findings are contrary to current AHA guidelines that rely solely on aneurysm diameter as a predictor of thrombotic risk (Newburger et al. 2004). While all but one aneurysm in this group was >8 mm (Table 2), several large aneurysms had lower than average PRT and higher WSS. Hence, if confirmed in future clinical studies, criteria for anticoagulation based on geometry alone may lead to unnecessary anticoagulation in patients with large diameter aneurysms as well as failure to anticoagulate patients with smaller diameter aneurysms at higher risk of thrombosis due to unfavorable hemodynamic parameters.

Furthermore, some patients such as patient B may be at particularly high risk of thrombosis and importantly may still be at risk even with standard systemic anticoagulation. Such patients may benefit from more additional medical therapy such as more intensive anticoagulation with a higher target INR and/or more intensive antiplatelet therapy as well as more intensive monitoring such as serial CT angiograms to assess for the presence of thrombus. In addition, the role of the new oral thrombin or Factor Xa inhibitors (dabigatran, rivaroxaban, and apixaban) in KD remains to be determined. The assessment of patient-specific hemodynamics presented here may be of use in the design of clinical trials to evaluate these newer agents in KD patients.

Finally, our results suggest that fusiform aneurysms may confer a higher risk for thrombosis than previously appreciated, which goes counter to current clinical thinking that larger diameter, saccular aneurysms pose the highest risk. This provides motivation for future clinical studies that could compare patients with different aneurysm shapes. The sphericity index was lower for patients who developed thrombosis, suggesting that more fusiform aneurysms may actually have higher propensity for thrombus formation compared to saccular aneurysms. Additional patients with small and medium aneurysms are needed for comparison to strengthen these findings.

The correspondence between locations of low WSS and high PRTg for patient B and subsequent locations of thrombosis is a promising indicator of the predictive ability of the proposed simulation methodology. This patient had the lowest WSS values and the highest PRT among all patients in the cohort. Regions of prolonged PRTg were located in regions of subsequent thrombosis, suggesting possible locations of initiation. This patient’s unique history provided a valuable opportunity to compare simulation predictions with patient outcome. Future studies could incorporate additional parameters such as coherent vortices, as well as biochemistry models of thrombosis.

Prior clinical studies have also examined the relationship between WSS and aneurysm shape and have raised awareness of the importance of abnormal hemodynamics. A 2007 study of Ohkubo et al. estimated WSS from flow wire measurements in 111 KD patients, classifying into giant aneurysm, aneurysm, and normal groups (Ohkubo et al. 2007). WSS levels were correlated with the presence of thrombus detected by intravascular ultrasound. Over 90 % of aneurysms were found at left coronary branching sites, with significantly reduced WSS in giant aneurysms with disturbed flow. However, the accuracy of measuring maximum velocity using flow wires remains a challenge, as WSS values were estimated by assuming laminar steady flow in a circular pipe, and thus could not fully account for the complex geometry or flow variations among patients.

There are several important differences between this and prior studies of aneurysm hemodynamics. First, aneurysms caused by KD do not typically rupture, which is the primary concern with abdominal or cerebral aneurysms. Instead, the primary concern is the risk of occlusive thrombosis leading to myocardial infarction. This makes hemodynamic factors more important in KD compared to other common aneurysms, in which the material properties, stresses, strains, and growth of the wall over time are of primary importance. Additionally, following the initial acute phase of KD when the aneurysms form, their size remains relatively constant in time, unlike other common aneurysms where prediction of growth and remodeling is critical for rupture prediction. Treatment of KD is also distinct from other aneurysm types, as the primary decision is whether to prescribe anticoagulation therapy, which poses a significant risk in children. Other treatments are less commonly performed, including coronary artery bypass grafting and percutaneous interventions, but typically only in symptomatic patients with signs of ischemia.

We recognize several strengths and limitations to our study. First, the computational methodology includes physiologically realistic coronary boundary conditions and incorporates patient-specific anatomy and clinical data. Second, this paper provides the first quantitative comparison of flow conditions in aneurysms of KD patients with subsequent patient outcomes. Third, these results suggest that a followup prospective clinical study is warranted to construct a clinical index based on simulation data that could be used to better select patients for anticoagulant therapy. Hemodynamic data from a larger study could then be used in the future to replace or augment the current AHA guidelines, leading to better selection criteria for anticoagulation therapy in KD patients.

The major limitation of this study was the small sample size. A substantially larger cohort and computational effort will be required to demonstrate statistical significance in comparisons of patients with and without thrombus. An initial power analysis predicted that we will need a sample size of at least 100, assuming approximately 25 subjects develop a clinical cardiovascular endpoint, to achieve approximately 80 % power to detect a correlation of 0.82 (assuming a null correlation of 0.5), based on a two-sided α = 0.05 [R version 2.14.0 (www.r-project.org)]. In addition to the challenges of patient identification and selection, a further limitation in expanding the cohort size and in creating a useful clinical tool is the time- and labor-intensive procedure for the model construction and simulations. In the future, these protocols could be streamlined by improved methods for automated image segmentation, further advances in high performance computing such as the use of GPU computing, and efficiency gains by improving the computational solver methodology. Limitations of the modeling methods include the use of rigid walls, a Newtonian flow model, and the assumptions required for assignment of lumped parameter boundary condition values.

While previous studies have found differences in WSS between rigid and deformable wall simulations (Bazilevs et al. 2009), smaller WSS differences have been found in coronary arteries (Siogkas et al. 2011). However, there remains a need to quantify the effects of translation due to cardiac contraction, and radial expansion of the blood vessel walls over the cardiac cycle. A few prior studies have examined the hemodynamic impacts of coronary vessel wall motion. Prior work in Fontan surgery simulations showed little impact of FSI on PRT values (Long et al. 2012). Zeng et al. (2008) quantified differences in WSS between deformable wall simulations of the right coronary artery incorporating both translational and radial wall motion, against rigid wall simulations of the same anatomy. WSS magnitude and the temporal gradient of the local WSS were relatively unchanged, and differences in WSS between rigid and deformable simulations were negligible in the proximal regions of the CFD domain. Increasing differences down the length of the deformable vessels are likely explained by flow waveform damping due to compliant walls (Kung et al. 2011). It should be noted that the present study modeled the coronary anatomy at a fixed point in the cardiac cycle (at diastole) from the available clinical CT data. Effects of changing curvature and movement due to cardiac contraction should be considered in detail in future studies and could effect the conclusions.

Our FSI simulation of the left coronary aneurysm of patient A revealed acceptable differences in WSS between rigid and deformable simulations. These differences were well below those reported between aneurysmal and non-aneurysmal geometries, and between thrombosed and non-thrombosed vessels. Comparable differences were found between simulation and phase-contrast MRI experimental measurements in a recent in vitro validation study using a programmable flow pump and a model of the right coronary artery of patient A. As in prior studies, we also found a smaller deformation-induced WSS impact in the proximal region compared to the distal region. These findings suggest that with a combination of careful selection of CFD domain bounds and appropriate proximal boundary conditions, hemodynamics in the coronaries may be reasonably well captured via rigid wall simulations. In addition, most KD aneurysms have calcification, which stiffens the vessels and reduces deformation. However, the impact of fluid–solid interaction should continue to be investigated in future studies using full anatomical models in multiple patients. More realistic material models of the vessel wall are warranted in future studies to adequately describe the material response of individual layers (Holzapfel et al. 2005). To adequately prescribe coronary vessel movement, translation, and radial expansion, high-resolution time-resolved CT images, which are not currently clinical standard of care, may be required.

While we have provided justification for the necessary assumptions related to our choice of coronary boundary condition values, a comprehensive uncertainty quantification study should be performed, following methods proposed in recent work (Sankaran and Marsden 2011). Sensitivity analysis should be used to assess the effect of varying material properties with FSI, blood composition with age, boundary condition assumptions, waveform shape, cardiac mass, and other factors. A further limitation is the use of hemodynamic surrogates to predict thrombotic risk. Future studies could attempt reduced order modeling of the biochemical processes of thrombus formation (Xu et al. 2009). The work of Biasetti et al. (2011) provides a particularly elegant solution for relating coherent vortices from hemodynamics to platelet activation and should be incorporated in future studies of KD. This work revealed that vortical structures provided insight into locations of thrombus formation in abdominal aortic aneurysms and revealed important differences between Newtonian and non-Newtonian models. Finally, because this was a retrospective study, some variability in medical treatment and timing of imaging studies was unavoidable. Although we note that all patients with aneurysms in the study were treated with anticoagulant therapy prior to the imaging studies with no major changes in the treatment during the study period, we do not have clinical details regarding INR target, monitoring of INR, or patient compliance. We also note that there was a large variation in patient age, which may contribute to inhomogeneities in patient characteristics and assumptions.

This pilot study provided the first quantitative evidence that current AHA guidelines for determining thrombotic risk based on aneurysm diameter in patients with aneurysms caused by Kawasaki disease may be inadequate. This constitutes a compelling hypothesis that hemodynamics may more accurately select for thrombotic risk compared to aneurysm diameter alone, which should be tested in the future studies. More accurate patient selection for anticoagulation could avoid unnecessary treatment in some patients with large aneurysms, while identifying other at-risk patients who would benefit from systemic anticoagulation. A much larger cohort of patients is needed to construct a statistically significant clinical index to validate and corroborate these findings.