Estimated Risk Level of Unified SBRT Dose Tolerance Limits for Spinal Cord

Abstract

A literature review of more than 200 SBRT spine articles from the past 20 years found only a single manuscript that provided dose-volume data and outcomes for each spinal cord of a clinical dataset: the Gibbs 2007 article (2), which essentially contains the first 100 SBRT spine treatments from Stanford University Medical Center. The dataset is modeled and compared in detail to the rest of the literature review, which found 59 dose tolerance limits for the spinal cord in 1–5 fractions. We partitioned these limits into a unified format of high-risk and low-risk dose tolerance limits. To estimate the corresponding risk level of each limit we used the Gibbs 2007 clinical spinal cord dose-volume data for 102 spinal metastases in 74 patients treated by spinal radiosurgery. Fifty of the patients were previously irradiated to a median dose of 40 Gy in 2–3 Gy fractions and 3 patients developed treatment-related myelopathy. These dose-volume data were digitized into the DVH Evaluator software tool where parameters of the probit dose response model were fitted using the maximum likelihood approach (3). Based on this limited dataset, for de novo cases the unified low-risk dose tolerance limits yielded an estimated risk of spinal cord injury of ≤1% in 1–5 fractions, and the high-risk limits yielded an estimated risk of ≤3%. The QUANTEC Dmax limits of 13 Gy in a single fraction and 20 Gy in 3 fractions had less than 1% risk estimated from this dataset, so we consider these among the low-risk limits. In the previously irradiated cohort, the estimated risk levels for 10 Gy and 14 Gy maximum cord dose limits in 5 fractions are 0.4% and 0.6%, respectively. Longer follow-up and more patients are required to improve the risk estimates and provide more complete validation.

Spinal cord dose tolerance is of critical importance in stereotactic body radiation therapy (SBRT). Numerous studies have presented outcomes data and dose tolerance guidelines for the spinal cord in 1 to 5 fractions (2, 4–9). From these and other studies, several treatment planning constraints for the spinal cord have emerged (1). Using a DVH Risk Map (10) these spinal cord planning constraints can be organized into a unified format of high-risk and low-risk limits, based on the assumption that higher doses have relatively higher risk than the more conservative limits. With the addition of dose-response modeling, the DVH Risk Map can be enhanced to include statistically estimated risk levels of each dose tolerance limit based on clinical outcomes data. To date, assessment of associated risk of spinal cord complication has not been well quantified for SBRT and few dose-response models based on clinical data have been published. Gibbs et al. (2) previously published a dataset of relatively detailed dose-volume points for 102 spinal metastases in 74 patients in which there were 3 events of spinal injury. Treatment planning constraints for SBRT have become plentiful in the literature (1), but the relationship between these constraints and clinical outcomes has not yet been well established.

In order to develop a dose response model based on clinical data, we analyzed the Gibbs et al. published dataset with a probit dose response model and maximum likelihood parameter fitting to estimate spinal cord risk. In this report, we propose a method by which the estimated spinal cord risks from this analysis are included in the DVH Risk Map to develop a unified format of high-risk and low-risk spinal cord dose limits that can be used by clinicians to optimize treatment planning. Although this is not a sufficient amount of data to attain final estimates of risk, it is important to assess initial clinical validation of currently used dose tolerance limits as data emerges.

First 100 Spine SBRT Cases from Stanford

This article began as a literature review of spinal cord dose tolerance in 1–5 fractions. After searching 200 articles from the past 20 years, we determined that Gibbs 2007 (2) is the only article providing dose-volume data for each patient’s spinal cord and the corresponding outcomes. Essentially the Gibbs 2007 article represents the first 100 spine SBRT cases treated at Stanford University Medical Center. Given the profound rarity of such a dataset, the original authors were contacted, along with a team of key experts from several other institutions, in order to gain a more complete understanding of these cases, the models, and implications.

The literature review identified 59 dose constraints for spinal cord tolerance limits (1). We partitioned these limits into a unified format of high-risk and low-risk dose tolerance limits as elaborated in Appendix e1, and used statistical analysis of the Gibbs 2007 (2) published dataset of clinical outcomes to estimate the corresponding risk level of each limit. From the previously published series of 102 spinal radiosurgery treatments for 74 patients at Stanford University Medical Center with the Cyberknife radiosurgery system (Accuray, Inc., Sunnyvale, CA) from 1996 to 2005 by Gibbs et al. (2), we performed detailed dose-volume data analysis. The treatment planning and delivery details of the patient population were previously reported (2). In this series, the median follow-up was 9 months and there were 3 events of treatment-related severe radiation myelopathy; 50 patients had previously received radiation in 2–3 Gy fractions near or overlapping the SBRT site.

On the recommendation of Report Committee 25 of the International Commission on Radiation Units & Measurements (ICRU), we used the equieffective dose, EQDX_α/β, to account for the effects of different dose-time-fractionation schedules (11). Based on the Withers formulation (12) we defined the equieffective dose as EQDX_α/β = D(d + α/β)/(X + α/β), where d is the dose per fraction, D the total dose and X the reference dose per fraction. Two special cases of EQDX_α/β are 1) the 2Gy Equivalent Dose, EQD2_α/β, and 2) the Biologically Effective Dose (BED), EQD0_α/β, which is the limit as the reference dose per fraction X becomes infinitesimally small. For some of the comparisons, the same basic form of the linear quadratic (LQ) equation Nd₂ = n₁d₁ (d₁ + α/β)/(d₂ + α/β) was used to determine the N-fraction Equivalent Dose (NfxED), to convert from n₁ fractions of d₁ Gy to N fractions of d₂ Gy, by solving for d₂. Whenever possible the raw physical dose in Gy, was used except where one of these derived quantities is specifically stated. The original data from Gibbs et al. was described in terms of BED₃ (which is the same as EQD0₃). Thus, the dose response modeling was performed in terms of EQD0₃, and wherever possible we performed comparisons in terms of 3fxED since it is the parameter closest to a physical dose, and centered midway between 1 fraction and 5 fractions.

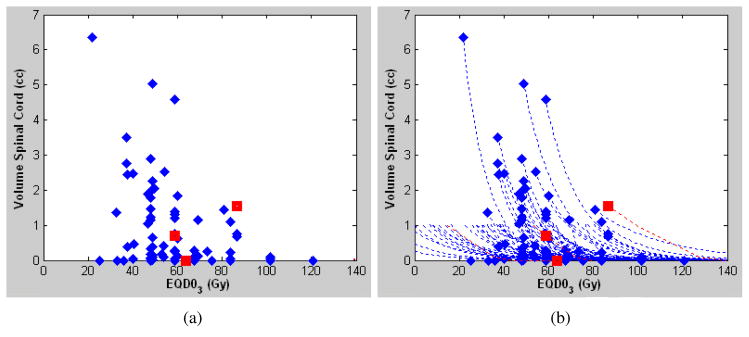
Seventy-two data points are discernible from the figure in the report by Gibbs et al. (2) and these data points, shown in Fig. 1(a), are the basis for the analysis in this report. Of these 72 visible datapoints from 102 metastases in 74 patients, 19 were from the 24 de novo patients and 53 were from the 50 previously irradiated patients. As may be seen from Grimm et al. (1), the most popular dose tolerance limits for spinal cord for SBRT have been the maximum point dose (D_max), the D_0.1cc, and the D_1cc, where D_V is the minimum dose to the “hottest volume” V. Dose response modeling was performed using the probit model for of each of the three parameters, D_1cc, D_0.1cc and D_max, separately for the de novo and re-treatment cases, as described below. For de novo cases, a sufficient number of published treatment planning constraints exist (1) to construct a DVH Risk Map, which is a comparative graph of dose tolerance, as previously described in Srivastava et al. (10). The estimated risk level of each dose tolerance limit was computed from the dose response model Eq. (1) as follows:

Figure 1.

Spinal cord dose-volume plot (a) from Gibbs et al. (2) and (b) with an approximated exponential DVH (dashed lines). The diamonds correspond to cases without complications and the squares correspond to cases with complications. Data points are the volume of spinal cord receiving 80% of the reference prescription dose or more.

Modeling Methods

All dose calculations used the MultiPlan Ray Tracing algorithm and all modeling was done in terms of EQD0₃. In order to approximate the dose corresponding to each parameter D_1cc, D_0.1cc, and D_max, an exponential y = y₀e^{−λ(x−x₀)} was used, where (x₀, y₀) are the coordinates of the data point in Fig. 1(a) in the manuscript, and a volume of y=0.05cc was considered to be sufficiently small to approximate the maximum dose. These approximated maximum doses were given to the authors of the Gibbs 2007 article, and they confirmed that all except two of them matched the actual doses within 3.5Gy, in terms of 3-fraction equivalent doses with α/β=3 Gy. The actual maximum doses were then provided as supplemental information by the Gibbs et al. (1) authors, along with the annotation of which of the dose-volume data corresponded to the cases that had previously received radiation. These actual maximum dose data points were combined with the data points of Fig. 1(a) to solve λ for each pair to generate the curves in Fig. 1(b). Furthermore, the exact D_1cc, D_0.1cc, and D_max doses for the three myelopathy cases were also provided, and also agreed with the approximations. Throughout the analysis the known doses were used wherever available. Each data point in Fig. 1(a) corresponds to a single approximated DVH curve in Fig. 1(b).

From the approximated DVH curves in Fig. 1(b), the doses at three volumes, D_1cc, D_0.1cc, and D_max, were interpolated for use in a probit dose response model:

$$\mathit{NTCP}=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^t{e}^{-x^2/2}dx$$ (1)

where t = (D_V − TD₅₀ (V))/(m × TD₅₀ (V)), m is the normalized slope. Dose corresponding to a variety of volumes are used in the literature including V=1 cc, V=0.1 cc, and V=0 (D_max) (1). Therefore we separately fit the model to the complications data for each of these volumes. The analytical dose response curves were each optimized independently, using the maximum likelihood technique (3) in two dimensions:

$$L({\gamma }_1,{\gamma }_2)=\prod _{\begin{array}{c}m\\ \mathit{complications}\end{array}}{\mathit{NTCP}}_m({\gamma }_1,{\gamma }_2)\times \prod _{\begin{array}{c}n\\ no\mathit{complications}\end{array}}(1-{\mathit{NTCP}}_n({\gamma }_1,{\gamma }_2))$$ (2)

For the model in Eq. (1), the two parameters to be solved are γ₁ = m and γ₂ = TD₅₀ (V), jointly in two dimensions; the analysis was performed separately for each volume (1 cc, 0.1 cc and D_max), for de novo cases. Only D_max was analyzed for the re-treatment cases. The fitted m and TD₅₀(V) parameters (Table 1) were constrained to clinically realistic values; any such limitations are clearly explained in the Results section. When the prior cord dose is known techniques are available to account for it (16). However, in this clinical dataset the re-treatment cases had a median prior dose of 40 Gy (range: 13–62 Gy) in 2–3 Gy fractions at a median time interval of 14.6 months (range: 2–354 months) (1) although detailed prior spinal cord dose information was not available.

Table 1.

Dose-response parameters for probit model

Group	Volume V (cc)	EQD03		3fxED
		m	TD50(V), (Gy)	TD50(V), (Gy)
De novo	1.0	0.2506	108.0	27.0
De novo	0.1	0.2506	164.3	34.2
De novo	0 (Dmax)	0.2680	188.0	36.9
Re-treatment	0 (Dmax)	0.3438	188.0	36.9

^*The slope for D_1cc was constrained not to exceed the slope for D_0.1cc or D_max.

^†The TD₅₀(V) for the re-treatment cases was constrained not to exceed that for the de novo cases.

Confidence intervals were determined using the profile likelihood method (17, 18), with the value of 0.495 from the χ² distribution as the threshold to obtain a contour on the three-dimensional log-likelihood function corresponding to the 68% confidence region. The effects of the confidence region on the dose response curve were determined by considering all combinations of m and TD₅₀ (V) within this contour, and plotting the full extents as the dashed green confidence intervals in the figures.

Emami et al. (19) gave the 5% and 50% risk levels for many critical structures in conventional fractionation, and this is convenient both clinically and mathematically, since the TD₅₀(V) is one of the main modeling parameters. However, for the most critical structures like spinal cord, the 50% risk level is not acceptable clinically, so this modeling parameter will continue to be quite uncertain. In fact, if left unconstrained for the re-treatment cases this clinical dataset, the TD₅₀(V) values would exceed EQD0₃=500Gy, which is more than double that of the cases without prior irradiation. It is not expected that the tolerance dose for re-treatment cases would exceed that of the de novo cases, so in this work we have constrained the TD₅₀(V) for re-treatment cases not to exceed the corresponding TD₅₀(V) for de novo cases.

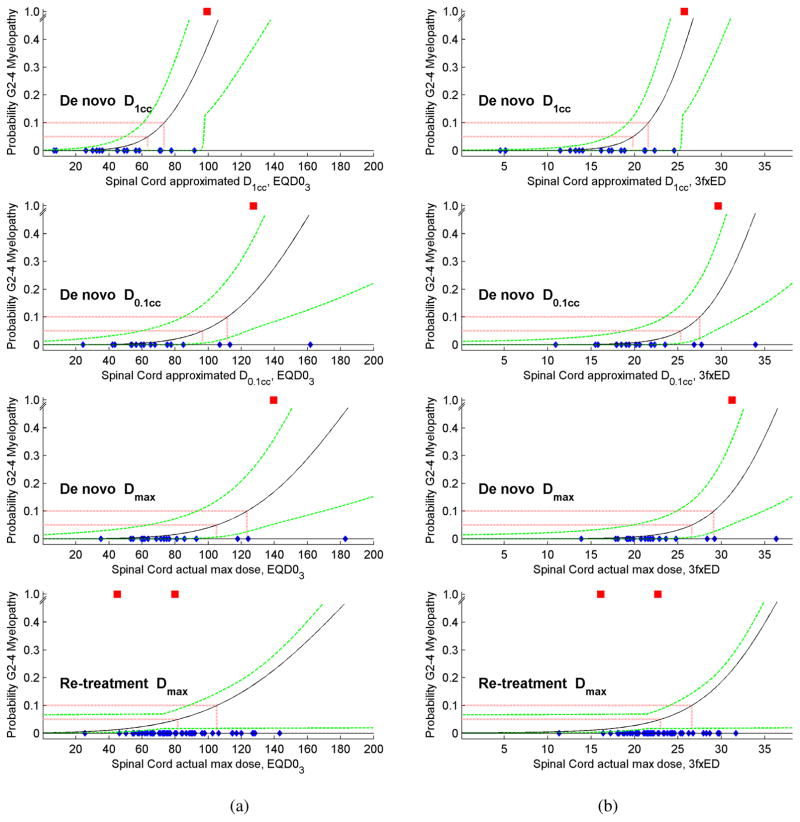
One other modeling issue due to the sparseness of the dataset is that in the top subplot of Fig. 2 it is apparent that the D_1cc of the myelopathy case is higher than the D_1cc of any of the other cases. This means that if left unconstrained, the fitted slope from the maximum likelihood algorithm would tend towards infinity, which is clinically unrealistic. This was easily overcome by constraining the slope for D_1cc to not be steeper than any other slope in this dataset, which corresponds to the normalized slope value m=0.2506 of the D_0.1cc parameter. For any such constraints on the algorithm, the confidence intervals were computed both with and without the constraint and the widest range was plotted, to see the full impact of the uncertainty.

Figure 2.

The probability of Grade 2–4 Myelopathy was modeled (a) as it was computed in terms of EQD0₃, and (b) after conversion to 3-fraction equivalent doses (3fxED). For de novo cases the subplots are for D_1cc, D_0.1cc and D_max, and for the re-treatment cases the subplot is for the SBRT D_max only, without volumetric data. The myelopathy cases are plotted as red squares, the cases without complications are plotted as blue diamonds, the probit model is the solid black line, the 5% and 10% risk levels are plotted as red dashed lines, and the 68% confidence intervals are plotted as dashed green lines.

Dose Tolerance Results

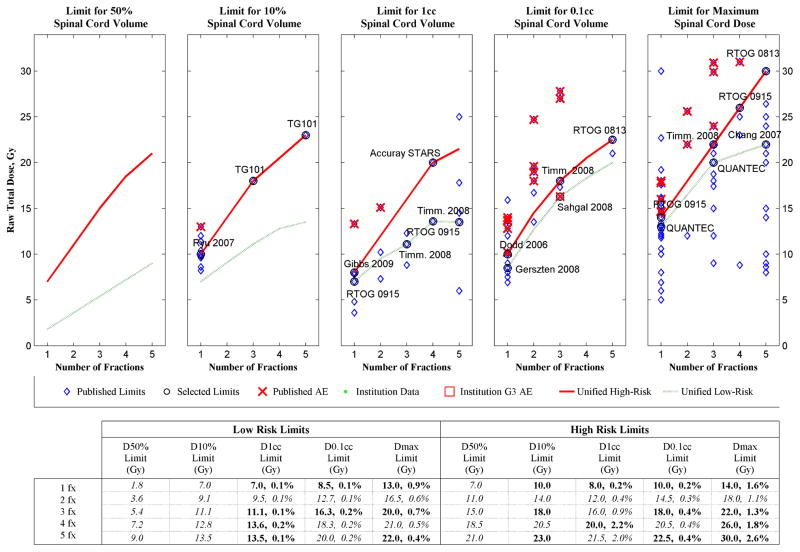
Dose response modeling of probability of Grade 2–4 myelopathy results are shown in Fig. 2, both in terms of EQD0₃ and converted to 3fxED. From these analytical dose response curves, the table in Fig. 3 shows the estimated risk level corresponding to the dose tolerance limits found in the literature review (1) as part of a DVH Risk Map (10). Instead of creating yet another set of dose tolerance limits, whenever possible we used the clinical data to validate limits from existing publications, only adding new limits where they were missing from the high risk and low risk partitions, as may be seen from Appendix e1 and from the DVH Risk Map in Fig. 3.

Figure 3.

DVH Risk Map for spinal cord toxicity showing estimated risk level of unified SBRT spinal cord dose tolerance limits for de novo treatments, in terms of raw physical dose (Gy). Bolded limits are published data and italicized limits are interpolated or extrapolated, the blue diamonds correspond to the published dose tolerance limits from the literature review (1), the circled diamonds with text labels are the selected limits from Appendix e1, the red X’s are dose-volume points corresponding to published adverse events, the red solid lines are the unified high-risk limits, and the green dashed lines are the unified low-risk limits. In the tabular portion of the figure, within the 1 cc, 0.1 cc and Max Limit cells the number on the left is the dose tolerance limit in Gy, and the number on the right is the corresponding risk level estimated from this dataset.

Spinal cord definitions, imaging and contouring techniques, and treatment types varied substantially among the dose tolerance limits found in the literature review (1), as may be seen from Table e2 in Appendix e1, to the extent that very few publications had the same combination of these parameters. However, the clinical dataset used to construct the dose response model is entirely from a single institution with one set of these parameters. Therefore, regardless of the origin of the dose tolerance limits in Fig. 3, the estimated risk level is applicable for the single configuration of actual spinal cord contoured on MRI-CT fusion for spinal metastases treated with CyberKnife spine tracking, and all the other exact circumstances of Gibbs et al. (2). Differences from any of these factors must be considered before applying these results in any other conditions.

For re-treatment cases, the literature review (1) showed that much less dose-volume data is available, therefore only the model for D_max was included in Fig 2. In five fractions, the estimated risk levels of the typical 10 Gy and 14 Gy maximum cord dose limits are 0.4% and 0.6%, respectively.

For de novo cases, the DVH Risk Map in Fig. 3 includes a graphical comparison of a partition of high-risk and low-risk dose tolerance limits in 1–5 fractions, each for five specified volumes, D_50%, D_10%, D_1cc, D_0.1cc and D_max. According to this analysis the selected D_0.1cc limits all have less than 0.5% risk. The selected low-risk D_1cc limits use doses that are about half that of the corresponding high-risk D_1cc limits, and as a consequence the low-risk D_1cc limits all have 0.2% or lower estimated risk. In this series the high-risk D_1cc and D_max limits represent the highest risk of complication, although the overall incidence is so low that much additional data will be required to determine the most reliable estimates.

Discussion

Although stereotactic body irradiation has become an important technique in the arsenal of the radiation oncologist, understanding radiation dose tolerance of the spinal cord to these hypo-fractionated radiation regimens remains elusive. A number of guidelines for spinal cord dose tolerance are currently in use. However, few dose-response models based on clinical data have been published. By using a clinical dataset in which spinal toxicity was observed, we have applied the dose-volume parameters to guidelines currently in use to ascertain initial quantitative estimates of toxicity risk. Based on this limited dataset, for de novo cases, the unified low-risk dose tolerance limits yielded an estimated risk of spinal cord injury of 1% or less in 1–5 fractions, and the high-risk limits yielded an estimated risk of 3% or less.

The rare incidence of myelopathy presents a challenge to clinicians because it is the primary dose-limiting factor of spinal treatments, yet without a sufficient number of reported complications clinicians have not had a way to validate the dose tolerance limits they must use. At the time of the Sahgal 2013 review (4), only 9 cases of radiation myelopathy following SBRT had been found in the literature. Since it is not likely for a large amount of complications data to emerge soon, it is important to glean the most information possible from the available published data. Examination of the confidence intervals in Fig. 2 can provide additional insight into the limitations of the present analysis. For D_1cc at effective doses of 25Gy or higher in 3 fractions, the confidence intervals are quite loose, and the sharp angle of the confidence interval above 25Gy is due to uncertainty of the probit model slope parameter. However, despite the limitation, it may be seen that in the range of most of the clinical data at D_1cc<20Gy, the confidence intervals become reasonably tight. Hence the confidence intervals depict what we already know clinically; until the response at higher doses is better understood, the predominance of clinical data is likely to remain at the lower doses.

For the re-treatment cases the complications occurred at lower doses than in the de novo cases, and within the re-treatment data no dose response is evident. If dose were not a factor, the complication probability would be 2/53 = 3.8% for any dose, and it is apparent that this value is within the confidence intervals in Fig. 2. However, it does not seem likely that the tolerance for the re-treatment cases could be higher than for the de novo cases, so we constrained the TD₅₀(V) of the re-treatment cases not to exceed that of the de novo cases. The confidence intervals have been generated by taking into account both possibilities with and without this constraint, and they are still reasonably tight throughout the majority of the current clinical range, diverging at doses above which there is not much data.

While we tend to be very conservative clinically, these models of dose-volume effects in high-risk and low-risk categories could be useful to clinicians to in several ways. Firstly, this strategy of modeling may allow clinicians to evaluate alternative treatment plans based on acceptable risk levels appropriate for each unique clinical situation in order to better optimize radiation treatment. In addition, this approach may also allow clinicians to become more comfortable in devising more aggressive regimens when necessary such as for radioresistant tumors in order to improve the effectiveness of treatment.

A key parameter in this study was the choice of α/β for late spinal cord effects. In conventional fractionation QUANTEC estimated α/β= 0.87 Gy (95% CI: 0.54–1.19 Gy) for cervical cord but were unable to achieve a good fit for thoracic cord (9). For purposes of roughly comparing different regimens QUANTEC used α/β=3 Gy for their Tables 3 and 4, but cautioned that “it is not appropriate to extrapolate cord tolerance data obtained at a low dose per fraction to regimens using 10 Gy or more/fraction” (9). Although α/β values ranging from 1–4 Gy have been used for spinal cord (9) our analysis is based on an α/β=3 Gy because the clinical dataset from Gibbs et al. (2) reported its findings based on α/β=3 Gy. In terms of EQD0 this could cause a difference of up to 145.7% for the doses encountered in this manuscript, but in terms of equieffective physical dose in 1–5 fractions the corresponding difference is only about 4%. The largest absolute dose difference in terms of EQD0 will occur at the highest biologically effective doses, which will be the 14Gy in 1 fraction RTOG 0915 max dose limit, or the 30Gy in 5 fractions RTOG 0813 max dose limit, depending on which α/β is used. Based on the analysis in this manuscript, a risk level of 2.6% is associated with EQD0₃ = 90Gy, which corresponds to 30Gy in 5 fractions, 24.3Gy in 3 fractions, and 15Gy in 1 fraction. Using α/β=1, the 24.3Gy in 3 fractions converts to 14.4Gy in 1 fraction and 30.8Gy in 5 fractions, which only differ from the α/β=3 counterparts by 4.1% and 2.8%, respectively. The EQD0₁ of 24.3Gy in 3 fractions is 221.1Gy which differs by 145.7% from the EQD0₃ of 90Gy which might seem problematic, but the equieffective physical dose to the patient differs by less than 1Gy for the different assumed values of α/β.

Daly et al. (5) demonstrated that spinal cord dose tolerance in a single fraction is dramatically different than predicted by the Lyman-Kutcher-Burman (LKB) parameters (13). Neither the LKB nor Schultheiss parameters (9, 14) for conventional radiation therapy were found to be suitable for SBRT spinal cord tolerance (5). Therefore, instead of using maximum likelihood techniques to optimize the α/β ratio as in Daly et al. (5), we have fixed α/β and used maximum likelihood to estimate new TD₅₀(V) and m values for a probit model based on the available approximated dose-volume points.

The QUANTEC report (9) stated that the reported risk of myelopathy is low (<1%) when the maximum spinal cord dose is limited to 13 Gy in a single fraction or 20 Gy in three fractions. Our estimated risk levels for those limits are 0.9% and 0.7%, respectively, which confirms their opinion.

The recent paper by Sahgal et al. (4) is a landmark study for spinal cord tolerance specific to spine SBRT. In that study it is important to note that the complete DVH data were centrally reviewed for each of the 9 radiation myelopathy (RM) cases and the 66 controls, and that it is a multi-institutional study spanning various treatment platforms. Detailed analysis for volumes ranging from a point maximum to 2 cc was provided and as yet these data are unparalleled in quality. They also based their analysis on the thecal sac as a surrogate for the true cord as there are several factors that make spinal cord delineation a challenge, and several sources of uncertainty in treatment planning and delivery such that the dose delivered to the spinal cord can be greater than that expected from the treatment planning system. As compared to the current analysis and other sources of expert recommendations, the Sahgal estimates are lower than this study. For example, using the LQ model with α/β=2 Gy, 25.3 Gy in 5 fractions is estimated by Sahgal et al. (4) to have a ≤5% risk level, whereas this study estimated the RTOG 0813 limit of 30 Gy in 5 fractions to only have a 2.6% risk level. The most likely reason is that the actual risk of RM from SBRT is quite low in general, within a narrow range of what we would consider reasonably safe practice, and in the Sahgal study there were cases of RM secondary to quite low and unexpected point maximum doses that drove the model to be more conservative than that generated by the current study. For example, amongst the 9 RM cases point maximum doses of 10.6 Gy in 1 fraction, 13.1 in 1 fraction, and 14.8 Gy in 1 fraction resulted in RM and this was again confirmed with central review of the raw DVH data. Nevertheless, Sahgal et al. (4) have presented a landmark analysis of spinal cord tolerance for SBRT with quite reasonable agreement to QUANTEC and the results of this study, which all combined should help provide confidence for clinical practice. Analysis of the Gibbs et al. data demonstrates that the low-risk limits compiled from review of many publications yielded estimated spinal cord complication probability less than 1%. Indeed even in the setting of previously irradiated patients, our results show that spinal cord complications from SBRT are very rare.

To the purist modelers such sparse data is frustrating. From a clinical perspective, however, we are glad that the spinal cord dataset has the fewest complications of all, and we hope that these side effects continue to be rare. We feel it is best to fully extract as much information as possible from this dataset that already exists because is not likely that much more data will emerge soon, with only 9 reported cases of myelopathy reported worldwide in de novo SBRT treatments (4), and no further case of new myelopathy at Stanford in the past 10 years.

Conclusions

Spinal cord dose tolerance for SBRT in 1 to 5 fractions is dramatically different than what can be accurately extrapolated from conventional fractionation. Many publications have provided preliminary insight at least sufficient to prove clinical feasibility, but much work still remains to determine statistically reliable limits for optimal clinical use. Since the risk of complications appears to be low under current clinical procedures, a large amount of data will be required to attain more reliable statistical estimates of risk. By partitioning the currently published SBRT spinal cord dose tolerance limits into a unified format of high-risk and low-risk groups, and estimating the risk level of each limit based on clinical data, we provide a potentially useful technique to help physicians to optimize radiation treatment plans for each patient. We have presented preliminary estimates of risk for 18 commonly used dose tolerance limits in a unified format of high and low risk, to provide initial validation of current clinical practice.