Some Behavioral Science Measurement Concerns and Proposals

Abstract

Primarily from a measurement standpoint, we question some basic beliefs and procedures characterizing the scientific study of human behavior. The relations between observed and unobserved variables are key to an empirical approach to building explanatory theories and we are especially concerned about how the former are used as proxies for the latter. We believe that behavioral science can profitably reconsider the prevailing version of this arrangement because of its vulnerability to limiting idiosyncratic aspects of observed/unobserved variable relations. We describe a general measurement approach that takes into account idiosyncrasies that should be irrelevant to the measurement process but can intrude and may invalidate it in ways that distort and weaken relations among theoretically important variables. To clarify further our major concerns, we briefly describe one version of the measurement approach that fundamentally supports the individual as the primary unit of analysis orientation that we believe should be preeminent in the scientific study of human behavior.

Behavioral science is generally not considered to be “hard” science like physics, chemistry, or astronomy. Nevertheless, behavioral science is very difficult science. It is difficult because its focus is the behavior of human beings rather than attributes of inanimate objects such as prisms, plastics, and planets. We do not accept the idea, however, that because of the difficulties behavioral science is forever doomed to be inferior to the so-called “hard” sciences. To the contrary, we think there is reason for optimism provided that some fundamental adaptations are made to the ways we theorize about measurement, conduct the measurement process, and use the resulting measurements in research and theory construction. The arguments we will present here are mainly conceptual rather than statistical and empirical. We do this because we aim to communicate with as broad an array of behavioral science colleagues as possible about matters that are absolutely fundamental to the scientific study of behavior. Rigorous technical presentations, both past and contemplated, are essential components of our agenda but in this instance we have opted not to rely on them. Similarly, we have chosen not to address some philosophy of science matters that are ultimately interesting and important. It is our hope that others will examine such matters in future work.

We contend that measurement in behavioral science reflects insufficiently that our primary unit of study–the behaving organism–is animate rather than inanimate and that the methods developed and used effectively by physical science disciplines give rise to serious problems when slavishly applied to the behavior of living organisms. We will explain our concerns regarding measurement in detail and describe an approach to measurement and modeling that illustrates a different way to think about these matters; one that we believe can be helpful in alleviating the concerns we raise.

Scientifically Studying Human Behavior

Measurement is fundamental to science. In our view, major problems in conducting behavioral science are first encountered at the measurement stage where they are not resolved optimally and, as a consequence, are further exacerbated at later stages, including modeling and theory development and testing. The negative effects are systemic because any subsequent use of already problematic measurements to model and explain behavior and behavior change is correspondingly flawed. The “downstream” negative effects of measurement problems undermine the development and rigorous testing of theory, thereby jeopardizing prediction and explanation–two primary activities of successful scientific disciplines.

We embrace the development of theory involving latent (not directly observed) variables to formalize lawful relations concerning the behavior of living organisms. Latent variables are illustrated, for example, in such venerable, but for our purposes here still useful, hypothesized relations as “Frustration produces Aggression.” Both Frustration and Aggression are latent variables, not directly observed. Because of the indispensable role observation plays in empirical inquiry, the business of measurement in behavioral science is very much focused on clarifying and quantifying the links between these unobserved latent variables and the observed, manifest variables that represent them, so that the relations among the former can be tested, evaluated, revised, and further tested. Aggression, for example, is a latent variable that can manifest in many different observed variables, some verbal (e.g., swearing), some mental (plotting revenge), some physical (hitting or slapping). Because Aggression cannot be measured directly, we must infer its presence from witnessing its observed manifestations. Frustration is a state that is not directly observed but which is inferred from the presence of circumstances that may be different for different people. Therefore, to test empirically the validity of an hypothesis such as “Frustration produces Aggression,” convincing links must be forged between the two latent variables and the observed manifest variables used to infer the presence of the latent ones. Forging these links well is a primary concern of measurement.

Science is mainly about accounting for similarities in the objects being studied and variables are the primary reference frame for such accounting.¹ For behavioral scientists, lawful relations describe similarities, not dissimilarities, in behavioral attributes. Kluckhohn and Murray (1953) observed that “… for general scientific purposes the observation of uniformities, uniformities of elements and uniformities of patterns, is of first importance. This is so because without the discovery of uniformities there can be no concepts, no classifications, no formulations, no principles; no laws; and without these no science can exist (pp. 55–56).”

The “Frustration produces Aggression” example implies similarities, at some level, in the way frustrated people behave. But different individuals actually manifest Aggression in different ways just as it takes different kinds of events to frustrate different individuals. The measurement problems to which we alluded earlier are intimately tied to the nature of manifest (observed) variables and are thus amplified by the differences in how appropriately given observed variables represent particular latent (unobserved) variables in different individuals. If every individual invariably slapped everyone who frustrated them, we would be well on the way to forming a law at the manifest variable level, but slapping someone when frustrated is not how most people behave. Nevertheless, observation is critical to behavioral science, so let us take a closer look at the scientific role played by manifest variables in trying to characterize important features of behaving organisms.

Substituting two manifest variables for the two latent variables Frustration and Aggression limits, perhaps greatly, the scope regarding behavioral similarities among individuals. Whereas “Frustration produces Aggression” applies generally to individuals and includes a variety of different circumstances and behaviors, an empirically testable version such as “Inability to solve a math problem (from which we infer Frustration) produces swearing (from which we infer Aggression)” may not apply to even most people and certainly not to those who do not swear or who have no investment at all in mathematics. The point is that lawful relations, to be general, employ latent variables, rather than manifest ones. Nevertheless, given the integral role of observation in conducting empirical science, we have to emphasize and respect the crucial role of linkages between latent variables and the manifest variables by which we infer them–as noted above, a key role of measurement.

Accounting for similarities in human behavior is not a simple task. Consider the sentiment “No two people are alike.” with which it is difficult to disagree–even when observing the behavior of monozygotic twins. Taken simply at face value the sentiment negates applying scientific methods to the study of people. But “No two people are alike.” characterizes only some of the behaving individuals’ attributes, not all of them, and part of the scientist’s responsibility is to distinguish between the variables on which there are similarities and those on which “No two people are alike.” Rather than signifying hopelessness regarding the study of human behavior “No two people are alike.” can be taken as a cautionary reminder that there may be some aspects of behavior that do not yield to conventional scientific examination.²

Nesselroade (2010) attempted to characterize an approach to studying behavior that falls somewhat outside of the two disciplines of scientific psychology–experimental and differential–so effectively identified by Cronbach (1957) a half-century ago but which fits closely with the ideas being promoted here. Essential features of this third approach are: (1) the focal unit of analysis is the individual, not averages and not the differences among individuals (see e.g., Cervone, 2005; Molenaar, 2004); (2) the primary source of variation under scrutiny is intra-individual–the varying of a person over time and/or situations and conditions³ (see e.g., Nesselroade & Molenaar, 2010); (3) behavior is modeled primarily at the latent variable level with data arising from repeated, multivariate measurement of manifest variables; and (4) it is the identification of similarities among individuals more than the assessment of their differences that directs theory development and its attendant empirical research. Elements of this third approach have been practiced for a long time (see e.g., Robinson, 2011), but it has yet to attain the straightforward coherence of the differential and experimental disciplines.

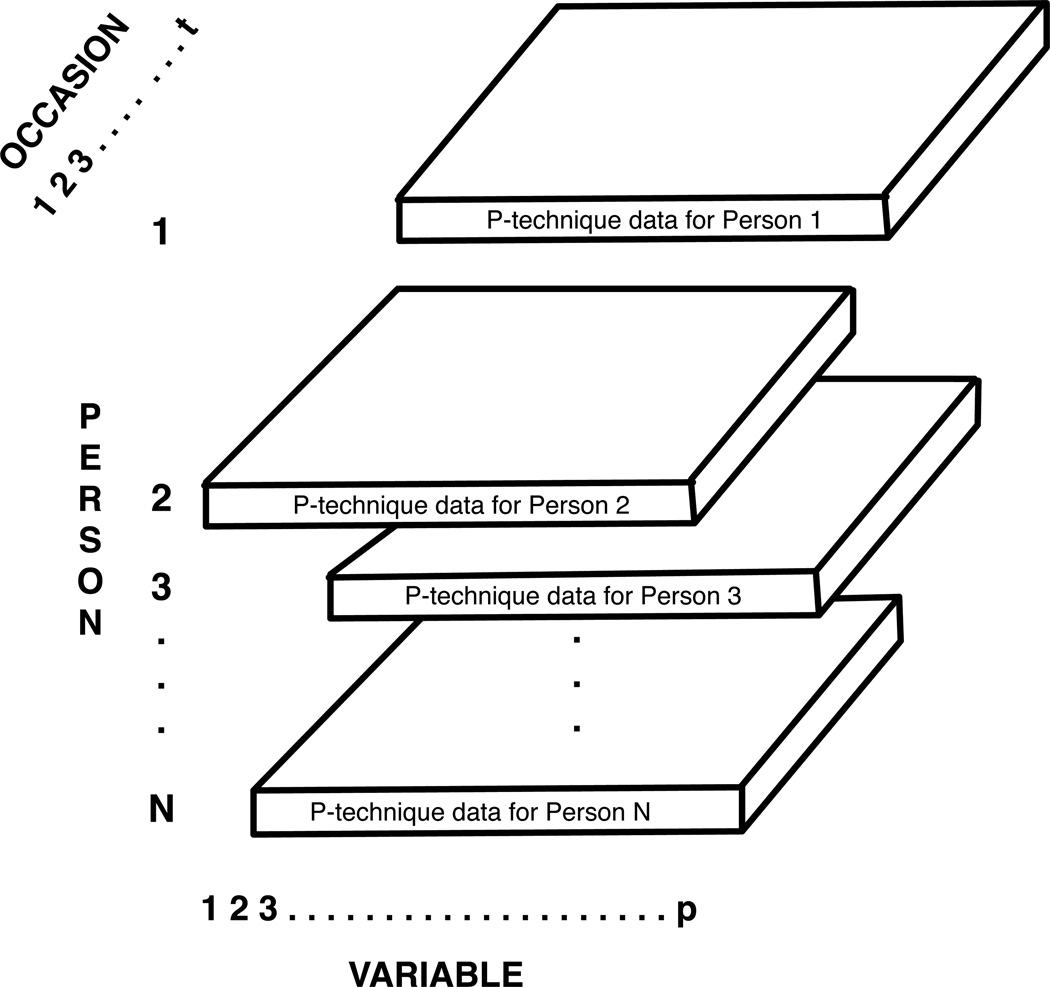
Nesselroade and Ford (1985) discussed the case for multivariate, single-subject research designs with built-in replications as a promising approach to studying behavior. In brief, their proposal was to conduct several multivariate, single-subject factor analytic research designs in concert in order (a) to identify patterns of individual behavior that might then (b) be shown to be replicable over individuals rather than to simply pool individuals’ data initially and define common patterns ipso facto on the pooled data. Operationally, such designs amount to collecting multivariate time series (MTS) data on each of multiple participants. Inferences can then be rested on the outcome of fitting models to each individual’s MTS data separately then attempting to establish similarities and differences in those individual models, primarily in their similarities. The basic data-gathering design is depicted in Figure 1. Fitting the common factor model to the MTS of one individual was labeled P-technique factor analysis by Cattell (see e.g., Cattell, Cattell, & Rhymer, 1947; Cattell, 1963), a term that seems now well-ensconced in the multivariate literature.⁴ Nesselroade and Ford (1985) called this configuration the MRSRM design (Multivariate Replicated Single-subject Repeated Measurement design) and recommended it for conducting research that falls within the tradition contrasted above with the experimental and differential traditions. Use of MRSRM designs has been well-illustrated in, for example, the domain of self-reported affect (e.g., Lebo & Nesselroade, 1978; Zevon & Tellegen, 1982). In those studies, the MTS of self-reported affect scores were first factor analyzed individual by individual (a series of P-technique factor analyses) and then the factor solutions were examined for similarities across the participants. As reported by Nesselroade (2007), the results of the Lebo and Nesselroade (1978) study revealed strong between-person similarities more so at the level of factor intercorrelations than factor loadings.

Figure 1.

Multivariate Replicated Single-Subject Repeated Measurements (MRSRM) Data Consisting of a p variables × t occasions Data Matrix (P-technique data) for each of N persons.

Questioning the Sanctity of Observable Variables

To foreshadow what is coming, the major departure from measurement orthodoxy in what we will be proposing is to hypothesize and test latent variable interrelations by using possibly different manifest variable representations of the same latent variables for different individuals because given manifest variables may not adequately represent a given latent variable for all individuals. In other words, with regard to behavior we question the sanctity of observed variables as a sine qua non of empirical science. That sanctity seems to be a fundamental tenet of empirical science and one seemingly taken for granted; incorrectly so, we believe. The challenge attendant to our questioning is how to define the same latent variable when different manifest variables are used to anchor it empirically. Subsequently, this matter will be delved into more extensively.

Nesselroade and Ford (1985) registered some uneasiness regarding the use of manifest variables to represent latent variables that has since blossomed into the major concern being articulated in the present article. They asserted that: “The possibility that a given observable may have a different significance for different persons, or that different observables may signify the same thing to different persons raises doubts about the mindless aggregation of data in group designs. The distinction between observable behaviors and inferred constructs, which has been a central aspect of P-technique research since its inception, provides a conceptually powerful way to address the matter of replicability either at the level of observables, where it may or may not be found, or at the level of unobservables inferred from multivariate covariation patterns (p. 67).” With the term replicability, they were referring to similarities in relations across different individuals.

As noted earlier, the key role of manifest variables in building and evaluating theory is to provide access to the latent variables involved in articulating lawful relations. The fundamental reason for the measurement difficulties to which we alluded earlier is that the manifest variables on which we rely to represent the latent variables of theory do not dependably provide a reference frame for making and using observations that has the same meaning from one person to another. Yet our methods, which rest heavily on the aggregation of information across multiple individuals, tacitly assume that manifest variables do provide such a common reference frame. For the moment, assume that Frustration produces Aggression. One who elects empirically to test the hypothesis by examining whether or not “presenting an insoluble problem results in slapping someone who is handy” will find that the relation obtains for a certain number of people–certainly not all; not because “Frustration produces Aggression” doesn’t hold, but because not everyone is Frustrated by trying to solve an insoluble problem nor does everyone who is thusly Frustrated display Aggression by slapping someone nearby. The failure isn’t with the general principle but with the observable (empirically testable) representation of the general principle. But behavioral science, with its roots still tapping the deep waters of operationism, tends to eschew this interpretation and, instead, accepts that the relation between Frustration and Aggression is unfortunately a weakened one that can best be expressed probabilistically.⁵

Put simply, we contend that manifest variables may not provide generally trustworthy access to latent variables. This is not a felicitous situation because much of the quantitative modeling of behavior being done today leans heavily on these manifest/latent variable relations–the so-called measurement model in much of contemporary behavioral science modeling. We note that the basic ideas being articulated here have antecedents and correlates strewn widely through the behavioral science literature. Kagan’s discussions of homotypic and heterotypic continuity (Kagan, 1971), for instance, recognize the plasticity of the manifest/latent variable linkages. We take the notion further by allowing those linkages to vary from person to person to the extent that a given manifest variable might not even be considered to be the same variable across individuals. For example, in a far remove from the developmental literature, Rijmen, de Boek, and Leuven (2002) introduced an Item Response Theory (IRT) model that contains both item parameters and person parameters such that not only do the person parameters affect performance but the item features can “have a different effect across persons on the probability of success”(p.272). In other words, a given item may very well not reflect the same properties from one individual to another. The concept of Differential Item Functioning (DIF) in IRT has some pertinence to the present discussion. Also in the general IRT framework, considerable work has been done on the development of measurement devices that are “tailored” to the attributes of the individual (see e.g., Woodcock & Johnson, 1990). Embretson and her colleagues (e.g., Embretson, 1999; Embretson & Poggio, 2012) have examined relevant matters in great detail, including important issues of measurement device construction. Such work is tantamount to attempting to measure a given latent variable with different manifest variables for different individuals. As will be seen subsequently, we offer a particular rationale for why this orientation to measurement seems to us compelling.

Breakdowns in the relations between manifest and latent variables is obviously problematic–but it happens and the literature is replete with examples. Several instances of problematic manifest/latent variable relations will now be considered. Subsequently, we will identify the problems in the context of the data box (see e.g., Cattell, 1966b).

Psychologists rely a great deal on self-report in one form or another. But the continuity in meaning of even the same adjective as might be used in self-ratings is not guaranteed. Even persons who share a common language use its words somewhat idiosyncratically. Anxious means nervous and jittery to one person and eager to another person. Sanctions can be supportive in the case of sponsoring events or detrimental when punishments are being meted out. Sometimes the ambiguities are reduced by supplying contextual information but other times such information is omitted. What does it mean when such mixed-message data are aggregated over many individuals and used to render calculations such as averages?

Also in the self-report framework, anyone can examine a rose and respond to the question, On a 10-point scale, how beautiful is this? The rose is the same objective piece of organic matter but to assume that the rating given by an accomplished still-life painter is commensurate with the rating given by a hyper-allergic sneezer is untenable, we believe. More to the point, we question whether the different individuals’ recorded observations of the flower’s beauty are sufficiently commensurate to justify aggregating them across individuals. If not, such measurements should not be the basis for attempting to develop lawful relations. To use such ratings to create averages, draw inferences about aesthetic sensitivities, etc., confuses, distorts, and confounds matters.

In the cognitive area, it has been known for a long time that scores on a learning task (manifest variable) can reflect differences in factor composition (latent variables) from one group of trials to another (e.g., Fleishman & Fruchter, 1960). In a repeated memorization task, for example, early trial performance might reflect memory ability and later trial scores might reflect reasoning ability as the importance of being able to form strategies comes into play. Thus, the relations between manifest and latent variables differs from trial to trial. And that is within the same individual. The problem is likely to be compounded between individuals. Similarly, constructing a list of words (to provide manifest variable scores) to measure spelling ability (latent variable) can be problematic if used with a range of ages. The very same list of words used in a spelling test can reflect spelling ability at age 10 and interest, motivation, attention, etc., at age 16. Also from the cognitive arena, Luce (2000) drew attention to the substantial subject-specificity of human decision making, even in simple standard experimental tasks, concluding that “Each axiom should be tested in as much isolation as possible, and it should be done in-so-far as possible for each person individually, not using group aggregations (p. 29).”

In a very different arena, specificity of response in regard to the functioning autonomic nervous system highlights another class of variables that may well not have the same meaning from one individual to another (see e.g., Stemmler, 1992). For instance, respiration rate (manifest variable) has something in common across individuals but it also reflects unique histories of learning and conditioning that can make it different, as an indicator variable, from one person to another.

Another example comes from brain imaging in cognitive neuroscience. Even in the so-called resting state (when no task is being performed), as well as under task conditions the effective networks connecting brain regions of interest are found to be subject-specific to a substantial degree. The heterogeneity is great enough that pooling across subjects can lead to nonsensical results, including the emergence of so-called phantom connections which do not exist for any of the subjects involved in the pooling, necessitating new methodological innovations that can deal with it (see e.g., Gates & Molenaar, 2012).

The foregoing examples illustrate how the same latent constructs can be manifested differently for different individuals as well as differently for the same individual at different times. A related aspect is that despite different manifestations over time an underlying latent processes can be invariant over individuals. That the same latent processes can manifest themselves differently across replications or across time arises in different scientific disciplines, including the “hard” sciences. Consider the example schematized in Figure 2. To estimate the direction-of-arrival of airplanes by means of radar, and using the simplest possible scenario to describe it, consider a linear array of M equidistant radar stations, with distance Δ between adjacent stations. The reflected electromagnetic radiation by the d^th airplane, d=1,2,…,D, can be represented by a plane wave if the airplanes are sufficiently far away. The angle of the straight line connecting the d^th airplane with each radar station is approximately θ_d. Define the so-called spatial frequency ${\mu }_d=-2\frac{\pi }{\lambda }\mathrm{\Delta }\mathit{\text{sin}}{\theta }_d$, where λ = f_c/c, f_c is the carrier frequency of the radar signal and c the speed of light.

Figure 2.

Direction-of-Arrival Estimation in Aircraft Control as a Factor Model. Δ is the distance between adjacent stations and θ_d is the angle of the straight line connecting the d^th airplane with each radar station.

The true signal reflected by the d^th airplane and received at the m^th station is: S_md(t) = Re{s_d(t)exp[i(m−1)μ_d]}, where s_d(t) is the radar signal reflected by the d-th plane, i is the imaginary unit and Re{.} denotes the real part. Introduce the M-dimensional vector y(t) containing the received signals at the M radar stations at time t. Then the observed signals at each radar station are given by the following D-factor model: y(t) = As(t) + ε(t), where ε(t) is M-dimensional measurement error and the d^th column of A, d=1,2,…,D, is given by: a_d(μ_d)^T = {1, exp[iμ_d], exp[2iμ_d],…, exp[(M−1)iμ_d]} At each time t this is a complex-valued nonlinear D-factor model. But the D planes move and therefore all θ_d, and hence all a_d(μ_d), are time-varying. Applying standard criteria for measurement equivalence would yield the nonsensical conclusion that each of the D planes differs qualitatively as time proceeds. For further details, including explicit analytic expressions for s (t) and generalizations to non-equidistant and non-linear arrays of radar stations (see e.g., Chen, Godeka, & Yu, 2010). The point is that latent processes manifest differently over time. Measurement schemes in the “hard” sciences must accommodate this fact. We believe it is no less important to do so in behavioral science.

Further examples could be produced but do not seem to be necessary to hammer home the point that an observed variable may not be the same manifest variable from one individual to another and therefore not an appropriate basis on which to perform the various aggregation operations that behavioral scientists are wont to do in their efforts to work with latent variables. It is not that this will always be the case but that is not the issue. The salient matter is that a given observable variable cannot be unquestioningly relied on to be the same from one person to another. When it is not, how can it confidently be used as an empirical anchor for what one hopes to be the same latent variable from one individual to another? Obviously, it can not be. It seems that in order to have an empirical science of behavior other devices for anchoring abstract concepts to observations must be identified. Before considering alternatives, however, we will examine this key matter of sameness of meaning at the observable level from another perspective.

The matter can be well-illustrated with the heuristic device that Cattell (1966b) referred to as the data box. For our purposes the simpler version of the data box, the three-dimensional one bounded by person, variable, and occasion axes will suffice. A graphic representation of this heuristic is shown in Figure 3. Any 3-way intersection of a row with a column with the remaining dimension is one datum—a score for a given person on a given variable at a given occasion of measurement. For the data box to have integrity as a cube, each given person (1, 2, …, N) must be the same person across all levels of the variable dimension. Similarly, and here is what we believe to be a major sticking point, each given variable (1, 2, …, p) is presumed to be the same variable across all persons, as stressed by the heavy vertical arrows in the figure. In this case three variables (2, p-k, and p) are emphasized but the concerns apply to all variables being measured. This last premise is typically unquestioned and, as we pointed out with several examples, is potentially a very serious problem.

Figure 3.

The Data Box. Heavy Vertical Arrows Emphasize the Usually Tacit Assumption that a Given Variable is the Same Variable for All Individuals.

Very commonly, working data consist of a “slice” of the data box which is a two-dimensional array (matrix) bounded by samplings of two of the three sets of entities defining the three dimensions of the data box. A typical cross-sectional data set consisting of a persons by variables score matrix for one occasion of measurement (R-Data) is illustrated in Figure 4. These data might represent college students’ self-reported emotions at final exam time (e.g., anxiety, depression, fatigue, etc) or professional baseball players’ performance scores for a particular season (e.g., batting average, walks, home runs, etc.). One more such example–if students nearing semester’s end are reporting how “worried” they are, some might be responding with regard to a particular exam when others are responding with regard to their GPA. To fairly portray such information as an intact data matrix requires that the assumptions regarding persons and variables being the same across all levels of each other be met. However, with regard to variables across persons this can be a particularly troublesome assumption as we have noted with many examples in the current section.

Figure 4.

Multivariate, Cross-Sectional R-Data (Persons by Variables) as a One-Occasion Slice Taken From the Data Box.

We reiterate that the assumption of continuity in meaning of variables over persons is not questioned by most empirical researchers. We view its possible untenability, however, as a fundamental measurement problem and possibly a major culprit underlying the seemingly weak relations that have helped lead to characterizing behavioral science as difficult. We realize that our questioning of the sanctity of manifest variables conflicts with the tenets of empirically-oriented research but we believe that the matter deserves serious consideration and further debate. The implications, if our questioning is on target, are considerable. We examine some of these in the following section.

Consequences of the Lack of Continuity of Meaning in Manifest Variables Across Persons

Consider some of the consequences when the assumption that a manifest variable is the same variable across individuals doesn’t hold. The primary one is that the data box no longer exists as a coherent three-dimensional array as portrayed in Figure 3. Rather, we now have a situation that can be better depicted as in Figure 5. Now, there is a variables by occasions “slice” of the data box for each person (P-technique data) because the data box has been de-coupled across persons to depict the possibility that variables are not the same from one person to another. The “slices” cannot be properly arrayed as in the data box of Figure 3, presented earlier.⁶ This somewhat “exploded” view of the data box now consists of a series of 2-dimensional arrays of data (p variables × t occasions)–one for each person–but the p variables are not necessarily the same p variables from one person to another even though they may be (and usually are in some research designs) labeled the same. In other words, the data box is no longer a box. It has been “deconstructed” in light of concerns regarding the sanctity of observed variables.

Figure 5.

The Multivariate Replicated Single-Subject Repeated Measurements (MRSRM) Design which capitalizes on P-technique data for studying behavior at the individual level (Nesselroade & Ford, 1985). Off-set slices emphasize that variables with the same name might or might not be the same for different individuals.

There are some notable precedents for the data array of Figure 5 in the scientific literature. To an economist, the arrays form a group of multivariate time series–one multivariate time series for each individual. To a differential psychologist, the arrays are a group of P-technique data sets (Cattell, 1952). But note that Figure 5 is the research design identified earlier and advocated by Nesselroade and Ford (1985)—the Multivariate Replicated Single-Subject Repeated Measurements (MRSRM) design depicted in Figure 1—for emphasizing the individual as the proper unit of analysis in studying behavior.

In addition to leading to a decoupling of the data box, there is a second major consequence of recognizing that variables may not have the same meaning from one individual to another. That consequence is the inability to identify a fundamentally important kind of invariance–factorial invariance–which has severe implications for measurement. We will briefly elaborate.

Statements of the kind “If X then Y” and “Given A, if X then Y” exemplify invariant relations, the establishment of which is a fundamental objective of science. The second statement has more limited applicability than the first but nevertheless represents an invariant relation between X and Y in the presence of A. To illustrate: If the opposite poles of two bar magnets are brought into close proximity then attraction occurs whereas if the same poles of two bar magnets are brought into close proximity then repelling occurs. This relation between polarity and action is the same (invariant) at sea level or at high altitudes. Now, consider the relation between temperature and the boiling point of water. If its temperature reaches 212° F then water boils, but this holds only at sea level. At higher altitudes, water boils when reaching lower temperatures.

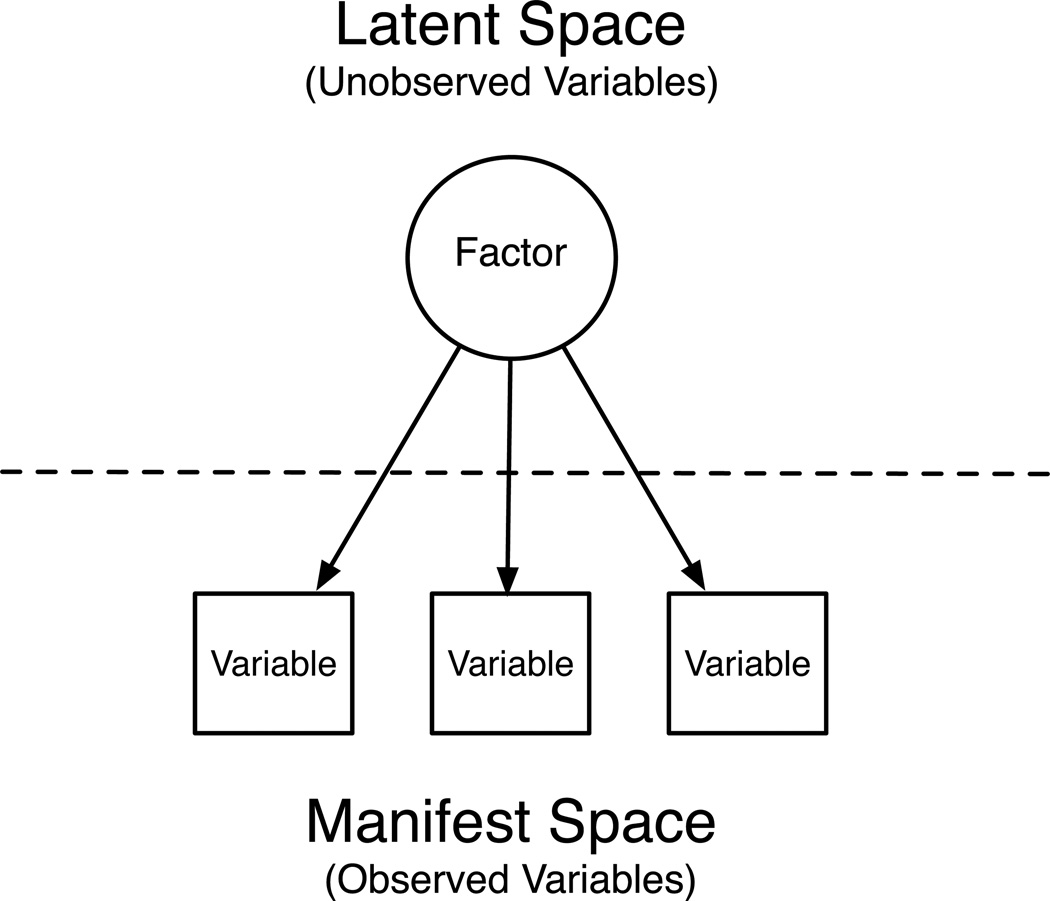
Behavioral science generally has actively participated in the explicit search for invariant relations. Psychophysical laws relating physical values of stimuli to subjective experience (e.g., Stevens, 1958) and relations between the resistance of a learned behavior to extinction and the reinforcement schedule under which the behavior was acquired (Skinner, 1953) are but two examples of areas in which behavioral science, with some success, has invested heavily in identifying invariant relations. In the study of individual differences and its handmaiden–psychometrics–a precise and powerful embodiment of the invariance concept is found in the domain of factor analysis with an explicit focus on factor loading pattern invariance (e.g., Ahmavaara, 1954; Cattell, 1944; Guilford, 1977; Horn, McArdle, & Mason, 1983; McArdle & Cattell, 1994; Meredith, 1964a, 1964b, 1993; Millsap, 2011; Thurstone, 1947, to name a few). For good reasons, demonstrating invariant relations between manifest variables and latent factors has long been a key ingredient in measurement and theory development. Factor loadings embody the relations between the manifest variables and the latent factors that we have already noted are so important for empirical science. Indeed, factor loadings continue to play the pivotal role of bridging the empirical and theoretical worlds (see e.g. Hox, Leeuw, & Zijlmans, 2015; Lommen, Schoot, & Engelhard, 2014), as noted in Figure 6.

Figure 6.

Factor Loadings (arrows)—Bridges Between Manifest and Latent Space.

Thurstone (1947) devoted considerable space in Multiple Factor Analysis to defining and exploring the implications of invariance of factor loadings. He proposed that a test should keep the same loading when it was moved from one battery of tests to another battery of tests involving the same common factors. Demonstrating such factorial invariance was taken as evidence that one had indeed captured an important scientific entity and not just a statistical artifact and had available convincing assessment tools to render the entity operational. Thurstone had in mind an essential (and large) set of transformations under which factor loading invariance was critical–changes in the test battery.⁷

In behavioral and social science, explications of factor invariance have had a major impact on the development of both the common factor model per se (e.g., Cattell, 1944; McArdle & Cattell, 1994; Meredith, 1964a, 1964b, 1993; Millsap, 2011) and its applications such as the measurement model in structural equation modeling (Jöreskog & Sörbom, 1993; Meredith, 1993; Millsap, 2011) and, in studying developmental change, for instance, as a prime basis for distinguishing between qualitative and quantitative change patterns (Nesselroade, 1970).

In longitudinal data–panel studies, for instance–loading pattern invariance over occasions provides for an easy interpretation of observed changes (e.g., whether or not one is measuring “the same thing” at different ages). The basic idea is that in order for observed changes or differences to be meaningful the pertinent values on which the change score or difference is defined represent amounts of the same attribute (see e.g., Bereiter, 1963; Cronbach & Furby, 1970). A compelling way to establish this condition is by demonstrating factorial invariance across occasions of measurement (or across groups when differencing means). The fundamental idea is easily illustrated with change scores. Consider the basic factor specification equation (e.g., Cattell, 1957):

$$a_{ji}=b_{j1}+F_{1i}+b_{j2}{F}_{2i}+\cdots +b_{jk}{F}_{ki}+u_{ji}$$

where a_ji represents an observed score for person i on variable a_j, b_jp is the loading of variable a_j on factor p, F_pi is the score for person i on factor p, and u_ji is the unique part of person i’s a_j score. Consider a second equation where the prime symbol indicates that individual i has been remeasured at a later time, resulting perhaps in a different value of a_j:

$$a_{ji\prime }=b_{j1}+F_{1i\prime }+b_{j2}{F}_{2i\prime }+\cdots +b_{jk}{F}_{ki\prime }+u_{ji\prime }$$

To indicate factorial invariance over the two measurement occasions, the corresponding factor loadings (the bs) are set equal in the two equations. The factor scores, however, are not so restricted and a given person’s score on a given factor can differ (signifying a change on that factor) over time. Subtracting the first equation from the second to obtain the observed change score on the left side of the equation results in:

$$a_{ji\prime }-a_{ji}=b_{j1}+F_{1i\prime }+b_{j2}{F}_{2i\prime }+\cdots +b_{jk}{F}_{ki\prime }+u_{ji\prime }-b_{j1}{F}_{1i}-b_{j2}{F}_{2i}-\cdots -b_{jk}{F}_{ki}-u_{ji}.$$

Rearranging terms yields:

$$a_{ji\prime }-a_{ji}=b_{j1}(F_{1i\prime }-F_{1i})+b_{j2}(F_{2i\prime }-F_{2i})+\cdots +b_{jk}(F_{ki\prime }-F_{ki})+(u_{ji\prime }-u_{ji}).$$

The observed change is on the left side of the equation and the accounting of the observed change by the factors is on the right. Thus, under the imposed condition of factor loading pattern invariance over occasions, the observed change scores reflect the same factor pattern as the separate occasions on which they are based and are attributable to changes across time in the (unobserved) factor scores. This is a clear and concise statement regarding the nature of observed changes; one made possible by the condition of factor loading pattern invariance.⁸ The formulation gives an unambiguous answer to the question: What has changed-the person or what the test is measuring? As such, it plays a key role in the conceptions of developmental science.

The foregoing makes it obvious why psychometricians cling so avidly to the traditional conception of factorial invariance. It is a powerful conception that, if in play, lends rigor to the measurement of unobservable psychological entities. However, the conception has been somewhat undermined by factor analysts themselves by the introduction of less rigorous invariance conceptions such as configural invariance (see e.g., Horn et al., 1983; Thurstone, 1957) and partial invariance. Of course such accommodations extend the concept of invariance to more data sets but they lose the advantage provided by the rigorous version of the concept as shown above. Even Meredith (1993), perhaps the most convincing and effective proponent of using the tools of factorial invariance, considered the various levels of invariance to be “idealizations” that might be empirically somewhat elusive.

But there is a major problem with the factorial invariance formulation that we have started to lay bare and will now identify more fully. Factorial invariance as discussed above rests fully on the tacit assumption that the observed variables do have the same meaning from one instance involved in the invariance search to another in the sense that scores for different individuals (or groups) can be legitimately arrayed in a vector format as per our earlier discussion of the data box. Whether invariance is being examined across individuals or across subgroups, the observed variables that are given the same name are taken to have the same meaning in order to proceed with an evaluation of factorial invariance. Typically, if invariance is not demonstrable, the determination is simply that invariance doesn’t hold rather than that what are ostensibly the same observed variables are actually different across comparison entities. Thus, there seems to be a fatal kind of circularity involved. We assume that the observed variables have the same meaning in order to test whether or not they have the same factorial composition (test for factor invariance). If invariance holds, this “same meaning” interpretation seems reasonable. If invariance is not demonstrable, is it because the observed variables don’t have the same meaning or because their factorial composition is different–or both? Said another way, a distinction is being made between a variable having the same meaning across units versus having the same factorial composition across units. Having the same meaning across units is a necessary condition for being able to test whether or not the factorial composition is invariant. The same meaning is tacitly assumed by most empirical scientists. The same factorial composition is then to be a testable proposition. We see this to be a troubling situation for such a key measurement concern, making it timely to cast around for alternate invariance conceptions that might be helpful. We strongly encourage such activity. We will illustrate one such effort–the idiographic filter measurement approach–which can be teamed with the MRSRM design.

The Idiographic Filter Approach to the Measurement of Psychological Constructs

Measurement experts have wrestled long and hard with how to answer the question whether or not the same latent variable or construct is being measured; across occasions, across subgroups, across cultures, etc. In many cases, the proposed solutions involve some application of factor analysis and the concept of factorial invariance discussed above. However, as was noted, the procedures for evaluating invariance in the traditional manner rests on the more basic assumption that an observable or manifest variable is the same variable from one instance of use to another. But, as also noted earlier, there is ample justification for questioning the tenability of this assumption. We seriously doubt that blind acceptance of such continuity of meaning across individuals or groups is a proper stance to assume in the measurement of behavior.

Concerns regarding the sanctity traditionally afforded manifest variables by empirical scientists led to a proposal to tailor the measurement of latent variables such that the configuration of relations between observable or manifest variables and the “same” latent variable could be different from one person to another, thereby offering a way to deal with idiosyncratic aspects of manifest variables (Nesselroade, 2007; Nesselroade, Gerstorf, Hardy, & Ram, 2007). This tailoring, which recognized explicitly the idiosyncratic nature of relations between manifest and latent variables, was dubbed the idiographic filter.⁹ Within this framework, the goal of building a nomothetic science remains intact (see e.g., Molenaar, 2004) but idiosyncratic features associated with manifest variables that might otherwise hinder approaching the goal are filtered out.

As discussed by Nesselroade and Molenaar (2010) four principal considerations are involved in implementing the idiographic filter within the MRSRM design. First, individual–level modeling is initially conducted, even though the ultimate goal is to reach general conclusions. Second, first-order factor loading patterns are allowed to reflect idiosyncracies. Third, obtaining idiosyncratic loading patterns is accomplished while constraining the interrelations among the first-order factors (e.g., factor intercorrelations) to be invariant across individuals.¹⁰ Fourth, if the model with invariant factor intercorrelation matrices can be fitted to the different individuals, one can fit a second-order factor solution with invariant loadings across individuals. Thus, by virtue of the third and fourth considerations a traditional conception of invariance is re–established, albeit at the second-order factor level. Whether or not this higher–order of invariance can be demonstrated has to be determined from one’s data but there are ways of doing this rigorously (see e.g., Molenaar & Nesselroade, 2012; Zhang, Browne, & Nesselroade, 2011). If it can be so demonstrated, important implications exist both for measurement operations and the development and refinement of theory.

Rather than emphasizing the primary factor loadings as the locus of invariant relations as has been the dominant activity for many decades, the idiographic filter proposal, as noted, placed invariant relations at the level of factor intercorrelations. This was done to retain a conception of invariance as a basis for arguing that the “same” latent variables were being targeted from one instance to another while, at the same time, allowing the relations between observed variables and primary factors (loadings) to take an idiosyncratic look appropriate to the data. In this way, we try to accommodate a lack of consistency of meaning in the manifest variables while maintaining consistency of meaning for the latent variables. If one thinks of the inter-relations of the factors as indications of some mechanism, for instance, then the interpretation of invariance at that level is that the data reflect a common abstract mechanism that may actually manifest somewhat differently in different instances. Harking back to our earlier example, Frustration produces Aggression can take different forms in different people but the Frustration producing Aggression relation is invariant across individuals.

Invariant factor intercorrelations lead to a common (invariant) second-order factor solution of the traditional kind. Thus, with the idiographic filter, invariant factor loadings remain a key part of the solution but they are now at the more abstract, second-order factor level. For this reason, the procedure was also termed higher–order invariance. The essential model has been more formally discussed by Zhang et al. (2011) and Molenaar and Nesselroade (2012). Judd and Kenny (2010) have provided a concise discussion of its implementation in the context of social psychological research.

Within the context of the MRSRM design discussed earlier, the idiographic filter proposal allowed first-order factor loading patterns to differ from individual to individual in line with the notion that the observed variables might not have the same meaning or the same factor composition for different individuals. But, at the same time, rigor was maintained because a locus of invariant relations was established at the factor intercorrelation level. In other words, the conceptually rich, highly desirable feature of factorial invariance was not abandoned but redefined as to its level of abstraction in order to cope with the idiosyncrasies of individuals which, although irrelevant to the measurements could interfere with the measurement process. For individuals, this arrangement implied a common underlying mechanism (expressed in the higher-order factors) that could manifest somewhat idiosyncratically in the observed variables. So, for instance, the first-order factor loadings could reflect the idiosyncrasies of observed variables due to different individuals’ unique histories of conditioning, learning, language usage, etc., and thus act as a filter to remove irrelevant, idiosyncratic material from the measurement process that would otherwise interfere with demonstrating invariant relations.¹¹

Reiterating, implementing the idiographic filter as described above results in a factor solution that meets the traditional definition of factor invariance albeit with the invariant factors being at least one level removed in abstraction from the typical level at which invariance is sought i.e., at the second–order level instead of the first–order level. A bonus is that one can calculate the loadings of the observed variables directly on the invariant, higher–order factors via transformations such as Cattell–White and Schmidt–Leiman (e.g., Cattell, 1966a; Loehlin, 1998; Schmidt & Leiman, 1957) which allows one to define invariant higher order constructs with individually tailored observed variable configurations.

With the advent of dynamic factor models (Browne & Nesselroade, 2005; Molenaar, 1985; Nesselroade, McArdle, Aggen, & Meyers, 2002) MRSRM data can now be even more fully exploited than was the case with traditional P-technique factor models. Molenaar and Nesselroade (2012) discuss applying the idiographic filter measurement approach to dynamic factor modeling and show that the model can be statistically evaluated and is falsifiable in a rigorous way. In its essence, the approach involves fitting MRSRM data with the dynamic factor model such that the latent variable relations (concurrent and lagged) are invariant from one individual to another but the measurement models that define the latent variables can differ idiosyncratically from individual to individual. This development opens the way to modeling processes (as defined by dynamic factor models) that are invariant across individuals but can manifest in different observed variable patterns. Thus, for example, older individuals can develop patterns of emotion regulation (Carstensen, 1993) that are ostensibly quite different from one another but are arrived at by a common change process. Or, in another arena, children can undergo a common socialization process with very different family configurations (e.g., one- vs. two-parent families) and very different outcomes (e.g., social dominance vs. social submissiveness). From the idiographic filter perspective the nomothetic goal of identifying general processes is thus served by confronting the threat of idiosyncratic observed behavior head on and dispelling it, rather than ignoring it and allowing it to weaken empirically derived relations among variables. What the idiographic filter approach to measurement offers at a general level is a way for behavioral scientists to apply rigorous procedures to the development and articulation of lawful relations while circumventing idiosyncratic features of observable behavior that are real but which, if allowed to intrude into the measurement process, can wreck empirical inquiry.

We don’t expect our proposals to be the final word but we do believe they point to an important divergence from orthodoxy that deserves consideration. Harking back to the earlier quote from Kluckhohn and Murray (1953) we must look for uniformities but we most certainly are not going to find them by letting our investigative apparatus be undermined by idiosyncrasies.

The traditional factor invariance model (presented earlier) is a special case of the idiographic filter. If the former can be fitted satisfactorily to a given data set, there is no need to invoke the idiographic filter and one can take advantage of the powerful properties of measurement invariance at the primary factor level as presented earlier. If it can not, however, one can attempt to fit the idiographic filter. By making the idiographic filter falsifiable via statistical test, one has a rigorous basis for concluding that it is inappropriate for one’s data.

Simulation Example

To illustrate some of the matters being discussed more precisely, and give interested readers some guidance in conducting the kinds of analyses being proposed, we consider a set of simulated data. The illustration has a limited purpose: to show one way in which the presence of subject-specific factor loadings can be detected while the correlations among the factors are invariant across subjects. The subject-specific factor loadings are an indication that the manifest variables have different meaning for different subjects; the invariant correlations among the factors are an indication that their meaning is invariant across subjects. Several necessary steps in the data analysis, such as preliminary identification of the dimension of the latent state process and a posteriori model validation, are not considered here.

The simulated data consist of 5 replicated 6-variate time series of length T=100. Replications in this illustration refer to different subjects or participants. The simulation model is a state-space model with bivariate state process described by a first-order vector-autoregressive model, (A), consisting of:

$${\mathbf{y}}^{(i)}(t)={\mathbf{\Lambda }}^{(i)}{\eta }^{(i)}(t)+{\epsilon }^{(i)}(t)\hspace{1em}\mathit{\text{cov}}[{\epsilon }^{(i)}(t),{\epsilon }^{(i)}(t-u)\prime ]=\delta (u){\mathbf{\Theta }}^{(i)}$$

1. $${\eta }^{(i)}(t+1)=\mathbf{B}{\eta }^{(i)}(t)+{\zeta }^{(i)}(t+1)\hspace{1em}\mathit{\text{cov}}[{\zeta }^{(i)}(t+1),{\zeta }^{(i)}(t+1)\prime ]=\delta (u)\mathbf{\Psi }$$

2. i = 1,2,‥5; t=1,2,‥,100.

Note: Boldface lowercase letters denote column vectors; boldface uppercase letters denote matrices; and the prime symbol denotes transposition.

y⁽ⁱ⁾(t) is a 6-variate, zero mean manifest time series of subject i; η⁽ⁱ⁾(t) is a 2-variate latent state process; Λ⁽ⁱ⁾ is a (6,2)-dimensional matrix of factor loadings; ε⁽ⁱ⁾(t) is zero mean Gaussian measurement error with covariance function %(u)Θ⁽ⁱ⁾, where δ(u) is the Kronecker delta (equal to 1 if u = 0 and equal to 0 if u ≠ 0) and Θ⁽ⁱ⁾ is a (6,6)-dimensional diagonal covariance matrix; B is a (2,2)-dimensional matrix of regression coefficients; ζ⁽ⁱ⁾(t) is 2-variate zero mean Gaussian process noise with covariance function δ(u)Ψ, where Ψ is a (2,2)-dimensional full covariance matrix. Notice that the matrices of factor loadings Λ⁽ⁱ⁾ are subject-specific, but that B and Ψ, the parameters in the VAR(1) describing the latent state process, are invariant across subjects.

The true values of the parameter matrices in this state-space model, the Fortran simulation program and the simulated data set can be obtained on request from the authors. In what follows it is assumed that the appropriate preliminary data analyses have been carried out. In particular, it is assumed that single-subject analyses have shown that the data of each subject are stationary and obey a state-space model with 2-variate latent state process. The matrix of factor loadings in each subject-specific state-space model has fixed loadings λ₆₁ = λ₁₂ = 0 to guarantee identifiability (cf. Bai & Wang, 2012). In addition, the latent state process has to be scaled; this is accomplished in different ways depending on the model fitted to the data (see below).

All model fits were carried out with mkfm6. This program and manual can be downloaded from: http://quantdev.ssri.psu.edu/resources/. Mkfm6 is a Fortran program with which state-space models can be fitted to replicated time series data by means of the raw data likelihood method (prediction error decomposition; (cf. Durbin & Koopman, 2012).

Three analyses were carried out:

1. State-space models with 2-variate latent state process without any constraints across replications. To scale the latent state process the diagonal of Ψ in (A) is fixed at 1. This yields a baseline −2*log-likelihood = 3493.846 with 105 free parameters. Akaike’s Information Criterion AIC = 3703.846.

2. The same state-space models as in (1) were fitted while constraining B and Ψ in (A) to be invariant across subjects. This yields −2*log-likelihood = 3514.629 with 85 free parameters. AIC = 3684.629.

3. The same state-space models as in (1) were fitted while constraining the matrix of factor loadings to be invariant across subjects, Λ⁽ⁱ⁾ = Λ. To scale the latent state process the factor loadings λ₁₁ and λ₆₂ were fixed at 1, while leaving the diagonal of Ψ free. The alternative scaling of η(t) is necessary in order to avoid confounding the test of invariant factor loadings with differences in the scale of the latent state processes. This yields −2*log-likelihood = 4591.404 with 73 free parameters. AIC = 4737.404.

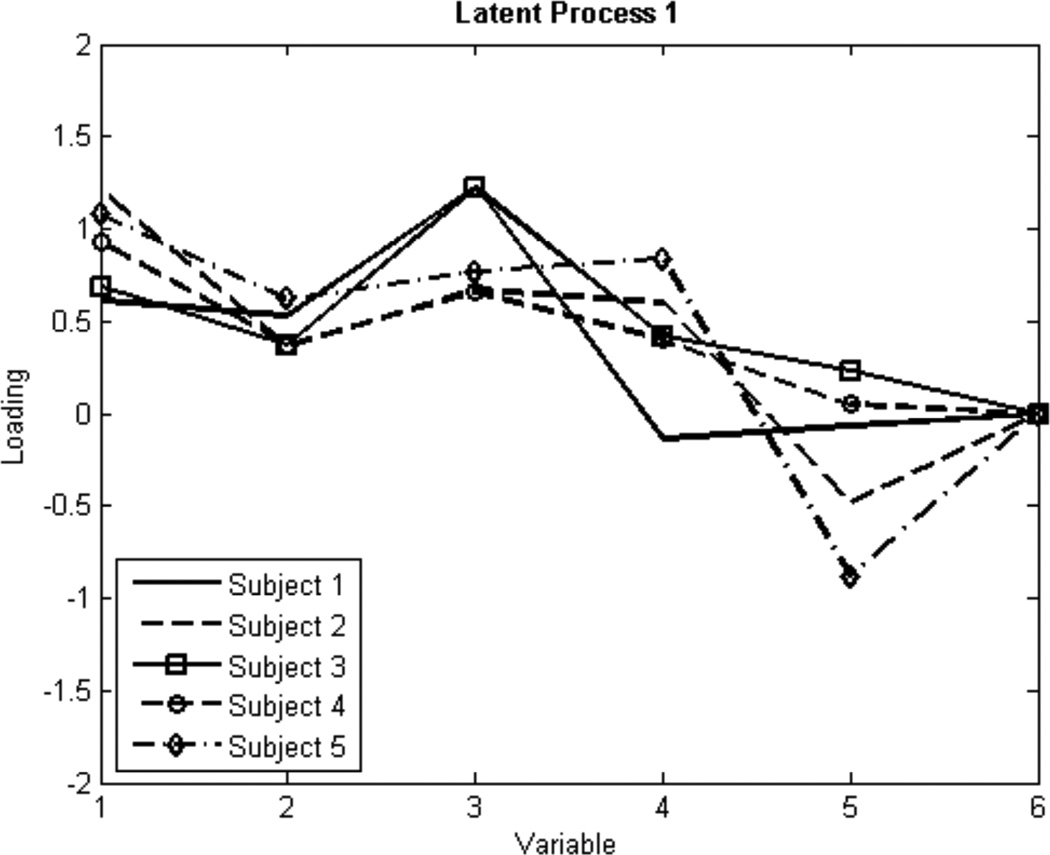
The model fitted in (2) yields the smallest AIC and therefore is selected. It is the model with which the data have been simulated. For illustrative purposes, the mkfm6 input file used to fit model (2) above is given in Appendix A. The estimated subject-specific factor loadings are depicted in Table 1 and presented graphically in Figure 7 and Figure 8 for Latent Process 1 and Latent Process 2, respectively. The estimated regression coefficients for the two latent state processes in the Replication-Invariant Model, VAR(1), are found in Table 2, and the covariance matrix for the Process Noise in Replication-Invariant VAR(1) for Latent State Processes (P1 and P2) is found in Table 3.

Table 1.

Estimated Loadings for Six-Variable, Replication-Invariant VAR(1) Latent State Processes (P1 and P2) Involving Five Replications (R1–R5).

	R1		R2		R3		R4		R5
Var	P1	P2	P1	P2	P1	P2	P1	P2	P1	P2
1	.61*	.00	1.21*	.00	.69*	.00	.93*	.00	1.08*	.00
2	.53*	.27*	.36*	−.17*	.37*	−1.10*	.37*	−.60*	.62*	−.85*
3	1.23*	−.07	.67*	−.21*	1.22*	−.93*	.66*	−1.34*	.77*	−.52*
4	−.14	.15*	.60*	1.06*	.42*	1.28*	.40*	.92*	.84*	.94*
5	−.07	.49*	−.48*	.40*	.23*	.62*	.05	.38*	−.88*	1.49*
6	.00	1.05*	.00	1.87*	.00	1.22*	.00	.74*	.00	1.58*

(Values indicated by * represent nominal α = .01 level.)

Figure 7.

Graphical Representation of Estimated Loadings for Latent Process 1 on Six Variables for Five Replications (see Table 1).

Figure 8.

Graphical Representation of Estimated Loadings for Process 2 on Six Variables for Five Replications (see Table 1).

Table 2.

Regression Matrix in Replication-Invariant VAR(1) for Latent State Processes (P1 and P2).

	P1	P2
P1	.73	.01
P2	.53	.66

Table 3.

Covariance Matrix of Process Noise in Replication-Invariant VAR(1) for Latent State Processes (P1 and P2).

	P1	P2
P1	1.00
P2	.72	1.00

Where to Then?

At any point in the development of a scientific discipline, there is some reluctance to embrace a significant departure from established dogma and accepted practices. In the broader scheme, such inertia is a positive feature, because it protects us from plunging willy-nilly into a lot of resource-wasting dead ends. Clearly, the views concerning measurement that we have been espousing deliberately challenge more orthodox ones regarding how measurement is conducted in behavioral science. We do so because it seems to us that, except for some further tinkering, accepted practice may have reached the limits of what it can contribute and it is time to try some alternatives. One already sees hints of redirecting measurement efforts in medicine, for example, with a growing interest in individually-tailored treatments and outcome measures for certain diseases.

Behavioral scientists desire to have an empirical science but human beings are not bars of iron or vessels of glass that wait unfeelingly, even patiently, for stimuli to be applied and reactions to be assessed. We are sentient creatures, motivated by complex influences and shaped by unique genetic configurations and learning and conditioning histories such that neither a measurable stimulus nor an observable response can be relied on to represent the same experiential event from one person to another. In light of that, we firmly believe that the way the measurement of behavior is practiced can be productively altered by keeping some procedural features intact while modifying others. To have a powerful, empirically-based science of behavior a common reference frame across individuals is needed and if observed variables cannot be unequivocally relied on to provide it–our fundamental argument here–other paths must be found. In the context of the idiographic filter, we have explored the idea that such a common reference frames can be established at the level of unobserved or latent variable interrelations.

Emphasizing the building of relations among variables at the latent level but being able to test them at the manifest variable level has long been accepted practice but what is different in our proposal is that the empirical testing part of the method cannot rely on a slavish application of standardized measurement procedures. Rather, measurement procedures should respect the individual and his/her idiosyncrasies even as they filter out those idiosyncrasies while still affording empirical tests of the latent relations. We are persuaded of the importance of building theoretical conceptions and using latent or unobserved variables to do it. Thus, it remains essential to anchor latent variables to the empirical world, but this does not have to be done (cannot be done?) within the rigid framework of the physical sciences that has prevailed for the past couple of centuries.

Although it is difficult to know just how to say it, our contention is that behavioral science has not discriminated carefully enough between features of behavior that can be studied scientifically and those that can not. A major problem, in our estimation, is a rigid insistence on anchoring empirical inquiry on manifest (observed) variables in the traditional ways it has been done. We have asserted the idea that anchoring principles of behavior on latent variables and their interrelations is more promising provided–and this is key–manifest variables can somehow still be used in rigorous tests of the empirical implications of those latent variable interrelations. We have illustrated this argument explicitly elsewhere (Molenaar & Nesselroade, 2012).

One of the corollaries of the foregoing is that there are interesting questions and issues that fall outside of our purview when the focus is on other questions and issues. For example, if one is trying to examine the relation between Frustration and Aggression, one shouldn’t confound with it the question of why Joe is frustrated by event X but not event Y whereas Mary is frustrated by event Y but not event X. Similarly, why do Joe and Mary display their aggression in such very different ways? To study the relation between Frustration and Aggression, we need to look at what frustrates Joe and his resulting aggressive behavior and, similarly, we need to look at what frustrates Mary and her resulting aggressive behavior, accepting that Mary and Joe may well be different at the manifest level. Why X frustrates Joe but not Mary or vice versa is a different question that can be attacked but not as a germane piece of the Frustration/Aggression relation.

Boiled down to essentials, another way to think about the matter is: Do we want different measurement rules or different modeling rules? The idiographic filter, for example, absorbs idiosyncrasies at the measurement stage (the measurement model). Current approaches tend to absorb them at the modeling stage with different models for different people or different subgroups. From the standpoint of building a science of behavior that emphasizes the similarities in how people behave, we think a strong argument can be made for explanatory models that are common across persons and that these can be determined and evaluated using measurement approaches that are different for different people. At the very least, this puts the scientific study of behavior on a footing that we believe is more secure than the one that forces the measurement of behavioral attributes to be standardized over persons at the cost of different models of behavior for different subgroups or individuals.

We emphasize the phrase fundamentally different measurement approaches. Some approaches that seem to respect idiosyncrasy (e.g., IRT and measurement invariance models) rely on the manifest variables as having the same meaning, if not the same factor composition over individuals in the sense that different individuals’ scores can be meaningfully arrayed in the same score vector. We are arguing for the possibility that manifest variable scores for different persons may not even be meaningfully arrayed as a vector. Recall it is discontinuity in meaning at that level that was described earlier as destroying the integrity of the data box.

Measurement perspectives such as the idiographic filter bring to the fore the use of factor analytic methodology for discovering latent variable explanations for observable events. However, not just any arbitrarily chosen set of manifest variables can be expected to yield higher order invariance. There is clearly a place for selection, refinement, and retesting of variables in developing explanatory frameworks. That is why we have tried to emphasize the development of rigorous model testing methods.

One of our general purposes here has been to elaborate further the importance of recognizing the individual as the primary unit of analysis for studying behavior. Toward that end, we have emphasized the idiographic filter approach to the measurement of psychological entities. We have tried to foster the use of MRSRM designs, primarily as a way of enhancing the role of the individual as the proper unit of analysis for the study of behavior. As a consequence, we have also called attention to a third discipline of scientific psychology that offers some key features that we think are not given enough emphasis in the experimental and differential disciplines. Our very broad aim, in line with the introductory comments, is to assist in making psychology a less difficult science while, at the same time making it a “harder” science. We believe it is timely to explore accomplishing this by modifying measurement activities in ways that seem appropriate to the study of behavior.

Admittedly, the idiographic filter approach almost certainly is not the final word regarding measurement in behavioral science. We want the idea to be tried out extensively but, even more important than this particular “fix,” is to recognize the possibility that there are serious problems with the dominant approaches to the scientific study of behavior that need to be addressed. Breaking the bonds that have so tightly constrained the nature of manifest/latent variable relations to free up the representation of the latter by taking idiosyncrasy into account at the measurement stage seems to us to be an important step toward making behavioral science “harder” but at the same time less difficult.

We mention two final considerations in closing. First, a reminder that there are indeed likely to be instances in which the manifest variables do have the same meaning for different individuals. This is a special case of the more general situation, we believe. As such, the traditional conception of measurement invariance may well prevail and it makes sense to examine that possibility. Filters still function when there are no impurities as well as when there are.

Second, the matter of generalizability looms large, especially when one is emphasizing the individual as the unit of analysis and calling for many repeated measurements on multiple variables. A decade ago Molenaar (2004) pointed out the rapidly growing ability to manage incredibly large amounts of individual data. The current popularity of “big data” gives credence to the importance of generalizability and can help us identify perhaps more fruitful ways to conceptualize it. Thus, future work, including applications of the MRSRM design, can most likely involve large samples of individuals–when this is desirable. A caution is in order, however. When one is investigating processes, synthesizing by averaging over large numbers of individuals will be fruitless if the processes are manifested in an idiosyncratic manner.¹² It seems far more appropriate to apply tools that emphasize first understanding individuals well and then identifying similarities across persons; thus accruing generalizability gradually than initially fitting models to heterogeneous samples in order to claim generalizability. Large, diverse samples of individuals may put a gleam in a demographer’s eye but a wide array of observed differences, however universal the underlying mechanisms may be, can blind the behavioral scientist to the identification of general processes.