Abstract
The latent growth curve modeling (LGCM) approach has been increasingly utilized to investigate longitudinal mediation. However, little is known about the accuracy of the estimates and statistical power when mediation is evaluated in the LGCM framework. A simulation study was conducted to address these issues under various conditions including sample size, effect size of mediated effect, number of measurement occasions, and R2 of measured variables. In general, the results showed that relatively large samples were needed to accurately estimate the mediated effects and to have adequate statistical power, when testing mediation in the LGCM framework. Guidelines for designing studies to examine longitudinal mediation and ways to improve the accuracy of the estimates and statistical power were discussed.
Keywords: accuracy of mediated effects, indirect effects, latent growth curve modeling, longitudinal mediation, statistical power
Assessing mediation is a critical part of social science research. Researchers hypothesize the underlying causal mechanism and assess how the effect of the independent variable on the dependent variable is carried out through the hypothesized intervening variables (Baron & Kenny, 1986; Sobel, 1990). For example, alcohol researchers hypothesize that drinking alcohol reduces attention capacity, which, in turn, facilitates aggressive behaviors because individuals with reduced attention capacity are likely to attend to more salient cues, such as provocation from others (Steele & Josephs, 1990; Taylor & Leonard, 1983). For another example, the theory of cognitive dissonance (Festinger, 1957) suggests that behaviors that are incongruent with an individual's attitudes produce an unpleasant dissonance state, and thus lead to attitude change in an effort to reduce the unpleasantness.
Statistical approaches to testing mediation have been actively studied in recent years (Baron & Kenny, 1986; Collins, Graham, & Flaherty, 1998; Kenny, 2008; MacKinnon, Fairchild, & Fritz, 2007; MacKinnon, Lockwood, Hoffman, West, & Sheets, 2002; Preacher & Hayes, 2004; Sobel, 1990). The majority of these methods are based on a variable-centered approach, in which researchers focus on the relations among the independent variable, the mediator, and the outcome variable. MacKinnon et al. (2002) examined Type I error rates and statistical power of 14 variable-centered methods that were widely used for testing mediation in various disciplines. Other researchers take a person-centered approach and focus on individuals' response patterns that are consistent or inconsistent with the mediation hypothesis (Collins et al., 1998; Robins & Greenland, 1992). Mediation analysis has been extended and applied to investigating mediational processes in more complicated study designs such as longitudinal studies (Cheong, MacKinnon, & Khoo, 2003; Cole & Maxwell, 2003), studies with multilevel data structure (Bauer, Preacher, & Gil, 2006; Kenny, Korchmaros, & Bolger, 2003; Krull & MacKinnon, 1999, 2001; Raudenbush & Sampson, 1999), and studies investigating the combination of mediation and moderation (Bauer et al., 2006; Edwards & Lambert, 2007; Fairchild & MacKinnon, 2009; Morgan-Lopez & MacKinnon, 2006).
Although advances have been made regarding the accuracy of estimates and statistical power to detect mediation effects for basic mediation models (MacKinnon et al., 2002; MacKinnon, Lockwood, & Williams, 2004; Shrout & Bolger, 2002), our understanding about testing longitudinal mediation is still limited. Several studies (Cheong et al., 2003; Cole & Maxwell, 2003; Fritz & MacKinnon, 2008) introduced and illustrated different modeling techniques for investigating longitudinal mediation, and empirical studies (Jagers, Morgan-Lopez, Howard, Browne, & Flay, 2007; Roesch et al., 2009; Simons-Morton, Haynie, Saylor, Crump, & Chen, 2005) began to utilize these modeling techniques. However, simulation studies are needed to examine statistical performance of these techniques and to provide researchers with guidelines for analyzing existing data or designing future studies that involve testing longitudinal mediation. In this study, a simulation study was conducted to examine how accurately the mediated effects were estimated and how statistical power changed under different conditions when the methods for testing mediation were utilized in the latent growth curve modeling (LGCM) framework.
An example of a growth curve model for investigating longitudinal mediation is shown in Figure 1. Based on the repeated measures of the mediator and the outcome made on the same individuals, the trajectories of the mediator and the outcome are modeled as two parallel processes that are influenced by the independent variable. Figure 1 presents a single mediator parallel process latent growth model with five measurement occasions, in which the trajectories of the mediator and the outcome variables are modeled as linear with equal intervals between measurement occasions.
Figure 1.
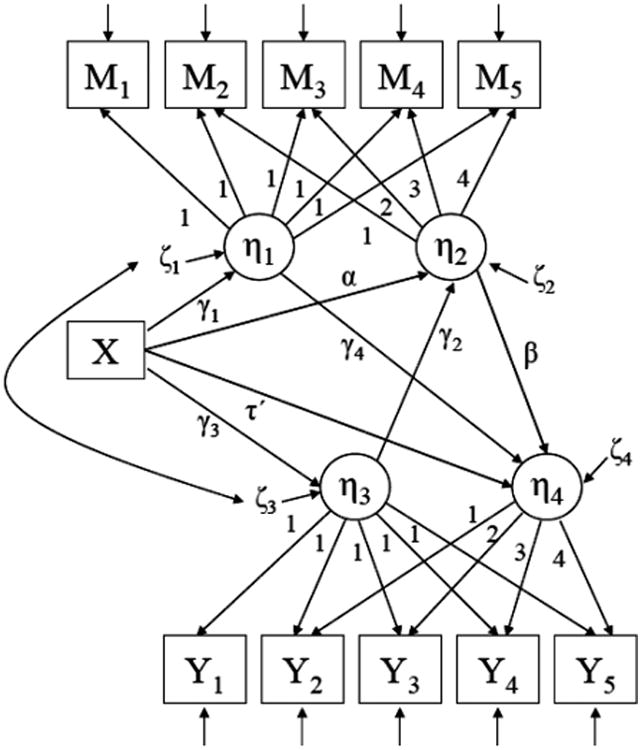
A parallel process latent growth model for mediation. X = independent variable; Y = outcome; M = mediator; η1 = intercept (initial status) factor of mediator; η3 = intercept (initial status) factor of outcome; η2 = slope (growth rate) factor of mediator; η4 = slope (growth rate) factor of outcome.
Estimating the parallel process mediation model requires several steps. The growth trajectory of the mediator and the growth trajectory of the outcome are modeled separately to determine the trajectory shapes and to estimate the overall changes in the mediator and the outcome. These two processes are modeled in the measurement models as follows:
| (1) |
| (2) |
In the preceding equations, the superscripts m and y denote the mediator and the outcome process, respectively. Mi and Yi are T × 1 vectors of the repeated measures of the mediator M and the outcome Y for the individual i across T measurement occasions; and are T × 1 vectors of the intercepts of the repeated measures; Λ(m) and Λ(y) are T × J matrices of factor loadings on the latent growth factors (j = 1, 2, …, J, where j = the number of growth factors); and are J × 1 vectors of the latent growth factors; and and are T × 1 vectors of the measurement errors of the repeated measures of the mediator and the outcome processes. In Figure 1, the two latent growth factors in each process are the common intercept factor and the slope factor. The means of the common intercept factors estimate the average initial level of the mediator and the average initial level of the outcome in the study sample. The means of the slope factors estimate the average growth rates of the mediator and the outcome processes. The variances of the intercept and the slope factors estimate the variability in the initial levels and the variability in the growth rates among individuals. Once the growth curves of the mediator and the outcome are modeled adequately, supporting the hypothesized trajectory shapes, and the variances of the latent growth factors are statistically significant, the latent factors can be regressed on the independent variable X to investigate the effects of the independent variable on the growth trajectory of the mediator and the growth trajectory of the outcome.
Mediational process is modeled by combining the two growth curve models estimated in the previous steps and relating the growth factors and the independent variable X in the structural model. When the growth trajectories of the mediator and the outcome are modeled as linear, the meditational process can be expressed as follows:
| (3) |
| (4) |
| (5) |
| (6) |
In these equations, , and denote the regression intercepts of the growth factors, and ζ1i, ζ2i, ζ3i, and ζ4i denote the residuals. Path coefficients γ1 in Equation 3 and γ3 in Equation 5 indicate the effects of X on the initial level of the mediator process and the initial level of the outcome process, respectively. These coefficients can be modeled to be 0, for example, when the independent variable represents the groups individuals are randomly assigned to. In such cases, the groups are expected to be equivalent on the pretreatment measures and thus, the group membership is not expected to be related to the baseline measures (initial levels) of the mediator and the outcome. Path coefficients γ2 and γ4 in Equations 4 and 6 represent the effects of the initial levels on the growth rates. Reflecting the interrelatedness between the mediator and the outcome variables and modeling the temporal sequence of the initial level at Time 1 and the growth rate estimated based on the multiple measurements from Time 1 to Time T, the initial level can be modeled to have direct effect on the growth rate of the other process. Path coefficient α represents the effect of the independent variable X on the growth rate of the mediator (i.e., change in M per time unit), controlling for the other predictors in the model. Path coefficient β indicates the effect of the growth rate of the mediator process on the growth rate of the outcome process, controlling for the effects of the independent variable and the intercept factor of the mediator. Path coefficient τ′ represents the effect of X on the growth rate of the outcome process that is not mediated by the mediator process, or the direct effect.
In the model described in Figure 1 and the preceding equations, mediational process can be hypothesized in several ways. First, one can hypothesize that the independent variable X affects the growth rate of the mediator process, η2, and subsequently affects the growth rate of the outcome process, η4 (i.e., X → η2 → η4). Another potential mediational pathway is the independent variable affecting the growth rate of the outcome process via the initial level of the outcome process, η3, and the growth rate of the mediator process, η2 (i.e., X → η3 → η2 → η4). It is also possible to hypothesize a mediational process such that the independent variable influences the initial level of the mediator, which, in turn, affects the growth rate of the outcome process (i.e., X → η1 → η4). This study focuses on the first type of mediational process. The question of interest here is whether the independent variable influences the trajectory of the outcome process through its effects on the trajectory of the mediator process. Thus, the mediation is defined by the pathway from the independent variable X through the growth rate of the mediator process to the growth rate of the outcome process, X → η2 → η4.
Among a number of methods for testing the significance of the mediated effects (see MacKinnon et al. (2002) for review of these methods), some of the most widely used are the joint significance test and the methods classified as the product of coefficients methods. Three of these methods were examined in this study (Table 1) to examine statistical power to detect significant mediation effects. In the joint significance test, the mediated effect is evaluated by examining the extent to which the independent variable X affects the growth rate of the mediator process (path coefficient α) and the extent to which the growth rate of the mediator affects the growth rate of the outcome (path coefficient β). Significant mediation is claimed when both path coefficients are statistically significant. The joint significance test does not estimate the mediated effect or calculate confidence intervals to test the significance of the mediated effect.
Table 1. Three Methods for Testing Mediated Effects Examined in the Current Simulation Study.
| Method | Estimate of Mediated Effect | Test of Significance | |
|---|---|---|---|
| First-order solution (Sobel, 1982) | α̂β̂ |
|
|
| Asymmetric confidence interval (MacKinnon & Lockwood, 2001) | α̂β̂ |
|
|
| Joint significance test (Cohen & Cohen, 1983) | None |
|
In the product of coefficients tests, the mediated effects are estimated by the product of the two coefficients, α̂β̂. For the Sobel first-order test, the significance of mediation is tested by comparing the ratio of the estimated mediated effect to its standard error against the standard normal distribution. The assumption here is that the product of the two coefficients, α̂β̂, is normally distributed. However, the distribution of the product of the two coefficients is not always normal, often being asymmetric with high kurtosis. To take into account the nonnormality of the distribution of α̂β̂, MacKinnon and Lockwood (2001) proposed the asymmetric confidence interval test. In the asymmetric confidence interval test, the significance of mediation is tested by constructing the confidence interval of the mediated effect based on the distribution of the product of two normally distributed random variables (Meeker, Cornwell, & Aroian, 1981). Unlike the typical cases of confidence intervals, the confidence intervals obtained in this method are asymmetric because it accommodates the nonnormality of the distributions of the product of two random variables.1 When the confidence interval does not include zero, the mediated effect is considered statistically significant.
The purpose of this simulation study was to examine the statistical performance of testing mediation in the LGCM framework, focusing on the accuracy of the estimates of the mediated effects and statistical power to detect significant mediation for the tests previously described (Table 1). Simulation data were generated under various conditions defined by the combination of effect size of mediated effect, sample size, number of measurement occasions, and R2 of the measured variables; that is, proportion of the variance of the measured mediator and the outcome explained by the growth factors. Effect size and sample size were chosen as simulation factors based on prior simulation studies carried out in the multiple regression framework, as they (e.g., MacKinnon et al., 2002) found that effect size of the mediated effect and sample size were critical factors that affected the accuracy of the estimates of the mediated effects and statistical power of the methods for testing mediation. Thus, it was expected that the accuracy of estimates and power of mediation tests would be enhanced as sample size and effect size increase when the longitudinal mediation is tested in the LGCM framework.
The other two simulation conditions, the number of measurement occasions and R2 of the measured variables, are related to the precision and reliability of growth curves. When mediational processes are modeled in the LGCM framework, accurate and reliable estimation of growth trajectories is crucial and thought to affect statistical performance of the methods for testing mediation. Precision of a growth curve (Singer & Willet, 2003) is the extent to which the growth rate estimates the true rate of change in the sample and is improved by increasing the number of measurement occasions. As such, it was found that statistical power to detect group differences in the mean of the slope factor in a single growth curve model improved dramatically as the number of measurements increased (Muthen & Curran, 1997). In this study, it was expected that an increased number of measurements, given the same magnitude of growth over time, would improve the precision of growth curve and consequently, enhance the accuracy of the estimates of the mediated effects and statistical power to detect the significant mediation effect.
Finally, R2 of the measured variable was thought to affect the accuracy of estimates and statistical power. R2 of the measured variable is the proportion of the total variance of the measured variable that is accounted for by the growth factors. The R2 value is calculated at each measurement time point and can vary across time. A large R2 value indicates that the variance of the measured variable at time t is well explained by the hypothesized growth trajectory. In a simulation study examining statistical power to detect the significant covariance between the slope factors of two growth curves (Hertzog, Lindenberger, Ghisletta, & Oertzen, 2006), R2 at Time 1 (i.e., the proportion of the measured variable at Time 1 explained by the intercept factor), was found to be an important factor for statistical power. In this study, the R2 of the measured variable was defined as the proportion of the variance of the measured variable accounted for by both intercept and slope factors, and it was expected that greater R2 would improve the accuracy of estimation and statistical power for the mediation tests.
Method
Statistical Model
In this simulation study, the longitudinal mediation model was similar to the model in Figure 1. All the variables (X, M, and Y) in the model were simulated to be continuous. The growth trajectories of the mediator and the outcome were modeled as linear with equal intervals between measurements. The mediational process was modeled in the relations among the independent variable, the slope of the mediator trajectory, and the slope of the outcome trajectory. As the main research questions examined in the growth curve models center around the growth rates over time and the individual differences in the growth rates, the mediation effect in this study was defined as the independent variable affecting the growth rate of the outcome via the growth rate of the mediator.
The parameters in the growth trajectories were selected based on prior simulation studies on single growth trajectory models (Muthén & Curran, 1997) and the author's prior experiences in longitudinal data analyses. Specifically, the means of the intercept factors (η1 and η3) were set to be 1.0 with variances of 0.5. The growth of the mediator and the growth of the outcome over the multiple measurement occasions were modeled to be the same in magnitude, such that the level at the last measurement occasion was 1 SD above the mean of the baseline level (i.e., M1 and Y1). In addition, the intercept factors of the mediator and the outcome processes (η1 and η3) were simulated to be correlated with each other (r = .30) but unrelated with the independent variable X to mimic the randomized trials, where individuals are randomly assigned to the levels of the independent variable, and thus, the mediator and the outcome measures at baseline are equivalent across different levels of the independent variable. The covariances between the intercept factors and the disturbances of the slope factors were set to be −0.1. The relations between the intercept factors and the slope factors of the other processes (e.g., the intercept factor of the mediator and the slope factor of the outcome) were also set to be −0.1. These negative relations of the intercept and the slope factors reflected the situations frequently observed in the empirical studies using the LGCM technique, where the individuals with higher levels at the initial measurement time point showed smaller changes at the later time points (Duncan, Duncan, & Strycker, 2006; Hancock & Lawrence, 2006).
Conditions of Simulation Study
The simulation study was conducted in a 3×2×2×6 factorial design in the combination of the following four factors. All simulations were carried out using Mplus (Muthén & Muthén, 2006) software program (version 4.1). In each of the 72 conditions, a total of 1,000 replications were conducted. Out of 1,000 replications in each condition, any replications in which estimates of variances were negative or the model was not converged were excluded, and then the first 500 replications were selected for the subsequent analyses. Thus, a total of 36,000 replications were included in the analyses to examine statistical performance of the mediation tests.
Effect size of mediated effect
Effect size of the mediated effect was defined by the proportion mediated, that is, the ratio of the mediated effect to the total effect [αβ/(αβ + τ′)]. Three different values of the proportion mediated were chosen: 0.1, 0.3, and 0.5. The different values of the proportion mediated measure were obtained by varying the size of the path coefficients α and β, while setting the size of the direct effect, τ′, to be constant. For the proportion mediated of 0.1 (i.e., 10% of the total effect is mediated), the coefficient α was 0.18 and β was 0.16. For the proportion mediated of 0.3, α was 0.31 and β was 0.35. For the proportion mediated of 0.5, α was 0.52 and β was 0.49. In all conditions, the path coefficient τ′, the direct effect, was 0.25.
R2 of measured variables
Two different values for R2 of the measured mediator and outcome variables were chosen to represent moderate and large proportion of variance accounted for by the latent growth factors: 0.5 and 0.8. The R2 values were set to be constant across time to reflect that the growth trajectory explained the variances of the measured variables equally across the measurement occasions. In addition, the same R2 values were set for both mediator and outcome processes. As the variance explained by the growth factors at each time point was a function of the time scores represented by the factor loadings and the variances and covariances of the growth factors, the total variances of the measured variables increased over time in the current simulations. Thus, with the constant R2 values across the measurement occasions, the error variance increased across time as well.
Number of measurement occasions
The number of measurement occasions was chosen to be three and five time points. The number of measurements was modeled to be the same for both mediator and outcome processes. Since the growth of the mediator and the outcome at the last measurement occasion was defined as 1 SD above the mean of the initial level at Time 1, the level at the last measurement was the same regardless of the number of measurement occasions. In other words, increasing the measurement occasions in this study corresponded to adding more measurement occasions for a given study period.
Sample size
Sample sizes were varied by six different sizes: 100, 200, 500, 1,000, 2,000, and 5,000. These sample sizes were chosen to represent the sample sizes used in research studies in social sciences and prevention science.
Simulation Outcome Measures
Measure of accuracy of estimate of mediated effect and standard error
Relative bias was used to assess the accuracy of the point estimate of the mediated effect and the standard error of estimate. As shown next, relative bias of the point estimate of the mediated effect was calculated by the ratio of the difference between the estimate and the true value of the mediated effect to the true value.
| (7) |
In Equation 7, ω̂ is the point estimate of the mediated effect based on the simulated data and ω is the true value of the mediation effect. Out of three tests examined in this study, mediated effects are not estimated in the joint significance test. In the other two methods, the mediated effects are estimated by the product of the two path coefficients, α̂β̂. Thus, the relative bias of the mediated effect was obtained for the product of coefficients, α̂β̂.
For the relative bias of the standard error of the mediated effect, the first-order delta-method standard error (Sobel, 1982) was calculated as shown in Table 1 for each of 500 replications. The mean of these 500 standard error estimates was then used as the estimate of the standard error of the mediated effect. The true value of the standard error was obtained by the standard deviation of the estimated mediated effects across 500 replications (Yang & Robertson, 1986). A relative bias smaller than .10 was considered acceptable (Kaplan, 1988).
Empirical power
Estimation of statistical power in this study was empirically based. To estimate power empirically, the mediated effect was calculated and tested for significance repeatedly for 500 replications in each simulation condition using each of the three methods in Table 1. The proportion of replications, in which the mediated effect was statistically significant at the Type I error rate of .05, was computed as an estimate of statistical power for each condition and for each method for testing mediation. Because the true values of α and β were not 0 in this study, the proportion of replications that the mediated effect was significant provided the measure of statistical power.
Results
Accuracy of Estimates of Mediated Effects
The relative biases of the mediated effect estimates (α̂β̂) are reported in Table 2. The relative biases were generally larger when R2 was .50 compared to the conditions with R2 of .80, especially when the number of measurement occasions was reduced (i.e., three time points). With R2 of .50 across three measurement occasions, the relative bias was smaller than .10 only when the sample size was 1,000 or larger. With two additional measurements on both mediator and outcome variables, the relative bias decreased tremendously: Relative bias was larger than .10 only with the sample size of 100. When R2 was .80, the estimates of mediated effects were quite accurate. Specifically, only when the sample size was 100 with three measurement occasions, the relative bias was larger than .10. In other conditions with R2 of .80, the relative bias of the estimated mediated effect was smaller than .10.
Table 2. Relative Bias of Mediated Effect across Simulation Conditions.
| Number of Measurements | Effect Size | Sample Size | |||||
|---|---|---|---|---|---|---|---|
|
| |||||||
| 100 | 200 | 500 | 1,000 | 2,000 | 5,000 | ||
| Three occasions | |||||||
| R2 = .5 | Small | 1.240 | 1.502 | 0.201 | 0.110 | 0.046 | 0.027 |
| Medium | 1.617 | 0.610 | 0.126 | 0.079 | 0.026 | 0.017 | |
| Large | 0.779 | 0.342 | 0.137 | 0.054 | 0.026 | 0.018 | |
| R2 = .8 | Small | 0.195 | −0.006 | 0.041 | 0.020 | −0.009 | −0.004 |
| Medium | 0.110 | 0.047 | 0.005 | 0.022 | 0.011 | −0.002 | |
| Large | 0.153 | 0.050 | 0.020 | 0.009 | 0.002 | 0.003 | |
| Five occasions | |||||||
| R2 = .5 | Small | 0.352 | 0.079 | 0.014 | 0.004 | 0.020 | 0.005 |
| Medium | 0.271 | 0.093 | 0.025 | 0.021 | 0.011 | 0.007 | |
| Large | 0.184 | 0.076 | 0.017 | 0.011 | 0.002 | 0.004 | |
| R2 = .8 | Small | 0.077 | 0.028 | 0.032 | 0.009 | −0.003 | −0.003 |
| Medium | 0.023 | −0.001 | 0.001 | −0.003 | 0.000 | 0.000 | |
| Large | 0.014 | 0.004 | 0.005 | 0.000 | 0.001 | 0.000 | |
Note. Effect size was defined as the proportion mediated: small = .10, medium = .30, and large = .50. R2 was the proportion of variances of the measured mediator and outcome accounted for by both intercept and slope factors.
Accuracy of Standard Errors
The relative biases of the standard errors of the mediated effects calculated for the first-order delta-method are reported in Table 3. Similar to the result patterns found in the relative biases of the mediated effect estimates, the relative biases of the standard error were larger than .10 when R2 was .50, with relatively smaller sample sizes, such as 100 or 200, and with three measurement time points. With two additional measurements, the relative bias of the standard error of estimate decreased. When the mediator and the outcome are measured over five occasions and R2 of the measures is .80, the relative bias of the standard error was smaller than .10 across all the conditions.
Table 3. Relative Bias of Standard Error of Mediated Effect across Simulation Conditions.
| Number of Measurements | Effect Size | Sample Size | |||||
|---|---|---|---|---|---|---|---|
|
| |||||||
| 100 | 200 | 500 | 1,000 | 2,000 | 5,000 | ||
| Three occasions | |||||||
| R2 = .5 | Small | 2.926 | 1.115 | −0.082 | −0.055 | −0.007 | 0.006 |
| Medium | 9.514 | 1.694 | −0.025 | 0.032 | −0.022 | −0.032 | |
| Large | 9.741 | 1.265 | 0.028 | −0.057 | −0.025 | −0.008 | |
| R2 = .8 | Small | −0.024 | 0.024 | −0.070 | −0.049 | 0.003 | −0.020 |
| Medium | −0.040 | 0.025 | 0.023 | −0.011 | 0.026 | 0.029 | |
| Large | −0.124 | −0.006 | −0.052 | 0.022 | 0.007 | −0.006 | |
| Five occasions | |||||||
| R2 = .5 | Small | −0.124 | −0.007 | −0.032 | 0.007 | 0.008 | 0.027 |
| Medium | −0.090 | −0.041 | −0.010 | −0.033 | 0.026 | 0.008 | |
| Large | −0.148 | −0.058 | −0.034 | −0.019 | 0.040 | −0.060 | |
| R2 = .8 | Small | 0.052 | −0.034 | −0.048 | 0.031 | −0.085 | 0.030 |
| Medium | 0.009 | 0.003 | −0.003 | −0.009 | −0.075 | −0.014 | |
| Large | −0.062 | 0.020 | −0.056 | 0.010 | −0.023 | −0.057 | |
Note. Effect size was defined as the proportion mediated: small = .10, medium = .30, and large = .50. R2 was the proportion of variances of the measured mediator and outcome accounted for by both intercept and slope factors. Standard error of mediated effect was obtained by Sobel's (1982) first-order delta-method.
Empirical Power
The results on empirical power are presented in Figures 2 and 3: Figure 2 for power under the three measurement occasions and Figure 3 for power under the five measurement occasions. In each figure, the top row represents the R2 value of .50 and the bottom row represents the R2 value of .80. Power curves are represented as a function of sample size for each method for testing mediation.
Figure 2.
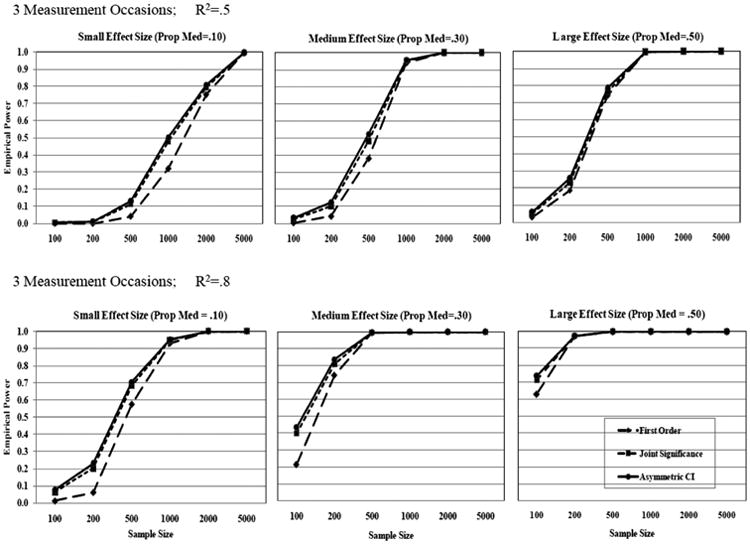
Empirical power: Three measurement occasions.
Figure 3.
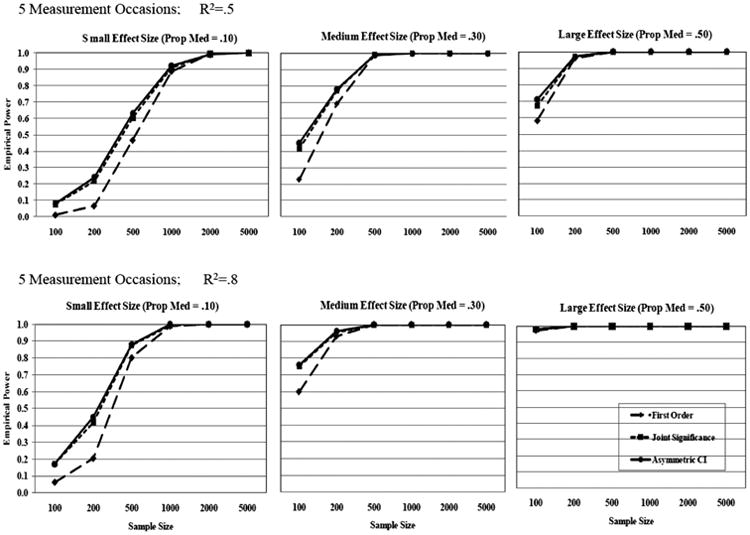
Empirical power: Five measurement occasions.
As expected, empirical power was affected by the factors varied across simulation conditions. In addition, power varied depending on the methods used for testing mediation. The test using Sobel's first-order solution (Sobel, 1982) had relatively lower power than the other tests. The joint significance test (Cohen & Cohen, 1983) and the asymmetric confidence interval test (MacKinnon & Lockwood, 2001) had equivalent power. Examining empirical power under the conditions with three measurement occasions in Figure 2, power greater than .80 required extremely large samples when the R2 value was .50. When using the joint significance test and the asymmetric confidence interval test with R2 of .50 across three measurement occasions, the sample size required for .80 power was approximately 2,000, 1,000, and 500, for small, medium, and large effect sizes, respectively. The Sobel test needed larger samples than the joint significance test or the asymmetric confidence interval test under the same conditions. With the increase in R2 (i.e., .80) of the measured variables, power improved. However, the sample size needed for .80 power was still large when the effect size of mediation was small. For example, the joint significance test and the asymmetric confidence interval test needed a sample size of approximately 750 to have .80 power with R2 of .80 across three measurement occasions. When the effect size of the mediated effect was medium and the R2 value was .80 across three measurement occasions, a sample size of 200 was needed for power greater than .80, except for the Sobel test. The Sobel test needed a sample size larger than 200 to have .80 power, when the effect size was medium and the R2 value was .80 across three measurement occasions.
As can be seen in Figure 3, the additional two measurements (i.e., five measurement occasions) increased power substantially. However, when the effect size was small with the R2 value of .50 across five measurements, the sample size needed for .80 power was still as large as approximately 750 for the joint significance test and the asymmetric confidence interval test. For the Sobel test, the sample size needed for .80 power was 1,000 under the same condition. With the R2 value of .80 over five measurements and small mediated effect, the required sample size for .80 power was approximately 500 for the Sobel test and slightly smaller for the other two tests. When the effect size of the mediated effect was medium or large, a sample size of approximately 200 was enough to have power greater than .80 across different R2 values for the joint significance and the asymmetric confidence interval tests; however, when the R2 value was .50 with the medium effect size, the Sobel test needed a sample size greater than 200.
Discussion
This study examined the accuracy of estimated mediated effects and statistical power of different methods for testing mediation when the mediation was investigated in the parallel process LGCM framework. As expected, the factors varied across simulation conditions in this study affected the accuracy of estimates and statistical power to detect significant mediated effects. As sample size, effect size of the mediated effect, number of measurement occasions, and R2 of the measured variables increased, the estimates of the mediated effect and its standard error were more accurate and statistical power improved. However, in general, large samples were needed for accurate estimates of mediation and decent statistical power. The accuracy of the estimates of mediated effects suffered, particularly when R2 was .50 across three measurement occasions. In such conditions, a sample size of approximately 1,000 was needed. With the additional two measurements on both mediator and outcome variables, the accuracy of the estimated mediated effects improved tremendously, except for the small sample size (i.e., 100) with R2 of .50.
For statistical power of .80 or higher, large samples, such as a sample size of approximately 1,000, were needed for most of the methods for testing mediation, when the effect size of mediation is medium and R2 was .50 across three measurement occasions. With the additional two measurements, the sample size needed for .80 power under the same condition decreased to approximately 200. Increases in the number of measurements and in the R2 value of the measured variables improved statistical power substantially, although quite large samples were still needed when the effect size of mediation was small.
Based on the findings of this study, it appears that researchers could improve statistical power to detect mediation in the LGCM framework by securing large samples, increasing the effect size of the mediated effect, increasing the number of measurement occasions, and increasing R2 of the measured variables. Considering that the resources are often limited, increasing R2 of the measured variables appears to be an efficient way to improve statistical power to detect the mediation effect. This finding is consistent with prior work by Hertzog et al. (2006), which examined power to detect the correlations between the slope factors of two growth curves. Large R2 can be achieved by reducing the proportion of the residual variances of the measured variables. One way to reduce the proportion of the residual variances of the measures is to reduce random measurement errors by choosing reliable measures for the mediator and the outcome. Alternatively, one could use multiple indicators in measuring the mediator and the outcome and model them as latent variables to separate out the measurement errors from the true estimates of the mediator and the outcome at each time point. In such cases, the growth of the mediator and the growth of the outcome can be modeled as growth of factors using second-order latent variable models (Hertzog et al., 2006; Sayer & Cumsille, 2001). However, modeling the growth of the latent factors might require larger sample sizes due to the complexity of the models.
Another factor to consider for statistical power was the choice of method for testing mediation. The method using Sobel's first-order solution, which assumes that the mediated effect (α̂β̂) is normally distributed, showed the lowest power among the three methods examined in this study. The distributions of (α̂β̂) are often nonnormal and thus, testing mediation by using the critical values under the standard normal distribution leads to low statistical power. Among the three methods examined in this study, the joint significance test does not estimate the mediated effects and the asymmetric confidence interval test is based on the distribution of the product of two normally distributed random variables (see MacKinnon et al., 2002, for more details). These two tests showed essentially the same statistical power; however, the asymmetric confidence interval test would be preferable because one can obtain the point estimate of the mediated effect and also construct confidence limits of the mediated effect. Another set of tests that were not examined in this study but need to be noted are those based on resampling methods such as bootstrapping (Efron & Tibshirini, 1993). These methods create empirical distributions of the mediated effects, adjusting for the nonnormality of the distribution of the product of the two coefficients (MacKinnon et al., 2004; Preacher & Hayes, 2004; Shrout & Bolger, 2002). Future study is warranted to examine statistical power of these resampling methods when mediation effects are evaluated in the LGCM framework.
Although the parallel process LGCM approach is a superior method for investigating longitudinal mediation, there are several issues researchers should note. The foremost strength of the parallel process LGCM approach is that researchers estimate the longitudinal changes based on the repeated measures across multiple occasions. Consequently, one can estimate the changes in the mediator and the outcome that are closer to true values and, thus, evaluate mediation more accurately. However, the difficulties in causal interpretation of the meditational process remain in this approach, without the design aspects and theoretical rationale supporting the causal directions. When the independent variable represents random assignment to conditions, the path coefficient α in Figure 1 can be interpreted as causal effect. The causal interpretation of coefficient β is still not clear, as the relation between the two slope factors is correlational and it is possible that the outcome actually causes the mediator (Holland, 1988; MacCallum, 1986), especially when the mediator and the outcome are concurrently measured. The causal interpretation of the relation between the growth rate in the mediator and the growth rate in the outcome should depend on other factors, such as time precedence of the mediator or clear theoretical rationale. Another issue is that in the parallel process LGCM approach, the overall, as opposed to time-specific, mediation effect is estimated based on the repeated measures across time. If researchers are interested in examining whether the effect of the independent variable on the mediator and the effect of the mediator on the outcome vary across time or assessing when the mediated effect ceases to occur in longitudinal studies, the cross-lagged model approach (Cole & Maxwell, 2003) might be more suitable. If the mediation effects of interest are based on the change scores between two measurement occasions, rather than the overall changes across several measurement occasions, latent difference score models (Ferrer & McArdle, 2003; McArdle, 2001) can be applied.
Given the recent increased use of the LGCM approach to mediation, the findings reported here provide researchers with important information that can be utilized in designing longitudinal studies or analyzing existing data; however, there are several limitations of this study. First, the LGCM mediation in the current study was modeled in a relatively simple model. Researchers might run into more complicated modeling issues. For example, the growth might take nonlinear forms, the number of occasions might be different for the mediator and the outcome processes, the R2 values might vary over time, the two path coefficients involved in the meditational process (α and β) might show discrepancy in magnitude, and the independent variable might be modeled as another growth process. In such cases, the mediation models become more complicated than the current model and the accuracy of estimates and statistical power could be reduced in the similar conditions. Second, the independent variable in this study was simulated as a continuous variable. Although the independent variable in this study was not simulated as a dichotomous variable, it is speculated that the results for the dichotomous independent variable might not be different from the results presented here, as other simulation studies found the similarities in the results when comparing continuous and categorical independent variables, if other conditions are equivalent for the model parameters (Fritz & MacKinnon, 2008; MacKinnon et al., 2002). Third, this study did not examine Type I error rates. Based on the findings from a prior simulation study on mediation carried out in the multiple regression framework (MacKinnon et al., 2002), it is expected that the Type I error rates would be lower than the conventional level when using the joint significance test, the Sobel's first-order solution test, and the asymmetric confidence interval test. However, it is not clear to what extent the Type I error rates would be biased when mediation is modeled in an LGCM framework. Issues of Type I error rates and other modeling aspects should be investigated in future studies. Finally, effect size of the mediated effect in this study was defined as the proportion mediated. Proportion mediated is one of the most frequently used effect size measures; however, it tends to be stabilized with relatively large samples. Future study is needed to examine whether similar results are obtained with different effect size measures, such as the ratio of the mediated effect to the direct effect (α̂β̂/τ̂′) and R2 measures (Fairchild, MacKinnon, Taborga, & Taylor, 2009).
Acknowledgments
This project was supported by Grants R01-DA07356 and R01 AA13117-01A awarded to Dr. David MacKinnon. The author thanks Dr. David MacKinnon for his generous support and valuable comments on this study. The author also thanks Drs. Siek Toon Khoo and Matthew Fritz for their helpful comments and acknowledges the members of the Prevention Science Methodology Group for their comments on the presentations related to this study.
Footnotes
The asymmetric confidence intervals of estimated mediated effects can be obtained directly using a program called PRODCLIN (MacKinnon, Fritz, Williams, & Lockwood, 2007), which can be downloaded on the Web (http://www.public.asu.edu/∼davidpm/ripl/Prodclin/).
References
- Baron RM, Kenny DA. The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Bauer DJ, Preacher KJ, Gil KM. Conceptualizing and testing random indirect effects and moderated mediation in multilevel models: New procedures and reecommendations. Psychological Methods. 2006;11(2):142–163. doi: 10.1037/1082-989X.11.2.142. [DOI] [PubMed] [Google Scholar]
- Cheong J, MacKinnon DP, Khoo ST. Investigation of mediational processes using parallel process latent growth curve modeling. Structural Equation Modeling. 2003;10(2):238–262. doi: 10.1207/S15328007SEM1002_5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen J, Cohen P. Applied multiple regression/correlation analysis for the behavioral sciences. Hillsdale, NJ: Lawrence Erlbaum Associates, Inc; 1983. [Google Scholar]
- Cole DA, Maxwell SE. Testing mediational models with longitudinal data: Questions and tips in the use of structural equation modeling. Journal of Abnormal Psychology. 2003;112(4):558–577. doi: 10.1037/0021-843X.112.4.558. [DOI] [PubMed] [Google Scholar]
- Collins LM, Graham JW, Flaherty BP. An alternative framework for defining mediation. Multivariate Behavioral Research. 1998;33:295–312. doi: 10.1207/s15327906mbr3302_5. [DOI] [PubMed] [Google Scholar]
- Duncan TE, Duncan SC, Strycker LA. An introduction to latent variable growth curve modeling: Concepts, issues, and applications. Mahwah, NJ: Lawrence Erlbaum Associates, Inc; 2006. [Google Scholar]
- Edwards JR, Lambert LS. Methods for integrating moderation and mediation: A general analytical framework using moderated path analysis. Psychological Methods. 2007;12(1):1–22. doi: 10.1037/1082-989X.12.1.1. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirini RJ. An introduction to the bootstrap. Boca Raton, FL: Chapman & Hall/CRC Press; 1993. [Google Scholar]
- Fairchild AJ, MacKinnon DP. A general model for testing mediation and moderation effects. Prevention Science. 2009;10(2):87–99. doi: 10.1007/s11121-008-0109-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fairchild AJ, MacKinnon DP, Taborga MP, Taylor AB. R-squared effect size measures for mediation analysis. Behavioral Research Methods. 2009;41:486–498. doi: 10.3758/BRM.41.2.486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrer E, McArdle JJ. Alternative structural models for multivariate longitudinal data analysis. Structural Equation Modeling. 2003;10:493–524. [Google Scholar]
- Festinger L. A theory of cognitive dissonance. Palo Alto, CA: Stanford University Press; 1957. [Google Scholar]
- Fritz MS, MacKinnon DP. An exponential decay model for mediation; Paper presented at the Society for Prevention Research; San Francisco, CA. 2008. May 27, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock GR, Lawrence FR. Using latent growth models to evaluate longitudinal change. In: Hancock GR, Mueller RO, editors. Structural equation modeling: A second course. Greenwich, CT: Information Age; 2006. pp. 171–196. [Google Scholar]
- Hertzog C, Lindenberger U, Ghisletta P, von Oertzen T. On the power of multivariate latent growth curve models to detect correlated change. Psychological Methods. 2006;11(3):244–252. doi: 10.1037/1082-989X.11.3.244. [DOI] [PubMed] [Google Scholar]
- Holland PW. Causal inference, path analysis, and recursive structural equations models. In: Clogg CC, editor. Sociological methodology. Washington, DC: American Sociological Association; 1988. pp. 449–493. [Google Scholar]
- Jagers RJ, Morgan-Lopez AA, Howard TL, Browne DC, Flay BR. Mediators of the development and prevention of violent behavior. Prevention Science. 2007;8(3):171–179. doi: 10.1007/s11121-007-0067-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaplan D. The impact of specification error on the estimation, testing, and improvement of structural equation models. Multivariate Behavioral Research. 1988;23:69–86. doi: 10.1207/s15327906mbr2301_4. [DOI] [PubMed] [Google Scholar]
- Kenny DA. Reflections on mediation. Organizational Research Methods. 2008;11(2):353–358. [Google Scholar]
- Kenny DA, Korchmaros JD, Bolger N. Lower level mediation in multilevel models. Psychological Methods. 2003;8(2):115–128. doi: 10.1037/1082-989x.8.2.115. [DOI] [PubMed] [Google Scholar]
- Krull JL, MacKinnon DP. Multilevel mediation modeling in group-based intervention studies. Evaluation Review. 1999;23(4):418–444. doi: 10.1177/0193841X9902300404. [DOI] [PubMed] [Google Scholar]
- Krull JL, MacKinnon DP. Multilevel modeling of individual and group level mediated effects. Multivariate Behavioral Research. 2001;36(2):249–277. doi: 10.1207/S15327906MBR3602_06. [DOI] [PubMed] [Google Scholar]
- MacCallum R. Specification searches in covariance structure modeling. Psychological Bulletin. 1986;100:107–120. [Google Scholar]
- MacKinnon DP, Fairchild AJ, Fritz MS. Mediation analysis. Annual Review of Psychology. 2007;58:593–614. doi: 10.1146/annurev.psych.58.110405.085542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Fritz MS, Williams J, Lockwood CM. Distribution of the product confidence limits for the indirect effect: Program PRODLIN. Behavior Research Methods. 2007;39(3):384–389. doi: 10.3758/bf03193007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM. Unpublished manuscript. Arizona State University; Tempe, AZ: 2001. Distribution of products tests for the mediated effect. [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychological Methods. 2002;7(1):83–104. doi: 10.1037/1082-989x.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Williams J. Confidence limits for the indirect effect: Distribution of the product and resampling methods. Multivariate Behavioral Research. 2004;39(1):99–128. doi: 10.1207/s15327906mbr3901_4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McArdle JJ. A latent difference score approach to longitudinal dynamic structural analysis. In: Cudeck R, du Toit S, Sörbom D, editors. Structural equation modeling: Present and future A festschrift in honor of Karl Jöreskog. Lincolnwood, IL: Scientific Software International; 2001. pp. 341–380. [Google Scholar]
- Meeker WQ, Cornwell LW, Aroian LA. Selected tables in mathematical statistics: Vol VII The product of two normally distributed random variables. Providence, RI: American Mathematical Society; 1981. [Google Scholar]
- Morgan-Lopez AA, MacKinnon DP. Demonstration and evaluation of a method for assessing mediated moderation. Behavior Research Methods. 2006;38(1):77–87. doi: 10.3758/bf03192752. [DOI] [PubMed] [Google Scholar]
- Muthén BO, Curran PJ. General longitudinal modeling of individual differences in experimental designs: A latent variable framework for analysis and power estimation. Psychological Methods. 1997;4(2):371–402. [Google Scholar]
- Muthén BO, Muthén L. Mplus user's guide. Los Angeles, CA: Muthén & Muthén; 2006. [Google Scholar]
- Preacher KJ, Hayes AF. SPSS and SAS procedures for estimating indirect effects in simple mediation models. Behavior Research Methods, Instruments, & Computers. 2004;36(4):717–731. doi: 10.3758/bf03206553. [DOI] [PubMed] [Google Scholar]
- Raudenbush SW, Sampson R. Assessing direct and indirect effects in multilevel designs with latent variables. Sociological Methods and Research. 1999;28(2):123–153. [Google Scholar]
- Robins DR, Greenland S. Identifiability and exchangeability for direct and indirect effects. Epidemiology. 1992;3:143–155. doi: 10.1097/00001648-199203000-00013. [DOI] [PubMed] [Google Scholar]
- Roesch SC, Norman GJ, Adams MA, Kerr J, Sallis JF, Ryan S, et al. Patrick K. Latent growth curve modeling of adolescent physical activity testing parallel process and mediation models. Journal of Health Psychology. 2009;14(2):313–325. doi: 10.1177/1359105308100216. [DOI] [PubMed] [Google Scholar]
- Sayer AG, Cumsille PE. Second-order latent growth models. In: Collins LM, Sayer AG, editors. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001. pp. 177–200. [Google Scholar]
- Shrout PE, Bolger N. Mediation in experimental and nonexperimental studies: New procedures and recommendations. Psychological Methods. 2002;7(4):422–445. [PubMed] [Google Scholar]
- Simons-Morton B, Haynie D, Saylor K, Crump AD, Chen RA. Impact analysis and mediation of outcomes: The going places program. Health Education & Behavior. 2005;32(2):227–241. doi: 10.1177/1090198104272002. [DOI] [PubMed] [Google Scholar]
- Singer JD, Willet JB. Applied longitudinal data analysis: Modeling change and event occurrence. New York, NY: Oxford University Press; 2003. [Google Scholar]
- Sobel ME. Asymptotic confidence intervals for indirect effects in structural equation models. In: Leinhardt S, editor. Sociological methodology. Washington, DC: American Sociological Association; 1982. pp. 290–312. [Google Scholar]
- Sobel ME. Effect analysis and causation in linear structural equation models. Psychometrika. 1990;55(2):337–352. [Google Scholar]
- Steele C, Josephs R. Alcohol myopia: Its prized and dangerous effects. American Psychologist. 1990;45:921–933. doi: 10.1037//0003-066x.45.8.921. [DOI] [PubMed] [Google Scholar]
- Taylor S, Leonard K. Alcohol and human physical aggression. In: Geen R, Donnerstein E, editors. Aggression: Theoretical and empirical reviews. Vol. 2. New York, NY: Academic Press; 1983. pp. 77–101. [Google Scholar]
- Yang MCK, Robertson DH. Understanding and learning statistics by computer. Singapore: World Scientific; 1986. [Google Scholar]


