Neurons in macaque Area V4 are tuned for complex spatio-temporal patterns

Abstract

To deepen our understanding of object recognition, it is critical to understand the nature of transformations that occur in intermediate stages of processing in the ventral visual pathway, such as area V4. Neurons in V4 are selective to local features of global shape, such as extended contours. Previously we found that V4 neurons selective for curved elements exhibit a high degree of spatial variation in their preference. If spatial variation in curvature selectivity was also marked by distinct temporal response patterns at different spatial locations, then it might be possible to untangle this information in subsequent processing based on temporal responses. Indeed, we find that V4 neurons whose receptive fields exhibit intricate selectivity also show variation in their temporal responses across locations. A computational model that decodes stimulus identity based on population responses benefits from using this temporal information, suggesting that it could provide a multiplexed code for spatio-temporal features.

INTRODUCTION

Visual information impinging on the photoreceptors in the retina is initially processed in the retinal circuit (Field and Chichilnisky, 2007) before being relayed via the Lateral Geniculate Nucleus (LGN) on to the primary visual cortex. Processing of visual shape continues downstream in a set of cortical areas in the ventral cortical pathway in the temporal lobe (DiCarlo et al., 2012). At the earliest stages of visual processing in the retina, systems identification techniques, such as reverse correlation, have spurred progress for understanding of how visual inputs are pooled to give rise to the receptive fields (RFs) of visual neurons (Field et al., 2010; Schwartz et al., 2012). Similar approaches have provided key insights about the population RFs of LGN afferents that make monosynaptic connections to neurons in the primary visual cortex (V1) (Jin et al., 2011) and the detailed spatial structure of RFs in the secondary visual cortex (V2) (Anzai et al., 2007; Tao et al., 2012). At later stages of processing along the ventral stream it has been much more difficult to constrain such mechanistic models of receptive field structure. However, there has been considerable progress towards understand what information is encoded based on decoding population responses (Pasupathy and Connor, 2002; Rust and DiCarlo, 2010). Area V4 lies at a critical intermediate juncture in the transformations that occur between V1/V2 and the final stages of shape processing in the inferotemporal cortex (areas TEO and TE). Earlier studies in V4 found that many neurons were selective to extended contours that form curved shapes (Pasupathy and Connor, 2001; 1999). A detailed understanding of RF organization in V4 remains crucial for understanding the more invariant forms of object recognition that then follow in inferotemporal cortex.

In a recent study (Nandy et al., 2013) we examined the fine spatial structure of V4 RFs using reverse correlation techniques to estimate the tuning for curvature. We found that V4 neurons exhibit a tradeoff between curvature selectivity and spatial invariance. Neurons tuned to curved shapes exhibited very limited spatial invariance, while those that preferred straight contours tended to show spatially invariant tuning. This diversity was explained by the fine-scale RF structure: fine-scale maps of orientation tuning across the RF for neurons preferring curved contours showed heterogeneous local variation, whereas tuning was homogeneous and thus translation invariant for neurons preferring straight contours.

This previous analysis examined a temporally averaged static picture of the RF structure. Here we investigate whether the homogeneity/heterogeneity observed in the spatial domain extended to the temporal domain as well. We find that the fine-scale RFs in V4 often show previously unappreciated spatio-temporal structure. Some neurons have progressively shifting spatial kernels. Others show distinct temporal signatures in different RF sub-regions, while others have spatial kernels that dissipate over time from the center to the edges.

As in the spatial domain, the complexity of these temporal patterns varied with the heterogeneity of the fine-scale receptive field map: neurons with spatially varying shape tuning have distinct temporal response patterns that unfold across RF locations. In contrast, neurons with spatially invariant shape tuning have similar temporal response patterns across RF locations. We find that computational models that use this temporal information to decode stimulus identity far outperform simpler models based on time averaged spike counts. We suggest that this tradeoff between simple/complex shape selectivity and homogeneity/heterogeneity in both the spatial and temporal domains could potentially reflect a spatio-temporal shape code in area V4.

RESULTS

We analyzed responses from 86 well-isolated neurons in area V4 of two awake, behaving male macaques (see Experimental Procedures). The stimuli consisted of oriented bars that served to map each neuron’s RF and orientation preference at a fine spatial scale, as well as composite contours that served to map the neuron’s shape preference at a coarser spatial scale (Fig 1). The temporal evolutions of the fine-scale RF structure of 4 example neurons are shown in Fig 2 (upper panels). Each panel depicts the fine-scale structure of the receptive field at different time-points after stimulus onset (non-overlapping 8.33ms time bins). Neuron I has two distinct spatial sub-regions (‘sub-fields’ with different orientation preferences, color-coded with different hues, upper panels) with very different temporal patterns. The red sub-field emerges earlier and persists longer as compared to the yellow sub-field, which emerges later and has a much shorter duration. Neuron II exhibits a clear and progressive spatial shift in the spatio-temporal RF (STRF) over time. These temporal patterns in the evolution of the RFs are not correlated to systematic drifts in fixational eye movements (Supp Fig 1A,B). Example neuron III illustrates a third STRF pattern that we observe in our data: receptive fields that dissipate outward over time from a central region. Finally, neuron IV is an example in which the receptive field remains fixed in place over time.

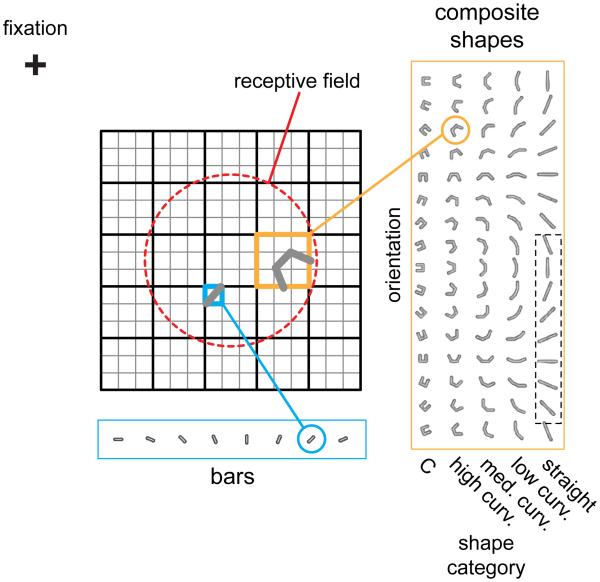
Fig 1. Stimuli and selectivity.

V4 receptive fields were probed with fast reverse correlation sequences drawn randomly from a set of bars or bar-composite shapes while the animal maintained fixation for 3s. Bars were presented at 8 orientations on a fine 15×15 location grid centered on the neuron’s receptive field (red dashed circle, drawn for illustrative purposes only). The composite stimuli were composed of 3 bars. The end elements were symmetrically linked to the central element at 5 different conjunction angles (0°,22.5°,45°,67.5° and 90°). These 5 conjunction Ι evels (straight, low curvature, medium curvature, high curvature and “C”), together with 16 orientations, yielding a total of 72 unique stimuli (although shown for aesthetic completion, the lower half of the zero curvature shapes [dotted box] is identical to the upper half and was not presented). The composite shapes were presented on a coarser 5×5 location grid that spanned the finer grid. A pseudo-random sequence from the combined stimulus set was shown in each trial. The stimulus duration was 16 ms with an exponentially distributed mean delay of 16 ms between stimuli.

Fig 2. Fine-scale spatio-temporal receptive fields (STRFs).

For 4 example neurons: Upper panels, temporal evolution of smoothed fine-scale orientation maps. Smoothing was achieved by linear interpolation of the respective fine-scale maps obtained using the oriented bars on the 15×15 grid (Fig 1). The maps are color-coded as follows: hue indicates local orientation preference, saturation indicates sharpness of orientation tuning and value indicates normalized average response. The color cone in the inset illustrates the hue-saturation-value color-coding scheme. Time points indicate the center of non-overlapping time bins relative to stimulus onset (bin width = 8.33ms). Lower panels, response contours at 5 response levels (90, 80, 70, 60 and 50% of local peak) are shown superimposed on orientation-averaged fine-scale maps (shown in gray scale). Contour lines are only shown for significant time bins (see Experimental procedures). The response contours are color coded as in the inset. The red ‘+’ depicts the centroid of the 90% contour. The 4 example neurons illustrate representative temporal patterns in our data: I has different spatial sub-fields (‘red’, ‘yellow’) with different temporal dynamics; II shows a progressively shifting spatial kernel; the spatial kernel for III emerges at the center and dissipates over time toward the edges in a ring-like fashion; neuron IV has no appreciable spatial excursion over time.

To capture these spatial excursions, we tracked the center of mass of each RF as it unfolded over time. We generated response contours from the fine-scale STRFs (Fig 2, lower panels; see Experimental Procedures) and calculated contour centroids. By connecting successive centroids, we could generate spatial trajectories of the fine-scale STRFs. Fig 3A illustrates the spatial trajectory of the centroids over time (yellow) superimposed over the time-averaged spatial RFs for the 4 example neurons in Fig 2 (centroid trajectories shown only for the 80% response level). There are 20 trajectories in each panel, each corresponding to a jackknifed subset of the data. This pattern of stability holds for all response levels (Supp Fig 1C) and for completely disjoint subsets of the data (Supp Fig 1D; first 50% of trials compared to last 50% of trials). Thus, V4 neurons exhibit very stable, repeatable patterns in the temporal evolution of their RFs.

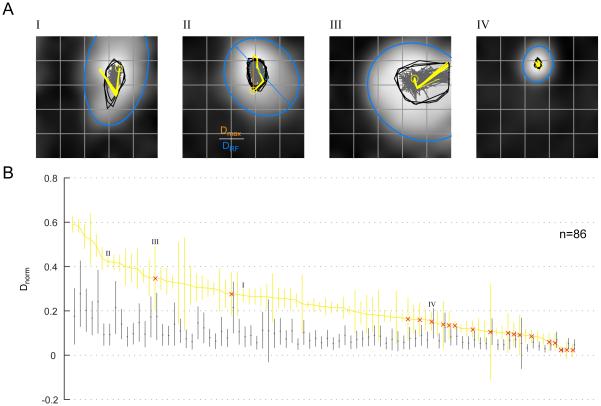
Fig 3. Fine-scale STRF trajectories.

(A) Spatial trajectories of the 80% contour centroids over time are shown superimposed on the temporally averaged receptive fields (gray) for the four example neurons in Fig 2. Each yellow trajectory shows the temporal progression of the centroids for a jackknifed subset of the data. There are 20 trajectories corresponding to 20 jackknives (each using 95% of the data). The yellow circle depicts the centroid location for the first significant time bin. The gray trajectories in the background are a subset of null trajectories obtained by random temporal permutations of the data (see Experimental Procedures). Gray polygons depict the convex hulls of the entire set of null trajectories (1000, obtained using a bootstrap procedure). The blue ellipse is the least-squares best-fit ellipse to the 50% response contour of the temporally averaged receptive field. (B) The normalized spatial excursion of the trajectories, D_norm, is plotted for each neuron in our population (n=86; mean ± std. dev.). The normalized distance was calculated by dividing the maximum Euclidean distance between any two points on a trajectory by the length of the major axis of the best-fit ellipse to the RF (blue ellipses in A). Also shown in gray are the normalized distances obtained from the null trajectories (mean ± std. dev.). The 4 example neurons are marked with Roman numerals. The neurons with normalized distances that were not significantly different from chance (p = 0.05) are marked with red ‘x’s.

We next quantified whether these temporal patterns were significantly different from the range of temporal patterns expected from stationary RFs. For each trajectory we identified the pair of STRF time-bins that contributed to a maximum spatial separation (D_max) among the corresponding pair of centroids. To facilitate comparison across the population of neurons with varying RF sizes, we calculated a normalized measure of the maximum spatial excursion (D_norm). This was done by dividing D_max by the major axis of an elliptical fit (D_RF) to the time-averaged spatial RF (Fig 3A; see Experimental Procedures). Trajectories with minimal spatial excursions will have D_norm values close to 0, while those with excursions spanning the width of the RF will have values close to 1. This normalized measure, D_norm, is plotted in rank-order for every unit in our population in Fig 3B (example units in Fig 2 are highlighted with corresponding numerals). Several units have large spatial excursions compared to the size of the RF, some exceeding half the width of the RF. These findings were robust across time and not due to any non-stationarities in recordings, as reflected by similar results when we repeated the analysis using the first and second halves of the data (Supp Fig 1E). To compute whether these spatial excursions were statistically significant, we compared D_norm to those obtained from a null distribution. The null distribution, D_{norm-shuffled}, assumed that the spatial RF remained stationary throughout the temporal response, such that temporally shuffling response bins per location would have no appreciable effect on the computation of the centroid and thus our D_norm measure. Because the average temporal response varies over time, often with a sharp transient to start, we first normalized responses per time bin before shuffling. A bootstrap procedure was then used to compute the null distribution (see Experimental Procedures). We reasoned that if the trajectories in the data were not due to any underlying temporal structure, then the statistics of the temporally shuffled data would not be significantly different from the statistics computed on the unshuffled data. The null distribution for each unit is also shown in Fig 3B (gray error bars). By this measure, 67 out of the 86 units were significantly different from chance (p < 0.05; non-significant units marked with ‘x’ in the figure). Thus a majority of units (78%) had spatial patterns in the temporal evolution of their RFs that could not be attributed to chance.

In an earlier study (Nandy et al., 2013), we found that V4 neurons selective for curved composite shapes exhibited considerable spatial heterogeneity in their tuning. The above analysis reveals that the center of mass of V4 RFs undergoes considerable excursions in visual space as the RF unfolds over time and that these excursions cannot be attributed to chance. This raises the possibility that the shape tuning heterogeneity in the spatial domain that was reported in the earlier study might extend to the temporal domain as well. In particular, we wondered if neurons with spatial heterogeneity in their shape tuning might also exhibit heterogeneity in their temporal response profiles. We thus investigated the temporal response properties of our population to the composite shape stimuli. We examined the coarse-scale STRFs (obtained from the composite shape stimuli) and first observed that shape selectivity at a particular RF location remained stable over time (Fig 4A,B and Supp Fig 2). To quantify this we computed a dispersion metric of peak shape selectivity in shape space (see Experimental Procedures). Across the population the dispersion metric is highly skewed toward low values (Fig 4C). We compared the dispersion metric for each unit to a null distribution obtained from temporally shuffled data. 82 out of 86 units had dispersion metrics that were not significantly different from null (p > 0.05). Shape tuning across time was thus highly conserved for the population.

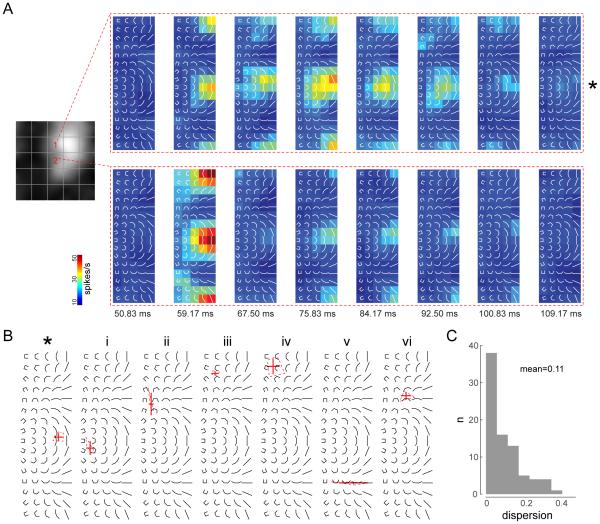
Fig 4. Coarse-scale STRFs show stable shape selectivity across time.

(A) Neuronal response maps to the set of composite shapes are shown for two spatial locations (on the 5×5 coarse grid) for an example neuron (neuron I in Fig 2). The spatial locations are marked by numbers on the temporal average RF (left panel). The composite stimuli are overlaid on the response maps for ease of reference. (B) Summary plots showing the dispersion of peak shape selectivity across significant temporal bins for seven example neurons at their maximally responsive spatial location. The error bars show the mean and standard deviation of peak response locations (centroid of contour at 90% of peak response) across time in shape space. The dotted polygon is the convex hull of the peak response locations. The neuron marked with an asterisk is the same example neuron in (A). The STRFs for the other neurons (i-vi) are shown in Supp Fig 2. (C) Histogram of dispersion of peak shape selectivity for the population. Dispersion is plotted as the area of the convex hull of the peak response locations (dotted polygons in B) as a fraction of shape space. Mean of the distribution is 0.11 or 11% of shape space, illustrating the temporal stability of shape selectivity.

However, the temporal response profiles were different in different parts of the RF for some neurons (example unit shown in Fig 4A). To investigate this further, we extracted the temporal response patterns (temporal kernel) to the composite stimuli at different locations within each neuron’s spatial RF (see Experimental Procedures). Temporal kernels are illustrated for two example neurons in Fig 5A-B. The first example neuron has spatially varying shape selectivity (Fig 5A, top row) and diverse temporal kernels in different parts of its RF (Fig 5B, top row). In contrast, the second example neuron has spatially homogeneous shape selectivity and very similar temporal kernels in different parts of the RF (Fig 5A,B; bottom row).

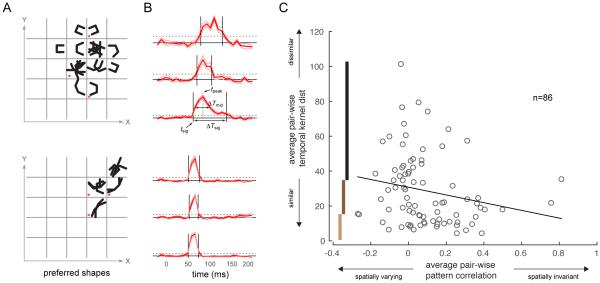
Fig 5. Neurons with spatially diverse shape selectivity have distinct temporal responses across spatial locations.

(A) For two example neurons (rows), the location-specific shape or set of shapes to which the neuron responded preferentially, at all spatially significant locations. Shapes are superimposed at each grid location. The example neuron in the top row is neuron II in Figs 2,3. (B) Normalized temporal response profiles (red, mean ± s.e.m.) to the composite shapes at the spatial locations marked with asterisks in A. The temporal responses were calculated across all stimuli whose responses were above 70% of local peak response. The black solid line indicates baseline response and the black dotted line indicates 4 standard deviations above baseline. Four purely temporal aspects of the response profiles are indicated: t_sig, the time point at which the temporal kernel first reaches significance; ΔT_sig, the period over which the temporal kernel remains significant; t_peak, the time point at which the response reaches its peak; and ΔT_mid, the duration over which the response remains at a level greater than half-way between the peak and baseline response levels. (C) The average pair-wise temporal kernel distance (see Experimental Procedures; average of all values in right column in Supp Fig 4) is plotted against the average pair-wise pattern correlation (average of all values in middle column of Supp Fig 4) for our entire population of neurons. There is a significant negative correlation (Spearman’s ρ = −0.28, p = 0.01) between the two quantities. The vertical bars mark the ranges for the lower, middle and upper third percentiles of the temporal kernel distances used for the analysis in Fig 6C.

To quantify the diversity of temporal kernels, we extracted four purely temporal aspects of each response kernel: the time point at which the response first reaches significance, t_sig; the duration over which the response remained significant, ΔT_sig; the time point at which the response reached its peak, t_peak; and the duration over which there was a sustained response at a level above the half-way mark between peak and baseline, ΔT_mid (Fig 5B and Supp Fig 3A; see Experimental Procedures). Because several of these temporal measures are related (Supp Fig 3B), we performed a principal components analysis (PCA) on this four dimensional space to reduce its dimensionality (Supp Fig 3). The first principal component is dominated by ΔT_sig, a measure of response duration, while the second gets roughly equal contributions from the other three parameters and is related to response latency (Supp Fig 3D). These two components accounted for 88% of the variance (Supp Fig 3E). Each kernel could then be represented as a point in the 2D plane defined by the first two principal components. The Euclidean distance between two such points gives a measure of similarity between the corresponding pair of temporal kernels (Supp Fig 4, last column).

To quantify the diversity of shape tuning, we calculated a measure of the similarity of shape tuning between pairs of spatial locations within the RF (pattern correlation; see Experimental Procedures). High pattern correlation values indicate spatially homogeneous tuning, while low values indicate spatially heterogeneous tuning (Supp Fig 4, middle column).

To investigate the relationship between spatial diversity of shape tuning and the spatial diversity of temporal kernels, we computed the average pairwise pattern correlation and temporal kernel distance for each neuron across all pairs of RF locations with significant response. Fig 5C shows the scatterplot of average temporal kernel distance versus average pattern correlation for all neurons in our population. Neurons with high pattern correlation show a relatively low temporal response distance. Neurons with low average pattern correlation exhibit a wide range of temporal kernel distances. Overall, we find that pattern correlation and temporal kernel distance are inversely correlated across the neural population (Spearman’s ρ = −0.28, p = 0.01). Spatial and temporal heterogeneity are thus correlated with one another. Neurons with spatially invariant tuning tend to have similar temporal kernels across RF locations. Although neurons with spatially varying tuning exhibit a large scatter in their average temporal kernel distances, a large subset have diverse temporal kernels. This inverse relationship is even stronger if we restrict our analysis to the subset of units whose D_norm values are in the top 50^th percentile (top 43 units in Fig 3B; Supp Fig 3F; Spearman’s ρ = −0.43, p = 0.005). Temporal kernel distance is positively correlated with D_norm (ρ = 0.19, p = 0.04), suggesting the involvement of the fine-scale STRF dynamics in shaping the temporal kernels; conversely, pattern correlation is negatively correlated with D_norm (ρ = −0.16, p = 0.03).

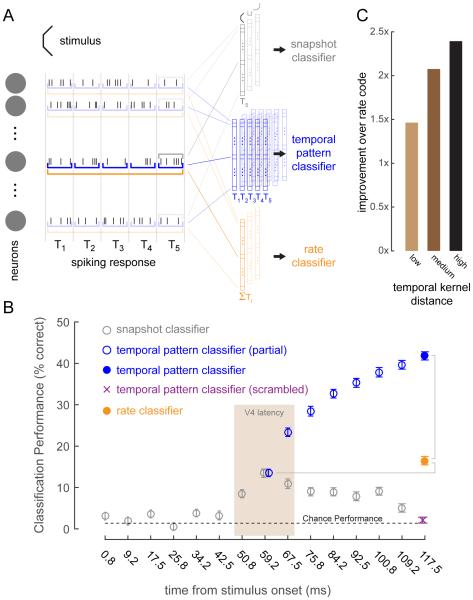
Finally, we investigated the potential role of the observed temporal dynamics in neural coding. We took the neural response of all 86 units as a population code, and asked whether a temporal code can outperform a mean-rate-based code. We trained classifiers (random forest classifiers, see Experimental Procedures) to perform a 72-way classification of the shape data (corresponding to the 72 composite shapes, Fig 1) in a position-invariant manner. Classifiers were trained on three categories of population codes (Fig 6A). The snapshot classifiers (Fig 6A, gray) were trained on data from individual time-bins. The temporal pattern classifier was trained on the temporal patterns of responses across a subset of time-bins (Fig 6A, blue). The rate classifier was trained on the sum total response across the same subset of time bins as the temporal pattern classifier (Fig 6A, orange). As expected, the snapshot classifiers (Fig 6B, gray symbols) exhibit chance performance at time-bins less than 50ms. Performance for these classifiers peaks at around 60ms, which corresponds to the expected latency of V4 neurons. The rate classifier (Fig 6B, orange symbol), which was trained on the total neuronal responses in the 8 time-bins between 50 and 120ms, performs only marginally better than peak snapshot performance at V4 latency. However, the temporal pattern classifier (Fig 6B, solid blue symbol) with access to the pattern of responses in these 8 time-bins far outperforms the rate classifier with about a 3x improvement in performance. This shows that there is rich information contained in the temporal response patterns that a decoder can potentially exploit in decoding shape information. By shuffling the temporal response patterns (random shuffle for each sample provided to the classifier), we verified that the improved performance was not due to the larger number of features used by the temporal pattern classifier as compared to the rate classifier (Fig 6B, purple ‘x’ symbol).

Fig 6. A population code of temporal response patterns far outperforms one with only rate information.

(A) Schematic illustrating the three different categories of population codes that were used to train classifiers to identify composite shapes. The snapshot classifier (gray) had access to the response for a particular time bin. The temporal pattern classifier (blue) had access to the temporal response pattern across multiple time bins. The rate classifier (orange) was given the sum total response across multiple time-bins. (B) Classification performance for different population codes (n=86) using a random forest classifier. The gray symbols are the performance for the snapshot classifiers for 15 time-bins after stimulus onset (non-overlapping 8.33ms time-bins; time-bin centers indicated on x-axis). Performance peaks at ~60ms which corresponds to the latency of V4 responses. The blue symbols are the temporal pattern classifier performances. Each successive open blue symbol is for a classifier with incremental temporal pattern information. The first has information from the time-bin at 59.2ms, the second from time-bins at 59.2ms and 67.5ms, and so on. The solid blue symbol is for the classifier that has the entire temporal pattern from 59.2ms to 117.5ms. The orange symbol is for the rate classifier that is given the total response for all time-bins from 59.2ms to 117.5ms. The rate classifier is only marginally better than the peak snapshot classification performance at 59.2ms. The full temporal pattern classifier is ~3x better than the rate classifier. The purple cross symbol is for the full temporal pattern classifier, but with scrambled temporal patterns. The dotted line represents chance performance of 1/72. Symbols are mean ± std. dev. of classification performance across 100 classifier runs. (C) Improvement in performance of the temporal pattern classifier over the rate classifier for neurons divided into three sub-populations according to their average temporal kernel distance (vertical bars in Fig 5C indicate corresponding ranges): low, neurons whose temporal kernel distances lie in the lower third percentiles (n=29); medium, middle third percentile (n=28); high, upper third percentiles (n=29).

We verified this improvement in performance using two other kinds of classifiers: decision tree and support vector machine (SVM). Absolute performance values for the decision tree classifiers are lower compared to the random forest, as expected, but the pattern of improvement remains the same (Supp Fig 5A). Since SVM does not directly support multi-way classification, we used a standard method (one-vs-one, see Experimental Procedures) to adapt SVM for multi-way classification. As with the other classifiers, the SVM-based classifier shows a similar pattern of improvement, with the temporal pattern classification exhibiting improved performance over the rate and snapshot classifiers (Supp Fig 5B)

We next subdivided our population into three sub-populations based on their average temporal kernel distances: neurons whose distances lay in the lower third, middle third and upper third percentiles (ranges indicated by vertical bars in Fig 5C). Performance improvement of the temporal patterns classifiers over the rate classifier increases with increasing diversity of temporal kernels in the sub-population (Fig 6C), further supporting the idea that temporal response patterns in V4 are information rich.

Control condition

We recorded from a small subset of neurons (n = 6) where the stimuli were presented for longer duration (200ms) in addition to the fast reverse correlation (16ms) method. As in our previous study (Nandy et al., 2013) where we found virtually identical shape tuning for both slow and fast stimuli, here we find that the temporal response patterns within 120ms of stimulus onset are essentially similar for both stimulus durations (Supp Fig 6). To quantify this, we extracted the temporal kernel parameters (used in the PCA analysis above) from the responses to both the slow and fast stimuli. This was done for all spatially significant response locations among the subset of units (n=36). The temporal kernel parameters for the two stimulus conditions are highly correlated: ρt_sig = 0.79, ρt_peak = 0.93, ρΔT_sig = 0.69, ρΔT_mid = 0.65, all p << 0.01.

DISCUSSION

The current findings show significant variation in the temporal response of V4 neurons across their receptive fields. We find that in addition to their diverse spatial selectivity (Nandy et al., 2013), neurons that are tuned to curved contours also exhibit diverse temporal response patterns and that a decoder with access to such response patterns can outperform a rate code decoder. This improvement is larger for neurons with greater diversity of temporal response patterns. This suggests that V4 neurons may employ the temporal domain to encode shape information. Although the importance of a temporal code in the shape processing pathway has been appreciated for a long time (McClurkin et al., 1991), our study provides the first quantification of this benefit in area V4 which is a critical locus in this pathway. Diverse temporal kernels could allow a neuron to multiplex information about multiple features. This finding also suggests a possible disambiguation of the V4 shape code. We previously found that V4 neurons tuned to curved shapes exhibit very limited spatial invariance (Nandy et al., 2013). These neurons preferred different curved shapes in different parts of their RF. If such neurons employed a purely spatial code, then their output signal (input to a recipient area such as the posterior infero-temporal cortex) would necessarily be ambiguous, since the code will not contain any additional information about the particular curved shape that the neuron was responding to. Such ambiguity could be partially resolved if different sub-fields in the RF had different temporal kernels (Fig 5). The temporal response patterns would then contain information about the particular shape that the neuron was signaling. This proposal is purely hypothetical, though here we have demonstrated the existence of neurons in V4 with the requisite heterogeneity in space and time. It is important to note that our classification analysis is based on the full temporal pattern of the neuronal response and it therefore assumes a perfect memory or storage of the response patterns. Memory for these patterns may in fact be more leaky than a mean rate code. To the extent that this holds, on the time scale of the classifier (120 ms), our model may overestimate the relative advantage of the temporal code. Further studies, both empirical and theoretical, are necessary to investigate whether these neurons serve to support this type of spatio-temporal code, what role they play in perception and how such a code could be decoded in a recipient area such as the infero-temporal cortex.

A related question is how these differential temporal patterns may emerge. Parafoveal V4, from which our neurons were recorded, receives inputs from both areas V1 and V2 (Ungerleider et al., 2008). Segregated inputs from different functional domains, both within and across these earlier visual areas, into sub-domains of V4 RFs, along with the dynamics of feature selectivity in these earlier visual areas (Hegdé and Van Essen, 2004; Ringach et al., 1997) are candidate mechanisms for the differential temporal dynamics we observe in our data. Our previous results concluded that the homogeneity/heterogeneity in shape selectivity could be accounted for by pooling over more or less homogeneous pools of orientation signals (Nandy et al., 2013). Our new analysis shows that V4 neurons that pool over homogeneous pools of orientation signals show the most homogenous temporal kernels. This suggests that the diversity of pooling in the orientation domain is reflected in the diversity of temporal response patterns across the RF. The patterns of V1 and V2 innervations that contribute to a V4 RF remain exciting avenues for future research.

It has been proposed that curvature selectivity in V4 is refined at longer latencies due to possible recurrent or feedback connections (Yau et al., 2012). The rapid reverse correlation procedure that we used may have mainly captured the feed-forward component of the neural response. These data suggests that the intricate spatio-temporal structure in the feed-forward sweep contain enough rich dynamics to enable rapid object recognition (Potter and Levy, 1969; Thorpe et al., 1996). The shifting temporal patterns that we observe in our data could also serve as the neural underpinnings of the reports of direction selectivity in V4 (Desimone and Schein, 1987; Ferrera et al., 1994; Li et al., 2013; Tolias et al., 2005), and suggests a role of V4 neurons in motion processing as well. Our study suggests that V4 neurons might possess the requisite spatio-temporal dynamics to participate in more complex and perhaps more informative forms of perception such as form from motion e.g. biological motion (Blake and Shiffrar, 2007).

EXPERIMENTAL PROCEDURES

Electrophysiology

Neurons were recorded in area V4 in two rhesus macaques. Surgical and electrophysiological procedures have been described previously (Nandy et al., 2013; Reynolds et al., 1999). In brief, a recording chamber was placed over the prelunate gyrus, on the basis of preoperative MRI imaging. All procedures were approved by the Institutional Animal Care and Use Committee and conformed to NIH guidelines. Neuronal signals were recorded extracellularly, filtered, and stored using the Multichannel Acquisition Processor system (Plexon, Inc). Single units were isolated in the Plexon Offline Sorter based on waveform shape and were included only if they formed an identifiable cluster, separate from noise and other units, when projected into the principal components of waveforms recorded on that electrode.

Task, Stimuli and Inclusion Criteria

Experimental procedures have been described in detail previously (Nandy et al., 2013). In brief, stimuli were presented on a computer monitor placed 57 cm from the eye. Eye position was continuously monitored with an infrared eye tracking system. Trials were aborted if eye position deviated more that 1° from fixation. Experimental control was handled by NIMH Cortex software (http://www.cortex.salk.edu/). At the beginning of each recording session, preliminary neuronal RFs were mapped using subspace reverse correlation in which Gabor (eight orientations, 80% luminance contrast, spatial frequency 1.2 cpd, Gaussian half-width 2°) or ring stimuli (80% luminance contrast) appeared at 60 Hz.

For the main task, the monkey began each trial by fixating a central point for 200 ms and then maintained fixation through the trial. Each trial lasted 3s during which neuronal responses to a fast-reverse correlation sequence (16 ms stimulus duration, exponential distributed delay between stimuli with mean delay of 16 ms, i.e. 0 ms delay p=1/2, 16 ms delay p=1/4, 32 ms delay p = 1/8 and so on) were recorded. The stimuli were comprised of oriented bars (8 orientations) or bar-composites (16 orientations × 5 conjunction angles, total of 72 unique stimuli, Fig 1). The 5 conjunction levels created 5 categories of shapes: zero curvature/straight, low curvature, medium curvature, high curvature and “C”. A pseudo-random sequence from the combined stimulus sets was presented in each trial. The composite stimuli were presented on a uniform 5×5 location grid (‘coarse grid’) centered on the estimated spatial RF based on the preliminary mapping. The grid locations were separated by one-fourth of the RF eccentricity (for e.g., for a RF centered at 6°, the grid-spacing was 1.5° and the grid covered a visual extent of 3°-9°). The oriented bar stimuli were pre sented on a finer 15×15 location grid (‘fine grid’) that spanned the larger 5×5 grid in equal spaced increments. Stimuli were scaled by RF eccentricity, such that each single bar element spanned approximately the diagonal length of the fine grid. The receptive fields of all neurons reported in the study were in the parafoveal region between 2°and 12°in the inferior right visual field.

Only well isolated units were considered as potential candidates for the analysis. Among these, only those neurons that were significantly spatially responsive and shape selective were selected for further analysis (n=86). The details of inclusion criteria have been described previously (Nandy et al., 2013). In brief, we first determined a spatial Z-score for each location on the 5×5 grid based on the average response across all composite stimuli at the spatial location. A grid location was marked as spatially significant if it exceeded the significance level of 0.05 (corrected for 25 multiple comparisons). We next determined if the neuron was significantly shape selective at that spatial location by calculating a shape Z-score for each composite shape. The spatial location was considered as shape selective if the maximum among the shape Z-scores exceeded the 0.05 significance level (corrected for 72×M multiple comparisons, where M=the number of spatially significant grid locations). A neuron was considered significantly shape selective, if it had at least one spatially significant grid location that was also significantly shape selective.

Data analysis

Spatio-temporal receptive fields (STRFs) were computed as follows: a temporal window between 30 and 120 ms after stimulus onset was used to identify a temporal interval of significant visual response, T_sig. The temporal window was divided into non-overlapping 8.33 ms bins for determining the peri-stimulus time histogram (PSTH). T_sig was taken as those PSTH bins where the mean firing rate averaged across all stimulus conditions exceeded the baseline rate by 4 standard deviations. The baseline rate was determined from a temporal window between 0 and 20 ms after stimulus onset. For each significant time bin, we determined the neuronal response, r(x, y, s, t_i; t_i ∈ T_sig) to a particular stimulus, s, at grid location (x, y), as the average firing rate across stimulus repeats. This was done separately for the composite stimuli and the oriented bars, to yield STRFs at both the coarse (Fig 4) and fine (Fig 2, upper panels) spatial scales.

Estimation of temporal trajectories of the fine-scale STRFs

The fine-scale STRF was first averaged across all 8 orientations for each spatial location, $\widehat{r}$ (x, y, t_i; t_i ∈ T_sig). This orientation averaged STRF was spatially interpolated using 2D nearest neighbor interpolation (20 interpolation points, Fig 2, lower panels). We calculated response contours at 90%, 80%, 70%, 60% and 50% of local peak at each significant time-bin (Fig 2, lower panels), and further, the centroid of each contour. The trajectory of the centroids across the spatial extent of the RF (Fig 3A, Supp Fig 1C) was then used to compute the spatial excursion of the temporal response (Fig 3B). The spatial excursion was quantified as follows: for each trajectory, we calculated the maximum Euclidean distance (D_max) between any pair of points on the trajectory. We also estimated the spatial extent of the RF as the length of the major axis (D_RF) of the least-squares best-fit ellipse to the 50% response contour of the temporally averaged RF (i.e. average across all STRF significant time-bins). We used the normalized maximum Euclidean distance as a measure of the spatial excursion of the temporal response:

$$D_{\text{norm}}=\frac{D_{\text{max}}}{D_{\text{RF}}}.$$

To obtain error bounds on this estimate, we performed a jackknife analysis on the data (N_j = 20 jackknifes, each using 95% of trials). For each jackknife, we calculated contour centroids at each response level (90, 80, …, 50%). We thus obtained 20 centroid trajectories for each response level (Fig 3A, Supp Fig 1C; colored lines). We then estimated D_norm, by calculating D_max (using the same time bins that contributed to D_max in the full data set) and D_RF for each jackknife.

To estimate whether these spatial excursions were statistically significant, we calculated a distribution of null trajectories as follows: we reasoned that if spatial selectivity within the RF did not have temporal structure, then the statistics of trajectories obtained by temporal shuffling will not be significantly different from the original (unshuffled) trajectories; if on the other hand, spatial selectivity had specific temporal signatures, then the shuffled trajectories will be markedly different. We first generated temporally shuffled versions of the orientation averaged STRF, $\widehat{r}$_shuffled(x, y, t_i; t_i ∈ T_sig-permute), by random permutations of the response values across time for each spatial location (x, y). To avoid non-stationarity in the mean temporal responses (averaged across spatial positions) due to shuffling, we first normalized the data per time bin prior to shuffling. For each shuffled STRF we obtained the temporal trajectory of the contour centroids (gray trajectories in Fig 3A and Supp Fig 1C) and the normalized maximum distance (D_{norm-shuffled}) as with the original unshuffled data (using the same time bins that contributed to D_max in the unshuffled data). This was repeated 1000 times to obtain a distribution of null temporal excursions.

Temporal stability of shape tuning

To examine the stability of the coarse-scale STRFs over time, we computed the peak shape selectivity (centroid of contour at 90% of peak response) across significant temporal bins at the maximally responsive spatial location on the 5×5 grid (Fig 4A,B). We computed a dispersion metric for shape selectivity as the ratio of the area of the convex hull of the peak response locations across time in shape space (dotted polygons in Fig 4B) over the area of the entire shape space (Fig 4C). Stability of shape tuning would imply a low dispersion metric. To estimate whether the dispersion was statistically significantly different from a null distribution, we performed a bootstrap analysis on temporally shuffled data that was essentially similar to the D_{norm-shuffled} procedure described above, but performed on the coarse-scale data. We thus obtained a null distribution of the dispersion metric against which to compare the metric from the empirical data in order to assess statistical significance.

Pair-wise pattern correlation (ρ) for composite stimuli

As described previously (Nandy et al., 2013), for each neuron we first determined the spatial locations with significant response on the 5×5 coarse grid. For each pair of spatially significant coarse grid locations, we then estimated the empirical distribution of correlation coefficients between the response patterns to the composite stimuli at the two locations using a bootstrap procedure (Efron and Tibshirani, 1993). The response patterns were calculated from the average response to each composite shape across all significant time bins, T_sig. The pair-wise pattern correlation (ρ) was taken as the expected value of a Gaussian fit to this empirical distribution (see Supp Fig 4 in Nandy et al., 2013). Pair-wise pattern correlations for example neurons are shown in Supp Fig 4 (middle column).

Pair-wise temporal kernel distance (D) for composite stimuli

For each significant spatial location (x, y) on the 5×5 grid, we calculated the temporal kernel K_x,y(t) as the average time course to the set of composite stimuli which elicited responses that were above 70% of local peak in the temporally averaged responses $\widehat{r}$(x, y, s) (averaged across all significant time bins). For each temporal kernel, we calculated (a) the time point, t_sig, at which the response first reached significance (4 standard deviations above baseline; baseline calculated from a time window between 0 and 20 ms from stimulus onset), (b) the duration, ΔT_sig, over which the response remained significant, (c) the time point, t_peak, at which the response reached its peak and (d) the duration, ΔT_mid, over which the response was above the half-way mark between peak response and baseline (Fig 5B). Each temporal kernel can be represented as point in a 4D space defined by t_sig, ΔT_sig, t_peak and ΔT_mid. We then performed a principal components analysis (PCA) on this 4D space (Supp Fig 3D,E). The first two principal components accounted for 88% of the variance in the data (Supp Fig 3E). We then projected each point in the 4D space to the lower dimensional 2D plane defined by the two principal components (Supp Fig 3D). The Euclidean distance, D, between pairs of points in this 2D plane serves as a measure of similarity between temporal kernels. Such pair-wise distances for example neurons are shown in Supp Fig 4 (right column).

Shape classification

For each neuron in our population, we calculated the empirical distribution of firing rates in 8.33ms non-overlapping time-bins within a temporal window 0 to 120ms after stimulus onset, using a bootstrap procedure (resampling with replacement, 1000 iterations) (Efron and Tibshirani, 1993). This was done separately for each of the 72 composite stimuli on each of the 25 spatial locations in the 5×5 coarse grid. Firing rates were normalized to a neuron’s peak response. Each of the empirical distributions was very well fit with a Gaussian. In this fashion, we obtained a statistical description of the firing rate for each {neuron [n=86], spatial location [n=25], stimulus [n=72], time-bin [n=16]}-tuple. We chose the resampling approach since stimulus repeats varied across neurons due to varying durations of isolation and also due to the pseudo-random presentation sequences for the fast reverse-correlation procedure (28.3 ± 4.2 presentations across all neurons, locations and stimuli). We next trained classifiers to perform a 72-way classification of stimulus identity in a position-invariant manner as follows. For each sample that was input to the classifier we first chose a random location on the 5×5 grid and a random stimulus identity from the set of 72. For this combination of location and stimulus, we generated a population response vector, which along with the stimulus identity (scalar, [1…72]) served as a training or a test sample for the classifiers. We assessed classification performance for three categories of population codes: (a) snapshot classifier: for this classifier, the population response vector consisted of responses (drawn from the empirical distributions) from a particular time-bin for each neuron (Fig 6A, gray). We had 16 such classifiers for each of the 16 time-bins; (b) temporal pattern classifier: here the population response vector consisted of the train (or pattern) of responses across a subset of time-bins for each neuron (Fig 6A, blue); (c) rate classifier: here the population response vector consisted of the sum of the responses across a subset of time-bins for each neuron (Fig 6A, orange). For each classification run, 3000 such population vector samples along with the corresponding stimulus identities were given to the classifier for training and testing with cross-validation. We assessed classification performance using both an ensemble based random forest classifier (Breiman, 2001) (Fig 6B) and a decision tree classifier (Rokach and Maimon, 2008) (Supp Fig 5A). A random forest is a meta-estimator that fits a number of decision tree classifiers on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting. The sub-sample size is always the same as the original input sample size but the samples are drawn with replacement. Classification performance for the random forest classifiers was reported as 1 – Out-Of-Bag-Error (Breiman, 1996). We used random forest classifiers with 50 decision trees, as this was the number of trees for which the Out-Of-Bag-Error was saturated. Classification performance for the decision tree classifiers was the ten-fold cross-validated performance (90% of samples used for training, 10% for test; 10 such runs leaving out independent sets for test).

We also assessed classification performance using a more traditional support vector machine (SVM) approach with a linear kernel (Supp Fig 5B). Since SVM does not directly support multi-way classification, we used a one-versus-one (OVO), also known as an all-versus-all, approach (Hastie and Tibshirani, 1998) to build a bank of binary classifiers whose predictions are combined using hamming decoding to generate the multi-way classification (Allwein et al., 2000). For each stimulus pair, we trained a binary classifier to perform a positive-class versus negative-class categorization. With 72 unique stimuli, we thus had a total of $\left(\begin{array}{c}\hfill 72\hfill \\ \hfill 2\hfill \end{array}\right)=2556$ binary classifiers whose predictions were combined as described in (Allwein et al., 2000) to achieve the multiclass classification. The number of training samples was reduced from 3000 to 500 in order to prevent boosting due to the large number of binary classifiers in the multi-way SVM. Classification performance was assessed with ten-fold cross validation. Machine learning software for all three types of multi-way classification analyses was implemented in MATLAB (r2014b), using the Statistics Toolbox.