Abstract
The existing, semisupervised, spectral clustering approaches have two major drawbacks, i.e., either they cannot cope with multiple categories of supervision or they sometimes exhibit unstable effectiveness. To address these issues, two normalized affinity and penalty jointly constrained spectral clustering frameworks as well as their corresponding algorithms, referred to as type-I affinity and penalty jointly constrained spectral clustering (TI-APJCSC) and type-II affinity and penalty jointly constrained spectral clustering (TII-APJCSC), respectively, are proposed in this paper. TI refers to type-I and TII to type-II. The significance of this paper is fourfold. First, benefiting from the distinctive affinity and penalty jointly constrained strategies, both TI-APJCSC and TII-APJCSC are substantially more effective than the existing methods. Second, both TI-APJCSC and TII-APJCSC are fully compatible with the three well-known categories of supervision, i.e., class labels, pairwise constraints, and grouping information. Third, owing to the delicate framework normalization, both TI-APJCSC and TII-APJCSC are quite flexible. With a simple tradeoff factor varying in the small fixed interval (0, 1], they can self-adapt to any semisupervised scenario. Finally, both TI-APJCSC and TII-APJCSC demonstrate strong robustness, not only to the number of pairwise constraints but also to the parameter for affinity measurement. As such, the novel TI-APJCSC and TII-APJCSC algorithms are very practical for medium- and small-scale semisupervised data sets. The experimental studies thoroughly evaluated and demonstrated these advantages on both synthetic and real-life semisupervised data sets.
Keywords: All-compatibility, flexible constrained spectral clustering (FCSC), robustness, semisupervised clustering, spectral clustering
I. Introduction
Spectral clustering is one of the significant techniques of clustering learning in pattern recognition. Despite its history not being as long as those of other classic clustering methods, such as the partition-based [1]–[3] and hierarchy-based [4], [5] methods, spectral clustering has caused an increasing amount of interest over the past two decades owing to its distinctive merits of owning (nearly) global optima [6], [7] as well as fitting both convex and nonconvex data sets. The advantages of spectral clustering have been validated by many actual applications, such as information retrieval [8], load balancing [9], and image segmentation [7], [10]. The literature regarding spectral clustering is so abundant that it cannot be thoroughly summarized. The representative review is as follows. Several graph-partition criteria, e.g., minimum cut [11], normalized cut (NC) [7], ratio cut [12], average cut [13], and min–max cut [14], had been put forward over the last 20 years. Most of these criteria, especially NC, have become the important theoretical bases in spectral clustering, and there have been numerous follow-up studies [15]–[17]. The surveys on spectral clustering presented in [18]–[21] provide the overall understanding of the spectral clustering origin, mechanism, and relationship to other theories. Two strategies for speeding up conventional spectral clustering approaches were separately studied in [16] and [22], so that they can deal with large-scale data sets or online data streams. Moreover, the combinations of spectral clustering and the other state-of-the-art techniques, e.g., semisupervised learning [23], multitask [24], multiview [25], coclustering [26], and transfer learning [27], still belong to very hot research topics, and several correlative approaches have been developed [23], [28]–[40].
As is well known, similar to other conventional clustering methods, the effectiveness of spectral clustering is sensitive to the purity of the data set, which signifies that spectral clustering could be inefficient and even invalid if the data were distorted by noise or interference information. We believe that transfer learning and semisupervised learning are two of the most feasible pathways to address this issue as both attempt to enhance the learning performance on the target data set by means of adopting partially given information as the reference. The distinction between them lies in the source of the prior information. That is, transfer learning extracts the desired information from other correlated scenarios (source domains) and applies this information to the current scenario (target domain) [27], whereas semisupervised learning works solely on one scenario (data set), which indicates that the known information not only comes from this data set but is also utilized on itself [10], [31]. In this paper, we focus on the latter, i.e., on studying constrained (semisupervised) spectral clustering and separately proposing our own frameworks and approaches.
To date, there has been quite a bit of effective work associated with constrained spectral clustering. We now review the related work from two perspectives 1) the possible types of supervision (partially known information) in semisupervised learning and 2) the ways of using the supervision. The data instance label is the most ordinary but straightforward category of prior knowledge [19], [23], [28], [35], whereas the pairwise constraint [29]–[31], [33], [34], also referred to as the must-link or cannot-link constraint, belongs to another kind of user supervision with comparatively more flexibility and practicability, as it is independent on some insightful knowledge, such as the cluster number and the involved clusters in the prior information, which, however, are sensitive in the case of data labels. The grouping information [10] is the third possible type of supervision, which often appears in the application of image segmentation where several regions are definitely marked in an image and all of the pixels within each region should be assigned into the same cluster. The schemas regarding how to use the supervision also pose two strategies. One is to directly manipulate the affinity matrix (or equally, the Laplacian matrix) according to some conditions generated from the specified supervision, either data labels or pairwise constraints. For example, the affinity matrix-oriented constraints and the affinity propagation based on instance-level constraints were studied in [19] and [40], respectively. The other strategy is to construct a combined framework in terms of the objective function or the subjection condition so as to satisfy both the supervision and original optimization conditions as much as possible. For instance, the constraint conditions added to subjection conditions were investigated in [30] and [31]. One constrained, multiway, spectral clustering approach with the determination of the cluster number was presented in [29]. A partial grouping information-based approach for image segmentation was proposed in [10].
Nevertheless, in the progress of constrained spectral clustering, there is no relatively completely effective method, which can address all types of supervision with the perfect combination of simultaneous affinity constraints and framework optimization so far. Motivated by this challenge, we devise two novel types of constrained spectral clustering frameworks with full compatibility, high flexibility, and strong robustness in this paper. We separately designate them as type-I affinity and penalty jointly constrained formulation (TI-APJCF) and type-II affinity and penalty jointly constrained formulation (TII-APJCF) and name their corresponding algorithms as type-I affinity and penalty jointly constrained spectral clustering (TI-APJCSC) and type-II affinity and penalty jointly constrained spectral clustering (TII-APJCSC), respectively. In general, the primary contributions of this paper can be summarized as follows.
-
1)
Both TI-APJCSC and TII-APJCSC pose the affinity and penalty jointly constrained strategies for semisupervised spectral clustering. In particular, the constraints lie not only in the explicit pairwise constraints added to the affinity matrix and the objective expression separately, but also in the implicit efficacy that both TI-APJCF and TII-APJCF indirectly adjust the affinity measurement to a certain extent, which consequently enhances the eventual effectiveness and robustness of both TI-APJCSC and TII-APJCSC.
-
2)
Both TI-APJCSC and TII-APJCSC are compatible with the three existing categories of supervision, i.e., class labels, pairwise constraints, and grouping information, which makes them more practical than those only partial category-oriented methods.
-
3)
Both TI-APJCSC and TII-APJCSC feature high flexibility, which is achieved from two aspects. First, it helps us avoid specifying the threshold for the constraint term [30], [31] to introduce the constraint term (penalty term) into the objective function rather than into the subjection condition. Second, after normalizing the ranges of both the original spectral clustering term and the semisupervised penalty term, a simple tradeoff factor taking values within the interval (0, 1] is able to balance their individual roles to the overall framework in any data scenario.
-
4)
Benefiting from the affinity and penalty jointly constrained strategies, both TI-APJCSC and TII-APJCSC are robust with respect to the parameter in the affinity measurement as well as the number of pairwise constraints. The only slight performance difference between them lies in their separate insensitivity to the tradeoff factor. That is, TII-APJCSC seems generally steadier against the tradeoff factor than TI-APJCSC.
The remainder of this paper is organized as follows. In Section II, the work related to our research is briefly reviewed. In Section III, two types of affinity and penalty jointly constrained formulation: TI-APJCF and TII-APJCF, several associated definitions and theorems, the corresponding algorithms TI-APJCSC and TII-APJCSC, and the parameter setting are sequentially introduced. In Section IV, the experimental validation of the correlated algorithms is presented and discussed. In Section V, the conclusions are presented.
II. Background and Preliminaries
A. Graph and Common Notations
Given a data set X = {xi|xi ∈ Rd, i = 1,2, . . . , N}, where d is the data dimensionality and N is the data size. Let G = (V, E, W) denote an undirected, weighted graph on X, where each data instance in X corresponds to a vertex (node) in V; all the edges between any two vertices in V compose the edge set E, and each edge in E is weighted by a similarity that is an entry of the affinity (similarity) matrix W. Suppose there exist K (2 ≤ K < N) potential groups (clusters) in X. Now, in terms of the graph G, the purpose of clustering can be reformulated as a partition of the graph, in which the edges among different groups have very low weights while the edges within a group have high ones. To determine this ideal partition, several partition criteria were developed, such as minimum cut [11], NC [7], and ratio cut [12]. Among them, as mentioned in Section I, NC is currently studied more extensively.
Some important notations need to be explicitly introduced before continuing our work, and these notations will be recruited throughout this paper.
Suppose the N × N affinity (similarity) matrix W of the graph G = (V, E, W) is calculated according to a certain affinity function, e.g., the well-known radial basis function
| (1) |
Let D = diag(d11, . . . , dN N) denote the degree matrix with and L = D – W denote the Laplacian matrix. Moreover, make and measure the total weights of graph G. Putting them together, the common notations regarding our work are listed in Table I.
TABLE I.
Common Notations Regarding Graph
| Symbol | Meaning |
|---|---|
| G | The graph G = (V, E, W) on the given data set X |
| W | The affinity (similarity) matrix |
| D | The degree matrix |
| L | The Laplacian matrix |
| vol(G) | The total weights of the graph G |
B. Normalized Cut and Normalized Spectral Clustering
The primitive theories of NC and the spectral clustering algorithm were presented in [7]. For related research, see [10], [15], [16], and [18]–[23]. We now briefly review NC and the normalized spectral clustering algorithm as follows.
The objective function of NC can be represented as [18]
| (2) |
where y is the relaxed clustering indicator vector and 1 is a constant vector whose entries are all 1.
Suppose y = D−1/2v and L̃ = D−1/2LD−1/2, then (2) becomes
| (3) |
where L̃ is called the normalized Laplacian matrix and v is the new clustering indicator vector.
It is easy to prove that (3) is equivalent to the standard eigensystem using the Lagrange optimization
| (4) |
where λ is the eigenvalue and v is the matching eigenvector. As revealed in [7], the eigenvector corresponding to the second smallest eigenvalue of (4) can be adopted as the optimal solution of (3) for the two-class partition issue. As for the multiclass problem, namely, there being multiple clusters (K > 2) in the target data set, the well-known normalized spectral clustering algorithm (Algorithm 1) is available [7], [10], [18].
Algorithm 1.
Normalized Spectral Clustering
| Step 1: | Construct the graph G on the given data set X and calculate the similarity matrix W; |
| Step 2: | Generate the normalized Laplacian matrix L̃ = D–1/2LD–1/2; |
| Step 3: | Obtain the K relaxed continuous solutions (the first K eigenvectors) of Eq. (4) based on the eigenvalue decomposition on L̃; |
| Step 4: | Generate the final discrete solution via K-means [18] or spectral rotation [6], [10] based on these continuous solutions. |
C. Supervision Types
In general, there are three categories of prior information for semisupervised learning: 1) class labels; 2) pairwise constraints; and 3) grouping information.
Class labels are widely enlisted as the reference in various supervised or semisupervised learning approaches [28]. In the sense of the class number existing in the given information, here there may be two cases: 1) only partial class labels are involved and 2) all class labels are covered, i.e., the case of full class labels.
Pairwise constraints, also referred to as must-link or cannot-link constraints, belong to the second type of supervision [31]. Depending on the specific information offered by users, pairwise constraints can be in the forms of a must-link set (MLS) in which the pairs of samples must be assigned to the same cluster, a cannot-link set (CLS) in which the pairs of data instances cannot be assigned to the same cluster, or both.
As for grouping information, it usually appears in the application of image segmentation [10] where several regions are explicitly drawn as the groups in an image and all of the pixels within each region should be assigned to the same cluster.
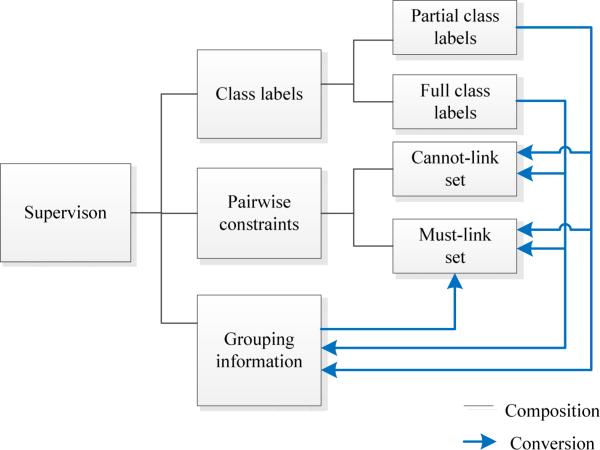
These three types of supervision are actually not isolated from each other, and there are some conversions among them. The supervision types as well as their feasible conversions are shown in Fig. 1. More specifically, the practicable conversions among them can be stated as follows.
Fig. 1.
Composition of three types of supervision and feasible conversions among them.
1) Class Labels → Must-Link & Cannot-Link Sets
Both cases of partial class labels and full class labels can be easily converted into the must-link or cannot-link constraints, depending on the specific cases of sample labels existing in the supervision data. According to the different sample labels, the given supervision data can be divided into several groups. Only one group exists, as a special case, if and only if all the given sample labels are consistent. Suppose the data capacity of each group is greater than 1, then any two samples within one group can certainly be used to constitute the MLS, and any sample pair whose members are from two separate groups should be an entry in the CLS. In the special case of only one group, the MLS is available but not the CLS.
2) Class Labels → Grouping Information
Likewise, both cases of partial class labels and full class labels can be conveniently converted into the grouping information, and the number of groups equals the number of different sample labels existing in the supervision data. Each group is composed of all data instances owning the same label.
3) Grouping Information → Must-Link Set
It is definite that any two members of each group in the grouping information should belong to the MLS. However, the cannot-link constraints are not obtainable due to the uncertain relations between any two groups in this case.
The purpose of semisupervised learning is to strengthen as much as possible the practical performance of intelligent algorithms in terms of any category of supervision.
III. Affinity and Penalty Jointly Constrained Spectral Clustering
As shown in Fig. 1, in light of the fact that all three supervision categories can eventually be represented as the MLS or the CLS or both, we only need to focus on pairwise constraints in this paper. How to sufficiently make use of the prior knowledge in the form of pairwise constraints for semisupervised spectral clustering is the first challenge which we have to face. To resolve this issue, we propose two affinity and penalty jointly constrained strategies as follows.
A. Affinity and Penalty Jointly Constrained Strategies
It should be pointed out that our affinity and penalty jointly constrained strategies exist not only in the constraints added to both the affinity matrix and the framework, but also in the essential connections between them. Next, we introduce our work in detail.
1) Pairwise Constraints on the Affinity Matrix
Without loss of generality, we assume that both MLS and CLS are available throughout this paper. It is worth noting that some rules for propagating must-link and cannot-link constraints can be applied before our work in order to further enlarge the pairwise sizes in MLS and CLS [34], [40].
Based on the final MLS and CLS, we manipulate the affinity matrix W according to the following rules:
| (5) |
where 〈i, j〉 signifies any pairwise of constraint in MLS or CLS and i and j are the separate indices of the matching data instances in the entire data set X.
The strategy of directly updating the affinity matrix according to the pairwise constraints is definitely the least sophisticated modality in semisupervised spectral clustering. Actually, it is a double-edged sword. On the one hand, it can offer the most straightforward constraints, as the affinity measurement is the foundation of all spectral clustering methods. On the other hand, it simultaneously disrupts the overall consistency regarding similarity measurement, so that some unexpected cases usually occur in those approaches relying solely on affinity constraints [19]. This phenomenon will be disclosed in the Section IV-B. For this reason, most state-of-the-art techniques in semisupervised spectral clustering do not currently value the pure affinity constraint mechanism. Therefore, this type of constraints added to the affinity matrix W is only the basis of our research, and other more reliable constraint strategies are required as the significant supplements. To this end, we present the following two core formulations for constrained spectral clustering based on NC.
2) Type-I Affinity and Penalty Jointly Constrained Formulation
As we know well, each entry vi (i = 1, . . . , N) in the clustering indicator vector v in (3) is relaxed to take the continuous value. In particular, vi > 0 indicates xi belongs to cluster + and vi < 0 to cluster – in the case of bipartition. As in the case of bipartition. for the multiclass partition problem, the K-way partition strategy [7], [10], [18] is always enlisted as the standard means in spectral clustering, in which each way is also treated as a bipartition issue. In this regard, we present the first formulation for constrained spectral clustering as follows.
Definition 1
Let nM and nC denote the numbers of pairwise constraints in MLS and CLS, respectively. Suppose y = (y1, . . . , yN)T is the clustering indicator vector in normalized spectral clustering, then the TI-APJCF can be defined as
| (6) |
where 〈i, j〉 signifies any pairwise constraint in MLS, and i and j are the indices of the corresponding data instances in the entire data set X; 〈k, l〉 signifies the one in CLS, and k and l are also the indices of the matching samples.
Equation (6) is constructed based on the premise that, for any must-link constraint 〈i, j〉 ∈ MLS, the signs of the entries yi and yj in the clustering indicator vector y should keep the same and the values of yi and yj should be as close as possible. Therefore, the first term in should consequently be as small as possible. In contrast, for any cannot-link constraint 〈k, l〉 ∈ CLS, the signs of yk and yl should be opposite, i.e., one is negative and the other is positive, which causes the term in to favor a smaller value. Combining them, the optimal solution that best meets the constraints in both MLS and CLS should minimize . Considering the potential pairwise size diversity between MLS and CLS, we prefer the form of averages in .
Definition 2
For any must-link constraint indicator 〈i, j〉 ∈ MLS, the must-link indicator matrix ML〈i,j〉 is defined as
 |
(7) |
that is, aside from the two entries, (i, j) and (j, i), which are set to 1, the others in ML〈i,j〉 are all 0.
Definition 3
For any cannot-link constraint 〈k, l〉 ∈ CLS, the type-I cannot-link indicator matrix is defined as
 |
(8) |
that is, the two entries (k, l) and (l, k) are set to −1, whereas the others in are all 0.
We now yield the matrix form of in (6) in terms of Definitions 2 and 3.
Theorem 1
With the notations being the same as those declared in Definitions 1–3, let , , and S1 = ML + CLT1, then TI-APJCF in the form of (6) can be represented by the following formula:
| (9-1) |
where
| (9-2) |
diag(·) denotes the generating function of diagonal matrix in terms of the vector argument, and 1N×1 is a constant vector with all N entries being 1.
Proof
It is easy to prove that the objective expression of NC [see min (2)]. min yTLy, can be rewritten as min , in which wij is the affinity between any two samples xi and xj in X [18]. Therefore, making the transformation from W to L as the reference, we can prove this theorem.
As ML and CLT1 are both symmetric, S1 is consequently symmetric. Moreover, it is explicit that here the roles of H1 and S1 to (6) are similar to those of D and W in , respectively. Thus, we arrive at .
As in evident, belongs to a kind of penalty-based framework constraint for semisupervised spectral clustering; however, it is also of another efficacy in this paper, i.e., it delicately establishes a full connection to the affinity measurement W, which will be explained in detail hereinafter. Therefore, we call it one of the affinity and penalty jointly constrained formulations.
3) Type-II Affinity and Penalty Jointly Constrained For mulation
The distinctive merit of is that it can build the complete connection between the affinity- and penalty-based constraint manners in this paper. Nevertheless, the second term and is not the only modality preferred in this paper for measuring the consistency between the clustering indicator y and CLS, as it is merely a necessary condition for successful clustering partitions. This indicates that, in some extreme cases, a clustering indicator y, whose many pairs of entries belonging to CLS are assigned to the same signs, can also cause the term to take smaller values as long as the gap of any pair of |yk| and |yl| is large enough. However, such cases a little violate the original intention of NC, i.e., the signs of samples from different clusters should keep opposite. In this regard, we put forward the other more concise model for measuring CLS in Definition 4.
Definition 4
If the notations are the same as those in Definition 1, the TII-APJCF can be defined as
| (10) |
The first term in is the same as that in ; however, the second one is different. For any cannot-link constraint 〈k, l〉 in CLS, the ideal signs of vk and vl can only be inconsistent, such that the second term in remains as small as possible. Therefore, the new measurement can eliminate the flaw of in in theory.
Definition 5
For any cannot-link constraint cannot-link 〈k, l〉 ∈ CLS, the type-II indicator matrix is defined similar to (8) except that the entries (k, l) and (l, k) are 1.
Theorem 2
With the notations being the same as those defined in Theorem 1 and Definitions 4 and 5, let , then TII-APJCF in the form of (10) can also be represented by the following formula:
| (11-1) |
where
| (11-2) |
Proof
First, in terms of and CLT2, it is clear that can directly be represented as yT CLT2y. Then, for , likewise, taking the transformation from W to L in NC as the reference, we generate the new matrices H2 = diag(ML · 1N×1) and Q2 = H2 – ML whose roles are separately similar to those of D and L in . Combining them, this theorem is proved.
B. Flexible, Normalized Frameworks for Affinity and Penalty Jointly Constrained Spectral Clustering
Based separately on (9) and (11), we can immediately propound our own two different frameworks for constrained spectral clustering
| (12) |
where γ > 0 is the regularization coefficient.
In (12), we place yT Piy in the objective function as a penalty term with the regularization coefficient γ rather than adding it as another subjection condition, which helps us avoid specifying a definite value for yT Piy as in [30] and [31]; meanwhile, the parameter γ is able to balance the impact of yT Piy to the whole expression.
In Theorem 1, in the sight of ML and CLT1, we can easily find that each pair of must-link constraints in MLS equals setting the entries S1_ij and S1_ji in S1 to 1/nM and each one in CLS equals setting the entries S1_kl and S1_lk in S1 to −1/nC. Now, let us come back to (12), where yT Ly + γ yT P1y = yT (L + γ P1)y. Let T = L + γ P1, then T equals being generated from the generalized affinity matrix W′ = W + γ S1, which means that we set for each constraint in MLS as well as for each constraint in CLS.
As for P2 corresponding to in Theorem 2, as only the first term in (10) is the same as that in (6), P2 is only partially associated with L (or equally, W), whereas its second term can offer us a more reliable measurement for the consistency between the clustering indicator y and CLS, which facilitates the total effectiveness of from another different perspective.
Based on the above analyses, our proposed frameworks in the form of (12) for constrained spectral clustering, in terms of either TI-APJCF or TII-APJCF, exhibit not only the explicit penalty term-based framework constraints but also two different degrees of implicit influence to the affinity measurement. We collectively call them affinity and penalty jointly constrained frameworks.
Theorem 3
The affinity and penalty jointly constrained spectral clustering frameworks in the form of (12) are equivalent to the following flexible optimization problems with the delicate normalized frameworks:
| (13-1) |
where
| (13-2) |
| (13-3) |
| (13-4) |
v is the new clustering indicator vector, η ∈ (0, 1] is a tradeoff factor, I is the N × N identify matrix, λmin_P̃i and λmax_P̃i denote the minimal and maximal eigenvalues of P̃i separately, λmin_L̃ and λmax_L̃ denote the minimal and maximal ones of L̃, and v0 represents the trivial eigenvector corresponding to the smallest eigenvalue 0 with respect to Si.
Proof
Let y = D−1/2v, L̃ = D−1/2LD−1/2, and P̃i = D−1/2PiD−1/2, then (12) can be represented as
| (14) |
Given a real, symmetric matrix A, we can obtain the following inequality according to Rayleigh quotient [7], [41] and the min–max theorem [42]:
| (15) |
where λmin_A and λmax_A denote the minimal and maximal eigenvalues of A, respectively.
Due to vTv = vol(G) in (14), (15) equals
| (16) |
As P̃i and L̃ are both symmetric, based on (16), we attain
| (17) |
| (18) |
Moreover, via (16), it is evident that
| (19) |
As we previously discussed, the role of the regularization coefficient γ in this paper is to balance the impact of the penalty term vTP̂iv to the whole expression. Whereas the current ranges of both vTL̂v and vTP̂iv are normalized into the same interval from 0 to 1, we can substitute a tradeoff factor η ∈ (0, 1] for the regularization coefficient γ as
| (20) |
As for the reason of v ≠ v0 see Theorem 4.
It should be noted that converting (12) into (13) is not trivial from the viewpoint of practicability, as the estimation of the proper range of the regularization coefficient γ in (12) is more intractable than that of the tradeoff factor η in (13). More specifically, based on our extensively empirical studies, the solution of (12) is more sensitive to γ than that of (13) to η, as the orders of magnitude of yT Ly and yT Piy in (12) differ and their gap dependent on the pairwise sizes of both MLS and CLS could be huge sometimes. This is the reason why we normalize the ranges of both vTL̂v and vTP̂iv in (13) into the same interval from 0 to 1. In this way, with the tradeoff factor η varying in the fixed interval (0, 1], our schemes can cope with any data scenario. Consequently, we think such delicate normalized frameworks in the form of (13) are more flexible and practical than the original one in (12).
Theorem 4
The novel normalized frameworks of constrained spectral clustering in the form of (13) further equals the standard eigensystems of
| (21) |
where λ and v signify the eigenvalue as well as the matching eigenvector, respectively. Moreover, for two-class, constrained spectral clustering, the second smallest eigenvector of the eigensystem is the eventual solution to (13), and for the multiclass case, the K -way partition strategy is needed.
Proof
The solution of (13) can be derived by the Lagrange optimization. Let
| (22) |
where λ is the Lagrange multiplier. As both L̂ and P̂i are symmetric, we obtain
| (23) |
We immediately arrive at (21) by rearranging (23). Moreover, as vT v = vol(G) > 0, we can deduce
| (24) |
| (25) |
Combining (24) and (25), we arrive at
| (26) |
As Si = ηL̂+(1 – η)P̂i is symmetric, according to Rayleigh quotient and the min–max theorem, (26) indicates that all of the eigenvalues of Si are larger than or equal to 0, i.e., Si is a positive, semidefinite matrix. Comparing (21) with (4), we immediately know that (21) can also be regarded as a standard eigensystem with λ and v being the eigenvalue and the corresponding eigenvector separately. Thus, similar to (4), the second smallest eigenvector is the solution to (13) for the two-cluster case, and the K-way trick can be recruited for the multicluster situation. Furthermore, as the minimal eigenvalue of Si is 0, the corresponding eigenvector v0 is a trivial solution, which should be eliminated, because all the entries are almost the same.
C. Algorithms
Based on TI-APJCF/TII-APJCF and Theorems 1–4, we now depict our core algorithms, i.e., TI-APJCSC or TII-APJCSC, in Algorithm 2.
Algorithm 2.
Type-I/Type-II Affinity and Penalty Jointly Constrained Spectral Clustering
| Step 1: | Convert the known supervision into MLS and CLS; |
| Step 2: | Calculate the affinity matrix W of the given data set X, manipulate W according to (5), generate the Laplacian matrix L, the degree Matrix D, and calculate vol(G); |
| Step 3: | Construct the constraint matrix Pi (i = 1 or 2) based on Theorem 1 or Theorem 2, respectively; |
| Step 4: | Generate L̂ and P̂i (i = 1 or 2) according to Theorem 3, and attain Si = ηL̂ + (1 - η)P̂i, i = 1 or 2; |
| Step 5: | Obtain the first K smallest eigenvectors of Si (i = 1 or 2) using eigenvalue decomposition and construct the continuous solution matrix UN×K; |
| Step 6: | Based on UN×K, yield the normalized U′N×K with the norm of each row being 1, and generate the final discrete solution of (13) via K-means [18] or spectral rotation [6], [10] on U′N×K. |
D. Parameter Setting
Our proposed algorithms, either TI-APJCSC or TII-APJCSC, only involve two core parameters: 1) the affinity parameter σ in (1) and 2) the tradeoff factor η in (13). Similar to other conventional clustering issues, it belongs to the open problems today to adjust these involved parameters self-adaptively and optimally. Currently, the grid-search strategy is widely used for approximating the parameter setting in pattern recognition. It is also well known that this strategy is dependent on validity indices, and current validity indices can be roughly divided into two categories, i.e., external criteria (label-based) and internal criteria (label-free). The external criterion, e.g., normalized mutual information (NMI) [43], Rand index (RI) [43], and cluster purity [28], evaluates the degree of agreement between the achieved and known data structures and is usually adopted on synthetic or benchmark data sets where the data labels are given, even in testing sets. In contrast, the internal criterion, such as Davies–Bouldin index (DBI) [44] and Dunn index [44], evaluates the result of an algorithm using only quantities and features inherent to the data set and, thus, better suits real data situations where the testing data are certainly unlabeled.
In addition, this paper belongs to the semisupervised learning problem in which the supervision can also be employed as the reference for parameter approximation. In this regard, besides the above, existing external criteria or internal criteria, we design the dedicated metric CONS for our constrained spectral clustering problems, as shown in (27), which measures the consistency between the achieved clustering outcomes and the pairwise constraints in MLS and CLS
| (27-1) |
where
| (27-2) |
lbi denotes the achieved label corresponding to the data instance xi, and nM and nC represent the pairwise number of MLS and CLS separately.
IV. Experimental Results
A. Setup
In this section, we focus on evaluating the realistic performance of the developed TI-APJCSC and TII-APJCSC algorithms. For this purpose, in addition to TI-APJCSC and TII-APJCSC, six other state-of-the-art algorithms were enlisted for comparisons, i.e., multiclass spectral clustering (MSC) [6], spectral learning with affinity modification (SLAM) [19], flexible constrained spectral clustering (FCSC) [31], clustering through ranking on manifolds (CRMs) [35], actively self-training clustering (ASTC) [28], and partial grouping constrained spectral clustering (PGCSC) [10]. Except for MSC, the other seven algorithms belong to semisupervised spectral clustering. The supervision categories and the constraint mechanisms regarding correlative algorithms are listed in Table II. As shown in Table II, SLAM relies solely on affinity constraints; both FCSC and PGCSC work based on the supplemental subjection conditions of supervision; CRM and ASTC are dependent on the penalty optimizations added to their objective functions; our proposed TI-APJCSC and TII-APJCSC work with the delicate affinity and penalty jointly constrained strategies. As for the compatible categories of supervision, SLAM, FCSC, TI-APJCSC, and TII-APJCSC can cope with all of the existing three types of supervision, and the others only partially support them.
TABLE II.
Categories of Supervision and Constraints of Involved, Semisupervised Algorithms
| Categories | Algorithms | ||||||
|---|---|---|---|---|---|---|---|
| SLAM | FCSC | CRM | ASTC | PGCSC | TI-APJCSC | TII-APJCSC | |
| Supervision | CL, PC, GI | CL, PC, GI | CL | CL | CL,GI | CL, PC, GI | CL, PC, GI |
| Constraints | A | S | P | P | S | A + P | A + P |
Note: A - Affinity constraints; S - Subjection condition; P - Penalty optimization; CL - Class labels; PC - Pairwise constraints; GI - Grouping information.
Our experiments were implemented on both synthetic and real-life data sets. Four validity indices, i.e., NMI, RI, DBI, and the dedicated CONS metric defined in (27), as well as the running time were employed to verify the clustering performance of these adopted algorithms. Before introducing our detailed experimental content, the definitions of NMI, RI, and DBI are first, briefly reviewed as follows.
1) Normalized Mutual Information
| (28) |
where Ni,j denotes the number of agreements between cluster i and class j, Ni is the number of data points in cluster i, Nj is the number of data points in class j, and N is the size of the whole data set.
2) Rand Index
| (29) |
where f00 denotes the number of any two sample points belonging to two different clusters, f11 denotes the number of any two sample points belonging to the same cluster, and N is the total number of sample points.
3) Davies–Bouldin Index
| (30-1) |
where
| (30-2) |
C denotes the cluster number in the data set, denotes the data instance belonging to cluster Ck, and nk and vk separately denote the data size and the centroid of cluster Ck.
Both NMI and RI take values from 0 to 1, and larger values of them indicate better clustering performance. In contrast, smaller values of DBI are preferred as they indicate that the levels of both intercluster separation and intracluster compactness are concurrently high. Nevertheless, similar to other internal criteria, DBI has the potential drawback that the minimum does not necessarily imply the best information retrieval.
The grid-search strategy was adopted in our experiments for parameter optimization. The affinity parameter σ in (1) is the common one in all involved algorithms, and its specific setting in each algorithm on the related data sets will be stated separately in Tables VI and X. The values or the trial intervals of the other primary parameters in the associated algorithms are listed in Table III. For the parameters in the competitive algorithms, such as CRM, ASTC, and FCSC, we respected the authors’ recommendations in their literature as well as adjusting them according to our practice. For example, FCSC is especially sensitive to the threshold β for the constraint condition. The number of positive eigenvalues in FCSC increases as β decreases, whereas the semisupervised information could not be sufficiently utilized if β is too small. In this regard, we set β = (λmax_K–1 + λmax _K)vol(G)/2 throughout this paper, where λmax _K–1 and λmax _K denote the (K–1)th and Kth largest eigenvalues of the constraint matrix Q̄, so as to obtain enough, feasible real-value eigenvectors as well as utilize the supervision as much as possible.
TABLE VI.
Recommended Optimal Settings of TI-/TII-APJCSC on Synthetic Databases
| Algorithms | Datasets | |||||
|---|---|---|---|---|---|---|
| X 1 | X 2 | X 3 | ||||
| 5% | 10% | 5% | 10% | 5% | 10% | |
| TI-APJCSC | σ ∈ | σ ∈ | σ ∈ | σ ∈ | σ ∈ | σ ∈ |
| [0.033,0.045] | [0.059,0.065] | [0.011,0.021] | [0.013,0.017] | [0.023,0.037] | [0.025,0.035] | |
| σ ∈ [0.7,0.9] | η = 0.8 | η = 0.9 | σ ∈ [0.1,0.4] | η = 0.9 | η = 0.9 | |
| TII-APJCSC | σ ∈ | σ ∈ | σ ∈ | σ ∈ | σ ∈ | σ ∈ |
| [0.021,0.045] | [0.015,0.063], | [0.015,0.023] | [0.013,0.017] | [0.025,0.037] | [0.017,0.033] | |
| σ ∈ [0.5,0.9] | σ ∈ [0.5,0.7] | σ ∈ [0.6,0.8] | σ ∈ [0.3,0.8] | σ ∈ [0.8,0.9] | σ ∈ [0.8,0.9] | |
Note: Each interval or specific value of optimal settings is achieved by 10 times of implementations of TI-/TII-APJCSC on the same dataset but with different supervision. If the ten results are inconsistent, the interval form is attained; otherwise, the specific value is given.
TABLE X.
Parameter Trial Ranges of All Algorithms and Recommended Optimal Settings of TI-/TII-APJCSC on Real-Life Data Sets
| Datasets | Trial ranges (σ) | Recommended optimal settings | |
|---|---|---|---|
| TI-APJCSC | TII-APJCSC | ||
| Banana | [0.015:0.002:0.085] | σ = 0.043, η = 0.5 | σ = 0.037, η = 0.3 |
| Wisconsin | [0.05:0.02:0.85] | σ = 0.11, η = 0.3 | σ = 0.11, η = 0.1 |
| Led7digit | [0.277:0.02:1.077] | σ ∈ = [0.517,0.737], η ∈ [0.7,0.9] | σ ∈ [0.697,0.957], η ∈ [0.3,0.4] |
| Wine | [0.05:0.02:1.55] | σ ∈ [0.25,0.29], η ∈ [0.8,0.9] | σ ∈ [0.27,0.31], η ∈ [0.5,0.8] |
| Waveform-21 | [0.3:0.02:1.3] | σ ∈ [0.34,0.74], η ∈ [0.2,0.9] | σ ∈ [0.92,1.1], η ∈ [0.8,0.9] |
| USPS-3568 | [0.3:0.02:2.2] | σ ∈ [1.12,1.3], η ∈ [0.6,0.7] | σ ∈ [0.5,0.72], η = 0.9 |
| JAFFE | [0.5:0.035:5.1] | σ ∈ [2.67,3.3], η ∈ [0.2,0.7] | σ ∈ [2.32,3.23], η ∈ [0.2,0.9] |
| 20news | [0.3:0.05:2.3] | σ ∈ [0.45,0.55], η ∈ [0.1,0.3] | σ ∈ [0.35,0.45], η ∈ [0.1,0.3] |
| Berke-296059 | [0.01:0.0012:0.08] | σ = 0.0220, η = 0.8 | σ = 0.0484, η = 0.3 |
Note: Each interval or specific value of optimal settings is achieved by 10 times of implementations of TI-/TII-APJCSC on the same dataset but with different supervision (Except for the three KEEL datasets, where the supervision is invariant). If the ten results are inconsistent, the referenced interval is listed; otherwise, the specific value is given.
TABLE III.
Values or Intervals of Primary Parameters in Employed Algorithms
| Algorithms | Parameter settings |
|---|---|
| MSC | K equals the number of clusters. |
| SLAM | K equals the number of clusters. |
| FCSC | K equals the number of clusters; Threshold β=(λmax_K–i + λmax_K)vol(G)/2 where λmax_K–1 and λmax_K denote the (K-1)th and Kth largest eigenvalues of the normalized constraint matrix Q̄. |
| CRM | K equals the number of clusters; Parameter α ∈ {0.5,0.7,0.9,0.99,0.999,0.9999}. |
| ASTC | K equals the number of clusters; Parameter αu ∈ {0.5,0.7,0.9,0.99,0.999,0.9999}. |
| PGCSC | K equals the number of clusters. |
| TI-APJCSC | K equals the number of clusters; Trade-off factor η ∈ [0.1:0.1:1]. |
| TII-APJCSC | K equals the number of clusters; Trade-off factor η ∈ [0.1:0.1:1]. |
All experiments were carried out on a computer with Intel Core i3-3240 3.4-GHz CPU and 4-GB RAM, Microsoft Windows 7, and MATLAB 2010a.
B. On Synthetic Data Sets
1) Experimental Setup
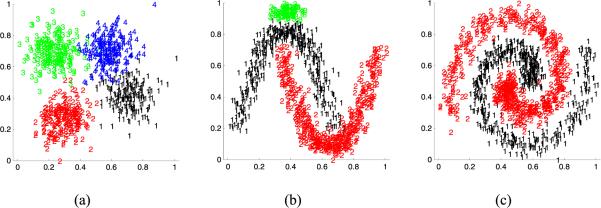
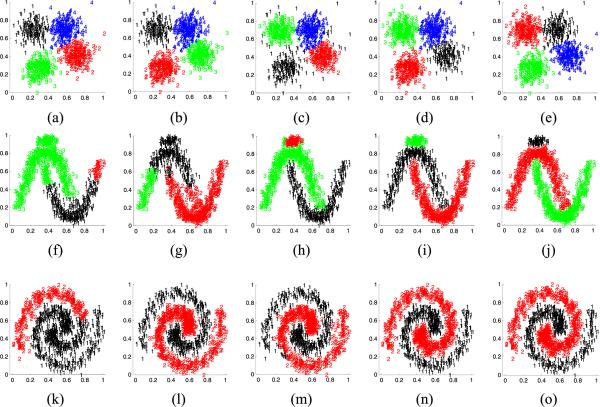
We generated three, artificial, 2-D data sets, X1, X2, and X3, as the synthetic data sets, as shown in Fig. 2. The cluster numbers of X1, X2, and X3 are 4, 3, and 2, respectively, and their data sizes are separately 800, 1010, and 1200. In addition, X1, X2, and X3 were all normalized before our experiments. As is evident, because there are a few overlaps in almost all of the clusters and their neighbors in these data sets, the clustering work on these data sets is a challenge for most of the conventional clustering approaches, and they are good validation data sets for evaluating the actual performance of the recruited algorithms in our experiments.
Fig. 2.
Synthetic data sets. (a) X1 data set. (b) X2 data set. (c) X3 data set.
Among these employed approaches, aside from MSC, the others work relying on the supervision. For fair comparisons, we consistently used the sample labels, which were randomly and separately chosen at different ratios from X1, X2, and X3 as the supervision for all of the semisupervised clustering approaches. In particular, we first generated each of the ten subsets from each data set at 1%, 3%, 5%, 7%, 10%, 13%, 16%, and 20% sampling ratios of the whole data size, respectively. We then ran SLAM, FCSC, CRM, ASTC, PGCSC, TI-APJCSC, and TII-APJCSC on X1, X2, and X3 with the labels in each of their sampled subsets acting as the prior information separately and evaluated their clustering performance in terms of the NMI, RI, DBI, and CONS indices as well as the running time (in seconds). As for MSC, whereas it is the original, normalized spectral clustering method and does not need any supervision, it was directly and separately performed on X1, X2, and X3.
2) Results of the Experiments
In this section, we would like to report the clustering effectiveness and robustness of the involved approaches with brief and varied forms. As such, the clustering outcomes of seven, semisupervised algorithms on each artificial data set with 5% and 10% sampling ratios are listed in Table IV in the forms of means and standard deviations of NMI, RI, DBI, CONS, and running time, respectively. The results of the original MSC algorithm are shown in Table V with ten times repeated running on each data set. By the way, as MSC is irrelevant to any supervision, the CONS index is definitely unsuitable to MSC.
TABLE IV.
Clustering Performance in Terms of NMI, RI, DBI, CONS, and Running Time of Seven Semisupervised Spectral Clustering Algorithms on Synthetic Data Sets
| Datasets | Metrics | Algorithms | |||||||
|---|---|---|---|---|---|---|---|---|---|
| SLAM | FCSC | CRM | ASTC | PGCSC | TI | TII | |||
| X 1 | 5% | NMI-m | 0.8908 | 0.8522 | 0.8727 | 0.8876 | 0.8898 | 0.8986 | 0.9016 |
| NMI-s | 0.0016 | 0.0245 | 0.0158 | 0.0016 | 0.0034 | 0.0088 | 0.0024 | ||
| RI-m | 0.9695 | 0.9526 | 0.9533 | 0.9590 | 0.9676 | 0.9714 | 0.9711 | ||
| RI-s | 0.0012 | 0.0121 | 0.0055 | 0.0015 | 0.0007 | 0.0025 | 0.0007 | ||
| DBI-m | 0.6755 | 0.6917 | 0.6988 | 0.6882 | 0.6783 | 0.6667 | 0.5333 | ||
| DBI-s | 0.0036 | 0.0110 | 0.0102 | 0.0021 | 0.0030 | 0.3055 | 0.3512 | ||
| CONS-m | 1 | 0.9870 | 0.9880 | 0.9877 | 1 | 0.9425 | 0.9928 | ||
| CONS-s | 0 | 0.0225 | 0.0020 | 0.0025 | 0 | 0.0653 | 0.0124 | ||
| Time-m | 1.2133 | 9.007 | 0.4925 | 0.4473 | 1.3499 | 0.5223 | 0.5591 | ||
| Time-s | 0.0618 | 0.9381 | 0.0189 | 0.1601 | 0.0523 | 0.0126 | 0.0018 | ||
| 10% | NMI-m | 0.8824 | 0.8845 | 0.8779 | 0.8766 | 0.8829 | 0.8909 | 0.8884 | |
| NMI-s | 0.0035 | 0.0054 | 0.0051 | 0.0012 | 0.0051 | 0.0048 | 0.0011 | ||
| RI-m | 0.9660 | 0.9630 | 0.9568 | 0.9560 | 0.9660 | 0.9675 | 0.9675 | ||
| RI-s | 0.0001 | 0.0015 | 0.0007 | 0.0011 | 0.0001 | 0.0025 | 0.0024 | ||
| DBI-m | 0.6754 | 0.6778 | 0.6841 | 0.6864 | 0.6750 | 0.4215 | 0.4333 | ||
| DBI-s | 0.0033 | 0.0019 | 0.0010 | 0.0055 | 0.0052 | 0.2646 | 0.2082 | ||
| CONS-m | 1 | 1 | 0.9823 | 0.9877 | 1 | 0.9747 | 1 | ||
| CONS-s | 0 | 0 | 0.0083 | 0.0025 | 0 | 0.0438 | 0 | ||
| Time-m | 1.1235 | 9.4850 | 0.4727 | 0.3674 | 1.2161 | 0.5242 | 0.5588 | ||
| Time-s | 0.0446 | 0.4850 | 0.0012 | 0.1587 | 0.0467 | 0.0145 | 0.0104 | ||
| X 2 | 5% | NMI-m | 0.9190 | 0.8544 | 0.9097 | 0.9082 | 0.9156 | 0.9207 | 0.9325 |
| NMI-s | 0.0099 | 0.0836 | 0.0066 | 0.0077 | 0.0066 | 0.0109 | 0.0231 | ||
| RI-m | 0.9758 | 0.9536 | 0.9660 | 0.9654 | 0.9746 | 0.9758 | 0.9794 | ||
| RI-s | 0.0032 | 0.0299 | 0.0036 | 0.0029 | 0.0012 | 0.0032 | 0.0082 | ||
| DBI-m | 1.1512 | 1.6108 | 1.1583 | 1.1620 | 1.1399 | 1.0206 | 1.0997 | ||
| DBI-s | 0.0078 | 0.8279 | 0.0082 | 0.0146 | 0.0037 | 0.1732 | 0.2309 | ||
| CONS-m | 0.8764 | 1 | 0.9890 | 1 | 0.8764 | 1 | 1 | ||
| CONS-s | 0.2141 | 0 | 0.0010 | 0 | 0.2141 | 0 | 0 | ||
| Time-m | 2.7255 | 17.0034 | 1.2992 | 0.5175 | 2.1397 | 1.0153 | 1.0697 | ||
| Time-s | 0.0878 | 1.3347 | 0.6661 | 0.1098 | 0.1051 | 0.0333 | 0.0268 | ||
| 10% | NMI-m | 0.3648 | 0.9102 | 0.9248 | 0.9253 | 0.9165 | 0.9330 | 0.9366 | |
| NMI-s | 0.0673 | 0.0267 | 0.0216 | 0.0128 | 0.0239 | 0.0247 | 0.0266 | ||
| RI-m | 0.6690 | 0.9745 | 0.9705 | 0.9716 | 0.9734 | 0.9785 | 0.9805 | ||
| RI-s | 0.0271 | 0.0080 | 0.0073 | 0.0040 | 0.0084 | 0.0085 | 0.0098 | ||
| DBI-m | 1.0987 | 1.3430 | 1.1680 | 1.1659 | 1.1362 | 1.0341 | 1.0239 | ||
| DBI-s | 0.1536 | 0.3446 | 0.0241 | 0.0229 | 0.0302 | 0.2777 | 0.1939 | ||
| CONS-m | 1 | 1 | 0.9893 | 0.9883 | 1 | 1 | 1 | ||
| CONS-s | 0 | 0 | 0.0006 | 0.0015 | 0 | 0 | 0 | ||
| Time-m | 2.7928 | 17.6024 | 1.1485 | 0.4837 | 2.1009 | 1.0122 | 1.0683 | ||
| Time-s | 0.0967 | 1.4077 | 0.4569 | 0.0962 | 0.0891 | 0.0293 | 0.0175 | ||
| X 3 | 5% | NMI-m | 0.8956 | 0.7237 | 0.8853 | 0.8868 | 0.8914 | 0.9033 | 0.9035 |
| NMI-s | 0.0111 | 0.0658 | 0.0243 | 0.0166 | 0.0074 | 0.0089 | 0.0091 | ||
| RI-m | 0.9731 | 0.9034 | 0.9621 | 0.9631 | 0.9715 | 0.9753 | 0.9753 | ||
| RI-s | 0.0034 | 0.0340 | 0.0081 | 0.0052 | 0.0025 | 0.0028 | 0.0028 | ||
| DBI-m | 6.4415 | 8.0839 | 6.1906 | 6.4519 | 6.4266 | 5.7511 | 5.7058 | ||
| DBI-s | 0.1177 | 3.4620 | 0.5492 | 0.3011 | 0.0402 | 0.1025 | 0.1349 | ||
| CONS-m | 1 | 1 | 0.9798 | 0.9917 | 1 | 1 | 1 | ||
| CONS-s | 0 | 0 | 0.0211 | 0.0047 | 0 | 0 | 0 | ||
| Time-m | 3.2666 | 13.7548 | 0.7066 | 0.4121 | 4.6916 | 1.6856 | 1.8101 | ||
| Time-s | 0.3502 | 2.2228 | 0.0481 | 0.0700 | 0.0520 | 0.0886 | 0.0329 | ||
| 10% | NMI-m | 0.8972 | 0.7942 | 0.9011 | 0.8882 | 0.9004 | 0.9015 | 0.9014 | |
| NMI-s | 0.0048 | 0.1323 | 0.0052 | 0.0048 | 0.0065 | 0.0027 | 0.0029 | ||
| RI-m | 0.9737 | 0.9255 | 0.9675 | 0.9637 | 0.9742 | 0.9748 | 0.9748 | ||
| RI-s | 0.0016 | 0.0666 | 0.0019 | 0.0016 | 0.0019 | 0.0009 | 0.0009 | ||
| DBI-m | 6.3587 | 5.4516 | 6.0547 | 6.3895 | 6.3620 | 6.2377 | 6.3255 | ||
| DBI-s | 0.0868 | 1.1024 | 0.2106 | 0.0746 | 0.0744 | 0.2129 | 0.1745 | ||
| CONS-m | 1 | 1 | 0.9943 | 1 | 0.8333 | 1 | 1 | ||
| CONS-s | 0 | 0 | 0.0045 | 0 | 0.2887 | 0 | 0 | ||
| Time-m | 3.2024 | 12.3624 | 0.7028 | 0.3740 | 4.2121 | 1.6924 | 1.8049 | ||
| Time-s | 0.0657 | 1.2427 | 0.0212 | 0.2277 | 0.1241 | 0.0222 | 0.0155 | ||
Note: *-m and *-s denote the values of the mean and standard deviation, respectively; TI and TII are the separate abbreviations of our proposed TI-APJCSC and TH-APJCSC algorithms.
TABLE V.
Clustering Results in Terms of NMI, RI, DBI, and Running Time of the Conventional MSC Algorithm on Synthetic Data Sets
| Metrics | Datasets | ||
|---|---|---|---|
| X 1 | X 2 | X 3 | |
| NMI-m | 0.8897 | 0.5728 | 0.2727 |
| NMI-s | 0 | 0 | 0 |
| RI-m | 0.9684 | 0.7970 | 0.5810 |
| RI-s | 0 | 0 | 0 |
| DBI-m | 0.6734 | 0.7683 | 1.7183 |
| DBI-s | 1.4E-16 | 0 | 2.7E-16 |
| Time-m | 1.2276 | 3.3082 | 3.9013 |
| Time-s | 0.0932 | 0.0244 | 0.0314 |
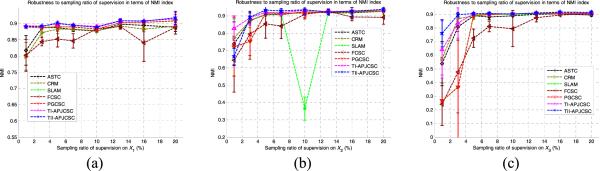
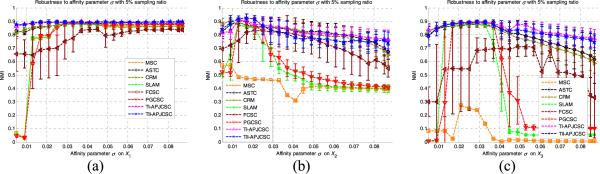
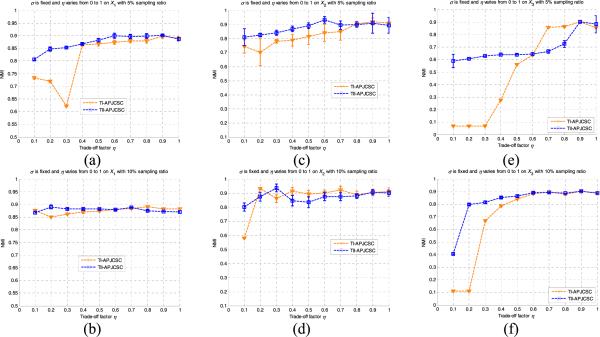
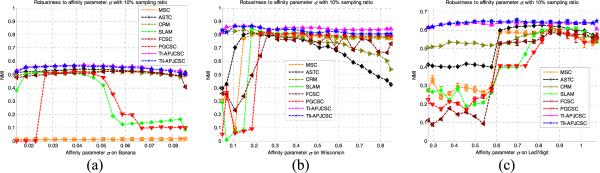
In addition to the clustering effectiveness, as is well known, the robustness (i.e., stability) is another primary factor affecting the practicability of intelligent algorithms. To this end, in order to appraise the clustering robustness of each algorithm on these artificial data sets, our work proceeded from two aspects in terms of the most authoritative, well-accepted NMI index. On the one hand, we studied the robustness of all recruited semisupervised methods, i.e., SLAM, FCSC, CRM, ASTC, PGCSC, TI-APJCSC, and TII-APJCSC, regarding different sampling ratios. That is, by means of the NMI scores of each algorithm running on X1, X2, and X3 individually with the sampled subsets of different sampling ratios, i.e., 1%, 3%, 5%, 7%, 10%, 13%, 16%, and 20%, acting as the supervision, respectively, we drew the clustering effectiveness curves of these algorithms with respect to the different sampling ratios, as shown in Fig. 3. On the other hand, we also investigated the performance robustness of our proposed TI-APJCSC and TII-APJCSC approaches regarding their core parameters, i.e., the affinity parameter σ in (1) and the tradeoff factor η in (13). In light of the fact that the affinity parameter σ is involved in all eight algorithms (including MSC), we compare their NMI score curves together with the parameter σ varying within the same range from 0.005 to 0.087. Due to the limitation of paper space, we only report the outcomes of these algorithms on X1, X2, and X3 with a 5% sampling ratio, respectively, as shown in Fig. 4. As for the robustness regarding the tradeoff factor η enlisted in both TI-APJCSC and TII-APJCSC, with the affinity parameter σ being fixed as the individual optima, we separately recorded the best NMI scores of TI-APJCSC and TII-APJCSC, while parameter η took values from 0.1 to 1. In addition, also due to the limitation of paper space, we just indicate the individual sensitivity of TI-APJCSC and TII-APJCSC to the tradeoff factor η on three synthetic data sets with 5% and 10% sampling ratios, respectively, as shown in Fig. 5.
Fig. 3.
Robustness to sampling ratios. (a) NMI curves of seven algorithms to sampling ratios on X1. (b) NMI curves of seven algorithms to sampling ratios on X2. (c) NMI curves of seven algorithms to sampling ratios on X3.
Fig. 4.
Robustness to affinity parameter σ. (a) NMI curves of eight algorithms to σ on X1. (b) NMI curves of eight algorithms to σ on X2. (c) NMI curves of eight algorithms to σ on X3.
Fig. 5.
Robustness to tradeoff factor η. (a) NMI curves of TI-APJCSC and TII-APJCSC to η on X1 with a 5% sampling ratio. (b) NMI curves of TI-APJCSC and TII-APJCSC to η on X1 with a 10% sampling ratio. (c) NMI curves of TI-APJCSC and TII-APJCSC to η on X2 with a 5% sampling ratio. (d) NMI curves of TI-APJCSC and TII-APJCSC to η on X2 with a 10% sampling ratio. (e) NMI curves of TI-APJCSC and TII-APJCSC to η on X3 with a 5% sampling ratio. (f) NMI curves of TI-APJCSC and TII-APJCSC to η on X3 with a 10% sampling ratio.
A few intuitive clustering results of the partial algorithms on three artificial data sets are shown in Fig. 6. For saving the paper space, here we only exhibit one of the partition scenarios of MSC, SLAM, FCSC, TI-APJCSC, and TII-APJCSC with a 10% sampling ratio on each data set.
Fig. 6.
Partition results of partial algorithms on synthetic data sets. (a) MSC on X1. (b) SLAM on X1. (c) FCSC on X1. (d) TI-APJCSC on X1. (e) TII-APJCSC on X1. (f) MSC on X2. (g) SLAM on X2. (h) FCSC on X2. (i) TI-APJCSC on X2. (j) TII-APJCSC on X2. (k) MSC on X3. (l) SLAM on X3. (m) FCSC on X3. (n) TI-APJCSC on X3. (o) TII-APJCSC on X3.
All of the experiments of eight algorithms were finished with the affinity parameter σ ranging within the same interval [0.005:0.002:0.087], and the recommended, optimal parameter settings of TI-APJCSC and TII-APJCSC on these artificial data sets with 5% and 10% sampling ratios are shown in Table VI.
Based on these experimental results, we can make some analyses as follows.
-
1)
In general, the seven, semisupervised spectral algorithms overcome the original, unsupervised MSC algorithm. Furthermore, benefiting from the distinctive affinity and penalty jointly constrained mechanism, both TI-APJCSC and TII-APJCSC outperform the others. As shown in Table IV, the top two ranks of NMI and RI, two well-accepted validity indices, are achieved by either TI-APJCSC or TII-APJCSC, even though the advantage in some comparisons is not overwhelming, particularly comparing their scores with those of ASTC, CRM, and PGCSC.
-
2)
The robustness of our proposed TI-APJCSC and TII-APJCSC algorithms to both the sampling ratio and the affinity parameter σ are demonstrated in our experiments. As shown in Fig. 3, the NMI curves of TI-APJCSC and TII-APJCSC regarding different sampling ratios seem relatively stable and almost always rank at top 1 or top 2 on all of the artificial data sets. In particular, when the sampling ratios are <10%, the stability and the effectiveness of TI-APJCSC or TII-APJCSC, which also indicate the practicability, are definitely valuable. Moreover, Fig. 4 further shows the insensitivity of TI-APJCSC and TII-APJCSC to the parameter σ in the affinity function. In particular, taking Fig. 4(a) as an example, each node of each curve in this subfigure was the average score of the NMI index achieved by the matching algorithm running ten times with the same setting of affinity parameter σ but different subsets of X1 as the supervision. Therefore, the stability of both TI-APJCSC and TII-APJCSC to the affinity parameter σ is especially valuable, which means that they can work well as long as σ takes values approximately within the appropriate range. This guarantees their practicability in another way.
-
3)
ASTC and CRM exhibit more excellent effectiveness and robustness on all three artificial data sets, which are only worse than those of our novel TI-APJCSC and TII-APJCSC approaches. However, they can only work based on the supervision in the form of class labels, and this restricts their realistic applications.
-
4)
In the view of the clustering effectiveness, PGCSC also performs well on three artificial data sets. Nevertheless, its robustness, particularly to the affinity parameter σ, is distinctly worse than that of TI-APJCSC or TII-APJCSC, as it is just essentially compatible with the must-link constraints.
-
5)
Both the effectiveness and the robustness of FCSC are unsatisfactory in practice despite its all-compatibility with all categories of supervision. Figs. 3 and 4 intuitively show that the overall effectiveness of FCSC is distinctly worse than that of TI-APJCSC/TII-APJCSC and its instability is sensitive not only to the capacity of supervision (i.e., the sampling ratio) but also to the parameter of affinity measurement.
-
6)
SLAM is one of the straightforward, semisupervised, spectral clustering methods that work based merely on the affinity constraints, among all of these employed algorithms. Nevertheless, Table IV and Figs. 3(b) and 6(g) clearly show its instability. More precisely, in terms of the NMI index, it achieved approximately the 0.919 score with the 5% sampling ratio on X2; however, it abnormally obtained the 0.3648 score with the 10% sampling ratio on the same data set. Actually, such phenomena commonly occur in other similar, semisupervised, spectral clustering approaches relying only on affinity constraints.
-
7)
In addition to the effectiveness and robustness verified in our experiments, both TI-APJCSC and TII-APJCSC have two other distinguished merits: 1) the all-compatibility and 2) the flexibility. The all-compatibility is that they can deal with all existing categories of supervision, including class labels, pairwise constraints, and group information. As for the flexibility, it is dependent on the transformation from (12) to (13). Our previous empirical studies suggest that the regularization coefficient γ in (12) is always associated with the specific constrained matrix Pi, which causes the uncertainty of its range. In contrast, benefiting from the normalized frameworks in (13), both TI-APJCSC and TII-APJCSC can handle any semisupervised scenario by only assigning the consistent interval (0, 1] to the tradeoff factor η. In addition, putting the penalty term yT Piy in the objective function rather than in the subjection condition helps us avoid specifying a threshold for this constraint term, such as in FCSC [31] and CSC-L1R [30], which further enhances the practicability as well as the flexibility of TI-APJCSC and TII-APJCSC. By means of the grid-search strategy and the feasible validity metrics, e.g., NMI or DBI, the tradeoff factor η in both TI-APJCSC and TII-APJCSC will eventually arrive at an appropriate value within the interval (0, 1]. Whereas this procedure is finished self-adaptively, both TI-APJCSC and TII-APJCSC are able to automatically determine the impact of the constraint term yT Piy to the overall objective expression in (13).
-
8)
The constraint formulation of TII-APJCSC, i.e., TII-APJCF in the form of (10), differs from that of TI-APJCSC. It keeps the same first term as that in TI-APJCSC for must-link constraints in order to establish the implicit but incomplete connection between the penalty and affinity constraints. However, via the inconsistent second term for cannot-link constraints, TII-APJCSC is able to further optimize the clustering indicator vector. As such, the clustering performance of TI-APJCSC and TII-APJCSC is generally close to each other, and the slight performance distinction between them exists in their sensitivity to the tradeoff parameter η. In particular, TII-APJCSC generally appears more insensitive to the tradeoff factor η than TI-APJCSC, as shown in Fig. 5, although both of them demonstrate the basically similar robustness against the affinity parameter σ (see Fig. 4).
-
9)
In the sight of running time of all candidate algorithms, as shown in Table IV, TI-APJCSC and TII-APJCSC are averagely at the moderate levels. We would like to discuss the running time of FCSC as it exhibits distinctly high computing cost against the others. The formulation of FCSC is equivalent to one generalized eigensystem [31], and the MATLAB built-in function, eig(), was employed to compute the eigenvalue decomposition issues throughout this paper, and we noticed that the computing time of this function noticeably increased when it coped with the generalized eigenvalue decomposition cases. Such phenomenon is particularly recognizable when the data capacity is near or larger than 1000.
C. On Real-Life Data Sets
1) Experimental Setup
In this section, we evaluated the performance of all eight algorithms on nine real-life data sets, including: 1) three KEEL data sets: Banana, Wisconsin, and Led7digit1; 2) two UCI data sets: Wine and Waveform-212; 3) the USPS handwritten digit data set: USPS-35683; 4) the human facial data set: Japanese female facial expression (JAFFE)4; 5) the text data set: 20news5; and 6) the Berkeley segmentation data set: Berke-296059.6 Some data sets were resized in this paper due to the well-known computing burden occurred in most of the spectral clustering approaches.
The constructions and the arrangements regarding these data sets in our experiments are briefly introduced as follows.
-
1)
As in the dedicated, KEEL semisupervised data sets, the supervision is given with the fixed sampling ratio of 10%, and we just straightforwardly performed all algorithms on Banana, Wisconsin, and Led7digit with ten repetitions.
-
2)
As for USPS-3568, JAFFE, and 20news, likewise, we first randomly sampled each data set ten times using an invariant ratio of 10% to obtain ten subsets of each of them, after that, the seven, semisupervised algorithms were carried out on each data set with its each subset being adopted as the supervision.
-
3)
The USPS-3568 data set was generated by randomly extracting 1564 samples from four handwritten digits, 3, 5, 6, and 8, in the USPS database.
-
4)
The JAFFE data set was obtained from the JAFFE database. We selected 10 × 20 female facial images from the original database, i.e., 10 different persons and 20 facial images per person. One frontal face image of each person is shown in Fig. 7. To enlarge the size of the data set, we also rotated anticlockwise each image at angles of 5° and 10°, respectively. We then performed the principal component analysis processing on the raw pixel-gray features of each image, and obtained the final JAFFE data set with the data size and dimension being 600 and 599, respectively.
-
5)
The 20news data set was composed of 2000 data instances chosen randomly from four subcategories in the 20 newsgroups database: 1) comp.sys.mac.hardware; 2) rec.autos; 3) sci.med; and 4) talk.politics.guns. The BOW toolkit [45] was used to reduce the data dimension, which was originally as high as 43 586. The eventual 20news data set contains 350 effective features in our experiment.
-
6)
As for Berke-296059, we attempted to evaluate the effectiveness of those algorithms compatible with must-link or cannot-link constraints, such as FSCS, PGCSC, TI-APJCSC, and TII-APJCSC. For this purpose, one, hand-labeled, animal image numbered 296 059 in the Berkeley segmentation data sets was enlisted in this paper, and we resized it into 70 × 46 resolution and relabeled it by hand, as shown in Fig. 8(a). The Berke-296059 data set was composed of the features of hue, saturation, and value (HSV) of each pixel in this images. Furthermore, we drew six regions with different colors on this image as the pairwise constraints or grouping information, as shown in Fig. 8(b). The regions belong to the same class only if they are marked in the same color. Table VII summarizes the details of these real-life data sets involved in our experiments. All data sets were also normalized before our experiments.
Fig. 7.
Human facial data set JAFFE.
Fig. 8.
Image segmentation data set Berke-296059. (a) Three clusters labeled by hand. (b) Pairwise constraints.
TABLE VII.
Description of Real-Life Benchmark Data Sets for Experiments
| Dataset Type | Dataset Name | Size | Dimensions | Classes | Sampling Ratio |
|---|---|---|---|---|---|
| KEEL dedicated semi-supervised learning | Banana | 2650 | 2 | 2 | 10% |
| Wisconsin | 683 | 9 | 2 | 10% | |
| Led7digit | 500 | 7 | 10 | 10% | |
| UCI | Wine | 178 | 13 | 3 | 10% |
| Waveform-21 | 2500 | 21 | 3 | 10% | |
| Handwritten digit | USPS-3568 | 1564 | 256 | 4 | 10% |
| Human face | JAFFE | 600 | 599 | 10 | 10% |
| Text data | 20news | 2000 | 350 | 4 | 10% |
| Berkeley segmentation | Berke-296059 | 3220 | 3 | 3 | By hand |
2) Results of the Experiments
We first performed the classic MSC approach on all these real-life data sets, and the values of involved validity indices are listed in Table VIII. Only SLAM, FCSC, PGCSC, TI-APJCSC, and TII-APJCSC were performed on Berke-296059 due to the compatibility with pairwise constraints or grouping information. On the other data sets, all seven, semisupervised approaches were carried out, and their results are listed in Table IX.
TABLE VIII.
Clustering Performance of MSC on Real-Life Data Sets
| Metrics | Datasets | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Banana | Wisconsin | Led7digit | Wine | Wave form-21 | USPS-3568 | JAFFE | 20news | Berke-296059 | |
| NMI-m | 0.0147 | 0.8055 | 0.5939 | 0.8120 | 0.3723 | 0.6112 | 0.2208 | 0.1083 | 0.6155 |
| NMI-s | 0 | 0 | 0.0013 | 0 | 0.0026 | 7.4E-4 | 0.0050 | 1.8E-4 | 0 |
| RI-m | 0.5113 | 0.9392 | 0.8957 | 0.8699 | 0.6714 | 0.8205 | 0.2947 | 0.5917 | 0.7198 |
| RI-s | 0 | 0 | 0.0020 | 1.4E-16 | 1.5E-4 | 4.2E-4 | 0.0042 | 0.0011 | 0 |
| DBI-m | 1.0481 | 0.8030 | 1.3479 | 1.3766 | 1.5130 | 2.2246 | 3.7791 | 5.4758 | 0.7307 |
| DBI-s | 0 | 1.4E-16 | 0.0254 | 0 | 0.0356 | 4.7E-4 | 0.0280 | 0.0210 | 0 |
| Time-m | 21.8386 | 0.4401 | 0.1977 | 0.0471 | 30.1275 | 13.4835 | 3.9337 | 29.5338 | 11.8847 |
| Time-s | 0.3731 | 0.0115 | 0.0140 | 0.0090 | 0.9683 | 0.0417 | 0.2579 | 0.0050 | 0.4389 |
Note: *-m and *-s denote the values of mean and standard deviation, respectively.
TABLE IX.
Clustering Results in Terms of NMI, RI, DBI, CONS, and Running Time of Seven Semisupervised Algorithms on Real-Life Data Sets
| Datasets | Metrics | Algorithms | ||||||
|---|---|---|---|---|---|---|---|---|
| SLAM | FCSC | CRM | ASTC | PGCSC | TI | TII | ||
| Banana | NMI-m | 0.5164 | 0.5342 | 0.5356 | 0.5430 | 0.5237 | 0.5756 | 0.5662 |
| NMI-s | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RI-m | 0.7990 | 0.8021 | 0.7986 | 0.8080 | 0.8116 | 0.8373 | 0.8352 | |
| RI-s | 0 | 1.4E-16 | 0 | 0 | 1.4E-16 | 0 | 0 | |
| DBI-m | 9.1997 | 8.9751 | 7.3475 | 7.7922 | 6.0164 | 7.0240 | 6.4169 | |
| DBI-s | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| CONS-m | 1 | 1 | 0.9940 | 0.9973 | 0.8333 | 0.9019 | 0.8992 | |
| CONS-s | 0 | 0 | 0.0048 | 0.0017 | 0.2887 | 0 | 0 | |
| Time-m | 25.0206 | 205.9835 | 6.2195 | 3.4858 | 28.4171 | 5.6457 | 6.0950 | |
| Time-s | 0.4568 | 2.1845 | 0.0124 | 0.0081 | 0.9151 | 0.1845 | 0.1169 | |
| Wisconsin | NMI-m | 0.8431 | 0.8486 | 0.8440 | 0.8290 | 0.8144 | 0.8662 | 0.8654 |
| NMI-s | 1.4E-16 | 1.4E-16 | 0 | 0 | 0 | 1.4E-16 | 0 | |
| RI-m | 0.9544 | 0.9454 | 0.9316 | 0.9523 | 0.9392 | 0.9585 | 0.9616 | |
| RI-s | 0 | 0 | 0 | 1.4E-16 | 0 | 1.4E-16 | 0 | |
| DBI-m | 0.7965 | 0.8150 | 0.8314 | 0.7940 | 0.8062 | 0.8010 | 0.7675 | |
| DBI-s | 0 | 0 | 0 | 1.4E-16 | 0 | 0 | 0 | |
| CONS-m | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| CONS-s | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Time-m | 0.4246 | 2.7636 | 0.3073 | 0.3234 | 0.4977 | 0.3786 | 0.3425 | |
| Time-s | 0.0265 | 0.0291 | 0.0363 | 0.0206 | 0.0141 | 0.0219 | 0.0106 | |
| Led7digit | NMI-m | 0.6239 | 0.6026 | 0.6066 | 0.6283 | 0.6121 | 0.6503 | 0.6591 |
| NMI-s | 0.0025 | 0.0160 | 0 | 0 | 0.0039 | 0.0023 | 0.0030 | |
| RI-m | 0.9082 | 0.8927 | 0.9008 | 0.9020 | 0.8995 | 0.9197 | 0.9252 | |
| RI-s | 0.0010 | 0.0110 | 0 | 0 | 0.0051 | 0.0055 | 0.0004 | |
| DBI-m | 1.2998 | 1.5942 | 1.8240 | 1.4937 | 1.4238 | 1.3538 | 1.2364 | |
| DBI-s | 0.0110 | 0.2173 | 2.7E-16 | 0 | 0.0118 | 0.1639 | 0.0093 | |
| CONS-m | 0.8060 | 0.9817 | 0.9962 | 0.9943 | 0.9911 | 0.8077 | 0.9191 | |
| CONS-s | 0.0360 | 0.0213 | 0.0053 | 0.0038 | 0.0077 | 0.0418 | 0.0121 | |
| Time-m | 0.2867 | 1.0037 | 0.1689 | 0.1107 | 0.2431 | 0.2232 | 0.1945 | |
| Time-s | 0.0076 | 0.0707 | 0.0045 | 0.0051 | 0.0173 | 0.0209 | 0.0075 | |
| Wine | NMI-m | 0.9253 | 0.8160 | 0.8680 | 0.8901 | 0.9263 | 0.9317 | 0.9317 |
| NMI-s | 0.0247 | 0.0832 | 0.0135 | 0.0335 | 0.0247 | 0.0216 | 0.0216 | |
| RI-m | 0.9750 | 0.9246 | 0.9444 | 0.9543 | 0.9750 | 0.9774 | 0.9774 | |
| RI-s | 0.0088 | 0.0373 | 0.0066 | 0.0124 | 0.0088 | 0.0076 | 0.0076 | |
| DBI-m | 1.3780 | 1.4074 | 1.4065 | 1.4003 | 1.3780 | 1.1781 | 1.2766 | |
| DBI-s | 0.0025 | 0.0397 | 0.0063 | 0.0107 | 0.0025 | 0.0025 | 0.0115 | |
| CONS-m | 1 | 1 | 0.9962 | 0.9940 | 1 | 1 | 1 | |
| CONS-s | 0 | 0 | 0.0053 | 0.0038 | 0 | 0 | 0 | |
| Time-m | 0.0328 | 0.2321 | 0.0671 | 0.0559 | 0.0402 | 0.0516 | 0.0619 | |
| Time-s | 0.0023 | 0.0104 | 0.0020 | 0.0064 | 0.0040 | 0.0017 | 0.0086 | |
| Waveform-21 | NMI-m | 0.3816 | 0.4388 | 0.4678 | 0.4964 | 0.3873 | 0.4860 | 0.4837 |
| NMI-s | 1.9E-5 | 0.0326 | 0.0114 | 0.0106 | 0.0036 | 0.0132 | 0.0212 | |
| RI-m | 0.7192 | 0.7235 | 0.7692 | 0.7681 | 0.6797 | 0.7570 | 0.7558 | |
| RI-s | 8.7E-5 | 0.0211 | 0.0106 | 0.0105 | 0.0026 | 0.0110 | 0.0154 | |
| DBI-m | 9.7754 | 2.2163 | 2.1605 | 2.1702 | 1.6890 | 2.0529 | 2.1418 | |
| DBI-s | 2.1733 | 0.0710 | 0.0553 | 0.0500 | 0.0201 | 0.1328 | 0.0480 | |
| CONS-m | 0.6564 | 1 | 0.9923 | 1 | 1 | 0.6316 | 0.6328 | |
| CONS-s | 0.0358 | 0 | 0.0020 | 0 | 0 | 0.0099 | 0.0097 | |
| Time-m | 31.7048 | 247.5292 | 6.0845 | 7.1319 | 33.9353 | 7.2836 | 7.7212 | |
| Time-s | 0.3075 | 10.4529 | 0.2558 | 0.0381 | 1.2736 | 0.0252 | 0.0977 | |
| USPS-3568 | NMI-m | 0.7332 | 0.8064 | 0.8317 | 0.8405 | 0.6457 | 0.8397 | 0.8615 |
| NMI-s | 0.0138 | 0.0136 | 0.0053 | 0.0102 | 0.0060 | 0.0144 | 0.0081 | |
| RI-m | 0.8864 | 0.9408 | 0.9250 | 0.9490 | 0.8287 | 0.9434 | 0.9622 | |
| RI-s | 0.0367 | 0.0079 | 0.0018 | 0.0038 | 0.0009 | 0.0067 | 0.0023 | |
| DBI-m | 2.6784 | 2.8119 | 2.7395 | 2.7570 | 2.2378 | 2.1318 | 2.3635 | |
| DBI-s | 0.0318 | 0.0245 | 0.0006 | 0.0015 | 0.0277 | 0.0365 | 0.0269 | |
| CONS-m | 0.9756 | 1 | 0.9865 | 0.9937 | 0.8600 | 1 | 1 | |
| CONS-s | 0.0422 | 0 | 0.0065 | 0.0040 | 0.0799 | 0 | 0 | |
| Time-m | 8.2979 | 70.5778 | 7.2742 | 5.7583 | 8.8198 | 5.8785 | 6.0986 | |
| Time-s | 0.0339 | 1.2188 | 0.2229 | 0.0420 | 0.1161 | 0.0573 | 0.0117 | |
| JAFFE | NMI-m | 0.2635 | 0.2310 | 0.3421 | 0.3134 | 0.2701 | 0.5070 | 0.3811 |
| NMI-s | 0.0182 | 0.0051 | 0.0274 | 0.0137 | 0.0189 | 0.0410 | 0.0282 | |
| RI-m | 0.3239 | 0.3186 | 0.5525 | 0.7257 | 0.4337 | 0.8237 | 0.7008 | |
| RI-s | 0.0285 | 0.0205 | 0.0387 | 0.0153 | 0.0172 | 0.0573 | 0.0819 | |
| DBI-m | 5.3146 | 3.6118 | 7.5782 | 9.3607 | 4.2364 | 5.7232 | 5.8227 | |
| DBI-s | 0.2453 | 0.3839 | 0.4257 | 0.1263 | 0.2470 | 0.8505 | 0.5714 | |
| CONS-m | 0.9893 | 0.8881 | 0.9923 | 0.9903 | 0.6765 | 0.8613 | 0.8640 | |
| CONS-s | 0.0140 | 0.0120 | 0.0020 | 0.0025 | 0.0933 | 0.0207 | 0.0921 | |
| Time-m | 0.6178 | 4.0853 | 0.4075 | 0.5269 | 0.7839 | 0.6182 | 0.6476 | |
| Time-s | 0.0531 | 0.5997 | 0.0533 | 0.0225 | 0.0121 | 0.1479 | 0.0965 | |
| 20news | NMI-m | 0.1564 | 0.1543 | 0.1914 | 0.1879 | 0.1250 | 0.2556 | 0.2238 |
| NMI-S | 0.0036 | 0.0014 | 0.0018 | 0.0033 | 0.0062 | 0.0143 | 0.0153 | |
| RI-m | 0.3317 | 0.3274 | 0.4894 | 0.4443 | 0.6166 | 0.5433 | 0.4681 | |
| RI-s | 0.0014 | 0.0012 | 0.0407 | 0.0957 | 0.0164 | 0.0646 | 0.0801 | |
| DBI-m | 9.3337 | 10.526 | 7.8736 | 7.8657 | 6.1765 | 6.5541 | 6.5224 | |
| DBI-s | 0.3082 | 0.2342 | 0.8057 | 0.4107 | 0.2036 | 0.0222 | 0.0516 | |
| CONS-m | 1 | 1 | 0.5000 | 0.9903 | 0.7823 | 0.8983 | 0.9300 | |
| CONS-s | 0 | 0 | 0 | 0.0025 | 0.0473 | 0.1702 | 0 | |
| Time-m | 28.9717 | 124.7176 | 22.1992 | 21.1076 | 29.5331 | 23.4338 | 24.7605 | |
| Time-s | 0.1455 | 2.0669 | 0.0424 | 0.1506 | 0.5522 | 0.6306 | 0.0368 | |
| Berke-296059 | NMI-m | 0.6409 | 0.5131 | — | — | 0.6190 | 0.7515 | 0.7600 |
| NMI-s | 0.0350 | 0.0202 | — | — | 0 | 0 | 0 | |
| RI-m | 0.8084 | 0.6710 | — | — | 0.7193 | 0.9007 | 0.9029 | |
| RI-s | 0.0612 | 0.0165 | — | — | 0 | 0 | 0 | |
| DBI-m | 0.9765 | 3.2890 | — | — | 0.7051 | 1.1556 | 1.1209 | |
| DBI-s | 0.1448 | 1.2200 | — | — | 0 | 0 | 0 | |
| CONS-m | 0.8063 | 0.7337 | — | — | 0.7546 | 1 | 1 | |
| CONS-s | 0.0553 | 0.0050 | — | — | 0 | 0 | 0 | |
| Time-m | 15.1517 | 124.1676 | — | — | 18.4191 | 6.3568 | 5.9789 | |
| Time-s | 0.6538 | 0.7005 | — | — | 0.1123 | 0.2013 | 0.2822 | |
Note: TI and TII are the separate abbreviations of TI-APJCSC and TII-APJCSC.
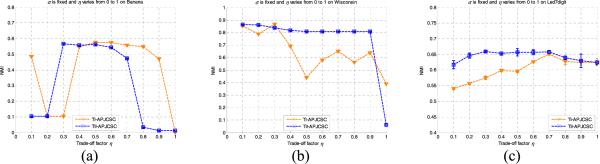
Likewise, we have also concurrently conducted the robustness studies of these algorithms on these real-life data sets. Due to the limitation of space, we cannot report more detailed results, and only the NMI-based parameter robustness regarding related algorithms on the three, dedicated, KEEL data sets are shown in Figs. 9 and 10. In particular, the robustness of all eight algorithms with respect to the affinity parameter σ is shown in Fig. 9, and the sensitivity investigations regarding the tradeoff factor η of TI-APJCSC and TII-APJCSC are shown in Fig. 10.
Fig. 9.
Robustness to affinity parameter σ on semisupervised KEEL benchmark data sets. (a) NMI curves of eight algorithms to σ on Banana. (b) NMI curves of eight algorithms to σ on Wisconsin. (c) NMI curves of eight algorithms to σ on Led7digit.
Fig. 10.
Robustness to tradeoff factor η on semisupervised KEEL benchmark data sets. (a) NMI curves of TI-APJCSC and TII-APJCSC to η on Banana. (b) NMI curves of TI-APJCSC and TII-APJCSC to η on Wisconsin. (c) NMI curves of TI-APJCSC and TII-APJCSC to η on Led7digit.
As seen in these results, our proposed TI-APJCSC and TII-APJCSC algorithms generally overcome the others once again from the perspectives of their effectiveness and stability. Considering the paper space constraint, we do not present the detailed analyses regarding each algorithm on these data sets, as the analyses and conclusions which we performed on the artificial data sets also generally hold here. Owing to the affinity and penalty jointly constrained strategies as well as the flexible normalized frameworks, both TI-APJCSC and TII-APJCSC demonstrate comparatively high effectiveness and strong robustness even on these real-world data sets, which are full of uncertainties, such as noise, outliers, or mislabeling. Moreover, TII-APJCSC overall features better stability to the tradeoff factor η than TI-APJCSC due to their different semisupervised formulations in the forms of (6) and (10), respectively.
The segmentation results of partial approaches, i.e., PGCSC, SLAM, TI-APJCSC, and TII-APJCSC, on the Berke-296059 data set are shown in Fig. 11. Comparing the index scores of the related algorithms listed in Table IX with the realistic segmentation diagrams shown in Fig. 11, the flaw of the DBI index is intuitively confirmed that the minimal value does not necessarily represent the most reasonable result. For example, in terms of the DBI metric, PGCSC should be the best one; however, its corresponding NMI score is only 0.619, which is definitely worse than those of TI-APJCSC and TII-APJCSC. Fig. 11(a) shows that it cannot successfully partition the image into three desirable parts with DBI equaling 0.7051.
Fig. 11.
Segmentation illustrations of partial algorithms. (a) Result of PGCSC. (b) Result of SLAM. (c) Result of TI-APJCSC. (d) Result of TII-APJCSC.
Last but not least, the trial ranges of the affinity parameter σ of all recruited algorithms on these real-life data sets as well as the recommended optimal parameter settings of TI-APJCSC and TII-APJCSC are listed in Table X.
V. Conclusion
In this paper, two affinity and penalty jointly constrained formulations, TI-APJCF and TII-APJCF, respectively, were first devised to cope with the semisupervised, spectral clustering problem. Based on these formulations, by means of the min–max theorem, two flexible, normalized, constrained, spectral clustering frameworks as well as their corresponding algorithms, referred to as TI-APJCSC and TII-APJCSC, were eventually proposed. The comparisons among TI-APJCSC/TII-APJCSC and the other six state-ofthe-art approaches on both the artificial and real-life semisupervised data sets demonstrated that our proposed schemas for constrained spectral clustering concurrently have three, distinctive merits: 1) full compatibility; 2) high flexibility; and 3) strong robustness. This further suggests that both TI-APJCF and TII-APJCF have desirable practicability in those medium-and small-scale, semisupervised data scenarios.
There are two aspects of work need to be continued in depth in the future. One is the computational burden of our propounded TI-APJCSC and TII-APJCSC approaches in large-scale data scenarios, and the other is how to adjust the core parameters involved in TI-APJCSC and TII-APJCSC self-adaptively. Such two issues indeed restrict the practicability of our developed schemas for semisupervised spectral clustering to a great extent.
Acknowledgment
The authors would like to thank B. Hami from MA, USA, for the editorial assistance in the preparation of this paper.
This work was supported in part by the National Cancer Institute of the National Institutes of Health, USA, under Grant R01CA196687, in part by the Research and Development Frontier Grant of Jiangsu Province under Grant BY2013015-02, in part by the Natural Science Foundation of Jiangsu Province, China, under Grant BK201221834, and in part by the National Natural Science Foundation of China under Grant 61202311, Grant 61272210, and Grant 61572236.
Biography
 Pengjiang Qian (M'12) received the Ph.D. degree from Jiangnan University, Wuxi, China, in 2011.
Pengjiang Qian (M'12) received the Ph.D. degree from Jiangnan University, Wuxi, China, in 2011.
He is currently an Associate Professor with the School of Digital Media, Jiangnan University. He is also a Research Scholar with Case Western Reserve University, Cleveland, OH, USA, where he is involved in research in medical imaging processing. He has authored over 30 papers in international/national authoritative journals and conferences. His current research interests include data mining, pattern recognition, bioinformatics and their applications, such as analysis and processing for medical imaging, intelligent traffic dispatching, and advanced business intelligence in logistics.
 Yizhang Jiang (M'12) is currently pursuing the Ph.D. degree with the School of Digital Media, Jiangnan University, Wuxi, China.
Yizhang Jiang (M'12) is currently pursuing the Ph.D. degree with the School of Digital Media, Jiangnan University, Wuxi, China.
He is a Research Assistant with the Computing Department, Hong Kong Polytechnic University, Hong Kong, for almost one year. He has authored several papers in international journals, including IEEE Transactions on Fuzzy Systems and the IEEE Transactions on Neural Networks and Learning Systems. His current research interests include pattern recognition, intelligent com putation, and their applications.
 Shitong Wang received the M.S. degree in computer science from the Nanjing University of Aeronautics and Astronautics, Nanjing, China, in 1987.
Shitong Wang received the M.S. degree in computer science from the Nanjing University of Aeronautics and Astronautics, Nanjing, China, in 1987.
He visited London University, London, U.K., Bristol University, Bristol, U.K., Hiroshima International University, Higashihiroshima, Japan, Osaka Prefecture University, Osaka, Japan, The Hong Kong University of Science and Technology, Hong Kong, and Hong Kong Polytechnic University, Hong Kong, as a Research Scientist, for over six years. He is currently a Full Professor with the School of Digital Media, Jiangnan University, Wuxi, China. He has authored about 100 papers in international/national journals and has authored seven books. His current research interests include artificial intelligence, neurofuzzy systems, pattern recognition, and image processing.
 Kuan-Hao Su received the Ph.D. degree from National Yang-Ming University, Taipei, Taiwan, in 2009.
Kuan-Hao Su received the Ph.D. degree from National Yang-Ming University, Taipei, Taiwan, in 2009.
He is currently a Research Associate with the Department of Radiology, Case Western Reserve University, Cleveland, OH, USA. His current research interests include molecular imaging, tracer kinetic modeling, pattern recognition, and machine learning.
 Jun Wang received the Ph.D. degree in mechanical engineering from Jiangnan University, Wuxi, China, in 2009.
Jun Wang received the Ph.D. degree in mechanical engineering from Jiangnan University, Wuxi, China, in 2009.
He is currently an Associate Professor with the School of Mechanical Engineering, Jiangnan University. He has authored or co-authored over 40 research papers in international/national journals. His current research interests include mechatronics, machine learning, robot, and their applications.
 Lingzhi Hu received the Ph.D. degree in medical imaging from Washington University in St. Louis, St. Louis, MO, USA, in 2012.
Lingzhi Hu received the Ph.D. degree in medical imaging from Washington University in St. Louis, St. Louis, MO, USA, in 2012.
He is currently a Research Scientist with Philips Electronics North America, Highland Heights, OH, USA. He has authored or co-authored over 30 papers in internationally recognized journals and conferences. His current research interests include system design, image reconstruction, and processing for radiological imaging device.
Dr. Hu has been invited to review top journals and conferences in medical imaging over 20 times.
 Raymond F. Muzic, Jr. (M'90–SM'00) received the Ph.D. degree from Case Western Reserve University, Cleveland, OH, USA, in 1991.
Raymond F. Muzic, Jr. (M'90–SM'00) received the Ph.D. degree from Case Western Reserve University, Cleveland, OH, USA, in 1991.
He is currently an Associate Professor of Radiology, Biomedical Engineering, and General Medical Sciences–Oncology with Case Western Reserve University. He has also had the pleasure of serving as an Advisor for Ph.D. students. He has authored or coauthored approximately 50 peer-reviewed articles. His current research interests include development and application of quantitative methods for medical imaging.
Dr. Muzic has led or been a Team Member on numerous funded research projects.
Footnotes
Contributor Information
Pengjiang Qian, School of Digital Media, Jiangnan University, Wuxi 214122, China.
Yizhang Jiang, School of Digital Media, Jiangnan University, Wuxi 214122, China.
Shitong Wang, School of Digital Media, Jiangnan University, Wuxi 214122, China.
Kuan-Hao Su, Case Center for Imaging Research, Department of Radiology, University Hospitals, Case Western Reserve University, Cleveland, OH 44106 USA.
Jun Wang, School of Mechanical Engineering, Jiangnan University, Wuxi 214122, China (wangj_1982@jiangnan.edu.cn)..
Lingzhi Hu, Philips Electronics North America, Highland Heights, OH 44143 USA (hlingzhi@gmail.com)..
Raymond F. Muzic, Jr., Case Center for Imaging Research, Department of Radiology, University Hospitals, Case Western Reserve University, Cleveland, OH 44106 USA.
REFERENCES
- 1.Höppner F, Klawonn F, Kruse R, Runkler T. Fuzzy Cluster Analysis: Methods for Classification, Data Analysis and Image Recognition. Wiley; New York, NY, USA: 1999. [Google Scholar]
- 2.Bezdek JC, Hathaway RJ. Numerical convergence and interpretation of the fuzzy c-shells clustering algorithm. IEEE Trans. Neural Netw. 1992 Sep;3(5):787–793. doi: 10.1109/72.159067. [DOI] [PubMed] [Google Scholar]
- 3.Wu K-L, Yu J, Yang M-S. A novel fuzzy clustering algorithm based on a fuzzy scatter matrix with optimality tests. Pattern Recognit. Lett. 2005;26(5):639–652. [Google Scholar]
- 4.Heller KA, Ghahramani Z. Bayesian hierarchical clustering. Proc. 22th Int. Conf. Mach. Learn.; Bonn, Germany. Aug. 2005.pp. 297–304. [Google Scholar]
- 5.Guha S, Rastogi R, Shim K. CURE: An efficient clustering algorithm for large databases. Proc. ACM SIGMOD Int. Conf. Manage. Data; Seattle, WA, USA. Jun. 1998.pp. 73–84. [Google Scholar]
- 6.Yu SX, Shi J. Multiclass spectral clustering. Proc. 9th IEEE Int. Conf. Comput. Vis.; Nice, France. Oct. 2003.pp. 313–319. [Google Scholar]
- 7.Shi J, Malik J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000 Aug;22(8):888–905. [Google Scholar]
- 8.Han J, Kamber M. Data Mining: Concepts and Techniques. Academic; San Francisco, CA, USA: 2006. [Google Scholar]
- 9.Hendrickson B, Leland R. An improved spectral graph partitioning algorithm for mapping parallel computations. SIAM J. Sci. Comput. 1995;16(2):452–469. [Google Scholar]
- 10.Yu SX, Shi J. Segmentation given partial grouping constraints. IEEE Trans. Pattern Anal. Mach. Intell. 2004 Feb;26(2):173–183. doi: 10.1109/tpami.2004.1262179. [DOI] [PubMed] [Google Scholar]
- 11.Wu Z, Leahy R. An optimal graph theoretic approach to data clustering: Theory and its application to image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 1993 Nov;15(11):1101–1113. [Google Scholar]
- 12.Hagen L, Kahng AB. New spectral methods for ratio cut partitioning and clustering. IEEE Trans. Comput.-Aided Design Integr. Circuits Syst. 1992 Sep;11(9):1074–1085. [Google Scholar]
- 13.Sarkar S, Soundararajan P. Supervised learning of large perceptual organization: Graph spectral partitioning and learning automata. IEEE Trans. Pattern Anal. Mach. Intell. 2000 May;22(5):504–525. [Google Scholar]
- 14.Ding CHQ, He X, Zha H, Gu M, Simon HD. A min-max cut algorithm for graph partitioning and data clustering. Proc. IEEE Int. Conf. Data Mining; San Jose, CA, USA. Nov./Dec. 2001.pp. 107–114. [Google Scholar]
- 15.Wang Y, Jiang Y, Wu Y, Zhou Z-H. Spectral clustering on multiple manifolds. IEEE Trans. Neural Netw. 2011 Jul;22(7):1149–1161. doi: 10.1109/TNN.2011.2147798. [DOI] [PubMed] [Google Scholar]
- 16.Qian P, Chung F-L, Wang S, Deng Z. Fast graph-based relaxed clustering for large data sets using minimal enclosing ball. IEEE Trans. Syst., Man, Cybern. B, Cybern. 2012 Jun;42(3):672–687. doi: 10.1109/TSMCB.2011.2172604. [DOI] [PubMed] [Google Scholar]
- 17.Dhillon IS, Guan Y, Kulis B. Weighted graph cuts without eigenvectors: A multilevel approach. IEEE Trans. Pattern Anal. Mach. Intell. 2007 Nov;29(11):1944–1957. doi: 10.1109/TPAMI.2007.1115. [DOI] [PubMed] [Google Scholar]
- 18.von Luxburg U. A tutorial on spectral clustering. Statist. Comput. 2007;17(4):395–416. [Google Scholar]
- 19.Kamvar SD, Klein D, Manning CD. Spectral learning. Proc. 18th Int. Joint Conf. Artif. Intell., Acapulco, Mexico. 2003 Aug;:561–566. [Google Scholar]
- 20.Chung FRK. Spectral Graph Theory. AMS; Providence, RI, USA: 1997. [Google Scholar]
- 21.Ng AY, Jordan MI, Weiss Y. On spectral clustering: Analysis and an algorithm. Proc. Conf. Adv. Neural Inf. Process. Syst.; Vancouver, BC, Canada. Dec. 2001.pp. 849–856. [Google Scholar]
- 22.Ning H, Xu W, Chi Y, Gong Y, Huang TS. Incremental spectral clustering by efficiently updating the eigen-system. Pattern Recognit. 2010;43(1):113–127. [Google Scholar]
- 23.Zhu X, Ghahramani Z, Lafferty J. Semi-supervised learning using Gaussian fields and harmonic functions. Proc. 20th Int. Conf. Mach. Learn.; Washington, DC, USA. Aug. 2003.pp. 912–919. [Google Scholar]
- 24.Caruana R. Multitask learning. Mach. Learn. 1997;28(1):41–75. [Google Scholar]
- 25.Jiang Y, Chung F-L, Wang S, Deng Z, Wang J, Qian P. Collaborative fuzzy clustering from multiple weighted views. IEEE Trans. Cybern. 2015 Apr;45(4):688–701. doi: 10.1109/TCYB.2014.2334595. [DOI] [PubMed] [Google Scholar]
- 26.Dhillon IS, Mallela S, Modha DS. Information-theoretic co-clustering. Proc. 9th ACM SIGKDD Int. Conf. Knowl. Discovery Data Mining; Washington, DC, USA. Aug. 2003.pp. 89–98. [Google Scholar]
- 27.Pan SJ, Yang Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010 Oct;22(10):1345–1359. [Google Scholar]
- 28.Nie F, Xu D, Li X. Initialization independent clustering with actively self-training method. IEEE Trans. Syst., Man, Cybern. B, Cybern. 2012 Feb;42(1):17–27. doi: 10.1109/TSMCB.2011.2161607. [DOI] [PubMed] [Google Scholar]
- 29.Wacquet G, Poisson-Caillault É, Hébert P-A. Computational Intelligence. Vol. 465. Springer; Berlin, Germany: 2013. Semi-supervised K-way spectral clustering with determination of number of clusters; pp. 317–332. [Google Scholar]
- 30.Kawale J, Boley D. Constrained spectral clustering using L1 regularization. Proc. SIAM Int. Conf. Data Mining; Austin, TX, USA. May 2013.pp. 103–111. [Google Scholar]
- 31.Wang X, Davidson I. Flexible constrained spectral clustering. Proc. 16th ACM SIGKDD Int. Conf. Knowl. Discovery Data Mining; Washington, DC, USA. Jul. 2010.pp. 563–572. [Google Scholar]
- 32.Zeng H, Cheung Y-M. Semi-supervised maximum margin clustering with pairwise constraints. IEEE Trans. Knowl. Data Eng. 2012 May;24(5):926–939. [Google Scholar]
- 33.Rangapuram SS, Hein M. Constrained 1-spectral clustering. Proc. 15th Int. Conf. Artif. Intell. Statist.; La Palma, Spain. Apr. 2012.pp. 1143–1151. [Google Scholar]
- 34.Lu Z, Carreira-Perpinan MA. Constrained spectral clustering through affinity propagation. Proc. IEEE Conf. Comput. Vis. Pattern Recognit.; Anchorage, AK, USA. Jun. 2008.pp. 1–8. [Google Scholar]
- 35.Breitenbach M, Grudic GZ. Clustering through ranking on manifolds. Proc. 22nd Int. Conf. Mach. Learn.; Bonn, Germany. Aug. 2005.pp. 73–80. [Google Scholar]
- 36.Jiang WH, Chung F-L. Machine Learning and Knowledge Discovery in Databases (Lecture Notes in Computer Science) Vol. 7524. Springer; Berlin, Germany: 2012. Transfer spectral clustering; pp. 789–803. [Google Scholar]
- 37.Gu Q, Li Z, Han J. Learning a kernel for multi-task clustering. Proc. 25th AAAI Conf. Artif. Intell.; San Francisco, CA, USA. Aug. 2011.pp. 368–373. [Google Scholar]
- 38.Kumar A, Rai P, Daumé H., III Co-regularized multi-view spectral clustering. Proc. 25th Annu. Conf. Neural Inf. Process. Syst.; Granada, Spain. Dec. 2011.pp. 1413–1421. [Google Scholar]
- 39.Shi X, Fan W, Yu PS. Efficient semi-supervised spectral co-clustering with constraints. Proc. IEEE 10th Int. Conf. Data Mining; Sydney, NSW, Australia. Dec. 2010.pp. 1043–1048. [Google Scholar]
- 40.Givoni IE, Frey BJ. Semi-supervised affinity propagation with instance-level constraints. Proc. 12th Int. Conf. Artif. Intell. Statist.; Clearwater Beach, FL, USA. Apr. 2009.pp. 161–168. [Google Scholar]
- 41.Surhone LM, Timpledon MT, Marseken SF, editors. Rayleigh Quotient: Mathematics, Hermitian Matrix, Conjugate Transpose, Eigenvalue, Eigenvector and Eigenspace, Min-Max Theorem, Rayleigh Quotient Iteration, Numerical Range, Euclidean Vector. Betascript Press; Saarland, Germany: 2010. [Google Scholar]
- 42.Liu S-T, Luo X-L. A method based on Rayleigh quotient gradient flow for extreme and interior eigenvalue problems. Linear Algebra Appl. 2010;432(7):1851–1863. [Google Scholar]
- 43.Liu J, Mohammed J, Carter J, Ranka S, Kahveci T, Baudis M. Distance-based clustering of CGH data. Bioinformatics. 2006;22(16):1971–1978. doi: 10.1093/bioinformatics/btl185. [DOI] [PubMed] [Google Scholar]
- 44.Desgraupes B. Clustering Indices. Apr, 2010. [Online]. Available: https://cran.r-project.org/web/packages/clusterCrit/vignettes/clusterCrit.pdf.
- 45.McCallum AK. Bow: A Toolkit for Statistical Language Modeling, Text Retrieval, Classification and Clustering. [Online] Sep, 1998. Available: http://www.cs.cmu.edu/~mccallum/bow.