Abstract
Here I analyze the observed and projected surface temperature anomalies over land between 50°S-50°N for the period 1950–2099 by large-scale ecoregion and find strongest warming consistently and persistently seen over driest ecoregions such as the Sahara desert and the Arabian Peninsula during various 30-year periods, pointing to desert amplification in a warming climate. This amplification enhances linearly with the global mean greenhouse gases(GHGs) radiative forcing and is attributable primarily to a stronger GHGs-enhanced downward longwave radiation forcing reaching the surface over drier ecoregions as a consequence of a warmer and thus moister atmosphere in response to increasing GHGs. These results indicate that desert amplification may represent a fundamental pattern of global warming associated with water vapor feedbacks over land in low- and mid- latitudes where surface warming rates depend inversely on ecosystem dryness. It is likely that desert amplification might involve two types of water vapor feedbacks that maximize respectively in the tropical upper troposphere and near the surface over deserts, with both being very dry and thus extremely sensitive to changes of water vapor.
The observed global mean surface temperature has increased by 0.85 °C for the period 1880–2012 and this warming has been attributed mostly to the increase in anthropogenic greenhouse gases(GHGs) in the atmosphere1. Global coupled atmosphere-ocean general circulation models(AOGCMs) driven by a set of scenarios of anthropogenic forcings, Representative Concentration Pathways(RCPs), project a further warming up to 4.8 °C for 2081–2100 relative to 1986–20051. Observational and model studies of temperature change, climate feedbacks and variations in the Earth’s energy budget together provide confidence in the magnitude of global warming in response to past and future forcing1.
The positive GHGs-induced radiative forcing is global-scale but can be amplified or dampened by various atmospheric and terrestrial feedbacks2,3. Over land, evapotranspiration(ET) is a primary process driving energy and water exchanges in the interface of hydrosphere, atmosphere and biosphere4. It can largely weaken this positive forcing and thus determine spatial patterns of surface warming among different ecosystems. After analyzing observed land surface air temperature trends in low- and mid- latitudes for the period 1979–2012, Zhou et al.5 found a spatial dependence of observed surface warming on terrestrial dryness, with the strongest warming rate seen over the driest ecoregions such as the Sahara desert and the Arabian Peninsula, suggesting a warming amplification mechanism over deserts(i.e., desert amplification). Based on a comprehensive analysis of observations, reanalysis data and historical simulations for the period 1979–2012, Zhou et al.6 proposed that desert amplification may result mainly from stronger GHGs-enhanced downward longwave radiation reaching the surface associated with water vapor feedbacks over drier ecoregions, rather from land surface processes as the deserts have too limited amounts of vegetation and soil moisture(SM) to influence ET. This finding, if true, has important implications for understanding climate sensitivity to anthropogenic forcings, uncovering mechanisms of spatiotemporal patterns of climate change, and assessing climatic impacts6.
However, desert amplification was proposed based on the analysis of only 34 years of data(1979–2012), which are too short to detect a climate signal and particularly overlap with the global warming hiatus1. Furthermore, simple linear trends were calculated to estimate the warming rates and the linear trend for a short time series depends strongly on the choice of the beginning and end points of data. This raises an important question of whether this amplification is a true long-term signal of global warming or simply short-term climate variability for the period 1979–2012. Here I analyze observational temperatures and historical and projected simulations of 26 AOGCMs (Table S1) over land for the period 1950–2099 (see Method for detail) to further this amplification at longer time scales. Unlike the previous studies6,7 which estimated the linear trends and analyzed primarily land surface variables, different 30-year average anomalies relative to the same reference period 1961–1990 are used to quantify the warming magnitude over different periods and atmospheric profiles are also examined to further the linkage between water vapor and the amplification.
The observations (OBS) are obtained from the ensemble mean of three widely used surface air temperature datasets for the period 1950–2013. There are two groups of historical simulations for the period 1950–2005: one with both anthropogenic and natural forcings (referred to as ALL) and the other with only natural forcings (referred to as NAT). For the projected climate from 2006 to 2099, the simulations under RCP45 and RCP85 are used. These two pathways represent contrasting mitigation efforts between a concerted rapid CO2 mitigation and a ‘business-as-usual’ scenario (CO2 concentrations could increase to 538 and 936 ppm by 2100, according to RCP45 and RCP85, respectively)7. As averaging over multiple members enhances the forcing signal and reduces noise from internal variability and errors from individual models1, I simply average available simulations to obtain the multi-model ensemble mean for the period 1950–2099.
I calculate the 9-month (March-November) mean anomalies of observations and CMIP5 simulations relative to the reference period 1961–1990 for every year, and then average the anomalies into five 30-year periods: 1950–1979, 1980–2009, 2010–2039, 2040–2069, and 2070–2099. My primary focus is long-term temperature anomalies and so a fixed reference period makes the comparison of the anomalies consistent over time. A satellite-measured vegetation greenness index, enhanced vegetation index (EVI)8 for the period 2000–2013, is aggregated to create the 9-month mean climatology of EVI. EVI largely reflects the geographical distribution of amount of vegetation and SM and thus ET at large scales9,10. The latitudinal zones beyond 50 °N and 50 °S and three winter months (DJF) are excluded because polar amplification and albedo feedbacks dominate the high-latitude surface warming5,6. My study region (50°N-50°S) consists of 1538 land grid boxes. For simplicity, I refer to several mostly used variables, surface air temperature, surface air specific humidity, surface downward longwave radiation, surface downward shortwave radiation, surface upward longwave radiation, total atmospheric water vapor content, atmospheric air temperature and specific humidity as T2m, q2m, DLR, DSR, ULR, TAWV, T and q, respectively.
Desert amplification by large-scale ecoregion
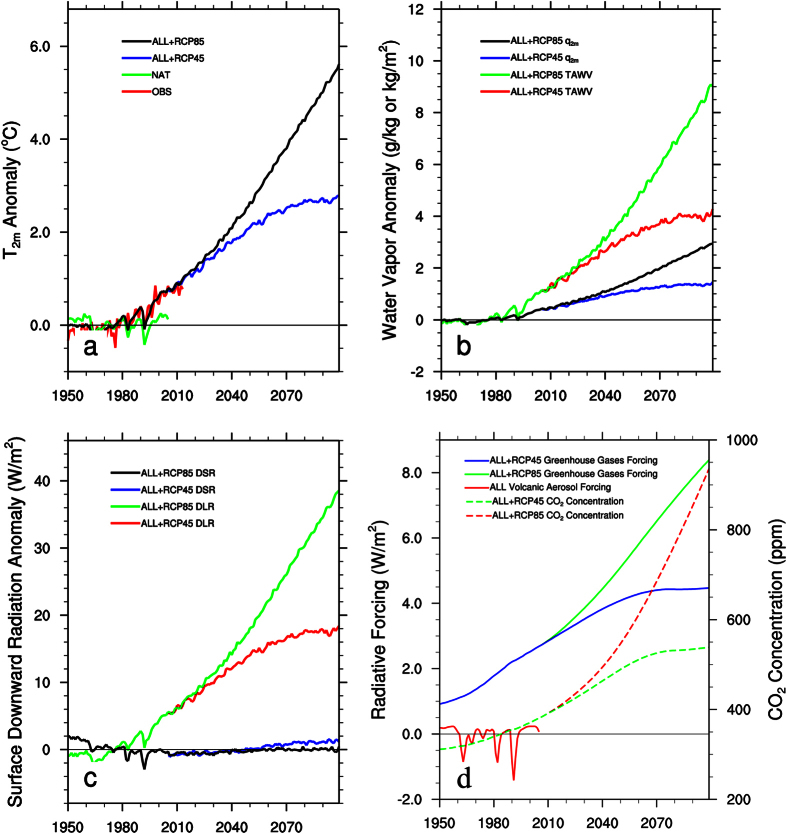
Figure 1a shows the regional mean T2m anomalies for the period 1950–2099 over the entire study region. OBS shows strong interannual variability in 1950–1979 but a persistent warming trend thereafter. ALL generally reproduces the observed warming with a slightly smaller magnitude and also captures the large-scale cooling associated with volcanic eruptions on shorter time scales1 (Fig. 1d). NAT simulates this short-term variability but exhibits no apparent warming trend. The projected T2m increases persistently and is 2.8 and 5.6 °C warmer in 2099 than the 1961–1990 averages under RCP45 and RCP85, respectively.
Figure 1. Interannual variations in regional mean March-November anomalies averaged over the entire study region, relative to the 1961–1990 reference period, of surface air temperature (T2m, °C), surface specific humidity (q2m, g/kg), total atmospheric water vapor (TAWV, kg/m2), downward longwave radiation (DLR, W/m2) and downward shortwave radiation (DSR, W/m2) at the surface from observations (OBS) for 1950–2013 and simulations (ALL, NAT, RCP45 and RCP85) for 1950–2099, together with the corresponding total global mean greenhouse gases and volcanic aerosol radiative forcing (W/m2) and atmospheric CO2 concentration (ppm) provided in Meinshausenet al.7.
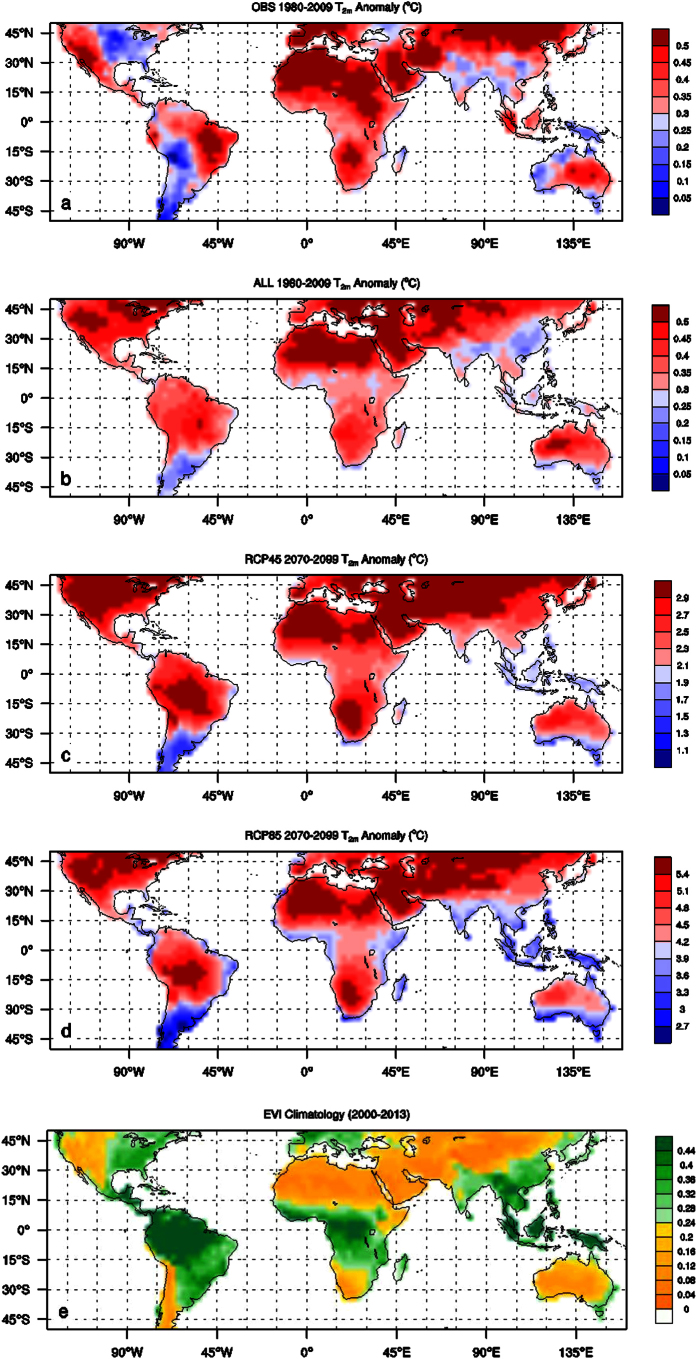
Figure 2 shows spatial patterns of 30-year mean T2m anomalies for two periods: 1980–2009 and 2070–2099, together with the climatology of EVI. The observed and projected T2m increases everywhere relative to the reference period 1961–1990 and the strongest warming occurs mostly in arid and semi-arid regions such as Northern Africa, Middle East, Northern Asia, and western U.S. Noticeable regional warming is also observed or projected over several non-dry regions such as southern Amazon, Europe, and eastern U.S., likely related to decreased SM11 or dynamical processes linked to changes in circulation and sea surface temperature patterns5,6. Although the warming rate increases with time and is stronger in RCP85 than RCP45, OBS and projections exhibit spatial patterns of T2m anomalies that are similar to those projected for the later 21st century and are highly correlated with EVI, with a spatial correlation ranging from −0.42 to −0.45 (p < 0.001, n = 1538). Note that T2m is not a linear function of EVI. Overall the warming is generally strongest over the driest or least vegetated ecoregions such as the Sahara desert and the Arabian Peninsula.
Figure 2.
Spatial patterns of 30-year mean surface air temperature anomalies (T2m, °C) relative to the 1961–1990 averages for two periods: (a) OBS 1980–2009, (b) ALL 1980–2009, (c) RCP45 2070–2099, and (d) RCP85 2070–2099, and (e) spatial patterns of climatological EVI (unitless) for the period 2000–2013, in 2.5° × 2.5° grid boxes over land. Map was created using CISL’s NCAR Command Language (NCL) (https://www.ncl.ucar.edu/) Version 6.0.0.
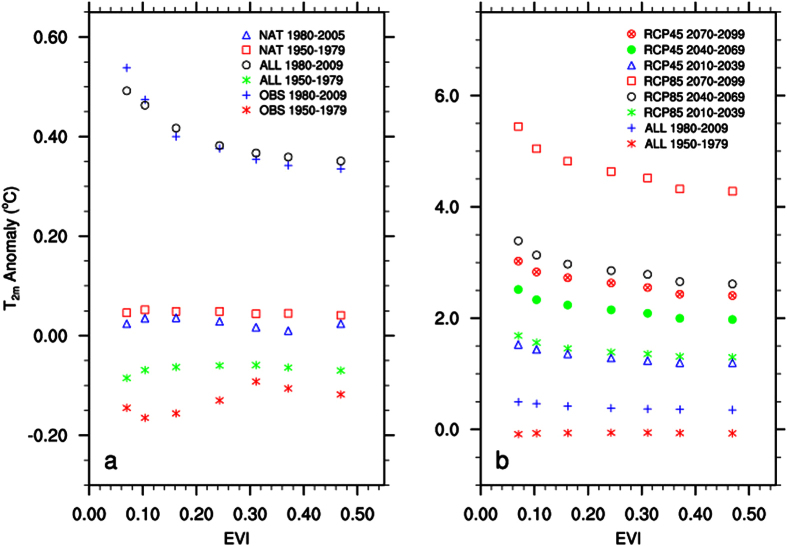
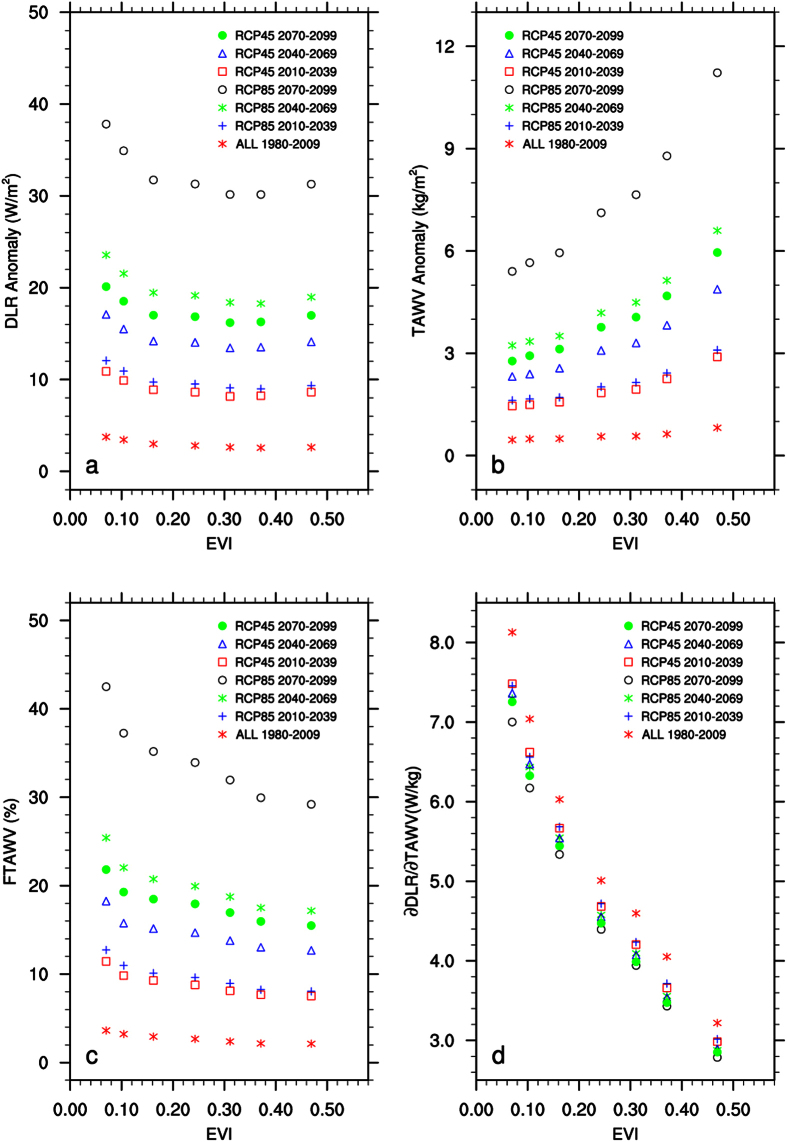
To minimize data noise and variability at small scales, I classify the study region into 7 large-scale ecoregions from barren deserts to dense rainforests based on the climatological EVI values, and then analyze how the 30-year mean T2m anomalies vary as a function of EVI by ecoregion via least squares fitting (Fig. 3; Fig. S1). Evidently, the warming rate depends strongly on ecoregions and increases dramatically with decreasing EVI. Four regression lines (exponential, linear, logarithmic, and power) are fit between T2m and EVI over different 30-year periods, all consistently showing the largest warming over the driest ecoregions for the period after 1980s (Fig. S1). The goodness of fit (R2) measures the fraction of data variations captured by the fit. Among the four regressions, the power and logarithmic are comparable and have the highest R2 (Fig. S1), which are consistent with previous findings for the period 1979-20125,6. For example, the R2 value for the logarithmic (power) fit is 96% (97%) in OBS 1980–2009, 98% (98%) in ALL 1980–2009, and 98% (98%) in RCP85 2070–2099 in the case of 7 ecoregions (Fig. S1). The corresponding R2 value for the linear (exponential) fit is 79% (84%) in OBS 1980–2009, 86% (88%) in ALL 1980–2009, and 88% (90%) in RCP85 2070–2099. To examine whether the T2m-EVI relationship depends on how the ecoregions are classified, I perform the same fitting by considering 14, 21, 28, and 35 ecoregion (Fig. S1; Table 1). All results show consistently that the negative power and logarithmic fits capture well the T2m-EVI relationship by large-scale ecoregion in both OBS and different periods of CMIP5 projection. When more ecoregions are considered, R2 decreases because more small-scale factors affect the spatial variations of T2m. Nevertheless, during each 30-year period the fitted coefficients (C0 and A0) remain stable independent of the number of ecoregions classified – indicating that the fitted T2m-EVI relationship remains robust.
Figure 3. Relationship between 30-year mean surface air temperature anomalies (T2m, °C) relative to the 1961–1990 averages and the climatological EVI by large-scale ecoregion for different periods from 1950 to 2099.
Here only the results for 7 ecoregions are shown.
Table 1. Fitted coefficients and goodness of fit (R2) of the logarithmic and power functions between 30-year mean T2m anomalies (°C) and the climatological EVI by large-scale ecoregion for four different periods from 1980–2099.
| Ecoregions | T2m = A0*ln(EVI)+C0 | T2m = C0*(EVI)A0 | T2m = A0*ln(EVI)+C0 | T2m = C0*(EVI)A0 |
|---|---|---|---|---|
| R2 (C0, A0) | R2 (C0, A0) | R2 (C0, A0) | R2 (C0, A0) | |
| OBS (1980–2009) | ALL (1980–2009) | |||
| 7 | 0.95(0.23, −0.11) | 0.97(0.27, −0.25) | 0.98(0.29, −0.07) | 0.98(0.30, −0.18) |
| 14 | 0.91(0.23, −0.11) | 0.93(0.27, −0.25) | 0.94(0.29, −0.07) | 0.93(0.30, −0.18) |
| 21 | 0.89(0.24, −0.10) | 0.91(0.27, −0.25) | 0.91(0.29, −0.07) | 0.91(0.30,−0.17) |
| 28 | 0.86(0.24, −0.10) | 0.88(0.27, −0.25) | 0.89(0.29, −0.07) | 0.88(0.30, −0.17) |
| 35 | 0.84(0.24, −0.10) | 0.86(0.27, −0.25) | 0.86(0.29, −0.07) | 0.85(0.30, −0.17) |
| RCP85 (2010–2039) | RCP45 (2010–2039) | |||
| 7 | 0.97(1.12, −0.20) | 0.98(1.15, −0.14) | 0.99(1.03, −0.18) | 0.99(1.06, −0.13) |
| 14 | 0.90(1.12, −0.20) | 0.89(1.15, −0.14) | 0.92(1.03, −0.18) | 0.91(1.06, −0.13) |
| 21 | 0.85(1.12, −0.20) | 0.85(1.15, −0.14) | 0.89(1.04, −0.18) | 0.88(1.06, −0.13) |
| 28 | 0.82(1.12, −0.20) | 0.82(1.15, −0.14) | 0.85(1.04, −0.18) | 0.84(1.06, −0.13) |
| 35 | 0.79(1.12, −0.20) | 0.78(1.15, −0.14) | 0.82(1.04, −0.18) | 0.81(1.06, −0.13) |
| RCP85 (2040–2069) | RCP45 (2040–2069) | |||
| 7 | 0.98(2.30, −0.39) | 0.99(2.36, −0.13) | 0.98(1.75, −0.27) | 0.98(1.79, −0.12) |
| 14 | 0.92(2.29, −0.39) | 0.91(2.36, −0.13) | 0.91(1.75, −0.28) | 0.90(1.79, −0.12) |
| 21 | 0.89(2.30, −0.39) | 0.88(2.36, −0.13) | 0.88(1.75, −0.27) | 0.87(1.79, −0.12) |
| 28 | 0.85(2.30, −0.39) | 0.84(2.36, −0.13) | 0.84(1.75, −0.27) | 0.83(1.79, −0.12) |
| 35 | 0.83(2.30, −0.39) | 0.82(2.36, −0.13) | 0.82(1.75, −0.27) | 0.81(1.79, −0.12) |
| RCP85 (2070–2099) | RCP45 (2070–2099) | |||
| 7 | 0.98(3.79, −0.59) | 0.98(3.87, −0.12) | 0.98(2.16, −0.32) | 0.98(2.20, −0.12) |
| 14 | 0.92(3.78, −0.59) | 0.91(3.87, −0.12) | 0.91(2.15, −0.32) | 0.90(2.20, −0.12) |
| 21 | 0.89(3.79, −0.59) | 0.88(3.87, −0.12) | 0.88(2.16, −0.32) | 0.87(2.20, −0.12) |
| 28 | 0.85(3.79, −0.59) | 0.84(3.87, −0.12) | 0.84(2.16, −0.32) | 0.83(2.20, −0.12) |
| 35 | 0.83(3.79, −0.59) | 0.82(3.87, −0.12) | 0.81(2.16, −0.32) | 0.80(2.20, −0.12) |
Overall the negative power and logarithmic fit describes well the T2m-EVI relationship by ecoregion in both OBS and projected climate, indicating the strongest warming over the driest ecoregions. ALL generally reproduces the observed features of regional mean T2m anomalies (Fig. 1a), spatial patterns of 30-year mean T2m anomalies (Fig. 2b), and the spatial dependence of warming on EVI by ecoregion (Fig. 3a; Fig. S1; Table 1). It has slightly weaker warming rates and smaller interannual variability than OBS, which is expected as the multi-model ensemble mean represents primarily the forced signal of GHGs1.
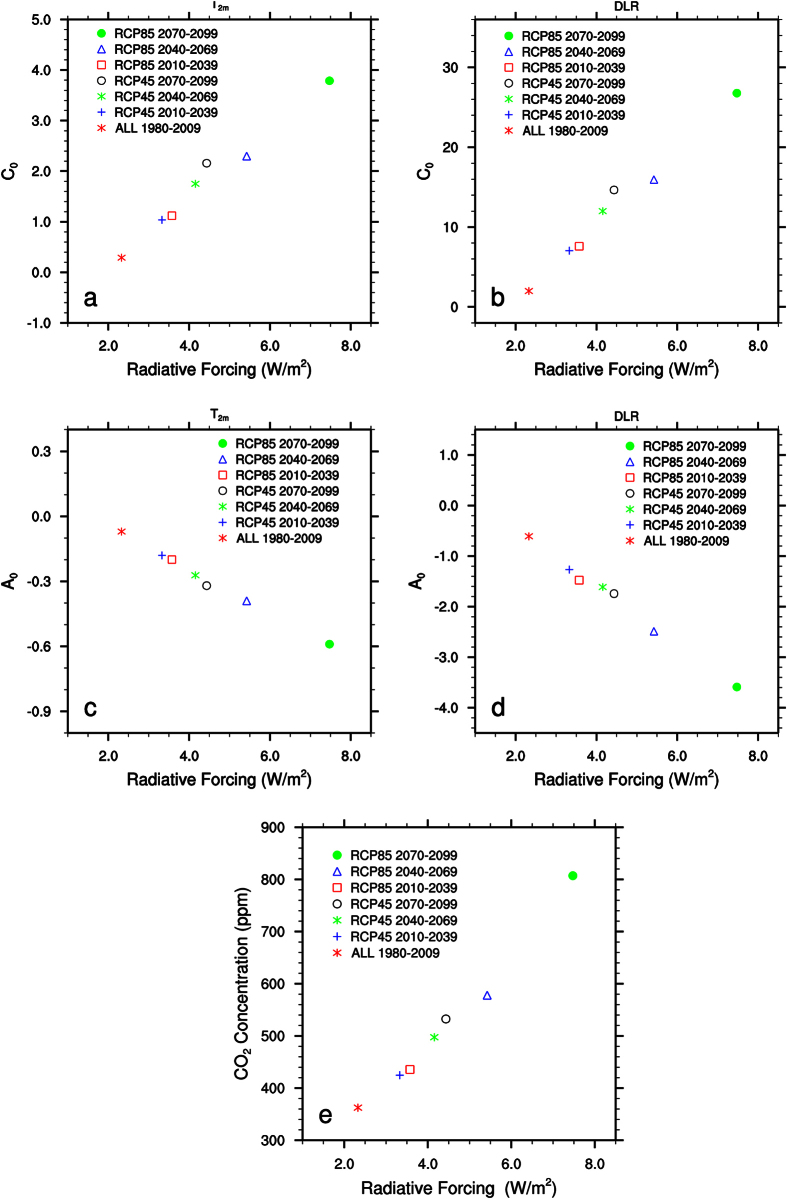
For the power, T2m = C0*(EVI)A0, and logarithmic, T2m = A0*ln(EVI)+C0, function, C0 is the T2m anomaly for EVI = 1, which approximates the warming rate for dense rainforests. The negative scaling factor, A0, represents the growth rate of warming from the rainforests to dry deserts, i.e., the magnitude of desert amplification. Mathematically the negative power and logarithmic fits exhibit the almost identical T2m-EVI relationship within the valid range of EVI. Interestingly, the magnitude of fitted coefficients for T2m (C0 and A0) both increases linearly with the global mean GHGs radiative forcing from 1950 to 2099 (Fig. 4a,c), meaning that not only the warming rate over humid rainforests becomes stronger with time, but also the magnitude of desert amplification becomes larger. These results consistently indicate that desert amplification is a persistent signal in a warming climate and it intensifies with the radiative forcing associated with increased GHGs.
Figure 4.
Scatter plots of fitted coefficients (C0 and A0 for the logarithmic fit of T2m and DLR) and atmospheric CO2 concentration as a function of the global mean GHGs radiative forcing (W/m2, Fig. 1d) for different 30-year periods: (a) C0 for surface air temperature anomalies (T2m, °C), (b) C0 for surface downward longwave radiation (DLR, W/m2), (c) A0 for T2m, (d) A0 for DLR, and (e) atmospheric CO2 concentration (ppm). For each period, the arithmetic mean fitted coefficients are obtained from Tables 1, 2.
Changes in surface radiation and energy budget
To understand the above warming patterns, I first examine the changes in surface radiative and non-radiative fluxes (DLR, DSR, ULR, upward solar radiation, net shortwave and longwave radiation, latent and sensible heat). Zhou et al.6 performed a comprehensive analysis of observations, reanalysis and CMIP5 data from this perspective for the period 1979–2012. They found that GHGs-enhanced DLR is the primary driver for desert amplification, while ecosystem feedbacks associated with SM and vegetation play a secondary role. I perform the same analyses for different 30 periods and obtain similar results, some of which are briefly summarized below.
The warming rate of T2m depends on surface radiative forcing2,3,4,12. Figure 1c shows the regional mean anomalies of DLR and DSR over the study region for the period 1950–2099. DLR displays a persistent increasing trend, while DSR varies slightly after 1991 between −0.8 and +1.1 W/m2. The DLR anomaly reaches 18.4 W/m2 under RCP45 and 38.6 W/m2 under RCP85 in 2099, which are substantially larger than the DSR anomalies. DLR is slightly higher in clear-sky than all-sky while the opposite is true for DSR, due to a small decreasing trend in total cloud cover (Fig. S2). Hence the positive DLR anomalies should dominate the surface radiative forcing, while the DSR forcing is small and has a secondary effect.
The warming rate of T2m also depends on land surface properties and ecosystem feedbacks in response to the surface radiative forcing, particularly upward shortwave and longwave radiation and the partitioning of net radiation between sensible and latent heat4,12. Figure S2 show the regional mean anomalies of related surface fluxes over the study region for the period 1950–2099. ULR displays similar but slightly smaller anomalies than DLR, reaching 16.5 W/m2 under RCP45 and 34.1 W/m2 under RCP85 in 2099, while the upward shortwave radiation decreases slightly by 0.8 W/m2 under RCP45 and 1.0 W/m2 under RCP85 in 2099. The surface latent heat increases slightly with time after 1980s and its anomaly in 2099 is 1.0 W/m2 under RCP45 and 1.7 W/m2 under RCP85. The sensible heat shows similar but slightly larger increases, reaching 2.2 W/m2 and 4.8 W/m2 under RCP45 and RCP85 in 2099, respectively.
I then perform similar analyses as done above for T2m to each of the surface fluxes but can only identify two variables (DLR and ULR) showing features similar to T2m at both the grid and ecoregion level (Figs 5, S3 and S4). Note that DLR and ULR resemble T2m because DLR is the primary radiative forcing for surface warming while ULR is mainly a consequence of the warming following the Stefan–Boltzmann law. Compared to other ecoregions, deserts are least opaque to thermal infrared radiation due to least amounts of water vapor and cloud cover in the atmosphere and thus are most effective in emitting terrestrial radiation to space. Consequently, the DLR anomalies are mostly balanced by the ULR anomalies over the driest ecoregions. I also analyze interannual variations of cloud and precipitation anomalies and their spatial dependences on EVI but cannot identify any statistical meaningful relationship with the warming patterns.
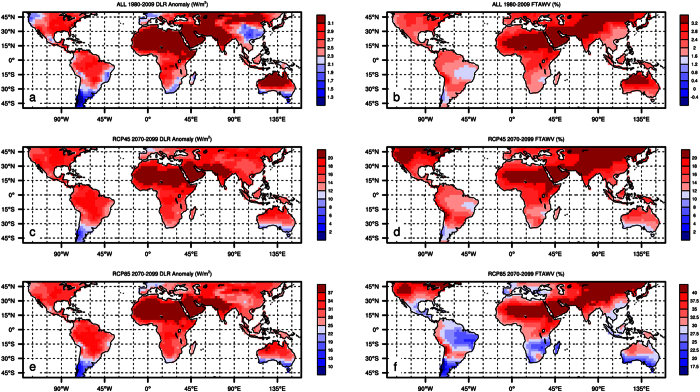
Figure 5.
Spatial patterns of 30-year mean anomalies, relative to the 1961–1990 averages, of surface downward longwave radiation (DLR, W/m2) for (a) ALL 1980–2009, (c) RCP45 2070–2099, and (e) RCP85 2070–2099, and fractional changes in total atmospheric water vapor content (FTAWV, %) for (b) ALL 1980–2009, (d) RCP45 2070–2099, and (f) RCP85 2070–2099. Map was created using CISL’s NCAR Command Language (NCL) (https://www.ncl.ucar.edu/) Version 6.0.0.
For a given forcing, land surface warms less due to more evaporative cooling via ET over ecoregions with more SM and vegetation13. However, desert amplification is most evident over the driest ecoregions where SM and vegetation are too limited to have a noticeable impact on ET6. Furthermore, the Bowen ratio, which is controlled by vegetation and SM, decreases slightly over deserts, with time during different 30-year periods (Fig. S5), indicating its limited role in controlling the surface warming patterns. Again these results suggest that DLR is the primary radiative forcing for desert amplification, while other processes related to SM and vegetation play a secondary role.
Strong coupling between DLR and atmospheric water vapor content
Radiative forcing due to increasing GHGs drives much of long-term climate change2,3 and increasing TAWV is closely linked to surface and tropospheric warming5,6,14,15,16. As DLR depends strongly on near surface humidity and temperature17,18, next I examine its associations with T2m, TAWV and q2m. Because most of TAWV is confined near the surface, the changes in TAWV and q2m are very similar at both grid and ecoregion levels. Hence most of my results are shown for TAWV for brevity. TAWV and q2m display a persistent increasing trend along with DLR over the study region for the period 1950–2099 (Fig. 1b). The temporal increases in T2m, TWAV, q2m and DLR resemble these in the global mean GHGs radiative forcing and the atmospheric CO2 concentration under RCP45 and RCP85 (Fig. 1d). Hence, the positive DLR forcing associated with enhanced GHGs, particularly water vapor, should primarily determine the observed and projected large-scale warming patterns.
Scatter plots of CMIP5 data (Fig. S6) clearly demonstrate a power function of DLR on TAWV as shown in previous studies6,19,20,21, DLR = C0*(TAWV)0.25, where C0 varies 156–165 W/m2 among different periods. This function is evident in NAT, ALL, RCP45 and RCP85 despite their differences in atmospheric CO2 concentration. Note that the greenhouse effect is roughly proportional to changes in the logarithm of the GHGs concentration14,15,16. The derivative of DLR versus TAWV (∂DLR/∂TAWV) resemble a negative power (or logarithmic) function (Table 2), indicating that for a unit amount of TAWV increase, the largest efficiency in increasing DLR will occur over the driest regions with the least TAWV. Therefore, the negative power and logarithmic T2m-EVI relationships shown above may result from a warmer and moister atmosphere with increasing GHGs. This can be tested next by analyzing the collective changes in DLR, q2m, TAWV, and T2m.
Table 2. Fitted coefficients and goodness of fit (R2) of the logarithmic and power functions between 30-year mean surface DLR anomalies (W/m2) and the climatological EVI by large-scale ecoregion for four different periods from 1980–2099.
| Ecoregions | DLR = A0*ln(EVI)+C0 | DLR = C0*(EVI)A0 | DLR = A0*ln(EVI)+C0 | DLR = C0*(EVI)A0 |
|---|---|---|---|---|
| R2 (C0, A0) | R2 (C0, A0) | R2 (C0, A0) | R2 (C0, A0) | |
| OBS (1980–2009) | ALL (1980–2009) | |||
| 7 | 0.94(1.97, −0.63) | 0.95(2.12, −0.20) | ||
| 14 | 0.88(1.99, −0.61) | 0.89(2.13, −0.20) | ||
| 21 | 0.85(2.00, −0.61) | 0.86(2.14, −0.20) | ||
| 28 | 0.82(2.00, −0.60) | 0.84(2.15, −0.19) | ||
| 35 | 0.80(2.01, −0.60) | 0.81(2.15, −0.19) | ||
| RCP85 (2010–2039) | RCP45 (2010–2039) | |||
| 7 | 0.86(7.56, −1.51) | 0.87(7.86, −0.15) | 0.83(6.99, −1.30) | 0.83(7.24, −0.14) |
| 14 | 0.78(7.58, −1.49) | 0.79(7.88, −0.14) | 0.76(7.02, −1.28) | 0.77(7.26, −0.14) |
| 21 | 0.73(7.60, −1.47) | 0.74(7.90, −0.14) | 0.72(7.04, −1.26) | 0.72(7.28, −0.13) |
| 28 | 0.70(7.63, −1.46) | 0.71(7.91, −0.14) | 0.69(7.06, −1.25) | 0.70(7.29, −0.13) |
| 35 | 0.67(7.64, −1.45) | 0.68(7.92, −0.14) | 0.66(7.07, −1.25) | 0.67(7.30, −0.13) |
| RCP85 (2040–2069) | RCP45 (2040–2069) | |||
| 7 | 0.84(15.86, −2.56) | 0.85(16.31, −0.12) | 0.78(11.95, −1.65) | 0.78(12.21, −0.11) |
| 14 | 0.76(15.92, −2.51) | 0.77(16.35, −0.12) | 0.70(11.98, −1.63) | 0.70(12.24, −0.11) |
| 21 | 0.70(15.96, −2.48) | 0.71(16.39, −0.12) | 0.64(12.00, −1.61) | 0.65(12.26, −0.11) |
| 28 | 0.67(16.00, −2.46) | 0.68(16.42, −0.12) | 0.61(12.02, −1.59) | 0.62(12.27, −0.10) |
| 35 | 0.63(16.02, −2.44) | 0.65(16.43, −0.12) | 0.59(12.04, −1.58) | 0.59(12.29, −0.10) |
| RCP85 (2070–2099) | RCP45 (2070–2099) | |||
| 7 | 0.82(26.62, −3.70) | 0.82(27.21, −0.11) | 0.77(14.59, −1.79) | 0.78(14.85, −0.10) |
| 14 | 0.74(26.72, −3.63) | 0.74(27.28, −0.11) | 0.70(14.62, −1.76) | 0.70(14.88, −0.10) |
| 21 | 0.67(26.79, −3.58) | 0.68(27.34, −0.11) | 0.64(14.65, −1.74) | 0.64(14.90, −0.10) |
| 28 | 0.64(26.85, −3.53) | 0.64(27.39, −0.10) | 0.61(14.68, −1.72) | 0.61(14.92, −0.10) |
| 35 | 0.60(26.89, −3.51) | 0.61(27.42, −0.10) | 0.57(14.70, −1.71) | 0.58(14.94, −0.09) |
First, I examine the spatial patterns of changes in DLR and water vapor at the grid level for three periods: ALL 1980–2009, RCP45 2070–2099, and RCP85 2070–2099. If the increase in DLR and associated water vapor are the primary driver of the warming patterns, one would expect to see a spatial coupling between these variables. As expected, the changes in TAWV and q2m are very similar even at the grid level (Fig. S7), with a spatial correlation of 0.95–0.96 (p < 0.001, n = 1538). Figure 5 shows the spatial patterns of changes in DLR and fractional changes in TAWV (referred to as FTAWV), with a spatial correlation of 0.55–0.78 (p < 0.001, n = 1538). The spatial correlation between T2m and DLR is 0.52–0.55 (p < 0.001, n = 1538). Note that the correlations of DLR-T2m and DLR-FTAWV are lower than the TAWV-q2m correlations because DLR depends nonlinearly on the changes in both atmospheric temperatures and humidity. The driest ecoregions such as the Sahara desert and the Arabian Peninsula where DLR increases most have the largest increases in FTAWV, resembling the spatial patterns of warming of T2m. The widespread increase of water vapor in ALL 1980–2009 is consistent with surface synoptic observations and reanalysis data6. As expected, URL (Fig. S4) shows patterns similar to DLR (Fig. 5), with a spatial correlation of 0.62–0.77 (p < 0.001, n = 1538). These results suggest a stronger linkage between surface warming and increasing water vapor over drier ecosystems.
Second, I analyze the spatial dependence of DLR on EVI by large-scale ecoregion as done for T2m. If DLR is responsible for desert amplification, one would expect to see similar features in DLR as shown in T2m. As expected, TAWV increases with EVI and thus has the largest increase over dense rainforests (Fig. 6b). However, it is the fractional change in water vapor (i.e., FTAWV) that matters in the change in DLR22,23. Despite their smallest increases in TAWV, the driest regions have the largest fractional increases in water vapor (Fig. 6c) and thus the strongest increase in DLR (Fig. 6a). ∂DLR/∂TAWV resembles a negative power (or logarithmic) function (Fig. 6d), indicating the strongest sensitivity of DLR to TAWV changes over the driest regions. For example, R2 is 95% (94%) for the power (logarithmic) fit in the case of 7 ecoregions. Again, this feature remains consistent under different ecoregion classifications and during different 30-year periods (Table 2). The fitted two coefficients for DLR (C0 and A0) both increase in magnitude during all five 30-year periods from 1950–2099, meaning that DLR over humid rainforests and its difference from the deserts become stronger with time. These results resemble those of T2m (Fig. 4b,d) discussed above.
Figure 6.
Same as Fig. 3 but for (a) surface downward longwave radiation (DLR, W/m2), (b) total atmospheric water vapor content (TAWV, kg/m2), (c) fractional changes in TAWV (FTAWV, %), and (d) the ratio of changes in DLR to changes in TAWV (∂DLR/∂TAWV, W/kg).
Third, I analyze the spatial dependence of maximum and minimum T2m on EVI by ecoregion. Arid regions generally have the deepest well-mixed atmospheric boundary layer (ABL) at daytime but a very shallow and stable (atmospheric stratification) condition at nighttime. For a given DLR forcing, the surface warming rate depends inversely on the ABL depth24,25, indicating the sensitivity of T2m to changes in DLR is stronger at nighttime when ABL is mostly stable and persistently stratified26,27,28,29. My analyses of maximum and minimum T2m support a much stronger effect of DLR on T2m at nighttime than at daytime (not shown).
Fourth, I examine the response of T2m changes to DLR for special cases when water vapor changes little over the study period. The spatial dependence of warming on ecoregion in a warming climate for periods after 1980 are absent from (i) the period 1950–1979 when the warming is small and (ii) NAT when the natural forcings is only considered. The largest increases in T2m, fractional changes in q2m, FTAWV, and DLR over the driest regions seen above disappear in these two cases (not shown), pointing to human cause of anthropogenic GHGs in increasing DLR and T2m over the deserts. This inference is consistent with previous analyses of observations, reanalysis data and AOGCM simulations5,6,30,31.
It is worth noting again that the magnitude of fitted coefficients (C0 and A0) for both DLR and T2m increases similarly and linearly along with the global mean GHGs radiative forcing (Fig. 4). Also there is a strong positive correlation between the GHGs forcing versus the atmospheric CO2 concentration (Fig. 4e), indicating that increasing GHGs warm all ecoregions via enhanced DLR and broaden the differences in T2m and DLR between the driest and wettest ecoregions.
Summary and Discussion
This study analyzes the observed and projected surface temperature anomalies over land between 50°S-50°N for the period 1950–2099 by large-scale ecoregion and finds that the warming rate increases dramatically with decreasing vegetation cover. The strongest warming is consistently and persistently seen over driest ecoregions such as the Sahara desert and the Arabian Peninsula during various 30-year periods, pointing to a fundamental pattern of desert amplification in a warming climate over land in low- and mid- latitudes where surface warming rates depend inversely on ecosystem dryness. This amplification enhances linearly with the global mean GHGs radiative forcing, meaning that both the warming rates of all ecoregions and the warming differences between rainforests and deserts intensify with increasing GHGs. My analyses suggest that desert amplification is driven primarily by a stronger GHGs-enhanced downward longwave radiation forcing that reaches and heats the surface over drier ecoregions.
The increase in DLR is likely a consequence of a warmer and thus moister atmosphere associated with water vapor feedbacks due to increasing GHGs. Fig. S8 shows the changes in atmospheric air temperature (T) and the fractional changes in specific humidity (referred to as qf) for six pressure levels from 1000 mb to 200 mb for RCP85 2079–2099 relative to ALL 1961–1990 as a function of EVI by ecoregion. Vertically, the increase in qf enhances with height and maximizes in the upper troposphere (UT). Horizontally, it enhances with surface dryness and maximizes over the deserts in the lower troposphere (LT) but the opposite is seen in the UT. T exhibits roughly similar vertical and horizontal changes as qf, with the strongest warming effect in the UT over the densest rainforests and in the near surface LT layers over the driest ecoregions. The large water vapor increases could not occur without the temperature increases and thus are a reasonable consequence of warming with a relatively stable relative humidity1. The strongest warming and moistening effects are seen over the wettest ecoregions in the UT but such effects reverse in the LT. Although wave propagation in the UT reduces the horizontal gradients in T and q profiles observed in ABL, one would expect to see the largest water vapor feedback in the UT over the wettest ecoregions where the near surface relative humidity is highest and deep moist convection occurs most, which in turn warms and moistens the atmosphere most22. Hence, the enhanced DLR is a cascade effect of the collective increases in atmospheric T and q.
With a substantial surface radiative forcing of DLR, the land surface basically has three ways to balance this additional energy (i.e., cooling processes) due to the absorption of DLR by latent heat via ET, sensible heat via convection and turbulence, and thermal emission via ULR. Among these three terms, latent heat is the most effective way to transfer heat from the surface to the above atmosphere. Over very wet ecoregions, latent heat dominates the surface budget and hence the surface and atmospheric air can be warmed at similar rates via ET. Over very dry ecoregions, sensible heat and ULR dominates the surface budget and hence the surface needs to warm much more than the above air to increase the upward transfer of sensible heat, which depends on the surface-air temperature gradient and near-surface wind speed, and ULR, which is mostly proportional to the fourth power of surface temperature. The increase in URL is much more effective than sensible heat over the dry regions and thus primarily balances the increase in DLR as shown above over the deserts.
I speculate that two types of water vapor feedbacks might be involved32. The first is the well-known positive water vapor feedback that amplifies the GHGs induced warming by moistening the atmosphere, which is defined from the perspective of top of atmosphere (TOA) radiation budget. The water vapor feedback is strongest in the tropical UT where the warming profile is close to moist adiabatic and the fractional changes in water vapor concentration are largest with increasing GHGs14,15,22,33. In the UT where the temperature is cold and very dry, TOA radiation budget is very sensitive to water vapor changes. The warmer and thus moister atmosphere enhances DLR in the LT because of the water vapor greenhouse effect. It is very likely that drier ecoregions are less opaque to DLR because of smaller amounts of clouds and water vapor. Consequently the UT water vapor effect can be propagated more to the surface and thus have stronger influence on surface warming over drier ecoregions. The second is an additional water vapor feedback near the surface over drier ecoregions. This feedback is similar to the water vapor feedback in the UT but from the perspective of surface energy budget. The deserts are extremely dry near the surface and thus are very sensitive to the fractional changes of water vapor. Any near surface warming over deserts could be amplified by increased water vapor as well. For example, the increases in DLR associated with a strong water vapor feedback near the surface are used to explain the rapid warming in Europe34. The stronger warming over other non-dry regions such as south Amazon as mentioned previously can be explained similarly because of decreases in SM content projected in the later 21 century11.
My attribution of desert amplification is certainly not conclusive and other mechanisms are possible. The focus of the present study is the detection of desert amplification, while its attribution needs to consider all relevant atmosphere and surface processes. For example, how do increasing GHGs modify the heating and cooling profiles of the atmosphere? How do convection and other dynamic heat transfer processes affect the atmospheric profiles and regional climate? Do other climate feedbacks such as Planck feedback and lapse-rare feedback also play a role in desert amplification? These questions are challenging and will be addressed in future work. Nevertheless, this study draws attention to an important issue that requires further investigation. Deserts make up ~33% of the global land surface area and climate models project increasing drought and desert extent with elevated CO2 concentrations35,36,37. Consequently, desert amplification may accelerate over arid and semi-arid ecosystems in a warming climate and thus have important societal and economic consequences.
Method
Observed surface temperature datasets
This study uses the ensemble mean of three global gridded monthly surface air temperature (T2m) datasets: CRU38, GISS2 and NCDC39, for the period 1950–2013. The three datasets have been widely used for long-term temperature variability and trend analysis. Despite sharing some similarities in input data sources, they differ substantially in their data processing approaches39. For example, satellite data is used extensively in GISS, used very limited in NCDC, and not used at all in CRU39. Nevertheless, the three datasets show very similar temperature changes and so their ensemble mean is used to reduce redundancy as done in Zhou et al.5,6. Although some observations are available starting 1880, here only the data after 1950 is chosen to maximize spatial coverage of in situ measurements.
Satellite measured vegetation greenness data
This study uses enhanced vegetation index (EVI), an optimized vegetation greenness index measured by the MODerate resolution Imaging Spectroradiometer (MODIS) satellite sensor8 for the period 2000–2013, to examine the spatial dependence of observed and projected surface warming rates on large-scale ecoregions. EVI does not saturate, even over dense forests, and correlates highly with ET, particularly at large scales9,10.
CMIP5 simulations
This study uses historical and projected simulations of 26 global coupled atmosphere-ocean general circulation models (AOGCMs) developed for the Coupled Model Intercomparison Project phase 5 (CMIP5)40. For the historical simulations, there are two groups: one with time-evolving changes in anthropogenic (greenhouse gases and sulfate aerosols) and/or natural (solar and volcanic) forcing agents (referred to as ALL) and the other with only natural forcings (referred to as NAT). Although the ALL and NAT simulations are available starting 1850, I focus only on the period 1950–2005 because AOGCMs are generally able to reproduce the observed warming at large scales, especially after the 1950s1. For the projected climate after 2005, the simulations with data from the Representative Concentration Pathways 4.5 (RCP45) and 8.5 (RCP85) are considered. These two pathways represent contrasting mitigation efforts between a concerted rapid CO2 mitigation and a ‘business-as-usual’ scenario (CO2 concentrations could increase to 538 and 936 ppm. by 21007, according to RCP45 and RCP85, respectively. Monthly means of surface variables: air temperature (T2m), specific humidity (q2m), downward shortwave and longwave radiation (DSR and DLR), net longwave and solar radiation, upward longwave and shortwave radiation, latent heat, and sensible heat; and atmospheric variables: air temperature (T), specific humidity (q), cloud cover, precipitation, and total atmospheric water vapor (TAWV) are examined.
Data processing
This study analyzes monthly output of observations and CMIP5 simulations for the period 1950–2099. All variables are spatially re-projected into grid boxes (2.5° by 2.5°). The monthly data are converted into monthly anomalies relative to the 1961–1990 reference period and then temporally averaged to generate 9-month mean anomalies during March to November (M-N). The monthly EVI is aggregated to create the climatology of M-N mean EVI. I average the yearly M-N anomalies into five 30-year periods: 1950–1979, 1980–2009, 2010–2039, 2040–2069, and 2070–2099. The latitudinal zones beyond 50°N and 50°S and three winter months (DJF) are excluded because polar amplification and albedo feedbacks dominate the high-latitude surface warming5,6. My study region consists of 1538 land grid boxes. As averaging over multiple members enhances the forcing signal and reduces noise from internal variability and errors from individual models1, this study simply averages the available multi-model simulations to obtain the multi-model ensemble mean in NAT, ALL, RCP45 and RCP85.
Analyses by ecoregions
This study evaluates T2m changes at aggregated large-scale ecoregions to minimize small-scale temperature variability and data noise. The 1538 land grids are classified into 7, 14, 21, 28, and 35 large-scale ecoregions from barren land to dense forests based on the climatological EVI values (referred to as EVI)8 and then analyze how T2m anomaly varies with EVI by ecoregion via least squares fitting. The goodness of fit (R2) is used to measure how successful the fit is in approximating the fraction of the data variations. Different classifications are used to test whether the fitted T2m–EVI relationship is robust. For each classification, every ecoregion contains about the same number of grid boxes. Same analyses are also performed for other T2m-related variables. The regional mean time series is calculated using area-weighted averaging over land grids within each ecoregion. For brevity, only results of 7 and 35 ecoregions, which represent the least and most ecoregions classified, are shown in figures, while those of other classifications are listed in tables.
Additional Information
How to cite this article: Zhou, L. Desert Amplification in a Warming Climate. Sci. Rep. 6, 31065; doi: 10.1038/srep31065 (2016).
Supplementary Material
Acknowledgments
This study was supported by National Science Foundation (NSF AGS-1247137 and AGS-1535426).
Footnotes
The authors declare no competing financial interests.
Author Contributions L.Z. contributed the ideas, analysed all of the data, and wrote this paper
References
- IPCC, Climate Change 2013: The Physical Science Basis, the contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (ISBN 978-1-107-05799-1). Cambridge Univ. Press, Cambridge (2013). [Google Scholar]
- Hansen J., Ruedy R., Sato M. & Lo K. Global surface temperature change. Rev. Geophys. 48, RG4004, doi: 10.1029/2010RG000345 (2010). [DOI] [Google Scholar]
- Thorne P. W., Lanzante J. R., Peterson T. C., Seidel D. J. & Shine K. P. Tropospheric temperature trends: history of an ongoing controversy, Wiley Interdisciplinary Reviews: Climate Change, doi: 10.1002/wcc.80 (2010). [DOI] [Google Scholar]
- Wang K. C. & Dickinson R. E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev Geophys. 50, doi: 10.1029/2011rg000373 (2012). [DOI] [Google Scholar]
- Zhou L., Chen H. & Dai Y. Stronger warming amplification over drier ecoregions observed since 1979. Environ. Res. Lett. 10(2015) 064014, doi: 10.1088/1748-9326/10/6/064012, 2015 (2015). [DOI] [Google Scholar]
- Zhou L., Chen H., Hua W., Dai Y. & Wei N. Mechanisms for stronger warming over drier ecoregions observed since 1979. Clim. Dyn. doi: 10.1007/s00382-016-3007-9 (2016). [DOI] [Google Scholar]
- Meinshausen M. et al. The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Climatic Change 109, 213–241, doi: 10.1007/s10584-011-0156-z (2011). [DOI] [Google Scholar]
- Huete A. et al. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 83, 195–213 (2002). [Google Scholar]
- Suzuki R. & Masuda K. Interannual co-variability found in evapotranspiration and satellite-derived vegetation indices over northern Asia. J. Meteorol. Soc. Jpn. 82(4), 1233–1241 (2004). [Google Scholar]
- Nagler P. L. et al. Evapotranspiration on western US rivers estimated using the enhanced vegetation indices from MODIS and data from eddy covariance and Bowen ratio flux towers. Remote Sens. Environ. 97(3), 337–351 (2005). [Google Scholar]
- Dai A. Increasing drought under global warming in observations and models. Nat. Clim. Change. 3, 52–58, doi: 10.1038/NCLIMATE1633 (2013). [DOI] [Google Scholar]
- Wang K. C. & Dickinson R. E. Contribution of solar radiation to decadal temperature variability over land. Proc. Nat. Acad. Sci. 110, 37, 14877–14882, doi: www.pnas.org/cgi/doi/10.1073/pnas.1311433110 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seneviratne S. I. et al. Investigating soil moisture-climate interactions in a changing climate: A review. Earth-Science Reviews 99, (3–4), 125–161 (2010). [Google Scholar]
- IPCC, Climate Change 2007: The Physical Science Basis, Contribution of Working Group I to the Fourth Assessment Report of the IPCC (ISBN 978 0521 88009-1), Cambridge Univ. Press, Cambridge (2007). [Google Scholar]
- Dessler A. E. & Davis S. M. Trends in tropospheric humidity from reanalysis systems. J. Geophys. Res. 115, D19127, doi: 10.1029/2010JD014192 (2010). [DOI] [Google Scholar]
- Myhre G., Highwood E. J., Shine K. P. & Stordal F. New estimates of radiative forcing due to well-mixed greenhouse gases. Geophys. Res. Lett. 25, 2715–2718 (1998). [Google Scholar]
- Wang K. C. & Liang S. Global atmospheric downward longwave radiation over land surface under all-sky conditions from 1973 to 2008. J. Geophys. Res. 114, D19101, doi: 10.1029/2009JD011800 (2009). [DOI] [Google Scholar]
- Wang K. & Dickinson R. E. Global atmospheric downward longwave radiation at the surface from ground-based observations, satellite retrievals, and reanalyses. Rev. Geophys. 51, 150–185, doi: 10.1002/rog.20009 (2013). [DOI] [Google Scholar]
- Ruckstuhl C., Philipona R., Morland J. & Ohmura A. Observed relationship between surface specific humidity, integrated water vapor, and longwave downward radiation at different altitudes. J Geophys. Res. 112, L19809, doi: 10.1029/2005GL023624 (2007). [DOI] [Google Scholar]
- Rangwala I., Sinsky E. & Miller R. J. Amplified warming projections for high altitude regions of the northern hemisphere mid-latitudes from CMIP5 models. Environ. Res. Lett. 8, 024040, doi: 10.1088/1748-9326/8/2/024040 (2013). [DOI] [Google Scholar]
- Naud C. M., Chen Y.-H., Rangwala I. & Miller J. R. Sensitivity of downward longwave surface radiation to moisture and cloud changes in a high elevation region. J. Geophys. Res. 118 (17), 10,072–10,081, doi: 10.1002/jgrd.50644 (2013). [DOI] [Google Scholar]
- Held I. M. & Soden B. J. Water vapor feedback and global warming. Annu. Rev. Energy Environ. 25, 441–475 (2000). [Google Scholar]
- Dessler A. E., Zhang Z. & Yang P. Water‐vapor climate feedback inferred from climate fluctuations, 2003–2008. Geophys. Res. Lett. 35, L20704, doi: 10.1029/2008GL035333 (2008). [DOI] [Google Scholar]
- Dirmeyer P. A., Jin Y., Singh B. & Yan X. Trends in land-atmosphere interactions from CMIP5 simulations. J. Hydrometeorol. 829–849, doi: 10.1175/JHM-D-12-0107.1 (2013). [DOI] [Google Scholar]
- Davy R. & Esau I. Global climate models’ bias in surface temperature trends and variability. Environ. Res. Lett. 9(11) (2014). [Google Scholar]
- Zhou L., Dickinson R. E., Tian Y. & Vose R. S. Impact of vegetation removal and soil aridation on diurnal temperature range in a semiarid region – Application to the Sahel. Proc. Natl. Acad. Sci. USA 104(46), 17937–17942 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou L. et al. Spatial dependence of diurnal temperature range trends on precipitation from 1950 to 2004. Clim. Dyn. 32, 429–440, doi: 10.1007/s00382-008-0387-5 (2009). [DOI] [Google Scholar]
- Zhou L., Dickinson R. E., Dai A. & Dirmeyer P. Detection and attribution of anthropogenic forcing to diurnal temperature range changes from 1950 to 1999: Comparing multi-model simulations with observations. Clim. Dyn. 35, 1289–1307, doi: 10.1007/s00382-009-0644-2 (2010). [DOI] [Google Scholar]
- McNider R. T. et al. Response and sensitivity of the nocturnal boundary layer over land to added longwave radiative forcing. J. Geophys. Res. 117, D14106 (2012). [Google Scholar]
- Dai A. Recent climatology, variability and trends in global surface humidity. J. Climate 19, 3589–3606 (2006). [Google Scholar]
- Simmons A. J., Willett K. M., Jones P. D., Thorne P. W. & Dee D. P. Low-frequency variations in surface atmospheric humidity, temperature, and precipitation: Inferences from reanalyses and monthly gridded observational data sets. J. Geophys. Res. 115 (2010). [Google Scholar]
- Pierrehumbert R. T. Busy week for water vapor. Available online at http://www.realclimate.org/index.php/archives/2005/11/busy-week-for-water-vapor/ (2005).
- Schneider T., O’Gorman P. A. & Levine X. J. Water vapor and the dynamics of climate changes. Rev. Geophys. 48, RG3001, doi: 10.1029/2009RG000302 (2010). [DOI] [Google Scholar]
- Philipona R., Durr B., Ohmura A. & Ruckstuhl C. Anthropogenic greenhouse forcing and strong water vapor feedback increase temperature in Europe. Geophys. Res. Lett. 32, L19809, doi: 10.1029/2005GL023624 (2005). [DOI] [Google Scholar]
- Seager R., Naik N. & Vecchi G. A. Thermodynamic and dynamic mechanisms for large-scale changes in the hydrological cycle in response to global warming. J. Clim. 23, 4651–4668 (2010). [Google Scholar]
- Trenberth K. E. et al. Global warming and changes in drought. Nat. Clim. Change 4, 17–22 (2013). [Google Scholar]
- Huang J., Yu H., Guan X., Wang G. & Guo R. Accelerated dryland expansion under climate change. Nature Climate Change 6, 166–171, doi: 10.1038/nclimate2837 (2016). [DOI] [Google Scholar]
- Harris I. & Jones P. D. CRU TS3.22: Climatic Research Unit (CRU) Time-Series (TS) Version 3.22 of high resolution gridded data of month-by-month variation in climate (Jan. 1901- Dec. 2013). NCAS British Atmospheric Data Centre, 24th September 2014. doi: 10.5285/18BE23F8-D252-482D-8AF9-5D6A2D40990C (2014). [DOI]
- Vose R. S. et al. NOAA’s merged land-ocean surface temperature analysis. Bull. Amer. Meteor. Soc. 93, 1677–1685, doi: 10.1175/BAMS-D-11-00241.1 (2012). [DOI] [Google Scholar]
- Taylor K. E., Stouffer R. J. & Meehl G. A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 93, 485–498 (2012). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.