Iterative Potts and Blake–Zisserman minimization for the recovery of functions with discontinuities from indirect measurements

Abstract

Signals with discontinuities appear in many problems in the applied sciences ranging from mechanics, electrical engineering to biology and medicine. The concrete data acquired are typically discrete, indirect and noisy measurements of some quantities describing the signal under consideration. The task is to restore the signal and, in particular, the discontinuities. In this respect, classical methods perform rather poor, whereas non-convex non-smooth variational methods seem to be the correct choice. Examples are methods based on Mumford–Shah and piecewise constant Mumford–Shah functionals and discretized versions which are known as Blake–Zisserman and Potts functionals. Owing to their non-convexity, minimization of such functionals is challenging. In this paper, we propose a new iterative minimization strategy for Blake–Zisserman as well as Potts functionals and a related jump-sparsity problem dealing with indirect, noisy measurements. We provide a convergence analysis and underpin our findings with numerical experiments.

1. Introduction

Problems involving reconstruction tasks for functions with discontinuities appear in numerous biological and medical applications. Examples are the steps in the rotation of the bacterial flagella [1,2], the cross-hybridization of DNA [3–5] and single-molecule fluorescence resonance energy transfer [6]. A more classical engineering example is crack detection in fracture mechanics. In general, signals with discontinuities appear in many applied problems ranging from mechanics, electrical engineering to biology and medicine. For further examples, we refer to the papers [7–9] and the references therein. The latter references in particular deal with various aspects concerning the reconstruction of piecewise constant signals.

For reconstruction tasks, it is quite usual to use a variational approach: an energy functional consisting of a data fidelity term, and a regularizing term is minimized. It is well known that using classical regularizing terms based on Hilbert–Sobolev semi-norms $\parallel \mathrm{\nabla }u{\parallel }_{L^2}^2$ performs poorly for the recovery of functions with discontinuities. Much better results are obtained by non-smooth non-convex minimizers such as the Mumford–Shah functional and the piecewise-constant Mumford–Shah functional [10,11]. These functionals penalize the ‘size’ (i.e. the outer Hausdorff measure) of the discontinuity set and, only on its complement, measure some qth variation. However, their analysis is more demanding because they are non-smooth and non-convex. Some references concerning Mumford–Shah functionals are [12–15] and also the references therein; see also the book [16]. Mumford–Shah functionals are the maybe most well-known representative of the class of free-discontinuity problems introduced by De Giorgi [17].

The concrete data acquired in applications are usually indirectly measured. Furthermore, they consist of measurements on a discretized grid and are typically corrupted by noise. In practical applications, the task is to restore the signal and, in particular, to recover the discontinuities from these measurements. In order to deal with indirect linear measurements, data terms of the form ∥Au−f∥², where A represents the measurement device and f is the given data, are considered. To deal with the discrete data, typically, the energy functional is discretized.

Discretizations of the Mumford–Shah functional and the piecewise-constant Mumford–Shah functional are known under the names Blake–Zisserman functionals and Potts functionals, respectively. The weak string model as it is called by Blake & Zisserman in [18] is given in its univariate version by

$$\begin{array}{cc}\text{minimize}\gamma \sum _{i}min(|u_i-u_{i-1}{|}^q,s^q)+\parallel Au-f{\parallel }_2^2.& \text{(}{\mathcal{B}}_{\gamma ,s}\text{)}\end{array}$$

Here, the data f live in a real-valued finite dimensional linear space. The parameter γ>0 controls the balance between data fidelity and regularizing term. The parameter s>0 determines the discontinuity. More precisely, the underlying signal models are piecewise smooth functions with discontinuities. In a discrete set-up, we say there is a jump (a discontinuity) between i,i+1 if the distance between u_i+1,u_i is at least s. The penalty for a jump is then independent of its magnitude. If the distance between consecutive members of u is smaller than s, the penalty is just chosen as the (discrete) qth variation of u. We allow for $q\in [1,\mathrm{\infty })$. References related to Blake–Zisserman functionals are [13,18–20].

The Potts model [21–23] is a discrete variant of the piecewise-constant Mumford–Shah model. It assumes that the underlying signal is constant between its discontinuities. The corresponding minimization problem is given by

$$\begin{array}{cc}\text{minimize}\gamma \parallel \mathrm{\nabla }u{\parallel }_0+\parallel Au-f{\parallel }_2^2,& \text{(}{\mathcal{P}}_{\gamma }\text{)}\end{array}$$

where ∥∇u∥₀=|{i:u_i≠u_i+1}| denotes the number of jumps of the target variable u. The name Potts model is frequently used in statistics as well as signal and image processing [24–28]; it is a tribute to Renfrey B. Potts and his work in statistical mechanics [21] where the above priors were used for the first time. For recent work concerning the reconstruction of piecewise constant signals, we refer to the papers [7,8] of Little & Jones; the first paper includes an overview, and the second paper in particular deals with methods.

Formally, the Potts problem (${\mathcal{P}}_{\gamma }$) might be seen as the ‘Lagrange formulation’ of the following constrained optimization problem which we call J-jump sparsity problem. It is given by

$$\begin{array}{cc}\begin{array}{rl}\text{minimize}& \parallel Au-f{\parallel }_2^2\\ \text{subject to}& \parallel \mathrm{\nabla }u{\parallel }_0\le J,\end{array}\}& \text{(}{\mathcal{S}}_J\text{)}\end{array}$$

where $J\in {\mathbb{N}}_0.$ We later see that the relation between the Potts problem (${\mathcal{P}}_{\gamma }$) and the J-jump sparsity problem is only of formal nature; they are not equivalent. To the best of our knowledge, the J-jump sparsity problem (${\mathcal{S}}_J$) for general A has only recently appeared in the literature [29]; the authors obtain asymptotic statements in the context of inverse regression. The situation A=id is well studied. References on the J-jump sparsity problem (${\mathcal{S}}_J$) for A=id are [30,31]. Related sparsity problems were considered in [32].

Finding solutions of all the above problems is challenging because they are NP hard; for the Blake–Zisserman problem (${\mathcal{B}}_{\gamma ,s}$), this has been shown in [33], and for the Potts problem, in [34]. Thus, for real applications, there is no hope to find a global minimizer in reasonable time. However, owing to the practical importance, several approximative strategies have been proposed. Fornasier & Ward [19] (see also Artina et al. [35]) rewrite the Blake–Zisserman problem as a pointwise-penalized problem and derive generalized iterative thresholding algorithms for the rewritten problem. They show that their method converges to a local minimizer. Further theoretical results concerning the pointwise penalized problem were derived by Nikolova [20]. Related algorithms are iterative soft thresholding for ℓ¹ penalized problems, analysed by Daubechies et al. [36], and the iterative hard thresholding algorithms for ℓ⁰ penalizations, analysed by Blumensath & Davies in [32,37]. For the Potts problem, the authors of this paper have proposed a strategy based on the alternating methods of multipliers in [34]. Furthermore, Candès et al. [38] use iteratively re-weighted total variation minimization for piecewise constant recovery problems. Results of compressed sensing type related to the Potts problem have been derived by Needell & Ward [39,40]: under certain conditions, minimizers of the Potts functional agree with total variation minimizers. For the case of Blake–Zisserman functionals we are not aware of similar results. However, in the presence of noise, total variation minimizers might significantly differ from minimizers of the Potts problem. But, the minimizers of the Potts problem are the results frequently desired in practice.

In this paper, we propose a new iterative minimization strategy for Blake–Zisserman as well as Potts functionals and the J-jump sparsity problem dealing with indirect, noisy measurements. Our methods belong to the class of majorization–minimization or forward–backward splitting methods of Douglas–Rachford type [41]. In contrast to the approaches in [19] and [32,37], which lead to thresholding algorithms, our approach leads to non-separable yet computationally tractable problems in the backward step. Facing the additional challenge owing to the non-separability of the backward step, we provide a convergence analysis. Most notably, we obtain convergence statements towards local minimizers. We further establish a relation between stationary points of the iterations and local and global minimizers. We also show that the Potts problem (${\mathcal{P}}_{\gamma }$) and the J-jump sparsity problem (${\mathcal{S}}_J$) are not equivalent. From an experimental side, we show the applicability of each of our algorithms in several signal recovery experiments. In particular, we consider deconvolution problems with full and partial data. We apply our methods to real data: we estimate the steps in the rotation of the bacterial flagellar motor [1].

The paper is organized as follows. In §2, we consider the variational recovery of signals with jumps. We properly introduce the considered problems and derive iterative algorithms for their solution. This is done for the Potts problem in §2a, for the J-jump sparsity problem in §2b, and for the Blake–Zisserman problem in §2c. In §3, we gather our analytical results. They are formulated in §3a, and the proofs are supplied in the following sections. In §4, we apply the algorithms derived in this paper to concrete reconstruction problems.

2. Variational recovery of signals with jumps and related algorithms

We consider the Potts problem and the J-jump sparsity problem dealing with piecewise constant signals in §2a and b, respectively. The Blake–Zisserman problem dealing with piecewise smooth signals is treated in §2c.

(a). The Potts problem

We start with the Potts problem (${\mathcal{P}}_{\gamma }$). Here, the underlying signal models are the piecewise constant functions. The idea is to minimize the functional in (${\mathcal{P}}_{\gamma }$) for corrupted, indirectly measured noisy data to obtain a parsimonious piecewise constant estimate for the underlying signal.

We first of all record the existence of minimizers for this non-continuous problem.

Theorem 2.1 —

The Potts problem (${\mathcal{P}}_{\gamma }$) has a minimizer.

Proofs are, e.g. given in [19] or in [34] where also more general ℓ^p data terms (which lead to a non-Hilbert space setup) are considered. The minimizers of the Potts problem are not unique in general—even if A is injective; but, at least, for A=id, the set of data and parameters γ for which minimizers are not unique are known to be a negligible set [42]. It is worth mentioning that the time-continuous formulation of the Potts problem need not have solutions in general. Here, additional regularization, e.g. by $L^{\mathrm{\infty }},$ constraints is needed. Then, under further suitable assumptions, the minimizers of the Potts problem converge to piecewise constant minimizer of a continuous Potts functional (or, synonymously, piecewise constant Mumford–Shah functional), as sampling gets finer [25]. This also holds in the presence of noise [25,26,43]. For related results on Potts functionals with L¹ data terms, we also refer to Weinmann et al. [44].

Iterative Potts minimization algorithms. Because the Potts problem is NP hard (cf. [34]), there is no hope to find a practically applicable algorithm that computes a global minimizer within reasonable time. The challenge is to derive practically applicable algorithms that produce ‘good solutions’—‘good’ from the practical point of view—and to obtain analytic guarantees, at least locally. We here derive an algorithm that does so. Later on, we show convergence towards a local minimizers. To this end, we consider the Potts functional

$$P_{\gamma }(u)=\gamma \parallel \mathrm{\nabla }u{\parallel }_0+\parallel Au-f{\parallel }_2^2.$$ 2.1

Here, the target variable u lives in ${\mathbb{R}}^L,$ data f consisting of s measurements live in ${\mathbb{R}}^s$ and A is a real-valued s×L matrix. The corresponding surrogate functional P^surr_γ is given by

$$P_{\gamma }^{\mathrm{surr}}(u,v)=\gamma \parallel \mathrm{\nabla }u{\parallel }_0+\parallel Au-f{\parallel }_2^2-\parallel Au-Av{\parallel }_2^2+\parallel u-v{\parallel }_2^2.$$ 2.2

Expanding and rearranging the terms on the right-hand side, we see that

$$P_{\gamma }^{\mathrm{surr}}(u,v)=\gamma \parallel \mathrm{\nabla }u{\parallel }_0+\parallel u-v+A^{\ast }Av-A^{\ast }f{\parallel }_2^2+C,$$ 2.3

with some constant C which is independent of u and thus negligible. It follows that

$$\arg \underset{u}{min}{P}_{\gamma }^{\mathrm{surr}}(u,v)=\arg \underset{u}{min}\{\gamma \parallel \mathrm{\nabla }u{\parallel }_0+\parallel u-v+A^{\ast }Av-A^{\ast }f{\parallel }_2^2\}.$$ 2.4

We now successively compute $u^{k+1}=\arg \underset{u}{min}{P}^{\mathrm{surr}}(u,u^k).$ We obtain the following iterative Potts minimization algorithm given by the iteration

$$\begin{array}{rl}{d}^{k+1}& =(I-A^{\ast }A)u^k+A^{\ast }f\\ \text{and}{u}^{k+1}& =\arg \underset{u}{min}\gamma \hspace{0.17em}\parallel \mathrm{\nabla }u{\parallel }_0+\parallel u-d^{k+1}{\parallel }_2^2,\end{array}\}$$ 2.5

where I denotes the identity matrix. The first step consists of simple matrix–vector multiplications which can be done in quadratic time. The crucial observation is that the second step consists of minimizing a Potts functional with A=id, given by

$$P_{\gamma }^{\mathrm{id}}(u)=\gamma \parallel \mathrm{\nabla }u{\parallel }_0+\parallel u-d{\parallel }_2^2,$$ 2.6

for data d=d^k+1. For the special case A=id, a global minimizer can be computed in quadratic complexity as explained in the next paragraph. Hence, both steps of the iteration can be computed efficiently.

The Potts problem for A=id. The Potts problem (2.6) (with A=id) can be solved exactly by dynamic programming [10,11,13,23,31,45–47]. Because it is a basic building block of our method, we briefly describe the basic idea of the dynamic programming algorithm for its solution. For a more detailed description, we refer, e.g. to [45]. We assume that we have already computed minimizers u^l of the Potts functionals P^id_γ associated with the partial data (d₁,…,d_l) for each l=1,…,r and some r smaller than the number L of full data items. Using this information, the Potts functional associated with data (d₁,…,d_r+1) can be efficiently minimized via

$$\underset{u\in {\mathbb{R}}^{r+1}}{min}{P}_{\gamma }^{\mathrm{id}}(u)=\underset{l=1,\dots ,r+1}{min}{P}_{\gamma }^{\mathrm{id}}(u^{l-1})+\gamma +{ϵ}_{[l,r+1]},$$ 2.7

where ϵ_[l,r+1] is the quadratic deviation of the data (d_l,…,d_r+1) from its mean. Here, we use the convention that u⁰ is an empty vector and P^id_γ(u⁰)=−γ. A corresponding minimizer reads u^r+1= (u^l*−1,w_[l*,r+1]), where l* is a minimizing argument of the right-hand side of (2.7) and w_[l*,r+1]=(μ,…,μ) with μ being the mean value of (d_l*,…,d_r). We obtain a minimizer for full data d by successively computing u^l for each l=1,…,L. The described method can be implemented in O(L²) using pre-computation of the moments and storing only jump locations [45]. Furthermore, there are strategies to prune the search space which speed up the computations in practice [48,49]. Besides the dynamic programming approach there are greedy algorithms which perform well in practice but which come without theoretical guarantees; for a discussion, see [7,8].

Relations to iterative hard thresholding. In [19], Fornasier and Ward transform Blake–Zisserman problems with ℓ² data terms to sparsity-related problems and solve the resulting problem by iterative thresholding algorithms. The same technique can also be applied to the Potts problem (cf. [34]). We obtain the sparsity problem

$$\text{minimize}\gamma \parallel v{\parallel }_0+\parallel A^{\mathrm{\prime }}{\mathrm{\nabla }}^{+}v-f^{\mathrm{\prime }}{\parallel }_2^2,$$ 2.8

Here, ∇⁺ is the pseudo-inverse of the discrete difference operator ∇. The transformed matrix A′ and the transformed data f′ are obtained from A,f by

$$A_{kj}^{\mathrm{\prime }}=A_{kj}-\frac{{\overline{A}\hspace{0.17em}}_k\sum _{i=1}^m{\overline{A}\hspace{0.17em}}_i{A}_{ij}}{\sum _{i=1}^m{\overline{A}\hspace{0.17em}}_i^2},$$ 2.9

with ${\overline{A}\hspace{0.17em}}_i$ given by ${\overline{A}\hspace{0.17em}}_i=\sum _{j=1}^n{A}_{ij}$,

$$f_k^{\mathrm{\prime }}=f_k-\frac{{\overline{A}\hspace{0.17em}}_k\sum _{i=1}^m{\overline{A}\hspace{0.17em}}_i{f}_i}{\sum _{i=1}^m{\overline{A}\hspace{0.17em}}_i^2}.$$ 2.10

Then, the iterative thresholding algorithm proposed by Blumensath & Davis [32,37] can be applied to (2.8). This thresholding algorithm consists of a gradient or Landweber step for the data f′ and the matrix A′∇⁺ followed by a hard thresholding step. In contrast, the proposed method in this paper uses Potts minimization for A=id working on the direct problem instead of thresholding on a transformed problem. Solving the Potts problem for A=id is of quadratic complexity as opposed to the linear complexity of thresholding. Thus, the proposed algorithm might seem computationally more expensive than the iterative hard thresholding. However, the involved matrix–vector multiplications have already quadratic complexity in general. Even if A is a band matrix or of convolution type (and thus diagonalizable by Fourier methods), the matrix A′∇⁺ is typically full or not of convolution-type anymore. This is because ∇⁺ is a full lower triangular matrix. So in either way, the complexity is quadratic.

(b). The J-jump sparsity problem

We here consider the J-jump sparsity problem (${\mathcal{S}}_J$). As for the Potts problem, the underlying signal model is the piecewise constant functions. We minimize the constrained functional in (${\mathcal{P}}_{\gamma }$) for corrupted, indirectly measured noisy data to obtain a parsimonious J-jump sparse estimate for the underlying signal. To the best of our knowledge, the J-jump sparsity problem (${\mathcal{S}}_J$) for general A has only recently appeared in the literature [29]. However, the situation A=id has been considered, for example, in optimum quantization [30] and computational biology [31]. Related sparsity problems were considered in [32].

We first state the existence of minimizers.

Theorem 2.2 —

The J-jump sparsity problem (${\mathcal{S}}_J$) has a solution.

Although the functional is not continuous, the proof is trivial: fix arbitrary J indices M, consider u's which have their (left) jump set contained in J. These u form a vector space of dimension J on which the quadratic functional u↦Q(u)=∥Au−f∥² has a minimizer, say u^M. Variation over all jump sets M of size J (which are finitely many) yields a candidate u^M for each jump set M. Now, one can just take a candidate u* with the smallest Q(u^M)-value among all M.

The minimizers of the J-jump sparsity problem are not unique in general. This is a consequence of theorem 3.1, because Potts solutions are solutions of the J-jump sparsity problems, and Potts solutions are not unique.

We record that the problem of finding one or all minimizers of the J-jump sparsity problem (${\mathcal{S}}_J$) is NP-hard.

Theorem 2.3 —

The J-jump sparsity problem (${\mathcal{S}}_J$) is NP-hard.

This can be seen easily seen by the following argument. One (theoretic) way to obtain a solution for the Potts problem for specific parameter γ is to compute a J-jump sparse solution u^J for all J, J smaller than the signal length. Then, we compare the values P_γ(u^J) and choose a minimal one. This is a minimizer of the Potts problem for γ. Hence, there is a strategy to find a solution of the NP-hard Potts problem by solving at most L J-jump sparsity problems (${\mathcal{S}}_J$), where L is the problem size. Therefore, the NP-hardness of the Potts problem implies the NP-hardness of the J-jump sparsity problem (${\mathcal{S}}_J$).

By these considerations, finding global minimizer within reasonable time is infeasible. Instead, we derive a practically applicable algorithm that performs well in practice and derive at least statements on local optimality.

Iterative J-jump sparsity algorithms. We consider the J-jump sparsity problem

$$\text{minimize}\hspace{0.17em}Q(u)=\parallel Au-f{\parallel }_2^2,\text{s. t. }\hspace{0.17em}\parallel \mathrm{\nabla }u{\parallel }_0\le J,$$ 2.11

and the corresponding constrained surrogate problem

$$Q^{\mathrm{surr}}(u,v)=\parallel Au-f{\parallel }_2^2-\parallel Au-Av{\parallel }_2^2+\parallel u-v{\parallel }_2^2,\text{s. t. }\parallel \mathrm{\nabla }u{\parallel }_0\le J.$$ 2.12

We may rewrite Q^surr(u,v) to obtain the problem

$$\text{minimize }\parallel u-v+A^{\ast }Av-A^{\ast }f{\parallel }_2^2,\text{s. t. }\parallel \mathrm{\nabla }u{\parallel }_0\le J.$$ 2.13

We see that this problem is a J-jump sparsity problem with A=id which is computationally feasible as explained below; the complexity is quadratic. Then, minimizing Q^surr(u,v) (or, more precisely, the constrained surrogate problem) with respect to u and taking the result as new input v yields the iteration

$$\begin{array}{rl}{d}^{k+1}& =(I-A^{\ast }A)u^k+A^{\ast }f\\ \text{and}{u}^{k+1}& =\arg min\parallel u-d^{k+1}{\parallel }_2^2,\text{s.t. }\parallel \mathrm{\nabla }u{\parallel }_0\le J.\end{array}\}$$ 2.14

We call this iteration iterative J-jump sparsity algorithm.

The J-jump sparsity problem for A=id. In (2.13), we have to solve a J-jump sparsity problem for A=id of the form

$$\text{minimize }\parallel u-d{\parallel }_2^2,\text{s. t. }\parallel \mathrm{\nabla }u{\parallel }_0\le J,$$ 2.15

for data d=d^k+1=(I−A*A)u^k+A*f. As the Potts problem, it can be solved exactly using dynamic programming. The algorithm was reinvented several times in different contexts; we refer to [30,31]. Let us assume that we have solutions of (2.15) for all numbers of jumps j=0,…,J and for all partial data (d₁,…,d_l) for all l=1,…,r with r being smaller than the number L of data items. For j jumps and length l, we denote a corresponding solution by u^l,j. We want to compute a minimizer for data (d₁,…,d_r+1). We first note that the zero jump solution u^r+1,0 is given by the mean of d_[1,r+1]:=(d₁,…,d_r+1). For j jumps, j=1,…,J, we use that

$$\underset{u\in {\mathbb{R}}^{r+1},\parallel \mathrm{\nabla }u{\parallel }_0\le j}{min}\parallel u-d_{[1,r+1]}{\parallel }_2^2=\underset{l=1,\dots ,r+1}{min}\parallel u^{l-1,j-1}-d_{[1,l-1]}{\parallel }_2^2+{ϵ}_{[l,r+1]},$$

where ϵ_[l,r+1] is again the quadratic deviation of the data (d_l,…,d_r+1) from its mean value. Corresponding minimizers are given by u^r+1,j=(u^l*−1,j−1,w_[l*,r+1]), where l* is a minimizing index of the right-hand side of the above equation and the components of w_[l*,r+1] are given by the mean value on d_[l*,r+1]. A solution for the full data is obtained by successively computing u^l,j for all j=0,…,J and l=1,…,n. Compared with the minimization algorithm for the Potts problem, it is more expensive, because, actually, minimizers for all j=0,…,J have to be computed. Nonetheless, the method has quadratic complexity with respect to the data size L. As in the case of the Potts problem with A=id, there are greedy algorithms which may perform well, in practice, but which do not guarantee a global optimum; see [7,8] for a discussion.

Relation to iterative hard thresholding. Similar to (2.8), the J-jump sparsity problem can be transformed to the constrained sparsity problem

$$\text{minimize }\parallel A^{\mathrm{\prime }}{\mathrm{\nabla }}^{+}v-f^{\mathrm{\prime }}{\parallel }_2^2\text{s.t. }\parallel v{\parallel }_0\le J,$$ 2.16

with A′ and f′ given by (2.9) and (2.10), respectively. Then, the iterative constrained hard thresholding algorithms of Blumensath & Davis [32,37] can be applied to (2.16). This thresholding algorithm involves a hard thresholding variant keeping the J items with highest absolute value. When applying this approach to the J jump sparsity problem, the resulting complexity of one iteration step is again quadratic. This is because the same arguments as given for hard thresholding in the section on Potts problems also apply to iterative constrained hard thresholding. Hence, the approach via iterative constrained hard thresholding has the same complexity as the iterative J-jump sparsity algorithm proposed in this paper.

(c). The Blake–Zisserman problem

Until now, we have only considered piecewise constant signals. We now also allow the signal to vary smoothly in-between the jumps; this corresponds to piecewise smooth signals as underlying signal model. In a discrete set-up, we allow for small qth variations in-between the jumps. These small variations are reflected by the Blake–Zisserman regularizers given in (${\mathcal{B}}_{\gamma ,s}$).

We first of all note that the Blake–Zisserman problem has a minimizer.

Theorem 2.4 —

The Blake–Zisserman weak string problem (${\mathcal{B}}_{\gamma ,s}$) has a solution.

Theorem 2.4 has been shown in [19] for general A. Convergence results of Blake–Zisserman functionals towards Mumford–Shah functionals are given in [13].

Iterative Blake–Zisserman algorithm. We derive an iterative Blake–Zisserman minimization algorithm in analogy to the iterative algorithm derived for the Potts problem. The Blake–Zisserman functional B_γ,s was given by

$$B_{\gamma ,s}(u)=\gamma \sum _{i}min(|u_i-u_{i-1}{|}^q,s^q)+\parallel Au-f{\parallel }_2^2.$$ 2.17

In analogy to the Potts problem, we consider its surrogate functional B^surr_γ,s(u,v) =B_γ,s(u) $-\parallel Au-Av{\parallel }_2^2$ $+\parallel u-v{\parallel }_2^2.$ After some calculation, we see that

$$B_{\gamma ,s}^{\mathrm{surr}}(u,v)=\gamma \sum _{i}min(|u_i-u_{i-1}{|}^q,s^q)+\parallel u-v+A^{\ast }Av-A^{\ast }f{\parallel }_2^2+C,$$ 2.18

where C is independent of u and can therefore be omitted. Iteratively minimizing this functional, using the previous minimizer as new input v, leads to the iterative Blake–Zissermann minimization algorithm

$$\begin{array}{rl}{d}^{k+1}& =(I-A^{\ast }A)u^k+A^{\ast }f\\ \text{and}{u}^{k+1}& =\arg \underset{u}{min}\gamma \sum _{i}min(|u_i-u_{i-1}{|}^q,s^q)+\parallel u-d^{k+1}{\parallel }_2^2.\end{array}\}$$ 2.19

We note that the second line constitutes a Blake–Zisserman problem for A=id for which there is again a computationally feasible algorithm as explained next.

The Blake–Zisserman problem for A=id. The Blake–Zisserman functional B^id_γ,s(u) for A=id is given by

$$B_{\gamma ,s}^{\mathrm{id}}(u)=\gamma \sum _{i}min(|u_i-u_{i-1}{|}^q,s^q)+\parallel u-d{\parallel }_2^2.$$ 2.20

It is a basic building block of our iterative Blake–Zissermann minimization algorithm (2.19). For the particular case A=id, the dynamic programming principle as explained for the Potts problem before, can be applied to the Blake–Zissermann problem to obtain an algorithm computing an exact solution [10,11,13,23,45]. We use the basic dynamic program explained in the corresponding paragraph concerning the Potts problem, where we reinterpret (2.7). In the context of Blake–Zisserman functionals, the deviation ϵ_[l,r] of (2.7) from the data (d_l,…,d_r) is given by

$${ϵ}_{[l,r]}=\underset{w\in {\mathbb{R}}^{r-l+1}}{min}\gamma \parallel \mathrm{\nabla }w{\parallel }_q^q+\parallel w-(d_l,\dots ,d_r){\parallel }_2^2.$$ 2.21

Then, minimizers of B^id_γ,s have the form (u^l*−1,w_[l*,r]), where w_[l*,r] is a minimizer of (2.21). We note that, in contrast to the Potts problem, w_[l*,r] need not be constant. The functional (2.21) is convex for all p≥1 which makes it accessible for standard convex optimization techniques such as the primal–dual strategy of Chambolle & Pock [50]. The special case p=2 reduces to solving a linear system of equations.

Relation to thresholding algorithms. In [19], Fornasier and Ward transform Blake–Zisserman problems to sparsity type problems of the form (2.8) with the sparsity term in (2.8) replaced by $\sum _{i}min(|u_i{|}^q,s^q)$. Then, they solve the resulting transformed problem by iterative thresholding algorithms with a corresponding suitable thresholding function. In contrast, we directly work on the non-transformed problem here.

3. Analysis

(a). Main analytic results

The problems (${\mathcal{P}}_{\gamma }$) and (${\mathcal{S}}_J$) both deal with an underlying piecewise constant signal model. They are intimately connected; in particular, one can formally interpret the Potts problem (${\mathcal{P}}_{\gamma }$) as the Lagrange formulation of the J-jump sparsity problem (${\mathcal{S}}_J$). However, we see that this formal connection is not given analytically.

Theorem 3.1 —

The problems (2.5) and (${\mathcal{S}}_J$) are not equivalent. More precisely, if u* is a solution of the Potts problem (2.1) with γ>0 then it is also a solution of the constrained problem (${\mathcal{S}}_J$) with parameter k=∥∇u*∥₀. On the other hand, a minimizer of (${\mathcal{S}}_J$) need not necessarily be a minimizer of (${\mathcal{P}}_{\gamma }$) – not even for some parameter.

Proof. —

Because u* is a minimizer of the Potts functional, it minimizes the problem

$$\underset{u}{min}||Au-f|{|}_2^2,\text{s.t.}\parallel \mathrm{\nabla }u{\parallel }_0=k.$$

We further have that $||Av-f|{|}_2^2>||A{u}^{\ast }-f|{|}_2^2$ for all v with ∥∇v∥₀<k. This is because ∥∇v∥₀<∥∇u*∥₀, and u* is a minimizer of the Potts functional (${\mathcal{P}}_{\gamma }$). Thus, u* is a solution of (${\mathcal{S}}_J$), which shows the first assertions.

To show the second assertion, we give an example of a solution of (${\mathcal{S}}_J$) which is not a solution of (${\mathcal{P}}_{\gamma }$). To this end, we consider f=(0,2,0), A=id. For J=0, we get the solution $u^0=(\frac{2}{3},\frac{2}{3},\frac{2}{3}).$ It has functional value $P_{\gamma }(u^0)=\frac{8}{3}.$ The possible solutions, for J=1, u¹=(0,1,1) and u¹=(1,1,0), attain the functional value P_γ(u¹)=γ+2. The 2-jump solution u²=f has the functional value P_γ(u²)=2γ. It follows that P_γ(u₁)>P_γ(u₀) for all γ>1 and that P_γ(u₁)>P_γ(u₂) for γ<2. Hence, there is no γ>0 such that the solutions for J=1 of (${\mathcal{S}}_J$) are solutions of (${\mathcal{P}}_{\gamma }$). This shows the second assertion. ▪

The above proposition shows that it can happen that even (theoretically) scanning the whole parameter range of γ of the Potts problem (${\mathcal{P}}_{\gamma }$) will not even yield at least one (not speaking about all) J-jump sparse solution for some J.

We learned that theorem 3.1 can also be proved as follows: one rewrites (${\mathcal{P}}_{\gamma }$) and (${\mathcal{S}}_J$) as the equivalent sparsity problems (2.8) and (2.16) and uses the recent results by Nikolova [51] on the relation between these sparsity problems. There, under additional assumptions, also quasi-equivalence has been shown. For A=id, this has been already addressed in, e.g. [26]. However, the proof next to the theorem 3.1. is short and instructive, and moreover, it generalizes to arbitrary data terms of the form $||Au-f|{|}_p^p,$ p≥1, whereas the equivalence to the sparsity problems is only true for p=2.

In the following theorems, we always assume that the measurement matrix A fulfills ∥A∥<1 with respect to the operator norm on ℓ². This is a set-up that can always be achieved by rescaling. More precisely, multiply the functional under consideration with λ², where λ is chosen such that ∥λA∥<1. This results in a corresponding problem with rescaled data λf, and rescaled parameters for which our results apply (because ∥λA∥<1). We note that rescaling with λ<1 results in a smaller step size in the respective algorithm.

We first analyse iterative Potts minimization for which we obtain the following convergence results.

Theorem 3.2 —

We let ∥A∥<1. Then, the iterative Potts minimization algorithm (2.5) converges to a local minimizer of the inverse Potts functional (2.1) for any starting point. The convergence rate is linear. Furthermore, we have the following relation between local minimizers $\mathcal{L},$ global minimizers $\mathcal{G}$ and the fixed points $\mathrm{Fix}(\mathbb{I})$ of the iteration (2.5),

$$\mathcal{G}\subset \mathrm{Fix}(\mathbb{I})\subset \mathcal{L}.$$ 3.1

This result is shown in §3b.

We next consider the constrained J-jump sparsity problem (${\mathcal{S}}_J$). We derive a convergence result for the J-jump sparsity algorithm (2.14). Its formulation is somewhat more involved than theorem 3.2 for the Potts problem (${\mathcal{P}}_{\gamma }$) which is owing additional assumptions. These additional assumptions are usually met in noisy data situations (which are the typical situation in practice) as discussed below.

We recall that u is J-jump sparse if it has at most J jumps, i.e. at most J indices with u_i≠u_i+1.

Theorem 3.3 —

We let ∥A∥<1 and assume that the unrestricted problem of minimizing ∥Au−f∥² with respect to $u\in {\mathbb{R}}^L$ has at most one J-jump sparse solution. (This is, for example, the case if A is injective.)

If the unrestricted problem has no J-jump sparse solution, then the iterative J-jump sparsity algorithm (2.14) converges towards a local minimizer of (2.11).

Otherwise, the iterative J-jump sparsity algorithm (2.14) produces iterates u^k that either converge to a local minimizer of (2.11) with (exactly) J jumps or they have a cluster point which is a global minimizer of (2.11) with (strictly) less than J jumps. If, in this situation, f is in the range of A and A is injective, then the iterates converge to a local minimizer (which is a global minimizer when it has (strictly) less than J jumps.)

This result is shown in §3c. We briefly discuss the assumptions of the theorem and give some applications.

We first consider measurements from time/translation-invariant systems with full measurement data. These systems are described by a convolution operator represented by a corresponding Töplitz matrix A. If the Fourier transform of the underlying convolution kernel is non-zero, and we are given full measurement data, A is invertible and theorem 3.3 yields convergence to a local minimizer for any starting point.

Theorem 3.3 also applies to inpainting or missing data situations with noisy data. The simplest cases are missing data problems for direct measurements. Here, A equals the identity matrix with some rows missing, and the data f are a noisy version of the underlying signal with some items removed. Because f is noisy, it is typically not J-jump sparse for a smaller number of jumps J. Therefore, there is typically no J-jump sparse solution of the unrestricted problem, because all such solutions equal f on the non-missing part. Hence, theorem 3.3 may be applied to obtain convergence. Obviously, this argumentation generalizes to missing and noisy data situations for more general problems, in particular to deconvolution problems.

Theorem 3.3 can also be applied to certain missing data situations for noise-free data. Because noise-free data appears rather infrequently in practice, they are not our primary interest. However, for completeness, we give a simple example as example 3.11 in §3c. We note that, in case of non-noisy few data situations, theorem 3.3 is rather restrictive. In this situation, the corresponding statement theorem 3.2 we derived for the Potts problem is stronger because it also deals with this situation without additional requirements.

Besides considering piecewise constant signal models, we also consider piecewise smooth signals. In a discrete set-up, this corresponds to small variations in-between the jumps. In this context, we introduced the iterative Blake–Zisserman minimization algorithm in §2c. Regarding its analysis, we obtain the following convergence results.

Theorem 3.4 —

For ∥A∥<1, the iterative Blake–Zisserman minimization algorithm (2.19) converges to a local minimizer of the Blake–Zisserman functional (2.17) for any starting point. Furthermore, the relation (3.1) holds true in the context of the Blake–Zisserman functionals B_γ,s of (2.17) as well.

This result is shown in §3d.

(b). Analysis of the iterative Potts minimization algorithm

We first need some well-known results for surrogate functionals of the form F(u)=γJ(u)+∥Au−f∥² [19,32,36]. We first need the implementation J(u)=∥∇u∥₀ counting the number of jumps of u. In §3d, we also consider the Blake–Zisserman regularizer $J(u)=\sum _{i}min(|u_i-u_{i-1}{|}^q,s^q)$.

Lemma 3.5 —

Consider the functionals F(u)=γJ(u)+∥Au−f∥² (where, for our purposes, J is either the Potts regularizer J(u)=∥∇u∥₀ or the Blake–Zisserman regularizer $J(u)=\sum _{i}min(|u_i-u_{i-1}{|}^q,s^q).$) We assume that the operator norm of A on ℓ² fulfills ∥A∥<1. Then, we obtain, for the associated surrogate functional, F^surr given by (2.2) (with J as regularizer), that

• — the inequality

  $$F_{\gamma }^{\mathrm{surr}}(u,v)\ge F_{\gamma }(u)$$

  holds for all v; and equality holds if and only if u=v;
• — the functional value F_γ(u^k) of the sequence u^k given by the surrogate iteration $u^{k+1}=\arg \underset{u}{min}{F}_{\gamma }^{\mathrm{surr}}(u,u^k)$ are non-increasing, i.e.

  $$F_{\gamma }(u^{k+1})\le F_{\gamma }(u^k);$$ 3.2
• — the distance between consecutive members of the previous surrogate sequence u^k converges to 0, i.e.

  $$\underset{k\to \mathrm{\infty }}{lim}\parallel u^{k+1}-u^k\parallel =0.$$ 3.3

For proofs of this general statement on surrogate functionals, we exemplarily refer to the above-mentioned papers [19,32,36]. The statements actually hold for general real-valued surrogate functionals and do not rely on the specific structure of the problems considered here.

We now invoke specific properties of Potts functionals. We first show that minimizers of the Potts functional P^id_γ (with A=id) have a minimal jump height which only depends on the scale parameter γ but not on the particular input data.

Lemma 3.6 —

Consider the Potts functional P^id_γ given by (2.6) for data f. Then, there is a constant c>0 which is independent of the minimizer u*, and the data f such that the minimal jump height $h_{min}(u^{\ast })$ of u* fulfills

$$h_{min}(u^{\ast })\ge c.$$ 3.4

Proof. —

We let

$$c=\sqrt{\frac{\gamma }{L}},$$ 3.5

where L is the length of the underlying signal u. We now assume that $h_{min}(u^{\ast })<c,$ which means that the minimizer u* has a jump of height smaller than c. We construct an element u′ with a smaller P^id_γ value which contradicts u* being a minimizer. To this end, denote the (left) jump points of u* by j_i. By assumption there, is some jump point j_i0 such that the corresponding jump height h_i0<c. We let I₁ be the (discrete) interval between j_i0−1+1 and j_i0 (corresponding to the plateau of u* to the left of j_i0) and I₂ be the (discrete) interval between j_i0+1 and j_i0+1 (corresponding to the plateau of u* to the right of j_i0). Here, we use the convention that j_i0−1=0 if j_i0 is the first jump of u*, and j_i0+1=L if j_i0 is the last jump of u*. We let m₁,m₂ and m be the mean of f on I₁,I₂ and I₁∪I₂, respectively. We define

$$u^{\prime }(l)=\{\begin{array}{ll}m& \text{for }l\in I_1\cup I_2\\ u^{\ast }(l)& \text{elsewhere. }\end{array}$$ 3.6

We have by construction that

$$\parallel \mathrm{\nabla }{u}^{\prime }{\parallel }_0=\parallel \mathrm{\nabla }{u}^{\ast }{\parallel }_0-1.$$ 3.7

Furthermore, because u* is a minimizer of P^id_γ, it equals m₁ on I₁ as well as m₂ on I₂. We get, because u* and u′ only differ on I₁∪I₂, that

$$\parallel u^{\prime }-f{\parallel }^2=\parallel u^{\ast }-f{\parallel }^2+l_1|m_1-m{|}^2+l_2|m_2-m{|}^2<\parallel u^{\ast }-f{\parallel }^2+L{c}^2.$$ 3.8

where l₁ is the length of I₁ and l₂ is the length of I₂. Combining (3.7) and (3.8) we obtain

$$\begin{array}{rl}{P}_{\gamma }^{\mathrm{id}}(u^{\prime })& =\gamma \parallel \mathrm{\nabla }{u}^{\prime }{\parallel }_0+\parallel u^{\prime }-f{\parallel }^2\\ & <\gamma \parallel \mathrm{\nabla }{u}^{\ast }{\parallel }_0-\gamma +\parallel u^{\ast }-f{\parallel }^2+L{c}^2\\ & \le \gamma \parallel \mathrm{\nabla }{u}^{\ast }{\parallel }_0+\parallel u^{\ast }-f{\parallel }^2=P_{\gamma }^{\mathrm{id}}(u^{\ast }).\end{array}$$

The last inequality is a consequence of (3.5). Summing up, u′ has a smaller P^id_γ value than u* which contradicts u* being a minimizer. This shows the assertion of the lemma. ▪

Proposition 3.7 —

The iteration (2.5) converges to a local minimizer of (2.1). The convergence rate is linear.

Proof. —

The proof is subdivided into three steps. We first show that the jump sets of the iterates u^k get fixed after sufficiently many iterations. Using this, we proceed by showing that the algorithm (2.5) converges and conclude by showing that the limit point is a local minimizer.

(1) We start out by showing that the jump sets of the u^k get fixed. The iterate u^k of the algorithm (2.5) is a minimizer of a Potts functional P^id_γ (with A=id) given by (2.6) for data d^k=(I−A*A)u^k−1+A*f. The parameter γ is the same for all k. By lemma 3.6, there is a constant c>0 which is independent of u^k and the data d^k such that the minimal jump height u^k fulfills

$$h_{min}(u^k)\ge c,\text{for all }k.$$ 3.9

If now two consecutive members u^k,u^k−1 have different jump locations, then their distance in the ℓ² sense fulfills ∥u^k−u^k−1∥>c/2. This can happen only in the initial steps because by (3.3), we have ∥u^k−u^k−1∥→0 as k increases. In consequence, there is an index K such that all following members u^k have the same jump set.

(2) We use this observation to show the convergence of (2.5). We consider iterates u^k with k≥K (all having the same jump set and all jumps with minimal jump height c) and denote the corresponding (left) jump locations by j_i and the corresponding (discrete) intervals on which the iterates are constant by I_i. Using the notation mean_I(g) for the mean value of g on the interval I, the corresponding orthogonal projection reads

$$P(g):=\sum _i{\mathrm{mean}}_{I_i}(g)1_{I_i}.$$

For all k≥K, we can now write the iteration (2.5) as

$$u^{k+1}=P(d^{k+1})=P((I-A^{\ast }A)u^k+A^{\ast }f).$$ 3.10

Because u^k=Pu^k and P is an orthogonal projection we further obtain

$$P((I-A^{\ast }A)u^k+A^{\ast }f)={(I-(AP)}^{\ast }AP)u^k+{(AP)}^{\ast }f.$$

Hence, the iteration (3.10) may be interpreted as Landweber iteration on the image space P(ℓ²) for the matrix AP and data f. The Landweber iteration converges at a linear rate; cf. e.g. [52]. Thus, the iteration (3.10) convergences and, in turn, we obtain the convergence of (2.5) to some u*.

(3) It remains to show that u* is a local minimizer. Because u* is the limit of the iterates u^k, the jumps of u* also have minimal height c, the number of jumps are equal to those of the u^k for k≥K, and the locations are the same as those of the u^k for k≥K. We choose a vector h and consider u*+th for small $t\in \mathbb{R}.$ If the jump set of h is contained in that of u* and, in turn, in that of the u^k for k≥K, it follows that P_γ(u*+th)≥P_γ(u*) for all t. This is because u* equals the limit of the above Landweber iteration on P(ℓ²) and is thus a minimizer on P(ℓ²). It remains to consider the case where the jump set of h is not contained in that of u*. Then, for small t, t<c/∥h∥, the jump set of the vector u*+th is a proper superset of the jump set of u*. This is because u* has jumps of height at least c. Hence, ∥∇(u*+th)∥₀ ≥∥∇u*∥₀+1. Because N(u)=∥Au−f∥² is a continuous function of u, there is a neighbourhood of u* with |N(u*)−N(u)|<γ for all u in this neighbourhood. Hence, for small enough t, u*+th is contained in this neighbourhood and therefore,

$$\begin{array}{rl}{P}_{\gamma }(u^{\ast }+th)& =\gamma \parallel \mathrm{\nabla }(u^{\ast }+th){\parallel }_0+\parallel (u^{\ast }+th)-f{\parallel }^2\\ & >\gamma \parallel \mathrm{\nabla }{u}^{\ast }{\parallel }_0+\gamma +\parallel u^{\ast }-f{\parallel }^2-\gamma =P_{\gamma }^{\mathrm{id}}(u^{\ast }).\end{array}$$

Together, this shows that u* is a local minimizer of the Potts functional P_γ. ▪

Proposition 3.8 —

The global minimizers 𝒢 and the local minimizers ℒ of the Potts functional (2.1) and the fixed points $\mathrm{Fix}(\mathbb{I})$ of the Potts iteration given by (2.5) (which we here denote by $\mathbb{I}$) fulfill the inclusions

$$\mathcal{G}\subset \mathrm{Fix}(\mathbb{I})\subset \mathcal{L}.$$

Proof. —

We first show that any global minimizer of the Potts functional (2.1) appears as a stationary point of the algorithm (2.5). We start the algorithm with a global minimizer u* as initialization. Then, we have for all v with v≠u*,

$$\begin{array}{rl}{P}_{\gamma }^{\mathrm{surr}}(v,u^{\ast })& =P_{\gamma }(v)-\parallel Av-A{u}^{\ast }{\parallel }^2+\parallel v-u^{\ast }{\parallel }^2\\ & >P_{\gamma }(v)\ge P_{\gamma }(u^{\ast })=P_{\gamma }^{\mathrm{surr}}(u^{\ast },u^{\ast }).\end{array}$$ 3.11

This means that u* is the minimizer of v↦ P^surr_γ(v,u*) and hence the iterate u¹ of the algorithm (2.5) equals u* when the iteration is started with u*. Thus, the global minimizer u* is a stationary point of (2.5).

It remains to show that each stationary point of (2.5) is a local minimizer of the Potts functional (2.1). This has essentially already been done in the proof of proposition 3.7: start the iteration (2.5) with a stationary point u′. Its limit equals u′ which is a local minimizer by proposition 3.7. ▪

Proof of theorem 3.2 —

The statement follows by propositions 3.7 and 3.8. ▪

(c). Analysis of the iterative constrained jump-sparsity algorithm

Here, we analyse the iterative constrained jump-sparsity algorithm (2.14). In analogy to lemma 3.5, lemma 3.9 gathers the relevant facts on constrained surrogate functionals of the form (2.12). Related assertions may be found in [32] where also proofs or sketches of the proof are given. For the sake of completeness and because this case might be less well known, we give short proofs after stating the assertions.

Lemma 3.9 —

For the surrogate functional Q^surr given by (2.12) of the constrained jump-sparsity problem (2.11) we have

• — the inequality

  $$Q^{\mathrm{surr}}(u,v)\ge Q(u)$$

  holds for all v, and equality holds if and only if u=v;
• — the functional value Q(u^k) of the sequence u^k given by the surrogate iteration $u^{k+1}=\arg \underset{u}{min}{Q}^{\mathrm{surr}}(u,u^k)$ are non-increasing, i.e.

  $$Q(u^{k+1})\le Q(u^k);$$ 3.12
• — the distance between consecutive members of the surrogate sequence u^k (defined above) converges to 0, i.e.

  $$\underset{k\to \mathrm{\infty }}{lim}\parallel u^{k+1}-u^k\parallel =0.$$ 3.13

Proof. —

For the first statement, note that we can rewrite the term ∥u−v∥²−∥Au− Av∥²=〈(I−A*A)(u−v),u−v〉 appearing in the definition (2.12). Because ∥A∥<1 the positive matrix I−A*A has its spectrum in (0,1] and is in particular invertible. Hence, 〈(I−A*A)(u−v),u−v〉≥0 and it equals 0 if and only if u=v.

For the second statement, we consider the kth iterate u^k which is J-jump sparse. We have Q(u^k)=Q^surr(u^k,u^k), and so a J-jump sparse minimizer u^k+1 of Q^surr(⋅,u^k) fulfills Q^surr(u^k+1,u^k)≤Q(u^k). (This is because the candidate u^k is admissible.) Because Q(u^k+1)≤Q^surr(u^k+1,u^k), the second statement holds true.

For the last assertion, note that, for some C>0,

$$\begin{array}{rl}\parallel u^{k+1}-u^k{\parallel }^2& \le C⟨(I-A^{\ast }A)(u^{k+1}-u^k),u^{k+1}-u^k⟩\\ & =C(Q^{\mathrm{surr}}(u^{k+1},u^k)-Q(u^{k+1}))\le C(Q(u^k)-Q(u^{k+1})).\end{array}$$

Here, the last inequality follows from the minimizing property of u^k+1. Now, we have that Q(u^k)−Q(u^k+1)→0 as $k\to \mathrm{\infty },$ because the bounded below sequence Q(u^k) is monotone and thus convergent. This completes the proof. ▪

We need specific properties of a minimizer of the J-jumps sparsity problem (2.15) (with A=id).

Lemma 3.10 —

Consider a minimizer u* of the J-jump sparsity problem (2.15) (with A=id) for data f and assume that the Jth jump of u* has height at most ε. Then, there is a constant C independent of f such that ∥u*−f∥<Cε.

Proof. —

Enumerate the (left) jump points of u* by j_i with i=1,…,J. Let j_i0 be the smallest jump point of u* and let I₀ and I₁ be the intervals of constance of u* neighbouring j_i0 to the left and right, respectively. Let furthermore m₁,m₂ and m be the mean of f on I₁,I₂ and I₁∪I₂. We define u′ by (3.6) and observe as in the proof of lemma 3.6 that

$$\parallel u^{\prime }-f{\parallel }^2<\parallel u^{\ast }-f{\parallel }^2+L{\epsilon }^2,$$ 3.14

where L is the length of u*. By construction, u′ has at least one jump less than u*.

If ∥u′−f∥<C′ε for some C′>0, then the assertion of the lemma is shown because $\parallel u^{\prime }-u^{\ast }\parallel <\sqrt{L}\epsilon$. We enumerate the jump points of u′ by j′_i and let, for a given index l, the integer d_l be the distance of the index l to the left next jump location of u′. We scan u′ starting from the leftmost index l=1, and increase l until |u(l′)−f(l′)|>2^d_l′Lε for some l′. If there is no index l′ fulfilling this inequality, we have found a corresponding C′ and the proof is complete. Otherwise, we construct u′′ with

$$\parallel u^{″}-f{\parallel }^2<\parallel u^{\prime }-f{\parallel }^2-L{\epsilon }^2.$$ 3.15

We attach the index l′ to the jump set of u′ and denote the corresponding left and right intervals I₃ (between l′ and its leftmost neighbour in the jump set of u′) and I₄, respectively. We denote the mean of f on I₃,I₄ and I₃∪I₄ by m₃,m₄ and m′. We define u′′ by

$$u^{″}(l)=\{\begin{array}{ll}{m}_3,& \text{for}\hspace{0.17em}l\in I_3,\\ m_4,& \text{for}\hspace{0.17em}l\in I_4,\\ u^{\prime }(l),& \text{elsewhere.}\end{array}$$

The jump set of u′′ is the index l′ together with the jump set of u′. So, ∥∇u′′∥₀≤J and u′′ is admissible. We show that u′′ fulfills (3.15). By the definition of u′′, we obtain

$$\begin{array}{rl}\parallel u^{\prime }-f{\parallel }^2-\parallel u^{″}-f{\parallel }^2& =\parallel (f-m^{\prime }){|}_{I_3\cup I_4}{\parallel }^2-\parallel (f-m_3){|}_{I_3}{\parallel }^2-\parallel (f-m_4){|}_{I_4}{\parallel }^2\\ & =|I_3|{(m_3-m^{\prime })}^2+|I_4|{(m_4-m^{\prime })}^2.\end{array}$$ 3.16

Here, the symbols |I₃|,|I₄| denote the length of the corresponding intervals. We consider the interval I₃. For all indices l in I₃ smaller than l′, we have that |u(l)−f(l)|≤2^d_lLε and, for the index l′ (which is the last in I₃ by construction), that |u(l′)−f(l′)|>2^d_l′Lε. Hence, |m₃−m′|>Lε/|I₃|, and therefore,

$$|I_3|{(m_3-m^{\prime })}^2>L{\epsilon }^2.$$

Plugging this into (3.16) shows (3.15). Now, we combine (3.15) and (3.14) to obtain

$$\parallel u^{″}-f{\parallel }^2<\parallel u^{\prime }-f{\parallel }^2-L{\epsilon }^2<\parallel u^{\ast }-f{\parallel }^2$$

with u′′ having at most J jumps. This contradicts u* being a minimizer and so shows the assertion. ▪

We next give the proof of theorem 3.3.

Proof of theorem 3.3 —

We arrange the jump height of each iterate u^k in decreasing order and denote the Jth highest jump by h_k. If u_k has less than k jumps we let h_k=0. We distinguish two cases according to whether $\underset{k}{lim inf}{h}_k>0$ or not.

(1) If $c:=\underset{k}{lim inf}{h}_k>0,$ then there is an index K′ such that for all greater indices k each member u_k has J jumps with each jump being at least c>0 in height with c independent of k. By (3.13), we have ∥u^k−u^k−1∥→0 as k increases. Hence, there is an index K such that all following members u^k have the same jump set. This is because otherwise we would have ∥u^k−u^k−1∥>c/2 if u^k+1 and u^k have different jump points. Then, we may argue as in the proof of proposition 3.7 to conclude that, in this case, u^k converges to a local minimizer of (2.11).

(2) If $\underset{k}{lim inf}{h}_k=0,$ then there is a subsequence k_i such that h_ki converges to 0 as i increases. This means that, given ε>0, there is an I such that for all i≥I, the Jth jump of u^k_i is smaller than ε. Lemma 3.10 implies that, for d^k_i defined by (2.14),

$$\parallel d^{k_i}-u^{k_i}\parallel \le C\epsilon$$ 3.17

with C independent of i.

Rewriting the definition of d^k_i in (2.14), we have d^k_i =u^k_i−1 +A*(f−Au^k_i−1). Hence, we may estimate

$$\begin{array}{rl}\parallel A^{\ast }(f-A{u}^{k_i-1})\parallel & \le \parallel d^{k_i}-u^{k_i-1}\parallel \\ & \le \parallel d^{k_i}-u^{k_i}\parallel +\parallel u^{k_i}-u^{k_i-1}\parallel \to 0,\end{array}$$ 3.18

as i increases. Here, the first summand converges to 0 by (3.17), and the second summand converges to 0 by (3.13).

Now, we decompose each

$$u^{k_i-1}=v^{k_i-1}+w^{k_i-1}$$

with $w^{k_i-1}\in \ker A$ and v^k_i−1 in its orthogonal complement. The sequence v^k_i is bounded because otherwise

$$A^{\ast }(f-A{u}^{k_i-1})=A^{\ast }(f-A{v}^{k_i-1})\to \mathrm{\infty }.$$

This would contradict (3.18). Therefore, v^k_i is bounded, and thus contains a convergent subsequence, denoted by v^k_j. We denote the corresponding limit by v*. Using (3.18), we obtain

$$\begin{array}{rl}\parallel A^{\ast }(f-A{v}^{\ast })\parallel & =\underset{j}{lim}\parallel A^{\ast }(f-A{v}^{k_j-1})\parallel \\ & =\underset{j}{lim}\parallel A^{\ast }(f-A{u}^{k_j-1})\parallel =0.\end{array}$$ 3.19

Hence, v* is a minimizer of the unrestricted functional u→∥Au−f∥² on ${\mathbb{R}}^L.$ Then, the solution space for the unrestricted problem is $v^{\ast }+\ker A.$ By (3.19),

$$\mathrm{dist}(u^{k_j},v^{\ast }+\ker A)\to 0\text{as }j\to \mathrm{\infty }.$$ 3.20

Passing to a further subsequence u^k_r of u^k_j, we may assume that the u^k_r have the same jump sets. Hence, they are all elements of the same subspace U with dimension lower than or equal to J. By our assumption, the unrestricted problem has at most one J-jump sparse solution, now denoted u*. This means that either $U\cap v^{\ast }+\ker A=\mathrm{\varnothing }$ or $U\cap v^{\ast }+\ker A=\{u^{\ast }\}.$ (Note that we have chosen a particular subspace which a priori need not be a subspace where u* is in.)

(2a) In the first case, $U\cap v^{\ast }+\ker A=\mathrm{\varnothing }$, these affine subspaces do not intersect which contradicts (3.20). Hence, in this case (where there is no J-jump sparse minimizer of the unrestricted problem), situation (2) of this proof does not apply (and the subsequence we chose before necessary belongs to a subspace also u* is in if it exists.) This shows that if there is no J-jump sparse minimizer of the unrestricted problem, then (1) of this proof applies and we then have the convergence to a local minimizer.

(2b) So, it remains to consider the case where $U\cap v^{\ast }+\ker A=\{u^{\ast }\}.$ Then, u^k_r converges to u* which is a J-jump sparse minimizer; actually, u* has strictly less than J jumps. This is because u^k_r converges to u* which implies that the jump set of u* is contained in the jumps sets of all u^k_r with sufficiently high r. The subsequence u^k_r is chosen such that jump sets are fixed, and the height h_kr of the smallest jump approaches 0 which implies that the limit does not have this jump.

(3) Finally, we show convergence for the case (2b) when the data f lie in the image space of A and A is injective. By (2b), we have that the subsequence u^k_r converges to u* which is a minimizer of the unrestricted problem with less than J jumps. Then, by assumption, ∥Au*−f∥=0. For a given index k we choose the next bigger index k_r of the convergent subsequence u^k_r. Then,

$$\parallel A{u}^k-f\parallel \le \parallel A{u}^{k_r}-f\parallel \to \parallel A{u}^{\ast }-f\parallel =0$$

as $r\to \mathrm{\infty }.$ The first inequality is a consequence of (3.12). Hence, u^k converges because A is lower bounded, i.e. ∥Ax∥≥m∥x∥ for some m>0, as an injective operator on finite dimensional space. Then, the limit equals that of the subsequence which is u*. ▪

As pointed out, we conclude this part by giving a simple example of a particular situation where theorem 3.3 applies to a deconvolution problem with missing data in a noise-free set-up. Although the noise-free set-up is not our primary interest (because it rather infrequently appears in practice), we give such an example for completeness.

Example 3.11 —

We consider cyclic convolution on (the cyclic group consisting of) L elements, which may be described as a cyclic L×L matrix. Let $K=\frac{1}{2}{\delta }_0+\frac{1}{2}{\delta }_1$ be the moving average of size 2 and B be the corresponding cyclic L×L matrix. We let m be a positive integer which divides L, and we remove every mth row of B to obtain A. We consider data f=Ag with g having n<m jumps. Let s be the number of (left) jump points of g in the set {m,2m,…}. We are interested in the corresponding J-jump sparsity problem for J≤m−1−n+s. In this case, we may apply theorem 3.3, because each element in $g+\ker (A)$ has at least m−1−n+s jumps which means that the corresponding unrestricted problem has at most one J-jump sparse solution. If $J<min(m-1-n+s,n),$ theorem 3.3 yields convergence to a local minimizer because $g+\ker (A)$ has no J-jump sparse member. If $J=min(m-1-n+s,n),$ then $g+\ker (A)$ has no or precisely one J-jump sparse member. In the first case, the previous argument applies. In the second case, theorem 3.3 yields either convergence to a local minimizer or a cluster point which is a global minimizer and which has less than $J=min(m-1-n+s,n)$ jumps. Because the latter situation cannot occur (as discussed above), theorem 3.3 also yields convergence in this situation.

(d). Analysis of the iterative Blake–Zisserman minimization algorithm

Here, we analyse the iterative Blake–Zisserman algorithm (2.19). Besides the facts on surrogate functionals gathered in lemma 3.5 we need lemma 3.12 on the minimizers of Blake–Zisserman functionals B^id_γ,s (with A=id). In the context of Blake–Zisserman functionals, an index l with difference |∇u(l)|≥s might be interpreted as a jump. In this interpretation, lemma 3.12 states that minimizers either take a jump of height bigger than s+c or have differences |∇u(l)|≤s−c, i.e. there is a 2c-gap, with c only dependent on the parameters γ,s and q (the underlying qth variation) but not on the input data.

Lemma 3.12 —

Consider the Blake–Zisserman functional B^id_γ,s given by (2.20) for data f and a corresponding (global) minimizer u*. Then, there is a constant c>0 which is independent of u* and the data f such that

$$|\mathrm{\nabla }{u}^{\ast }(l)|\notin (s-c,s+c).$$ 3.21

Proof. —

Lemma 3.12 can be proven directly by a quite tedious argumentation. However, it is also possible to base the argumentation on results derived in [19]. We decided to do the latter.

We consider a global minimizer u* of B^id_γ,s. Then, v*=∇u* is a global minimizer of the functional 𝒥_p defined by (22) in [19]. By [19], Theorem 5.1, the global minimizer v* is a fixed point of the iteration (36) in [19]. For any output vector v of this iteration, there is a constant c>0 which is independent of the iterate v and the data f, but dependent on the parameters γ,s, such that

$$v(l)\notin (s-c,s+c)\text{for all }l.$$ 3.22

This is a direct consequence of [19], Proposition 4.3. Then (3.22) also holds for v* because it is a fixed point. In consequence, u*, which is related to v* via v*=∇u*, fulfills (3.21) which shows the assertion of the lemma. ▪

Proposition 3.13 —

The iteration (2.19) converges to a local minimizer of (2.17).

Proof. —

(1) We first show that the jump sets of the iterates u^k are identical for sufficiently large k. We recall that, in the context of Blake–Zisserman functionals, an index l is a (left) jump point of u, if |u(l+1)−u(l)|≥s. Each iterate u^k of the iterative Blake–Zisserman minimization algorithm (2.19) is a global minimizer of a Blake–Zisserman functional B^id_γ,s of the form (2.20) for certain data d^k. The parameters γ and s are the same for all k. By lemma 3.6, there is a constant c>0 which is independent of u^k and the data d^k such that, for each u^k,

$$|\mathrm{\nabla }{u}^k(l)|\notin (s-c,s+c).$$ 3.23

Now, (3.3) states that ∥u^k−u^k−1∥→0 as $k\to \mathrm{\infty }.$ Hence, for sufficiently large k, |u^k(l)−u^k−1(l)|<c/2 for all l. Therefore, |∇u^k(l)−∇u^k−1(l)|<c. Hence, if u^k−1 has a jump at l, u^k does so, too. This is because

$$|\mathrm{\nabla }{u}^k(l)|\ge |\mathrm{\nabla }{u}^{k-1}(l)|-|\mathrm{\nabla }{u}^k(l)-\mathrm{\nabla }{u}^{k-1}(l)|>s-c,$$

which implies that |∇u^k(l)|≥s+c by (3.23). If u^k−1 has no jump at l,

$$|\mathrm{\nabla }{u}^k(l)|\le |\mathrm{\nabla }{u}^{k-1}(l)|+|\mathrm{\nabla }{u}^k(l)-\mathrm{\nabla }{u}^{k-1}(l)|<s+c,$$

which implies that |∇u^k(l)|≤s−c by (3.23). This shows that the jump sets of the u^k get fixed for sufficiently large k.

(2) We now show the convergence of (2.19). Let K be sufficiently large such that, for all indices k≥K, the iterates u^k have the same jump set. We denote the jump set by Z. When the jump set is fixed, then minimizing the Blake–Zisserman functional (2.20) given by

$$B_{\gamma ,s}^{\mathrm{id}}(u)=\gamma \sum _{i}min(|u_{i+1}-u_i{|}^q,s^q)+\parallel u-d^k{\parallel }_2^2$$

is equivalent to minimizing the functional

$$V_{\gamma }^q(u)=\gamma \sum _{\{i:i\notin Z\}}|u_{i+1}-u_i{|}^q+\parallel u-d^k{\parallel }_2^2$$ 3.24

This is because the jump sets are fixed, and thus the corresponding costs are the fixed number of jumps times γs^q, regardless whatever the candidate u looks like whenever it is admissible. The functional $V_{\gamma }^q$ in (3.24) is a convex functional of qth variation type or TV type for q=1 (appearing in similar form in inpainting problems based on TV type functionals). Replacing the Blake–Zisserman functional B^id_γ,s by the convex functional $V_{\gamma }^q$ in the algorithm (2.19) we obtain a classical forward–backward splitting algorithm (cf. [41]) for the problem

$$F_1(u)+F_2(u):=\gamma \sum _{\{i:i\notin Z\}}|u_{i+1}-u_i{|}^q+\parallel Au-f{\parallel }_2^2.$$ 3.25

Obviously, F₁+F₂ has a minimizer. Furthermore, the Lipschitz constant of the gradient of F₂ equals ∥A∥ which is smaller than 1 by assumption. Thus, we may apply, e.g. [53], Theorem 3.4 to obtain that the corresponding forward–backward splitting algorithm for F₁+F₂ converges to a minimizer of F₁+F₂. Hence, the algorithm (2.19) converges to some limit u*.

(3) We finally show that u* is a local minimizer of the Blake–Zisserman functional B_γ,s. By (2) of this proof, the sequence of iterates fulfills (3.23) which implies that the same is also true for its limit u*, i.e. —∇u*(l)|∉(s−c,s+c).

We first consider an arbitrary vector h and the corresponding perturbation u*+th for small $t\in \mathbb{R}.$ More precisely, we consider h with $\parallel h{\parallel }_{\mathrm{\infty }}<1$ and t with t<c/2. All these candidates u*+th fulfill

$$|(u^{\ast }+th)(l+1)-(u^{\ast }+th)(l)|>|u^{\ast }(l+1)-u^{\ast }(l)|-c\ge s+c-c=s,$$

for all indices l in the jump set Z of u*. Hence, B_γ,s(u*+th)=(F₁+F₂)(u*+th)+|Z| (with F₁+F₂ from (3.25)). Because u* is a minimizer of F₁+F₂ by part (2), we have

$$B_{\gamma ,s}(u^{\ast })=(F_1+F_2)(u^{\ast })+|Z|\le (F_1+F_2)(u^{\ast }+th)+|Z|=B_{\gamma ,s}(u^{\ast }+th),$$

for all h,t with $\parallel h{\parallel }_{\mathrm{\infty }}<1$ and t<c/2. This shows that u* is a local minimizer of the Blake–Zisserman functional B_γ,s. ▪

Proposition 3.14 —

The global minimizers 𝒢 and the local minimizers ℒ of the Blake–Zisserman functional (2.17) are related to the fixed points $\mathrm{Fix}(\mathbb{I})$ of the iterative Blake–Zisserman iteration given by (2.19) (which we here denote by $\mathbb{I}$) by

$$\mathcal{G}\subset \mathrm{Fix}(\mathbb{I})\subset \mathcal{L}.$$ 3.26

Proof. —

We start with the second inclusion and show that each stationary point u′ of $\mathbb{I}$ is a local minimizer of B_γ,s. To this end, we start the iteration (2.19) with a fixed point u′. Its limit equals u′ which is a local minimizer by proposition 3.13.

It remains to show the first inclusion which means that any global minimizer of a Blake–Zisserman functional of the form (2.17) is a fixed point of the iteration (2.19). Starting the algorithm (2.19) with a global minimizer u*, the estimate (3.11) with the Potts functional P_γ replaced by the Blake–Zisserman functional B_γ,s remains valid and we obtain $B_{\gamma ,s}^{\mathrm{surr}}(u^{\ast },u^{\ast })<B_{\gamma ,s}^{\mathrm{surr}}(v,u^{\ast })$ for all v with v≠u*. Hence, the first iterate produced by the autonomous system (2.19) for input u* equals u* which means that it is a fixed point. This shows the statement. ▪

Proof of theorem 3.4 —

The assertion follows by propositions 3.13 and 3.14. ▪

4. Numerical results

We first present a relaxation strategy for the initial steps of the algorithms. This strategy improves the performance of the proposed methods in practice. Then, we employ the derived algorithms for the deconvolution of noisy signals with discontinuities. We also deal with the situation where data is missing. Finally, we consider real data: we estimate steps in the rotation of the bacterial flagellar motor.

(a). A relaxation strategy for the initial steps of the algorithms

Because we deal with non-smooth non-convex problems, the set of (local) minimizers usually is neither unique nor convex. Thus, the solutions produced by our iterative methods typically depend on the starting point. Without additional a priori information, we use the initial guess A*f in the experiments. However, it turns out that this guess is, in practice, often close to an undesired local minimum. Instead of trying to choose another starting point (without additional a priori information), we propose a relaxation strategy for the initial steps of the algorithm. This strategy addresses the empirical observation that the unrelaxed iteration suffers from fixing partitions too early. We note that the corresponding convergence statements remain true unchanged, because only the initial steps of the iterations of the autonomous system are relaxed.

Let us first consider the iterative Potts minimization algorithm (2.5). We start with a small regularization parameter γ_k which we successively increase during the first k₀ iterations until we reach the desired parameter γ. In our examples, we choose the sequence γ_k given by

$${\gamma }_k=\{\begin{array}{ll}\gamma {(1-\frac{k}{k_0})}^2,& \text{if }k<k_0,\\ \gamma ,& \text{else.}\end{array}$$ 4.1

In our experiments, the value k₀=1000 turned out to be a reasonable choice. For the J-jump sparsity problem, we use the sequence

$$J_k=\{\begin{array}{ll}tJ-k,& \text{if }tJ-k>J,\\ J,& \text{else.}\end{array}$$

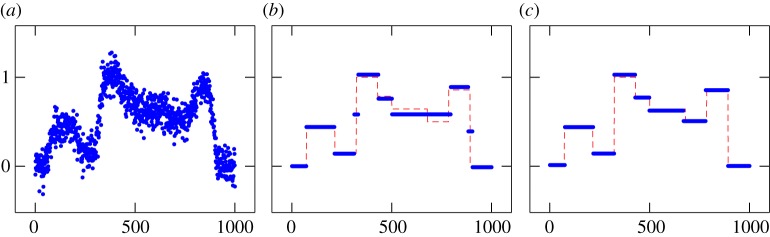
with t=20. For the Blake–Zisserman problem, we keep the s-parameter fixed and use the relaxation (4.1) for the γ-parameter. Figure 1 illustrates the practical gain of the relaxation. There, A represents the convolution with Gaussian kernel of standard deviation 16, and the noise is zero-mean Gaussian distributed with standard deviation σ=0.1.

Figure 1.

Iterative Potts minimization (γ=0.7) for the deconvolution of a noisy signal: effect of the relaxation strategy proposed in §4a. The runtime is 1.1 s without relaxation and 43.8 s with relaxation. (a) Blurred and noisy data. (b) Without relaxation. (c) With relaxation. (Online version in colour.)

(b). Deconvolution of signals with discontinuities

As application, we consider deconvolution problems. Deconvolution problems actually cover all measurement systems A which are translation- or time-invariant.

In our test cases, A is a L×L Töplitz matrix describing a discrete convolution by a Gaussian kernel of standard deviation 16. As common setup, we deal with signals of length L=1000. We simulate data f by f=Ag+η, where g is the underlying true signal and η is a Gaussian-distributed random vector consisting of independent zero mean random variables with standard deviation σ=0.1. To simulate incomplete data, we randomly select a set of 500 missing data points which we remove from the data vector f. We further adapt the matrix A by removing the corresponding rows. For all our algorithms, we employ the following stopping criterium. We stop the iterations when the term ∥u^k−u^k+1∥/(∥u^k∥+∥u^k+1∥), measuring a kind of relative ℓ² ‘distance’ between two consecutive iterates u^k,u^k+1, falls below a threshold which we here chose as 10⁻⁶. A Matlab implementation of the algorithms developed in this work is available online.¹ All experiments were conducted on a desktop computer with Intel Xeon E5 (3.5 GHz).

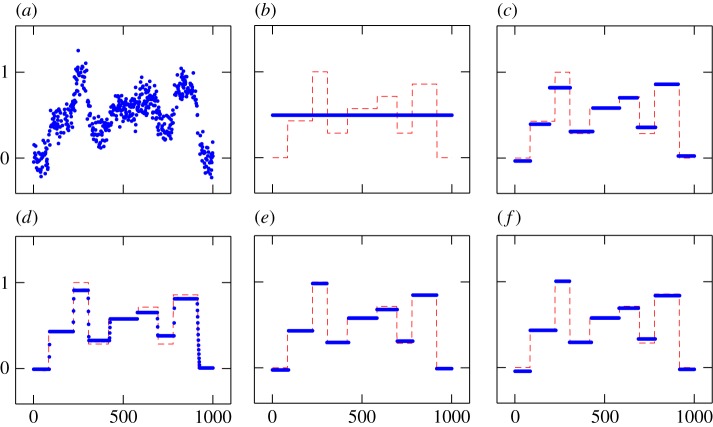
In our first experiment (figure 2), we reconstruct a piecewise constant signal from blurry and noisy data. (In the figures, we display the data points and the computed results as dots and the ground truth as dashed line.) We compare our results to those of iterative thresholding. To this end, we use (2.8) and (2.16) to obtain corresponding separable problems. Then, we apply the iterative thresholding algorithms proposed by Blumensath & Davies [32,37] using the toolbox ‘sparsify 0.5’.² We also compare with total variation minimization, i.e.

$$\text{minimize}\gamma \sum _i|u_i-u_{i-1}|+\parallel Au-f{\parallel }_2^2,$$

which may be seen as the convex state of the art method for the corresponding task. In the experiment (figure 2), we see that total variation minimization tends to produce transitional points at the jumps and to decrease the contrast. The iterative thresholding approach to the Potts problem gets stuck in a constant result. The result of the thresholding approach to the J-jump sparsity problem is satisfactory. We observe an almost perfect reconstruction using the proposed iterative Potts and J-jump sparsity algorithms.

Figure 2.

Reconstruction of a piecewise constant signal. Total variation minimization tends to produce transitional points at the jumps and to decrease the contrast. The iterative thresholding approach to the Potts problem gets stuck in a constant result. The result of the thresholding approach to the J-jump sparsity problem is satisfactory. Iterative Potts minimization and the iterative J-jump sparsity algorithm recover the piecewise constant signal almost perfectly. (a) Blurred and noisy data. (b) Iterative thresholding algorithm for (${\mathcal{P}}_{\gamma }$), γ=0.7. (c) Iterative thresholding algorithm for (${\mathcal{S}}_J$), J=8. (d) Total variation solution, λ=1.5. (e) Iterative Potts algorithm for (${\mathcal{P}}_{\gamma }$) (proposed method), γ=0.7. (f) Iterative J-jump sparsity algorithm for (${\mathcal{S}}_J$) (proposed method), J=8. (Online version in colour.)

Next, we study the influence of the model parameter. In figure 3, we show the results of the iterative Potts algorithm for various parameters γ. We observe that the majority of the partitions is recovered robustly over a large range of parameters.

Figure 3.

Influence of the parameter γ on the result of the iterative Potts algorithm: for smaller values of γ, some additional jumps appear, and for larger values of γ, some jumps vanish. Despite this variation, the result is stable for a large parameter range on the majority of the partitions. (a) Blurred and noisy data. (b) γ=0.25. (c) γ=0.5. (d) γ=1. (e) γ=2. (f) γ=4. (Online version in colour.)

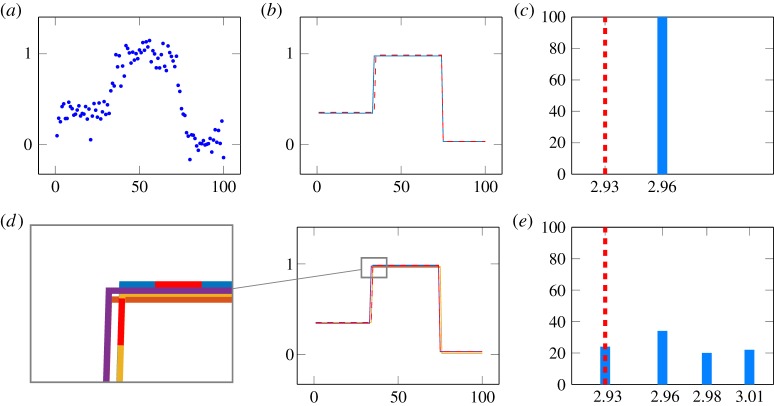
In the next experiment, we look at the influence of the starting value on the result. To this end, we start the iteration with perturbed starting values u⁰=A*(f+η), where η is a Gaussian distributed random vector with zero mean. We consider a particularly simple experiment where we can compute the global minimizer explicitly using brute force. (We used 100 data points, two jumps, Gaussian convolution of standard deviation 3.) In figure 4, we see the results of two series of the iterative Potts algorithm for 100 realizations of η, one with smaller perturbations and one with larger perturbations. For the small standard deviation τ=0.01 of η (nearby starting points), we end up in the same local minimizer, which is rather near to the global minimizer. The case of large standard deviation τ=0.5 of η illustrates the dependence of the solution on the starting point; we get different nearby solutions which also include the global minimizer.

Figure 4.

Influence of the starting point on the result of the iterative Potts algorithm (γ=1): for small random perturbations of the starting point, we end up the same local minimizer for all 100 realizations. The result is near to the global minimizer which is displayed as dashed line (b). For large random perturbations, we obtain four different nearby results (d). The histogram shows their frequency where the abscissa displays their functional values (e). The dashed line indicates the global optimum which could be computed for this particularly simple example by brute force. (a) Blurred and noisy signal. (b) Result with perturbed starting point (τ=0.01). (c) Histogram of the local minimizers (τ=0.01). (d) Results with perturbed starting point (τ=0.5). (e) Histogram of the local minimizers (τ=0.5). (Online version in colour.)

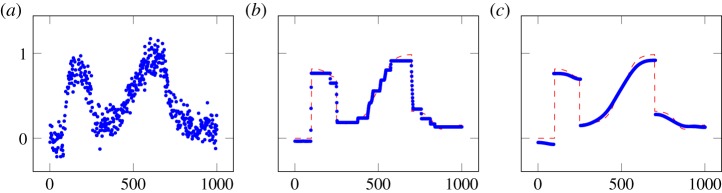
Figure 5 shows the reconstruction of a piecewise smooth function. Total variation minimization produces the typical ‘staircasing’ effects. The iterative Blake–Zisserman algorithm yields a very satisfactory reconstruction.

Figure 5.

Reconstruction of a piecewise smooth signal. Total variation minimization produces so-called staircasing. The iterative Blake–Zisserman minimization reconstructs the underlying signal almost perfectly. (a) Blurred and noisy signal. (b) Total variation solution, λ=1. (c) Iterative Blake–Zisserman solution, γ=1000, s=0.04. (Online version in colour.)

(c). Estimating steps in the rotation of the bacterial flagellar motor

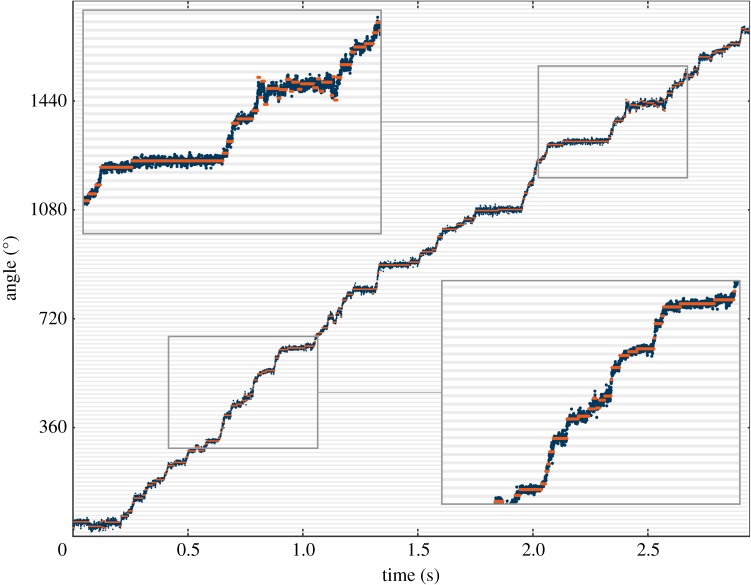
The bacterial flagellar motor is a rotary molecular machine that is embedded in the bacterial cell envelope. It propels many species of swimming bacteria [1,2]. Sowa et al. [1] observed steps in the rotation of the flagellar motor over time; on average, they found approximately 26 steps per revolution. The present dataset is a time series of the angular position of the flagellar motor. The data were acquired using back-focal plane interferometry (BFP) using around 4000 recordings per second. The maximum number of steps that can be detected is around 200 per second [1]. This measurement set-up motivates to model the measurements as convolution with zero mean Gaussian with a standard deviation such that the [−σ,σ] interval spreads over 20 data points. This leads to σ=2.5⋅10⁻³ s. For this rather large dataset of 11 912 elements, we used k₀=10 in the relaxation strategy (4.1). The result of the iterative Potts algorithm is shown in figure 6. The exact runtime for this experiment was 106.6 s. We obtain a reasonable estimate of the steps.

Figure 6.

The points represent the angle of the bacterial flagellar motor over time. The grid lines are in a distance of (360/26)≈13.8 degree. We obtain a reasonable estimate of the steps using the iterative Potts algorithm (solid line, γ=900). (Original data by courtesy of Y. Sowa et al. [1].) (Online version in colour.)

5. Conclusion and future research

We have considered the problem of restoring signals with discontinuities from indirect noisy measurements. For piecewise smooth signals, we have employed Blake–Zisserman functionals. We have derived an iterative Blake–Zisserman minimization algorithm. We have shown its convergence to a local minimizer. For piecewise constant signals, we have considered the Potts and the J-jump sparsity problem. We have seen that these two problems are related but not equivalent. For both problems, we have derived iterative algorithms and obtained convergence results. We have shown the practical potential of all proposed methods in numerical experiments on signal deconvolution. In particular, the proposed methods are preferable to total variation-based relaxation for jump/discontinuity/step detection.

Future research includes the extension of the proposed approaches to the multivariate set-up.

Data accessibility

Data and code are available at http://pottslab.de/.

Author contributions

The paper was developed and written by both authors.

Funding statement

This work was supported by the German Federal Ministry for Education and Research under SysTec grant no. 0315508. A.W. acknowledges support by the Helmholtz Association within the young investigator group VH-NG-526. M.S. acknowledges support from the European Research Council under the European Union's Seventh Framework Programme (FP7/2007-2013) / ERC grant agreement no. 267439.

Conflict of interests

We declare we have no competing interests.