1. Introduction
Volume computed tomography dose index (CTDIvol) and dose length product (DLP) values are frequently used to represent radiation doses from a CT scan. The limitation of CTDIvol and DLP is that they are surrogates for patient dose, providing information about the scanner output for only a very specific standardized condition [1]. The dose received by a patient depends on both patient size and scanner output. Turner et al. showed that using CTDIvol as a normalization factor, organ dose estimates can be obtained for a specific patient size [2], and that the relationship to patient size was consistent across scanner models [3]. Their results showed a promising approach to estimating size-dependent, scanner-specific, and exam-specific organ doses based on patient size and the CTDIvol reported by the scanner. Hence, obtaining accurate information about patient size is crucial to estimating patient dose in CT.
Report 204 from the American Association of Physicists in Medicine (AAPM) described the use of a size metric that involved the physical dimensions of the patient (anteroposterior [AP], lateral, AP+lateral, or effective diameter), in combination with scanner output (CTDIvol), to determine size-specific dose estimates (SSDE) from CT scanning [4]. Patient dimension can be determined using physical or electronic tools. Physical devices, such as the calipers that were frequently used in radiography before the routine use of phototiming, may be used to measure patient thickness in the AP or lateral directions. Alternatively, electronic measurement tools can be used to measure physical dimensions from either the CT localizer radiograph or an axial CT image. The conversion factors used to calculate SSDE from CTDIvol reported in AAPM Report 204 were derived from experimental and Monte Carlo data and normalized to patient size in terms of water- or tissue-equivalent materials.
For the task of calculating SSDE, geometric size was used as a surrogate for a patient's x-ray attenuation. However, x-ray attenuation is the fundamental physical parameter affecting the absorption of x-rays and is thus more relevant than geometric patient size in determining the radiation dose absorbed by the patient. For example, regions of the thorax and abdomen could have the same external physical dimensions. However, because the lungs are less dense and of different composition than abdominal tissue, the thorax would attenuate fewer x-ray photons than would the abdomen. For the same scanner output (CTDIvol), the thorax region would experience a higher radiation fluence and, hence, have a higher absorbed dose than an abdominal region having the same geometric dimensions. While CT operators can measure a patient's AP or lateral width, they currently have no practical way to measure attenuation. Both a CT localizer radiograph and CT projection data are measurements of the integrated x-ray attenuation along a ray path, and a CT image is a cross-sectional map of the linear attenuation coefficients of the materials in the image, normalized to the linear attenuation of water. Therefore, the CT localizer radiograph, the CT projection data, and the CT image all contain information that can be used to estimate patient attenuation.
The charge of AAPM Task Group 220 was to develop a robust and scientifically sound metric for automatically estimating patient size in CT that would account for patient attenuation and allow routine determination of SSDE for all patients, with little or no user intervention. This task group had a specific goal of developing a practical, standardized approach to estimating patient size that could be implemented by CT scanner manufacturers and others using CT localizer radiographs, axial CT images, or other data derived from the scanning process (e.g., projection data). Advantages and limitations of different methods were considered during task group deliberations and are summarized in this report. This includes comparing the SSDE calculated using various geometric size metrics, such as AP or lateral dimensions and effective diameter, and attenuation metrics, such as water equivalent diameter. Finally, recommendations are presented on the adoption and implementation of a standardized approach to estimating patient size.
This report is organized as follows. First, the concept of water equivalent diameter (Dw) is presented, and the methodology of calculating it from either a CT image or a CT localizer radiograph image is described. Second, data are provided comparing the accuracy of Monte Carlo dose estimates made using geometrical-based versus attenuation-based metrics for a series of virtual abdomen and thorax phantoms and their respective virtual CT images, and for patient images. Third, data are provided comparing Dw calculations from CT image and CT localizer radiograph phantom measurements. Fourth, practical considerations involved in implementing either approach are discussed, and recommendations for users and for manufacturers are provided. Finally, a road map for commercial adoption is suggested such that both patient size and SSDE can be calculated in a robust and consistent fashion across CT scanner manufacturers, and the resultant values stored in either the DICOM image header or the DICOM-structured dose report.
2. Water Equivalent Diameter (Dw)
Previous work has expressed the x-ray attenuation of a patient in terms of a water cylinder having the same x-ray absorption [5-9]. The area and diameter of such a cylinder of water are referred to as the water equivalent area (Aw) and water equivalent diameter (Dw), respectively. While the concepts of water equivalent area and diameter were proposed in these studies, doses to the scanned object and its water equivalent cylinder were not actually compared in order to demonstrate that use of a water equivalent cylinder to estimate the dose of an object would yield the correct dose to that object. This question was evaluated by Wang et al., who used Monte Carlo and analytical approaches to demonstrate that because clinical CT systems use a beam-shaping filter, use of water equivalent diameter to estimate an object's dose indeed yields an accurate value for absorbed dose [9].
2.1. Determination of Dw from the CT Image
The attenuation values, or CT numbers, in the axial CT image are expressed using a special unit known as Hounsfield Units (HU):
| (1) |
where μ(x,y) is the linear attenuation coefficient for a voxel in an axial CT image at position (x,y). Because μ(x,y) is normalized to the attenuation of water in the definition of CT number, Aw can be represented in terms of CT numbers, as shown in Equation 2,
| (2a) |
| (2b) |
where Apixel is the area of a pixel in the CT image and CT(x,y) is the CT number of a voxel. The parameter α determines the weighting of the linear attenuation coefficients relative to water. In previous works on the estimation of Aw from CT images [5–7], a linear dependence (α = 1) was assumed. Wang et al. used analytical and Monte Carlo methods to demonstrate that this assumption is valid when a bowtie filter is used for CT scanning [9].
Aw can be calculated using the mean CT number within a region of interest (ROI). The ROI must be large enough to include the entire patient cross section, but should not include irrelevant objects such as the patient table, since it is only the dose to the patient that is of interest. Equation 2b can then be expanded as,
| (3a) |
| (3b) |
| (3c) |
| (3d) |
where is the mean CT number in the ROI, Npixel is the number of pixels in the region of interest, and , which is the total area of the ROI. The ROI may include the air surrounding the patient, since voxels that have an attenuation coefficient of nearly zero negligibly change the value of the sum in Equation 2b. The water equivalent diameter, Dw is equal to:
| (4a) |
| (4b) |
Thus, Dw of an object can be calculated from the mean CT number in an ROI containing that object. The mean CT number can be evaluated using tools readily available on most CT operator consoles or workstations, although this would require user manual intervention, which may not be practical. Alternatively, automatic segmentation algorithms could be used.
2.2. Determination of Dw from the CT Localizer Radiograph
Estimating Dw from axial CT images can only be performed after the CT scan is finished and images are reconstructed. However, knowledge of patient attenuation may be desirable in order to calculate SSDE prior to scanning. Two studies have shown that patient attenuation can be estimated using the CT localizer radiograph, although the results were not described in terms of Dw [6,7]. Wang et al. derived the expected value of Dw from the CT localizer radiograph image and demonstrated agreement with the results obtained from the axial CT image using a range of phantoms [8, 9].
Conceptually, each horizontal line of a CT localizer radiograph image is associated with a different section of anatomy along the z-axis of the patient; the section width along the z-axis is determined by the collimation settings used by the manufacturer. Each pixel in a CT localizer radiograph image is associated with an x-ray path from the focal spot, through the patient, to the detector, and the pixel value is proportional to the total attenuation along this x-ray path (typically referred to as a ray sum). The width of each ray sum is determined by the detector spacing S. The total attenuation through a patient is the sum of the linear attenuation coefficients (μi) of each tissue type times their associated lengths (li) along the path of the x-ray beam. It should be noted that the line integral of the attenuation in a CT localizer radiograph will include attenuation of the patient table that must be accounted for in the calculation of Dw.
Because Aw is linearly dependent on the object attenuation, the equivalent path length through water can be found by normalizing the total attenuation by μwater, which is represented by the water equivalent length (Lw),
| (5) |
Assuming that the pixel values in an appropriately scaled CT localizer radiograph represent ray sums having a mean width at isocenter equal to the detector spacing S at isocenter, the water equivalent area associated with each ray sample is equal to Lw × S. An estimate of the overall water equivalent attenuation of the patient at a particular position along the z-axis can be determined by summing the attenuation associated with each ray sample. That is,
| (6) |
where the sum is taken over a horizontal line of a CT localizer radiograph. Having computed Aw, Dw can be easily obtained using Equation 4a.
3. Comparison between Geometric- and Attenuation-based Metrics
Using Monte Carlo simulation, the average dose to simulated abdomen and thorax phantoms was calculated for adult and pediatric models, as described in Khatonabadi et al. [10]. A bowtie filter was used for all abdomen and thorax phantoms in the Monte Carlo method to simulate a realistic scanning scenario. The Dw of each virtual phantom was calculated with Equation 4b. The radiation dose to a water cylinder was obtained for each Dw value using the same Monte Carlo method and compared with the dose to its corresponding abdomen or thorax phantom. The use of attenuation information did not affect the accuracy of dose estimates in the abdomen, but, as expected, it increased the accuracy of dose estimates for the thorax.
In separate work using patient image data and a validated Monte Carlo technique for estimation of organ dose, Khatonabadi et al. [10] calculated dose to the lungs and kidney for both fixed tube current and modulated tube current scenarios. The correlation of two patient size metrics (effective diameter derived only from cross-sectional area and Dw derived using Equation 4b) to normalized organ dose was determined using the mean CTDIvol from the thoracic (lung) or abdominal (kidney) regions. For the kidney, better correlation was observed for Dw than for effective diameter (R2 = 0.89 and 0.78, respectively). For the lung, better correlation was again observed for Dw compared to effective diameter (R2 = 0.92 and 0.78, respectively).
These and other Monte Carlo studies are consistent with theoretical predictions that dose is most accurately estimated when patient attenuation is taken into account in estimating patient size.
4. Comparison between Dw from CT Localizer Radiographs and Dw from CT Images
Wang et al. studied three sets of abdomen phantoms and two types of thorax phantoms for size ranges from neonate to large adult (Figure 1) [8]. The AP and lateral dimensions and cross-sectional area of the abdomen and thorax phantoms were measured from CT images. Calibration of CT localizer radio-graph pixel values to water thickness was performed using a series of custom-made, torso-shaped phantoms filled with water, which were used to create a variety of thicknesses of water along the AP axis (Figure 1b). For each of the phantoms, effective diameter was calculated using two geometry-based methods: (1) taking the average of lateral and AP dimensions of the phantom and (2) calculating from the cross-sectional area of the phantom. Two attenuation-based methods were used to calculate Dw: (1) using the CT image and (2) using the CT localizer radiograph image.
Figure 1.
Phantoms used for estimating Dw from CT localizer radiographs and CT images: (a) water cylinders, (b) torso-shaped phantoms with a PMMA shell filled with water, (c) water equivalent torso phantoms, (d) semi-anthropomorphic thorax phantom with extension rings for mimicking larger patient sizes, and (e) anthropomorphic thorax phantom.
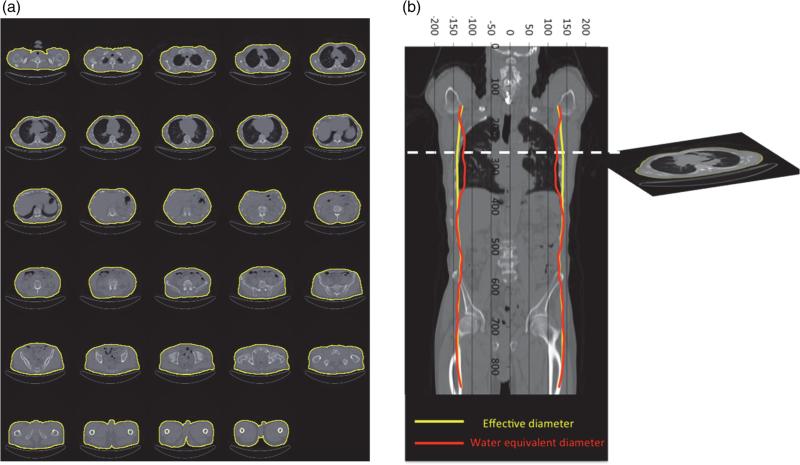
Calculated values of effective diameter and Dw for the abdomen and thorax phantoms are listed in Table 1 (abdomen) and Table 2 (thorax). Results were normalized to Dw values calculated using the CT images. For abdomen phantoms, Dw was consistently larger than the effective diameter, although the difference was no larger than about 5% (Table 1). In thorax phantoms, effective diameter, which considers only geometry, was 4.3% to 21.5% larger than Dw, which takes into account object attenuation (Table 2). For thorax and abdomen phantoms, Dw calculated using the CT localizer radiograph was very similar to the CT image-based method, which is consistent with the theoretical equivalence of these two methods shown in Section II. Dw calculated using the CT localizer radiograph was consistently larger compared to Dw calculated using the CT image, although the difference was no larger than 4%. Figure 2 provides a visual comparison between effective diameter and Dw in a patient data set: effective diameter is equivalent to Dw in the abdomen, but is greater than Dw in the thorax. Thus if attenuation is not considered, patient size will be overestimated in the thorax, leading to an underestimation of SSDE.
Table 1. Abdominal phantom.
AP and lateral dimensions, effective diameters calculated using phantom dimensions, and water equivalent diameters (Dw) calculated using CT images and CT localizer radiographs. Effective and water equivalent diameter values were normalized to Dw calculated from the CT images. The absolute value of Dw calculated using the CT image is shown in parentheses. (Adapted with permission from Wang et al. [8].)
| Phantom | Phantom Size | Phantom Dimension (cm) | Effective Diameter (%) | Water Equivalent Diameter (%) | |||
|---|---|---|---|---|---|---|---|
| AP | LAT | (AP + LAT)/2 | From CT Image** | From CT Localizer Radiograph | |||
| Water Cylinder | 20 cm | 20 | 20 | 98.0 | 98.0 | 100 (20.4) | 101.0 |
| 30 cm | 30 | 30 | 98.0 | 98.0 | 100 (30.6) | 102.0 | |
| Abdomen Water Phantom | 15 cm*^ | 11.2 | 15 | 97.0 | 98.5 | 100 (13.5) | 103.7 |
| 20 cm* | 14.9 | 20 | 97.2 | 98.9 | 100 (18.0) | 102.2 | |
| 25 cm* | 18.6 | 25 | 96.0 | 98.2 | 100 (22.7) | 100.9 | |
| 30 cm* | 22.4 | 30 | 96.3 | 98.2 | 100 (27.2) | 100.7 | |
| 35 cm* | 26.1 | 35 | 96.8 | 98.7 | 100 (31.6) | 101.6 | |
| 40 cm* | 29.8 | 40 | 96.7 | 98.6 | 100 (36.1) | 101.7 | |
| 45 cm* | 33.6 | 45 | 97.0 | 99.0 | 100 (40.5) | 102.5 | |
| Tissue Equivalent Abdomen Phantom | Newborn | 8.9 | 10.6 | 96.1 | 99.0 | 100 (10.2) | 102.9 |
| 1 Yr | 11.4 | 14 | 95.5 | 98.5 | 100 (13.3) | 101.5 | |
| 5 Yr | 13.9 | 18 | 95.8 | 98.8 | 100 (16.7) | 101.2 | |
| 10 Yr | 15.9 | 20.6 | 95.8 | 98.4 | 100 (19.1) | 101.0 | |
| 15 Yr | 18.4 | 24 | 95.1 | 98.2 | 100 (22.3) | 100.9 | |
| Small Adult | 22 | 30 | 95.6 | 98.5 | 100 (27.2) | 101.1 | |
| Medium Adult | 24.9 | 32.4 | 96.3 | 99.3 | 100 (29.8) | 101.7 | |
| Large Adult | 30.7 | 38.9 | 95.1 | 98.4 | 100 (36.6) | 101.4 | |
| Mean ± Standard Deviation | 96.4 ±0.9% | 98.5 ±0.4% | - | 101.6 ±0.8% | |||
AP = anteroposterior, LAT = lateral
Lateral width of the phantom
Absolute value in parenthesis (cm)
Size of a newborn.
Table 2. Thorax Phantom.
AP and lateral dimensions, effective diameters calculated using phantom dimensions, and water equivalent diameters Dw calculated using CT images and CT localizer radiographs. Effective and water equivalent diameter values were normalized to Dw calculated from the CT images. The absolute value of Dw calculated using the CT image is shown in parentheses. (Adapted with permission from Wang et al. [8].)
| Phantom | Phantom Size | Phantom Dimension (cm) | Effective Diameter (%) | Water Equivalent Diameter (%) | |||
|---|---|---|---|---|---|---|---|
| AP | LAT | (AP + LAT)/2 | From CT Image** | From CT Localizer Radiograph | |||
| Tissue Equivalent Thorax Phantom | 30 cm* | 20 | 30 | 119.6 | 121.5 | 100 (20.9) | 100.0 |
| 35 cm* | 25 | 35 | 109.9 | 112.5 | 100 (27.3) | 100.7 | |
| 40 cm* | 30 | 40 | 105.4 | 107.5 | 100 (33.2) | 101.5 | |
| Anthro-pomorphic Phantom | 21.6 | 31.8 | 104.3 | 112.1 | 100 (25.6) | 100.0 | |
| Mean ± Standard Deviation | 109.8 ±7.0% | 113.4 ±5.9% | - | 100.6 ±0.7% | |||
AP = anteroposterior, LAT = lateral
Lateral width of the phantom
Absolute value in parenthesis (cm).
Figure 2.
Comparison of effective diameter and Dw for a patient data set. A threshold of −383 HU was used to remove the patient table for every 10th image in the data set. The segmented ROIs are shown in (a). The area and mean CT number of the ROI in each axial image were used to calculate effective diameter and Dw,, which are superimposed on a coronal reformation of the patient data in (b). This visually demonstrates that the use of effective diameter will overestimate Dw in the thorax.
5. Implementation Issues and Recommendations When a CT Localizer Radiograph is Used to Determine Patient Size
5.1. Measurement of AP or Lateral Dimensions from a CT Localizer Radiograph
The American College of Radiology (ACR) has developed a CT Dose Index Registry for the purposes of gathering large samples of CT dose index data from across the nation. These data will greatly facilitate the establishment of a national reference and achievable dose levels [11–13]. However, there are currently no established measures of patient size or surrogates, such as weight or body mass index, recorded in the DICOM metadata. This presents a considerable barrier to the use of the acquired data, as binning of similarly sized patients cannot be accomplished without prohibitively large amounts of manual data entry to inform the registry of each patient's size. Thus, in the absence of automated methods of calculating Dw being widely available, the data collection software was modified by the ACR to allow the collection of localizer radiographs (starting with Triad version 4.0). Although CT localizer radiographs are not required for the registry, they are highly encouraged, as this allows more meaningful analyses of registry data according to patient size categories, or by calculating SSDE.
To facilitate collection of AP or lateral dimensions from a transmitted lateral or AP CT localizer radiograph, respectively, the registry software uses a segmentation algorithm to automatically extract a patient's body contour and measure a patient's width. Christianson et al. evaluated a range of segmentation techniques for robustness and accuracy across a range of patient data sets [14]. Additionally, they determined an empirical correction factor for use in the thorax to account for the differences in tissue density between water and lungs [14]. A pixel value threshold of 30% of the maximum value along each row of the CT localizer radiograph and a correction factor of 0.85 was used to adjust for the lower attenuation of lung tissue. SSDE values calculated based on their segmentation and correction method agreed with attenuation-based methods of estimating Dw from cross-sectional CT images to within 5% [14].
5.2. Measurement of Dw from the CT Localizer Radiograph
Prior to the scan, some estimate of patient attenuation may be desired, either for determining the scanner output that should be delivered to achieve the required level of image quality or for calculating SSDE prior to scan initiation. The CT localizer radiographs are created from patient attenuation measurements and are used by manufacturers to prescribe the tube current modulation to be used in the patient scan [15]. Thus, they can be used to estimate Dw. Several important issues, however, may limit the accuracy of this approach.
5.2.1. Need for Calibration of CT Localizer Radiograph Pixel Values in Terms of Water Attenuation
Unlike CT numbers, the pixel values of a CT localizer radiograph image are not reported in absolute units; the relationship between attenuation and pixel value can vary among scanner models and manufacturers. Therefore, the CT localizer radiograph-based method to estimate Dw is not recommended for the user community because it requires careful calibration of CT localizer radiograph pixel values in terms of water attenuation. Although this can be established through a series of experiments, the constancy of such calibrations over time, across software versions, or even across scanners from the same manufacturer, has not been established. Therefore, we recommend that the CT localizer radio-graph image method to estimate Dw be implemented only by scanner manufacturers, who know the relationship between water attenuation and CT localizer radiograph pixel values.
5.2.2. Need to Account for Patient Table Attenuation
The pixel values in the CT localizer radiograph are a measure of the total x-ray attenuation of all material located between the x-ray source and the detector. This includes the attenuation of the patient and the patient table supporting the patient. Thus, in order to estimate only the attenuation of the patient, the attenuation of the patient table must be known for each z position of the table, expressed in terms of water equivalent path length and subtracted from the total attenuation measured in the CT localizer radiograph. Failure to correct for the attenuation of the table will cause greater errors in estimating Dw for smaller patients than for larger patients.
5.2.3. Need for Use of Non-edge-enhanced CT Localizer Radiographs
To assist the operator in identifying anatomic landmarks, various edge-enhancement filters are applied by manufacturers to CT localizer radiograph attenuation measurements. These filters can modify the relationship between attenuation and pixel value in a nonlinear fashion. Hence, in order to estimate patient attenuation from a CT localizer radiograph image according to equations 5 and 6, non-edge-enhancing image filters must be used. However, non-edge-enhanced CT localizer radiograph images are not currently available from all manufacturers.
5.2.4. Need for Careful Patient Centering or for Acquiring Orthogonal CT Localizer Radiographs
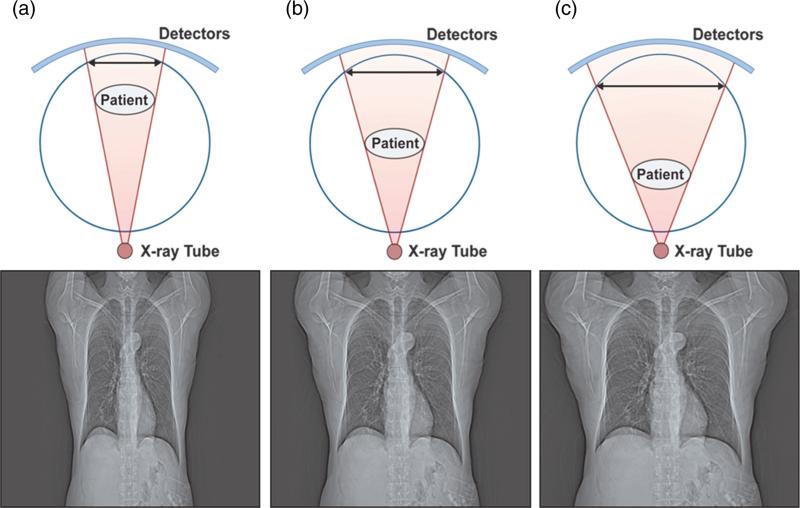
Clinically, the patient table is not always positioned such that the patient is centered in the gantry (Figure 3) [7]. Moving a 30-cm diameter water cylinder 5 cm and 10 cm closer to the x-ray tube was shown to lead to overestimation of Dw by 4.5% and 9.9%, respectively [8]. Moving the table 5 cm farther away from the tube led to underestimation of Dw by 4.2% [8]. These errors happen because CT systems calibrate S (detector spacing) with respect to isocenter. When the patient is farther away from the tube relative to the distance from the tube to isocenter (Figure 3a), the patient's image is minified, and the CT localizer radiograph underestimates the amount of attenuation within the field of view (FOV). Conversely, when the patient is closer to the tube compared to the distance to isocenter (Figure 3c), the patient's shadow is magnified, and the CT localizer radiograph overestimates the amount of attenuation in the FOV. Thus, even if the CT localizer radiograph pixel values are properly calibrated in terms of water attenuation, the magnification error caused by patient mis-centering could lead to errors in size estimation [7, 16].
Figure 3.
Minification (a) or magnification (c) of the patient's lateral dimensions occurs when the patient is not well centered in the FOV (b).
Since it is difficult to guarantee patient centering in practice, correction for this potential error is important. Li et al. proposed a correction algorithm which requires the use of an orthogonal CT localizer radiograph to estimate and correct for patient mis-centering [16]. They found that the error in Dw was linearly dependent on the table height offset caused by mis-centering, but that the use of an orthogonal CT localizer radiograph to more accurately determine the width of each ray sum reduced this error. Because patients are typically easier to center on the table in the left to right direction compared to in the anterior to posterior direction, a lateral CT localizer radiograph may be less susceptible to mis-centering errors.
5.2.5 Recommendation Regarding Use of CT Localizer Radiograph Images to Estimate Dw
This task group considers the value of Dw determined from full FOV axial CT images to be the reference standard for measuring patient x-ray attenuation.
This task group also recognizes that the CT localizer radiograph can be used to calculate reasonable estimates of Dw, but that potential errors can occur when using a CT localizer radiograph to estimate Dw. Because there are some advantages in using CT localizer radiograph images to estimate Dw (e.g., estimates of SSDE can be provided prior to the scan acquisition), and since most manufacturers already use the CT localizer radiograph to estimate attenuation for use with automated exposure control systems, the task group considers this to be an acceptable approach, provided that the implemented method can be shown to determine Dw to within 20% of the reference value over a range of patient sizes and centering conditions. The task group strongly recommends that potential sources of error be taken into account by:
calibrating CT localizer radiograph pixel values in terms of water attenuation,
accounting for patient table attenuation in the calculation of Dw,
using a non-edge-enhancing filter to produce the image used to estimate Dw, and
mitigating patient centering issues through acquiring two orthogonal radiographs or implementing an appropriate correction technique.
Estimates of Dw made from CT localizer radiograph images prior to the scan should be replaced after the scan, when possible, provided that Dw is computed using a full field-of-view (FOV) reconstructed axial image or projection data (which will be discussed in the next section).
6. Implementation Issues and Recommendations when a CT Acquisition is Used to Determine Dw
6.1. Use of Acquisition Data in Projection Space or Image Space
Fundamentally, all information related to the patient's size and attenuation is contained in both the projection and image domains. When care is taken (1) to avoid truncation of views or anatomy (e.g., by making sure that the patient's anatomy is fully contained in the projection data set and in the reconstruction FOV) and (2) to ensure accurate attenuation calibrations (e.g., in water and air) and corrections (e.g., scatter and beam hardening) are performed, the measurements of attenuation should be similarly accurate, whether performed using a reconstructed CT image or from the projection data used to reconstruct the CT image. This assumes that the reconstruction process, including the reconstruction kernel applied, introduces no artifacts or other errors in CT number accuracy. This is typically a safe assumption; however, some reconstruction kernels are edge-enhancing or otherwise nonlinear and can alter CT number accuracy, which is not acceptable for the task of using CT numbers to estimate patient attenuation.
Thus, if images are to be used to estimate Dw, the FOV should cover all patient anatomy in the beam, and a linear, quantitative kernel must be used, possibly requiring additional reconstruction data sets. For the user community, such axial CT images provide the easiest route to determining Dw off-line, using either a user-developed software tool or a third-party software package. In this case, extra reconstructions may be necessary and must be integrated into an acceptable clinical workflow.
For manufacturers, the most efficient commercial implementation may be to perform the calculations in projection space, thus avoiding the need to reconstruct any additional (i.e., full field of view or different kernel) images. In the remaining sections of this report, measurement of Dw from a reconstructed axial CT image is described in detail. It should be understood that sinogram and image data are complementary forms of the same data set, and that either form could be used, provided that the described criteria (such as not truncating any patient information and not including attenuation information for objects that are not part of the patient, like the patient table) are able to be met.
6.2. Measurement of Dw from a Reconstructed Axial CT Image
6.2.1. Need for a Full Field of View (FOV) Reconstruction
Use of the reconstructed axial CT image is an accurate way to estimate the patient attenuation because, by definition, an axial CT image gives a cross-sectional map of tissue attenuation. In order to provide an accurate estimate of Dw, it is essential that all patient tissue be included in the reconstructed image. This requires that a full FOV image encompassing the entire patient cross section be reconstructed. For clinical applications where a full FOV image is not reconstructed, such as for imaging of the heart or spine, an additional reconstruction using the full FOV would be required. To minimize additional reconstruction time, an image thickness of not greater than 5 mm and a nonoverlapping reconstruction interval are recommended. Off-line calculations of Dw can then be performed using these full FOV images.
It is anticipated that Dw will eventually be automatically calculated by the scanner for each reconstructed image and the values stored in yet-to-be-specified DICOM data elements. In this scenario, the manufacturer could automatically reconstruct a full FOV image series using a wide image thickness, nonoverlapping interval, and possibly even a decreased matrix size (e.g., 256 × 256) for the sole purpose of calculating Dw. This process could be fully automated in such a fashion that the user would not ever see this special “low resolution, full FOV image series.” This is analogous to the current practice by some manufacturers of reconstructing very thin axial images in a hidden series from which to generate coronal or sagittal images.
As noted in Section 6.1, the manufacturer could calculate the total attenuation in a projection that includes all of the patient (and the table) and then subtract the known attenuation level of the table off of the integrated attenuation measurement. Details with regard to the numbers of projections required, the preferred projection orientation(s), geometrical factors (e.g., fan or rebinned parallel data sets) are left to the manufacturers’ discretion, albeit no matter which method is selected, the final implementation must yield Dw results that agree with those calculated using full FOV images to within 10%.
6.2.2. Need to Omit Non-patient Sources of Attenuation from the Measurement
When using the axial CT image to estimate patient attenuation, care should be taken to define the ROI to include all of the patient, yet minimal amounts of other attenuating materials, such as the patient table. Including large amounts of the patient table can lead to overestimation of patient attenuation, particularly for very small pediatric patients due to their relatively small size. Li et. al. [16] showed that the CT table can contribute up to 12% of the total attenuation for small objects. A manually drawn ROI that conforms more closely to the patient contour than a circular ROI could be used, but this requires more time and effort by the user. As shown in Wang et al., placing a circular ROI around the patient, without attempting to exclude all portions of the patient table, provides acceptable results [9].
Alternatively, automated methods can perform calculations on a voxel-by-voxel basis, as opposed to having to measure the ROI mean and area, as required by Equation 4b. Instead, voxel-by-voxel calculations can be performed using Equation 3a: In this manner, no ROI needs to be drawn manually by a user or automatically through boundary recognition. Voxels having CT numbers that are essentially air can be identified and ignored. Thus, a simple thresholding can remove all voxels with a CT number below, for example, −900 HU. Then Equation 3d can be used with the remaining voxels in the image. As discussed above, it improves accuracy if the table is not included for very small patient sizes, and table removal could be implemented through manufacturer-provided tools or a table recognition algorithm in the software.
The presence of foreign objects in the beam, particularly highly attenuating objects such as metallic implants or bismuth shields, pose a fundamental limitation to the accuracy of Dw and SSDE calculations. Methods to address these limitations are not addressed by this task group report. However, it should be noted that such overestimation of Dw will lead to an underestimation of SSDE. Conversely, in very large patients having tissue outside the scan FOV (typically 50 cm in diameter), the total attenuation in the beam may be underestimated, which could lead to a small overestimation of SSDE.
7. Longitudinal Position at Which to Measure Dw
Patient dimension and attenuation can vary considerably along the longitudinal axis. When tube current modulation is used, scanner output also varies along the longitudinal axis of a patient according to changes in patient attenuation.
The mean scanner output per rotation normalized to the tube-current time product (CTDIvol/mAs) is easily measured or can be determined from the scanner's accompanying documents. The mean effective mAs per rotation is easily calculated by the scanner, or it can be determined from image header information. By multiplying the mean effective mAs per rotation at every image location along the z-axis with the nominal CTDIvol/mAs, the scanner output at each location can be calculated. This information can be recorded as a series of CTDIvol values for each reconstructed image, which we refer to as CTDIvol(z). SSDE can then be calculated at each position z along the longitudinal direction,
| (7) |
where fDw(z) is the size-specific conversion factor from AAPM Report 204. The mean SSDE over the entire scan range can be expressed as
| (8) |
where N is the total number of images.
This approach requires that Dw be calculated for each table location. This would allow the determination of the mean SSDE over the scan range using the fDw(z) and CTDIvol(z) at each longitudinal position.
Leng et al. showed, however, that the mean SSDE over a scan range calculated using Equation 8 correlated extremely well with a mean SSDE calculated using the Dw from a central image in the scan range and the mean CTDIvol(z) over the entire scan range [17]. Thus, for the purpose of estimating a single SSDE value for a given patient, the “shortcut” of using the scanner-reported mean CTDIvol and the Dw from a central location in the scan range (e.g., the center of the prescribed scan range on the CT localizer radiograph or the central image of the CT images) appears acceptable. It is highly recommended, however, that z-specific values of Dw be provided in a standardized DICOM tag. This may provide future opportunities to estimate organ doses by having attenuation (and mAs information) along the longitudinal patient axis [18].
8. Summary and Road Map for Adoption
This task group was charged with developing and analyzing robust and scientifically sound metrics for automatically estimating patient size in CT that would account for patient attenuation and allow routine determination of SSDE with little or no human intervention (e.g., no drawing of ROIs and no manual calculations). Specifically, the size metric water equivalent diameter was described and two approaches for obtaining this value were evaluated: (a) one based on the CT localizer radiograph and (b) one based on an axial CT image reconstructed using a full FOV.
Pragmatically, patient attenuation needs to be determined using automated methods implemented on the scanner so that a patient-specific size metric can be included as part of the dose report information. This would allow SSDE to be automatically calculated and saved in DICOM data elements. A standardized methodology should be approved by an appropriate standards organization and implemented in a consistent manner by all scanner manufacturers.
This task group recommends:
Adopt water equivalent diameter as the preferred patient size metric. This value reflects the x-ray attenuation of the patient and is a sound descriptor of patient size.
The preferred method to obtain water equivalent diameter values would be that they be calculated from projection or full FOV CT image data. This approach would provide a more robust estimate of patient size compared to use of the CT localizer radiograph. This task group understands that there may be practical limitations to implementing this approach, including the possible need to perform additional full FOV images, which would increase reconstruction time and create more images to review, transfer, and archive.
- A reasonable method to obtain estimates of water equivalent diameter using the CT localizer radiograph must take into account potential sources of error by requiring the following:
- Pixel values are calibrated in terms of water attenuation.
- The attenuation of the table is accounted for in the calculation of Dw.
- Non-edge-enhancing filters are used in producing the image used to estimate Dw.
- Patient centering issues are mitigated by acquiring two orthogonal radiographs or using some other method of correcting for magnification error.
If the CT localizer radiograph method is used, then the Dw and SSDE values after the scan should be automatically calculated and used to replace pre-scan values for Dw and SSDE (estimated using the CT localizer radiograph); these post-scan results are the ones that should be stored in DICOM data elements.
If the difference between the pre- and post-scan values for Dw and SSDE can be shown by a manufacturer to be consistently less than 10% of the pre-scan values across a range of patient size and habitus, the pre-scan values may be used as the final values.
The preferred approach is to obtain Dw values at multiple locations along the z-axis of the patient, at intervals not to exceed 5 mm; however, reasonable estimates of SSDE may be obtained with a single Dw value from the central image of the scanned range.
Both scanner manufacturers and third-party suppliers of dose metric tracking tools need to quickly develop an implementation strategy to allow the appropriate DICOM working groups to include the needed data fields in the next version of the DICOM standard.
To facilitate testing of the various implementation strategies, deidentified test data and the associated reference Dw values should be made available to manufacturers for use in their development and testing processes. Systems that meet the criteria described in this document and produce root mean square errors of less that 10% relative to the reference values for the test patient cases are considered to be compliant with this report's recommendations.
Considering the rapid rate of adoption of SSDE in the clinical and research communities, and given the continued interest in assessing patient-specific dose models, it is imperative that scanner manufacturers and other dose metric tracking software providers automatically calculate Dw at z-axis intervals of no larger than 5 mm and store these data in clearly labeled DICOM data fields, in both the image and the Radiation Dose Structured Report, as soon as possible. Additionally, scanner manufacturers are urged to provide the angular and longitudinal modulation tube current values in a separate DICOM data array to allow CTDIvol and SSDE to be calculated for z-axis ranges that are clinically relevant, e.g., over the entire thorax or over just the heart. While the mean tube current value per image, or over a 5 mm z-axis interval, provide important and useful information, the individual tube current values for different view angles (x-ray source angles) should be provided at reasonable intervals (such as every 1 degree or every 5 degrees).
The strongly expressed goal of the CT stakeholder community is that this work be completed and begin shipping on software versions released in 2016. This will provide users sophisticated metrics for assessing size-specific patient doses in an automated and reproducible manner for use in many quality and safety initiatives.
Appendix
Clarification Regarding the Use of the Term “Effective Diameter” Instead of Dw in AAPM Report 204
The conversion factors in AAPM Report 204 were derived with water- or tissue-equivalent materials. In the case of the PMMA phantoms used by Toth and Strauss, the attenuation was expressed in terms of water attenuation by correcting for the increased density of PMMA relative to water. Thus, although the phrase “effective diameter” was used in the report, all measurements and calculations were in terms of Dw. Thus, in Equation A–1 of AAPM Report 204, which describes the best fit to the data shown in Figures 4–6, patient size is already expressed in terms of Dw:
| (A-1) |
where the coefficients are given in the table below:
| Figure Number | X parameter | Y parameter | a | b |
|---|---|---|---|---|
| 4 | Dw (cm) | Conversion Factor | 3.704369 | 0.03671937 |
| 5 | Dw (cm) | Conversion Factor | 4.378094 | 0.04331124 |
| 6 | Dw (cm) | Conversion Factor | 1.874799 | 0.03871313 |
When Dw values are available, they should be used in Tables 1 and 2 and in Equation A–1 of AAPM Report 204. No additional corrections are required when substituting Dw for effective diameter.
In the thorax, use of effective diameter instead of Dw will lead to an overestimation of patient attenuation and an underestimation of SSDE. However, as noted in AAPM Report 204 and shown in Table 2 of this report, when attenuation is not considered, errors in the estimate of thoracic size are below 20%. In the abdomen, the errors are much smaller, in the range of a few percent. Thus, even though use of Dw is recommended, when only geometric data are available to the user, it is still reasonable to calculate SSDE based on any of the geometric input parameters shown in Report 204: AP, LAT or AP+LAT, or effective diameter.
Additionally, when the cross-sectional area of the patient is known (without attenuation information), use of effective diameter as the input parameter is preferable to the use of AP, LAT, or AP+LAT. This is because knowledge of cross-sectional area allows calculation of effective diameter directly, without any assumptions regarding the shape of the patient (i.e., without assuming that the patient cross-section is elliptical).
In all cases, knowledge of both patient attenuation and cross-sectional area allows the most accurate calculation of Dw. and hence the most accurate calculation of SSDE.
Table A-1.
This table provides conversion factors based on the use of the 32 cm diameter PMMA phantom for CTDIvol. Other than the clarification that the effective diameter in the data table is equivalent to Dw, it is identical to Table 1 in AAPM Report 204.
| Table 1A | Table 1B | Table 1C | Table 1D | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lat + AP | Dw | Conversion | Lateral | Dw | Conversion | AP | Dw | Conversion | Dw | Conversion |
| Dim (cm) | (cm) | Factor | Dim (cm) | (cm) | Factor | Dim (cm) | (cm) | Factor | (cm) | Factor |
| 16 | 7.7 | 2.79 | 8 | 9.2 | 2.65 | 8 | 8.8 | 2.68 | 8 | 2.76 |
| 18 | 8.7 | 2.69 | 9 | 9.7 | 2.60 | 9 | 10.2 | 2.55 | 9 | 2.66 |
| 20 | 9.7 | 2.59 | 10 | 10.2 | 2.55 | 10 | 11.6 | 2.42 | 10 | 2.57 |
| 22 | 10.7 | 2.50 | 11 | 10.7 | 2.50 | 11 | 13.0 | 2.30 | 11 | 2.47 |
| 24 | 11.7 | 2.41 | 12 | 11.3 | 2.45 | 12 | 14.4 | 2.18 | 12 | 2.38 |
| 26 | 12.7 | 2.32 | 13 | 11.8 | 2.40 | 13 | 15.7 | 2.08 | 13 | 2.30 |
| 28 | 13.7 | 2.24 | 14 | 12.4 | 2.35 | 14 | 17.0 | 1.98 | 14 | 2.22 |
| 30 | 14.7 | 2.16 | 15 | 13.1 | 2.29 | 15 | 18.3 | 1.89 | 15 | 2.14 |
| 32 | 15.7 | 2.08 | 16 | 13.7 | 2.24 | 16 | 19.6 | 1.81 | 16 | 2.06 |
| 34 | 16.7 | 2.01 | 17 | 14.3 | 2.19 | 17 | 20.8 | 1.73 | 17 | 1.98 |
| 36 | 17.6 | 1.94 | 18 | 15.0 | 2.13 | 18 | 22.0 | 1.65 | 18 | 1.91 |
| 38 | 18.6 | 1.87 | 19 | 15.7 | 2.08 | 19 | 23.2 | 1.58 | 19 | 1.84 |
| 40 | 19.6 | 1.80 | 20 | 16.4 | 2.03 | 20 | 24.3 | 1.52 | 20 | 1.78 |
| 42 | 20.6 | 1.74 | 21 | 17.2 | 1.97 | 21 | 25.5 | 1.45 | 21 | 1.71 |
| 44 | 21.6 | 1.67 | 22 | 17.9 | 1.92 | 22 | 26.6 | 1.40 | 22 | 1.65 |
| 46 | 22.6 | 1.62 | 23 | 18.7 | 1.86 | 23 | 27.6 | 1.34 | 23 | 1.59 |
| 48 | 23.6 | 1.56 | 24 | 19.5 | 1.81 | 24 | 28.7 | 1.29 | 24 | 1.53 |
| 50 | 24.6 | 1.50 | 25 | 20.3 | 1.76 | 25 | 29.7 | 1.25 | 25 | 1.48 |
| 52 | 25.6 | 1.45 | 26 | 21.1 | 1.70 | 26 | 30.7 | 1.20 | 26 | 1.43 |
| 54 | 26.6 | 1.40 | 27 | 22.0 | 1.65 | 27 | 31.6 | 1.16 | 27 | 1.37 |
| 56 | 27.6 | 1.35 | 28 | 22.9 | 1.60 | 28 | 32.6 | 1.12 | 28 | 1.32 |
| 58 | 28.6 | 1.30 | 29 | 23.8 | 1.55 | 29 | 33.5 | 1.08 | 29 | 1.28 |
| 60 | 29.6 | 1.25 | 30 | 24.7 | 1.50 | 30 | 34.4 | 1.05 | 30 | 1.23 |
| 62 | 30.5 | 1.21 | 31 | 25.6 | 1.45 | 31 | 35.2 | 1.02 | 31 | 1.19 |
| 64 | 31.5 | 1.16 | 32 | 26.6 | 1.40 | 32 | 36.0 | 0.99 | 32 | 1.14 |
| 66 | 32.5 | 1.12 | 33 | 27.6 | 1.35 | 33 | 36.8 | 0.96 | 33 | 1.10 |
| 68 | 33.5 | 1.08 | 34 | 28.6 | 1.30 | 34 | 37.6 | 0.93 | 34 | 1.06 |
| 70 | 34.5 | 1.04 | 35 | 29.6 | 1.25 | 35 | 38.4 | 0.91 | 35 | 1.02 |
| 72 | 35.5 | 1.01 | 36 | 30.6 | 1.20 | 36 | 39.1 | 0.88 | 36 | 0.99 |
| 74 | 36.5 | 0.97 | 37 | 31.7 | 1.16 | 37 | 39.8 | 0.86 | 37 | 0.95 |
| 76 | 37.5 | 0.94 | 38 | 32.7 | 1.11 | 38 | 40.4 | 0.84 | 38 | 0.92 |
| 78 | 38.5 | 0.90 | 39 | 33.8 | 1.07 | 39 | 41.1 | 0.82 | 39 | 0.88 |
| 80 | 39.5 | 0.87 | 40 | 34.9 | 1.03 | 40 | 41.7 | 0.80 | 40 | 0.85 |
| 82 | 40.5 | 0.84 | 41 | 36.1 | 0.98 | 41 | 42.3 | 0.78 | 41 | 0.82 |
| 84 | 41.5 | 0.81 | 42 | 37.2 | 0.94 | 42 | 42.8 | 0.77 | 42 | 0.79 |
| 86 | 42.4 | 0.78 | 43 | 38.4 | 0.90 | 43 | 43.4 | 0.75 | 43 | 0.76 |
| 88 | 43.4 | 0.75 | 44 | 39.6 | 0.87 | 44 | 43.9 | 0.74 | 44 | 0.74 |
| 90 | 44.4 | 0.72 | 45 | 40.8 | 0.83 | 45 | 44.4 | 0.73 | 45 | 0.71 |
Table A-2.
This table provides conversion factors based on the use of the 16 cm diameter PMMA phantom for CTDIvol. Other than the clarification that the effective diameter in the data table is equivalent to Dw, it is identical to Table 2 in AAPM Report 204.
| Table 2A | Table 2B | Table 2C | Table 2D | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lat + AP | Dw | Conversion | Lateral | Dw | Conversion | AP | Dw | Conversion | Dw | Converion |
| Dim (cm) | (cm) | Factor | Dim (cm) | (cm) | Factor | Dim (cm) | (cm) | Factor | (cm) | Factor |
| 12 | 5.7 | 1.50 | 6 | 8.2 | 1.36 | 6 | 5.8 | 1.50 | 6 | 1.49 |
| 13 | 6.2 | 1.47 | 7 | 8.7 | 1.34 | 7 | 7.3 | 1.41 | 7 | 1.43 |
| 14 | 6.7 | 1.44 | 8 | 9.2 | 1.32 | 8 | 8.8 | 1.33 | 8 | 1.38 |
| 15 | 7.2 | 1.42 | 9 | 9.7 | 1.29 | 9 | 10.2 | 1.26 | 9 | 1.32 |
| 16 | 7.7 | 1.39 | 10 | 10.2 | 1.26 | 10 | 11.6 | 1.19 | 10 | 1.27 |
| 17 | 8.2 | 1.36 | 11 | 10.7 | 1.24 | 11 | 13.0 | 1.13 | 11 | 1.22 |
| 18 | 8.7 | 1.34 | 12 | 11.3 | 1.21 | 12 | 14.4 | 1.07 | 12 | 1.18 |
| 19 | 9.2 | 1.31 | 13 | 11.8 | 1.19 | 13 | 15.7 | 1.02 | 13 | 1.13 |
| 20 | 9.7 | 1.29 | 14 | 12.4 | 1.16 | 14 | 17.0 | 0.97 | 14 | 1.09 |
| 21 | 10.2 | 1.26 | 15 | 13.1 | 1.13 | 15 | 18.3 | 0.92 | 15 | 1.05 |
| 22 | 10.7 | 1.24 | 16 | 13.7 | 1.10 | 16 | 19.6 | 0.88 | 16 | 1.01 |
| 23 | 11.2 | 1.22 | 17 | 14.3 | 1.08 | 17 | 20.8 | 0.84 | 17 | 0.97 |
| 24 | 11.7 | 1.19 | 18 | 15.0 | 1.05 | 18 | 22.0 | 0.80 | 18 | 0.93 |
| 25 | 12.2 | 1.17 | 19 | 15.7 | 1.02 | 19 | 23.2 | 0.76 | 19 | 0.90 |
| 26 | 12.7 | 1.15 | 20 | 16.4 | 0.99 | 20 | 24.3 | 0.73 | 20 | 0.86 |
| 27 | 13.2 | 1.13 | 21 | 17.2 | 0.96 | 21 | 25.5 | 0.70 | 21 | 0.83 |
| 28 | 13.7 | 1.10 | 22 | 17.9 | 0.94 | 22 | 26.6 | 0.67 | 22 | 0.80 |
| 29 | 14.2 | 1.08 | 23 | 18.7 | 0.91 | 23 | 27.6 | 0.64 | 23 | 0.77 |
| 30 | 14.7 | 1.06 | 24 | 19.5 | 0.88 | 24 | 28.7 | 0.62 | 24 | 0.74 |
| 31 | 15.2 | 1.04 | 25 | 20.3 | 0.85 | 25 | 29.7 | 0.59 | 25 | 0.71 |
| 32 | 15.7 | 1.02 | 26 | 21.1 | 0.83 | 26 | 30.7 | 0.57 | 26 | 0.69 |
| 33 | 16.2 | 1.00 | 27 | 22.0 | 0.80 | 27 | 31.6 | 0.55 | 27 | 0.66 |
| 34 | 16.7 | 0.98 | 28 | 22.9 | 0.77 | 28 | 32.6 | 0.53 | 28 | 0.63 |
| 35 | 17.2 | 0.97 | 29 | 23.8 | 0.75 | 29 | 33.5 | 0.51 | 29 | 0.61 |
| 36 | 17.6 | 0.95 | 30 | 24.7 | 0.72 | 30 | 34.4 | 0.50 | 30 | 0.59 |
| 37 | 18.1 | 0.93 | 31 | 25.6 | 0.70 | 31 | 35.2 | 0.48 | 31 | 0.56 |
| 38 | 18.6 | 0.91 | 32 | 26.6 | 0.67 | 32 | 36.0 | 0.46 | 32 | 0.54 |
| 39 | 19.1 | 0.89 | 33 | 27.6 | 0.65 | 33 | 36.8 | 0.45 | 33 | 0.52 |
| 40 | 19.6 | 0.88 | 34 | 28.6 | 0.62 | 34 | 37.6 | 0.44 | 34 | 0.50 |
| 42 | 20.6 | 0.84 | 35 | 29.6 | 0.60 | 35 | 38.4 | 0.42 | 35 | 0.48 |
| 44 | 21.6 | 0.81 | 36 | 30.6 | 0.57 | 36 | 39.1 | 0.41 | 36 | 0.47 |
| 46 | 22.6 | 0.78 | 37 | 31.7 | 0.55 | 37 | 39.8 | 0.40 | 37 | 0.45 |
| 48 | 23.6 | 0.75 | 38 | 32.7 | 0.53 | 38 | 40.4 | 0.39 | 38 | 0.43 |
| 50 | 24.6 | 0.72 | 39 | 33.8 | 0.51 | 39 | 41.1 | 0.38 | 39 | 0.41 |
| 52 | 25.6 | 0.70 | 40 | 34.9 | 0.48 | 40 | 41.7 | 0.37 | 40 | 0.40 |
| 54 | 26.6 | 0.67 | 41 | 36.1 | 0.46 | 41 | 42.3 | 0.36 | 41 | 0.38 |
| 56 | 27.6 | 0.64 | 42 | 37.2 | 0.44 | 42 | 42.8 | 0.36 | 42 | 0.37 |
| 58 | 28.6 | 0.62 | 43 | 38.4 | 0.42 | 43 | 43.4 | 0.35 | 43 | 0.35 |
| 60 | 29.6 | 0.60 | 44 | 39.6 | 0.40 | 44 | 43.9 | 0.34 | 44 | 0.34 |
| 62 | 30.5 | 0.57 | 45 | 40.8 | 0.39 | 45 | 44.4 | 0.34 | 45 | 0.33 |
| 64 | 31.5 | 0.55 | 46 | 42.1 | 0.37 | 46 | 44.8 | 0.33 | 46 | 0.32 |
| 66 | 32.5 | 0.53 | 47 | 43.3 | 0.35 | 47 | 45.2 | 0.33 | 47 | 0.30 |
| 68 | 33.5 | 0.51 | 48 | 44.6 | 0.33 | 48 | 45.6 | 0.32 | 48 | 0.29 |
| 70 | 34.5 | 0.49 | 49 | 45.9 | 0.32 | 49 | 46.0 | 0.32 | 49 | 0.28 |
| 72 | 35.5 | 0.47 | 50 | 47.2 | 0.30 | 50 | 46.4 | 0.31 | 50 | 0.27 |
| 74 | 36.5 | 0.46 | 51 | 48.5 | 0.29 | 51 | 46.7 | 0.31 | 51 | 0.26 |
| 76 | 37.5 | 0.44 | 52 | 49.9 | 0.27 | 52 | 47.0 | 0.30 | 52 | 0.25 |
| 78 | 38.5 | 0.42 | 53 | 51.3 | 0.26 | 53 | 47.2 | 0.30 | 53 | 0.24 |
| 80 | 39.5 | 0.41 | 54 | 52.7 | 0.24 | 54 | 47.5 | 0.30 | 54 | 0.23 |
| 82 | 40.5 | 0.39 | 55 | 54.1 | 0.23 | 55 | 47.7 | 0.30 | 55 | 0.22 |
Footnotes
DISCLAIMER: This publication is based on sources and information believed to be reliable, but the AAPM, the authors, and the publisher disclaim any warranty or liability based on or relating to the contents of this publication.
The AAPM does not endorse any products, manufacturers, or suppliers. Nothing in this publication should be interpreted as implying such endorsement.
References
- 1.McCollough CH, Leng S, Yu L, Cody DD, Boone JM, McNitt-Gray MF. CT Dose Index and Patient Dose: They Are Not the Same Thing. Radiology. 2011;259:311–316. doi: 10.1148/radiol.11101800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Turner AC, Zankl M, DeMarco JJ, et al. The Feasibility of a Scanner-Independent Technique to Estimate Organ Dose from MDCT Scans: Using CTDIvol to Account for Differences between Scanners. Med Phys. 2010;37:1816–1825. doi: 10.1118/1.3368596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Turner AC, Zhang D, Khatonabadi M, et al. The Feasibility of Patient Size-Corrected, Scanner-Independent Organ Dose Estimates for Abdominal CT Exams. Med Phys. 2011;38:820–829. doi: 10.1118/1.3533897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.American Association of Physicists in Medicine . Size-Specific Dose Estimates (SSDE) in Pediatric and Adult Body CT Examinations (Task Group 204) American Association of Physicists in Medicine; College Park, MD: 2011. [Google Scholar]
- 5.Huda W, Scalzetti EM, Roskopf M. Effective Doses to Patients Undergoing Thoracic Computed Tomography Examinations. Med Phys. 2000;27:838–844. doi: 10.1118/1.598949. [DOI] [PubMed] [Google Scholar]
- 6.Menke J. Comparison of Different Body Size Parameters for Individual Dose Adaptation in Body CT of Adults. Radiology. 2005;236:565–571. doi: 10.1148/radiol.2362041327. [DOI] [PubMed] [Google Scholar]
- 7.Toth T, Ge Z, Daly MP. The Influence of Patient Centering on CT Dose and Image Noise. Med Phys. 2007;34:3093–3101. doi: 10.1118/1.2748113. [DOI] [PubMed] [Google Scholar]
- 8.Wang J, Christner JA, Duan X, Leng S, Yu L, McCollough CH. Attenuation-based Determination of Patient Size for the Purpose of Size Specific Dose Estimation in CT: Part II. Implementation on Abdomen and Thorax Phantoms Using Cross Sectional CT Images and Scanned Projection Tadiograph Images. Med Phys. 2012;39:6772. doi: 10.1118/1.4757586. [DOI] [PubMed] [Google Scholar]
- 9.Wang J, Duan X, Christner JA, Leng S, Yu L, McCollough CH. Attenuation-based Estimation of Patient Size for the Purpose of Size Specific Dose Estimation in CT. Part I. Development and Validation of Methods Using the CT Image. Med Phys. 2012;39:6764. doi: 10.1118/1.4754303. [DOI] [PubMed] [Google Scholar]
- 10.Khatonabadi M, Oria D, Mok K, Cagnon CH, DeMarco JJ, McNitt-Gray MF. Calculating Size Specific Dose Estimates (SSDE): The Effect of Using Water Equivalent Diameter (WED) Vs. Effective Diameter (ED) on Organ Dose Estimates when Applying the Conversion Coefficients of TG 204.. 55th Annual AAPM Meeting; Indianapolis, Indiana. 2013. [Google Scholar]
- 11.McCollough C, Branham TA, Herlihy V, et al. Diagnostic Reference Levels from the ACR CT Accreditation Program. JACR Journal of the Americal College of Radiology. 2011;8:795–803. doi: 10.1016/j.jacr.2011.03.014. [DOI] [PubMed] [Google Scholar]
- 12.National Council on Radiation Protection and Measurements . Reference Levels and Achievable Doses in Medical and Dental Imaging: Recommendations for the United States. National Council on Radiation Protection and Measurements; Bethesda, MD: 2012. Report No. 172. [Google Scholar]
- 13.American College of Radiology Dose Index Registry. 2012 [Google Scholar]
- 14.Christianson O, Li X, Frush D, Samei E. Automated Size-specific CT Dose Monitoring Program: Assessing Variability in CT Dose. Med Phys. 2012;39:7131–7139. doi: 10.1118/1.4761871. [DOI] [PubMed] [Google Scholar]
- 15.Kalra MK, Maher MM, Toth TL, et al. Techniques and Applications of Automatic Tube Current Modulation for CT1. Radiology. 2004;233:649–657. doi: 10.1148/radiol.2333031150. [DOI] [PubMed] [Google Scholar]
- 16.Li B, Behrman RH, Norbash AM. Comparison of Topogram-based Body Size Indices for CT Dose Consideration and Scan Protocol Optimization. Med Phys. 2012;39:3456–3465. doi: 10.1118/1.4718569. [DOI] [PubMed] [Google Scholar]
- 17.Leng S, Shiung M, Duan X, Yu L, Zhang Y, McCollough CH. Size Specific Dose Estimation in Abdominal CT: Impact of Longitudinal Variations in Patient Size.. AAPM Annual Meeting; Indianapolis, Indiana. 2013. [Google Scholar]
- 18.Khatonabadi M, Kim HJ, Lu P, et al. The Feasibility of a Regional CTDIvol to Estimate Organ Dose from Tube Vurrent Modulated CT Exams. Med Phys. 2013;40:051903. doi: 10.1118/1.4798561. [DOI] [PMC free article] [PubMed] [Google Scholar]