Abstract
The performance of fragment-based ab initio 1H, 13C, 15N and 17O chemical shift predictions is assessed against experimental NMR chemical shift data in four benchmark sets of molecular crystals. Employing a variety of commonly used density functionals (PBE0, B3LYP, TPSSh, OPBE, PBE, TPSS), we explore the relative performance of cluster, two-body fragment, and combined cluster/fragment models. The hybrid density functionals (PBE0, B3LYP and TPSSh) generally out-perform their generalized gradient approximation (GGA)-based counterparts. 1H, 13C, 15N, and 17O isotropic chemical shifts can be predicted with root-mean-square errors of 0.3, 1.5, 4.2, and 9.8 ppm, respectively, using a computationally inexpensive electrostatically embedded two-body PBE0 fragment model. Oxygen chemical shieldings prove particularly sensitive to local many-body effects, and using a combined cluster/fragment model instead of the simple two-body fragment model decreases the root-mean-square errors to 7.6 ppm. These fragment-based model errors compare favorably with GIPAW PBE ones of 0.4, 2.2, 5.4, and 7.2 ppm for the same 1H, 13C, 15N, and 17O test sets. Using these benchmark calculations, a set of recommended linear regression parameters for mapping between calculated chemical shieldings and observed chemical shifts are provided and their robustness assessed using statistical cross-validation. We demonstrate the utility of these approaches and the reported scaling parameters on applications to 9-tertbutyl anthracene, several histidine co-crystals, benzoic acid and the C-nitrosoarene SnCl2(CH3)2(NODMA)2.
1 Introduction
Hydrogen, carbon, nitrogen and oxygen-containing functional groups play a central role in the structures, chemical reactivity, and solubility of biological and pharmaceutical compounds.1 Advances in instrumentation and methodology over recent decades have made nuclear magnetic resonance (NMR) spectroscopy a particularly potent tool for investigating structural features associated with 1H, 13C, 15N, and 17O nuclei. However, even with modern multi-dimensional NMR experiments, structure elucidation can prove challenging due to the complexity of the spectra and the subtle effects of chemical environment on the chemical shifts.
Computational tools play an increasingly prominent role in NMR spectral assignment and structure elucidation. Early ab initio chemical shielding prediction began with small cluster models, often employing simple charge-embedding schemes to mimic the crystal environment.2,3 The inherent limitations of such models resulting from their approximate treatment of the crystal lattice limited their widespread application. On the other hand, periodic density functional theory (DFT) is well-suited for modeling chemical shieldings in extended crystal systems, and the plane wave DFT-based gauge-including projector augmented wave (GIPAW) method4–6 has now become the method of choice for chemical shift prediction for molecular crystals.
The success of the GIPAW technique has contributed significantly to the rapidly expanding field of NMR crystallography, which combines solid state NMR, diffraction methods and ab initio chemical shielding predictions to solve crystal structures.7–11 However, despite the widespread success of plane wave DFT methods, they suffer from two main limitations. First, plane wave calculations are limited to GGA-type density functionals in practice. Hybrid density functionals can offer improved accuracy for NMR chemical shift prediction,12–14 but they typically require at least an order of magnitude more computational effort to evaluate in a plane wave basis compared to a GGA functional. In contrast, the cost premium for hybrid density functionals in Gaussian basis sets is typically less than a factor of two.
The second limitation lies in the mapping of absolute shifts obtained from calculations to empirically determined chemical shifts. This mapping is generally performed using a simple linear regression model relating experimental and chemical shifts. However, the linear regression parameters are specific to a given functional/basis set combination.15 Regression models obtained from plane wave/pseudopotential GIPAW calculations in periodic crystals are not transferable to chemical shieldings computed from all-electron models in non-periodic systems, such as an enzyme active site.
By decomposing the molecular crystal into a series of interacting molecules, fragment methods provide an accurate, low-cost alternative to plane wave techniques for computing a variety of chemical properties, including NMR chemical shieldings.12,16–20 Fragment methods pave the way for routine use of hybrid density functionals or perhaps even a high-accuracy wave function-based correlation treatment of magnetic properties. Further, fragment methods allow the same density functionals, basis sets and empirically derived scaling parameters to be applied across systems ranging from molecular crystals to molecules in solution or even biomolecules.
We have recently shown that both GIPAW and an electrostatically embedded two-body fragment model reproduce the experimental 13C isotropic shifts in a set of 25 organic molecular crystals to within a root mean square error of 2.1-2.2 ppm when using the PBE functional.13 However, using a hybrid density functional like PBE021 or B3LYP22 in the fragment model instead decreases the error by a third to 1.4 ppm.13 The same study also found good performance for the principal components of the shielding tensors. Furthermore, the chemical shielding scaling parameters obtained here have been successfully applied to the NMR characterization of the 2-aminophenol quininoid intermediate in the mechanism of tryptophan synthase.23
Building upon the success of fragment-based methods in the context of 13C chemical shift predictions,13 the present work explores the application of fragment, cluster, and combined cluster/fragment approaches to predicting the isotropic chemical shifts of 1H, 15N and 17O nuclei, and it compares the performance of these models to the widely used GIPAW approach. For the sake of consistency, we also slightly revise the earlier 13C chemical shift test results13 here using the identical geometry optimization protocol and sets of density functionals across all four nuclei. These four nuclei were chosen because of their ubiquity in organic and biological systems and their importance in NMR studies of these systems. Their widespread use in NMR also means that relatively large sets of experimental shifts could be drawn from studies found in the literature. Because reliable shielding tensor data is harder to find for these nuclei, we focus only on isotropic shifts in this work.
Previous work has shown that the many-body expansion converges more slowly for 15N and 17O compared with 1H and 13C.12 It is particularly important, therefore, to assess the viability of fragment methods for these nuclei. To do so, we have compiled three new benchmark sets of molecular crystals consisting of 80 1H, 51 15N, and 28 17O experimentally measured isotropic chemical shifts. These benchmark sets augment our previously developed 13C set consisting of 169 shifts. These new sets include diverse chemical shifts that span the ranges observed in most common biological and pharmaceutical species.24,25 The use of molecular crystals with well-defined and largely static structures helps mitigate the influence of confounding variables such as solvation or conformational dynamics. It enables more direct assessment of fragment-based methods and produces linear regression parameters that properly account for an explicit chemical environment. Because common benchmark data sets are extremely useful for validating and comparing models developed by different researchers, complete optimized crystal structures and tabulated chemical shifts for these test sets are provided as ESI.†
Developing a robust set of chemical shielding scaling parameters for 1H, 15N, and 17O nuclei is challenging. 15N and 17O exhibit broad chemical versatility, and the shifts of all three nuclei types can be affected by proton dynamics, particularly in hydrogen bonding situations. Nitrogen, for example, bonds with most other elements, has oxidation numbers ranging from −3 to +5, coordination numbers from 1 to 6, and bond orders up to 3.24 Such diversity manifests in a chemical shift range spanning ~1100 ppm. An even greater diversity in chemical shifts is observed for oxygen, with the chemical shifts for water and dioxygen separated by nearly ~2000 ppm.25 However, in the context of organic molecular crystals and biologically relevant applications, these ranges span ~400 and ~1000 ppm for 15N and 17O, respectively.26 Proton isotropic shifts are generally limited to a more modest ~20 ppm range. On the other hand, hydrogen is much more susceptible to dynamics such as methyl group rotation or rapid proton exchange between hydrogen-bonded partners or even nuclear quantum effects. In all cases, care must be taken to adequately represent the desired range of chemical shieldings and to avoid errors introduced in the calculations by neglecting the dynamical averaging occurring in the NMR experiments.
Despite efforts to include a wide variety of chemical environments in each molecular crystal test set, biases resulting from the composition of the test set could impact both the reported accuracy of a given method and the general transferability of the scaling parameters. To assess the degree to which the composition of the training and validation sets impact performance and transferability, a series of statistical cross-validation numerical experiments were performed. In agreement with cross-validation results obtained previously for 13C chemical shifts,13 the analysis here reveals relatively little impact of training/validation set composition on both overall accuracy or scaling parameters.
Using these benchmark sets, we examine the impact of electrostatic embedding, two-body fragment and cluster cut-off distance, and the choice of density functional on the chemical shift predictions. Specifically, we compare the hybrid density functionals PBE0 and B3LYP, the GGA-based functionals PBE27 and OPBE,28 as well as the meta-GGA functional TPSS and its hybrid variant TPSSh.29 The meta-GGA and hybrid meta-GGA functionals performed well for 15N chemical shift tensors in a recent study using symmetry-adapted cluster calculations.14
Although this work primarily focuses on the fragment-based approaches, we have also benchmarked GIPAW across the same test sets for comparison. Despite its widespread use for chemical shift prediction, extensive GIPAW benchmarks for nuclei like hydrogen and oxygen are hard to find. The test sets developed here provide scaling parameters for mapping GIPAW chemical shieldings for these four nuclei to chemical shifts, which may prove useful in other applications.
Through these benchmarks, we demonstrate that with the PBE functional, the fragment-type approaches perform competitively with plane wave GIPAW, especially for hydrogen, carbon, and nitrogen. As we found in our previous study of 13C chemical shifts,13 however, hybrid density functionals provide statistically improved accuracy over GGAs. In particular, fragment PBE0 calculations out-perform GIPAW PBE ones in terms of the root-mean square (rms) errors and the maximal errors for 1H, 13C, and 15N. Oxygen chemical shifts, which are more sensitive to many-body effects, prove more difficult to model with the fragment approach. Nevertheless, the 17O cluster/fragment PBE0 results are almost as accurate as the GIPAW PBE ones, with the differences in root-mean-square error between the two functionals being comparable to typical experimental uncertainties in 17O chemical shifts. Given the high computational expense associated with using hybrid functionals in plane wave GIPAW calculations, these results provide further support for using fragment-based approaches over GIPAW methods for NMR chemical shielding predictions in organic molecular crystals.
Finally, we provide a collection of illustrative examples demonstrating the utility of fragment-based methods coupled with the chemical shielding scaling parameters derived from these training sets. First, we help assign the previously unpublished 1H/13C heteronuclear correlation spectrum for the 9-tertbutyl anthracene ester (9-TBAE) molecular crystal. Second, the prediction of both 1H and 15N isotropic shieldings for a particularly challenging set of histidine co-crystals is assessed. Third, we briefly examine issues of proton exchange dynamics using 17O chemical shielding predictions applied to crystalline benzoic acid. Finally, we assess the accuracy of predicted 17O chemical shieldings for a challenging organometallic C-nitrosoarene whose experimental chemical shift30 lies far outside the range of oxygen chemical shifts included in the test set.
2 Theory
2.1 Many-body expansion for ab initio shielding tensor calculations
The chemical shielding tensor describes the screening of the external magnetic field experienced at the nucleus by the surrounding electron density. This change in local magnetic field at the nucleus results directly from interaction between the external magnetic field and the local electron density. Formally, the NMR chemical shielding tensor element σαβ for atom A is defined as the second derivative of the electronic energy with respect to the α-th component of the external magnetic field Bα and the β-th component of the nuclear magnetic moment on atom A, :
| (1) |
As discussed previously,12 differentiating the many-body decomposition of the energy allows one to express the total chemical shielding tensor of atom A on molecule i in a crystal as a sum of one-body, two-body, and higher-order terms,
| (2) |
where is the shielding tensor for atom A on the isolated monomer i, is the two-body contribution to the shielding tensor arising from the interaction of monomer i with monomer j,
| (3) |
and is the three-body contribution to the shielding tensor and is defined as
| (4) |
Note that because atom A lies on monomer i and not monomer j or k, terms like and in Eqs 3 and 4 are actually zero.
2.2 Fragment and cluster methods
For each atom on each symmetrically unique molecule in the unit cell, the summations in Eq 2 are carried out over all unique sets of fragments (dimers, trimers, etc.) Evaluation of the one- and two-body contributions can be done inexpensively, but the cost of the three-body and higher terms grows rapidly, giving rise to a significantly larger computational burden if contributions beyond two-body are included. However, assessment of the many-body expansion for 13C chemical shielding tensors has demonstrated that the contributions from three-body and higher terms are small relative to the inherent errors from density functional theory, especially if electrostatic embedding models are employed to mimic the crystal lattice.12,13 Accordingly, a two-body fragment model approximates the shielding tensor as
| (5) |
where and are the one and two-body contributions with each monomer and dimer calculation carried out in an electrostatic embedding environment which will be discussed below.
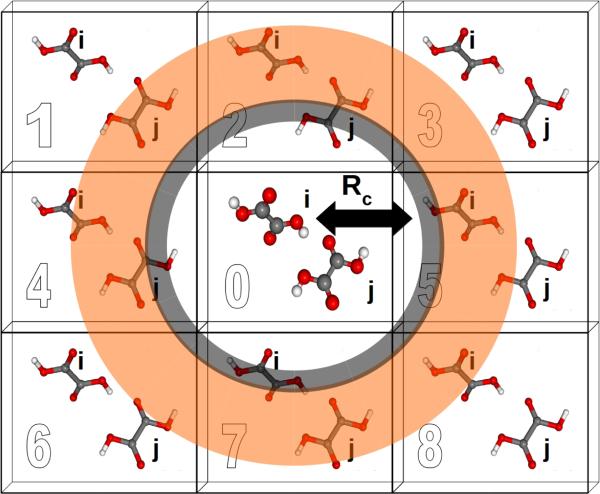
A two-body fragment-based calculation in a molecular crystal is carried out by defining a cut off radius Rc around the asymmetric unit, as illustrated in Figure 1. The chemical shielding tensor for each atom in the asymmetric unit is then approximated by calculating the two-body contributions for all dimers involving that monomer in the asymmetric unit and any other monomer lying within the defined cut off according to Eq 5. For example, using the labeling and cut-off defined in Figure 1, the total chemical shielding tensor for atom A on monomer i is given by:
| (6) |
| (7) |
By focusing these many-body expansions on molecules in the asymmetric unit, the fragment approach readily exploits space group symmetry to achieve additional computational savings. Nevertheless, it still computes chemical shielding tensors for every symmetrically unique atom in the crystal. Further computational savings can be achieved by exploiting locally dense basis sets, which use smaller basis sets on all atoms outside the molecules in the asymmetric unit, as described in Section 3.2.
Fig. 1.
Schematic illustrating the application of fragment and cluster-based methods to molecular crystal systems. Rc denotes the cut off distance for a given model. Each cell is labeled for ease of reference.
If a two-body fragment method proves insufficient, a cluster-based calculation can be constructed by including all monomers within the defined cut off radius Rc in a single supermolecular chemical shielding calculation. This effectively amounts to summing the many-body expansion through all orders for the subset of molecules lying closest to the molecule of interest. Additional chemical shielding contributions from more distant molecules in the crystal lattice can then be approximated in a pairwise (two-body) fashion. Specifically, one computes the two-body contributions between the molecule of interest and any other molecule outside the initial cluster but inside a second two-body fragment cut off (orange region in Figure 1). Cluster-based calculations improve the treatment of local many-body effects, albeit with a substantial increase in computational cost since DFT methods typically scale O(N3) with system size for moderately sized systems.
Electrostatic embedding provides a secondary strategy for approximating both long-range and many-body effects which can be beneficial for both cluster and fragment-based calculations. In the present work, we use a simple electrostatic embedding model based upon point charges obtained from Gaussian distributed multipole analysis (GDMA).31–33 GDMA point charges are positioned at each atomic center for every monomer within a user-defined charge-embedding radius of molecule i in the central unit cell. The presence of these point charges mimics many-body effects by polarizing the monomer and dimer fragment calculations. Long-range electrostatic effects are captured by extending the charge embedding cut off well into the surrounding lattice. Previous work has demonstrated that a 30 Å charge-embedding cut off ensures convergence in the calculated shieldings,12 and that cut off is used here as well.
2.3 Computational efficiency
For a typical small-molecule organic crystal, the computational efficiency of GIPAW PBE and fragment 2-body PBE are similar. Our software implementation automatically fragments the crystal, generating the necessary jobs which can then be run with an external electronic structure package, such as Gaussian. The software then combines the results of those fragment jobs into the final set of shielding tensors. For a crystal with a single molecule in the asymmetric unit (Z′ = 1) and a 6 Å two-body cut off, the fragmentation procedure generates one monomer calculation and typically ~20–25 dimer calculations.
Perfect computational comparisons between GIPAW and the fragment approach are difficult due to differences in the basis sets, grids, etc. Nevertheless, for a typical small-molecule organic crystal with a handful of molecules in the unit cell, two-body fragment PBE and GIPAW PBE require similar amounts of total CPU time. Several computational features of the fragment method are notable, however. First, the cost premium for using the hybrid functionals in the fragment approach is typically only ~50%, making them routinely applicable. In contrast, hybrid functionals are rarely employed in GIPAW due to their high computational expense.
Second, due to the local nature of the two-body interactions and exploitation of space group symmetry, the cost of the fragment approach depends on the number of molecules in the asymmetric unit, rather than the total number of molecules in the unit cell. The time to compute chemical shielding tensors for a four-molecule unit cell crystal and an eight-molecule cell polymorph will be identical, as long as Z′ = 1 for both. Doubling the number of molecules in the asymmetric unit from Z′ = 1 to Z′ = 2 will double the cost of the shielding tensor calculation.
Third, the fragment approach achieves high parallel efficiency. Each of the two dozen or so fragment jobs can be run simultaneously with minimal internode communication. Each individual fragment job can be run in parallel across 1–2 dozen processor cores. Together, these two tiers of parallelization enable the chemical shielding tensor calculation to be run very efficiently on hundreds of processor cores. If one has several hundred processor cores available, chemical shifts on a Z′ = 1 crystal structure of a 70–80 atom molecule can be obtained within a few hours, irrespective of the size of the unit cell.
The cluster/fragment approach is substantially more expensive than the two-body fragment, since it requires computing chemical shifts for a large 10–15 molecule cluster. Still, such calculations are very feasible for clusters containing hundreds of atoms or more due to efficient and/or linear-scaling chemical shift algorithms.34–36
3 Computational Methods
3.1 Crystal Structures
Separate benchmark sets of molecular crystal structures were constructed for hydrogen, nitrogen and oxygen to augment our previously developed13 carbon set. Specific molecular crystals were chosen based on the availability of both high-resolution room temperature NMR chemical shift data in the literature with unambiguous spectral assignment as well as high-quality x-ray or neutron diffraction crystal structures. Structural data for each compound in the study was obtained either from the literature or from the Cambridge Structure Database (CSD) maintained by the Cambridge Crystallographic Data Center.
The hydrogen, carbon, nitrogen and oxygen benchmark sets consist of 13, 25, 24 and 15 crystal structures, respectively. In the interest of providing a uniform set of scaling parameters obtained using a single computational procedure outlined below, we update our predicted 13C shifts here for the carbon test set, though the differences in the 13C predicted shifts here and in our earlier work13 are trivial (less than 0.1 ppm difference in root-mean-square error). Each of the species in the hydrogen, nitrogen, and oxygen sets are depicted in the ESI,† along with their common names and CSD reference codes. The carbon set species were shown previously.13 Each set was chosen to include a variety of intermolecular interactions which are representative of common interactions in pharmaceutical and biological compounds. Experimental chemical shifts for 1H and 13C are reported relative to neat TMS under magic angle spinning (MAS) conditions,37 the 15N shifts are given relative to external solid NH4Cl also under MAS, and 17O shifts are relative to liquid water. Conversions to other chemical shift scales can be accomplished as described by Ref 37; for expediency, several of the most common conversions are given in the ESI.† The CSD reference codes and experimental references for NMR data for the three test sets are:
Hydrogen (13 structures, 80 shifts): CIMETD,1 INDMET,38 URACIL,39 co-crystal of 4,5-Dimethylimidazole and 3,5-Dimethylpyrazole,40 AMBACO05,41 PHBARB06,42 IPMEPL,7 COYRUD11,43 FPAMCA11,8 BAPLOT01,8 WEZCOT,8 FLUBIP,44 ZIVKAQ.45
Carbon (25 structures, 169 shifts, see Ref 13): MBDGAL02, MEMANP11, MGALPY01, MGLUCP11, XYLOBM01, SUCROS04, RHAMAH12, FRUCTO02, GLYCIN03, LALNIN12, LSERIN01, LSERMH10, ASPARM03, LTHREO01, GLUTAM01, LTYROS11, LCYSTN21, NAPHTA36, ACENAP03, TRIPHE11, HXACAN09, INDMET, SULAMD06, ADENOS12, PERYTO10.
Nitrogen (24 structures, 51 shifts): BITZAF,46 GEHHAD,46 GEHHEH,46 GEHHIL,46 LHISTD02,47 LHISTD13,47 TEJWAG,47 GLYCIN03,26 FUSVAQ01,48 CYTSIN,48 THYMIN01,48 URACIL,48 CIMETD,1 BAPLOT01,49 Compound 1,50 LTYRHC10, CYSCLM11, LSERIN01, GLUTAM01, ASPARM03, LCYSTN21, ALUCAL04, GLYHCL01, LGLUAC11.
Oxygen (15 structures, 28 shifts): LALNIN12,26 ALAHCL,26 VALEHC11,26 LTYRHC10,26 CYSTIN,51 ACANIL03,52 BZAMID07,53 GLYCHL01,26 LGLUTA03,54 MBNZAM10,52 FEQYUM,55 LILEUC10,55 PHALNC01,55 CYSCLM11,55 TPEPHO02.56
A number of the nitrogen chemical shifts (those without a citation given above) were measured and reported here, as discussed in Section 4.
3.2 Computational techniques
Experimental crystal structures were subjected to all-atom geometry optimizations with fixed lattice parameters using the freely available, open-source Quantum Espresso software package.57 All geometry optimizations were performed using the PBE27 density functional and the D2 dispersion correction,58 ultrasoft pseudopotentials with a plane wave cut off of 80 Ry, and typically a 3×3×3 Monkhorst-Pack k-point grid. This grid typically corresponds to a spacing of 0.04 Å−1 between nearest k-points and, for all but a few structures, a spacing no larger than 0.07 Å−1. Larger numbers of k-points were used in some of the smaller unit cells as needed based on chemical shift convergence tests. See ESI for details. We used the pseudopotentials H.pbe-rrkjus.UPF, C.pbe-rrkjus.UPF, N.pbe-rrkjus.UPF, O.pbe-rrkjus.UPF, S.pbe-n-rrkjus_psl.0.1.UPF, F.pbe-n-rrkjus_psl.0.1.UPF, Cl.pbe-n-rrkjus_psl.0.1.UPF, I.pbe-n-rrkjus_psl.0.2.UPF, Na.pbe-spn-rrkjus_psl.0.2.UPF, K.pbe-n-mt.UPF, and P.pbe-n-rrkjus_psl.0.1.UPF from http://www.quantum-espresso.org.
The use of fixed room-temperature experimental lattice parameters effectively compensates for the appreciable increases in volume that occur between the minimum electronic energy structure and the finite temperature structure.59,60 Note that the use of fixed experimental lattice parameters reduces sensitivity to the specific dispersion correction. The root-mean-square errors in the predicted 13C chemical shifts obtained here using PBE-D2 geometries differ by less than 0.1 ppm from those obtained previously for the same crystals using PBE-TS geometries.13
Molecular crystal fragmentation through two-body was carried out using our hybrid many-body interaction (HMBI) code.16,61,62 Individual fragment shielding tensor calculations were performed using Gaussian0963 with the B3LYP, PBE0, PBE, OPBE, TPSS, and TPSSh density functionals. Calculations were performed using a locally dense basis set and the GIAO approximation. Unless otherwise stated, a 6 Å fragment cut off Rc was used for both fragment and cluster/fragment models, and a 4 Å cluster was used in cluster/fragment calculations. All calculations used a 6-311+G(2d,p) basis64–67 for all atoms on the central monomer of interest, a 6-311G(d,p) basis for all neighboring atoms out to 4 Å, and a 6-31G68,69 basis for all atoms beyond 4 Å. This locally dense basis set70,71 combination has proved effective in previous studies12,72 and is simply referred to here as our “mixed basis.” The ATZP basis73 was used on the tin atom for the nitrosoarene in Section 7.4.
As described in previous work,12 a large DFT integration grid consisting of 150 radial and 974 Lebedev angular points was used to approach rotational invariance and mitigate the introduction of noise from fragment contributions given by symmetrically equivalent molecules with different orientations. After constructing the raw shielding tensors via the fragment or cluster/fragment approach, the tensors are symmetrized and diagonalized to compute the principal components. Isotropic shieldings are reported as the average of these diagonal values. Note that if one is only interested in predicting the isotropic shifts, one can use the raw isotropic shieldings for each fragment instead of the full tensors. However, the tensor approach used here is more general.
Distributed multipoles computed with the GDMA package33,74 were used to construct the embedding environment. The GDMA charges were calculated using the same functional and 6-311+G(2d,p) basis set as the chemical shielding calculation. The GDMA point charges were then placed on all molecules lying within 30 Å of any atom in the asymmetric unit cell, as described in previous work.12,13
Gauge-including projector augmented wave (GIPAW) chemical shielding calculations were performed at the same optimized PBE-D2 (Quantum Espresso) geometries without further relaxation. Calculations were performed using CASTEP75 with the PBE functional, ultrasoft pseudopotentials generated on-the-fly and an 850 eV plane wave basis set cut off. Electronic k-points were sampled on a Monkhorst-Pack grid to give a maximum separation between k-points of 0.05 Å−1. The basis set cut off and k-point density were chosen based on chemical shift convergence tests (see ESI†). The basis set plane wave cut off energy was chosen to converge absolute chemical shifts to within 0.4 ppm and, more importantly, relative chemical shifts to 0.05 ppm or better. Chemical shielding was found to be fairly insensitive to the density of the k-point grid. Full space group symmetry was used in all GIPAW calculations.
3.3 Chemical shift linear regression and statistical cross-validation
The experimentally observed chemical shift δi represents the difference between the absolute chemical shielding σi of nucleus i and the absolute shielding σre f of a reference compound. Thus, comparison of predicted shifts with experimental NMR spectra requires mapping between the computed absolute shieldings σi and the experimentally referenced chemical shift δi. Numerous techniques exist for performing this mapping.15 Here we adopt a linear regression approach which addresses the shift referencing and helps correct for systematic errors in the calculations.
| (8) |
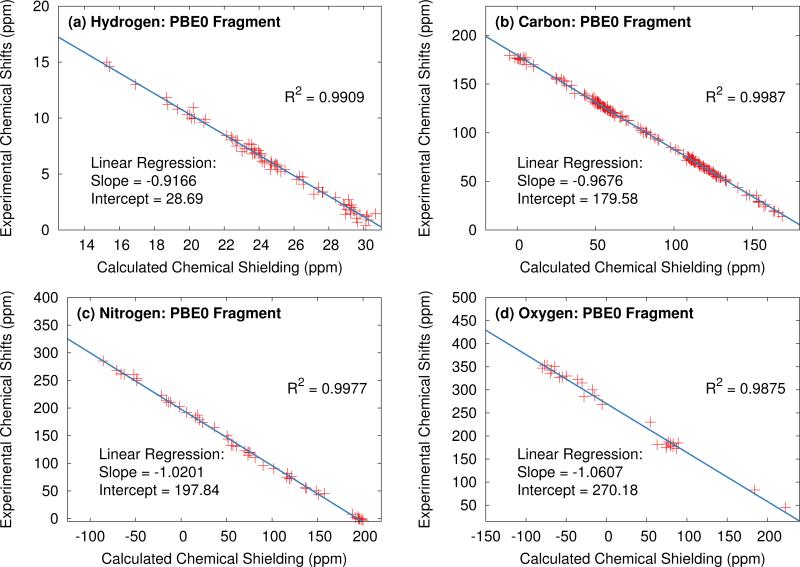
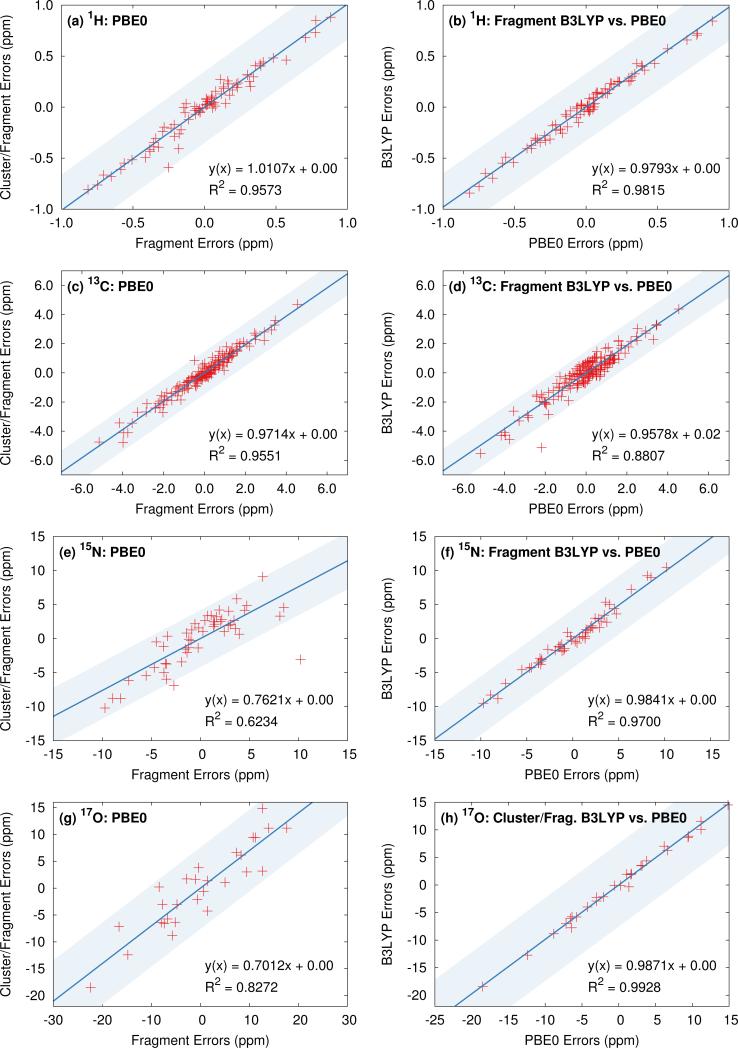
In the absence of any systematic error, A would take a value of −1, and B would simply be the absolute shielding of the reference compound σre f . However, obtaining these parameters via a linear least-squares fit between the calculated and experimental data for each of the test sets provides scaling parameters for each type of nucleus which partially mitigate systematic errors present in the calculations. Further, assuming these regression parameters are fitted to a sufficiently broad and representative test set, they can be used to scale predicted shifts obtained for compounds not included in the test set and can even be applied in the context of non-crystalline systems. Figure 2 illustrates the application of this approach using the hydrogen, carbon, nitrogen and oxygen test sets using PBE0 fragment two-body calculation.
Fig. 2.
Plot of experimental vs. calculated isotropic shifts for the (a) 1H, (b) 13C, (c) 15N and (d) 17O benchmark sets. Predicted shifts were obtained from two-body fragment calculations at the PBE0/mixed basis level with a 6 Å two-body cut off distance.
In an effort to asses the robustness of the linear regression parameters, exhaustive N-choose-5 cross-validation was performed for each test. The cross-validation procedure consists of partitioning the N crystal structures into a training set with N - 5 training structures and 5 validation structures. In this way, 1287, 53130, 42504 and 3003 different partitionings were formed for the hydrogen, carbon, nitrogen and oxygen test sets, respectively. Linear regression and error analysis was then performed for each partitioning to obtain distributions of errors and linear regression parameters.
4 Experimental methods
Most experimental chemical shifts considered here were obtained from the literature. However, we found relatively few examples of high-quality, small-molecule crystals with primary amine nitrogen chemical shifts in the literature. Therefore, new experimental 15N NMR chemical shifts for many amino acids (structures 8 and 16 through 24 in the nitrogen test set) are reported here. The experimental 1H and 13C chemical shifts for 9-tertbutyl anthracene (Section 7.1) are also reported here for the first time.
4.1 9-Tertbutyl Anthracene Ester
Two-dimensional 1H, 13C heteronuclear-correlation (HETCOR) experiments76 were performed at 14.1 T (600.01 MHz 1H, 150.87 MHz 13C) on a Bruker AV600 spectrometer equipped with a triple resonance 1.3 mm MAS probe with a sample spinning rate of 50 kHz (±2 Hz). Less than 2 mg of microcrystalline sample were packed into each rotor. For these experiments, cross polarization (CP) was established using a 2 ms contact time with nutation frequencies of 125 kHz for 1H and 75 kHz for 13C; high power 1H decoupling during 13C acquisition was implemented using XiX (125 kHz, 2.85 τr).77 Chemical shifts were indirectly referenced to neat TMS using an external sample of adamantane in which the 1H resonance was set to 1.87 ppm and the down-field 13C peak to 38.48 ppm.78,79
4.2 15N Solid-state NMR
15N Cross-polarization magic-angle-spinning (CPMAS) solid-state NMR experiments were performed at 9.4 T (1H frequency 400.37 MHz, 15N frequency 40.57 MHz) on a Bruker AVANCE III spectrometer equipped with a double resonance 4 mm MAS probe, spinning at a MAS rate of 8 kHz. 83 kHz 1H π/2 and decoupling pulses were used throughout, along with a 2 ms CP and high power (83 kHz) 1H decoupling during acquisition. During CP the 15N nutation rate was set to 46 kHz and the 1H nutation rate ramped from 31–41 kHz. For each spectrum, 2048 complex data points with a dwell of 20 μs (spectral width 50 kHz, total acquisition time 41 ms) were acquired with a recycle delay between 4 and 60 s. Chemical shifts were referenced to external 15NH4Cl set to 0.0 ppm. Samples of nitrogen test set crystal structures 8, 16, and 21 were obtained from Sigma Aldrich, structure 22 from Acros Organics, 18 from Alfa Asar, structures 20 and 24 from Fisher Scientific, and structure 19 from MP Biomedical. These crystal samples were used directly from the supplier without recrystallization. The crystal structures of the samples were confirmed via powder x-ray diffraction.
5 Results and Discussion
We begin by first examining the performance of fragment and cluster/fragment models for each of the four nuclei, assessing both the impact of electrostatic embedding as well as two-body cut-off distance. Second, we compare the predicted shifts for fragment, cluster and cluster/fragment approaches across six different commonly used density functionals. Third, the accuracy of the various fragment-type approaches relative to the widely used GIPAW is assessed. Fourth, we examine the statistical robustness of the linear regression parameters using statistical cross-validation. Finally, we apply fragment methods along with our scaling parameters to four chemically interesting problems which involve species not included in the benchmark test sets.
5.1 Performance of fragment and cluster/fragment models
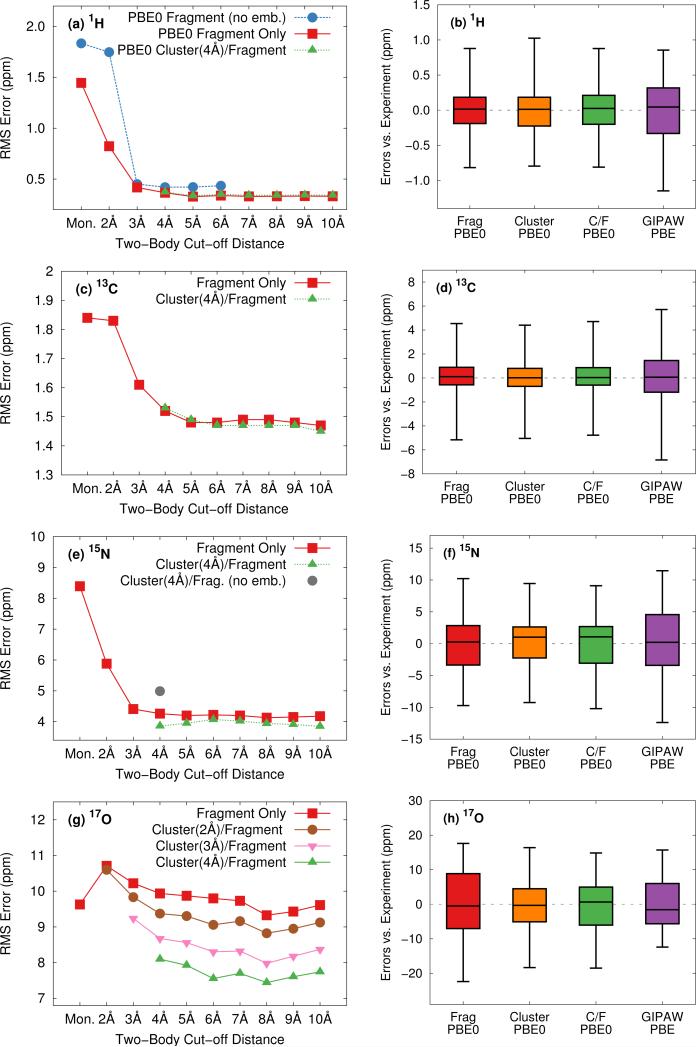
To ensure that the chemical shift predictions are well-converged with respect to the fragment contributions included, we first examine the impact of the two-body cut off distance for both fragment and cluster/fragment models. Figure 3 illustrates the root-mean-square errors in the isotropic chemical shifts relative to experiment for (a) hydrogen, (c) carbon, (e) nitrogen and (g) oxygen as a function of two-body cut-off distance. Linear regression models of the form presented in Eq 8 were applied separately to each model/cut-off combination using the experimental isotropic shifts for the respective test sets (see ESI† for details). All calculations were performed using the locally dense basis set defined previously in Section 3.2.
Fig. 3.
Assessment of two-body cut off distance dependence as well as relative performance of fragment and cluster/fragment models on the rms errors (left) and error distributions (right) for the calculated isotropic shifts relative to experiment for all hydrogen (a,b), carbon (c,d) nitrogen (e,f) and oxygen (g,h) structures. Calculations were performed with PBE0 and the locally dense basis defined in Section 3.2. Electrostatic embedding was employed unless otherwise specified. Cluster-based calculations reported in the error distributions (right) use a 4 Å cluster. Error distributions given in (b),(d), (f), and (h) for fragment and cluster/fragment calculations were obtained using a 6 Å two-body cut off.
All four nuclei demonstrate a dramatic reduction in rms errors once sufficient two-body terms are included to capture all hydrogen-bonding partners (2-3 Å two-body cut off). As noted previously for 13C,13 reasonable convergence is achieved for both hydrogen and nitrogen once all nearest-neighbor molecules are included in the fragment calculation using a 4 Å two-body cutoff.
As a result of the inherently local character of the chemical shielding, two-body contributions decrease rapidly with increasing distance between the two molecules. Extending the two-body cut off beyond 6 Å has a very small impact on the predicted 1H, 13C, and 15N isotropic shifts (Figures 3a, 3c, and 3e). Isotropic shifts for 17O display a slightly greater dependence on long-range two-body contributions (Figure 3g) and could perhaps benefit slightly from an 8 Å two-body cut off. Nevertheless, for the sake of consistency with calculations on other nuclei, we adopt a 6 Å cut off throughout.
Figures 3a and 3b show that both electrostatic embedding and cluster-based calculations provide minimal improvements in the predicted 1H isotropic shifts compared to a simple, un-embedded fragment two-body model. Carbon benefits slightly more from electrostatic embedding,13 while nitrogen and oxygen demonstrate a much greater dependence on it. Fragment-based calculations for 15N and 17O without point charge embedding (not shown) proved unreliable, with absolute errors almost uniformly exceeding 20 ppm. These results indicate a greater sensitivity of 15N and 17O nuclei to both long-range electrostatics as well as local many-body effects when compared with 1H and 13C. For 15N, electrostatic embedding is largely sufficient for capturing local many-body effects, as evidenced by the relatively uniform behavior of the fragment and cluster/fragment approaches both in terms of overall rms error (Figure 3e) as well as the error distributions (Figure 3f).
In contrast, explicit treatment of local many-body contributions using a small cluster becomes much more important for 17O chemical shieldings. Both cluster and combined cluster/fragment methods improve the accuracy of predicted isotropic 17O shifts relative to the two-body fragment model. Cluster/fragment calculations using a 4 Å cluster uniformly improve the overall rms errors relative to two-body fragment calculations by ~2 ppm (Figure 3g). These results highlighting the impact of local many-body effects on 17O shieldings agree with earlier work indicating larger three-body contributions for 17O compared with 1H, 15N and 13C.12 Of course, measuring oxygen chemical shifts experimentally is also challenging, due to the line broadening resulting from the quadrupolar interaction. Experimental uncertainties range ~0.5–5 ppm26,51–55 and likely contribute to the errors seen for oxygen here.
The error distributions presented as box plots in Figures 3b, 3d, 3f and 3h demonstrate similar trends to those observed for the rms errors. Hydrogen, carbon, and nitrogen show comparable performance between fragment and cluster/fragment methods. On the other hand, oxygen clearly shows a noticeably broadened error distribution for the two-body fragment methods compared with cluster-based approaches. Further, individual chemical shifts converge at the same rate with respect to the two-body cut off as the rms errors presented in Figure 3 show (see Figure S6 in ESI†). We therefore conclude that in the presence of electrostatic embedding, a two-body fragment approach with a 6 Å cut off is the method of choice for calculating 1H, 13C, and 15N shifts. On the other hand, high accuracy 17O calculations benefit from the use of a central 4 Å cluster and perhaps a longer 8 Å two-body cut off.
5.2 Relative performance of DFT functionals
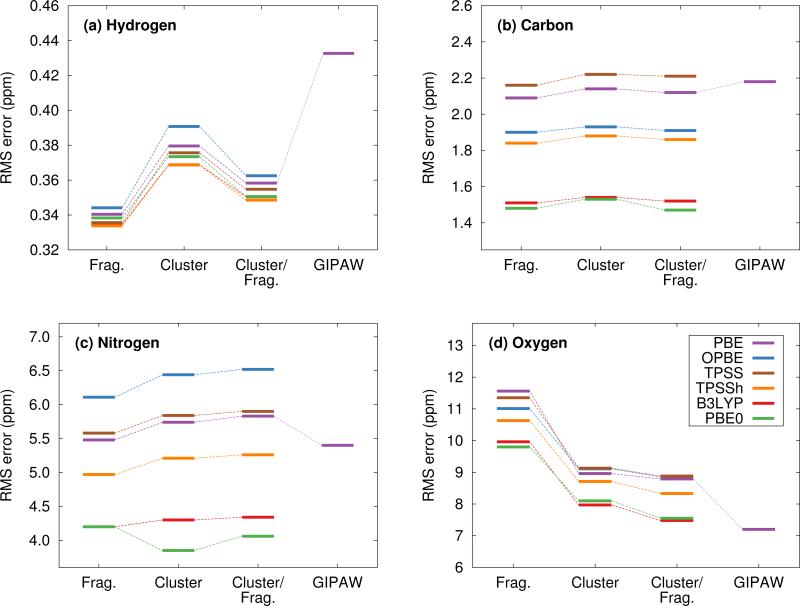
We now assess the performance of various commonly used density functionals for NMR chemical shift prediction in molecular crystals using these models. Specifically, we benchmark two GGA functionals (PBE, OPBE), two hybrid density functionals (PBE0, B3LYP) and a meta-GGA (TPSS) and its hybrid variant (TPSSh). TPSS and TPSSh performed well in a recent molecular crystal study.14 Using the fragment, cluster, and combined cluster/fragment models, rms errors for each of the 1H, 13C, 15N, and 17O chemical shifts on their respective molecular crystal test sets are given in Figure 4. Table 1 summarizes the rms errors along with linear regression parameters for each nucleus and density functional included in the present work. Results for GIPAW PBE are also included in the table and figures and will be discussed in Section 5.3.
Fig. 4.
Root-mean-square errors broken down by functional and method for (a) 1H, (b) 13C, (c) 15N and (d) 17O isotropic chemical shifts.
Table 1.
Linear regression parameters and rms errors for the 1H, 13C, 15N and 17O test sets using two-body fragment, cluster/fragment (with a 4 Å cluster), and GIPAW calculations. All cluster and fragment calculations employ the mixed basis, electrostatic embedding and a two-body fragment cut off of 6 Å. We recommend these scaling parameters be used for general applications.
| Two-body Fragment | Cluster/Fragment | GIPAW | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Atom | Functional | RMSE | Slope | Intercept | RMSE | Slope | Intercept | |||
| Hydrogen | OPBE | 0.34 | −0.9391 | 29.28 | 0.36 | −0.9324 | 29.05 | |||
| PBE | 0.34 | −0.9335 | 29.05 | 0.36 | −0.9260 | 28.78 | 0.43 | −0.8730 | 27.19 | |
| TPSS | 0.33 | −0.9366 | 29.46 | 0.35 | −0.9291 | 29.20 | ||||
| TPSSh | 0.33 | −0.9294 | 29.27 | 0.35 | −0.9238 | 29.07 | ||||
| PBE0 | 0.34 | −0.9169 | 28.69 | 0.35 | −0.9111 | 28.49 | ||||
| B3LYP | 0.33 | −0.9210 | 28.95 | 0.35 | −0.9140 | 28.71 | ||||
| Carbon | OPBE | 1.90 | −1.0603 | 194.78 | 1.91 | −1.0592 | 194.66 | |||
| PBE | 2.09 | −1.0273 | 180.43 | 2.12 | −1.0240 | 180.25 | 2.18 | −0.9902 | 169.19 | |
| TPSS | 2.16 | −1.0442 | 185.91 | 2.21 | −1.0419 | 185.75 | ||||
| TPSSh | 1.84 | −1.0179 | 184.94 | 1.86 | −1.0162 | 184.82 | ||||
| PBE0 | 1.48 | −0.9676 | 179.58 | 1.47 | −0.9661 | 179.49 | ||||
| B3LYP | 1.51 | −0.9702 | 173.83 | 1.52 | −0.9685 | 173.70 | ||||
| Nitrogen | OPBE | 6.11 | −1.1296 | 215.63 | 6.52 | −1.1067 | 215.41 | |||
| PBE | 5.48 | −1.0808 | 197.53 | 5.83 | −1.0609 | 197.72 | 5.40 | −1.0165 | 184.98 | |
| TPSS | 5.55 | −1.1061 | 206.39 | 5.90 | −1.0859 | 206.27 | ||||
| TPSSh | 4.97 | −1.0797 | 205.63 | 5.26 | −1.0616 | 205.52 | ||||
| PBE0 | 4.20 | −1.0201 | 197.84 | 4.06 | −0.9997 | 197.15 | ||||
| B3LYP | 4.20 | −1.0177 | 191.02 | 4.34 | −0.9996 | 191.18 | ||||
| Oxygen | OPBE | 11.01 | −1.1461 | 278.91 | 8.85 | −1.1347 | 281.53 | |||
| PBE | 11.56 | −1.1440 | 262.61 | 8.79 | −1.1291 | 264.15 | 7.20 | −1.0663 | 248.30 | |
| TPSS | 11.35 | −1.1632 | 276.67 | 11.35 | −1.1505 | 278.32 | ||||
| TPSSh | 10.63 | −1.1265 | 278.45 | 8.33 | −1.1153 | 280.05 | ||||
| PBE0 | 9.80 | −1.0607 | 270.18 | 7.55 | −1.0502 | 271.60 | ||||
| B3LYP | 9.96 | −1.0646 | 264.15 | 7.48 | −1.0551 | 266.32 | ||||
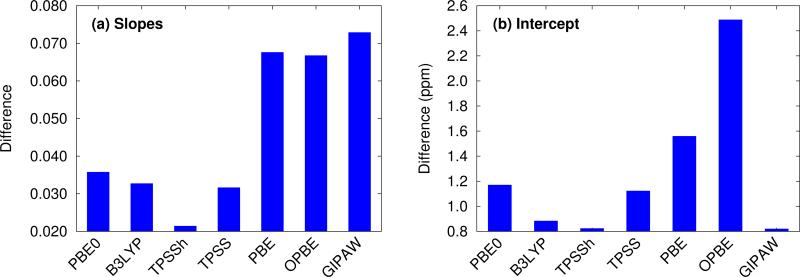
Figure 4 reveals several insightful trends. First, the three hybrid functionals demonstrate improved rms errors relative to the GGA-type and meta-GGA functionals across all functionals and atom types. The PBE0 and B3LYP hybrid functionals clearly give rise to the lowest rms errors for 13C, 15N and17O, notably outperforming the GGA, meta-GGA and meta-hybrid functionals. For 1H, the differences in rms error across the different functionals are a trivial few hundredths of a ppm. Second, the trends regarding the relative performance of the different computational models reported for PBE0 in the previous section hold across all functionals for 1H, 13C and 15N nuclei. Root-mean-square errors for the GGA-type functionals differ by only a couple tenths of a ppm across fragment, cluster and cluster/fragment calculations. For oxygen, on the other hand, the rms errors for the two-body fragment model are up to several ppm larger than those for the cluster or cluster/fragment models, reiterating the importance of capturing many-body effects when predicting 17O chemical shifts.
Third, it was recently reported that the meta-GGA density functional TPSS demonstrated improved agreement with experiment relative to GGA functionals using a GIAO/symmetry-adapted cluster model in predicting the principal components of the chemical shielding tensor for 13C, 15N, 19F and 31P nuclei.14 Here, no such behavior is observed for the isotropic 13C and 17O chemical shifts. For nitrogen, the meta-GGA TPSS does perform slightly better than PBE or OPBE, but the differences are ~0.1 ppm or less between TPSS and OPBE. For 1H, all six functionals are essentially indistinguishable from one another in terms of accuracy.
Holmes et al14 also observed that PBE0 performed worse than the GGA and meta-GGA functionals they tested for nitrogen, while it and B3LYP perform the best here. The reasons for the discrepancy between that study and the current one are unclear, but the studies do differ in a few notable ways. First, Ref 14 focuses on principal components of the chemical shielding tensors, while the work here is based on isotropic chemical shifts. On the one hand, shielding tensor principal components contain more detailed information about the local environment that is averaged out in the isotropic shift, making them a more sensitive probe for the structure and more challenging for models to predict. On the other hand, measuring tensor components is inherently less precise than extracting isotropic chemical shifts, which could increase the experimental errors in the tensor data used in the benchmarking. Second, no van der Waals dispersion correction was employed when performing all-atom crystal structure optimizations in Ref 14. Dispersion is critical in molecular crystals,80–83 though freezing the lattice parameters at their experimental values partially mitigates problems arising from its neglect.84 Third, the clusters used in Ref 14 typically contain 13– 17 molecules, which are similar in size to the 4 Å clusters used here, and did not employ charge-embedding. As seen in Figure 3, the effects of charge embedding and longer-range interactions beyond 4 Å are modest but non-zero. While further investigation is needed to sort out these details, hybrid functionals stand out here as the functionals of choice for NMR chemical shift calculations for all nuclei under consideration.
Fourth, the slopes in the regression lines of the best-performing hybrid functionals mostly deviate from the ideal −1 by a few percent. Such deviations are fairly typical15 and they help compensate for various systematic errors, including the omission of dynamics, vibrational averaging, etc.85–89 Interestingly, the deviations from −1 in the hydrogen slopes are much larger at 8–9%. This might reflect the particular importance of dynamics and nuclear quantum effects for hydrogen.90
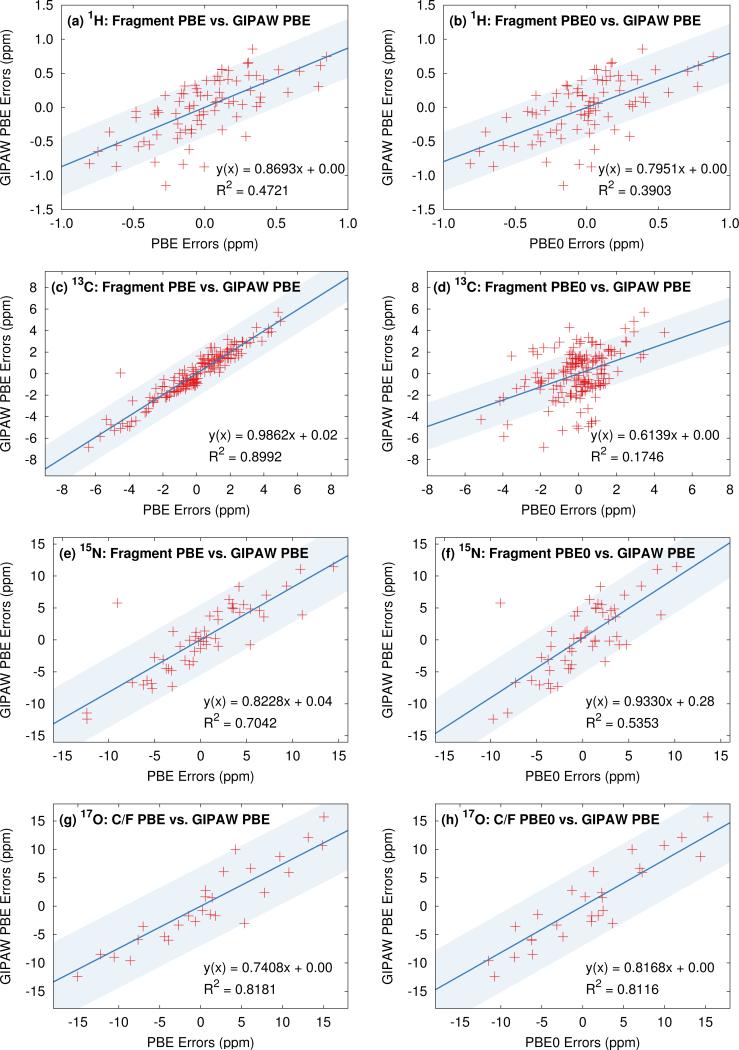
Finally, we examine the degree to which similarities in the predicted chemical shifts among various computational models and density functionals extend to individual atoms. To provide visual context for the scatter plot, the shaded region in these plots indicates plus or minus the rms error for the method on the y-axis. Figure 5 plots the correlations between a collection of top-performing model/density functional combinations. Previous results for 13C isotropic chemical shifts demonstrate relatively uniform performance at the individual atom level across both functional class and fragment model,13 and comparable results are seen here in Figures 5c and 5d. Figure 5a illustrates the correlations in the errors for the isotropic 1H shifts relative to experiment for PBE0 fragment and cluster/fragment calculations. Figure 5b plots the similar comparison between fragment-based PBE0 and B3LYP calculations. The corresponding linear fits demonstrate both high correlation coefficients as well as slopes near unity, indicating that fragment and cluster/fragment models using either PBE0 or B3LYP predict very similar 1H shieldings. Similar results are observed for 15N and 17O when comparing across hybrid functionals (see Figures 5f and 5h).
Fig. 5.
(left) Correlation of the errors predicted with the two-body fragment and cluster/fragment PBE0 models and (right) correlation of the errors between the PBE0 and B3LYP functionals with two-body fragment (or cluster/fragment for oxygen) models. The shaded region indicates ±RMSE from the model on the y-axis for a visual guide.
On the other hand, both 15N and 17O show slightly reduced correlation for fragment and cluster/fragment errors (Figures 5e and 5g). In the case of 17O these results are not surprising given the reduction in rms errors observed for cluster-based approaches. However, the differences in the predicted 15N isotropic shifts betwe6en fragment and cluster/fragment methods is more surprising given the uniform performance in terms of rms errors.
5.3 Comparison of fragment and GIPAW approaches
Given the widespread use of plane wave GIPAW (particularly with the PBE functional) for chemical shift prediction in molecular solids,6 it is interesting to compare the accuracy of fragment-based approaches against GIPAW ones. The right column in Figure 3 plots the error distributions for GIPAW PBE across the four test sets. Figure 4 plots the rms errors for GIPAW PBE on each test set against the various fragment models and functionals described in the Section 5.2, and Table 1 summarizes the resulting linear regression parameters and rms errors.
Consider first how GIPAW and fragment approaches compare when using the same PBE functional. As shown in Table 1, GIPAW PBE predicts the chemical shifts with rms errors of 0.42 ppm for 1H, 2.2 ppm for 13C, 5.4 ppm for 15N, and 7.2 ppm for 17O. We previously demonstrated that GIPAW and the two-body fragment PBE model behave very similarly for 13C.13 This observation is reiterated here, where the two-body fragment model obtains an rms error of 2.1 ppm for 13C versus 2.2 ppm for GIPAW. Similarly, both the two-body fragment and GIPAW models perform about the same for 15N with PBE (rmse 5.5 ppm).
Interestingly, GIPAW PBE (rmse 0.42 ppm) performs notably worse for 1H than the two-body fragment model in the same functional (rmse 0.33 ppm). Though this difference is fairly small in absolute terms, the larger GIPAW errors stand out notably from the highly consistent results obtained for the fragment-type methods with different functionals in Figure 4. The reasons underlying the larger GIPAW 1H errors are unclear. Of course, the experimental uncertainties for 1H are often ~0.1 ppm, so the difference between the fragment and GIPAW approaches may not be statistically significant.
Only for oxygen does GIPAW PBE (rmse 7.2 ppm) significantly out-perform the two-body fragment PBE model (rmse 11.6 ppm). As discussed above, many-body effects are particularly important for oxygen, and these are only approximated via point charge embedding in the two-body fragment model. Switching to the combined cluster/fragment PBE model improves the oxygen chemical shifts substantially, reducing the rms error down to 8.8 ppm. Still, even this smaller rms error remains ~25% larger than the GIPAW one.
As discussed in Section 5.2, a key advantage of the fragment approaches is that they enable routine use of hybrid functionals for chemical shift prediction with only modest additional computational effort. For the nuclei other than hydrogen, hybrid functionals appreciably improve the quality of the chemical shift predictions. In 13C, two-body PBE0 or B3LYP rms errors of 1.5 ppm are about a third smaller than the GIPAW PBE ones (2.2 ppm). For 15N, the two-body fragment PBE0 and B3LYP errors are 1.2 ppm (~20%) smaller than those from GIPAW PBE. For 17O, switching to a hybrid functional reduces the rms error to 7.5–7.6 ppm, eliminating most of the difference in the errors between the cluster/fragment and plane wave methods. Indeed, the ~0.3 ppm difference in statistical errors between cluster/fragment PBE0 and GIPAW PBE is comparable to or smaller than the magnitude of the uncertainties in the experimental oxygen chemical shifts.
How these rms errors translate into the overall error distributions can be seen in the box plots in Figure 3. For 1H, 13C, and 15N, two-body fragment PBE0 exhibits both more small errors (as indicated by the smaller box sizes, which delineate the middle 50% of the data) and smaller-magnitude maximum errors (as indicated by the box whiskers). For oxygen, the GIPAW PBE and cluster/fragment PBE0 have a similarly sized boxes (i.e. many of the errors are comparable), but the worst errors have larger magnitude with the cluster/fragment approach.
It is also interesting to compare correlations between individual shifts predicted with GIPAW and the fragment approaches. Several such plots are shown in Figure 6. To provide visual context for the scatter plot, the shaded region in these plots indicates plus or minus the GIPAW PBE rms error. For 13C, individual shifts predicted with GIPAW and two-body fragment PBE are very similar, as demonstrated by the excellent correlation in Figure 6c. Virtually all of the variation between the two models is within the magnitude of the rms errors for the models (shaded region). On the other hand, individual two-body fragment PBE0 13C shifts are somewhat different (and statistically better) than the GIPAW PBE ones (Figure 6d). A moderate fraction of these differences are larger than the magnitude of the rms errors for GIPAW. For 1H, GIPAW PBE correlates relatively poorly with either two-body fragment PBE or PBE0 (Figure 6a–b), as might be expected from the overall larger rms errors seen with GIPAW. On the other hand, differences in the individual predicted shifts between the fragment and plane wave models are largely comparable in magnitude to the GIPAW rms error.
Fig. 6.
The left column plots the correlation between the fragment PBE and GIPAW PBE isotropic shift errors for each nucleus, while the right column compares fragment PBE0 and GIPAW PBE. For oxygen, the cluster/fragment data is shown. The shaded region indicates ±RMSE from GIPAW for a visual guide.
For 15N, the correlation between two-body PBE and GIPAW is moderate (Figure 6e), despite their statistically similar errors. In other words, the two models do predict moderately different shifts for individual atoms, but the variations in individual shifts between the two models generally appear to be comparable to or less than the overall rms errors of 5.5 ppm. Just as for carbon, the fragment PBE0 shifts correlate less well with GIPAW shifts than the PBE ones do (Figure 6f). Again, as with carbon, PBE0 shifts differ from PBE ones for individual atoms, and those differences lead to smaller statistical errors across the test sets. Finally, for oxygen, the correlations with GIPAW PBE are reasonable for both cluster/fragment PBE and PBE0 (Figure 6g–h), despite the differences in the rms errors for the different models.
Taken together, these results indicate that individual chemical shifts predicted by the different models are generally similar. For the most part, the variations seen for individual chemical shifts among the different models are on par with the statistical errors relative to experiment observed in these test sets.
Finally, the errors seen here compare well with those found in other solid-state benchmarks. Previous DFT cluster and/or GIPAW benchmark studies in molecular crystals found errors of ~0.3 ppm for hydrogen7 and ~1.5–2 ppm for carbon.7,14,91 Fewer statistics on large sets of molecular crystals are available for 15N and 17O nuclei. Holmes et al14 report rms errors of ~15 ppm for principal components of 15N shielding tensors, compared to errors of less than ~5 ppm for isotropic shifts here. Isotropic shifts are generally much easier to predict correctly, and the ratio of ~3 between the errors in the principal components and isotropic shift is consistent with the analogous ratios observed in 13C benchmarks.13,91 A different cluster model study by Rorick et al reports a mean absolute deviation of 13 ppm for a dozen 17O isotropic shifts spanning a broad range of organic and inorganic environments.56 Our results are also compatible with smaller-scale GIPAW studies on nitrogen92–94 and oxygen nuclei.92,93,95–97 See the review article by Bonhomme et al6 for additional GIPAW examples.
In summary, the results presented in these sections clearly demonstrate excellent performance for fragment-based NMR chemical shielding calculations for 1H, 13C, 15N and 17O isotropic chemical shieldings. Hybrid functionals like B3LYP and PBE0 consistently out-perform GGA functionals for all four nuclei. Statistically, the use of hybrid functionals allows fragment-based approaches to nearly match (17O) or improve upon (1H, 13C, and 15N) the quality of isotropic chemical shifts obtained with GIPAW PBE. Coupled with the general utility of Gaussian basis set wave function-based ab initio shielding calculations, the present work provides compelling support for more widespread use of fragment-based methods.
6 Statistical cross-validation of the regression models
When training a model against a set of benchmark results, as is done here for the linear regressions that convert absolute chemical shieldings to observed chemical shifts (Eq 8), there is always the danger that the fit parameters will not transfer well to systems that were not part of the training set. Accordingly, it is important to validate the performance of the models on species not included in the training set.
Instead of arbitrarily partitioning the test sets collected here into distinct training and validation subsets, we assess the robustness of the linear regression parameters obtained here using exhaustive N-choose-k cross validation trials for each nucleus and density functional. Here, N is the number of crystals in the benchmark set, and k is the number of crystals in the validation subset. The cross-validation procedure then considers all possible ways of partitioning the N crystals into N − k training crystals and k validation crystals. For example, the oxygen set contains N = 15 crystal structures. Setting k = 5 results in 3,003 possible combinations in which the regression model is trained on 10 of the crystal structures and then validated on the remaining 5 structures. Comparing the statistical performance of the model over all 3,003 combinations to the original value obtained by fitting to the entire benchmark set provides a measure of the robustness of the linear regression models. This same approach was applied previously to our carbon test set.13 That earlier work found that k values between 5 and 9 gave very similar cross-validation results in the 25 crystal 13C test set.
Table 2 summarizes the mean rms errors and linear regression parameters obtained across the thousands of fits. Standard deviations in the mean linear regression parameters are also reported. Comparison of these values with those obtained from the original fits against the entire benchmark sets (listed in Table 1) provides a measure of robustness of the regression models and chemical shift error estimates.
Table 2.
Cross-validation analysis for isotropic shifts. Data reported for 1H, 13C and 15N nuclei was obtained using the charge-embedded two-body fragment method (R2b = 6 Å, Remb = 30 Å). Cluster/fragment results are reported for 17O (R2b = 6 Å, Remb = 30 Å, 4 Å cluster). Uncertainties in the slope and deviation represent the standard deviations in the fit parameters observed over all cross-validation fits.
| Atom | Functional | Original RMSE | Cross-validation RMSE | Mean slope (A) | Mean intercept (B) |
|---|---|---|---|---|---|
| Hydrogen | OPBE | 0.34 | 0.37 | −0.9382 ± 0.0134 | 29.26 ± 0.32 |
| PBE | 0.34 | 0.36 | −0.9327 ± 0.0127 | 29.03 ± 0.30 | |
| TPSS | 0.33 | 0.36 | −0.9358 ± 0.0124 | 29.45 ± 0.30 | |
| TPSSh | 0.33 | 0.36 | −0.9287 ± 0.0119 | 29.25 ± 0.29 | |
| PBE0 | 0.34 | 0.36 | −0.9160 ± 0.0116 | 28.67 ± 0.28 | |
| B3LYP | 0.33 | 0.36 | −0.9327 ± 0.0127 | 29.03 ± 0.30 | |
| PBE (GIPAW) | 0.43 | 0.47 | −0.8731 ± 0.0182 | 27.20 ± 0.47 | |
| Carbon | OPBE | 1.90 | 1.91 | −1.0602 ± 0.0023 | 194.77 ± 0.25 |
| PBE | 2.09 | 2.13 | −1.0273 ± 0.0028 | 180.42 ± 0.27 | |
| TPSS | 2.16 | 2.22 | −1.0441 ± 0.0031 | 185.89 ± 0.35 | |
| TPSSh | 1.84 | 1.87 | −1.0178 ± 0.0024 | 184.93 ± 0.29 | |
| PBE0 | 1.48 | 1.51 | −0.9676 ± 0.0014 | 179.58 ± 0.15 | |
| B3LYP | 1.51 | 1.49 | −0.9701 ± 0.0016 | 173.83 ± 0.18 | |
| PBE (GIPAW) | 2.18 | 2.25 | −0.9901 ± 0.0028 | 169.18 ± 0.25 | |
| Nitrogen | OPBE | 6.11 | 6.40 | −1.1220 ± 0.0058 | 215.37 ± 0.82 |
| PBE | 5.48 | 5.75 | −1.0755 ± 0.0049 | 197.44 ± 0.68 | |
| TPSS | 5.55 | 5.81 | −1.1001 ± 0.0051 | 206.23 ± 0.70 | |
| TPSSh | 4.97 | 5.20 | −1.0747 ± 0.0043 | 205.50 ± 0.62 | |
| PBE0 | 4.20 | 4.41 | −1.0200 ± 0.0033 | 197.83 ± 0.50 | |
| B3LYP | 4.20 | 4.42 | −1.0176 ± 0.0034 | 191.00 ± 0.50 | |
| PBE (GIPAW) | 5.40 | 5.65 | −1.0117 ± 0.0046 | 184.95 ± 0.64 | |
| Oxygen | OPBE | 8.85 | 10.29 | −1.1393 ± 0.0267 | 281.52 ± 1.22 |
| PBE | 8.79 | 10.06 | −1.1331 ± 0.0233 | 264.06 ± 1.33 | |
| TPSS | 8.88 | 10.19 | −1.1548 ± 0.0248 | 278.28 ± 1.31 | |
| TPSSh | 8.33 | 9.45 | −1.1188 ± 0.0209 | 280.03 ± 1.27 | |
| PBE0 | 7.55 | 8.42 | −1.0525 ± 0.0151 | 271.56 ± 1.19 | |
| B3LYP | 7.48 | 8.36 | −1.0574 ± 0.0150 | 266.26 ± 1.19 | |
| PBE (GIPAW) | 7.20 | 8.14 | −1.0687 ± 0.0152 | 248.21 ± 1.21 |
The mean cross-validation rms error for 13C and 15N nuclei across all functionals is only ~1–5% larger than the corresponding value obtained by fitting against the entire set. Larger increases in the rms error are observed for 1H and 17O nuclei, ranging from ~6–8% and ~9–15%, respectively. These differences likely result from a combination of test set size, inherent challenges in predicting chemical shieldings for certain nuclei, as well as uncertainties in the experimental data. Note too that the overall cross-validation behaviors of the fragment and GIPAW approaches are qualitatively similar.
Comparing the mean linear regression parameters obtained via cross-validation (Table 2) with those reported in Table 1 also reveals close agreement in the regression parameters. The mean slopes differ only in the third decimal place, while the intercepts generally agree to within a few hundredths of a ppm. The standard deviations in the cross validation parameters are roughly one order of magnitude larger. For 13C, 15N and 17O, these uncertainties in the regression model parameters have minimal effect on the predicted chemical shifts. Proportionally, the uncertainties in the 1H scaling parameters are much larger, however, the relatively uniform rms errors for each partitioning indicate a degree of compensation between the slope and intercept.
Overall, these tests demonstrate the robustness of the regression model parameters obtained in the benchmarks here. The reported scaling factors in Table 1 should prove useful in future molecular crystal studies or in other cases such as biological systems where the explicit treatment of the environment is necessary for accurate chemical shift prediction. The next section discusses four illustrative applications which apply these scaling parameters to systems which are not found in the benchmark sets.
7 Applications
The purpose of developing the regression models in the previous sections is to enable chemical shift prediction in new systems which are not included in the test sets. The following sections provide example applications of the regression models for each of the four nuclei studied here. In assessing the quality of the predictions, one should consider the distributions of errors observed in the benchmark test sets. As shown in Figure S5 in the ESI,† the error distributions are somewhat Gaussian, particularly for the larger test sets. Notably, 65–75% of the errors fall within one standard deviation of the mean (zero error), and 92–97% of the errors fall within two standard deviations. These percentages compare favorably with the 68% and 95% probabilities expected for data lying within one and two standard deviations in an ideal normal distribution.
Accordingly, as a rule of thumb, we consider any predicted shift that lies within twice the root-mean-square error of the experimental value to be in reasonable agreement. For example, based on two-body fragment (or cluster/fragment for oxygen) data from Table 1, this means that individual PBE0 shift errors of 0.64 ppm for 1H, 3.0 ppm for 13C, 8.6 ppm for 15N, and 15.2 ppm for 17O should be considered acceptable. Larger errors will sometimes occur, of course, but relatively rarely (~5% of the time). When considering larger sets of predicted shifts, one might similarly hope that the rms errors would be similar in magnitude to the test set rms errors. One could attempt to make this latter argument more rigorous using a χ2 test, for instance, but we do not do so here.
7.1 9-Tertbutyl Anthracene Ester
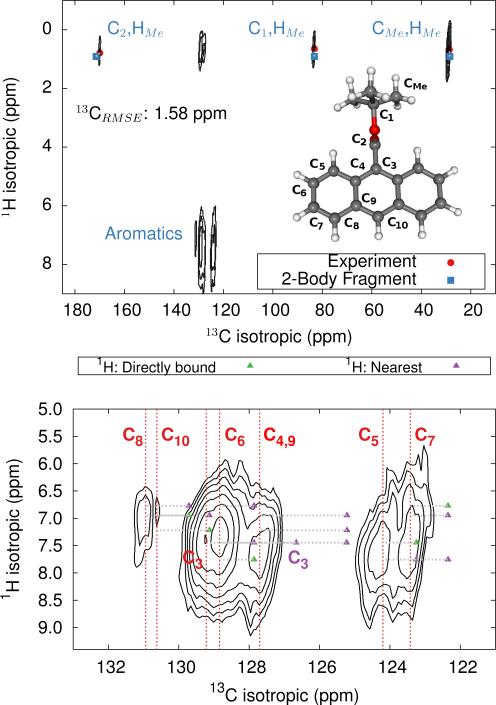
The 9-tertbutyl anthracene ester (9-TBAE) has been the subject of recent experimental interest in light of its unique photochemical properties. Previous work demonstrated a photodimerization-induced expansion of the molecular crystal nanorods of up to 15%.98,99 Although initial evidence characterized the photodimerized product as a metastable intermediate, the mechanism for the expansion remains unclear. In the present work we present tentative 1H and 13C assignments in the heteronuclear correlation (HETCOR) spectra for the 9-TBAE monomer (Figure 7).
Fig. 7.
HETCOR 1H/13C spectrum for 9-TBAE (top) and zoom focusing on the aromatic region (bottom). The location of the experimental 13C peaks are given by red dashed lines. Predicted cross-peak locations are illustrated in green for protons directly bound to the carbon and in purple for the nearest neighboring proton.
A previous x-ray diffraction study of the 9-TBAE crystal structure revealed two distinct configurations of the t-butyl side chain with a 69%/31% occupancy ratio at low temperature, which disappears above 100 K.99 Hydrogen-only plane wave geometry optimizations with fixed lattice parameters were performed on each configuration (see Section 3.2 for further details). Fragment-based NMR chemical shelding calculations using the PBE0 functional and mixed basis described above with a 6 Å two-body cut off were performed on both optimized crystal structures. The predicted chemical shieldings were converted to chemical shifts using the test-set-derived PBE0 scaling parameters presented in Table 1. The predicted chemical shifts for each configuration were then weighted according to the site occupancy to obtain final predicted chemical shifts for assigning the spectrum. The methyl carbon and hydrogen shifts were also averaged under the assumption of fast dynamics.
The upper panel of Figure 7 illustrates the HETCOR spectrum with the experimental peaks labeled in red and the corresponding predicted peaks in blue. While unambiguous assignment of CMe, C1, C2 and HMe is possible upon inspection of Figure 7, the aromatic region requires more careful analysis. The lower panel in Figure 7 shows an expansion of the aromatic region of the HETCOR spectrum. The experimental 13C shifts are indicated as dashed red lines. Predicted cross-peaks to carbon are illustrated using green triangles for directly bound hydrogen atoms and purple for nearest-neighbor hydrogens. The predicted cross-peaks agree well with the experimental HETCOR spectrum, with the largest 13C error approximately ~2.5 ppm.
Tables 3 and 4 present tentative spectral assignments based on the fragment NMR calculations. Most carbon shifts in the aromatic region can be plausibly assigned based on the sequential ordering of the predicted carbon shifts. Two pairs of carbon atoms, C8/C10 and C4/C9, are difficult to resolve unambiguously due to their very similar experimental shifts, but our predicted shieldings provide candidate assignments. C3 has no directly bound hydrogen and should exhibit weak cross-peaks to neighboring protons, so it was assigned to the weak peak at 129.22 ppm. C4 and C9 exhibit similarly weak cross-peaks, but were assigned to the larger peak at 127.70 ppm due to their predicted overlapping resonances. Based on these assignments, two-body fragment PBE predicts an overall 13C rms error of only 1.57 ppm. GIPAW PBE calculations lead to the same assignments, albeit with a larger 13C rms error of 2.17 ppm relative to experiment.
Table 3.
Experimental 13C isotropic shifts (in ppm) along with tentative carbon assignments based on two-body fragment PBE0 NMR calculations using PBE0 and a mixed basis. GIPAW PBE shifts are also listed. See Figure 7 for atom numbering.
| Atom | Expt. | 2-Body PBE0 | Error | GIPAW PBE | Error |
|---|---|---|---|---|---|
| CMe | 28.63 | 28.52 | 0.11 | 24.05 | 4.58 |
| C1 | 83.21 | 83.27 | −0.06 | 85.00 | −1.79 |
| C2 | 169.94 | 171.43 | −1.49 | 170.06 | −0.12 |
| C3 | 129.22 | 126.69 | 2.53 | 126.95 | 2.27 |
| C4 | 127.70 | 125.26 | 2.44 | 124.95 | 2.75 |
| C5 | 124.20 | 123.28 | 0.92 | 122.79 | 1.41 |
| C6 | 128.84 | 127.89 | 0.95 | 127.57 | 1.27 |
| C7 | 123.42 | 122.38 | 1.04 | 122.10 | 1.32 |
| C8 | 130.94 | 129.73 | 1.21 | 129.39 | 1.55 |
| C9 | 127.70 | 125.25 | 2.45 | 125.57 | 2.13 |
| C10 | 130.62 | 129.16 | 1.46 | 129.01 | 1.61 |
| RMSE: | 1.57 | 2.17 |
Table 4.
Possible cross-peak assignments of the 9-TBAE HETCOR spectrum, based on the carbon assignments from Table 3, along with the corresponding predicted 1H chemical shifts. All shifts in ppm. Listed atom pairs correspond to hydrogens either directly bonded to the carbon or on nearest-neighbor carbons.
| 1H/ 13C Expt. | Cross-Peak Assignment | 2-Body PBE0 1H | GIPAW PBE 1H |
|---|---|---|---|
| 0.68/28.63 | HMe / CMe | 0.89 | 0.67 |
| 0.65/83.21 | HMe / C1 | 0.89 | 0.67 |
| 0.79/ 169.94 | HMe / C2 | 0.89 | 0.67 |
| 7.41 / 129.22 | H5 /C3 | 7.45 | 6.82 |
| 7.72/ 127.70 | H5 / C4,C9 | 7.45 | 6.82 |
| H10 / C4,C9 | 7.22 | 6.42 | |
| 7.70/ 124.20 | H5 / C5 | 7.45 | 6.82 |
| H6 / C5 | 7.76 | 7.27 | |
| 7.31/ 128.84 | H5 / C6 | 7.45 | 6.82 |
| H6 / C6 | 7.76 | 7.27 | |
| H7 /C6 | 6.77 | 6.42 | |
| 7.37/ 123.42 | H6 /C7 | 7.76 | 7.27 |
| H7 /C7 | 6.77 | 6.42 | |
| H8 /C7 | 6.95 | 6.33 | |
| 6.90/ 130.94 | H7 /C8 | 6.77 | 6.42 |
| H8 /C8 | 6.95 | 6.33 | |
| H10 / C8 | 7.22 | 6.42 | |
| 6.90/ 130.62 | H8 / C10 | 6.95 | 6.33 |
| H10 / C10 | 7.22 | 6.42 |
Given the degree of overlap in the proton resonance for the aromatic region, spectral assignment of the 1H shifts proves more difficult. Table 4 lists the prominent, experimentally observed cross peaks in the HETCOR spectrum. Combining the carbon assignments and the assumption that the resonances will be dominated by contributions involving either directly bonded or nearest-neighbor hydrogen atoms, we propose the possible assignments listed in the table. Based on the assignments for C8 and C10, for instance, the two cross peaks at 6.9 ppm for 1H likely correspond to H8/C8 and H10/C10 correlations, perhaps with smaller contributions from dipolar couplings to nearest-neighbor hydrogens (e.g. H7/C8, H10/C8, and H8/C10). As shown in Figure 7 and Table 4, the predicted two-body fragment PBE0 1H shifts for these assignments are generally within a few tenths of a ppm of the experimental values.
Performing the analysis with 1H GIPAW PBE shifts instead of two-body PBE0 leads to the same qualitative cross-peak assignments. For the hydrogen shifts associated with the methyl, C6, and C7 atoms, GIPAW PBE performs comparably well or up to a few tenths of a ppm better than two-body PBE0. On the other hand, GIPAW PBE underestimates the hydrogen shifts by ~0.5–1 ppm for cross-peaks associated with C3, C4, C5, C8, and C10. Overall, the 1H and 13C isotropic chemical shifts predicted with either the two-body fragment PBE0 model or GIPAW PBE can help assign the HETCOR spectrum of 9-TBAE. However, the fragment PBE0 predictions provide moderately better agreement with experiment.
7.2 15N Chemical shift predictions in histidine co-crystals
Hydrogen bonding between imidazole and carboxylate moieties occurs frequently in biological systems. Given that both functional groups have similar pKa values, enhanced proton mobility is often observed.100 In an effort to characterize these ubiquitous interactions better, a recent study used solid-state NMR spectroscopy to probe the magnetic properties of a collection of histidine-containing molecular co-crystals.100
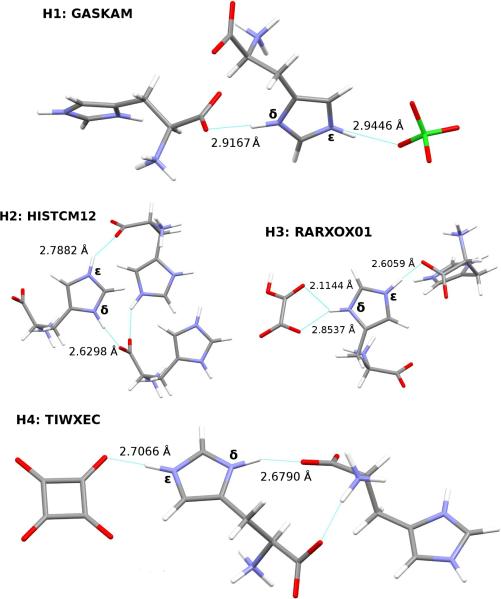
Here, we investigate the ability of our fragment-based chemical shift predictions to discriminate among the two imidazole ring nitrogens and between the different crystal environments found in four such co-crystals: L-histidine perchlorate (H1), L-histidine monohydrochloride monohydrate (H2), L-histidine hydrogen oxalate (H3), and L-histidine hydrogen oxalate co-crystals (H4). The hydrogen bonding and CSD reference codes for these crystals are shown in Figure 8.
Fig. 8.
Hydrogen bonding in optimized histidine structures. N-O bond lengths are given in Å.
Each co-crystal was subjected to an all-atom geometry optimization using fixed lattice parameters, as described in Section 3.2. Both GIPAW PBE and fragment PBE0 chemical shielding calculations were performed on each of the optimized structures. The raw shieldings were scaled according to Eq 8 using the test-set derived scaling parameters reported in Table 1.
A comparison of the experimental and predicted 15N isotropic shifts for each of the histidine co-crystals is given in Figure 9. The predicted 15N isotropic shifts systematically overshoot the experimental values (Figure 9) by between 3–9 ppm for fragment PBE0 and 2–10 ppm for GIPAW PBE. The fragment PBE0 rms error of 6.9 ppm is larger than the nitrogen test set rms error of 4.3 ppm (Table 2), but it still lies well within the expected error distribution. In fact, close examination of the predicted shifts for comparable sp2 hybridized nitrogen atoms hydrogen-bonded to a carboylate group in the nitrogen benchmark set (e.g. see structures 3, 5, 6, 7, and 9 in the ESI†) reveals a similarly large rms error. In other words, these particular nitrogen environments prove slightly harder to model than other ones. For comparison, cluster/fragment PBE0 predicts the shifts with an rms error of 6.1 ppm, while GIPAW PBE gives an rms error of 6.6 ppm.
Fig. 9.
(a) Comparison between two-body fragment PBE0 predicted and experimental imidazole nitrogen chemical shifts for the histidine co-crystals H1–H4 shown in Figure 8. (b) Comparison of GIPAW PBE versus experiment.
As a side note, the systematic nature of the over-estimation of the chemical shifts with all three methods means that one could reduce the rms errors by directly fitting the predicted shieldings to the experimental shifts via Eq 8. For example, doing so with the two-body PBE0 data reduces the error to 2.7 ppm. Of course that approach lacks the transferability of the scaling models developed here.
The differences between the δ and ε N chemical shifts in a given co-crystal range from 3-13 ppm. Except for L-histidine perchlorate (H1), the predicted chemical shifts correctly order the δ and ε nitrogen shifts, which would be important when using these calculations to assign the histidine nitrogen features. H1 exhibits the smallest difference between the two nitrogen shifts (3.4 ppm), and both the fragment PBE0 and the GIPAW PBE results incorrectly order those shifts.
A more stringent test comes from considering the ordering of the chemical shifts across all four co-crystals. Fragment PBE0 orders most of the shifts correctly, except for those in H1 and the ε nitrogen in H4. The δ nitrogens in H2, H3, and H4, all of which exhibit short N-O distances, are over-estimated by 8–9 ppm, while the ε nitrogen in H4 has the smallest error of 3 ppm, leading to the incorrect ordering. GIPAW does better for H4ε, correctly predicting that it occurs further downfield from H2ε and H3δ . Overall, despite imperfect reproduction of the qualitative trends, the predicted chemical shifts derived from the nitrogen scaling parameters provide a useful tool for investigating how chemical environment impacts these 15N chemical shifts.
7.3 Benzoic acid
In the crystalline state, benzoic acid molecules form symmetric carboxylic acid dimers (Figure 10). There are two possible configurations for the hydrogens in the carboxylic acid dimer, and these configurations inhabit slightly different environments in the crystal,101 as shown in Figure 10. In configuration A, the protonated oxygen is closer to the meta hydrogen in the neighboring co-planar dimer, while in configuration B it is closer to the ortho hydrogen.
Fig. 10.
Predicted cluster/fragment PBE0 17O chemical shifts for benzoic acid. Though the isolated dimers would be symmetric, symmetry of the two configurations is broken in the crystal. The protonated oxygen is closer to either the (a) meta hydrogens in configuration A or (b) ortho hydrogens of the neighboring benzoic acid dimers in configuration B.
Given four oxygens per dimer and two unique dimer configurations, one might expect up to eight oxygen chemical shifts. However, the oxygens diagonal to one another within a given dimer are equivalent by symmetry, which reduces the number of potential shifts to four. At room temperature, fast proton exchange further dynamically averages over configurations A and B. In the end one expects to observe two unique 17O shifts. The experimental NMR spectrum shows a single, broad 17O peak at 230 ppm under magic angle spinning conditions.53 The carboxyl carbon appears at 173–174 ppm.102,103
Such dynamical effects can be modeled by computing the chemical shifts for the two different possible proton positions and Boltzmann averaging over them. This has been done for the carboxylic acid dimers in aspirin and salicyclic acid,104 for instance. We perform similar analysis here. The chemical shift tensors were averaged over configurations A and B according to:
| (9) |
| (10) |
| (11) |
where PA and PB are Boltzmann weights for the two configurations,
| (12) |
To test the performance of the scaling models derived here, configuration A was generated by optimizing the experimental benzoic acid crystal structure (CSD code BENZAC02) using periodic PBE-D2 (all atom, fixed lattice parameters). Configuration B was generated by transferring the hydrogens to the opposite oxygens and re-optimizing. The resulting energies predict that configuration B is more stable by 1.13 kJ/mol, so PA = 0.387 and PB = 0.613 at 298 K. Fragment, cluster/fragment, and GIPAW NMR chemical shielding calculations were then performed using each density functional. For each model, the final isotropic chemical shifts were obtained by diagonalizing the tensors obtained from Eqs 9–11, averaging the principal components to obtain isotropic shieldings, and converting the shieldings to shifts according to the linear regression parameters reported in Table 1.
Figure 10 shows the two unique 17O chemical shifts predicted for each of the two configurations at the cluster/fragment PBE0 level. The shifts resulting from room-temperature Boltzmann-averaging according to Eqs 9–12 are summarized in Table 5 for all six functionals using the fragment and cluster/fragment models. As expected from previous results13 and the discussion in Sections 5.1 and 5.2, the carboxyl carbon shift predicted with each functional varies by only ~0.1–0.3 ppm between the fragment and cluster/fragment methods. The fragment approach shifts differ from the GIPAW PBE value by 1–1.5 ppm, but they still lie within 1–2 ppm of the experimental 13C shift. Similarly good agreement is seen for OPBE, PBE0, and B3LYP.
Table 5.
Predicted and experimental carboxyl-13C and 17O isotropic chemical shifts for benzoic acid.
| Functional | 13C Fragment | 13C Cluster/Fragment | 13C GIPAW | 17O Fragment | 17O Cluster/Fragment | 17O GIPAW |
|---|---|---|---|---|---|---|
| OPBE | 175.5 | 175.3 | 215.2,233.4 | 216.4,238.8 | ||
| PBE | 175.3 | 175.1 | 173.8 | 211.2,229.6 | 213.1,235.8 | 211.6,237.8 |
| TPSS | 176.7 | 176.5 | 212.9,231.3 | 214.5,237.2 | ||
| TPSSh | 176.7 | 176.5 | 213.0,231.6 | 214.6,237.3 | ||
| PBE0 | 175.4 | 175.2 | 212.0,231.0 | 213.7,236.5 | ||
| B3LYP | 175.7 | 175.4 | 210.8,229.7 | 212.8,235.7 | ||
| Experiment | 173–174a | 230b |
Analysis of the oxygen atoms is slightly more difficult, since the experimental study did not resolve the two distinct shifts. Nevertheless, the predicted two-body fragment PBE0 shifts (213 and 231 ppm) and the cluster/fragment PBE0 shifts (214 and 237 ppm) are reasonably consistent with the broad experimental peak assigned to 230 ppm. They are also within a couple ppm of the GIPAW PBE predictions of 212 and 238 ppm. Similar shifts are obtained with fragment-based approaches for most of the other functionals, too. In summary, the fragment approaches predict these carboxylic acid atom shifts in good agreement with both GIPAW and experiment.
7.4 C-Nitrosoarene complex
C-Nitroso compounds represent an important class of organic compounds with chemical, biological and pharmaceutical relevance.30,105 Of particular interest for the present work is the wide span of chemical shieldings nitrosoarene-metal complexes display. For instance, (NODMA) has one of the largest 15N chemical shift anisotropies known.106,107 In the present work, we examine the 17O chemical shielding for SnCl2(CH3)2(NODMA)2, hereafter refered to as compound 2 and depicted in Figure 11. Strong tin-oxygen interactions give rise to an experimental 17O isotropic chemical shift of 717 ppm relative to liquid water.30 The largest chemical shift included in the 17O test set is approximately 350 ppm, therefore the chemical shift for compound 2 lies well outside the range of shifts which comprise the test set. This test case allows us to simultaneously assess the accuracy of fragment methods in the context of organometallic molecular crystals and the accuracy of the scaling parameters when applied to chemical environments significantly different from those included in the test set.
Fig. 11.
Structure of compound 2: SnCl2(CH3)2(NODMA)2.
Compound 2 exhibits static disorder about the oxygen-nitrogen bond. The two dominant configurations were observed with occupancy rations of about 3:1 in the x-ray crystallography. We performed all-atom optimizations with fixed lattice parameters on each of the three possible crystal structures for compound 2 (CSD code BISVII01) as outlined in Section 3.2. The two minor configurations had stabilities of +2.5 and +9.9 kJ/mol relative to the major one, and the corresponding room temperature Boltzmann factors suggest populations of approximately 72%, 26%, and 1%, in good agreement with the 3:1 ratio cited experimentally for the two most important structures. The original experimental study of this nitrosoarene ascribes the oxygen shift of 717 ppm to the dominant configuration,30 so we focus on that structure here. Though oxygen chemical shift calculations benefit appreciably from explicit treatment of many-body effects via the cluster/fragment approach, pairwise-only fragment calculations with a 6 Å two-body cut off and electrostatic embedding were performed instead due to the large size of this system. Table 6 reports the absolute and scaled isotropic shifts and the error in the predicted shifts relative to the experiment.
Table 6.
Predicted isotropic 17O chemical shifts (in ppm) for compound 2 using a two-body fragment method and scaling parameters reported in Table 1. The experimental shift is 717 ppm.
| Functional | Absolute Shielding | Scaled Shift | Error |
|---|---|---|---|
| OPBE | −428.6 | 770.1 | 53.1 |
| PBE | −444.9 | 771.6 | 54.6 |
| TPSS | −399.7 | 741.6 | 24.6 |
| TPSSh | −404.5 | 734.1 | 17.1 |
| PBE0 | −450.5 | 748.0 | 31.0 |
| B3LYP | −452.1 | 745.4 | 28.4 |
| GIPAW (PBE) | −499.6 | 781.0 | 64.0 |
First, we observe that hybrid functionals reproduce the 17O isotropic shieldings to within ~20 ppm, while GGA functionals exhibit errors nearly double that. Interestingly, the TPSS and TPSSh notably out-perform the other functionals here, with errors of only 11 and 8 ppm, respectively. The ~20 ppm errors for the hybrid and ~10 ppm errors for the meta-GGA/hybrid functionals are large but are plausibly within the error distributions one expects for oxygen with the two-body fragment method based on the test set results (cf Figure 3h). On the other hand, GIPAW PBE dramatically overestimates this shift by 64 ppm, which is an order of magnitude larger than the GIPAW oxygen test set rms errors.
Second, the errors reported in Table 6 reflect contributions from both the fragment DFT calculations and the extrapolation of the scaling parameters well-outside the range for which they were fitted. Although the statistical cross-validation studies demonstrate low sensitivity of the regression parameters to the choice of fitting set, those studies included only shifts in the ~50–350 ppm range. If, hypothetically, one were to expand the test set to include compound 2, comparing the resulting linear regression parameters with those from the initial test set would provide further insights into the robustness of the regression parameters.
Figure 12 illustrates the differences in the linear regression parameters for the 17O test set upon including compound 2. The magnitude of the differences in regression parameters in Figure 12 directly correlate with the magnitude of the errors given in Table 6. Accordingly, both the TPSS and TPSSh density functionals demonstrate the smallest variations in the regression parameters upon including compound 2. With these new regression parameters for the cluster/fragment model, individual predicted shifts in the oxygen test set would vary by an rms ~2 ppm. However, the overall rms errors versus experiment would increase by only a few tenths of a ppm.
Fig. 12.
Differences in linear regression parameters for the 17O test set resulting from the inclusion of compound 2 for the (a) slopes and (b) intercepts.
These results raise the question of whether compound 2 should be included in the test set. Its inclusion would improve the prediction for its oxygen chemical shift and would extend the range of oxygen chemical shifts upon which the regression parameters are included. That could improve the realm of applicability of the regression parameters. On the other hand, due to its extreme 717 ppm chemical shift, this single data point has an outsized effect on the regression line through the more typical ~50–350 ppm range of oxygen shifts. For that reason, we excluded this shift from the test set. Even without including this particular shift in the test set, the ~10-20 ppm errors obtained for this oxygen with the fragment approach remain tolerable, demonstrating the broad range of applicability of the test-set-derived parameters. Of course, if one is interested in chemical shifts outside the more typical range, one might wish to include compound 2 and perhaps other similar species in constructing the regression model.
8 Conclusions
In conclusion, a series of benchmark calculations assessing the performance of fragment, cluster and combined cluster/fragment models for predicting 1H, 13C, 15N, and 17O isotropic chemical shifts in molecular crystals using a variety of density functionals have been carried out. Test sets have been assembled for each nucleus which enable one to validate chemical shift predictions against experiment. The following key conclusions can be drawn from this work.
Fragment, cluster, and combined cluster/fragment methods using a 6 Å two-body cut off and a 4 Å cluster size demonstrate comparable performance for 1H, 13C, and 15N isotropic shift prediction. However, local many-body effects result in improved accuracy (~2 ppm reduction in rms error) for predicted 17O isotropic shifts using a cluster-based approach. Accordingly, the two-body fragment approach can be used for most applications, but a cluster/fragment approach should be used for oxygen when higher accuracy is needed.
Hybrid functionals out-perform GGA-type functionals for 1H, 13C, 15N, and 17O nuclei, regardless of the model used. Among the functionals tested, the hybrid functionals PBE0 and B3LYP stand out as the functionals of choice for modeling NMR chemical shifts. Whether the improved performance of hybrid functionals is seen for other NMR active nuclei will be explored in future work. The benchmarks here do not reproduce earlier findings which found particularly good performance for the TPSS and TPSSh meta-GGA/hybrid functionals. Those functionals do perform particularly well for the unusual oxygen chemical shift in nitrosoarene compound 2, though it is unclear how broadly one should generalize from that single data point.
The fragment-based approaches exhibit accuracy that is highly competitive with GIPAW. Two-body fragment PBE0 and B3LYP out-perform GIPAW PBE on the 1H, 13C, and 15N test sets by 20-30%. For 17O, where many-body effects are particularly important, the cluster/fragment PBE0 and B3LYP models produce rms errors that are about half a ppm (8%) worse than those from GIPAW PBE.
Linear regression parameters mapping absolute chemical shieldings to observable chemical shifts have been provided for six different density functionals (OPBE, PBE, TPSS, PBE0, B3LYP, and TPSSh) using both fragment and cluster/fragment methods and the locally dense 6-311+G(2d,p)/6-311G(d,p)/6-31G basis combination. Mean scaling parameters obtained via statistical cross-validation (Table 2) are in excellent agreement with those obtained directly from the test set (Table 1), with only small variations in the regression parameters for any of the nuclei and density functionals included in the analysis. For general applications, we recommend the use of the linear regression parameters presented in Table 1.
The applicability of these regression parameters for each nucleus to systems not included in the test set was demonstrated on several systems, including assignment of the 1H and 13C HETCOR spectrum of 9-TBAE, investigation of the nitrogen chemical shifts in histidine co-crystals, analysis of the carboxylic acid group shifts in benzoic acid, and prediction of the unusually far downfield oxygen chemical shift of oxygen bound to a tin atom in a C-nitrosoarene.
These models provide practical, high-accuracy alternatives to existing plane wave methods in organic molecular crystals. In the future, it will be interesting to explore the performance of these models more widely. Fragment methods generally perform well in systems with sufficiently large band gaps,108–110 and so one might expect the chemical shift prediction methods developed here to be effective in a variety of non-metallic systems. On the other hand, some nuclei (like 17O) are more sensitive to many-body effects, so the impact of the truncating the many-body expansion should be tested on other nuclei.
Supplementary Material
Table 7.
Linear regression parameters for the 17O test set with compound 2 included. Errors in the predicted shieldings for compound 2 using the linear regression parameters from the expanded test set.
| Functional | Slope | Intercept | Error |
|---|---|---|---|
| OPBE | −1.0794 | 276.42 | 22.0 |
| PBE | −1.0765 | 261.05 | 22.9 |
| TPSS | −1.1316 | 275.55 | 10.9 |
| TPSSh | −1.1052 | 277.63 | 7.7 |
| PBE0 | −1.0250 | 269.02 | 13.7 |
| B3LYP | −1.0319 | 263.27 | 12.8 |
| PBE (GIPAW) | −0.9934 | 247.48 | 26.7 |
Acknowledgments
Funding for this work from the National Science Foundation (CHE-1362465 for J.H. and G.B., NSF DMR-1508099 for R.K. and L.M.), the National Institutes of Health (R01GM097569 for L.M.), and supercomputer time from XSEDE (TG-CHE110064 to G.B.) are gratefully acknowledged. GMD thanks the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013)/ERC through grant agreement n. 307358 (ERC-stG-2012-ANGLE), and acknowledges the ARCHER UK National Supercomputing Service via UK's HEC Materials Chemistry Consortium membership, which is funded by the EPSRC (EP/L000202). We thank Robert Young for many helpful discussions. We thank B.P.T. Fokwa and H. Park for their assis tance with the powder x-ray diffraction experiments.
Footnotes
Electronic Supplementary Information (ESI) available: All crystal structures used, experimental chemical shifts, convergence tests, detailed benzoic acid results, and the predicted fragment PBE0 and GIPAW PBE chemical shifts are reported for each of the test sets studied here.
References
- 1.Tatton AS, Pham TN, Vogt FG, Iuga D, Edwards AJ, Brown SP. Cryst. Eng. Comm. 2012;14:2654. [Google Scholar]
- 2.Ferraro MB, Facelli JC. J. Mol. Struct. 2002;603:159–164. [Google Scholar]
- 3.Stueber D. Concepts Magn. Reson. A. 2006;28:347–368. [Google Scholar]
- 4.Pickard C, Mauri F. Phys. Rev. B. 2001;63:245101. [Google Scholar]
- 5.Yates JR, Pickard CJ, Mauri F. Phys. Rev. B. 2007;76:024401. [Google Scholar]
- 6.Bonhomme C, Gervais C, Babonneau F, Coelho C, Pourpoint F, Azais T, Ashbrook SE, Griffin JM, Yates JR, Mauri F, Pickard CJ. Chem. Rev. 2012;112:5733–5779. doi: 10.1021/cr300108a. [DOI] [PubMed] [Google Scholar]
- 7.Salager E, Day GM, Stein RS, Pickard CJ, Elena B, Emsley L. J. Am. Chem. Soc. 2010;132:2564–2566. doi: 10.1021/ja909449k. [DOI] [PubMed] [Google Scholar]
- 8.Baias M, Widdifield CM, Dumez J-N, Thompson HPG, Cooper TG, Salager E, Bassil S, Stein RS, Lesage A, Day GM, Emsley L. Phys. Chem. Chem. Phys. 2013;15:8069–8080. doi: 10.1039/c3cp41095a. [DOI] [PubMed] [Google Scholar]
- 9.Kalakewich K, Iuliucci R, Harper JK. Cryst. Growth Des. 2013;13:5391–5396. [Google Scholar]
- 10.Mueller LJ, Dunn MF. Acc. Chem. Res. 2013;46:2008–2017. doi: 10.1021/ar3003333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dračínský M, Hodgkinson P. RSC Adv. 2015;5:12300–12310. [Google Scholar]
- 12.Hartman JD, Beran GJO. J. Chem. Theory Comput. 2014;10:4862–4872. doi: 10.1021/ct500749h. [DOI] [PubMed] [Google Scholar]
- 13.Hartman JD, Monaco S, Schatschneider B, Beran GJO. J. Chem. Phys. 2015;143:102809. doi: 10.1063/1.4922649. [DOI] [PubMed] [Google Scholar]
- 14.Holmes ST, Iuliucci RJ, Mueller K, Dybowski C. J. Chem. Theory Comput. 2015;11:5229–5241. doi: 10.1021/acs.jctc.5b00752. [DOI] [PubMed] [Google Scholar]
- 15.Michael Lodewyk DJT, Siebert Mattew R. Chem. Rev. 2012;112:1839–62. doi: 10.1021/cr200106v. [DOI] [PubMed] [Google Scholar]
- 16.Beran GJO, Nanda K. J. Phys. Chem. Lett. 2010;1:3480–3487. [Google Scholar]
- 17.Kitaura K, Ikeo E, Asada T, Nakano T, Uebayasi M. Chem. Phys. Lett. 1999;313:701–706. [Google Scholar]
- 18.Tan H-J, Bettens RPA. Phys. Chem. Chem. Phys. 2013;15:7541–7. doi: 10.1039/c3cp50406a. [DOI] [PubMed] [Google Scholar]
- 19.Reid DM, Collins MA. Phys. Chem. Chem. Phys. 2015;17:5314–5320. doi: 10.1039/c4cp05116e. [DOI] [PubMed] [Google Scholar]
- 20.Gao Q, Yokojima S, Fedorov DG, Kitaura K, M S, S N. J. Chem. Theory Comput. 2010;6:1428–1444. [Google Scholar]
- 21.Adamo C, Barone V. J. Chem. Phys. 1999;110:6158. [Google Scholar]
- 22.Stephens PJ, Devlin FJ, Chabalowski CF, Frisch MJ. J. Phys. Chem. 1994;98:11623âĂŞ–11627. [Google Scholar]
- 23.Young RP, Caulkins BG, Borchardt D, Bullo ch DN, Larive CK, Dunn MF, Mueller LJ. Angew. Chem. Int. Ed. 2016;55:1350–1354. doi: 10.1002/anie.201508898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mason J. Chem. Rev. 1981;81:205. [Google Scholar]
- 25.Lemaitre V, Smith ME, Watts A. Soild State Nuc. Magn. Reas. 2004;26:215–235. doi: 10.1016/j.ssnmr.2004.04.004. [DOI] [PubMed] [Google Scholar]
- 26.Gervais C, Dupree R, Pike KJ, Bonhomme C, Profeta M, Pickard CJ, Mauri F. J. Phys. Chem. A. 2005;109:6960–6969. doi: 10.1021/jp0513925. [DOI] [PubMed] [Google Scholar]
- 27.Perdew JP, Burke K, Ernzerhof M. Phys. Rev. Lett. 1996;77:3865. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 28.Zhang Y, Wu A, Xu X, Yan Y. Chemical Physics Letters. 2006;421:383–388. [Google Scholar]
- 29.Tao J, Perdew J, Staroverov V, Scuseria G. Phys. Rev. Lett. 2003;91:146401. doi: 10.1103/PhysRevLett.91.146401. [DOI] [PubMed] [Google Scholar]
- 30.Wu G, Zhu J, Wang R, Terskikh V. J. Am. Chem. Soc. 2010;132:5143–5155. doi: 10.1021/ja909656w. [DOI] [PubMed] [Google Scholar]
- 31.Stone AJ. Chem. Phys. Lett. 1981;83:233–239. [Google Scholar]
- 32.Stone AJ, Alderton M. Mol. Phys. 1985;56:1047–1064. [Google Scholar]
- 33.Stone AJ. J. Chem. Theory Comput. 2005;1:1128–1132. doi: 10.1021/ct050190+. [DOI] [PubMed] [Google Scholar]
- 34.Ochsenfeld C, Kussmann J, Koziol F. Angew. Chem. Int. Ed. 2004;43:4485–4489. doi: 10.1002/anie.200460336. [DOI] [PubMed] [Google Scholar]
- 35.Zienau J, Kussmann J, Ochsenfeld C. Mol. Phys. 2010;108:333–342. [Google Scholar]
- 36.Loibl S, Manby FR, Schütz M. Mol. Phys. 2010;108:477–485. [Google Scholar]
- 37.Harris RK, Becker ED, Cabral de Menezes SM, Granger P, Hoffman RE, Zilm KW. Pure Appl. Chem. 2008;80:59–84. [Google Scholar]
- 38.Bradley JP, Velaga SP, Antzutkin ON, Brown SP. Cryst. Growth Des. 2011;11:3463–3471. [Google Scholar]
- 39.Uldry AC, Griffin JM, Yates JR, Torralba MP, Maria MD, Webber AL, Beaumont ML, Samoson A, Claramunt RM, Pickard CJ, Brown SP. J. Am. Chem. Soc. 2008;130:945–954. doi: 10.1021/ja075892i. [DOI] [PubMed] [Google Scholar]
- 40.Sardo M, Santos SM, Babaryk AA, Lopez C, Alkorta I, Elguero J, Claramunt RM, Mafra L. Soid State Nuc. Magn. Res. 2015;65:49–63. doi: 10.1016/j.ssnmr.2014.12.005. [DOI] [PubMed] [Google Scholar]
- 41.Harris RK, Jackson P. J. Phys. Chem. Solids. 1987;48:813–818. [Google Scholar]
- 42.Abraham A, Apperley DC, Gelbrich T, Harris RK, Griesser UJ. Can. J. Chem. 2011;89:770–778. [Google Scholar]
- 43.Carignani E, Borsacchi S, Bradley JP, Brown SP, Geppi M. J. Phys. Chem. C. 2013;117:17731–17740. [Google Scholar]
- 44.Yates JR, Dobbin SE, Pickard CJ, Mauri F, Ghi PY, Harris RK. Phys. Chem. Chem. Phys. 2005;7:1402–1407. doi: 10.1039/b500674k. [DOI] [PubMed] [Google Scholar]
- 45.Harris RK, Hodgkinson P, Zorin V, Dumez JN, Herrmann BE, Emsley L, Salager E, Stein RS. Magn. Reason. Chem. 2010;48:S103–S112. doi: 10.1002/mrc.2636. [DOI] [PubMed] [Google Scholar]
- 46.Sharif S, Schagen D, Toney M, Limbach H. J. Am. Chem. Soc. 2007;129:4440–4455. doi: 10.1021/ja066240h. [DOI] [PubMed] [Google Scholar]
- 47.Wei Y, Dios AC, McDermott AE. J. Am. Chem. Soc. 1999;121:10389–10394. [Google Scholar]
- 48.Hu JZ, Facelli JC, Alderman DW, Pugmire RJ, Grant DM. J. Am. Chem. Soc. 1998;120:9863–9869. [Google Scholar]
- 49.Smith ED, Hammond RB, Jones MJ, Roberts KJ, Mitchell JB, Price SL, Harris RK, Apperkey DC, Cherryman JC, Docherty R. J. Phys. Chem. B. 2001;105:5818–5826. [Google Scholar]
- 50.Li ZJ, Abramov Y, Bordner J, Leonard J, Medek A, Trask AV. J. Am. Chem. Soc. 2006;128:8199. doi: 10.1021/ja0541332. [DOI] [PubMed] [Google Scholar]
- 51.Wu G, Dong S, Ida R, Reen N. J. Am. Chem. Soc. 2002;124:1768. doi: 10.1021/ja011625f. [DOI] [PubMed] [Google Scholar]
- 52.Yamada K, Dong S, Wu G. J. Am. Chem. Soc. 2000;122:11602–11609. [Google Scholar]
- 53.Dong S, Yamada K, Wu G. Z. Naturforsch. 2000:55a, 21–28. [Google Scholar]
- 54.Lemaitre V, Pike K, Watts A, Anupold T, Samoson A, Smith M, Dupree R. Chem. Phys. Lett. 2003;371:91–97. [Google Scholar]
- 55.Pike KJ, Lemaitre V, Kukol A, Anupold T, Samoson A, Howes AP, Watts A, Smith ME, Dupree R. J. Phys. Chem. B. 2004;108:9256–9263. [Google Scholar]
- 56.Rorick A, Michael M, Yang L, Zhang Y. J. Phys. Chem. B. 2015;119:11618–11625. doi: 10.1021/acs.jpcb.5b06536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Giannozzi P, Baroni S, Bonini N, Calandra M, Car R, Cavazzoni C, Ceresoli D, Chiarotti GL, Cococcioni M, Dabo I, Dal Corso A, de Gironcoli S, Fabris S, Fratesi G, Gebauer R, Gerstmann U, Gougoussis C, Kokalj A, Lazzeri M, Martin-Samos L, Marzari N, Mauri F, Mazzarello R, Paolini S, Pasquarello A, Paulatto L, Sbraccia C, Scandolo S, Sclauzero G, Seitsonen AP, Smogunov A, Umari P, Wentzcovitch RM. Journal of Physics: Condensed Matter. 2009;21:395502, 19. doi: 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]
- 58.Antony J, Grimme S. Phys. Chem. Chem. Phys. 2006;8:5287–5293. doi: 10.1039/b612585a. [DOI] [PubMed] [Google Scholar]
- 59.Heit YN, Nanda KD, Beran GJO. Chem. Sci. 2016;7:246–255. doi: 10.1039/c5sc03014e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Heit YN, Beran GJO. Acta Cryst. B. 2016:72. doi: 10.1107/S2052520616005382. in press. [DOI] [PubMed] [Google Scholar]
- 61.Beran GJO. J. Chem. Phys. 2009;130:164115. doi: 10.1063/1.3121323. [DOI] [PubMed] [Google Scholar]
- 62.Wen S, Beran GJO. J. Chem. Theory Comput. 2011;7:3733–3742. doi: 10.1021/ct200541h. [DOI] [PubMed] [Google Scholar]
- 63.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery JA, Jr., Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas Ã, Foresman JB, Ortiz JV, Cioslowski J, Fox DJ. Gaussian 09 Revision A.1. Gaussian Inc.; Wallingford CT: 2009. [Google Scholar]
- 64.Krishnan R, Binkley JS, Seeger R, Pople JA. J. Chem. Phys. 1980;72:650–654. [Google Scholar]
- 65.McLean AD, Chandler GS. J. Chem. Phys. 1980;72:5639–5648. [Google Scholar]
- 66.Frisch MJ, Pople JA, Binkley JS. J. Chem. Phys. 1984;80:3265–3269. [Google Scholar]
- 67.Clark T, Chandrasekhar J, Spitznagel GW, Schleyer P. v. R. J. Comp. Chem. 1983;4:294–301. [Google Scholar]
- 68.Hehre WJ, Ditchfield R, Pople JA. J. Chem. Phys. 1972;56:2257–2261. [Google Scholar]
- 69.Hariharan PC, Pople JA. Theor. Chim. Acta. 1973;28:213–222. [Google Scholar]
- 70.Chesnut DB, Moore KD. Journal of Computational Chemistry. 1989;10:648–659. [Google Scholar]
- 71.Chesnut DB, Rusiloski BE, Moore KD, Egolfs DA. J. Comp. Chem. 1993;14:1364–1375. [Google Scholar]
- 72.Hartman JD, Neubauer TJ, Caulkins BG, Mueller LJ, Beran GJO. J. Biomol. NMR. 2015;62:327–340. doi: 10.1007/s10858-015-9947-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Martins LSC, de Souza FAL, Ceolin GA, Jorge FE, de Barredo RC, Campos CT. Comput. Theor. Chem. 2013;1013:62–69. [Google Scholar]
- 74.GDMA . Distributed Multipole Analysis of Gaussian Wavefunctions, version 2.2.09. A. J. Stone; [May 28, 2014]. http://www-stone.ch.cam.ac.uk/pub/gdma/. [Google Scholar]
- 75.Clark SJ, Segall MD, Pickard CJ, Hasnip PJ, Probert MI, Refson K, Payne MC. Z. Kristallogr. 2005;220:567–570. [Google Scholar]
- 76.Caravatti P, Braunshweller L, Ernst RR. Chem. Phys. Lett. 1983;100:305–310. [Google Scholar]
- 77.Detken A, Hardy EH, Ernst M, Meier BH. Chem. Phys. Lett. 2002;356:298–304. [Google Scholar]
- 78.Morcombe CR, Zilm KW. J. Magn. Reson. 2003;162:479–486. doi: 10.1016/s1090-7807(03)00082-x. [DOI] [PubMed] [Google Scholar]
- 79.Harris RK, Becker ED, Cabral DM, Sonia M, Granger P, Hoffman RE, Zilm KW. Solid State NMR. 2008;33:41–56. doi: 10.1016/j.ssnmr.2008.02.004. [DOI] [PubMed] [Google Scholar]
- 80.Civalleri B, Zicovich-Wilson CM, Valenzano L, Ugliengo P. CrystEngComm. 2008;10:405–410. [Google Scholar]
- 81.Otero-de-la Roza A, Johnson ER. J. Chem. Phys. 2012;137:054103. doi: 10.1063/1.4738961. [DOI] [PubMed] [Google Scholar]
- 82.Kronik L, Tkatchenko A. Acc. Chem. Res. 2014;47:3208–3216. doi: 10.1021/ar500144s. [DOI] [PubMed] [Google Scholar]
- 83.Beran GJO. Chem. Rev. 2016;116:5567–5613. doi: 10.1021/acs.chemrev.5b00648. [DOI] [PubMed] [Google Scholar]
- 84.van de Streek J, Neumann MA. Acta Cryst. B. 2010;66:544–58. doi: 10.1107/S0108768110031873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Dumez J-N, Pickard CJ. J. Chem. Phys. 2009;130:104701. doi: 10.1063/1.3081630. [DOI] [PubMed] [Google Scholar]
- 86.Gortari ID, Portella G, Salvatella X, Bajaj VS, van der Wel PCA, Yates JR, Segall MD, Pickard CJ, Payne MC, Vendruscolo M, De Gortari I, Portella G, Salvatella X, Bajaj VS, van der Wel PCA, Yates JR, Segall MD, Pickard CJ, Payne MC, Vendruscolo M, Gortari ID, Wel PCAVD, Yates XJR. J. Am. Chem. Soc. 2010;132:5993–6000. doi: 10.1021/ja9062629. [DOI] [PubMed] [Google Scholar]
- 87.Dračínský M, Hodgkinson P. CrystEngComm. 2013;15:8705. [Google Scholar]
- 88.Exner TE, Frank A, Onila I, Möller HM. J. Chem. Theory Comput. 2012;8:4818–4827. doi: 10.1021/ct300701m. [DOI] [PubMed] [Google Scholar]
- 89.Teale AM, Lutnaes OB, Helgaker T, Tozer DJ, Gauss J. J. Chem. Phys. 2013;138:024111. doi: 10.1063/1.4773016. [DOI] [PubMed] [Google Scholar]
- 90.Dračínský M, Bouř P, Hodgkinson P. J. Chem. Theory Comput. 2016;12:968–973. doi: 10.1021/acs.jctc.5b01131. [DOI] [PubMed] [Google Scholar]
- 91.Holmes ST, Iuliucci RJ, Mueller KT, Dybowski C. J. Chem. Phys. 2014;141:164121. doi: 10.1063/1.4900158. [DOI] [PubMed] [Google Scholar]
- 92.Gervais C, Dupree R, Pike KJ, Bonhomme C, Profeta M, Pickard CJ, Mauri F. J. Phys. Chem. A. 2005;109:6960–6969. doi: 10.1021/jp0513925. [DOI] [PubMed] [Google Scholar]
- 93.Zhu J, Geris AJ, Wu G. Phys. Chem. Chem. Phys. 2009;11:6972–6980. doi: 10.1039/b906438a. [DOI] [PubMed] [Google Scholar]
- 94.O'Dell LA, Schurko RW, Harris KJ, Autschbach J, Ratcliffe CI. J. Am. Chem. Soc. 2011;133:527–546. doi: 10.1021/ja108181y. [DOI] [PubMed] [Google Scholar]
- 95.Yates JR, Pickard CJ, Payne MC, Dupree R, Profeta M, Mauri F. J. Phys. Chem. A. 2004;108:6032–6037. [Google Scholar]
- 96.De Gortari I, Galván M, Ireta J, Segall M, Pickard CJ, Payne M. J. Phys. Chem. A. 2007;111:13099–13105. doi: 10.1021/jp0751817. [DOI] [PubMed] [Google Scholar]
- 97.Wong A, Howes AP, Yates JR, Watts A, Anupõld T, Past J, Samoson A, Dupree R, Smith ME. Phys. Chem. Chem. Phys. 2011;13:12213–12224. doi: 10.1039/c1cp20629j. [DOI] [PubMed] [Google Scholar]
- 98.Al-Kaysi RO, Muller AM, Bardeen CJ. J. Am. Chem. Soc. 2006;128:15938–15939. doi: 10.1021/ja064535p. [DOI] [PubMed] [Google Scholar]
- 99.Zhu L, Agarwal A, Lai J, Al-Kaysi R, Tham F, Ghaddar T, Mueller L, Bardeen C. J. Mat. Chem. 2011;21:6258–6268. [Google Scholar]
- 100.Song X, Rienstra CM, McDermott AE. Magn. Reason. Chem. 2001;39:S30–S36. [Google Scholar]
- 101.Li R, Zeitler JA, Tomerini D, Parrott EPJ, Gladden LF, Day GM. Phys. Chem. Chem. Phys. 2010;12:5329. doi: 10.1039/b926536h. [DOI] [PubMed] [Google Scholar]
- 102.Kempf J, Spiess HW, Haeberlen U, Zimmermann H. Chem. Phys. 1974;4:269–276. [Google Scholar]
- 103.Nagaoka S, Terao T, Imashiro F, Saika A, Hirota N, Hayashi S. Chem. Phys. Lett. 1981;80:580–584. [Google Scholar]
- 104.Kong X, Shan M, Terskikh V, Hung I, Gan Z, Wu G. J. Phys. Chem. B. 2013;117:9643–9654. doi: 10.1021/jp405233f. [DOI] [PubMed] [Google Scholar]
- 105.Rice W, Schaeffer C, Harten B, Villinger F, South T, Summers M, Henderson L, Bess W, Arthur L, McDougal S, Orloff L, Mendeleyev J, Kun E. Nature. 1993;361:473–475. doi: 10.1038/361473a0. [DOI] [PubMed] [Google Scholar]
- 106.Lumsden M, Wu G, Wasylishen R, Curtis R. J. Am. Chem. Soc. 1993;115:2825–2832. [Google Scholar]
- 107.Salzmann R, Wojdelski M, McMahon M, Havlin R, Oldfield E. J. Am. Chem. Soc. 1998;120:1349–1356. [Google Scholar]
- 108.Gordon MS, Fedorov DG, Pruitt SR, Slipchenko L. Chem. Rev. 2012;112:632–672. doi: 10.1021/cr200093j. [DOI] [PubMed] [Google Scholar]
- 109.Collins MA, Bettens RPA. Chem. Rev. 2015;115:5067–5642. doi: 10.1021/cr500455b. [DOI] [PubMed] [Google Scholar]
- 110.Raghavachari K, Saha A. Chem. Rev. 2015;115:5643–5677. doi: 10.1021/cr500606e. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.