Abstract
Purpose
To develop and evaluate an automated algorithm to segment intramuscular adipose (IMAT) and connective (IMCT) tissue from musculoskeletal MRI images acquired with a dual echo Ultrashort TE (UTE) sequence.
Theory and Methods
The dual echo images and calculated structure tensor images are the inputs to the multichannel fuzzy cluster mean (MCFCM) algorithm. Modifications to the basic MCFCM include an adaptive spatial term and bias shading correction. The algorithm was tested on digital phantoms simulating IMAT/IMCT tissue under varying conditions of image noise and bias and on ten subjects with varying amounts of IMAT/IMCT.
Results
The MCFCM including the adaptive spatial term and bias shading correction performed better than the original MCFCM and adaptive spatial MCFCM algorithms. IMAT/IMCT was segmented from the unsmoothed simulated phantom data with a mean Dice coefficient of 0.933 ± 0.001 when contrast-to-noise (CNR) was 140 and bias was varied between 30% and 65%. The algorithm yielded accurate in-vivo segmentations of IMAT/IMCT with a mean Dice coefficient of 0.977 ± 0.066.
Conclusion
The proposed algorithm is completely automated and yielded accurate segmentation of intramuscular adipose and connective tissue in the digital phantom and in human calf data.
Keywords: Intramuscular connective and Adipose tissue, automated segmentation, lower leg calf muscle, intramuscular connective tissue (IMCT), intramuscular adipose tissue (IMAT), fuzzy cluster mean segmentation, ultrashort TE (UTE), structure tensor maps
INTRODUCTION
Recent studies have identified the important role of the network of intramuscular connective tissue (IMCT), represented by the extracellular matrix (ECM), in loss of muscle force in conditions ranging from normal aging, sarcopenia, to muscular dystrophies such as Duchenne muscular dystrophy (DMD) (1–3). For example, in DMD, the increase in connective tissue is generally regarded as a compensatory replacement for muscle loss. However, several clinical studies have documented the extensive increase of connective tissue even prior to the onset of muscle degeneration in DMD (3). A functional consequence of structural changes in the extracellular matrix is the reduction in lateral transmission of force, which is mediated by the connective tissue network. In aging rats, a 50% loss of lateral transmission of force - potentially one of the biggest contributors to the loss of muscle force with age - has been reported (2). The increase in connective tissue is also often accompanied by fatty infiltration as seen in DMD (4,5) as well as in sarcopenia (6,7). The ability to non-invasively image and segment intramuscular connective and intramuscular adipose tissue (IMAT) is critical to quantifying muscle compositional changes and provides the potential to explore correlations of changes in adipose and connective tissue to muscle function.
Direct visualization of connective tissue is challenging since the T2 of the highly collagenous connective tissue is extremely low (< 2 ms) and does not have appreciable signal intensity in routine MR images. In the current paper, a novel ultra-short TE (UTE) double echo gradient echo sequence is used with the first TE at 8 μs to capture signal from the low species as well. A second echo at a longer TE (3 ms) is used to suppress long species in the subtracted image (TE1 − TE2). In these UTE images, the adipose and connective tissue have low values. Though the T2 of adipose is long (45 ms at 3 T), the is low due to the presence of J-coupling among the protons of a lipid molecule. Manual segmentation of the IMCT and IMAT is challenging and tedious since these tissues are distributed in thin filament like structures (forming a 3D network) through the muscle belly. It should be noted that the resolution of the UTEs images (0.78 mm in plane with thickness of 5 mm) limits the visualization of IMAT and IMCT to the thicker peri- and epimysial structures whose effective width is of the order of the image resolution. Few studies have reported algorithms for automated segmentation of intramuscular adipose tissue from fat and water images of the muscle (8,9) and even fewer groups have attempted to automatically extract IMCT (6). Simple thresholding, region growing or even level set based algorithms do not provide accurate results due to partial volume effects, severe shading artifacts, and the many small, disjoint regions. The lack of algorithms to segment IMCT is primarily due to the paucity of MR imaging studies that directly visualize the IMCT. It should be noted that recent advances in MR imaging sequences enable voxel wise determination of the relative amount of adipose tissue.
Fuzzy cluster mean (FCM) algorithms have been extensively used in medical image processing applications (12,13) to segment tissue by clustering based on voxel intensities or other features. An extension to FCM is the multichannel FCM (MCFCM) that integrates additional data channels (e.g. multiple echo intensities). However the MCFCM doesn’t incorporate spatial connectivity in the clustering; modifications to the MCFCM include the spatial similarity term for homogeneous regions and bias correction to account for the intensity shading artifacts. The goal of this paper is to develop an automated tool to segment the low components of the intramuscular tissue (adipose and connective tissue) from UTEs double echo images. In the UTEs images, it is not possible to discriminate between adipose and connective tissue based on either intensity (overlapping values) or structure (both present as filament/sheet network). The paper includes 1: Theory of the 3D fuzzy classifier-based segmentation algorithm that uses intensity and structure tensor derived features (‘vesselness index’ to capture the linear filament/planar sheet shape of the IMAT and IMCT (10)). The fuzzy classifier incorporates spatial connectedness and bias field correction. 2: Generation of a digital phantom simulating muscle and IMAT/IMCT-like tissue incorporating different levels of noise and bias; the range of bias and noise was chosen to be in the range found in in-vivo data. 3: Evaluation of the algorithm on the phantom and on whole lower leg calf muscle images with segmentation into four classes (muscle/bone marrow, cortical bone, intramuscular connective/adipose tissue and background). The in-vivo segmentation is compared to expert-guided semi-automated segmentation of intramuscular connective and adipose tissue in select slices of the muscle volume. It should be noted that accurate semi-manual segmentation is extremely tedious and is in fact, the rationale for development of the automated algorithm. 4: Evaluation of the algorithm on segmented triceps surae muscles (Medial Gastrocnemius (MG), Lateral gastrocnemius (LG) and Soleus). This restricts the segmentation to a single muscle compartment which has reduced intensity shading artifacts due to the smaller anatomic extent and the presence of only three classes of tissue: muscle and intramuscular connective/adipose tissue and background. The manual segmentations from the previous section are used in the evaluation.
THEORY
Multichannel fuzzy cluster mean (MCFCM) Algorithm
A modified fuzzy c-means clustering algorithm incorporating both spatial connectedness and bias field corrections was chosen to label the voxels of the lower leg volume. Fuzzy cluster mean (FCM) partitions a set of n voxels at location x = (x, y, z) in d-dimensional space into k (1 < k < n) fuzzy clusters with d-dimensional cluster centroids, νk. FCM segmentation provides a statistical measure of determining the probability of belonging to a specific tissue class (12,13). MCFCM is an extension of FCM where several data types (channels) are used to create an input feature in the multidimensional space associated with that voxel. Modes (tissue type) are found within the data set and the statistical probability of belonging to that class is found by assigning a fuzzy membership probability to each data point based on its proximity to the cluster centroids in multi-feature space. The fuzzy clustering of voxels is described by a fuzzy matrix U whose elements uk,x denote the degree of membership of a voxel in the k-th cluster. In MCFCM, the objective function JMCFCM is minimized with respect to the both membership values U and cluster centroids ν:
| [1] |
with membership class constraint
| [2] |
where m is any real number greater than 1; the matrix U = {uk,x} is a fuzzy c-partition of the multi-feature input data set with uk,x as the degree of membership of a voxel’s feature in the kth-cluster, where the coordinate of a voxel is x = (x, y, z); and I is the domain defining the multi-feature input data set. The distance metric d measures the similarity between any data and the kth-cluster center (νk). The objective function is minimized when high membership values are assigned to a voxel with distance metric that indicates a similarity (small values) between a particular class’s center and data, while low membership values are given to classes with large distance metrics. In conventional FCM formulation, the distance metric d is the Euclidean Norm (L2 norm) and defined as:
| [3] |
where s(x) is the d-dimensional feature input data and νk is the d-dimensional kth-cluster center.
Spatial Similarity term and Bias field compensation
One of the challenges in the proposed segmentation is the presence of large intensity shading artifacts that confound membership classification. In both conventional FCM and MCFCM each voxel is assumed to be independent of every other voxel within the volume, as is evident from the objective functions where the cluster assignment does not include any correlation between data points. To include a term for neighborhood voxel similarity, the fuzzy c-means objective function was modified to incorporate spatial similarity of voxels (26 nearest voxels around the central voxel are considered; the term selectively modifies the labeling of voxels in homogeneous regions). The bias field is incorporated within the distance metric and the condition for minimization of the objective function, JMCFCM with respect to the bias field is determined (14). The method for spatial similarity and bias field correction follows closely that in (14) and is not detailed here. Extending the work in (14), an ‘unregularized’ version of the bias correction was also implemented to account for severe bias fields; the term selectively modifies the labeling of voxels in homogeneous regions. The bias field is incorporated within the distance metric and the condition for minimization of the objective function, JMCFCM with respect to the bias field is determined (14). The method for spatial similarity and bias field correction follows closely that in (14) and is not detailed here. Extending the work in (14), an ‘unregularized’ version of the bias correction was also implemented to account for severe bias fields.
Structure Tensor
In the current implementation, the input set of features for the fuzzy clustering were the intensities of the dual echo images as well indices derived from the structure tensor. The rationale for the structure tensor was that the IMCT and IMAT have an in-plane linear and a 3D sheet structure. The structure tensor, evaluated from the Hessian, is used to isolate voxels that have a specific structure, e.g., the linear/sheet structure of the connective and adipose tissue. The present implementation follows the Frangi filter that was initially proposed for vessel segmentation (15). The Hessian matrix (H) is a second derivative-based measure, which was evaluated with a 3D Gaussian filter whose standard deviation (σ) was varied within a predefined range to determine the maximum response as a function of sigma at that voxel. This was performed at each voxel in order to sensitize to different thickness of IMAT and IMCT tissue.
| [4] |
where the gaussian function is:
| [5] |
For a 3D image, the resulting eigenvalue matrix is given by:
| [6] |
The structure of a voxel’s neighborhood can be inferred from a comparison of the eigenvalues of the Hessian matrix (arranged in ascending order, λ1 ≤ λ2 ≤ λ3). If λ1 ≈ λ3, the neighborhood is isotropic, indicating that the pixel is either noise or in a homogeneous region of the image (e.g., muscle, bone marrow). If, on the other hand λ1 ≪ λ2 and λ2 ≈ λ3, the structure in the neighborhood has a clear orientation, implying that it is a linear pixel. The last alternative is that λ1 ≈ λ2 and λ1 ≪ λ3, in this case, the structure is distinctly planar. The main advantage of comparing eigenvalues of the Hessian is that it provides a robust method for determining edges without prior knowledge of edge direction. Boundaries of tissue types can be found by grouping pixels with very different eigenvalues. The map containing the boundary information is called the structure tensor. The coefficients used within the structure map are the: i) linearity coefficient (LC), ii) planar coefficient (PC), iii) spherical coefficients (SC), and iv) second order structureness (SOS). The coefficients are given in terms of eigenvalues by (x = (x, y, z) refer to voxel coordinates):
| [7] |
| [8] |
| [9] |
| [10] |
| [11] |
The structure weight index, SW, that highlights linear and planar structures is calculated at each voxel as:
| [12] |
The value for α was set low in the calculation of SW such that the contribution from the spherical term, SC is around 10%. While the structure weight was successful in highlighting the ‘tube’ and ‘plate’ like structures, there was also some unwanted enhancement in the background noise regions. In order to filter these voxels, a noise filter, NF was calculated that compared the magnitude of the structure eigenvalues to β; the value was empirically determined to filter noise (β was set at 110 and 150 for TE1 and TE2 respectively).
| [13] |
The resulting structure tensor (ST) was calculated for each voxel for different values of scale, (σ in Eq. 5), stepping through values of σ from 0.05 to 1 in steps of 0.01.
| [14] |
The range of σ was set from empirical observations that the maximum response was within this range (0.05 to 1) for the range of in-vivo thickness of IMAT/IMCT tissue. The range was adjusted to (.01–5.0 in steps of 0.01) for the synthetic phantom to accommodate a larger range of thickness in the simulated IMAT/IMCT tissue.
The structure tensor maps derived from the TE1 and TE2 images form the input to the MCFCM algorithm along with the intensities of the TE1 and TE2 images. The input at each voxel is a 4 dimensional feature vector consisting of the original voxel intensities in the TE1 and TE2 images as well as the ST map (Eq. 14) derived from TE1 and TE2 images respectively (note: ST values are calculated at each voxel; the voxel index x = (x, y, z) has been dropped for convenience from LC, PC, SC, SOS, SW and NF (Eq. 8–13) for convenience).
METHODS
Acquisition
Ten subjects were scanned using a FAST Gradient-echo based, 2D dual echo UTE sequence (TE1 = 8 μs, TE2 = 3 ms). The sequence includes a short 40 to 80 μs RF pulse for excitation followed by dual echo radial ramp sampling. The sequence parameters included: FOV = 20 cm, TR = 200 μs, TE1 = 8 μs, TE2 = 3 ms, FA = 30°, BW = ±62.5 kHz, NEX = 2, Matrix 256 × 256, slice thickness 5 mm with 5 mm gap, two sets of ≈ 22 interleaved slices and a scan time of 14 min for both scans.
Synthetic Phantom
A digital phantom was synthesized to simulate a 3D network of IMAT/IMCT tissue embedded in muscle tissue. The IMAT/IMCT filaments were synthesized with varying diameters (thickness) and probability distributions of IMAT/IMCT; voxels with values less than one simulated partial volume effects with muscle. Both straight and curved segments of IMAT/IMCT type tissue were synthesized to reflect the IMAT/IMCT pathways. The dual echo images of an UTE acquisition were synthesized using values of 30 ms and 2 ms for muscle and IMAT/IMCT tissue respectively. The signal intensity at any voxel (Svoxel) was generated from:
| [15] |
where TE is 8 μs or 3 ms, k is a constant adjusted to give an intensity similar to the in-vivo data and p is the probability of IMAT/IMCT tissue. Several phantom datasets were generated with a Gaussian noise that yielded a contrast-noise-ratio (CNR) value of 140 (contrast between muscle and connective tissue) and bias shading across the phantom ranging from ∼ 0% to 100%. The CNR was set at the median value determined from the in-vivo images and bias values were varied (in-vivo bias values ranged from 30% to 65%). The dual echo images were then processed in a manner identical to that of the in-vivo human subject scans. The advantage of the digital phantom is that the ground truth (voxel based probability of muscle and IMAT/IMCT classes) is known which is not available for the in-vivo dataset.
Preprocessing
Prior to any image processing, images were manually edited to remove the subcutaneous fat tissue, then denoised with a custom 3D anisotropic filter and corrected for shading artifacts using the algorithm in 3D Slicer (3DSlicer; http://wiki.slicer.org/slicerWiki/index.php/Documentation/4.4/Modules/N4ITKBiasFieldCorrection; Planning Laboratory, Harvard Medical School, Boston, MA, USA). While this bias correction addresses some of the shading artifacts, there was residual shading that was corrected within the fuzzy c-means clustering algorithm. Further, the individual muscle compartments (MG, LG and Soleus) were manually segmented by an expert (RC); masks corresponding to the muscles were used in all the evaluations as well in the segmentation of the IMCT/IMAT from individual muscles.
Tissue labeling
The probability map output(s) of the proposed algorithm were converted to tissue labels and two approaches were evaluated: a hard threshold based on an examination of the histogram of the probability values for the IMAT+IMCT cluster distribution and a soft threshold which was the probability map output of the fuzzy clustering. A 50% probability value was selected for the hard threshold based on examination of the histograms as well as by visual comparison to the UTE’s TE2 image and its corresponding structure tensor map. Subsequent to the hard threshold, isolated pixels were removed using morphological reconstruction for in-vivo images.
Evaluation
For in-vivo data, completely manual segmentation of the IMCT and IMAT, where an expert manually delineates the IMCT and IMAT tissue, is impossible due to the distributed network within the muscle body as well as the complexity of partial voluming and shading artifact confounders. Here, a semi-manual segmentation using region growing was performed on select slices under expert guidance for comparison to the automated segmentation. Thresholds and seed points guided by the ST maps from UTE TE2 images were defined by the expert to initiate the region growing algorithm available in Osirix (16). This was followed by manual editing of each region.
The ROI used in the evaluation was the muscle compartments (MG, LG, or Soleus) contoured by the expert at given axial location. The evaluation was performed at three slice locations for each subject with the slices located approximately in the proximal, middle and apical regions of the muscle. These anatomical locations were selected as they represent the range of bias field and SNR across the volume.
For the synthetic phantom data, the tissue probabilities are known at each voxel and was the reference standard for the soft threshold evaluation. The accuracy of segmentation for the soft thresholded data was the mean of the square of the residual difference (MSRD); the residual was the difference in the probabilities of the reference and the output of the automated algorithm. For the evaluation of the hard threshold a value of 80% was used for the synthetic and segmented phantom data. For both (hard and soft threshold evaluations), the mean for a slice was taken over all phantom voxels and the average of all 16 slices is reported. The accuracy of the in-vivo segmented data as well as the phantom data (hard threshold) was based on two performance indices. If the true segmentation or synthetic phantom is denoted by T (manual segmentation for in-vivo data, and the synthetic phantom thresholded at 80% for the phantom evaluation) and the automatic segmentation by R, then the True Positive (TP), True Negative (TN), False Positive (FP) and False Negative (FN) are: TP = R ∩ T; ; ; . The algorithm performance was evaluated using the Dice coefficient (IDC) which was defined in terms of TP, TN, FP and FN as:
| [16] |
Comparison of IMAT/IMCT Segmentation from Whole Calf/Individual muscle
In the comparison of the segmentation of the whole calf to that of the individual muscles, the following indices were adopted to test how close the IMAT/IMCT segmentations were for the two datasets. The three indices to quantify the agreement between these two segmentations are (for each individual muscle):
| [17] |
| [18] |
| [19] |
Here, WC is the whole calf muscle, M is one of the three triceps-surae muscles (MG, LG, and Soleus). When the two segmentations agree exactly C1 will be 1, C2 and C3 will be zero.
RESULTS
Phantom
The segmentation of IMAT/IMCT-like tissue using the hard threshold (80%) is shown for the digital phantom (CNR and bias field of 140 and 50%, respectively) using the Multichannel Fuzzy Cluster Mean, the Adaptive Spatial Multichannel Fuzzy Cluster Mean, and the Adaptive Spatial Multichannel Fuzzy Cluster Mean with Bias shading correction (Figure 1). The improvement in the classification with added spatial and spatial/bias terms is evident when comparing rows 2 and 3 with row 1.
Figure 1.

The digital phantom (CNR = 140, Bias = 50%) with muscle and IMAT/IMCT like tissue generated at TE1 (a) and TE2 (b) simulating the input double echo UTE images. Straight line and curved segments of varying thickness were simulated to represent IMCT/IMAT tissue distribution in muscle. The structure tensor images derived from the double echo images are shown in (c) and (d). Row 2 shows the segmented clusters based on the Multichannel Fuzzy Cluster Mean algorithm: background (e), IMAT/IMCT cluster (f) and the muscle cluster (g). The effect of bias is clearly seen in the output field. The other two rows show the same clusters with the Adaptive Spatial Multichannel Fuzzy Cluster Mean (third row), and Adaptive Spatial Multichannel Fuzzy Cluster Mean with Bias shading correction (last row). The improvements in segmentation in rows 3 and 4 are clearly evident. It should be noted that the smallest arc (also widest) with 20% connective tissue was identified as ≈ 100% muscle since the structure was more blob-like than linear or planar.
Table 1 lists the accuracy of the three different algorithms: MCFCM, Adaptive Spatial MCFCM, and the Adaptive Spatial MCFCM algorithm with bias term corrections for digital phantoms simulated at different bias levels and CNR of 140. The MCFCM with spatial and bias corrections has the best performance (lowest MSRD, highest Jaccard and Dice scores). Highly accurate segmentations are realized at the CNR of 140 (typical CNR of in-vivo images) and all bias values (0–100%) when the data is smoothed; the accuracy is reduced (higher MSRD and lower Jaccard and Dice scores) though still at an acceptable range for unsmoothed images with a CNR of 140 and bias in the range observed in human subjects (30%–65%). It should be noted that smoothing was performed on all the in-vivo images.
Table 1.
Segmentation Accuracy of Digital Phantom†
| Bias Field TE1 % |
Bias Field TE2 % |
Dice coefficient IDC (Mean Square Residual Difference, MSRD)
|
||
|---|---|---|---|---|
| MCFCM‡ | MCFCM + SPATIAL⋄ | MCFCM + SPATIAL + BFC⋆ | ||
| smoothed data
| ||||
| 0 | 0 | 0.889 (0.068) | 0.893 (0.076) | 1 (0.062) |
| 10 | 10 | 0.879 (0.069) | 0.881 (0.076) | 1 (0.063) |
| 20 | 20 | 0.874 (0.069) | 0.876 (0.077) | 1 (0.064) |
| 30 | 30 | 0.871 (0.070) | 0.871 (0.078) | 1 (0.064) |
| 40 | 40 | 0.866 (0.070) | 0.866 (0.079) | 1 (0.065) |
| 50 | 50 | 0.863 (0.071) | 0.869 (0.079) | 1 (0.065) |
| 60 | 60 | 0.858 (0.071) | 0.865 (0.079) | 1 (0.065) |
| 70 | 70 | 0.856 (0.074) | 0.874 (0.079) | 1 (0.065) |
| 80 | 80 | 0.857 (0.083) | 0.874 (0.079) | 1 (0.065) |
| 90 | 90 | 0.854 (0.105) | 0.879 (0.079) | 1 (0.065) |
| 100 | 100 | 0.854 (0.129) | 0.872 (0.079) | 1 (0.065) |
|
| ||||
| unsmoothed | ||||
|
| ||||
| 30 | 40 | 0.791 (0.091) | 0.752 (0.097) | 0.932 (0.098) |
| 30 | 50 | 0.790 (0.091) | 0.751 (0.098) | 0.932 (0.098) |
| 40 | 60 | 0.831 (0.089) | 0.844 (0.087) | 0.934 (0.083) |
| 40 | 30 | 0.834 (0.090) | 0.846 (0.087) | 0.933 (0.089) |
| 50 | 30 | 0.834 (0.089) | 0.824 (0.087) | 0.931 (0.083) |
| 55 | 60 | 0.784 (0.094) | 0.744 (0.088) | 0.931 (0.089) |
| 60 | 40 | 0.831 (0.089) | 0.843 (0.087) | 0.934 (0.083) |
| 60 | 55 | 0.832 (0.094) | 0.845 (0.088) | 0.933 (0.083) |
| 60 | 65 | 0.781 (0.127) | 0.742 (0.099) | 0.934 (0.089) |
| 65 | 60 | 0.832 (0.123) | 0.846 (0.098) | 0.933 (0.083) |
, where S is signal intensity, was 140 for all the simulations and the performance indices are the average over all 16 slices.
Multichannel Fuzzy Cluster Mean (MCFCM); MSRD given in brackets
Adaptive Spatial MCFCM (MCFCM+Spatial); MSRD given in brackets
MCFCM+Spatial with Bias correction (MCFCM+Spatial+Bias); MSRD given in brackets
In-vivo Data
Figure 2 shows the segmentation of IMCT and IMAT using the Multichannel Fuzzy Cluster Mean, the Adaptive Spatial Multichannel Fuzzy Cluster Mean, and finally the Adaptive Spatial Multichannel Fuzzy Cluster Mean with Bias shading correction (soft threshold). The improvement in the segmentation by the successive modifications to the MCFCM algorithm can be appreciated by comparing the dark segments within the muscle compartments (adipose and connective tissue) in the UTE’s TE2 image as well as the bright segments on the corresponding structure tensor-derived image to the segmented image. Table 2 is a quantitative comparison of the three algorithms using the manual contouring as the reference and clearly shows that MCFCM with spatial and bias field correction has the best performance. The segmentations reported in the following sections are based on the Adaptive Spatial Multichannel Fuzzy Cluster with Bias shading correction.
Figure 2.

The input images (segmented medial gastrocnemius, MG) to the algorithm are shown in the first row: UTE TE1 (a), UTE TE2 (b), Structure Tensor from UTE TE1 (c), and Structure Tensor UTE TE2 (d). The following rows are the output of the Multichannel Fuzzy Cluster Mean algorithm (second row); the Adaptive Spatial Multichannel Fuzzy Cluster Mean (third row); and Adaptive Spatial Multichannel Fuzzy Cluster Mean with Bias shading correction (last row). Each output row depicts from left to right the following clusters: Background, IMAT/IMCT and Muscle respectively. The improvement in the clustering can be seen with the successive modifications to the basic Multichannel Fuzzy Cluster Mean algorithm.
Table 2.
Comparison of the segmentation accuracies of the three algorithms
| Patient‡ | Dice coefficient*
IDC
|
||
|---|---|---|---|
| MCFCM† | MCFCM + SPATIAL⋄ | MCFCM + SPATIAL + BFC⋆ | |
| Y1 | 0.401 | 0.679 | 0.997 |
| Y2 | 0.347 | 0.616 | 0.997 |
| Y3 | 0.333 | 0.560 | 0.998 |
| Y4 | 0.368 | 0.671 | 0.997 |
| Y5 | 0.373 | 0.645 | 0.997 |
| O1 | 0.352 | 0.446 | 0.789 |
| O2 | 0.456 | 0.632 | 0.997 |
| O3 | 0.472 | 0.517 | 0.997 |
| O4 | 0.452 | 0.730 | 0.998 |
| O5 | 0.518 | 0.826 | 0.998 |
The indices are calculated on select slices corresponding to the manually segmented slices and the average of the select slices is reported.
The subjects are labeled as Young(Y) or Old(O).
Multichannel Fuzzy Cluster Mean (MCFCM)
Adaptive Spatial MCFCM (MCFCM+Spatial)
MCFCM+Spatial with Bias correction (MCFCM+Spatial+Bias)
Segmentation of IMAT and IMCT from whole calf muscle
The segmentation was performed on the whole calf muscle with the subcutaneous fat cropped from the data. Figure 3 shows the original UTEs images, the corresponding structure tensor images, the expert guided manual, soft threshold and hard threshold automated segmentations for two subjects. These two subjects represent cases of small and large volume of IMAT/IMCT to evaluate the range of applicability of the algorithm. The small volume of IMAT/IMCT is from a young subject (26 years) and that of the larger volume IMAT/IMCT is from an older subject (83 years).
Figure 3.
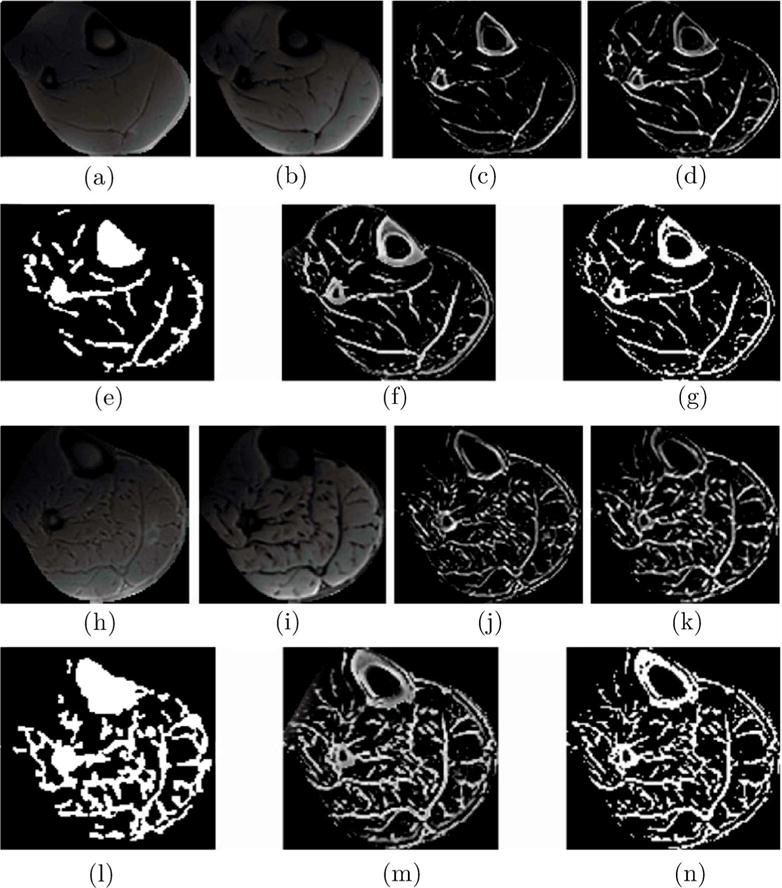
The panel shows segmentation of a slice from one subject with a small volume of IMAT/IMCT (top two rows) and another subject with a large volume of IMAT/IMCT (last two rows). Rows 1 and 3 are the input images (whole calf muscle with subcutaneous fat manually edited) to the algorithm, from left to right: UTE TE1 (a and h), UTE TE2 (b and i), Structure Tensor from UTE TE1 (c and j), and Structure Tensor UTE TE2 (d and k). Rows 2 and 4 are from left to right: expert supervised segmentation of IMAT/IMCT (e and l), the output of the algorithm corresponding to the cluster of IMAT/IMCT and cortical bone, soft threshold (f and m) and hard threshold (g and n). Cortical bone is clustered with IMAT/IMCT since it is connective tissue (thus has the same intensity patterns on the UTEs TE1 and TE2) and is a relatively thin structure.
Segmentation of IMAT and IMCT from individual muscles
The segmentation was performed on the segmented MG, LG and Soleus muscles (Fig. 4, 5 and 6). In order to facilitate comparison, the same slices are shown for the individual muscles as for the whole calf muscle segmentation. Figure 7 shows the 3D reconstruction of the hard thresholded segmented volume of IMCT/IMAT in the medial gastrocnemius for a young and old subject. Interactive 3D reconstructed volumes of young and old are available as Supplement Figures S1 and S2 respectively. Table 3 lists the performance of the proposed algorithm using the expert-guided semi-automated segmentation as the reference for each of the ten subjects for segmentation of IMCT/IMAT from whole muscle and masked muscles. As there was no significant difference in the accuracy of segmentation between the three different locations (proximal, middle, distal), the average accuracy is reported in Table 3. The evaluation indices confirm the visual examination (Figs. 2–6) that the accuracy of the automated segmentation algorithm is high for both individual muscles and whole muscle IMAT and IMCT segmentation.
Figure 4.
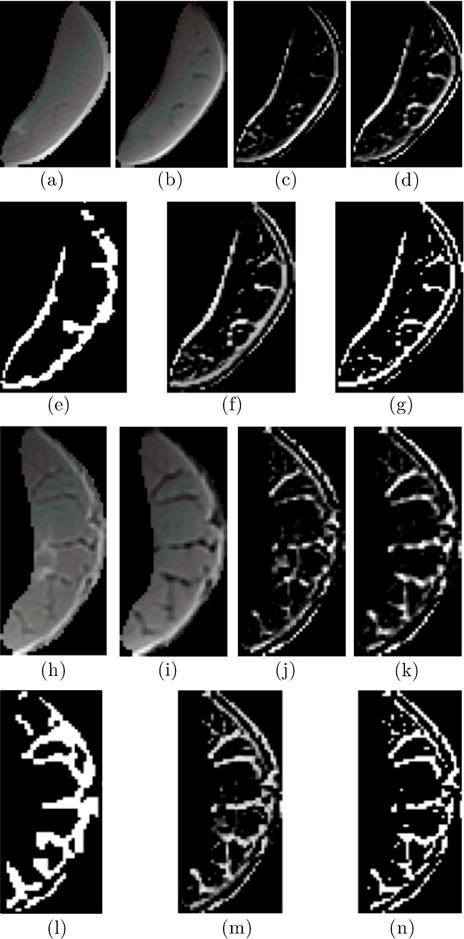
The panel shows segmentation of IMAT/IMCT from the MG from one subject with a small volume of IMAT/IMCT (top two rows) and another subject with a large volume of IMAT/IMCT (last two rows). Rows 1 and 3 are the input images (medial gastrocnemius) to the algorithm, from left to right: UTE TE1 (a and h), UTE TE2 (b and i), Structure Tensor from UTE TE1 (c and j), and Structure Tensor UTE TE2 (d and k). Rows 2 and 4 are from left to right: expert supervised segmentation of IMAT/IMCT (e and l), the output of the algorithm corresponding to the cluster of IMAT/IMCT, soft threshold (f and m) and hard threshold (g and n).
Figure 5.
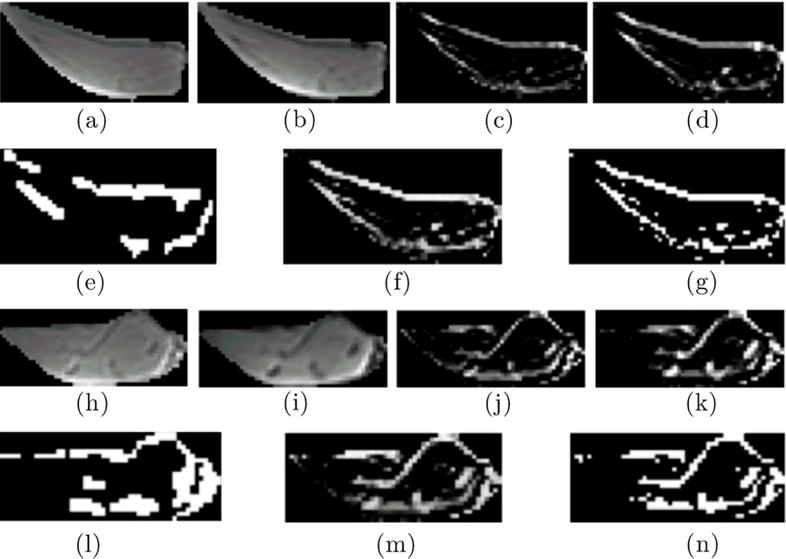
The panel shows segmentation of IMAT/IMCT from the LG from one subject with a small volume of IMAT/IMCT (top two rows) and another subject with a large volume of IMAT/IMCT (last two rows). Rows 1 and 3 are the input images (lateral gastrocnemius) to the algorithm, from left to right: UTE TE1 (a and h), UTE TE2 (b and i), Structure Tensor from UTE TE1 (c and j), and Structure Tensor UTE TE2 (d and k). Rows 2 and 4 are from left to right: expert supervised segmentation of IMAT/IMCT (e and l), the output of the algorithm corresponding to the cluster of IMAT/IMCT, soft threshold (f and m) and hard threshold (g and n)
Figure 6.

The panel shows segmentation of IMAT/IMCT from the soleus from one subject with a small volume of IMAT/IMCT (top two rows) and another subject with a large volume of IMAT/IMCT (last two rows). Rows 1 and 3 are the input images (soleus) to the algorithm, from left to right: UTE TE1 (a and h), UTE TE2 (b and i), Structure Tensor from UTE TE1 (c and j), and Structure Tensor UTE TE2 (d and k). Rows 2 and 4 are from left to right: expert supervised segmentation of IMAT/IMCT (e and l), the output of the algorithm corresponding to the cluster of IMAT/IMCT, soft threshold (f and m) and hard threshold (g and n)
Figure 7.
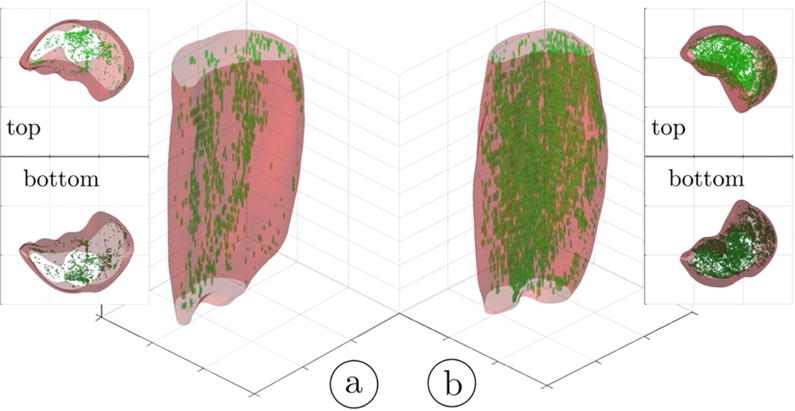
3D rendering of the hard thresholded (52%) volumes of IMCT/IMAT tissue in the triceps surae muscles; young subject (a) and older subject (b). It should be noted that the aponeurosis surrounding each muscle was selectively eroded in order to provide a better view of the IMCT/IMAT. The top and bottom views are given as 3D volume projections.
Table 3.
Segmentation accuracy of in-vivo human subject data†
| Patient‡ | Dice coefficient*
IDC
|
|||
|---|---|---|---|---|
| MG† | LG† | SOL† | WC† | |
| Y1 | 0.995 | 0.997 | 0.997 | 0.997 |
| Y2 | 0.996 | 0.998 | 0.997 | 0.997 |
| Y3 | 0.999 | 0.997 | 0.996 | 0.998 |
| Y4 | 0.996 | 0.999 | 0.996 | 0.997 |
| Y5 | 0.997 | 0.994 | 0.996 | 0.997 |
| O1 | 0.867 | 0.868 | 0.722 | 0.789 |
| O2 | 0.997 | 0.997 | 0.995 | 0.997 |
| O3 | 0.996 | 0.996 | 0.997 | 0.997 |
| O4 | 0.998 | 0.997 | 0.997 | 0.998 |
| O5 | 0.997 | 0.998 | 0.998 | 0.998 |
The indices are reported for IMCT/IMAT segmentation from individual muscles (Medial gastrocnemius (MG), Lateral Gastrocnemius (LG), and Soleus (SOL) and from the whole calf (WC).
The subjects are labeled as Young(Y) or Old(O).
The indices are calculated on select slices corresponding to the manually segmented slices and the average of the select slices is reported.
Comparison of the two data sets used for segmentation (whole calf vs the individual muscles)
There was perfect agreement between the segmentation outputs for the two data inputs when the same threshold was applied (C1 = 1, C2 = C3 = 0; average over all the subjects). When the segmentations were thresholded individually based on the optimum value from the histograms of the probability distributions, the average indices were C1 = 0.95, C2 = 0.025 and C3 = 0.025.
DISCUSSION
Algorithm
Clustering is a process for classifying image voxels such that all samples in a cluster are more similar to each other than to samples in any other cluster. Both hard clustering and fuzzy clustering have been explored with the latter being more suited for medical image segmentation due to various acquisition factors: limited spatial resolution, intensity shading artifacts, noise, and poor contrast. The fuzzy c-means (FCM) is popular due to its robustness but it has limitations: it does not include any spatial term, which makes it sensitive to noise and image artifacts. Further, segmentation accuracy can be very sensitive to image intensity shading artifacts when clustering small structures (prone to partial volume effects) with poor contrast. The successive improvements in segmentation (assessed visually and by quantitative performance indices) confirm that the modifications to the basic MCFCM result in more accurate identification of IMAT/IMCT (Figs. 1,2 and Tables 1, 2). Considering the input images to the classifier, clustering based only on the differences in intensity patterns of the muscle and IMAT/IMCT did not provide sufficient discrimination between the two types of tissues, especially at the thin segments (which suffered from partial volume effects) of the IMAT/IMCT. The indices obtained from the structure tensor provided a discriminatory feature as the IMAT and IMCT have linear/planar structures in contrast to the muscle which is a blob-like structure. The residual intensity shading does not affect the structure maps as these are based on second order spatial derivatives of the intensity. Further, as the indices were customized at each voxel for the strongest response, IMAT/IMCT with a range of thicknesses could be identified (Eq. 5). This was important as the IMAT/IMCT width varied from 2–3 voxels in the aponeuroses to sub voxel levels within the muscle belly.
The proposed structure tensor has been shown to be optimal for detecting linear structures (17) and has also been applied effectively to the detection of blood vessels from angiograms (15). The structure tensor has additional advantages of noise suppression (through the Gaussian filter) and ability to detect structures of different widths (through the smoothing scale, sigma). In the current paper, the structure detection was extended to planar structures to accommodate the distribution of IMAT/IMCT which had linear (tube structure) and planar components (sheet structure). Two other structure tensors that were explored used different weights on gradient values in the structure weight index as:
| [20] |
| [21] |
Compared to the structure weight index in Eq. 12 which emphasizes both the linear and planar components, the above two structure weight indices emphasize only the linear component (SWalt1) or only the planar component (SWalt2). The structure weight index in Eq. 12 yielded the best results and highlights the linear and planar morphology of the IMAT/IMCT. Though other structure weight indices have been defined for applications such as vessel enhancement (15), the ones proposed here were designed for the linear and planar structure of the IMAT/IMCT.
The standard Euclidean distance measure in Eq. 3 works only for spherical clusters; in order to process non-spherical cluster distributions, the FCM with the Mahalanobis distance was also implemented and tested on the dataset (18). The Mahalanobis distance (MD) method shortens the number of iteration steps at the expense of computational time; the additional time arises from computing the covariance matrix between different features. The MD distance method was implemented in the non-bias field corrected algorithm and offered no improvement in the accuracy of the segmentation compared to the Euclidean distance metric. The accuracy of the subject segmentations using the MCFCM and spatial method for the two metrics was very close: the Dice coefficient for the Mahalanobis metric was 0.641 while that of the Euclidean metric was 0.632 while the computational time increased by 1.5 over the Euclidean method. Further, the problem with including a non-spherical method is that it cannot be readily integrated into the bias field correction extension as the method would require modification of the resulting minimization conditions for both the cluster center and bias field coefficients. Additionally, the proposed method includes several features that help distinguish each tissue class and a non-spherical metric is not needed.
The algorithm can be extended to include the segmentation of bone and subcutaneous fat tissue as well. The FCM algorithm when applied to the whole calf (including the subcutaneous fat) yields the following non-background clusters (Supplemental Fig. 3): muscle and bone marrow (cluster 1); IMAT, IMCT, cortical bone and subcutaneous fat (cluster 2). To identify the subcutaneous fat, cluster 1 will be processed with morphological closing to fill in the holes in this cluster followed by a connected component analysis to identify a mask that includes all tissue except subcutaneous fat. The mask obtained from cluster 1 will be used to identify the subcutaneous fat in the cluster 2 (all non-zero voxels in cluster 2 outside this mask are subcutaneous fat). Once the subcutaneous fat has been identified in cluster 2, a connected component analysis on the remaining voxels in cluster 2 will isolate cortical bone from IMAT/IMCT. Other automated checks such as the shape of the segmented volumes will be integrated into the algorithm to ensure that the tissue labels are accurate.
Phantom Images
The phantom enables the accurate evaluation of the algorithm’s performance since the ground truth is known and allows one to determine the noise/bias limits for accurate segmentation. From the phantom data (Table 1), a CNR of 140 (typical of the UTEs data) and a bias range from 0%–100% yielded highly accurate segmentations for smoothed images. For unsmoothed data, the algorithm yielded lower segmentation accuracies (still greater than 90%) even within a smaller range of bias fields (Table 1). This identifies the role of noise in reducing accuracy as well as the effectiveness of the denoising algorithm used here. It should be noted that all in-vivo images were denoised prior to segmentation.
In addition to assessing the hard threshold, the phantom was also evaluated using soft threshold (MSRD) since the simulated probability values are available. An inaccurate segmentation will yield results close to 1 while a perfect segmentation will yield a value close to zero; the low values close to zero in Table 1 show that the automated algorithms perform well. The improvement in performance (based on both soft and hard thresholds) of the Adaptive Spatial MCFCM with Bias Correction over the other two algorithms is especially evident at the larger bias fields and the former algorithm is robust even at the highest simulated bias fields.
Noise and Bias Fields in in-vivo calf images
The 3D Slicer was used for the initial correction of the bias fields in the images and noise was reduced with a 3D anisotropic diffusion filter but this pre-processing did not sufficiently reduce noise and shading artifacts to provide accurate segmentation of small structures. The inclusion of the adaptive spatial similarity term in the FCM objective function allows voxels in homogenous regions to form one cluster even in the presence of noise. However, the spatial term alone could not address the shading artifacts, which required the integration of a bias field correction term in the objective function for accurate segmentation (14). The challenge in implementing the bias field correction was that it made the minimization process computationally intensive (since the number of variables was the same size as the object). In order to increase the speed to convergence, the cluster output of the adaptive spatial MCFCM served as the initial cluster centers for the bias corrected adaptive spatial MCFCM. The ‘unregularized’ bias field correction was not required for any of the images analyzed here as such severe bias was not seen in any of the in-vivo images.
Hard versus soft threshold
It is difficult to select a hard threshold value that retains all the partial volume segments without including parts of the muscle tissue. The soft threshold provided a more realistic segmentation since the thinner segments of the IMAT/IMCT have sub-pixel occupancy, and intensities are based on the partial volume of muscle and non-muscle within one voxel. Soft threshold approaches have been implemented successfully in other structures, which suffer from partial volume effects such as the trabecular bone which have a small width and form a network (19).
It is not possible to evaluate the in-vivo soft thresholded (probability value maps) images as the manual contour is of necessity a hard threshold (while manual contouring is challenging, manual assignment of probability values is impossible). Thus comparisons are only possible for the hard thresholded data for the in-vivo studies (Table 2). The soft thresholded evaluation is conducted for the phantom data which shows very small residual errors reflecting a highly accurate segmentation (Table 1). In the case of the in-vivo data, expert visual comparison of the hard and soft thresholds confirmed the increased accuracy and realistic segmentation with the latter method.
The automated algorithm was tested on a total of 440 images (44 images per subject ×10 subjects); the dataset included subjects with IMCT and IMAT ranging from small volumes in 5 young subjects to much larger volumes in 5 old subjects. Further, the anatomical images included varying extent of bias fields and signal to noise ratio depending on the relative location with respect to the radio-frequency coil. Thus, the test data included the range of IMCT/IMAT infiltration as well as bias fields and SNR that are likely to be encountered in any clinical scan and the applicability and accuracy of the automated segmentation algorithm is shown across this dataset.
Manual segmentation and Algorithm Validation
Manual segmentation of IMAT/IMCT is extremely challenging as these tissues form a distributed and often fragmented network (since the IMAT/IMCT are short, disjoint segments at MR resolutions). Thus, it is critical to develop accurate, automated algorithms for the segmentation of IMAT/IMCT. For the present validation, considerable effort was spent in performing the manual segmentations. Validation is performed in the current paper by comparing the automated segmentation to manual segmentation by an expert; further validation using biochemical assays to extract and quantify the IMAT and IMCT volumes is clearly not possible in human subjects. However, the accuracy of the proposed segmentation for different bias and noise levels as well as for a range of IMAT/IMCT effective widths was validated using phantom data that simulated in-vivo conditions and for which the ground truth is known. It should be noted that simulated phantom data have been used in other studies; e.g., to verify the accuracy of segmentation of brain white/gray/CSF tissues since in the latter case also the ground truth cannot be determined for the in-vivo condition (20).
IMACT/IMCT segmentation from whole calf muscle versus individual muscles
The rationale for segmentation of IMAT and IMCT from individual muscles was that (1) the single muscle spatial extent was lower than the entire calf resulting in smaller bias shading within the region, and (2) there were only two tissue clusters in each individual muscle: muscle and non-muscle (IMAT and IMCT). The quantitative comparison between the IMAT/IMCT segmentation from whole calf versus individual muscles shows that the two methods yielded very similar results. This confirms that the algorithm can handle relatively large intensity shading artifacts as well as many tissue types, since the whole calf also included bone marrow and cortical bone in addition to muscle and IMAT/IMCT.
Extraction of IMCT maps
The focus of this paper is the segmentation of IMAT and IMCT tissue from the UTEs image volumes. However, the ultimate clinical goal may be to quantify each component, (i.e., IMAT and IMCT) separately. Based only on the UTEs intensities and the indices extracted from the structure tensor, the two tissues cannot be disambiguated. Further, the IMAT/IMCT is also localized to the same anatomical regions. Recently, quantitative sequences such as Iterative decomposition of water and fat with echo asymmetry and least-squares estimation (IDEAL) that directly provide the fat fraction in each voxel (IMAT) are available on MR scanners (10,11). It would be straightforward to combine the IMAT fraction maps from such sequences with the IMAT/IMCT fraction maps (soft threshold) obtained here to produce separate IMAT and IMCT maps. In this context it should also be mentioned that the aponeurosis has the same intensity and structure as the IMAT/IMCT and is also segmented as the IMAT/IMCT cluster. If the aponeuroses need to be excluded from the segmentation the individual muscle masks have to be defined within the boundaries set by the aponeuroses or alternatively, a morphological erosion can be performed on the individual muscle masks to exclude the aponeuroses. It should be noted here that the intramuscular adipose tissue is defined as those voxels that are completely within the individual muscle masks (MG, LG, Soleus). The intermuscular adipose tissue which is not evaluated in this study are those voxels in between the muscle masks. This definition is consistent with that used in (2). Since the intensities on the dual echo images as well as the morphology of the connective and adipose tissue are similar in the intra- and in the inter-muscular regions, the proposed algorithm (based on intensities and local structure) clusters both type of tissues (inter- and intra-muscular IMAT/IMCT) in the same class. In the current paper, the intermuscular IMAT/IMCT was distinguished from the intramuscular IMCT was enabled by application of the masks of each individual muscle (MG, LG, and Soleus) that were manually contoured. A completely automated algorithm that includes identification of the individual muscle compartments (21) is challenging and our future work will include this so that muscle compartments, inter- and intra-muscular IMCT/IMAT will be classified in automatically.
Quantifying IMAT and IMCT has relevance in several clinical conditions: increase in IMAT of the quadriceps muscle has been shown to be associated with knee arthritis (22) and in type 2 diabetes mellitus, IMCT of the lower extremities has been linked to insulin resistance (23) and quantitative estimation of IMAT can be used as an objective marker of disease severity in several dystrophies (24–26). Recent studies have also shown that remodeling of the extracellular matrix in sarcopenia and muscular dystrophies results in increases in the intramuscular connective tissue (3–7). This increase in the IMCT volume has been shown to correlate with the decrease in lateral force transmission which leads to loss of total muscle force (2,27). Thus quantification of IMAT and IMCT will potentially provide quantitative imaging biomarkers of disease severity, and for monitoring therapeutic, exercise and nutrition interventions in several musculoskeletal diseases (24–28).
In conclusion, the proposed method provides accurate segmentation of the intramuscular connective and adipose tissue in a completely automated fashion. The multimodal input included a set of robust features that incorporates intensity and structure maps that provided accurate clustering. A phantom simulated with IMAT/IMCT structures resembling in-vivo tissue in terms of size and contrast as well as noise and bias similar to the in-vivo images was used to validate the proposed segmentation algorithm for hard and soft thresholds. Both phantom and in-vivo validation confirmed that the Adaptive Spatial MCFCM with Bias Correction is the best of the proposed three algorithms and that the automated algorithm yielded highly accurate segmentations when evaluated against the reference segmentations. Given that accurate manual segmentation is extremely difficult since the structures are filament like and distributed, an accurate automated algorithm should be of great utility in clinical applications.
Supplementary Material
Figure S1: 3D volume of the lower leg with the segmented IMCT/IMAT tissue (green) of a young subject. The user can rotate and adjust display options to view the 3D volume. The amount of IMCT/IMAT tissue is much smaller in the younger subject than in the older subject.
Figure S2: 3D volume of the lower leg with the segmented IMCT/IMAT tissue (green) of an older subject. The user can rotate and adjust display options to view the 3D volume. The amount of IMCT/IMAT tissue is much larger in the older subject than in the younger subject (Fig. S1).
Figure S3: To illustrate the extensibility of the proposed algorithm, the subcutaneous fat is included in the analysis. The top row shows the acquired images UTE TE1 (a) and UTE TE2 (b). The lower row shows the background cluster (c), cluster 1 containing muscle and bone marrow voxels (d), and cluster 2 containing subcutaneous fat, cortical bone, IMAT and IMCT voxels (e).
Acknowledgments
This work was supported by the National Institute of Arthritis and Musculoskeletal and Skin Diseases Grant 5RO1-AR-053343-07 (S.S.).
References
- 1.Zhang C, Gao Y. Effects of aging on the lateral transmission of force in rat skeletal muscle. J Biomech. 2014;47:944–948. doi: 10.1016/j.jbiomech.2014.01.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ramaswamy KS, Palmer ML, van der Meulen JH, Renoux A, Kostrominova TY, Michele DE, Faulkner JA. Lateral transmission of force is impaired in skeletal muscles of dystrophic mice and very old rats. J Physiol. 2011;589:1195–1208. doi: 10.1113/jphysiol.2010.201921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Klingler W1, Jurkat-Rott K, Lehmann-Horn F, Schleip R. The role of fibrosis in Duchenne muscular dystrophy. Acta Myol. 2012;31:184–195. [PMC free article] [PubMed] [Google Scholar]
- 4.Kim HK, Merrow AC, Shiraj S, Wong BL, Horn PS, Laor T. Analysis of fatty infiltration and inflammation of the pelvic and thigh muscles in boys with Duchenne muscular dystrophy (DMD): grading of disease involvement on MR imaging and correlation with clinical assessments. Pediatr Radiol. 2013;43:1327–1335. doi: 10.1007/s00247-013-2696-z. [DOI] [PubMed] [Google Scholar]
- 5.Torriani M1, Townsend E, Thomas BJ, Bredella MA, Ghomi RH, Tseng BS. Lower leg muscle involvement in Duchenne muscular dystrophy: an MR imaging and spectroscopy study. Skeletal Radiol. 2012;41:437–445. doi: 10.1007/s00256-011-1240-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Csapo R, Malis V, Sinha U, Du J, Sinha S. Age-associated differences in triceps surae muscle composition and strength - an MRI-based cross-sectional comparison of contractile, adipose and connective tissue. BMC Musculoskelet Disord. 2014;15:209–219. doi: 10.1186/1471-2474-15-209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kent-Braun JA, Ng AV, Young K. Skeletal muscle contractile and noncontractile components in young and older women and men. J Appl Physiol (1985) 2000;88:662–668. doi: 10.1152/jappl.2000.88.2.662. [DOI] [PubMed] [Google Scholar]
- 8.Makrogiannis S1, Serai S, Fishbein KW, Schreiber C, Ferrucci L, Spencer RG. Automated quantification of muscle and fat in the thigh from water-, fat-, and nonsuppressed MR images. J Magn Reson Imaging. 2012;35:1152–1161. doi: 10.1002/jmri.22842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Valentinitsch A1, Karampinos DC, Alizai H, Subburaj K, Kumar D, Link TM, Majumdar S. Automated unsupervised multi-parametric classification of adipose tissue depots in skeletal muscle. J Magn Reson Imaging. 2013;37:917–927. doi: 10.1002/jmri.23884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Reeder SB, McKenzie CA, Pineda AR, Yu H, Shimakawa A, Brau AC, Hargreaves BA, Gold GE, Brittain JH. Water-fat separation with IDEAL gradient-echo imaging. J Magn Reson Imaging. 2007;25:644–652. doi: 10.1002/jmri.20831. [DOI] [PubMed] [Google Scholar]
- 11.Reeder SB, Pineda AR, Wen Z, Shimakawa A, Yu H, Brittain JH, Gold GE, Beaulieu CH, Pelc NJ. Iterative decomposition of water and fat with echo asymmetry and least-squares estimation (IDEAL): application with fast spin-echo imaging. Magn Reson Med. 2005;54:636–644. doi: 10.1002/mrm.20624. [DOI] [PubMed] [Google Scholar]
- 12.Pham DL, Prince JL. Adaptive fuzzy segmentation of magnetic resonance images, IEEE Trans. Med Imaging. 1999;18:737–752. doi: 10.1109/42.802752. [DOI] [PubMed] [Google Scholar]
- 13.Yang X, Fei B. A multiscale and multiblock fuzzy C-means classification method for brain. MR images Med Phys. 2011;38:2879–2891. doi: 10.1118/1.3584199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liew AW, Yan H. An adaptive spatial fuzzy clustering algorithm for 3-D MR image segmentation. IEEE Trans Med Imaging. 2003;22:1063–1075. doi: 10.1109/TMI.2003.816956. [DOI] [PubMed] [Google Scholar]
- 15.Frangi FA, Niessen WJ, Vincken KL, Viergever MA. Multiscale vessel enhancement filtering. In: MICCAI’98Wells WM, Colchester A, Delp SL, editors. Lecture Notes in Computer Science. Vol. 1496. 1998. pp. 130–137. [Google Scholar]
- 16.Rosset A, Spadola L, Ratib O. OsiriX: An Open-Source Software for Navigating in Multidimensional DICOM Images. J Digit Imaging. 2004;17:205–216. doi: 10.1007/s10278-004-1014-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Li Q, Sone S, Doi K. Selective enhancement filters for nodules, vessels, and airway walls in two- and three-dimensional CT scans. Med Phys. 2003;30:2040–2051. doi: 10.1118/1.1581411. [DOI] [PubMed] [Google Scholar]
- 18.Liu HC, Jeng BC, Yih JM, Yu YK. Fuzzy C-Means Algorithm Based on Standard Mahalanobis Distances. Proc 2009 International Symposium on Information Processing (ISIP’09); Huangshan, P. R. China. August 21–23, 2009; pp. 422–427. [Google Scholar]
- 19.Moreno R, Borga M, Smedby Ö. Soft Classification of trabeculae in Trabecular Bone. IEEE International Symposium on Biomedical Imaging: From Nano to Macro. 2011:1641–1644. [Google Scholar]
- 20.Kwan RKS, Evans AC, Pike GB. MRI simulation-based evaluation of image-processing and classification methods. IEEE Trans Med Imag. 1999;18:1085–1097. doi: 10.1109/42.816072. [DOI] [PubMed] [Google Scholar]
- 21.Ghanbari BH, Hamarneh G, Changizi N, Ward AD, Reid WD. MRI-Based 3D Shape Analysis of Thigh Muscles: Patients with Chronic Obstructive Pulmonary Disease Versus Healthy Adults. Academic Radiology. 2011;18:155–166. doi: 10.1016/j.acra.2010.09.008. [DOI] [PubMed] [Google Scholar]
- 22.Kumar D, Karampinos DC, MacLeod TD, Lin W, Nardo L, Li X, Link TM, Majumdar S, Souza RB. Quadriceps intramuscular fat fraction rather than muscle size is associated with knee osteoarthritis. Osteoarthritis Cartilage. 2014;22:226–234. doi: 10.1016/j.joca.2013.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Karampinos DC, Baum T, Nardo L, Alizai H, Yu H, Carballido-Gamio J, Yap SP, Shimakawa A, Link TM, Majumdar S. Characterization of the regional distribution of skeletal muscle adipose tissue in type 2 diabetes using chemical shift-based water/fat separation. J Magn Reson Imaging. 2012;35:899–907. doi: 10.1002/jmri.23512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Willis TA, Hollingsworth KG, Coombs A, Sveen ML, Andersen S, Stojkovic T, Eagle M5, Mayhew A, de Sousa PL, Dewar L, Morrow JM, Sinclair CD, Thornton JS, Bushby K, Lochmuller H, Hanna MG, Hogrel JY, Carlier PG, Vissing J, Straub V. Quantitative magnetic resonance imaging in limb-girdle muscular dystrophy 2I: a multinational cross-sectional study. PLoS One. 2014;9:e90377. doi: 10.1371/journal.pone.0090377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Janssen BH, Voet NB, Nabuurs CI, Kan HE, de Rooy JW, Geurts AC, Padberg GW, van Engelen BG, Heerschap A. Distinct disease phases in muscles of facioscapulohumeral dystrophy patients identified by MR detected fat infiltration. PLoS One. 2014;9:e85416. doi: 10.1371/journal.pone.0085416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Johnston JH, Kim HK, Merrow AC, Laor T, Serai S, Horn PS, Kim DH, Wong BL. Quantitative Skeletal Muscle MRI: Part 1, Derived T2 Fat Map in Differentiation Between Boys With Duchenne Muscular Dystrophy and Healthy Boys. AJR Am J Roentgenol. 2015;205:W207–W215. doi: 10.2214/AJR.14.13754. [DOI] [PubMed] [Google Scholar]
- 27.Zhang C, Gao Y. Effects of aging on the lateral transmission of force in rat skeletal muscle. J Biomech. 2014;47:944–948. doi: 10.1016/j.jbiomech.2014.01.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gillies AR, Lieber RL. Structure and function of the skeletal muscle extracellular matrix. Muscle Nerve. 2011;44:318–331. doi: 10.1002/mus.22094. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1: 3D volume of the lower leg with the segmented IMCT/IMAT tissue (green) of a young subject. The user can rotate and adjust display options to view the 3D volume. The amount of IMCT/IMAT tissue is much smaller in the younger subject than in the older subject.
Figure S2: 3D volume of the lower leg with the segmented IMCT/IMAT tissue (green) of an older subject. The user can rotate and adjust display options to view the 3D volume. The amount of IMCT/IMAT tissue is much larger in the older subject than in the younger subject (Fig. S1).
Figure S3: To illustrate the extensibility of the proposed algorithm, the subcutaneous fat is included in the analysis. The top row shows the acquired images UTE TE1 (a) and UTE TE2 (b). The lower row shows the background cluster (c), cluster 1 containing muscle and bone marrow voxels (d), and cluster 2 containing subcutaneous fat, cortical bone, IMAT and IMCT voxels (e).


