Abstract
Classical 3-point rigid water models are most widely used due to their computational efficiency. Recently, we introduced a new approach to constructing classical rigid water models [S. Izadi et al., J. Phys. Chem. Lett. 5, 3863 (2014)], which permits a virtually exhaustive search for globally optimal model parameters in the sub-space that is most relevant to the electrostatic properties of the water molecule in liquid phase. Here we apply the approach to develop a 3-point Optimal Point Charge (OPC3) water model. OPC3 is significantly more accurate than the commonly used water models of same class (TIP3P and SPCE) in reproducing a comprehensive set of liquid bulk properties, over a wide range of temperatures. Beyond bulk properties, we show that OPC3 predicts the intrinsic charge hydration asymmetry (CHA) of water — a characteristic dependence of hydration free energy on the sign of the solute charge — in very close agreement with experiment. Two other recent 3-point rigid water models, TIP3PFB and H2ODC, each developed by its own, completely different optimization method, approach the global accuracy optimum represented by OPC3 in both the parameter space and accuracy of bulk properties. Thus, we argue that an accuracy limit of practical 3-point rigid non-polarizable models has effectively been reached; remaining accuracy issues are discussed.
I. INTRODUCTION
Molecular modeling and simulations are routinely employed to study the structure and function of biological molecules in applications ranging from structural biology to bio-medicine and rational drug design.1,2 Accurate, classical water models are just as important for these modeling efforts as water is for life.3–5 The simplest, and most widely used, atomistic water models are fixed-charge, rigid, non-polarizable models,6–11 implemented in virtually every modeling package.12–15 However, despite at least three decades of effort, there is still significant room for much needed improvement.16,17 As more physical realism is added to such models either through more complex geometry or/and by inclusion of electronic polarization effects, the cost of finding the accuracy optimum in the large parameter space grows exponentially. As a result, available parametrizations are virtually guaranteed to be sub-optimal with respect to faithfully reproducing key experimental properties of water, hindering predictive potential of these models. Critically, even modest inaccuracies of water models can drastically affect the outcomes of atomistic biomolecular modeling in an unpredictable, adverse manner. For example, even ∼2% change in the strength of water-water hydrogen bonds can make a critical difference.18 While in some cases fortuitous cancellation of errors between solute-solvent and solvent-solvent interactions leads to seemingly reasonable agreement with experiment, the balance cannot be maintained in general if the solvent-solvent part is wrong. For example, the popular TIP3P model6 leads to ∼40% error (∼6 kcal/mol) relative to experiment in small ligand (host-guest) binding enthalpy estimates.1 For larger protein-ligand systems, the discrepancies between binding energies can exceed 10 kcal/mol for commonly used water models,19 which is unacceptable for quantitative molecular modeling efforts. Likewise, widely used water models fail to predict correct experimental size of intrinsically disordered proteins20 or the balance between RNA tetraloop populations,21 regardless of the underlying force-field used.
Accurate water models are also critical for studying pure water. Water is the most extensively studied substance,22,23 yet our understanding of its unique properties is incomplete.3 Despite decades of research, investigations are still active to characterize water in many respects, including, among many others, bulk properties,17 phase diagram,17 hydrogen bonding,24 and dynamics crossover.25 Most such investigations rely on molecular simulations using fixed-charge rigid non-polarizable water models.
The most popular — mainly due to their computational efficiency in practical molecular simulations — are 3-point models that utilize 12-6 Lennard-Jones (LJ) and Coulombic electrostatic potentials. These models of water are about as simple as one can possibly make them suitable for atomistic simulations (successful 2-point models were developed for coarse-grained simulations26). Despite their continued popularity, most commonly used 3-point water models (TIP3P6 and SPCE10) cannot faithfully reproduce bulk properties at 298 K and 1 bar pressure at once. For instance, while TIP3P produces the enthalpy of vaporization and dielectric constant reasonably well, it underestimates the density and significantly overestimates the self-diffusion coefficient.17 In contrast, SPCE fairly accurately reproduces the density and self-diffusion; however, it overestimates the enthalpy of vaporization and underestimates the dielectric constant. Unfortunately, both of these commonly used models lead to poor reproduction of the temperature dependence of liquid water properties. For instance, the density maximum experimentally observed at 277 K is not present in the density profile of these two models in the range of temperatures normally studied for water.
The modern quest for better 3-point classical water models — the type most commonly used in practice — has continued for at least three decades,6,17,27,28 with no apparent end in sight. It may come as a surprise that it has been so extraordinarily difficult to find, once and for all, a combination of just 5 model parameters, e.g., Fig. 1, to best reproduce, by some reasonable metric,17 a limited set of the most relevant experimental bulk properties of liquid water. At present, there are at least two interrelated reasons for the difficulty. First, the “charge–distances–angle” parameters conventionally varied during water model optimization affect model’s electrostatics, and hence the resulting bulk properties, in a convoluted manner, leading to a great multitude of local optima in this parameter space. Some of these optima represent water models developed so far.6,8–10 However, for a complex optimization landscape with multiple local optima, no method except for an exhaustive search in the entire relevant parameter space can guarantee that a global optimum is found. And this is where the second problem lies: identifying such global optimum is very difficult because water properties are extremely sensitive to the model parameters in the “charge–distances–angles” sub-space. For example, a change of the |OH| distance by as little as 10−2 Å can change the calculated self-diffusion constant by as much as 30%.29 Requiring a more realistic 3% accuracy relative to experiment would imply that the discretization in the parameter space needs to be at least 10−3 Å along just one spatial dimension, or a total of 103 grid points, assuming that an unrestricted search along this coordinate spans 1 Å. Thus, a reasonably fine-grain exhaustive search along just three dimensions would take about 109 evaluations of model water properties. Since some of these, such as estimates of dielectric constant or self-diffusion coefficient, involve tens of nanoseconds of Molecular Dynamics (MD) simulations, it is clear that such an exhaustive search is extraordinarily difficult in the traditional parameter space, unless the search is limited to a small subspace of “intuitively expected” geometries, Fig. 1. However, this geometry can be very far from electrostatically optimal charge distribution, which is what matters for classical water models.11,30 Recently introduced highly sophisticated and powerful force-field optimization methods27 expand the boundaries of the traditional approach, resulting in improvements in water model quality. Still, the key question remains: how far are the most accurate existing practical 3-point rigid water models from the true optimum, at least as far as most important liquid properties are concerned? And if a globally optimal 3-point model can be found, how far its properties would be from reality? Given that tens of thousands of atomistic modeling and simulation studies are published each year31 that use simplified classical water models, the question is highly relevant.
FIG. 1.
TIP3P: widely used 3-point water model. Liquid properties of the model are determined by 5 parameters: geometry of the triangle (l and Θ), partial charge q, and two Lennard-Jones parameters of the oxygen center (σLJ and ϵLJ, see Table II).
Recently we proposed a new approach to constructing classical water models that can deliver novel highly accurate optimal n-point water models.11 In contrast to the mainstream water modeling parametrization techniques, the key feature of the new approach is the complete abandonment of any constraint on the point charge geometry, except the fundamental symmetry of water molecule, in favor of an unconstrained exhaustive search in the subspace of low order electrostatic multipole moments. This subspace is directly relevant to the electrostatic properties of water, which makes the resulting “model quality” landscape “simple,” without multiple local optima. The dimensionality of the search space can also be effectively reduced, along with the number of search points along each dimension needed to locate the global optimum. The 4-point OPC water model previously developed based on this new approach was shown to reproduce the key liquid state properties significantly more accurately than the commonly used water models,11 and was, in fact, more accurate than any other model of the same class that OPC was tested against. OPC can deliver noticeable accuracy improvement in molecular simulations of solvated biomolecules even with existing force-fields. Improvements have been reported specifically in RNA21 and DNA32,33 simulations, thermodynamics of ligand binding,1 and small molecule hydration.11
Motivated by the notable popularity of the simple 3-point models in practical molecular simulations, here we apply our new approach to construct (within the most widely used pairwise Coulombic and 12-6 Lennard-Jones framework) a 3-point version of the optimal point charge water model referred to as OPC3. We compare OPC3 with the two most commonly used models (TIP3P and SPCE) and also with two more recent 3-point models obtained by independent optimizations based on completely different methods (TIP3PFB27 and H2ODC28).
II. METHODS
A. Optimization procedure
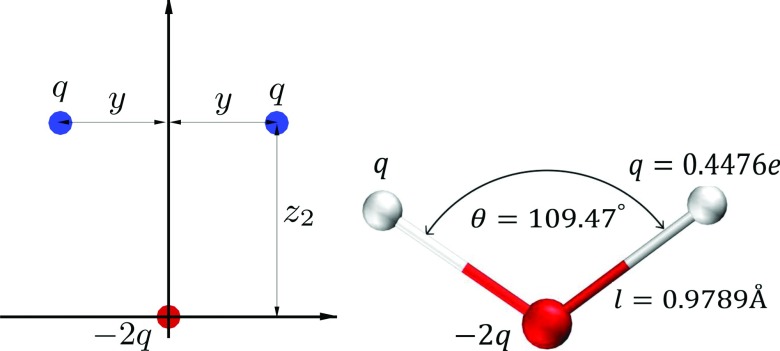
The first key feature of our approach is to abandon any and all (seemingly intuitive) constraints on point charge values or their relative positions (other than the fundamental C2v symmetry of water molecule) in search for an optimal electrostatic charge distribution that best approximates liquid properties of water. The most general configuration for a 3-charge 3-point model consistent with C2v symmetry of the water molecule is shown in Fig. 2. Note that the position of the negative charge in a 3-point model has to coincide with the position of the oxygen atom (the van der Waals center), but the position of the positive charges is allowed to vary (Fig. 2). As a result, the charge distribution in 3-charge 3-point models has an additional geometry constraint compared to 4-point 3-charge models7,8,11 in which charges are completely unconstrained (except for the C2v symmetry).11
FIG. 2.
Left. The most general configuration for a 3-charge 3-point water model consistent with C2v symmetry of the water molecule. The charge distribution parameters (y, z, and q) are calculated to optimally reproduce a given set of dipole and quadrupole moments. The value of the positive and negative charges is q and −2q, respectively. The single Lennard-Jones interaction is centered on the origin (oxygen). Right. The final, optimized geometry of the proposed OPC3 water model.
Based on the concept of optimal point charge approximation,30 the parameters of the charge distribution shown in Fig. 2 can be optimized so that the most important dipole and the quadrupole moments of the water molecule are reproduced exactly (note that the monopole is zero).11,30 In the coordinate system shown in Fig. 2, the charge distribution characterized by z, y and q can fully reproduce a given set of dipole (μ) and quadrupole (Q0 and QT) moments for the water molecule by requiring
| (1) |
| (2) |
| (3) |
The above three equations are solved to find three parameters (z, y and q) as follows:
| (4) |
| (5) |
| (6) |
where μ, Q0, and QT moments are related to the more traditional Cartesian components of the traceless multipole moments of water molecule as μ = μz, Q0 = Qzz, QT = 1/2(Qyy − Qxx).34–36 The above set of analytical expressions enables us to independently vary the moments of the charge distribution, which makes it computationally feasible to fully explore in the relevant subspace of the moments (μ, Q0 and QT).
The Q0 component of the quadrupole moment (linear quadrupole) is known to be relatively small for water molecule and is not expected to be very important.35 We fix this value to zero, which automatically results in fully tetrahedral angle: by setting Q0 = 0 in Eq. (2) we obtain that translates to θ = 109.47∘ (Fig. 2).
This leaves the two more important moments, the dipole (μ) and the square quadrupole (QT), as the two key search parameters we vary exhaustively. For the case of 3-point model, we vary μ within the range of 2.3 D–2.5 D, and QT within 1.6 D Å –2.4 D Å, which reflect the ranges for commonly used and recently developed water models of the same class. For every pair of trial values of μ and QT (and the fixed value of Q0 = 0) the optimal charge and geometry parameters of the test model (q, z, and y, Fig. 2) are uniquely determined via the set of closed-form analytical expressions (Eqs. (4)–(6)).
The usual 12-6 Lennard-Jones (LJ) potential is employed to model the van der Waals interaction among the oxygens. The Lennard-Jones potential function, ELJ, can be written as
| (7) |
where roo is the distance between the oxygen sites of two molecules, and ϵLJ and σLJ are the strength and the size of the LJ center, and . Unlike σLJ and ϵLJ, the ALJ and BLJ parameters can be optimized nearly independently due to the weak coupling between them.35 For every charge distribution calculated as described above, the value ALJ of the 12-6 Lennard-Jones (LJ) potential, which is mainly responsible for the liquid structure,35 is selected so that the location of the first peak g(roo) of the oxygen-oxygen radial distribution function (RDF) is in agreement with most recent experimental data.37 The value of BLJ is optimized so that the experimental value of water density is achieved.
Using the procedure above, we can obtain a test water model for each trial combination of μ and QT within the search space. We evaluate the performance of each of these models in reproducing six targeted liquid water properties at 298.16 K and 1 bar: static dielectric constant ϵ0, self-diffusion coefficient D, heat of vaporization ΔHvap, density ρ, and the position roo1 and height g(roo1) of the first peak in oxygen-oxygen pair distribution functions. For calculations of thermodynamic and dynamical bulk properties we use standard protocols;8,11 the details are summarized in the supplementary material.40
The quality of each test water model — corresponding to a μ, QT point on the map — is characterized by a quality score function suggested by Vega and Abascal17 based on the same six key bulk properties used for the fitting. For a calculated property x and the corresponding experimental value of xexp, the assigned score is obtained as17
| (8) |
where the tolerance (tol) is assigned to 0.5% for density and position of the first peak in the RDF, and 2.5% for the remaining properties. The quality score assigned to each test model is equal to the average of the scores in bulk properties considered.
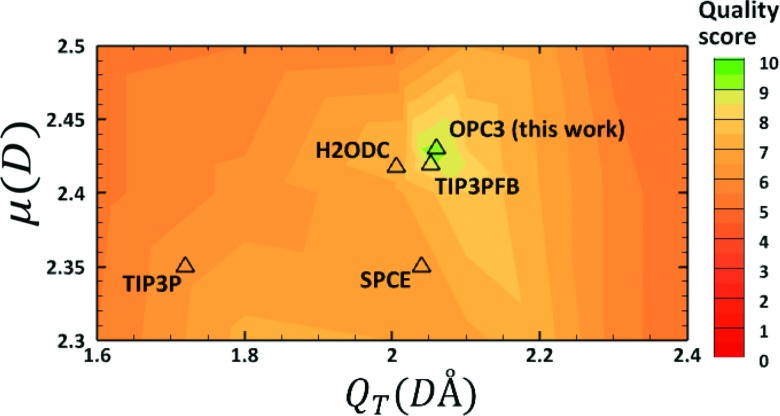
The result of the above search procedure is a “quality map” of all possible water models in the μ-QT space (Fig. 3): the proposed model is the one with the highest quality score.
FIG. 3.
The quality score distribution of test water models in the space of dipole (μ) and quadrupole (QT). Each fine grain point on the plot represents a model tested. Scores (from 0 to 10) are calculated based on the accuracy of predicted values for six key properties of liquid water (see text). The resulting proposed optimal model is termed OPC3. For reference, the μ and QT values of commonly used and the very recently developed 3-point water models (triangles, quality score given by the color at the symbol position) are placed on the same map (see also Table I).
B. Simulation details
Unless specified otherwise, we use the following MD simulations protocol. Simulations in the NPT ensemble (1 bar, 298.16 K) were carried out using the AMBER 14 MD software package.12 A cubic box with edge length of 30 Å was filled with 804 water molecules. Periodic boundary condition was implemented in all directions. Long-range electrostatic interactions, calculated via the particle mesh Ewald (PME) summation, and the van der Waals interactions were cut off at distance 8 Å; the van der Waals interactions beyond the cutoff distance are accounted for via a continuum model (vdwmeth = 1 in AMBER,12 DispCorr = EnerPres in GROMACS14). Dynamics were conducted with a 2 fs time step and all intra-molecular geometries were constrained with SHAKE. The NPT simulations were performed using Langevin thermostat with a coupling constant 2.0 ps−1 and a Berendsen barostat with coupling constant of 1.0 ps−1 for equilibration and 3.0 ps−1 for production.
We perform a 3-tier search for the best fit in the 2D space of (μ, QT), Fig. 3. The initial search is on 0.05 × 0.05 grid in the 2D (μ, QT) space shown in Fig. 3. The refinement is on 0.01 × 0.01 grid, limited to vicinity of the optimum (green area), followed by the final comparison of a few candidates within a very small area (dark green). The simulation time was 6 ns for the first stage, 15 ns for the second, and 65 ns for the final stage and all of the properties of water models shown here. These long simulation times are needed to obtain well-converged averages of some properties, such as static dielectric constant.29
C. Charge hydration asymmetry (CHA) calculations
Accurate, to within 1 kcal/mol, estimation of a reference value for charge hydration asymmetry (CHA) from solvation energies of cation/anion pairs is fraught with technical and fundamental difficulties,41–43 both experimental and computational. For example, estimates of CHA for K+/F− from the available comprehensive experimental sets44–46 of ion hydration energies differ by as much as 300%, or tens of kcal/mol.41 From the theoretical prospective, obtaining a computational estimate of hydration free energy of a charged species that directly corresponds to a concrete experiment is also anything but straightforward.47
Here we employ an alternative CHA reference free from all of these defects: we use two pairs of CHA-conjugate molecules (3-methyl butanoic acid, N-methylacetamide) and (pentanoic acid, N-methylacetamide), analogous to K+/F− pair with respect to CHA, in a sense precisely defined in Ref. 41. Briefly, the anion-like (cation-like) molecule has one relatively highly charged “CHA-dominant” atom, e.g., the amide oxygen of N-methyl acetamide (carboxylic hydrogen of pentanoic acid) that behaves like F− (or K+) with respect to the structuring of water around it. The effect of the opposite charges within each molecule is much more diffuse and cannot cancel the dominant asymmetric contribution from this one atom. Mathematically, the difference between hydration free energies of the two molecules within each CHA-conjugate pair behaves just like the difference between K+ and F− hydration energies with respect to the symmetry-breaking perturbation that breaks the tetrahedral symmetry of water molecule.41 The difference between experimental hydration energies within each CHA-conjugate pair of neutral molecules quantifies the intrinsic charge-asymmetric response of real water, accurately, and free of extrinsic, complicating factors such as the energetic cost of charge species to cross the liquid/vapor boundary. Critically, unlike the corresponding quantity for ions, the measured hydration free energy of small neutral molecules is accurate to within a fraction of kcal/mol, which makes the corresponding CHA reference value accurate enough. From computational standpoint, estimation of hydration free energy of a neutral solute is also straightforward and accurate.48 We quantify the charge hydration asymmetry of these two pairs by their relative experimental CHA, , where for each pair (A,B) of molecules, ΔΔG is the difference in their hydration energies ([ΔG(A) − ΔG(B)]), and 〈ΔG〉 is the average of their hydration energies ((1/2)[ΔG(A) + ΔG(B)]).41 The numbers reported in Table IV are averages over the two CHA-conjugate pairs. Molecule topology and coordinate files for the small molecules used here were prepared in an earlier work,49 using GAFF50 small molecule parameters assigned by Antechamber 14,51 and the partial charges were assigned using the Merck-Frosst implementation of AM1-BCC.52 The hydration free energy calculations in OPC3 (this work) explicit water were performed in GROMACS 4.6.514 using standard free energy perturbation (FEP) calculations49 — the Coulomb and van der Waals coupling was reduced from 1 to 0 using 20 intermediate λ values. Molecules were solvated in triclinic box with at least 12 Å from the solute to the nearest box edge. Real space electrostatic cutoff was 10 Å, and long-range electrostatic interactions were calculated using periodic boundary conditions via the particle mesh Ewald (PME) summation53,54 and all bonds were restrained using the LINCS algorithm. Production simulations were 5 ns in length at each λ value, and free energies and the associated uncertainties were computed using the Bennett acceptance ratio (BAR), namely, the gbar feature in GROMACS 4.6.5.
TABLE IV.
Relative CHA propensity, η∗, of various water models compared to experiment. The experimental and calculated η∗ for TIP5P, TIP3P, TIP4PEw, OPC11 water models are taken from Ref. 41. The calculation of η∗ value for OPC3’s is described in Sec. II C. Although no η∗ for TIP3PFB and H2ODC were reported in the original references, we expect the values to be close to those of OPC3, based on the over-all proximity of these models in the multipole parameter space.
| Exp | TIP5P | TIP3P | TIP4PEw | OPC | OPC3 |
|---|---|---|---|---|---|
| 0.485 | 0.11 | 0.43 | 0.55 | 0.45 | 0.49 |
III. RESULTS
A. The proposed OPC3 model
The result of the above search procedure is a “quality map” of all possible test water models in the μ–QT space, Fig. 3: the proposed OPC3 model is the one with the highest quality score.
The OPC3’s point charge positions and values and the LJ parameters are listed in Table II. The |O–q+| distances for OPC3 are slightly longer (0.978 88 Å) than the corresponding experimental values of |O − H| bond. We stress that it is the |O–q+| and not the |O − H| distance that is of critical importance for classical water models with a single LJ center on the oxygen atom. The ∠q+Oq+ angle (Fig. 2) is equal to (109.47∘) which is a direct consequence of setting Q0 = 0 (see Sec. II).
TABLE II.
Force field parameters of OPC3 (see Fig. 2), some commonly used, and recently developed 3-point water models. Here σLJ = (ALJ/BLJ)1/6 and . For comparison, water molecule geometry in the gas phase is also included.
| q(e) | l (Å) | Θ (deg) | σLJ (Å) | ϵLJ (kJ/mol) | |
|---|---|---|---|---|---|
| EXP (gas) | NA | 0.9572 | 104.52 | NA | NA |
| TIP3P | 0.417 | 0.9572 | 104.52 | 3.150 61 | 0.6364 |
| SPCE | 0.4238 | 1.0 | 109.47 | 3.166 | 0.65 |
| TIP3PFB | 0.424 22 | 1.0118 | 108.15 | 3.1780 | 0.652 14 |
| H2ODC | 0.4238 | 0.958 | 109.47 | 3.184 00 | 0.593 |
| OPC3 | 0.447 585 | 0.978 88 | 109.47 | 3.174 27 | 0.683 69 |
Compared to the commonly used 3-point models shown, OPC3 reproduces the multipole moments of water molecule in the liquid phase substantially better (Table I): OPC3’s μ (2.43 D) is closer to the accepted range of values inferred from indirect experimental estimates and QM predictions.36,38,39,55–58 OPC3’s QT (2.06 D Å) is also larger than that of the commonly used TIP3P and SPCE, and is in better agreement with the values from quantum calculations.36,39,56,57 The improved multipole moments of OPC3 are achieved due to the “unconstrained” search for model’s optimal parameters in the space of moments.
TABLE I.
Water molecule multipole moments centered on oxygen: from experiment, liquid phase quantum calculations, some common and recent 3-point models, and OPC3 model (this work).
B. Bulk properties at 298.16 K, 1 bar
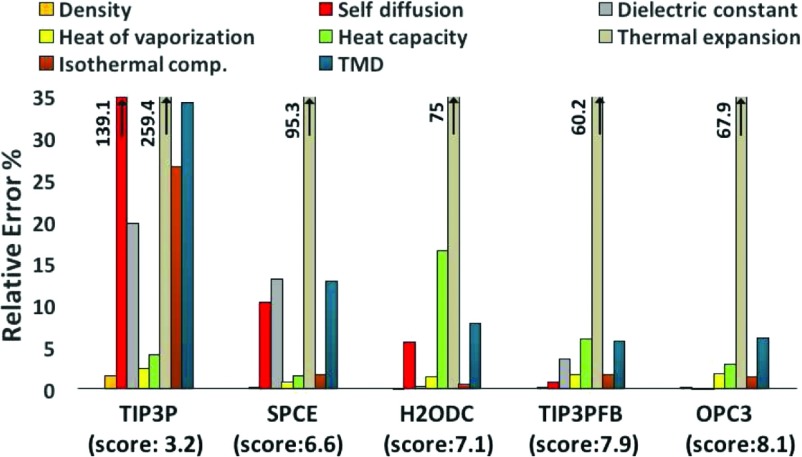
The quality of the OPC3 model in reproducing experimental bulk water properties at ambient conditions and a comparison with other most commonly used and recently developed 3-point models are presented in Table III. For each of 10 key liquid properties (Table III) against which water models are most often benchmarked,8,17,59 the deviations of OPC3’s computed properties from the corresponding experimental values are less than 6%, except for the thermal expansion coefficient that deviates from experiment by about 67.9% (see Fig. 4). Note that the parametrization of OPC3 involved a fitting to only 5 of the properties reported in Table III, yet the model is accurate in estimating several other properties that were not included in the optimization, such as isobaric heat capacity Cp, isothermal compressibility κT, thermal expansion coefficient αp, and the temperature of maximum density (TMD) (see Fig. 4).
TABLE III.
Model vs. experimental bulk properties of water at ambient conditions (298.16 K, 1 bar): dipole μ, density ρ, static dielectric constant ϵ0, self-diffusion coefficient D, heat of vaporization ΔHvap, first peak position in the RDF roo1, isobaric heat capacity Cp, thermal expansion coefficient αp, and isothermal compressibility κT. The temperature of maximum density (TMD) is also shown. Bold fonts denote the values that are closest to the corresponding experimental data (EXP). Statistical uncertainties (±) are given where appropriate.
| Property | TIP3P9,17 | SPCE17,27 | TIP3PFB27 | H2ODC | OPC3 | EXP17,37,59 |
|---|---|---|---|---|---|---|
| μ (D) | 2.348 | 2.352 | 2.42 | 2.42 | 2.43 | 2.5–3 |
| ρ (g/cm3) | 0.980 | 0.994 | 0.995 | 0.9975 | 0.996 ± 0.001 | 0.997 |
| ϵ0 | 94 | 68 | 81.3 | 78.7 | 78.4 ± 1 | 78.4 |
| D (109 m2/s) | 5.5 | 2.54 | 2.28 | 2.17 | 2.30 ± 0.02 | 2.3 |
| ΔHvap (kcal/mol) | 10.26 | 10.43 | 10.71 | 10.36 | 10.73 ± 0.004 | 10.52 |
| roo1 (Å) | 2.77 | 2.75 | 2.755 | … | 2.755 | 2.8 |
| Cp (cal/(K mol)) | 18.74 | 20.7 | 19.1 | 20.98 | 18.54 ± 0.05 | 18 |
| αp (10−4 K−1) | 9.2 | 5.0 | 4.1 | 4.48 | 4.3 ± 0.1 | 2.56 |
| κT (10−6 bar−1) | 57.4 | 46.1 | 44.5 | 45.0 | 46.0 ± 1 | 45.3 |
| TMD (K) | 182 | 241 | 261 | 255 | 260 | 277 |
FIG. 4.
Comparing the accuracy of OPC3 to some old and very recent rigid 3-point water models TIP3P,6 SPCE,10 H2ODC,28 and TIP3PFB.27 The quality scores (see Methods) represent the overall performance of each model in reproducing eight key properties. Density ρ, self-diffusion coefficient D, static dielectric constant ϵ0, heat of vaporization ΔHvap, isobaric heat capacity Cp, isothermal compressibility κT and thermal expansion coefficient αp, and the temperature of maximum density (TMD). Note that four of these properties are different from those used for scoring in Fig. 3.
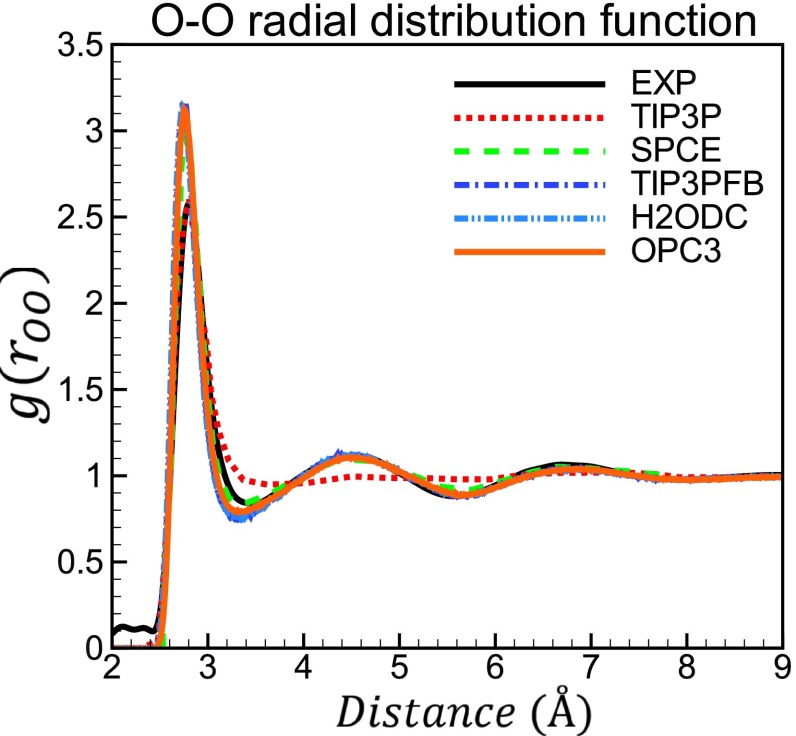
The O–O radial distribution functions (RDFs), g(rOO), for OPC3 are presented in Fig. 5. By design, the experimental position of first peak in O–O RDF is accurately reproduced by OPC3. The position and height of other peaks are also closely reproduced by OPC3. The height of the first peak is overestimated by all of the models shown in Fig. 5, except for TIP3P. While TIP3P accurately reproduces the height of the first peak, it fails completely to describe the experimental RDF beyond the first peak (Fig. 5). In the case of OPC3 the overestimated height of the first peak is likely due to the use of a too repulsive LJ potential (r−12) at short range, which is known to create an over structured liquid.16,60 A “softer” repulsive potential may correct the height of the first O–O RDF peak,60,61 which might entail further accuracy gains in bulk water properties. Whether a more accurate first peak height would lead to immediate accuracy gains in practical biomolecular simulations beyond pure water would not be straightforward to ascertain: major force-fields (and packages) almost invariably employ 12-6 LJ potentials, implying that the solute-solvent and even solute-solute parts of the total interaction may need to be refitted if a different functional form were to be used for the solvent.
FIG. 5.
O–O radial distribution functions of liquid water at 298.16 K, 1 bar. The OPC3 model is compared to the commonly used 3-point models (TIP3P and SPCE), and two more recent 3-point models (TIP3PFB and H2ODC). The experimental data are taken from Ref. 37.
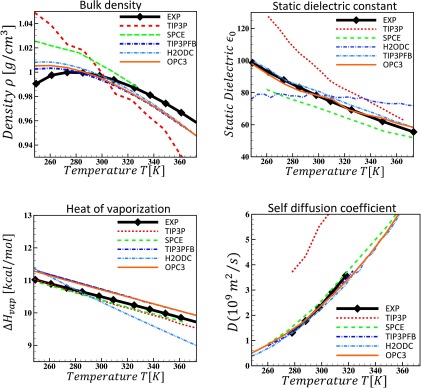
C. Temperature dependent behavior
The ability of OPC3 to reproduce the temperature dependence of four key water properties is shown in Fig. 6. Overall, OPC3 provides a much more accurate description of the temperature dependence of water properties compared to SPCE and TIP3P. In particular, in contrast to TIP3P and SPCE that do not exhibit a maximum in the density of liquid water in the range of temperatures studied, OPC3 yields a maximum density at 260 K. The diffusion coefficient and dielectric constant of OPC3 are in perfect agreement with the experimental values over the large range of temperatures. OPC3’s heat of vaporization is slightly higher than that produced by SPCE and TIP3P. OPC3 has larger dipole and quadrupole moments, which can yield stronger hydrogen bonds and therefore a higher value for heat of vaporization.
FIG. 6.
Calculated temperature dependence of water properties of OPC3 compared to the two most commonly used and two very recent 3-point water models, and experiment. TIP3P results are from Refs. 6, 27, 59, and 62, SPCE from Refs. 27 and 63, TIP4PFB from Ref. 27, and H2ODC from Ref. 28.
Given that OPC3 resulted from a search in the space of only two parameters (μ and QT) at only one temperature (298.16 K), the overall good performance of the model in reproducing bulk properties across a wide range of temperatures, where no fitting was performed, is remarkable. A similarly good performance in temperature dependence of recent rigid models (TIP3PFB and H2ODC) is achieved by employing massive and more specialized fits, and sometimes, over a wide range of thermodynamic conditions, as described below.
D. A consensus in the parametrization of 3-point rigid models
Here we compare OPC3 with two recent 3-point water models: TIP3PFB27 and H2ODC,28 which are parametrized using completely different strategies. TIP3PFB is developed based on the state-of-the-art ForceBalance parametrization method,27 which essentially evaluates the simulated properties in NPT ensemble and calculates their parametric derivatives to use in the optimization. The search for TIP3PFB was performed in the space of the bond length, angle, charge, and van der Waals parameters, using the geometry of TIP3P and SPCE as the starting point. H2ODC is specifically designed to reproduce the correct experimental dielectric constants, along with the more common target properties such as density and enthalpy of vaporization.28 The starting geometry of H2ODC is a fixed tetrahedral angle and a bond length equal to the experimental gas-phase value (Table II). The search for H2ODC was performed in the space of σLJ, ϵLJ and q that are uniformly scaled to fit experimental values for density, heat of vaporization, and dielectric constant, respectively. In contrast to these two models, OPC3 is obtained from an unconstrained exhaustive search in the electrostatic parameter space (key multipole moments) so that six key properties are best reproduced.
For comparison, the μ and QT values of two most recently developed 3-point water models (TIP3PFB27 and H2ODC28) are placed on the quality score map in Fig. 3 (see also Table I). Surprisingly, TIP3PFB and H2ODC are both clustered in the vicinity of the same small high quality region on the map, close to OPC3. Overall, there is also a close agreement between the model parameters (Table II), multipole moments (Table I), and bulk properties (Table III and Fig. 6) for these models. Note that for consistency here we report previously published results for all of the models other than OPC3. However, the properties reported in the original papers may be calculated based on somewhat different protocols from those used in this work, which may lead to slight variation in the computed accuracy, especially outside the T ∼ 300 K point targeted by most model for best fit to experiment. Specifically, our calculations (not shown) suggest that, overall, H2ODC performs equally well as OPC3 and TIP3PFB in describing temperature dependence of density ρ, static dielectric constant ϵ0, self-diffusion coefficient D, and heat of vaporization ΔHvap, shown in Fig. 6. Given the fundamental differences in the optimization of these three models, close agreement of the model parameters and accuracy of OPC3 with values from H2ODC and TIP3PFB points out to a “consensus” for the optimal parametrization of 3-point water models.
E. OPC3 versus OPC
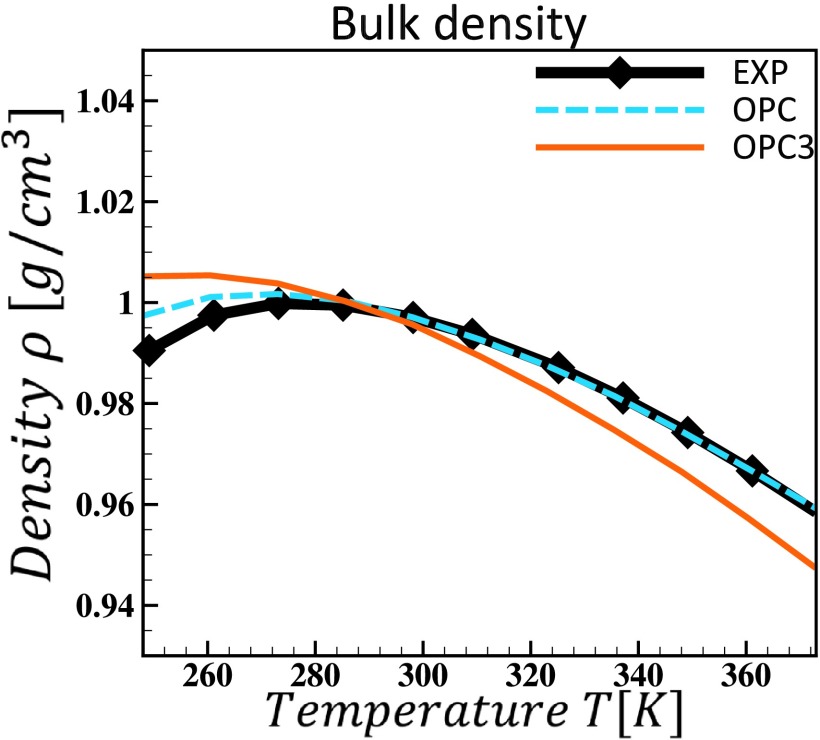
Although we found that OPC3 performs well in most of water bulk properties over a wide range of temperatures (see Table III and Fig. 6), essentially with the same level of accuracy as previously reported 4-point OPC (OPC results not shown here, see Ref. 11 for details), OPC3, as just any other 3-point model, provides a much poorer description of the temperature dependence of water density (Fig. 7). Such a drawback translates into much lower accuracy of OPC3 in calculated thermal expansion at ambient condition: the deviation from experimental value of OPC3 (67.9%) (Fig. 4) is much larger than that of OPC (5%). This discrepancy may lead to a larger deviation of critical parameters of OPC3 from experiment; however, a detailed evaluation64–66 of OPC3’s performance in reproducing critical points and phase diagram of water is beyond the scope of this introductory work.
FIG. 7.
Calculated temperature dependence of water density of OPC3 and OPC. 4-point OPC reproduces the density over a wide range of temperature more accurately than 3-point OPC3.
The lower accuracy of OPC3 compared to OPC is mainly due to its poorer representation of the multiple moments of the water molecule. For instance, OPC’s dipole moment is slightly larger (closer to the accepted range of values for liquid phase) than that of OPC3 (2.48D vs 2.43D, respectively). A more profound distinction is seen in the value of square quadrupole QT, which is 2.3 D Å and 2.06 D Å for OPC and OPC3, respectively. Note that, despite an exhaustive search in the space of μ and QT, neither μ nor QT was used as target properties by OPC3 or OPC. However, the negative charge of OPC is allowed to shift from the oxygen, which enables the model to optimally reproduce a given set of moments up to the octupole.11,30 In contrast, the negative charge of OPC3 is constrained to the oxygen, and consequently the analytical expressions derived for OPC3 (Eqs. (4)-(6)) do not necessarily optimally reproduce the moments beyond the quadrupole order. As a result, although the dipole and quadrupole moments of OPC3 can be set to the values that are in better agreement with QM predictions, doing so might introduce severe errors in the representation of its higher order moments (e.g., octupole), and therefore the resulting bulk properties of the model. Overall, OPC3’s moments seem to be the best compromise between the dipole, quadrupole, and higher moments, which is presently achievable by a 3-point model (Table I). In fact, the dipole and octupole moments of OPC3 are still in reasonable agreement with the QM predictions (Table I) but an overall reasonable balance may have been obtained at the expense of having a relatively low quadrupole moment.
We speculate that the poorer performance of OPC3 in reproducing the temperature dependent properties can be due to its lower value of QT,36 compared to that of OPC. The large quadrupole of water has been known to be crucial for obtaining good tetrahedral structure, which yields a better representation of the phase diagram and temperature dependent properties of water.36,67 The contribution of the higher order multipole moments to electrostatic potential can also be significant at close distances, which are relevant to water-water and water-ion interactions in liquid phase.
The fact that OPC3 is less accurate than 4-point OPC in reproducing some of bulk properties of water does not necessarily mean that OPC3 will deliver poorer performance than OPC in all practical atomistic simulation of biomolecules. This is because accuracy of simulations of solvated molecules depends on a combined effect of water-water, water-solute and solute-solute interactions, therefore OPC3 might perform as well as OPC in some practical simulations based on existing imperfect force fields. It remains to be seen if OPC3 can provide accuracy gains in simulations of biomolecules similar to those already reported for OPC in thermodynamics of ligand binding,1 solvation free energies of small molecules,11 and RNA21 and DNA32,33 simulations.
What is clear is that OPC3 provides a noticeably better description of the electrostatics and bulk properties of water compared to older, commonly used 3-point models. Thus, OPC3 may be a good candidate to eventually replace these models in simulations of solvated biomolecules in situations where the 30% extra speed compared to some of the more accurate 4-point models is critical, while the accuracy loss can be tolerated. These improvements and considerations warrant further analysis and practical tests of OPC3 in biomolecular simulations.
As a first test of OPC3 beyond bulk properties, we have assessed its accuracy in reproducing experimental response of water to microscopic hydrated charge — an obvious prerequisite68 for accurate description of hydrated molecules, especially polar ones. While hydration free energies of small molecules might seem like an obvious reference quantity, we argue that the use of a differential and relative quantity instead41 will minimize uncertainties associated with parametrization of the solute probe. We therefore compute and compare with experiment the relative propensity of OPC3 to cause charge hydration asymmetry41,48,68–80 (CHA). A classical illustrative example of CHA is the large difference between hydration free energies of ions of the same size81 such as K+ and F−, although here we use a different pair of solute probes41 for an accurate comparison with experiment, see Sec. II C. As shown in Table IV, the relative CHA propensity calculated for OPC3 is in best agreement with experiment compared to most commonly used TIPnP water models and even OPC, which is itself very close. Since the CHA propensity characterizes response of water to microscopic electric fields, its reasonable agreement with experiment is necessary for good performance of the model in atomistic modeling studies.41
As the first sanity check of the new model in realistic biomolecular simulations, we preformed 0.5 μ NPT MD simulation of ubiquitin at 300 K solvated in OPC3: the protein was found to be quite stable, with the backbone RMS deviation from the starting crystal structure remaining below 1 Å.
We cautiously recommend the Joung/Cheatham ion parameters82 developed for TIP3P to be used with OPC3 in biomolecular simulations, while awaiting the development of OPC3-specific ions parameters, possibly along the lines described in Ref. 83. The suggestion is based on comparing the Ion-Oxygen Distances (IODs) for 3 monovalent ions (Na+, K+, and Cl-) solvated in TIP3P and OPC3: we found that the Joung/Cheatham ion parameters82 developed for use with TIP3P well reproduce the target IOD values84 (within ±0.05 Å) when used with OPC3.
IV. CONCLUSION
Recently we proposed a new approach to constructing point charge water models. The novelty of the approach is that an unconstrained search for optimal parameters of fixed-point charge models is performed in the electrostatically most relevant, low-dimensional sub-space of lowest multipole moments, rather than in the convoluted high-dimensional charges-distances-angles space native to point-charge models. As a result, a global optimum can be reliably located. The global optimization can be difficult, or impossible, to achieve in models constructed based on common parametrization techniques that impose geometry constraints on the location of the point charges, or search in the charges-distances-angles space.
Here we show that the OPC3 model developed based on the approach above gives significantly better agreement with experimental bulk water properties, compared to most commonly used 3-point models. OPC3 is made to reproduce the bulk properties at only one temperature (298.16 K), yet it improves thermodynamic and dynamic properties over a wide range of temperature. A comparison of the OPC3 model with two recent models developed based on completely different parametrization procedures indicates a consensus for the optimal parametrization of 3-point water models. Given that very different parameter optimizations, including a virtually exhaustive search for a global optimum in the “appropriate” electrostatic parameter space, yield essentially the same result, we conclude that the accuracy limits for 3-point rigid, non-polarizable models (within the most common pairwise Coulombic and 12-6 Lennard-Jones framework) have been reached, at least as far as key properties of liquid water are concerned at biologically relevant temperatures and pressures. As modern force-fields are becoming more accurate, with more emphasis on first principles in their development, the community can no longer rely on fortuitous error cancellations between gas-phase and solvent terms: in that respect, water models that describe the liquid phase accurately become even more important.
We emphasize that, operationally, OPC3 is the same as TIP3P or SPCE: users can immediately replace these older models with OPC3 in the same applications that need atomistic water models. We plan to make OPC3 available as an option in AMBER 2017 and have already tested it in AMBER and GROMACS 4.6.5.
Acknowledgments
This work was supported by the NIH No. GM076121. The authors acknowledge Advanced Research Computing at Virginia Tech for providing computational resources and technical support that have contributed to the results reported within this paper. URL: http://www.arc.vt.edu.
REFERENCES
- 1.Gao K., Yin J., Henriksen N. M., Fenley A. T., and Gilson M. K., J. Chem. Theory Comput. , 4555 (2015). 10.1021/acs.jctc.5b00676 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gilson M. K. and Zhou H. X., Annu. Rev. Biophys. Biomol. Struct. , 21 (2007). 10.1146/annurev.biophys.36.040306.132550 [DOI] [PubMed] [Google Scholar]
- 3.Stillinger F. H., Science , 451 (1980). 10.1126/science.209.4455.451 [DOI] [PubMed] [Google Scholar]
- 4.Karplus M. and Kuriyan J., Proc. Natl. Acad. Sci. U. S. A. , 6679 (2005). 10.1073/pnas.0408930102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Dill K. A., Truskett T. M., Vlachy V., and Hribar-Lee B., Annu. Rev. Biophys. Biomol. Struct. , 173 (2005). 10.1146/annurev.biophys.34.040204.144517 [DOI] [PubMed] [Google Scholar]
- 6.Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. , 926 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- 7.Abascal J. L. F. and Vega C., J. Chem. Phys. , 234505 (2005). 10.1063/1.2121687 [DOI] [PubMed] [Google Scholar]
- 8.Horn H. W., Swope W. C., Pitera J. W., Madura J. D., Dick T. J., Hura G. L., and Head-Gordon T., J. Chem. Phys. , 9665 (2004). 10.1063/1.1683075 [DOI] [PubMed] [Google Scholar]
- 9.Mahoney M. W. and Jorgensen W. L., J. Chem. Phys. , 8910 (2000). 10.1063/1.481505 [DOI] [Google Scholar]
- 10.Berendsen H. J. C., Grigera J. R., and Straatsma T. P., J. Phys. Chem. , 6269 (1987). 10.1021/j100308a038 [DOI] [Google Scholar]
- 11.Izadi S., Anandakrishnan R., and Onufriev A. V., J. Phys. Chem. Lett. , 3863 (2014). 10.1021/jz501780a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Case D., Berryman J., Betz R., Cerutti D., Cheatham T. III, Darden T., Duke R., Giese T., Gohlke H., Goetz A., Homeyer N., Izadi S., Janowski P., Kaus J., Kovalenko T., amd Lee A., LeGrand S., Li P., Luchko T., Luo R., Madej B., Merz K., Monard G., Needham P., Nguyen H., Nguyen H., Omelyan I., Onufriev A., Roe D., Roitberg A., Salomon-Ferrer R., Simmerling C., Smith W., Swails J., Walker R., Wang J., Wolf R., Wu X., York D., and Kollman P., Amber 2015, University of California, San Francisco, 2015.
- 13.Brooks B. R., Brooks C. L., Mackerell A. D., Nilsson L., Petrella R. J., Roux B., Won Y., Archontis G., Bartels C., Boresch S., Caflisch A., Caves L., Cui Q., Dinner A. R., Feig M., Fischer S., Gao J., Hodoscek M., Im W., Kuczera K., Lazaridis T., Ma J., Ovchinnikov V., Paci E., Pastor R. W., Post C. B., Pu J. Z., Schaefer M., Tidor B., Venable R. M., Woodcock H. L., Wu X., Yang W., York D. M., and Karplus M., J. Comput. Chem. , 1545 (2009). 10.1002/jcc.21287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pronk S., Pll S., Schulz R., Larsson P., Bjelkmar P., Apostolov R., Shirts M. R., Smith J. C., Kasson P. M., van der Spoel D., Hess B., and Lindahl E., Bioinformatics , 845 (2013). 10.1093/bioinformatics/btt055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Phillips J. C., Braun R., Wang W., Gumbart J., Tajkhorshid E., Villa E., Chipot C., Skeel R. D., Kal L., and Schulten K., J. Comput. Chem. , 1781 (2005). 10.1002/jcc.20289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Guillot B., J. Mol. Liq. , 219 (2002). 10.1016/S0167-7322(02)00094-6 [DOI] [Google Scholar]
- 17.Vega C. and Abascal J. L. F., Phys. Chem. Chem. Phys. , 19663 (2011). 10.1039/c1cp22168j [DOI] [PubMed] [Google Scholar]
- 18.Chaplin M., “Water’s hydrogen bond strength,” in Water and Life (CRC Press, 2010), pp. 69–86. [Google Scholar]
- 19.Izadi S., Aguilar B., and Onufriev A. V., J. Chem. Theory Comput. , 4450 (2015). 10.1021/acs.jctc.5b00483 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Piana S., Donchev A. G., Robustelli P., and Shaw D. E., J. Phys. Chem. B , 5113 (2015). 10.1021/jp508971m [DOI] [PubMed] [Google Scholar]
- 21.Bergonzo C. and Cheatham T. III, J. Chem. Theory Comput. , 3969 (2015). 10.1021/acs.jctc.5b00444 [DOI] [PubMed] [Google Scholar]
- 22.Kale S. and Herzfeld J., J. Chem. Phys. , 084109 (2012). 10.1063/1.3688228 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tu Y. and Laaksonen A., Chem. Phys. Lett. , 283 (2000). 10.1016/S0009-2614(00)01026-5 [DOI] [Google Scholar]
- 24.Laage D. and Hynes J. T., Science , 832 (2006). 10.1126/science.1122154 [DOI] [PubMed] [Google Scholar]
- 25.Demontis P., Guln-Gonzlez J., Masia M., Sant M., and Suffritti G. B., J. Chem. Phys. , 244507 (2015). 10.1063/1.4922930 [DOI] [PubMed] [Google Scholar]
- 26.Izvekov S. and Voth G. A., J. Chem. Phys. , 134105 (2005). 10.1063/1.2038787 [DOI] [PubMed] [Google Scholar]
- 27.Wang L. P., Martinez T. J., and Pande V. S., J. Phys. Chem. Lett. , 1885 (2014). 10.1021/jz500737m [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Fennell C. J., Li L., and Dill K. A., J. Phys. Chem. B , 6936 (2012). 10.1021/jp3002383 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wu Y., Tepper H. L., and Voth G. A., J. Chem. Phys. , 024503+ (2006). 10.1063/1.2136877 [DOI] [PubMed] [Google Scholar]
- 30.Anandakrishnan R., Baker C., Izadi S., and Onufriev A. V., PLoS One , e67715 (2013). 10.1371/journal.pone.0067715 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Schlick T., Collepardo-Guevara R., Halvorsen L., Jung S., and Xiao X., Q. Rev. Biophys. , 191 (2011). 10.1017/S0033583510000284 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Galindo-Murillo R., Robertson J. C., Zgarbov M., Šponer J., Otyepka M., Jurčeka P., and Cheatham I. T. E., J. Chem. Theory Comput. , 4114–4127 (2016). 10.1021/acs.jctc.6b00186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Häse F. and Zacharias M., Nucleic Acids Res. gkw607 (2016). 10.1093/nar/gkw607 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Stone A., The Theory of Intermolecular Forces, International Series of Monographs on Chemistry (Clarendon Press, 1997). [Google Scholar]
- 35.Rick S. W., J. Chem. Phys. , 6085 (2004). 10.1063/1.1652434 [DOI] [PubMed] [Google Scholar]
- 36.Niu S., Tan M. L., and Ichiye T., J. Chem. Phys. , 134501 (2011). 10.1063/1.3569563 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Skinner L. B., Huang C., Schlesinger D., Pettersson L. G. M., Nilsson A., and Benmore C. J., J. Chem. Phys. , 074506 (2013). 10.1063/1.4790861 [DOI] [PubMed] [Google Scholar]
- 38.Gregory J. K., Clary D. C., Liu K., Brown M. G., and Saykally R. J., Science , 814 (1997). 10.1126/science.275.5301.814 [DOI] [PubMed] [Google Scholar]
- 39.Coutinho K., Guedes R., Cabral B. C., and Canuto S., Chem. Phys. Lett. , 345 (2003). 10.1016/S0009-2614(02)02026-2 [DOI] [Google Scholar]
- 40.See supplementary material at http://dx.doi.org/10.1063/1.4960175 E-JCPSA6-145-018630 for the definition of thermodynamic and dynamic bulk properties.
- 41.Mukhopadhyay A., Tolokh I. S., and Onufriev A. V., J. Phys. Chem. B , 6092 (2015). 10.1021/acs.jpcb.5b00602 [DOI] [PubMed] [Google Scholar]
- 42.Kathmann S. M., Kuo I.-F. W., Mundy C. J., and Schenter G. K., J. Phys. Chem. B , 4369 (2011). 10.1021/jp1116036 [DOI] [PubMed] [Google Scholar]
- 43.Donald W. A. and Williams E. R., Pure Appl. Chem. , 2129 (2011). 10.1351/PAC-CON-11-08-15 [DOI] [Google Scholar]
- 44.Tissandier M. D., Cowen K. A., Feng W. Y., Gundlach E., Cohen M. H., Earhart A. D., Coe J. V., and Tuttle T. R., J. Phys. Chem. A , 7787 (1998). 10.1021/jp982638r [DOI] [Google Scholar]
- 45.Schmid R., Miah A. M., and Sapunov V. N., Phys. Chem. Chem. Phys. , 97 (2000). 10.1039/a907160a [DOI] [Google Scholar]
- 46.Marcus Y., Chem. Rev. , 1475 (1988). 10.1021/cr00090a003 [DOI] [Google Scholar]
- 47.Lin Y.-L., Aleksandrov A., Simonson T., and Roux B., J. Chem. Theory Comput. , 2690 (2014). 10.1021/ct500195p [DOI] [PubMed] [Google Scholar]
- 48.Mobley D. L., Barber A. E., Fennell C. J., and Dill K. A., J. Phys. Chem. B , 2405 (2008). 10.1021/jp709958f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Mobley D. L., Bayly C. I., Cooper M. D., Shirts M. R., and Dill K. A., J. Chem. Theory Comput. , 350 (2009). 10.1021/ct800409d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wang J., Wolf R., Caldwell J., Kollman P., and Case D., J. Comput. Chem. , 1157 (2004). 10.1002/jcc.20035 [DOI] [PubMed] [Google Scholar]
- 51.Wang J., Wang W., Kollman P. A., and Case D. A., J. Mol. Graphics Modell. , 247 (2006). 10.1016/j.jmgm.2005.12.005 [DOI] [PubMed] [Google Scholar]
- 52.Jakalian A., Jack D. B., and Bayly C. I., J. Comput. Chem. , 1623 (2002). 10.1002/jcc.10128 [DOI] [PubMed] [Google Scholar]
- 53.Essmann U., Perera L., Berkowitz M. L., Darden T., Lee H., and Pedersen L. G., J. Chem. Phys. , 8577 (1995). 10.1063/1.470117 [DOI] [Google Scholar]
- 54.Darden T., York D., and Pedersen L., J. Chem. Phys. , 10089 (1993). 10.1063/1.464397 [DOI] [Google Scholar]
- 55.Gubskaya A. V. and Kusalik P. G., J. Chem. Phys. , 5290 (2002). 10.1063/1.1501122 [DOI] [Google Scholar]
- 56.Silvestrelli P. L. and Parrinello M., J. Chem. Phys. , 3572 (1999). 10.1063/1.479638 [DOI] [Google Scholar]
- 57.Site L. D., Alavi A., and Lynden-Bell R. M., Mol. Phys. , 1683 (1999). 10.1080/00268979909483112 [DOI] [Google Scholar]
- 58.Leontyev I. and Stuchebrukhov A., Phys. Chem. Chem. Phys. , 2613 (2011). 10.1039/c0cp01971b [DOI] [PubMed] [Google Scholar]
- 59.Vega C., Abascal J. L. F., Conde M. M., and Aragones J. L., Faraday Discuss. , 251 (2009). 10.1039/B805531A [DOI] [PubMed] [Google Scholar]
- 60.Kiss P. T. and Baranyai A., J. Chem. Phys. , 204507 (2013). 10.1063/1.4807600 [DOI] [PubMed] [Google Scholar]
- 61.Te J. A. and Ichiye T., Chem. Phys. Lett. , 219 (2010). 10.1016/j.cplett.2010.09.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Jorgensen W. L. and Jenson C., J. Comput. Chem. , 1179 (1998). [DOI] [Google Scholar]
- 63.English N. J., Mol. Phys. , 1945 (2005). 10.1080/00268970500105003 [DOI] [Google Scholar]
- 64.Vega C., Abascal J. L. F., and Nezbeda I., J. Chem. Phys. , 034503 (2006). 10.1063/1.2215612 [DOI] [PubMed] [Google Scholar]
- 65.Vega C., Sanz E., Abascal J. L. F., and Noya E. G., J. Phys.: Condens. Matter , 153101 (2008). 10.1088/0953-8984/20/15/153101 [DOI] [Google Scholar]
- 66.Bauer B. A. and Patel S., J. Chem. Phys. , 084709 (2009). 10.1063/1.3200869 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Abascal J. L. F. and Vega C., J. Phys. Chem. C , 15811 (2007). 10.1021/jp074418w [DOI] [Google Scholar]
- 68.Mukhopadhyay A., Fenley A. T., Tolokh I. S., and Onufriev A. V., J. Phys. Chem. B , 9776 (2012). 10.1021/jp305226j [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Buckingham A. D., Discuss. Faraday Soc. , 151 (1957). 10.1039/df9572400151 [DOI] [Google Scholar]
- 70.Rashin A. A. and Honig B., J. Phys. Chem. , 5588 (1985). 10.1021/j100272a006 [DOI] [Google Scholar]
- 71.Hirata F., Redfern P., and Levy R. M., Int. J. Quantum Chem. , 179 (1988). 10.1002/qua.560340716 [DOI] [Google Scholar]
- 72.Roux B., Yu H. A., and Karplus M., J. Phys. Chem. , 4683 (1990). 10.1021/j100374a057 [DOI] [Google Scholar]
- 73.Hummer G., Pratt L. R., and Garcia A. E., J. Phys. Chem. , 1206 (1996). 10.1021/jp951011v [DOI] [Google Scholar]
- 74.Bell R. M. L. and Rasaiah J. C., J. Chem. Phys. , 1981 (1997). 10.1063/1.474550 [DOI] [Google Scholar]
- 75.Rajamani S., Ghosh T., and Garde S., J. Chem. Phys. , 4457 (2004). 10.1063/1.1644536 [DOI] [PubMed] [Google Scholar]
- 76.Grossfield A., J. Chem. Phys. , 024506 (2005). 10.1063/1.1829036 [DOI] [PubMed] [Google Scholar]
- 77.Bardhan J. P., Jungwirth P., and Makowski L., J. Chem. Phys. , 124101 (2012). 10.1063/1.4752735 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Scheu R., Rankin B. M., Chen Y., Jena K. C., Ben-Amotz D., and Roke S., Angew. Chem., Int. Ed. , 9560 (2014). 10.1002/anie.201310266 [DOI] [PubMed] [Google Scholar]
- 79.Bardhan J. P. and Knepley M. G., J. Chem. Phys. , 131103 (2014). 10.1063/1.4897324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Reif M. M. and Hünenberger P. H., J. Phys. Chem. B (published online, 2016). 10.1021/acs.jpcb.6b02156 [DOI] [Google Scholar]
- 81.Latimer W. M., Pitzer K. S., and Slansky C. M., J. Chem. Phys. , 108 (1939). 10.1063/1.1750387 [DOI] [Google Scholar]
- 82.Joung I. S. and Cheatham I. T. E., J. Phys. Chem. B , 9020 (2008). 10.1021/jp8001614 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Li P., Song L. F., and Merz J. K. M., J. Chem. Theory Comput. , 1645 (2015). 10.1021/ct500918t [DOI] [PubMed] [Google Scholar]
- 84.Marcus Y., J. Chem. Soc., Faraday Trans. , 2995 (1991). 10.1039/FT9918702995 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1063/1.4960175 E-JCPSA6-145-018630 for the definition of thermodynamic and dynamic bulk properties.