Approaches to reducing photon dose calculation errors near metal implants

Abstract

Purpose:

Dose calculation errors near metal implants are caused by limitations of the dose calculation algorithm in modeling tissue/metal interface effects as well as density assignment errors caused by imaging artifacts. The purpose of this study was to investigate two strategies for reducing dose calculation errors near metal implants: implementation of metal-based energy deposition kernels in the convolution/superposition (C/S) dose calculation method and use of metal artifact reduction methods for computed tomography (CT) imaging.

Methods:

Both error reduction strategies were investigated using a simple geometric slab phantom with a rectangular metal insert (composed of titanium or Cerrobend), as well as two anthropomorphic phantoms (one with spinal hardware and one with dental fillings), designed to mimic relevant clinical scenarios. To assess the dosimetric impact of metal kernels, the authors implemented titanium and silver kernels in a commercial collapsed cone C/S algorithm. To assess the impact of CT metal artifact reduction methods, the authors performed dose calculations using baseline imaging techniques (uncorrected 120 kVp imaging) and three commercial metal artifact reduction methods: Philips Healthcare’s o-mar, GE Healthcare’s monochromatic gemstone spectral imaging (gsi) using dual-energy CT, and gsi with metal artifact reduction software (mars) applied. For the simple geometric phantom, radiochromic film was used to measure dose upstream and downstream of metal inserts. For the anthropomorphic phantoms, ion chambers and radiochromic film were used to quantify the benefit of the error reduction strategies.

Results:

Metal kernels did not universally improve accuracy but rather resulted in better accuracy upstream of metal implants and decreased accuracy directly downstream. For the clinical cases (spinal hardware and dental fillings), metal kernels had very little impact on the dose calculation accuracy (<1.0%). Of the commercial CT artifact reduction methods investigated, the authors found that o-mar was the most consistent method, resulting in either improved dose calculation accuracy (dental case) or little impact on calculation accuracy (spine case). gsi was unsuccessful at reducing the severe artifacts caused by dental fillings and had very little impact on calculation accuracy. gsi with mars on the other hand gave mixed results, sometimes introducing metal distortion and increasing calculation errors (titanium rectangular implant and titanium spinal hardware) but other times very successfully reducing artifacts (Cerrobend rectangular implant and dental fillings).

Conclusions:

Though successful at improving dose calculation accuracy upstream of metal implants, metal kernels were not found to substantially improve accuracy for clinical cases. Of the commercial artifact reduction methods investigated, o-mar was found to be the most consistent candidate for all-purpose CT simulation imaging. The mars algorithm for gsi should be used with caution for titanium implants, larger implants, and implants located near heterogeneities as it can distort the size and shape of implants and increase calculation errors.

1. INTRODUCTION

Many patients receiving external beam radiation therapy have metal implants that can complicate the treatment process. In a survey conducted by the American Association of Physicists in Medicine’s Task Group 63, it was found that 1%–4% of all radiation therapy patients have a prosthetic device that could affect their treatment.¹ This percentage does not include the large number of patients with dental fillings that affect the treatment of head and neck cancer. These metal implants negatively impact the dose calculation accuracy of patient treatment plans. Dose calculation errors associated with metal implants stem from computed tomography (CT) imaging artifacts, as well as limitations in modern dose calculation algorithms.

Metal implants cause well-known imaging artifacts in the CT images that are used for treatment planning.² These metal streak artifacts make it difficult to confidently delineate the tumor and surrounding organs and can also negatively impact dose calculation accuracy. Imaging artifacts result in errors in CT numbers, which propagate to density assignment errors and subsequently to dose calculation errors.^3,4 Recently, commercial metal artifact reduction (AR) methods have become available for CT imaging. One of these commercial solutions, the algorithm for orthopedic implants (o-mar) developed by Philips Healthcare (Cleveland, OH), is becoming increasingly popular for CT simulation imaging in radiation oncology clinics. The o-mar algorithm is an iterative projection modification solution that identifies projection data corrupted by the presence of the metal implant and corrects it based on nearby uncorrupted data.⁵ Another approach to metal artifact reduction is the use of dual-energy CT. Dual-energy CT has many applications for diagnostic imaging,^6–8 but few studies have looked at its use for treatment planning.^9–11 One such dual-energy CT system, GE Healthcare’s Discovery CT750 HD (Milwaukee, WI), acquires dual-energy projection data via fast kilovoltage switching with a single x-ray source. This dual-energy projection data can then be reconstructed to generate virtual monochromatic images at various energy levels (from 40 to 140 keV), called gemstone spectral imaging (gsi). These monochromatic images depict how an object would look if it were imaged using a monoenergetic x-ray source¹² and have reduced beam hardening artifacts in comparison to conventional polyenergetic images.^7,8,13 To further reduce artifacts, GE has developed metal artifact reduction software (mars) specifically for use with gsi monochromatic images.¹⁴ The mars algorithm combines the benefits of virtual monochromatic imaging with the benefits of a dedicated artifact reduction algorithm. While it has been investigated for reducing artifacts caused by an orthopedic prosthesis,^11,14 spinal hardware,^11,15 dental work,¹¹ and fiducial markers,¹⁶ these efforts have been focused on image quality and visualization, which can be very different issues than dose calculation accuracy. Our group, Huang et al.,¹¹ has previously evaluated these commercial artifact reduction methods (o-mar and gsi with and without mars) based on metrics of interest in treatment planning (CT number accuracy, metal size accuracy, and success of artifact reduction) but the dosimetric impact of these artifact reduction methods was not investigated in this study.

In addition to calculation errors associated with imaging artifacts, errors also result from the limited ability of modern dose calculation algorithms to accurately model radiation transport in and near metal implants. The convolution/superposition (C/S) method is the current standard of care in commercial treatment planning systems (TPSs) for photon dose calculations. In the C/S method, the energy released by photon interactions in the patient is described by the TERMA (total energy released per unit mass), while the process of energy deposition via secondary electrons and scattered photons is described by the energy deposition kernel. The TERMA and energy deposition kernel are convolved to calculate the absorbed dose. While C/S methods can accurately calculate the attenuation caused by a metal implant in ideal cases (in which the density and physical dimensions of the implant are well-defined), C/S methods result in dose calculation errors near the metal/tissue interfaces, underestimating the backscatter dose enhancement at the proximal interface and overestimating the dose directly downstream of the implant.¹ Although these errors are typically confined to the local region near metal/tissue interfaces (within a few centimeters of the interfaces), local errors can be as high as 30%, depending on the photon energy and the type of metal.^17,18 One source of this dose calculation error is that for commercial C/S algorithms, the energy deposition kernels are based on photon interactions and scatter in water, and these water-based kernels are simply scaled in dimension based on the local density to perform heterogeneous dose calculations (density scaling approximation). Though this approximation is reasonable for tissue, it is less accurate for materials that differ greatly from water in their atomic composition.¹⁹ Recently, our group, Huang et al.,²⁰ generated kernels for several metals and highlighted that the shape of metal kernels (MK) differed from that of water kernels, indicating that density scaling of water kernels is inadequate to describe photon interactions in metals. We also found, promisingly, that implementing these metal kernels in a commercial algorithm resulted in increased backscatter dose and decreased dose directly downstream of metals.²⁰ Therefore, metal kernels have the potential to correct the calculation errors at metal/tissue interfaces that have been observed with conventional C/S algorithms.

Although we have previously investigated the shape and nature of metal kernels,²⁰ as well as the success of commercial CT artifact reduction methods for reducing artifacts associated with common implants,¹¹ the magnitude of the improvement in dose calculation accuracy due to these strategies is not known. Thus, the purpose of this study was to investigate these error-reduction strategies using several types of phantoms. Both strategies were first evaluated in a simple geometric phantom (with two different metal inserts) and then in two anthropomorphic phantoms. The anthropomorphic phantoms were chosen to mimic clinical cases (a spinal hardware case and a dental fillings case) for which beam arrangements traversing metal implants are difficult to avoid.

2. METHODS AND MATERIALS

2.A. Geometric phantom

2.A.1. Phantom geometry

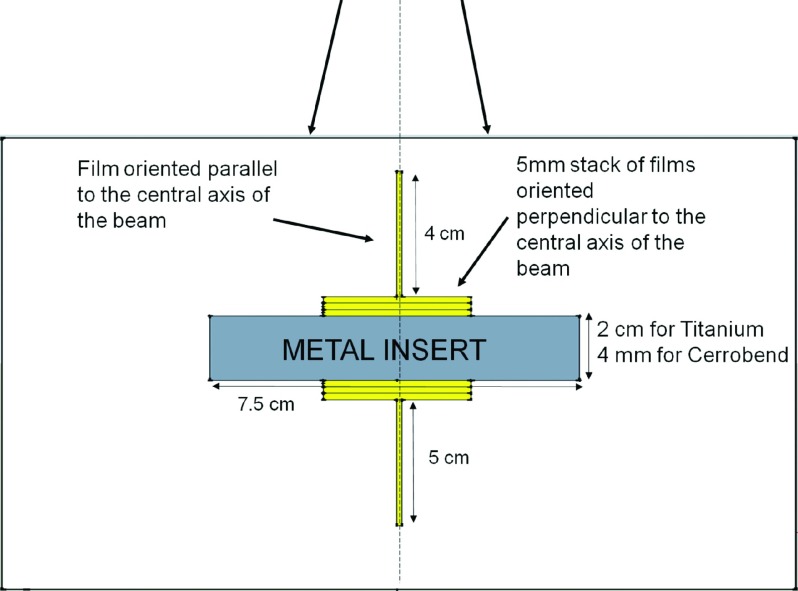
Both strategies (metal artifact reduction methods and metal kernels) were first evaluated using a simple slab phantom. This geometric phantom, illustrated in Fig. 1, was composed of 30 cm × 30 cm high-impact polystyrene slabs with a rectangular cavity that could accommodate a metal insert [either titanium (4.51 g/cm³) or Cerrobend (9.4 g/cm³)]. Both the type of metal and the thickness of the metal implants were chosen to mimic common implants (hip prostheses and spinal hardware for titanium^21–24 and dental fillings for Cerrobend¹⁸). To measure the dose as close as possible to the metal/tissue interfaces with high spatial resolution, we placed stacks of 3 cm × 3 cm EBT2 radiochromic films (Gafchromic, Ashland, Wayne, NJ), totaling 5 mm in thickness and oriented perpendicular to the central axis of the radiation beam, at both the proximal and distal interfaces. To measure the dose further away from metal/tissue interfaces, we placed films upstream and downstream of the stacked films on the central axis, oriented parallel to the beam direction (Fig. 1).

FIG. 1.

Schematics of the measurement phantom used for this study, showing the location of the metal insert along the central axis and the locations of films used to measure the dose upstream and downstream of the metal.

2.A.2. Phantom irradiation and film analysis

The phantom was irradiated using a single gantry angle with the beam pointed vertically down (100 cm source-to-surface distance); the photon beam was a flattened 6-MV photon beam from a Varian Clinac 21iX linear accelerator with a 5 × 5 cm field size. For each of the two metal implants, measurements were repeated three times to create an average percent depth dose curve. The optical density (OD) of the irradiated films was obtained using a CCD Microdensitometer for Radiochromic Film model CCD100 (Photoelectron Corp., Lexington, MA) approximately four days after irradiation. For the interface films oriented perpendicular to the beam, ImageJ (1.44P, National Institute of Health, Bethesda, MD) was used to obtain the mean OD value for a 30 × 30 pixel region of interest (0.76 cm²) centered on the central axis. For the films oriented parallel to the beam, ImageJ was used to obtain average OD values (for a 30-pixel-wide region of interest centered on the central axis) as a function of depth. A background OD value, measured from an un-irradiated film of the same batch, was subtracted from all irradiated films. In order to convert the net OD to absorbed dose, we generated a calibration curve (third-degree polynomial fit) by irradiating films to absorbed doses ranging from 0.5 to 15 Gy. The measured dose from the parallel and perpendicular films was then combined to create a depth dose curve.

2.B. Anthropomorphic phantoms

2.B.1. Phantom design

To mimic a patient with spinal hardware, a thoracic anthropomorphic phantom was used. This thoracic phantom was designed by the Imaging and Radiation Oncology Core (IROC) Houston Quality Assurance Center, formerly known as the Radiological Physics Center, and contains structures representing the heart and lungs.²⁵ For this study, the spine insert of this phantom, which contains structures representing the spinal cord, bone, and esophagus, was replaced with a high impact polystyrene insert that could accommodate two titanium rods (9.5 mm in diameter) to mimic spinal fixation rods, as well as four Exradin A1SL 0.057cc ion chambers (Standard Imaging, Middleton, WI) and an axial film plane that intersected the titanium rods. For some of our measurements, the titanium rods were replaced with high impact polystyrene rods to investigate the level of accuracy that could be achieved with no metal implants (no-metal case).

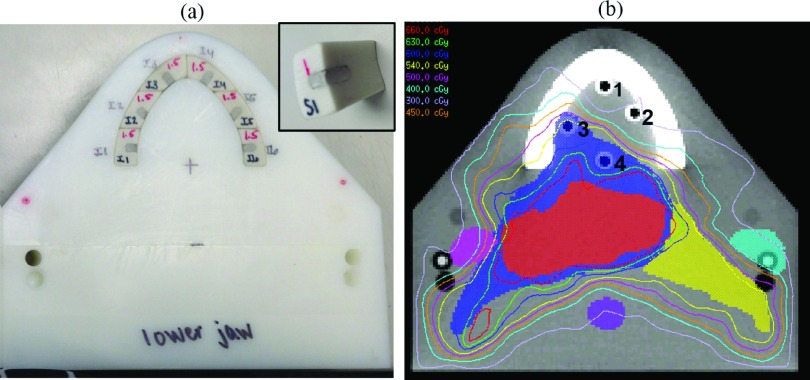
To mimic the case of a head and neck cancer patient with dental fillings, we custom-built a phantom; this phantom contained two halves (mimicking an upper and lower jaw) composed of high impact polystyrene. Each half of the phantom contained tooth structures made of Gammex 450 cortical bone substitute (Middleton, WI). One set of teeth contained cortical bone material only and was used to quantify the level of accuracy that could be achieved without metal (no-metal case), while a second set of teeth was modified to contain Dispersalloy® dental amalgam (Dentsply, Milford, DE). For the set of teeth modified to hold dental amalgam, 12 fillings were simulated, 6 in the upper set of teeth and 6 in the lower set of teeth. The locations and dimensions of the fillings were selected by a dental oncologist to be clinically realistic [Fig. 2(a)]. As with the spine phantom, the dental phantom was designed to accommodate four Exradin A1SL ion chambers at various locations in the oral cavity, as well as an axial film plane between the upper and lower jaws of the phantom.

FIG. 2.

(a) A photograph of the inferior half of the dental phantom illustrating the cortical bone tooth structures that have been modified to hold amalgam fillings. The inset shows an individual tooth structure with dental amalgam. (b) A CT image of the dental phantom (without fillings) illustrating the locations of the three target structures (high, intermediate, and low risk), the parotid glands, spinal cord, and the four ion chambers (numbered) used to measure dose at various locations in the oral cavity. The isodose lines for the resultant treatment plan are also shown.

2.B.2. Treatment planning

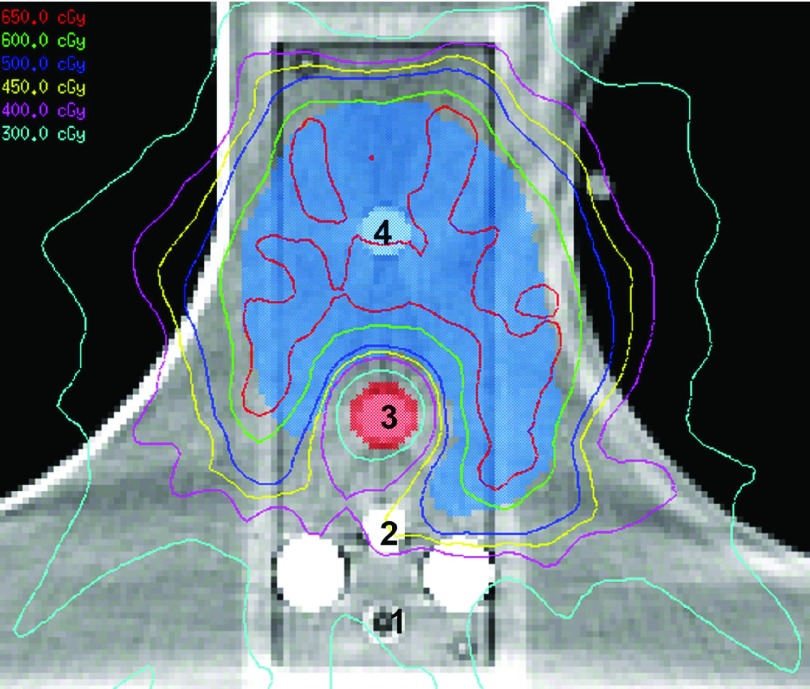
For the two anthropomorphic phantoms, treatment plans were created using the pinnacle ³ v9.0 treatment planning system (Philips Healthcare, Andover, MA) following our institution’s clinical planning procedures. For the spine case, a stereotactic spine radiosurgery (SSRS) treatment plan was created using nine posteriorly incident 6 MV step-and-shoot IMRT beams. The prescribed dose to the planning target volume was 6 Gy in a single fraction (with >90% coverage), and the resulting plan met the dose constraints for the spinal cord, heart, esophagus, skin, and whole lung according to IROC Houston’s credentialing guidelines for the spine phantom. Figure 3 illustrates the location of the target, spinal cord, titanium rods, and the four ion chambers used to measure dose, as well as the isodose lines of the treatment plan for the spine case. For the dental case, a treatment plan was created using nine 6 MV step-and-shoot IMRT beams. Three target structures were created to represent high, intermediate, and low risk disease areas with prescription doses of 6.6, 6.0, and 5.4 Gy, respectively, in one fraction. The parotid glands, oral cavity, brainstem, and spinal cord were contoured and used as avoidance structures in the optimization process [Fig. 2(b)]. For both cases, plans were optimized using pinnacle’s inverse planning direct machine parameter optimization (DMPO) algorithm, and the dose variation across contoured ion chamber cavities was restricted to <2% standard deviation to ensure reliable measurements.

FIG. 3.

A CT image of the spine phantom illustrating the location of the two posterior titanium rods, the four ion chambers (numbered) used to measure dose at various distances from the titanium rods, the target structure, and the spinal cord. The isodose lines for the resultant treatment plan are also shown.

2.B.3. Phantom irradiation and analysis

Phantom irradiation was performed using a Varian Clinac 2100 linear accelerator. For each phantom, four Exradin A1SL ion chambers were used to measure the dose along with an axial EBT2 radiochromic film plane that intersected both the target structure and the metal implants. For each phantom, the treatment plan was delivered twice with the metal implant in place and twice with no metal implants to verify the reproducibility of the measurements and to quantify the level of accuracy that can be achieved in the ideal case without metal.

To compare the measured radiochromic film dose against the calculated dose, film registration and analysis were performed using a matlab-based software program developed at IROC Houston based on the known locations of pinpricks and landmarks in each phantom.²⁵ Once spatial registration was performed, the film-measured dose was normalized to perform relative 2D gamma analysis comparisons against calculated dose using a ±2%/2 mm criteria and a region of interest chosen to highlight calculation differences near the metal implants. The ±2%/2 mm criteria was chosen rather than the more clinically common ±3%/3 mm criteria in order to better highlight dose calculation differences due to artifact reduction methods and metal kernels.

2.C. Imaging

In order to quantify the dosimetric impact of using various CT metal artifact reduction methods, we imaged all phantoms using baseline, uncorrected 120 kVp imaging, as well as o-mar, gsi, and mars artifact reduction imaging. Each phantom in this study was scanned using both a Philips Brilliance (Cleveland, OH) and a GE Discovery CT750 HD (Milwaukee, WI) scanner. For the Philips scanner, the phantom was scanned using a 120 kVp protocol and reconstructed with and without the o-mar algorithm. For the GE scanner, the phantom was scanned using polyenergetic imaging (120 kVp) and with its dual-energy mode, which allowed for monoenergetic image reconstruction. For the gsi dual-energy scan, images were reconstructed at 140 keV, the highest energy available, with and without the mars algorithm. The 140 keV energy level was chosen based on previous work that indicated that 140 keV was more successful than lower energies at reducing metal artifacts.¹¹ In order to draw a fair comparison between the two vendors, we matched the CT protocols based on various acquisition and reconstruction parameters. All protocols for the phantoms used in this study are listed in Table I. All reconstructed images were 12-bit depth images. In summary, phantom images were obtained using baseline, uncorrected imaging methods (“Philips 120 kVp” and “GE 120 kVp”) and the artifact reduction methods under investigation (“o-mar,” “gsi 140 keV,” and “mars 140 keV”).

TABLE I.

Scan protocols for phantom scans using the Philips Brilliance and the GE Discovery CT750 HD CT scanners. All protocols are helical scans.

Phantom insert	Protocol	Pitch	mA	Tube rotation time (s)	Filter	Slice thickness (cm)	DFOV (cm)	Recon kernel	CTDIvol (mGy)
Titanium geometric phantom	Philips 120 kVp	0.938	231	0.75	B	3.0	50	B	12.3
	GE 120 kVp	0.984	265	0.6	Medium	2.5	50	Standard	13.2
	GE gsi preset #41	0.984	360	0.6	Medium	2.5	50	Standard	13.1
Cerrobend geometric phantom	Philips 120 kVp	0.688	206	0.75	B	3.0	50	B	26.7
	GE 120 kVp	0.516	280	0.6	Medium	2.5	50	Standard	26.8
	GE gsi preset #32	0.516	375	0.6	Medium	2.5	50	Standard	26.4
Spine phantom	Philips 120 kVp	0.938	375	0.75	B	1.5	50	B	19.9
	GE 120 kVp	0.969	440	0.5	Medium	1.25	50	Standard	20.3
	GE gsi preset #35	0.969	630	0.5	Medium	1.25	50	Standard	20.2
Dental phantom	Philips 120 kVp	0.688	202	0.75	B	3.0	50	B	26.2
	GE 120 kVp	0.516	375	0.6	Medium	2.5	50	Standard	26.0
	GE gsi preset #32	0.516	290	0.6	Medium	2.5	50	Standard	26.4

2.D. M3D dose calculations

To quantify dose calculation accuracy, we compared measured dose with dose calculations performed using Mobius3D v1.3.1 (Mobius Medical Systems, Houston, TX), a commercial TPS verification tool that calculates dose using a collapsed cone C/S algorithm similar to pinnacle’s collapsed cone algorithm (CCC).²⁶ For heterogeneity corrections, CT number-to-density conversion curves (for both 120 kVp polyenergetic images and 140 keV monoenergetic images) were created for the M3D system using the RMI 467 tissue characterization phantom (Gammex, Middleton, WI). Because this study sought to assess the improvement in dose calculation accuracy due to the application of different metal artifact reduction methods, we wanted the density mapping of the metal implants to be consistent across the different imaging techniques. Therefore, for all dose calculations, the saturated Hounsfield unit (HU) values in the images were mapped to the known density of the metal implants, essentially performing a density override for the metal region in the CT images.

To assess how metal kernels impact dose calculation accuracy, we implemented metal kernels into M3D’s collapsed cone C/S algorithm. For dose calculations with the titanium implants (geometric phantom and spine case), titanium kernels were used. For dose calculations with the Cerrobend implant and the dental case, silver kernels were used because this is a high-Z material that falls within the range of various dental amalgams in terms of atomic number and physical density and therefore was selected to be a reasonable representative for such high-Z metals.^27–29 These metal energy deposition kernels were simulated using the EGSsnrc Monte Carlo system, characterized in previous work,²⁰ and implemented in the M3D algorithm using a density threshold. For voxels with an assigned density greater than the threshold value (e.g., 4.0 g/cm³), metal kernels were used to describe the energy deposition for energy released from those voxels. For voxels with assigned density less than the metal threshold, water kernels were used. Kernel density scaling was still employed for voxels with a density that did not exactly match one of the two kernel materials (water or metal).

2.E. Evaluation of dose calculation accuracy

2.E.1. Geometric phantom

For the geometric phantom, M3D-calculated dose (using a uniform 1.5 mm dose grid) was compared to the measured dose, and a mean % error was reported for both the upstream region (from d_max to the proximal interface) and the downstream region (from the distal interface to the deepest point of measurement, approximately 5 cm beyond the metal implant). To investigate the impact of using commercial metal artifact reduction methods, the dose calculation error obtained with artifact-corrected images was compared to that of uncorrected CT images. In order to study the impact of implementing metal kernels for photon dose calculations without the confounding effects of the imaging artifacts, we chose to perform dose calculations using metal kernels in an “ideal” phantom geometry. This ideal geometry was created using CT images acquired as described in Sec. 2.C but modified with density overrides for the metal insert and the streak artifacts in the high-impact polystyrene portion of the phantom, based on the known dimensions of the phantom geometry and the known densities of the materials. The dose was then calculated using the M3D collapsed cone algorithm using both the traditional implementation of density scaling of water kernels and the novel implementation using metal kernels. For comparison, the dose for these ideal phantom plans was also calculated using the pinnacle ccc and the eclipse aaa algorithms (Varian Medical Systems, Palo Alto, CA).

2.E.2. Anthropomorphic phantoms

M3D dose calculations were performed for both phantom cases (spine and dental) using a uniform 1.5 mm dose grid size. For each phantom, the impact of both error-reduction strategies was investigated. Dose calculations were performed using uncorrected imaging (“baseline” calculation) and metal artifact reduction methods (o-mar, gsi, and mars), both with water kernels only and repeated with water and metal kernels. Thus, for each metal artifact reduction method studied, there were four dose calculations to compare in terms of accuracy (baseline calculation, baseline with metal kernels, artifact reduction calculation, and artifact reduction with metal kernels).

3. RESULTS

3.A. Geometric phantom

3.A.1. Metal artifact reduction study

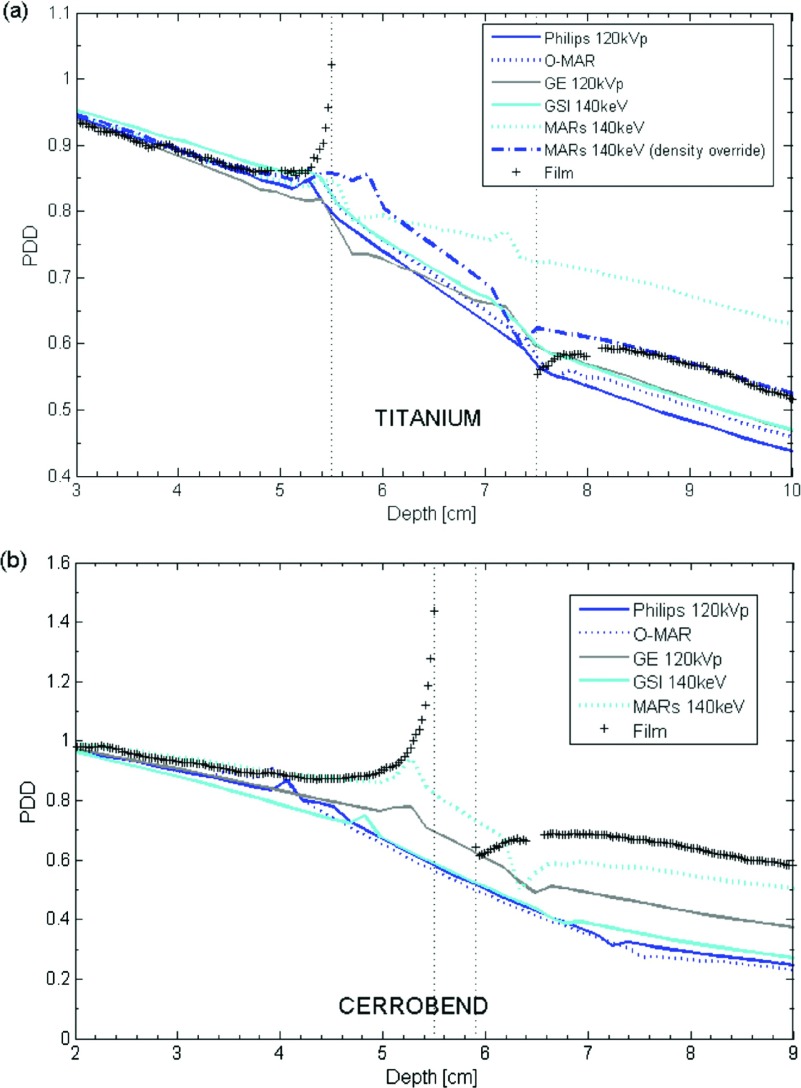
As described in Sec. 2.E.1, the dosimetric impact of CT metal artifact reduction methods was investigated by acquiring images of the geometric phantom with titanium and Cerrobend inserts using both uncorrected imaging techniques (Philips 120 kVp and GE 120 kVp) and metal artifact reduction methods (o-mar, gsi 140 keV, and mars 140 keV). We then performed depth dose calculations using these image sets (Fig. 4). On the uncorrected CT scans, substantial errors were observed. The average error upstream was only 1%–2% for titanium and 7%–10% for Cerrobend, but at the interface the dose error exceeded 20% for titanium and 50% for Cerrobend. Large systematic errors were seen in the downstream region, on average more than 10% for titanium and more than 30% for Cerrobend. For the repeated film measurements, the uncertainty in the mean absolute percent error is estimated to be approximately 0.3%.

FIG. 4.

Percent depth dose (PDD) curves calculated for (a) titanium and (b) Cerrobend using baseline imaging techniques (Philips 120 kVp and GE 120 kVp) and metal artifact reduction methods (o-mar, gsi 140 keV, and mars 140 keV). The images show that the dose calculations largely fail to describe the dose effects at the interface, but also highlight that the position of the interface is substantially displaced from the true interface because of artifacts in the CT image. (a) also illustrates the effect of overriding the incorrect low-density values assigned to the inner portion of the titanium implant caused by the mars algorithm.

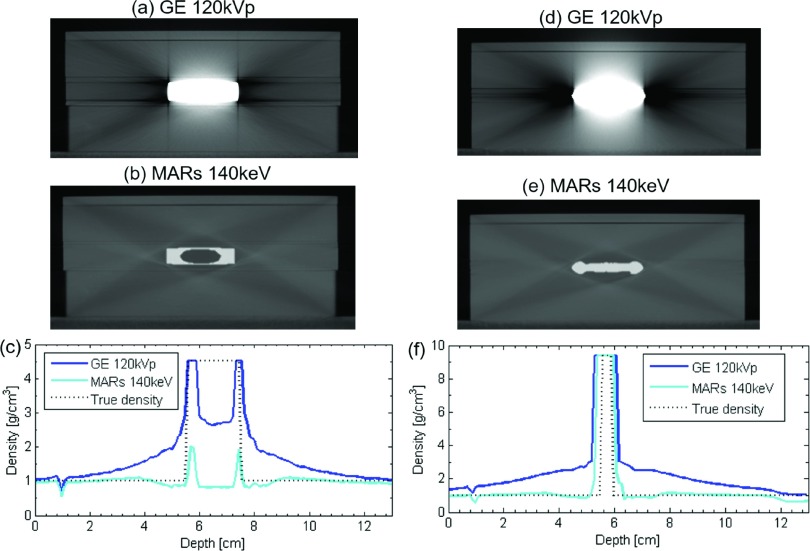
Application of the artifact reduction methods often provided some benefit, but sometimes produced substantially erroneous results. For the titanium insert, o-mar was successful in reducing the error in the downstream region (from 15.0% to 11.1%) in comparison to uncorrected imaging. gsi 140 keV imaging had no effect on the overall error in the upstream region or the downstream region. The mars algorithm was successful in reducing error in the upstream region; however, it greatly increased the error in the downstream region in comparison to uncorrected imaging (from 9.0% to 21.8%). This large increase in the error arose from the artificial creation of a low-density pocket within the titanium implant by the mars algorithm [Fig. 5(b)]. If no manual intervention was performed to override the incorrect densities assigned to this pocket [Fig. 5(c)], the attenuation caused by the titanium implant was highly underestimated, resulting in a substantial overestimation of dose downstream of the metal. However, when the correct density was assigned to the pocket, the dose calculation accuracy in the downstream region was greatly improved, yielding a mean absolute error of 2.0% [Fig. 4(a)]. This accuracy could be achieved because the mars algorithm was otherwise successful at reducing streak artifacts and at accurately representing the external dimensions of the titanium implant. The streak artifacts in the uncorrected, baseline images of the titanium implant result in an overestimation of the density along the central axis, with this overestimation getting worse as one gets closer to the metal implant, while the mars algorithm corrected this behavior [Fig. 5(c)].

FIG. 5.

(a) and (d) show uncorrected 120 kVp images of the titanium and Cerrobend phantom configurations, respectively, while (b) and (e) show the same image slice using mars 140 keV imaging, illustrating the artificial introduction of a low-density pocket within the titanium insert in (b). (c) and (f) show the density assignment along the central (vertical) axis using both imaging methods, along with the true density.

The 4 mm-thick Cerrobend implant was a much more challenging case for dose calculation in general. Most of the imaging methods overestimated the attenuation caused by the Cerrobend implant as seen in Fig. 4(b). This overestimation of attenuation was caused in part by the metal streak artifacts, which artificially inflated density assignment values near the metal, but the dominant factor was actually the misrepresentation of the metal implant’s size in the images. Most of the imaging methods, including artifact reduction methods, severely overestimated the thickness of the Cerrobend implant and thus overestimated the attenuation caused by the metal. The only artifact reduction method that was able to reduce dose calculation errors was the mars algorithm. In comparison to GE baseline imaging, which overestimated the thickness of the Cerrobend [Fig. 5(d)], the mars algorithm reduced the severe artifacts caused by the high-density metal [Fig. 5(e)] and more accurately represented the thickness of the implant [Fig. 5(f)]. Accordingly, in the upstream region, mars reduced the mean absolute % error from 7.3% to 2.5% in comparison to uncorrected imaging, while in the downstream region, mars reduced the error from 33.0% to 14.7%. mars did not artificially create a low-density pocket in the Cerrobend insert, probably because the insert was much thinner than the titanium insert.

3.A.2. Metal kernel study

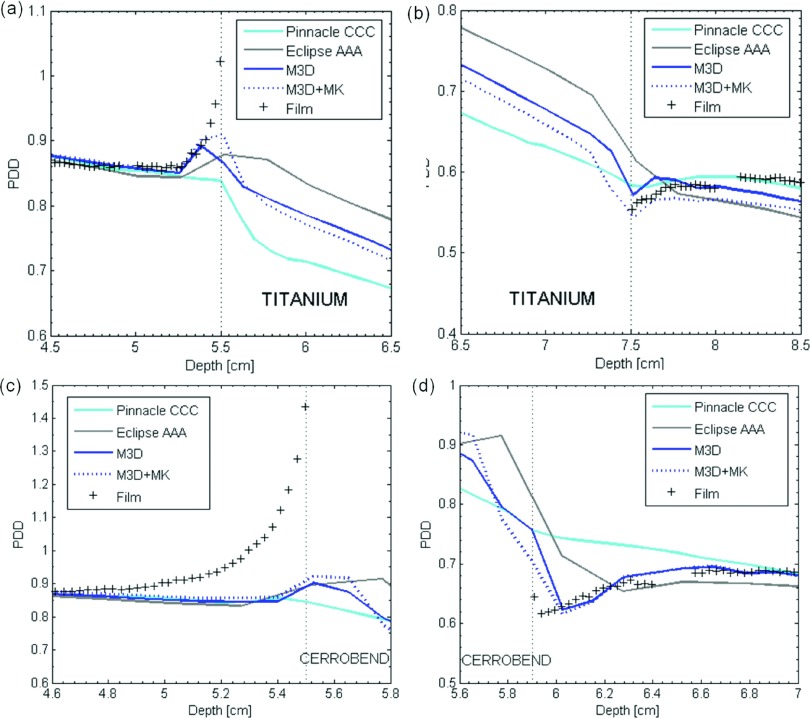
The dosimetric impact of implementing metal kernels for the geometric phantom without the confounding effects of imaging artifacts was investigated using a virtual (i.e., ideal) phantom geometry. The percent depth dose curves for M3D dose calculations with and without metal kernels, along with the dose calculated with pinnacle’s CCC and Eclipse’s AAA algorithms, are shown in Fig. 6. The mean absolute % errors in the 1-cm region upstream of the proximal interface (e.g., from 4.5 to 5.5 cm for titanium) and the 1-cm region downstream of the distal interface (e.g., from 7.5 to 8.5 cm for titanium) are listed in Table II for both metals. Based on repeated film measurements, the estimated uncertainty in the % absolute error is estimated to be approximately 0.1%. These data reveal that metal kernels generally improved dose calculation accuracy in the upstream region but generally worsened accuracy in the downstream region. It can also be seen from Table II that metal kernels generally yielded more accurate calculations as the dose grid size decreased.

FIG. 6.

Percent depth dose (PDD) curves for dose calculations performed using M3D with (“M3D+MK”) and without (“M3D”) metal kernels using a 1.25-mm dose grid, pinnacle ccc, and eclipse aaa at (a) the proximal interface of the titanium insert, (b) the distal interface for titanium, (c) the proximal interface for Cerrobend, and (d) the distal interface for Cerrobend.

TABLE II.

The mean absolute % error between calculated and film-measured dose for M3D calculations performed with and without MK, pinnacle ccc, and eclipse aaa. Dose calculations were performed for virtual (ideal) phantom geometries. The % error is reported for the region 1 cm upstream of the proximal interface and the region 1 cm downstream of the distal interface.

		Titanium: Mean absolute % error		Cerrobend: Mean absolute % error
Dose calculation method	Dose grid size (mm)	Upstream 1 cm	Downstream 1 cm	Upstream 1 cm	Downstream 1 cm
M3D (no MK/MK)	1.25	1.5/1.2	2.4/3.7	9.2/8.2	2.6/2.0
M3D (no MK/MK)	1.5	1.4/1.8	2.2/6.1	9.0/7.5	2.8/6.6
M3D (no MK/MK)	3.0	1.7/1.8	4.5/7.9	9.4/8.2	3.7/4.3
pinnacle ccc	1.5 × 1.5 × 1.0	2.6	1.6	9.2	9.2
eclipse aaa	2.5	2.2	5.0	9.8	6.3

3.B. Anthropomorphic phantoms

3.B.1. Spine phantom

The results for ion chamber measurements for the SSRS treatment plan delivered to the spine phantom are listed in Table III. The reproducibility of repeat ion chamber measurements was within 0.5% for all measurement locations, and this repeatability was taken as the precision in the measurements. Chambers 3 and 4, located in the spinal cord and target, respectively, were minimally affected by the presence of the metal rods (<0.6% impact on the measured dose). Additionally, the % error (between calculated and measured dose) with versus without metal were within 0.2% for both chambers, indicating that the treatment planning system was able to calculate the dose to these chambers equally well regardless of the presence of the metal. The two chambers (1 and 2) that were closest to the titanium rods were more affected by the presence of the metal implants. Chamber 1 showed no actual impact on the dose from the metal rods (the measured dose was effectively unchanged); however, the dose calculation accuracy worsened from 3.5% error to 4.2% error. Chamber 2 showed a decrease in measured dose (by 2.7%) caused by attenuation in the titanium rods and an increase in calculation error caused by the rods (from 1.3% up to 1.8%). We chose to focus our analysis on chambers 1 and 2 since both showed a decrease in calculation accuracy caused by the metal (increases in error by 0.7% and 0.5%, respectively).

TABLE III.

Ion chamber results for the spine and dental phantoms (averaged over 2 repeat irradiations). For each chamber location, the ratio of the measured dose with metal implants in place to the dose measured without metal is presented to highlight the true impact of the metal. Additionally, the % error between calculated (Philips 120 kVp uncorrected imaging) and measured doses are shown for both the no-metal case and the case with metal implants.

			% error(calculated vs measured)
Phantom	Ion chamber	Measured ratio (with metal/no metal)	No metal	With metal
Spine phantom	1	0.999	3.5	4.2
	2	0.973	1.3	1.8
	3	1.006	1.8	1.6
	4	1.002	−0.8	−0.7
Dental phantom	1	0.999	3.0	−11.5
	2	1.004	1.7	−7.5
	3	0.977	−0.9	−10.2
	4	0.966	0.8	−0.3

For chambers 1 and 2, the percent error for dose calculations performed with metal artifact reduction and/or metal kernels is listed in Table IV. The artifact reduction methods and metal kernels generally did not have a large or even positive effect on dose calculation accuracy. In fact, o-mar and gsi typically caused small increases in error (although they were generally <1%). More drastically, the mars algorithm decreased accuracy for both measurement locations. For chamber 2, mars increased the error from 2.3% to 5.0% in comparison to uncorrected images. The mars algorithm has previously been shown to underestimate the size of titanium implants.^11,14 Therefore, the observed overestimation in dose was likely the result of an underestimation of the size of the titanium rods in the mars images and a subsequent underestimation of attenuation caused by the rods. Using metal kernels in the dose calculations also had a relatively small effect on accuracy (generally <0.5%), although improvements in accuracy were seen for chamber 2. In combining the two error-reduction strategies, some successes were found (particularly for chamber 2 with gsi), but results were routinely comparable or slightly worse than using uncorrected 120 kVp images with water kernels.

TABLE IV.

Errors between calculated and ion chamber measured dose for the spine case. The baseline calculation error for uncorrected CT imaging is listed as well as the absolute change in calculation error when CT artifact reduction methods are used (o-mar, gsi, and mars), when metal kernels are used (MK), and when artifact reduction and metal kernels are used together for the dose calculation. Positive results indicate increased errors (i.e., worse performance).

	Chamber 1	Chamber 2	Average
Baseline % errora	4.3%	2.0%	3.2%
Absolute change in % error
o-mar	+0.7	+0.1	+0.4
gsi 140 keV	+0.7	−0.4	+0.2
mars 140 keV	+1.4	+2.7	+2.1
MK	+0.1	−0.3	−0.1
O-MAR + MK	+0.9	−0.1	+0.4
GSI + MK	+0.8	−0.5	+0.2
MARS + MK	+1.4	+2.7	+2.1

^aAverage % error based on two uncorrected CT imaging methods (GE 120 kVp and Philips 120 kVp).

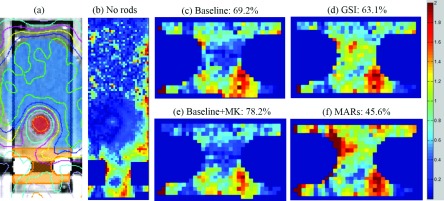
To spatially evaluate the agreement between calculated and measured dose, particularly in closer proximity to the titanium rods, gamma analysis was also performed for an axial film plane that intersected the titanium rods. Metal kernels affect the dose calculation near metal/tissue interfaces,²⁰ and the streak artifacts in the spine phantom were the most severe medial to the two titanium rods. Thus, we focused our analysis on the portion of the film in close proximity to the titanium rods [Fig. 7(a)]. For the two films irradiated with the titanium rods in the spine phantom, the average results are reported in Table V. Although most of the changes in percentage of pixels passing were not significant based on the reproducibility of our repeat films (approximately 5% pixels passing standard deviation), some of the more illustrative results are shown in Fig. 7. For the film measurements performed with titanium rods in place, gsi and mars decreased passing rates, while metal kernels increased the passing rate. The largest change was seen for the mars dose calculation, in which mars resulted in a decrease in the percentage of pixels passing from 69.2% to 45.6%. These results broadly agree with our ion chamber results that showed small changes from the application of o-mar or gsi, small changes (but improvement) from the application of metal kernels, and a substantial decrease in dose calculation accuracy from the application of mars.

FIG. 7.

Film gamma analysis results for the spine case. (a) shows the location of the region of interest (in orange) used for gamma analysis in (c)–(f), (b) shows the results for the entire film plane using ±3%/3 mm criteria for an irradiation without metal rods (86.6% pixels passing), and (c)–(f) show the results for an irradiation with titanium rods using ±2%/2 mm criteria for a sample of dose calculations using artifact reduction methods (gsi and mars) and metal kernels (MK). The baseline dose calculation was performed using GE uncorrected 120 kVp images.

TABLE V.

The mean percentages of pixels passing for gamma analysis (±2%/2 mm criteria) comparing film-measured dose to calculated dose for two repeated film measurements (with metal implants in place). Comparisons were performed for the four possible combinations of the two error-reduction strategies (CT AR methods and MK).

		Mean % pixels passing
Phantom	AR method	Baselinea	AR	Baseline + MK	AR + MK
Spine phantom	o-mar	81.0	77.9	82.9	80.2
	gsi 140 keV	74.3	62.4	80.7	60.3
	mars 140 keV	74.3	43.5	80.7	46.4
Dental phantom	o-mar	69.8	72.0	70.5	71.8
	gsi 140 keV	68.1	67.3	69.0	66.7
	mars 140 keV	68.1	71.6	69.0	70.4

^aBaseline imaging was Philips 120 kVp for o-mar and GE 120 kVp for both gsi 140 keV and mars 140 keV imaging.

3.B.2. Dental phantom

The ion chamber results for the base of tongue treatment plan delivered to the dental phantom are listed in Table III. The reproducibility of repeat ion chamber measurements was within 0.7% for all measurement locations. In comparison to the spine phantom, the amalgam fillings had a greater effect on the measured dose, decreasing the dose by 2.3%–3.4% in the target (chambers 3 and 4). Furthermore, the dose calculation accuracy was more affected by the presence of the fillings than the titanium spinal rods. While the dose calculation was within 3% when no metal was present, the calculation errors were as high as 12% when the fillings were present. Interestingly, for chamber 4, the measurement location in which the fillings decreased the dose the most, the calculation accuracy was very good (error <1.0%) both with and without metal. In contrast, the chambers that were actually less affected by the fillings had substantial errors (>5.0%) introduced into the dose calculations. Since all four chambers either had decreased measured dose or decreased calculation accuracy due to the metal fillings, all ion chamber locations were analyzed.

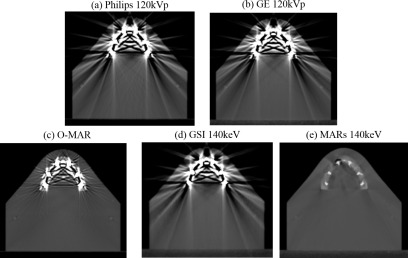
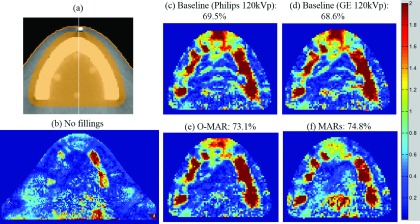
The percent error for various dose calculations performed with artifact reduction methods and/or metal kernels for the dental phantom with fillings is listed in Table VI. In comparison to baseline (with metal), uncorrected CT images, o-mar was able to reduce errors for the three chamber locations that had the largest calculation errors, and increased the accuracy by 1.8% on average over all four chambers. gsi also generally reduced errors, though the gains in calculation accuracy were more modest than those observed with o-mar. mars was the most successful of the three methods for reducing calculation errors based on our ion chamber results, increasing the accuracy by 4.0% averaged over all four chambers, and resulting in errors <4.0% for all four chamber locations. The success of the mars algorithm can be explained by looking at the CT images of the dental phantom shown in Fig. 8. In comparison to the other artifact reduction methods, mars resulted in not only excellent artifact reduction but also better visualization of the size of the individual amalgam fillings [Fig. 8(e)]. Though o-mar showed some artifact reduction [Fig. 8(c)], residual artifacts still existed, making it difficult to discern the size of the fillings and the bone/metal and bone/tissue interfaces. Thus, by using mars images for the dose calculation, the attenuation caused by the fillings was more accurately calculated and not overestimated as much as with the other imaging methods. For the dental phantom, use of metal kernels in the dose calculation algorithm generally improved accuracy, though again the magnitude of the effect was generally small for our ion chamber measurements (≤0.6%).

TABLE VI.

Errors between calculated and ion chamber measured dose for the dental case. The baseline calculation error for uncorrected (with metal) CT imaging is listed as well as the absolute change in calculation error when CT artifact reduction methods are used (o-mar, gsi, and mars), when metal kernels are used (MK), and when artifact reduction and metal kernels are used together for the dose calculation.

	Chamber 1	Chamber 2	Chamber 3	Chamber 4	Average
Baseline % errora	−10.8%	−6.2%	−9.2%	−0.8%	−6.7%
Absolute change in % error
o-mar	−3.4	−2.6	−2.1	+0.9	−1.8
gsi 140 keV	−1.4	−0.2	+0.8	−0.9	−0.4
mars 140 keV	−7.9	−4.7	−6.0	+2.7	−4.0
MK	−0.6	−0.2	+0.1	−0.0	−0.2
O-MAR + MK	−4.1	−2.8	−1.8	+0.8	−2.0
GSI + MK	−2.0	+0.1	+0.9	−0.9	−0.4
MARS + MK	−7.9	−4.7	−5.7	+2.7	−3.9

^aAverage % error based on two uncorrected CT imaging methods (GE 120 kVp and Philips 120 kVp).

FIG. 8.

CT images of the dental phantom with amalgam fillings (window level = 500 and window width = 2500) using baseline, uncorrected imaging methods (Philips 120 kVp and GE 120 kVp) and artifact reduction methods (o-mar, gsi 140 keV, and mars 140 keV).

Table V shows the results of gamma analysis for a region of interest that contains the fillings, the bone material, and the oral cavity of the dental phantom [Fig. 9(a)]. This region of interest was chosen in order to highlight the area most affected by the streak artifacts and the region where metal kernels were most likely to affect the dose calculation. Though most of the changes in percentage of pixels passing were small, Fig. 9 highlights areas in which artifact reduction improved the agreement between calculated and measured dose. The gamma index maps for both o-mar and mars showed improved agreement in comparison to uncorrected images, particularly anteriorly and near the teeth [Figs. 9(e) and 9(f)]. Furthermore, when the dose was calculated using uncorrected images, disagreement was seen at the locations of the streaks in the oral cavity [Figs. 9(c) and 9(d)]; these streaks of disagreement were improved when o-mar and mars were used for dose calculations.

FIG. 9.

Film gamma analysis results for the dental phantom. (a) shows the location of the region of interest (in orange) used for gamma analysis in (c)–(f), (b) shows results for the entire film plane using ±3%/3 mm criteria for an irradiation without fillings (91.7% pixels passing), and (c)–(f) show results using ±2%/2 mm criteria for an irradiation with fillings for uncorrected, baseline images and artifact reduction methods (o-mar and mars).

4. DISCUSSION

In this study, we investigated the dosimetric impact of several commercial CT metal artifact reduction methods and the impact of implementing metal energy deposition kernels in a commercial collapsed cone C/S algorithm. Both strategies for reducing dose calculation errors for patients with metal implants were evaluated using a simple slab phantom geometry as well as two anthropomorphic phantoms representing clinical scenarios, the case of a patient with spinal hardware receiving SSRS and the case of a patient with dental fillings receiving head and neck radiation therapy. Our results indicate that although both strategies can improve dose calculation accuracy in some cases, neither is globally effective, and users should be aware of the scenarios in which these strategies may worsen dose calculation accuracy.

In general, we found that the higher Z materials (Cerrobend and dental amalgam fillings) created more severe artifacts than lower Z titanium and therefore there were larger dose calculation errors associated with the higher Z metals. In investigating how different metal artifact reduction methods affected calculations errors, we found that there were two sources of errors that stem from metal artifacts. The first is the effect of the streak artifacts which caused fairly local dose calculation errors [e.g., in the oral cavity in Figs. 9(c) and 9(d)]. The second is metal size representation in the CT images. For very dense metals such as Cerrobend, the CT numbers in the image can saturate, not only inside the metal itself but also in nearby pixels. This blooming or spreading of saturated CT numbers causes the physical dimensions of the implant to be overestimated. If there is no prior knowledge of the dimensions of the implant that can be used to perform manual density overrides, and if extended bit-depth CT images are not available, this overestimation of metal size can lead to large dose calculation errors. The dosimetric impact of metal size accuracy was especially evident from our geometric phantom data with the Cerrobend insert, in which uncorrected CT images resulted in systematic errors greater than 30% in the downstream region. Surprisingly, in our clinical cases, the largest dosimetric impact due to the metal artifact reduction algorithms stemmed not from successful artifact reduction but rather from an improvement in metal size accuracy. Proper representation of the size of the metal implants was highly variable between approaches and made a substantial difference for dose calculation accuracy. In the most dramatic instance, we observed that the mars algorithm caused a low-density pocket in the center of a rectangular titanium implant [Fig. 5(b)]. This behavior of the mars algorithm to create low-density pockets¹¹ and distort the size/shape of metal implants has been documented previously.^14–16 In our study, use of the mars algorithm for this rectangular titanium insert resulted in higher dose errors than use of uncorrected CT images, when the low-density pocket was left uncorrected. For the clinical spinal case, the mars algorithm also resulted in a substantial increase in dose calculation errors, more than doubling the error in one measurement location (from 2.3% to 5.0%), due to an underestimation of the titanium rod diameter in the mars images.^11,14 Based on these data, it is not advisable to use the mars algorithm with titanium implants because it can lead to an overestimation of dose downstream of metal and thus an overestimation of target coverage. In contrast, the mars algorithm resulted in substantial improvements in metal thickness accuracy and dose calculation accuracy for our Cerrobend insert and the clinical dental case, indicating that the success of mars may be dependent on the type of metal and the size of the implant, a feature that may be unattractive given the wide variety of implants that can be encountered in radiation oncology.

In summarizing the success of the artifact reduction methods in this study, the mars algorithm resulted in the largest dosimetric impact of the three methods investigated, though the results were inconsistent. mars increased calculation errors for titanium (both for the geometric phantom and the clinical spine case) while decreasing errors for the Cerrobend insert and the dental case. o-mar was a more consistent artifact reduction method, either decreasing errors (dental case) or having little effect on calculation accuracy (spine case), although its benefit in the dental case was much less pronounced than for the mars algorithm. o-mar has been investigated in the literature for radiation therapy treatment planning without any findings indicating that it is detrimental for dose calculations.^30,31 The last metal artifact reduction method, gsi without mars, had very little effect on calculation accuracy and was not successful in reducing artifacts associated with high-Z dental fillings. Though gsi dual-energy CT imaging may not be as successful as a dedicated artifact reduction algorithm, such as o-mar or mars, dual-energy CT nonetheless has many applications in radiation therapy aside from metal artifact reduction and still has the potential to improve the accuracy of treatments in other ways.^10,32,33

In summary, our results indicate that of the three methods investigated, o-mar is the safest option for all-purpose metal artifact reduction in CT simulation imaging. mars showed the greatest potential, but had serious limitations. mars was developed primarily for diagnostic imaging and has not been fine-tuned for CT simulation and radiotherapy purposes. Thus, mars should be used with great caution, especially for titanium implants, larger implants, and implants located near heterogeneities, as it can lead to metal distortion and introduce secondary artifacts.¹¹

In addition to CT metal artifact reduction methods, we also investigated the dosimetric impact of implementing metal kernels in a commercial collapsed cone C/S dose calculation algorithm. We found that the dosimetric impact of metal kernels is a local effect; the dose differences between dose calculations with and without metal kernels only extend up to 1 cm from the interface. Unfortunately, metal kernels did not universally improve dose calculation accuracy. In an ideal phantom geometry without artifacts, metal kernels generally improved the accuracy at the proximal interface but worsened accuracy at the distal interface in comparison to dose calculations using water kernels only. For our two clinical cases, we typically found some benefit from using metal kernels, although the dosimetric impact was generally small (<1.0%). However, the maximum dosimetric benefit of metal kernels may not have been achieved in these clinical cases because the imaging artifacts resulted in messy and sometimes undiscernible metal/tissue interfaces and the many beam angles in these clinical intensity-modulated plans washed out the effects of the kernels to some extent. Despite the limited success of metal kernels in this study, there are clinical benefits to further pursuing more accurate calculation near metal implants. Modern treatment planning systems are not able to predict the backscatter dose enhancement due to metals.²¹ For cases in which spinal hardware is close to the spinal cord, this limitation can lead to an underestimation of dose to the spinal cord, the dose-limiting structure for spinal treatments. For dental work, the local dose enhancement can lead to adverse reactions in the oral mucosa, and more accurate dose calculations could predict and prevent these painful oral complications.²⁷ It is also important to note that we observed that several commercial algorithms (Mobius3D, pinnacle ccc, and eclipse aaa) handled the sharp metal/tissue interfaces differently. It is possible that markedly different results would be obtained if metal kernels were implemented into the pinnacle ccc algorithm or the eclipse aaa algorithm.

A limitation of this study is that other approaches to improving calculation accuracy for patients with metal implants, namely the use of other calculation methods (e.g., Monte Carlo³⁴ and Grid-Based Boltzmann Solvers³⁵) and MV imaging,³⁶ were not investigated. Another limitation is that in our evaluation of various commercial artifact reduction algorithms we chose clinical cases in which treatment beams traverse metal implants. For both the case of spinal hardware and dental fillings, this choice is in line with clinical procedures. However, as a result, our study evaluates both the dosimetric impact of streak artifact reduction and metal size accuracy as a cumulative effect, rather than isolating the error associated with each individual component. Therefore, our conclusions about the success of the three commercial artifact reduction methods may not hold if there is no need for using beams that traverse metal implants and the only concern is successful streak artifact reduction.

5. CONCLUSIONS

The presence of metal was found to induce substantial dose calculation errors, in excess of 10% for a clinical treatment involving dental fillings. Strategies to mitigate these problems were examined, but tended to show mixed or only moderate results. In comparison to dose calculations with water kernels only, use of metal kernels resulted in better modeling of the increased backscatter dose at the proximal metal interface but decreased dose calculation accuracy directly downstream of the metal. In clinical cases, the accuracy was typically improved with metal kernels, but only minimally (<1.0%). Of the commercial CT metal artifact reduction methods investigated, o-mar was found to be the most consistent method for reducing calculation errors, either decreasing errors (dental case) or having little effect on calculation accuracy (spine case), and thus was a strong candidate for all-purpose CT simulation imaging. We found that the mars algorithm resulted in metal distortion in some cases, substantially increasing dose calculation errors for certain types of metal implants (a rectangular titanium insert and titanium spinal hardware). Therefore, the mars algorithm should be used with caution for dose calculations, especially for titanium implants, larger implants, and implants located near tissue heterogeneities. On the other hand, the mars algorithm was also clearly the most successful method for reducing calculation errors associated with dental fillings. gsi without mars was unsuccessful at reducing the severe artifacts caused by high-Z dental fillings and generally had little impact on dose calculation accuracy.

CONFLICT OF INTEREST DISCLOSURE

The authors have no COI to report.