The aerodynamics and control of free flight manoeuvres in Drosophila

Abstract

A firm understanding of how fruit flies hover has emerged over the past two decades, and recent work has focused on the aerodynamic, biomechanical and neurobiological mechanisms that enable them to manoeuvre and resist perturbations. In this review, we describe how flies manipulate wing movement to control their body motion during active manoeuvres, and how these actions are regulated by sensory feedback. We also discuss how the application of control theory is providing new insight into the logic and structure of the circuitry that underlies flight stability.

This article is part of the themed issue ‘Moving in a moving medium: new perspectives on flight’.

1. Introduction

Why should we care about how a fruit fly flies? Dragonflies are more powerful, butterflies more elegant, honey bees more economically relevant and hoverflies more dazzling. We only notice fruit flies when they flitter about our wine glasses or settle on our fruit salad. Surely, there are better models for studying aerodynamics and control than these annoying tiny creatures?

The general collapse of a once diverse array of model organisms in biology is regrettable, and we do not intend to lure scholars away from studies of other flying animals. Indeed, over the past few years, research has advanced substantially on various flight-related topics in other insects including motor planning and prey capture in dragonflies [1], nocturnal vision in hawkmoths [2,3], navigation in bees [4] and spatial memory in wasps [5]. The advent of transgenic techniques such as the CRISPR/Cas9 system [6] will soon allow researchers to pursue questions in these non-genetic model species at finer levels of granularity, as is already happening in mosquitos [7,8]. Nevertheless, the fruit fly (Drosophila melanogaster) will continue to provide unique experimental opportunities in flight research for several reasons. First, the genetic tools in Drosophila, which were originally developed to study developmental and cell biology, are now well suited for questions related to flight physiology, neurobiology and biomechanics. A second, less obvious, advantage of fruit flies is that their size and natural history make them especially convenient for behavioural experiments in the laboratory. Unlike many larger insects, Drosophila fly well when tethered, and free flight experiments do not require awkwardly large chambers. Because fruit flies are most active at dawn and dusk, they are also adapted to fly in the relatively dim conditions of laboratories. This is largely why fruit flies hover around your kitchen fruit bowl instead of slamming themselves repeatedly against the window. Pioneers of Drosophila flight research, including Karl Götz [9], Martin Heisenberg and Reinhard Wolf [10], Steven Vogel [11–13] and Charles David [14,15], exploited the experimental tractability of fruit flies for studies of aerodynamics and flight control long before it was possible to apply genetic tools to these problems. Indeed, the quantitative experimental tradition founded by these individuals continues to impact the field and informs the implementation of the latest genetic approaches.

The constraints of both physics and evolution on animal flight also elevate the general importance Drosophila research. There are a limited number of ways to fly with flapping wings, a fact that accounts for the striking similarity between the hovering kinematics of fruit flies and hummingbirds [16]. The insect brain is also structurally conservative and many core flight control circuits, such as those used for navigation [17,18], likely emerged very early in the arthropod lineage that gave rise to all pterygote insects [19]. The ubiquity of this ‘Devonian toolkit’ [20] makes it possible to study these general questions in fruit flies, or any convenient insect for that matter. Although our review will focus on Drosophila, most of the principles we describe will likely apply to a wide variety of species.

2. Hovering flight

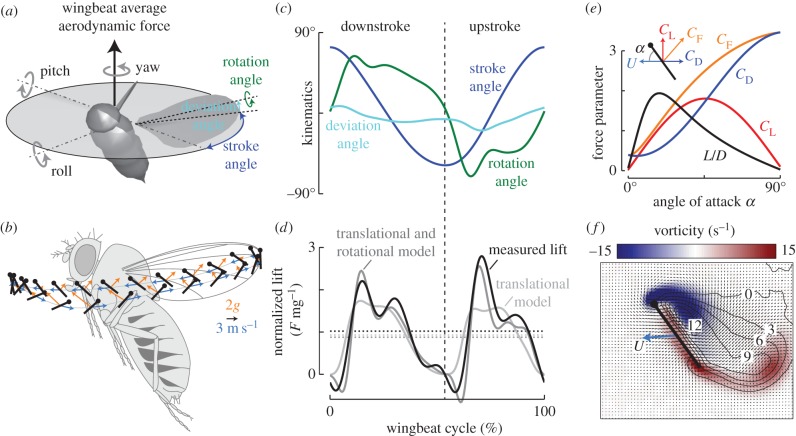
The advent of affordable methods for high-speed videography revolutionized the study of flight aerodynamics in flies. Using high-speed film, Ellington [21] and Ennos [22] were the first to capture free flight data on Drosophila, but film requires extremely high light levels and the full three-dimensional motion of the wing—especially the time course of the angle of attack—is difficult to accurately measure with a single camera view. The first attempt to capture the full three-dimensional kinematics of hovering flies employed quite low-resolution video cameras by today's standards [23,24], but the data remain consistent with subsequent efforts using more accurate methods [25,26]. Unlike flying vertebrates, flies contain no active joints in their wings and the path of the wingtip can be traced on the surface of a sphere; consequently, wing kinematics are conveniently described using three Euler angles in a stroke plane reference frame (stroke position, deviation and wing rotation angle; figure 1a–c). While hovering, this stroke plane is roughly horizontal, so fruit flies move their wings back and forth rather than up and down (figure 1b). The reciprocal wing movement can be divided into a ‘forward’ and ‘reverse’ stroke, which by convention are misleadingly called the ‘downstroke’ and ‘upstroke’. The wings deviate upward at the end of each half stroke, and the wing path during the downstroke is higher than the wing path during the upstroke. The resulting tip path creates a shape like the grin of the Cheshire cat, which has significant consequences for the time history of forces and moments (figure 1b). During the mild downward plunge at the beginning of each half stroke, the drag generated by the wing is angled slightly upward, thus contributing to the net vertical force [23,24,31]. (Throughout this review, we use the term ‘lift’ and ‘drag’ according to the conventional meaning of the force components perpendicular and parallel to the wing velocity vector, respectively, as shown in figure 1e). The wing rotates about its long axis such that it operates at a nearly constant and very high angle of attack (approx. 45°) during both the upstroke and downstroke (figure 1b). As mentioned above, there is nothing extraordinary about this pattern of wing motion, in that it is remarkably similar to what has been observed in hummingbirds [16,32], honey bees [32] and hawk moths [33]. Whether this pattern is optimal with respect to energetics is not entirely clear [34]; nevertheless, the similarity among species is noteworthy and suggests that a combination of physical and biological constraints restrict the solutions available to hovering animals.

Figure 1.

Kinematics and aerodynamics of fruit flies. (a) According to the helicopter model, a fly controls flight by modulating the magnitude of the wingbeat-average aerodynamic force and rotating its body around the roll, pitch and yaw axes. The required force and torque modulations are controlled by adjusting wing kinematics, which can be described by three Euler angles in the stroke plane reference frame: stroke angle, deviation angle and wing rotation angle. (b) Wingtip path and wing rotation angle (lollypop symbols), wing velocities (blue vectors) and instantaneous aerodynamic forces (orange vectors) at 25 equally spaced points in time throughout the wingbeat of a hovering fly (wingbeat frequency is 189 Hz) [27]. (c) Time history of wing Euler angles during steady flight. (d) Time history of vertical aerodynamic force. The light grey trace shows results from a quasi-steady aerodynamic model based on translational forces only; the dark grey trace is from a quasi-steady model that includes both translational and rotational forces [28]. The black trace shows the vertical force from a robotic fly experiment [27] and thus also includes unsteady aerodynamic effects such as wake capture and added mass forces. (e) Aerodynamic forces produced by a revolving robotic Drosophila wing model for a variable angle of attack [29]. The total force coefficient (C_F) is the resultant of the lift and drag components (C_L and C_D, respectively), and is oriented roughly perpendicular to the wing. All force coefficients are normalized by wing surface area and dynamic pressure. The ratio between C_L and C_D provides the lift-to-drag ratio L/D (black). (f) The flow field around a wing section (at 56% span) of a robotic Drosophila wing model moving at wing velocity U, measured using stereoscopic particle image velocimetry (PIV). Arrows indicate instantaneous in-plane fluid velocity, iso-lines show out-of-plane flow velocity in centimetres per second (positive indicates flow towards wingtip), and colour indicates fluid vorticity. The blue patch of high clockwise vorticity is the leading edge vortex (LEV), which enhances aerodynamic force production. Adapted from [30].

The time history of forces and moments generated during hovering is of course just as stereotyped as the pattern of wing motion that produces them (figure 1d). The wings generate peak force during the middle of the upstroke and downstroke. The upstroke peak is slightly higher because the midstroke velocity is greater during the upstroke than the downstroke. Quasi-steady aerodynamic models predict the time history of mid-stroke forces with remarkable accuracy [23] (figure 1d,e), a fact that is due to the peculiar stability of a flow structure known as the leading edge vortex (LEV), a region of high vorticity that forms on wings moving at high angles of attack [29,35,36]. Experiments with dynamically scaled robots [37–39] and computational fluid dynamics (CFD) simulations [40] demonstrate that revolving wings create a stable LEV, and as a consequence, elevated force coefficients (figure 1e,f). The stability (i.e. the lack of time dependence) of the LEV is noteworthy; a model fly wing revolving like a propeller at a fixed angle of attack quickly develops an LEV and maintains it as long as the wing continues spinning [41]. This explains why the quasi-steady model based on measured force coefficients works as well as it does (figure 1d). Many hypotheses have been put forward to explain the stable attachment of the LEV [35,38]. One explanation that has received the most attention recently is the role of Coriolis forces that are present when the ratio of translational to rotational velocity is sufficiently low [41], a condition quantified by the Rossby number (Ro). A wing translating as that of an airplane has an infinitely high Ro and develops an LEV at start-up that quickly sheds. By contrast, a low aspect ratio wing rotating as a propeller has a Ro close to zero and the resulting LEV remains attached. CFD simulations of revolving wings in which the Coriolis term of the Navier–Stokes equation is removed predict rapid shedding of the LEV [40]. Fruit flies and other small hovering animals flap their wings with relatively high rotational velocity compared with their translational velocity [21], thus ensuring a low Ro number and large Coriolis effects.

This strategy for generating an upward force is, however, horribly inefficient. Although the LEV does generate very high forces, the force vector is directed roughly perpendicular to the surface of the wing and thus a wing translating at a 45° angle of attack will generate lift and drag in nearly equal measure. Thus, flies pay a very dear price in drag for the lift they generate by way of the LEV. They would be much better off flapping their wings faster and using a lower angle of attack with a more advantageous lift-to-drag ratio [42]. Why fruit flies do not flap their wings faster is not entirely clear, but it is likely that flapping frequency is limited by the physiology of their indirect flight muscles. In other words, flies can only flap their wings so fast, so they must do so at a high angle of attack to generate sufficient lift, thereby suffering the consequences of high drag. Note that even the maximum lift-to-drag ratio (approx. 2) achievable by fruit flies (figure 1e) is very low compared with bird and aeroplane wings, which reflects the detrimental influence of viscosity at low Reynolds numbers (approx. 100) [42].

Unlike the midstroke forces, the quasi-steady model does a poor job of predicting the time history of flight forces during stroke reversal. The prediction is a bit better if the model is augmented with the addition of a term that accounts for the circulation generated when the angle of attack is changing (figure 1d) [28]. Even with this so-called rotational lift term, the augmented quasi-steady model is imperfect as it does not account for added mass effects and the complex interactions between the wing and its wake as the wing quickly changes direction [29]. The flow dynamics during stroke reversal, although captured reasonably well in the most accurate CFD simulations [43,44], are difficult to incorporate in simpler quasi-steady models.

3. Free flight manoeuvres

Based on body orientation measurements in a wind tunnel, David proposed that the control of forward speed boils down to the task of regulating pitch and throttle [45]. According to this model, a fly—like a helicopter—pitches nose-down to accelerate, thereby directing the mean force vector forward. The reorientation of the force vector results in a slight drop in its vertical component, for which a fly must compensate by slightly increasing force magnitude to avoid descending as well as to balance the increase in forward drag. In experiments on tethered flies, Götz & Wandel [46] directly demonstrated that the orientation of the mean flight force vector remains fixed relative to the stroke plane and body axis. The helicopter analogy, though useful, is not 100% accurate, because pilots control the pitch of a helicopter by tilting the rotor plane relative to the airframe by means of the swash plate, whereas flies possess two wings that they can modulate independently. Nevertheless, it still serves as a useful analogy. For example, although it was developed to explain the control of forward flight, recent work indicates that the helicopter model is equally apt for changes in heading. Like many species of flies [47–50], Drosophila employ a flight pattern consisting of straight segments interspersed with rapid changes in heading termed body saccades [51,52]. During both routine body saccades [53] and faster escape manoeuvres [27], flies alter heading by executing a banked turn (figure 2). As in David's original studies, these experiments employed the species Drosophila hydei, because their slightly larger body size provides more accurate kinematics measurements than are possible in D. melanogaster. The turns consist of four overlapping actions: (i) a rapid bank that redirects the mean force vector in the intended direction of motion, (ii) a counter-bank that rotates the force vector back to a more vertical orientation, (iii) a slower yaw rotation that aligns the body axis with the new direction of motion, and (iv) an increase in the total aerodynamic force. (We use the slightly awkward terms ‘bank’ and ‘counter-bank’ instead of the ‘roll’ and ‘counter-roll’—as is common in aeronautics—so that we can reserve ‘roll’ and ‘pitch’ to denote rotation about particular morphological axes.) The manoeuvres are quite analogous to the banked turns of helicopters and aeroplanes, as well as birds [54] and bats [55], and was first elegantly demonstrated in blowflies by Schilstra and van Hateren by experiments in which they tracked the angular orientation of the body and head using tiny magnetic coils [56].

Figure 2.

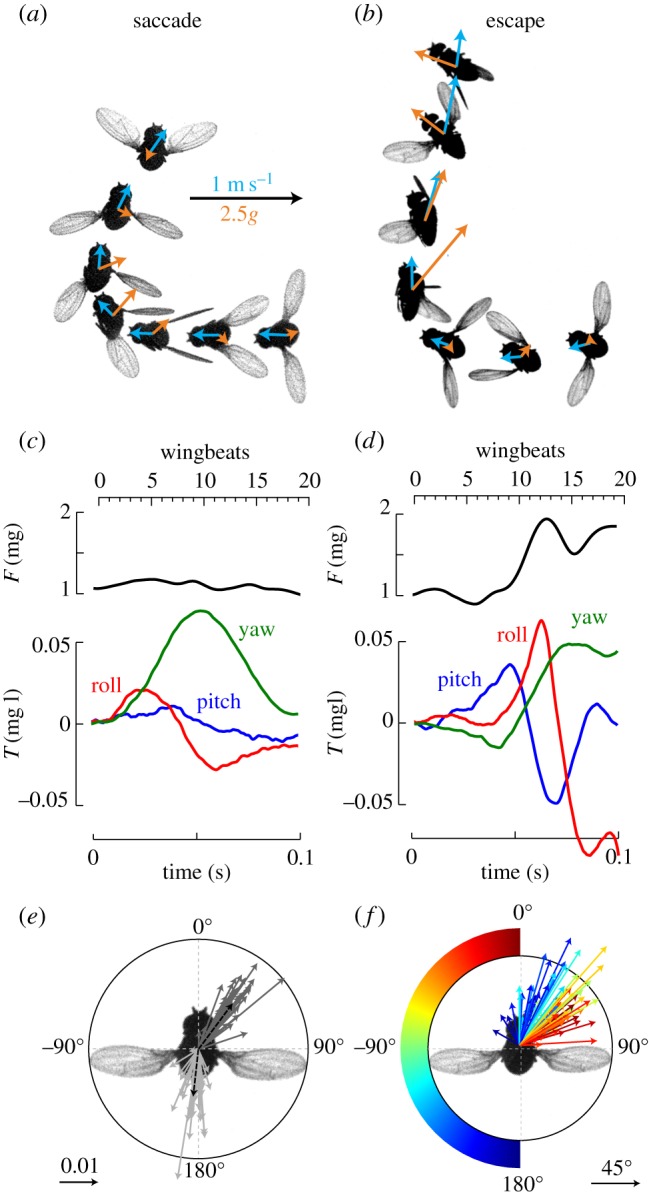
Body saccade and escape manoeuvre. (a) Photomontage from a high-speed video of a fly performing a saccadic turn adapted from [53]. (b) Photomontage of evasive manoeuvre elicited by looming visual stimulus adapted from [27]. In both (a,b), the fly changes course by approximately 90°. The instantaneous flight velocity (blue vectors) and the horizontal component of the aerodynamic force produced by the fly (orange vectors) are overlaid on each fly image. (c) Time course of the total aerodynamic force and body torques produced throughout the saccadic turn shown in (a). (d) Equivalent data for the escape manoeuvre shown in (b). Forces are normalized by body mass (mg) and torques are normalized by the product of body mass and wing length (mg l). (e) Torque vectors for the bank (dark grey) and counter-bank phases (light grey) of 44 body saccades, adapted from [53]. The length of each vector depicts normalized torque magnitude. The black dashed vectors depict the averages for all manoeuvres. (f) Vectors indicating magnitude and orientation of body rotation during the bank phase of 92 evasive manoeuvres, adapted from [27]. The colour of each vector indicates the position of the looming stimulus that elicited each trail.

Flies are capable of changing heading via a pure yaw manoeuvre with no adjustment in roll or pitch [24,57], but banked turns appear to be the preferred means of changing direction. An analysis of flight trajectories within a wind tunnel found that body saccades account for 80% of all changes in heading [58]. Banking by just 30°—which a fly can perform in a couple wingbeats—creates a sideways vector equal to 50% of its total aerodynamic force. To generate a comparable yaw turn, a fly must rotate a full 90^o about its yaw axis, which would only serve to redirect the rather meagre horizontal component of its net aerodynamic force. Thus, banked turns provide a much faster means of changing direction. However, because banked turns involve rotation about three axes and require throttle control, they are more complicated than a pure yaw turn. For example, during a yaw turn, a fly could minimize motion blur via yaw movements of the head relative to the body. By contrast, a fly must also stabilize its head position about the roll and pitch axes during a banked turn [56].

A comparison of body saccades and escape manoeuvres indicates that flies can adjust the magnitude of a turn by two different mechanisms (figure 2; electronic supplementary material, movies S1 and S2). In the case of the more stereotyped body saccades, flies always bank about the same two axes in body-centred coordinates (figure 2e). These axes are not perfectly aligned, however; flies bank about an axis that is approximately 35° off the longitudinal body axis, whereas they counter-bank about an axis that is more nearly aligned with the roll axis. The reason for this discrepancy can be explained by the fact that while the animal banks it also begins to yaw. Yawing at a banked angle results in a nose-down motion (in the world reference frame), and as a consequence the fly can regain an upright pose by producing a pure roll, without generating any nose-down pitch. Flies regulate the turn angle of the saccade by adjusting the amount of torque they generate and not by changing the orientation of rotation relative to the body frame. The situation is quite different for escape manoeuvres, which to be effective must allow the fly to direct its motion away from the location of the looming threat. In this case, the flies rotate about different axes in the azimuthal plane depending upon the angular position of the visual stimulus (figure 2f). A threat from directly ahead elicits a pitch-up manoeuvre whereas an attack from behind elicits a pure roll. This flexibility in the escape response demonstrates that flies quickly transform visual information into a motor code that generates the appropriate combination of pitch and roll torque.

In the case of both body saccades and escape responses, the end of the counter-bank leaves the fly with a new heading, which if not corrected, would result in a misalignment of the body axis with the new direction of motion (figure 2a,b). This so-called sideslip is reduced by the production of yaw torque, but the temporal dynamics of this compensatory action are different for saccades and escapes. During a saccade, yaw torque is produced simultaneously with the bank and counter-bank, resulting in only a small amount of sideslip at the end of the heading change. This is not the case for the evasive manoeuvre; in fact, the fly typically produces negative yaw torque during the initial phase of the manoeuvre, resulting in an increase in sideslip. As a result, flies experience substantial sideslip following an evasive banked turn and they continue to generate positive yaw to correct the misalignment long after the initial change in heading (figure 2c).

Assuming that the initial command to bank is generated by an internal signal, is the counter-bank also the result of a (slightly delayed) feed-forward command or is it triggered by sensory feedback resulting from the early phases of the manoeuvre, and if so, which modalities are involved? The time course of bank, counter-bank and yaw during free flight manoeuvres along with data from tethered flight experiments provide useful insight into these questions. In typical tethered flight studies, flies are glued to a rigid wire and their fictive turns are observed either by measuring yaw torque [9,59] or bilateral changes in stroke amplitude [59]. In some studies, either a thin flexible fibre [60] or a ‘magno-tether’ is employed which allows the fly to rotate freely about its yaw axis [61]. Tethered flies exhibit spontaneous behaviours—either fictive turns on a rigid tether or actual turns on a magno-tether—that researchers have interpreted as the manifestations of spontaneous free flight saccades. Likewise, tethered flies respond to expanding visual objects with what are presumably the fictive equivalents of escape manoeuvres [62]. However, the knowledge that saccades and escape manoeuvres consist of banked turns—and not pure yaw rotations—complicates these interpretations.

The most parsimonious way of amalgamating observations from free and tethered flight is to assume that the fictive saccades of rigidly tethered animals represent only the feed-forward component of the manoeuvre, and that this consists of the commands to bank and yaw, but not to counter-bank. In tethered flight experiments, the bilateral changes in stroke amplitude associated with fictive saccades are unidirectional and show no evidence for the counter-torque expected of a complete banked turn. Fictive saccades last much longer than free flight manoeuvres and are substantially larger in terms of measured changes in stroke amplitude. These observations make sense if we assume that a sensory signal present only in free flight triggers the rapid counter-bank phase of the turn. The fly then uses additional cues to determine that the yaw correction at the end of the manoeuvre is complete.

Sensory signals experienced by an animal due to its own deliberate actions are known as ‘reafference’ [63]. What reafferent feedback, experienced during the initial bank, might trigger the counter-bank? The time delay between the initial bank and counter-bank for an escape manoeuvre is approximately 25 ms (or five wingbeats), which seems too short for visual feedback. The most likely source of fast feedback during flight manoeuvres are the mechanoreceptors on the rapidly oscillating halteres, a subset of which are thought to act as gyroscopes by detecting Coriolis forces resulting from body rotation [64,65]. The subset of campaniform sensilla that are best positioned to detect Coriolis forces as the haltere oscillates are also those that make direct electrotonic synapses with a steering motor neuron that has been implicated in fast alterations of wing kinematics [66,67]. Clever, free flight experiments in which a magnetic coil system is used to impart a rapid rotation of a fly indicate that some sensory system—most probably the halteres—can trigger compensatory reactions within about three wingbeats (approx. 15 ms) [68], consistent with the time delay between the bank and counter-bank phases of a flight manoeuvre. Other modalities that might trigger the counter-roll include campaniform sensilla on the wing, which are the serial homologues of those on the haltere [69], Johnston's organ of the antennae [70,71] and the ocelli [72–74]. These sensory systems might be of particular importance for controlling flight manoeuvres in non-dipteran insects that do not possess halteres [75,76].

What sensory cues act to terminate the yaw correction at the end of a saccade? Although manipulating visual feedback during a magno-tether saccade does not alter the dynamics of the turn, changing haltere sensitivity does. Flies with slightly weighted halteres (which increase the Coriolis forces they detect) exhibit shorter saccades, whereas flies with partially ablated halteres exhibit longer saccades [77]. These observations suggest that reflexes mediated by the haltere act to reduce angular velocity about the yaw axis at the end of the manoeuvre. One problem with this model is that as angular rate sensors, halteres are ill suited for guiding the fly to a particular yaw angle, for instance, an angle that would align the body with the new direction of motion. The antennae, which can detect bilateral differences in airspeed [74], or the visual system, which can detect the optic flow created by the fly's forward motion, are much better suited for a reflex that could align the body axis so that it was tangent to the flight path. Tethered flies actively fixate (i.e. steer towards) the pole of visual expansion [78], provided that the expansion rate is sufficiently low. This reflex has the correct feedback sign to ensure that a fly completes a turn by trimming its sideslip angle to zero with respect to the new heading.

This model of free flight saccades emerging from behavioural experiments is relevant to an intriguing phenomenon recently observed in electrophysiological recordings from visual interneurons in tethered flies. The lobula plate, a fourth-order visual neuropil in the fly's brain, contains an array of neurons that are thought to act as matched-filters for particular modes of ego-motion during locomotion [79,80]. A set of three lobula plate neurons called the horizontal system (HS) cells are matched to yaw rotation, and are thought to underlie the compensatory optomotor response that stabilizes the flight path [81–83]. Electrophysiological recordings from these cells in head-fixed, tethered flying animals exhibit transient potentials that co-occur with the changes in wing motion during fictive saccades, even though these neurons are traditionally considered to be sensory and not motor interneurons [84,85]. Furthermore, the sign of these membrane voltage deflections are such that they would tend to negate the sensory input that the HS cells would experience during a turn. This has been interpreted as evidence for a so-called efferent-copy mechanism [85], by which an internal signal during the execution of a motor action is used to attenuate reafferent sensory input [63,86]. The mechanism would allow an animal to perform a voluntary manoeuvre, such as a rapid turn, by inhibiting compensatory reflexes that would normally act to maintain a steady course. Whereas the evidence for visual suppression during saccades is very strong in HS cells, it is much weaker in the cells that detect rotation in the azimuthal plane, the so-called vertical system (VS) cells [85]. This difference suggests that the flies' ability to turn is not impaired by reafferent feedback during the bank and counter-bank—perhaps because these actions are too fast to be inhibited by compensatory visual reflexes. Alternatively, perhaps the head motor system can adequately stabilize gaze during the bank and counter-bank [87], whereas suppression of the HS cells is required to enable the yaw correction at the end of the saccade. This phenomenon is an exciting example of the fruitful convergence of biomechanics and neurobiology that is now possible in Drosophila.

4. Kinematic control of forces and moments

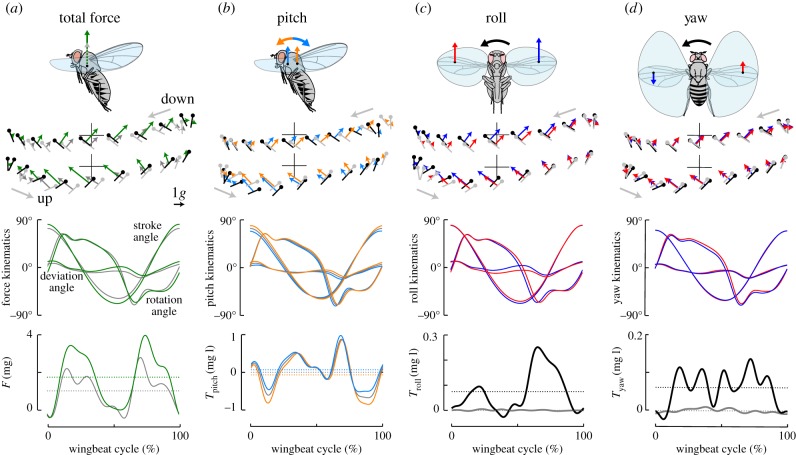
According to the helicopter model, flies manoeuvre by regulating the magnitude of the net force and tilting their stroke plane in the desired direction of motion. The requisite actions may be conveniently broken down into four control modes: throttle (i.e. changes in mean force) and torque production around the roll, pitch and yaw axes. Recent analysis of free flight manoeuvres, in conjunction with physical and mathematical models, has made it possible to determine how flies adjust their pattern of wing motion to generate the requisite forces and moments. In generating any manoeuvre, flies subtly distort the time course of stroke position, deviation and wing rotation angles (figures 1a and 3). One strategy for untangling the relative contributions of these three parameters is to measure the forces and moments created by synthetic wing strokes on a dynamically scaled robot in which one kinematic parameter changes as it does during actual free flight manoeuvres, while other parameters remain as in the normal hovering pattern [27]. In this way, it is possible to measure the aerodynamic effects of kinematic features in isolation and quantify the interactions among different features.

Figure 3.

Drosophila adjust wing kinematics to control total force, pitch torque, roll torque and yaw torque, adapted from [27,53]. In all top schematic panels, the net wingbeat-average forces and torques acting on the fruit fly are shown (not to scale). The second row shows the time history of wing movements and forces on the wings, whereby crosses define the wing hinge location for each half stroke, and serve as 10° reference scales for stroke and deviation angles. The third row shows the Euler angles as defined by figure 1a, and the bottom panels show the corresponding normalized forces or torques. (a) Forces and wing kinematics for a steady hovering fly (grey data) and for a fly that generates an increased flight force (green/black data). The corresponding wingbeat frequencies were 189 Hz and 230 Hz, respectively. (b) Comparison of the wing kinematics, forces and torques throughout a wingbeat that generates pitch down torque (orange data and grey lollypops), pitch up torque (blue data and black lollypops) and zero pitch torque (grey data in time-series plots). The changes in kinematics result in a shift in the position of the stroke-averaged centre of pressure, as illustrated in the top cartoon. (c) Wing kinematics, forces and torques of a fly producing roll torque. Upward rotating wing is indicated by black lollypops and blue data; downward rotating wing is indicated by grey lollypops and red data. The bottom panel shows roll torque throughout steady (grey) and roll-generating (black) wingbeat. (d) Wing kinematics, forces and torques of a fly producing yaw torque. Forward rotating wing is indicated by grey lollypops and red data, backwards rotating wing is indicated by black lollypops and blue data. The bottom panel shows yaw torque throughout the steady (grey) and yaw-generating (black) wingbeat.

To throttle, flies must increase the magnitude of the mean force vector without tilting its orientation. They accomplish this primarily by increasing the amplitude and frequency of the stroke, the combined effect of which is to raise the mean velocity of the wings (figure 3a). Owing to the squared dependence on velocity, even small changes in amplitude and frequency have substantial effects on flight force. Flies also alter the pattern of stroke deviation when they throttle, creating slightly stronger plunging movements at the start of each half stroke. Although this effect is secondary to that of the changes in frequency and amplitude, this also serves to increase wing velocity (because the wing must follow a longer path) and results in larger forces immediately after stroke reversal (because the plunging action redirects drag in an upward direction) [31]. By comparison, the changes in the time history of the wing rotation angle, which largely determines the aerodynamic angle of attack, are quite small.

Flies regulate pitch torque through a combined alteration of all three wing kinematic angles (figure 3b). The most important change based on measurements using a robotic fly, however, is a distortion in the time course of the stroke angle such that the dorsal excursion of the wing shifts either forward or backward, depending upon whether the fly desires to increase or decrease nose-up pitch torque, respectively (figure 3b). Such adjustments have the effect of changing the position of the stroke-averaged centre of pressure relative to the fly's centre of mass. Changes in stroke deviation and wing rotation angle do contribute to pitch, however, and their effects are amplified by the fact that they alter aerodynamics when the wings are near their dorsal and ventral extremes, where the effects on pitch moments are greatest [27]. When creating nose-up pitch, for example, flies slightly advance the timing of wing rotation and plunge the wing further downward at the start of the upstroke (figure 3b).

Unlike throttle and pitch control, changes in roll and yaw involve asymmetrical alterations in the stroke kinematics of the two wings. Flies generate roll moments through a combined alteration of all three wing angles, for which the changes in stroke angle and wing rotation are most important (figure 3c,d). On the outside of the roll (i.e. the wing on the side that will rotate upward), flies increase stroke amplitude, advance wing rotation and elevate the path of the wing upward during ventral stroke reversal, while making the opposite adjustments on the contralateral wing. The net effect is a large roll moment generated at the beginning of the upstroke (figure 3c). The results provide support for an old hypothesis that flies turn in part by regulating the timing of the wing rotation during the ‘ventral flip’, the fast rapid supination of the wing during the downstroke-to-upstroke transition [88], and illustrate how very subtle kinematic changes during stroke reversal can nevertheless have large effect on forces and moments.

The regulation of yaw is somewhat unique in that flies appear to create the requisite torque almost exclusively via changes in wing rotation angle with very little contribution from changes in stroke angle or deviation [53,57]. The most conspicuous change is a tonic offset in the wing rotation angle of one wing relative to the other (figure 3d). This creates a situation in which the angle of attack increases on one wing while it simultaneously decreases on the other. The situation then reverses on the alternate half stroke. This differential change in the angle of attack creates net yaw torque, because during the first half stroke one wing generates more drag than the other, whereas the situation reverses during the subsequent half stroke [89]. Flies also adjust the timing of wing rotation during ventral stroke reversal, similar to the changes executed to create roll, enabling the fly to generate yaw torque at a time in the stroke when the translational velocity of the wing is near zero [53].

5. Stability and inner-loop architecture

The flight behaviour of a fly may be coarsely simplified as a control system with both inner- and outer-loop components. The outer-loop system is not necessary for the instantaneous stability of the system, but rather allows the animal to respond to specific sensory cues such as looming objects, odour plumes or navigational landmarks. By contrast, inner-loop reflexes are necessary for maintaining a stable pose and velocity in the face of external and internal perturbations (figure 4). Evidence suggests that flies possess multiple inner-loop circuits, the dynamics of which are determined by the inertia and damping associated with each degree of freedom. As demonstrated by Hasselberg & Lehmann [92], the rotational damping of a flying fly is dominated by the drag created by the reciprocally flapping wings. As a consequence, damping is particularly large about the yaw axis, because it is normal to the stroke plane of the flapping wings, whereas damping about the roll and pitch axes is substantially less [93]. In contrast to damping, the inertia about the three rotational axes is quite similar. As a consequence of the increased passive damping, flies should be more resilient to perturbations in yaw than to those in roll and pitch. On the other hand, the fly will be less responsive about its yaw axis during active manoeuvres, and this may explain the advantages of changing direction via banked turns. This trade-off between stability and manoeuvrability is regarded as a fundamental feature of both engineered [94] and natural [95] locomotor systems, although direct experimental evidence is lacking.

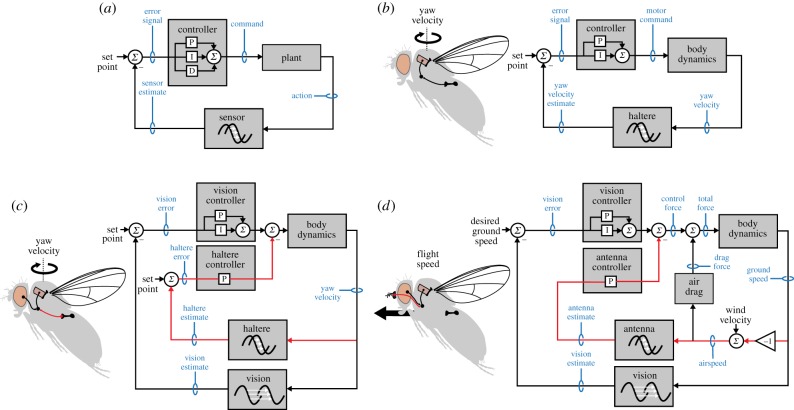
Figure 4.

Control theory models of flight stabilization reflexes in Drosophila. (a) General from of simple proportional, integral and derivative (PID) feedback controller. In this and all other panels, delays are only indicated for the sensor block, although in actual systems they might occur throughout the feedback loop. (b) A simple PI controller for yaw velocity, based on [68]. (c) Another model of yaw stabilization that incorporates both visual and haltere feedback, based on results of [84,90]. The embedded loop using short-delay haltere feedback (red traces) acts to stabilize the outer loop using long-delay visual feedback. The haltere loop increases the stability of the vision loop by adding damping to the body dynamics. (d) A model for speed control based on [91]. As in yaw velocity controller shown in (c), a long-delay visual feedback loop is stabilized through the action of a short-delay mechanosensory loop (red traces), in this case mediated by the antennae. In this model, the action of the antennal loop in augmenting the passive damping of the system (indicated by ‘air drag’) is shown explicitly.

A common theme in recent studies is the use of control theory and systems identification techniques to quantitatively model inner-loop reflexes. For flies, such approaches have been used to model velocity control [96–98], pose stabilization [99,100], gust responses [91], landmark fixation [101] and optic flow stabilization [102]. Although these behaviours are undoubtedly nonlinear and depend on many sensory inputs, the salient features of inner-loop reflexes are often well approximated by simpler linear models. A generic feedback controller for a motor action is shown in figure 4a. In the simplest case, a proportional controller, the system possesses a sensor that measures some state variable, such as angular velocity. This measurement is then compared to a desired set point (e.g. zero angular velocity) to create an internal error signal. The error signal is scaled linearly to generate a compensatory motor response, which acts to reduce the measured state variable until the system equilibrates at zero error. The motor actions act on the ‘plant’, which incorporates the passive inertia and damping terms for the relevant degrees of freedom.

One linear feedback system widely used in engineered systems is the PID (proportional, integral and derivative) controller [103]. In a PID controller, the error signal is processed in three separate pathways: one that applies a simple proportional gain to the error signal, one that continuously integrates it and another that differentiates it (figure 4a). The three pathways then converge to create a composite signal that creates the compensatory motor command. An intuitive interpretation of such a system is that while the proportional term allows the system to respond to the current value of system error, the derivative and integral terms allow the system to respond to estimates of the future and past error, respectively. In an engineered system, the gains of the proportional, derivative and integral pathways are carefully adjusted to optimize the performance of the system, and presumably natural selection has acted to tune the fly's nervous system as well. Flying flies fuse information from different sensors (e.g. eyes, ocelli, halteres, antennae) to measure errors, whereas the reactions are actuated primarily via the action of the wing steering muscles. Because of variation in the intrinsic adaptation rates of different sensory neurons (e.g. ‘tonic’ versus ‘phasic’ campaniform sensilla on the wing [104]), or the physics involved in the sensory apparatus, feedback is often automatically in a form that is appropriate (or inappropriate) for either proportional or derivative control.

Feedback based entirely on a proportional term is subject to several systematic problems, which are well illustrated by recent research on flies. For example, a purely proportional feedback system has difficulties in reducing steady-state error to zero, a phenomenon known as droop. The addition of an integral term corrects this problem because the integrator ‘winds up’ the small error term over time into a signal sufficient to effect full compensation. Integrating the error signal also serves to reduce high-frequency noise. The responses of flies to very fast angular perturbation in free flight suggest that the inner-loop circuits that stabilize yaw and pitch institute a form of PI feedback (figure 4b) [68,100]. The rapidity of these reflexes suggests that mechanosensory systems are involved, most probably the halteres, although the means by which integration is performed on the raw sensory signals is not known.

The role of integration in haltere-mediated reflexes is more likely to be noise reduction and amplification of small signals than correction of steady-state error per se, because the halteres are inherently insensitive to low angular velocities [105]. When placed in a dark magno-tether, flies tend to spin continuously about the yaw axis, an effect that is accentuated if one wing is clipped so as to create asymmetric torque [77]. Turning on the lights to provide visual feedback stabilizes the flies, confirming that the visual system is better suited to detect and stabilize slow rotation [105]. Another situation where integration of haltere signals might be important is the yaw controller for saccadic turns. As mentioned earlier, flies on a magno-tether with slightly weighted halteres exhibit shorter saccades, whereas flies with partially ablated halteres exhibit longer saccades [77]. These results suggest that feedback from the halteres helps determine saccade duration. Because the haltere cannot measure sideslip, however, the continuous tuning of body orientation and flight direction is most probably mediated by vision or feedback from the antennae. This visual–motor loop regulating yaw also exhibits integration, but operates over a much longer time scale than the haltere loop [84].

Unlike derivative and proportional gain, which is easily implemented by routine membrane properties of neurons, integration is more difficult to explain, because it involves a form of memory that is longer than membrane time constants of most cells. Physiological experiments suggest that slow calcium dynamics within the terminals of the HS cells—which influence the synaptic output of the cell—might be responsible for computing the integration within the optomotor pathway [84].

The delays inherent in transduction and subsequent motion processing create substantial problems when vision-based estimates are used for inner-loop control. A proportional controller operating with substantial sensory delay relative to the system dynamics tends to overshoot or oscillate in response to a perturbation, especially when operating at high gain. The two simplest ways of correcting for this instability are to reduce the feedback gain or to add a derivative term to add damping to the system. However, these solutions are problematic because reducing the gain diminishes the responsiveness of the system and adding a derivative term amplifies noise. Although the inner-loop system that stabilizes yaw benefits from the elevated passive damping about the yaw axis discussed earlier [92,93], simulations using a flapping robot suggest that this passive damping alone could not fully stabilize visually mediated feedback [90]. Physical simulations suggest that flies can negate these deleterious effects of delay using a fast reflex loop mediated by the halteres (figure 4c). This creates active damping that augments the passive damping and allows the visual–motor loop to operate at higher gain without making the fly unstable [90]. Flies without halteres are unstable about the poorly damped pitch axis and cannot fly unless additional passive damping is added in the form of a long tail [99], although such experiments must be interpreted cautiously because the halteres are likely to serve many other sensory functions in flight besides acting as gyroscopes [64,106]. If true, this role of the haltere in creating active damping would complement its function in detecting fast perturbations [68,107]. Another advantage of active damping is that, unlike passive damping, it may be turned off to facilitate fast manoeuvres. Indeed, halteres evolved from hind wings, and presumably the ancestors of all dipterans experienced particularly strong passive damping due to the flapping of all four wings. By replacing the hind wings with a sensory structure that can quickly mediate active damping as required, dipterans have achieved greater manoeuvrability with little loss in stability. Although speculative, this may explain both the evolution of halteres and the impressive agility of dipterans as a group.

A control architecture similar to that posited above for yaw control (figure 4c) may also operate in the circuit that maintains forward flight speed (figure 4d). Fruit flies regulate forward velocity using vision [96,108], a reflex that enables them to maintain constant ground speed in the presence of a variable headwind. However, flies whose aristae have been ablated—thereby impairing antennal function—exhibit oscillations in forward velocity, suggesting that their vision-based speed controller is unstable under these conditions [91]. A set of experiments in which flies were subjected to controlled gusts suggests that, like the role of halteres in stabilizing yaw, the antennae mediate a fast motor reflex that actively increases damping in response to a change in air speed [91]. Again, an embedded loop relying on short-latency feedback from mechanoreceptors stabilizes a longer delay loop based on vision. Although these hypotheses need to be tested more rigorously, they suggest a general principle by which flies accommodate the various limitations of different sensory modalities. Prior models of visual and haltere feedback posited a simple additive system in which the low- and high-pass characteristics of the visual system and halteres combine to provide a broader bandwidth [109]. These new results suggest that the actual means by which the fly fuses multimodal information is more complicated and takes advantage of short-latency information provided by mechanosensors and the absolute spatial information provided by vision.

One intriguing new theme in fly research is that all of the major sensory structures involved in flight control—eyes, halteres and antennae—can influence each other's sensitivity via the action of specialized motor systems. For example, the halteres are equipped with a complex set of control muscles that receive descending visual input [110]. This interaction is reciprocal, because haltere mechanoreceptors project to motor neurons that regulate head motion [111]. Two recent independent studies have explored the functional consequences of this interaction between proprioceptive and visual pathways by manipulating feedback from the halteres and wings and examining the effect on visual reflexes [112,113]. The results are somewhat enigmatic, in that haltere ablation attenuates visual responses to large field motion or looming objects, but can actually enhance the fixation of small targets. Interpreting the results of these ablation experiments is complicated by the likely possibility that the haltere functions both as a gyroscope and as a metronome to provide phasic input to the wing steering system—and both these submodalities might be influenced by descending control via the haltere muscles. The antennae also possess muscles that alter the organ's orientation in response to visual motion [114]. Apparently each relevant sensory modality has the capacity to alter the sensitivity of every other modality, thus creating a densely connected sensory motor network [71].

As commented above, freely flying flies can execute rapid turns using remarkably small changes in wing motion. This fact is superficially at odds with the large changes in motion exhibited by tethered flies in response to open-loop presentations of visual stimuli. Why are flies capable of creating such large changes in wing motion when subtle alterations suffice for the fastest flight manoeuvres? One explanation for this discrepancy is that mechanosensory-based, inner-loop reflexes that increase active damping allow vision-based reflexes to operate at very high gain, and thus the exaggerated open-loop responses are expected [90]. Another possibility is that the system has evolved to compensate for large internal perturbations, such as asymmetrical wing damage. Unlike birds that can replace lost or damaged feathers through moulting and bats that can regenerate their damaged wing membrane, insects cannot repair wing damage and even small reductions in wing length and area have large aerodynamic consequences. Integral feedback, along with a large dynamic range, would allow an optomotor loop to wind-up kinematic changes to the large values required to trim forces and moments produced by damaged wings [115]. In this interpretation, the classic open-loop optomotor response is largely a manifestation of the feedback specialization required for damage compensation, and is consistent with the slow time-evolution of the tethered flight optomotor response as well as the flies' remarkable ability to turn continuously in free flight when presented with rotatory visual motion [52]. The challenges associated with internal imbalances might also explain the slow postural responses of tethered flies. In response to optomotor stimuli, flies bend their abdomen and legs like a rudder [116]. These postural changes are perplexing, because the resulting aerodynamic moments are very small compared with those generated by the wings [117], and have not been observed during fast free flight manoeuvres. However, they may provide a means of creating the small but constant torque required to trim out errors due to asymmetries in wing length due either to damage or natural variation [117].

The application of control theory has already provided great insight into the function of the flight aerodynamics and will no doubt emerge as an essential tool going forward. Like all modelling, however, control theory is most powerful when used iteratively with experiments, and there are several pitfalls associated with its application. First, systems identification ultimately boils down to parameter fitting, and the data from any set of experiments could be explained by an infinite number of feedback models. Although relying on parsimony is perhaps the most prudent strategy, there is no guarantee that the simplest model is indeed the correct one. More problematic is the fact that block diagrams may often be re-arranged in a number of different ways that superficially appear to represent alternative models, but actually reduce to the same set of differential equations. For this reason, one should not be seduced into believing that the elements in a block diagram represent actual neural pathways and computations. Finally, the computations relevant to control systems, such as differentiation and integration, are automatically performed by neurons and muscles as part of their intrinsic operation. It may be tempting to see every example of such an operation as a functional feature of the system, but in some cases it may simply represent a bug or epiphenomenon due to the hard constraints of the underlying cell biology. Only careful experimental analysis can resolve this tricky ‘feature versus bug’ problem. It is also important to appreciate that the stimuli most useful for performing systems identification are not necessarily good proxies for the perturbations that an animal experiences in nature. For example, whereas it has been informative to subject flies to brief perturbations in free flight [68,91], measurements of airflow in natural settings indicate that flies would rarely, if ever, experience perturbations at such short temporal scales [118–120]. They are much more likely to have to deal with large, long gusts and the design of their control system should be interpreted accordingly.

6. Future directions

Whereas control theory provides a rigorous mathematical framework with which to understand flight behaviour, most biologists will not be fully satisfied until they have identified the actual circuitry and mechanical hardware that enables insects to fly. Although the past literature on the neuroethology of other insects such as locusts is particularly rich [121], the ability to use genetic tools in Drosophila to target identified neurons for imaging, electrophysiology, silencing and activation could lead to profound changes in our understanding of the neural computations that underlie flight behaviour (e.g. [122]). Genetic approaches can also be applied to study flight muscle [123,124], which could help in elucidating the function of the dipteran wing hinge—perhaps the most impenetrable black box in our current model of fly flight [125]. Nearly all the flight behaviours described in this review are implemented by a sparse set of about 15 steering muscles [126], but due to the nearly incomprehensible morphological complexity of the hinge, we have a poor understanding of how they control the subtle changes in wing motion required for flight manoeuvres. However, based on the speed with which other tough problems are yielding due to the experimental advantages of Drosophila, even this old chestnut may crack in the near future.

Authors' contributions

Both authors wrote the paper.

Competing interests

The authors have no confliction interests.

Funding

This work was supported by grants from the Netherlands Organization for Scientific Research, NWO-VENI-863-14-007 (F.T.M.), and the National Science Foundation, IOS 1452510 (M.H.D.).