Decision-making by a soaring bird: time, energy and risk considerations at different spatio-temporal scales

Abstract

Natural selection theory suggests that mobile animals trade off time, energy and risk costs with food, safety and other pay-offs obtained by movement. We examined how birds make movement decisions by integrating aspects of flight biomechanics, movement ecology and behaviour in a hierarchical framework investigating flight track variation across several spatio-temporal scales. Using extensive global positioning system and accelerometer data from Eurasian griffon vultures (Gyps fulvus) in Israel and France, we examined soaring–gliding decision-making by comparing inbound versus outbound flights (to or from a central roost, respectively), and these (and other) home-range foraging movements (up to 300 km) versus long-range movements (longer than 300 km). We found that long-range movements and inbound flights have similar features compared with their counterparts: individuals reduced journey time by performing more efficient soaring–gliding flight, reduced energy expenditure by flapping less and were more risk-prone by gliding more steeply between thermals. Age, breeding status, wind conditions and flight altitude (but not sex) affected time and energy prioritization during flights. We therefore suggest that individuals facing time, energy and risk trade-offs during movements make similar decisions across a broad range of ecological contexts and spatial scales, presumably owing to similarity in the uncertainty about movement outcomes.

This article is part of the themed issue ‘Moving in a moving medium: new perspectives on flight’.

1. Introduction

Individuals typically respond to changes in their internal state [1,2] and environment [3,4] by changing their location or behaviour, presumably trying to maximize benefit and minimize the associated costs of time or energy, under the constraints associated with motion and navigation capacities [5]. Superimposed on these plastic responses are innate variations in the tendency of individuals to take risks such as predation, exhaustion, or failure to find food that might lead to starvation [6]. Decisions about when, where and how to move (i.e. the movement mode) can affect their performance, and ultimately fitness. For instance, soaring–gliding flight is an energetically efficient movement mode because it decreases energy expenditure by using external energy resources [7–9]. Individuals gain altitude by soaring on ascending air currents, and then glide to achieve horizontal displacement. These ascending currents could be generated by topography or by thermal convective currents (air close to the ground heated by solar radiation). Soaring–gliding species (mostly large birds) spend most of their time foraging within their home range (or in their wintering grounds), with movement at this scale motivated by a diverse set of needs [10,11]. Yet, soaring–gliding flight has been investigated mostly by observing differences among species, and mostly limited to the context of long-distance migration [12–15]. While traditional tracking methods allow biologists to describe space-use patterns of individuals, recent technological advances provide the means to approach the short time-scales at which decision-making takes place. This progress, together with the development of tools for relating movement paths to associated behaviours [16–18] and with environmental factors [19], enables examination of how intrinsic and extrinsic factors affect decision-making and the resulting movement path [20,21].

The dependence of soaring flight on environmental resources places the individual under trade-off constraints of time, energy and risk. In general, flying slower is less risky and energetically cheaper (to a certain minimum speed required for staying aloft). Shifting from soaring to flapping flight elevates energetic costs but does not necessarily imply faster movement or less risky flight. Similarly, variation in risk-sensitive behaviour is not distinctly related to either energy and time minimization and can lead different outcomes. Thereby, a soaring–gliding animal can alter its flight in different ways, with variable consequences for minimizing time, energy and risk. We thus suggest relaxing the common conceptions that energy and time minimization represent two opposing ends of the same axis, and that risk merely reflects one of these two basic costs. Here, we propose three proxies (soaring–gliding efficiency, flapping activity and risk-averse flight behaviour) to represent minimization of time, energy and risk, respectively (figure 1). We define each of these proxies to directly reflect each component, and to make them conceptually independent from each other.

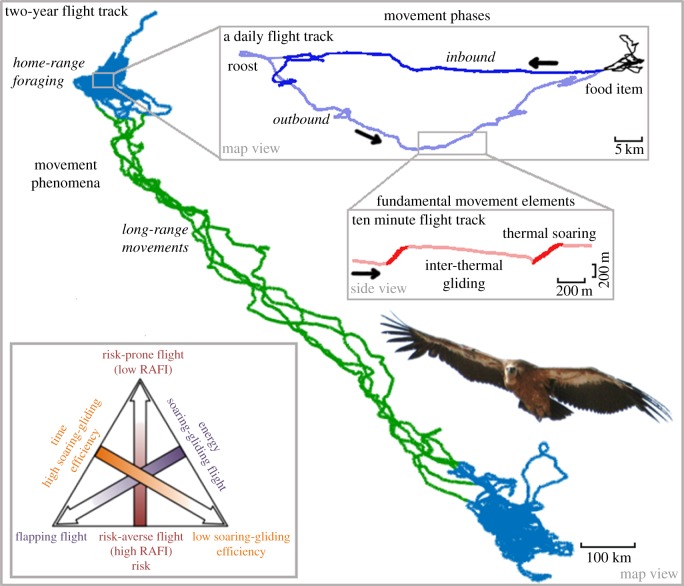
Figure 1.

A description of a vulture's track over three spatio-temporal scales, illustrating some basic concepts of soaring–gliding flight. A large-scale movement track reveals different movement phenomena (home-range foraging and long-range movements). Nested within foraging are movement phases, inbound and outbound flights, from and to the central place (roost), respectively. At finer scales, movement phases comprise different fundamental movement elements (thermal soaring and inter-thermal gliding). The triangle on the bottom left represents the trade-off between minimizations of time, energy and risk for soaring–gliding birds. Each of these components is estimated by a proxy, soaring–gliding efficiency, flapping activity and risk-aversion flight index (RAFI), respectively. Arrows represent gradients starting from the best minimization for each component; best time minimization: vultures exhibit high soaring–gliding efficiency resulting in fast cross-country speed; best energy minimization: vultures soar and glide without wing flaps; best risk minimization: vultures glide relatively slowly between thermals (high RAFI).

(a). Time: soaring–gliding efficiency

Time minimization does not exclusively depend on either climbing or gliding performance, but on how both phases jointly determine cross-country speed; essentially, a glider should strive to decrease time spent in thermals with respect to the displacement obtained during inter-thermal gliding [22]. A bird that glides faster between thermals might achieve a slower cross-country speed if it spends too much time climbing a thermal, compared with a slower inter-thermal glider that spends shorter durations in thermals. Here, we introduce for the first time, to the best of our knowledge, the use of soaring–gliding efficiency (calculated as inter-thermal displacement divided by climbing time), a well-known metric in human glider competitions [22], as a useful time-minimization metric for studies of soaring birds. Essentially, soaring–gliding efficiency and cross-country flight speed (calculated overall displacement divided by overall time) constitute two different parameters that are highly correlated; yet, they are not synonymous but reflect, respectively, the decision-making process and its outcome.

(b). Energy: flapping activity

Flapping flight dramatically influences energy balance because it requires high-energy expenditure: up to a 20-fold rate increase in birds compared with the basal metabolic rate [23]. Because flapping flight is less restricted to specific environmental conditions needed for soaring–gliding flight, it can also save time either by relaxing the need to spend time soaring in thermals or by providing flight opportunities when the soaring conditions are not good enough. Yet, flapping flight tends to be slower than soaring–gliding flight for relatively large birds [24]. Therefore, flapping rate is expected to have a non-trivial relationship with cross-country flight speed, especially for large soaring–gliding birds.

(c). Risk: risk-averse flight index

The relationship between flight speed and sink rate is portrayed by the glide polar [25]. There is an inherent association between horizontal speed and sinking rate, and a bird can adjust its wing shape to minimize sink or maximize displacement. When a gliding bird sinks faster, it runs the risk of being forced to land or to perform costly flapping flight at lower altitudes to reach the nearest thermal [26]. Two specific speeds on the glide polar are the best-glide speed that minimizes altitudinal loss per unit of forward distance and the optimal (‘MacCready’) speed that maximizes cross-country speed by adjusting airspeed to the rate of ascent in thermals [27]. These speeds are integrated within a risk-averse flight index (RAFI), which is the ratio of actual to theoretical risk-averse gliding airspeed in inter-thermal gliding [26]. RAFI measures the level of risk aversion; hence, more risk-prone flights with faster sinks are indicted by lower RAFI values. We note, however, that a faster sink between thermals does not necessary imply a faster cross-country speed, because a bird taking a more risk-prone flight might fail to find a suitable thermal, and might thus be forced to land or switch to potentially slower flapping flight.

The movement track of an individual has nested flight modes across several spatio-temporal scales [28]. Over large scales, long-range movements are characterized by directional movements between geographically separated regions (e.g. migration or long-distance dispersal); during these movement, individuals are challenged to traverse long distances with an ensuing need to minimize energetic cost of transport [29], overall time [30], or a weighted combination of these two under risk-avoidance constraints. In contrast, home-range foraging movements are motivated by a need to obtain food within a restricted region, and a time minimization imperative is less likely to be operating than during long-range movements [31]. At this intermediate scale, foraging trips contain different movement phases, which are sequences of steps associated with the fulfilment of a particular set of goals [5]. For central-place foragers, a simple dichotomy is to separate outbound flights, primarily motivated by food finding, from inbound flights, motivated to return back to the roost/nest [32]. Each of these phases, in turn, contains repeated and homogeneous small-scale segments called fundamental movement elements [28], such as thermal soaring and inter-thermal gliding used by soaring birds (figure 1).

To explore the trade-offs between time, energy and risk, we tracked year-round movements of Eurasian griffon vultures (Gyps fulvus) in Israel and France. These vultures are obligate scavengers that rely almost exclusively on soaring–gliding flight. We hypothesized that vultures optimize flight performance by considering time, energy and risk factors in a context-dependent manner that varies with the internal state of the individual and the external factors of its local environment. We predicted that when moving towards a known destination, individuals will fly faster and more efficiently in terms of both (i) time minimization and (ii) energy minimization, and (iii) will take more risks compared with individuals who fly to less known destinations. To test this first set of predictions we compared long-range movements versus home-range foraging (at large spatial scales), and inbound flights versus outbound flights (at intermediate spatial scales). Both long-range movements and inbound flights reflect known destinations (migration direction, roost), whereas home-range foraging and outbound flights consist mostly of search flights with an unknown destination site (e.g. a carcass). To further elucidate the potential mechanisms underlying soaring–gliding flight decisions, we examined the effects of variation in the internal state of the individual (breeding status, age and sex) and external conditions (wind velocity) over movements at these two scales. As a second set of predictions, we predicted that: (i) older, more experienced individuals will show better flight performance than juveniles; (ii) because Eurasian griffon vultures exhibit no sexual dimorphism or sex-related behavioural difference [33], we do not expect flight decisions to depend on sex (as it would if only one sex made long-range forays); (iii) time constraints for breeding individuals will be stronger, owing to the need to engage in nesting and food provisioning activities; (iv) individuals will be more risk prone during favourable environmental conditions (e.g. tailwinds) and risk-averse under unfavourable environmental conditions (e.g. head wind, low thermal availability).

2. Methods

(a). Study species and sites

The Eurasian griffon vulture (G. fulvus; Hablizl 1783) is a large raptor (6–11 kg) with relatively high wing loading that is favourable for obtaining high inter-thermal gliding speed, but limits the ability to use weak thermals and increases the energetic cost of flapping flight compared with smaller soaring–gliding species [34,35]. Eurasian griffon vultures can be considered as partial migrants during the first years of life, becoming mostly sedentary after first breeding, though some adults eventually engage in long-range forays presumably reflecting unsuccessful breeding attempts [36,37]. These two movement phenomena that are characterized by directional movements between geographically separated regions were grouped in our analysis under long-range movements. Because predators rarely threaten vultures during flight, their in-flight decisions are probably motivated by time and energy considerations and the need to encounter suitable rising air currents. Furthermore, being exclusive scavengers, vultures can swallow 1.5 kg of meat during a meal, which can increase their body mass by 10–20% and may affect their flight performance and decisions. In our study sites, vultures breed from January till August [38], and as central place foragers, typically return to the same roost (or nest) before the end of each foraging day.

In this study, we combine two datasets obtained at distinct regions that differ in their topographic structures, atmospheric conditions and food distribution patterns: the Negev desert in Israel (30.8° N, 34.8° E) and the Grands Causses (semi-steppe tabular mountains) in France (44.1° N, 3.0° E). No genetic [39] or morphometric (table 1) differences were found between the populations. In Israel, the population size was approximately 50 pairs, and estimated foraging range is 12 000 km² (mean 95% kernel distribution estimator) [36]. In France, the population size was more than 350 pairs in 2012, and foraging range is 10 000 km² (mean 95% kernel distribution estimator) [33]. In both regions, food resources are mainly provided at feeding stations (116 tonnes of carcasses per year deposited at 25 stations in Israel compared with 111 tonnes per year at 100 stations together with unknown biomass of carcasses found in the wild in France; see details in electronic supplementary material, S1).

Table 1.

Comparisons of movement properties between GPS tracking datasets (mean ± s.d.).

	Israel low-resolution	Israel high-resolution	France high-resolution
tracked individuals (#)	38	19	8
sex ratio (male : female : unknown)	11 : 19 : 8	5 : 7 : 7	2 : 4 : 2
age group (less than 2 months : older)	9 : 29	9 : 10	0 : 8
age (years)	7.5 ± 4.1	5.3 ± 3.4	15.0 ± 7.5
breeding (individuals)	—	8	7
tracking duration (days)	106 ± 100	29.9 ± 29.1	8.9 ± 9.5
body mass (kg)	8.16 ± 0.64		8.46 ± 0.99
folded wing (mm)	725 ± 25		716 ± 18
daily tracks characteristics
daily distance travelled (km)	90 ± 30	160 ± 110	141 ± 92
straightness of the daily path	0.35 ± 0.06	0.6 ± 0.13	0.65 ± 0.04
daily maximum displacement (km)	30.4 ± 13.4	32.5 ± 15. 3	23.8 ± 11.6
flight altitude above ground (m)	442 ± 124	462 ± 58	338 ± 75
movement phenomena (days)
long-range movements	86
home-range foraging	6903
movement phases (events)
inbound flights		230
outbound flights		549
fundamental movement elements
linear soaring (events per individual)	207 ± 293	15.8 ± 18.1	2.3 ± 1.5
thermal soaring (events per individual)	1229 ± 1115	194 ± 267	88 ± 162
inter-thermal glides (events per individual)	1291 ± 1461	217 ± 261	78 ± 143
climb rate (vertical speed) (m s−1)	1.2 ± 0.7	1.2 ± 1.0	1.4 ± 0.9
inter-thermal glide speed (m s−1)	16.7 ± 1.1	16.6 ± 1.9	16.2 ± 2.9

(b). Tracking data

Vultures in Israel were tracked using global positioning system (GPS; including accelerometer) transmitters (e-obs GmbH, Munich, Germany), deployed with a body-loop harness (for more details regarding trapping, biometry and molecular sexing, see [1,36]). Vultures in France were tracked using GPS transmitters (UvA-BiTS, Amsterdam, The Netherlands) [40] deployed with a leg-loop harness [41,42]. No adverse effects on behaviour (either breeding or survival rate), were observed during the study. Data were collected in the daytime only, with a duty cycle of approximately 13 h in both regions, and a subset of tracks were sampled at relatively high resolution. First, we used tracks (Israel and France) sampled continuously all day at 1–3 s intervals (hereafter high-resolution data) during flight, as determined onboard by a threshold instantaneous speed value (more than 2 m s⁻¹). Second, we used tracks (Israel) sampled at 1 min intervals (hereafter low-resolution). In addition, triaxial acceleration (ACC) data were sampled in Israel every 1 or 5 min with 10 Hz bursts lasting 3.8 s, to identify flapping and feeding behaviours [1,16]. Flight altitudes above ground level (i.e. ‘absolute altitude’ in aviation terminology) were calculated by subtracting ground elevation (referenced to the WGS84/EGM96 geoid) and the estimated difference between the geoid and ellipsoid for each GPS sample (referenced to the WGS84 ellipsoid). The ground elevation map was based on approximately 30 m resolution ASTER GDEM data (https://lpdaac.usgs.gov/data_access/data_pool), and negative altitude above ground level values (frequently occurring near gorges) were set to be zero. To explore the effect of environmental conditions on flight decisions, we annotated the tracks with meteorological data using the regional atmospheric modelling system [43] (see electronic supplementary material, S2 for details on track annotation with environmental data).

(c). Track segmentation and identifying path characteristics

In the high-resolution dataset, we identified the fundamental movement elements using a two-step process. First, we identified thermal soaring elements by searching for self-intersections of the path in two dimensions (indicating loops or circles on a horizontal plane). Because a typical thermal circle takes approximately 15 s, we set a minimum of 45 s and positive net altitudinal gain for elements defined as thermal soaring. Second, we identified interthermal gliding and linear soaring elements that contained at least 90% of the fixes with either positive or negative altitudinal change, respectively; we also excluded other elements that failed to satisfy either of these conditions. Linear soaring elements were below 10% of the soaring elements and were excluded from the analyses. In our analyses, we focused on subsets of the data that were longer than 120 s (i.e. made up of a sequence of the same fundamental movement elements, such as in extended gliding or continuous thermal climbing) in contrast to, say, flights that mixed climbing and gliding into a fundamental movement element. We logged the type of each fundamental movement element (thermal soaring or inter-thermal gliding), its mean vertical speed (commonly abbreviated ‘climb rate’ if more than zero and ‘sink rate’ if less than zero), flight altitude at the beginning of the segment, ground speed, airspeed, tail and side wind components, variance of the wind vector over the specific movement phase.

In the low-resolution dataset, we used the distribution of vertical speed (V_z) and the distance between adjacent GPS locations (D) in order to classify the three fundamental movement elements: (i) thermal soaring is characterized by circular flights with altitude gain (V_z > 0 m s⁻¹, D < 500 m within a minute); (ii) inter-thermal gliding by relatively directional flights with altitude loss (V_z < 0 m s⁻¹) and (iii) linear soaring is a directional flight with zero or positive altitude gain (V_z > 0 m s⁻¹, D > 500 m). Low-resolution daily tracks were classified into home-range foraging or long-range movements based on the distance from the mode main roost of the population [36], and based on daily travel distance (DTD) and the straightness of the daily path (SDP) which was calculated as the maximum daily displacement divided by the distance travelled from roost to the location of maximum daily displacement.

We classified home-range foraging (distance to mode roost smaller than 300 km, DTD smaller than 200 km and SDP larger than 0.5) and long-range movements (distance to mode roost greater than 300 km, DTD larger than 200 km and SDP larger than 0.7). Foraging movements were observed at the high-resolution dataset focusing on days with a foraging effort (DTD > 15 km). Feeding events were defined based on ACC identification of feeding behaviour in Israel and by recognizing stops on the ground in feeding station or outside the roosts area in France. Here, we distinguished between outbound flights in which individuals started from a roost/nest and ended in a feeding event and inbound flights where individuals started from a feeding place and were directed towards a recently visited roost (return trip).

(d). Data analysis, model comparison and selection

To understand the differences in vulture flight we focused on three decision-making proxies: (i) soaring–gliding efficiency, as a proxy for time minimization, was estimated by calculating the distance travelled when gliding divided by the preceding thermal soaring duration (i.e. soaring–gliding efficiency); (ii) flapping activity, as a reverse proxy for energy minimization, was estimated whether a flight segment included flapping flight; and (iii) the RAFI as a proxy for risk minimization. RAFI values are based on the glide polar that was calculated using average values for the species of body mass, wing area and wingspan [25] (see table 1). A RAFI value of zero represents risk-prone flight behaviour with higher airspeed, and a value of unity stand for risk-averse flight behaviour [26]. However, birds may fly non-optimally (i.e. out of the range of the best glide to ‘MacCready’ speed) and therefore the values are not limited to this interval (0–1). We also verified our assertion (see §1) that cross-country speed should correlate with soaring–gliding efficiency, but not with the other two proxies (electronic supplementary material, figure S1).

To investigate the factors affecting vultures' decisions, we analysed separately the high- and low-resolution datasets using general linear-mixed models (GLMM) with a multimodal-model inference framework. The response variables were the three decision-making proxies, and the predictors consisted of external factors reflecting wind conditions (tailwind, side wind and variance of the wind velocity over the movement phase), internal factors, such as age (juveniles under two months, representing individuals that may exhibit inferior flight skills, and older than two months), sex (M, F, unknown) and breeding status (breeding and non-breeding), and categorical classification of movement type to home-range foraging versus long-range movements, and inbound versus outbound flight. Soaring–gliding efficiency and RAFI were modelled using a Gaussian distribution, and flapping activity was modelled using a binomial distribution. No significant correlations were found among the proxies (electronic supplementary material, figure S1). We also accounted for variation in flight altitude, gliding speed and climb rate: these parameters also reflect decision-making, but cannot be directly associated with either time, energy or risk minimization; hence, we explored their relationships with the decision-making proxies and their variation across movement phenomenon and movement phase. We used two-sample t-tests for testing differences in DTD, daily maximum displacement and flight altitude between the regions (electronic supplementary material, figure S2). Models were ranked based on Akaike's information criterion (AICc), and goodness of fit of the best model was evaluated with marginal and conditional R² [44]. Statistical analyses were performed using R v. 3.2.2 statistical software (R Development Core Team 2009) with lme4 package [45].

3. Results

In the low-resolution dataset, we tracked 38 individuals over 105.9 ± 99.9 days. In the high-resolution dataset, we tracked 19 individuals over 29.9 ± 29.1 days in Israel (2010–2015) and eight individuals over 8.9 ± 9.5 in France (2011–2012). These datasets jointly represent a total of 4.4 million GPS fixes during flight (see table 1 for summary statistics).

(a). Long-range movements versus home-range foraging

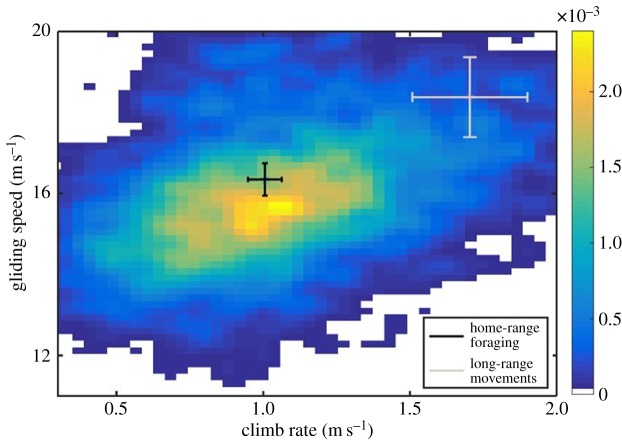
Gliding speeds during inter-thermal glides and climb rates in thermal soaring were higher during long-range movements than during home-range foraging (figure 2). Results from the GLMM models for the decision-making proxies show that during long-range movements vultures (i) had higher soaring–gliding efficiency (figure 3a); (ii) flapped less frequently (figure 3b); and (iii) displayed lower RAFI values (i.e. more risk-prone flight) compared with home-range foraging (figure 3c). Furthermore, compared with home-range foraging, the mean daily flight altitude was higher during the long-range movements (figure 4a). Inexperienced individuals (less than two months of flight) exhibited lower soaring–gliding efficiency, more flapping activity and slightly lower RAFI compared with older individuals. Sex had no significant effect on either of the proxies (table 2 and electronic supplementary material, S3).

Figure 2.

Probability–density plot of the daily gliding ground speed, as a function of the daily climb rate during thermal soaring (yellow colours represent higher probabilities). The 95% confidence intervals around the mean for home-range foraging (black) and long-range movements (grey) are presented. The figure is based on the low-resolution dataset collected in Israel.

Figure 3.

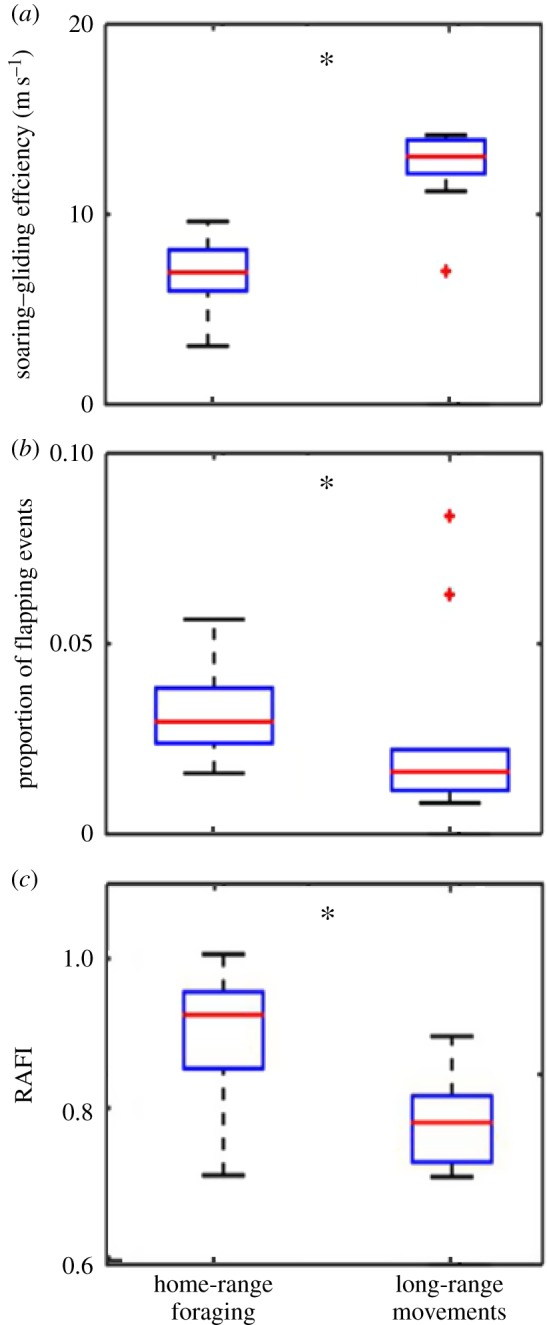
Differences in time-, energy- and risk-related proxies for soaring–gliding decision-making between two large-scale movement phenomena. (a) Soaring–gliding efficiency measured by dividing cross-country distance during inter-thermal glides by the time soaring in thermals; (b) proportion of flapping events and (c) the estimated RAFI (higher values indicate risk-averse flight behaviour). The boxplots represent averaged individual data of daily means with population median (red line), 1.5 interquartile distance (whiskers) and outliers (red crosses). See table 3 for statistical modelling of these currencies (asterisks indicate significant statistical differences with p < 0.05). The figure is based on the low-resolution dataset.

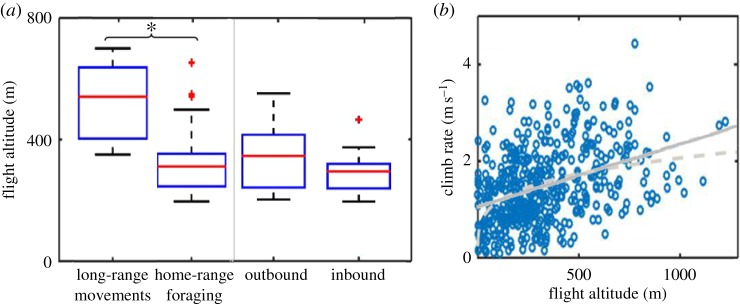
Figure 4.

Variation in flight altitude above ground across different scales. (a) During long-range movements individuals showed higher mean flight altitude compared to home-range foraging movements (large-scale analysis based on the low-resolution dataset). No significant differences were found between the movement phases (inbound and outbound flights, based on intermediate scale analysis of the high-resolution dataset). The boxplots represent averaged individual data of daily means with median (red line), 1.5 interquartile distance (whiskers) and outliers (red crosses). Asterisks indicate significant statistical differences. (b) A positive trend was observed between flight altitude and climb rate at thermal soaring elements (based on the high-resolution dataset). The solid line is a linear fit and the dashed line is a power-law fit.

Table 2.

Soaring–gliding decision-making at different movement phenomena based on the low-resolution dataset collected in Israel. Vultures made different decisions during long-range movements and home-range foraging as indicated by the strongest effect movement phenomena have on each of the dependent variables. The estimates and t-Wald values for the different effects on the response variables (Y; columns) were modelled using GLMMs with individual's identity and time of day as random factors. Model fitted was Y approximately 0 + (1 | individual) + (1 | time) + movement phenomena + age + sex + altitude. N = 11 332 observations from 38 birds. The reference categories were home range for movement phenomena, juveniles for age and females for sex. Significance codes are: n.s., not significant, *0.01–0.05, **0.001–0.01, ***<0.001. For full model results, see electronic supplementary material, S3.

fixed effects	soaring–gliding efficiency		flapping activity		RAFI
	estimate	t-Wald	estimate	t-Wald	estimate	t-Wald
movement phenomena	1.10	21.3***	−2.02	−3.9***	−0.49	10.5***
age	0.28	2.6**	−0.74	−6.3***	0.16	8.5***
sex	0.15	1.3 n.s.	−0.24	−1 n.s.	0.01	0.3 n.s.
flight altitude	0.59	19.1***	−0.09	−1.7 n.s.	−0.07	−11.7***

(b). Inbound versus outbound flights

At intermediate scale, we focused on the different movement phases within foraging, using the high-resolution dataset. During inbound flights, individuals showed higher soaring–gliding efficiency, less flapping activity and were more risk-prone (figure 5a) compared with outbound flights (table 3 and electronic supplementary material, S4). Outbound flights were longer than inbound flights, with a mean DTD of 87.5 ± 61.5 km and 51.2 ± 29.9 km, respectively. Overall, the foraging patterns in the two studied regions were quite similar (table 1). Vultures in France travelled at lower flight altitudes than in Israel (ca 340 versus 460 m, respectively, table 1; two-sample t-test, t_18,7 = 4.6, p < 0.001) and remained closer to their starting point (daily maximum displacement of 24 versus 33 km, respectively, table 1; t_18,7 = 2.3, p = 0.02; see also electronic supplementary material, figure S3), but there were no differences in DTD (t_18,7 = 1.3, p = 0.2) and ground speed (t_18,7 = 1, p = 0.3).

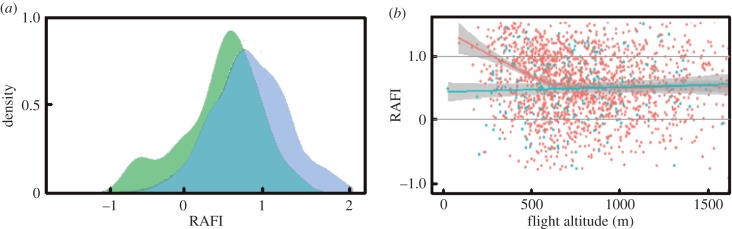
Figure 5.

Risk-averse flight behaviour in foraging movements. (a) Scaled kernel density plot for outbound (blue) and inbound flights (green) shows individuals flew in a more risk-prone manner (i.e. lower RAFI values) during inbound flights. (b) RAFI as a function of flight altitude of breeding individuals (blue) and non-breeding individuals (red). Breeding status had no effect on RAFI at high flight altitudes, but non-breeding vultures were more risk-prone at low-flight altitudes. Horizontal lines mark RAFI values of zero and unity that represent optimal (‘MacCready’) speed and best-glide speed, respectively.

Table 3.

Soaring–gliding decision-making during inbound and outbound flights (movement phase) based on the high-resolution dataset collected in Israel and France. The estimates and t-Wald values for the different effects were obtained using GLMMs for the response variables (columns) with an individual identity and time of day as random factors (flapping activity is based on the Israel dataset only). Competing models were ranked with AIC and only predictions that were included in the best fitted model are presented. n = 615 observations from 21 birds. Significance codes are: n.s., not significant, *0.01–0.05, **0.001–0.01, ***<0.001. The reference categories were outbound flights for movement phase, juveniles for age and females for sex. For full model results and model comparison, see electronic supplementary material, S4.

fixed effects	soaring–gliding efficiency		flapping activity		RAFI
	estimate	t-Wald	estimate	z-Wald	estimate	t-Wald
movement phase	0.20	12.2***	0.26	−3.5**	−0.13	3.6***
breeding					−0.01	−0.2 n.s.
age	−0.04	−1.8 n.s.	−0.2	−0.2 n.s.	0.07	3.9***
sex	−0.01	−0.5 n.s.			−0.04	−0.2 n.s.
flight altitude	0.11	7.3***	−0.13	0.2 n.s.	−0.05	−2.9**
tailwind					−0.38	−26.2***
side wind					−0.07	−5.3***
wind variance	−0.02	1.6 n.s.			0.04	2.8**
marginal/conditional R2	0.07/0.11		0.44/0.50		0.47/0.57

Older individuals tended to take less risk (higher RAFI) than juveniles. Also at this scale, sex had no significant effect in any of the proxies (table 3 and electronic supplementary material, S4). Breeding individuals did not show higher soaring–gliding efficiency than non-breeding birds, but were more risk-prone and flew at lower flight altitudes (figure 5b). Individuals showed lower RAFI values when flying with stronger tail or side winds, but higher values in conditions of high variance in wind speed. Flight altitude showed a positive relationship with the achieved climb rate (power-law coefficient, a = 0.49 ± 0.13, b = 0.21 ± 0.06, R² = 0.11; figure 4b), had a positive effect on soaring–gliding efficiency and a negative effect on RAFI (table 3).

4. Discussion

We examined the decision-making process of large terrestrial birds specialized in soaring–gliding flight and its consequences for flight performance by analysing movement tracks over several spatio-temporal scales. We introduce a simple framework to analyse the three major costs of soaring flight, using three different, uncorrelated proxies, one for each type of cost. Proxy values were estimated using a dataset of unprecedentedly high temporal resolution to evaluate vultures' context-dependent decisions across multiple scales, and to assess how changes in the internal state of individuals and external conditions affect these decisions. Overall, individuals considered time, energy and risk trade-offs in a fairly consistent way across different spatio-temporal scales, ranging from minute-long local thermal soaring–gliding cycles to long-range flights spanning hundreds of kilometres. We attribute the consistency across a range of scales, as we further explain below, to similarity in the uncertainty in movement outcomes at these different scales. To the best of our knowledge, this is the first time that this type of analysis has been carried out across such a range of scales in soaring birds, presumably because the movement data of sufficient detail and duration have not been available in the past.

(a). Comparison of decision-making proxies between movement phenomena and phases

During long-range movements, vultures minimized both time (higher soaring–gliding efficiency; i.e. gained longer forward displacement in relation to time spent climbing in thermals) and energy expenditure (less flapping activity), and flew in a more risk-prone manner (lower RAFI) than during home-range foraging (figure 3). During such migration and long-range forays, vultures presumably traverse unknown landscapes though in a known direction. The motivation in these flights is probably to complete the journey as fast as possible [30], as suggested for short- and long-distance migratory raptors, thereby opting to take risks associated with high gliding speed [14]. Furthermore, during these long-range movements, vultures feed less frequently [36], highlighting the importance of reducing energy expenditure during these periods of low intake. The tendency to minimize time or energy may not be exclusive of one another and may be affected by motivation, such as in the case of spring versus autumn migration [15]. By contrast, during home-range foraging, individuals search for food in familiar landscapes. Despite reliance on feeding stations, food locations are rather unpredictable, because carcass drop-off is variable in time and place (see electronic supplementary material, S1) [1,33]. Therefore, food search might take time, forcing individuals to remain aloft while minimizing energy expenditure and to favour a more risk-averse flight behaviour. Yet, the relatively high availability of food within the home range probably relaxes the acute need to minimize energy expenditure experienced during long-range movements.

These explanations are further strengthened by considering the higher flight altitudes during long-range movements compared with home-range foraging. Flying at higher altitudes offers an insurance from possible costs that may rise during risk-prone flights: when flying high, a bird has more time to act before reaching the ground [26], and flying high is associated with an increased climb rate (figure 4b), presumably reflecting better conditions or increased options in choosing stronger thermals to reach overall higher cross-country speeds [46]. Vultures foraging within their home range, however, fly primarily to locate food on the ground. Hence, they may fly at relatively low altitudes (between 300 and 400 m) [47], as also shown in an interspecific comparison of vultures foraging, where a negative relationship between flight altitude and ground speed was found [48]. The higher flapping activity during home-range foraging may also reflect higher expected food intake. Alternatively, frequent flapping may not be related to actual cross-country flight and might result from more landing and take-off events at feeding sites, which often require flapping bouts before finding a suitable thermal. We also note that individuals flapped mostly at the beginning of interthermal glides (electronic supplementary material, figure S4), and not at the end of the segment, as would be expected if individuals take excessive risk and fail to find the next thermal. The flapping bouts we observed might act like wing tucks proposed to reflect fine-scale adjustments to turbulent gusts [49] or intensive sink when leaving thermals.

The above-mentioned differences at the larger scale are mirrored at our intermediate scale, despite the difference in the spatio-temporal scale itself. As with the long-range movements, foraging birds taking inbound flights minimized both time and energy, and flew in a more risk-prone manner compared with outbound flights (table 3). We suggest that these differences reflect relaxation from the need to search for food that characterize outbound but not inbound flights, coupled with certainty about the movement destination in the latter but not the former case. As for long-range movements, when vultures flew in a more risk-prone manner, we would have expected higher flight altitudes during inbound flights compared with outbound flights, but we did not find such differences. This could be explained by the expected effect of additional food load of foraging birds returning to their central place after feeding (inbound flights). Heavier birds should climb more slowly in thermals and sink faster while gliding; hence they are expected to fly at lower altitudes in home-range foraging than in long-range movements. Because extra weight also yields faster airspeed when gliding, individuals may compensate for this food-load handicap and for the associated longer time required to climb thermals by faster gliding; this explains our finding that soaring–gliding efficiency was actually higher during inbound flights. Similar compensation was found in dynamic soaring seabirds that change their behaviour to account for wind drift and extra meal-load during inbound flights [50]. While no significant variation in flight decisions was found between inbound and outbound flights in other studied terrestrial soaring birds (the lesser kestrels [32]), foraging-related flight decisions await further investigation.

(b). Internal and external factors explaining variation in decision-making proxies

The effect of individual's age was consistent across scales. Vultures in their first two months of flight showed lower soaring–gliding efficiency, used more flapping and had higher RAFI. These differences indicate suboptimal flight performance, probably owing to the need for young birds to learn the difficult technique of soaring–gliding flight [51]. The effect of such differences may be enhanced at larger scales with other age-related differences, such as better migratory performance [52], or superior navigation capacity of adult birds [4,15,53], which may affect survival rates [52]. Sexes did not differ in their flight performance, as expected for this species with similar morphology and chick rearing behaviours [33]. Breeding individuals were slightly more risk-prone, mainly at low-flight altitudes than non-breeders (figure 5), but overall we did not find significant differences in time, energy and risk considerations between breeding and non-breeding birds. This finding is surprising, because breeding entails strong demands on vultures, as it does on most bird species, especially in food provisioning stages [54]. Breeding individuals may increase their overall food intake in order to meet their nestling needs by altering either their behaviour during feeding (being more aggressive and dominant at feeding events, decreasing duration of rests), or activity hours (making few foraging bouts in a day). Overall, these behaviours are expected to result in higher energy expenditure than non-breeding individuals [55,56].

Movement decisions were affected by local environmental conditions. During inter-thermal gliding, individuals took more risk with increased tailwinds, presumably because ground speed was higher and the probability of reaching the next thermal increased. The finding of frequent risk-prone flight in side winds may be attributed to minimizing the drift resulting from side winds [57,58]. In addition, as expected, higher environmental unpredictability (measured by variance in wind velocity) was associated with more risk-averse flight. The response of raptors to variation in environmental resources has also been found in golden eagles (Aquila chrysaetos) that change their flight strategy over the migratory season [59]. It has been shown in another specialized (dynamic) soaring–gliding bird, the wandering albatross (Diomedea exulans), that climate change resulted in changes in wind patterns that increased flight efficiency which, in turn, has increased their breeding success over the past 20 years [60]. Future studies should determine how soaring–gliding birds recognize changes in their environments, and whether or not they use them differently.

To better understand how individual vultures cope with the challenges and trade-offs they face during flight, we need to characterize how context affects variation in their movement patterns at different scales. A mechanistic understanding of decision-making processes and the resulting movement patterns of mobile animals might enhance our ability to predict their response to their changing environment. Here, we suggest that vulture flight behaviour (e.g. choosing riskier flight or more energetically expensive flight) reflects a response to particular dilemmas that need to be solved. These dilemmas converge to management of uncertainty about movement destination or outcome, which leads to similar behavioural response in terms of three main movement costs at different spatio-temporal scales. The findings obtained here are likely generalizable to other large soaring–gliding birds, and perhaps other animals as well. Formulating and testing this and other generalizations are likely to become increasingly feasible with the accumulation of high-quality datasets for animals on the move.

Ethics

The Israeli project was conducted with permission from the Israel Nature and Parks Authority and the ethics committee of the Hebrew University of Israel (NS-07-11063-2). The French study was conducted with the permission of the Centre for Bird Population Studies (CRBPO) of the Natural History Museum (MNHN, Paris). All care was taken to reduce discomfort to the birds. Logger mass was less than 1% of bird body mass. Logger harnesses were designed to fall off after a few years to prevent these long-lived birds carrying their load during their entire life.

Data accessibility

The data used in the manuscript are available under the following Movebank (http://www.movebank.org/) projects: Eurasian Griffon Vultures 1 Hz HUJ (Israel), Eurasian Griffon Vultures 1 min HUJ (Israel) and Eurasian Griffon Vulture in Grands Causses (France) - 0.3 Hz dataset. Should anyone wish to use these data please contact R.N. regarding the data collected in Israel and O.D. regarding the data collected in France.

Authors' contributions

R.H., O.S., W.M.G., R.N. and O.D. designed the study; R.H., O.S., O.D., O.H. and J.F. performed the fieldwork; W.B. provided materials and processed the GPS data; R.H., O.S. and N.H. analysed the data. R.H., R.N., O.D. and O.S. led the writing of the manuscript, and all other authors contributed substantially to revisions and gave final approval for publication.

Competing interests

The authors have no competing interests.

Funding

This Israeli project was supported by the NIH (GM083863 to W.M.G.), U.S.-Israel bi-national Science Foundation and the special BSF Multiplier Grant Award from the Rosalinde and Arthur Gilbert Foundation (BSF255/2008 to R.N. and W.M.G.), and the Adelina and Massimo Della Pergola Chair of Life Sciences and the Minerva Center for Movement Ecology (to R.N.). The French project was supported by ANR (ANR-07-BLAN-0201), coordinated by F.S. and Carmen Bessa-Gomes. R.H. was supported by the Israeli Ministry of Science, Technology and Space. O.S. was supported by NSF grant (DEB-1456730 to A Sih). J.F. was supported by the French national parks (Parc National des Cévennes, Parc National des Pyrénées and Parcs Nationaux de France) and the doctoral school ‘Gaia’ from University of Montpellier.