Tendon-Driven Continuum Robot for Neuroendoscopy: Validation of Extended Kinematic Mapping for Hysteresis Operation

Abstract

Purpose

The hysteresis operation is an outstanding issue in tendon-driven actuation—which is used in robot-assisted surgery—as it is incompatible with kinematic mapping for control and trajectory planning. Here, a new tendon-driven continuum robot, designed to fit existing neuroendoscopes, is presented with kinematic mapping for hysteresis operation.

Methods

With attention to tension in tendons as a salient factor of the hysteresis operation, extended forward kinematic mapping (FKM) has been developed. In the experiment, the significance of every component in the robot for the hysteresis operation has been investigated. Moreover, the prediction accuracy of postures by the extended FKM has been determined experimentally and compared with piecewise constant curvature assumption (PCCA).

Results

The tendons were the most predominant factor affecting the hysteresis operation of the robot. The extended FKM including friction in tendons predicted the postures in the hysteresis operation with improved accuracy (2.89 mm and 3.87 mm for the single and the antagonistic tendons layouts, respectively). The measured accuracy was within the target value of 5 mm for planning of neuroendoscopic resection of intraventricle tumors.

Conclusion

The friction in tendons was the most predominant factor for the hysteresis operation in the robot. The extended FKM including this factor can improve prediction accuracy of the postures in the hysteresis operation. The trajectory of the new robot can be planned within target value for the neuroendoscopic procedure by using the extended FKM.

Introduction

Endoscopic neurosurgery has proven to be useful in the management of noncommunicating hydrocephalus and intracranial cysts, as well as in tumor biopsy procedures. The utility of endoscopic approaches to the ventricular system of the brain provides minimally intensive access to these lesions, whose location in a region of numerous important neurovascular structures renders surgical approaches potentially hazardous [1]. After the first report published by Gaab in 1998 [2], neuroendoscopy has increasingly focused the interest of neurosurgeons on further expanding this approach to the pure endoscopic resection of soft tumors smaller than 2 cm [1–4]. Specifically, this approach is beneficial for deep-seated lesions in a posterior third ventricle or pineal region [2–4]. Feletti, et al. reported that a flexible endoscope can fully use its bending capability to access tumors on the posterior third ventricle from a right precoronal burr hole, while reducing the mechanical stress on the brain [3]. Although this approach provides a safe, effective way to radically resect small soft tumors in difficult locations, Feletti, et al. stressed that only expert endoscopists should perform the procedure. As aspirated fragments of the tumors were very small, inadvertent aspiration of surrounding structures must be avoided by carefully and accurately positioning the tip of the endoscope on just the tumoral portions [3]. Therefore, further improvements to this approach are needed to enable a wider range of endoscopists to perform this procedure.

A potential solution to lower the difficulty of this procedure is to house the flexible camera in a multi-section continuum robot. By using multiple bending sections, the endoscopists can achieve an optimal tip position corresponding to topology of the tumor and the surrounding portions and can control other degree-of-freedom (DOF) motions to adjust the tip position in a confined space in the ventricles. Moreover, planning of accessing postures of the multi-section continuum robot before the endoscopic procedure for each patient may provide effective and minimally invasive access to the ventricles as suitable for the individual. An estimation of the robot posture is a key to success in the precision control and planning.

Among different actuation principals of the multi-section continuum robot, in particular, a tendon-driven continuum robot is an ideal choice for neuroendoscopy, as the tendon-driven continuum robot can provide adequate power through narrow, tortuous pathways and allow the actuators to be located at a safe distance from the patient [5]. While these tendon-driven mechanisms are commonly applied as manually-operated instruments, noteworthy efforts have been made to robotize them for catheters [6–12] and endoscopes [13–16] with higher DOF motion. In particular for tendon-driven endoscopes, tendon-driven mechanism is used to aim cameras to intended surgical sites while avoiding complexity of control for multiple bending sections and multiple tendons. In catheter applications, the tendon-driven mechanism is useful to aim catheter tip to a target lesion, such as optimal ablation sites in a catheter ablation therapy for atrial fibrillation.

In the safe and efficient operation of tendon-driven mechanism, the accurate estimation of the posture of the devices is mandatory. Most common approaches researchers have taken are kinematic modeling with simplification that captures salient features for their application. Jones et al. [17,18] proposed a constant curvature assumption (PCCA) for the kinematic model of the tendon-driven continuum robot. The constant curvature can facilitate analytical frame transformations and additional analysis of topics such as differential kinematics and real-time control [5]. Camarillo, et al. [6,7] reported a tendon-driven steerable catheter using multisections. For independent control of multisections, they proposed a linear beam configuration model that transformed beam configuration to tendon displacement, including both mechanical and geometrical coupling among multisections in intra-cardiac catheter operations. Rucker, et al. [19] presented the model for kinematics and dynamics of the tendon-driven continuum robot with general tendon routing paths. The model was derived by coupling the classical Cosserat-rod and Cosserat-string models, and took into account a general external loading condition.

In some of the studies above, hysteresis operation has been reported to be a cause of error in estimating the posture of tendon-driven devices. Camarillo, et al. [6] observed the hysteresis in their tendon-driven robot, and estimated that the hysteresis may have been stemmed from the friction between tendons and robots. Penning, et al. also reported in [20] that their tendon-driven robotic catheter using the PCCA showed strong dependence on pretensioning of tendons. Penning et al. also stated that this hysteresis operation may be caused by friction between tendons and their guide structures [20]. From these articles, one can conclude that 1) the tension profile across the tendons cannot be assumed to be uniform, 2) the tension profile depends on the time history of applied forces, and 3) the PCCA may not be suitable for predicting the hysteresis operation. To the best of our knowledge, however, no study has modeled hysteresis operation in kinematic modeling of tendon-driven robot.

In this study, we attempted to overcome the aforementioned issues by extending the tension propagation model that is known to be more suitable than PCCA model in tendon-driven robot. In the extended tension propagation model, we newly developed a predictive hysteresis model based on time-varying direction and magnitude of friction forces between the pulling tendons and the robot’s core structure. To test this extended propagation model, we also developed tendon-driven continuum robot miniaturized to the size of a real neuroendoscope, and observed the improvement brought by the extended propagation model over the PCCA model.

Materials and Methods

Miniaturized tendon-driven continuum robot for neuroendoscopy

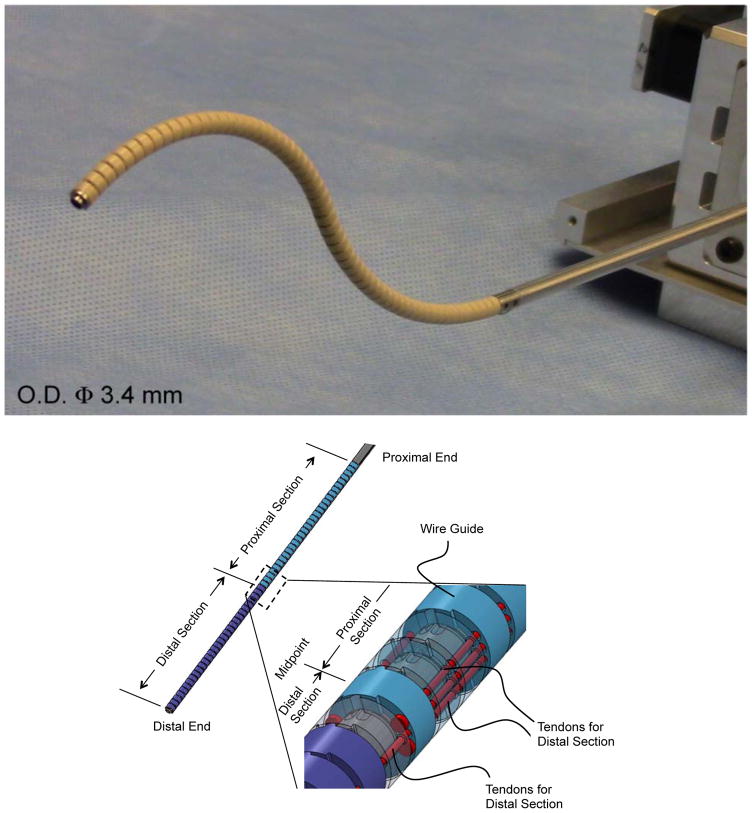
The tendon-driven continuum robot we newly miniaturized for this study is intended for use in neuroendoscopy and has an outer diameter (O.D.) of 3.4 mm, a length of 120 mm, and a 1.4 mm-diameter tool channel (Fig. 1). The O.D. of the robot is indistinguishable to the actual sheath size of neuroendoscopes in present clinical practice [21]. All subsequent modeling and validation were performed based on this newly developed tendon-driven robot.

Fig. 1.

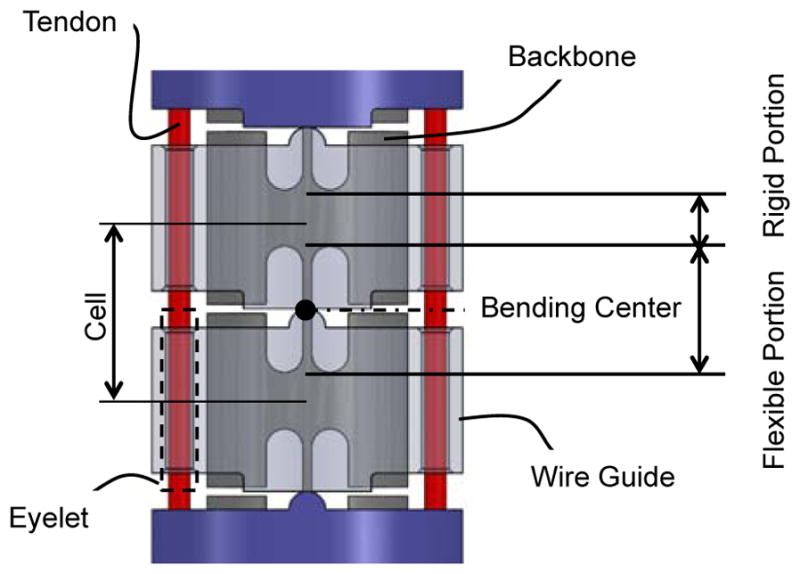
Tendon-driven continuum robot. (Top) Perspective view of the tendon-driven continuum robot. (Center) Perspective view of the component formation of the robot. The robot comprises two bending sections, i.e. the distal and the proximal sections. Two pairs of three tendons run through the wire guides. One antagonistic pair of tendons is terminated at the distal end. Two antagonistic pairs of tendons are terminated at the midpoint of the robot. (Bottom) Side view of the cascaded spring system. The wire guides are made of polyether ether ketone (PEEK), and the backbone is monolithically machined from super elastic TiNi alloy (Nitinol) with laser cutting. The hinges of the wire guides are aligned with the bending center of the flexible portion in the backbone by stacking the wire guides without an additional alignment process

The articulation structure of this robot comprises two bending sections, each with one degree of freedom (Fig. 1, Center). Two groups of three tendons run through eyelets in wire guides. The tendons are spread apart 1.4 mm from the centroid of the robot. The one antagonistic pair of tendons (tendons for distal section in Fig. 1, Center), which is on the bending plane, is fixed at the distal end of the robot. The other two pairs of tendons (tendons for distal section in Fig. 1, Center) are fixed at the midpoint of the robot. These pairs of tendons run through the equidistant eyelets symmetrically located from the bending plane. By pulling tendons terminated at the distal end or the midpoint, the two bending sections can bend independently. For instance, to perform an S-shaped posture in Fig. 1 Top, the tendons terminated at the distal end pull the distal section toward opposite direction from the bending direction of the proximal section pulled by tendons terminated at the midpoint.

The bending sections comprise cascaded spring systems—referred to as the cell (Fig. 1, Bottom). A monolithic backbone includes rigid and flexible portions and extends from a proximal end to the tip of the robot. These flexible and rigid portions render the cells as tandem rotational springs. Each cell is a unit of curvature when bent by the robot and has a length of 2 mm. The bending stiffness of one cell is 8.6 × 10⁻³ Nm/rad measured after fabrication. Each section of the robot has thirty cells.

The wire guides include trapezoidal and curved projections and are piled up along the backbone. The trapezoidal and curved projections touch each other between adjacent wire guides and create a pivot aligned to a bending center in the flexible portion of the backbone. Since a flat plane on the trapezoidal projection contacts the curved projection, the pivot can narrow its touching area into a line. Therefore, this configuration enhances the rolling motion of the pivot while minimizing slipping motions during robot articulation.

Kinematic mapping with a tension propagation model with friction propagation

Modeling tension propagation in a tendon-driven robot with careful attention to friction between the tendon and the surrounding structure has been actively discussed in literature, yet without attention to hysteresis operation. Zhang et al. proposed a kinematic model that included constant friction in a single tendon for steerable electrode arrays [22]. This model maps the tension in a single tendon to the robot posture, accounting for the constant friction force and the elasticity of the robot. Kato et al. [23] presented the tension propagation model with varying friction along the course of propagation. This model was applied to an antagonistic tendon pair in a pull-pull configuration, and found to be accurate at least in the arching motion. Our preliminary study indicated that the Kato et al’s propagation model produces hysteresis operation in the arching and extending cycle. Therefore, here we propose a new a tension propagation model, based on Kato et al’s approach, that hypothesizes that the direction of friction is motion dependent and has to be incorporated into the kinematic mapping of the tendon-driven continuum robot.

Impact of components on hysteresis operation

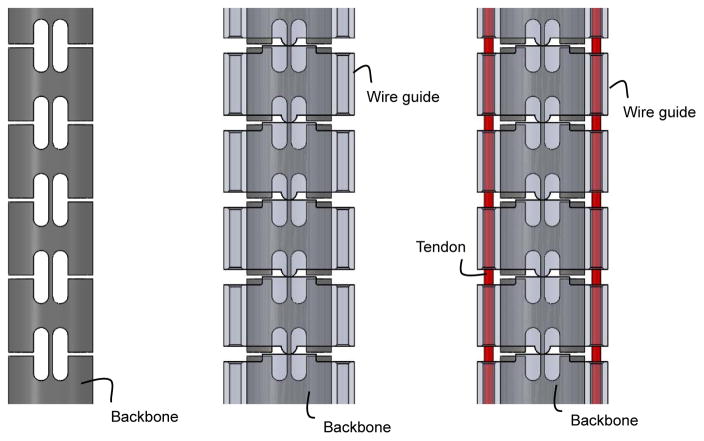
Before we formulated the tension propagation with consideration for the directionality of friction, we measured hysteresis curves of articulation by varying the complexity of physical bending bodies consisting of combinations of or the entirety of the backbone, the wire guides, and the tendons, as follows: the backbone only; the backbone and the wire guides; and all three components (Fig. 2). Our goal was to find an essential set of subcomponents in the tendon-driven robot that affects behavior of the propagation model and motion hysteresis. In the experimental set-up (depicted in Fig. 3), the bending bodies were mounted horizontally to a vertical mounting base. We applied an identical axial compression force of 4 N for both bending bodies with the wire guides and tendons. On a tip of the bending body, we attached a string and put tensions on this string running parallel to the x-axis. While moving the bending body to a planned x position (hereafter, lateral tip position), the tension on the string was measured using a load cell through two round trips of articulation.

Fig. 2.

Side views of bending bodies for significance validation. (Left) Backbone: The backbone is a control of the validation. (Center) Backbone with wire guides: The wire guides fitted the identical backbone to the control. The wire guides were drawn as transparent parts to show the geometrical relationship between the wire guides and the backbone. (Right) Backbone with wire guides and tendons: An antagonistic pair of tendons went through and pressed the wire guides with a pretensioning of 4 N. The wire guides were drawn as transparent parts to show geometrical relationship between the wire guides and the backbone

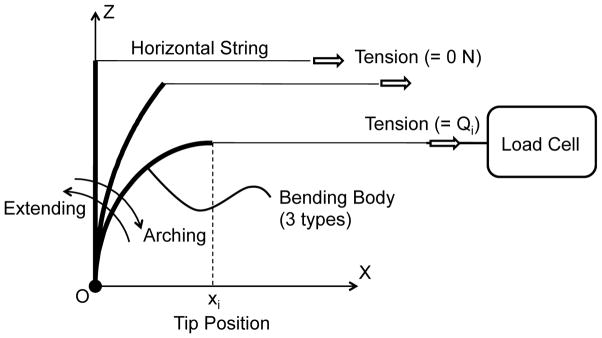
Fig. 3.

Experimental setup of significance validation for hysteresis operation. The setup holds a proximal end of a bending body. A horizontal string pulled the tip of the bending body along in a direction parallel to the x-axis. Lateral positions of the tip were set to the preplanned values by using measurement microscope (STM-UM, Olympus, Tokyo, Japan). A load cell (LTS-2KA, Kyowa Electronic Instruments, Tokyo, Japan) connected to the signal conditioner (CDV-700A, Kyowa Electronic Instruments) measured a pulling tension on the string. The bending body bends along an arching direction by the lateral position of 44 mm and returns to the lateral position of 0 mm (a straight initial position) along an extending direction. These round-trip articulation experiments were performed twice for each bending body to create the hysteresis curve

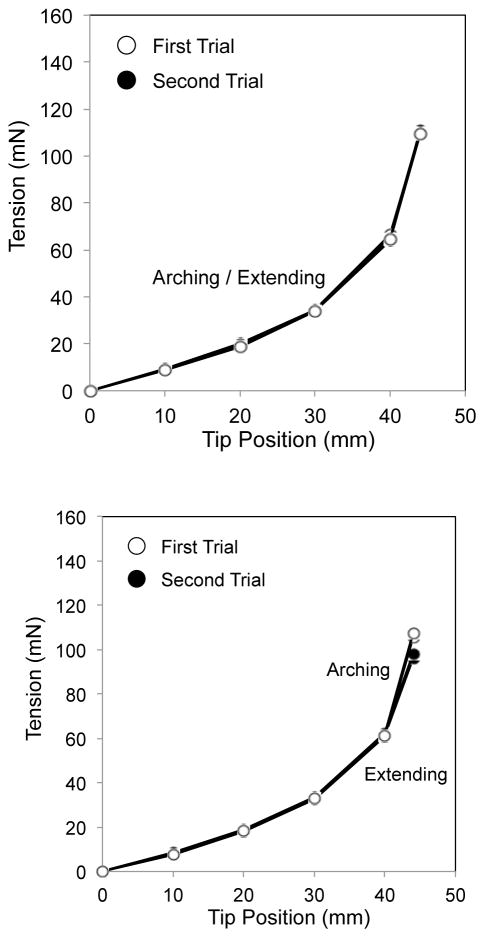
The measured curves of the backbone and of the backbone with the wire guides were identical between the arching and extending motions and did not exhibit the hysteresis operation (Fig. 4, Top and Center). On the other hand, the measured curve of the backbone with the wire guides and the tendons showed the hysteresis characteristic (Fig. 4, Bottom).

Fig. 4.

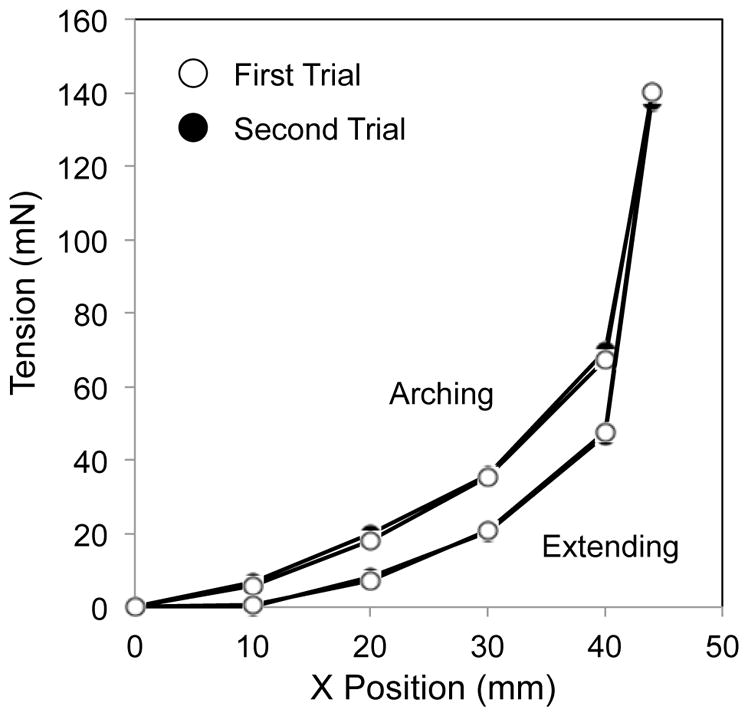
Hysteresis curve in three sets of bending bodies. White circles signify the first trial of bending in arching and extending. Black circles are for the second trial. (Top) The backbone. (Center) The backbone with the wire guides. (Bottom) The backbone with the wire guides and tendons

The tension discrepancy between the values in arching and extending at the same lateral tip position showed tendons were the most significant element for the hysteresis operation (Fig. 5). Thus, we concluded that the friction between the tendons and the wire guides is a primary factor in the hysteresis operation of the tendon-driven continuum robot. We therefore focus on the tendons and the wire guides in kinematic mapping.

Fig. 5.

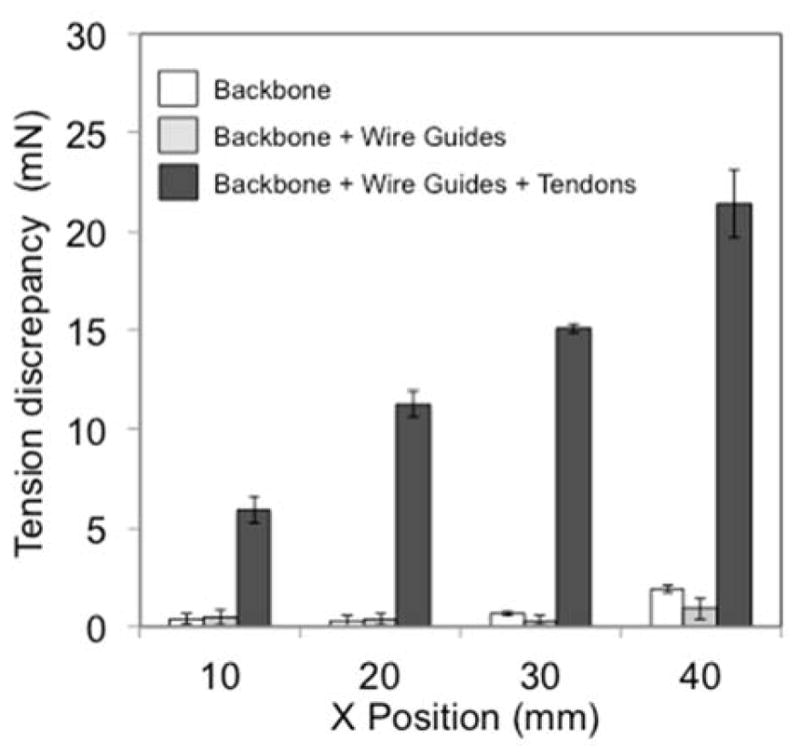
Tension discrepancy in three sets of bending bodies. White, light gray, and heavy gray bars signify the backbone, the backbone with the wire guides, and the backbone with the wire guides and the tendons, respectively. The bars denote averages of the tension discrepancy. Error bars indicate maximum and minimum measured values. The backbone with the wire guides and tendons showed a larger tension discrepancy ranging from 5.9 to 21.4 mN, while the backbone with the wire guides ranged from 0.1 to 1.9 mN. Since the backbone ranged from 0.3 to 1.9 mN for the discrepancy, the wire guides did not induce the hysteresis operation from the curve of the backbone

Extended forward kinematic mapping

This section describes our newly proposed forward kinematic mapping incorporating the directionality and time history of friction between the tendon and the robot’s wire guides.

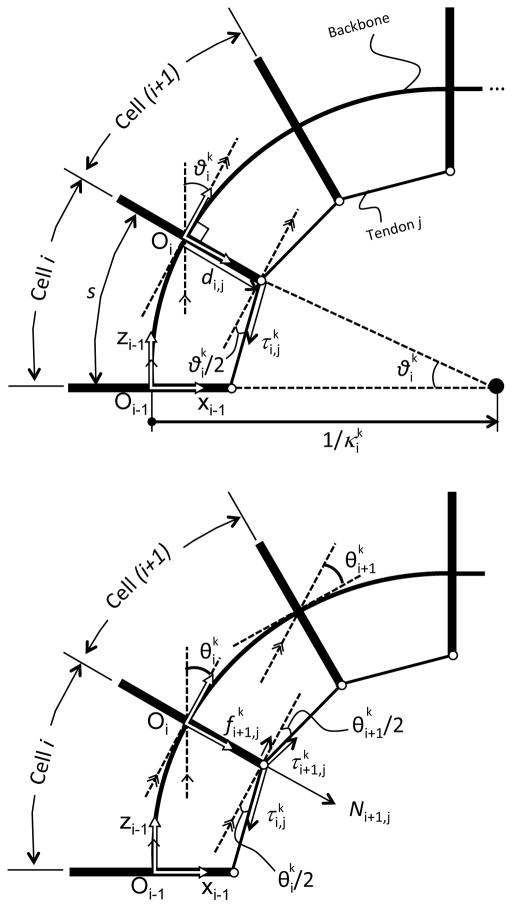
Fig. 6 defines a schematic joint configuration and frame convention of the tendon-driven continuum robot we developed. The frame of each cell in the section of the tendon-driven continuum robot was set as individual joint coordinates. These coordinates represent the robot posture. A set of cells in the section of the robot is modeled as under-actuated joints at each section of the robot. Given the tensions in tendons, the posture (in position and orientation of set of all cells) of the robot is calculated as:

$${\mathit{\tau }}_{\mathbf{1}}\mapsto {\mathit{X}}_{\mathit{c}}$$ (1)

where τ₁ is a tension vector of tendons at cell 1, and X_c is a coordinate vector of the robot.

Fig. 6.

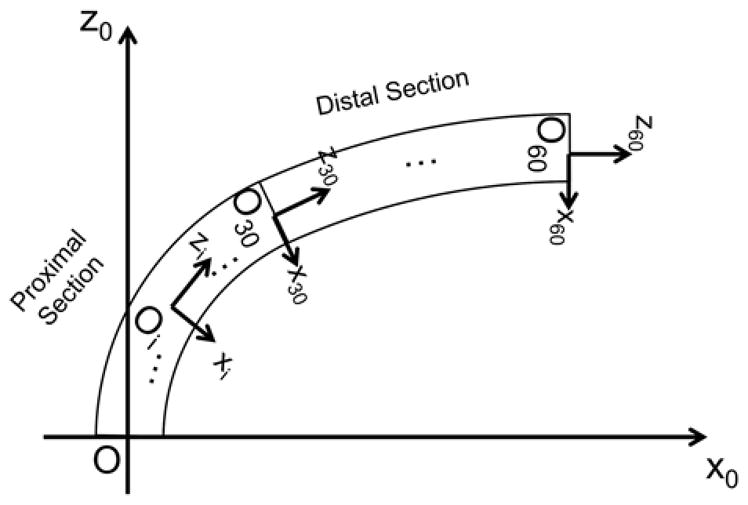
Frame convention of robot. The proximal end of the tendon-driven continuum robot is mechanically grounded on the task space coordinate. The +z-axis is defined as tangent to the base of the robot. Each of the proximal and distal sections of the robot has thirty joint coordinates

In this study, we proposed to extended the forward kinematic mapping (FKM) in form of Eq. (1) presented in [23] to compute the hysteresis operation of the tendon-driven continuum robot. To handle the hysteresis in the extended FKM, we defined bending angles of n cells in the robot from the coordinate of each cell as the following vector of discrete time variables,

$${\mathit{\theta }}^{\mathit{k}}=\left[\begin{array}{ccccc}{\theta }_1^k& \dots & {\theta }_i^k& \dots & {\theta }_n^k\end{array}\right]$$ (2)

where θ^k is the bending angle vector at time k.

In the tension propagation model proposed in [23], as well as our proposed model in this study, we consider the tendon-driven continuum robot as a lumped-parameter model as in Fig. 7. The following are the assumptions for this model:

Fig. 7.

Tension propagation model. (Top) Bending equilibrium at cell i. (Bottom) Tension propagation from cell i to cell i+1. Tension ${\mathrm{\tau }}_{\mathrm{i},\mathrm{j}}^{\mathrm{k}}$ is transformed with friction force ${\mathrm{f}}_{\mathrm{i}+1,\mathrm{j}}^{\mathrm{k}}$ to tension ${\mathrm{\tau }}_{\mathrm{i}+1,\mathrm{j}}^{\mathrm{k}}$

• A1The robot does not extend or contract in the longitudinal direction because the wire guides do not transfer axial forces to the backbone.
• A2Each cell bends into a circular shape. This assumption was confirmed in [6] for a tendon-driven continuum robot without a longitudinal contraction.
• A3The inclined angle between wires and wire guides is small. This assumption is valid when the robot has a sufficient number of cells to make the bending angles of cells small.
• A4Eyelets in the wire guide are assumed to be points. The wire is subject to friction forces at every eyelet. Friction forces and normal forces acting on the wires are concentrated forces. The direction of normal forces is tangential to a backbone in each cell.
• A5Quasi-static equilibrium is satisfied. The friction force is proportional to the normal force at eyelets.
• A6The gravitational force against bending shape is ignored. For a small millimeter-sized continuum robot, this assumption was verified in [24].
• A7The tendons do not extend or contract elastically in the longitudinal direction.

In a typical tendon-driven robot as well as ours, each cell has a backbone with a linear spring constant for bending, as illustrated in Fig. 3. To establish a framework for mapping between tensions in the tendons to the curvatures of all cells, we began by analyzing a simple one-tendon system (Fig. 7). The tendon j applies actuation force ${\mathrm{\tau }}_{\mathrm{i},\mathrm{j}}^{\mathrm{k}}$ at cell i shown in Fig. 3A. Assuming A2 and A3, the moment arm of ${\mathrm{\tau }}_{\mathrm{i},\mathrm{j}}^{\mathrm{k}}$ for cell i equals the offset distance d_i,j of the eyelet from the centroid. Therefore, the bending angles is is described as,

$${\theta }_i^k={\kappa }_i^{k}s=\frac{d_{i,j}{\tau }_{i,j}^k}{K_{\theta }}$$ (3)

where K_θ is the bending stiffness of one cell, and s is a length of one cell. These two parameters are design parameters and constant for every cell and time k.

To determine tension of the tendon at cell i+1, we analyzed propagation of tension in the tendon with a friction force between adjoining cells. Fig. 7 - Bottom shows this relationship, combining bending angles for cells i and i+1. Tension ${\mathrm{\tau }}_{\mathrm{i},\mathrm{j}}^{\mathrm{k}}$ is subjected to friction force ${\mathrm{f}}_{\mathrm{i}+1,\mathrm{j}}^{\mathrm{k}}$ when tension propagates from from cell i to cell i+1 beyond the eyelet. Under assumptions A4 and A5, and assuming $sin({\mathrm{\theta }}_{\mathrm{i}}^{\mathrm{k}}/2)\approx sin({\mathrm{\theta }}_{\mathrm{i}+1}^{\mathrm{k}}/2)$, a tension ratio between ${\mathrm{\tau }}_{\mathrm{i}+1,\mathrm{j}}^{\mathrm{k}}$ and ${\mathrm{\tau }}_{\mathrm{i},\mathrm{j}}^{\mathrm{k}}$ is described explicitly as,

$${\alpha }_{i,j}^k=\frac{{\tau }_{i+1,j}^k}{{\tau }_{i,j}^k}={\left(\frac{1-\mu sin(\mid {\theta }_i^k\mid /2)}{1+\mu sin(\mid {\theta }_i^k\mid /2)}\right)}^{sgn(d_{i,j})sgn\left({\theta }_i^k-{\theta }_i^{k-1}\right)}$$ (4)

where μ is a friction coefficient that is a proportional constant between the friction force ${\mathrm{f}}_{\mathrm{i}+1,\mathrm{j}}^{\mathrm{k}}$ and the the corresponding normal force ${\mathrm{N}}_{\mathrm{i},\mathrm{j}}^{\mathrm{k}}$.

Eq. (4) transforms the tension at cell i to tension at cell i+1 with bending angles of cell i at time k–k–1 and k. Specifically, the sign function in Eq. (4) determines the direction of the friction force against against tension in the tendon to express the hysteresis operation of the robot. The sign function of ( ${\mathrm{\theta }}_{\mathrm{i}}^{\mathrm{k}}-{\mathrm{\theta }}_{\mathrm{i}}^{\mathrm{k}-1}$) denotes the direction of velocity of the robot and the sign function of d_i,j is consistent with the sign of d_i,j on the x-axis in the frame of cell i. When the bending angle increases ( $\left({\mathrm{\theta }}_{\mathrm{i}}^{\mathrm{k}}-{\mathrm{\theta }}_{\mathrm{i}}^{\mathrm{k}-1}\right)>0$) from time k – 1 to time k, tension ${\mathrm{\tau }}_{\mathrm{i},\mathrm{j}}^{\mathrm{k}}$ in Fig. 3B decreases to ${\mathrm{\tau }}_{\mathrm{i}+1,\mathrm{j}}^{\mathrm{k}}$.

The assumption of $sin({\mathrm{\theta }}_{\mathrm{i}}^{\mathrm{k}}/2)\approx sin({\mathrm{\theta }}_{\mathrm{i}+1}^{\mathrm{k}}/2)$ gives an approximation of the variation ratio of the bending angle of adjoining cells in many situations when there are a sufficient number of cells in the robot. Eq. (4) allows one to calculate tension ${\mathrm{\tau }}_{\mathrm{i}+1,\mathrm{j}}^{\mathrm{k}}$ by using only cell i parameters. Using Eqs. (3) and (4) (4) alternately, tensions and curvatures for all cells in the robot are calculated in our newly proposed model. To extend this mapping to a multi-tendon situation, we assumed that there are m appropriately distributed tendons available to us for multisections of the robot. This configuration enables the writing of the tension of tendons at cell i at time k with the following vector:

$${\mathit{\tau }}_{\mathit{i}}^{\mathit{k}}={\left[\begin{array}{ccccc}{\tau }_1^k& \dots & {\tau }_j^k& \dots & {\tau }_m^k\end{array}\right]}^{\mathrm{T}}$$ (5)

In the same manner, tendon moment arms in the robot can be defined by a matrix form. When tendons 1 to i are fixed at the tip of the robot, e.g., cell n, and tendons i+1 to m are fixed at cell q that is that is the top of the proximal section, the tendon moment-arm matrix is described as

$$\mathit{D}=\left[\begin{array}{c}{\mathit{d}}_{\mathbf{1}}\\ ⋮\\ {\mathit{d}}_{\mathit{q}}\\ {\mathit{d}}_{\mathit{q}+\mathbf{1}}\\ ⋮\\ {\mathit{d}}_{\mathit{n}}\end{array}\right]=\left[\begin{array}{cccccc}{d}_{1,1}& \dots & d_{1,l}& d_{1,l+1}& \dots & d_{1,m}\\ & ⋮& & & ⋮& \\ d_{q,1}& \dots & d_{q,l}& d_{q,l+1}& \dots & d_{q,m}\\ d_{q+1,1}& \dots & d_{q+1,l}& 0& \dots & 0\\ & ⋮& & & ⋮& \\ d_{n,1}& \dots & d_{n,l}& 0& \dots & 0\end{array}\right]$$ (6)

where zero components in Eq. (6) denotes that tendons are fixed at the previous cell. In the same fashion, tendon moment-arm matrix D can express the tendon routing for any number of multisections of the robot by placing zero value components.

Eq. (3) is vectorized as the inner product of the tendon moment arm vector d_i and the tension vector ${\mathbf{\tau }}_{\mathbf{i}}^{\mathbf{k}}$ for cell i.

$${\theta }_i^k=\frac{1}{K_{\theta }}{\mathit{d}}_{\mathit{i}}{\mathit{\tau }}_{\mathit{i}}^{\mathit{k}}$$ (7)

Tension vector ${\mathbf{\tau }}_{\mathbf{i}}^{\mathbf{k}}$ is transformed to ${\mathbf{\tau }}_{\mathbf{i}+\mathbf{1}}^{\mathbf{k}}$ by a tension ratio matrix A_i,

$${\mathit{\tau }}_{\mathit{i}+\mathbf{1}}^{\mathit{k}}={\mathit{A}}_{\mathit{i}}{\mathit{\tau }}_{\mathit{i}}^{\mathit{k}}$$ (8)

where the matrix A_i is the following diagonal matrix,

$${\mathit{A}}_{\mathit{i}}=\left[\begin{array}{ccccc}{\alpha }_{i,1}^k& & & & 0\\ & \ddots & & & \\ & & {\alpha }_{i,j}^k& & \\ & & & \ddots & \\ 0& & & & {\alpha }_{i,m}^k\end{array}\right]$$ (9)

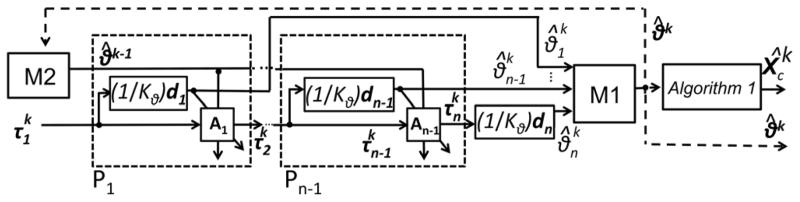
We derived the entire forward kinematic mapping from ${\mathbf{\tau }}_{\mathbf{1}}^{\mathbf{k}}$ to θ^k as a block diagram in Fig. 8. In the diagram, the dashed blocks P₁ to P_n-1 with Eqs. (7) and (8) perform mechanics transformations leading to to the bending angle ${\mathrm{\theta }}_{\mathrm{i}}^{\mathrm{k}}$ for each cell from the tension vector ${\mathbf{\tau }}_{\mathbf{i}}^{\mathbf{k}}$. This transformation propagates tension in in tendons in a cell-by-cell calculation from the proximal to the distal cell. Once the bending angle vector θ^k is determined, the algorithm 1 block transforms this bending angle vector θ^k to the coordinate vector ${\mathit{X}}_{\mathit{c}}^{\mathit{k}}$ of the robot on the task coordinate. This transformation is the kinematic (geometric) transformation. To attain this transformation in the algorithm 1 block, we used a homogeneous transformation matrix parameterized by the arc parameters in [5] and applied the matrix to the frame of a set of all cells in the robot. By multiplying this transformation matrix by the number of cells, the position of a set of all cells in the robot can be determined.

Fig. 8.

Block diagram of extended FKM. The memory block M2 provides the information on bending angles at the previous time k–1. By comparing this information with the present bending angles at time time k in the block associated with Eq. (8), the extended FKM determines the appropriate direction of the the friction force, considering the tendon layout even when the robot has an antagonistic pair of tendons. The mapping can manage a hysteresis operation of the robot, i.e., the dependency of the bending angles toward the bending direction.

This extended FKM requires a rotational spring constant of the backbone and a friction coefficient between the tendon and the wire guide to predict the robot posture and does not include any fitting parameters to regulate computing results. For the computation of this study, we plugged values we measured for each part in advance into the extended FKM.

Validation of prediction accuracy by the extended FKM

To validate the prediction accuracy of the robot posture by the extended FKM, we measured the robot postures experimentally and computed the discrepancy between these measured postures and the values predicted by the extended FKM. The experimental set-up is depicted in Fig. 9, where the measurement method of the robot posture was identical to the experiment in the previous section for evaluation of impact of the components on hysteresis motion. The difference between this experiment and the experiment in the previous section is the bending method of the robot. In this experiment, we bend the robot by pulling tendons in the robot with pre-planned input tensions at the proximal end of the tendons.

Fig. 9.

Experimental apparatus for articulation experiment. The single section of the tendon-driven continuum robot was positioned with its bending plane aligned horizontally, and it supported its articulation posture by itself. The tendon was fixed to the tractor through the idler pulley. The tractor was mounted on the slide stage and pulled with the load cell (LTS-2KA, Kyowa Electronic Instruments) that connected to the signal conditioner (CDV-700A, Kyowa Electronic Instruments) to measure the tension in the tendon during actuation. The posture of the robot was observed with the measurement microscope (STM-UM, Olympus). The digitized position stage in the microscope recorded the position of the hinges as the posture. For the antagonistic tendons layout, we used a weight to apply gravitational forces on the tendon on the other side from the load cell (−x direction from the centroid of the robot in Fig. 2). The weight was hung on the end of tendons via idler pulleys so as to pull the tendon horizontally.

The tendons were organized into two distinct layouts to evaluate the dependency of friction directionality in the tendons on the geometry between the tendons and the bending direction of the robot. The first layout was a single-tendon layout. In this layout, we set the single tendon embedded on one side (+x direction from the centroid of the robot in Fig. 6). This single-tendon layout enabled evaluation of the extended FKM with the simplest form. Specifically, this layout confirmed the sign function of ( ${\mathrm{\theta }}_{\mathrm{i}}^{\mathrm{k}}-{\mathrm{\theta }}_{\mathrm{i}}^{\mathrm{k}-1}$) in Eq. (4), which determined the direction of the friction force associated with the velocity of the robot, fixing the other sign function of d_i,j in the equation. The second layout used an antagonistic pair of tendons. In this layout, we set the two tendons on both sides of robot (+ x and − x direction from the centroid as is in Fig. 6) with the identical moment arms. This layout allowed us to evaluate the sign function of d_i,j in Eq. (4) that manages the directionality of friction in the tendons determined by the geometry between tendons and the bending direction of the robot.

The input tensions ascended from 0.0 N to 0.40 N at 0.10 N intervals for the single-tendon layout and from (0.12, 0.12) N to (0.12, 0.65) N for the antagonistic-tendons layout; they descended in the opposite way at the same intervals. At these input tensions, we measured the position of thirty hinges of the robot and the tip of the robot, and determined the position of thirty cells by calculating midpoints between adjoining measured points. We performed three trials for all postures and recorded one posture for each input tension in one trial. After the measurement, these measured postures were interpreted as two items, namely dependency of the robot posture on bending direction and prediction accuracy of the robot posture.

First, the dependency of the robot posture on bending direction was evaluated by calculating the discrepancy of the robot postures at the same input tension between the arching motion and the extending motion. The discrepancy of the robot postures is defined as the average distance between the tips in arching and extending motions among the three trials. Second, the prediction accuracy of the robot posture was evaluated by calculating the discrepancy between the measured tip positions and the values predicted by the extended FKM. This discrepancy was also compared with the discrepancy between the measured tip positions and the values predicted by the conventional PCCA in [6,17,18] to evaluate improvement of the prediction accuracy.

Each discrepancy was summarized as mean, maximum, and minimum values of the three trials and was compared with the target value of 5 mm. We defined this target value from a tumor size of 2 cm resectable by using neuroendoscope [1–4]. From the literature, we estimated that mean values of error of 5 mm give good margins for planning to aim at a tumoral area of 2 cm, when the kinematic model is used to predict the robot posture.

Results

Dependency of the robot posture on bending direction

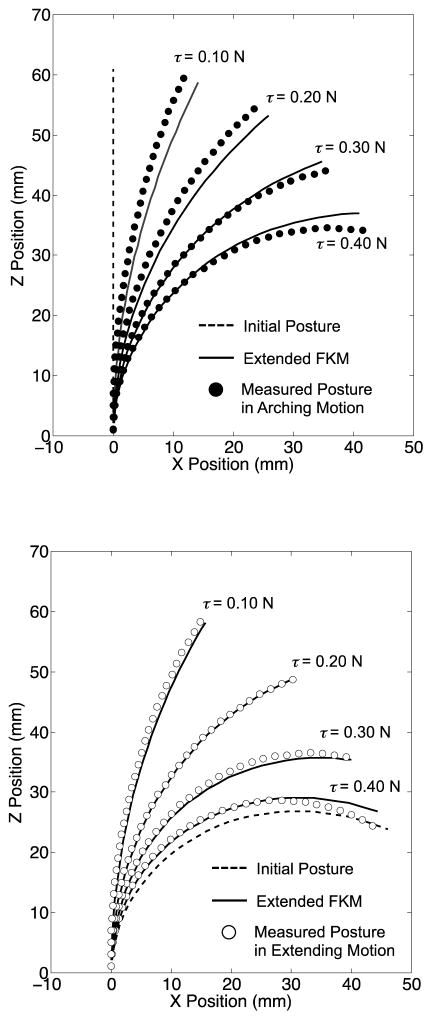
The mean discrepancies of the tip position between arching and extending motions were 9.8 mm at 0.4 N for the single tendon and 13.2 mm at (0.12, 0.48) N for the antagonistic tendons (Fig. 10 and 11).

Fig. 10.

Result of the articulation experiment with the single-tendon layout. The dotted line signifies the initial posture for each measurement. (Top) Arching posture: the mean postures among three trials (black circles) were achieved from the straight initial posture. (Bottom) Extending posture: the mean postures among three trials (white circles) were achieved from the initial posture in maximum bending of the robot

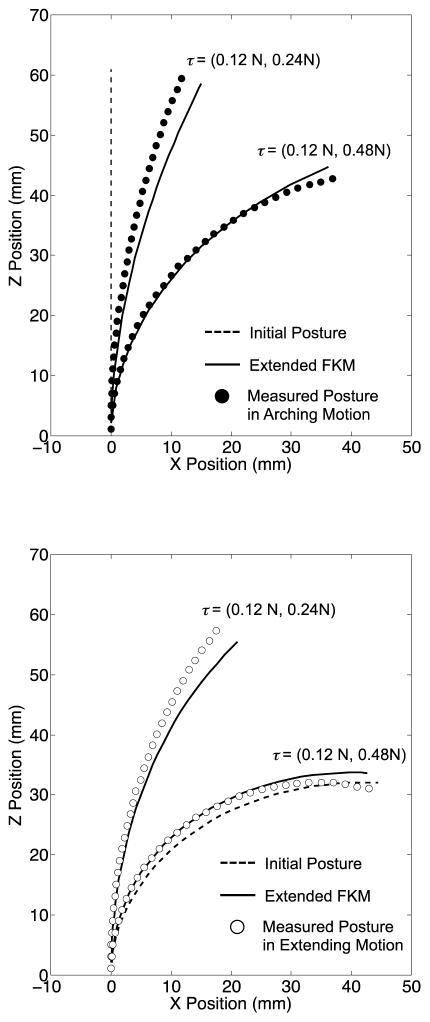
Fig. 11.

Result of the articulation experiment with the antagonistic-tendons layout. The dotted line signifies the initial posture for each measurement. (Top) Arching posture: the mean postures among three trials (black circles) were achieved from the straight initial posture, (Bottom) Extending posture: the mean postures among three trials (white circles) were achieved from the initial posture in maximum bending of the robot

The postures in the extending motion at every input tension performed greater bending than the posture in the arching motion Overall, the robot in both the single- and the antagonistic-tendons layouts showed a discrepancy of the robot postures between arching and extending motions.

Prediction accuracy of the robot posture

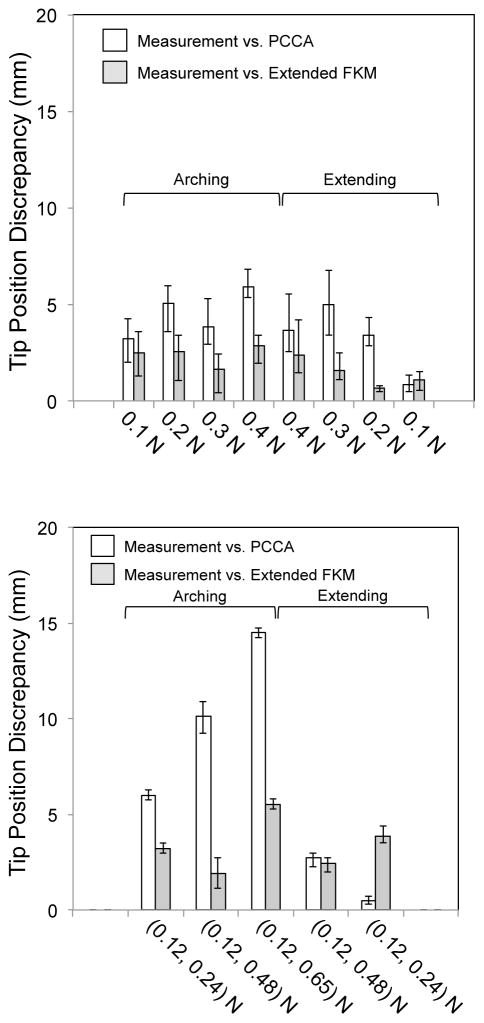
Fig. 12 summarizes the prediction accuracy of the extended FKM and PCCA. In the single-tendon layouts, the prediction accuracy of the extended FKM was within the target value of 5 mm (2.9 mm at maximum in Fig. 12, Top). In the antagonistic-tendons layout, the prediction accuracy was approximately 10% larger than the target value at the highest input tension of (0.12, 0.65) N (5.5 mm in Fig. 12, Bottom). The prediction accuracy of PCCA in the single-tendon layout was larger than the target value at three input tension conditions (5.1 mm at 0.2 N, 5.9 mm at 0.4 N in arching motion, and 5.0 mm at 0.3 N in extending motion in Fig. 12, Top). In the antagonistic-tendons layout, the prediction accuracy exceeded the target value in arching motions [6.0, 10.1, and 14.6 mm at (0.12, 0.24), (0.12, 0.48), and (0.12, 0.65) N, respectively, in Fig. 12, Bottom].

Fig. 12.

Tip position discrepancy for the single-tendon and antagonistic-tendons layouts. White bars signify a discrepancy between the measurement and the values predicted with PCCA. Gray bars indicate discrepancy between the measurement and the values predicted with the extended FKM. (Top) Single-tendon layout. (Bottom) Antagonistic-tendons layout

In a comparison of the prediction accuracies of the extended FKM and PCCA, the extended FKM improved the prediction accuracy in all input tension conditions except for in the lowest input tension in the extending motion. Specifically, the improvement was the largest in the antagonistic-tendons layout in the arching motion [81% and 62% at (0.12, 0.48) and (0.12, 0.65) N, respectively].

Discussion

This study presented a tendon-driven continuum robot for neuroendoscopy and proposed an extended FKM incorporating the tension propagation model [23] to compute the hysteresis operation of the robot. The prediction accuracy of the extended FKM was experimentally validated and compared with that of conventional PCCA, with attention to dependency on the bending direction. This validation indicated that the extended FKM predicted the measured posture within a prediction accuracy of 5.5 mm (2.9 mm for the single-tendon and 5.5 mm for the antagonistic-tendons layout) both in arching motion and in extending motion. We also found that the extended FKM improved the prediction accuracy from the values of the conventional PCCA [81%, 62% at (0.12, 0.48), (0.12, 0.65) N].

Our primal motivation of the adoption of the tension propagation model is to improve prediction accuracy of the tip position of the robot. With the improved prediction accuracy of the tip position, the preoperative planning may provide better consistency with the actual operation of the robot. We suppose this consistency is crucial to determine the localization of the accessible trajectory of the robot in the planning stage for the neuroendoscopic approaches to the ventricular system since the multi-curved trajectory of the robot is not intuitive for endoscopists.

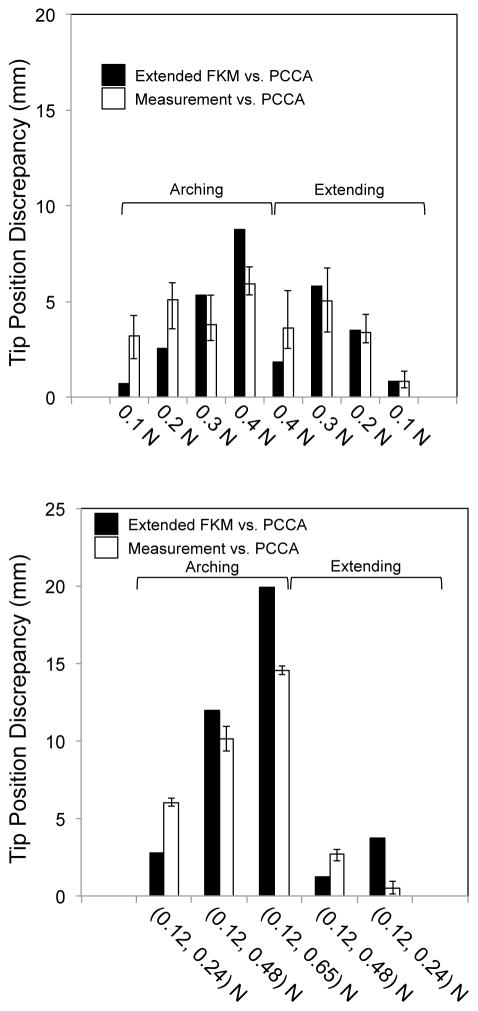
In the experiment, we observed the unique tendency of the discrepancy of tip positions between the measured values and the values predicted by PCCA. In the arching motion, the discrepancy tended to increase as the input tension increased. However, at the beginning of the extending motion, the discrepancy decreased in both the single- and the antagonistic-tendons layout. Moreover, in the extending motion with single-tendon layout, we observed another peak as the input tension decreased to zero. To explain these tendencies, we compared these discrepancies with the discrepancy of predicted values between the extended FKM and the PCCA (Fig. 13). This discrepancy showed an almost identical tendency to the observed discrepancy in PCCA and correlated strongly to the observed discrepancy in PCCA (correlation coefficients were 0.74 and 0.92 for the single- and the antagonistic-tendons layout). Therefore, the temporal decrease and peak of the discrepancy in PCCA in the extending motion seems to stem from the friction effect that the extended FKM considers. Specifically, the friction effect changes the tension distribution along the longitudinal direction of the robot, while PCCA considers the tension distribution constant. The tension distribution is associated with the tip position by integrating local relative bending angles of each cell from the adjacent cell, which is proportional to the tension in the tendon locally at each cell. The tip position calculated by different tension distributions may cause the distinctive tendency of the tip position discrepancy between the values measured and predicted by PCCA.

Fig. 13.

Comparison of tip position discrepancy between measurements vs. PCCA and the extended FKM vs. PCCA. Black bars signify a calculated discrepancies between the extended FKM and PCCA. White bars were measured values for PCCA in Fig. 12

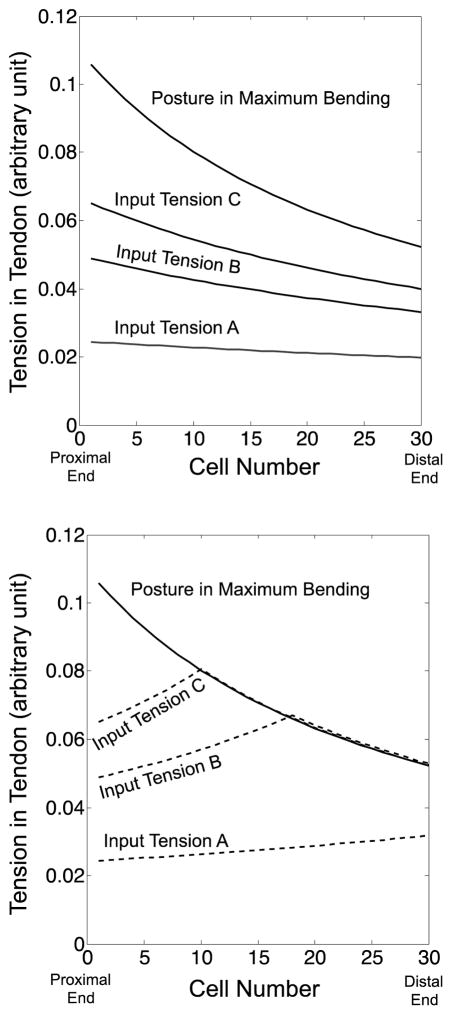
To delineate this tendency by using the tension distribution, we simulated the tension distribution by using the extended FKM and compared the values by PCCA with the extended FKM as follows. Fig. 14 shows the simulation of tension distribution calculated by the extended FKM. This simulation corresponds to the articulation experiment with the single tendon layout. In this simulation, we elevated input tension from A to C and the tension for the maximum bending for the arching motion. After the arching motion, we decreased input tension from C to A for the extending motion. In the arching motion, the tension in the tendon decreased from the proximal to the distal end because of the friction force between the tendon and the wire guides. As increasing input tension from A to C, the tension became larger values, while the monotonic decreasing distribution from the proximal to the distal end was identical among inputs A, B, and C (Fig. 14, Top).

Fig. 14.

Tension variation in a tendon calculated by the extended FKM from proximal to distal ends. The lines signify the tension variation at different input tensions A, B, and C. (Top) Arching motion. (Bottom) Extending motion

In the extending motion, the tension in the tendon increased from the proximal to the distal end just like the distribution at input A in Fig. 14, Bottom, since the tendon was fed into the robot instead of pulling in the extending motion. Specifically, in the beginning of the extending motion, the tension distribution presented a peak distribution in input tensions B and C. The tension near to the proximal end increased monotonically toward the distal side. At the point of the tension in the posture at the maximum bending, the tension started to decrease along the tension distribution of the maximum bending. This tension distribution with the peak is equivalent to a transition state of tension in a driving cable for a cable-conduit system reported in [25,26].

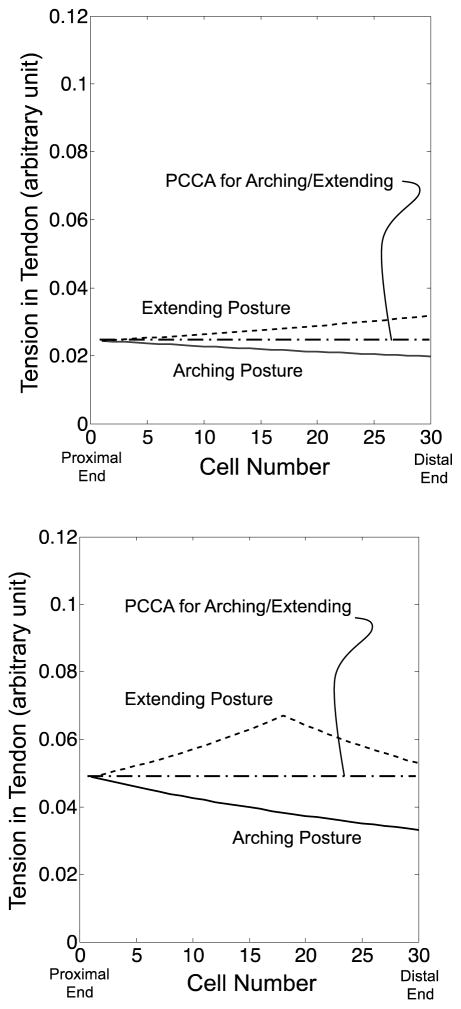
Fig. 15 compares the tension distribution calculated by the FKM and PCCA side by side. At input tension A (Fig. 15, Top), the FKM-predicted tension distributions for the arching and the extending motions are similar to the PCCA-predicted values since the friction effect was small in these bending angles. Therefore, the tip position discrepancies between the values measured and predicted with PCCA also are minimal at input tension A for the arching and the extending motion. At input tension C (Fig. 15, Bottom), the FKM-predicted values for the extending motions presented the peak distributions. PCCA-predicted values crossed these FKM-predicted values for the extending motion. Since PCCA-predicted values were lower on the proximal side and higher on the distal side than the FKM-predicted values, the discrepancies between the extended FKM and PCCA were cancelled out for computation of the tip position. From the FKM-predicted values for the arching motion, PCCA included a large discrepancy between them since the FKM-predicted values decreased monotonically. Consequently, PCCA presented a smaller tip position discrepancy at the beginning of the extending motion than at the end of the arching motion.

Fig. 15.

Comparison of tension variation at the same input tension between the values calculated by the extended FKM and PCCA. Solid and dotted lines signify the values calculated by the extended FKM in arching and extending motions. An alternate long and short dash line denotes the values calculated by PCCA. (Top) Input tension A. (Center) Input tension B. (Bottom) Input tension C

At input tension B (Fig. 15, Center), PCCA widened the discrepancy to the FKM-predicted values for the extending motion and contracted the discrepancy to the FKM-predicted values for the arching motion. This discrepancy validation elucidated the peak of the tip position discrepancy with PCCA in the extending motion.

As the above-mentioned analysis shows, the extended FKM can compute a potential tip position discrepancy between the actual robot and PCCA for a specific motion. Therefore, we expect the extended FKM is also useful to identify the applicable motion range of PCCA for the actual robot within certain error criteria. Since PCCA has a great advantage in real-time control [5], this information is important for design of the continuum robot if the robot can work with a relatively small bending angle. Specifically, the extended FKM does not include any fitting parameters to compute the postures of the robot. This evaluation can be performed even before development of the robot and can provide or before the robot actually perform the certain task or motions.

In the articulation experiment, the extended FKM tended to predict larger bending angles for a set of cells of the robot than the measured values at lower tensions and smaller bending angles at higher tensions. This tendency was consistent in the arching and the extending posture for any tendon layouts. Therefore, the discrepancy between the extended FKM-predicted and measured values results from some factors of conservative quantity rather than the hysteresis quantity. We expected that this factor was probably the nonlinearity of the spring constant of the backbone that the extended FKM does not take into account. The backbone having been made of Nitinol may account for the Young’s modulus’ soft spring effect. The mechanical design of the backbone is expected to be helpful in reducing the unpleasant nonlinearity and in the development of a robot with suitable control.

The friction model in tendon-driven systems has been proposed for a cable-conduit system where cables pass through conduits to actuate remote instruments [25,26]. These studies proposed a tension transmission model in tendons with a fixed-path routing. The variation of tension due to friction effects is modeled as an exponential function that has similar monotonically reducing or increasing effect on Eq. (4). Our main contribution is that of mapping the tension distribution in tendons to the posture of the tendon-driven continuum robot. To determine the continuum robot posture, we defined a series of linear springs in the routing of tendons and combined the mechanics model of the springs.

Implications of the direct adoption of these friction models in the prior studies [25,26], which are more complex models than in this study, may include large computation process to determine the robot posture since these models solve large simultaneous equations about force equilibrium between an elastic body of the robot and driving and friction forces directly. We supposed that this large computation process was a possible improvement in the adoption of these complex friction models. To reduce this large computation process, in this study, we provided a simple matrix form for kinematics of the tendon-driven continuum robot with attention to friction forces even when the robot has multiple tendons and multisection. Moreover, we expect that our approach can be integrated into feedback control loops with sensors and trajectory planning using a simple computational algorithm.

In summary, we have developed a tendon-driven continuum robot for neuroendoscopy and shown that the extended FKM can predict the hysteresis operation of the tendon-driven continuum robot with improved accuracy in comparison to the FKM in [23]. We expect the extended FKM to lead to active usage of the tendon-driven continuum robot, particularly in neuroendoscopy in which the multisections of the robot can promote greater dexterity and flexibility of neuroendoscopes.