A Bending Test for Determining the Atterberg Plastic Limit in Soils

Abstract

The thread rolling test is the most commonly used method to determine the plastic limit (PL) in soils. It has been widely criticized, because a considerable subjective judgment from the operator that carries out the test is involved during its performance, which may affect the final result significantly. Different alternative methods have been put forward, but they cannot compete with the standard rolling test in speed, simplicity and cost.

In an earlier study by the authors, a simple method with a simple device to determine the PL was presented (the "thread bending test" or simply "bending test"); this method allowed the PL to be obtained with minimal operator interference. In the present paper a version of the original bending test is shown. The experimental basis is the same as the original bending test: soil threads which are 3 mm in diameter and 52 mm long are bent until they start to crack, so that both the bending produced and its related moisture content are determined. However, this new version enables the calculation of PL from an equation, so it is not necessary to plot any curve or straight line to obtain this parameter and, in fact, the PL can be achieved with only one experimental point (but two experimental points are recommended).

The PL results obtained with this new version are very similar to those obtained through the original bending test and the standard rolling test by a highly experienced operator. Only in particular cases of high plasticity cohesive soils, there is a greater difference in the result. Despite this, the bending test works very well for all types of soil, both cohesive and very low plasticity soils, where the latter are the most difficult to test via the standard thread rolling method.

Download video file ^{(30.3MB, mp4)}

Introduction

Liquid Limit (LL) and Plastic Limit (PL) are the two most important soil consistency limits of those defined by Atterberg in 1911¹. LL marks the boundary between liquid and plastic states, and PL between plastic and semisolid states. LL is obtained around the world according to several standards through the Casagrande method^2,3 or the penetration test⁴. Both methods are conducted mechanically by devices; thereby, minimal operator interference is involved. In the case of PL, the so called "thread rolling test" is the most popular and standardized method for its determination^2,5. This test is based on rolling soil into 3 mm threads by hand until the operator considers the soil to be crumbling. For this reason it has been widely criticized because the skill and judgment of the operator play a critical role in the outcome of the test. Standard rolling test is importantly affected by many uncontrolled factors, such as the pressure applied, the contact geometry, the friction, the speed of rolling, the size of the sample and the type of soil^6,7. The American Society for Testing and Materials (ASTM) developed the ASTM D 4318 standard which includes a simple device in order to minimize the operator interference^2,8, however significant differences have been reported in some soils when comparing the manual rolling test against the test performed by the ASTM D4318 device⁹.

PL is a very important parameter for geotechnical purposes, since Plasticity Index (PI) is obtained from it (PI = LL - PL); PI is used to classify the soil in accordance with the Plasticity Chart shown in ASTM D 2487¹⁰, based on the research of Casagrande^11,12. Errors in the PL affect negatively this classification¹³, and for this reason, a new test for PL determination is required.

Pfefferkorn test, cone penetrometer, capillary rheometer, torque rheometer or stress-strain tests are some examples of alternative methods for measuring soil plasticity¹⁴, but these are not adequate to obtain the PL. With the special instance of fall cone tests, a large number of researchers have attempted to define a new methodology for PL determination using different penetrometer designs^15-20, but without reaching any real agreement. Furthermore, all of it is based on the assumption that the shear strength at the PL is 100 times that at the LL²¹, which is not true²².

Barnes^23,24 developed an apparatus that emulated the rolling conditions of soil cylinders in an attempt to lay down a clear criterion for PL determination. Nevertheless, some shortcomings are identified with this approach, such as its complexity, test duration and mainly the questionable means of calculating the PL²⁵. The success of the standard rolling test lies in its simplicity, quick performance and low cost, so no alternative method will be able to replace it, unless it meets these three requirements and other ones, such as high accuracy and low operator interference.

In a previous study by the authors, a new PL approach was proposed²⁵: the original thread bending test (or simply bending test) allowed the PL to be obtained from a graph in which it was represented the relationship between water content and bending deformations. The authors obtained and plotted several experimental points for each soil (the protocol followed to get these points was the same as that indicated in the present paper), so that the correlation of the points could be defined in two ways without compromising in any way the correct definition of the point path: as a parabolic curve, named the bending curve (Figure 1A), and as two intersecting straight lines with different slope, named the stiff-plastic line and the soft-plastic line. The stiff-plastic line is the steepest one, and PL was calculated from it as the moisture percentage corresponding to the cutoff point of this with the y-axis (Figure 1B). In this cutoff point the bending produced is zero, which is in accordance with the concept of plastic limit, i.e., PL is the moisture content at which the soil is not capable of withstanding deformations below this threshold (semisolid state) but it does bear them above it (plastic state). Although in the original study, the PL could not be obtained directly by the bending curve (this does not intersect the y-axis), this line was very useful because considering that the bending curve and the intersecting lines follow very similar paths, the bending curve equation obtained from the experimental data was used to obtain extra points to, firstly, correct any deviation, and, secondly, to carry out the test with just a few points as shown in Figure 1B.

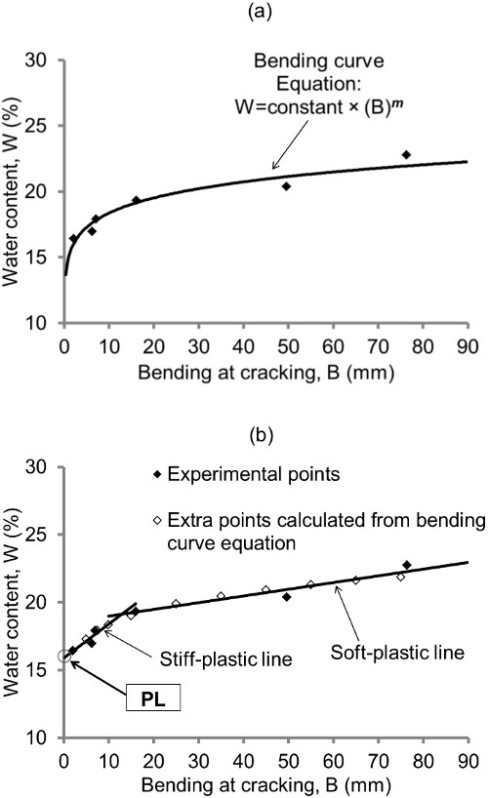Figure 1. Graphical representation of the B-W points in a tested soil by the original bending test. (A) The correlation of the points is represented as a parabolic curve, named the bending curve whose equation is included. (B) The correlation of the points is defined by two intersecting lines and other extra points are added (they were calculated from the bending curve equation). B values are obtained as B=52.0-D (where D is the average distance measured between the tips at the time of cracking in mm) and the PL is calculated as the water content corresponding to the cutoff point of the stiff-plastic line with the y-axis. This figure has been modified from Moreno-Maroto & Alonso-Azcárate²⁵. Please click here to view a larger version of this figure.

All the results were in excellent agreement with those achieved through the traditional thread rolling method by a highly experienced operator. However, the original bending test remained slower than the standardized thread rolling test. In an attempt to further economize test time, a one-point version was put forward. It was based on the average bending slope (m) obtained in the 24 tested soils, which was 0.108 (m is the slope of the bending curve when it is represented in double logarithmic scale; m appears on the bending curve equation in Figure 1A). By means of an equation where this factor was included, both the stiff-plastic and soft-plastic lines were graphically drawn, and thus the PL was estimated. These results were also highly correlated with both the multi-point bending test and the standard rolling test. In spite of this one-point version being even faster than the traditional test, the PL calculation was more complex because plotting was necessary. For this reason, on the basis of statistical criteria a new equation for PL calculation has been developed in this study, so that plotting is not required and results can be achieved with only one point, whereas the experimental protocol is the same as the original bending test. This new version meets the necessary requirements to replace the outdated thread rolling method.

Protocol

1. Collect, Dry and Sieve the Test Sample

1. Collect a soil sample in the field (use a shovel or a trowel) and store it in a polyethylene bag. Note: The volume of the sample varies depending on the type of soil: in fine soils (clays and silts) between 100 and 1,000 g is generally sufficient, but in sandy soils and those containing gravel and pebbles, large amounts may be required, from a few to several kg.

2. Reduce the sample by quartering in the laboratory if this is too voluminous (use a soil splitter if necessary).

3. Place the sample on a tray and dry the soil at a temperature not exceeding 60 °C. Note: Both oven-drying and air-drying are valid. Even the drying step may be ignored in very fine soils if they contain suitable natural moisture for the test (water content above the plastic limit without actually being sticky).

4. Disaggregate the soil manually by a mortar. Be careful not to break sand particles, so it is better to use a rubber covered pestle.

5. Pass the sample through a 0.40 mm (or a 0.425 mm) sieve. Keep only the fractions of under 0.40 mm or 0.425 mm (remove the soil fraction retained by the sieve).

2. Prepare Two Wet Soil Balls

1. Add distilled water with a wash-bottle to approximately 20-40 g of soil on a nonabsorbent smooth glass plate and knead with a metal spatula until a homogeneous soil-water mixture is obtained.

2. Shape a soil ball by hand from the soil-water mixture which is between 3 and 5 cm in diameter approximately (it is preferable to wear latex gloves).

3. Repeat steps 2.1 and 2.2 for the same soil sample to obtain another ball with different water content.

   1. Add more or less water to the soil in the step 2.1 to get this different water content, or simply shape a larger soil ball in the step 2.2 than that indicated in that step (for example one of 6-7 cm in diameter), take a portion of this and dry it slightly by hand or add water to this to get a soil ball of different moisture content. Note: Regarding the steps 2.1 to 2.3, in cohesive soils (mainly clayey soils), the amount of added water should provide a consistency at which the soil could be rolled without sticking to the hands. This is elaborated further in the Discussion.

4. Wrap each soil ball with cling film and put them inside an airtight bag for 24 hr under hermetic conditions.

3. Carry Out the Bending Test

1. Weigh an empty container and record the weight to a precision of at least 0.01 g.

2. After the tempering period, take one of the soil balls and flatten it by hand on the nonabsorbent smooth glass plate (use latex gloves to prevent loss of moisture) until the thickness is slightly higher than 3 mm. At this point, complete the flattening with the thread molder (Figure 2A,B,C) in order to obtain a thickness of exactly 3 mm. Note: The thread molder is designed in such a way that there is a space of exactly 3 mm between the part which shapes the soil thread and the glass plate (Figure 2A).

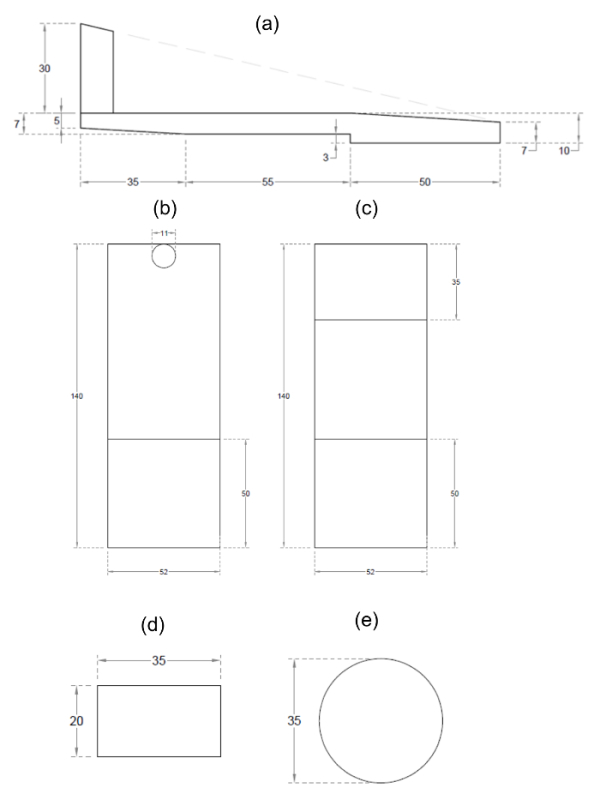Figure 2. Drawings and dimensions in mm of the thread molder and the steel pushers. (A) Side view, (B) top view, and (C) bottom view of the thread molder; (D) front view and (E) top view of the steel pushers. This figure has been modified from Moreno-Maroto & Alonso-Azcárate²⁵. Please click here to view a larger version of this figure.

1. Cut the jagged edges of the flattened soil mass with a spatula (the cut must be straight).

2. Cut with a spatula a soil strip that is at least 52 mm long and a square section of approximately 3 × 3 mm.

3. Shape a cylindrical soil thread of exactly 3 mm in diameter and 52 mm long.

   1. Roll and round the 3 × 3 mm section soil strip with the thread molder: move the thread molder successively backwards and forwards by hand until the exact moment at which the initially square section of the soil thread becomes round, so now it must be 3 mm in diameter.

      1. If the initial soil strip is difficult to roll with the thread molder (e.g., in low cohesive soils or even in plastic soils in water contents close to the PL), at the beginning, round the square section by hand very carefully (use gloves). Just after, roll the soil thread with the thread molder as described in the step 3.5.1 until an exactly 3mm in diameter soil thread is obtained.
      2. Place the soil thread and the front side of the thread molder close together. Use the width of the thread molder as a template and cut the tips of the soil thread with a metal spatula in order to obtain a soil cylinder of exactly 52 mm in length. Note: The thread molder measures 52 mm wide as shown in Figure 2 B,C.
4. Bend the soil thread until the point of cracking (Figure 3).

   1. Turn the thread molder upside down, so that now it is supported by its cylindrical piece and the device rear. Put the cylindrical piece of the thread molder in contact with the central part of the 3 mm in diameter × 52 mm long soil thread.
   2. Place the steel pushers (Figure 2D,E) in contact with the center of the soil thread (Figure 3A), so that the soil thread is located between the two steel pushers (these work as mobile supporting points) and the cylindrical part of the thread molder (this works as a fixed supporting point).
   3. Move carefully the steel pushers from the center to the tips of the soil thread (Figure 3B) in an approximately circular path. Repeat this motion until the point of cracking (Figure 3C); at this point, stop bending.

      1. If the crack appears out of the central third of the soil thread (Figure 3D), i.e., near one of the thread tips, keep bending around the other tip until another crack appears (Figure 3D,E). This way, two cracks are obtained along the soil thread.
   4. Right afterwards, remove the thread molder and measure the distance between the tips (D) of the thread with a caliper and record it to a precision of 0.1 mm. Take this measurement from the central part of the tips (Figure 3C,E).

      1. Put the soil thread into the container whose weight was previously recorded (step 3.1) and cover it to prevent moisture loss.
      2. If bending deformations are so large that even the thread tips come into contact, i.e., D=0 mm (Figure 3F), remove the pushers and thread molder and bend the soil thread by hand until the point of cracking as is shown schematically in Figure 3G. Measure the distance between the thread tips as shown in Figure 3H and record it with a negative sign. Finally, repeat step 3.6.4.1.

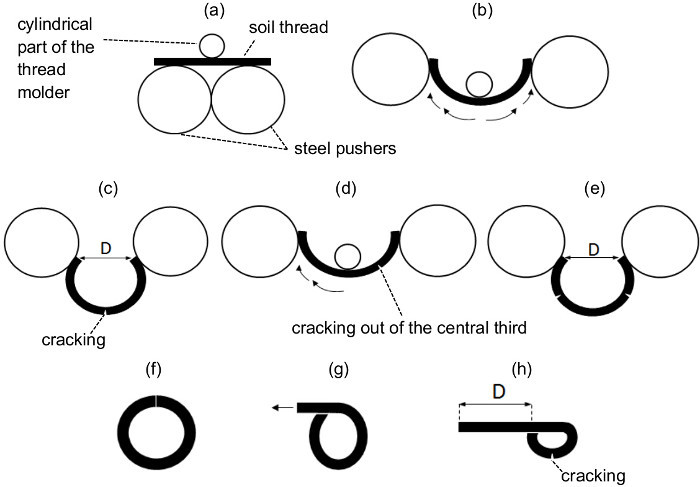Figure 3. Schematic drawing where bending and tips distance measurement techniques are detailed. (A) Initial position of the steel pushers, the soil thread and the cylindrical part of the thread molder on the glass plate. (B) Usual bending technique by means of an approximately circular path from the center to the tips which is carried out very carefully (see the arrows path). (C) Usual tip distance measurement technique of a thread that has cracked in its central part. (D) Soil thread that has cracked out its central third and bending technique to be followed around the other tip (that indicated by the arrows). (E) Usual tip distance measurement technique of a thread that has cracked out of its central third. (F) Soil thread in which tips come into contact and can form a closed ring. (G) Bending technique to be conducted when the soil thread is able to bend beyond a closed ring and (H) tip distance measurement technique for this last case. This figure has been modified from Moreno-Maroto & Alonso-Azcárate²⁵. Please click here to view a larger version of this figure.

1. Shape other soil threads from the same flattened soil mass according to steps 3.4, 3.5.1, 3.5.1.1. Do not cut their tips. Finally, put them into the container and cover it (step 3.6.4.1). Note: The role of these threads is simply to obtain enough material to correctly determine the moisture content. If the contact surfaces (the glass plate and the thread molder) were dirty after shaping a thread, clean them with a damp cloth and dry them with a piece of paper quickly.

2. Repeat steps 3.4 through 3.6.4.2 for at least another soil thread. Shape these threads with a certain alternation with respect to those obtained in the step 3.7. If the second measurement of tip distance (D) is the same or quite similar to that obtained in the first soil thread, do not bend more threads. If not, shape and bend at least one further soil thread. Note: The term "a certain alternation" means that it is recommended that the bent threads are not shaped one after the other, i.e., they should not be taken from the same area of the flattened soil mass in order to obtain representative measurements of the whole soil mass. Thus, some of those soil threads that are not cut and bent (step 3.7) should be shaped between the bent ones. If there was an inhomogeneous moisture distribution in the flattened soil mass (which is unlikely), it would be corrected this way.

3. Weigh the container with the soil threads to a precision of at least 0.01 g. Shape and add more threads according to steps 3.4, 3.5.1, 3.5.1.1 if the weight of the soil threads is less than 5 g, until this weight is exceeded (a weight between 5 and 7 g is suitable).

4. Repeat steps 3.1 through 3.9 for the other soil ball (the ball shaped in step 2.3).

   1. In the case of very low plasticity soils, omit step 3.10 if the plasticity of the soil is too low to carry out the test properly for two balls with different water content (so that only a soil ball would be tested).

4. Determine the Moisture Content (W) of the Soil

1. Place the two containers (corresponding to the two soil balls tested) with their respective soil threads in an oven at 105 ± 5 °C for a minimum of 18 hr (if the step 3.10.1 is applied, there is only one container with soil to dry). After this period, leave the containers with the dry soil in a desiccator and when they are cool, record their weights to a precision of at least 0.01 g.

2. Place the containers with the dry soil again into the oven at 105 ± 5 °C for a minimum of 6 hr. Then allow them to cool and record their weights again as indicated in the step 4.1. If the weight is constant, i.e., if this weight is essentially the same as the obtained in the step 4.1, the soil is completely dry, therefore use this data to calculate the moisture content (W) in the step 5.2.

   1. If the weight is different, repeat step 4.2 as many times as necessary until the weight of the container with the dry soil is constant.

5. Calculate the Bending at Cracking (B) and the Moisture Content (W)

1. Calculate the bending at cracking (B) in mm as follows: B=52.0-D where 52.0 refers to the length in mm of the soil thread, and D is the average distance measured between the tips at the time of cracking in mm: D=(D₁+D₂…+D_n)/n where n is at least 2 (see step 3.8)

2. Calculate the moisture content (W) in percentage as follows: W= (M1-M2)/(M2-M3)×100 where: M1 is the weight of the container with the wet soil (see step 3.9) M2 is the weight of the container with the dry soil (see step 4.2) M3 is the weight of the container (see step 3.1)

6. Calculate the Plastic Limit (PL)

1. Calculate the plastic limit of the first soil ball as follows: PL₁ = W × (B/2.135)^-0.108 where 2.135 refers to the average B on the bending curve at which PL was obtained in 24 soils according to the original bending test, whereas -0.108 refers to the average bending slope (m) of the bending curve of these 24 soils (Table 1 and Figure 4).

2. Repeat step 6.1 for the second soil ball and obtain PL₂.

3. Calculate the PL as the average of PL₁ and PL₂ PL = (PL₁ + PL₂)/2 Note: If more than two experimental points had been obtained, the PL is also the average of the PL results, i.e., PL=(PL₁+PL₂…+PL_n)/n.

4. Omit Steps 6.2 and 6.3 if only one experimental point has been obtained (see step 3.10.1), therefore in this case: PL = PL₁ Note: It is important to highlight that in the present study the PL calculated through the step 6 has been named PL_nb in order to differentiate it from the PL results achieved with the original bending test and the standard thread rolling test, which have been named PL_ob and PL_st respectively.

Representative Results

The PL equation shown in the step 6.1 of the protocol was achieved through a statistical study of the 24 soils tested in a previous study of the authors²⁵ (Table 1). The objective was to know the most probable bending slope (the term m in the bending curve equation, which appears in Figure 1A) and the average value of B on the bending curve at which PL was obtained according to the original bending test (the original test was conducted with more than 3 experimental points and graphs were needed to obtain the PL, as shown in Figure 1). The B value corresponding to the PL was calculated by the next equation, which was deduced from the bending curve equation (Figure 1A):

B_PLob=10^{((log PL_ob - log z)/m)}

where, PL_ob is the PL obtained with the original multi-point bending test²⁵; B_PLob is the value of bending at cracking in the bending curve corresponding to the moisture content of PL_ob; z is the constant of the bending curve equation (see Figure 1A) and m is the bending slope (see Figure 1A). The average m is 0.108 with a standard deviation of 0.032 and the average B_PLob is 2.135 mm with a standard deviation of 0.901 as shown in Table 1 and in a more schematic manner in Figure 4. The PL with the new bending method was calculated for each experimental point with the equation shown in the step 6.1 of the protocol, so the final PL for each sample was the average of those results (see the Note in step 6.3).

Soil	PLob  (original multi-point  bending test)	z	m	BPLob
M1	19.1	18.375	0.113	1.408
M2	15.9	13.900	0.139	2.630
M3	19.7	18.136	0.097	2.346
M4	12.4	10.772	0.129	2.977
M5	21.8	20.985	0.061	1.868
M6	13.6	14.125	0.093	0.665
M7	14.9	14.846	0.124	1.030
M8	32.8	33.759	0.193	0.861
M9	52.9	54.097	0.072	0.733
M10	20.9	20.851	0.057	1.042
M11	12.9	11.279	0.133	2.745
M12	24.3	22.481	0.130	1.819
M13	36.2	33.906	0.072	2.482
M14	17.5	14.990	0.129	3.321
M15	15.0	13.337	0.101	3.201
M16	15.4	13.952	0.101	2.658
M17	16.8	14.727	0.099	3.782
M18	15.6	15.448	0.079	1.132
M19	11.6	9.932	0.145	2.917
M20	19.2	17.617	0.085	2.752
M21	11.5	9.901	0.140	2.914
M22	15.9	15.020	0.087	1.924
M23	17.4	16.111	0.095	2.248
M24	14.3	13.343	0.120	1.781
		Average	0.108	2.135
		Std. Dev.	0.032	0.901

Table 1. Data source from which the equation to determine the PL is obtained. M1 to M24 are the 24 soil samples used in this statistical study; PL_ob is the result of PL obtained with the original multi-point bending test²⁵; z and m are the constant and the bending slope of the bending curve equation obtained with the original bending test respectively²⁵ and B_PLob is the value of bending at cracking in the bending curve corresponding to the moisture content of PL_ob. The average and standard deviation (Std. Dev.) of m and B_PLob are indicated.

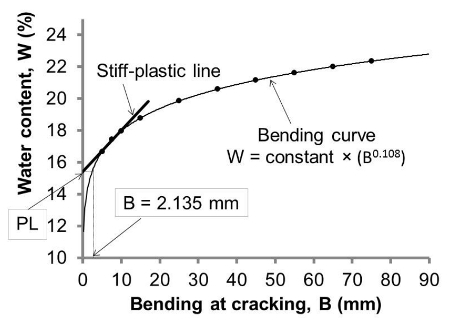Figure 4. Schematic graph of the average bending at cracking (B) at which PL occurs in the bending curve. PL is obtained from the cutoff point of the stiff-plastic line with the y-axis, and that PL value is plotted in the bending curve in order to know its corresponding bending at cracking (B) in the curve. Therefore, B=2.135 refers to the average B value obtained in 24 soils and m=0.108 is the average bending slope of the bending curve in those 24 soils. Please click here to view a larger version of this figure.

The PL results obtained with the new bending test (PL_nb) proposed in this paper, and those corresponding to the original bending test (PL_ob) and the standard rolling test by a highly experienced operator (PL_st) are shown in Table 2. Apart from the 24 soils studied in the previous research (soils M1 to M24)²⁵ other 6 different soils (soils S1 to S6) were tested in order to check the feasibility of the method with independent soils, i.e., these other soils were not used in the initial statistical study to get the PL equation and, in addition, only two experimental points were obtained in these soils, therefore PL was calculated as shown in step 6.3. The low standard deviation and coefficient of variation (CV) values shown in Table 2 are indicative of a good repeatability of the method, i.e., the PL results obtained from each experimental point are very similar to each other with the new bending method; in fact, all soils except M8 have a CV value that is less than 10 so the dispersion of the results can be considered as low. In accordance with Figure 5, the PL results obtained through the new bending test are highly correlated with the original bending test (R² = 0.9648) and the standard thread rolling test (R² = 0.9531), and most results are distributed very close to the 1:1 line, which indicates that the results are very similar, even in very low plasticity soils (the most difficult to test by an operator).

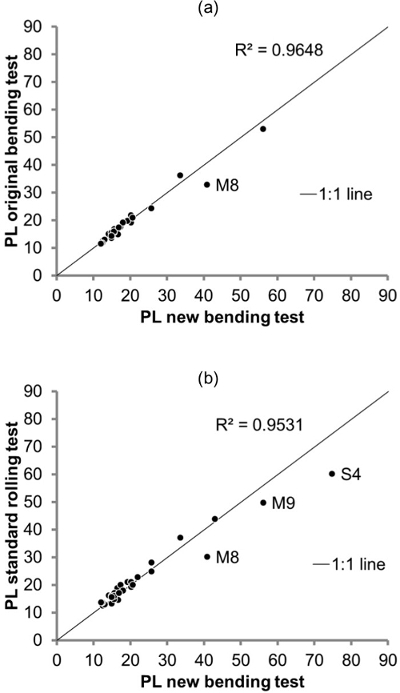Figure 5. Graphical representation and R² of the PL results obtained with the new bending test against other PL methods. (A) Representation of the PL results achieved through the new bending test against the original bending test²⁵ in 24 soils. (B) Representation of the PL results achieved through the new bending test against the standard thread rolling test in 30 soils. Please click here to view a larger version of this figure.

When the two bending tests are compared (Figure 5A) only in soil M8 is a greater PL difference observed, whereas the soils M8, M9 and S4 are the three ones that exhibit greater PL variations when the new bending test is compared with the traditional thread rolling test (Figure 5B, Table 2). In these samples the new bending test overestimates the results, especially in M8 and S4 that are two soils with particular characteristics: on the one hand, M8 was reported in the previous authors' study as an unusual soil because despite the fact that it has high LL and PI, it exhibits a poor resistance to bending that could be caused by its composition (it has a great deal of calcite combined with smectite clay)²⁵, and on the other hand, S4 is a sepiolite which is a very rare clay in which very high values of PL and PI are normal²⁶. Soils M8, M9 and S4 have in common high PL values (greater than 30). This fact suggests that the new bending test could overestimate the PL result with respect to the standard thread rolling test or the original bending test in some very high PL soils, even though it does not happen in other highly plastic soils, such as M12, M13 and S1 in which results are quite similar or even slightly lower than those obtained with the other tests.

Table 2. PL results achieved with the new bending test and comparison with other tests. In the first three columns the name of the soil, its location and a general description are indicated. The column "Experimental points" indicates the number of points used to determine the PL (for soils M1 to M24 more than 3 points are used because these points are the same as those obtained in the original bending test²⁵). PL, LL and PI (PI=LL-PL) refer to Plastic Limit, Liquid Limit³ and Plasticity Index results respectively, and the subscripts ob, st, nb refer to "original bending test²⁵", "standard thread rolling test^2,5" and "new bending test" respectively (this last one, the object of this study). The standard deviation and the coefficient of variation of the PL results obtained with the new bending test are indicated as "Std. Dev. PL_nb" and "CV (%) PL_nb" respectively. The difference between the PL results achieved with the new bending test and the other two methods is also included, as well as the Casagrande Classification¹⁰ (in bold those symbols in which the classification differs). NA = Not applicable. Please click here to view a larger, unified version of this table.

However the similarity among the new bending test and the other two methods is ratified in Table 3, where after checking that both high plasticity soils (soils M8, M9, M12, M13, S1 and S4) and low-medium plasticity soils (the rest of the soils) are normally distributed according to Shapiro-Wilk test (p-Values are greater than 0.05, the alpha-level), a Student's T test indicates that there are no significant differences among the new bending method results and those achieved by both the other original bending test and the traditional thread rolling test (the obtained p-Values are also greater than the 0.05 alpha-level). In Table 2 the LL results obtained by the Casagrande method³ are also shown, so both the Plasticity Index (PI) and the Casagrande classification¹⁰ corresponding to each PI value are also presented. Only in three soils (M8, M15 and S4) the classification changes when the new bending test is used, but the PL result in M15 is quite similar regarding the other two methods. In the cases of M8 and S4, classification changes from CH to MH and from CH/MH to MH, respectively, i.e., with the new bending test M8 and S4 are considered as high plasticity silts (they are considered high plasticity clays if the other PL results are taken into account), which could be in line with the bibliography^25,26, so it also appears to be valid.

Variable	p-Value
Shapiro-Wilk test for PLob of high plasticity soils	0.700
Shapiro-Wilk test for PLst of high plasticity soils	0.753
Shapiro-Wilk test for PLnb of high plasticity soils	0.703
Shapiro-Wilk test for PLob of low-medium plasticity soils	0.708
Shapiro-Wilk test for PLst of low-medium plasticity soils	0.563
Shapiro-Wilk test for PLnb of low-medium plasticity soils	0.252
Student's T bilateral test for high plasticity soils: PLnb vs PLob	0.345
Student's T bilateral test for high plasticity soils: PLnb vs PLst	0.237
Student's T bilateral test for low-medium plasticity soils: PLnb vs PLob	0.861
Student's T bilateral test for low-medium plasticity soils: PLnb vs PLst	0.065

Table 3. Statistical study to check whether there are significant differences between the PL results achieved with the new bending test and the other two methods for an alpha-level of 0.05. The subscripts ob, st, nb refer to "original bending test²⁵", "standard thread rolling test^2,5" and "new bending test" respectively. As the soils are very heterogeneous, two different populations are differentiated: high plastic soils (which are the samples M8, M9, M12, M13, S1 and S4), and medium and low plasticity soils (the rest of the soils). The p-Values of a Shapiro-Wilk test are shown for each type of results. Shapiro-Wilk statistical test is necessary to know that the results are normally distributed, which is a necessary condition to perform a Student's T test (in this case, the Shapiro-Wilk test was performed using the software SPSS Statistic). In bold the p-Values results achieved with a Student's T test in which the PL results obtained with the new bending test are compared with those obtained with the original bending test and thread rolling test in order to check if significant differences exist.

Discussion

The Atterberg plastic limit¹ is a very important parameter in soils, mainly because it is widely used for geotechnical purposes^10,11,12. The standard thread rolling test for PL determination has been widely criticized because it is highly dependent on the skill and judgment of the operator who is conducting the test and consequently new approaches to obtain the PL are claimed^{6,7,9,13,15-20, 23-25}. However the simplicity, low cost and quick performance of the standard PL test give it an advantage over the unsuccessful alternatives proposed to date, despite the fact that the subjectivity of the operator is reduced in most of alternative methods, like those carried out by fall cones^15-20.

The method presented in this study (the thread bending test or simply bending test) is based on the measurement of bending deformations, so the subjective judgments from the operator are minimized²⁵. This is a very rapid method, since only one experimental point is necessary to calculate the PL through an equation (although two data points are recommended in order to be more accurate), and it is also inexpensive because only a very simple device is required to carry out the test.

With respect to the protocol, there are some critical steps that should be taken into account: In step 1.3, the drying period cannot be predetermined because it will depend on the type and volume of soil and its moisture content, thus the soil should be dried until it can be disaggregated and sieved properly (which can take from a few hours to several days), because if the soil is wet it can adhere to mortar during the disaggregation and the aggregates can be retained on the sieve following the steps 1.4 and 1.5. In any case, the laboratory operator can perceive if the soil is dry simply by touching it with the fingers. Regarding the steps 2.1 to 2.3, for cohesive soils (mainly clays) it is recommended that at least one of the balls shows certain stiffness, which would indicate that the moisture content is close to the PL. In the case of soils with low or very low cohesion (mainly silts and sandy soils), the soil ball consistency should be soft, but without an excess of water (this soft consistency is required because in low plasticity soils the soil threads are usually too difficult to shape at water contents in which the soil consistency becomes stiff). It is important to highlight that the amount of water that is added at these steps varies depending on the type of soil, so the operator must judge in its sole discretion when the soil has the appropriate consistency to perform the test properly, because the soil threads are difficult to shape if the soil is too dry (it could crumble) or too wet (it could be sticky), even when the step 3.5.1.1 is followed. In the step 2.4 the tempering period can be prolonged (for example in high plasticity clays) or shortened (in low plasticity soils), but in order to unify the criteria the 24 hr period is a good option because the PL test implementation and its results can be affected by this factor (soils usually show more plasticity when this time is prolonged). Regarding the step 3.2, it is recommended that the surface of the flattened soil mass remains covered with cling film in order to minimize the loss of water by evaporation, especially in sandy soils which can lose water quickly, so if the soil mass is not covered, the first rolled soil threads might present greater moisture contents than those obtained at the end of the step 3. For this reason just after a soil thread is shaped and put into the container, it should be covered immediately (for example with a watch glass) during the step 3 (see step 3.6.4.1).

One of the limitations of the test is that the bending motion is performed manually; since there is not any device to do it (the thread molder and the steel pushers are simply used as supporting points). The bending motion should be smooth and progressive as shown in Figure 3B (the soil thread should not be bent all at once, unless the soil is close to the PL, where it barely bends, as often happens in cohesive soils), so that this movement should be repeated more than once. Therefore, the step 3.6.3 is critical in the outcome of the test because if the bending technique is not adequate, the soil thread could crack before it should, or even the cracks could appear out of the central third of the thread (this latter case often occurs when the soil has a soft consistency, especially in sandy soils and silts). These shortcomings are solved on the one hand, by bending two or more threads (step 3.8) in order to check that all measurements are quite similar, and on the other hand, by bending the thread as indicated in the step 3.6.3.1 when cracking occurs near of the thread tips. After bending, it is important to highlight that the thread tips may move during the tip distance measurement (step 3.6.4). There are two options to prevent it: 1) do not remove the steel pushers during the measurement (however, the steel pushers are sometimes placed in such a way that could hinder the measurement) or 2) press the thread tips slightly against the glass plate with the fingers and remove the steel pushers to measure the tip distance properly. With respect to the step 3.6.4.2 the bending technique that this step indicates is more difficult to implement than that explained in the step 3.6.3. For this reason, whenever feasible, it is preferable to prepare the soil ball with an amount of water at which D<0 mm is avoided (this usually occurs when the soil is very wet and also in low cohesion soils).

The results obtained with the new bending test in 30 soils are in excellent agreement with those obtained by a highly experience operator through both the standard thread rolling method^2,5 and the previous multi-point version of the bending test (that previous version was slower than the new one and plotting was required to get the PL²⁵). It should be pointed out that the new bending test works very well not only in cohesive soils, but also in low and very low plasticity soils, which are the types of soil most difficult to test by laboratory operators. Only in particular cases of very high plasticity soils with PL values greater than 30 (such as soils M8, M9 and S4), the new bending test could overestimate the PL results regarding the standard thread rolling test or the original bending test. When the PL result is greater than 30 and the soil is clearly cohesive (it can be rolled easily by hand), a good way to find out whether we are facing a soil of this type is by: (1) checking the two PL results obtained with the equation shown in the step 6.1, because in these particular cases the difference between the two PL results may be very large (even of more than 4 percentage points) which also results in large standard deviations and coefficients of variation (like those indicated for soil M8 in Table 2) and could be indicative of a much steeper bending slope than m=0.108 (see for example m for soil M8 in Table 1), and (2) checking the B values, because despite the fact that these soils (such as M8 and S4) are very cohesive (they can be rolled easily) the bending deformations tend to be small (for example, B<5 mm or even B<2 mm, so for larger B values soil becomes sticky and difficult to handle), which involves that these soils could exhibit B values at the PL much lower than the average B=2.135 mm (see B_PLob of soils M8 and M9 in Table 1). In these particular cases (which are very unusual), the use of the original multi-point bending test²⁵ could be justified, although from a statistical point of view it would not be compulsory since the Student's T test (Table 3) indicates that the differences between the methods are not significant and hence, the new bending test would be valid for a wide variety of soils, even for those with very high plasticity and special characteristics.

In spite of the particular cases above indicated related to some highly plastic soils, the new bending test proposed in this paper (based on a previous study by the authors²⁵) is accurate, quick, cheap and simple, which give it an advantage over the traditional thread rolling test and also over other alternative methods for PL determination (like those based on cone penetrometers^15-20). The implementation of the new bending test in geotechnical and soil laboratories would involve an improvement in the PL test performance, because in addition to the abovementioned features, now the criteria to obtain and calculate the PL would be clear, the skill or experience of the operator would not be a decisive factor for conducting the test properly and the subjective interpretation from the operator would also be minimized. In this way, the potential errors that are committed with the standard thread rolling method (for example, those in which the PL result is greater than the LL, something that, theoretically is not possible) and that affect negatively the Casagrande classification¹³, could be avoided. Although an interlaboratory study would be required, it is expected that the results between different operators are quite similar with the new bending test, something that in many occasions does not happen when the traditional thread rolling test is conducted, especially in low plasticity soils in which the skill and experience of the operator are decisive in the final result. For these reasons, the bending test has potential to be standardized in order to become a real alternative to replace the inaccurate thread rolling test in geotechnical and soil laboratories around the world.

Disclosures

The authors have nothing to disclose.