Abstract
Due to the higher computational cost relative to pure molecular mechanical (MM) simulations, hybrid quantum mechanical/molecular mechanical (QM/MM) free energy simulations particularly require a careful consideration of balancing computational cost and accuracy. Here we review several recent developments in free energy methods most relevant to QM/MM simulations and discuss several topics motivated by these developments using simple but informative examples that involve processes in water. For chemical reactions, we highlight the value of invoking enhanced sampling technique (e.g., replica-exchange) in umbrella sampling calculations and the value of including collective environmental variables (e.g., hydration level) in metadynamics simulations; we also illustrate the sensitivity of string calculations, especially free energy along the path, to various parameters in the computation. Alchemical free energy simulations with a specific thermodynamic cycle are used to probe the effect of including the first solvation shell into the QM region when computing solvation free energies. For cases where high-level QM/MM potential functions are needed, we analyze two different approaches: the QM/MM-MFEP method of Yang and co-workers and perturbative correction to low-level QM/MM free energy results. For the examples analyzed here, both approaches seem productive although care needs to be exercised when analyzing the perturbative corrections.
1 Introduction
Using theoretical and computational approaches to understand catalysis in solution and biomolecules has a long history that dates back to the beginning of the development of quantum chemistry.1 More systematic efforts began with the pioneering developments of molecular dynamics simulations of biomolecules2 and hybrid quantum mechanical/molecular mechanical (QM/MM) methodologies,3 as recognized by the Nobel prize of Chemistry in 2013. After decades of methodology developments,4–14 QM/MM simulations have become a powerful tool for the analysis of enzyme catalysis15–20 and can aide effectively in exciting applications such as drug design,21 enzyme/protein engineering22–24 and systems biology.14 Despite much success, one may argue that the field of computational enzymology is still at its infancy,25,26 in the sense that it remains challenging to make quantitative predictions on the catalytic proficiency of an arbitrary enzyme with an entirely generic computational approach. Therefore, much work is needed to push forward QM/MM based techniques toward the next level of maturity and robustness.
Central to most QM/MM applications is the computation of free energy differences. In the context of enzyme catalysis, for example, the relevant quantities27 include the binding affinity of the substrate (often related but not necessarily equivalent to the Michealis constant KM) and the free energy profile for the chemical step(s), which contain information about kcat; to understand the proficiency of enzyme catalysis, it is also important to determine the free energy profile for the uncatalyzed reaction(s) in solution. Accordingly, two types of free energy simulations are involved: alchemical simulations for binding and potential of mean force (PMF) simulations for chemical reactions. The division of the techniques is certainly not absolute; for example, PMF type of simulations can also be used to compute the absolute binding free energy of ligands to protein receptors.28
For both types of free energy simulations, it is well appreciated that the key challenge is to strike the proper balance between potential energy accuracy and the degree of conformational sampling. This is particularly the case for QM/MM based free energy simulations, since the cost of QM calculations is substantially higher than that of classical force field based calculations. For example, work in our group has targeted metalloenzymes that feature active sites that are particularly dynamical in nature, allosterically regulated, and/or have a significant degree of solvent accessibility; good examples include biomolecular motors,29,30 DNA repair enzymes,31–33 ion transporters34–36 and enzymes that feature a high degree of catalytic promiscuity.37–42 In addition to their biological significance, these problems were chosen because they have been difficult to tackle with existing methodologies. On one hand, the involvement of metal ions calls for the use of a reliable QM approach; on the other hand, the particular dynamical nature of these systems demands adequate sampling.
In this contribution, we briefly review the two types of QM/MM free energy simulations with most examples motivated by our own research. The goal is to illustrate state-of-the-art techniques, recent developments and technical issues relevant for realistic applications using model systems. We focus on problems in which a direct sampling of the QM/MM potential function is important, although we also discuss the elegant minimum free energy path method of Yang and co-workers11 (also see Ref.43,44), in which the QM and MM fluctuations are decoupled and therefore finite-temperature sampling is done mainly for the MM degrees of freedom. For direct sampling, it is crucial to develop a low-level QM/MM potential that provides a semi-quantitative description of the underlying potential energy surface. One approach is to develop system-dependent semi-empirical QM/MM potentials, based on either minimum energy paths,45–47 force-matching48 or para-dynamics.49 The alternative approach, which is what we follow, is to develop a general-purpose approximate QM method so that refitting is (ideally) not required when studying a new system. In particular, we have been pursuing an approximate density functional theory, density functional tight binding (DFTB50,51), for biologically relevant systems. As reviewed elsewhere recently,52–54 the latest version of the DFTB methodology, referred to as DFTB3,55 provides encouraging results for a fairly broad class of systems of biological interest; the accuracy is often comparable to density functional theory with the generalized gradient approximation (DFT/GGA) and a double-zeta-plus-polarization quality basis set, while the computational cost is similar to conventional semi-empirical methods56 such as AM1 and PM3, making it routine to conduct nano-second simulations based on DFTB3/MM potentials. For metalloenzyme applications, recent developments have led to promising parameterizations for several metal ions that include the alkali metals,57 magnesium, zinc58 and copper.59 The DFTB3 method in the current form is most reliable for structural properties, including for fairly complex bi-metallic motifs in several enzymes;40,41,58,60,61 for energetic properties, the results are less robust as compared to DFT/GGA62,63 but can often be improved to satisfying accuracy with single point energy calculations at high QM(/MM) level, making DFTB3 a promising low-level approach in dual-level QM/MM free energy simulations, a topic that we will also discuss here.
In the following, we first summarize the basic theoretical foundation of the two types of QM/MM free energy simulations and relevant techniques (e.g., metadynamics and finite-temperature string) for various applications. Next, we discuss a number of condensed phase model systems to illustrate these free energy methods and relevant technical issues. Finally, we draw a few conclusions and highlight a few pressing challenges for future investigations.
2 Theory and Methods
In this section, we first discuss methods for computing reaction free energy profiles and pathways, and then move on to alchemical free energy computations, including multi-level free energy calculations that integrate low- and high-level QM(/MM) potential functions.
2.1 Reaction free energy profile and pathways
2.1.1 Sampling along pre-determined order parameters
For relatively simple chemical reactions, such as localized proton/atom transfers, umbrella sampling64 along one or several pre-defined order parameter(s) is likely an effective approach. These order parameters are usually geometrical parameters, such as an antisymmetric stretch involving the atom being transferred and the respective donor and acceptor atoms;65 in some applications, energetic parameters such as the energy gap between the relevant diabatic states66,67 are also useful. The potential function in umbrella sampling (UUS) takes the following form, which includes both the unbiased potential energy (U0) and the umbrella potential (Ub),
| (1) |
The umbrella potential of the ith window typically takes the form of a harmonic restraint on the order parameter ξ (i.e., k(i)(ξ − ξ(ref,i))2), although more complex functional forms or numerical values can be used in, for example, adaptive umbrella sampling;68 the bias can also take the form of a constraint69,70 rather than a restraint, thus fixing the value of the order parameter to be specific reference values, ξ(ref,i). When a restraining potential is used, statistics of the order parameter(s) from all windows are collected and analyzed using, typically, Weighted Histogram analysis (WHAM)71 to generate the underlying PMF, W(ξ) (Eq. 29). In constrained simulations,69 the mean gradient of the order parameter(s), 〈∇ξ(U0 − β−1 log |J|)〉ξ, is integrated to generate W(ξ) (where 〈·〉ξ is the conditional average ∫ dX(·) exp[−βU0]δ(ξ(X) − ξ)/∫ dX exp[−βU0]δ(ξ(X) − ξ), β is the inverse temperature, and we have formally included the Jacobian of the coordinate transformation, but left the transformation unspecified). Because it is straightforward to decompose atomic contributions to (mean) force when pair-wise MM potential or QM-MM interactions are used, constrained simulations are valuable for decomposing atomic contributions72 to W(ξ), provided that care is exercised to include the Jacobian contribution.73,74
As discussed in recent studies, the WHAM approach relies on the assumption that data from different windows are drawn from globally equilibrated simulations, thus care needs to be exercised to design the restraining potentials and to monitor convergence;75 a promising alternative is to analyze the data using a discrete transition based reweighting analysis (dTRAM,76 a similar idea was published in Ref.75), which provides maximum-likelihood estimates of free energy quantities without the assumption of global equilibrium. Another technical issue often encountered in umbrella sampling for complex system is that the degrees of freedom orthogonal to the order parameters are sampled differently in different windows. One promising approach to improve the convergence is replica-exchange umbrella sampling (REUS77,78), which is a variant of the Hamiltonian replica-exchange method.77,79 In REUS, different umbrella windows are run in parallel; at a given frequency, an attempt is made to exchange configurations from two windows (m ↔ n) with the acceptance probability following a Metropolis criterion:
| (2) |
where . If there are significant barriers along the orthogonal directions for all important ξ values, REUS alone does not help overcome these barriers; when the orthogonal barrier is only high in certain ξ windows, however, REUS is expected to be effective.80 For the acceptance probability to fall in the reasonable range, exchange is usually attempted for neighboring windows.
Another popular variant of the adaptive umbrella sampling technique is metadynam-ics,81–83 in which Gaussian potentials are deposited with a time interval of τG along a molecular dynamics simulation. The Gaussian potentials, with width δG and height ωG, are functions of the order parameters, which are referred to as the collective variables (CVs) in the metadynamics literature. Addition of the Gaussian functions elevates the potential wells and eventually facilitates transition over barriers in the CV space. In the long time limit, when the dynamics in the CV space becomes diffusive, the accumulated Gaussian potential,
| (3) |
approaches the negative PMF in the CV space, i.e., limt→∞ VG(ξ, t) ~ −W(ξ); it is straight-forward to generalize Eq.3 to multi-dimensional cases. In addition to the choice of the CVs, which is a common issue to any form of umbrella sampling technique, the convergence behavior of metadynamics simulations has been thoroughly discussed in the literature,81,84 including the choice of the key parameters (δG, ωG and τG). Approximate expressions have been derived for metadynamics, although in practice, the error in the computed PMF profile is more conveniently estimated by comparing independent runs or using block averaging. In well-tempered metadynamics,85 the height of the Gaussian potential is automatically scaled as the simulation proceeds, which leads to a smoother convergence behavior,84
| (4) |
Here ΔT is an input parameter, which determines the long-time limit of the accumulated Gaussian potential,
| (5) |
For ΔT = 0, regular MD is recovered, while the regular metadynamics corresponds to the limit of ΔT → ∞.
The challenge for studying reactions in a complex environment is that many degrees of freedom are likely involved. If a large number of order parameters/CVs are chosen, umbrella sampling and metadynamics simulations will be prohibitively expensive for thoroughly exploring the multi-dimensional PMF. One possible solution is to maintain a small number of CVs, but couple metadynamics with replica-exchange/simulated tempering simulations to enhance the sampling of the orthogonal or transverse degrees of freedom.81 Another choice is bias exchange metadynamics,86 in which replica-exchange is conducted for multiple meta-dynamics simulations that bias different sets of CVs. The other alternative is to search for a minimum free energy path rather than exploring the entire multi-dimensional PMF surface. In this case, only a one-dimensional object is sought for, regardless of the number of CVs used to parameterize the path, thus the computation formally scales much more favorably compared to multi-dimensional umbrella sampling/metadynamics. We turn to this subject in the next section.
2.1.2 Free energy path sampling
The search of minimum energy path (MEP), also known as the intrinsic reaction coordinate,87 has a long history in quantum chemistry. For reactions in the liquid phase or biomolecules, which feature very rugged potential energy surfaces, a small number of MEPs are often insufficient for a quantitative description of the reaction,9,45,88 since the potential energy profiles can vary greatly among them and it’s not trivial to evaluate the weights of these MEPs in terms of contribution to the reaction flux at a finite temperature.89
The alternative is to determine the path(s) on a free energy surface. Again, there has been many developments motivated by somewhat different applications, and here we focus on those most relevant to QM/MM type of simulations; we limit the discussion to pathways in the configurational space only, as sampling in the trajectory space (transition path sampling90) is most important for understanding dynamical (non-equilibrium) effects associated with a reaction. In this context, we again first define the CV space spanned by a set of order parameters most relevant to the reaction process: ξ⃗(X) = (ξ1(X), ξ2(X),···, ξn(X)); the CVs can range from a combination of internal coordinates to a set of Cartesian coordinates for the most essential atoms. Then the free energy surface (or PMF) in this n-dimensional space is defined as,
| (6) |
where Z is the configuration integral. The minimum free energy path (MFEP) on this surface is a curve (or a “string”) defined by the condition that the projection of the mean force perpendicular to the path vanishes,
| (7) |
where Mij= 〈∇X*ξi · ∇X*ξj〉ξ⃗ is the metric tensor associated with the transformation to the space of collective variables, and X* are mass-weighted coordinates. As discussed in detail in Ref.,91 the MFEP is the path of maximum likelihood for the reaction if two conditions are met: (i). the set of collective variables is adequate to approximate the committor function, which is taken to be the true reaction coordinate that describes the mechanism of the reaction;90,92–96 (ii). most reactive trajectories are contained in narrow ‘transition’ tubes, which are separated by significant energy barriers.
In practical implementations, the MFEP is optimized with the chain-of-states methods,97 similar to the nudged elastic band98 and its variations for MEP computations. The string is discretized into a set of N equidistant points (or images91) , with i ∈ [1 … N] and to each point a separate simulation system is assigned, which is used to compute the metric tensor M(ξ⃗) and the free energy gradient ∇W(ξ⃗) that appear in Eq. 7. Starting from an initial condition for the string , the points are updated iteratively until a discretized version of condition Eq. 7 is satisfied. A straightforward iterative method is to first advance the string using steepest descent:99
| (8) |
followed by reparametrization,91 i.e., an interpolation step that enforces equal distances between adjacent images:
| (9) |
In Eq. (9), τ→i is the vector tangent to the string at , and λi are chosen such that | | are equal for i ∈ {1 … N − 1}.99,100
M and ∇W in Eq. (8) are computed from simulations with harmonic restraints , and the parameters Δt and γ are adjusted empirically to accelerate convergence to the MFEP.91,100 For the special case of Δt=dt, where dt is the time step in the molecular simulation used to compute M and ∇W, the string was shown to converge to the MFEP rapidly,101,102 provided that the friction γ was taken sufficiently large. However, in this case the optimized path satisfies the condition
| (10) |
which differs from Eq. (7) by the temperature-dependent term β−1∇·M. The differences in the paths and free energies based on Eqs. (7) and (10) were found to be small for the solvated alanine dipeptide.101,102 It is noteworthy that the reparametrization step of Eq. (9) is a relatively expensive collective computation involving all points (i.e., possibly all processors), and thus a larger Δt is typically chosen to avoid performing this step too frequently.
An indirect approach to approximate the solution to Eq. (10) is the swarm-of-trajectories string method (STS).103 In STS, a collection of independent unbiased trajectories of (usually short) duration Δt are launched from configurations of the molecular systems conditioned on , and the evolution in Eq. (8) is replaced by
| (11) |
where α is a scaling parameter that can be used to optimize convergence and accuracy (α=1 is a typical starting choice). are then obtained from Eq. (9). To iterate further, one must recondition the molecular systems to satisfy , which can be achieved using e.g., restrained simulations. Although the original STS approach assumed diffusive dynamics of the CV variables under which condition the optimized path is the most probable transition path (i.e., the system has the highest probability of being on the path), it was subsequently shown that the approach is also valid when the CV dynamics is in the inertia regime,102,104 and the path converges to MFEP.
In practical applications of the string methods, the most important decisions include the choice of the CVs, the initial string ( ) and the values of the restraining force constants. The choices are often not straightforward and can influence results significantly. We will discuss some of the issues using examples in Sect.3.1.2.
When the QM method is expensive, such as an ab initio or DFT method, direct sampling is usually not affordable. One promising solution is the QM/MM-MFEP approach pioneered by Yang and co-workers11,105 that searches for MFEP with the CVs corresponding to the Cartesian coordinates of the QM region; i.e., one searches the MFEP on the PMF surface for the QM degrees of freedom,
| (12) |
and the key is to compute the gradient with respect to the QM coordinates,
| (13) |
In practice, this is done by decoupling the fluctuations of the QM and MM regions, and extensive sampling is only done for the MM degrees of freedom in the presence of frozen QM atoms that are represented by partial charges (and possibly polarizabilities106); related methods have also been developed by others.43,44 To facilitate convergence, the QM geometry/path optimization is done in an iterative process106 in which a fixed MM ensemble is used when QM structure is relaxed according to an approximate expression for Eq.13 (see below). Once the QM structure is fully relaxed, the MM ensemble is updated with a frozen QM region, and the process is repeated till convergence. For MM sampling and QM structural relaxation, the QM density/partial charges are determined using the corresponding MM ensemble and a mean-field approximation. This allows the approximate separation of electrostatically embedded QM/MM energy into the sum of a QM internal term and classical QM-MM electrostatics,
| (14) |
where Ψmf is the mean-field wave function for the QM region, includes only the electrostatic embedding operators for the mean-field QM-MM interactions, NMM–ens is the number of configurations in the MM ensemble included in the mean-field calculations, and is the ESP charge for the i-th QM atom determined by the mean-field calculations; we will examine whether the mean-field approximation is a good model below using solution reactions. Accordingly, the PMF gradient can be written as,
| (15) |
where includes the classical electrostatic interactions between the QM ESP charges and MM charges, along with other classical QM/MM terms such as van der Waals and bonded contributions.4 In practice, since a fixed MM ensemble is used for each cycle of QM structural relaxation, the ensemble average in Eq.15 needs to be re-weighted with the QM structure used to generate the MM ensemble as a reference; i.e.,
| (16) |
where 〈···〉MM,ref emphasizes that the MM ensemble is generated using a reference QM structure (for example, the converged structure from the previous cycle of QM structural relaxation). Note that the difference in the QM internal energy relative to the QM reference structure in principle contributes to the Boltzmann factor in Eq. 16, but, with the mean-field approximation, such contributions cancel out in the numerator and denominator.
Since the QM structures are relaxed with local minimizations, only harmonic fluctuations around the stationary points along the MFEP can be estimated using normal mode analysis.106 Anharmonic effects and larger scale changes for the QM region, such as extensive rearrangement of hydrogen bonding networks during the reaction, are not captured, thus the method may not be optimal for systems with a high degree of flexibility and/or solvent accessibility.
Finally, we note that an entirely different approach is to use enhanced sampling techniques to let the QM region overcome chemical barriers without biasing specific geometrical coordinates. Then the free energy surface can be projected onto desirable CVs for analysis. Several attempts have been made in the past under the name of “chemical flooding”.107 The most recent example featured the use of selective integrated tempering sampling (SITS108) for the QM atoms in a QM/MM framework. In ITS,109 an effective Hamiltonian is constructed by integrating the distributions at multiple temperatures, and sampling using this effective Hamiltonian allows overcoming enthalpic barriers; in SITS,108 only the effective temperature for selected degrees of freedom and their coupling to the environment is scaled, similar to solute tempering,110 allowing the enhancement of sampling for specific degrees of freedom. The method has been successfully used to study Claisen rearrangement in different solutions.111 In the future, it is interesting to explore whether this promising method remains effective when the QM region is large and therefore there are many ways to partition the energy boost introduced through the higher temperature distributions.
2.2 Alchemical and multi-level free energy computations
2.2.1 Alchemical free energy simulations
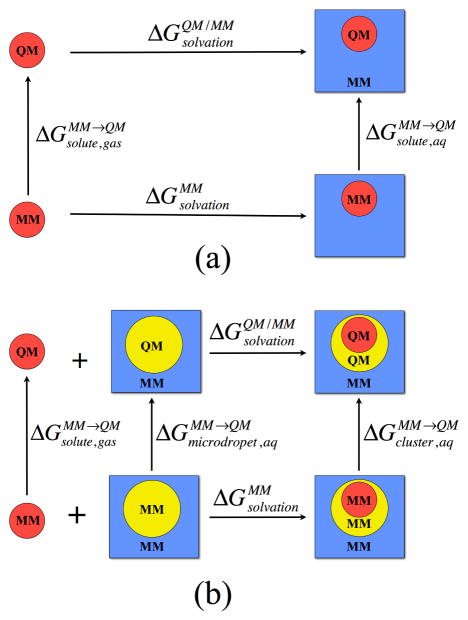
When only the relative free energy of two species/states, rather than the path that connects them, is of interest, alchemical free energy simulations112–114 are often used. Specifically for QM/MM applications, typical examples include the solvation free energy of a QM solute, and the binding affinity of a QM ligand to a protein active site; in the first case, the two states correspond to the QM solute in the gas phase and water, respectively, while in the latter case, the two states are the QM ligand in water and in the protein active site, respectively. Alternatively, we might be interested in the relative solvation free energy of two QM solutes in water, or the relative binding affinity of two QM ligands to the same protein active site. To minimize the cost of sampling, QM/MM alchemical free energy simulations are often carried out using a thermodynamic cycle pioneered by Gao5 and Warshel66 in which pure MM simulations are used as a reference; an example is described in Fig. 1a, which describes the solvation free energy calculation of a QM solute.
Figure 1.
Thermodynamic cycles used to compute the solvation free energy of a QM solute in (a) a pure MM environment and (b) when nearby solvent molecules are also described at the QM level. In both cases, a pure MM solvation free energy calculation (bottom horizontal process) is used as a reference; to obtain the desired QM solvation free energies, various vertical processes need to be studied in which the solute (colored red) or a micro droplet (colored yellow) is converted between a MM and a QM model either in the gas phase or in an MM solution environment (in blue).
Following the thermodynamic cycle, the step that requires most sampling is done with an inexpensive MM potential ( ), while “alchemical mutations” are used to convert the solute between MM and QM representations; such conversion is expected to converge quickly due to the generally small differences between QM and MM potentials for stable species. Using the state nature of free energy, it is easy to see,
| (17) |
This type of thermodynamic cycle can be easily generalized to connect QM descriptions at different levels as well, which we discuss in the next subsection.
For highly polar and charged solutes, it might be preferable to treat also the first solvation shell as QM. In this case, the thermodynamic cycle only requires a minimal degree of revision, as shown in Fig. 1b. The additional step involves converting the microdroplet, which corresponds to the first solvation shell solvent molecules in the absence of the solute, between MM and QM representations,
| (18) |
In terms of computational cost, the alchemical steps that involve MM/QM conversion are most likely to dominate. When QM is an ab initio or DFT method, it is desirable to minimize the degree of QM sampling, a topic we discuss in the next subsection. When the QM is a semi-empirical method, direct sampling is possible although it may still be costly. Thus it is fruitful to develop methods to speed up alchemical free energy computations that mix different potential functions. We recently developed the integrated Hamiltonian sampling (IHS),115 which can be regarded as an extension of the ITS approach;109 it is also intimately related to the enveloping distribution sampling of van Gunsteren and co-workers.116 In IHS, we introduce an effective potential (UIHS(R)) whose canonical distribution is the integrated distributions of multiple potential functions,
| (19) |
where Ω(λ) is a weight function to be determined (see Ref.115 for discussion of algorithms) and Uλ takes the usual form,
| (20) |
In the specific case of MM→QM conversion, U0 and U1 correspond to pure MM and QM/MM potential functions, respectively. In general applications, U0 can be the potential function of a realistic system while U1 the potential function of a fictitious system introduced to enhance sampling; e.g., specific torsional barriers or non-bonded interactions are scaled down.
2.2.2 Multi-level QM/MM free energy methods
As mentioned above, the thermodynamic cycle in Fig. 1a can be easily generalized to connect low-level and high-level QM potentials in QM/MM simulations. This can be applied to improve the relative free energy of the same molecule in different environments (e.g., solvation free energy) or of different chemical states in the same environment (e.g., reactant vs. transition state in an enzyme active site). In practice, the challenge is that the computational cost for any calculation involving the high-level QM is so high that canonical sampling has to be at a minimal level or avoided altogether. For example, several studies computed the free energy profile (e.g., PMF along a pre-defined order parameter) with a low-level QM/MM potential function, and correction is estimated based on the difference between the low- and high-level QM/MM results along one or several MEPs;117,118 for systems with a dynamical active site, the energetics of MEPs may fluctuate significantly as functions of the protein conformation, 9,45,88 thus the correction may also have significant uncertainties. In other studies, sampling is done exclusively with the low-level QM/MM potential, and a one-step free energy perturbation is used to estimate the free energy change to high-level QM/MM;41,119–122 as expected, the quantitative accuracy and convergence of the results depends critically on the overlap of distributions with different QM/MM potentials,121,123 thus some authors advocated to carry out at least short sampling using high-level QM/MM potential rather than relying entirely on trajectories sampled with low-level QM/MM.13,124,125
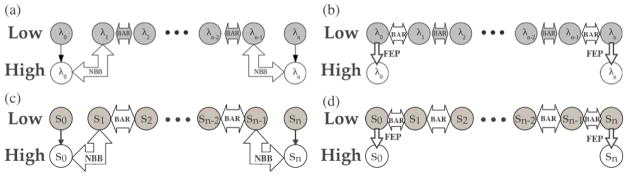
One interesting recent development in multi-level free energy computation is the Non-Boltzmann Bennet (NBB) approach,122 which treats the low-level simulation ensemble as that from a high-level simulation under a biasing potential being nothing but the energy difference between the low- and high-level potentials. This allows, for example, directly connecting the λ0 window at high-level and λ1 window at the low-level method (Fig. 2a); by coupling regular BAR simulations at the low-level for the intermediate λ windows and NBB for the end states (λ0, λn windows), one recovers the free energy difference between the end states with the high-level potential. The working expression for NBB combines the BAR equation and the familiar reweighting formula;64 for the high-level λ0/low-level λ1 free energy difference, for example, we have,
Figure 2.
Two different routes to compute the free energy change as the potential function is switched between a low level and a high level. (a–b) illustrate the routes for alchemical free energy calaculations and (c–d) illustrate the corresponding calculations along a path (e.g., an optimized string). In the NBB route, a low-level window (e.g., ) is connected with a neighboring high-level (e.g., ) by re-weighting the data. In the FEP(+BAR) route, free energy change due to a switch in the potential function is calculated only for the same (e.g., λ0) window; different λ/s windows (e.g., λ0/λ1 or s0/s1) are connected with the low-level potential function using BAR. See text for the corresponding equations for the free energy changes (compare Eqs. 21 and 23).
| (21) |
in which C is the constant to be determined in the BAR iteration, f is the Fermi function: , and in the energy difference between the low- and high-level potential functions for the λ0 window. The notation 〈···〉λ0,L highlights that the ensemble average is over the simulation at the low-level.
The NBB approach has been tested using a series of solvation free energy simulations with both explicit and implicit solvent models;122 the low-level has been taken as either a MM model, or a low-level QM method, while the high-level is taken to be a DFT or correlated ab initio method. Encouraging results have been obtained. Nevertheless, the question is whether NBB offers a significant advantage over the more traditional approach in which the low- and high-level methods are connected at only specific windows (e.g., λ0, λn) via one-step free energy perturbation. At the λ0 window, for instance, one has,
| (22) |
Therefore, the and windows can alternatively be connected by combining and a BAR computation for λ0, λ1 at the low level (Fig. 2b):
| (23) |
Comparing Eqs.21 and 23, one sees that the two pathways of connecting and windows indeed have similar expressions. As well appreciated in the literature,126 both FEP and BAR methods require a good overlap of distributions between the two states being considered; numerically, BAR is more robust and therefore less sensitive to the degree of overlap, which likely motivated the development of NBB. We note, however, the numerical behavior of Eq.23 depends on the overlap between the low- and high-level distributions for the same (λ0) window and the overlap between two λ windows at the same (low- level) theory, while Eq.21 depends on the overlap between the high-level distribution for λ1 and the low-level distribution for λ0; i.e., both the level of theory and λ values are changed simultaneously in NBB. Therefore, intuitively, NBB is expected to work less well than the traditional FEP+BAR route, despite the intrinsic numerical advantage of BAR. At a quantitative level, one possible way to compare the two approaches is to evaluate the variances of the two free energy difference estimators. This was done recently by Jia et al.,127 who showed for , for example,
| (24) |
The variance is actually the sum of contributions from BAR between and (though with configurations sampled at low-level for both λ values) and FEP between and ; a similar expression can be obtained for by replacing by in the first two terms on the right hand side of Eq. 24. The variance tends to be dominated by the FEP variance term, thus the result confirms our expectation that, with the same degree of sampling, the variance of NBB is unlikely better than the FEP+BAR route. It is nevertheless interesting to analyze the two approaches under broader context since variance alone may not be sufficient to characterize the reliability of the multi-level free energy result.
The discussions are straightforwardly generalized to free energy correction along a reaction path, such as for images along a string. With the NBB scheme (Fig. 2c), for example, the argument of the Fermi function would include also the restraining potentials associated with different images in a string calculation, e.g., . It is of interest to compare the results to the traditional “one-step” FEP route (Fig. 2c vs. 2d) for specific images (e.g., those correspond to the reactant and transition state), as we do in Sect.3.2.2.
3 Model and realistic examples
3.1 Reaction free energy profile and pathways
3.1.1 Umbrella sampling, replica-exchange umbrella sampling and metadynamics
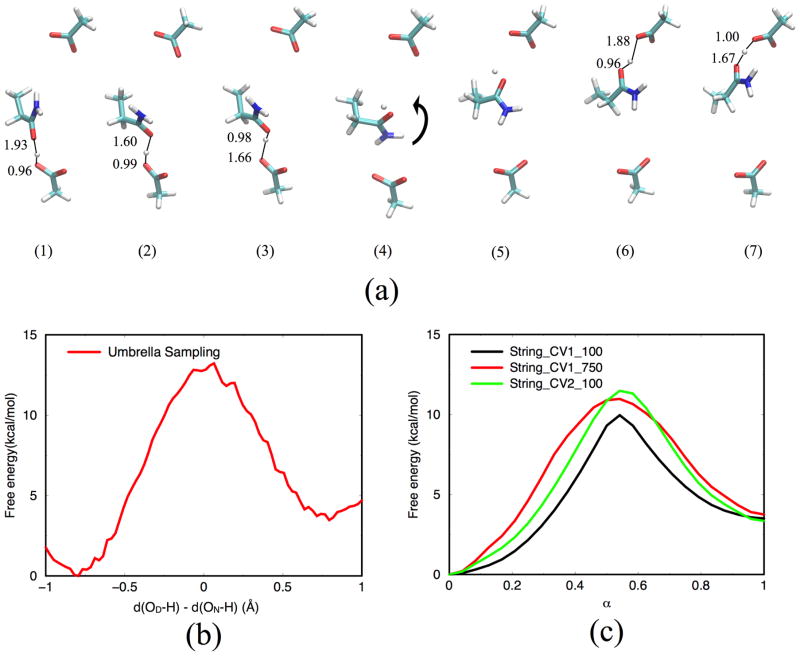
We’ll use a simple model to illustrate the comparison between umbrella sampling, replica-exchange umbrella sampling (REUS) and metadynamics. As illustrated in Fig. 4a, the model describes proton transfer between two small water droplets through a “channel”; the confinement effect of the channel is implemented using a set of restraints available in CHARMM128 and a set of point dipoles are included to stabilize the excess proton in the low-dielectric region of the model. This type of model was used in our previous studies to explore the definition of order parameters for long-range proton transfers,129 to understand the impact of boundary potential, including an external membrane potential,130 on proton transfers, and to compare different parameterizations of DFTB3 for studying the free energy of proton transfers.54 Here we use the model to illustrate the value of REUS for computing free energy profiles over regular umbrella sampling, and to illustrate the flexibility of choosing CVs in metadynamics simulations for gaining new mechanistic insights.
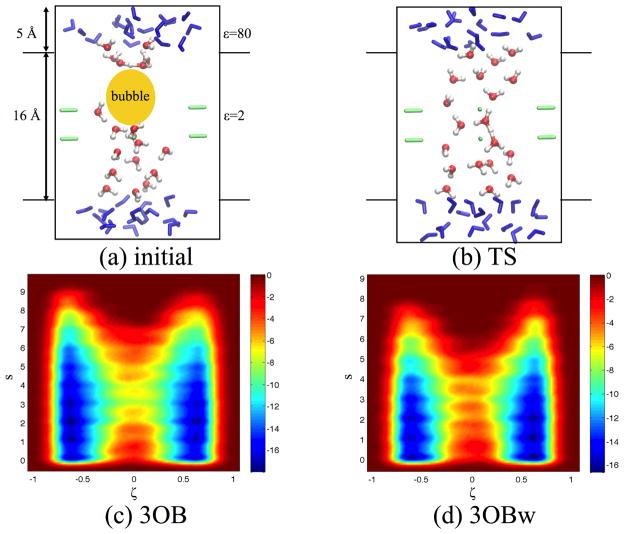
Figure 4.
2D metadynamics simulations for proton transfer in a model channel to illustrate the coupling between hydration level change and proton transfer. (a)–(b) Snapshots for the reactant and transition state regions, respectively. The “bulk” MM water molecules are shown in blue, and the QM water molecules are colored by atom type. The dipoles are shown in green. (c)–(d) Two dimensional PMF from well-tempered metadyanmics simulations using DFTB3/3OB133 (barrier 9.8 kcal/mol) and DFTB3/3OBw54 (barrier 11.5 kcal/mol), respectively. ζ describes the proton transfer and s describes the level of channel hydration (see text).
The model includes a water chain consisting of 19 QM water molecules and one excess proton; the distance from the first to the last oxygen is 16 Å. The length of the chain is motivated by the typical size of proton conducting channels in biomolecules. The water chain is held in the model channel by a cylindrical potential to each of the oxygen atoms:
| (25) |
with kcyl = 125 kcal·mol−1·Å−2; r is the distance of the water oxygen atom from the central axis of the channel, r0 is 3.5 Å, and Θ is the Heaviside step function. To ensure appropriate solvation of the excess proton at the ends of the water chain, 34 MM water molecules are added to each end of the chain. These “bulk” water molecules are subject to a set of quartic constraints to maintain a cubic shape of 10 × 10 × 5 Å3. To stabilize the hydronium in the center of the channel, eight dipoles with modest dipole moments composed of two opposite charges (|q| = 0.5 e and d = 1.5 Å) are circularly arranged around the channel. The system is then embedded into a dielectric environment to mimic a lipid membrane (see Fig. 4a for dimensionality); the dielectric constants for the membrane and bulk water are set to be 2 and 80, respectively.
To study the proton transfer, we carry out 1D REUS simulations as well as 2D metadynamics simulations and compare those to our recent study that used the standard 1D umbrella sampling.54 The order parameter used to describe the proton transfer itself is the ζ coordinate defined in our previous studies: it is based on the modified center of excess charge (mCEC)129 and takes the form,
| (26) |
where ξ is the mCEC, D denotes the proton donor heavy atom, A is the proton acceptor heavy atom and d is the distance; one MM water molecule in each “bulk” region of the model is fixed and taken to be the donor/acceptor group. Therefore, a ζ value of ±0.6 represents the excess proton being solvated by water molecules near the entrance/exit of the model channel and corresponds to the PMF minimum (see Figs. 3–4).
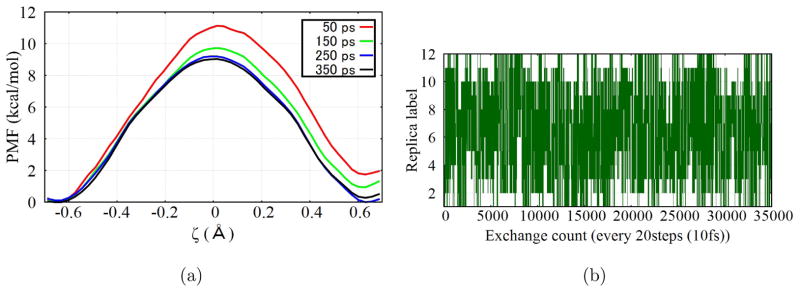
Figure 3.
Results for the proton transfer in a model channel (see Fig. 4) from 1D REUS simulation along the ζ coordinate. (a) Convergence of the PMF as a function of simulation time per replica; (b) Illustration of the exchange behavior of replicas during the REUS simulation, using replica 2 as an example.
In the metadynamics simulations, a second coordinate is used to describe the level of solvation at the center of the channel. As discussed below, this was motivated by the observation that in the reactant state (i.e., when the excess proton is in the “bulk” region), a vacuum region (or a “bubble”) is observed between the excess proton and the other side of the channel; this likely reflects the “amphiphilic” nature of the hydronium,131 which prefers to remain at the air/water interface. It is therefore of interest to explicitly study the coupling between proton transfer and wetting of the channel. The solvation number81,132 of the channel center is described using s, which is defined by,
| (27) |
Here, the channel center is represented by a fixed dummy atom, and
| (28) |
where rij is the distance between atom i and j and d0, r0 are set to be 2.5 and 0.5 Å, respectively.
In REUS, the same 13 set of umbrella windows with equal spacing in ζ as Ref.54 is used. Exchange of configurations between a randomly selected pair of neighboring windows is attempted every 10 fs. Simulations are run till 350 ps for each replica, thus the total simulation time is comparable to that of Ref.54 The DFTB3/3OB model133 is used to describe the QM region. In the 2D metadynamics simulation, well-tempered metadynamics85 is employed with a bias factor of 15. The initial values for Gaussian height are set to be 0.1 kcal/mol for ζ and 0.2 kcal/mol for s. A new Gaussian potential is added every 2.5 ps during the simulation so as to leave sufficient time for the system to respond to changes in the CVs. Two sets of DFTB3 O-H repulsive potential are tested, the standard 3OB133 and a recent 3OBw54 set developed based on improved description of bulk water. Each set of simulation is ran for 1.5 ns.
With the standard 1D umbrella sampling, the computed PMF in Ref.54 still suffers from minor convergence issues after 500 ps of sampling per window. Indeed, the PMF is not symmetrical and has a small exothermicity of about 1 kcal/mol with the DFTB3/3OB model; the barrier measured from the more stable minimum is about 10.0 kcal/mol. With the 1D REUS (Fig. 3a), we see indeed the computed PMF features a significant level of asymmetry at the early stage of the simulation. As simulation proceeds, however, the degree of asymmetry decreases and a practically symmetrical and converged PMF is obtained after about 250 ps per replica. The diffusive behavior of the exchange moves (Fig. 3b) also confirms the efficiency of REUS. Therefore, the simple example illustrates the value of REUS over the standard umbrella sampling in terms of convergence.
As noted above, in the reactant, a vacuum region (or a “bubble”, see Fig. 4a) is formed between the excess proton and the other side of the channel. Therefore, it is expected that hydration level change (i.e., wetting) of the channel is explicitly coupled with the proton transfer. The key question regards whether such wetting is an energy demanding process. As shown by the 2D PMF from metadynamics, proton transfer indeed requires a substantial change in the level of hydration. The barrier along ζ is sufficiently low only when s is in the range of 3–4; as s further increases, the barrier along ζ remains fairly constant. However, the free energy profile along s is rather flat for s ≤ 6 when the excess proton remains in either side of the “bulk” region (i.e., when ζ ~ ±0.6). Therefore, wetting of the channel, at least with the current model, appears to be a rather facile process. This explains why the barriers from the 2D metadynamics simulation and the 1D umbrella sampling/REUS calculations are, in fact, very similar, regardless of the DFTB3 model used.
The general behaviors we found here are similar to the findings from a recent study of proton transfer across a carbon nanotube by Voth and co-workers using the MS-EVB model.134 It was found that the presence of the excess proton at one end of the nanotube induces spontaneous wetting of the tube and facilitates the subsequent proton transfer; interestingly, such favorable wetting behavior was not observed with other monovalent cations (e.g., Na+) or a classical model of the hydronium ion (H3O+), suggesting that the delocalized nature of the excess proton in water is essential. This delocalized nature is captured in our study with the use of a QM model (DFTB3), and the relatively similar barrier heights between 3OB and 3OBw suggests that the qualitative behavior is not highly sensitive to the quantitative description of proton solvation.
The fact that local wetting around an excess proton does not appear to be energetically demanding even in a rather hydrophobic environment (low-dielectric in our model and carbon nanotube in Ref.134) has important implications to proton transfer in biomolecules. Proton transfer pathways are often identified by examining hydrogen bonding networks135,136 visible in protein structures from crystallography or equilibrium MD simulations in the absence of an excess proton. The current discussion highlights that the hydrogen bonding network may in fact change rather significantly in the presence of the excess proton to facilitate its transport. Depending on the specific molecular environment, the wetting process may or may not involve a substantial energy cost. Therefore, one should not rule out proton transfer pathways based purely on hydrogen-bonding network seen in structures obtained in the absence of the excess proton,137 and it is essential to explicitly include the local hydration level 35,36 as one of the order parameters to characterize the energetics and kinetics of proton transfers.
3.1.2 String method in collective variables
To illustrate some of the practical issues in a string simulation, we study a seemingly simple proton transfer reaction inspired by the D-channel in cytochrome c oxidase.34 The model contains two aspartate sidechains separately by an asparagine sidechain, and the entire system is immersed in a water droplet of 20 Å radius. One aspartate is initially protonated, and the proton is transferred from the carboxylate to the carbonyl of the asparagine, which in turn rotates upward to deliver the proton to the upper aspartate (see Fig. 5). The positions of the three sidechain models are adjusted to make the proton transfer pathway feasible with only modest conformational isomerization of the asparagine. The model is constructed to explore whether an asparagine sidechain can relay proton transfers in biomolecules. The three sidechains are treated with DFTB3/3OB, and the water environment is treated with TIP3P under the stochastic boundary condition.
Figure 5.
Study of a proton transfer process inspired by the D-channel in cytochrome c oxidase. (a) Representative structures along the optimized string with key distances (in Å) labeled (water molecules are excluded for clarity); (b) PMF for the first step of proton transfer (approximately corresponding to 1→3 in panel a) studied by umbrella sampling; (c) PMFs for the first step of proton transfer studied by the string method with different collective variables and restraining force constants (indicated in the legend in kcal/mol/Å2).
For the string calculation, 56 images are included, and the CV space is spanned by all the pairwise distances between heavy atoms in the three amino acid analogues and the distances involved the extra proton, leading to 62 distances. The friction coefficient γ in Eq. 8 is 100 ps−1. MD sampling is carried out for 1.5 ns per image at 300 K with a time step of 0.5 fs; string evolution and reparameterizations are performed every 0.5 ps.
A few critical structures along the converged string are shown in Fig. 5a to illustrate the process of interest. The calculations are repeated with different values of the restraining force constants, which range from 5 to 20 kcal/mol/Å2. The structural features of the converged strings do not seem to vary notably with respect to the restraining force constants, while the estimated free energy along the string does vary significantly (not shown). Although the free energy derivatives computed from string simulations were shown to converge as O(k−1)91 (where k is the restraint force constant), the optimal value for k in an arbitrarily-dimensioned CV space is not obvious. For example, choosing a very high value precludes the use of replica-exchange between adjacent string points that can substantially accelerate convergence.100
To emphasize the importance of choosing a good CV set, we recall that two types of free energies can be computed from string calculations. The first is simply the integral of the n-dimensional PMF, W(ξ⃗) along the converged path
| (29) |
in which the free energy gradient is evaluated using restrained MD simulations, and α is used to parametrize the string curve. Since the gradients are evaluated at the discrete images , numerical quadrature must be used to evaluate Eq. (29), such as the trapezoid rule.100 This free energy profile, however, does not generally capture the energetics that govern the reaction because ΔW(α) does not contain the contributions due to the thermal fluctuations of the CVs orthogonal to the string. The proper 1D free energy quantity is the free energy as a function of the committor,100,138 denoted by F(α), which is obtained by integrating over hypersurfaces orthogonal to the string. ΔW(α) and F(α) are equivalent only if the transition tube is infinitely narrow or has identical cross sections along the reaction path. Alternatively speaking, entropic effects associated with the CVs orthogonal to the string are not properly included in ΔW(α). This consideration suggests that one should be particularly careful when choosing the CVs. Too few CVs clearly won’t describe the reaction process well (i.e., the committor is poorly parameterized); on the other hand, including too many CVs might effectively freeze out many potentially relevant degrees of freedom and greatly perturb the computed free energy profile. Moreover, including too many CVs also means that finer discretization is needed to avoid missing important changes in a few degrees of freedom.
To illustrate the sensitivity of the free energy profile from string calculations, we focus on the first proton transfer step, which approximately corresponds to the transition from structure 1 to 3 in Fig. 5a; to further simplify the situation, the Asn sidechain is fixed to coordinates in structure 1. First, we study the PMF for this step using the regular umbrella sampling, using the antisymmetric stretch, d(OAsp-H) - d(OAsn-H), as the order parameter; 21 windows (0.1 Å spacing) are used with 500 ps simulations for each window and the uniform force constant of 300 kcal/mol· Å2. Next, we carry out string calculations for this first proton transfer step. 25 images are used to discretize the string, and the force constants used in the restrained simulations are varied from 100 to 750 kcal/mol· Å2 and the friction coefficient γ is set to 100 ps−1. Different CV sets are also used: CV1 set consists of the two distances in the antisymmetric stretch, d(OAsp-H) and d(OAsn-H); CV2 set includes 13 distances between the transferring proton and all heavy atoms in the model side chains. MD sampling is carried out for 1 ns per image at 300 K with a time step of 0.5 fs; string evolution and reparameterizations are performed every 0.5 ps. For the last 500 ps, image centers are fixed and free energy gradients are calculated and used for analysis.
As shown in Fig. 5b, the proton transfer from an aspartic acid to an asparagine in this model is only moderately endothermic by ~4 kcal/mol with a barrier of ~ 13 kcal/mol. Considering that the asparagine model is fixed thus the proton donor/acceptor distance has only a modest degree of flexibility (the O-O distance changes from ~2.9 Å in the reactant to ~2.6 Å in the barrier region), the barrier height computed here should be an upper bound. Therefore, asparagine should not be ruled out as a proton relay group in biological proton transfers. With the string calculations, the calculated free energy profile ΔW(α) depends on both the choice of CV and the restraining force constant, especially near the barrier. With CV1, the free energy barrier changes by about 1 kcal/mol as the restraining force constant is increased from 100 to 750 kcal/mol/Å2. With the same restraining force constant, using two different CV sets also leads to a barrier difference of 1–2 kcal/mol; this level of difference is not unexpected considering that the two CV sets differ significantly in terms of dimensionality (2 vs. 13). In all three cases shown in Fig. 5c, the barrier appears too low compared to the umbrella sampling result by 2–3 kcal/mol; considering the local nature of the proton transfer, the 1D umbrella sampling result is expected to be more reliable.
The results highlight that free energy calculations using string methods should be treated with great care, even for a fairly simple local proton transfer. For more complex processes that involve both chemistry and conformational transitions, such as those in Fig. 5a, the energetics results appear even more sensitive to the choice of the CV space and restraining force constants. A more systematic analysis, including the comparison of F(α) and ΔW(α), is being carried out and will be presented elsewhere.
3.1.3 Decoupling of QM and MM fluctuations in minimum free energy path calculations
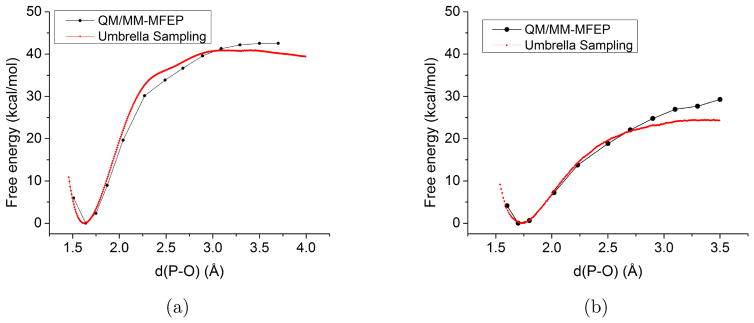
To explore the impact of approximations in the QM/MM-MFEP framework of Yang and coworkers, 11,105,106 we study the dissociation of pNPP2− (para-nitrophenyl phosphate) in water. pNPP2− is a substrate of alkaline phosphate, which catalyzes the hydrolysis of pNPP2− with great proficiency.38 Given the simplicity of the dissociation reaction (leading to para-nitrophenyl and metaphosphate), we use the distance between the leaving group oxygen and phosphorus (dOlgP) as the order parameter and carry out adiabatic mapping along dOlgP on the QM-region PMF surface. The results are then compared to 1D umbrella sampling along the same order parameter in which regular MD sampling is done with the same QM/MM potential function. By comparing the adiabatic mapping and umbrella sampling results, we will be able to evaluate two key approximations in the adiabatic PMF mapping methodology: (i). the decoupling of QM and MM thermal fluctuations; and (ii). the mean-field approximation used to describe the QM region wavefunction for MM sampling and QM structural relaxation. The analysis is done with two sets of QM/MM potentials, which employ B3LYP139,140 and DFTB3 as the QM, respectively, to treat pNPP2−. In the B3LYP calculations, 6–31+G(d,p) is used as the basis set; in DFTB3, the 3OB/OPhyd parameterization63 is used. These two methods are chosen to evaluate the robustness of the findings with different levels of sampling.
As a reference, regular umbrella sampling calculations are done using standard QM/MM with pNPP2− solvated in a TIP3P water droplet of 20 Å radius under the stochastic boundary condition.141 A series of 32 (22) umbrella windows are used for DFTB3/MM (B3LYP/MM) to cover dOlgP between 1.4 (1.4) Å and 4.5 (3.5) Å. The umbrella force constant is chosen to be 300 kcal/mol·Å2 for all windows and each window is calculated for 500 ps (25 ps) for DFTB3/MM (B3LYP/MM). The probability distributions are combined together by WHAM to obtain the PMF along dOlgP. Convergence of the PMF is checked by examining the overlap of dOlgP distributions sampled in different windows and by evaluating the effect of leaving out segments of trajectories.
For the adiabatic PMF mapping, dOlgP is constrained at a set of values between 1.5 and 3.5 Å, while all other solute degrees of freedom are optimized on the QM-region PMF surface. During each iterative cycle to relax the QM geometry, 80 ps production run is carried out after 50 ps equilibration to generate the MM ensemble (including 400 snapshots) used to evaluate the PMF gradients (Eq.15). In the mean-field calculations (Eq. 14), only MM atoms within 8 (10) Å of any QM atoms are included for B3LYP/MM (DFTB3/MM) calculations to reduce the computational cost; test calculations with different cut-off radii confirm that these values are appropriate. For each iterative QM structural relaxation cycle, geometry optimization is terminated with a threshold of 0.5 kcal/mol/ Å; typically, each cycle involves 10–20 steps of QM geometry relaxation, and 3–4 cycles are needed for each fixed dOlgP value. After the structures along the adiabatic PMF mapping are optimized, free energy perturbation calculations (with the BAR implementation) are used to obtain a better estimate of the free energy profile along the adiabatic path; in these calculations, which include 200 ps MD for each structure, the QM geometry is frozen and represented with mean-field ESP charges (Mulliken charges are used for DFTB3) from the converged adiabatic mapping calculations.
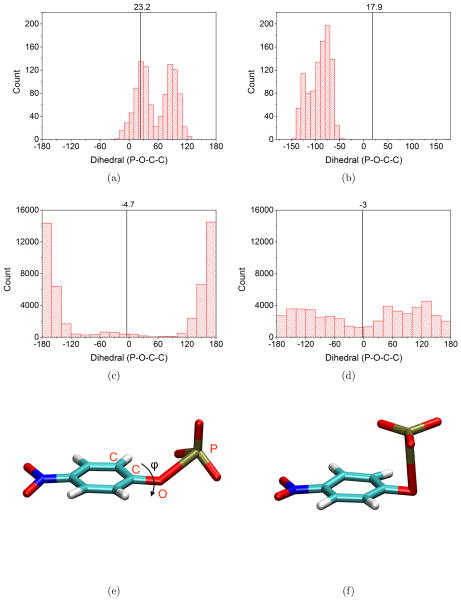
First, we compare the B3LYP/MM and DFTB3/MM results using umbrella sampling simulations. As shown in Fig. 6, the computed PMFs at the two levels of theory differ substantially, with the endothermicity of being about 40 kcal/mol with DFTB3/MM but only about 23 kcal/mol with B3LYP/MM; the value of dOlgP for the reactant well also differs slightly, being ~1.6 Å with DFTB3/MM and ~1.7 Å with B3LYP/MM. Clearly, as highlighted by Ref.,63 the 3OB/OPhyd parameterization remains problematic for a balanced description of associative and dissociative pathways of phosphoryl transfers. The significant difference between DFTB3/MM and B3LYP/MM, however, is valuable to the analysis of multi-level free energy simulations, as we discuss in Sect. 3.2.2. Finally, we note that the orientation of the leaving group with respect to the (meta)phosphate group also differs somewhat between DFTB3/MM and B3LYP/MM (Fig. 7): at equilibrium dOlgP distance, DFTB3/MM samples mainly the parallel orientation (with the P-O-C-C dihedral close to be ±180°) while B3LYP/MM also samples the perpendicular orientations with notable populations; at long (3.1 Å) dOlgP distance, as expected, both methods sample a fairly broad range of orientations (DFTB3/MM samples both positive and negative values of the P-O-C-C dihedral due to the longer simulation time).
Figure 6.
Computed PMFs (red lines) for the dissociation of pNPP2− in solution along the order parameter dOlgP based on (a) DFTB3/MM and (b) B3LYP/MM simulations; pNPP2− is treated as QM and water with TIP3P. For DFTB3, the 3OB/OPhyd parameterization is used; for B3LYP, the 6–31+G(d,p) basis set is used. Also shown in black are the results from adiabatic PMF mapping along dOlgP using DFTB3/MM and B3LYP/MM simulations. See text for additional details.
Figure 7.
Structural properties of pNPP2− from (a–b) B3LYP/MM and (c–d) DFTB3/MM simulations. The dihedral angle is the P-O-C-C angle indicated in panel (e), which illustrates a “parallel” type of configuration; in (f), a “perpendicular” configuration is illustrated. The histograms in the left (right) column are collected from the dOlgP =1.9 (3.1) Å window; note the different numbers of configurations from B3LYP/MM and DFTB3/MM windows. The vertical black line and the numerical value in each histogram indicate the result of adiabatic PMF mapping calculation for the corresponding dOlgP window.
Next, we note that the adiabatic PMF scan gives rather similar results as the umbrella sampling with both B3LYP/MM and DFTB3/MM potentials. The adiabatic PMF result is a few kcal/mol higher than the umbrella sampling value at long dOlgP values, and the difference is about 3 kcal/mol for B3LYP/MM at dOlgP ~ 3.1 Å (see Fig. 6); this is not unexpected because the entropic component associated with the dissociation of the QM solute is not included in the adiabatic PMF mapping. For instance, as discussed above, the relative orientation between the leaving group and the phosphate has a broader distribution at long dOlgP distances in umbrella sampling simulations, an effect not captured in the adiabatic PMF scans (see vertical lines in Fig. 7). The solute entropic contribution can be estimated by quasiharmonic analysis142,143 for dOlgP =1.7 and 3.1 Å by running 200 ps DFTB3/MM simulations with constrained dOlgP; such estimated TΔSvib contribution is about 3.3 kcal/mol.
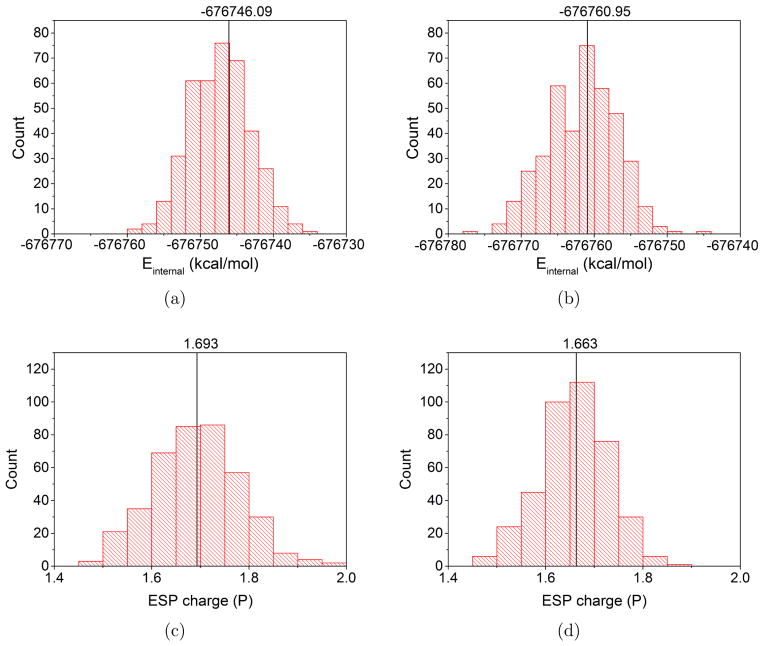
Finally, we explicitly comment on the mean-field approximation. Table 1 summarizes the difference between QM-MM electrostatic interactions calculated using a mean-field approximation (i.e., in Eq.14) and using direct embedding calculations (i.e., fully self-consistent QM/MM interaction for each configuration in the MM ensemble), and the deviation is about 1 kcal/mol with a standard deviation of ~ 2 kcal/mol for DFTB3/MM and ~ 4 kcal/mol for B3LYP/MM. Similarly, in Fig. 8, we compare the QM internal energy (i.e., not including QM-MM electrostatic interaction) from the mean-field calculation (Eq. 14, which leads to a single value for a given MM ensemble) and from self-consistent QM/MM calculations (which lead to different values for different MM configurations); clearly, the mean-field approximation captures the peak value of the distribution, which has a width of about 10 kcal/mol. This is also reflected by the ESP charges from mean-field and self-consistent QM/MM calculations; the results are shown for the phosphorus atom in Fig. 8c-d. Therefore, although instantaneous polarization of the QM region is clearly missing from the mean-field treatment, the average polarization effect is captured and seems to be adequate for describing the energetics of a reaction process.
Table 1.
Comparison (average and standard deviation of the difference, in kcal/mol) of electrostatic QM-MM interaction energies calculated using a mean-field approximation relative to self-consistent electrostatic embedding QM/MM calculationsa
| QM method (dOlgP window) | Average deviation | Standard deviation |
|---|---|---|
| B3LYP (1.9 Å) | −1.2 | 4.3 |
| B3LYP (3.1 Å) | −0.7 | 4.8 |
| DFTB3 (1.8 Å) | 0.2 | 2.0 |
| DFTB3 (3.7 Å) | 1.0 | 2.4 |
400 solvent configurations are included for each MM ensemble.
Figure 8.
Properties from B3LYP/MM simulations for pNPP2− dissociation in solution. The left (right) columns are for dOlgP =1.9 (3.1) Å, and each window includes 400 MM configurations. (a-b) illustrate distributions of the QM internal energy (i.e., QM/MM electrostatic energy from self-consistent electrostatic embedding calculation minus the classical QM-MM electrostatic interaction energy), (c-d) illustrate distributions of ESP charge on P. The vertical black line and numerical value indicate results from mean-field calculations (e.g., see Eq. 14 for the internal QM energy).
In short, our test calculations here suggest that the two key approximations of the QM/MM-MFEP framework (decoupling of QM and MM fluctuations and the mean-field approximation) are appropriate, at least for the current example of pNPP2− dissociation.
3.2 Alchemical and multi-level free energy computations
3.2.1 Solvation free energy
In our recent study,54 using the thermodynamic cycle in Fig. 1a, we have computed the solvation free energy of several small molecules at the DFTB3/3OB level relative to the CHARMM22 force field,144 which has been well calibrated for solvation free energies145,146 (although the value for charged species remains uncertain147–149). As also summarized in Table 2 for acetate and acetic acid, the DFTB3/3OB model gives slightly (~3–5 kcal/mol) more favorable solvation free energy than the CHARMM 22 force field. Although part of such mild degree of oversolvation is probably due to the fact that van der Waals parameters150 have not been reoptimized for the QM atoms at the DFTB3 level, another likely reason is that the electrostatic interactions between DFTB3 and MM (TIP3P) atoms employed a simple Coulombic model.151 As discussed in Ref.,152 a more appropriate model would consider the finite size of the QM charge distribution and therefore damp the interaction at short range, such as in a Klopman-Ohno (KO) model. Further optimization of the KO parameters and (charge-dependent153) van der Waals parameters for DFTB3 is an important task for ongoing work that aims to improve the robustness of DFTB3/MM for condensed phase applications.54
Table 2.
Relative Solvation Free Energy ΔΔGgas→aq(MM→QM) (in kcal/mol) with Different Size of QM Regiona
| Solute | MM ref. (Exp.)b | DFTB3/3OBc small QM region |
DFTB3/3OBd large QM region |
|---|---|---|---|
| CH3COOH | −3.7 (−6.7) | −3.41 ± 0.07 | +1.49 ± 0.11 |
| CH3COO− | −85.4 (−77.6) | −5.36 ± 0.04 | +3.21 ± 0.09 |
Thermodynamic cycle shown in Figure 1 is used. MM force field is the CHARMM22 force field and water is described with a modified TIP3P model. The QM atoms use the standard CHARMM22 van der Waals parameters. GSBP154,155 (inner region 20 Å) is used for all the calculations here.
The “MM ref.” values are absolute solvation free energies computed following the standard protocol. Values in parentheses are experimental values. 156
The small QM region includes the solute only.
The large QM region includes the solute and 27 water molecules in the first coordination shell of the solute. To ensure the QM water molecules are always nearest the metal ion, Flexible Inner Region Ensemble Separator (FIRES157) restraining potential is imposed to any outer sphere MM water molecules that are closer to the ion than the most distant inner sphere QM water molecule.
Alternatively, one could describe the first solvation shell of the solute also with the DFTB3 model. This likely reduces the sensitivity of DFTB3/MM simulations to QM/MM coupling scheme and parameters, although for the study of heterogeneous systems like an enzyme, it is likely that any deficiency of QM/MM boundary will eventually propagate back to the active site of interest (Roston and Cui, private communication). To test this hypothesis, we compute the change of solvation free energies of acetate and acetic acid when the solute and its first solvation shell water molecules are converted from CHARMM 22 to DFTB3/3OB. As discussed in Sect.2.2.1, this requires a slightly revised thermodynamic cycle as illustrated in Fig. 1b. The results are also summarized in Table 2. Compared to CHARMM 22, the DFTB3 treatment now leads to slightly smaller solvation free energies, by ~1–3 kcal/mol. From a technical point of view, the alchemical free energy simulations employ 11 λ windows even spaced between 0 and 1, and each window is equilibrated for 200 ps, which is followed by a production run of 500 ps. As shown in Table 2, this level of sampling leads to very small statistical errors as evaluated via block averaging, highlighting the advantage of converting between generally similar models for the solutes (CHARMM22 vs. DFTB3). As shown in Refs.,54,115 convergence can be further enhanced with the IHS approach.
3.2.2 Dual-level QM/MM PMF
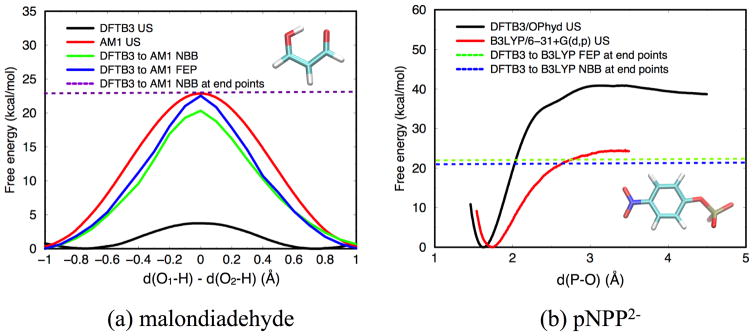
In this last subsection, we discuss several issues related to multi-level QM/MM free energy simulations using two simple solution reactions. One fitting example is the pNPP2− dissociation discussed in Sect.3.1.3, because DFTB3/MM and B3LYP/MM results have notable differences for both structures and energetics (see Figs.6–7). The other example is the intra-molecular proton transfer in malondiadehyde in solution (a water droplet of 20 Å radius), for which we compare DFTB3/MM and AM1/MM simulations because they lead to rather similar structural properties but very different energetics. The low computational cost of these methods makes it straightforward to compute the reference 1D PMFs using umbrella sampling (see Fig. 9a); the reaction coordinate is defined as distance(O1-H) - distance(O2-H), 21 windows with an equal spacing of 0.1 Å are used for each PMF, and each window is sampled for 500 ps. We treat DFTB3/MM as the “low-level” theory for both systems, and the aim is to explore whether (or when) the dual-level free energy sampling schemes discussed in Sect.2.2.2 (see Fig. 2) are able to reproduce the “high-level” PMF in a numerically efficient and robust fashion.
Figure 9.
Potential of mean force (PMF) computed via standard umbrella sampling (US), and perturbation of the PMF following the NBB and FEP routes (see Fig. 2) for (a) intra-molecular proton transfer in malondiadehyde in solution (b) p-nitrophenyl phosphate (pNPP2−) dissociation in solution. For the NBB and FEP calculations, the “low-level” method is taken to be DFTB3/MM for both reactions, while the “high-level” method is AM1/MM for (a) and B3LYP/MM for (b). For the NBB/FEP perturbations at the endpoints, only two reactant windows and two transition state windows are used, as shown in Fig. 2, leading to “corrected” barrier heights indicated by dashed lines (also see text). For (a), s0 = −1.0 Å, s1 = −0.9 Å, sn−1 = −0.1 Å, sn=0.0 Å; for (b), s0 = 1.6 Å, s1 = 1.7 Å, sn−1 = 3.1 Å, sn=3.2 Å.
We first discuss the case of proton transfer in malondiadehyde. As shown in Fig. 9a, AM1/MM and DFTB3/MM give barrier heights that differ by more than 15 kcal/mol; it is likely that the overestimation at the AM1 level is more significant, 133 although this is not the focus of this study. Due to the symmetry of the problem, the barrier location is consistent at the two levels, while the reactant region at the DFTB3/MM level occurs at slightly smaller absolute values of the order parameters (~ ±0.8 Å vs. ~ ±1.0 Å at the AM1 level). In terms of “correction” of the DFTB3/MM results, in addition to comparing the NBB and FEP+BAR routes, we also compare making corrections along the entire range of the order parameter, so as to obtain a corrected PMF, with making corrections only at the reactant/barrier windows so as to obtain only a corrected barrier height. When making corrections along the entire path, we see that the FEP+BAR route appears to lead to a better agreement in the barrier height (by ~ 2 kcal/mol) than the NBB route with the actual AM1/MM umbrella sampling result; overall, however, both schemes lead to substantially “improved” barriers. On the other hand, with both schemes, the “corrected” PMF is narrower than the umbrella sampling result. When the “correction” is applied to the reactant (s0=−1.0 Å) and barrier (sn=0.0 Å) windows only, however, the barrier height is in good agreement with the original AM1/MM umbrella sampling (see Fig. 9a). Our interpretation is that when correction is applied along the entire path, errors due to the limited overlap between the two levels of theory (DFTB3/MM vs. AM1/MM) accumulate, leading to a larger error in the barrier height. Therefore, making perturbations only in the key windows seems more robust for practical applications.
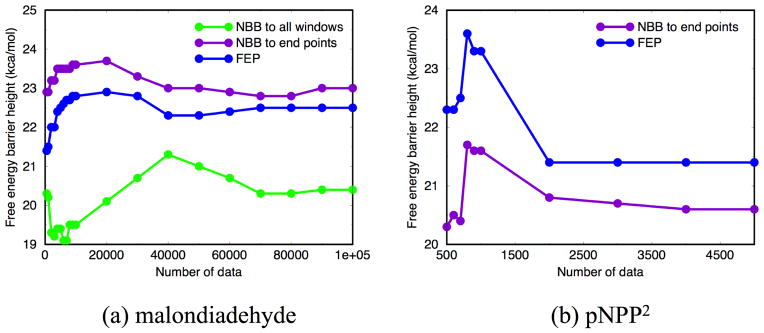
In Fig. 10a, we further compare the convergence behavior of the “corrected” barrier height with different schemes when applied along the entire path or only to the reactant/ barrier windows. Again, it is seen that the latter protocol leads to better convergence, with a variation of < 0.5 kcal/mol in the barrier height when from a few thousands to 105 number of configurations are included. This contrasts with the situation when NBB is applied along the entire path, where the variation in the barrier height is about 2 kcal/mol, not to mention the fact that the estimated barrier with 105 configurations per window is still 2 kcal/mol too low compared to the reference AM1/MM umbrella sampling result.
Figure 10.
Corrected free energy barrier height via NBB/FEP using different numbers of data points per window. Convergence plots are shown for (a) intra-molecular proton transfer in malondiadehyde in solution (b) p-nitrophenyl phosphate (pNPP2−) dissociation in solution. NBB/FEP at end points (i.e., reactant and transition state windows) only requires adequate overlaps between s0-s1 and sn−1-sn windows, thus the results are less dependent on the number of data points.
For the pNPP2− dissociation reaction in solution, only 5,000 data points per window are used for the reactant and “barrier” windows because the B3LYP/MM calculations are substantially more expensive; the reactant window and the “barrier” window are taken to be dOlgP =1.6 and 3.2 Å, respectively. Thus only a correction in the barrier height through either the NBB or the FEP+BAR route is obtained. Moreover, as we noted in Sect.3.1.3, DFTB3/MM has a shorter equilibrium dOlgP distance than B3LYP/MM (1.6 vs. 1.7 Å); thus the difference of ~3 kcal/mol in the B3LYP/MM PMF at these two dOlgP distances is included in the NBB/FEP corrected barrier height. As shown in Fig. 9b, the two routes lead to rather similar barrier heights; they still differ ~ 2 kcal/mol from the B3LYP/MM umbrella sampling result (see below), although the improvement is quite encouraging considering the large (~ 20 kcal/mol) difference between the original DFTB3/MM and B3LYP/MM results. Examination of the convergence behavior (Fig. 10b) suggests that 5,000 data points appears to lead to a reasonable estimate for the barrier height correction, although whether this level of sampling is indeed adequate in general needs to be explored with more systems.
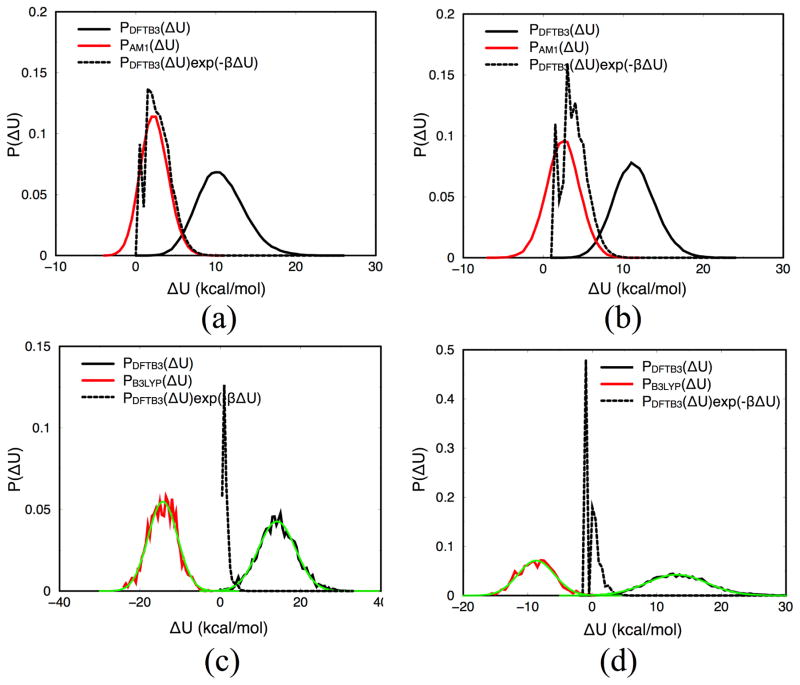
In an attempt to measure the reliability of the NBB/FEP+BAR correction schemes, we have also computed the variance of the corrections using the expression discussed in Sect.2.2.2 (e.g., Eq.24 for NBB). As shown in Table 3, the computed values seem rather small and substantially lower than 1 kcal/mol. These values, however, only report on the estimated statistical uncertainty for the corresponding free energy estimators. As discussed in Ref.,126 there can be substantial bias in the estimated free energy even when the variance is small. To illustrate this point, we plot the distributions for the energy difference between the low- and high-levels of theory (ΔULH) with configurations sampled from the two levels of theory; this comparison is made for both the reactant and barrier windows for the two example reactions. Also plotted is the product of ΔULH distribution (sampled with the low-level trajectory) multiplied with the Boltzmann factor for ΔULH; free energy perturbation type of calculations are expected to be reliable only when this product closely matches the ΔULH distribution sampled at the high-level,126 considering an identity associated with free energy perturbation,
Table 3.
Free energy correction and variance (in parentheses) of multi-level free energy estimatorsa
| Perturbations | PT in malondiadehydeb | pNPP−2 dissociationc | ||||
|---|---|---|---|---|---|---|
|
| ||||||
| FEP | NBB | LRA | FEP | NBB | LRA | |
| Reactantd | 8240.7 (0.012/0.007) | −8241.1 (0.012/0.007) | 8241.0 | −654205.5 (0.06) | 654206.4 (0.06) | −654208.9 |
| Transition statee | 8260.3 (0.011/0.005) | 8260.4 (0.011/0.005) | 8260.2 | −654227.9 (0.32) | −654228.0 (0.33) | −654227.4 |
| Free energy barrierf | 22.5 | 23.0 | 22.2 | 21.4g | 20.7g | 25.3g |
All values are in kcal/mol. In FEP and NBB, only low (L) level simulations are conducted and perturbations to the high (H) level are computed following different routes (see Fig. 2). In LRA, both L and H trajectories are used in a linear response model. For PT in malondiadehyde, L=DFTB3/MM, H=AM1/MM; for pNPP−2 dissociation, L=DFTB3/MM, H=B3LYP/MM.
5000/105 data points are included per window.
5000 data points are included.
FEP and LRA calculates the free energy difference , while NBB calculates . For PT in malondiadehyde, s0 = −1.0 Å, s1 = −0.9 Å; for pNPP−2 dissociation, s0 = 1.6 Å, s1 = 1.7 Å.
FEP and LRA calculates the free energy difference , while NBB calculates . For PT in malondiadehyde, sn−1 = −0.1 Å, sn=0.0 Å; for pNPP−2 dissociation, sn−1 = 3.1 Å, sn=3.2 Å.
Corrected free energy barrier . For PT in malondiadehyde, the reference value (at “high”-level) is 22.9 kcal/mol; for pNPP−2 dissociation, the reference value is 24.9 kcal/mol.
The corrected barrier height contains the 3 kcal/mol difference between 1.6 and 1.7 Å at the B3LYP/MM level (see text).
| (30) |
As shown in Fig. 11a–b, good match is indeed observed for the proton transfer in malondiadehyde; this is consistent with the fact both NBB and FEP+BAR schemes lead to satisfactory “corrections” of the barrier height. For the pNPP2− example, however, the DFTB3/MM and B3LYP/MM have broad and significantly different ΔULH distributions (Fig. 11c–d) that have almost vanishing overlap; as a result, the product PDFTB3/MM(ΔULH)e−βΔULHdeviates substantially from PB3LY P/MM(ΔULH). Thus, it is rather surprising that the one-step FEP seems to lead to fairly adequate correction of the barrier height as shown in Fig. 9b.
Figure 11.
Distribution of energy difference between the low- and high-levels of theory, ΔULH, using trajectories from the two levels of theory; also plotted is the integrand of the FEP expression using the low-level trajectory (i.e., exp(–βΔULH)PL(ΔULH)). The ΔULH data are shifted with a different amount in (a–d) for plotting purposes; see Table 3 for absolute free energy perturbation results. The plots are for: (a) reactant in malondiadehyde proton transfer (b) transition state in malondiadehyde proton transfer (c) reactant in pNPP2− dissociation (d) transition state in pNPP2− dissociation. In (a)-(b), PAM1(ΔU) has a similar shape from PDFTB3(ΔU)exp(-βΔU)), thus FEP and NBB calculations yield reliable barrier corrections. In (c)-(d), the ΔULH distributions are remarkably broader and data at different levels have almost vanishing overlap, thus it seems challenging for FEP and NBB to obtain reliable barrier corrections, although the Gaussian nature of the ΔULH distributions (fit shown explicitly in green) suggests that a linear response model works well (see Table 3).
We rationalize this finding by the observation that ΔULH distributions are fairly Gaussian in nature at both the low- and high-levels of theories for the two reactions studied here; although variances of the ΔULH distributions differ at the low- and high-levels in some cases (e.g., see Fig. 11d, the variances are 4.7 and 2.9 kcal/mol at DFTB3/MM and B3LYP/MM levels, respectively), the difference is not large. Since second-order cumulant expansion for the FEP expression is exact for a Gaussian distribution,158 free energy difference can be evaluated based solely on ΔULH data along the trajectory sampled at either level of theory when the ΔULH variance is not sensitive to the level of theory:
| (31) |
| (32) |
There is of course no formal reason that the variances are the same at the two levels of theory, thus a better approach would be to compute ΔULH using trajectories sampled at both levels of theory and then compute the free energy difference using a linear response approximation (LRA), as recommended by Warshel and co-workers.13 Using this protocol would lead to a corrected barrier of 25.3 kcal/mol for pNPP2− dissociation, indeed better than using only the low-level (DFTB3/MM) trajectories with NBB or FEP+BAR (see Fig. 9 and Table 3). In practical applications, this requires running at least short trajectories with high-level QM/MM, which may not always be feasible when the QM region is large.
In short, using two simple solution reactions, we show that perturbation schemes following either a NBB or a FEP+BAR route can indeed lead to a notable correction of the reaction free energy. The correction is more robust when perturbations are done only for selected windows, such as for the reactant and transition state windows to obtained an improved barrier height. The NBB approach does not seem to provide any major advantage over the FEP+BAR route. To judge whether the correction is robust, computing the variance of the free energy estimator is unlikely sufficient while examining the Gaussian nature of ΔULH distributions would be more informative, especially if ΔULH distributions at both low- and high-levels of theory can be examined. Finally, the correction scheme is expected to be meaningful only when critical structures on the free energy surface (reactant, intermediate, transition state) are similar at different levels of theory, thus determining/confirming these structures at the high-level of theory using, for example the QM/MM-MFEP approach, is expected to be an essential and practical option for realistic applications.
4 Concluding Remarks
Reliable free energy simulations are critical to both mechanistic analysis and computational designs. Since QM/MM calculations are generally more expensive compared to pure MM calculations, it is particularly worthwhile to carefully consider the best free energy practices for QM/MM simulations. In this contribution, we briefly review several recent developments in free energy calculations and discuss a number of topics stimulated by those developments using relatively simple processes in water.
When a low-level of QM theory, such as a semi-empirical method, is adequate, both potential of mean force and alchemical free energy simulations can be readily carried out with several established techniques, such as umbrella sampling, metadynamics and free energy perturbation; various enhanced sampling techniques such as replica-exchange/parallel tempering and their variations can be integrated to improve the computational efficiency. For complex reactions, minimum free energy path methods have become more prevalent, although we caution that the results, especially free energy profiles, can be sensitive to several parameters in these calculations, such as the choice of the CV space used to span the string and force constants used to estimate the mean force with restrained molecular dynamics. A practical strategy might be to compare the results of string calculations with other techniques for a local segment of the reaction (e.g., a local proton transfer step in a long-range proton transport) so as to calibrate key parameters in the string calculations. Finally, it is also productive to integrate metadynamics with finite temperature string type of calculations to explore the mechanism of complex reactions; metadynamics using well-chosen CVs can be very effective at identifying new reaction channels and therefore provide good initial guess for string calculations, which are local in nature and therefore rely on well-chosen initial pathways.
The best strategy to employ high-level QM/MM potentials likely depends on the problem in hand. When the QM region is fairly rigid and fluctuations orthogonal to the reaction path are largely harmonic in nature, the QM/MM-MFEP framework pioneered by Yang and co-workers is expected to work well; the necessary mean-field approximation seems to be satisfactory at least for the example analyzed here. When the QM region is highly dynamical, an appropriate alternative is to determine the minimum free energy pathway at a semiquantitative level using direct sampling with a low-level (semi-empirical) QM/MM method and then correct the energetics for key regions following perturbative schemes (Fig. 2). Provided that the key structures on the free energy surface remain similar at different levels of theory, our tests indicate that the perturbative schemes can lead to substantially improved barriers and in favorable cases, only low-level sampling is needed. In general, to make sure that perturbative schemes give meaningful results, however, it is essential to conduct careful analysis of the energy difference distributions and key structural features using trajectories at different levels of theory. In this context, even local structural minimization (e.g., adiabatic PMF mapping) in the QM/MM-MFEP framework again can be highly informative.
Regarding future efforts, we anticipate that continuing developments in the area of reliable low-cost QM methods for diverse elements, robust enhanced sampling methods, efficient ways to include polarization in both low-cost QM method and MM models will be particularly important. Another fruitful direction is the integration of free energy sampling with automated and systematic reaction path search,159,160 which may find great value in timely applications such as annotation of protein functions,161 understanding of enzyme evolution162,163 and design of novel enzymes. Finally, although we focused our discussions on solution and biological systems, the developments are also equally important to chemical processes in other complex environments, such as liquid/solid interfaces that are prevalent in materials science, heterogeneous catalysis and energy/environmental research.164
Acknowledgments
The work has been supported by grants from the National Science Foundation grants CHE-1300209 and by the National Institutes of Health R01GM106443. Computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by NSF grant number OCI-1053575, are greatly appreciated; computations are also supported in part by NSF through a major instrumentation grant (CHE-0840494) to the Chemistry department. We also thank Dr. Jia and his co-workers for sending the manuscript for Ref.127 prior to publication; discussions with Dr. Woodcock and König about NBB are also acknowledged.
References
- 1.Pauling L. The Nature of the Chemical Bond and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry. 3. Cornell University Press; Ithaca: 1960. [Google Scholar]
- 2.McCammon JA, Gelin BR, Karplus M. Dynamics of Folded Proteins. Nature. 1977;267:585–590. doi: 10.1038/267585a0. [DOI] [PubMed] [Google Scholar]
- 3.Warshel A, Levitt M. Theoretical Studies of Enzymic Reactions - Dielectric, Electrostatic and Steric Stabilization of Carbonium-Ion in Reaction of Lysozyme. J Mol Biol. 1976;103:227–249. doi: 10.1016/0022-2836(76)90311-9. [DOI] [PubMed] [Google Scholar]
- 4.Field MJ, Bash PA, Karplus M. A Combined Quantum-Mechanical and Molecular Mechanical Potential for Molecular-Dynamics Simulations. J Comput Chem. 1990;11:700–733. [Google Scholar]
- 5.Lipkowitz KB, Boyd DB, editors. J. Gao, In Reviews in Computational Chemistry VII. VCH; New York: 1995. p. 119. [Google Scholar]
- 6.Vreven T, Morokuma K. On the application of the IMOMO (integrated molecular orbital plus molecular orbital) method. J Comput Chem. 2000;21:1419–1432. [Google Scholar]
- 7.Friesner RA, Guallar V. Ab intio QM and QM/MM methods for studying enzyme catalysis. Annu Rev Phys Chem. 2005;56:389–427. doi: 10.1146/annurev.physchem.55.091602.094410. [DOI] [PubMed] [Google Scholar]
- 8.Gao JL, Ma SH, Major DT, Nam K, Pu JZ, Truhlar DG. Mechanisms and free energies of enzymatic reactions. Chem Rev. 2006;106:3188–3209. doi: 10.1021/cr050293k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Riccardi D, Schaefer P, Yang Y, Yu H, Ghosh N, Prat-Resina X, Konig P, Li G, Xu D, Guo H, Elstner M, Cui Q. Feature Article: Development of effective quantum mechanical/molecular mechanical (QM/MM) methods for complex biological processes. J Phys Chem B. 2006;110:6458–6469. doi: 10.1021/jp056361o. [DOI] [PubMed] [Google Scholar]
- 10.Zhang Y. Pseudobond ab initio QM/MM approach and its applications to enzyme reactions. Theor Chem Acc. 2006;116:43–50. [Google Scholar]
- 11.Hu H, Yang WT. Free Energies of Chemical Reactions in Solution and in Enzymes with Ab Initio Quantum Mechanics/Molecular Mechanics Methods. Annu Rev Phys Chem. 2008;59:573–601. doi: 10.1146/annurev.physchem.59.032607.093618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Senn HM, Thiel W. QM/MM methods for biomolecular systems. Angew Chem Int Ed. 2009;48:1198–1229. doi: 10.1002/anie.200802019. [DOI] [PubMed] [Google Scholar]
- 13.Kamerlin SCL, Haranczyk M, Warshel A. Progress in Ab Initio QM/MM Free-Energy Simulations of Electrostatic Energies in Proteins: Accelerated QM/MM Studies of pK(a), Redox Reactions and Solvation Free Energies. J Phys Chem B. 2009;113:1253–1272. doi: 10.1021/jp8071712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Brunk E, Rothlisberger U. Mixed Quantum Mechanical/Molecular Mechanical Molecular Dynamics Simulations of Biological Systems in Ground and Electronically Excited States. Chem Rev. 2015;115:6217–6263. doi: 10.1021/cr500628b. [DOI] [PubMed] [Google Scholar]
- 15.Gao JL, Truhlar DG. Quantum mechanical methods for enzyme kinetics. Annu Rev Phys Chem. 2002;53:467–505. doi: 10.1146/annurev.physchem.53.091301.150114. [DOI] [PubMed] [Google Scholar]
- 16.Monard G, Merz KMJ. Combined quantum mechanical/molecular mechanical methodologies applied to biomolecular systems. Acc Chem Res. 1999;32:904–911. [Google Scholar]
- 17.Shaik S, Cohen S, Wang Y, Chen H, Kumar D, Thiel W. P450 Enzymes: Their Structure, Reactivity, and Selectivity-Modeled by QM/MM Calculations. Chem Rev. 2010;110:949–1017. doi: 10.1021/cr900121s. [DOI] [PubMed] [Google Scholar]
- 18.Garcia-Viloca M, Gao J, Karplus M, Truhlar DG. How enzymes work: Analysis by modern rate theory and computer simulations. Science. 2004;303:186–195. doi: 10.1126/science.1088172. [DOI] [PubMed] [Google Scholar]
- 19.Nashine VC, Hammes-Schiffer S, Benkovic SJ. Coupled motions in enzyme catalysis. Curr Opin Chem Biol. 2010;14:644–651. doi: 10.1016/j.cbpa.2010.07.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.van der Kamp MW, Mulholland AJ. Combined Quantum Mechanics/Molecular Mechanics (QM/MM) Methods in Computational Enzymology. Biochem. 2013;52:2708–2728. doi: 10.1021/bi400215w. [DOI] [PubMed] [Google Scholar]
- 21.Lonsdale R, Mulholland AJ. QM/MM modelling of drug-metabolizing enzymes. Curr Top Med Chem. 2014;14:1339–1347. doi: 10.2174/1568026614666140506114859. [DOI] [PubMed] [Google Scholar]
- 22.Reetz MT, Puls M, Carballeira JD, Vogel A, Jaeger KE, Eggert T, Thiel W, Bocola M, Otte N. Learning from directed evolution: Further lessons from theoretical investigations into cooperative mutations in lipase enantioselectivity. Chem Bio Chem. 2007;8:106–112. doi: 10.1002/cbic.200600359. [DOI] [PubMed] [Google Scholar]
- 23.Fruschicheva MP, Mills MJL, Schopf P, Singh MK, Prasad RB, Warshel A. Computer aided enzyme design and catalytic concepts. Curr Opin Chem Biol. 2014;21:56–62. doi: 10.1016/j.cbpa.2014.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wietek J, Wiegert JS, Adeishvili N, Schneider F, Watanabe H, Tsunoda SP, Vogt A, Elstner M, Oertner TG, Hegemann P. Conversion of Channelrhodopsin into a Light-Gated Chloride Channel. Science. 2014;344:409–412. doi: 10.1126/science.1249375. [DOI] [PubMed] [Google Scholar]
- 25.Kraut DA, Carroll KS, Herschlag D. Challenges in enzyme mechanism and energetics. Annu Rev Biochem. 2003;72:517–571. doi: 10.1146/annurev.biochem.72.121801.161617. [DOI] [PubMed] [Google Scholar]
- 26.Zalatan JG, Herschlag D. The far reaches of enzymology. Nat Chem Biol. 2009;5:516–520. doi: 10.1038/nchembio0809-516. [DOI] [PubMed] [Google Scholar]
- 27.Fersht A. Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding. W.H. Freeman and Company; 1999. [Google Scholar]
- 28.Deng YQ, Roux B. Computations of Standard Binding Free Energies with Molecular Dynamics Simulations. J Phys Chem B. 2009;113:2234–2246. doi: 10.1021/jp807701h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sweeney HL, Houdusse A. Structural and Functional Insights into the Myosin Motor Mechanism. Annu Rev Biophys. 2010;39:539–557. doi: 10.1146/annurev.biophys.050708.133751. [DOI] [PubMed] [Google Scholar]
- 30.Yang Y, Yu H, Cui Q. Extensive conformational changes are required to turn on ATP hydrolysis in myosin. J Mol Biol. 2008;381:1407–1420. doi: 10.1016/j.jmb.2008.06.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Song CX, He C. Potential functional roles of DNA demethylation intermediates. Trends in Biochem Sci. 2013;38:480–484. doi: 10.1016/j.tibs.2013.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yi C, Jia G, Hou G, Dai Q, Zheng G, Jian X, Yang CG, Cui Q, He C. Iron-Catalyzed Oxidation Intermediates Captured in A DNA Repair Monooxygenase. Nature. 2010;468:330–333. doi: 10.1038/nature09497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nabel CS, Kohli RM. Demystifying DNA demethylation. Science. 2011;333:1229–1230. doi: 10.1126/science.1211917. [DOI] [PubMed] [Google Scholar]
- 34.Kaila VR, Verkhovsky MV, Wikström M. Proton-coupled electron transfer in cytochrome c oxidase. Chem Rev. 2010;110:7062–7081. doi: 10.1021/cr1002003. [DOI] [PubMed] [Google Scholar]
- 35.Goyal P, Lu J, Yang S, Gunner MR, Cui Q. Changing hydration level in an internal cavity modulates the proton affinity of a key glutamate in Cytochrome c Oxidase. Proc Natl Acad Sci US A. 2013;110:18886–18891. doi: 10.1073/pnas.1313908110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Goyal P, Yang S, Cui Q. Microscopic basis for kinetic gating in Cytochrome c oxidase: insights from QM/MM analysis. Chem Sci. 2015;6:826–841. doi: 10.1039/c4sc01674b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Khersonsky O, Roodveldt C, Tawfik DS. Enzyme promiscuity: evolutionary and mechanistic aspects. Curr Opin Chem Biol. 2006;10:498–508. doi: 10.1016/j.cbpa.2006.08.011. [DOI] [PubMed] [Google Scholar]
- 38.Lassila JK, Zalatan JG, Herschlag D. Biological phosphoryl transfer reactions: Understanding mechanism and catalysis. Annu Rev Biochem. 2011;80:669–702. doi: 10.1146/annurev-biochem-060409-092741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Babtie AC, Bandyopadhyay S, Olguin LF, Hollfelder F. Efficient catalytic promiscuity for chemically distinct reactions. Angew Chem Int Ed. 2009;48:3692– 3694. doi: 10.1002/anie.200805843. [DOI] [PubMed] [Google Scholar]
- 40.Hou GH, Cui Q. QM/MM analysis suggests that Alkaline Phosphatase (AP) and Nucleotide pyrophosphatase/phosphodiesterase (NPP) slightly tighten the transition state for phosphate diester hydrolysis relative to solution: implication for catalytic promiscuity in the AP superfamily. J Am Chem Soc. 2012;134:229–246. doi: 10.1021/ja205226d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hou GH, Cui Q. Stabilization of different types of transition states in a single enzyme active site: QM/MM analysis of enzymes in the alkaline phosphatase superfamily. J Am Chem Soc. 2013;135:10457–10469. doi: 10.1021/ja403293d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Duarte F, Amrein BA, Kamerlin SCL. Modeling catalytic promiscuity in the alkaline phosphatase superfamily. Phys Chem Chem Phys. 2013;15:11160–11177. doi: 10.1039/c3cp51179k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kosugi T, Hayashi S. QM/MM reweighting free energy SCF for geometry optimization on extensive free energ surface of enzymatic reaction. J Chem Theory Comput. 2012;8:322–334. doi: 10.1021/ct2005837. [DOI] [PubMed] [Google Scholar]
- 44.Rod TH, Ryde U. Accurate QM/MM Free Energy Calculations of Enzyme Reactions: Methylation by Catechol O-Methyltransferase. J Chem Theory Comput. 2005;1:1240–1251. doi: 10.1021/ct0501102. [DOI] [PubMed] [Google Scholar]
- 45.Cui Q, Karplus M. QM/MM Studies of the Triosephosphate isomerase (TIM) Catalyzed Reactions: The effect of geometry and tunneling on proton transfer rate constants. J Am Chem Soc. 2002;124:3093–3124. doi: 10.1021/ja0118439. [DOI] [PubMed] [Google Scholar]
- 46.Nam K, Cui Q, Gao J, York DM. A specific reaction parameterization for the AM1/d Hamiltonian for transphosphorylation reactions. J Chem Theory Comput. 2007;3:486–504. doi: 10.1021/ct6002466. [DOI] [PubMed] [Google Scholar]
- 47.Yang Y, Yu H, York D, Elstner M, Cui Q. Description of phosphate hydrolysis reactions with the Self-Consistent-Charge Density-Functional-Tight-Binding (SCC-DFTB) theory 1. Parametrization. J Chem Theory Comput. 2008;4:2067–2084. doi: 10.1021/ct800330d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Zhou Y, Pu J. Reaction Path Force Matching: A New Strategy of Fitting Specific Reaction Parameters for Semiempirical Methods in Combined QM/MM Simulations. J Chem Theory Comput. 2014;10:3038–3054. doi: 10.1021/ct4009624. [DOI] [PubMed] [Google Scholar]
- 49.Plotnikov NV, Kamerlin SCL, Warshel A. Paradynamics: An Effective and Reliable Model for Ab lnitio QM/MM Free-Energy Calculations and Related Tasks. J Phys Chem B. 2011;115:7950–7962. doi: 10.1021/jp201217b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Elstner M, Porezag D, Jungnickel G, Elsner J, Haugk M, Frauenheim T, Suhai S, Seifert G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys Rev B. 1998;58:7260–7268. [Google Scholar]
- 51.Elstner M, Frauenheim T, Suhai S. An approximate DFT method for QM/MM simulations of biological structures and processes. THEOCHEM. 2003;632:29–41. [Google Scholar]
- 52.Gaus M, Cui Q, Elstner M. Density Functional Tight Binding (DFTB): Application to organic and biological molecules. WIREs Comput Mol Sci. 2014;4:49–61. [Google Scholar]
- 53.Cui Q, Elstner M. Density Functional Tight Binding: values of semi-empirical methods in an ab initio era. Phys Chem Chem Phys. 2014;16:14368–14377. doi: 10.1039/c4cp00908h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Goyal P, Qian HJ, Irle S, Lu X, Roston D, Mori T, Elstner M, Cui Q. Feature Article: Molecular Simulation of Water and Hydration Effects in Different Environments: Challenges and Developments for DFTB Based Models. J Phys Chem B. 2014;118:11007–11027. doi: 10.1021/jp503372v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Gaus M, Cui Q, Elstner M. DFTB-3rd: Extension of the self-consistent-charge density-functional tight-binding method SCC-DFTB. J Chem Theory Comput. 2011;7:931–948. doi: 10.1021/ct100684s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Thiel W. Perspectives on semiempirical molecular orbital theory. Adv Chem Phys. 1996;93:703–757. [Google Scholar]
- 57.Kubillus M, Kubǎr T, Gaus M, Řezáč J, Elstner M. Parameterization of the DFTB3 Method for Br, Ca, Cl, F, I, K, and Na in Organic and Biological Systems. J Chem Theory Comput. 2015;11:332–342. doi: 10.1021/ct5009137. [DOI] [PubMed] [Google Scholar]
- 58.Lu X, Gaus M, Elstner M, Cui Q. Parameterization of DFTB3/3OB for Magnesium and Zinc for Chemical and Biological Applications. J Phys Chem B (Jorgensen Festschrift) 2015;119:1062–1082. doi: 10.1021/jp506557r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Gaus M, Jin H, Demapan D, Christensen AS, Goyal P, Elstner M, Cui Q. DFTB3 Parametrization for Copper: the importance of orbital angular momentum dependence of Hubbard parameters. J Chem Theory Comput. 2015;11:4205–4219. doi: 10.1021/acs.jctc.5b00600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Xu DG, Cui Q, Guo H. Quantum Mechanical/Molecular Mechanical Studies of Zinc Hydrolases. Int Rev Phys Chem. 2014;33:1–41. [Google Scholar]
- 61.Chakravorty DK, Wang B, Lee CW, Giedroc DP, Merz KM., Jr Simulations of Allosteric Motions in the Zinc Sensor CzrA. J Am Chem Soc. 2012;134:3367– 3376. doi: 10.1021/ja208047b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Mlynsky V, Banas P, Sponer J, van der Kamp MW, Mulholland AJ, Otyepka M. Comparison of ab Initio DFT and Semiempirical QM/MM Approaches for Description of Catalytic Mechanism of Hairpin Ribozyme. J Chem Theory Comput. 2014;10:1608–1622. doi: 10.1021/ct401015e. [DOI] [PubMed] [Google Scholar]
- 63.Gaus M, Lu X, Elstner M, Cui Q. Parameterization of DFTB3/3OB for Sulfur and Phosphorus for chemical and biological applications. J Chem Theory Comput. 2014;10:1518–1537. doi: 10.1021/ct401002w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Torrie GM, Valleau JP. Non-physical sampling distributions in Monte-Carlo free-energy estimation: Umbrella Sampling. J Comput Phys. 1977;23:187–199. [Google Scholar]
- 65.Neria E, Karplus M. Molecular dynamics of an enzyme reaction: proton transfer in TIM. Chem Phys Lett. 1997;267:23–30. [Google Scholar]
- 66.Warshel A. Computer Modeling of Chemical Reactions in Enzymes and Solution. Wiley; New York: 1991. [Google Scholar]
- 67.Mo YR, Gao JL. Ab initio QM/MM simulations with a molecular orbital-valence bond (MOVB) method: Application to an S(N)2 reaction in water. J Comput Chem. 2000;21:1458–1469. [Google Scholar]
- 68.Bartels C, Karplus M. Multidimensional adaptive umbrella sampling: Applications to main chain and side chain peptide conformations. J Comput Chem. 1997;18:1450–1462. [Google Scholar]
- 69.Darve E, Pohorille A. Calculating free energies using average force. J Chem Phys. 2001;115:9169–9183. [Google Scholar]
- 70.Sprik M, Ciccotti G. Free energy from constrained molecular dynamics. J Chem Phys. 1998;109:7737–7744. [Google Scholar]
- 71.Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. The weighted histogram analysis method for free-energy calculations on biomolecules I. The method. J Comput Chem. 1992;13:1011–1021. [Google Scholar]
- 72.Riccardi D, Koenig P, Guo H, Cui Q. proton transfer in carbonic anhdyrase is controlled by electrostatics rather than the orientation of the acceptor. Biochem. 2008;47:2369–2378. doi: 10.1021/bi701950j. [DOI] [PubMed] [Google Scholar]
- 73.den Otter WK. Thermodynamic integration of the free energy along a reaction coordinate in Cartesian coordinate. J Chem Phys. 2000;112:7283. [Google Scholar]
- 74.Henin J, Chipot C. Overcoming free energy barriers using unconstrained molecular dynamics simulations. J Chem Phys. 2004;121:2904–2914. doi: 10.1063/1.1773132. [DOI] [PubMed] [Google Scholar]
- 75.Rosta E, Hummer G. Free Energies from Dynamic Weighted Histogram Analysis Using Unbiased Markov State Model. J Chem Theory Comput. 2015;11:276–285. doi: 10.1021/ct500719p. [DOI] [PubMed] [Google Scholar]
- 76.Wu H, Mey ASJS, Rosta E, Noé F. Statistically optimal analysis of state-discretized trajectory data from multiple thermodynamic states. J Chem Phys. 2014;141:214106. doi: 10.1063/1.4902240. [DOI] [PubMed] [Google Scholar]
- 77.Sugita Y, Kitao A, Okamoto Y. Multidimensional replica-exchange method for free-energy calculations. J Chem Phys. 2000;113:6042–6051. [Google Scholar]
- 78.Murata K, Sugita Y, Okamoto Y. Free energy calculations for DNA base stacking by replica-exchange umbrella sampling. Chem Phys Lett. 2004;385:1–7. [Google Scholar]
- 79.Fukunishi H, Watanabe O, Takada S. On the Hamiltonian replica exchange method for efficient sampling of biomolecular systems: Application to protein structure prediction. J Chem Phys. 2002;116:9058–9067. [Google Scholar]
- 80.Park S, Kim T, Im W. Transmembrane Helix Assembly by Window Exchange Umbrella Sampling. Phys Rev Lett. 2012;108:108102. doi: 10.1103/PhysRevLett.108.108102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Laio A, Gervasio FL. Metadynamics: a method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep Prog Phys. 2008;71:126601. [Google Scholar]
- 82.Barducci A, Bonomi M, Parrinello M. Metadynamics. Wiley Inter Rev Comp Mol Sci. 2011;1:826–843. [Google Scholar]
- 83.Huber T, Torda A, van Gunsteren WF. Local elevation: a method for improving the searching properties of molecular dynamics simulation. J Comput Aided Mol Des. 1994;8:695–708. doi: 10.1007/BF00124016. [DOI] [PubMed] [Google Scholar]
- 84.Dama JF, Parrinello M, Voth GA. Well-Tempered Metadynamics Converges Asymptotically. Phys Rev Lett. 2014;112:240602. doi: 10.1103/PhysRevLett.112.240602. [DOI] [PubMed] [Google Scholar]
- 85.Barducci A, Bussi G, Parrinello M. Well-tempered metadynamics: A smoothly converging and tunable free-energy method. Phys Rev Lett. 2008;100:020603. doi: 10.1103/PhysRevLett.100.020603. [DOI] [PubMed] [Google Scholar]
- 86.Piana S, Laio A. A bias-exchange approach to protein folding. J Phys Chem B. 2007;111:4553–4559. doi: 10.1021/jp067873l. [DOI] [PubMed] [Google Scholar]
- 87.Fukui K. The path of chemical reactions - the IRC approach. Acc Chem Res. 1981;14:363–368. [Google Scholar]
- 88.Zhang YK, Kua J, Mccammon JA. Influence of structural fluctuation on enzyme reaction energy barriers in combined quantum mechanical/molecular mechanical studies. J Phys Chem B. 2003;107:4459–4463. [Google Scholar]
- 89.Wales DJ. Energy Landscapes. Cambridge University Press; 2003. [Google Scholar]
- 90.Bolhuis PG, Chandler D, Dellago C, Geissler PL. Transition path sampling: Throwing ropes over rough mountain passes, in the dark. Annu Rev Phys Chem. 2002;53:291–318. doi: 10.1146/annurev.physchem.53.082301.113146. [DOI] [PubMed] [Google Scholar]
- 91.Maragliano L, Fischer A, Vanden-Eijnden E, Ciccotti G. String method in collective variables: Minimum free energy paths and isocommittor surfaces. J Chem Phys. 2006;125:024106. doi: 10.1063/1.2212942. [DOI] [PubMed] [Google Scholar]
- 92.Dellago C, Bolhuis P, Geissler P. Transition Path Sampling. Adv Chem Phys. 2003;123:1–78. [Google Scholar]
- 93.EW, Ren W, Vanden-Eijnden E. Transition pathways in complex systems: Reaction coordinates, isocommittor surfaces, and transition tubes. Chem Phys Lett. 2005;413:242–247. [Google Scholar]
- 94.Best R, Hummer G. Reaction coordinates and rates from transition paths. Proc Natl Acad Sci USA. 2005;102:6732–6737. doi: 10.1073/pnas.0408098102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Peters B, Trout B. Obtaining reaction coordinates by likelihood maximization. J Chem Phys. 2006;125:054108. doi: 10.1063/1.2234477. [DOI] [PubMed] [Google Scholar]
- 96.Krivov SV, Karplus M. One-dimensional free-energy profiles of complex systems: Progress variables that preserve the barriers. J Phys Chem B. 2006;110:12689– 12698. doi: 10.1021/jp060039b. [DOI] [PubMed] [Google Scholar]
- 97.Elber R, Karplus M. A method for determining reaction paths in large biomolecules: application to myoglobin. Chem Phys Lett. 1987;139:375–380. [Google Scholar]
- 98.Henkelman G, Uberguaga B, Jónsson H. A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths. J Chem Phys. 2000;113:9978–9985. [Google Scholar]
- 99.EW, Ren W, Vanden-Eijnden E. Simplified and improved string method for computing the minimum energy paths in barrier-crossing events. J Chem Phys. 2007;126:164103. doi: 10.1063/1.2720838. [DOI] [PubMed] [Google Scholar]
- 100.Ovchinnikov V, Karplus M, Vanden-Eijnden E. Free energy of conformational transition paths in biomolecules: The string method and its application to myosin VI. J Chem Phys. 2011;134:085103. doi: 10.1063/1.3544209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Maragliano L, Vanden-Eijnden E. On-the-fly string method for minimum free energy paths calculation. Chem Phys Lett. 2007;446:182–190. [Google Scholar]
- 102.Maragliano L, Roux B, Vanden-Eijnden E. A Comparison between Mean Forces and Swarms-of-Trajectories String Methods. J Chem Theory Comput. 2014;10:524–533. doi: 10.1021/ct400606c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Pan AC, Sezer D, Roux B. Finding Transition Pathways Using the String Method with Swarms of Trajectories. J Phys Chem B. 2008;112:3432–3440. doi: 10.1021/jp0777059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Sanchez-Martinez M, Field M, Crehuet R. Enzymatic Minimum Free Energy Path Calculations Using Swarms of Trajectories. J Phys Chem B. 2014;119:1103–1113. doi: 10.1021/jp506593t. [DOI] [PubMed] [Google Scholar]
- 105.Hu H, Lu ZY, Yang WT. QM/MM minimum free-energy path: Methodology and application to triosephosphate isomerase. J Chem Theory Comput. 2007;3:390–406. doi: 10.1021/ct600240y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Hu H, Lu ZY, Parks JM, Burger SK, Yang WT. Quantum mechanics/ molecular mechanics minimum free-energy path for accurate reaction energetics in solution and enzymes: Sequential sampling and optimization on the potential of mean force surface. J Chem Phys. 2008;128:034105. doi: 10.1063/1.2816557. [DOI] [PubMed] [Google Scholar]
- 107.Muller EM, de Meijere A, Grubmuller H. Predicting unimolecular chemical reactions: Chemical flooding. J Chem Phys. 2002;116:897–905. [Google Scholar]
- 108.Yang LJ, Gao YQ. A selective integrated tempering method. J Chem Phys. 2009;131:214109. doi: 10.1063/1.3266563. [DOI] [PubMed] [Google Scholar]
- 109.Gao YQ. An integrate-over-temperature approach for enhanced sampling. J Chem Phys. 2008;128:064105. doi: 10.1063/1.2825614. [DOI] [PubMed] [Google Scholar]
- 110.Wang L, Friesner RA, Berne BJ. Replica exchange with solute scaling: a more efficient version of replica exchange with solute tempering (REST2) J Phys Chem B. 2011;115:9431–9438. doi: 10.1021/jp204407d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Zhang J, Yang YI, Yang LJ, Gao YQ. Conformational Preadjustment in Aqueous Claisen Rearrangement Revealed by SITS-QM/MM MD Simulations. J Phys Chem B. 2015;119:5518–5530. doi: 10.1021/jp511057f. [DOI] [PubMed] [Google Scholar]
- 112.Straatsma TP, McCammon JA. Computational alchemy. Annu Rev Phys Chem. 1992;43:407–435. [Google Scholar]
- 113.Kollman PA. Free-energy calculations - Applications to chemical and biochemical phenomena. Chem Rev. 1993;93:2395–2417. [Google Scholar]
- 114.Simonson T, Archontis G, Karplus M. Free energy simulations come of age: Protein-ligand recognition. Acc Chem Res. 2002;35:430–437. doi: 10.1021/ar010030m. [DOI] [PubMed] [Google Scholar]
- 115.Mori T, Hamers RJ, Pedersen JA, Cui Q. Integrated Hamiltonian Sampling: a simple and versatile method for free energy simulations and conformational sampling. J Phys Chem B. 2014;118:8210–8220. doi: 10.1021/jp501339t. [DOI] [PubMed] [Google Scholar]
- 116.Christ CD, van Gunsteren WF. Enveloping distribution sampling: A method to calculate free energy differences from a single simulation. J Chem Phys. 2007;126:184110. doi: 10.1063/1.2730508. [DOI] [PubMed] [Google Scholar]
- 117.Marti S, Moliner V, Tuñón I. Improving the QM/MM description of chemical processes: A dual level strategy to explore the potential energy surface in very large systems. J Chem Theory Comput. 2005;1:1008–1016. doi: 10.1021/ct0501396. [DOI] [PubMed] [Google Scholar]
- 118.Claeyssens F, Harvey JN, Manby FR, Mata RA, Mulholland AJ, Ranaghan KE, Schutz M, Thiel S, Thiel W, Werner HJ. High-accuracy computation of reaction barriers in enzymes. Angew Chem Int Ed. 2006;45:6856–6859. doi: 10.1002/anie.200602711. [DOI] [PubMed] [Google Scholar]
- 119.Woods CJ, Manby FR, Mulholland AJ. An efficient method for the calculation of quantum mechanics/molecular mechanics free energies. J Chem Phys. 2008;128:014109. doi: 10.1063/1.2805379. [DOI] [PubMed] [Google Scholar]
- 120.Retegan M, Martins-Costa M, Ruiz-Lopez MF. Free energy calculations using dual-level Born–Oppenheimer molecular dynamics. J Chem Phys. 2010;133:064103. doi: 10.1063/1.3466767. [DOI] [PubMed] [Google Scholar]
- 121.Polyak I, Benighaus T, Boulanger E, Thiel W. Quantum mechanics/molecular mechanics dual Hamiltonian free energy perturbation. J Chem Phys. 2013;139:064105. doi: 10.1063/1.4817402. [DOI] [PubMed] [Google Scholar]
- 122.König G, Hudson PS, Boresch S, Woodcock HL. Multiscale free energy simulations: An efficient method for connecting classical MD simulations to QM or QM/MM free energies using Non-Boltzmann Bennett reweighting schemes. J Chem Theory Comput. 2014;10:1406–1419. doi: 10.1021/ct401118k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Heimdal J, Ryde U. Convergence of QM/MM free-energy perturbations based on molecular-mechanics or semiempirical simulations. Phys Chem Chem Phys. 2012;14:12592–12604. doi: 10.1039/c2cp41005b. [DOI] [PubMed] [Google Scholar]
- 124.Plotnikov NV. Computing the Free Energy Barriers for Less by Sampling with a Coarse Reference Potential while Retaining Accuracy of the Target Fine Model. J Chem Theory Comput. 2014;10:2987–3001. doi: 10.1021/ct500109m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Nam K. Acceleration of Ab Initio QM/MM Calculations under Periodic Boundary Conditions by Multiscale and Multiple Time Step Approaches. J Chem Theory Comput. 2014;10:4175–4183. doi: 10.1021/ct5005643. [DOI] [PubMed] [Google Scholar]
- 126.Pohorille A, Jarzynski C, Chipot C. Good Practices in Free-Energy Calculations. J Phys Chem B. 2010;114:10235–10253. doi: 10.1021/jp102971x. [DOI] [PubMed] [Google Scholar]
- 127.Jia XY, Wang MT, Shao YH, König G, Brooks BR, Zhang JZH, Mei Y. Quantum Mechanical/Molecular Mechanical Calculation of Solvation Free Energy Based On a Decoupling Process. J Chem Theory Comput. 2015 Submitted. [Google Scholar]
- 128.Brooks BR, III, CLB, Mackerell AD, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, Caflisch A, Caves L, Cui Q, Dinner AR, Feig M, Fischer S, Gao J, Hodoscek M, Im W, Kuczera K, Lazaridis T, Ma J, Ovchinnikov V, Paci E, Pastor RW, Post CB, Pu JZ, Schaefer M, Tidor B, Venable RM, Woodcock HL, Wu X, Yang W, York DM, Karplus M. CHARMM: The Biomolecular Simulation Program. J Comput Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Koenig P, Ghosh N, Hoffman M, Elstner M, Tajkhorshid E, Frauenheim T, Cui Q. Towards theoretical analysis of long-range proton transfer kinetics in biomolecular pumps. J Phys Chem A. 2006;110:548–563. doi: 10.1021/jp052328q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Zienau J, Cui Q. Implementation of the Solvent Macromolecule Boundary Potential and Application to Model and Realistic Enzyme Systems. J Phys Chem B. 2012;116:12522–12534. doi: 10.1021/jp308218m. [DOI] [PubMed] [Google Scholar]
- 131.Petersen MK, Iyengar SS, Day TJF, Voth GA. The Hydrated Proton at the Water Liquid/Vapor Interface. J Phys Chem B. 2004;108:14804–14806. [Google Scholar]
- 132.Mori T, Hamers RJ, Pedersen JA, Cui Q. An explicit consideration of desolvation is critical to binding free energy calculations of charged molecules at ionic surfaces. J Chem Theory Comput. 2013;9:5059–5069. doi: 10.1021/ct400487e. [DOI] [PubMed] [Google Scholar]
- 133.Gaus M, Goez A, Elstner M. Parametrization and Benchmark of DFTB3 for Organic Molecules. J Chem Theory Comput. 2012;9:338–354. doi: 10.1021/ct300849w. [DOI] [PubMed] [Google Scholar]
- 134.Peng YX, Swanson JMJ, Kang SG, Zhou RH, Voth GA. Hydrated Excess Protons Can Create Their Own Water Wires. J Phys Chem B. 2015;119:9212–9218. doi: 10.1021/jp5095118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Silverman DN, McKenna R. Solvent-mediated proton transfer in catalysis by carbonic anhydrase. Acc Chem Res. 2007;40:669–675. doi: 10.1021/ar7000588. [DOI] [PubMed] [Google Scholar]
- 136.Sham YY, Muegge I, Warshel A. Simulating proton translocations in proteins: Probing proton transfer pathways in the Rhodobacter sphaeroides reaction center. Proteins: Struct, Funct & Bioinf. 1999;36:484–500. [PubMed] [Google Scholar]
- 137.Kato M, Pisliakov AV, Warshel A. The barrier for proton transport in Aquaporins as a challenge for electrostatic models: The role of protein relaxation in mutational calculations. Proteins: Struct Funct Bioinfor. 2006;64:829–844. doi: 10.1002/prot.21012. [DOI] [PubMed] [Google Scholar]
- 138.EW, Vanden-Eijnden E. Transition-Path Theory and Path-Finding Algorithms for the Study of Rare Events. Annu Rev Phys Chem. 2010;61:391–420. doi: 10.1146/annurev.physchem.040808.090412. [DOI] [PubMed] [Google Scholar]
- 139.Becke A. Density-functional thermochemistry. III. The role of exact exchange. J Chem Phys. 1993;98:5648–5652. [Google Scholar]
- 140.Lee C, Yang W, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys Rev B. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 141.Brooks CL, III, Karplus M. Deformable stochastic boundaries in molecular dynamics. J Chem Phys. 1983;79:6312–6325. [Google Scholar]
- 142.Karplus M, Kuschick JN. Method for estimating the configurational entropy of macromolecules. Macromol. 1981;14:325–332. [Google Scholar]
- 143.Schlitter J. Estimation of absolute and relative entropies of macromolecules using the covariance-matrix. Chem Phys Lett. 1993;215:617–621. [Google Scholar]
- 144.MacKerell AD, Jr, Bashford D, Bellott M, Dunbrack RL, Jr, Evenseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, III, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiórkiewicz-Kuczera J, Yin D, Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 145.Shivakumar D, Deng YQ, Roux B. Computations of absolute solvation free energies of small molecules using explicit and implicit solvent model. J Chem Theory Comput. 2009;5:919–930. doi: 10.1021/ct800445x. [DOI] [PubMed] [Google Scholar]
- 146.Deng YQ, Roux B. Hydration of amino acid side chains: Nonpolar and electrostatic contributions calculated from staged molecular dynamics free energy simulations with explicit water molecules. J Phys Chem B. 2004;108:16567–16576. [Google Scholar]
- 147.Lin Y, Aleksandrov A, Simonson T, Roux B. An overview of electrostatic free energy computations for solutions and proteins systems. J Chem Theory Comput. 2014;10:2690–2709. doi: 10.1021/ct500195p. [DOI] [PubMed] [Google Scholar]
- 148.Lu X, Cui Q. Charging free energy calculations using the Generalized Solvent Boundary Potential (GSBP) and periodic boundary condition: a comparative analysis using ion solvation and reduction potential in proteins. J Phys Chem B. 2013;117:2005– 2018. doi: 10.1021/jp309877z. [DOI] [PubMed] [Google Scholar]
- 149.Kastenholz MA, Hünenberger PH. Computation of methodology-independent ionic solvation free energies from molecular simulations. II. The hydration free energy of the sodium cation. J Chem Phys. 2006;124:224501 1–20. doi: 10.1063/1.2201698. [DOI] [PubMed] [Google Scholar]
- 150.Riccardi D, Li G, Cui Q. The importance of van der Waals interactions in QM/MM simulations. J Phys Chem B. 2004;108:6467–6478. doi: 10.1021/jp037992q. [DOI] [PubMed] [Google Scholar]
- 151.Cui Q, Elstner M, Kaxiras E, Frauenheim T, Karplus M. A QM/MM implementation of the self-consistent charge density functional tight binding (SCC-DFTB) method. J Phys Chem B. 2001;105:569–585. [Google Scholar]
- 152.Hou G, Zhu X, Elstner M, Cui Q. A modified QM/MM Hamiltonian with the Self-Consistent-Charge Density-Functional-Tight-Binding Theory for highly charged QM regions. J Chem Theory Comput. 2012;8:4293–4304. doi: 10.1021/ct300649f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Giese TJ, York DM. Charge-dependent model for many-body polarization, exchange, and dispersion interactions in hybrid quantum mechanical/molecular mechanical calculations. J Chem Phys. 2007;127:194101. doi: 10.1063/1.2778428. [DOI] [PubMed] [Google Scholar]
- 154.Im W, Berneche S, Roux B. Generalized solvent boundary potential for computer simulations. J Chem Phys. 2001;114:2924–2937. [Google Scholar]
- 155.Schaefer P, Riccardi D, Cui Q. Reliable treatment of electrostatics in combined QM/MM simulation of macromolecules. J Chem Phys. 2005;123:Art. No. 014905. doi: 10.1063/1.1940047. [DOI] [PubMed] [Google Scholar]
- 156.Marenich AV, Kelly CP, Thompson JD, Hawkins GD, Chambers CC, Giesen DJ, Winget P, Cramer CJ, Truhlar DG. Minnesota Solvation Database – version 2012. 2012 [Google Scholar]
- 157.Rowley CN, Roux B. The Solvation Structure of Na+ and K+ in Liquid Water Determined from High Level ab Initio Molecular Dynamics Simulations. J Chem Theory Comput. 2012;8:3526–3535. doi: 10.1021/ct300091w. [DOI] [PubMed] [Google Scholar]
- 158.Kubo R, Toda M, Hashitsume N. Statistical Physics II: Nonequilibrium Statistical Mechanics. Springer; 2003. [Google Scholar]
- 159.Maeda S, Ohno K, Morokuma K. Systematic exploration of the mechanism of chemical reactions: the global reaction route mapping (GRRM) strategy using the ADDF and AFIR methods. Phys Chem Chem Phys. 2013;15:3683–3701. doi: 10.1039/c3cp44063j. [DOI] [PubMed] [Google Scholar]
- 160.Habershon S. Sampling reactive pathways with random walks in chemical space: Applications to molecular dissociation and catalysis. J Chem Phys. 2015;143:094106. doi: 10.1063/1.4929992. [DOI] [PubMed] [Google Scholar]
- 161.Jacobson MP, Kalyanaraman C, Zhao SW, Tian BX. Leveraging structure for enzyme function prediction: methods, opportunities, and challenges. Trends Biochem Sci. 2014;39:363–371. doi: 10.1016/j.tibs.2014.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Tawfik DS. Accuracy-rate tradeoffs: how do enzymes meet demands of selectivity and catalytic efficiency? Curr Opin Chem Biol. 2014;21:73–80. doi: 10.1016/j.cbpa.2014.05.008. [DOI] [PubMed] [Google Scholar]
- 163.Toth-Petroczy A, Tawfik DS. The robustness and innovability of protein folds. Curr Opin Struct Biol. 2014;26:131–138. doi: 10.1016/j.sbi.2014.06.007. [DOI] [PubMed] [Google Scholar]
- 164.Murphy CJ, Vartanian AM, Geiger FM, Hamers RJ, Pederson J, Cui Q, Haynes CL, Carlson EE, Hernandez R, Klaper RD, Orr G, Rosenzweig Z. Biological Responses to Engineered Nanomaterials: Needs for the Next Decade. ACS Central. 2015;1:117–123. doi: 10.1021/acscentsci.5b00182. [DOI] [PMC free article] [PubMed] [Google Scholar]