Abstract
Modeling contagious diseases needs to incorporate information about social networks through which the disease spreads as well as data about demographic and genetic changes in the susceptible population. In this paper, we propose a theoretical framework (conceptualization and formalization) which seeks to model obesity as a process of transformation of one's own body determined by individual (physical and psychological), inter-individual (relational, i.e., relative to the relationship between the individual and others) and socio-cultural (environmental, i.e., relative to the relationship between the individual and his milieu) factors. Individual and inter-individual factors are tied to each other in a socio-cultural context whose impact is notably related to the visibility of anybody being exposed on the public stage in a non-contingent way. The question we are dealing with in this article is whether such kind of social diseases, i.e., depending upon socio-environmental exposure, can be considered as “contagious”. In other words, can obesity be propagated from individual to individual or from environmental sources throughout an entire population?
Keywords: contact dynamics, demography, mathematical modelling, obesity, social networks
Introduction
Social diseases are numerous and obesity can be considered as one of the most characteristic of what could be identified as a social “contagious” disease. Both stigmatization and mimicking1 constitute the method of dissemination of obesity into a family or a social network. Obesity is defined as an abnormal or excessive accumulation of fat in adipose tissue, more or less leading to important health problems at the individual level. Currently, obesity would be reaching an epidemic development worldwide: according to the latest world estimates of WHO (World Health Organization), obesity rate has tripled between 1980 and 2005.2,3 This rate of development suggests that this pathology involves a socio-cultural problem grafted into a predisposition at the individual level.
All specialists agree that, for decades, we have been witnessing an increase in worldwide obesity prevalence. This is true in developed as well as in developing countries. No society seems to be immunized against this epidemic. Classic data from MONICA WHO project2 shows that obesity prevalence in the majority of European countries increased in 10 y (1992–2002), going from 10% to 20% in men and from 10% to 25% among women. In France, between 1980 and 2006, obesity prevalence went from 6.4% to 14.3% in men and from 6.3% to 15.7% among women (International Association for the Study of Obesity 2000; Maillard et al. 19993,4). Based on these facts, several studies have been performed to identify risk factors associated with this condition as well as to contain the epidemic, because obesity became a real public health problem.5 It is well known that obesity has a genetic component as a familiar predisposition toward this condition. However, the genetic component does not explain the increasing (spectacular) progression of the disease prevalence. Additional behavioral, social, and economic factors must be considered.6-8 In this context, Christakis and Fowler recently showed the possibility of person to person obesity contagion in a social network.9 Moreover, Cohen-Cole and Fletcher suggested that obesity diffusion could occur via a common exogenous source applied to a set of individuals.10
Realistic models of contagious diseases now incorporate information about the social networks through which the disease spreads, as well as data about demographic and genetic changes in the susceptible population. They also include all the possible knowledge about the contacts between susceptible and sick individuals. In “Section Methods”, we will present the mathematical framework necessary to take into account, at a microscopic level, the dynamics of contacts between susceptible and obese individuals. Then we will introduce the description of the dynamics of obesity in the Results section, taking into account collective behaviors mimicking some dominant habits of nutrition transmitted through social networks. Obesity spread modeling will use the notion of homophilic graphs.
To investigate obesity in a multi-factorial manner, we have taken into account the impact through time that obese individual transformation may have on the social structure, by developing a network model in which individual interactions are in part due to homophilic selection/de-selection, i.e., a process of preferential attachment and detachment of inter-individual links according to characteristics of the individuals involved. Homophily is here defined as the tendency of an individual to create links with other individuals sharing similar attributes and to sever links with other dissimilar individuals. Homophily suggests that individuals tend to interact with those who resemble them. Second, and reciprocally, we study if obesity can be considered as a “contagious” social disease. So we can study the role which could be played by the structure of the social fabric in the increase and current development of obesity.
We evaluate the impact of relations between individuals (micro-level) as well as the impact of relations between districts (meso-level) and between countries (macro-level). This approach highlights the need to integrate the dynamics of each scale to better understand the evolution of the pathology. Two stochastic models are proposed: i) an epidemiological compartmental model and ii) an individual centered network model, considering 3 influences: exogenous heterogeneous (individual-cultural), exogenous homogeneous (individual-social) and endogenous (individual-individual). All together, this study of obesity will allow investigating the social and cultural dimension involved in being and transforming one's body.
In the Discussion section, we present elements of demographic dynamics to add to the social contagion dynamics as an obesity preventive policy, and eventually some perspectives about a new more realistic modeling of the contact dynamics.
Methods
General graph framework
Given that each individual is immersed in a social system, linked together with other individuals through diverse and complex interactions, each individual “i” can then be characterized, in a first approach, by its number of neighbors ki, whereas the overall system is characterized by the connection structure between individuals. To study the role played by social interactions in obesity spreading, 5 simple network topologies are considered to describe inter-individual connections: random (Erdös-Renyi), scale-free, small-world and 2 empirical networks.
The empirical networks are built from degree distributions found by Christakis and Fowler8 in real networks. In Figure 1, we can find examples of simulated architecture following the above topologies. We will use these architectures to start from initial configurations of the initial network, before applying the homophilic rule and converging to an “attractor” of its dynamics, i.e., a stable configuration of links and node states of the interaction graph related to the social network involved in the social contagion of the obesity.
Figure 1.
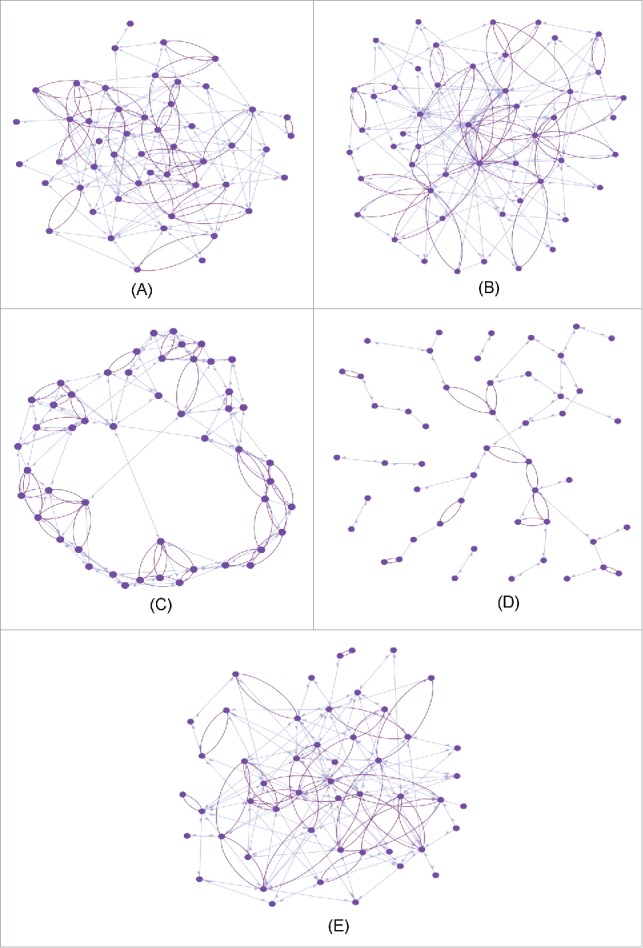
Simulation of various initial architectures: random, scale-free, small world, empirical (1 and 2). (A) Radom; (B) scale-free; (C) small-world; (D) empirical-1; (E) empirical-2.
Social contagion
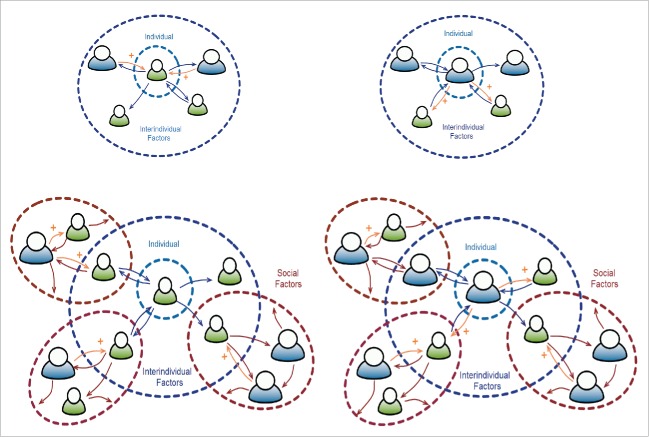
In Figure 2, each individual is represented in their social neighborhood: he/she can influence the narrow contexts to which he belongs, e.g, by transmitting a good opinion about his/her obese state (red arrow) or about his normal state (blue or brown arrows). Hence, each individual in a given social sub-network will receive indirect influence linked to his/her context. Under theses influences, some individual (in blue in Fig. 2) can become obese and others may not (in green in Fig. 2).
Figure 2.
Inter-individual relationships between obese and non-obese individuals in a social context.
We are interested in modeling the social contagion mechanisms through which the disease can propagate from individual to individual or from environmental sources through populations, individuals changing states like in biological regulatory networks for which many theoretical and numerical tools have been recently developed.11-14
In Figure 3, we have fixed the corporal state (obese, overweight and normal) following the distribution of the BMI (Body Mass Index) in Chilean children (population between the ages of 5 and 17)15 in 2011: obese (9.6%), overweight (23.2%) and normal (67.2%). The tolerance has been taken at the 0.25 level and the connection probability has been chosen following the Version 1. Directed (not directed) networks with 1000 nodes each have been simulated, with a probability of having forward directional (resp. bidirectional) links equal to a = 0.6 (resp b = 0.2). The node positioning has been done following the attraction-repulsion by the Fruchterman and Reingold algorithm.16
Figure 3.
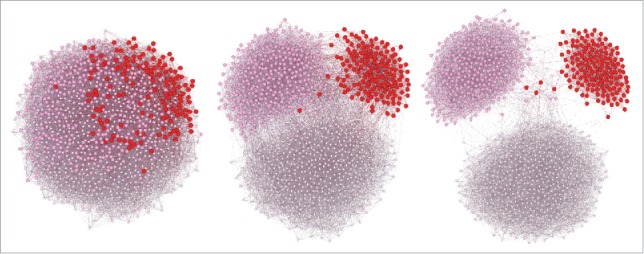
Dynamics with a progressive clusterization (from left to right) inside a small-world directed network with initial proportion of obese individuals in red (14,5%), overweight in pink (31.9%) and normal in white (53,6%), 0.25 tolerance and connection probability of the Version 1.
Homophilic Hebb graphs
The function homophily will be defined as the tendency of an individual to create links with other individuals sharing similar attributes and to sever links with other dissimilar individuals, by playing with the probability of having an infectious contact between agents having the same given state (e.g., normoweight susceptible S, overweight W and obese O). The tendency an agent or node i has to create or cut a link with another agent j in a social interaction graph G having N agents, depends on similarity distance d(i,j) in the graph, like the Hebbian rule of pruning/strengthening in neural networks, which is based on state correlations, destroying (resp. reinforcing) links between nodes weakly (resp highly) correlated.
For example, if the state x(t,i) of the ith node at time t equals 1 (S), 2 (W) or 3 (O), are considered as well as some biological characteristics like age A(t,i) and Body Adiposity Index B(t,i), social variables like sizes of the family F(t,i) and of the circle of friends C(t,i), environmental parameters like the numbers of accessible green areas G(t,i) and supermarkets M(t,i), behavioral variables like sedentary lifestyle index L(t,i) (resp. sport index S(t,i)), that is the number of hours at home (resp on a sports area) during the last 24h, they are all the components of a large state vector V(t,i), we can correlate with the vector V(t,j), e.g., by calculating the average cross-correlation between the V components during a defined timelapse.
Then, the Hebbian rule eliminates links between uncorrelated nodes and builds a positive (resp. negative) link between positively (resp negatively) sufficiently correlated nodes. The dynamics of creation/cancellation of links can be separated from the state dynamics, if it is slower : then we can first study, with a fixed architecture, the fast state dynamics, considered as autonomous and then study the bifurcations (in number and nature) of its attractors due to the slow link dynamics. Let us suppose that there are states x and y in the social graph and denote at time t by Lx,y(t) (resp. Lx,x(t), Lx(t) and L(t)) the number of heterophilic links (resp homophilic links of type x, links coming from type x nodes and total links) and by τ the relaxation time. We suppose in each time lapse of duration τ, a certain proportion of nodes (agents) create (resp. cancel) links toward nodes being in same (resp different) state, with a certain tolerance threshold, supposed to be the same in each state group. The simulation follows the successive steps:
At t = t0, generate the random value τ from an exponential distribution of parameter 1/β.
- At t = t0 + τ, do the following operations:
- choose a fraction Φ of nodes in G. Let M = ΦN.
- for each node i of these M nodes (i = 1,..,M), define its state x(k) (known initial conditions), its out-degree ki ∈ IN (equal to the number of links exiting from i), generate its tolerance to the difference, a real 0 ≤ hi ≤ 1, from a probability distribution g(h) and do the following operations:
- for ki = 0, connection from i to j:
- choose a node j by chance among N-1 other nodes.
- create a link from i to j with probability hid(i,j), where d(i,j) is the direct distance between i and j, with 3 levels: 0, 1 and 2, as follows:
- for ki ≤ 1, connection or disconnection from i to j:
- if V(i) denotes the set of neighbors of i, let choose a node j among the |V(i)| neighbors of i with the probability 1/ki. We will denote by V(j)\i the set of the neighbors of j, minus i.
- let r(i,j) be the total similarity distance between nodes i and j. The link between i and j will be cut with the probability 1-hir(i,j) where the total distance r is defined by:
where the indirect distance c is given by:
- if the link between i and j has been cut, we choose by chance a new node k in G \ V(i) \ (V(j)\i) and we create a link from i to k with the probability:
where is the number of nodes in G \ V (i)\ (V(j)\i) having the same state as k, i.e., nk is the number of nodes with state S (resp. W and O) if k is susceptible (resp overweight and obese). We will consider in the simulations 3 versions for the function f:-
Version 1: f(d(i,k)) = 1,if d(i,k) = 0;= 0 elsewhere.
-
Version 2: f(d(i,k)) = 1,if d(i,k) = 0 or 1;= 0 elsewhere
-
Version 3: f(d(i,k)) = 1,if d(i,k) = 0, 1or 2,
-
these versions being used in the individual centered network for representing 3 types of progressively increasing influence: exogenous heterogeneous (individual-cultural, Version 1), exogenous homogeneous (individual-social, Version 2), endogenous (individual-individual, Version 3).
Change the states x(j), for all j at the end of links created, by increasing their obesity weight of one level (S to W, W to O, O to O).
Generate a new τ and go to 2.
Stop when graph is no longer changing.
Results
Equilibrium configurations
Under the homophilic rule, the network converges until an attractor configuration of both links of the undirected graph architecture and node states, regardless of the initial architecture and initial state distribution (Fig. 3). By using a simulation engine of the social network, we can study the speed of convergence to this equilibrium for all the topologies proposed in the Methods section.
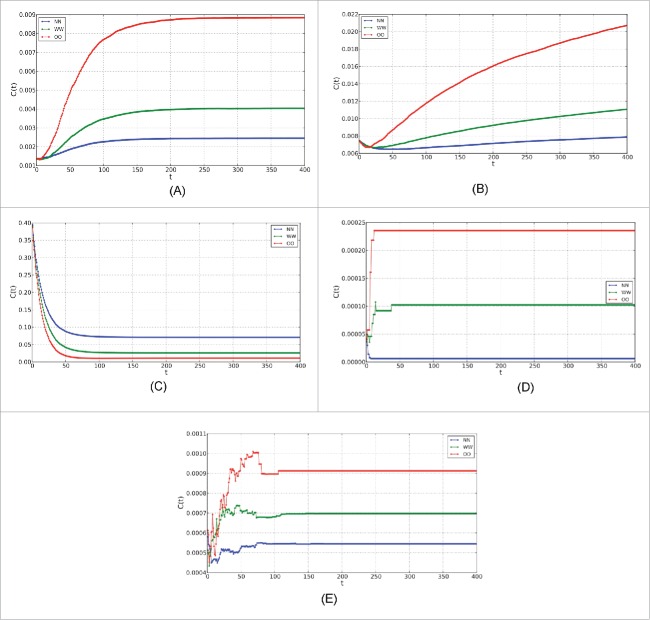
Figure 4 shows that the relaxation time to steady state (in connection with the speed of convergence to homophilic equilibrium) depends on the network topology. The shape of the initial and final “in-degree” (numbering of edges entering a node) distributions are about the same after applying the homophilic dynamics (Fig. 5). However, we can show that, paradoxically (with respect to the random topology) in the small-word initial topology, the mean clustering coefficient of a node i is the number of edges in V(i) divided by the maximum possible number of edges |V(i)|(1-|V(i)|)/2) calculated by state decreases (this phenomenon due to the modification of the state distribution).
Figure 4.
Evolution of the mean clustering coefficient for each state and for the architectures and initial distribution of states (normal in blue, overweight in green and obese in red) of Section 2, with tolerance equal to 0.25 and connection probability of the Version 3. (A) Radom; (B) scale-free; (C) small-world; (D) empirical-1; (E) empirical-2.
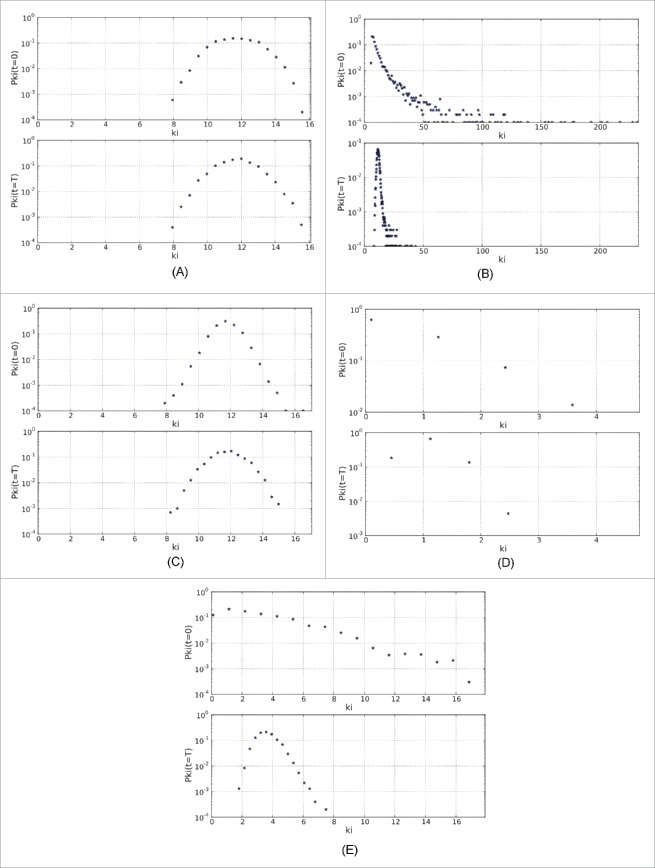
Figure 5.
Initial (top) and final (bottom) distributions of the “in-degree” for the architectures and initial distributions of states of Section Methods, with tolerance equal to 0.25 and connection probability of Version 3. (A) Radom; (B) scale-free; (C) small-world; (D) empirical-1; (E) empirical-2.
In order to improve this study, a theoretical estimation of the speed of convergence to the equilibrium configuration could be made, as well as the consideration of the robustness of the process: Do more than one equilibrium state exist, and if so, are there other attractors, e.g., only fixed states or possibly periodic configurations? Which network parameters are critical or sensitive to the dynamics, i.e., which parameter perturbation provokes a change in number or nature of attractors? Which perturbation of the initial configuration of the social network leads to a change of attraction (or stability) basin? All these questions will be addressed in a future work.
Examples of dynamics of obesity
Homophily defined as above suggests that individuals tend to interact with those who resemble them in terms of alimentary behavior. The structure of social fabric is involved in the increase and current development of obesity.17-29 By using the proposed simulation rules, we compare the simulated graphs with real data in case of obesity. Four situations have been tested: the pure random graph (links chosen by chance), the free scale graph (the distribution of out-degrees follows a power law), the small world graph (links around hub nodes are reinforced) and homophilic graphs, with different versions of probability of linking. The approach described above has highlighted the need to integrate a random dynamics at each scale to better understand the evolution of the obesity pathology, e.g., in Figure 5, the connectivity of the real social network representing obesity spread is better taken into account in the homophilic network Version 1 (the qualitative differences between homophilic versions being small) than in the other versions: random, scale-free or small world. Figure 6 shows the variation of the average homophily (left), based on the average level of tolerance for each studied network topology and the relaxation time (right) depending on the average tolerance to reach the steady-state (Fig. 7).
Figure 6.
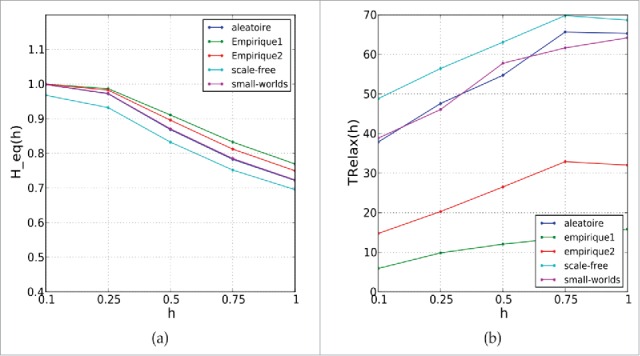
Left: with connection probability of the Version 3, evolution of the homophily coefficient at equilibrium as function of the mean tolerance. Right: Evolution of the relaxation time to equilibrium as function of the mean tolerance. (A) Connection version 3; (B) connection version 3.
Figure 7.
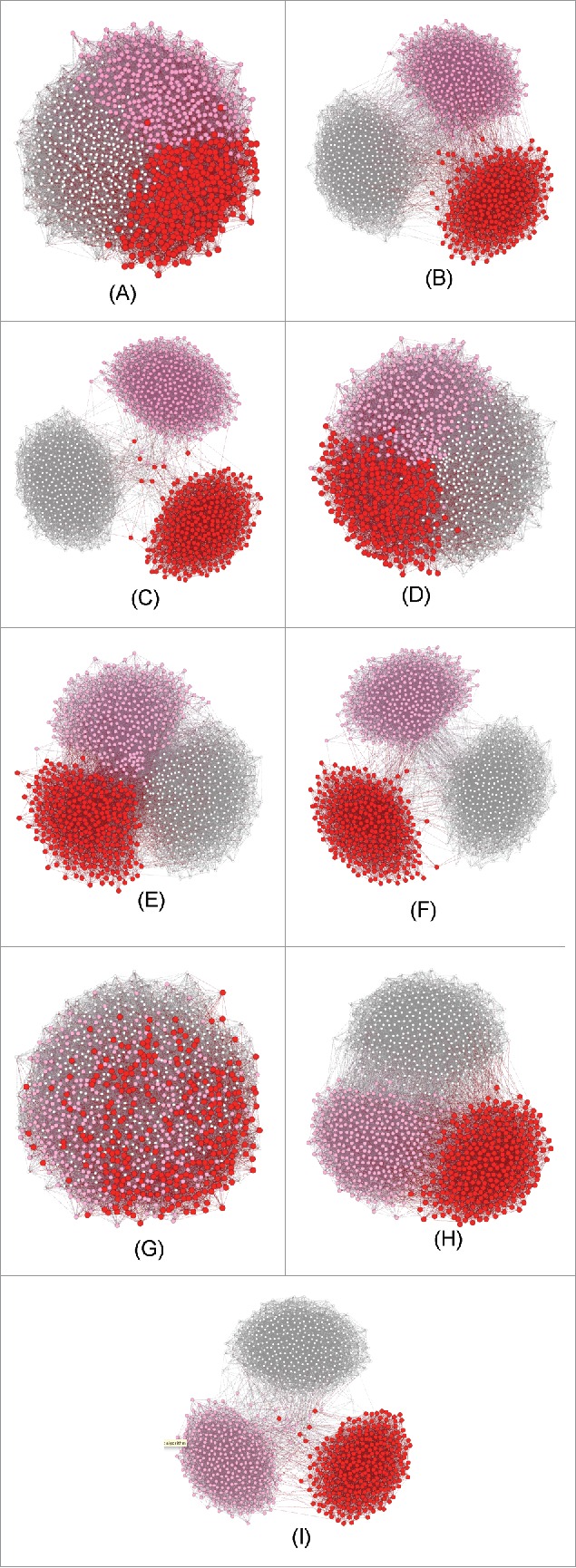
Homophilic dynamics representing obesity network for the architectures and initial distribution of states of Figure 5, with tolerance equal to 0.25 and connection probability of Version 3. Initial conditions (A), (D) and (G); middle configurations (B), (E) and (H) and final configurations (C), (F) and (I).
Demographic dynamics
For evaluating the number of susceptibles and defining them by age and sex (which are important factors in the occurrence of obesity), we need to develop a dynamic projection model by using key socio-demographic indicators of the studied population. The lack of comprehensive and documented data often not allow the use of international performance tools like Individual Based Model (IBM) demographic simulation such as FELICIE, DESTINIE, OMPHALE, MOGDEN, LIFEPATH,….17-19 So we proposed the DOPAMID model, which requires less raw data for its dynamic projection method.
DOPAMID model overview
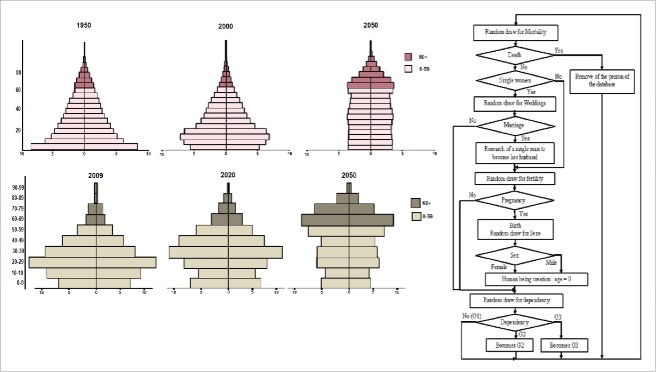
The objective of the model is to make a population evolve according to statistics based on its composition of age classes. This evolution allows expressing patterns in the composition of the population. Statistics used are: the distribution of the population according to the age and sex of the individuals, mortality, fertility, and composition of families as well as the dependency of individuals. Based on a population and respecting these statistics, the model advances in time over a period of up to 90 y. The members of this population will therefore age, reproduce, become dependent, die… Every year, the values of the population statistics are recalculated, they are saved on an Excel or Open Office-readable text format file and given in the classical pyramid format (Fig. 8).
Figure 8.
Aging algorithm applied each year for each human being, with DOPAMID simulations (bottom left) and World Bank data (top left from 20).
Model
A study of an important pathology associated to obesity, like type 2 diabetes,21 shows that the proportion of diabetics is equal to 3.5% in the normal weight Iranian population, and 6.4% and 14.3% respectively in overweight and obese population, representing an odd ratio of respectively 1.7 (the 95%-confidence interval being equal to [1.1–2.5]) and 4 (the 95%-confidence interval being equal to [2.7–5.8]). The demographic modeling allows calculating, for each age class, the proportion of obese and the risk of type 2 diabetes: in21 for example, the odd ratio per 10 y is equal to 1.2 (the 95%-confidence interval being equal to [1.1–1.4]). A precise distribution with respect to gender and age class can be found in.22
Discussion
Toward the proposal of an obesity preventive policy
The BMI was defined about 2 centuries ago by a Belgian physician (A. Quételet) and it represents the basic tool for diagnosing obesity and for therapeutic surveillance. New policies are now needed to contain the world pandemic and we suggest the following methods in order to watch and cure obesity:
Defining new optimal threshold for defining obesity states and associated risks from the classical BMI.23
Using a new index called the Body Adiposity Index (BAI) allowing differentiating muscular, skeletal and adipose masses.24
Elucidating all genetic factors involved in the obesity genesis (endogenous individual factors).25
Searching for all metabolic factors implied in the development of the disease: nutrition, as well as predisposition to use glycolytic pathway more than oxidative phosphorylation in order to produce energy, like in the Warburg effect.26,27
Identifying all social factors favoring the present epidemic, particularly exogenous environmental factors, in social networks involving young individuals (educative, sportive, familial, social,…) in order to actively prevent the disease before adult age (for example, cf. www.repop.fr) at school or during hospital stays.28
Studying all psycho-social factors leading to obesity stigmatization in relation to mental body image and self-esteem.29
Modeling carefully the connection between the demographic dynamics and the social networks. In the future, it needs deep knowledge (presently absent) regarding the structure by age class into the social networks, as well as on the rules of transmission and intergenerational inheritance of the alimentation and adapted physical activity habits. Nevertheless, the evolution of the size of the whole population has to be already introduced in order to fix the number of nodes and interaction links for calibrating our social networks models.
The Dynamics of Contacts
Influence of the contact duration
Let us now introduce contact duration τ and a contagion coefficient β possibly depending on τ.30 It is possible to retrieve the quadratic term of interaction already present in all the classical models of contagion30-40 by using a stochastic approach coming from the random chemistry of contacts41-57 for interpreting the proposed rules, more developed in.58
We have the demographic dynamics voiding the overweight transition:
where S(t) (resp. O(t)) is the size of the susceptible (resp obese) population at time t. The microscopic equation above leads to the mean differential equation ruling the expectations of the random variable S:
and to the macroscopic equation:
, in which we found the quadratic term of the classical models of contagion.
This quadratic term is also present in the interaction potential of Hopfield like networks in which the study of the robustness with respect to the contagion parameter changes has been performed59-69 as well as in recent studies taking into account the spatial character of the disease spread.70-78
Confinement and Saturation
The localization of contamination has been treated by different authors.79,80 When contagion occurs in confined locations (like professional, educational or residence buildings), we can use saturation dynamics terms coming from the enzymatic kinetics (cf. for example81,82) for expressing all the possibilities of meeting together k individuals from the S susceptible population and i from the O obese population in n contagion sites located in B buildings.
We call this quantity the partition function P(S,O) and is the total mean number of occupied sites, considered as proportional to the infection rate. Then, we have:
where the demographic parameters f (fecundity) and μ (mortality) are taken into account for the susceptible as well as for the obese population (f' and μ') and where ρ denotes the recovering rate at which an obese recovers to healthy weight.
An example of such a dynamics is the saturation Michaëlian one, if there is only one contagion site:
where (resp. ) is the probability for a susceptible (resp obese) to access a contagion site. If and , then the infection rate equals about and the equations of the dynamics are:
Complex threshold dynamics used in classical Hopfield like models59,69 are non-linear, but take into account only pair contacts, neglecting possible additional effects due to the presence and mutual interaction of more than 2 individuals in the contagion process.
It is now possible to introduce a synergy model, i.e., a formalism to be able of define non-linear n-uples interactions83 and simulate the model in a spatial Markovian context like in this study or in certain cases of remote spatial influence (due to new social networking on the web) in a renewal context,84 as well with different time scales modeling complex dynamics, for separating the local dynamics from the global trend of the obesity epidemic.85
Confrontation with data
Results shown in this paper about social networks involved in obesity have been obtained by modeling and simulating networks with various initial architectures (random, scale-free, small-world, empirical) evolving under the so-called social homophilic constraint. The computed evolution of these networks seems to be similar to the real one observed in developed countries for a socially “contagious disease:” obesity.
Complementary studies are now required based on large samples estimating the unobservable parameters linked both to initial network architecture (taking into account the specificity of the sub-populations of susceptibles, e.g., the differences between the schoolchildren, professional and elderly people networks) and to its interaction weights evolution, as well as incorporating the demographic dynamics and a more accurate model of social contacts through which the disease can spread. The choice of the homophilic rule is in agreement with the final proportions of each state group in Chilean population. Moreover, if we want to confront the residual number of the intergroup interactions (e.g., the number of links between overweight and obese), we have to look at inquiries in the field like those performed in Chile in 2011.86 In addition, data from such surveys should, in the future, document a differential tolerance, specific for each group in order to relax the constraint of the conservation of the total number of links. Eventually, we could introduce a new state, the obese with type II diabetes: indeed one-third of the population of obese suffer from type II diabetes,86,87 hence we would have the possibility of monitoring the effectiveness of prevention policies (e.g., using therapeutic education serious games88) for diabetes in the elderly. Additionally, 66% of cases of type II diabetes, 52% of cases of cholelithiasis, 29% of cases of hypertension and 22% of cases associated with cardiovascular disease can be attributed to obesity,89 while about 20% of all cancers in Chile could be avoided with strategies for the control and prevention of obesity, especially in children.90
Disclosure of Potential Conflicts of Interest
No potential conflicts of interest were disclosed.
Funding
We acknowledge the Projects “Investissements d'Avenir” VHP (Visual Home Presence inter@ctive), the PHC Maghreb SCIM (Systèmes Complexes et Ingénierie Médicale) and Conicyt - FONDEF “Plataforma de Integración Tecnológica para el Registro, Vigilancia y Alerta de Enfermedades de Notificación Obligatoria” IT13I10059.
References
- 1.Rosen J, Myers A. Obesity stigmatization and coping: relation to mental health symptoms, body image, and self-esteem. Int J Obesity Relat Metab Disord 1999; 23:221-230; PMID:10193866; http://dx.doi.org/ 10.1038/sj.ijo.0800765 [DOI] [PubMed] [Google Scholar]
- 2.Tunstall-Pedoe H, Project M. World's largest study of heart disease, stroke, risk factors, and population trends 1979-2002. Int J Epidemiol, WHO, Geneva, 2003. [Google Scholar]
- 3.ObEpi-Roche Enquête épidémiologique nationale sur le surpoids et l'obésité International Obesity Task Force Prevalence Data, Roche, Paris, 2009 and 2012. [Google Scholar]
- 4.Maillard G, Charles M, Thibault N, Forhan A, Sermet C, Basdevant A, Eschwege E. Trends in the prevalence of obesity in the French adult population between 1980 and 1991. Int J Obesity Relat Metab Disord 1999; 23:389-394; PMID:10340817; http://dx.doi.org/ 10.1038/sj.ijo.0800831 [DOI] [PubMed] [Google Scholar]
- 5.Barth J. What should we do about the obesity epidemic?. Pract Diab Inter 2002; 19:119-122; http://dx.doi.org/ 10.1002/pdi.341 [DOI] [Google Scholar]
- 6.de Saint-Pol T. Obésité et milieux sociaux en France : les inégalités augmentent, Bulletin Epidémiologique Hebdomadaire 2008; 20:175-179 [Google Scholar]
- 7.Laitinen J, Power C, Jarvelin M. Family social class, maternal body mass index, childhood body mass index, and age at menarche as predictors of adult obesity. Am J Clin Nutrit 2001; 74:287-294; PMID:11522550 [DOI] [PubMed] [Google Scholar]
- 8.Scharoun-Lee M, Adair L, Kaufman J, Gordon-Larsen P. Obesity, race/ethnicity and the multiple dimensions of socio-economic status during the transition to adulthood: A factor analysis approach. Social Sci Med 2009; 6:708-716; PMID:19136186; http://dx.doi.org/ 10.1016/j.socscimed.2008.12.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Christakis N, Fowler J. The spread of obesity in a large social network over 32 years. New Eng J Med 2006; 17:77-82. [DOI] [PubMed] [Google Scholar]
- 10.Cohen-Cole AM, Fletcher J. Is obesity contagious? Social networks vs. environmental factors in the obesity epidemic. J Health Economics 2008; 27:1382-1387; PMID:18571258; http://dx.doi.org/ 10.1016/j.jhealeco.2008.04.005 [DOI] [PubMed] [Google Scholar]
- 11.Demongeot J, Amor HB, Elena A, Gillois P, Noual M, Sené S. Robustness of regulatory networks. a generic approach with applications at different levels: physiologic, metabolic and genetic. Inter J Mol Sci 2009; 10:4437-4473; PMID:20057955; http://dx.doi.org/ 10.3390/ijms10104437 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Demongeot J, Elena A, Noual M, Sené S, Thuderoz F. Immunetworks, intersecting circuits and dynamics. J Theoretical Biol 2011; 280:19-33; PMID:21439971; http://dx.doi.org/ 10.1016/j.jtbi.2011.03.023 [DOI] [PubMed] [Google Scholar]
- 13.Demongeot J, Goles E, Morvan M, Noual M, Sené S. Attraction basins as gauges of environmental robustness in biological complex systems. PloS One 2010; 5, e11793; PMID:20700525; http://dx.doi.org/ 10.1371/journal.pone.0011793 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Demongeot J, Noual M, Sené S. Combinatorics of Boolean automata circuits dynamics. Dis Appl Mathe 2012; 160:398-415; http://dx.doi.org/ 10.1016/j.dam.2011.11.005 [DOI] [Google Scholar]
- 15.MINSAL Encuesta nacional de salud. 2010. http://web.minsal.cl/portal/url/item/bcb03d7bc28b64dfe040010165012d23.pdf [Google Scholar]
- 16.Fruchterman T, Reingold E. Graph drawing by force-directed placement. Software: Practice and Exp 1991; 21:1129-1164. [Google Scholar]
- 17.Gaymu J, Festy P, Poulain M, Beets G. From elderly population projections to policy implications, in: Future elderly living conditions in Europe (Felicie). Les cahiers de l'INED 2008; 162:267-290. [Google Scholar]
- 18.Duée M, Rebillard C. La dépendance des personnes âgées: une projection en 2040 Données sociales - La société française, INSEE, Paris, 2006. [Google Scholar]
- 19.Légaré J, Décarie Y. Using statistics Canada life paths micro-simulation model to project the health status of Canadian elderly. SEDAP Research Paper 227, SEDAP, Hamilton, 2008. [Google Scholar]
- 20.World Bank http://web.worldbank.org/WBSITE/EXTERNAL/DATASTATISTICS/, Washington, 2009 [Google Scholar]
- 21.Harati H, Hadaegh F, Saadat N, Azizi F. Population-based incidence of type 2 diabetes and its associated risk factors: results from a six-year cohort study in Iran. BMC Public Health 2009; 9, 186; PMID:19531260; http://dx.doi.org/ 10.1186/1471-2458-9-186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hosseinpanah F, Barzin M, Eskandary P, Mirmiran P, Azizi F. Trends of obesity and abdominal obesity in Tehranian adults: a cohort study. BMC Public Health 2009; 9, 429; PMID:19930668; http://dx.doi.org/ 10.1186/1471-2458-9-429 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dauphinot V, Wolff H, Naudin F, Gueguen R, Sermet C, Gaspoz J, Kossovsky M. New obesity body mass index threshold for self-reported data. J Epidemiol Com Health 2009; 63:128-132; PMID:18801799; http://dx.doi.org/ 10.1136/jech.2008.077800 [DOI] [PubMed] [Google Scholar]
- 24.Bergman R, Stefanovski D, Buchanan T, Sumner A, Reynolds J, Sebring N, Xiang A, Watanabe R. A better index of body adiposity. Obesity 2011; 19:1083-1089; PMID:21372804; http://dx.doi.org/ 10.1038/oby.2011.38 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Baranova A, Collantes R, Gowder S, Elariny H, Schlauch K, Younoszai SKA, Randhawa M, Pusulury S, Alsheddi T, Ong J, Martin L, Chandhoke V, Younossi ZM. Obesity-related differential gene expression in the visceral adipose tissue. Obesity Surgery 2005; 15:58-65; PMID:15768482; http://dx.doi.org/ 10.1381/0960892054222876 [DOI] [PubMed] [Google Scholar]
- 26.Demetrius L, Coy J, Tuszynski J. Cancer proliferation and therapy: the Warburg effect and quantum metabolism. Theoret Biol Med Mod 2010; 7, 2; PMID:20085650; http://dx.doi.org/ 10.1186/1742-4682-7-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Demetrius L, Tuszynski J. Quantum metabolism explains the allometric scaling of metabolic rates. J. Royal Soc. Interface 2010; 7:507-514; PMID:19734187; http://dx.doi.org/ 10.1098/rsif.2009.0310 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Delhumeau C, Demongeot J, Langlois F, Taramasco C. Modelling the hospital length of stay in diagnosis related groups data bases in: IEEE ARES-CISIS'09 IEEE Press, Piscataway:955-960, 2009. [Google Scholar]
- 29.Myers A, Rosen J. Obesity stigmatization and coping: relation to mental health symptoms, body image, and self-esteem. Int J Obes Relat Metab Disord 1999; 23:221-230; PMID:10193866; http://dx.doi.org/ 10.1038/sj.ijo.0800765 [DOI] [PubMed] [Google Scholar]
- 30.Demongeot J, Hansen O, Hessami H, Jannot A, Mintsa J, Rachdi M, Taramasco C. Random modelling of contagious diseases. Acta Biotheoretica 2013; 61:141-172; PMID:23525763; http://dx.doi.org/ 10.1007/s10441-013-9176-6 [DOI] [PubMed] [Google Scholar]
- 31.Bernoulli D. Essai d'une nouvelle analyse de la mortalité causée par la petite vérole, et des avantages de l'inoculation pour la prévenir Mém. Acad. Roy. Sci., Paris, 1760. [Google Scholar]
- 32.d'Alembert J. Onzième mémoire : sur l´application du calcul des probabilités à l´inoculation de la petite vérole ; notes sur le mémoire précédent ; théorie mathématique de l´inoculation, in: Opuscules mathématiques, David, Paris: 26-95, 1761. [Google Scholar]
- 33.Hamer W. The Milroy lectures on epidemic disease in England: the evidence of variability and persistency of type. Bedford Press, London: 733-739, 1906. [Google Scholar]
- 34.Ross R. Prevention of malaria John Murray, London, 1910. [Google Scholar]
- 35.Brownlee J. On the curve of the epidemic. Br Med J, 1915; 1:799-800; PMID:20767626; http://dx.doi.org/ 10.1136/bmj.1.2836.799 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ross R. Some a priori pathometric equations. Br Med J 1915; 1:546-547; PMID:20767555; http://dx.doi.org/ 10.1136/bmj.1.2830.546 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ross R. An application of the theory of probabilities to the study of a priori pathometry. part I. Proc Royal Soc London Series A 1916; 92:204-230; http://dx.doi.org/ 10.1098/rspa.1916.0007 [DOI] [Google Scholar]
- 38.Gibson M. Sir Ronald Ross and his contemporaries. J Royal Society of Medicine 1978; 71:611-618; PMID:20894263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kermack W, McKendrick A. A contribution to the mathematical theory of epidemics. Proc Royal Soc London, Series A 1927; 115:700-712; PMID:23797790; http://dx.doi.org/ 10.1098/rspa.1927.011823797790 [DOI] [Google Scholar]
- 40.Kermack W, McKendrick A. Contributions to the mathematical theory of epidemics. iii. further studies of the problem of endemicity. Proc Royal Soc London Series A 1933; 121:141-194. [Google Scholar]
- 41.Delbrück M. Statistical fluctuations in autocatalytic reactions. J Chem Phys 1940; 8:120-124; http://dx.doi.org/ 10.1063/1.1750549 [DOI] [Google Scholar]
- 42.Bartholomay A. On the linear birth and death processes of biology as Markov chains. Bull Math Biophys 1958; 20:97-118; http://dx.doi.org/ 10.1007/BF02477571 [DOI] [Google Scholar]
- 43.Bartholomay A. Stochastic models for chemical reactions: I. theory of the uni-molecular reaction process. Bull Math Biophys 1958; 20:175-190; http://dx.doi.org/ 10.1007/BF02478297 [DOI] [Google Scholar]
- 44.Bartholomay A. Stochastic models for chemical reactions: II. the unimolecular rate constant Bull Math Biophys 1959; 21:363-373; http://dx.doi.org/ 10.1007/BF02477895 [DOI] [Google Scholar]
- 45.McQuarrie D. Kinetics of small systems I. J Chem Phys 1963; 38:433-436; http://dx.doi.org/ 10.1063/1.1733676 [DOI] [Google Scholar]
- 46.McQuarrie D, Jachimowski C, Russell M. Kinetics of small systems. II. J Chem Phys 1964; 40:2914-2921; http://dx.doi.org/ 10.1063/1.1724926 [DOI] [Google Scholar]
- 47.Jachimowski C, McQuarrie D, Russell M. A stochastic approach to enzyme-substrate reactions. Biochem 1964; 3:1732-1736; PMID:14235340; http://dx.doi.org/ 10.1021/bi00899a025 [DOI] [PubMed] [Google Scholar]
- 48.McQuarrie D. Stochastic approach to chemical kinetics. J Appl Probab 1967; 4:413-478; http://dx.doi.org/ 10.2307/3212214 [DOI] [Google Scholar]
- 49.Hoare M. Molecular Markov processes. Nature 1970; 226:599-603; PMID:16057421; http://dx.doi.org/ 10.1038/226599a0 [DOI] [PubMed] [Google Scholar]
- 50.Bailey N. The simple stochastic epidemic: A complete solution in terms of known functions. Biometrika 1963; 50:235-240; http://dx.doi.org/ 10.1093/biomet/50.3-4.235 [DOI] [Google Scholar]
- 51.Dietz K. Epidemics and rumors: A survey. J Royal Stat Soc. Series A (General) 1967; 130:505-528; http://dx.doi.org/ 10.2307/2982521 [DOI] [Google Scholar]
- 52.Demongeot J. A stochastic model for the cellular metabolism in: Recent Developments in statistics, North Holland, Amsterdam:655-662, 1977. [Google Scholar]
- 53.Allen L. An introduction to stochastic epidemic models. Math Epidemiol 2008; 1945:81-130; http://dx.doi.org/ 10.1007/978-3-540-78911-6_3 [DOI] [Google Scholar]
- 54.Rhodes C, Demetrius L. Evolutionary entropy determines invasion success in emergent epidemics. PLoS One 2010; 5, e12951; PMID:20886082; http://dx.doi.org/ 10.1371/journal.pone.0012951 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Britton T. Stochastic epidemic models: a survey. Math Biosci 2010; 225:24-35; PMID:20102724; http://dx.doi.org/ 10.1016/j.mbs.2010.01.006 [DOI] [PubMed] [Google Scholar]
- 56.Gillespie D. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J Comput Phys 1970; 22:403-434; http://dx.doi.org/ 10.1016/0021-9991(76)90041-3 [DOI] [Google Scholar]
- 57.Magal P, Ruan S. Susceptible-infectious- recovered models revisited: From the individual level to the population level. Math Biosci 2014; 250:26-40; PMID:24530806; http://dx.doi.org/ 10.1016/j.mbs.2014.02.001 [DOI] [PubMed] [Google Scholar]
- 58.Taramasco C, Impact de l'obésité sur les structures sociales et impact des structures sociales sur l'obésité ? Facteurs individuels et environnementaux, PhD thesis, Ecole Polytechnique, Paris: 2011. [Google Scholar]
- 59.Aldana M, Cluzel P. A natural class of robust networks. Proc Natl Acad Sci USA 2003; 100:8710-8714; PMID:12853565; http://dx.doi.org/ 10.1073/pnas.1536783100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Demongeot J, Elena A, Sené S. Robustness in neural and genetic networks. Acta Biotheoretica 2008; 56:27-49; PMID:18379883; http://dx.doi.org/ 10.1007/s10441-008-9029-x [DOI] [PubMed] [Google Scholar]
- 61.Amor HB, Demongeot J, Elena A, Sené S. Structural sensitivity of neural and genetic networks. Lecture Notes Comp Sci 2008; 5317:973-986; http://dx.doi.org/ 10.1007/978-3-540-88636-5_92 [DOI] [Google Scholar]
- 62.Elena A, Demongeot J. Interaction motifs in regulatory networks and structural robustness in: IEEE ARES-CISIS'08, IEEE Press, Piscataway:682-686, 2008. [Google Scholar]
- 63.Elena A, Ben-Amor H, Glade N, Demongeot J. Motifs in regulatory networks and their structural robustness in: IEEE BIBE'08, IEEE Press, Piscataway:234-242, 2008. [Google Scholar]
- 64.Elena A, Robustesse des réseaux d´automates à seuil, PhD thesis, Université Joseph-Fourier, Grenoble, 2009. [Google Scholar]
- 65.Demongeot J, Elena A, Noual M, Sené S. Random Boolean networks and attractors of their intersecting circuits. in: Proceedings IEEE AINA'11, IEEE Proceedings, Piscataway:483-487, 2011. [Google Scholar]
- 66.Glade N, Elena A, Fanchon N, Demongeot J, Amor HB. Determination, optimization and taxonomy of regulatory networks. the example of Arabidopsis thaliana flower morphogenesis in: IEEE AINA'11, IEEE Press, Piscataway:488-494, 2011. [Google Scholar]
- 67.Demongeot J, Waku J. Robustness in genetic regulatory networks II, application to genetic threshold Boolean random regulatory networks (getbren). Comptes Rendus Mathématique, 2012; 350:225-228; http://dx.doi.org/ 10.1016/j.crma.2012.01.019 [DOI] [Google Scholar]
- 68.Demongeot J, Waku J. Robustness in genetic regulatory networks IV, application to genetic networks controlling the cell cycle. Comptes Rendus Mathématique 2012; 350:293-298; http://dx.doi.org/ 10.1016/j.crma.2012.02.005 [DOI] [Google Scholar]
- 69.Demongeot J, Drouet E, Moreira A, Rechoum Y, Sené S. Micro-RNAs: viral genome and robustness of the genes expression in host. Phil Trans Royal Soc A 2009; 367:4941-4965; PMID:19884188; http://dx.doi.org/ 10.1098/rsta.2009.0176 [DOI] [PubMed] [Google Scholar]
- 70.Koopman J, Longini I. The ecological effects of individual exposures and nonlinear disease dynamics in populations. Am J Public Health 1994; 84:836-842; PMID:8179058; http://dx.doi.org/ 10.2105/AJPH.84.5.836 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Kretzschmar M. Measures of concurrency in networks and the spread of infectious disease. Math Biosci 1996; 133:165-195; PMID:8718707; http://dx.doi.org/ 10.1016/0025-5564(95)00093-3 [DOI] [PubMed] [Google Scholar]
- 72.Sathik M, Rasheed A. Social network analysis in an online blogosphere. Inter J Eng Sci Technol 2011; 3:117-121, [Google Scholar]
- 73.Gaudart J, Giorgi R, Poudiougou B, Ranque S, Doumbo O, Demongeot J. Spatial cluster detection: principle and application of different general methods. Rev Epid Santé Pub 2007; 55:297-306; http://dx.doi.org/ 10.1016/j.respe.2007.04.003 [DOI] [PubMed] [Google Scholar]
- 74.Gaudart J, Touré O, Dessay N, Dicko A, Ranque S, Forest L, Demongeot J, Doumbo O. Modelling malaria incidence with environmental dependency in a locality of Sudanese savannah area, Mali. Malaria J 2009; 8, 61; PMID:19361335; http://dx.doi.org/ 10.1186/1475-2875-8-61 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Gaudart J, Ghassani M, Mintsa J, Rachdi M, Waku J, Demongeot J. Demography and diffusion in epidemics: Malaria and black death spread. Acta Biotheoretica 2010; 58:277-305; PMID:20706773; http://dx.doi.org/ 10.1007/s10441-010-9103-z [DOI] [PubMed] [Google Scholar]
- 76.Demongeot J, Gaudart J, Mintsa J, Rachdi M. Demography in epidemics modelling. Commun Pure Appl Analysis 2012; 11:61-82; http://dx.doi.org/ 10.3934/cpaa.2012.11.61 [DOI] [Google Scholar]
- 77.Demongeot J, Gaudart J, Lontos A, Promayon E, Mintsa J, Rachdi M. Least diffusion zones in morphogenesis and epidemiology. Int J Bifurcat Chaos 2012; 22: 50028; http://dx.doi.org/ 10.1142/S0218127412500289 [DOI] [Google Scholar]
- 78.Demongeot J, Ghassani M, Rachdi M, Ouassou I, Taramasco C. Archimedean copula and contagion modelling in epidemiology. Networks and Heterogeneous Media 2013; 8:149-170; http://dx.doi.org/ 10.3934/nhm.2013.8.149 [DOI] [Google Scholar]
- 79.Amarasekare P. Interactions between local dynamics and dispersal: insights from single species models. Theoret Populat Biol 1998; 53:44-59; PMID:9500910; http://dx.doi.org/ 10.1006/tpbi.1997.1340 [DOI] [PubMed] [Google Scholar]
- 80.Filipe J, Gibson G. Comparing approximations to spatio-temporal models for epidemics with local spread. Bull Math Biol 2001; 63:603-624; PMID:11497160; http://dx.doi.org/ 10.1006/bulm.2001.0234 [DOI] [PubMed] [Google Scholar]
- 81.Demongeot J, Laurent M. Sigmoidicity in allosteric models. Mathematical Biosciences 1983; 67:1-17; http://dx.doi.org/ 10.1016/0025-5564(83)90015-9 [DOI] [Google Scholar]
- 82.Demongeot J, Kellershohn N. Glycolytic oscillations : an attempt to an “in vitro” reconstitution of the higher part of glycolysis. Lectures Notes in Biomaths 1983; 49:17-31; http://dx.doi.org/ 10.1007/978-3-642-46475-1_2 [DOI] [Google Scholar]
- 83.Demongeot J, Sené S. The singular power of the environment on nonlinear Hopfield networks. in: CMSB´11, ACM Proceedings, New York:55-64, 2011. [Google Scholar]
- 84.Demongeot J, Fricot J. Random fields and renewal potentials. NATO ASI Serie F 1986; 20:71-84. [Google Scholar]
- 85.Barthélemy M, Nadal J, Berestycki H. Disentangling collective trends from local dynamics. Proc Natl Acad Sci USA 2010; 107:7629-7634; PMID:Can't; http://dx.doi.org/ 10.1073/pnas.0910259107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Garmendia M, Ruiz P, Uauy R. Obesidad y cáncer en Chile: estimación de las fracciones atribuibles poblacionales. Revista Médica de Chile 2013; 141:987-994; PMID:Can't; http://dx.doi.org/ 10.4067/S0034-98872013000800004 [DOI] [PubMed] [Google Scholar]
- 87.Fried M, Hainer V, Basdevant A, Buchwald H, Deitel M, Finer N, Willem J, Greve JW, Horber F, Mathus Vliegen E, Scopinaro N, Steffen R, Tsigos C, Weiner R, Widhalm K. Interdisciplinary European guidelines for surgery for severe (morbid) obesity. Obesity Surgery 2007; 17:260-270; PMID:17476884; http://dx.doi.org/ 10.1007/s11695-007-9025-2 [DOI] [PubMed] [Google Scholar]
- 88.Demongeot J, Elena A, Taramasco C, Vuillerme N. Serious games and personalization of the therapeutic education. Lecture Notes in Comp Sci 2015; 9102:270-281; http://dx.doi.org/ 10.1007/978-3-319-19312-0_22 [DOI] [Google Scholar]
- 89.Finkelstein E, Khavjou O, Thompson H, Trogdon J, Pan L, Sherry B, Dietz W. Obesity and severe obesity forecasts through 2030. Am J Prevent Med 2012; 42:563-570; PMID:22608371; http://dx.doi.org/ 10.1016/j.amepre.2011.10.026 [DOI] [PubMed] [Google Scholar]
- 90.Lipnowski S, LeBlanc C. Canadian Paediatric Society, healthy active living and sports medicine committee. healthy active living: Physical activity guidelines for children and adolescents. Paediatrics and Child Health 2012; 17:209-210; PMID:23543633 [DOI] [PMC free article] [PubMed] [Google Scholar]