Modeling household and community transmission of Ebola virus disease: Epidemic growth, spatial dynamics and insights for epidemic control

Abstract

The mechanisms behind the sub-exponential growth dynamics of the West Africa Ebola virus disease epidemic could be related to improved control of the epidemic and the result of reduced disease transmission in spatially constrained contact structures. An individual-based, stochastic network model is used to model immediate and delayed epidemic control in the context of social contact networks and investigate the extent to which the relative role of these factors may be determined during an outbreak. We find that in general, epidemics quickly establish a dynamic equilibrium of infections in the form of a wave of fixed size and speed traveling through the contact network. Both greater epidemic control and limited community mixing decrease the size of an infectious wave. However, for a fixed wave size, epidemic control (in contrast with limited community mixing) results in lower community saturation and a wave that moves more quickly through the contact network. We also found that the level of epidemic control has a disproportionately greater reductive effect on larger waves, so that a small wave requires nearly as much epidemic control as a larger wave to end an epidemic.

Abbreviation

EVD

Ebola virus disease

Introduction

An unprecedented epidemic of Ebola virus disease (EVD) got its start in a forested region of Guinea in December 2013 and has been spreading across Guinea, Sierra Leone, and Liberia for over a year.¹ Sporadic case importations into Nigeria, Senegal, Mali, and the United States have generated secondary cases in the range of zero to only a handful.² While prior outbreaks of Ebola have quickly subsided after a few generations of infections in relatively isolated communities,³ this time chains of transmission have been able to cross countries through a highly mobile population in a West African region inexperienced with the virus. The factors that have interacted to trigger this devastating epidemic include: 1) substantial delays in detecting Ebola outbreaks in the region, facilitating several chains of transmission getting a foothold in West Africa, 2) severely limited public health infrastructure including a lack of epidemiological surveillance systems, health care settings with appropriate infection control practices, 3) cultural practices that promote infection (e.g., touching the body of the deceased), and 4) resistance of some populations to follow guidelines set by authorities on how to prevent infection and spread the virus further. The number of EVD cases has reached 27341 including 11184 deaths as of June 17, 2015.² Toward the final months of 2014, after the peak incidence levels reported in August 2014, the epidemiological picture of Ebola dramatically improved in West Africa; the epidemic leveled off in Guinea and Sierra Leone while Liberia has recently reported a cluster of cases 2 months after having been declared Ebola-free in May 2015.² While the epidemic appears to be subsiding, the factors behind the differences in the spatial-temporal evolution of the epidemic in the most affected countries are still poorly understood.

The epidemic took off in December 2013 in the district of Guéckédou, a southern-forested area of Guinea most likely from a single spillover event originating from an infected bat.¹ The virus then spread to neighboring Liberia, generating a small wave of infections from late March to early June 2014, followed by a brief exponential growth dynamic in national case incidence to about mid-September 2014. Similarly, reports of EVD cases started to quickly increase in Sierra Leone in mid March 2014. The height of the epidemic occurred in August 2014, after which the epidemic significantly declined probably a result of a combination of factors including improved isolation and treatment capacity, behavior changes that reduce contact rates in the population, and a reduction in the time from the onset of symptoms to diagnosis.³

Mathematical modeling offers a valuable toolkit to comprehensively analyze the transmission dynamics of infectious diseases by developing models that connect the epidemiology of the disease, the underlying population structure, population behavior, available public health infrastructure to carry out contact tracing activities and isolation of infectious individuals, and public health interventions including education campaigns, social distancing (e.g., school closures) as well as treatment and vaccination campaigns.⁴ In the context of the 2014 Ebola epidemic, mathematical modeling has provided the opportunity to project transmission scenarios based on limited data,^5,6 assess the risk of international case importations,^7,8 and evaluate the impact of control interventions (e.g., construction of Ebola treatment units).^9-15 Yet, our understanding of the transmission characteristics and the role of control interventions in each of the most affected countries remain limited. For instance, at the subnational level, the 2014 epidemic in West Africa can be disaggregated into asynchronous local epidemics that are characterized largely by sub-exponential growth that levels off in just a few generations of the disease.¹⁶ Yet, the mechanisms behind the sub-exponential growth dynamics are not clearly understood. These dynamics could reflect a combination of reactive behavior changes, control interventions or simply a result of disease transmission in spatially constrained contact structures (e.g., high contact network clustering).¹⁶ It is critical to better understand the mechanisms and factors that have shaped the differences in Ebola transmission dynamics in order to improve our ability to forecast epidemics, guide cost-effective control strategies in each of the 3 countries and strengthen preparedness plans to confront future epidemics.

Here we use a relatively simple individual-based stochastic transmission model previously described by Kiskowski.¹⁷ This transmission model structures the population into communities of households to gain insights into the driving mechanisms of transmission of Ebola in West Africa. We vary properties of the network, in particular the distribution of contacts within the network to model well-and less-well-mixed populations, while overall measures of transmission such as the household and community reproductive numbers are kept fixed. This requires that the number of infectious contacts per infected individual and the probability of infections are fixed as the community size is varied. Epidemic control with delay is modeled by decreasing the reproductive numbers based on an external or internal clock. Using simulations we characterize patterns of the early growth phase of epidemics as well as the long-term disease dynamics with and without the role of control interventions.

Ebola Transmission

The Ebola virus is mainly transmitted by direct contact via body fluids or indirectly via contaminated surfaces. Also, the virus is most infectious when individuals are very ill or deceased.³ Consequently, the transmission scope of the EVD tends to be limited by its mode of transmission. EVD is frequently transmitted among caregivers at home or in health care settings (e.g., relatives, health care workers) and via unsafe burials when funeral attendants touch the infectious body of the deceased. After an average incubation period of 10 days (range 2–21 days),¹⁸ individual infectiousness increases as the disease progresses when infectious individuals are likely confined at home or in hospital.¹⁹ The epidemiological picture of the disease often includes nonspecific symptoms such as sudden onset of fever, weakness, vomiting, diarrhea, headache and a sore throat while only a small fraction of symptomatic individuals exhibit hemorrhagic manifestations.²⁰ Moreover, EVD is one of the most pathogenic viruses affecting humans.

These observations motivate a higher rate of infection among close contacts and a lower rate of infection among casual contexts. As in the stochastic transmission model previously described,¹⁷ close contacts with high rates of transmission occur among members of a household while casual contacts with low rates of transmission are assumed to occur among members in a local community.

In this 3-scale network of households within communities that comprise a larger total population, the community of an individual reflects a subset of the network for which that individual has an equiprobable chance of a casual interaction with other members of the same sub-network. A larger community size corresponds to interaction among a larger sub-population and greater community mixing overall in the population. One of the authors demonstrated¹⁷ that different community sizes (different community mixing rates) result in very different epidemic growth rates. Since the number of infectious contacts per infectious individual is assumed constant regardless of the community size, the probability of interaction with a particular community individual decreases with community size. Also, the community size does not affect R0, the rate of spread in a naive population.

Results

Short and long-term dynamics of an epidemic in a network with household-community structure

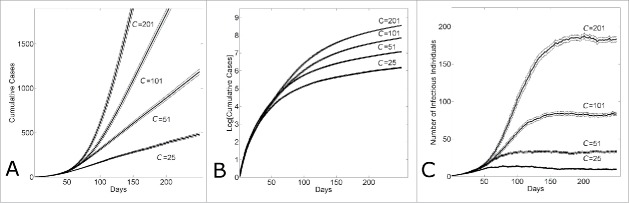
We have demonstrated¹⁷ that for a fixed household size H, varying the community mixing size C would result in different rates of epidemic growth. Figure 1A shows that the growth rate of cases increases systematically as the community size increases from C = 25 to C = 201. While the growth rate appears to transition from linear to exponential with the increase in community size, a log-normal plot of the number of cases per time shows that for all community sizes, the initial growth phase quickly transitions from exponential to sub-exponential as indicated by the strong curvature in the cumulative curve shown in Figure 1B. A leveling off of the number of infectious cases per day to a fixed constant value shows that for all community sizes, the long-term dynamic of epidemic growth is linear (Fig. 1C). Results shown in Figure 1 are for fixed reproductive numbers R_0H = 2, R_0C = 0.7; however, a sensitivity analysis confirmed that epidemic dynamics were qualitatively similar for all pairs of {R_0H, R_0C} that resulted in sustained epidemics

Figure 1.

Within several serial intervals, simulated epidemics transition from exponential to sub-exponential growth in cases. (A) Cumulative Ebola cases, (B) log-normal plot of cumulative Ebola cases and (C) number of infectious individuals versus simulation day for different community sizes (C = {25, 51, 101, 201}). Each curve shows the average and standard error of the results of 100 simulations seeded with one infectious individuals on the 1^st day.

The transition from exponential to sub-exponential growth can be understood by looking at the average saturation levels of infected individuals in affected communities. The average saturation of the communities of infected individuals steadily increases over time and reaches peak levels within 10—15 serial intervals (Fig. 2A). Saturation levels remain constant at these peak levels. A long-term dynamic of a constant number of infectious individuals over time (Fig. 1C) and a constant saturation level (Fig. 2A) suggests that the epidemic achieves a long-term endemic state. Indeed, the average reproductive number of infectious individuals decreases from 2.7 (this is the reproductive number of an individual in a naïve population) to approximately 1 in the same time frame of 10-15 serial intervals (Fig. 2B). Even though there is a large relative difference in the number of infectious individuals per day (Fig. 1C), the average community saturation of infectious individuals does not strongly depend on the community size (Fig. 2A).

Figure 2.

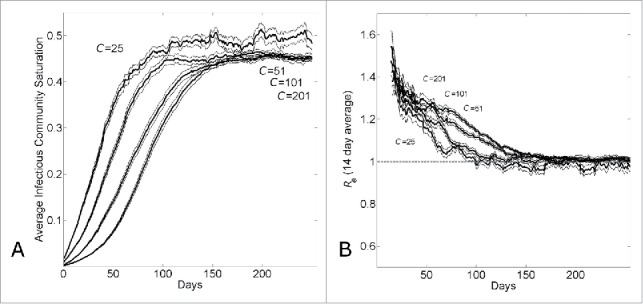
The transition from exponential to linear growth in a population with household-community structure is due to local saturation of communities. (A) Average saturation of the communities of infected individuals and (B) 14-day running effective reproductive number R_e14 vs. simulation day for different community sizes (C={25, 51, 101, 201}). Each curve shows the average and standard error of the results of 100 simulations seeded with one infectious individuals on the 1^st day.

The long-term dynamics characterized by long-term linear growth, constant community saturation levels of infected individuals and a constant reproductive number at R_e = 1 can be understood as an endemic state in which a wave of infections of fixed size and velocity passes through communities. This is demonstrated by visualizing the “spatial” spread of the epidemic through the network. Figure 3A shows the network location of infectious individuals (as a function of network distance from the first infectious individual) over time for a single epidemic simulation. A wave of infectious individuals moves through the network with an approximately uniform velocity. Since the ${\displaystyle H\times L}$ lattice geometry of our network permits 2 waves departing radially from the initialized infectious individual, the size of a wave (measured, for example, by the number of infectious individuals per day) as a function of community size is one half the total number of infectious individuals per day observed for that community size (Fig. 1C).

Figure 3.

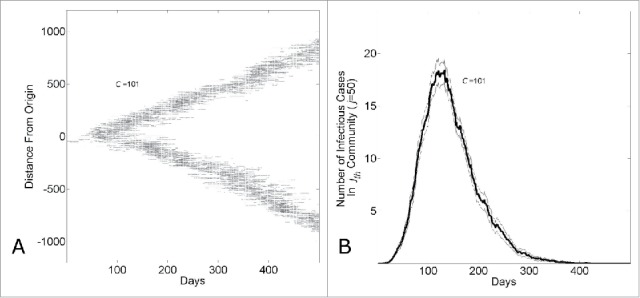
The endemic state of an epidemic moving through a network with household-community structure can be understood as a wave progressing at a fixed rate through the network. (A) The network location of all infected individuals versus simulation day in a single simulation (C = 101). The network location of an infectious individual is indicated as a darkened pixel at height ${\displaystyle \eta =j-j_0}$ (${\displaystyle \eta =j-j_0\text{ is }}$ the network distance of an infectious individual at node ${\displaystyle \left(i,j\right) }$ from the initial infected individual at node ${\displaystyle \left(i_0,j_0\right)}$). (B) The number of infectious cases in the j_th community vs. simulation day (j = 100, C = 101). The curve shows the average and standard error of the results of 100 simulations seeded with one infectious individuals on the 1^st day.

The epidemic wave can also be described from the perspective of a single community at a fixed location in the network. In a set of simulations with community size C = 101, we show the average number of infectious individuals in the j_th community where j = 50 over 100 simulations. As the epidemic passes through the community, the number of infectious cases increases, reaches a peak level and then decreases (Fig. 3B).

Distinguishing saturation versus control effects in an epidemic: epidemic control results in lower community saturation and epidemic waves that move faster through the network

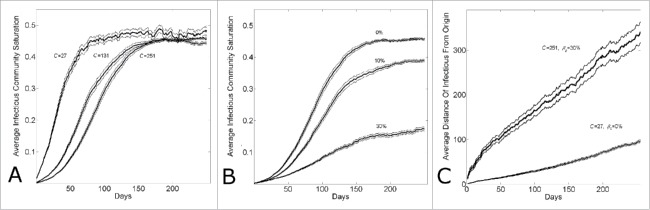
We have demonstrated¹⁷ that the different growth dynamics of Guinea, Sierra Leone and Liberia over the 6 months March 22^nd – August 22^nd were consistent with different community sizes. In Figure 4, we show that the different growth dynamics over this time period were consistent with both different community sizes (Panel A) or different levels of epidemic control (Panel B). Panel A shows that the growth dynamics are consistent with a community size that varies from C = 27 (reproducing Guinean dynamics) to C = 131 (reproducing Sierra Leonean dynamics) to C = 251 (reproducing Liberian dynamics), while Panel B shows that the growth dynamics are consistent with an epidemic control that varies from 30% (reproducing Guinean dynamics) to 10% (reproducing Sierra Leonean dynamics) to 0% (reproducing Liberian dynamics) while the community size is fixed at C = 251.

Figure 4.

Country variation in the 5 month time period (March22nd-August 22nd) of the epidemic is consistent with either different community structures or different levels of background control. (A) Cumulative number of Ebola cases (gray curves) for the community size C and temporal shift for the first day of the outbreak that provides the best fit of the reported WHO data (filled black circles) from March 22, 2014 to August 22, 2014 while all other parameters were held constant. For Guinea, Sierra Leone and Liberia, optimal fits were found for community sizes C = {27,131,251}, respectively while the temporal shift predicted that the epidemic in each country began (i.e., simulation “Day 1”) on Dec 29^th, 2013 for Guinea; April 15^th, 2014 for Sierra Leone and March 5^th, 2014 for Liberia. The (B) Cumulative number of Ebola cases (gray curves) for the level of epidemic control and temporal shift for the first day of the outbreak that provides the best fit of the reported WHO data (filled black circles) from March 22, 2014 to August 22, 2014 while all other parameters were held constant (C = 251). For Guinea, Sierra Leone and Liberia, optimal fits within the nearest 5% reduction were found for epidemic control levels ${\displaystyle {\beta }_0=\left\{0.3,0.1,0.0\right\}}$, respectively while the temporal shift predicted that the epidemic in each country began (i.e., simulation “Day 1”) on Dec 30^th, 2013 for Guinea; April 11^th, 2014 for Sierra Leone and March 5^th, 2014 for Liberia. Simulation results of cumulative Ebola cases results are shown as mean ± standard error of 100 simulations seeded with one infectious individual on the 1^st day.

Since the disparate country dynamics may be explained by 2 distinct hypotheses, varying community size or varying epidemic control, we sought to determine the extent to which these scenarios may in principle be distinguished. In particular, we focus on the competing hypothetical scenarios for Guinea and ask how it might be determined if the epidemic growth in Guinea is smaller than the epidemic growth in Liberia over the described time period due to (i) smaller community size (e.g.,, C = 27 for Guinea vs. C = 251 for Liberia, all other parameters equal) or (ii) greater epidemic control (e.g., β₀=0.3 for Guinea versus β₀=0.0 for Liberia, all other parameters equal).

Both sets of parameters for the 2 scenarios for Guinea result in steady state waves that propagate through the network. Observe that since either (i) smaller community size or (ii) greater epidemic control is consistent with the WHO Ebola case data March 22^nd – August 22^nd, the 2 hypotheses yield a comparable number of cases over the 180 days and thus have waves that are approximately the same size over the 180 days. Thus, the 2 scenarios would not be distinguished by the size of the waves over this time period. (The steady-state wave size is larger, however, for the case with greater epidemic control that best matched the WHO Ebola case data than the case with smaller community size best matching the data).

Although the size of the epidemic waves as measured by the infectious cases per day are comparable for the 2 scenarios for Guinea, the predicted community saturation levels do vary. For the first scenario in which a lower community size is used to fit the data, the equilibrium community saturation is approximately 49±1% whereas for the second scenario in which a higher epidemic control is used to fit the data, the equilibrium community saturation is approximately 17±1%. This is a consequence of the observation that the equilibrium community saturation is not very sensitive to the community size (Figs. 2A, 5A) but decreases significantly with epidemic control (Fig. 5B).

Figure 5.

Comparing simulation output parameters for epidemics with varying community size or levels of epidemic control. (A) Epidemics with different community sizes cannot be well distinguished by the equilibrium community saturation. The equilibrium community saturation of infectious individuals versus simulation day for different community sizes (C = {27,131,251}). (B) Community saturation decreases with increasing levels of epidemic control. The equilibrium community saturation of infectious individuals vs. simulation day for different levels of epidemic control (${\displaystyle {\beta }_0=\left\{0.3,0.1,0.0\right\}}$) for community size C = 251. (C) Epidemics with waves of comparable magnitude with lower levels of commuity saturation travel faster. The average distance of infectious individuals from the origin (location of the first infectious individual) verses simulation day for simulation parameters fitting Guinean case data with either large commuity size and high control (C = 251, β₀ = 0.3) or lower community size and lower control (C = 27, β₀ = 0.0). Curves shows the average and standard error of the results of 100 simulations seeded with one infectious individual on the 1^st day.

A consequence that the predicted sizes of the waves are the same, but that the predicted saturation levels differ, is that the speed of the waves through the network should vary. Indeed, the speed of the wave though the network in the case of a smaller community size (this being the one with higher equilibrium community saturation) is much slower than the speed of the wave through the network in the case of higher epidemic control (Fig. 5C)

Predictions regarding the ending of the epidemic

If the different growth dynamics of Guinea, Sierra Leone and Liberia are explained by different reproductive control, then Guinea has a much lower growth rate than Liberia due to a greater extent of epidemic control. At one extreme, for a community size of C = 251, Liberia would have 0% epidemic control with Guinea having 30% epidemic control. This is consistent with some analyses in the literature that the Liberian epidemic had been consistent with little or no epidemic control over this time period (21–23).

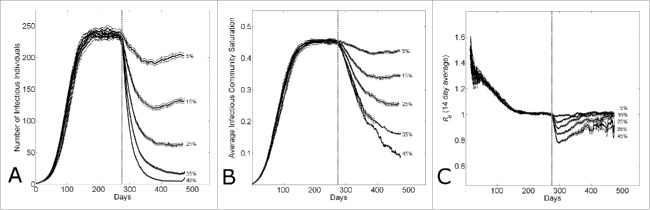
Whether the difference in Guinean, Sierra Leonean and Liberian dynamics is due to differences in community size or epidemic control, in either case further epidemic control is required to end the epidemic. In Figure 6, we investigate the effect of epidemic control applied to an established epidemic with a fixed delay. Figure 6A shows that the size of the epidemic wave decreases with the level of epidemic control applied at 6 months. Even with 45% epidemic control, there is a small epidemic wave. (While the epidemic control may be increased even further, resulting in still smaller waves, as the size of the waves decrease, with stochastic fluctuations there is a high probability of spontaneous extinction.) Figure 6B shows that community saturation levels decrease systematically with epidemic control, and the epidemic reproductive number vs. time in Figure 6C shows that the reproductive number initially dips (speculatively, since the community saturation is higher at that time than the new endemic steady state) and then begins to re-establish at R_e=1.

Figure 6.

The effect of epidemic control during an epidemic with household-community structure on the wave dynamics. The dotted vertical line indicates the simulation day (k=280) when epidemic control is applied. (A) The number of infectious individuals, (B) the average infectious community saturation and (C) the running 2-week reproductive number R_e14, per simulation day as the level of epidemic control on the k_th day is varied (${\displaystyle {\beta }_0=0.00-0.45)}$ for community size C=251. Curves shows the average and standard error of the results of 100 simulations seeded with one infectious individuals on the 1^st day.

If the different growth dynamics of Guinea, Sierra Leone and Liberia would be explained by different community mixing sizes, Figure 7A shows the relative effects of different amounts of control (applied at 6 months) on the steady-state number of infectious cases. While the number of infectious cases per day for small community sizes is already relatively small, and the number of infectious cases per day for large community sizes is relatively very large, this panel shows that small increases in epidemic control have a large effect for large community sizes. This observation is further illustrated in Figure 7B, where the effects of 35% epidemic control are compared for the different community sizes.

Figure 7.

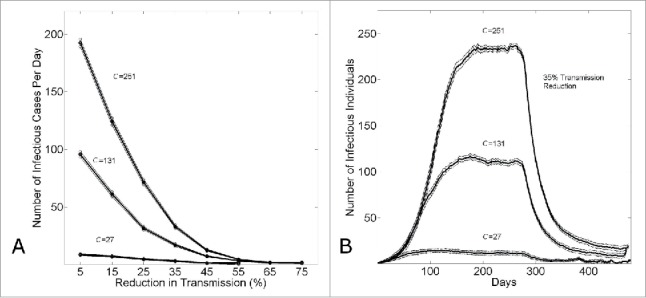
The effect of epidemic control to reduce the size of an epidemic wave. (A) The equilibrium number of infectious cases per day (measured on day k=480) versus the level of epidemic control ${\displaystyle ({\beta }_0=0.00-0.45)}$. (B) The number of infectious cases per day vs. the simulation day as the community size is varied (C = {27,131,251}) for a fixed level of epidemic control ${\displaystyle ({\beta }_0=0.35)}$. For both panels, in all simulations, epidemic control is applied on the the k_th day (k=280). Connected points in (A) and curves in (B) show the average and standard error of the results of 100 simulations seeded with one infectious individual on the 1^st day.

Discussion

In this paper we have employed a relatively simple stochastic individual-level transmission model that incorporates transmission within households and between communities of different sizes in order to capture the effects of different levels of population mixing.¹⁷ Our model is able to successfully capture the qualitative patterns of epidemic growth observed in Guinea, Liberia and Sierra Leone. Specifically, the model yields brief exponential growth during the first 2-3 generations of infections followed by sub-exponential epidemic growth during several disease generations. This is consistent with the local epidemic growth patterns observed for each of the EVD epidemics in the most affected countries in West Africa.⁶ The sub-exponential growth patterns provided by our model in the context of the Ebola epidemics in West Africa (even in the absence of control interventions or imposed behavior changes) contrasts with the exponential growth pattern typically derived from transmission models that assume random mixing of the population.²⁴

In the absence of control interventions or behavior changes, our models calibrated to the early growth patterns of EVD in the 3 most affected countries in West Africa yield an endemic state of disease reflecting a spatial traveling wave of new infections that moves through the host population over time with a reproduction number that is asymptotically 1.0. A reproductive number of approximately 1 indicates a stationary wave; that is neither shrinking nor growing, since each infected individual on average infects approximately one additional individual, and is analogous to the traveling waves of disease that can be derived from deterministic reaction diffusion models.)^25,26 The 14^th century Black Death is the flagship example of a spatially disseminating wave of disease.²⁷ Spatial-temporal profiles consistent with “traveling waves” of infectious disease have also been identified for dengue epidemics in Thailand.²⁸ and measles epidemics in the UK.²⁹

While the reproduction number for the ongoing Ebola epidemic in West Africa has been estimated on average around 2.0 during the early epidemic growth phase,^4,21-23,30 consistent with estimates from historical Ebola epidemics,³¹ the reproduction number quickly declines after a few generations of infections perhaps reflecting disease transmission in a confined/isolated setting, control interventions, or population behavior changes. It is worth noting that the ongoing epidemic in West Africa appears to have leveled off in some areas of Guinea and Sierra Leone, reaching an approximate effective reproduction number R_e of about 1.0 in some areas.³² Our model provides the additional perspective that an observed reproduction number R_e ≈ 1.0 is indicative of an endemic wave of infection traveling through the population

In this context, ‘endemic’ means that the infectious wave is in a steady equilibrium with a fixed size and speed. Our results indicate that the size and speed of the wave depends on the network properties of the population (e.g., community size) while the speed of the wave though a community, and net effect on the community, depends on the transmission characteristics of the disease (the reproductive numbers, in our case R_0H and R_0C, possibly modulated by control measures). In particular, the size of the wave (case incidence per day) increases starkly with community size and the fraction of the community affected increases with R₀. These results are consistent with those of,³³ whose spatial model of pathogen spread also resulted in a circular wave of spread from the pathogen source. They found for this cellular automata model with no household-community structure, the contact rate per susceptible also saturated and the resulting uniform level of saturation in the wake of the wave depended on the reproductive number as (1-1/R₀).

In principle, these results would apply to the progression of a disease in any network in which otherwise exponential growth must slow due to spread at a finite rate through the network. In sub-networks with low motility, such as a set of individuals within a school or employed at a hospital, regardless of the disease transmission dynamics, observe that an exponential phase must always be followed by extinction or a sub-exponential phase due to saturation effects as exponential growth depletes susceptibles within a small number of generations. The role of long-range infectious links are to “seed” the epidemic in more distant locations of the network that supply a new source of susceptibles. A question of interest for a network model of a given topology is the threshold fraction of long-range links for which the epidemic can be expected to grow exponentially rather than linearly.^34-37

Our model provides important insights on the level of control that would be required to contain Ebola epidemics. Specifically, findings suggest that a similar level of control effort would be required to bring the reproduction number below 1.0 in the 3 most affected countries if the transmission dynamics in each of the 3 countries are driven by different community sizes. This is somewhat surprising since the disease incidence (i.e., the number of infectious cases per day, or the size of the wave) increases starkly with the community size and implies that the size of an epidemic may not predict how difficult it is to control that epidemic. The fact that Liberia has been able to rid itself of the virus suggests that this population has been able to effectively mitigate transmission. In contrast, local reports indicate that the Guinean population has exhibited higher levels of resistance to education campaigns on how to avoid contracting and disseminating the virus,³⁸ which may explain the difficulties in halting transmission in this country where disease incidence has followed a relatively steady incidence pattern.

By comparing the predictions of decreasing the community size versus increasing of epidemic control we sought to determine the extent to which these competing explanations for a reduced epidemic growth rate can be distinguished. We found that for a fixed growth rate (for example, a growth rate matching observed case data), a greater level of epidemic control with correspondingly larger community size predicts lower community saturation than a lower level of epidemic control and corresponding smaller community size. Our model predictions would provide immediate interpretation if community seroprevalence rates of Ebola antibodies could be compared in areas of Guinea, Sierra Leone and Liberia for districts with different epidemic growth rates. In principle, if these rates were comparable among communities, then our model results predict that the difference in the district growth rates is due to differences in their network properties. On the other hand, if districts with lower epidemic growth rates have lower seroprevalence rates, this would suggest greater epidemic control in these areas. Since community size and epidemic control play a role together in epidemic dynamics, trends in seroprevalence rates may be able to discern the relative role of epidemic control over the course of the epidemic.

Our model is “spatially implicit,”³⁹ in that the defined distance between households corresponds to a distance within the network, and a decreased probability of contact, that only loosely corresponds, if at all, with spatial distance. For example, in West African countries, network distances may be shorter between villages and cities than between villages themselves, though of course this may not reflect geographic distances. Connectivity dependencies among villages were studied⁴⁰ and found, unsurprisingly, to be complex. Seven chiefdoms bordering the Gola forest in Sierra Leone were well connected to the city of Kenema, but there were also important lateral dependencies between villages. In our simulations, the community size varies over an order of magnitude from 125 to 1255. The community size is the subset of individuals that an infectious individual has an approximately equiprobable chance of interaction, even if that probability is very small in large communities. Heuristically, it may be thought of as the number of people drawn by the market where the infected individual shops or the number of children and teachers attending the same school. Small villages may represent natural upper bounds for community sizes. In a large city in contrast, certainly a thousand people might be expected to attend the same market or have children that attend the same school. A large village or city may be stratified with several partially overlapping communities (e.g., corresponding to overlapping school or market sub-networks, and different ethnic and socioeconomic groups). The extent of overlap from one community to the next would be expected to vary in a non-regular way. Our network model necessarily represents an extreme simplification and the ‘best-fit’ community size in simulations would represent a phenomenological weighted average of a distribution of community sizes in actual populations. Another limitation of our model is that it is relatively low-dimensional. Once transmission is established, the wave of infection may travel in only 2 directions within our simplified network. In complex real-world models, there are in principle no such limits in the dimensionality of the network. The low network-connectivity of our lattice is presumably a better description of more small or rural rather than urban communities, for which there would be more overlap expected among communities. For example, in a small, rural community, it would be more likely that the children of parents that work together also attend the same school. Simulating long-range links as the seeding of the epidemic to new communities, as done in Kiskowski et al 2014, increases the complexity of the network.

It is not expected that community size and epidemic control are constant or even that they vary monotonically over time. The 2014-2015 Ebola virus epidemic can be thought of as a superposition of asynchronous smaller outbreaks each with potentially different distributions of community sizes and levels of control. In Kiskowski, a systematic fitting algorithm was able to identify at least 2 distinct waves in Guinea over the 8 months March 22—October 15th. The first wave had a relatively low growth rate, for example consistent with a community size of only 45 individuals, but a second wave establishing in August had a much faster growth rate, consistent with a community size of 255 individuals. Similarly, Towers et al observed an increase in the effective reproductive number of the epidemic at this time when the outbreak in Guinea spread to Conakry. There is still much that can be learned by characterizing these individual district level outbreaks.

Our results underscore the importance of incorporating appropriate spatial structures into models of infectious disease transmission. Such considerations may be more important for infectious diseases that are transmitted via close contact such as Ebola and HIV.⁴¹ Such population structures used in models could be designed based on contact tracing data^42-44 or epidemic data of growth patterns in areas where interventions or population behavior changes are not suspected to have played a significant role such as the southern forested are of Guinea where the ongoing Ebola epidemic is suspected to have started back in December 2013.¹

Capturing the appropriate spatial structure in models of disease transmission is particularly important for epidemic forecasting because model-based predictions are highly sensitive to assumptions of contact structure with transmission models that assume homogeneous mixing^4,45 predicting the largest epidemic sizes in the absence of control interventions or behavior changes compared to population structured models (e.g., age structure, household-community structure).^{10,17,34,46,47} However, more work is needed to elucidate the dominant factors that have affected the epidemic trajectories in Guinea, Liberia and Sierra Lone.¹⁶ In addition to contact structure, other factors that may have played a significant role include the effects of specific control interventions such as social distancing, increased hygiene, increased safe burial rate, and improvement in health care infrastructure (e.g., increased bed capacity).

Methodology: Modeling Transmission Dynamics of Ebola Virus Disease (Evd)

SEIR network model for distinct transmission within households vs. communities

We use the 3-scale network based SEIR model described in detail¹⁷ to study the early transmission dynamics of EVD in Guinea, Sierra and Liberia. In this model, a hierarchical network is used to describe the household and community contacts of individuals within a population. At the smallest scale, individuals are organized within households of size H. At the second scale, each household is centered within a community of size C households. Communities are overlapping subsets of a much larger population of ${\displaystyle P=H\cdot L }$ individuals, where H is the number of individuals in a household and L is the total number of households.

This hierarchical structure is modeled on an ${\displaystyle H\times L }$ lattice so that each column of the lattice corresponds to a single household; the i_th column corresponds to the i_th household. Two households h_i and h_j on the lattice have a network distance η = |i-j| and they are in the same community if |i-j| < R_C, where R_C is the community radius (C = 2R_C + 1). The i_th community is the community centered at the i_th household containing households.

$${\displaystyle \left\{h_{i-R_C},h_{i-R_c+1},\dots ,h_i,h_{i+1},\dots h_{i+R_c}\right\}}$$

Without modification, this model can be viewed as a lattice-based reaction diffusion model with 2 interaction neighborhoods defined for each node (i, j): one smaller interaction neighborhood is the household (a ${\displaystyle H\times 1}$ vertical array corresponding to the entire column) and larger interaction neighborhood is the community (a ${\displaystyle H\times C}$ interaction neighborhood centered at the j_th lattice column) (Fig. 8).

Figure 8.

Two overlapping interaction neighborhoods for an arbitrary node (i,j) when the household size is H = 5 and the community radius R_c = 6. The depicted ${\displaystyle 5\times 26 }$ lattice corresponds to an ${\displaystyle H\times L }$ population of 130 individuals distributed among 26 households (5 individuals per household). An arbitrary node is indicated with a ‘∗’. The household interaction neighborhood for this node is the j_th column of the lattice indicated in dark gray. The community interaction neighborhood for this node is the ${\displaystyle 6\times 11 }$ sub-array of the lattice indicated with 2 shades of gray.

SEIR dynamics

Individuals on the lattice are assigned one of 4 states: S (susceptible), E (exposed), I (infectious) and R (refractory). States are updated at each time step with the following transition probabilities:

$${\displaystyle \begin{array}{c}p\left(S\to E\right)=probability that asusceptible will become exposed\\ =\left(1-probability of no exposures from any infected contacts\right)\\ =\left(1-{\left(1-t_H\right)}^{i_H}.{\left(1-t_C\right)}^{i_C}\right).\end{array}}$$

where ${\displaystyle t_H}$ and ${\displaystyle t_C}$ are the transmission probabilities within a household and within the community, respectively, and ${\displaystyle i_H}$ and ${\displaystyle i_C}$ are the number of infectious household and community contacts in the network, respectively

$$\begin{array}{l}p\left(E\to I\right)=probability that an exposed individual\\ becomes infectious=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\gamma $}\right.,\end{array}$$

where ${\displaystyle \gamma }$ is the average incubation period.

$$\begin{array}{l}p\left(I\to R\right)=probability thataninfectiousindividual\\ willbecomerefractory=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.,\end{array}$$

where ${\displaystyle \lambda }$ is the average infectious period.

Transmission in the context of no epidemic control

A susceptible individual becomes infected (exposed) with the probabilities t_H and t_C per household or community infected contact per day, respectively. Transmission can also be described in terms of the probability that a susceptible will become exposed when they are within one of the 2 neighborhoods of an infected individual. The probability that each susceptible individual in the household neighborhood will be exposed per day is given by the transmission probability t_H, and additionally the probability that each susceptible individual in the community neighborhood will be exposed per day is given by the transmission probability t_C.

In our model, the reproductive numbers ${\displaystyle R_{0H} }$ and ${\displaystyle R_{0C}}$ can be calculated as the expected number of susceptible individuals exposed by a single infectious individual that is placed on a lattice of susceptibles. Given that the expected lifetime of the infectious individual in days is ${\displaystyle \lambda }$, and that the size of the household and community neighborhoods are ${\displaystyle H\times 1 }$ and ${\displaystyle H\times C , }$ respectively, the expected number of exposures caused by the initial infected individual are:

$$R_{0H}\approx \lambda t_H\left(H-1\right),R_{0c}\approx \lambda t_C(C\cdot H-1)$$

And thus to define given values of ${\displaystyle R_{0H}}$ and ${\displaystyle R_{0C}}$, we define the transmission probabilities:

$${\displaystyle t_H:=\frac{R_{0H}}{\lambda \left(H-1\right)},t_C:=\frac{R_{0C}}{\lambda \left(C\cdot H-1\right)}}$$

Transmission in the Context of Global and Local Interventions

We define 2 types of epidemic control; external (global) and internal (local). For both types, epidemic control is modeled as a percent reduction in transmission probability. For externally applied epidemic control, the transmission reduction is a reduction in the transmission rate globally applied to the entire network. For internally applied epidemic control, the transmission reduction is calculated locally depending on the state of the interaction neighborhoods of each infectious individual.

For globally applied control, the household and community transmission probabilities are reduced by a factor ${\displaystyle {\beta }_0}$ ${\displaystyle \left(0\le {\beta }_0\le 1\right) }$ per timestep.

$${\displaystyle \begin{array}{l}p\left(S\to E\right)=probability thatasusceptiblewillbecomeexposed\\ =\left(1-probabilityofnoexposuresfromanyinfectedcontacts\right)\\ =\left(1-{\left(1-t_H\left(1-{\beta }_0\right)\right)}^{i_H}\cdot {\left(1-t_C\left(1-{\beta }_0\right)\right)}^{i_C}\right).\end{array}}$$

For locally applied epidemic control, the household and community transmission probabilities are maximally reduced by a factor ${\displaystyle {\beta }_0}$${\displaystyle \left(0\le {\beta }_0\le 1\right)}$ per timestep but the actual reduction ${\displaystyle \beta }$ is calculated for each infectious individual located at the node (i,j) using the Hill function increasing monotonically from 0 to ${\displaystyle {\beta }_0}$ with ${\displaystyle q_j}$:

$$\beta ={\beta }_0{\left(1+{\left(\frac{q_{1/2}}{q_j}\right)}^p\right)}^{-1}$$

Where ${\displaystyle q_j}$ is the total number of infectious or refractory individuals in the j_th community. i.e. ${\displaystyle q_j}$ would be the cumulative number of infectious (sympotomatic) individuals that a susceptible community individual has observed. The parameter ${\displaystyle q_{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$ determines the value of ${\displaystyle q_j}$ that results in ${\displaystyle \beta =0.5{\beta }_0}$.

Parameter values and initial conditions for simulations

Initially, all individuals (lattice nodes/network vertices) are susceptible (state S) except for one exposed individual (state I). In simulations, time steps are discrete and correspond to exactly one day. The average and standard error of simulation output parameters (described below) are computed for 100 simulations.

A simulation ends spontaneously when there are no exposed or infectious individuals remaining in the network, so output parameters versus time are calculated only for simulations that have not yet ended. The standard error is calculated as $\text{SE}=\frac{\sigma }{\sqrt{n}},$ where σ is the standard deviation and the number of simulation n is a non-increasing function of the simulation day (${\displaystyle n\le 100).}$ A description of the values (or ranges of values) for simulation parameters is provided in Table 1. In Figure. 4, Ebola case data is fit by varying either community size (Panel A) or the level of epidemic control (Panel B) and the calendar date for which the outbreak is initialized. The best pair of parameters is identified as the pair that minimized the R-square coefficient of determination comparing the simulated and Ebola case data.

Table 1.

Parameter values used in simulations. This table provides a description of each parameter used in simulations, the value or range that is used, and the reference source for the value that is used if applicable

Parameter	Description	Parameter Value (Range)	Source
${\displaystyle \gamma }$	Average incubation period	${\displaystyle 5.3}$ days	(48–51)
${\displaystyle \lambda }$	Average infectious period	5.6 days	(48–51)
H	Household size	5	(52)
C	Community size	25—251
${\displaystyle R_{0H}}$	Household reproductive number	2.0	(17) Appendix 3, Fig 1
${\displaystyle R_{0C}}$	Community reproductive number	0.7	(17) Appendix 3, Fig 1
${\displaystyle {\beta }_0}$	Transmission reduction factor	0—0.75	—
${\displaystyle q_{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$	Infected or susceptible quorum for half-response in Hill equation	0—250	—
p	Hill equation parameter	3	—

Output Parameters of Simulations

Average infectious cases, epidemic reproductive number and community saturation

Simulations track the states of individuals in the network as a function of the k_th day. An individual is defined as an Ebola case when they become infectious (assuming that an individual is not recognized as a case until they are infectious and that there is no delay in identifying infectious individuals). We calculate the average cumulative number of Ebola cases by the k_th day or the average number of cases per day.

The cumulative effective reproductive number ${\displaystyle R_e\left(k\right)}$ is calculated as a function of the k_th simulation day as the average number of infections resulting from all individuals that are refractory by day k:

$${\displaystyle R_e\left(k\right)=\frac{Total\#IndividualsExposedbyIndividualsRefractorybyDayk}{Total\#IndividualsRefractorybyDayk}}$$

Note that this calculation is equivalent to:

$${\displaystyle R_e\left(k\right)=\frac{\begin{array}{l} \\ Total \#Individuals Ever Exposed-\left(\begin{array}{ll}IndividualsExposedbyIndividuals& NotYetRefractory\end{array}\right) \end{array}}{Total\#IndividualsEverExposed-\left(IndividualsNotYetRefractory\right)}}$$

so that this ratio approaches 1 as a larger and larger fraction of ever-exposed individuals become refractory (as the serial interval becomes a smaller and smaller fraction of the days k). We therefore define a 2-week running effective reproductive number R_e14. The two-week running effective reproductive number is calculated as a function of the k_th simulation day as the average number of infections resultingrom all individuals that have become refractory in the last 14 days:

$${\displaystyle R_{e14}\left(k\right)=\frac{\begin{array}{l}Total\#IndividualsExposedbyIndividualsRefractory\\ BetweenDay\left(k-13\right)andDay\left(k\right)\end{array}}{Total\#ofIndividualsRefractoryBetweenDay\left(k-13\right)andDay\left(k\right)}}$$

The “community saturation” S of a single infectious individual located at the node ${\displaystyle \left(i,j\right)}$ is defined on the k_th day as the fraction of persons in their community that are no longer susceptible:

$${\displaystyle S\left(i,j,k\right)=\frac{\left(C\cdot H-1\right)-\left(\begin{array}{l}number of susceptible individuals in\\ jth community on the kth day\end{array}\right)}{C\cdot H-1}}$$

T average community saturation of a simulation on the k_th day is the community saturation averaged for all the individuals that are infected that day. Finally, the average community saturation averaged over N simulations on a given day is the average community saturation of all infected individuals among the N simulations – i.e., the final simulation average is weighted by the number of individuals that were infectious in each simulation. Averages on the 1^st day are always calculated for 100 simulations. However, simulations die out spontaneously and also as epidemics die out there may be very few infectious cases on a given day. A gap in the plot of average saturation vs. time may occur on the k_th day when there were no infectious cases on the k_th day. (This does not necessarily mean the epidemic is over since there may be incubating individuals.)

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.

Funding

GC acknowledges support from NSF grant #1414374 as part of the joint NSF-NIH-USDA Ecology and Evolution of Infectious Diseases program, United Kingdom Biotechnology and Biological Sciences Research Council grant BB/M008894/1, grant #1R01GM100471-01 from the National Institute of General Medical Sciences (NIGMS) at the National Institutes of Health, NSF grant 1318788 III: Small: Data Management for Real-Time Data Driven Epidemic simulation and RAPID NFS Grants#1518939 and NSF# 1518529, and the Division of International Epidemiology and Population Studies, The Fogarty International Center, NIH.