On the construction of general cubature formula by flat extensions

Abstract

We describe a new method to compute general cubature formulae. The problem is initially transformed into the computation of truncated Hankel operators with flat extensions. We then analyze the algebraic properties associated to flat extensions and show how to recover the cubature points and weights from the truncated Hankel operator. We next present an algorithm to test the flat extension property and to additionally compute the decomposition. To generate cubature formulae with a minimal number of points, we propose a new relaxation hierarchy of convex optimization problems minimizing the nuclear norm of the Hankel operators. For a suitably high order of convex relaxation, the minimizer of the optimization problem corresponds to a cubature formula. Furthermore cubature formulae with a minimal number of points are associated to faces of the convex sets. We illustrate our method on some examples, and for each we obtain a new minimal cubature formula.

1. Cubature formula

1.1. Statement of the problem

Consider the integral for a continuous function f,

$$I[f]=\underset{\mathrm{\Omega }}{\int }w(\mathbf{x})f(\mathbf{x})d\mathbf{x}$$

where Ω ⊂ ℝⁿ and w is a positive function on Ω.

We are looking for a cubature formula which has the form

$$\langle \sigma \mid f\rangle =\sum _{j=1}^r{w}_{j}f({\zeta }_j)$$ (1)

where the points ζ_j ∈ ℂⁿ and the weights w_j ∈ ℝ are independent of the function f. They are chosen so that

$$\langle \sigma \mid f\rangle =I[f],\forall f\in V,$$

where V is a finite dimensional vector space of functions. Usually, the vector space V is the vector space of polynomials of degree ≤ d, because a well-behaved function f can be approximated by a polynomial, so that Q[f] approximates the integral I[f].

Given a cubature formula (1) for I, its algebraic degree is the largest degree d for which I[f] = 〈σ|f〉 for all f of degree ≤ d.

1.2. Related works

Prior approaches to the solution of cubature problem can be grouped into roughly two classes. One, where the goal is to estimate the fewest weighted, aka cubature points possible for satisfying a prescribed cubature rule of fixed degree [9,24,26,29,30,33]. The other class focusses on the determination and construction of cubature rules which would yield the fewest cubature points possible [7,34,38–41,44,45]. In [34], for example, Radon introduced a fundamental technique for constructing minimal cubature rules where the cubature points are common zeros of multivariate orthogonal polynomials. This fundamental technique has since been extended by many, including e.g. [33,41,45] where notably, the paper [45] uses multivariate ideal theory, while [33] uses operator dilation theory. In this paper, we propose another approach to the second class of cubature solutions, namely, constructing a suitable finite dimensional Hankel matrix and extracting the cubature points using sub-operators of the Hankel matrix [18]. This approach is related to [21–23], which in turn are based on the methods of multivariate truncated moment matrices, their positivity and extension properties [11–13].

Applications of such algorithms determining cubature rules and cubature points over general domains occur in isogeometric modeling and finite element analysis using generalized Barycentric finite elements [17,1,35,36]. Additional applications abound in numerical integration for low dimensional (6–100 dimensions) convolution integrals that appear naturally in computational molecular biology [3,2], as well in truly high dimensional (tens of thousands of dimensions) integrals that occur in finance [32,8].

1.3. Reformulation

Let R = ℝ[x] be the ring of polynomials in the variables x = (x₁,…, x_n) with coefficients in ℝ. Let R_d be the set of polynomials of degree ≤ d. The set of linear forms on R, that is, the set of linear maps from R to ℝ is denoted by R^*. The value of a linear form Λ ∈ R^* on a polynomial p ∈ R is denoted by 〈Λ|p〉. The set R^* can be identified with the ring of formal power series in new variables y = (y₁,…, y_n):

$$\begin{array}{ll}\hfill R^{\ast }& \to ℝ[[\mathbf{y}]]\hfill \\ \hfill \mathrm{\Lambda }& \mapsto \mathrm{\Lambda }(\mathbf{y})=\sum _{\alpha \in {\mathbb{N}}^n}\langle \mathrm{\Lambda }\mid {\mathbf{x}}^{\alpha }\rangle {\mathbf{y}}^{\alpha }.\hfill \end{array}$$

The coefficients 〈Λ|x^α〉 of these series are called the moments of Λ. The evaluation at a point ζ ∈ ℝⁿ is an element of R, denoted by e_ζ, and defined by e_ζ : f ∈ R ↦ f(ζ) ∈ ℝ. For any p ∈ R and any Λ ∈ R^*, let p ★ Λ : q ∈ R ↦ Λ(pq).

Cubature problem

Let V ⊂ R be a vector space of polynomials and consider the linear form Ī ∈ V^* defined by

$$\begin{array}{ll}\hfill \overline{I}:V& \to ℝ\hfill \\ \hfill \mathbf{v}& \mapsto I[\mathbf{v}]\hfill \end{array}$$

Computing a cubature formula for I on V then consists in finding a linear form

$$\sigma =\sum _{i=1}^r{w}_i{\mathbf{e}}_{{\zeta }_i}:f\mapsto \sum _{j=1}^r{w}_{j}f({\zeta }_j),$$

which coincides on V with Ī. In other words, given the linear form Ī on R_d, we wish to find a linear form $\sigma ={\sum }_{i=1}^r{w}_i{\mathbf{e}}_{{\zeta }_i}$ which extends Ī.

2. Cubature formulae and Hankel operators

To find such a linear form σ ∈ R^*, we exploit the properties of its associated bilinear form H_σ : (p, q) ∈ R × R → 〈σ|pq〉, or equivalently, the associated Hankel operator:

$$\begin{array}{ll}\hfill H_{\sigma }:R& \to R^{\ast }\hfill \\ \hfill p& \mapsto p★\sigma \hfill \end{array}$$

The kernel of H_σ is kerH_σ = {p ∈ R | ∀q ∈ R, 〈σ|pq〉 = 0}. It is an ideal of R. Let 𝒜_σ = R/ker H_σ be the associated quotient ring.

The matrix of the bilinear form or the Hankel operator H_σ associated to σ in the monomial basis, and its dual are (〈Λ|x^α+β〉)_{α,β∈ℕⁿ}. If we restrict them to a space V spanned by the monomial basis (x^α)_α∈A for some finite set A ⊂ ℕⁿ, we obtain a finite dimensional matrix $[H_{\sigma }^{A,A}]={(\langle \mathrm{\Lambda }\mid {\mathbf{x}}^{\alpha +\beta }\rangle )}_{\alpha ,\beta \in A}$, and which is a Hankel matrix. More generally, for any vector spaces V, V′ ⊂ R, we define the truncated bilinear form and Hankel operators: $H_{\sigma }^{V,V^{\prime }}:(v,v^{\prime })\in V\times V^{\prime }\mapsto \langle \sigma \mid pq\rangle \in ℝ$ and $H_{\sigma }^{V,V^{\prime }}:v\in V\mapsto v★\sigma \in {V^{\prime }}^{\ast }$. If V (resp. V′) is spanned by a monomial set x^A for A ⊂ ℕⁿ (resp. x^B for B ⊂ ℕⁿ), the truncated bilinear form and truncated Hankel operator are also denoted by $H_{\sigma }^{A,B}$. The associated Hankel matrix in the monomial basis is then $[H_{\sigma }^{A,B}]={(\langle \mathrm{\Lambda }\mid {\mathbf{x}}^{\alpha +\beta }\rangle )}_{\alpha \in A,\beta \in B}$.

The main property that we will use to characterize a cubature formula is the following (see [22,20]):

Proposition 2.1

A linear form σ ∈ R^* can be decomposed as $\sigma ={\sum }_{i=1}^r{w}_i{\mathbf{e}}_{{\zeta }_i}$ with w_i ∈ ℂ \ {0}, ζ_i ∈ ℂⁿ iff

• H_σ : p ↦ p ★ σ is of rank r,

• ker H_σ is the ideal of polynomials vanishing at the points {ζ₁,…, ζ_r}.

This shows that in order to find the points ζ_i of a cubature formula, it is sufficient to compute the polynomials p ∈ R such that ∀q ∈ R, 〈σ|pq〉 = 0, and to determine their common zeroes. In Section 4 we describe a direct way to recover the points ζ_i, and the weights ω_i from suboperators of H_σ.

In the case of cubature formulae with real points and positive weights, we already have the following stronger result (see [22,20]):

Proposition 2.2

Let σ ∈ R^*.

$$\sigma =\sum _{i=1}^r{w}_i{\mathbf{e}}_{{\zeta }_i}$$

with w_i > 0, ζ_i ∈ ℝⁿ iff rankH_σ = r and H_σ ≽ 0.

A linear form $\sigma ={\sum }_{i=1}^r{w}_i{\mathbf{e}}_{{\zeta }_i}$ with w_i > 0, ζ_i ∈ ℝⁿ is called a r-atomic measure since it coincides with the weighted sum of the r Dirac measures at the points ζ_i.

Therefore, the problem of constructing a cubature formula σ for I exact on V ⊂ R can be reformulated as follows: Construct a linear form σ ∈ R^* such that

• rank H_σ = r < ∞ and H_σ ≽ 0.

• v ∈ V, I[v] = 〈σ|v〉.

The rank r of H_σ is given by the number of points of the cubature formula, which is expected to be small or even minimal.

The following result states that a cubature formula with dim(V) points, always exists.

Theorem 2.3. (See [42,4].)

If a sequence (σ_α)_{α∈ℕⁿ,|α|≤t} is the truncated moment sequence of a measure μ (i.e. σ_α = ∫ x^αdμ for |α| ≤ t), then it can also be represented by an r-atomic measure: for |α| ≤ t, ${\sigma }_{\alpha }={\sum }_{i=1}^r{w}_i{\xi }_i^{\alpha }$ where r ≤ s_t, w_i > 0, ζ_i ∈ supp(μ).

This result can be generalized to any set of linearly independent polynomials v₁,…, v_r ∈ R (see the proof in [4] or Theorem 5.9 in [22]). We deduce that the cubature problem always has a solution with dim(V) or less points.

Definition 2.4

Let r_c(I) be the maximum rank of the bilinear form $H_I^{W,W^{\prime }}:(w,w^{\prime })\in W\times W^{\prime }\mapsto I[w{w}^{\prime }]$ where W, W′ ⊂ V are such that ∀w ∈ W, ∀w′ ∈ W′, ww′ ∈ V. It is called the Catalecticant rank of I.

Proposition 2.5

Any cubature formula for I exact on V involves at least r_c(I) points.

Proof

Suppose that σ is a cubature formula for I exact on V with r points. Let W, W′ ⊂ V be vector spaces such that ∀w ∈ W, ∀w′ ∈ W′, ww′ ∈ V. Since $H_I^{W,W^{\prime }}$ coincides with $H_{\sigma }^{W,W^{\prime }}$, which is the restriction of the bilinear form H_σ to W × W′, we deduce that $r=\text{rank}{H}_{\sigma }\ge \text{rank}{H}_{\sigma }^{W,W^{\prime }}=\text{rank}(H_I^{W,W^{\prime }})$. Thus r ≥ r_c(I).

Corollary 2.6

Let W ⊂ V such that ∀w, w′ ∈ W, ww′ ∈ V. Then any cubature formula of I exact on V involves at least dim(W) points.

Proof

As we have ∀p ∈ W, p² ∈ V so that I(p²) = 0 implies p = 0. Therefore the quadratic form $H_I^{W,W}:(p,q)\in W\times W\to I[pq]$ is positive definite of rank dim(W). By Proposition 2.5, a cubature formula of I exact on V involves at least r_c(I) ≥ dim(W) points.

In particular, if V = R_d any cubature formula of I exact on V involves at least $dim{R}_{\lfloor \frac{d}{2}\rfloor }=\left(\begin{array}{c}\lfloor \frac{d}{2}\rfloor +n\\ n\end{array}\right)$ points.

In [25], this lower bound is improved for cubature problems in two variables.

3. Flat extensions

In order to reduce the extension problem to a finite-dimensional problem, we consider hereafter only truncated Hankel operators. Given two subspaces W, W′ of R and a linear form σ defined on W ·W′ (i.e. σ ∈ 〈W ·W′〉^*), we define

$$\begin{array}{ll}\hfill H_{\sigma }^{W,W^{\prime }}:W\times W^{\prime }& \to ℝ\hfill \\ \hfill (w,w^{\prime })& \mapsto \langle \sigma \mid w{w}^{\prime }\rangle .\hfill \end{array}$$

If w (resp. w′) is a basis of W (resp. W′), then we will also denote $H_{\sigma }^{\mathbf{w},{\mathbf{w}}^{\prime }}:=H_{\sigma }^{W,W^{\prime }}$. The matrix of $H_{\sigma }^{\mathbf{w},{\mathbf{w}}^{\prime }}$ in the basis w = {w₁,…, w_s}, ${\mathbf{w}}^{\prime }=\{w_1^{\prime },\dots ,w_{s^{\prime }}^{\prime }\}$ is [〈σ|w_iw_j〉]_{1≤i≤s,1≤j≤s′}.

Definition 3.1

Let W ⊂ V, W′ ⊂ V′ be subvector spaces of R and σ ∈ 〈V · V′〉^*. We say that $H_{\sigma }^{V,V^{\prime }}$ is a flat extension of $H_{\sigma }^{W,W^{\prime }}$ if $\text{rank}{H}_{\sigma }^{V,V^{\prime }}=\text{rank}{H}_{\sigma }^{W,W^{\prime }}$.

A set B of monomials of R is connected to 1 if it contains 1 and if for any m ≠ 1 ∈ B, there exist 1 ≤ i ≤ n and m′ ∈ B such that m = x_im′.

As a quotient R/ker H_σ has always a monomial basis connected to 1, so in the first step we take for w, w′, monomial sets that are connected to 1.

For a set B of monomials in R, let us define B⁺ = B ∪ x₁B ∪ ··· ∪ x_n, B and ∂B = B⁺ \ B.

The next theorem gives a characterization of flat extensions for Hankel operators defined on monomial sets connected to 1. It is a generalized form of the Curto–Fialkow theorem [13].

Theorem 3.2. (See [23,6,5].)

Let B ⊂ C, B′ ⊂ C′ be sets of monomials connected to 1 such that |B| = |B′| = r and C · C′ contains B⁺ · B′⁺. If σ ∈ 〈C · C′〉^* is such that $H_{\sigma }^{B,B^{\prime }}=\text{rank}{H}_{\sigma }^{C,C^{\prime }}=r$, then $H_{\sigma }^{C,C^{\prime }}$ has a unique flat extension H_σ̃ for some σ̃ ∈ R^*. Moreover, we have $\text{ker}{H}_{\stackrel{\sim }{\sigma }}=(ker{H}_{\sigma }^{C,C^{\prime }})$ and R = 〈B〉 ⊕ker H_σ̃ = 〈B′〉 ⊕ker H_σ̃. In the case where B′ = B, if $H_{\sigma }^{B,B}\succcurlyeq 0$, then H_σ̃ ≽ 0.

Based on this theorem, in order to find a flat extension of $H_{\sigma }^{B,B^{\prime }}$, it suffices to construct an extension $H_{\sigma }^{B^{+},{B^{\prime }}^{+}}$ of the same rank r.

Corollary 3.3

Let V ⊂ R be a finite dimensional vector space. If there exists a set B of monomials connected to 1 such that V ⊂ 〈B⁺ · B⁺〉 and σ ∈ 〈B⁺ · B⁺〉^* such that ∀v ∈ V, 〈σ|v〉 = I[v] and $\text{rank}{H}_{\sigma }^{B,B}=\text{rank}{H}_{\sigma }^{B^{+},B^{+}}=\mid B\mid =r$, then there exist w_i > 0, ζ_i ∈ ℝⁿ, i = 1,…, r such that ∀v ∈ V,

$$I[v]=\sum _{i=1}^r{w}_{i}v({\xi }_i).$$

This characterization leads to equations which are at most of degree 2 in a set of variables related to unknown moments and relation coefficients as described by the following proposition:

Proposition 3.4

Let B and B′ be two sets of monomials of R of size r, connected to 1 and σ be a linear form on 〈B′ ⁺ · B⁺〉. Then, $H_{\sigma }^{B^{+},{B^{\prime }}^{+}}$ admits a flat extension H_σ̃ such that H_σ̃ is of rank r and B (resp. B′) a basis of R/ker H_σ̃ iff

$$[H_{\sigma }^{B^{+},{B^{\prime }}^{+}}]=\left(\begin{array}{cc}\mathbb{Q}& {\mathbb{M}}^{\prime }\\ {\mathbb{M}}^t& \mathbb{N}\end{array}\right),$$ (2)

with $\mathbb{Q}=[H_{\sigma }^{B,B^{\prime }}],{\mathbb{M}}^{\prime }=[H_{\sigma }^{B,\partial B^{\prime }}],{\mathbb{M}}^t=[H_{\sigma }^{\partial B,B^{\prime }}],\mathbb{N}=[H_{\sigma }^{\partial B,\partial B^{\prime }}]$ such that ℚ is invertible and

$$\mathbb{M}={\mathbb{Q}}^t\mathbb{P},{\mathbb{M}}^{\prime }=\mathbb{Q}{\mathbb{P}}^{\prime },\mathbb{N}={\mathbb{P}}^t\mathbb{Q}{\mathbb{P}}^{\prime },$$ (3)

for some matrices ℙ ∈ ℂ^B×∂B′, ℙ′ ∈ ℂ^B′×∂B.

Proof

If we have 𝕄 = ℚ^tℙ, 𝕄′ = ℚℙ′, ℕ = ℙ^tℚℙ′, then

$$[H_{\sigma }^{B^{+},{B^{\prime }}^{+}}]=\left(\begin{array}{cc}\mathbb{Q}& \mathbb{Q}{\mathbb{P}}^{\prime }\\ {\mathbb{P}}^t\mathbb{Q}& {\mathbb{P}}^t\mathbb{Q}{\mathbb{P}}^{\prime }\end{array}\right)$$

has clearly the same rank as $\mathbb{Q}=[H_{\sigma }^{B,B^{\prime }}]$. According to Theorem 3.2, $H_{\sigma }^{B^{+},{B^{\prime }}^{+}}$ admits a flat extension H_σ̃ with σ̃ ∈ R^* such that B and B′ are bases of 𝒜_σ̃ = R/ker H_σ̃.

Conversely, if H_σ̃ is a flat extension of $H_{\sigma }^{B^{+},{B^{\prime }}^{+}}$ with B and B′ bases of 𝒜_σ̃ = R/ker H_σ̃, then $[H_{\stackrel{\sim }{\sigma }}^{B,B^{\prime }}]=[H_{\sigma }^{B,B^{\prime }}]=\mathbb{Q}$ is invertible and of size r = |B| = |B′|. As H_σσ is of rank r, $H_{\sigma }^{B^{+},{B^{\prime }}^{+}}$ is also of rank r. Thus, there exists ℙ′ ∈ ℂ^B′×∂B (ℙ′ = ℚ⁻¹𝕄′) such that 𝕄′ = ℚℙ′. Similarly, there exists ℙ ∈ ℂ^B×∂B′ such that 𝕄 = ℚ^tℙ. Thus, the kernel of $[H_{\sigma }^{B^{+},{B^{\prime }}^{+}}](\text{resp.}[H_{\sigma }^{{B^{\prime }}^{+},B^{+}}]={[H_{\sigma }^{B^{+},{B^{\prime }}^{+}}]}^t)$ is the image of $\left(\begin{array}{c}-{\mathbb{P}}^{\prime }\\ \mathbb{I}\end{array}\right)(\text{resp.}\left(\begin{array}{c}-\mathbb{P}\\ \mathbb{I}\end{array}\right))$. We deduce that ℕ = 𝕄^tℙ′ = ℙ^tℚℙ′.

Remark 3.5

A basis of the kernel of $H_{\sigma }^{B^{+},{B^{\prime }}^{+}}$ is given by the columns of $\left(\begin{array}{c}-{\mathbb{P}}^{\prime }\\ \mathbb{I}\end{array}\right)$, which represent polynomials of the form

$$p_{\alpha }={\mathbf{x}}^{\alpha }-\sum _{\beta \in B}{p}_{\alpha ,\beta }{\mathbf{x}}^{\beta }$$

for α ∈ ∂B. These polynomials are border relations which project the monomials x^α of ∂B on the vector space spanned by the monomials B, modulo ker $H_{\sigma }^{B^{+},{B^{\prime }}^{+}}$. It is proved in [6] that they form a border basis of the ideal ker H_σ̃ when $H_{\sigma }^{B^{+},{B^{\prime }}^{+}}$ is a flat extension and $H_{\sigma }^{B,B^{\prime }}$ is invertible.

Remark 3.6

Let A ⊂ ℕⁿ be a set of monomials such that 〈σ|x^α〉 = I[x^α]. Considering the entries of ℙ, ℙ′ and the entries σ_α of ℚ with α ∉ A as variables, the constraints (3) are multilinear equations in these variables of total degree at most 3 if ℚ contains unknown entries and 2 otherwise.

Example 3.7

We consider here V = R_2k for k > 0. By Proposition 3.4, any cubature formula for I exact on V has at least r_k := dim R_k points. Let us take B to be all the monomials of degree ≤ k so that B⁺ is the set of monomials of degree ≤ k + 1. If a cubature formula for I is exact on R_2k and has r_k points, then $H_{\sigma }^{B^{+},B^{+}}$ is a flat extension of $H_{\sigma }^{B,B}$ of rank r_k. Consider a decomposition of $H_{\sigma }^{B^{+},B^{+}}$ as in (2). By Proposition 3.4, we have the relations

$$\mathbb{M}=\mathbb{Q}\mathbb{P},\mathbb{N}={\mathbb{P}}^t\mathbb{Q}\mathbb{P},$$ (4)

where

• ℚ = (I[x^β+β′])_β,β′∈B,

• 𝕄 = (〈σ|x^β+β′〉)_{β∈B,β′∈∂B} with 〈σ|x^β+β′〉 = I[x^β+β′] when |β + β′| ≤ 2k,

• ℕ = (〈σ|x^β+β′〉)_{β,β′∈∂B},

• ℙ = (p_β,α)_{β∈B,α∈∂B}.

The equations (4) are quadratic in the variables ℙ and linear in the variables in 𝕄. Solving these equations yields a flat extension $H_{\sigma }^{B^{+},B^{+}}$ of $H_{\sigma }^{B,B}$. As $H_{\sigma }^{B,B}\succcurlyeq 0$, any real solution of this system of equations corresponds to a cubature for I on exact R_2k of the form $\sigma ={\sum }_{i=1}^{r_k}{w}_i{\mathbf{e}}_{{\zeta }_i}$ with w_i > 0, ζ_i ∈ ℝⁿ.

We illustrate the approach with R = ℝ[x₁, x₂], V = R₄, $B=\{1,x_1,x_2,x_1^2,x_1{x}_2,x_2^2\},B^{+}=\{1,x_1,x_2,x_1^2,x_1{x}_2,x_2^2,x_1^3,x_1^2{x}_2,x_1{x}_2^2,x_2^3\}$. Let

$$\sigma =8+17y_2-4y_1+15y_2^2+14y_1{y}_2-16y_1^2+47y_2^3-6y_1{y}_2^2+34y_1^2{y}_2-52y_1^3+51y_2^4+38y_1{y}_2^3-18y_1^2{y}_2^2+86y_1^3{y}_2-160y_1^4$$

be the series truncated in degree 4, corresponding to the first moments (not necessarily given by an integral).

$$H_{\sigma }^{B^{+},B^{+}}=\left[\begin{array}{cccccccccc}8& -4& 17& -16& 14& 15& -52& 34& -6& 47\\ -4& -16& 14& -52& 34& -6& -160& 86& -18& 38\\ 17& 14& 15& 34& -6& 47& 86& -18& 38& 51\\ -16& -52& 34& -160& 86& -18& {\sigma }_1& {\sigma }_2& {\sigma }_3& {\sigma }_4\\ 14& 34& -6& 86& -18& 38& {\sigma }_2& {\sigma }_3& {\sigma }_4& {\sigma }_5\\ 15& -6& 47& -18& 38& 51& {\sigma }_3& {\sigma }_4& {\sigma }_5& {\sigma }_6\\ -52& -160& 86& {\sigma }_1& {\sigma }_2& {\sigma }_3& {\sigma }_7& {\sigma }_8& {\sigma }_9& {\sigma }_{10}\\ 34& 86& -18& {\sigma }_2& {\sigma }_3& {\sigma }_4& {\sigma }_8& {\sigma }_9& {\sigma }_{10}& {\sigma }_{11}\\ -6& -18& 38& {\sigma }_3& {\sigma }_4& {\sigma }_5& {\sigma }_9& {\sigma }_{10}& {\sigma }_{11}& {\sigma }_{12}\\ 47& 38& 51& {\sigma }_4& {\sigma }_5& {\sigma }_6& {\sigma }_{10}& {\sigma }_{11}& {\sigma }_{12}& {\sigma }_{13}\end{array}\right]$$

where σ₁ = σ_5,0, σ₂ = σ_4,1, σ₂ = σ_3,2, σ₄ = σ_2,3, σ₅ = σ_1,4, σ₆ = σ_0,5, σ₇ = σ_6,0, σ₈ = σ_5,1, σ₉ = σ_4,2, σ₁₀ = σ_3,3, σ₁₁ = σ_2,4, σ₁₂ = σ_1,5, σ₁₃ = σ_0,6.

The first 6 × 6 diagonal block $H_{\sigma }^{B,B}$ is invertible. To have a flat extension $H_{\sigma }^{B^{+},B^{+}}$, we impose the condition that the sixteen 7 × 7 minors of $H_{\sigma }^{B^{+},B^{+}}$, which contains the first 6 rows and columns, must vanish. This yields the following system of quadratic equations:

$$\{\begin{array}{l}\begin{array}{l}-814592{\sigma }_1^2-1351680{\sigma }_1{\sigma }_2-476864{\sigma }_1{\sigma }_3-599040{\sigma }_2^2-301440{\sigma }_2{\sigma }_3-35072{\sigma }_3^2\\ -520892032{\sigma }_1-396821760{\sigma }_2-164529152{\sigma }_3+1693440{\sigma }_7-86394672128=0\end{array}\hfill \\ \begin{array}{l}-814592{\sigma }_2^2-1351680{\sigma }_2{\sigma }_3-476864{\sigma }_2{\sigma }_4-599040{\sigma }_3^2-301440{\sigma }_3{\sigma }_4-35072{\sigma }_4^2\\ +335275392{\sigma }_2+257276160{\sigma }_3+96277632{\sigma }_4+1693440{\sigma }_9-34904464128=0\end{array}\hfill \\ \begin{array}{l}-814592{\sigma }_3^2-1351680{\sigma }_3{\sigma }_4-476864{\sigma }_3{\sigma }_5-599040{\sigma }_4^2-301440{\sigma }_4{\sigma }_5-35072{\sigma }_5^2\\ +13226880{\sigma }_3+13282560{\sigma }_4-8227200{\sigma }_5+1693440{\sigma }_{11}+31714560=0\end{array}\hfill \\ \begin{array}{l}-814592{\sigma }_4^2-1351680{\sigma }_4{\sigma }_5-476864{\sigma }_4{\sigma }_6-599040{\sigma }_5^2-301440{\sigma }_5{\sigma }_6-35072{\sigma }_6^2\\ +212860736{\sigma }_4+162698880{\sigma }_5+51427456{\sigma }_6+1693440{\sigma }_{13}-13356881792=0\end{array}\hfill \\ \begin{array}{l}-814592{\sigma }_1{\sigma }_2-675840{\sigma }_1{\sigma }_3-238432{\sigma }_1{\sigma }_4-675840{\sigma }_2^2-837472{\sigma }_2{\sigma }_3\\ -150720{\sigma }_2{\sigma }_4-150720{\sigma }_3^2-35072{\sigma }_3{\sigma }_4+167637696{\sigma }_1-131807936{\sigma }_2\\ -150272064{\sigma }_3-82264576{\sigma }_4+1693440{\sigma }_8+54990043008=0\end{array}\hfill \\ \begin{array}{l}-814592{\sigma }_2{\sigma }_3-675840{\sigma }_2{\sigma }_4-238432{\sigma }_2{\sigma }_5-675840{\sigma }_3^2-837472{\sigma }_3{\sigma }_4-150720{\sigma }_3{\sigma }_5\\ -150720{\sigma }_4^2-35072{\sigma }_4{\sigma }_5+6613440{\sigma }_2+174278976{\sigma }_3+124524480{\sigma }_4\\ +48138816{\sigma }_5+1693440{\sigma }_{10}-746438400=0\end{array}\hfill \\ \begin{array}{l}-814592{\sigma }_3{\sigma }_4-675840{\sigma }_3{\sigma }_5-238432{\sigma }_3{\sigma }_6-675840{\sigma }_4^2-837472{\sigma }_4{\sigma }_5-150720{\sigma }_4{\sigma }_6\\ -150720{\sigma }_5^2-35072{\sigma }_5{\sigma }_6+106430368{\sigma }_3+87962880{\sigma }_4+32355008{\sigma }_5\\ -4113600{\sigma }_6+1693440{\sigma }_{12}-183201600=0\end{array}\hfill \\ \begin{array}{l}-814592{\sigma }_2{\sigma }_4-675840{\sigma }_2{\sigma }_5-238432{\sigma }_2{\sigma }_6-675840{\sigma }_3{\sigma }_4-599040{\sigma }_3{\sigma }_5\\ -150720{\sigma }_3{\sigma }_6-238432{\sigma }_4^2-150720{\sigma }_4{\sigma }_5-35072{\sigma }_4{\sigma }_6+106430368{\sigma }_2\\ +81349440{\sigma }_3+193351424{\sigma }_4+128638080{\sigma }_5+48138816{\sigma }_6\\ +1693440{\sigma }_{11}-21721986624=0\end{array}\hfill \\ \begin{array}{l}-814592{\sigma }_1{\sigma }_3-675840{\sigma }_1{\sigma }_4-238432{\sigma }_1{\sigma }_5-675840{\sigma }_2{\sigma }_3-599040{\sigma }_2{\sigma }_4\\ -150720{\sigma }_2{\sigma }_5-238432{\sigma }_3^2-150720{\sigma }_3{\sigma }_4-35072{\sigma }_3{\sigma }_5+6613440{\sigma }_1+6641280{\sigma }_2\\ -264559616{\sigma }_3-198410880{\sigma }_4-82264576{\sigma }_5+1693440{\sigma }_9+1312368000=0\end{array}\hfill \\ \begin{array}{l}-814592{\sigma }_1{\sigma }_4-675840{\sigma }_1{\sigma }_5-238432{\sigma }_1{\sigma }_6-675840{\sigma }_2{\sigma }_4-599040{\sigma }_2{\sigma }_5\\ -150720{\sigma }_2{\sigma }_6-238432{\sigma }_3{\sigma }_4-150720{\sigma }_3{\sigma }_5-35072{\sigma }_3{\sigma }_6+106430368{\sigma }_1\\ +81349440{\sigma }_2+25713728{\sigma }_3-260446016{\sigma }_4-198410880{\sigma }_5-82264576{\sigma }_6\\ +1693440{\sigma }_{10}+34550702464=0\end{array}\hfill \end{array}$$

The set of solutions of this system is an algebraic variety of dimension 3 and degree 52. A solution is σ₁ = −484, σ₂ = 226, σ₃ = −54, σ₄ = 82, σ₅ = −6, σ₆ = 167, σ₇ = −1456, σ₈ = 614, σ₉ = −162, σ₁₀ = 182, σ₁₁ = −18, σ₁₂ = 134, σ₁₃ = 195.

3.1. Computing an orthogonal basis of 𝒜_σ

In this section, we describe a new method to construct a basis B of 𝒜_σ and to detect flat extensions, from the knowledge of the moments σ_α of σ(y). We are going to inductively construct a family P of polynomials, orthogonal for the inner product

$$(p,q)\mapsto {\langle p,q\rangle }_{\sigma }:=\langle \sigma \mid pq\rangle ,$$

and a monomial set B connected to 1 such that 〈B〉 = 〈P〉.

We start with B = {1}, P = {1} ⊂ R. As 〈1, 1〉_σ = 〈σ | 1〉 ≠ 0, the family P is orthogonal for σ and 〈B〉 = 〈P〉.

We now describe the induction step. Assume that we have a set B = {m₁,…, m_s} and P = {p₁,…, p_s} such that

• 〈B〉 = 〈P〉;

• 〈p_i, p_j〉_σ ≠ 0 if i = j and 0 otherwise.

To construct the next orthogonal polynomials, we consider the monomials in $\partial B=\{m_1^{\prime },\dots ,m_l^{\prime }\}$ and project them on 〈P〉:

$$p_i^{\prime }=m_i^{\prime }-\sum _{j=1}^s\frac{{\langle m_i^{\prime },p_j\rangle }_{\sigma }}{{\langle p_j,p_j\rangle }_{\sigma }}{p}_j,i=1,\dots ,l.$$

By construction, ${\langle p_i^{\prime },p_j\rangle }_{\sigma }=0$ and $\langle p_1,\dots ,p_s,p_i^{\prime }\rangle =\langle m_1,\dots ,m_s,m_i^{\prime }\rangle$. We extend B by choosing a subset of monomials $B^{\prime }=\{m_{i_1}^{\prime },\dots ,m_{i_k}^{\prime }\}$ such that the matrix

$${[{\langle p_{i_j}^{\prime },p_{i_{j^{\prime }}}^{\prime }\rangle }_{\sigma }]}_{1\le j,j^{\prime }\le k}$$

is invertible. The family P is then extended by adding an orthogonal family of polynomials {p_s+1,…, p_s+k} constructed from { $p_{i_1}^{\prime },\dots ,p_{i_k}^{\prime }$}. If all the polynomials $p_i^{\prime }$ are such that ${\langle p_i^{\prime },p_j^{\prime }\rangle }_{\sigma }=0$, the process stops.

This leads to the following algorithm:

Algorithm 1

Input: the coefficients σ_α of a series σ ∈ ℂ[[y]] for α ∈ A ⊂ ℕⁿ connected to 1 with σ₀ ≠ 0.

• Let B := {1}; P = {1}; r := 1; E = 〈y^α〉_α∈A;

• While s > 0 and B⁺ · B⁺ ⊂ E do

  • Compute $\partial B=\{m_1^{\prime },\dots ,m_l^{\prime }\}$ and $p_i^{\prime }=m_i^{\prime }-{\sum }_{j=1}^s\frac{{\langle m_i^{\prime },p_j\rangle }_{\sigma }}{{\langle p_j,p_j\rangle }_{\sigma }}{p}_j$;

  • Compute a (maximal) subset $B^{\prime }=\{m_{i_1}^{\prime },\dots ,m_{i_k}^{\prime }\}$ of ∂B such that ${[{\langle p_{i_j}^{\prime },p_{i_{j^{\prime }}}^{\prime }\rangle }_{\sigma }]}_{1\le j,j^{\prime }\le k}$ is invertible;

  • Compute an orthogonal family of polynomials {p_s+1,…, p_s+k} from { $p_{i_1}^{\prime },\dots ,p_{i_k}^{\prime }$};

  • B := B ∪ B′, P := P ∪ {p_s+1,…, p_s+k}; r+ = k;

• If B⁺ · B⁺ ⊄ ⊂ E then return failed.

Output: failed or success with

• a set of monomials B = {m₁,…, m_r} connected to 1, and non-degenerate for 〈·, ·〉_σ;

• a set of polynomials P = {p₁,…, p_r} orthogonal for σ and such that 〈B〉 = 〈P〉;

• the relations ${\rho }_i:=m_i^{\prime }-{\sum }_{j=1}^s\frac{{\langle m_i^{\prime },p_j\rangle }_{\sigma }}{{\langle p_j,p_j\rangle }_{\sigma }}{p}_j$ for the monomials $m_i^{\prime }$ in $\partial B=\{m_1^{\prime },\dots ,m_l^{\prime }\}$.

The above algorithm is a Gramm–Schmidt-type orthogonalization method, where, at each step, new monomials are taken in ∂B and projected onto the space spanned by the previous monomial set B. Notice that if the polynomials p_i are of degree at most d′ < d, then only the moments of σ of degree ≤ 2d′ + 1 are involved in this computation.

Proposition 3.8

If Algorithm 1 outputs with success a set B = {m₁,…, m_r} and the relations ${\rho }_i:=m_i^{\prime }-{\sum }_{j=1}^s\frac{{\langle m_i^{\prime },p_j\rangle }_{\sigma }}{{\langle p_j,p_j\rangle }_{\sigma }}{p}_j$, for $m_i^{\prime }$ in $\partial B=\{m_1^{\prime },\dots ,m_l^{\prime }\}$, then σ coincides on 〈B⁺ · B⁺〉 with the series σ̃ such that

• rank H_σ̃ = r;

• B and P are bases of 𝒜_σ̃ for the inner product 〈·, ·〉_σ̃;

• The ideal I_σ̃ = ker H_σ̄ is generated by (ρ_i)_i=1,…,l;

• The matrix of multiplication by x_k in the basis P of 𝒜_σ̃ is

  $$M_k={\left(\frac{\langle \sigma \mid x_k{p}_i{p}_j\rangle }{\langle \sigma \mid p_j^2\rangle }\right)}_{1\le i,j\le r}.$$

Proof

By construction, B is connected to 1. A basis B′ of 〈B⁺〉 is formed by the elements of B and the polynomials ρ_i, i = 1,…, l. Since Algorithm 1 stops with success, we have ∀i, j ∈ [1, l], ∀b ∈ 〈B〉, 〈ρ_i, b〉_σ = 〈ρ_i, ρ_j〉_σ = 0 and ${\rho }_1,\dots ,{\rho }_l\in ker{H}_{\sigma }^{B^{+},B^{+}}$. As 〈B⁺〉 = 〈B〉 ⊕ 〈ρ₁,…, ρ_l〉, $\text{rank}{H}_{\sigma }^{B^{+},B^{+}}=\text{rank}{H}_{\sigma }^{B,B}$ and $H_{\sigma }^{B^{+},B^{+}}$ is a flat extension of $H_{\sigma }^{B,B}$. By construction, P is an orthogonal basis of 〈B〉 and the matrix of $H_{\sigma }^{B,B}$ in this basis is diagonal with non-zero entries on the diagonal. Thus $H_{\sigma }^{B,B}$ is of rank r.

By Theorem 3.2, σ coincides on 〈B⁺ ·B⁺〉 with a series σ̃ ∈ R^* such that B is a basis of 𝒜_σ̄ = R/I_σ̃ and $I_{\stackrel{\sim }{\sigma }}=(ker{H}_{\stackrel{\sim }{\sigma }}^{B^{+},B^{+}})=({\rho }_1,\dots ,{\rho }_l)$.

As 〈B⁺〉 = 〈B〉 ⊕ 〈ρ₁,…, ρ_l〉 = 〈P 〉 ⊕〈ρ₁,…, ρ_l〉 and P is an orthogonal basis of 𝒜_σ̄, which is orthogonal to 〈ρ₁,…, ρ_l〉, we have

$$x_k{p}_i=\sum _{j=1}^r\frac{\langle \sigma \mid x_k{p}_i{p}_j\rangle }{\langle \sigma \mid p_j^2\rangle }{p}_j+\rho$$

with ρ ∈ 〈ρ₁,…, ρ_l〉. This shows that the matrix of the multiplication by x_k modulo I_σ̄ = (ρ₁,…, ρ_l), in the basis P = {p₁,…, p_r} is $M_k={\left(\frac{\langle \sigma \mid x_k{p}_i{p}_j\rangle }{\langle \sigma \mid p_j^2\rangle }\right)}_{1\le i,j\le r}$.

Remark 3.9

It can be shown that the polynomials (ρ_i)_i=1,·,l are a border basis of I_σ̃ for the basis B [23,6,27,28].

Remark 3.10

If $H_{\sigma }^{B,B}\succcurlyeq 0$, then by Proposition 2.2, the common roots ζ₁,…, ζ_r of the polynomials ρ₁,…, ρ_l are simple and real ∈ ℝⁿ. They are the cubature points:

$$\overline{\sigma }=\sum _{i=1}^r{w}_j{\mathbf{e}}_{{\zeta }_j},$$

with w_j > 0.

4. The cubature formula from the moment matrix

We now describe how to recover the cubature formula, from the moment matrix $H_{\sigma }^{B^{+},{B^{\prime }}^{+}}$. We assume that the flat extension condition is satisfied:

$$\text{rank}{H}_{\sigma }^{B^{+},{B^{\prime }}^{+}}=H_{\sigma }^{B,B^{\prime }}=\mid B\mid =\mid B^{\prime }\mid .$$ (5)

Theorem 4.1

Let B and B′ be monomial subsets of R of size r connected to 1 and σ ∈ 〈B⁺ · B′⁺〉^*. Suppose that $H_{\sigma }^{B^{+},{B^{\prime }}^{+}}=\text{rank}{H}_{\sigma }^{B,B^{\prime }}=\mid B\mid =\mid B^{\prime }\mid$. Let $M_i={[H_{\sigma }^{B,B^{\prime }}]}^{-1}[H_{\sigma }^{x_i,B,B^{\prime }}]$ and ${(M_i^{\prime })}^t=[H_{\sigma }^{B,x_i{B}^{\prime }}]{[H_{\sigma }^{B,B^{\prime }}]}^{-1}$. Then,

1. B and B′ are bases of 𝒜_σ̃ = R/ker H_σ̃,

2. $M_i(\mathit{resp}.M_i^{\prime })$ is the matrix of multiplication by x_i in the basis B (resp. B′) of 𝒜_σ̃,

Proof

By the flat extension Theorem 3.2, there exists σ̄ ∈ R^* such that H_σ̃ is a flat extension of $H_{\sigma }^{B^{+},{B^{\prime }}^{+}}$ of rank r = |B| = |B′| and $ker{H}_{\overline{\sigma }}=(ker{H}_{\sigma }^{B^{+},{B^{\prime }}^{+}})$. As R = 〈B〉 ⊕ ker H_σ̄ and rank H_σ̃ = r, 𝒜_σ̃ = R/ker H_σ̄ is of dimension r and generated by B. Thus B is a basis of 𝒜_σ̃. A similar argument shows that B′ is also a basis of 𝒜_σ̃. We denote by π : 𝒜_σ̃ → 〈B〉 and π′ : 𝒜_σ̃ → 〈B′〉 the isomorphisms associated to these bases representations.

The matrix [ $H_{\sigma }^{B,B^{\prime }}$] is the matrix of the Hankel operator

$$\begin{array}{ll}\hfill {\overline{H}}_{\overline{\sigma }}:{\mathcal{A}}_{\stackrel{\sim }{\sigma }}& \to {\mathcal{A}}_{\stackrel{\sim }{\sigma }}^{\ast }\hfill \\ \hfill a& \mapsto a★\overline{\sigma }\hfill \end{array}$$

in the basis B and the dual basis of B′. Similarly, [ $H_{\sigma }^{x_{i}B,B^{\prime }}$] is the matrix of

$$\begin{array}{ll}\hfill {\overline{H}}_{x_{i★}\overline{\sigma }}:{\mathcal{A}}_{\stackrel{\sim }{\sigma }}& \to {\mathcal{A}}_{\stackrel{\sim }{\sigma }}^{\ast }\hfill \\ \hfill a& \mapsto a★x_i★\overline{\sigma }\hfill \end{array}$$

in the same bases. As x_i ★ σ̄ = σ̄ ○ M_i where M_i : 𝒜_σ̃ → 𝒜_σ̃ is the multiplication by x_i in 𝒜_σ̃, we deduce that H̄_xi★σ̄ = H̄_σ̄ ○ M_i and ${[H_{\sigma }^{B,B^{\prime }}]}^{-1}[H_{\sigma }^{x_{i}B,B^{\prime }}]$ is the matrix of multiplication by x_i in the basis B of 𝒜_σ̃. By exchanging the role of B and B′ and by transposition ( ${[H_{\sigma }^{B,B^{\prime }}]}^t=[H_{\sigma }^{B^{\prime },B}]$), we obtain that $[H_{\sigma }^{B,x_i{B}^{\prime }}]{[H_{\sigma }^{B,B^{\prime }}]}^{-1}$ is the transpose of the matrix of multiplication by x_i in the basis B′ of 𝒜_σ̃.

Theorem 4.2

Let B be a monomial subset of R of size r connected to 1 and σ ∈ 〈B⁺ · B⁺〉^*. Suppose that $\text{rank}{H}_{\sigma }^{B^{+},B^{+}}=\text{rank}{H}_{\sigma }^{B,B}=\mid B\mid =r$ and that $H_{\sigma }^{B,B}\succcurlyeq 0$. Let $M_i={[H_{\sigma }^{B,B^{\prime }}]}^{-1}[H_{\sigma }^{x_i,B,B^{\prime }}]$. Then σ can be decomposed as

$$\sigma =\sum _{j=1}^r{w}_j{\mathbf{e}}_{{\zeta }_j}$$

with w_j > 0 and ζ_j ∈ ℝⁿ such that M_i have r common linearly independent eigenvectors u_j, j = 1, …, r and

• ${\zeta }_{j,i}=\frac{\langle \sigma \mid x_i{\mathbf{u}}_j\rangle }{\langle \sigma \mid {\mathbf{u}}_j\rangle }$ for 1 ≤ i ≤ n, 1 ≤ j ≤ r;

• $w_j=\frac{\langle \sigma \mid {\mathbf{u}}_j\rangle }{{\mathbf{u}}_j({\zeta }_{j,1},\dots ,{\zeta }_{j,n})}$.

Proof

By Theorem 4.1, the matrix M_i is the matrix of multiplication by x_i in the basis B of 𝒜_σ̃. As $H_{\sigma }^{B,B}\succcurlyeq 0$, the flat extension Theorem 3.2 implies that H_σ̄ ≽ 0 and that

$$\overline{\sigma }=\sum _{j=1}^r{w}_j{\mathbf{e}}_{{\zeta }_j}$$

where w_j > 0 and ζ_j ∈ ℝⁿ are the simple roots of the ideal ker H_σ̄. Thus the commuting operators M_i are diagonalizable in a common basis of eigenvectors u_i, i = 1, …, r, which are scalar multiples of the interpolation polynomials at the roots ζ₁, …, ζ_r: u_i(ζ_i) = λ_i ≠ 0 and u_i(ζ_j) = 0 if j ≠ i (see [15, Chap. 4] or [10]). We deduce that

$$\langle \overline{\sigma }\mid {\mathbf{u}}_j\rangle =\sum _{k=1}^r{w}_k{\mathbf{u}}_j({\zeta }_k)=w_j{\lambda }_j\text{and}\langle \overline{\sigma }\mid x_i{\mathbf{u}}_j\rangle ={\zeta }_{j,i}{w}_j{\lambda }_j,$$

so that ${\zeta }_{j,i}=\frac{\langle \sigma \mid x_i{\mathbf{u}}_j\rangle }{\langle \sigma \mid {\mathbf{u}}_j\rangle }$. As u_i(ζ_i) = λ_i, we have $w_j=\frac{\langle \sigma \mid {\mathbf{u}}_j\rangle }{{\mathbf{u}}_j({\zeta }_{j,1},\dots ,{\zeta }_{j,n})}$.

Algorithm 2

Input: B is a set of monomials connected to 1, σ ∈ 〈 B⁺ · B⁺〉^* such that $H_{\sigma }^{B^{+},B^{+}}$ is a flat extension of $H_{\sigma }^{B,B}$ of rank |B|.

• Compute an orthogonal basis {p₁, …, p_r} of B for σ;

• Compute the matrices $M_k={\left(\frac{\langle \sigma \mid x_k{p}_i{p}_j\rangle }{\langle \sigma \mid p_j^2\rangle }\right)}_{1\le i,j\le r}$;

• Compute their common eigenvectors u₁, …, u_r.

Output: For j = 1, …, r,

• ${\zeta }_j=\left(\frac{\langle \sigma \mid x_1{\mathbf{u}}_j\rangle }{\langle \sigma \mid {\mathbf{u}}_j\rangle },\dots ,\frac{\langle \sigma \mid x_{in}{\mathbf{u}}_j\rangle }{\langle \sigma \mid {\mathbf{u}}_j\rangle }\right)$;

• $w_j=\frac{\langle \sigma \mid {\mathbf{u}}_j\rangle }{{\mathbf{u}}_j({\zeta }_{j,1},\dots ,{\zeta }_{j,n})}$.

Remark 4.3

Since the matrices M_k commute and are diagonalizable with the same basis, their common eigenvectors can be obtained by computing the eigenvectors of a generic linear combination l₁M₁ + ··· + l_nM_n, l_i ∈ ℝ.

5. Cubature formula by convex optimization

As described in the previous section, the computation of cubature formulae reduces to a low rank Hankel matrix completion problem, using the flat extension property. In this section, we describe a new approach which relaxes this problem into a convex optimization problem.

Let V ⊂ R be a vector space spanned by monomials x^α for α ∈ A ⊂ ℕⁿ. Our aim is to construct a cubature formula for an integral function I exact on V. Let i = (I[x^α])_α∈A be the sequence of moments given by the integral I. We also denote i ∈ V ^* the associated linear form such that ∀v ∈ V, 〈i | v〉 = I[v].

For k ∈ ℕ, we denote by

$${\mathcal{H}}^k(\mathbf{i})=\{H_{\sigma }\mid \sigma \in R_{2k}^{\ast },{\sigma }_{\alpha }={\mathbf{i}}_{\alpha }\text{for}\alpha \in A,H_{\sigma }\succcurlyeq 0\},$$

the set of semi-definite Hankel operators on R_t is associated to moment sequences which extend i. We can easily check that ℋ^k(i) is a convex set. We denote by ${\mathcal{H}}_r^k(\mathbf{i})$ the set of elements of ℋ^k(i) of rank ≤ r.

A subset of ${\mathcal{H}}_r^k(\mathbf{i})$ is the set of Hankel operators associated to cubature formulae of r points:

$${\mathcal{E}}_r^k(\mathbf{i})=\left\{H_{\sigma }\in {\mathcal{H}}^k(\mathbf{i})\mid \sigma =\sum _{i=1}^r{w}_i{\mathbf{e}}_{{\zeta }_i},{\omega }_i>0,{\zeta }_i\in {ℝ}^n\right\}.$$

We can check that ${\mathcal{E}}^k(\mathbf{i})={\cup }_{r\in \mathbb{N}}{\mathcal{E}}_r^k(\mathbf{i})$ is also a convex set.

To impose the cubature points to be in a semialgebraic set 𝒮 defined by equality and inequalities $\mathcal{S}=\{\mathbf{x}\in {ℝ}^n\mid g_1^0(\mathbf{x})=0,\dots ,g_{n_1}^0(\mathbf{x})=0,g_1^{+}(\mathbf{x})\ge 0,\dots ,g_{n_2}^{+}(\mathbf{x})\ge 0\}$, one can refine the space of ℋ^k(i) by imposing that σ is positive on the quadratic module (resp. preordering) associated to the constraints $\mathbf{g}=\{g_1^0,\dots ,g_n^0;g_1^{+},\dots ,g_n^{+}\}$ [19]. For the sake of simplicity, we don’t analyze this case here, which can be done in a similar way.

The Hankel operator $H_{\sigma }\in {\mathcal{E}}_r^k(\mathbf{i})$ associated to a cubature formula of r points is an element of ${\mathcal{H}}_r^k(\mathbf{i})$. In order to find a cubature formula of minimal rank, we would like to compute a minimizer solution of the following optimization problem:

$$\underset{H\in {\mathcal{H}}^k(\mathbf{i})}{min}\text{rank}(H)$$

However this problem is NP-hard [16]. We therefore relax it into the minimization of the nuclear norm of the Hankel operators, i.e. the minimization of the sum of the singular values of the Hankel matrix [37]. More precisely, for a generic matrix P ∈ ℝ^{s_t × s_t}, we consider the following minimization problem:

$$\underset{H\in {\mathcal{H}}^k(\mathbf{i})}{min}\text{trace}(P^{t}HP)$$ (6)

Let (A, B) ∈ ℝ^{s_k × s_k} × ℝ^{s_k × s_k} → 〈A, B〉 = trace(AB) denote the inner product induced by the trace on the space of s_k × s_k matrices. The optimization problem (6) requires minimizing the linear form H → trace(HPP^t) = 〈H, PP^t〉 on the convex set ℋ^k(i). As the trace of P^tHP is bounded by below by 0 when H ≽ 0, our optimization problem (6) has a non-negative minimum ≥ 0.

Problem (6) is a Semi-Definite Program (SDP), which can be solved efficiently by interior point methods. See [31]. SDP is an important ingredient of relaxation techniques in polynomial optimization. See [19,22].

Let ${\mathrm{\sum }}^k=\left\{p={\sum }_{i=1}^l{p}_i^2\mid p_i\in R_k\right\}$ be the set of polynomials of degree ≤ 2k which are sums of squares, let x^(k) be the vector of all monomials in x of degree ≤ k and let q(x) = (x^(k))^tPP^t x^(k) ∈ Σ^k. Let p_i(x) (1 ≤ i ≤ s_k) denote the polynomial 〈P_i, x^(k)〉 associated to the column P_i of P. We have $q(\mathbf{x})={\sum }_{i=1}^{s_k}{p}_i{(\mathbf{x})}^2$ and for any σ ∈ R_2k,

$$\text{trace}(P^t{H}_{\sigma }P)=\langle H_{\sigma }\mid P{P}^t\rangle =\langle \sigma \mid q(\mathbf{x})\rangle .$$

For any l ∈ ℕ, we denote by π_l: R_l → R_l the linear map which associates to a polynomial p ∈ R_l its homogeneous component of degree l. We say that P is a proper matrix if π_2k(q(x)) ≠ 0 for all x ∈ ℝⁿ.

We are thus looking for cubature formulae with a small number of points, which correspond to Hankel operators with small rank. The next result describes the structure of truncated Hankel operators, when the degree of truncation is high enough, compared to the rank.

Theorem 5.1

Let $\sigma \in R_{2k}^{\ast }$ and let H_σ be its truncated Hankel operator on R_k. If H_σ ≽ 0 and H_σ is of rank r ≤ k, then

$$\sigma \equiv \sum _{i=1}^{r^{\prime }}{\omega }_i{\mathbf{e}}_{{\zeta }_i}+\sum _{i=r^{\prime }+1}^r{w}_i{\mathbf{e}}_{{\zeta }_i}\circ {\pi }_{2k}$$

with ω_i > 0 and ζ_i ∈ ℝⁿ distinct for i = 1, …, r.

Proof

The substitution τ₀: S_[2k] → R_2k which replaces x₀ by 1 is an isomorphism of 𝕂-vector spaces. Let ${\tau }_0^{\ast }:R_{2k}^{\ast }\to S_{[2k]}^{\ast }$ be the pull-back map on the $\text{dual}({\tau }_0^{\ast }(\sigma )=\sigma \circ {\tau }_0)$. Let $\overline{\sigma }=\sigma \circ {\tau }_0={\tau }_0^{\ast }(\sigma )\in S_{[2k]}^{\ast }$ be the linear form induced by σ on S_[2k] and let $H_{\overline{\sigma }}:S_{[k]}\to S_{[k]}^{\ast }$ be the corresponding truncated operator on S_[k]. The kernel K̄ of H_σ̄ is the vector space spanned by the homogenization in x₀ of the elements of the kernel K of H_σ.

Let ≽ be the lexicographic ordering such that x₀ ≽ ··· ≽ x_n. By [14, Theorem 15.20, p. 351], after a generic change of coordinates, the initial J of the homogeneous ideal (K̄) ⊂ S is Borel fixed. That is, if x_ix^α ∈ J, then x_jx^α ∈ J for j > i. Let B̄ be the set of monomials of degree k, which are not in J. As J is Borel fixed and different from S_[2k], $x_0^k\in \overline{B}$. Similarly we check that if $x_0^{{\alpha }_0}\cdots x_n^{{\alpha }_n}\in J$ with α₁ = ··· = α_l−1 = 0, then $x_0^{{\alpha }_0+1}{x}_l^{{\alpha }_l-1}\cdots x_n^{{\alpha }_n}\in J$. This shows that B = τ₀(B̄) is connected to 1.

As 〈 B̄ 〉 ⊕〈J〉 = 〈 B̄ 〉 ⊕ K̄ = S_[k] where K̄ = ker H_σ̄, we have |B| = r. As B is connected to 1, deg(B) < r ≤ k and B⁺ ⊂ R^k.

By the substitution x₀ = 1, we have R_k = 〈B〉 ⊕ K with K = ker H_σ. Therefore, H_σ is a flat extension of $H_{\sigma }^{B,B}$. By the flat extension Theorem 3.2, there exist λ_i > 0, ζ̄_i = (ζ_i,0, ζ_i,1, …, ζ_i,n) ∈ ℝⁿ⁺¹ distinct for i = 1, …, r such that

$$\overline{\sigma }\equiv \sum _{i=1}^r{\lambda }_i{\mathbf{e}}_{{\overline{\zeta }}_i}\text{on}{S}_{[2k]}.$$ (7)

Notice that for any λ ≠ 0, e_ζ̄i = λ^−ke_λζ̄ion S_[2k].

By an inverse change of coordinates, the points ζ̄_i of (7) are transformed into some points ζ̄_i = (ζ_i,0, ζ_i,1, …, ζ_i,n) ∈ 𝕂ⁿ⁺¹ such that ζ_i,0 ≠ 0 (say for i = 1, …, r′) and the remaining r − r′ points with ζ_i,0 = 0. The image by ${\tau }_0^{\ast }$ of ${\mathbf{e}}_{{\overline{\zeta }}_i}\in S_{[2k]}^{\ast }$ with ζ_i,0 ≠ 0 is

$${\tau }_0^{\ast }({\mathbf{e}}_{{\zeta }_i})\equiv {\zeta }_{i,0}^{2k}{\mathbf{e}}_{{\zeta }_i}$$

where ${\zeta }_i=\frac{1}{{\zeta }_{i,0}}({\zeta }_{i,1},\dots ,{\zeta }_{i,n})$. The image by ${\tau }_0^{\ast }$ of ${\mathbf{e}}_{{\overline{\zeta }}_i}\in S_{[2k]}^{\ast }$ with ${\zeta }_{i,0}=0\text{is}\mathrm{a}\text{linear}\text{form}\in R_{2k}^{\ast }$, which vanishes on all the monomials x^α with |α| < 2k, since their homogenization in degree 2k is $x_0^{2k-\mid \alpha \mid }{\mathbf{x}}^{\alpha }$ and their evaluation at ζ̄_i = (0, ζ_i,1, …, ζ_i,n) gives 0. The value of ${\tau }_0^{\ast }({\mathbf{e}}_{{\overline{\zeta }}_i})$ at x^α with |α| = 2k, ${\zeta }_{i,1}^{{\alpha }_1}\cdots {\zeta }_{i,n}^{{\alpha }_n}={\mathbf{e}}_{{\zeta }_i}({\mathbf{x}}^{\alpha })$ where ζ_i = (ζ_i,1,…, ζ_i,n). We deduce that

$${\tau }_0^{\ast }({\mathbf{e}}_{{\overline{\zeta }}_i})\equiv {\mathbf{e}}_{{\zeta }_i}\circ {\pi }_{2k}.$$

By dehomogenization, we have ${\omega }_i={\lambda }_i{\zeta }_{i,0}^{2k}>0,{\zeta }_i=\frac{1}{{\zeta }_{i,0}}({\zeta }_{i,1},\dots ,{\zeta }_{i,n})\in {ℝ}^n$ for i = 1, …, r′ and ζ_i = (ζ_i,1, …, ζ_i,n) ∈ ℝⁿ for i = r′ + 1, …, n.

We exploit this structure theorem to show that if the truncation order is sufficiently high, a minimizer of (6) corresponds to a cubature formula.

Theorem 5.2

Let P be a proper operator and $k\ge \frac{deg(V)+1}{2}$. Assume that there exists ${\sigma }^{\ast }\in R_{2k}^{\ast }$ such that H_σ^* is a minimizer of (6) of rank r with r ≤ k. Then $H_{{\sigma }^{\ast }}\in {\mathcal{E}}_r^k(\mathbf{i})$ i.e. there exist ω_i > 0 and ζ_i ∈ ℝⁿ such that

$${\sigma }^{\ast }\equiv \sum _{i=1}^r{\omega }_i{\mathbf{e}}_{{\zeta }_i}.$$

Proof

By Theorem 5.1,

$${\sigma }^{\ast }\equiv \sum _{i=1}^{r^{\prime }}{\omega }_i{\mathbf{e}}_{{\zeta }_i}+\sum _{i=r^{\prime }+1}^r{w}_i{\mathbf{e}}_{{\zeta }_i}\circ {\pi }_{2k},$$

with ω_i > 0 and ζ_i ∈ ℝⁿ for i = 1, …, r.

Let us suppose that r ≠ r′. As $k\ge \frac{deg(V)+1}{2}$, the elements of V are of degree < 2k, therefore σ^* and ${\sigma }^{\prime }\equiv {\sum }_{i=1}^{r^{\prime }}{\omega }_i{\mathbf{e}}_{{\zeta }_i}$ coincide on V and H_σ′ ∈ ℋ^k(i). We have the decomposition

$$\text{trace}(P{H}_{{\sigma }^{\ast }}P)=\langle {\sigma }^{\ast }\mid q\rangle =\langle {\sigma }^{\prime }\mid q\rangle +\sum _{i=1}^{r^{\prime }}{\omega }_i{\pi }_{2k}(q)({\zeta }_i)$$

The homogeneous component of highest degree π_2k(q) of $q(\mathbf{x})={\sum }_{i=1}^{s_k}{p}_i{(\mathbf{x})}^2$ is the sum of the squares of the degree-k components of the p_i:

$${\pi }_{2k}(q)=\sum _{i=1}^{s_k}{({\pi }_k(p_i))}^2,$$

so that ${\sum }_{i=1}^{r^{\prime }}{\omega }_i{\pi }_{2k}(q)({\zeta }_i)\ge 0$. As trace(PH_σ*P) is minimal, we must have ${\sum }_{i=r^{\prime }+1}^r{\omega }_i{\pi }_{2k}(q)({\zeta }_i)=0$, which implies that π_2k(q)(ζ_i) for i = r′ + 1, …, r. However, this is impossible, since P is proper. We thus deduce that r′ = r, which concludes the proof of the theorem.

This theorem shows that an optimal solution of the minimization problem (6) of small rank (r ≤ k) yields a cubature formula, which is exact on V. Among such minimizers, we have those of minimal rank as shown in the next proposition.

Proposition 5.3

Let $k\ge \frac{deg(V)+1}{2}$ and H be an element of ℋ^k(i) with minimal rank r. If k ≥ r, then $H\in {\mathcal{E}}_r^k(\mathbf{i})$ and it is either an extremal point of ℋ^k(i) or on a face of ℋ^k(i), which is included in ${\mathcal{E}}_r^k(\mathbf{i})$.

Proof

Let $H_{\sigma }\in {\mathcal{E}}_r^k(\mathbf{i})$ be of minimal rank r.

By Theorem 5.1, $\sigma \equiv {\sum }_{i=1}^{r^{\prime }}{\omega }_i{\mathbf{e}}_{{\zeta }_i}+{\sum }_{i=r^{\prime }+1}^r{w}_i{\mathbf{e}}_{{\zeta }_i}\circ {\pi }_{2k}$ with ω_i > 0 and ζ_i ∈ ℝⁿ for i = 1, …, r. The elements of V are of degree < 2k, therefore σ and ${\sigma }^{\prime }\equiv {\sum }_{i=1}^{r^{\prime }}{\omega }_i{\mathbf{e}}_{{\zeta }_i}$ coincide on V. We deduce that H_σ′ ∈ ℋ^k(i).

As rank H_σ′ = r′ ≤ r and H_σ ∈ ℋ^k(i) is of minimal rank r, r = r′ and $H_{\sigma }\in {\mathcal{E}}_r^k(\mathbf{i})$.

Let us assume that H_σ is not an extremal point of ℋ^k(i). Then it is in the relative interior of a face F of ℋ^k(i). For any H_σ1 in a sufficiently small ball of F around H_σ, there exist t ∈ ]0, 1[ and H_σ2 ∈ F such that

$$H_{\sigma }=t{H}_{{\sigma }_1}+(1-t)H_{{\sigma }_2}.$$

The kernel of H_σ is the set of polynomials p ∈ R_k such that

$$0=H_{\sigma }(p,p)=t{H}_{{\sigma }_1}(p,p)+(1-t)H_{{\sigma }_2}(p,p).$$

As H_σi ≽ 0, we have H_σi (p, p) = 0 for i = 1, 2. This implies that ker H_σ ⊂ ker H_σi, for i = 1, 2. From the inclusion ker H_σ1 ∩ ker H_σ2 ⊂ ker H_σ, we deduce that

$$ker{H}_{\sigma }=ker{H}_{{\sigma }_1}\cap ker{H}_{{\sigma }_2}.$$

As H_σ is of minimal rank r, we have dim ker H_σ ≥ dim ker H_σi. This implies that ker H_σ = ker H_σ1 = ker H_σ2.

As r ≤ k, 𝒜_σ has a monomial basis B (connected to 1) in degree < k and R_k = 〈B〉 ⊕ ker H_σ. Consequently, H_σ (resp. H_σi) is a flat extension of $H_{\sigma }^{B,B}(\text{resp.}{H}_{{\sigma }_i}^{B,B})$ and we have the decomposition

$${\sigma }_1\equiv \sum _{i=1}^r{\omega }_{i,1}{\mathbf{e}}_{{\zeta }_i},{\sigma }_2\equiv \sum _{i=1}^r{\omega }_{i,2}{\mathbf{e}}_{{\zeta }_i},$$

with ω_i,j > 0, i = 1,…, r, j = 1, 2. We deduce that $H_{{\sigma }_1}\in {\mathcal{E}}_r^k(\mathbf{i})$ and all the elements of the line (H_σ, H_σ1) which are in F are also in ${\mathcal{E}}_r^k(\mathbf{i})$. Since F is convex, we deduce that $F\subset {\mathcal{E}}_r^k(\mathbf{i})$.

Remark 5.4

A cubature formula is interpolatory when the weights are uniquely determined from the points. From the previous theorem and proposition, we see that if a cubature formula is of minimal rank and interpolatory, then it is an extremal point of ℋ^k(i).

According to the previous proposition, by minimizing the nuclear norm of a random matrix, we expect to find an element of minimal rank in one of the faces of ℋ^k(i), provided k is big enough. This yields the following simple algorithm, which solves the SDP problem, and checks the flat extension property using Algorithm 1. Furthermore it computes the decomposition using Algorithm 2 or increases the degree if there is no flat extension:

Algorithm 3

• $k:=\lceil \frac{deg(V)}{2}\rceil$; notflat := true; P:= random s_k × s_k matrix;

• While (notflat) do

  • Let σ be a solution of the SDP problem: min_H∈ℋ^k(i) trace(P^tHP);

  • If $H_{\sigma }^k$ is not a flat extension, then k := k + 1; else notflat := false;

• Compute the decomposition of $\sigma ={\sum }_{i=1}^r{w}_i{\mathbf{e}}_{{\zeta }_i}$, ω_i > 0, ζ_i ∈ ℝⁿ.

6. Examples

We now illustrate our cubature method on a few explicit examples.

Example 6.1 (Cubature on a square)

Our first application is a well known case, namely, the square domain Ω = [−1, 1] × [−1, 1]. We solve the SDP problem (6), with a random matrix P and with no constraint on the support of the points. In the following table, we give the degree of the cubature formula (i.e. the degree of the polynomials for which the cubature formula is exact), the number N of cubature points, the coordinates of the cubature points and the associated weights.

Degree	N	Points	Weights
3	4	±(0.46503, 0.464462)	1.545
		±(0.855875, −0.855943)	0.454996
5	7	±(0.673625, 0.692362)	0.595115
		±(0.40546, −0.878538)	0.43343
		±(−0.901706, 0.340618)	0.3993
		(0, 0)	1.14305
7	12	±(0.757951, 0.778815)	0.304141
		±(0.902107, 0.0795967)	0.203806
		±(0.04182, 0.9432)	0.194607
		±(0.36885, 0.19394)	0.756312
		±(0.875533, −0.873448)	0.0363
		±(0.589325, −0.54688)	0.50478

The cubature points are symmetric with respect to the origin (0, 0). The computed cubature formula involves the minimal number of points, which all lie in the domain Ω.

Example 6.2 (Barycentric Wachpress coordinates on a pentagon)

Here we consider the pentagon C of vertices v₁ = (0, 1), v₂ = (1, 0), v₃ = (−1, 0), v₄ = (−0.5, −1), v₅ = (0.5, −1).

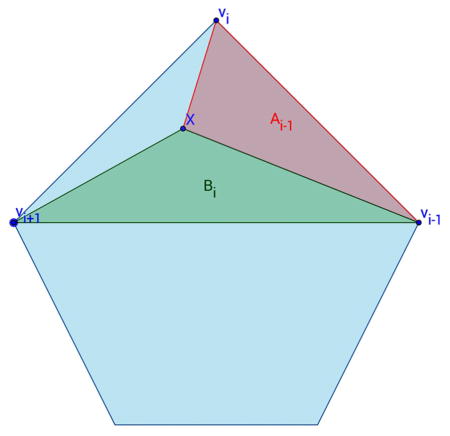
To this pentagon, we associate (Wachpress) barycentric coordinates [43], which are defined as follows. The weighted function associated to the vertex v_i is defined as:

$$w_i(\mathbf{x})=\frac{A_{i-1}-B_i+A_i}{A_{i-1}·A_i}$$

where A_i is the signed area of the triangle (x, v_i−1, v_i) and B_i is the area of (x, v_i+1, v_i−1). The coordinate function associated to v_i is:

$${\lambda }_i(\mathbf{x})=\frac{w_i(\mathbf{x})}{{\sum }_{i=1}^5{w}_i(\mathbf{x})}.$$

These coordinate functions satisfy:

• λ_i(x) ≥ 0 for x ∈ C

• ${\sum }_{i=1}^5{\lambda }_i=1$,

• ${\sum }_{i=1}^5{v}_i·{\lambda }_i(\mathbf{x})=\mathbf{x}$

For all polynomials p ∈ R = ℝ[u₀, u₁, u₂, u₃, u₄], we consider

$$I[p]=\underset{\mathbf{x}\in \mathrm{\Omega }}{\int }p\circ \lambda (\mathbf{x})d\mathbf{x}.$$

We look for a cubature formula σ ∈ R^* of the form:

$$\langle \sigma \mid p\rangle =\sum _{j=1}^r{w}_{j}p({\zeta }_j)$$ (8)

with w_i > 0, ζ_i ∈ ℝ⁵, such that I[p] = 〈σ | p〉 for all polynomials p of degree ≤ 2.

The moment matrix $H_{\sigma }^{B,B}$ associated to B = {1, u₀, u₁, u₂, u₃, u₄} involves moments of degree ≤ 2:

$$H_{\sigma }^{B,B}=\left(\begin{array}{cccccc}2.5000& 0.5167& 0.5666& 0.5167& 0.4500& 0.4500\\ 0.5167& 0.2108& 0.1165& 0.0461& 0.0440& 0.0992\\ 0.5666& 0.1165& 0.2427& 0.1165& 0.0454& 0.0454\\ 0.5167& 0.0461& 0.1165& 0.2108& 0.0992& 0.0440\\ 0.4500& 0.0440& 0.0454& 0.0992& 0.1701& 0.0911\\ 0.4500& 0.0992& 0.0454& 0.0440& 0.0911& 0.1701\end{array}\right)$$

Its rank is rank $(H_{\sigma }^{B,B})=5$.

We compute $H_{\sigma }^{B^{+},B^{+}}$. In this matrix, there are 105 unknown parameters. We solve the following SDP problem

$$\begin{array}{ll}min\hfill & \text{trace}(H_{\sigma }^{B^{+},B^{+}})\hfill \\ \text{s.t.}\hfill & H_{\sigma }^{B^{+},B^{+}}\succcurlyeq 0\hfill \end{array}$$ (9)

which yields a solution with minimal rank 5. Since the rank of the solution matrix is the rank of $H_{\sigma }^{B,B}$, we do have a flat extension. Applying Algorithm 1, we find the orthogonal polynomials ρ_i, the matrices of the operators of multiplication by a variable, their common eigenvectors, which gives the following cubature points and weights:

Points	Weights
(0.249888, −0.20028, 0.249993, 0.350146, 0.350193)	0.485759
(0.376647, 0.277438, −0.186609, 0.20327, 0.329016)	0.498813
(0.348358, 0.379898, 0.244967, −0.174627, 0.201363)	0.509684
(−0.18472, 0.277593, 0.376188, 0.329316, 0.201622)	0.490663
(0.242468, 0.379314, 0.348244, 0.200593, −0.170579)	0.51508