Significance
Touchscreens have redefined human–computer interfaces. Although flexibility in the design of interfaces has dramatically increased, users are still confronted with a flat, featureless glass plate that cannot provide any tactile cues. Exciting this plate with ultrasonic waves reduces the friction experienced by a user’s finger, enabling tactile feedback directly on the surface. For vibration amplitudes of ±3 μm, we measured a reduction of up to 95% in the friction force experienced by a sliding finger. Using special illumination techniques and microsecond imaging, we show that this reduction of friction is because of the skin bouncing on a layer of air trapped between the plate and the surface of the finger.
Keywords: acoustic, squeeze film, biotribology, roughness, haptics
Abstract
When touched, a glass plate excited with ultrasonic transverse waves feels notably more slippery than it does at rest. To study this phenomenon, we use frustrated total internal reflection to image the asperities of the skin that are in intimate contact with a glass plate. We observed that the load at the interface is shared between the elastic compression of the asperities of the skin and a squeeze film of air. Stroboscopic investigation reveals that the time evolution of the interfacial gap is partially out of phase with the plate vibration. Taken together, these results suggest that the skin bounces against the vibrating plate but that the bounces are cushioned by a squeeze film of air that does not have time to escape the interfacial separation. This behavior results in dynamic levitation, in which the average number of asperities in intimate contact is reduced, thereby reducing friction. This improved understanding of the physics of friction reduction provides key guidelines for designing interfaces that can dynamically modulate friction with soft materials and biological tissues, such as human fingertips.
Holding a glass of wine, searching for keys in one’s pockets, and assessing the quality of fabric are everyday tasks that involve precise and unambiguous perception of the friction between the skin and the environment. The somatosensory and motor control systems integrate multiple neural signals to determine the state of adhesion of the surface in contact with the skin, thus enabling perception (1–3) and in the context of grasp, ensuring that slippage is under control (4–6). Considering the central role of fingertip–surface friction in both manipulation and tactile perception, it is not surprising that many technologies attempt to control this effect to produce artificial and programmable tactile sensations (7–9). The use of transverse ultrasonic vibrations to reduce tactile friction (10) has proven to be a strong candidate for surface haptic displays that might be integrated with the ubiquitous touchscreen interface (11–13). A typical architecture consists of a glass plate—which may be placed in front of a graphical display—with piezoelectric actuators glued along one edge and used to excite a flexural resonance. The resonant frequency may be ∼30 kHz and the peak to peak vibration amplitude may be up to 5 μm at the antinodes. A finger placed on the plate experiences markedly reduced friction as the vibration amplitude is increased as shown in Movie S1.
A full understanding of the physical principle behind friction reduction has proven elusive. Two leading hypotheses have been put forward. The first hypothesis stems from an application of Reynolds’ lubrication theory to the thin film of air between the fingertip and vibrating plate. The vibrations lead to time-averaged compression of the air, thereby creating an overpressure that levitates the skin. The second hypothesis postulates that the skin does not stay in close contact with the surface but instead, bounces off of it, leading to shorter time in contact and therefore, a time-averaged reduction in friction.
We present evidence that the friction reduction effect cannot be fully explained by either of these theories. We argue that friction reduction is the result of a load sharing between compressed air and those asperities on the skin that are in intimate surface contact. Other recent evidence shows that the dynamics of the skin (in particular, its viscoelastic properties) is key to friction reduction (14). Combined with our evidence, the picture that emerges is of friction reduction by bouncing but bouncing off of compressed air as well as the surface.
Background
The roughness of the skin is often modeled as a random height profile following a normal distribution (15). When in contact with a plate, at rest or in motion, the contact area with the skin is formed by deformation of the highest peaks (asperities) when they come into intimate contact with the counterbody. This area, called the true area of contact, is often several orders of magnitude smaller than the apparent contact area seen at a macroscopic scale. Various models have been used to estimate the value of the true area as a function of the applied force. Greenwood and Williamson (16) treated asperities as spheres of constant radius and random heights. Bush et al. (17) went further to treat both the surface profile and the gradients as correlated random processes. In both papers, Hertzian contact mechanics were used to derive a relation between force and contact area (16, 17). More recently, Persson (18) has used a self-similar fractal model of the surface profile to derive the relation between the interfacial separation—the average gap between both surfaces—and the external load. Interestingly, all of these theories converge to the same relationship for small loads, wherein the true area of contact is proportional to the negative exponential of interfacial separation.
The true area of contact has a central role in friction. Each asperity making intimate contact can support an adhesive shear load proportional to its contact area. The friction force experienced by the finger is the sum of the shear loads on the contacting asperities (19). Because friction force is proportional to true area of contact, whic itself is proportional to load, according to multiscale theory of contact (15), we can appreciate the basis for Amonton’s first and second laws that state that friction is proportional to normal load and independent of the macroscopic apparent area. The value of the interfacial shear stress for the skin of fingertips on glass usually is found to be ∼4.8 kPa (20, 21). Measurement of the true area of contact by acoustical and optical methods supports this adhesive view of friction (22–24). Moisture significantly affects tactile friction by softening the stratum corneum, enabling it to conform better to the surface, which greatly increases the true area of contact (15, 25–27). In this study, moisture is likely responsible for much of the variability in friction force measurements. When a fingertip is pressed against a very flat surface, such as glass, the sweat glands are occluded, and moisture builds up rapidly. We also developed an artificial finger, enabling us to explore the mechanics of friction reduction without suffering from the measurement variability introduced by moisture.
Because all models of fingertip friction lead to the conclusion that friction is proportional to the true area of contact, we ask if this is also true in the case of ultrasonic friction reduction? Also, if this statement is true, by what mechanism does vibration reduce the time-averaged area of contact? In seeking answers, one consideration must be the role of air. It is well-known that acoustic waves in air create a radiation pressure when reflecting off an object (28). For smooth planar objects, stable levitation can occur when the acoustic radiation pressure balances the weight (29, 30). For levitation distances significantly smaller than the wavelength of sound (i.e., by at least three orders of magnitude), the behavior becomes dominated by the elasticity and viscosity of the fluid trapped between the actuator and the reflector surface (31, 32). This trapped fluid is known as a squeeze film. In this scenario, which is typical of tactile friction reduction devices, a squeeze film levitation model may be derived from the Reynolds’ lubrication equation to compute the levitation force (33–35). This model depends on a nondimensional “squeeze number” that is, essentially, a ratio of the time required to squeeze air out of the gap to the period of oscillation. For large-enough squeeze numbers, the air may be considered to be completely trapped, and the pressure may be shown to be , where is atmospheric pressure, α is the amplitude of motion, and u is the squeeze film thickness. Acoustic levitation does not on its own, however, explain the progressive reduction of friction with increasing vibration amplitude that is observed in tactile interfaces. Watanabe and Fukui (10) proposed that the load is shared between points in intimate contact and the overpressured film of air and presented a simple model. Their predictions, however, do not match the amplitude dependence that we present here, and they do not provide experimental validation (10).
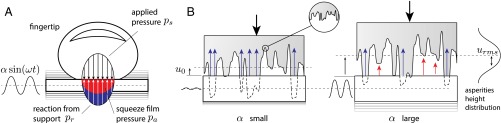
In this study, the contact area between a human fingertip and a vibrating glass plate was imaged by frustrated total internal reflection. This technique provides a detailed picture of the spatiotemporal behavior of the contact area, which is shown to be consistent with predictions stemming from a combination of squeeze film theory and an exponential contact model. Fig. 1 illustrates the balance of forces proposed in this research.
Fig. 1.
(A) Balance of time-averaged pressure when the plate undergoes ultrasonic vibrations. (B) View of the asperities. At low amplitude, the reaction from the support balances the pressing force completely. At high amplitude, both the reaction from the support and the squeeze film pressure contribute to balancing the pressing force. In addition, the average interfacial separation is increased.
Results and Discussion
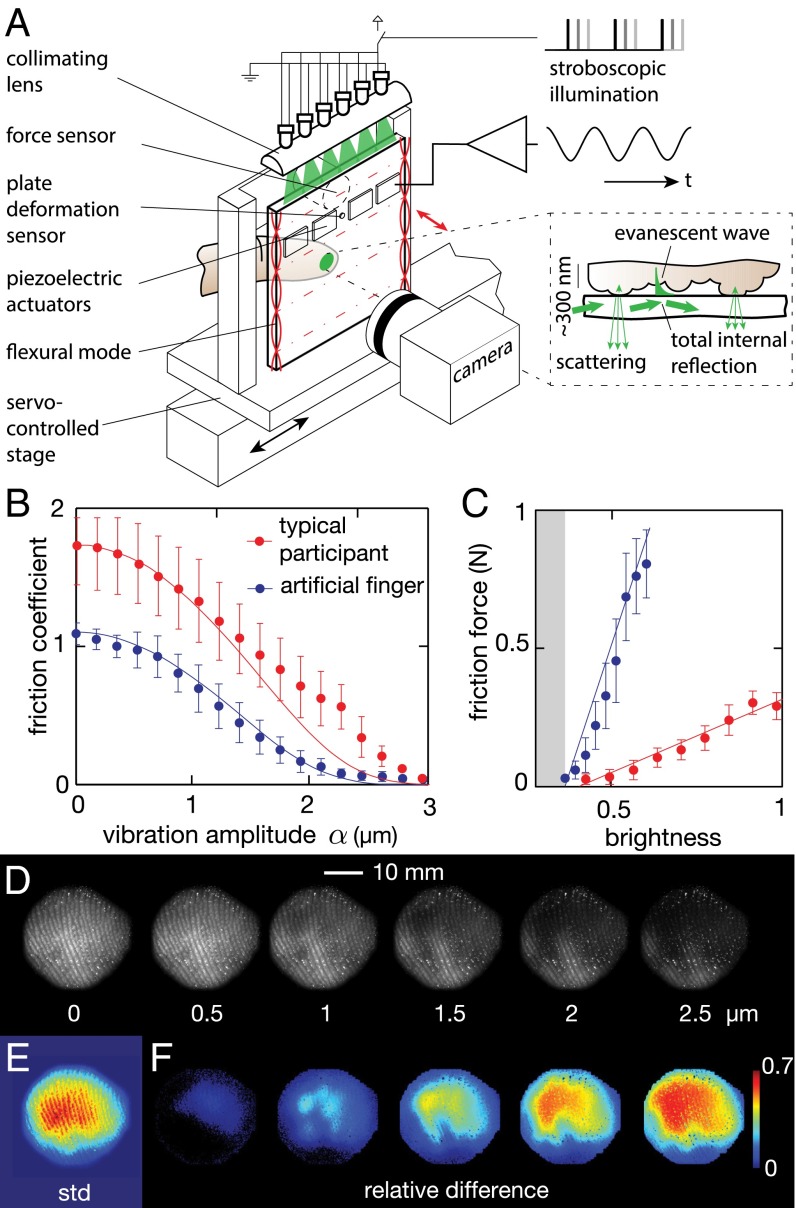
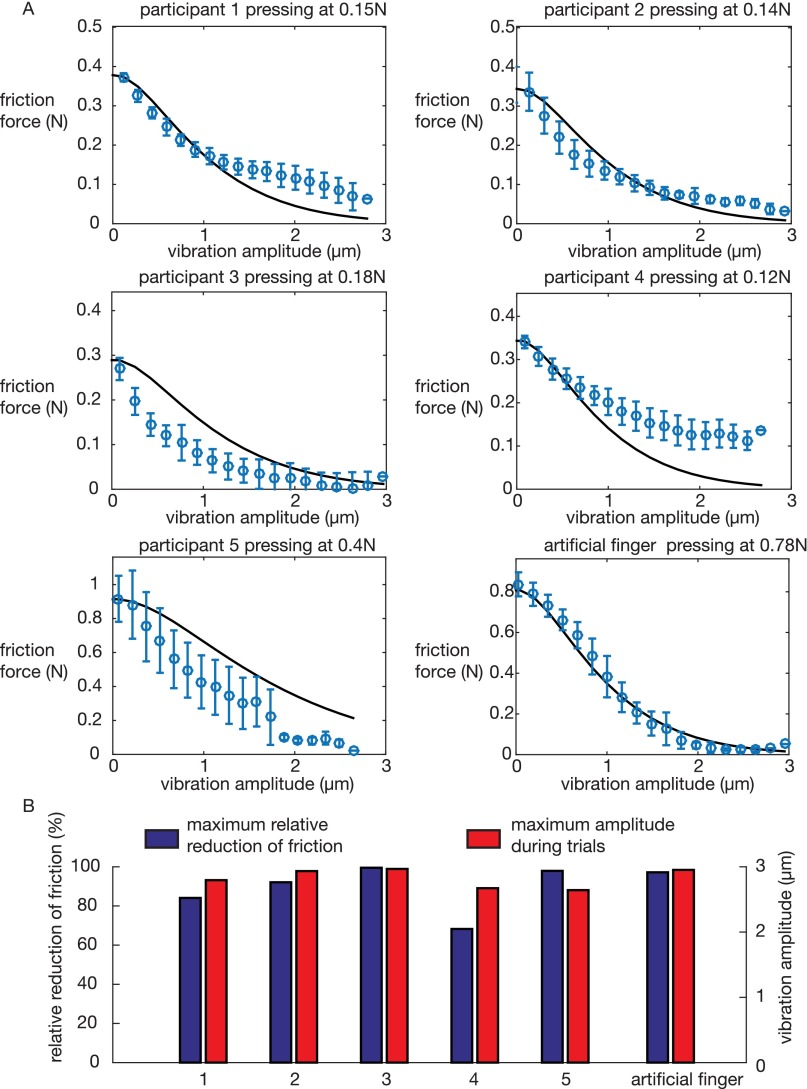
Each participant placed his or her finger on a glass plate that was driven side to side by a servomechanism for the purpose of measuring friction, and it experienced various amplitudes of ultrasonic vibration. The tribometric measurements confirmed that the friction force resisting the lateral motion consistently decreased as the amplitude of the out of plane oscillation increased. The reduction of friction reached 70% to 98%, with an average across participants of 90% at an amplitude of 3 μm and a frequency of 29 kHz. A schematic of the apparatus is shown in Fig. 2A and construction details are presented in SI Materials and Methods. No correlation with age or moisture of the skin could be established. The relation between amplitude and friction force is monotonic, and in some cases, a plateau is observed at low amplitude. For large-enough amplitudes, the curve flattens as it approaches near-frictionless contact, as seen in Fig. 2B. The relationship between friction force and amplitude of vibration for each participant is compared with the model in Fig. S1.
Fig. 2.
(A) Experimental setup. The vibrating plate is mounted on a servo-controlled stage equipped with a six-axis force sensor. Illumination from the side of the plate provides a uniform illumination of the true contact area through frustrated total internal reflection (A, Inset). (B) The sliding friction force gradually decreases with increasing vibration amplitude. The line represents the (C) brightness and friction force correlation. The illumination technique reveals those asperities that are within a few hundred nanometers of the plate; therefore, the spatial average of the brightness received by the camera is linearly correlated with the friction force and under the adhesive theory of friction, linearly correlated with the true area of contact. (D) Images of the contact area under ultrasonic vibration amplitudes of 0–2.5 μm. (E) Spatial distribution of the variation of brightness over a cycle where the amplitude of stimulation is slowly varying. The center of the contact experiences the most variation, whereas the edge remains unaffected. (F) The difference between the brightness at selected amplitudes and the brightness at rest highlight those areas that are more or less affected by vibration.
Fig. S1.
(A) Friction measurement for each participant compared with the prediction from the model, with . (B) Summary of the effectiveness of the friction reduction at the maximum vibration amplitude tested.
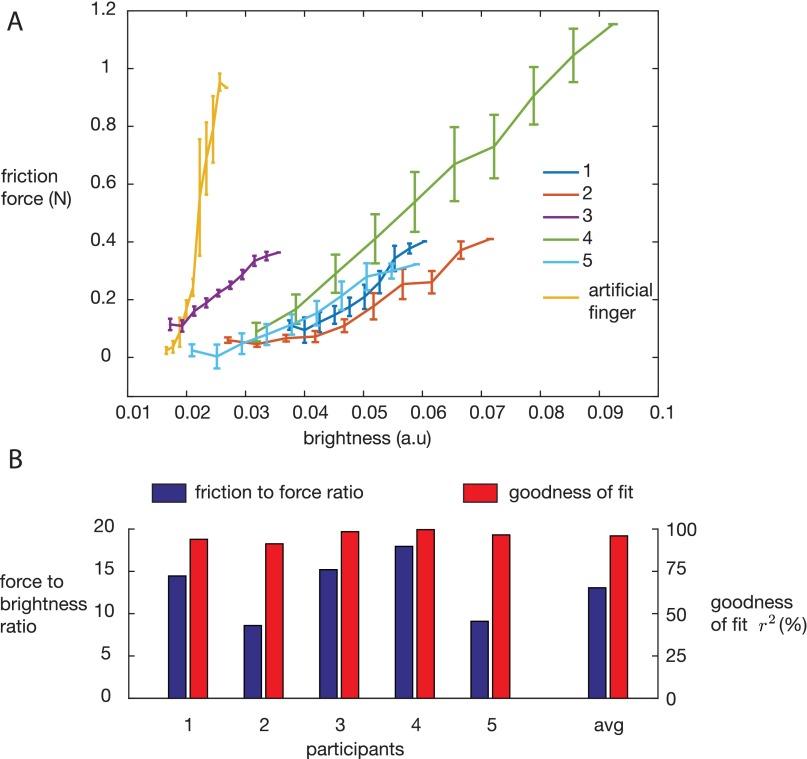
The contact imaging scheme used here leverages frustrated total internal reflection, which illuminates only those asperities that are within a few hundred nanometers of the glass plate, thus producing highly contrasted images of the area of contact. Each pixel of the image receives an amount of light that is proportional to the sum of the area made by every single asperity in intimate contact and thus, offers an estimation of the local true area of contact. A typical recording is shown in Movie S2. Simultaneous measurement of kinetic friction force and imaging of the scattered light from the skin reveals a remarkable correlation between the overall brightness of contact and the instantaneous friction force while sliding. A linear relationship was found between total brightness and friction force, with coefficients of determination r2 = 0.83–0.96 for the human subjects and r2 = 0.88 for the artificial finger. The error can be explained by the diffusivity of the skin and surroundings as well as force sensor noise. Data and regressions are given in Fig. 2C. This correlation is well in line with the adhesive theory of friction discussed above. The ratio between brightness and force remains within a 30% margin across participants. The variation is likely caused by differences in reflectance of the skin as well as the presence of moisture and the dynamics of friction. Movie S3 illustrates that the contact area fluctuates during steady-state sliding and exhibits dynamics after a rapid change in vibration amplitude. These effects explain some of the variation in friction force measurement. Because of a different reflectance, the artificial finger has a ratio of brightness to force eight times larger than the average human finger, but it shows the same linear correlation. The strong linear relationship seen in Fig. 2C and Fig. S2 is the basis for treating the frustrated total internal reflection measurement of contact area as a proxy for friction force. Notably, frustrated total internal reflection imaging provides data at temporal and spatial scales out of reach for standard force sensors.
Fig. S2.
(A) Relationship between friction force while sliding and the brightness of the contact patch. The observed linearity is expected, because both friction and brightness are proportional to the true area of contact. (B) The ratio of force to brightness for all human participants. The artificial finger has a value of 120 on this scale.
The reduction of contact area with increasing vibration amplitude is an indicator that the process involves squeeze film levitation and does not solely rely on intermittent contact of the finger. In fact, if a squeeze film did not support some of the normal load, the brightness of the contact, averaged over thousands of cycles, would remain constant, because the average contact force would necessarily balance the applied force. Clearly, this constant brightness is not the case. Thus, air plays a critical role in reducing the true area of contact by increasing the interfacial separation.
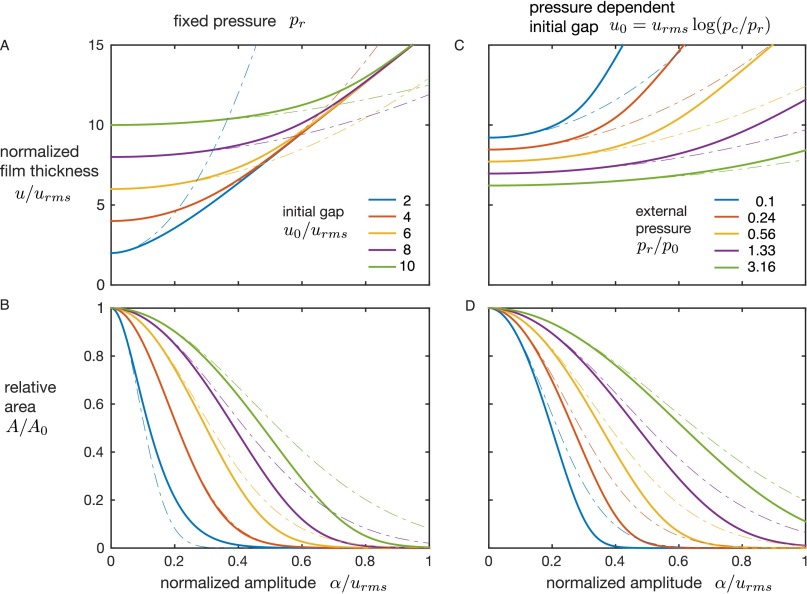
At the scale of the entire finger pad, the measurement fits well with the theory of squeeze film levitation. As the plate oscillates, the air trapped between it and the skin cannot escape and gets compressed. This compression follows a nonlinear process that creates a net force pushing the skin away from the plate and increasing the interfacial separation between the skin and the glass. However, because the roughness of skin is almost one order of magnitude larger than the increased separation, some contacting asperities never do break contact, leading to only partial reduction of friction. The pressing force that pushes the skin toward the glass is balanced by the force from squeeze film pressure as well as the resultant force from the asperities that remain in intimate contact. Both reaction forces depend on the interfacial separation u but with different relations. The contact forces typically fall off as , whereas the squeeze film force is proportional to . Because the pressing force is perfectly counterbalanced by the contact force when , the equilibrium may be written as . The full derivation is presented in SI Results and Discussion and results illustrated in Fig. S3. The comparison with measurement shows good agreement, especially in the low-amplitude regime where the acoustic force is small.
Fig. S3.
Representative results from the model. Solid lines are found by numerical solution of Eq. S11, and dashed lines are the first-order approximation described in S13. A and B are the interfacial separation and resulting relative area of contact for various initial separations and constant external pressures between conditions, respectively. C and D are the same output with an initial separation that depends of the external pressure. This last condition corresponds to the contact with an elastic body, which follows Eq. S2.
It is also instructive to look at the spatial distribution of brightness across the finger pad. The contact between the finger and the plate is roughly an ellipse shape as expected from the contact of an ellipsoid and a plane. The luminance field across this ellipse provides information about the local contact pressure, which may be calculated by multiplying the local brightness by the overall ratio of normal force to total brightness. The results show that normal pressure is maximum at the center of the ellipse and decreases toward the edges in a parabolic fashion, which is consistent with the Hertzian contact previously reported in the literature (21, 36, 37). The distribution of pressure fits , where r is the radial coordinate, is the lateral shift, and a is the radius of the apparent contact area. The goodness of fit for each participant varies between r2 = 0.92 and r2 = 0.98, and Hertzian pressure is on the order of kPa.
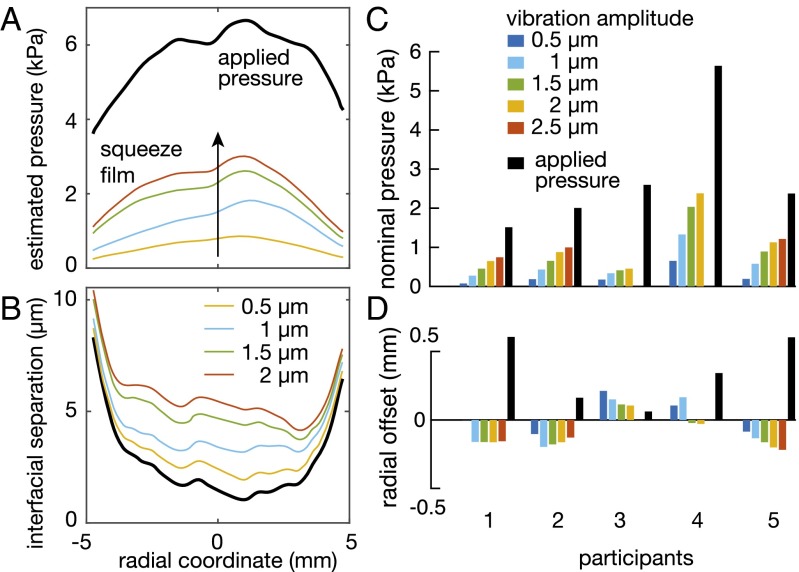
The addition of plate vibrations has a distinctive effect on the contact pressure. By subtracting the brightness of the resting finger from the brightness of the contact during vibration, the overpressure caused by the squeeze film can be estimated as illustrated in Fig. 3A. For each participant, the squeeze film pressure is highest in the center of the contact area and falls off to zero toward the edges. At first glance, it could be postulated that this distribution of squeeze film pressure is caused by an edge effect: the squeeze film pressure is constrained to be atmospheric at the edge and therefore, expected to increase toward a maximum value in the center. Such a broad edge effect, however, would be associated with an unrealistically small squeeze number. Fitting the distribution of pressure derived from the lubrication theory in the works in refs. 35, 38, and 39 to the data leads to squeeze number between 1 and 30, whereas the value derived from estimates of contact area, frequency, and interfacial displacement is between 150 and 1,000. At these higher values, the edge effect should be quite minimal. Instead, a more plausible explanation arises from the observation that the nominal gap between the skin and plate is not uniform across the contact because of the Hertzian pressure distribution. The applied pressure is maximum in the center, which in turn, means that the nominal interfacial separation is smaller at the center, producing a stronger squeeze film effect according to .
Fig. 3.
(A) Local brightness corresponds to the number of asperities in contact, which depends on pressure. Brightness scaled by the normal force reveals the pressure profile along the central axis of the contact. The squeeze film pressure is highest in the center of the contact. (B) Calculated interfacial separation. Larger applied pressure in the center results in a lower gap, which in turn, influences the acoustic radiation pressure created by the squeeze film of air. (C and D) Results from the fitting procedure with a Hertz contact model. The nominal pressure and the squeeze film pressure are asymmetric.
For convenience, the estimated acoustic pressure distribution was also fitted with a Hertzian profile, for which the goodness of fit reached . Although the nominal pressure increased with increasing amplitude (Fig. 3C), the lateral shift (Fig. 3D) and the estimated radius of action a remained within 10% of the average value across amplitudes. The estimated radius a of the acoustic pressure distribution was systematically smaller than the radius of the nominal contact area by an average of mm, which is likely to be because of the departure of acoustic pressure distribution from a Hertzian model. The position shift of the center of the squeeze film pressure distribution was also quite different from the normal pressure distribution. Although the normal pressure is shifted toward the proximal section of the fingertip, the squeeze pressure is, for the most part, shifted distally. This asymmetry is likely to be the result of the complex structure of the s.c. tissues and bone that have spatially dependent mechanical properties.
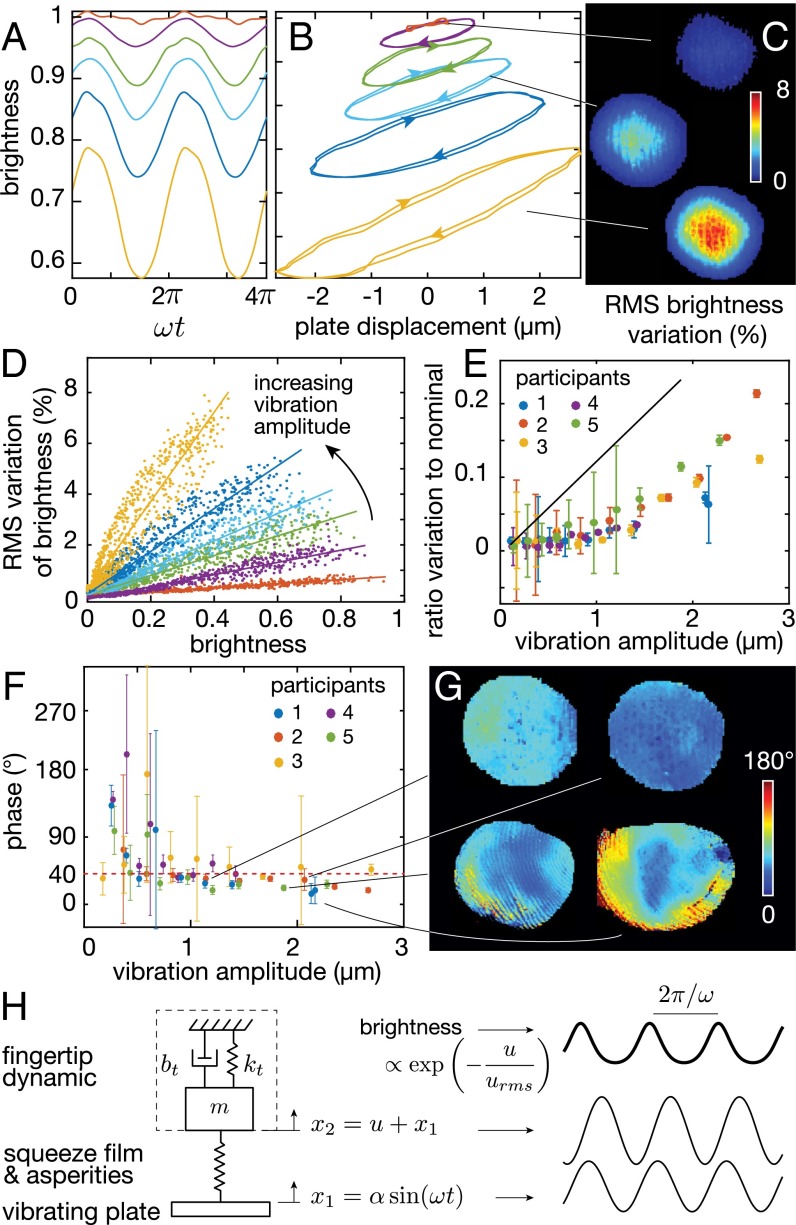
High-speed stroboscopy was used to image the intracycle contact area with a time resolution of 1 , revealing that dynamic effects are at play. Fig. 4 A and B illustrates the typical dependence of brightness on phase and plate displacement. Brightness of the contact is nearly sinusoidal at the plate vibration frequency, with total harmonic distortion between −10 and −8 dB for amplitudes higher than 0.5 . Consistent with long-exposure results, the average brightness decreases as the vibration amplitude increases. However, the peak to peak variation of brightness increases significantly with increasing amplitude, from 0% to 22% of the nominal brightness. Movie S4 depicts a representative sample of the brightness variations on a microsecond timescale.
Fig. 4.
(A) Time domain variation of brightness. Changes in brightness closely follow a sinusoidal pattern. (B) Phase portrait of brightness and plate position. Increased amplitude decreases the average brightness but increases the variation. (C) Selected images of the spatial distribution of brightness variation. (D) Variation and average brightness are correlated in each image. The lines are linear regressions. (E) The ratio is a function of the amplitude of stimulation. The prediction from a model with large skin roughness is in black. (F) Phase between motion of the plate and the interfacial separation as a function of amplitude and participant. (G) Selected spatially distributed phase plots. Large variations of phase occur across trials. (H) Simplified linear model of the skin bouncing off the film of air leads to behaviors similar to the experimental observations.
Remarkably, at a fixed amplitude of vibration, the temporal variation and nominal value of brightness are in proportion for the majority of pixels in the contact image as shown in Fig. 4D. This correlation can be explained if we consider that the true area of contact is , with u being the gap during levitation and being the gap at rest. The variation of levitation height caused by the combined motion of the plate and the skin induces a change in brightness so that . The ratio between fluctuation and average value of the brightness is fully derived in SI Results and Discussion, and experimental values of this ratio are graphed in Fig. 4E as a function of amplitude for each participant.
It is worth noting that the data lean toward refuting the hypothesis of intermittent contact and instead, favoring the hypothesis of load sharing between a squeeze film and asperities. Indeed, the maximum brightness observed with the stroboscopic illumination consistently decreased with increasing amplitude. This observation means that the smallest interfacial separation between the vibrating glass plate and the skin increases with increasing amplitude of the plate vibrations. If intermittent contact was the main mechanism, the impact caused by the collision would create a spike of brightness greater than that seen when the vibration is turned off. However, no spike in brightness was ever observed, ruling out the pure intermittent contact hypothesis.
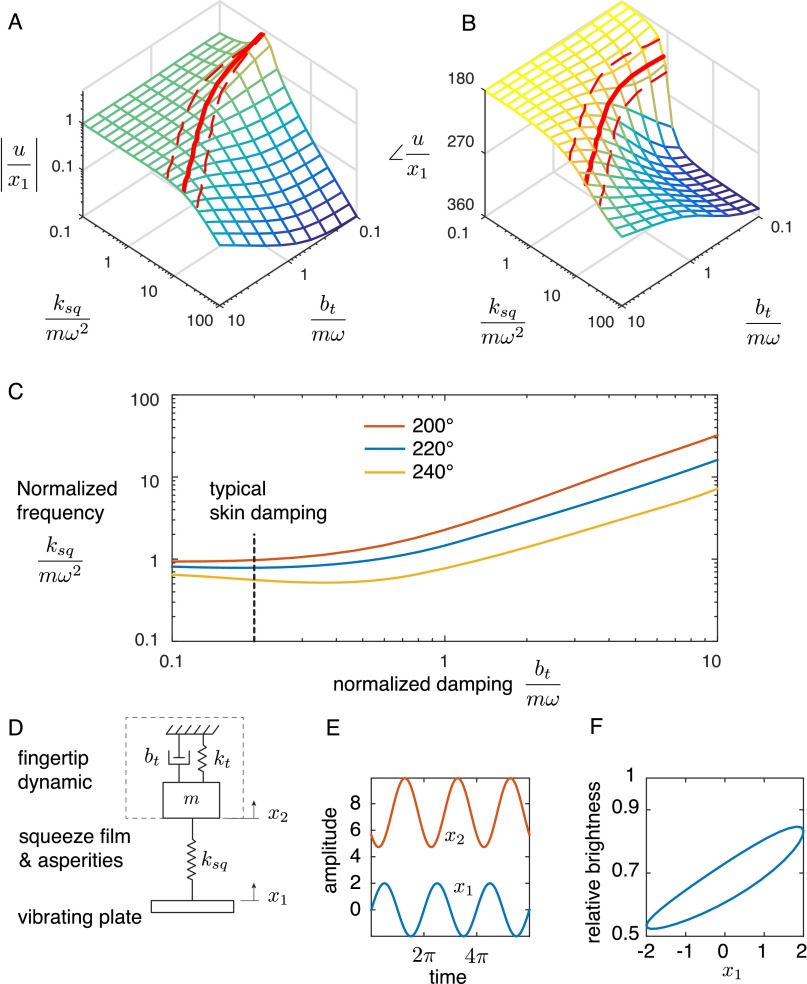
Nonetheless, the dynamics of skin seems to play a role as seen in the phase difference of the brightness fluctuations relative to the instantaneous displacement of the plate. A phase lead of the brightness fluctuation of is observed for each participant at amplitudes ranging from 0.5 to 2.5 without significant influence of amplitude as shown in Fig. 4F. The spatial distribution of the phase difference varies widely between subjects and trials. Representative distributions are shown in Fig. 4G. The phase lead is evidence that the dynamics of the finger tissue plays a significant role. If the tissues were to have a much lower impedance than the squeeze film and asperities, then very little brightness variation should occur. If, alternatively, the tissues were to have a much higher impedance, then the brightness variation would be in phase with the plate motion. However, the phase lead in brightness—which itself is out of phase with the instantaneous value of the gap—suggests that the skin motion actually lags the plate motion by a considerable amount. The lag can be attributed to the inertia of the skin and various energy dissipation mechanisms, including viscoelasticity, acoustic radiation, and scattering. To gain additional insight, the skin was modeled as a simple mass–spring–damper excited by an elastic squeeze film. Simulations confirmed that certain parameter values will, indeed, lead to a brightness phase lead of 40° (Fig. 4H and Fig. S4). Finger dynamics are discussed in greater detail in SI Results and Discussion.
Fig. S4.
Dynamics of the gap u as modeled by a second-order system excited with an elastic squeeze film . (A) Relative amplitude and (B) relative phase of the variation of the gap with respect to the vibration of the plate for a set of squeeze film springs and different skin dissipation . Each parameter is normalized to the impedance of the inertia. The thick red lines show the locus for which the phase difference is 220°, and the dashed lines represent a 20° tolerance. (C) Locus of squeeze film stiffness and skin damping values for which the phase of the gap with respect to the plate motion corresponds to the experimental data (i.e., from 200° to 240°). There is almost no sensitivity to normalized damping for values lower than 0.5, which highlights the robustness to variation in skin properties. (D) Illustration of the model. (E) Model prediction of the movement of the plate. (F) Estimated relative brightness, which matches relatively well the experimental data in Fig. 4, despite the assumption of linear dynamics.
The oscillation of the interfacial separation is an indicator that the skin is partially bouncing but without completely detaching, because brightness never reaches zero. Moreover, the absence of a brightness spike suggests that collisions are cushioned by the squeeze film of air, preventing the creation of new contact points.
The relation between average levitation gap and vibration amplitude does not seem to follow a linear relationship as predicted when squeeze film theory is applied to a flat, rigid plate (30, 32). One possible explanation is that the interfacial separation is strongly affected by the dynamics of the fingertip. For instance, if the fingertip were purely elastic, the skin and the plate would be in phase, and the time-averaged gap as well as the friction would be unaffected by vibration amplitude. However, the inertia and damping of the fingertip could make the skin oscillate out of phase with the plate, effectively doubling the time-averaged interfacial separation and thus, reducing the friction. Previous measurements with artificial fingers show that the dynamic properties of the material do have a large impact on friction reduction (14). Moisture also plays a role by increasing the adhesion between the surface and the skin as can be seen in Movie S5, which shows the formation of an air bubble underneath the contact with moist skin.
SI Materials and Methods
Friction Reduction Device.
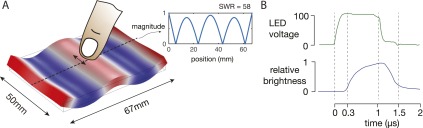
The friction reduction apparatus was built around a 67 × 50 × 5-mm3 borosilicate glass plate actuated by two piezoelectric transducers (smpl131w89t10; Steminc). The plate was excited in the 3 × 0 normal mode, which corresponds to a standing flexural wave with 19-mm nodal spacing at a resonant frequency of = 29,080 Hz. A finite element analysis (Comsol Multiphysics 5.0) presented in Fig. S5A shows the modal shape of the plate. The finite element analysis reveals that the standing wave ratio is 58 with a fingertip, modeled by 20 N⋅s/m damper, in contact with the center of the plate. In the experiment, only the center crest was used to provide the out of plane motion necessary to reduce friction. The amplitude of the center antinode varies by only 3% of its nominal value. The real time deformation of the glass is measured by a piezoelectric disk that was calibrated with a laser Doppler vibrometer. A power amplifier (A-303; A.A. Lab System Ltd) drives the actuators over a range of 200 V, which translates to a maximum unloaded displacement of 3 m, constant over the entire width of the plate.
Fig. S5.
(A) Finite element simulation of the flexural mode shape of the plate used in the experiments. Subjects placed their index finger in contact with the center antinode. The design of the plate is optimized for maximum uniformity of the vibration amplitude along the width of the plate. A, Inset shows the magnitude of the vibration along the length. The calculated standing wave ration (SWR) is 58. (B) Measurement of the time response of the LED during a short impulse. The pulse width is under , which gives an effective stroboscopic illumination bandwidth of 1 MHz.
Friction Experiment.
The ultrasonic plate and the illumination system were mounted on a servo-controlled stage (KR26; THK Co.) equipped with a six-axis force sensor (Nano 17; ATI Industrial Automation). The device measures normal and lateral forces while sliding the plate across the static finger at a 10-mm/s velocity. The stage was driven with a trapezoidal velocity profile to provide a constant velocity over the region of interest, avoiding the effect of the plate inertia on force measurements. The camera was placed at the other side of the plate pointed at the finger in contact with the glass. The position of the slide, forces acting on the glass, and amplitude of the vibration were measured by a 16-bit data acquisition board at a rate of 2 kHz. The data were numerically filtered by a zero-lag, four-pole Butterworth filter with a cutoff frequency 100 Hz, and then, they were down-sampled to match the timestamp provided by the camera. The resulting noise floor was 10 mN.
Imaging System and Image Processing.
The experiment used frustrated total internal reflection to provide a high contrast between the regions that are in intimate contact with the glass and the background. Frustrated total internal reflection imaging is based on the coupling of the material in contact (i.e., the skin) with the electromagnetic evanescent wave present at the surface of the glass plate. For an incident electromagnetic wave of wavelength-λ reflecting at an angle with the surface-θ, the evanescent wave decays exponentially with the distance z away from the plate, such that brightness , where , and is the relative refraction index between glass and air. In this experimental setup, the light was provided at the edge of the glass plate by 10 high-power green LEDs (XPEBGR, Cree Inc.) with a wavelength of nm focused to a narrow beam by a planoconvex lens over a 60-mm span. In the described condition, the brightness is reduced to 5% of its initial value when the objects are 300 nm apart.
To measure the time-averaged brightness of the contact, the illumination was driven by a constant current source of 1 A while the ultrasonic vibration was turned on. The skin and plate undergo a harmonic motion and reach steady state within milliseconds. High-speed imaging relies on the steady-state behavior by illuminating the contact with stroboscopic flashes that are synchronously triggered with the motion of the plate. The evolution of the contact is imaged at a reduced pace corresponding to the difference between the frequency of the ultrasonic vibration and the frequency of the light flashes. In these experiments, the rate is reduced to 1.0 Hz. The illumination was driven with 60-V pulse signal at a frequency Hz, where is the frequency of the ultrasonic vibration, and width is 1 s. The dynamic light source was verified with a photodiode having a 150-MHz frequency bandwidth (PDA10A; Thorlabs Inc.). The time response of the illumination is shown in Fig. S5B. The light pulse is shorter than 1.2 s, allowing for a time resolution of 30 points per cycle of the 30-kHz ultrasonic vibration. The delay between the rising edge of the pulse and the beginning of the light pulse was 0.4 s and accounted for during the postprocessing. The images of the contact were captured by a CCD camera (v5.1; Phantom Vision Research) equipped with a macrolens (Nikkor 105 mm; Nikon Corp.) at a rate of 50 images per second. The optical setup achieved a resolution of 18 m per pixel.
Microsecond imaging data were filtered to remove artifacts caused by tremors. To do so, the time evolution of each pixel was transformed into the Fourier domain, multiplied with a Dirac comb with the fundamental frequency as baseline, and then, converted back into the time domain.
SI Results and Discussion
Roughness and Nominal Separation.
When two elastic solids with rough surfaces are pressed together, they make contact only on a fraction of the apparent area composed by the contact of the tallest asperities. Larger normal pressures will increase the true area of contact by bringing more asperities into contact with the counterbody. The separation between the two surfaces as a function of lateral coordinates will vary in a random fashion and usually follow a normal distribution with SD (Fig. 1A). Many engineering and natural surfaces are self-affine fractal surfaces, where the roughness is defined at a certain level of magnification. In the case of skin, interferometer measurements of alginate casts reveal that the Hurst exponent is close to 0.8 and that the SD, when not compressed, is close to (15). The float borosilicate glass plate acting as a counterbody is considered perfectly rigid and smooth.
The Persson theory of contact states that the pressure from the reaction of the support is
| [S1] |
where is the absolute pressure coefficient that depends on the roughness and elastic properties of the material (18). In this case, is the magnification at which the rms of the height distribution is measured to be . is the Young’s modulus of the stratum corneum, and is its Poisson’s coefficient.
At rest, without any vibration, , the reaction from the support is equal in magnitude and opposite in direction to the external pressure , and the interfacial separation is denoted , which leads to an alternative expression for the Pearson pressure :
| [S2] |
This function leads to the following expression for the contact force: .
Levitation Forces from Squeeze Film Theory.
When subjected to transverse vibrations at ultrasonic frequencies, any air trapped between the rough surface of the skin and the plate undergoes a nonlinear compression cycle that results in a net levitation pressure. The Reynolds number under these conditions is typically in the order of , from which we conclude that inertia forces in the fluid are small compared with viscous forces and that the flow is laminar. Acoustic levitation pressure is then derived from the Reynolds equation:
| [S3] |
where is the instantaneous interfacial separation. The left-hand side captures Couette flow, and the right-hand side is the variation of molecular mass (time derivative of Boyle’s law). The squeeze number provides a nondimensionalized measure of the ratio between the elastic behavior of the air cushion and the viscous dissipation at the edge of the contact area. In the our configuration, the size of the contact is m, the angular frequency is , and the gap size is , which leads to a squeeze number .
The distribution of the squeeze pressure across the width of the contact is found to follow a uniform distribution within a 10% margin for squeeze numbers . For such a high number, the flow that escapes on the side of the contact is almost negligible. The reader can refer to refs. 35 and 38 for detailed analyses of the distribution of pressure.
Because no flow escapes the gap, the fluid mass remains constant or . The time integral of Eq. S3 over one cycle leads to
| [S4] |
with . Integrating twice over the spatial coordinate and noting that in the center of the contact leads to
| [S5] |
At the edge, the pressure is atmospheric, which leads to
| [S6] |
The rest of the contact undergoes isothermal expansion and contraction of the air; therefore, or . It follows that
| [S7] |
which leads to . The levitation pressure is the overpressure averaged across one cycle or
| [S8] |
for . For small separation u, the latter is well-approximated by the first term of its Taylor series expansion:
| [S9] |
Predictions from squeeze film theory are close to the prediction made by acoustic radiation pressure, which takes into account inertia. For a small gap, near-field acoustic pressure is , with the adiabatic index, ρ the air density, and the speed of sound in air. The acoustic radiation pressure predicts a force 50% smaller than squeeze film theory with large squeeze number. Zhao et al. (32) showed that, for small separation, the squeeze film theory is closer to the experimental. Conversely, as the levitation distance reaches a value for which the squeeze number , near-field acoustic levitation theory is more accurate (31).
Steady-State Equilibrium and Friction.
In steady state, the time-averaged pressing pressure is balanced by the time-averaged reaction of the support (Eq. S1) and the time-averaged acoustic pressure from the squeeze film (Eq. S9):
| [S10] |
and
| [S11] |
Solving this equation leads to the interfacial separation u as a function of the amplitude of vibration-α. The main result is that the levitation distance is a monotonic function of the amplitude of vibration. The results of the model are presented in Fig. S3 A and B. Indeed, as u increases, the exponential term approaches zero, and , which corresponds to the levitation distance that would result from the levitation of a smooth, rigid object (30).
Images of the contact and tribometry measurements both show a progressive decrease of contact area and friction force when the amplitude of vibration is increased. Larger interfacial separation will lead to fewer asperities in contact, therefore a reduced area of contact. Multiscale contact theory (16–18) notes that the true area of contact is proportional to the normal force, and therefore, we have the following relationship:
| [S12] |
with the true area of contact in the absence of vibrations. The model is compared with tribometry measurement for each participant in Fig. S1. A study of the evolution of the interfacial separation and relative area of contact is presented in Fig. S3. When α is small, we have and , which lead to the approximation of Eq. S11:
| [S13] |
and the true area of contact is closely approximated by a Gaussian centered at zero:
| [S14] |
with as the variance of the Gaussian function. Note that depends on the pressing force and the nominal roughness height of the skin .
However, the variation of brightness and it nominal value shown in Fig. 4 can be found if we consider that the interfacial separation is . Using this expression in S14, assuming , and using error propagation analysis, we find the rms of the variation to be
| [S15] |
This relationship is shown as the regression line in Fig. 4E. The data depart from this ideal model probably because of the bouncing behavior and other phenomena that are not captured.
Contact Dynamics.
Because the microsecond stroboscopy did not reveal any strong nonlinearities, it is fair to study the dynamics of the contact using linear time-invariant theory to the extent that the vibration amplitude remains small compared with the gap. At the range of frequencies used in this class of devices, the squeeze number is estimated to have a value higher than 300, which indicates that the film of air behaves elastically and that the dissipation induced by the airflow at the edge of the contact is small (38, 39).
The dynamic behavior of the skin can be modeled by a mass–spring–damper (m, , and ) that captures the density and viscoelasticity of the tissues as well as other dissipation mechanisms. In this model, the squeeze film is represented by a spring that connects the displacement of the vibrating plate, , to the displacement of the mass, . The force f applied by the spring to the mass is proportional to the instantaneous gap . The equations of motion expressed in the Fourier domain are
| [S16] |
and
| [S17] |
with . The previous equations can be combined into
| [S18] |
or
| [S19] |
The gap dynamics can be found by noting that :
| [S20] |
Measurement of the impedance at ultrasonic frequencies shows that the finger is contributing a mass of g, a damping of N⋅s/m, and a stiffness in the order of N/m (41). This model predicts that a phase of 220° ± 20° between the motion of the plate and the motion of the skin is achieved when the squeeze film contributes a stiffness of N/m, which is significantly higher than the stiffness of skin. This result is surprisingly robust to errors in evaluation of the damping, because less than 10% variation is observed for damping of the skin lower than N⋅s/m. Fig. S4 shows the evolution of the amplitude and phase of the gap with respect to the excitation as well as the effect of varying the dynamic parameters of the linear time-invariant model.
Conclusion
A finger placed against a plate vibrating out of plane at ultrasonic frequencies experiences reduced friction dependent on the amplitude of vibration. The precise mechanism underlying friction reduction has, however, never been clearly elucidated. In this study, a tribometer equipped with a unique optical setup enabled observation of the true area of contact with high spatiotemporal resolution. The measurements reveal that increases in amplitude lead to a clear reduction of the true area of contact and the interfacial friction. In addition, temporal variation of interfacial separation increases at higher amplitude. Phase data strongly suggest that the skin moves out of phase with the plate surface in a bouncing motion, but contrary to a previous hypothesis, it bounces against the squeeze film of air and not against the plate (40). Ongoing studies using laser Doppler interferometry measurement will shed additional light on the dynamics of the skin.
Overall, these results lead to a richer picture of the friction reduction mechanism, in which both the bouncing motion of the skin and the existence of a squeeze film are necessary to create an overpressure of air that partially supports the normal load and releases some asperities of the skin from contact, reducing friction. One application of these results is to the design of improved tactile interfaces for rendering virtual textures and shapes on flat plate surfaces. For instance, the results help elucidate sources of variability in the friction force and provide a basis for optimizing power consumption.
Materials and Methods
Friction Reduction Device.
The friction reduction apparatus was built around a 67 × 50 × 5-mm3 borosilicate glass plate actuated by two piezoelectric transducers vibrating at = 29,080 Hz in a 3 × 0 normal mode. This mode had a 19-mm nodal spacing and an unloaded Q factor of 150, which fell to 110 when a finger pushed with 0.5 N force. Only the center crest was used to provide the out of plane motion necessary to reduce friction. The plate deflects with a maximum unloaded displacement of ±3.0 , constant over the entire width of the plate (Fig. S5A). A piezoelectric sensor, bonded to the plate, measured the deformation of the plate in real time. The sensor was fed to an envelope detector and a sample and hold circuit to recover the envelope and the instantaneous vibration. Before each trial, the glass plate was cleaned with degreaser to remove any buildup of moisture or sebum. The ultrasonic plate and the illumination system were mounted on a servo-controlled stage driving the plate at a constant velocity of 10 mm/s. Interaction forces were measured with a six-axis force sensor providing a 10-mN noise floor.
Artificial Fingertip Manufacturing.
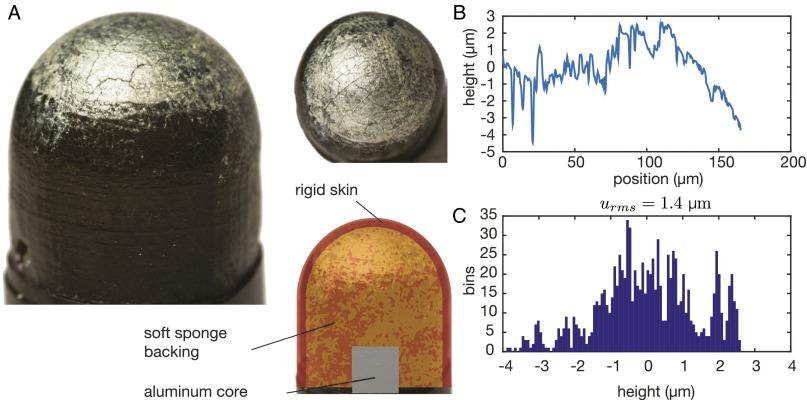
The artificial finger used in these experiments was constructed of an aluminum cylinder to represent bone, a sponge layer to represent soft tissue, and a 0.5-mm-thick half-spherical rubber-like covering of durometer Shore A 27 (which translates to a Young’s modulus of ∼1 MPa) to represent skin. This outer layer was chosen to be of a similar thickness and stiffness as human skin as well as for having damping properties more in line with human skin, and it was made of 3D printed rubber (14). A thin layer of acrylic paint was applied to the skin to both reduce the sliding friction coefficient of the finger into the range experienced by a real finger and aid in illumination. This final layer is also analogous to the stiff stratum corneum on the outermost layer of human skin. Interferometry measurement of the surface shows that at the -m scale. Fig. S6 shows a picture and results of the topography measurements.
Fig. S6.
(A) Picture of the artificial finger used in the study. (B) Results of interferometric measurement of the surface roughness. (C) Histogram of the surface profile.
Imaging System and Image Processing.
The experiment used frustrated total internal reflection to provide a high contrast between the regions that are in intimate contact with the glass and the background. Light from green LED is focused and fed into the thickness of the plate with a shallow angle. Based on a model of the total internal reflection, brightness is reduced by 95% when the distance between skin and glass plate is above ∼300 nm.
High-speed imaging is achieve by strobing the LED. The measured light pulse is shorter than 1.2 μs, which translates to a time resolution of 30 points per cycle of the ultrasonic vibration (Fig. S5B). The optical setup has 18-μm per pixel resolution. Histogram bracketing was used to increase contrast in Fig. 2 and Movies S1–S5. Stroboscopic videos were filtered using a Dirac comb in the temporal Fourier domain, which removed artifacts caused by tremors.
Participants.
The experiments were conducted under the approval of the Northwestern University Institutional Review Board. Participants gave their informed consent in writing before the experiment. In total, seven participants, including the lead authors, participated: two females and five males, with an average age of 26 y old. They did not report any skin condition, and their fingers did not present any scars. Two datasets were excluded because of a failure of the apparatus. After washing and drying their hands, participants sat comfortably on a chair in front of the apparatus. A cuff restricted the motion of their fingernails, leaving the skin of the fingertips free from mechanical contact. Subjects were instructed to relax their muscles and remain still. The experiment lasted less than 30 min, with a 10-min break between the friction measurements and stroboscopic analysis.
Supplementary Material
Acknowledgments
We thank Prof. Mitra Hartmann for lending us the high-speed camera. Michael Peshkin and Vincent Hayward provided valuable advice on the experimental setup and the manuscript. This work has been supported by National Science Foundation Grant IIS-1302422.
Footnotes
Conflict of interest statement: J.E.C. is a founder of Tanvas, Inc., which holds license to variable friction technology.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1603908113/-/DCSupplemental.
References
- 1.Cadoret G, Smith AM. Friction, not texture, dictates grip forces used during object manipulation. J Neurophysiol. 1996;75(5):1963–1969. doi: 10.1152/jn.1996.75.5.1963. [DOI] [PubMed] [Google Scholar]
- 2.Smith AM, et al. Roughness of simulated surfaces examined with a haptic tool: Effects of spatial period, friction, and resistance amplitude. Exp Brain Res. 2010;202(1):33–43. doi: 10.1007/s00221-009-2105-x. [DOI] [PubMed] [Google Scholar]
- 3.Wiertlewski M, Lozada J, Hayward V. The spatial spectrum of tangential skin displacement can encode tactual texture. IEEE Trans Robot. 2011;27(3):461–472. [Google Scholar]
- 4.Johansson RS, Westling G. Roles of glabrous skin receptors and sensorimotor memory in automatic control of precision grip when lifting rougher or more slippery objects. Exp Brain Res. 1984;56(3):550–564. doi: 10.1007/BF00237997. [DOI] [PubMed] [Google Scholar]
- 5.Westling G, Johansson RS. Responses in glabrous skin mechanoreceptors during precision grip in humans. Exp Brain Res. 1987;66(1):128–140. doi: 10.1007/BF00236209. [DOI] [PubMed] [Google Scholar]
- 6.Monzée J, Lamarre Y, Smith AM. The effects of digital anesthesia on force control using a precision grip. J Neurophysiol. 2003;89(2):672–683. doi: 10.1152/jn.00434.2001. [DOI] [PubMed] [Google Scholar]
- 7.Nara T, et al. Surface acoustic wave tactile display. IEEE Comput Graph Appl. 2001;21(6):56–63. [Google Scholar]
- 8.Bau O, Poupyrev I, Israr A, Harrison C. Proceedings of the 23nd Annual ACM Symposium on User Interface Software and Technology. ACM; New York: 2010. TeslaTouch: Electrovibration for touch surfaces; pp. 283–292. [Google Scholar]
- 9.Chubb E, Colgate J, Peshkin M. ShiverPaD: A glass haptic surface that produces shear force on a bare finger. IEEE Trans Haptics. 2010;3(3):189–198. doi: 10.1109/TOH.2010.7. [DOI] [PubMed] [Google Scholar]
- 10.Watanabe T, Fukui S. A method for controlling tactile sensation of surface roughness using ultrasonic vibration. IEEE Int Conf Robot Autom. 1995;1:1134–1139. [Google Scholar]
- 11.Winfield L, Glassmire J, Colgate JE, Peshkin M. Proceedings of the World Haptics Conference. IEEE; Piscataway, NJ: 2007. T-pad: Tactile pattern display through variable friction reduction; pp. 421–426. [Google Scholar]
- 12.Biet M, Giraud F, Lemaire-Semail B. Squeeze film effect for the design of an ultrasonic tactile plate. IEEE Trans Ultrason Ferroelectr Freq Control. 2007;54(12):2678–2688. doi: 10.1109/TUFFC.2007.596. [DOI] [PubMed] [Google Scholar]
- 13.Vezzoli E, et al. Physical and perceptual independence of ultrasonic vibration and electrovibration for friction modulation. IEEE Trans Haptics. 2015;8(2):235–239. doi: 10.1109/TOH.2015.2430353. [DOI] [PubMed] [Google Scholar]
- 14.Fenton Friesen R, Wiertlewski M, Peshkin MA, Colgate J. Proceedings of the World Haptics Conference. IEEE; Piscataway, NJ: 2015. Bioinspired artificial fingertips that exhibit friction reduction when subjected to transverse ultrasonic vibrations; pp. 208–213. [Google Scholar]
- 15.Persson B, Kovalev A, Gorb S. Contact mechanics and friction on dry and wet human skin. Tribol Lett. 2013;50(1):17–30. [Google Scholar]
- 16.Greenwood J, Williamson J. Contact of nominally flat surfaces. Proc R Soc Lond A Math Phys Sci. 1966;295(1442):300–319. [Google Scholar]
- 17.Bush A, Gibson R, Thomas T. The elastic contact of a rough surface. Wear. 1975;35(1):87–111. [Google Scholar]
- 18.Persson BN. Relation between interfacial separation and load: A general theory of contact mechanics. Phys Rev Lett. 2007;99(12):125502. doi: 10.1103/PhysRevLett.99.125502. [DOI] [PubMed] [Google Scholar]
- 19.Bowden F, Tabor D. The area of contact between stationary and between moving surfaces. Proc R Soc Lond A Math Phys Sci. 1939;169(938):391–413. [Google Scholar]
- 20.Adams M, Briscoe B, Johnson S. Friction and lubrication of human skin. Tribol Lett. 2007;26(3):239–253. [Google Scholar]
- 21.Warman PH, Ennos AR. Fingerprints are unlikely to increase the friction of primate fingerpads. J Exp Biol. 2009;212(Pt 13):2016–2022. doi: 10.1242/jeb.028977. [DOI] [PubMed] [Google Scholar]
- 22.Kendall K, Tabor D. An ultrasonic study of the area of contact between stationary and sliding surfaces. Proc R Soc Lond A Math Phys Sci. 1971;323(1554):321–340. [Google Scholar]
- 23.Dieterich JH, Kilgore BD. Direct observation of frictional contacts: New insights for state-dependent properties. Pure Appl Geophys. 1994;143(1-3):283–302. [Google Scholar]
- 24.Rubinstein SM, Cohen G, Fineberg J. Detachment fronts and the onset of dynamic friction. Nature. 2004;430(7003):1005–1009. doi: 10.1038/nature02830. [DOI] [PubMed] [Google Scholar]
- 25.Derler S, Schrade U, Gerhardt L. Tribology of human skin and mechanical skin equivalents in contact with textiles. Wear. 2007;263(7-12):1112–1116. [Google Scholar]
- 26.Pasumarty S, Johnson S, Watson S, Adams M. Friction of the human finger pad: Influence of moisture, occlusion and velocity. Tribol Lett. 2011;44(2):1–21. [Google Scholar]
- 27.Pailler-Mattei C, Bec S, Zahouani H. In vivo measurements of the elastic mechanical properties of human skin by indentation tests. Med Eng Phys. 2008;30(5):599–606. doi: 10.1016/j.medengphy.2007.06.011. [DOI] [PubMed] [Google Scholar]
- 28.Rayleigh L. On the pressure of vibrations. Philos Mag. 1902;3(15):338–346. [Google Scholar]
- 29.Chu BT, Apfel RE. Acoustic radiation pressure produced by a beam of sound. J Acoust Soc Am. 1982;72(6):1673–1687. [Google Scholar]
- 30.Hashimoto Y, Koike Y, Ueha S. Near-field acoustic levitation of planar specimens using flexural vibration. J Acoust Soc Am. 1996;100(4):2057–2061. [Google Scholar]
- 31.Li J, Cao W, Liu P, Ding H. Influence of gas inertia and edge effect on squeeze film in near field acoustic levitation. Appl Phys Lett. 2010;96(24):243507. [Google Scholar]
- 32.Zhao S, Mojrzisch S, Wallaschek J. An ultrasonic levitation journal bearing able to control spindle center position. Mech Syst Signal Process. 2013;36(1):168–181. [Google Scholar]
- 33.Salbu E. Compressible squeeze films and squeeze bearings. J Fluids Eng. 1964;86(2):355–364. [Google Scholar]
- 34.Wiesendanger M. 2001. Squeeze film air bearings using piezoelectric bending elements. PhD thesis (École polytechnique fédérale de Lausanne, Lausanne, Switzerland)
- 35.Minikes A, Bucher I, Haber S. Levitation force induced by pressure radiation in gas squeeze films. J Acoust Soc Am. 2004;116(1):217–226. [Google Scholar]
- 36.Delhaye B, Lefèvre P, Thonnard JL. Dynamics of fingertip contact during the onset of tangential slip. J R Soc Interface. 2014;11(100):20140698. doi: 10.1098/rsif.2014.0698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Johansson RS, Flanagan JR. Coding and use of tactile signals from the fingertips in object manipulation tasks. Nat Rev Neurosci. 2009;10(5):345–359. doi: 10.1038/nrn2621. [DOI] [PubMed] [Google Scholar]
- 38.Langlois W. Isothermal squeeze films. Q Appl Math. 1962;20(2):131–150. [Google Scholar]
- 39.Blech JJ. On isothermal squeeze films. J Lubrication Technol. 1983;105(4):615–620. [Google Scholar]
- 40.Dai X, Colgate J, Peshkin M. IEEE Haptics Symposium. IEEE; Piscataway, NJ: 2012. LateralPaD: A surface-haptic device that produces lateral forces on a bare finger; pp. 7–14. [Google Scholar]
- 41.Fenton Friesen R, Wiertlewski M, Colgate J. IEEE Haptics Symposium. IEEE; Piscataway, NJ: 2016. The role of damping in ultrasonic friction reduction; pp. 167–172. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.