A New Bayesian Lasso

Abstract

Park and Casella (2008) provided the Bayesian lasso for linear models by assigning scale mixture of normal (SMN) priors on the parameters and independent exponential priors on their variances. In this paper, we propose an alternative Bayesian analysis of the lasso problem. A different hierarchical formulation of Bayesian lasso is introduced by utilizing the scale mixture of uniform (SMU) representation of the Laplace density. We consider a fully Bayesian treatment that leads to a new Gibbs sampler with tractable full conditional posterior distributions. Empirical results and real data analyses show that the new algorithm has good mixing property and performs comparably to the existing Bayesian method in terms of both prediction accuracy and variable selection. An ECM algorithm is provided to compute the MAP estimates of the parameters. Easy extension to general models is also briefly discussed.

1 Introduction

In a normal linear regression setup, we have the following model

$$\mathit{y}=X\mathit{\beta }+\mathit{\epsilon },$$ (1)

where y is the n × 1 vector of centered responses; X is the n × p matrix of standardized regressors; β is the p × 1 vector of coefficients to be estimated and ε is the n × 1 vector of independent and identically distributed normal errors with mean 0 and variance σ².

The classical estimator in linear regression is the Ordinary Least Squares (OLS) estimator β̂_OLS = (X′X)⁻¹X′y, which is obtained by minimizing the residual sum of squares (RSS) = (y − Xβ)′(y − Xβ). It is well known that the OLS estimator is highly unstable in the presence of multicollinearity. Also, if p ≫ n, it is known to produce a non-unique estimator as X is less than full rank. To improve upon the prediction accuracy of OLS, least squares regression methods with various penalties have been developed. Ridge regression (Hoerl and Kennard, 1970) minimizes RSS subject to a constraint $\sum _{j=1}^p{|{\beta }_j|}^2\le t$. While ridge regression often achieves better prediction accuracy by shrinking OLS coefficients, it cannot do variable selection as it naturally keeps all the predictors. Frank and Friedman (1993) introduced bridge regression which minimizes RSS subject to a constraint $\sum _{j=1}^p{|{\beta }_j|}^{\alpha }\le t$, α ≥ 0. It includes ridge regression with α = 2 and subset selection with α = 0 as special cases. Among other developments, Fan and Li (2001) proposed the Smoothly Clipped Absolute Deviation (SCAD) penalty and Zhang (2010) introduced the minimum concave penalty (MCP), both of which result in consistent, sparse and continuous estimators in linear models (Fan and Li, 2001; Zhang, 2010).

Among penalized regression techniques, probably the most widely used method in statistical literature is the Least Absolute Shrinkage and Selection Operator (LASSO), which is a special case of bridge estimator with α = 1. The lasso of Tibshirani (1996) is obtained by minimizing

$$Q(\mathit{\beta })=(\mathit{y}-X\mathit{\beta })\prime (\mathit{y}-X\mathit{\beta })+\lambda {\Vert \mathit{\beta }\Vert }_1,\hspace{1em}\lambda >0.$$ (2)

Compared to ridge regression a remarkable property of lasso is that it can shrink some coefficients exactly to zero, which facilitates automatic variable selection. Various computationally efficient algorithms have been proposed to obtain the lasso and related estimators (Efron et al., 2004; Wu and Lange, 2008; Friedman et al., 2010). Given the tuning parameter(s), these algorithms are extremely fast. However, none of these algorithms provide a valid measure of standard error (Kyung et al., 2010), which is arguably a major drawback of these approaches.

Very recently, much work has been done in the direction of Bayesian framework. Tibshirani (1996) suggested that lasso estimates can be interpreted as posterior mode estimates when the regression parameters are assigned independent and identical Laplace priors. Motivated by this, different approaches based on scale mixture of normal (SMN) distributions with independent exponentially distributed variances (Andrews and Mallows, 1974) have been proposed (Figueiredo, 2003; Bae and Mallick, 2004; Yuan and Lin, 2005). Park and Casella (2008) introduced Gibbs sampling using a conditional Laplace prior specification of the form

$$\pi (\mathit{\beta }|{\sigma }^2)=\prod _{j=1}^p\frac{\lambda }{2\sqrt{{\sigma }^2}}\text{exp}\{-\frac{\lambda |{\beta }_j|}{\sqrt{{\sigma }^2}}\}$$ (3)

and non-informative scale-invariant marginal prior on σ², i.e. π(σ²) ∝ 1/σ². Park and Casella (2008) devoted serious efforts to address the important unimodality issue. They pointed out that conditioning on σ² is important for unimodality and lack of unimodality might slow down the convergence of the Gibbs sampler and make the point estimates less meaningful (Kyung et al., 2010). Other methods based on Laplace prior include Bayesian lasso via reversible-jump MCMC (Chen et al., 2011) and Bayesian lasso regression (Hans, 2009). Unlike their frequentist counterparts, Bayesian methods usually provide a valid measure of standard error based on a geometrically ergodic Markov chain (Kyung et al., 2010). Moreover, an MCMC-based Bayesian framework provides a flexible way of estimating the tuning parameter along with other parameters in the model.

In this paper, along the same line of Park and Casella (2008), we propose a new hierarchical representation of Bayesian lasso. A new Gibbs sampler is put forward utilizing the scale mixture of uniform (SMU) representation of the Laplace density. Empirical studies and real data analyses show that the new algorithm inherits good mixing property and yields satisfactory performance comparable to the existing Bayesian method. All statistical analyses and illustrations were conducted in R - 3.0.2 for Windows (64-bit). The remainder of the paper is organized as follows. In Section 2, we briefly review the SMU distribution. The Gibbs sampler is presented in Section 3. Some empirical studies and real data analyses are presented in Sections 4 and 5 respectively. Section 6 describes the ECM algorithm and easy extension to GLM is provided in Section 7. In Section 8, we provide conclusions and further discussions in this area. Some proofs and related derivations are included in an appendix.

2 Scale Mixture of Uniform Distribution

Proposition

A Laplace density can be written as a scale mixture of uniform distribution, the mixing density being a particular gamma distribution, i.e.

$$\frac{\lambda }{2}{e}^{-\lambda |x|}={\int }_{u>|x|}\frac{1}{2u}\frac{{\lambda }^2}{\mathrm{\Gamma }(2)}{u}^{2-1}{e}^{-\lambda u}du,\hspace{1em}\lambda >0.$$ (4)

Proof of this result is straightforward and included in Appendix A.

SMU distribution for regression models has been used in a few occasions in literature. Walker et al. (1997) used SMU distribution in normal regression models in non-Bayesian framework. Qin et al. (1998) provided Gibbs sampler by using SMU in variance regression models and also to derive Gibbs sampler for autocorrelated heteroscedastic regression models (Qin et al., 1998a). Choy et al. (2008) used it in stochastic volatility model by using a two-stage scale mixture representation of the student-t distribution. However, its use has been limited in penalized regression setting. We explore this fact by observing that the penalty function in lasso corresponds to a scale mixture of uniform distribution, the mixing distribution being a particular gamma distribution. Following Park and Casella (2008), we consider conditional Laplace priors of the form (3) on the coefficients and scale-invariant marginal prior on σ². Rewriting the Laplace priors as scale mixtures of uniform distributions and introducing the gamma mixing densites result in a new hierarchy. Under this new hierarchical representation, the posterior distribution of interest p(β, σ²|y) is exactly same as the original Bayesian lasso model of Park and Casella (2008) and therefore, the resulting estimates should exactly be same ‘theoretically’ for both Bayesian lasso models. We establish this fact by simulation studies and real data analyses. Conditioning on σ² ensures unimodal full posteriors in both Bayesian lasso models.

3 The New Bayesian Lasso

3.1 Model Hierarchy and Prior Distributions

Using (3) and (4), we formulate our hierarchical representation as follows:

$${\mathit{y}}^{n\times 1}|X,\mathit{\beta },{\sigma }^2~N_n(X\mathit{\beta },{\sigma }^2{I}_n),$$

$${\mathit{\beta }}^{p\times 1}|\mathit{u},{\sigma }^2~\prod _{j=1}^p\text{Uniform}(-\sqrt{{\sigma }^2}{u}_j,\sqrt{{\sigma }^2}{u}_j),$$ (5)

$${\mathit{u}}^{p\times 1}|\lambda ~\prod _{j=1}^p\text{Gamma}(2,\lambda ),$$

$${\sigma }^2~\pi ({\sigma }^2).$$

3.2 Full Conditional Posterior Distributions

Introduction of u = (u₁, u₂, …, u_p)′ enables us to derive the tractable full conditional posterior distributions, which are given as

$$\mathit{\beta }|\mathit{y},X,\mathit{u},\lambda ,{\sigma }^2~N_p({\hat{\mathit{\beta }}}_{\mathrm{O}\mathrm{L}\mathrm{S}},{\sigma }^2{(X\prime X)}^{-1})\prod _{j=1}^{p}I\{|{\beta }_j|<\sqrt{{\sigma }^2}{u}_j\},$$ (6)

$$\mathit{u}|\mathit{y},X,\mathit{\beta },\lambda ,{\sigma }^2~\prod _{j=1}^p\text{Exp}(\lambda )I\{u_j>\frac{|{\beta }_j|}{\sqrt{{\sigma }^2}}\},$$ (7)

$${\sigma }^2|\mathit{y},X,\mathit{\beta },\mathit{u},\lambda ~\text{Inverse-Gamma}(\frac{n-1+p}{2},\frac{1}{2}(\mathit{y}-X\mathit{\beta })\prime (\mathit{y}-X\mathit{\beta }))I\{{\sigma }^2>{\text{Max}}_j(\frac{{{\beta }_j}^2}{{u_j}^2})\},$$ (8)

where, I(․) denotes an indicator function. The derivations are included in Appendix A.

3.3 MCMC Sampling for the New Bayesian Lasso

3.3.1 Sampling Coefficients and Latent Variables

(6), (7) and (8) lead us to an exact Gibbs sampler that starts at initial guesses for β and σ² and iterates the following steps:

1. Generate u_j from the left-truncated exponential distribution (7) using inversion method which can be done as follows:

   1. Generate $u_j^{*}$ from an exponential distribution with rate parameter λ.
   2. Set, $u_j=u_j^{*}+\frac{|{\beta }_j|}{\sqrt{{\sigma }^2}}$.

2. Generate β from a truncated multivariate normal distribution proportional to (6). This step can be done by implementing efficient sampling technique developed by Li and Ghosh (2013).

3. Generate σ² from a left-truncated inverse-gamma distribution proportional to (8). This step can be done by utilizing the fact that the inverse of a left-truncated inverse-Gamma distribution is a right-truncated Gamma distribution. By generating σ^2* from the right-truncated gamma distribution proportional to

   $$\text{Gamma}(\frac{n-1+p}{2},\frac{1}{2}(\mathit{y}-X\mathit{\beta })\prime (\mathit{y}-X\mathit{\beta }))I\{{\sigma }^{2*}<\frac{1}{{\text{Max}}_j(\frac{{{\beta }_j}^2}{{u_j}^2})}\},$$

   and replacing ${\sigma }^2=\frac{1}{{\sigma }^{2*}}$, we can mimic sampling from the targeted left-truncated inverse-Gamma distrbution (8).

3.3.2 Sampling Hyperparameters

To update the tuning parameter λ, we work directly with the Laplace density marginalizing out the latent variables u_j’s. From (5), we observe that the posterior for λ given β is conditionally independent of y and takes the form

$$\pi (\lambda |\mathit{\beta })\propto {\lambda }^{2p}\text{ exp}\{-\lambda \sum _{j=1}^p|{\beta }_j|\}\pi (\lambda ).$$

Therefore, if λ has a Gamma(a,b) prior, its conditional posterior will also be a gamma distribution, i.e.

$$\lambda |\mathit{y},X,\mathit{\beta },{\sigma }^2\propto {\lambda }^{a+2p-1}\text{ exp}\{-\lambda (b+\sum _{j=1}^p|{\beta }_j|)\}.$$

Thus, we update the tuning parameter along with other parameters in the model by generating samples from $\text{Gamma}(a+2p,b+\sum _{j=1}^p|{\beta }_j|)$.

4 Simulation Studies

4.1 Prediction

In this section, we investigate the prediction accuracy of our method (NBLasso) and compare its performance with both original Bayesian lasso (OBLasso) and frequentist lasso (Lasso) across varied simulation scenarios. LARS algorithm of Efron et al. (2004) is used for lasso, in which 10-fold cross-validation is used to select the tuning parameter, as implemented in the R package lars. For Bayesian lassos, we estimate the tuning parameter λ by using a gamma prior distribution with shape parameter a = 1 and scale parameter b = 0.1, which is relatively at and results in high posterior probability near the MLE (Kyung et al., 2010). The Bayesian estimates are posterior means using 10, 000 samples of the Gibbs sampler after burn-in. To decide on the burn-in number, we make use of the potential scale reduction factor (Gelman and Rubin, 1992). Once R̂ < 1.1 for all parameters of interest, we continue to draw 10,000 iterations to obtain samples from the joint posterior distribution. The response is centered and the predictors are normalized to have zero means and unit variances before applying any model selection method. For the prediction errors, we calculate the median of mean squared errors (MMSE) for the simulated examples based on 100 replications. We simulate data from the true model

$$\mathit{y}=X\mathit{\beta }+\mathit{\epsilon },\hspace{1em}\mathit{\epsilon }~\mathrm{N}(\mathbf{0},{\sigma }^{2}I).$$

Each simulated sample is partitioned into a training set and a testing set. Models are fitted on the training set and MSE’s are calculated on the testing set. In all examples, detailed comparisons with both ordinary and Bayesian lasso methods are presented.

Example 1 (Simple Example - I)

Here we consider a simple sparse situation which was also used by Tibshirani (1996) in his original lasso paper. Here we set β^40×1 = (0^T, 2^T, 0^T, 2^T)^T, where 0^10×1 and 2^10×1 are vectors of length 10 with each entry equal to 0 and 2 respectively. The design matrix X is generated from the multivariate normal distribution with mean 0, variance 1 and pairwise correlations between x_i and x_j equal to 0.5. We experiment with four different scenarios by varying the sample size and σ². We simulate datasets wih {n_T, n_P} = {100, 400} and {200,200} respectively, where n_T denotes the size of the training set and n_P denotes the size of the testing set. We consider two values of σ : σ ∈ {9, 25}. The simulation results are summarized in Table 1 which clearly suggest that NBLasso outperforms both Lasso and OBLasso across all scenarios of this example.

Table 1.

Median mean squared error (MMSE) based on 100 replications for Example 1

{nT, nP}	σ2	Lasso	OBLasso	NBLasso
{200, 200}	225	279.72	249.79	244.4
{200, 200}	81	101.2	93.89	92.93
{100, 400}	225	354.19	268.74	259.85
{100, 400}	81	131.62	104.17	102.32

Example 2 (Difficult Example - I)

In this example, we consider a complicated model which exhibits a substantial amount of data collinearity. This example was presented in the elastic net paper by Zou and Hastie (2005). Here we simulate Z₁, Z₂ and Z₃ independently from N(0,1). Then, we let x_i = Z₁ + ε_i, i = 1(1)5; x_i = Z₂ + ε_i, i = 6(1)10; x_i = Z₃ + ε_i, i = 11(1)15 and x_i ~ N(0, 1), i = 16(1)30, where ε_i ~ N(0, 0.01), i = 1(1)15. We set β^30×1 = (3^T, 3^T, 3^T, 0^T)^T where 3^5×1 and 0^15×1 are vectors of length 5 and 15 with each entry equal to 3 and 0 respectively. We experiment with the same values of σ² and {n_T, n_P} as in Example 1. The simulation results are presented in Table 2. It can be observed that NBLasso is competitive with OBLasso in terms of prediction accuracy in all the scenarios presented in this example.

Table 2.

Median mean squared error (MMSE) based on 100 replications for Example 2

{nT, nP}	σ2	Lasso	OBLasso	NBLasso
{200, 200}	225	242.97	240.85	240.35
{200, 200}	81	90.01	88.98	88.92
{100, 400}	225	250.35	254.71	253.84
{100, 400}	81	93.36	95.34	94.49

Example 3 (High Correlation Example - I)

Here we consider a sparse model with strong level of correlation. We set β^8×1 = (3, 1.5, 0, 0, 2, 0, 0, 0)^T and σ² = {1, 9}. The design matrix X is generated from the multivariate normal distribution with mean 0, variance 1 and pairwise correlations between x_i and x_j equal to 0.95 ∀ i ≠ j. We simulate datasets with n_T = {20, 50, 100, 200} for the training set and n_P = 200 for the testing set. Table 3 summarizes our experimental results for this example. We can see that both Bayesian lassos yield similar performance and usually outperform their frequentist counterpart. As n_T increases, all the three methods yield equivalent performance.

Table 3.

Median mean squared error (MMSE) based on 100 replications for Example 3

nT	σ	Lasso	OBLasso	NBLasso
20	3	11.61	10.4	10.4
50	3	10.03	9.8	9.8
100	3	9.6	9.55	9.54
200	3	9.4	9.29	9.29
20	1	1.79	1.6	1.6
50	1	1.28	1.27	1.27
100	1	1.19	1.18	1.18
200	1	1.1	1.1	1.1

Example 4 (Small n Large p Example)

Here we consider a case where p ≥ n. We let β_1:q = (5, …, 5)^T, β_q+1:p = 0, p = 20, q = 10, σ = {1, 3}. The design matrix X is generated from the multivariate normal distribution with mean 0, variance 1 and pairwise correlations between x_i and x_j equal to 0.95 ∀ i ≠ j. We simulate datasets with n_T = {10, 20} for the training set and n_P = 200 for the testing set. It is evident from the results presented in Table 4 that the proposed method performs better than both OBLasso and Lasso in most of the situations. In one situation, OBLasso performs slightly better. Overall, Bayesian lassos significantly outperform frequentist lasso in terms of prediction accuracy.

Table 4.

Median mean squared error (MMSE) based on 100 replications for Example 4

nT	σ	Lasso	OBLasso	NBLasso
10	3	91.39	77.0	77.4
10	1	81.4	69.47	68.81
20	3	86.04	41.66	41.59
20	1	46.94	30.98	30.71

4.2 Variable Selection

In this section, we investigate the model selection performance of our method (NBLasso) and compare its performance with both original Bayesian lasso (OBLasso) and frequentist lasso (Lasso). Note that, the lasso was originally developed as a variable selection tool. However, in Bayesian framework, this attractive property vanishes as Bayesian lassos usually do not set any coefficient to zero. One way to tackle this problem is to use the credible interval criterion as suggested by Park and Casella (2008) in their seminal paper. However, it brings the problem of threshold selection. Moreover, credible intervals are not uniquely defined. Therefore, we will seek out an alternative strategy here. In Bayesian paradigm, it is a standard procedure to fully explore the posterior distribution and estimate λ by posterior median or posterior mean. Therefore, we can plug in the posterior estimate of λ in (2) and solve (2) to carry out variable selection. This strategy was recently used by Leng et al. (2014). For the optimization problem (2), we make use of the LARS algorithm of Efron et al. (2004).

For each simulated dataset, we apply three different lasso methods viz. NBLasso, OBLasso and Lasso and record the frequency of correctly-fitted models over 100 replications. For the Bayesian lassos, we assign a Gamma (1, 0.1) prior on λ to estimate the tuning parameter. Based on the posterior samples (10, 000 MCMC samples after burn-in), we calculate two posterior quantities of interest, viz. posterior mean and posterior median. Then we plug-in either posterior mean or posterior median estimate of λ in (2) and solve (2) to get the estimates of the coefficients. We refer to these different strategies as NBLasso-Mean, OBLasso-Mean, NBLasso-Median and OBLasso-Median, where NBLasso-Mean refers to NBLasso coupled with λ estimated by posterior mean, OBLasso-Median refers to OBLasso coupled with λ estimated by posterior median and so on. LARS algorithm is used for frequentist lasso, in which 10-fold cross-validation is used to select the tuning parameter. The response is centered and the predictors are normalized to have zero means and unit variances before applying any model selection method.

Example 5 (Simple Example - II)

This example was used in the original lasso paper to systematically compare the predictive performance of lasso and ridge regression. Here we set β^8×1 = (3, 1.5, 0, 0, 2, 0, 0, 0)^T and σ² = 9. The design matrix X is generated from the multivariate normal distribution with mean 0, variance 1 and pairwise correlations between x_i and x_j equal to 0.5^|i−j| ∀ i ≠ j. We simulate datasets with n_T = {20, 50, 100, 200} for the training set and n_P = 200 for the testing set. The simulation results are summarized in Table 5. From Table 5 we can see that NBLasso performs reasonably well outperforming both frequentist and original Bayesian lasso.

Table 5.

Frequency of correctly-fitted models over 100 replications for Example 5

nT	Lasso	OBLasso - Mean	NBLasso - Mean	OBLasso - Median	NBLasso - Median
20	15	13	22	11	17
50	11	14	20	12	15
100	16	21	25	20	25
200	11	16	17	16	16

Example 6 (Simple Example - III)

We consider another simple example from Tibshirani’s original lasso paper. We set β^8×1 = (5, 0, 0, 0, 0, 0, 0, 0)^T and σ² = 9. The design matrix X is generated from the multivariate normal distribution with mean 0, variance 1 and pairwise correlations between x_i and x_j equal to 0.5^|i−j| ∀ i ≠ j. We simulate datasets with n_T = {20, 50, 100, 200} for the training set and n_P = 200 for the testing set. The simulation results are presented in Table 6. For this example, we see that NBLasso always performs better than OBLasso although outperformed by frequentist lasso in many situations. The reason might be contributed to the fact that not much variance is explained by introducing the priors which resulted in poor model selection performance for the Bayesian methods.

Table 6.

Frequency of correctly-fitted models over 100 replications for Example 6

nT	Lasso	OBLasso - Mean	NBLasso - Mean	OBLasso - Median	NBLasso - Median
20	32	10	28	7	17
50	34	13	26	12	22
100	27	20	31	19	27
200	20	14	21	12	18

Example 7 (Difficult Example - II)

Here we consider a situation where lasso does not give consistent model selection. This example is taken from the adaptive lasso paper by Zou (2006). Here we set β^4×1 = (5.6, 5.6, 5.6, 0)^T and the correlation matrix of X is such that Cor(x_i, x_j) = −0.39, i < j < 4 and Cor(x_i, x₄) = 0.23, i < 4. Zou (2006) showed that for this example lasso is inconsistent regardless of the sample size. The experimental results are summarized in Table 7. None of the methods performed well for this example. Both Bayesian lassos yield similar performance and behave better than frequentist lasso in selecting the correct model.

Table 7.

Frequency of correctly-fitted models over 100 replications for Example 7

nT	σ	Lasso	OBLasso - Mean	NBLasso - Mean	OBLasso - Median	NBLasso - Median
120	5	0	6	6	5	6
300	3	0	10	8	12	10
300	1	0	9	12	12	12

Example 8 (High Correlation Example - II)

Here we consider a simple model with strong level of correlation. We set β^8×1 = (5, 0, 0, 0, 0, 0, 0, 0)^T and σ² = 9. The design matrix X is generated from the multivariate normal distribution with mean 0, variance 1 and pairwise correlations between x_i and x_j equal to 0.95 ∀ i ≠ j. We simulate datasets with n_T = {20, 50, 100, 200} for the training set and n_P = 200 for the testing set. Table 8 summarizes our experimental results for this example. It can be seen from the table that both Bayesian lassos yield similar performance and outperform frequentist lasso.

Table 8.

Frequency of correctly-fitted models over 100 replications for Example 8

nT	Lasso	OBLasso - Mean	NBLasso - Mean	OBLasso - Median	NBLasso - Median
20	8	19	22	17	19
50	11	18	20	18	19
100	8	17	17	17	17
200	5	16	16	16	16

4.3 Some Comments

We have considered a variety of experimental situations to investigate the predictive and model selection performance of NBLasso. Most of the simulation examples considered here have previously appeared in other lasso and related papers. From our extensive simulation experiments it is evident that NBLasso performs as well as, or better than OBLasso for most of the examples. For the simple examples, NBLasso performs the best whereas for other examples, NBLasso provides comparable and slightly better performance in terms of prediction and model selection. Note that, superiority of Bayesian lasso and related methods is already well-established in literature (Kyung et al., 2010; Li and Lin, 2010; Leng et al., 2014). We have found similar conclusion in this paper. For all the simulated examples, convergence of the corresponding MCMC chain was assessed by trace plots of the generated samples and calculating the Gelman-Rubin scale reduction factor (Gelman and Rubin, 1992) using the coda package in R. For n ≤ p situation, none of the methods performed well in model selection. Therefore, those results are omitted. In summary, based on our experimental results, it can be concluded that NBLasso is as effective as OBLasso with respect to both model selection and prediction performance.

5 Real Data Analyses

In this section, two real data analyzes are conducted using the proposed and the existing lasso methods. Four different methods are applied to the datasets: original Bayesian lasso (OBLasso), new Bayesian lasso (NBLasso), frequentist lasso (Lasso) and ordinary least squares (OLS). For the Bayesian methods, posterior means are calculated as estimates based on 10, 000 samples after burnin. To decide on the burn-in number, we make use of the potential scale reduction factor (Gelman and Rubin, 1992). Once R̂ < 1.1 for all parameters of interest, we continue to draw 10,000 iterations to obtain samples from the joint posterior distribution. The tuning parameter λ is estimated as posterior mean with a gamma prior with shape parameter a = 1 and scale parameter b = 0.1 in the MCMC algorithm. The convergence of our MCMC is checked by trace plots of the generated samples and calculating the Gelman-Rubin scale reduction factor (Gelman and Rubin, 1992) using the coda package in R. For the frequenstist lasso, 10-fold cross-validation (CV) is used to select the shrinkage parameter. The response is centered and the predictors are normalized to have zero means and unit variances before applying any model selection method.

5.1 The Diabetes Example

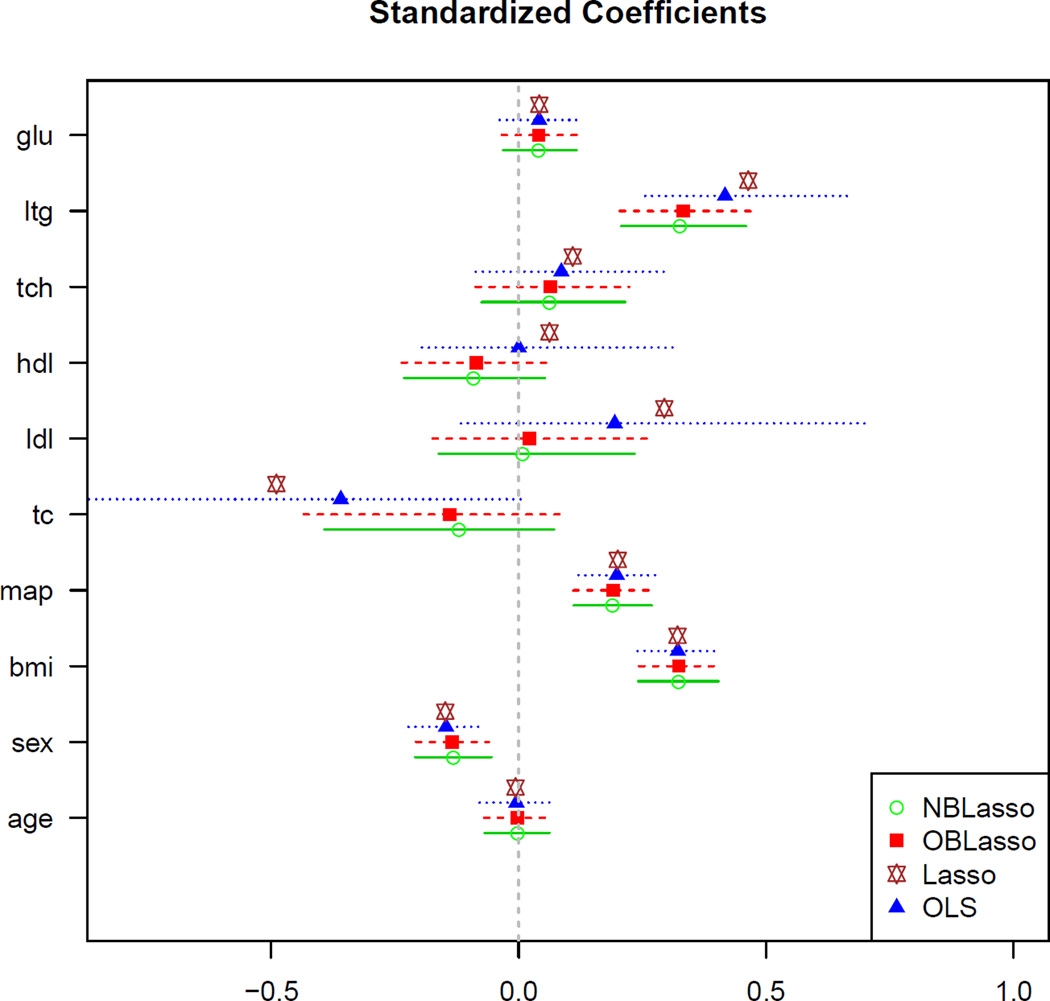
We analyze the benchmark diabetes dataset (Efron et al., 2004) which contains n = 442 measurements from diabetes patients. Each measurement has ten baseline predictors: age, sex, body mass index (bmi), average blood pressure (map) and six blood serum measurements (tc, ldl, hdl, tch, lth, glu). The response variable is a quantity that measures progression of diabetes one year after baseline. Figure 1 gives the 95% equal-tailed credible intervals along with posterior mean Bayesian lasso estimates of Diabetes data covariates along with frequentist lasso estimates, overlaid with OLS estimates with corresponding 95% confidence intervals. The estimated λ’s are 5.1 (2.5, 9.1) and 4.0 (2.2, 6.4) for NBLasso and OBLasso respectively. Figure 1 shows that two Bayesian lassos behave similarly for all the coefficients of this dataset. The 95% credible intervals are also similar. Any observed differences in parameter estimates can be contributed (up to Monte Carlo error) to the properties of the different Gibbs samplers used to obtain samples from the corresponding posterior distributions. The histograms of the Diabates data covariates based on posterior samples of 10,000 iterations are illustrated in Figure 2 (bottom panel). These histograms reveal that the conditional posterior distributions are in fact the desired stationary truncated univariate normals.

Figure 1.

Posterior mean Bayesian lasso estimates (computed over a grid of λ values, using 10,000 samples after burn-in) and corresponding 95% credible intervals (equal-tailed) of Diabetes data (n = 442) covariates. The hyperprior parameters were chosen as a = 1, b = 0.1. OLS estimates with corresponding 95% confidence intervals are also reported. For the lasso estimates, the tuning parameter was chosen by 10-fold CV of the LARS algorithm.

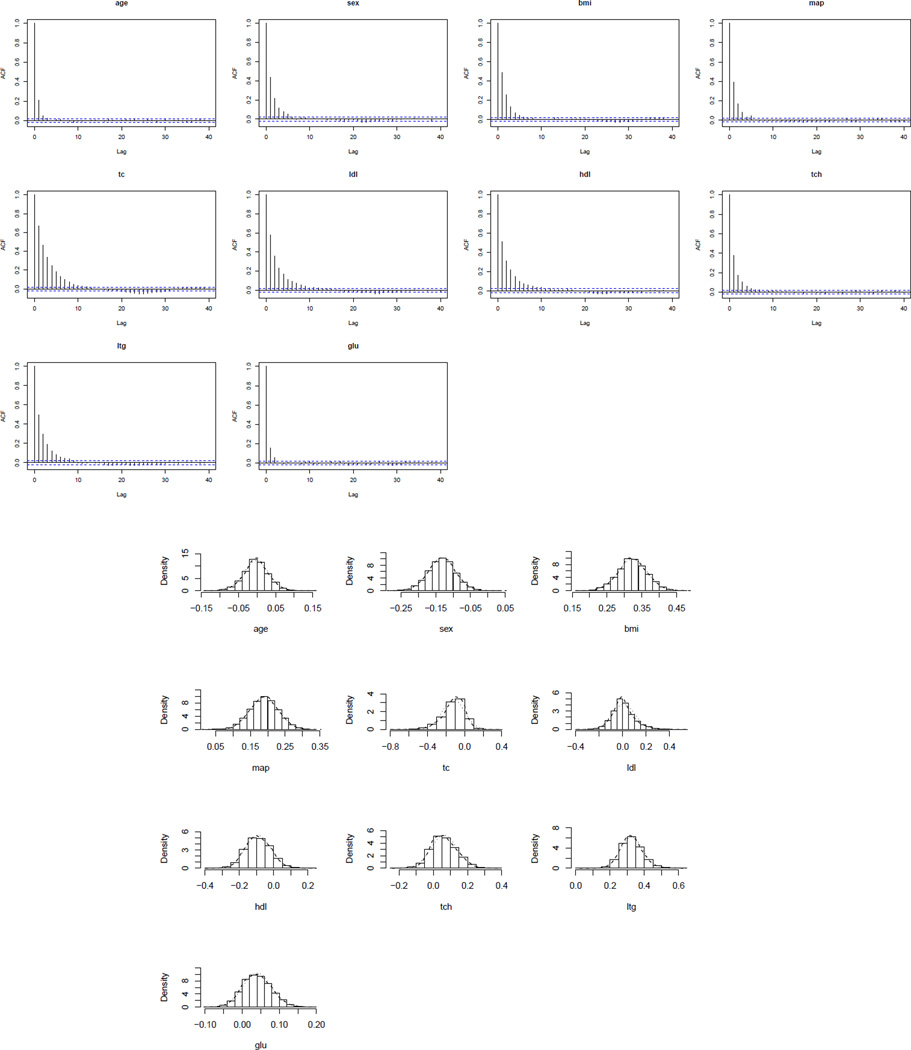
Figure 2.

ACF plots and histograms based on posterior samples of Diabetes data covariates.

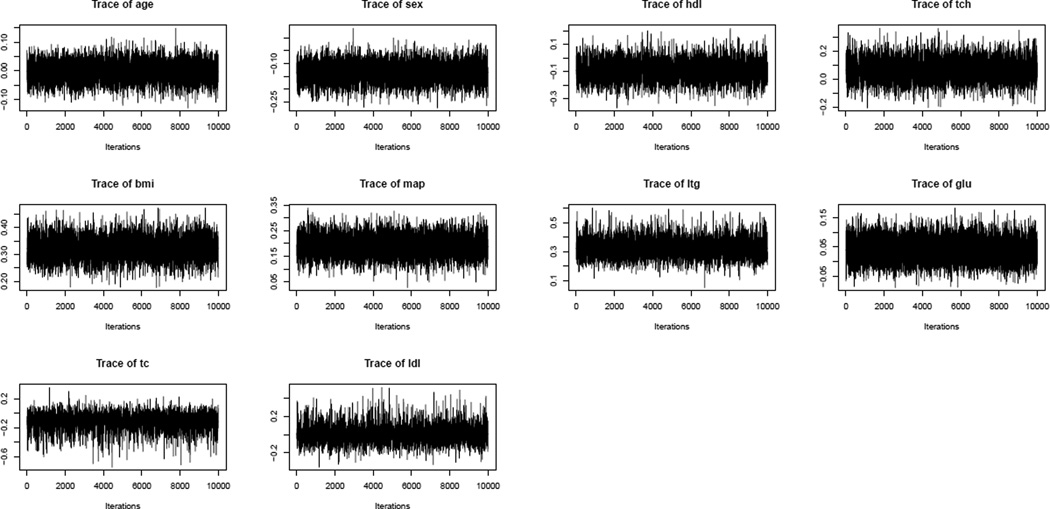
The mixing of an MCMC chain shows how rapidly the MCMC chain converges to the stationary distribution (Gelman et al., 2003). Autocorrelation function (ACF) plots and trace plots are good visual indicators of the mixing property. These plots are shown in Figures 2 (top panel) and 3 for the Diabetes data covariates. It is highly satisfactory to observe that for this benchmark dataset the samples traverse the posterior space very fast and the autocorrelations decay to zero rapidly. We also conduct the Geweke’s convergence diagnosis test and all the individual chains pass the tests. All these illustrate that the new Gibbs sampler has good mixing property.

Figure 3.

Trace plots of Diabetes data covariates.

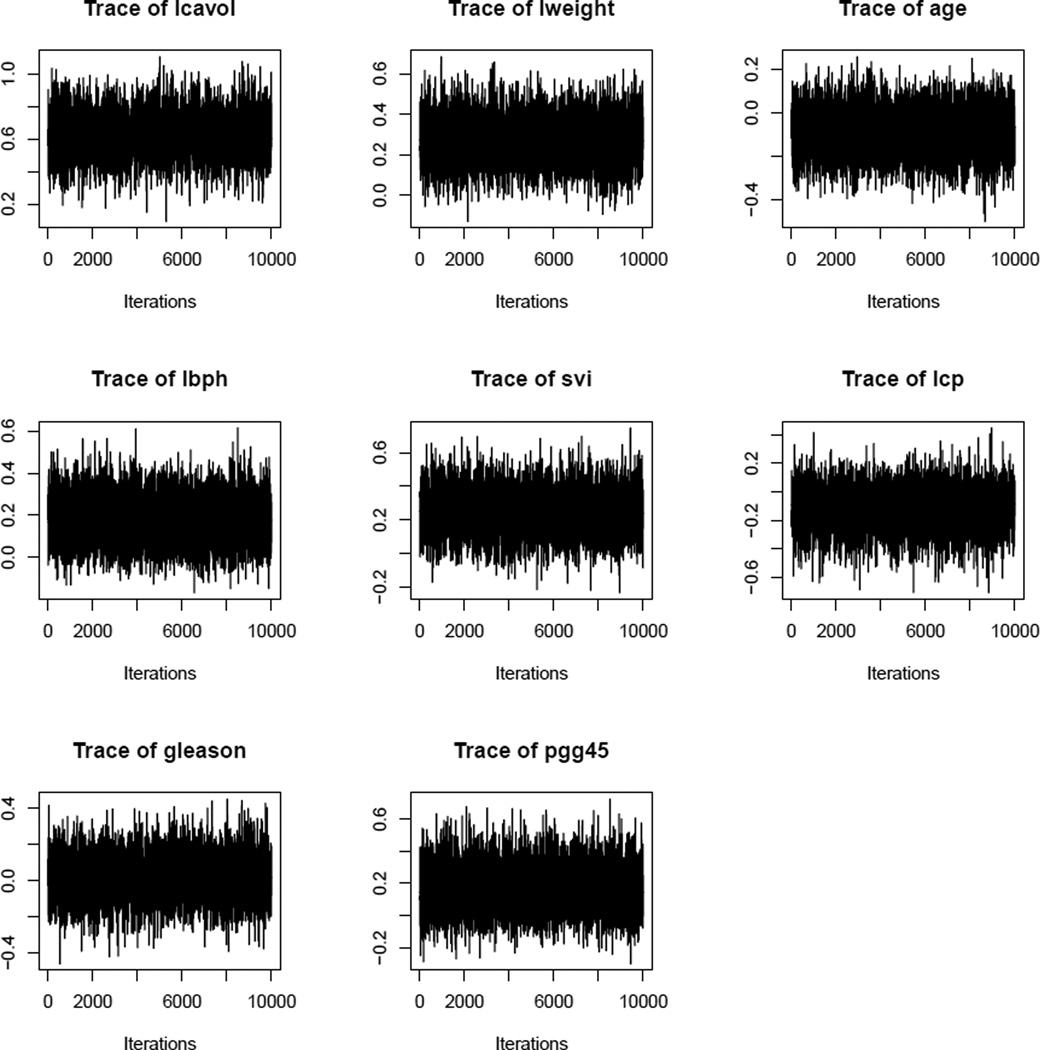
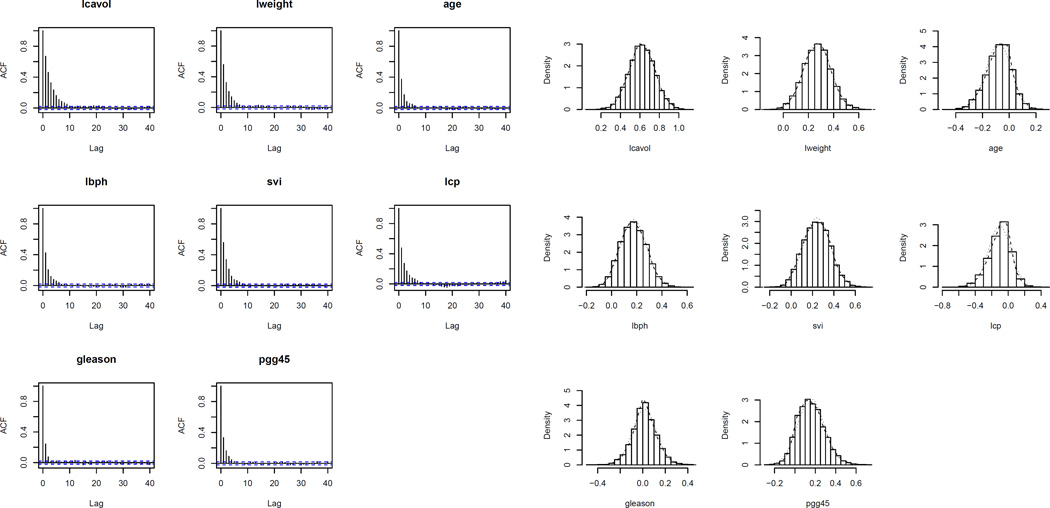
5.2 The Prostate Example

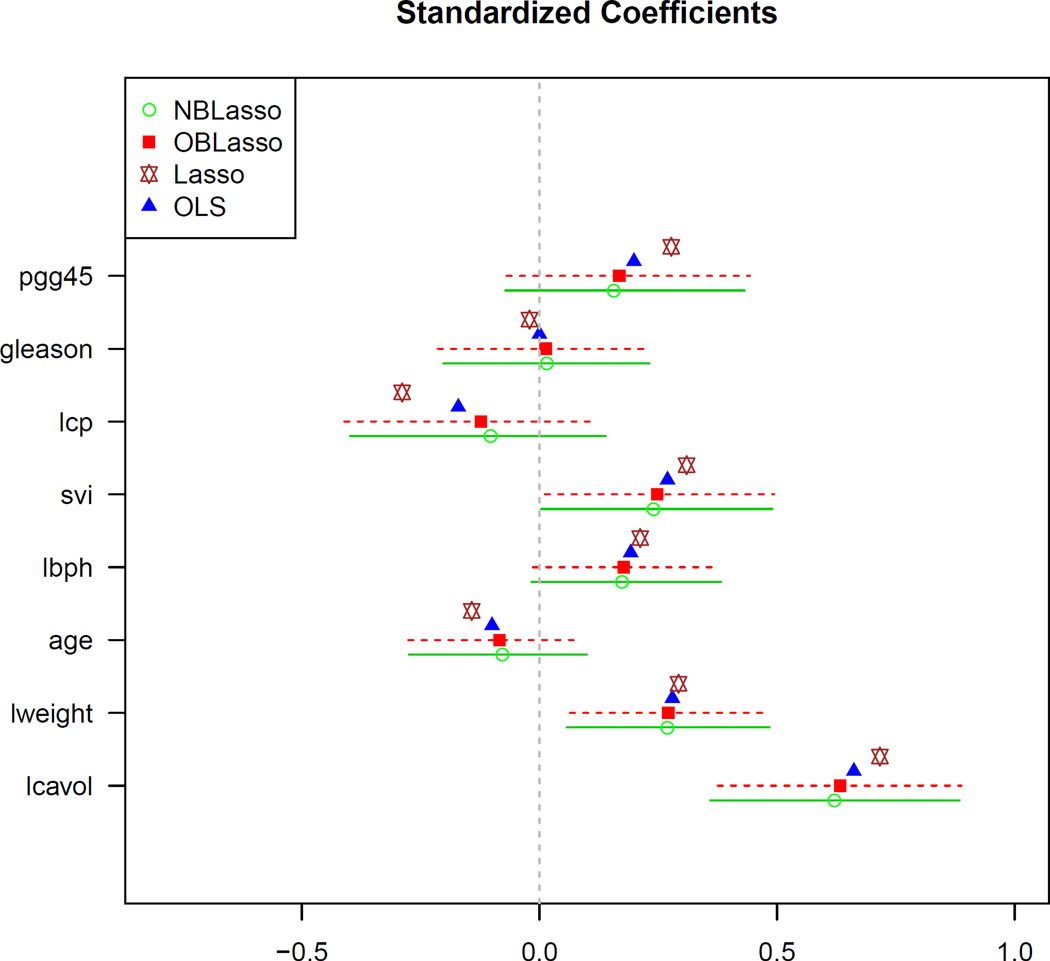
The data in this example is taken from a prostate cancer study (Stamey et al., 1989). Following Zou and Hastie (2005), we analyze the data by dividing it into a training set with 67 observations and a test set with 30 observations. Model fitting is carried out on the training data and performance is evaluated with the prediction error (MSE) on the test data. The response of interest is the logarithm of prostate-specific antigen. The predictors are eight clinical measures: the logarithm of cancer volume (lcavol), the logarithm of prostate weight (lweight), age, the logarithm of the amount of benign prostatic hyperplasia (lbph), seminal vesicle invasion (svi), the logarithm of capsular penetration (lcp), the Gleason score (gleason) and the percentage Gleason score 4 or 5 (pgg45). Figure 4 shows the 95% equal-tailed credible intervals for regression parameters of Prostate data based on the posterior mean Bayesian lasso estimates with point estimates of frequentist lasso and OLS estimates with corresponding 95% confidence intervals. The estimated λ’s are 3.5 (1.6, 7.3) and 3.1 (1.5, 5.3) for NBLasso and OBLasso respectively. The predictors in this dataset are known to be more correlated than those in the Diabetes data. Even for this dataset, the proposed method performs impressively. Figure 4 reveals that the two Bayesian lasso estimates are strikingly similar and the 95% credible intervals are almost identical for this dataset. Also, it is interesting to note that for this dataset all the estimates are inside the credible intervals which indicates that the resulting conclusion will be similar regardless of which method is used. Moreover, the new method outperforms both OBLasso and Lasso in terms of prediction accuracy (Table 9).

Figure 4.

Posterior mean Bayesian lasso estimates (computed over a grid of λ values, using 10,000 samples after burn-in) and corresponding 95% credible intervals (equal-tailed) of Prostate data (n = 67) covariates. The hyperprior parameters were chosen as a = 1, b = 0.1. OLS estimates with corresponding 95% confidence intervals are also reported. For the lasso estimates, the tuning parameter was chosen by 10-fold CV of the LARS algorithm.

Table 9.

Prostate Cancer Data Analysis - Mean squared prediction errors based on 30 observations of the test set for four methods : New Bayesian Lasso (NBLasso), Original Bayesian Lasso (OBLasso), Lasso and OLS

Method	NBLasso	OBLasso	Lasso	OLS
MSE	0.4696	0.4729	0.4856	0.5212

The trace plots and ACF plots shown in Figures 5 and 6 (left panel) demonstrate that the autocorrelations decay to zero very fast and the sampler jumps from one remote region of the posterior space to another in relatively few steps. Here also, we conduct Geweke’s convergence diagnosis test and all the individual chains pass the tests. All these establish good mixing property of the proposed Gibbs sampler. The histograms of the Prostate data covariates based on 10,000 posterior samples (Figure 6 right panel) reveal that the conditional posterior distributions are the desired stationary distributions viz. truncated univariate normals, which further validate our findings.

Figure 5.

Trace plots of Prostate data covariates.

Figure 6.

ACF plots and histograms based on posterior samples of Prostate data covariates.

6 Extensions

6.1 MCMC for General Models

In this section, we briefly discuss how NBLasso can be extended to several other models (e.g. GLM, Cox’s model, etc.) beyond linear regression. Our extension is based on the least squares approximation (LSA) by Wang and Leng (2007). Recently, Leng et al. (2014) used this approximation for Bayesian lasso. Therefore, here we only describe the algorithm for NBLasso. The algorithm for OBLasso can be found in Leng et al. (2014). Let us denote by L(β) the negative log-likelihood. Following Wang and Leng (2007), L(β) can be approximated by LSA as follows

$$L(\mathit{\beta })\approx \frac{1}{2}(\mathit{\beta }-\tilde{\mathit{\beta }})\prime \hat{\mathrm{\Sigma }}(\mathit{\beta }-\tilde{\mathit{\beta }}),$$

where β̃ is the MLE of β and Σ̂⁻¹ = σ²L(β)/γβ². Therefore, for a general model, the conditional distribution of y is given by

$$\mathit{y}|\mathit{\beta }~\text{exp }\{-\frac{1}{2}(\mathit{\beta }-\tilde{\mathit{\beta }})\prime \hat{\mathrm{\Sigma }}(\mathit{\beta }-\tilde{\mathit{\beta }})\}.$$

Thus, we can easily extend our method to several other models by approximating the corresponding likelihood by normal likelihood. Combining the SMU representation of the Laplace density and the LSA approximation of the general likelihood, the hierarchical presentation of NBLasso for general models can be written as

$$\mathit{y}|\mathit{\beta }~\text{exp }\{-\frac{1}{2}(\mathit{\beta }-\tilde{\mathit{\beta }})\prime \hat{\mathrm{\Sigma }}(\mathit{\beta }-\tilde{\mathit{\beta }})\},$$

$${\mathit{\beta }}^{p\times 1}|\mathit{u}~\prod _{j=1}^p\text{Uniform}(-u_j,u_j),$$ (9)

$${\mathit{u}}^{p\times 1}|\lambda ~\prod _{j=1}^p\text{Gamma}(2,\lambda ),$$

$$\lambda ~\text{Gamma}(a,b).$$

The full conditional distributions are given as

$$\mathit{\beta }|\mathit{y},X,\mathit{u},\lambda ~N_p(\tilde{\mathit{\beta }},\hat{\mathrm{\Sigma }})\prod _{j=1}^{p}I\{|{\beta }_j|<u_j\},$$ (10)

$$\mathit{u}|\mathit{y},X,\mathit{\beta },\lambda ~\prod _{j=1}^p\text{Exp}(\lambda )I\{u_j>|{\beta }_j|\},$$ (11)

$$\lambda |\mathit{y},X,\mathit{\beta }~{\lambda }^{a+2p-1}\text{ exp}\{-\lambda (b+\sum _{j=1}^p|{\beta }_j|)\}.$$ (12)

As before, an efficient Gibbs sampler can be easily carried out based on these full conditionals.

6.2 Simulation Examples for General Models

We now assess the performance of NBLasso in general models by means of two examples. For brevity, we only report the performance of various methods in terms of prediction accuracy. Three different lasso methods are applied to the simulated datasets. For the frequentist lasso, we use the R package glmnet which implements the coordinate descent algorithm of Friedman et al. (2010), in which 10-fold cross-validation is used to select the tuning parameter. We normalize the predictors to have zero means and unit variances before applying any model selection method. For the prediction errors, we calculate the median of mean squared errors (MMSE) for the simulated examples based on 100 replications. The design matrix X is generated from the multivariate normal distribution with mean 0, variance 1 and pairwise correlations between x_i and x_j equal to 0.5^|i−j| ∀ i ≠ j. We simulate datasets with n_T = {200, 400} for the training set and n_P = 500 for the testing set.

Example 9 (Logistic Regression Example)

In this example, observations with binary response are independently generated according to the following model (Wang and Leng, 2007)

$$P(y_i|x_i)=\frac{\text{exp}\{x_i^T\mathit{\beta }\}}{1+\text{exp}\{x_i^T\mathit{\beta }\}},$$

where β^9×1 = (3, 0, 0, 1.5, 0, 0, 2, 0, 0)^T. The experimental results are summarized in Table 10, which shows that NBLasso performs comparably with OBLasso. As the size of the training data increases, all the three methods yield equivalent performance.

Table 10.

Simulation Results for Logistic Regression

nT	Lasso	OBLasso	NBLasso
200	0.004	0.006	0.006
400	0.003	0.004	0.003

Example 10 (Cox’s Model Example)

In this simulation study, independent survival data are generated according to the following hazard function (Wang and Leng, 2007)

$$h(t_i|x_i)=\text{exp}\{x_i^T\mathit{\beta }\},$$

where t_i is the survival time from the ith subject and β^8×1 = (0.8, 0, 0, 1, 0, 0, 0.6, 0)^T. Also, independent censoring time is generated from an exponential distribution with mean u $\text{exp}\{x_i^T\mathit{\beta }\}$, where u ~ Uniform(1, 3). The experimental results are summarized in Table 11, which shows that both Bayesian lassos perform comparably, outperforming frequentist lasso. Thus, it is evident from the experimental results that NBLasso is as effective as OBLasso even for the general models.

Table 11.

Simulation Results for Cox’s Model

nT	Lasso	OBLasso	NBLasso
200	0.41	0.3	0.3
400	0.15	0.1	0.1

7 Computing MAP Estimates

7.1 ECM Algorithm for Linear Models

It is well known that the full conditional distributions of a truncated multivariate normal distribution are truncated univariate normal distributions. This fact motivates us to develop an ECM algorithm to estimate the marginal posterior modes of β and σ². At each step, we treat the latent variables u_j ’s and the tuning parameter λ as missing parameters and average over them to estimate β_j’s and σ² by maximizing the expected log conditional posterior distributions.

The complete data log-likelihood is

$$\text{log }p(\mathit{\beta },{\sigma }^2,\mathit{u},\lambda |\mathit{y},X)\propto \sum _{i=1}^n\text{log }p(y_i|X_i\mathit{\beta },{\sigma }^2)+\sum _{j=1}^p\text{log }p({\beta }_j|u_j,{\sigma }^2)+\sum _{j=1}^p\text{log }p(u_j|\lambda )+\text{log }p({\sigma }^2)+\text{log }p(\lambda )\propto \{\sum _{i=1}^n-\frac{1}{2{\sigma }^2}{(y_i-X_i\mathit{\beta })}^2+(a+2p-1)\text{log}\lambda -\lambda (b+\sum _{j=1}^p{u}_j)-\frac{(n-1+p)}{2}\text{ log }{\sigma }^2\}I\{u_j>\frac{|{\beta }_j|}{\sqrt{{\sigma }^2}},\forall j\}.$$ (13)

We initialize the algorithm by starting with a guess of β and σ². Then, at each step of the algorithm, we replace u and λ in the log joint posterior (13) by their expected values conditional on the current estimates of β and σ². Finally, we update β and σ² by maximizing the expected log conditional posterior distributions. The algorithm proceeds as follows:

• E-Step:

  $$u_j^{(t)}={\left(\frac{1}{\lambda }\right)}^{(t)}+\frac{|{\beta }_j^{(t)}|}{\sqrt{{\sigma }^{2(t)}}},$$

  $${\left(\frac{1}{\lambda }\right)}^{(t)}=\frac{1}{(b+\sum _{j=1}^p|{\beta }_j^{(t)}|)(a+2p-1)};$$
• CM-Steps: ${\beta }_j^{(t+1)}=\{\begin{array}{cc}-u_j^{(t)}\sqrt{{\sigma }^{2(t)}}\hfill & \text{if }{\beta }_j^{(t)}<-u_j^{(t)}\sqrt{{\sigma }^{2(t)}}\hfill \\ {\hat{\beta }}_{jOLS}\hfill & \text{if}-u_j^{(t)}\sqrt{{\sigma }^{2(t)}}<{\beta }_j^{(t)}<u_j^{(t)}\sqrt{{\sigma }^{2(t)}}\hfill \\ u_j^{(t)}\sqrt{{\sigma }^{2(t)}}\hfill & \text{if }{\beta }_j^{(t)}>u_j^{(t)}\sqrt{{\sigma }^{2(t)}},\hspace{1em}j=1(1)p\hfill \end{array}$,

  $${\sigma }^{2(t+1)}=\text{Max }\{\frac{(\mathit{y}-X{\mathit{\beta }}^{(t+1)})\prime (\mathit{y}-X{\mathit{\beta }}^{(t+1)})}{n+p+1},{\text{Max}}_j{\left(\frac{{\beta }_j^{(t+1)}}{{u_j}^{(t)}}\right)}^2\}.$$

  At convergence of the algorithm, we summarize the inferences using latest estimates of β and σ² and variances (Johnson et al., 1994).

7.2 ECM Algorithm for General Models

Similarly, an approximate ECM algorithm for general models can be given as follows:

1. E-Step:

   $$u_j^{(t)}={\left(\frac{1}{\lambda }\right)}^{(t)}+|{\beta }_j^{(t)}|,$$

   $${\left(\frac{1}{\lambda }\right)}^{(t)}=\frac{1}{(b+\sum _{j=1}^p|{\beta }_j^{(t)}|)(a+2p-1)}.$$

2. CM-Steps: ${\beta }_j^{(t+1)}=\{\begin{array}{cc}-u_j^{(t)}\hfill & \text{if }{\beta }_j^{(t)}<-u_j^{(t)}\hfill \\ {\hat{\beta }}_{j\mathrm{M}\mathrm{L}\mathrm{E}}\hfill & \text{if}-u_j^{(t)}<{\beta }_j^{(t)}<u_j^{(t)}\hfill \\ u_j^{(t)}\hfill & \text{if }{\beta }_j^{(t)}>u_j^{(t)},\hspace{1em}j=1(1)p,\hfill \end{array}$

3. Repeat 1 & 2 until convergence.

8 Concluding Remarks

In this paper, we have introduced a new hierarchical representation of Bayesian lasso using SMU distribution. It is to be noted that the posterior distribution of interest p(β, σ²|y) is exactly same for both original Bayesian lasso (OBLasso) and new Bayesian lasso (NBLasso) models. As such, all inference and prediction that is based on the posterior distribution should be exactly same ‘theoretically’. Any observed differences must be attributed (up to Monte Carlo error) to the properties of the different Gibbs samplers used to obtain samples from the corresponding posterior distributions. We establish this fact by real data analyses and empirical studies. Our results indicate that both Bayesian lassos perform comparably in different empirical and real scenarios. In many situations, the new method is competitive in terms of either prediction accuracy or variable selection. Moreover, NBLasso performs quite satisfactorily for general models beyond linear regression. Furthermore, the proposed Gibbs sampler inherits good mixing properties as evident from both empirical studies (data not shown due to too many predictors) and real data analyses. Note that, we do not have a theoretical result on the posterior convergence of our MCMC. Therefore, despite our encouraging findings, theoretical research is needed to investigate the posterior convergence of the proposed MCMC algorithm.

One should be aware that both non-Bayesian and Bayesian lasso are essentially optimization methods with the common goal of determining the model parameters that maximize some objective function. Therefore, a Bayesian approach can often lead to very different results than a traditional penalized likelihood approach (Hans, 2010). Apart from the advantages discussed above, the proposed Bayesian lasso also has some limitations as it carries forward all the drawbacks of frequentist lasso (Kyung et al., 2010). To overcome those limitations, one can easily adopt the adaptive lasso (Zou, 2006) by choosing variable-specific tuning parameter in the MCMC step. However, adopting the new hierarchical representation based on SMU distribution to other regularization methods viz. bridge estimator (Frank and Friedman, 1993), group lasso (Yuan and Lin, 2006; Meier et al., 2008), elastic net (Zou and Hastie, 2005), group bridge (Huang et al., 2009), adaptive group bridge (Park and Yoon, 2011) and adaptive elastic net (Zhou et al., 2010; Ghosh, 2011) remains an active area for future research.

A Appendix Section

Proof of Proposition

It is well known that

$${\int }_{z>\frac{|x|}{\sqrt{{\sigma }^2}}}\lambda e^{-\lambda z}dz=e^{-\lambda \frac{|x|}{\sqrt{{\sigma }^2}}}.$$

Therefore, the pdf of a Laplace distribution with mean 0 and variance $\sqrt{{\sigma }^2}/\lambda$ can be written as

$$\frac{\lambda }{2\sqrt{{\sigma }^2}}{e}^{-\lambda \frac{|x|}{\sqrt{{\sigma }^2}}}=\frac{\lambda }{2\sqrt{{\sigma }^2}}{\int }_{u>\frac{|x|}{\sqrt{{\sigma }^2}}}\lambda e^{-\lambda u}du={\int }_{-u\sqrt{{\sigma }^2}<x<u\sqrt{{\sigma }^2}}\hspace{1em}\frac{1}{2u\sqrt{{\sigma }^2}}\frac{{\lambda }^2}{\mathrm{\Gamma }(2)}{u}^{2-1}{e}^{-\lambda u}du.$$

Hence the proof (4).

Posterior Distributions

Assuming that priors for different parameters are independent, we can express the joint posterior distribution of all parameters as:

$$\pi (\mathit{\beta },\mathit{u},\lambda ,{\sigma }^2|\mathit{y},X)\propto \pi (\mathit{y}|X,\mathit{\beta },{\sigma }^2)\pi (\mathit{\beta }|\mathit{u},{\sigma }^2)\pi (\mathit{u}|\lambda )\pi (\lambda )\pi ({\sigma }^2)d{\sigma }^2$$

Conditional on y, X, u, λ, σ², the posterior distribution of β is

$$\pi (\mathit{\beta }|\mathit{y},X,\mathit{u},\lambda ,{\sigma }^2)\propto \pi (\mathit{y}|X,\mathit{\beta },{\sigma }^2)\pi (\mathit{\beta }|\mathit{u},{\sigma }^2)\propto \text{exp}\{-\frac{1}{2{\sigma }^2}(\mathit{y}-X\mathit{\beta })\prime (\mathit{y}-X\mathit{\beta })\prod _{j=1}^{p}I\{|{\beta }_j|<\sqrt{{\sigma }^2}{u}_j\}\propto \text{exp}\{-\frac{1}{2{\sigma }^2}(\mathit{\beta }-{\hat{\mathit{\beta }}}_{\mathrm{O}\mathrm{L}\mathrm{S}})\prime X\prime X(\mathit{\beta }-{\hat{\mathit{\beta }}}_{\mathrm{O}\mathrm{L}\mathrm{S}})\prod _{j=1}^{p}I\{|{\beta }_j|<\sqrt{{\sigma }^2}{u}_j\}.$$

Hence,

$$\mathit{\beta }|\mathit{y},X,\mathit{u},\lambda ,{\sigma }^2~N_p({\hat{\mathit{\beta }}}_{\mathrm{O}\mathrm{L}\mathrm{S}},{\sigma }^2{(X\prime X)}^{-1})\prod _{j=1}^{p}I\{|{\beta }_j|<\sqrt{{\sigma }^2}{u}_j\}.$$

(6)

Similarly,

$$\pi (\mathit{u}|\mathit{y},X,\mathit{\beta },\lambda ,{\sigma }^2)\propto \pi (\mathit{\beta }|\mathit{u},{\sigma }^2)\pi (\mathit{u}|\lambda )\propto \prod _{j=1}^p{e}^{-\lambda u_j}I\{u_j>\frac{|{\beta }_j|}{\sqrt{{\sigma }^2}}\}.$$

Therefore,

$$\mathit{u}|\mathit{y},X,\mathit{\beta },\lambda ,{\sigma }^2~\prod _{j=1}^p\text{Exponential}(\lambda )I\{u_j>\frac{|{\beta }_j|}{\sqrt{{\sigma }^2}}\}$$

(7)

Similarly,

$$\pi ({\sigma }^2|\mathit{y},X,\mathit{\beta },\mathit{u},\lambda )\propto \pi (\mathit{y}|X,\mathit{\beta },{\sigma }^2)\pi (\mathit{\beta }|\mathit{u},{\sigma }^2)\pi ({\sigma }^2)d{\sigma }^2\propto {\left(\frac{1}{{\sigma }^2}\right)}^{\frac{n-1+p}{2}+1}{e}^{-\frac{1}{2{\sigma }^2}(\mathit{y}-X\mathit{\beta })\prime (\mathit{y}-X\mathit{\beta })}I\{{\sigma }^2>{\text{Max}}_j(\frac{{{\beta }_j}^2}{{u_j}^2})\}.$$

Therefore,

$${\sigma }^2|\mathit{y},X,\mathit{\beta },\mathit{u},\lambda ~\text{Inverse}-\text{Gamma}(\frac{n-1+p}{2},\frac{1}{2}(\mathit{y}-X\mathit{\beta })\prime (\mathit{y}-X\mathit{\beta }))I\{{\sigma }^2>{\text{Max}}_j(\frac{{{\beta }_j}^2}{{u_j}^2})\}.$$

(8)