Matriarch: A Python Library for Materials Architecture

Abstract

Biological materials, such as proteins, often have a hierarchical structure ranging from basic building blocks at the nanoscale (e.g., amino acids) to assembled structures at the macroscale (e.g., fibers). Current software for materials engineering allows the user to specify polypeptide chains and simple secondary structures prior to molecular dynamics simulation, but is not flexible in terms of the geometric arrangement of unequilibrated structures. Given some knowledge of a larger-scale structure, instructing the software to create it can be very difficult and time-intensive. To this end, the present paper reports a mathematical language, using category theory, to describe the architecture of a material, i.e., its set of building blocks and instructions for combining them. While this framework applies to any hierarchical material, here we concentrate on proteins. We implement this mathematical language as an open-source Python library called Matriarch. It is a domain-specific language that gives the user the ability to create almost arbitrary structures with arbitrary amino acid sequences and, from them, generate Protein Data Bank (PDB) files. In this way, Matriarch is more powerful than commercial software now available. Matriarch can be used in tandem with molecular dynamics simulations and helps engineers design and modify biologically inspired materials based on their desired functionality. As a case study, we use our software to alter both building blocks and building instructions for tropocollagen, and determine their effect on its structure and mechanical properties.

1. INTRODUCTION

Despite the increasing interest in using hierarchically structured protein materials as low-cost, environmentally benign, and yet high-performance materials, the interplay between nanoscale structure and global properties is not well understood. Recent advances in algorithms for predicting a protein's structure from its amino acid sequence¹ have facilitated the engineering of new catalysts^2–4 and other proteins with new structures and functions.⁵ Biologically inspired engineering⁶ and materiomic engineering^7,8 seek to build multiscale hierarchical materials based on their desired functionality, and have the potential to generate many new materials on demand.⁹

Materials engineers explore the design-space for sequence, structure, and functionality of organic materials.^10,11 In this context, the building block replacement problem¹² poses the question of how global structure and function of a molecule is affected by basic building block substitutions, and furthermore how to use these substitutions to achieve desired properties. For example, in the case of proteins, one can consider the effect of replacing amino acids in a polypeptide by other amino acids. The building instructions, by which these building blocks are recursively put together into a structure for self-assembly, are an equally important part of the process. We refer to the combination of building blocks and associated building instructions as materials architecture.

Control over such architecture is of interest when there is an incomplete knowledge of a protein's final assembled structure. Specifically, during the creation of the initial structure for a molecular dynamics simulation, it may be useful to directly control both the sequence and the building instructions, such as the pitch of a helix or the gap distance of a fibril composite. Current software does not allow one to parametrically change such building instructions. To this end, we develop a domain-specific language of materials architecture and implement it in an open-source Python library, called Matriarch. This program, which is based on the mathematical field of category theory, is discussed in section 2. Although the mathematics applies to a wide variety of materials, Matriarch is currently restricted to proteins architecture.

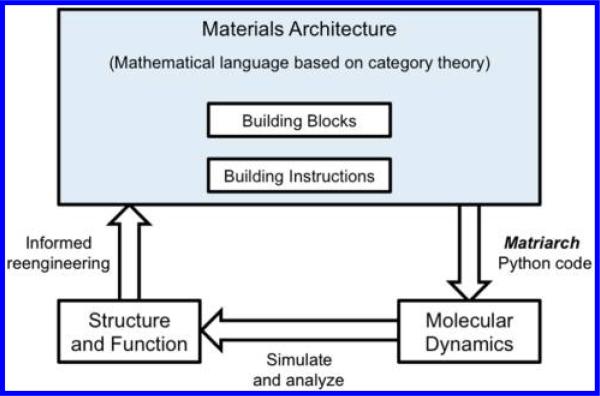
Matriarch approximates structures of proteins and generates atomic configurations from a given material architecture. Having a reasonable initial configuration, produced by Matriarch in the form of a PDB file, can significantly shorten molecular dynamics equilibration times and associated structure and function analysis. The engineer can then perform building block substitutions and variations on building instructions, using Matriarch, to study their effect on the functionality of a material. Matriarch thus facilitates the design process for the materials engineer (see Figure 1).

Figure 1.

Role of materials architecture in the engineering process. A material architecture consists of building blocks arranged according to building instructions, formalized using category theory. The building blocks of proteins are amino acids, which can be arranged in any number of forms by building instructions. Matriarch is a Python implementation of the mathematical formalism, which realizes the chosen materials architecture as a PDB file. The structure and function of the prearranged molecules can be obtained by molecular dynamics simulation. Using the data from many such simulations informs the design process for the materials engineer.

Section 3.2 provides a proof of concept for the utility of changing both building blocks and building instructions. We first develop a building instruction for forming tropocollagen-shaped molecules (triple-helices). We then systematically substitute parts of the tropocollagen polypeptide sequence, and shape the mutated polypeptide into a triple helix using our building instruction. Through equilibration and steered molecular dynamics simulations, we observe a large variation in the elastic moduli of the tropocollagen variants. Using Matriarch, similar methods can be extended to other building block replacement questions. Also in section 3, we parametrically create structures, such as a triangular helix of an amyloid, which would be extremely difficult and time-intensive to create using existing software.

2. THEORETICAL FRAMEWORK

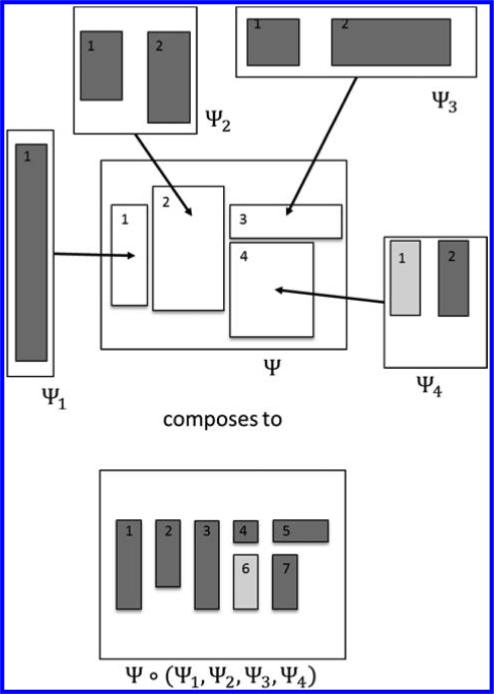
The language of materials architecture is formalized using a concept within category theory called operads, which can model the assembly of hierarchical structures.^13–15 Figure 2 provides a classical example from mathematics, in which the only building blocks are rectangles, and the building instructions are placements of nonoverlapping rectangles in a larger rectangle. The operad is the mathematical description of rectangle configurations as they are nested into hierarchies of arbitrary depth.

Figure 2.

Architecture of rectangle arrangements. Equivalent to an early example of an operad from mathematics called the little 2-cubes operad E₂. In the terminology of this paper, the only building blocks in E₂ are rectangles. A building instruction in E₂ is an arrangement of nonoverlapping rectangles within a larger rectangle. In the composition, the placements and aspect ratios of building blocks are retained, but sizes can change. The operad E₂ is the mathematical description of rectangle configurations as they are nested into hierarchies of arbitrary depth. The operad underlying Matriarch is far more complex than E₂, with more diverse building blocks and building instructions.

In the operad describing materials architecture, specifically that of hierarchical protein materials, both the building blocks and the building instructions are far more complex. It is useful to have such a mathematical language because it deals only with abstract building blocks and avoids the specifics of molecular geometry. That is, the abstractions offer a unified language for formal descriptions of intuitive building instructions, such as attach, twist, array, etc. Furthermore, the mathematical formalism provides rigorous type-checking for Matriarch and ensures that it operates on logical foundations. Matriarch is one of the first scientific applications of operads, and, to the best of our knowledge, it is the first use in the natural sciences. Although operads are quite abstract, they provide a concrete method by which to tackle the technical problem of materials architecture.

Our operad M has protein building block types as objects, and protein building instructions as morphisms. Forming a sequence of instructions, or program, in Matriarch corresponds to composing a tree of morphisms in the operad. A set-valued functor M → Set assigns to each object (building block type) the set of all building blocks of this type, and it assigns to each morphism (building instruction) a function that creates a new building block by combining or manipulating existing building blocks. The detailed mathematical framework is developed for experts in the Mathematics Supplement. A more practical formulation can be found in a User's Guide,¹⁶ and a summary is given in sections 2.1–2.2 below.

2.1. Building Blocks

A building block is abstracted to a set of oriented rigid bodies that are covalently bonded and embedded in space. The bond structure consists of a connection matrix as well as the building block interface. At these interfaces, building blocks can be attached. Attach is one of many building instructions that can be applied to form higher-level building blocks from more basic ones. The technical definition can be found in the Matriarch User's Guide¹⁶ and the Mathematics Supplement. Note that the current implementation of Matriarch assumes that all building blocks have a left–right orientation and covalent bonds can only be formed at the left–right interfaces.

To simplify the job of the materials engineer, we assign each protein a finite portion of the positive z-axis, called the axis line, by which to manipulate the protein. The axis line is equipped with a normal vector that is used by some building instructions. Each oriented rigid body, e.g., amino acid, is assigned a point in space, a backbone direction, a side-chain direction, and a projection onto the axis line (called axis projection).

2.2. Building Instructions

The most basic Matriarch command, chain, creates a building block from a sequence of PDB files. There are 20 amino acid PDB files, which come predefined with Matriarch, but the user can extend this set. New building blocks are then obtained by performing building instructions to existing building blocks. Table 1 summarizes the basic building instructions, as well as a few derived building instructions.

Table 1.

Functions of Common Basic Building Instructions^a

instruction	function
moveOrbs(Γ, g)	moves the atoms in Γ by rigid motion g
shiftOrbs(Γ, s)	shifts the atoms of Γ by s units in the z-direction
rotateOrbs(Γ, θ)	rotates the atoms of Γ by θ (in degrees) around the z-axis
twist(Γ, W)	twists Γ by the axis twister W, which describes the twisted and new building block axes
helix(Γ, rad, pitch, handed)	twists Γ into a helix with radius rad, pitch length pitch; the argument handed must be L or R, to choose the handed-ness of the helix.
pad(Γ, s)	pads Γ with blank space of length s at its left terminal
reverseOrbs(Γ)	reverses the direction of Γ
attach(Γ1, Γ2)	attaches Γ1 and Γ2 in series
attachSeries(Γ, n)	attaches n copies of Γ in series
overlay(Γ1, Γ2)	overlays Γ1 and Γ2 in the same space
makeArray(Γ, m, n, d, alt)	places mn copies of Γ into an m × n array, equally spaced at a distance d and either antiparallel (alt = true) or parallel (alt = false)
space(Γ1, Γ2, s)	spaces Γ1 and Γ2, with a distance s in between
spaceSeries(Γ, n, s)	places n copies of Γ in series, spaced at a distance s

^aThroughout, Γ₁ and Γ₂ represent building blocks and lowercase letters represent parameters.

Given a building instruction, Matriarch uses the formal definitions of its input building blocks to create a formal structure for its output (see User's Guide section 3¹⁶). For example, attach puts the building blocks next to each other, aligning them appropriately, and then adds a few new bonds at the interface.

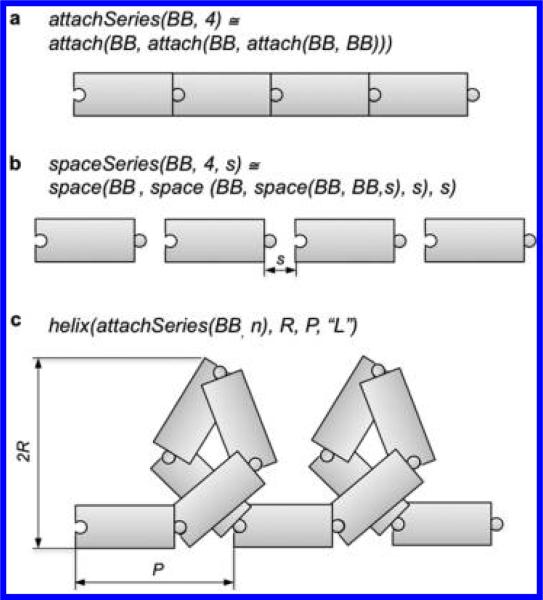
More complex building instructions can be derived from the predefined building instructions by recursively applying them. A few examples of such derived building instructions include: attachSeries (Figure 3a), spaceSeries (Figure 3b), helix (Figure 3c), collagen, triangle. See Table 1. Users can also program their own derived building instructions.

Figure 3.

Schematic of some building instructions. Building blocks are represented by the puzzle-piece rectangles, with left and right terminals indicated by lock and key. In the default case the left terminal of an amino acid is its amine group. (a) The instruction attachSeries is derived as a list version of the instruction attach, which connects two building blocks by bringing their left and right terminals together in space and making the necessary bonds. (b) The instruction spaceSeries is derived as a list version of the instruction space, which puts two building blocks next to each other at a distance s. In this case, no new bonds are formed. (c) A left-handed helix with pitch P and radius R is created by applying the instruction helix to an arbitrary sequence of building blocks.

3. MATRIARCH SOFTWARE PACKAGE

Matriarch is a language of building blocks and building instructions–the materials architecture–and is accessible as open source Python code.¹⁷ Although the underlying logic of Matriarch can be applied to a large variety of material systems, it has so far only been implemented for proteins. Complex materials architectures can be output in the form of PDB files, which are compatible with many molecular dynamics software packages and protein visualization tools.

As mentioned, each building block can be output as a file, but it can also be used as an argument to a further Matriarch building instruction. Matriarch adheres to the mathematics of operads in the way building blocks are defined and manipulated, as described in section 2. The particular framework of classes and instances reflects the mathematical structure in the well-known type-theoretic syntax for category theory,¹⁸ which establishes the type-checking for the Matriarch software.

More information about the use of the Matriarch software can be found in the User's Guide.¹⁶

3.1. Basic Matriarch Commands

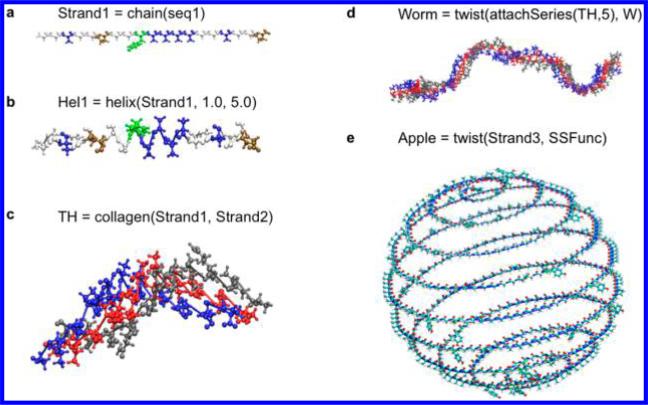
Figure 4 demonstrates the versatility of Matriarch, by showing sample outputs rendered in VMD.¹⁹ A single polypeptide strand can be obtained by attaching a sequence of amino acids, as shown in Figure 4a, using the Matriarch command chain. The function helix, with parameters for radius, pitch, and handedness, twists the strand into a helix, as shown in Figure 4b. The collagen command overlays and shifts three helices to form collagen-like structures, as shown in Figure 4c. The result of any of these commands is a building block, which can be output and studied (as we do in our case study, section 3.2) or further manipulated by Matriarch commands. For example, a collagen-like structure can be attached to itself in series (attachSeries) to form a longer helix, which can then be twisted to form a helix of helices; this is shown in Figure 4d. One could also stack these chains, helices, or collagen molecules into a fibril-like array, using the array command.

Figure 4.

Versatility of Matriarch. The result of any Matriarch building instruction is a building block, which can be further manipulated by Matriarch commands. The results can be output as (unequilibrated) PDB files. (a) A single polypeptide strand is obtained by attaching a sequence of amino acids using the Matriarch command chain. (b) The function helix, with parameters for radius and pitch, twists the strand into a helix. (c) The collagen command overlays and shifts three helices to form collagen-like structures. (d) The collagen-like structure can be attached to itself in series (attachSeries) to form a longer helix, which can then be twisted to form a larger-scale helix. (e) A building block can be twisted using any curve, such as a spherical spiral.

A building block can be twisted into any conceivable shape. That is, given a parametrized curve in 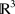, Matriarch will lay the sequence along that curve. The curve is automatically reparameterized by arclength so that amino acids are neither stretched nor compressed. Instead of providing a parametrized curve, the user can simply input a sequence of points in 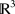. Matriarch will interpolate the points using a piecewise linear curve and subsequently smooth it. This is useful because most protein structures of interest do not follow analytical curves. In the future, we plan to add functionality to Matriarch by which a protein's sequence and backbone coordinates (as well as side-chain directions) can be imported to Matriarch from a PDB file. At this point, a building block is created with the smoothedPieceWiseLinear function, which is discussed in detail in the User's Guide.¹⁶ The user can further manipulate this building block, e.g., by twisting or by mutating the sequence, and then output it again. Although proteins of arbitrary backbone shape can be created in this way, the user currently has limited control over the side-chain configuration, though this will be addressed in a future Matriarch version.

Some structures, e.g., helices or stacked structures, can be created using analytical functions. Figure 4e shows an example in which the strand is twisted into a spherical spiral. Other examples in the User's Guide¹⁶ include a triangular helix (as found in amyloids) and an arbitrary mathematical curve.

In theory, Matriarch can create any protein structure (to the extent possible using rigid amino acid building blocks) from basic building instructions, as well as extend or modify existing protein structures. Users can extend the library of instructions by programming custom combinations of basic instructions. In the next section, this is demonstrated for the case of tropocollagen.

3.2. Case Study: Mutated Tropocollagen

Collagen, as one of the most important biological materials, has a wide range of potential applications, and considerable resources are currently being invested to synthetically engineer it within the next few years.^20,21 Engineers will benefit from exploring its design space to find variants that are tailored for specific mechanical applications. The ability of Matriarch to form arbitrary materials architectures (e.g., through targeted sequence mutations) makes it ideal for performing the series of computational experiments necessary for this exploratory phase.

As a case study, we perform such mutations on the α-1 and α-2 sequences from a type I collagen molecule from Rattus norvegicus,²² retrieved from RSCB sequence 3HQV. We select 57 representative amino acids between the 412th and 468th residues of each strand.²³ We then vary 18 amino acids of the α-2 strand by substituting sequences from rat collagen, rat elastin, and human elastin into the original tropocollagen, to form a total of ten molecules to be equilibrated using molecular dynamics. The structures are then mechanically tested via steered molecular dynamics (see Figure 5a), similar to the procedure used in refs 20, 23, and 24.

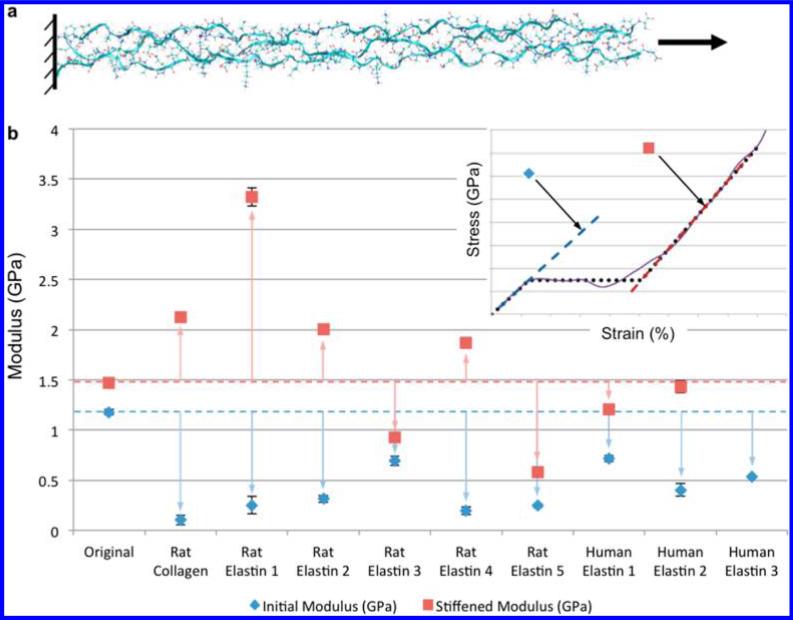
Figure 5.

Case study: tropocollagen mutations using Matriarch. (a) Schematic of the mechanical testing of tropocollagen molecule and nine mutations. The mutations are obtained by replacing 18 amino acids in the α-2 strand by various naturally occurring sequences, from rat collagen, rat elastin, and human elastin. For each tropocollagen mutant, the three strands are constrained at their left ends and pulled at their right ends, using steered molecular dynamics. (b) Two characteristic Young's moduli are determined from the tensile test, for each of the ten molecules. The initial moduli, shown in blue diamonds, are found to be consistently below that of the original tropocollagen structure, whereas the stiffened moduli, shown in red squares, do not show a consistent trend. The error bars indicate 95% confidence intervals of the regression. The results indicate that although the mutations form tropocollagen-like triple-helices, they display significant variation in mechanical properties. Such studies can be used to build databases of structure–function relationships.

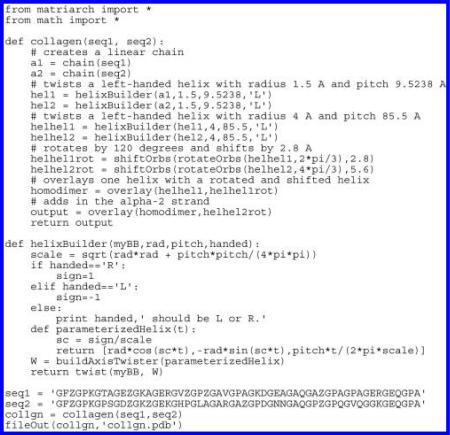
We create these ten structures using the function collagen(chain(seq1), chain(seq2)), which returns a triple helical heterotrimer whose α-1 and α-2 strands have sequences seq1 and seq2, respectively. The collagen command is a predefined script, defined as a composite of basic Matriarch functions, as shown in the appendix. After forming the original tropocollagen, we modify the amino acid sequence argument passed to this building instruction for each of the nine mutations. Matriarch generates the initial structures for all ten structures under the assumption that they would approximately coincide with those of nonmutated collagen. This assumption is valid in the sense that all mutations equilibrated into collagen-like triple helices, and the necessary equilibration times were dramatically reduced. Note that the structures are not necessarily stable. The stability is probably related to the types of noncovalent bonding between the amino acid functional groups in radial or circumferential direction. Other methods have been developed to predict stability upon mutation.²⁵

For mechanical testing of collagen variants, a possible design space can be formed by the initial elastic modulus and the so-called stiffened modulus (the modulus after unfolding of the structure), as shown in the schematic at the top-right of Figure 5b. The results for the ten structures show a large variation in the moduli, as shown in Figure 5b. All mutations show a lower initial modulus than the nonmutated collagen, which suggest that the native-state structure of this collagen may be well optimized to provide high initial elastic modulus for its role to provide structural support for tissues. The stiffened modulus varies significantly and nonuniformly; both much larger and smaller stiffened moduli occur. A Gaussian filter was applied to the stress–strain data of the tensile test, and local linear regression was applied to determine the moduli. The error bars in Figure 5b indicate 95% confidence intervals of the regression.

3.3. Comparison to Other Software Tools

Matriarch can be used to create a wide variety of initial structures, with the idea of vastly reducing the equilibration time needed for simulations. Note that it does not create topology files, but only geometry-based PDB files. Although the creation of topology files such as PSF files (VMD, NAMD) or TOPOL files (GROMACS) would be a relatively straightforward extension, the internal topology generators of these programs should generally be able to interpret Matriarch's output for non-overlapping structures. Of course, topology generation can fail for structures built with certain Matriarch programs, especially those involving the twist command or when atoms are placed with almost identical coordinates. A future version of the software will include a topology generator that uses the bond structure inherent in Matriarch building blocks.

The Matriarch software certainly shares features of other molecular design software packages, such as NanoEngineer, Materials Studio, CHARMM, and Sybil. The main advantage of Matriarch is the high complexity of possible conformations that can be easily created, from triple helices to multiple layers of strands. Furthermore, because Matriarch is an open source and freely available python library, it is possible to directly integrate the materials architecture creation into the runtime of molecular dynamics simulations, such as LAMMPS.

There are many other software tools for molecular design, both commercial and noncommercial.²⁶ Most of these (e.g., Packmol, FoldIt, Avogadro) involve scientifically informed guesses about secondary structures but are also limited in scope, e.g., to small molecules or to specific applications.

The THeBuSCR software²⁷ outputs triple helical molecules with arbitrary sequences, but it cannot be used to create any other structure. Its advantage over Matriarch is that it provides statistically derived conformations, specific to sequences found in collagen-like structures, whereas Matriarch arranges molecules in a user-specified shape (e.g., a triple helix).

Nanoengineer and Materials Studio have a user-friendly CAD interface, but they are feasible only for smaller molecules and DNA. Matriarch works on any length scale, with building blocks of arbitrary complexity and size. Sibyl enables the user to predefine secondary structures such as beta-sheets and alpha-helices, but it is often inconvenient when creating larger structures because the interface is not script-based. Although Materials Studio and Sibyl are extensive software packages that include molecular dynamics solvers, they require licenses and cannot be customized easily.

4. CONCLUSION

Here we presented Matriarch, a language of materials architecture, implemented as a Python library. It can be used to build the initial geometry of a large class of proteins using only a few basic building instructions. Matriarch returns PDB files that can be used as a starting point for molecular dynamics simulations. We have used this software to create various complex architectures and performed a sample study on the building block replacement problem for tropocollagen.

Future work involves several extensions to the Matriarch software package. Although users are currently able to create almost arbitrary configurations of amino acids using a combination of the basic building instructions, a detailed control over the conformation of the side-chain or the backbone dihedrals is not yet implemented. A next step is to introduce new parameters for controlling the side-chain configurations while creating protein structures. Furthermore, Matriarch will allow the user to import an existing PDB file or a simulation trajectory and to manipulate the protein using building instructions as well as modify its sequence. One important challenge for protein scientists is to obtain a good initial guess of a protein's structure based on its sequence. To this end we will create a database in the category theoretic framework that is automatically populated by results from peptide simulations and the protein database. This can be used to make a statistical prediction for the structure of an unknown protein by querying the database on subsets of its sequence.

Studies, such as the one discussed in section 3.2, can be used to build databases of structure–function relationships, as required to solve the building block replacement problem. For example, if the Matriarch python package were integrated with a molecular dynamics solver, a direct link could be made between the structural input and the property output, as sketched in Figure 1. Because each material architecture exists within a well-articulated mathematical design space, structural changes at runtime (by reading the simulation trajectory into Matriarch) and the associated material properties can be tracked and catalogued. When such a process is automated, it can be run repeatedly to optimize for any desired geometric feature or physical property, akin to the well-established structural optimization using finite element methods. This would be especially powerful in combination with machine-learning or genetic algorithms that can search the existing database for patterns that correlate with desired functionality and then propose similar structures for testing. Such patterns may exist, not only for short amino acid sequences, but for larger building blocks as well. Matriarch thus holds promise to be the core of a new molecular design process, where engineering decisions can be made at arbitrary scales.

APPENDIX: SAMPLE MATRIARCH SCRIPT