Arterial mechanics considering the structural and mechanical contributions of ECM constituents

Abstract

Considering the organization and engagement behavior of different extracellular matrix (ECM) constituents in the medial and adventitial layer of the arterial wall, in this study, we proposed a new constitutive model of ECM mechanics that considers the distinct structural and mechanical contributions of medial elastin, medial collagen, and adventitial collagen, to incorporate the constituent-specific fiber orientation and the sequential fiber engagement in arterial mechanics. Planar biaxial tensile testing method was used to characterize the orthotropic and hyperelastic behavior of porcine thoracic aorta. Fiber distribution functions of medial elastin, medial collagen, and adventitial collagen were incorporated into the constitutive model. Considering the sequential engagement of ECM constituents in arterial mechanics, a recruitment density function was incorporated into the model to capture the delayed engagement of adventitial collagen. A freely jointed chain model was used to capture the mechanical behavior of elastin and collagen at the fiber level. The tissue-level ECM mechanics was obtained by incorporating fiber distribution, engagement, and elastin and collagen content. The multi-scale constitutive model considering the structural and mechanical contributions of the three major ECM constituents allows us to directly incorporate information obtained from quantitative multi-photon imaging and analysis, and biochemical assay for the prediction of tissue-level mechanical response. Moreover, the model shows promises in fitting and predicting with a small set of material parameters, which has physical meanings and can be related to the structure of the ECM.

Introduction

Arteries have three layers: tunica intima, tunica media, and tunica adventitia. The tunica intima layer is made up of a single layer of endothelial cells and its main purpose is to provide hemocompatibility with the blood. The tunica media, the middle layer of the arterial wall, contains smooth muscle cells that are embedded in a matrix of elastic fibers, collagen fibers, as well as aqueous ground substance matrix containing proteoglycans. The outermost layer is the tunica adventitia that consists primarily of a dense network of collagen fibers.

Elastin and collagen are the major extracellular matrix (ECM) constituents in large elastic arteries. Human aorta is comprised of approximately 47% elastic fibers and undergoes billions of stretch cycles in the course of one's lifetime (Starcher and Galione, 1976). Elasticity is crucial for aortas to accommodate the pulsatile blood flow. Elastic fibers consist of an inner crosslinked elastin core surrounded by a mantle of fibrillin-rich microfibrils (Mecham, 2008). In elastic arteries such as the aorta, elastic fibers form thick concentric fenestrated layers of elastic lamellae, with inter-lamellar connecting fibers distributed radially through the vessel wall (O'Connell et al., 2008). Each elastic lamellae alternates with a layer of smooth muscle cells, collagen fibers, and together, organize into a lamellar unit which is considered as the functional unit of the vessel wall (Brooke et al., 2003). Collagen fibers primarily provide structural integrity and mechanical properties at higher strains. It has a triple helix structure of collagen molecules and these structures bundle together to form collagen fibrils. The structural and mechanobiological interrelations between elastin and collagen, the primary load-bearing components in the arterial wall, are important for properly functioning arteries.

With the help of optical techniques, many studies have attempted to quantify, and then, directly incorporate some of the structural information, such as fiber orientation and undulation properties, into structural-based constitutive models, pioneered by the work from Lanir (1979). In some of these studies, elastin and collagen fibers were assumed to be linear elastic material and the nonlinear response of tissues was considered to be the result of collagen recruitment. Later, Lokshin and Lanir (2009) investigated the sensitivity of elastin and collagen fiber dispersion as well as collagen undulation distribution.

Motivated by the tissue structure, varieties of constitutive formulations have been proposed for the study of biological tissues. Considering the fiber reinforced composite structure of arterial wall, Holzapfel et al. (2000) proposed an exponential-based constitutive model for the arterial wall in which they assumed multiple families of collagen fibers with preferred orientations. Later the model was extended to incorporate the 3D dispersion property of collagen fibers (Gasser et al., 2006). Some other models have been developed assuming one or multiple fiber families that are undulated with a stochastic nature (Wuyts et al., 1995; Zulliger et al., 2004; Cacho et al., 2007; Rezakhaniha et al., 2011; Zeinali-Davarani et al., 2013; Zeinali-Davarani et al., 2015). In these models the gradual recruitment of collagen fibers is responsible for the stiffening behavior of collagenous tissues.

Previous constitutive models have mainly focused on the undulation and distribution of adventitial collagen fibers in arterial mechanics, while the rest of the arterial structure was, to a large extent, treated as an isotropic matrix material. Our recent study coupling mechanical loading and multi-photon imaging provided new understandings on how medial elastin, medial collagen, and adventitial collagen play unique structural and mechanical roles in response to mechanical loading (Chow et al., 2014). Specifically, the three ECM constituents work cooperatively and are sequentially engaged with an immediate recruitment of the elastin and medial collagen, but a delayed engagement of adventitial collagen. The distinct contributions of the ECM constituents to arterial mechanics are important in modifying the dynamic behavior of the arterial wall, and need to be considered in constitutive modeling of arterial mechanics. In this study, a new constitutive model is proposed that considers the constitutional structural and mechanical contributions from medial elastin, medial collagen, and adventitial collagen fibers.

Materials and Methods

Biaxial Tensile Testing

Four porcine thoracic aortas from 12-24 month-old pigs were harvested from a local slaughter house and cleaned of adherent tissues. Two square aortic samples of about 20 mm × 20 mm were prepared from each thoracic aorta. Mechanical testing was performed within 48 hours of harvesting to minimize the effects of microstructural degradation on the artery. Equi- and nonequi-biaxial tensile tests were performed to characterize the mechanical behavior of the aortic tissue (n=7). Samples were preconditioned for 8 cycles with 10 s of half cycle time by applying an equi-biaxial tension of 30 N/m. Following the preconditioning cycles, a preload of 2 ± 0.050 N/m was applied in order to ensure tautness of the sutures. The preloaded configuration was chosen as the reference configuration for stress and stretch calculations. Eight cycles of one equibiaxial and two nonequi-biaxial tensions were applied to each aortic sample according to the following protocols: f_l:f_c = 2:3, 1:1, 3:2. Where f_l:f_c is the ratio of tension applied in the longitudinal and circumferential directions, respectively.

Constitutive Modeling

A constitutive model of ECM mechanics is developed that considers the contribution from medial elastin (ME), medial collagen (MC), and adventitial collagen (AC) constituents, and incorporates the constituent-specific distribution orientations R_i(θ) and the sequential fiber engagement in the hyperplastic and anisotropic arterial behavior. The total strain energy function of the arterial wall is the sum of the constituent strain energy, W_i, and can be represented as W = (Σ) W_i. Here and throughout the paper, i = ME, MC, AC correspond to medial elastin, medial collagen and adventitial collagen, respectively.

ECM constituent fiber network model

A fiber distribution network model is used to incorporate the experimentally measured fiber distribution function R_i (θ), and the elastin and collagen content n_i. The ECM constituent strain energy function, W_i, is assumed to be the sum of the individual fiber strain energies and can be expressed as:

$$W_i=n_i{\int }_{-\pi ∕2}^{\pi ∕2}{w}_i\left({\rho }_i\right)R_i\left(\theta \right)\mathrm{d}\theta$$ (1)

where w_i(ρ_i) is the strain energy function at the fiber level. The elasticity of elastin and collagen fibers is described by an entropy-based freely-jointed chain model, based on non-Gaussian statistical mechanics for large deformation (Kuhn and Grün, 1942):

$$w_i\left({\rho }_i\right)=kϴN_i\left(\frac{{\rho }_i}{N_i}{\beta }_{\rho }^i+\ln \frac{{\beta }_{\rho }^i}{\sinh {\beta }_{\rho }^i}\right)$$ (2)

In Equation (2) N_i is the number of rigid links within each chain, ρ_i is the normalized deformed chain length and is related to the fiber-level Green-Lagrange strain ε by ${\rho }_i=P_i\sqrt{2\epsilon +1}$, and $P_i=\sqrt{N_i}$ is the normalized undeformed chain length. ${\beta }_{\rho }^i={\mathcal{L}}^{-1}({\rho }_i∕N_i)$, where $\mathcal{L}\left(x\right)=\coth x-1∕x$ is the Langevin function. k = 1.38 × 10⁻²³ J/K is Boltzmann's constant, and Θ = 298K is the absolute temperature. Under affine assumption, the fiber-level Green-Lagrange strain (ε) can be related to tissue-level Green-Lagrange strain tensor E by ε = M^TEM, where $\mathbf{M}=\cos \theta \widehat{i}+\sin \theta \widehat{j}$ is the unit vector parallel to the fiber's long axis, and θ is the fiber angle with respect to the circumferential direction.

To maintain a stress-free state at the reference configuration, an additional term is needed in the strain energy function in Equation (2), and the new constituent strain energy function becomes:

$$W_i=n_i{\int }_{-\pi ∕2}^{\pi ∕2}{\psi }_i{R}_i\left(\theta \right)\mathrm{d}\theta$$ (3)

where ψ_i is the fiber level strain energy function with the additional term, and

$${\psi }_i=w_i-kϴP_i{\beta }_P^i\ln {\lambda }_f$$ (4)

where ${\lambda }_f=\sqrt{2\epsilon +1}$ is the fiber-level stretch. The Cauchy stress for each constituent can then be obtained by σ_i = J⁻¹FS_iF^T, where S_i = ∂W_i/∂E is the second Piola-Kirchhoff stress, F is the deformation gradient, and J = det (F). The corresponding constituent Cauchy stress is then:

$${\sigma }_i=\frac{n_{i}kϴ}{J}{P}_i{\int }_{-\pi ∕2}^{\pi ∕2}\left(\frac{{\beta }_{\rho }^i}{{\lambda }_f}-\frac{{\beta }_P^i}{{\lambda }_f^2}\right)\left(\mathbf{FM}\right){\left(\mathbf{FM}\right)}^{\mathrm{T}}{R}_i\left(\theta \right)\mathrm{d}\theta$$ (5)

Arterial mechanics considering the sequential engagement of ECM constituents:

Considering the sequential recruitment of ECM constituents in response to mechanical loading, a normal recruitment function ${\eta }_f^{AC}$ (Lanir, 1979) is included to capture the delayed adventitial collagen engagement, and

$${\eta }_f^{AC}=\frac{1}{\sqrt{2\pi }{d}_{AC}}\exp \left[-\frac{{(x-m_{AC})}^2}{2d_{AC}^2}\right]$$ (6)

where m_AC and d_AC are the mean and standard deviation of the normal distribution, defining the shape of the recruitment function. The total strain energy function considering the delayed adventitial collagen engagement is:

$$\begin{array}{c}\hfill W=n_{ME}{\int }_{-\pi ∕2}^{\pi ∕2}{\psi }_{ME}{R}_{ME}\left(\theta \right)\mathrm{d}\theta +n_{MC}{\int }_{-\pi ∕2}^{\pi ∕2}{\psi }_{MC}{R}_{MC}\left(\theta \right)\mathrm{d}\theta \hfill \\ \hfill n_{AC}{\int }_{-\pi ∕2}^{\pi ∕2}{\int }_1^{\lambda }{\psi }_{AC}(\lambda -x){\eta }_f^{AC}\mathrm{d}x{R}_{AC}\left(\theta \right)\mathrm{d}\theta \hfill \end{array}$$ (7)

The tissue-level Cauchy stress can then be expressed as σ = σ_ME + σ_MC + σ_AC.

Incorporation of structural and biological information into the model

Incorporation of ECM fiber distribution:

Based on model in equation (7), the fiber orientation distribution of the ECM constituents, R_i(θ), were incorporated into the model in two ways: A) the distributions of fiber orientation of each constituent are incorporated directly based on the analysis of multi-photon images (Chow et al., 2014); and B) the measured distribution functions of each constituent were fitted with a three-term von Mises distribution as:

$$R_i\left(\theta \right)=\sum _{j=1}^3\frac{1}{\pi I_0\left({\kappa }_j^i\right)}\exp \left\{{\kappa }_j^i\cos \left[2\left(\theta -{\mu }_j^i\right)\right]\right\}$$ (8)

where ${\mu }_j^i$ and ${\kappa }_j^i$ represent the mean and variance of the von Mises distribution to be obtained through parameter estimation. I₀ is the modified Bessel function of order 0 and is defined as:

$$I_0\left({\kappa }_j^i\right)=\frac{1}{2\pi }{\int }_0^{2\pi }\exp \left[{\kappa }_j^i\cos \left(\theta \right)\right]\mathrm{d}\theta$$ (9)

Determination of adventitial collagen recruitment function ${\eta }_f^{AC}$:

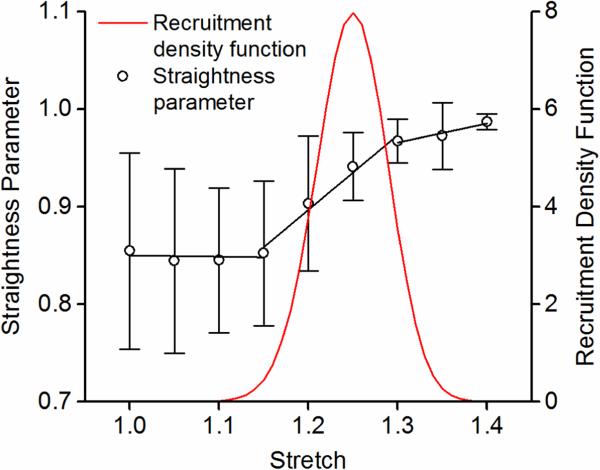
The collagen recruitment function was determined based on the straightness parameter analysis of adventitial collagen fibers from our previous study by Chow et al. (2014). Adventitial collagen was shown to exist as large wavy bundles of fibers that exhibit delayed fiber engagement. The values of the mean and standard deviation of the normal distribution, m_AC and d_AC, were fixed as 1.25 and 0.05, respectively, which captures a peak recruitment at about 1.25 stretch and an overall collagen engagement between 1.15-1.35 stretch (Figure 1).

Figure 1.

Straightness parameter of adventitial collagen fibers (from Chow et al., 2014), and the recruitment distribution density function that captures the delayed adventitial collagen engagement in response to mechanical loading.

Elastin and collagen content n_i

Parameter n_i is related to the content of ECM constituents. These parameters were not fixed in the model, but were rather allowed to vary within a physiologically meaningful range considering the elastin and collagen content in the arterial tissue. Based on the biochemical assay measurements of the elastin and collagen content in porcine thoracic aorta in our previous study (Chow, et al., 2013a; Chow, et al., 2013b), the content of the ECM constituent is enforced to satisfy the following relationship:

$$0.4614(n_{MC}+n_{AC})<n_{ME}<2.8315(n_{MC}+n_{AC})$$ (10)

Note that in the medial collagen and adventitial collagen content are indistinguishable from biochemical assay measurements. Meanwhile, since n_ikΘ is related to the initial modulus (Zhang et al., 2005), based on our past experience with the mechanics of arteries and elastin network (Zou and Zhang, 2009), n_i is set to be greater than 10²² 1/m³ so that the initial modulus is constrained to be at least larger than 10 pa. This is a rather loose constraint as the tangent modulus of elastin network and arteries are normally in the order of kPa.

Parameter Estimation

If the fiber distribution function of each constituent are incorporated directly based on the analysis of multi-photon images, then the model has six material parameters for method A: n_i and N_i (i = ME, MC, AC). The three-term von Mises distribution function has three fiber families with the same fiber property (N_i), but different fiber density (n_{i_1}, n_{i_2}, n_{i_3}) for each fiber family, thus the model has twelve material parameters for method B: n_{i_1}, n_{i_2}, n_{i_3,} and N_i (i = ME, MC, AC).

A penalty approach was employed to reinforce physiological meaningful constraints on the estimated parameters. In addition to constraints specified in Equation (10), it is also assumed that N_ME > N_MC > N_AC >1 to reinforce that the stiffness of medial elastin < medial collagen < adventitial collagen. This is in agreement with the fact that medial collagen contains much type III collagen, whereas adventitial collagen is composed mostly of type I collagen (Humphrey, 2002), and type III collagen has been shown to be more compliant than type I collagen (Eriksen et al., 2002).

The material parameters were determined by minimizing the following objective function:

$$\psi =\sum _{j=1}^m\left[{\left({\sigma }_{11}^c-{\sigma }_{11}^e\right)}_j^2+{\left({\sigma }_{22}^c-{\sigma }_{22}^e\right)}_j^2\right]$$ (11)

where m is the number of data points, and σ^c and σ^e represent Cauchy stress from the model and the biaxial tensile tests, respectively. Subscripts 1 and 2 correspond to the longitudinal and circumferential directions of the aortic sample, respectively. The objective function is minimized using the Nelder-Mead direct search method implemented in the fminsearch subroutine in Matlab (version R2013b, The MathWorks, Inc.).

To assess the fitting and predicting capability of the model, we 1) fit the model to experimental results from equi-biaxial tension f_l:f_c = 1:1, and predict the mechanical behavior under nonequi-biaxial tension f_l:f_c = 3:2 and 2:3 and compare with experimental measurements; 2) fit the model to experimental results from nonequi-biaxial tension f_l:f_c = 3:2 and 2:3, and predict the mechanical behavior under equi-biaxial tension f_l:f_c = 1:1 and compare with experimental measurements; and 3) fit the model to all experimental results from biaxial tension f_l:f_c = 3:2, 1:1, and 2:3. As a measure of the goodness of fit, the root mean square error measure is defined as (Holzapfel et al., 2005):

$$e=\frac{\sqrt{\frac{\psi }{m-q}}}{{\sigma }_{ref}}$$ (12)

where q is the number of parameters in the model, and σ_ref is determined from the sum of Cauchy stresses for each stress-strain curve divided by the number of data points m.

Statistical Analysis

Statistical analysis was performed to compare the fitting and predicting errors by JMP Pro (version 11.1.1, SAS Institute Inc.) using ANOVA followed by Tukey's post hoc comparisons. Differences are considered to be significant when p < 0.05.

Results

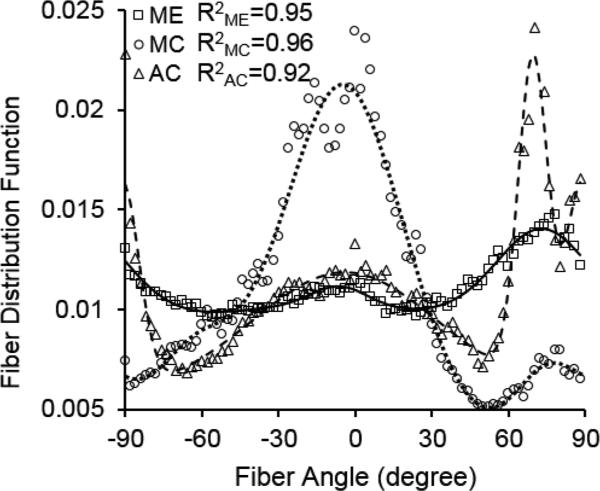
Figure 2 shows the averaged fiber orientation distribution function with three-term von Mises fitting for medial elastin, medial collagen, and adventitial collagen. The measurements were based on analysis of the multi-photon images from our previous study (Chow et al., 2014) when arterial tissue were subjected to an equi-biaxial stretch of 1.4. The fiber orientation distribution function shows remarkably different structural characteristics in ECM constituents. The elastic fibers are relatively more uniformly distributed compared to collagen. The medial collagen shows a preferred circumferential distribution, however the multi-fiber family distribution is evident in adventitial collagen. For all three ECM constituents, the three-term von Mises fittings were able to capture the fiber distributions in the arterial wall.

Figure 2.

Fiber orientation distributions of medial elastin (ME), medial collagen (MC), and adventitial collagen (AC) in porcine thoracic aorta when subjected to an equi-biaxial stretch of 140% in both the longitudinal and circumferential directions. Symbols represent measured distribution (Chow et al., 2014) and lines represent the corresponding three-term von Mises distribution function fitting. The R² values represent correlation coefficients between the measured and fitted fiber distributions.

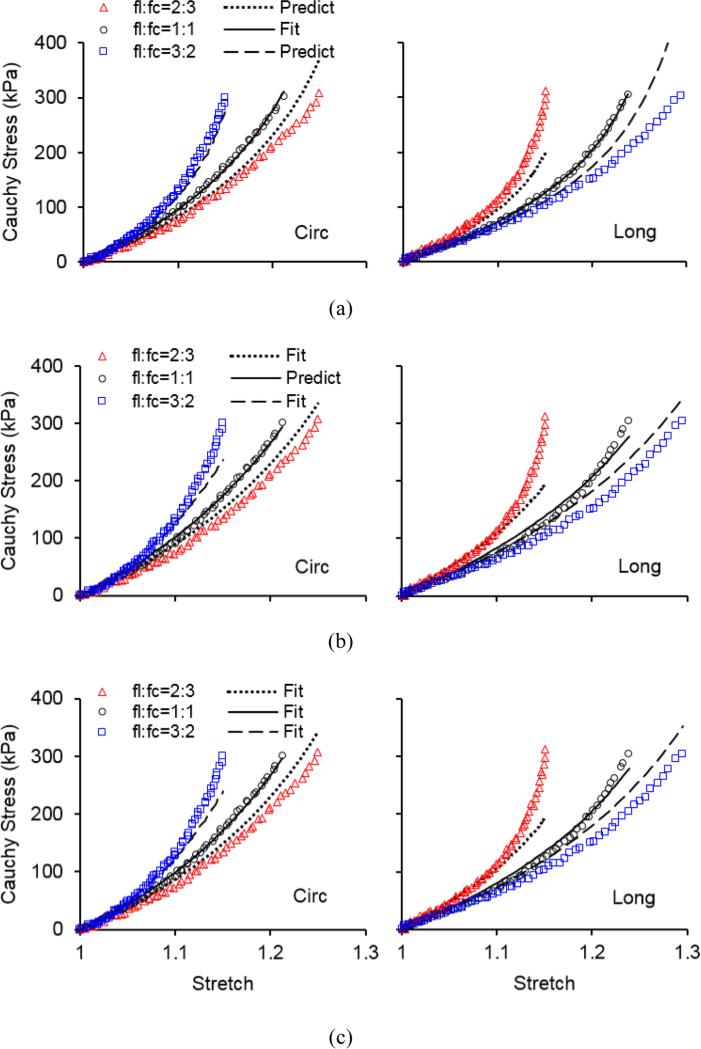
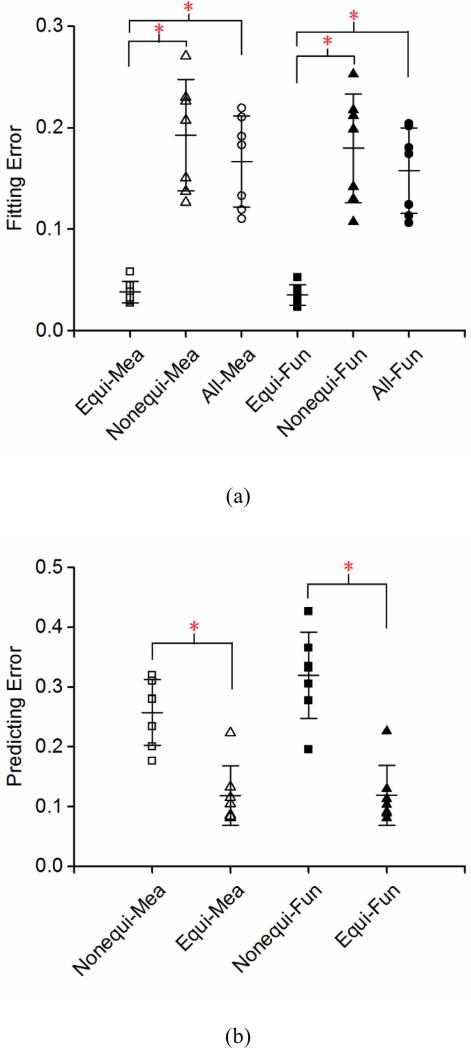
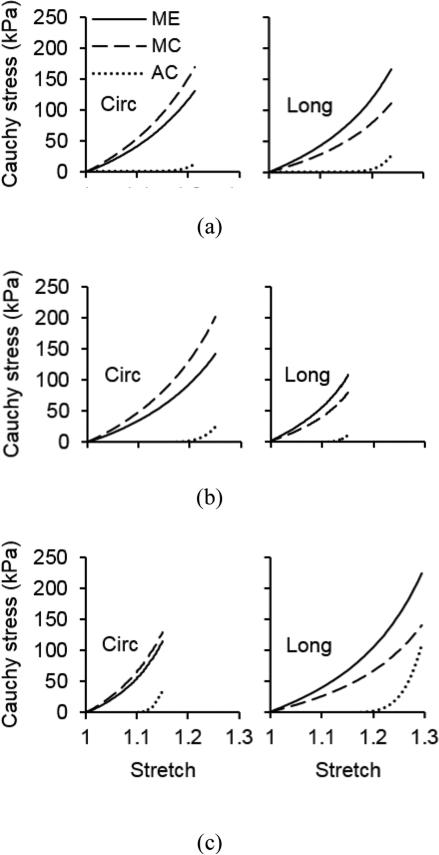
The representative stress-stretch behavior from biaxial tensile testing and constitutive modeling are shown in Figure 3. Overall the model is able to characterize the nonlinear and anisotropic behavior of arteries, however it appears that the predictability of the model is insufficient when fitting was performed to a single set of equi-biaxial tension data (Figure 3a). Fitting two sets of nonequi-biaxial tension data in Figure 3b improves the predictability of the model. This observation is further proved by quantifying the fitting and predicting errors in Figure 4. The fitting error from a single set of equi-biaxial tension data is significantly smaller than the error resulted from fitting two sets of nonequi-biaxial tension data and all three sets of biaxial tension data. However, fitting two sets of nonequi-biaxial tension data significantly decreases the predicting error. The complete list of estimated parameters, fitting and predicting errors are presented in Tables 1 and S1.

Figure 3.

Representative Cauchy stress vs. stretch in the circumferential (Circ) and longitudinal (Long) directions of sample 1 in Table 1 when (a) fitting equi-biaxial testing data f_l:f_c = 1:1 and predicting nonequi-biaxial testing data f_l:f_c = 2:3 and 3:2; (b) fitting nonequi-biaxial testing data f_l:f_c = 2:3 and 3:2 and predicting equi-biaxial testing data f_l:f_c = 1:1; and (c) fitting all equi-biaxial and nonequi-biaxial testing data. Symbols represent experimental measurements and lines represent modeling results.

Figure 4.

Quantification of (a) fitting and (b) predicting errors from the three fitting strategies in Figure 3 (Equi-, Nonequi-, All-) with the incorporation of directly measured orientation distribution functions (Mea) and the corresponding three-term von Mises distribution function (Fun) (n = 7). *p < 0.05.

Table 1.

Model parameters and fitting and predicting errors (Error_f and Error_p) from method A when the measured fiber orientation distribution function of medial elastin, medial collagen, and adventitial collagen was directly incorporated into the model.

Sample number	nME (1/m3)	NME	nMC (1/m3)	NMC	nAC (1/m3)	NAC	Errorf	Errorp
Fitting equi-biaxial testing data fl:fc = 1:1
1	1.02 × 1025	2.0815	1.00 × 1025	2.0815	5.42 × 1024	1.2325	0.0279	0.2812
2	4.67 × 1025	4.9990	7.55 × 1024	1.5478	9.36 × 1025	1.1578	0.0295	0.2345
3	9.99 × 1024	1.3848	1.00 × 1022	1.3791	2.09 × 1025	1.0000	0.0362	0.2798
4	1.71 × 1025	2.1244	2.95 × 1024	2.1244	3.09 × 1024	2.1244	0.0446	0.1765
5	4.16 × 1024	4.9541	8.99 × 1024	1.6103	3.38 × 1022	1.6103	0.0582	0.3200
6	2.11 × 1025	2.0348	4.88 × 1024	1.5646	2.56 × 1024	1.5646	0.0385	0.2003
7	1.34 × 1025	2.6391	2.91 × 1025	2.1392	1.09 × 1022	1.0001	0.0325	0.3103
Mean	1.75 × 1025	2.8882	9.07 × 1024	1.7781	1.79 × 1025	1.3842	0.0382	0.2575
SD	1.40 × 1025	1.4724	9.50 × 1024	0.3236	3.41 × 1025	0.4085	0.0105	0.0549
Fitting nonequi-biaxial testing data fl:fc = 2:3 and 3:2
1	2.28 × 1025	2.9107	7.90 × 1024	2.0182	1.53 × 1023	1.9447	0.2264	0.0867
2	3.55 × 1025	4.5885	1.23 × 1025	1.6706	2.34 × 1023	1.6703	0.1268	0.0816
3	3.20 × 1025	1.8935	1.00 × 1023	1.0569	6.92 × 1025	1.0000	0.2072	0.1333
4	2.89 × 1025	3.2538	6.12 × 1024	2.2048	4.08 × 1024	1.4121	0.1374	0.1049
5	2.53 × 1025	5.0000	1.81 × 1025	2.2161	2.55 × 1024	1.0292	0.2300	0.2232
6	5.64 × 1025	4.9991	1.32 × 1025	2.0784	6.70 × 1024	2.0783	0.1509	0.1156
7	3.38 × 1025	5.0000	5.31 × 1025	5.0000	1.13 × 1022	1.0000	0.2707	0.0839
Mean	3.35 × 1025	3.9494	1.58 × 1025	2.3207	1.18 × 1025	1.4478	0.1928	0.1184
SD	1.11 × 1025	1.2588	1.74 × 1025	1.2499	2.54 × 1025	0.4604	0.0547	0.0499
Fitting all equi-biaxial and nonequi-biaxial testing data
1	2.02 × 1025	2.7283	7.14 × 1024	1.9356	1.00 × 1022	1.9356	0.1916	-
2	3.29 × 1025	3.4276	1.16 × 1025	1.6687	2.38 × 1022	1.6687	0.1105	-
3	2.47 × 1025	1.7276	4.60 × 1023	1.2563	5.32 × 1025	1.0000	0.1831	-
4	2.20 × 1025	2.4964	5.17 × 1024	2.2081	2.58 × 1024	2.2081	0.1194	-
5	1.64 × 1025	4.9521	1.41 × 1025	1.8906	1.82 × 1024	1.0000	0.2103	-
6	3.41 × 1025	2.6298	1.20 × 1025	1.9863	4.63 × 1022	1.9863	0.1331	-
7	3.22 × 1025	5.0000	5.52 × 1025	5.0000	1.25 × 1024	4.7395	0.2193	-
Mean	2.61 × 1025	3.2802	1.51 × 1025	2.2779	8.41 × 1024	2.0769	0.1668	-
SD	7.00 × 1024	1.2601	1.83 × 1025	1.2370	1.98 × 1025	1.2663	0.0449	-

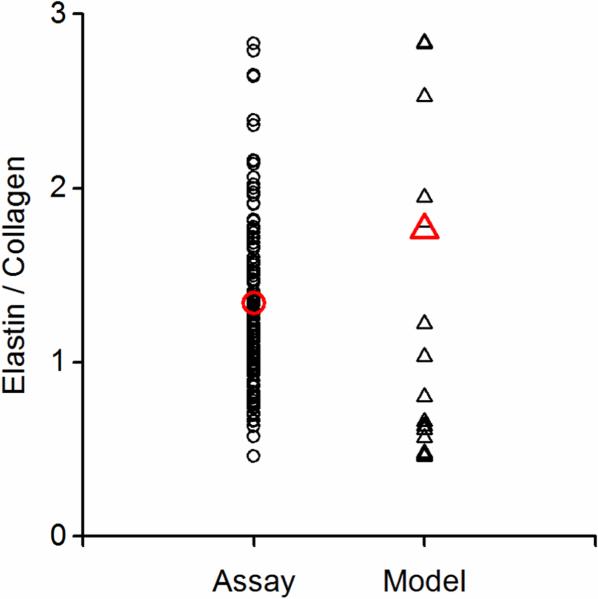
Parameter n corresponds to the ECM protein content. The ratio of elastin to collagen content obtained from the modeling, calculated by n_ME/(n_MC+n_AC), and from biochemical assay (Chow, et al., 2013a; Chow, et al., 2013b) is shown in Fig. 5. The fiber density from the three-term von Mises distribution function (n_{i_1}, n_{i_2}, n_{i_3}) was added together to represent the fiber density of the constituent. The ratio of elastin to collagen content from estimated parameters distributes evenly within the constraint obtained from biochemical assays and this indicates that the constraint applied is reasonable.

Figure 5.

The ratio of elastin to total collagen content obtained from biochemical assays (n = 118) and constitutive modeling (n = 42 combining all results listed in Tables 1 and S1).

The model allows us to study the contribution of individual ECM constituents to the mechanical behavior of the arterial wall. Figure 6 shows the stress-stretch relationship of medial elastin, medial collagen, and adventitial collagen when the arterial tissue is under equi- and nonequi-biaxial tension. The results suggest that that stress-stretch contribution of adventitial collagen is relatively low, which is related to the low stretch level achieved in the experiments. It is interesting that the medial collagen seems to contribute to the majority of the anisotropic response of the arterial wall under equi-biaxial tension condition, while all ECM constituents seem to contribute to the anisotropic behavior under nonequi-biaxial tension condition.

Figure 6.

Cauchy stress vs. stretch in medial elastin, medial collagen, and adventitial collagen of sample 1 in Table 1 in the longitudinal and circumferential directions when the tissue sample is subjected to (a) equi-biaxial tension f_l:f_c = 1:1, (b) nonequi-biaxial tension f_l:f_c = 2:3, and (c) nonequi-biaxial tension f_l:f_c = 3:2. The modeling results were obtained from fitting experimental results from equi-biaxial tension.

Discussion

Pathogenesis of many cardiovascular diseases has been associated with ECM changes such as elastin/collagen ratio, fibers orientation distributions, and collagen fiber undulations (Humphrey and Canham, 2000; Martinez-Lemus et al., 2009; Tsamis et al., 2013). There is a need for studies on the microstructural properties of ECM constituents and their association with the mechanical behavior of biological tissues to provide a better understanding of its structure-function relationship using constitutive models. In this study, a new constitutive model was developed that considers medial elastin, medial collagen, and adventitial collagen each play distinct structural and mechanical roles in arterial wall mechanics. The material parameters in the constitutive model, the constituent-specific fiber distribution, sequential fiber engagement, and elastin and collagen content, resemble key structural and biological information of the ECM, and are directly based on quantitative multi-photon imaging and analysis and biochemical assay.

Advances in optical methods and image processing techniques have made possible to explore\quantify the architecture of structural components of soft tissues at different scales (see review by Holzapfel 2008). Using multi-photon microscope, second harmonic generation and two-photon fluorescence signals have been simultaneously captured from arterial collagen and elastin in recent studies including ours (Hill et al., 2012; Wan et al., 2012; Fata et al., 2013; Zeinali-Davarani et al., 2013; Chow et al., 2014). Incorporation of experimentally measured collagen fiber distribution into the constitutive model has been studied previously (Sacks, 2003; Hill et al., 2012; Wan et al., 2012), and showed to improve the predictive capability of the model without significant loss in the goodness of fit. The fiber distribution function and adventitial collagen engagement function, obtained based on our previous study on elucidating the structural and functional interrelations between elastin and collagen in vascular function through coupled multi-photon imaging and biaxial mechanical loading, provide direct structural inputs to the model (Figure 2). Considering the structural characteristics and contributions of elastin, medial collagen, and adventitial collagen, the directly measured fiber orientation distributions were incorporated into the structurally motivated constitutive models and, hence, reduce the number of estimated parameters to only intrinsic fiber properties (associated with N) and fiber content (associated with n). The model predicts the biaxial mechanical behavior of arteries reasonably well, while requiring less mechanical datasets for reliable estimation.

Our previous multi-photon image analysis of biaxially stretched aortic tissues has shown that the medial collagen is being recruited throughout the stretching process while the adventitial collagen shows a delay in the fiber recruitment and starts to be recruited after 1.15-1.2 of equibiaxial stretch (Chow et al., 2014). Considering the sequential engagement of ECM constituents, in the present study, the medial collagen and elastin engages in load bearing from the onset of loading whereas the adventitial collagen is being recruited at a later stage of stretching. The shape of adventitial collagen recruitment distribution density function is determined based on the waviness measurements from our previous study (Chow et al., 2014). This procedure allows us to reinforce a physiological meaningful recruitment function (Figure 1), and in the meantime, reduce the number of optimization parameters. In fact, the likelihood of ill-conditioning is reduced with less unknown parameters.

With this constitutive model, we can study the mechanical contributions from the major load-bearing ECM constituents in the arterial wall (Figure 6). Understanding the mechanical contributions of ECM constituents in the arterial wall may shed light on the underlying mechanisms of vascular remodeling and disease progressions. The small load bearing of adventitial collagen at lower stretches is consistent with its role in preventing the artery from overstretch and rupture (Holzapfel et al., 2000; Humphrey, 2002). The arterial tissue is generally considered as anisotropic. Most previous models use an isotropic neo-Hookean model to represent elastin while the anisotropic of the tissue would originate from collagen (Zulliger et al., 2004; Gasser et al., 2006). However, purified aortic elastin network was revealed to possess an inherent anisotropy, with the circumference direction being stiffer than the longitude, from both uniaxial (Lillie et al., 2010) and biaxial tests (Zou and Zhang, 2009; Zou and Zhang, 2011). Several recent models made effort to account for the anisotropic material properties of elastin (Rezakhaniha and Stergiopulos, 2008; Kao et al., 2011; Rezakhaniha et al., 2011). The present study suggests that contributions from the ECM constituents to the mechanical behavior of the arterial wall are highly dependent on the mechanical loading conditions. It is important to understand the interactions between elastin and collagen in arterial wall, which are currently unclear. The coexistence of multiple ECM constituents and their interrelations may be important in maintaining the fiber distributions in the arterial wall and contributing to the anisotropic tissue behavior.

Either one set of equi-biaxial tensile testing data or two sets of nonequi-biaxial testing data were fitted to obtain material parameters in the model, which were then used to test the model predictive capability. The significantly improved predicting error from nonequi-biaxial fitting suggests that only a single equi-biaxial fitting is insufficient for an accurate prediction of mechanical response (Figures 3 and 4). A possible reason is perhaps that equi-biaxial protocol does not cover a large stretch ranges as in nonequi-biaxial testing, which leads to insufficient information for stress predictions (Polzer et al., 2015). It is important to note that materials parameters that produce the best fit to the stress-stretch curves are not unique, it is thus important to have constraints to enforce optimization within a physiological meaningful range, especially when the model has a large number of optimization variables. It happens that sometimes the values determined by the model are not freely estimated by fitting, but are rather determined by constraints, i.e. the constraints are active, as shown in Figure 5 when data points coincide with the limit.

The current study suggests that incorporation of structural fiber distribution information seems to be sufficient to capture and predict the mechanical response of an artery, as previously suggested by Wan et. al. (Wan et al., 2012). It also seems that the use of three-term von Mises distribution function does not provide much improvement to the fitting and predicting errors (Figure 4). However, it is important to realize that in method A, the anisotropic behavior of each constituent originated solely from the fiber orientation distribution function. This has been presented as a challenge in modeling the anisotropic behavior of purified elastin (results not shown). On the other hand, the three-term von Mises distribution function, in method B, allows for different fiber density (n_{i_1}, n_{i_2}, n_{i_3}) for each fiber family, which results in additional source and flexibility in capturing the anisotropic tissue behavior. Although not the focus of this study, this would be an interesting perspective in microstructural study and constitutive modeling of the anisotropic tissue behavior.

Limitations

The fiber orientation distribution used in this study was averaged data. Sample specific imaging and mechanical testing may improve the fitting and predicting capability of the model. The constitutive model developed in this study employs the assumption of affine deformation. It was suggested from previous studies that both medial and adventitial collagen fibers realign in the major direction of loading during the nonequi-biaxial deformation while medial elastin does not have a significant change in fiber orientation (Chow et al., 2014). Future studies need to take fiber rotation into consideration. The mechanical and structural interrelation between elastin and collagen was considered phenomenologically through the fiber engagement function. Future experiments are needed for a better understanding on the interrelations of ECM constituents. The contributions of other constituents, such as smooth muscle cell and ground substance, are assumed to be negligible in the current model of large elastic arteries. It is unlikely that the cells are viable and contractile during mechanical testing. Our previous study also showed that the decellularized ECM exhibited similar elastic behavior as the intact aorta (Zou and Zhang, 2012).

Conclusions

In this study, we developed a new multi-scale constitutive model of ECM mechanics from a fundamental mechanics perspective coupled with critical biophysical input. Contributions from medial elastin, medial collagen, and adventitial collagen were considered in the model to reflect the distinct mechanical and structural role of individual ECM component. The model uniquely integrates the ECM microstructural information, such as the constituent-specific fiber distribution, engagement, elastin and collagen content, and fiber properties, for tissue-level biomechanical function. Moreover, the integrated model shows promises in fitting and predicting with a small set of material parameters, which has physical meanings and can be related to the structure and properties of the ECM constituents. Future studies are needed to understand the intrinsic structural and mechanical interrelations among ECM constituents, which determine the mechanics of arteries and may carry important implications to vascular homeostasis and mechanobiology.