Speeding up Dynamic Spiral Chemical Shift Imaging With Incoherent Sampling and Low-Rank Matrix Completion

Abstract

Purpose

To improve the temporal and spatial resolution of dynamic ¹³C spiral chemical shift imaging via incoherent sampling and low-rank matrix completion (LRMC).

Methods

Spiral CSI data were both simulated and acquired in rats, and undersampling was implemented retrospectively and prospectively by pseudorandomly omitting a fraction of the spiral interleaves. Undersampled data were reconstructed with both LRMC and a conventional inverse nonuniform fast Fourier transform (iNUFFT) and compared with fully sampled data.

Results

Two-fold undersampling with LRMC reconstruction enabled a two-fold improvement in temporal or spatial resolution without significant artifacts or spatiotemporal distortion. Conversely, undersampling with iNUFFT reconstruction created strong artifacts that obscured the image. LRMC performed better at time points with strong metabolite signal.

Conclusion

Incoherent undersampling and LRMC provides a way to increase the spatiotemporal resolution of spiral CSI without degrading data integrity.

INTRODUCTION

Hyperpolarization of ¹³C-enriched agents provides signal enhancements on the order of 10,000, which makes it possible to track metabolically active substrates and their products in vivo (1–4). Dynamics can be studied noninvasively to determine metabolic rates under normal and pathological conditions (5–11). Examples so far include detecting tumors and their response to treatment (12,13), monitoring liver and cardiac function (14–17), and characterizing intracellular redox state (18).

The time window available for measurements is determined by the decay of polarization due to spin-lattice relaxation at a rate 1/T₁. Even in the best cases, T₁ ~ 1 min for ¹³C nuclei, so a fast imaging sequence is required to sample the spatiotemporal dynamics within a few-minute time frame. Spiral chemical shift imaging (spCSI) sequences are ideal for this situation because they have fast acquisition times, but their imaging bandwidth is limited by gradient strength and slew rate. The performance is reduced for ¹³C compared with ¹H, as carbon’s lower gyromagnetic ratio makes it necessary to acquire multiple spatial or spectral interleaves to fully interrogate the necessary k-space. For a fixed temporal resolution, these factors limit the spatial resolution that can be achieved, whereas for a fixed spatial resolution, they limit the temporal resolution as well as the total number of time points that can be sampled within the polarization lifetime.

SpCSI uses a sequence of spiral k-space trajectories during readout to encode both spectral and two-dimensional (2D)-spatial (i.e., x, y) information after a single excitation (19). The third (z) dimension can be acquired through a series of slice-selective measurements or phase encoding. Interleaving can be implemented by repeating the measurements with different spiral trajectories to cover more points in k-space [to increase spatial resolution/field-of-view (FOV)], or with the same trajectories at different offsets in time (to increase spectral bandwidth). For dynamic measurements, the full imaging sequence is repeated for a number of time points. For a three-dimensional (3D) sequence, the sequence time T for a single time point is then

$$T=N_p\times N_i\times TR$$ [1]

where N_p is the number of phase encode steps for z, N_i is the number of interleaves, and TR is the repetition time between consecutive excitations.

One way to reduce the acquisition time is to implement undersampling and a compressed sensing algorithm (20–22). Undersampling is already used to take advantage of sparsity in the spectral domain by reducing the number of spectral encoding steps below the Nyquist criterion and dealiasing the resulting spectrum (23). This is acceptable because ¹³C spectra are typically sparse, with only a few spectral lines, and overlap between peaks in the aliased spectrum can be avoided by selecting an appropriate receiver spectral width. Sparsifying compressed sensing algorithms can be applied to the spatial dimensions, and they are used extensively for speeding up ¹H imaging (20,24,25). Methods such as wavelet-in-time further extend the algorithms to take advantage of spatiotemporal sparsity, and they have been successfully applied to hyperpolarized ¹³C dynamic imaging (21).

Other methods rely on the fact that the spatiotemporal data are low-rank, meaning that they can be represented by a low-dimensional subspace model. Low-rank matrix completion (LRMC) algorithms use undersampling followed by iterative reconstruction to exploit the spatiotemporal correlations in time-resolved acquisitions. Redundant information in the time domain is used to reconstruct data points that were not sampled, thereby considerably reducing the artifacts typically created by undersampling. One family of LRMC algorithms includes SPICE (26–28) and SLIM (29), which can accelerate spectroscopic imaging in k,t space using the fact that spectral data are low-rank if the number of spectral lines or spectrally distinct tissue classes is limited. Another family of LRMC methods has been applied to dynamic imaging, such as cardiac and perfusion measurements (30,31), where there is a temporally correlated background.

In this work, we apply a low-rank algorithm to spCSI imaging of ¹³C-pyruvate metabolism by applying incoherent sampling to the interleaf dimension. This takes advantage of the fact that in dynamic metabolic MRI measurements, the locations of metabolite signal do not change substantially over time and thus exhibit a high level of spatiotemporal correlation. Using LRMC reconstruction on both simulated and in vivo data, we demonstrate a two-fold improvement in either temporal or spatial resolution without the creation of deleterious artifacts. We also provide guidelines for the selection of LRMC parameters to streamline reconstruction.

METHODS

Imaging Scheme

We implemented 3D spCSI (24 echoes, α_exc = 5.6°) using two parameter sets: (A) FOV = 80 × 80 × 60 mm³, 16 × 16 × 12 matrix, 4 spatial interleaves, SW = 276 Hz and (B) FOV = 70 × 70 × 60 mm³, 20 × 20 × 12 matrix, 8 spatial interleaves, SW = 280 Hz. Fully sampled data allowed temporal sampling at 6 and 12 s intervals, respectively. Undersampling by a factor of two was achieved by omitting half of the spatial interleaves, with different interleaves chosen pseudorandomly for each phase encode step and each time interval. This allows temporal sampling at 3 and 6 s intervals, respectively. The first case (A) represents a temporal speedup of two, whereas the second case (B) represents a two-fold increase in spatial resolution (nominal voxel size of 3.5 × 3.5 × 5 mm³ compared with 5 × 5 × 5 mm³).

Following acquisition, the fully sampled data from each time interval were first processed as described by Mayer et al. (23) Briefly, the x, y, and echo dimensions were zero filled by a factor of two, then the echo dimension was processed with Gaussian apodization and a fast Fourier transform (FFT) to convert it to the spectral domain. For each metabolite, unaliasing and linear phase correction were then applied to the spectra, and the remaining k-space dimensions, x, y, and z, were converted to raw images with a 2D inverse nonuniform FFT (2D-iNUFFT) (32) and a 1D inverse FFT, respectively. Here, the 2D-iNUFFT replaced gridding reconstruction used in previous works. Metabolic images were calculated for pyruvate, lactate, and alanine by phasing the spectrum in each voxel to produce maximum absorption-mode signal and integrating the resulting peak.

Next, a LRMC algorithm based on Otazo et al. (31), shown in Figure 1, was implemented to reconstruct the undersampled data. First, the data were preprocessed to convert the echo dimension to spectra for each metabolite, as described above. For each frequency point, the remaining dimensions were reshaped into an array d(ω_i) of k,t data with dimensions [n_x, n_y, n_z * n_t]. The LRMC algorithm was then run to find reconstructed dataset L by minimizing the equation

$$\underset{L}{min}\frac{1}{2}{\Vert R[E(L)-d]\Vert }_F^2+{\mathrm{\lambda }}_L{\Vert R(L)\Vert }_{\ast },$$ [2]

where d is the k,t data, L is a multidimensional array with x, y transformed into image space, E(L) is the 2D nonuniform FFT performed on the x, y dimensions of L, and λ_L is a constant. Here, ||||_F represents the Frobenius norm and ||||_* represents the nuclear norm. As these can only be calculated for matrices and not multidimensional arrays, their arguments are reshaped into dimensions [n_x * n_y, n_z * n_t ] for evaluation by the function R(.). The minimization is performed iteratively. First, inverse NUFFT is applied to the x and y dimensions of d, and the result is reshaped into a 2D matrix M_k–1 of size [n_x * n_y, n_z * n_t ]. M_k–1 is decomposed into singular values using soft singular value thresholding, with λ_L as the threshold parameter. For our data, λ_L = 0.0175 was selected, as described in Results. Next, the data are reconstructed from the remaining singular values to produce array L. A data-consistency algorithm is then implemented by subtracting the original k,t data d from E(L) to find the residuals, and then subtracting the transformed residuals, with x, y in image space, from L. The result is reshaped to produce a new matrix M_k on which the process is repeated until the convergence condition |M_k –M_k−1| < tol is reached. We chose tol = 2.5 × 10⁻³, which produced convergence in fewer than 500 iterations. The final M_k was reshaped and an inverse FFT was performed in the phase encode direction for each time point to produce a reconstructed series of 3D datasets in image space. After this reconstruction was performed for each frequency point, metabolic images were again calculated for each metabolite through integration as previously described.

FIG. 1.

LRMC algorithm. The preprocessed k-space data, d(ω_i), are converted to image space with an inverse nonuniform fast Fourier transform (iNUFFT). The resulting data M_k–1 are processed with soft singular value thresholding (SVT), which recreates the dataset L_k using only those singular values S > λ_LS_max, where S_max is the maximum singular value and λ_L is a constant. L_k is then converted back to k-space and the original k-space data are subtracted from it. The difference, representing residual aliasing artifacts, is converted to image space and subtracted from L_k to form the reconstructed data M_k. This process is iterated until |M_k – M_k−1| < tol, where tol is the desired tolerance for convergence.

The reconstruction code was written in MATLAB (The MathWorks, Natick, MA) and run on a computer with an Intel Core i7-4810MQ 2.80GHz CPU, 16 GB RAM, and an NVIDIA GeForce GTX 870M graphics card. GPU computing was implemented to speed up some matrix operations.

Simulations

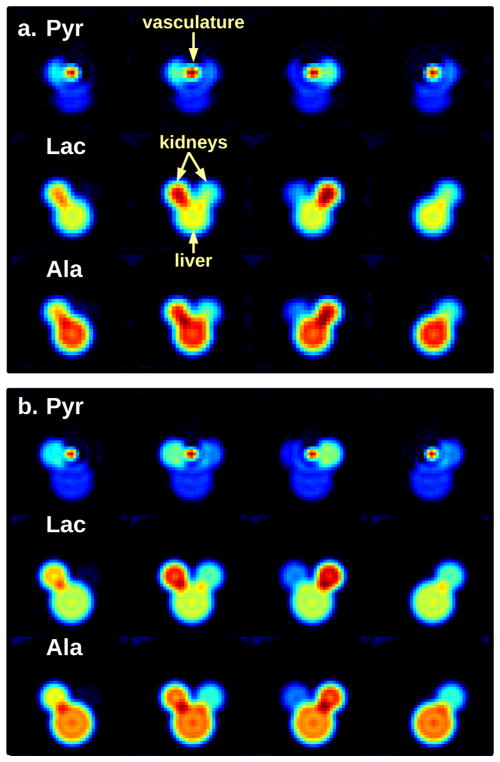
Simulated rat data were created with vasculature, kidneys, and liver/body defined by cylinders of appropriate length for each organ. The time course of signals from pyruvate, alanine, and lactate in each organ was based on typical dynamic measurements following hyperpolarized pyruvate injection. These data were fully sampled with the spCSI sequences using parameter sets (A) and (B) with temporal sampling at 3 and 6 s, respectively, and processed as described above to create reference datasets. The data were also undersampled by a factor of two and processed with LRMC for comparison. The simulation allows fully sampled and undersampled data to be acquired at the same rate so that they can be directly compared, which is not possible for in vivo imaging. Figure 2a,b show examples of fully sampled simulated images using parameters sets (A) and (B), respectively.

FIG. 2.

Four representative slices from the center of a rat phantom at the 12 s time point. Pyruvate, lactate, and alanine images are shown for (a) parameter set (A) and (b) parameter set (B). The model consists of cylinders representing kidneys, vasculature, and liver/body. Note that only pyruvate is modeled in the vasculature.

Animal Experiments

All animal studies were conducted with the approval of the Institutional Animal Care and Use Committee. Imaging was performed with a clinical GE 750w 3T MR scanner (GE Healthcare, Waukesha, WI) using a doubly tuned (¹H/¹³C) quadrature coil (80 mm diameter, USA Instruments Inc., Aurora, OH) for both RF excitation and signal reception. Healthy male Wistar rats (251–343 g) were anesthetized with 1–3% isoflurane in ~1.5 L/min oxygen. The rats were injected in a tail vein with ~3 mL of [1-¹³C]pyruvate (Pyr, ~80 or 125 mM), which was hyperpolarized to ~50% liquid state polarization via dynamic nuclear polarization using a GE SpinLab polarizer (Research Circle Technology, Niskayuna, NY). Data were acquired after Pyr injection with 3D spCSI using parameter sets (A) and (B), with temporal sampling at 6 s and 12 s intervals, respectively.

To test the effects of undersampling, two of four interleaves were retrospectively removed at random from each phase encode step, and the data were processed with the LRMC algorithm. Prospectively undersampled images were also acquired using parameter sets (A) and (B) by pseudorandomly sampling half the number of interleaves for each phase encode step, this time at sampling intervals of 3 s and 6 s, respectively. The data were processed with the same LRMC algorithm.

Image Analysis

To determine the performance of LRMC reconstruction of both simulated and retrospectively undersampled data, we compared the signal and noise properties with those of the fully acquired dataset. We also compared the results with inverse NUFFT reconstruction of the undersampled dataset to illustrate the types and size of artifacts produced by the undersampled acquisition, as well as their subsequent removal by LRMC reconstruction. We characterized the reconstruction artifacts by measuring the signal intensity in regions outside the rat body, where no real signals should be found. For real data, noise levels, σ, were determined using the average noise of lactate and alanine images at the first time point, before these metabolites are produced. Because phasing and integration of each voxel actually produces a magnitude image, the noise follows a Rayleigh distribution, and the true signal variance σ² is determined from the mean noise magnitude M̄ through the relationship $\overline{M}=\mathrm{\sigma }\sqrt{\mathrm{\pi }/2}$ (33). Artifact signals lead to an increase in the background signal above the noise. The calculated noise level, σ, was subtracted from the mean signal level outside the rat to find the artifact magnitude.

For simulated and retrospectively undersampled data, we characterized the reconstruction accuracy by calculating the pixel-by-pixel root-mean-square error (RMSE) between the full sets of undersampled images and fully sampled images, normalizing by the maximum signal of each dataset. This normalization emphasizes that the most important time points for metabolic imaging occur when signal strength is largest. Only the region inside the rat body was included, so that the known artifacts outside the body would not contribute to the error. We also compared the singular value decay curves for the three datasets by reshaping the image series to dimensions [n_x * n_y, n_z * n_t ] and calculating the singular values. Finally, we selected a slice through the kidneys and calculated time courses for the integrated metabolite signals within the kidneys, normalizing to the maximum kidney pyruvate signal. We compared the resulting time courses to characterize each algorithm’s reconstruction of the metabolite dynamics.

As prospectively undersampled data do not have a “gold standard” for comparison, we compared them to a fully sampled but lower resolution acquisition of the same rat. To partially account for variations in pyruvate concentration and polarization between experiments, we normalized by the total alanine signal measured in the body outside the kidneys. Singular value decay was also calculated as discussed above.

RESULTS

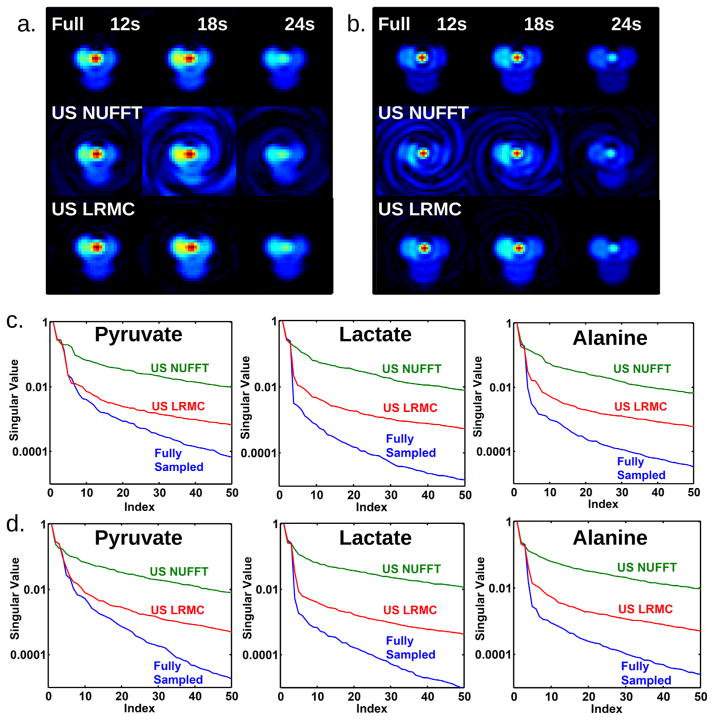
Figure 3 displays pyruvate images from a single slice through the rat kidneys of the simulated data. Figure 3a was acquired with parameter set (A) and 3 s sampling, while Figure 3b was acquired with parameter set (B) and 6 s sampling. Spiral artifacts are present when undersampled data is processed with inverse NUFFT reconstruction, but they are insignificant when the data are processed with LRMC. The LRMC images visually appear to match well with the fully sample images. Visually, there are some differences between the high- and low-resolution fully sampled images, due to blurring of the vasculature signal at low resolution and normalization by the maximum intensity, which occurs in the vasculature. Plots of singular value decay for the entire dataset (Fig. 3c,d) show that LRMC singular values better follow those of the fully sampled data, particular for the dominant singular values. The singular values decay quickly because the phantom pattern is relatively simple.

FIG. 3.

Simulated reconstructions using parameter sets (A) and (B). a and b: Reconstruction comparison for pyruvate in a kidney slice using parameter sets (A) and (B), respectively. The top row shows a fully sampled dataset reconstructed with inverse NUFFT. The middle row shows two-fold undersampled data reconstructed with inverse NUFFT, while the bottom row shows two-fold undersampled data reconstructed with LRMC. The inverse NUFFT reconstruction of undersampled data suffers from spiral artifacts, which are insignificant in the other reconstructions. c and d: Comparison of singular values for the complete image series from parameter sets (A) and (B), respectively. The largest 50 singular values are shown. The singular values of LRMC better follow those of the fully sampled reconstruction than inverse NUFFT.

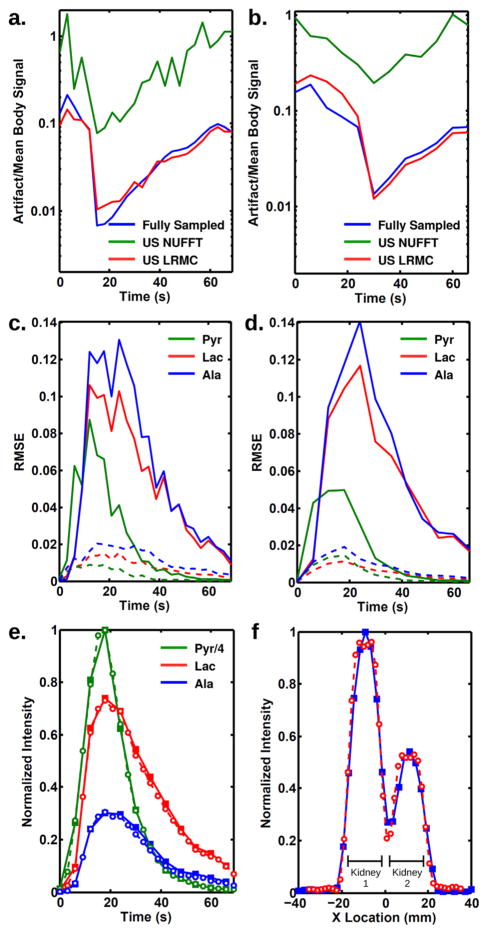
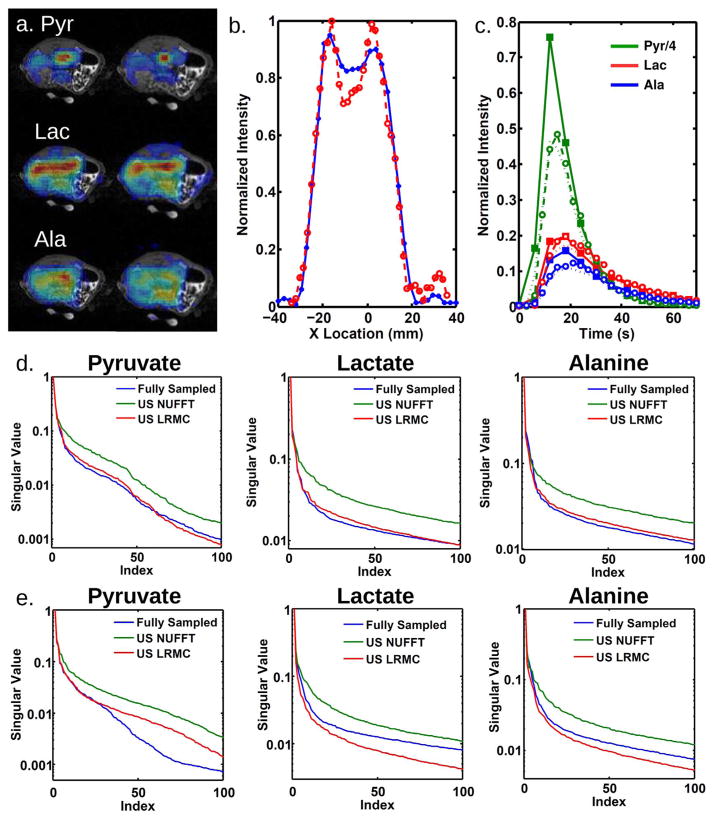
Further comparisons between the reconstructions demonstrate the strengths of LRMC. Figure 4a,b plot the mean pyruvate signal outside the rat body, normalized to the mean pyruvate signal inside the body at each respective time point. As expected, inverse NUFFT reconstruction does a poor job and produces artifacts between 10 and 100% of the body signals. Both fully sampled and LRMC data have nearly identical artifact magnitudes between 1 and 10% of the body signal. The relative artifact magnitude is higher at the beginning and ending time points, when the true signals are small. Even at its worst performing time points, LRMC removes at least 94% of the artifact caused by undersampling. Similar plots for alanine and lactate (not shown) follow the same trend, but with smaller artifact magnitude. Figure 4c,d plot the RMSE for each metabolite reconstructed with either inverse NUFFT or LRMC using the two parameter sets. The errors are on the order of 1–10%, with errors 5–10 time higher for inverse NUFFT than LRMC. The magnitude of errors for LRMC reconstruction is similar to values found by others and would not contribute significantly to the interpretation of the metabolic curves (21,31). An example of such curves is shown in Figure 4e, which compares the integrated intensities taken from kidney regions of interest (ROIs) for two acquisitions made with parameter set (A): fully sampled data acquired at 6 s time steps versus two-fold undersampled data acquired at 3 s time steps, then reconstructed with LRMC. The curves exhibit only minor differences, as expected given the magnitude of RMSE previously calculated. Figure 4f demonstrates the improved spatial resolution achievable with undersampling. Horizontal cross sections through the kidneys are plotted, taken from lactate images acquired with either the fully sampled parameter set (A) or the undersampled parameter set (B) reconstructed with LRMC. Both datasets were acquired at the same 6 s temporal resolution. The higher resolution cross section shows better delineation of the organ boundaries.

FIG. 4.

Comparison of noise and artifacts for three simulated reconstructions. The artifact for pyruvate images was characterized for (a) parameter set (A) and (b) parameter set (B) and normalized by the mean signal within the rat at each respective time point. In both cases, inverse NUFFT reconstruction of undersampled data produces significant artifacts, whereas LRMC reconstruction of the same dataset produces artifacts similar to fully sampled data. Reconstruction errors were characterized by the RMSE between fully sampled data and either inverse NUFFT (solid) or LRMC (dashed) reconstructions of undersampled data for (c) parameter set (A) and (d) parameter set (B). Each metabolite’s RMSE was normalized to the maximum signal of that metabolite in the image series. e: Integrated intensities taken from kidney ROIs for acquisitions made with parameter set (A). The solid lines with solid squares are from fully sampled data acquired at 6 s time intervals, while the dotted lines with open circles are taken from undersampled data acquired at 3 s time intervals and reconstructed with LRMC. f: Horizontal cross sections through the kidneys taken from lactate images acquired with the fully sampled parameter set (A) (blue, 5 mm nominal resolution) and the undersampled parameter set (B) reconstructed with LRMC (red, 3.5 mm nominal resolution). Both were acquired at 6 s time steps and normalized by the integrated intensity through the cross section.

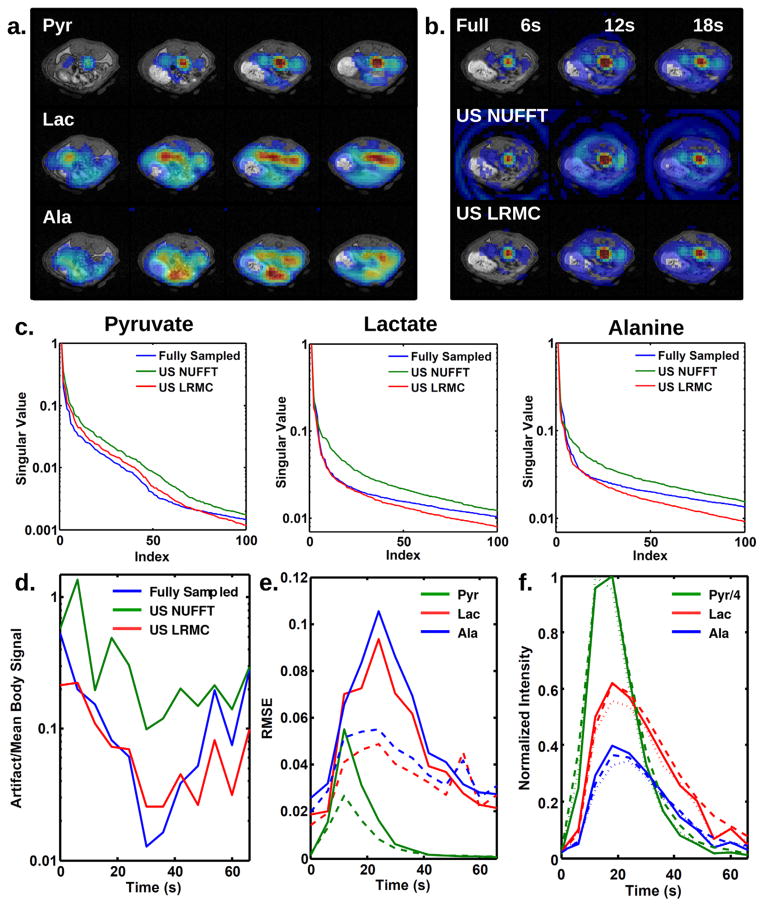
Figure 5 displays results for in vivo data acquired from a rat and retrospectively undersampled. Figure 5a shows typical fully sampled reconstructions for four slices through the kidney and liver. Figure 5b plots pyruvate images for the three reconstruction methods taken from a kidney slice at three time points. Pyruvate is predominantly concentrated in the vasculature and kidneys. A larger amount of artifact is present outside the animal than in simulations due to signal variations during the 3D acquisition, such as T₁ decay, inflow and outflow, and metabolic conversion. As in simulations, significant spiral artifacts are present when undersampled data are reconstructed with inverse NUFFT, whereas fewer artifacts are present when reconstructed using the LRMC algorithm. The resulting images closely match the fully sampled images. Singular value decay (Fig. 5c) is slower than in simulations due to the higher complexity of the images. LRMC better produces a matching decay curve, particularly for the largest singular values.

FIG. 5.

Reconstruction comparison for retrospectively undersampled data from a rat. a: Representative images from four slices through the liver and kidneys of the rat, taken from a fully sampled acquisition. b: Reconstructed slice through the kidneys at three time points for fully sampled data (top) and undersampled data reconstructed with inverse NUFFT (middle) and LRMC (bottom). As in the simulations, inverse NUFFT produces significant spiral artifacts, which are not present in fully sampled or LRMC reconstructions. c: Decay of the top 100 singular values for pyruvate, lactate, and alanine datasets. Singular values for LRMC match those of fully sampled data much better than inverse NUFFT, with the top 25 singular values for lactate and alanine nearly identical between LRMC and fully sampled datasets. d: Ratio of artifact to mean body signal. Undersampled data reconstructed with LRMC show artifacts similar in magnitude to fully sampled data, whereas artifacts for inverse NUFFT are up to an order of magnitude larger. e: RMSE between fully sampled data and either inverse NUFFT (solid) or LRMC (dashed) reconstructions of undersampled data. f: Integrated intensities within kidneys from fully sampled data (solid), data reconstructed with inverse NUFFT (dotted), and undersampled data reconstructed with LRMC (dashed).

The maximum ratio of kidney lactate signal to noise was 38 for the fully sampled dataset, 27 for inverse NUFFT reconstruction of the undersampled data, and 84 for LRMC reconstruction. The LRMC algorithm significantly denoises the image, as is typical for compressed sensing reconstruction (20). Artifact signals lead to an increase in the background signal above the noise. Figure 5d shows the artifact level over time for three reconstructions of pyruvate, normalized by the mean pyruvate signal within the body at each respective time point. Similar to the simulations, undersampled images reconstructed with inverse NUFFT have an artifact ~10 times higher than the fully sampled images and in some cases the same order of magnitude as the mean signal level. Again, LRMC removes at least 94% of the undersampling artifact and returns the ratio to nearly the same level measured from fully sampled data.

Figure 5e displays the RMSE between undersampled and fully sampled reconstructions. The inverse NUFFT reconstruction produces an RMSE as high as 10% of the maximum signal level. For LRMC, the error is roughly half that of inverse NUFFT, but still higher than that found using simulated data. Simulations show that noise is a significant component of the higher RMSE for real data and contributes ~2% to the lactate and alanine RMSE. The other 3–4% error may be due to other effects during acquisition that are not fully simulated, such as T₁ decay, flow, and metabolism. Nevertheless, signals integrated across kidney ROIs (Fig. 5f) are still quite similar for LRMC and fully sampled datasets, and the small differences would not interfere with interpretation of the metabolic curves.

Figure 6 displays results for prospectively undersampled acquisitions reconstructed with LRMC. The left column of Figure 6a was acquired using parameter set A and a full number of interleaves, while the right column was acquired using parameter set B with two-fold undersampling and reconstructed with LRMC. Undersampling allows a higher spatial resolution to be achieved in the same amount of time as A (6 s). Figure 6b shows horizontal cross sections taken through the kidneys from the lactate images in Figure 6a. The higher resolution image allows better delineation of the organ boundaries, which can help separate signal in the vasculature from signal in the kidneys. Figure 6c compares time courses from datasets acquired with different temporal resolutions using parameter set A, either fully sampled and acquired every 6 s or two-fold undersampled and acquired every 3 s. As is evident from these two datasets, the pyruvate dynamics can differ significantly between experiments. The higher temporal resolution is particularly useful when calculating metabolic rates from the time courses, as the results are sensitive to the dynamics of the pyruvate bolus (34). For example, with 6 s temporal resolution, the pyruvate peak is defined by only one or two points, which would be insufficient for fitting a model bolus function, whereas at 3 s temporal resolution there are enough points to perform a good fit. Moreover, with larger subjects such as humans requiring a larger number of spatial interleaves, even these temporal resolutions would not be possible without undersampling. Figure 6d,e display the singular value decay curves for acquisitions with higher spatial and temporal resolution, respectively. For both cases, the LRMC curve tracks the fully sampled curve well for the most important singular values, but the decay curves for increased spatial resolution track particularly well.

FIG. 6.

Reconstruction comparison for prospectively undersampled data from a rat. a: The left column was acquired using parameter set (A) and a full number of interleaves, while the right column was acquired using parameter set (B) with two-fold undersampling and reconstructed with LRMC. Time resolution was 6 s for both acquisitions. b: Horizontal cross sections through the kidneys taken from lactate images acquired with the fully sampled parameter set (A) (blue, 5 mm nominal resolution) and the undersampled parameter set (B) reconstructed with LRMC (red, 3.5 mm nominal resolution). Both were acquired at 6 s time steps and normalized by the integrated intensity through the cross section. c: Time courses of integrated intensities taken from kidney ROIs, for data acquired with parameter set (A), but two-fold undersampled and acquired every 3 s. Fully sampled data (solid lines with solid squares), data reconstructed with inverse NUFFT (dotted lines), and undersampled data reconstructed with LRMC (dashed lines with open circles) are shown. d: Decay of the top 100 singular values for the high spatial resolution acquisition shown in (a) and (b). e: Decay of the top 100 singular values for the high temporal resolution acquisition shown in (c).

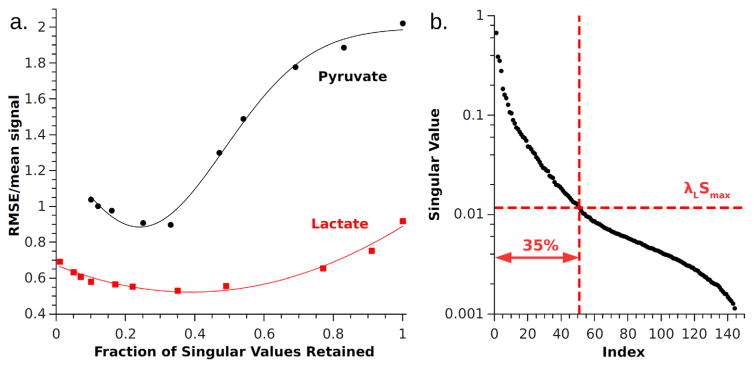
As in Otazo et al., we empirically determined an optimal value for λ_L using retrospectively undersampled data and used this value to reconstruct data acquired prospectively. We calculated the RMSE between the fully sampled dataset and the retrospectively undersampled dataset reconstructed using LRMC with various λ_L values (Fig. 7). The most accurate images were obtained when λ_L retained ~35% of the singular values during the first iteration at the frequency point of the strongest metabolite’s peak. In other words, if pyruvate was the strongest metabolite and its peak occurred at frequency f, then the optimal λ_L was found for each metabolite from the singular values at the first iteration of the reconstruction of frequency point f. If the n singular values are listed in order from S(1) = max (S) to S(n) = min (S), then λ_L ~S(0.35n)/S(1). The value of λ_L was then used for reconstruction of all other frequency points of that metabolite. For our data, optimal λ_L ≈ 0.0175 for all three metabolites.

FIG. 7.

a: Normalized RMSE between fully sampled reconstruction and LRMC using values of λ_L retaining different fractions of singular values during the first iteration. For both pyruvate and lactate, best results are obtained when the fraction is ~0.35. Gaussian curves are fit to guide the eye. Note that in this figure RMSE was normalized by mean signal of the image. b: The distribution of normalized singular values for pyruvate reconstruction with the 35% threshold indicated.

DISCUSSION AND CONCLUSIONS

LRMC provides an easy way to speed up metabolic imaging and is well-suited to spiral pulse sequences due to their use of interleaving. The same concept can be applied to many other sequences, including phase encoding used to acquire the z dimension. Further speed up might be gained by undersampling phase encode steps and performing LRMC reconstruction separately along z. Reconstruction might also be improved by interlacing the different interleaf spirals during each echo train, rather than performing an echo train on a single interleaf at a time. This would make the acquisition of the full k-space more evenly distributed in time.

One challenge of compressed sensing is finding the optimal reconstruction threshold parameters. We found that the best value for the singular value threshold, λ_L, calculated from retrospective undersampling worked equally well for reconstruction of the prospective data. Further studies of metabolic images with different spatiotemporal dynamics are needed to determine whether the 35% cutoff for determining λ_L is a general rule that could be applied to prospectively undersampled data, thereby removing the need for empirical optimization with fully sampled data. This is especially critical for hyperpolarized studies, where the limited quantities of polarized substrate and the extensive preparation required make calibration experiments undesirable.

Computationally, LRMC is more involved than conventional reconstruction and requires significantly more time due to the required iterations. Fortunately, for chemical shift imaging there are straightforward pathways to improvement. For example, each frequency point is independent and can be reconstructed in parallel. When run serially, the full reconstruction takes ~30 min for our datasets with three metabolites. This could be reduced to ~1 min using 48 separate processing units, one for each frequency. Conversely, larger spatiotemporal matrices will increase the time required for singular value decomposition, which cannot easily be sped up via parallelization. Although the reconstruction times may be long for human applications requiring large matrices, the higher resolution and/or FOV afforded by this technique makes it an acceptable trade-off, as the results from metabolic MRI exams are not likely to be required in real-time.

In conclusion, we have demonstrated that incoherent sampling and reconstruction with LRMC can substantially improve the temporal or spatial resolution of spiral CSI. This should make it possible to observe the dynamics within smaller ROI, making it easier to identify diseased tissue or small tumors.