Development and validation of a predictive model for detection of colorectal cancer in primary care by analysis of complete blood counts: a binational retrospective study

Abstract

Objective The use of risk prediction models grows as electronic medical records become widely available. Here, we develop and validate a model to identify individuals at increased risk for colorectal cancer (CRC) by analyzing blood counts, age, and sex, then determine the model’s value when used to supplement conventional screening.

Materials and Methods Primary care data were collected from a cohort of 606 403 Israelis (of whom 3135 were diagnosed with CRC) and a case control UK dataset of 5061 CRC cases and 25 613 controls. The model was developed on 80% of the Israeli dataset and validated using the remaining Israeli and UK datasets. Performance was evaluated according to the area under the curve, specificity, and odds ratio at several working points.

Results Using blood counts obtained 3–6 months before diagnosis, the area under the curve for detecting CRC was 0.82 ± 0.01 for the Israeli validation set. The specificity was 88 ± 2% in the Israeli validation set and 94 ± 1% in the UK dataset. Detecting 50% of CRC cases, the odds ratio was 26 ± 5 and 40 ± 6, respectively, for a false-positive rate of 0.5%. Specificity for 50% detection was 87 ± 2% a year before diagnosis and 85 ± 2% for localized cancers. When used in addition to the fecal occult blood test, our model enabled more than a 2-fold increase in CRC detection.

Discussion Comparable results in 2 unrelated populations suggest that the model should generally apply to the detection of CRC in other groups. The model’s performance is superior to current iron deficiency anemia management guidelines, and may help physicians to identify individuals requiring additional clinical evaluation.

Conclusions Our model may help to detect CRC earlier in clinical practice.

BACKGROUND AND SIGNIFICANCE

Electronic medical records (EMRs) have become increasingly available in recent years. ^1,2 As a result, many investigators are attempting to predict disease occurrence in individual patients by analyzing clinical parameters and constructing models that estimate the probability of development of a disease (commonly termed “risk score”). ³ Such models could be used by medical personnel to refer individuals at apparent increased risk for further clinical evaluation.

Colorectal cancer (CRC) is the third most commonly diagnosed cancer in men and the second in women worldwide. ⁴ Screening programs can reduce CRC mortality by 15–30%. ^5,6 Colonoscopy is often the preferred screening test in the United States, although fecal-based tests that detect occult bleeding are sometimes employed first. ^7–9 There have been attempts to detect CRC early by analyzing symptoms reported in general practice EMR databases. For example, Hippisley-Cox et al. ¹⁰ and Hamilton et al. ¹¹ have developed algorithms that showed good discrimination for the incident diagnosis of CRC in individuals with certain symptoms. However, symptom-based models have limitations, as symptoms may present only at an advanced stage of the illness; furthermore, patients may ignore or not report symptoms. In addition to symptoms, laboratory tests may also indicate presence of disease and have been found to contribute significantly to clinical prediction models and CRC prognosis. ^12–18

Unexplained iron deficiency anemia due to bleeding within the gastrointestinal tract ¹⁹ should be a “red flag” for CRC diagnosis, particularly in the elderly. ^20–23 However, some health care organizations do not use such guidelines, and even when available, these guidelines are often not followed. ^24–26 As we have previously suggested, recognition of a change in hemoglobin levels over time, rather than the current value alone, could improve detection of CRC. ²⁷

Here, we describe a novel approach for identifying individuals at increased risk of having CRC through computational analyses of their blood counts, age, and sex. Our approach is based on machine learning methods, mainly decision trees and cross-validation techniques, which enable generation and evaluation of data-driven prediction models. We developed and validated our approach on large retrospective data sets from 2 different countries.

MATERIALS AND METHODS

Datasets

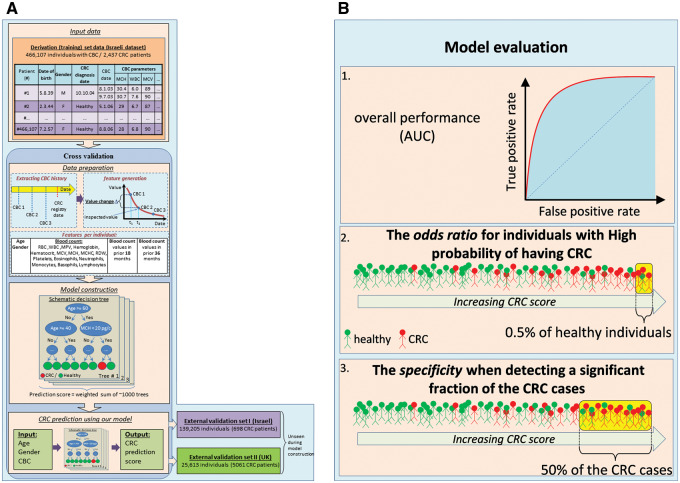
Data and methodology are illustrated in Figure 1 A. Study data were obtained from 2 independent sources, the Maccabi Healthcare Services and the United Kingdom Health Improvement Network (THIN). Maccabi Healthcare Services, the second largest Health Maintenance Organization (HMO) in Israel, with ∼2 million patients, provided the Israeli dataset, which consisted of all insured individuals above age 40 years. All patient records were anonymized and de-identified prior to analysis. This data source was randomly divided into a derivation dataset (80%) and a validation (20%) dataset. The UK dataset was derived from a subset of a de-identified UK primary care database that is broadly representative of the UK population in terms of age, sex, and prevalence of major medical conditions. ²⁸ We included individuals above age 40 years from this data to construct an external, independent validation set. The subset of the full database that was selected for the study contained all cancer cases in the years 2007–2012 and a random sampling of the cancer-free individuals (see Supporting Methods S1 for a detailed description of the information available in each data source.)

Figure 1:

(A) Model construction and evaluation. Shown is an illustration of the different steps of our model construction procedure. For every individual with CBC data, the input training data (top) consists of his/her age, gender, and all available sets of blood count panel parameters. In the data preparation phase (middle), the CBC data of every individual are aggregated (generating a CBC history), and features are generated, including the values of the parameters and the change in these values in the last 18 and 36 months. Next, in the model construction phase (lower middle), we automatically generate decision trees aimed at identifying CRC cases. The trees constructed are then combined into a single unified model. The parameters of the data preparation and model construction phases are optimized using cross-validation – we use 90% of the data as a learning set, construct a model, and evaluate its performance on the remaining 10%. This process is repeated 10 times by partitioning the data into different learning and testing sets. The resulting model can then use as input the age, gender, and CBC data of an unseen individual and produce a risk stratification score of having CRC (bottom left). The model is then validated on external datasets including previously unseen Israeli and UK populations (bottom right). (B) Model evaluation criteria. Shown are the 3 different measures used to evaluate model performance: (1) the area under the receiver operating characteristic curve (AUC) is used to measure overall performance, as it is a standard measure of performance in classification problems; (2) to assess the utility of our model for identifying individuals with the highest probability of having CRC, we consider a model threshold score that corresponds to false positive rate of 0.5% (i.e., a model score for which only 0.5% of the individuals without CRC score above it, representing the population with the highest scores), and use the odds-ratio measure to compare the CRC prevalence of individuals whose model score is above or below that threshold; (3) to examine the utility of our model for identifying a large portion of the CRC cases, we compute the fraction of individuals classified correctly as not having CRC (specificity) at a model score threshold that corresponds to 50% sensitivity (i.e., a model score for which 50% of the individuals with CRC score above it).

Input data

Sex and birth year were available for all individuals. We extracted all available blood count records from the period January 2003 to June 2011 in the Israeli dataset, and until May 2012 in the UK dataset, where blood counts were available as early as 1990, but became more common around 2004 (see Supporting Methods S1).

CRC registry

CRC and other cancer cases in the Israeli dataset were identified from the Israeli National Cancer Registry. ²⁹ The registry information of the derivation set was available during the model development, while the registry information of the Israeli validation set was made available only after completion of the model development. For the UK dataset, we created an ad hoc registry by scanning available records for malignancies or cancer treatment. The data were better recorded from 2007 (following the implementation of the Quality and Outcomes Framework in the UK ³⁰ ), and we therefore evaluated the model’s performance on this dataset only by scores assigned after 01/2007 (see Supporting Methods S1).

Generation of model features

For each complete blood count (CBC) record, we created a feature vector as input to our computational classifier. The vector records the individual’s demographics (age and sex) as well as the current CBC and the trends of the various CBC parameters. The current CBC includes 20 parameters, while the trends are represented by evaluating each parameter at 2 time points, viz. 18 and 36 months before the current CBC. The evaluation is performed using a linear regression model, which is selected from a repertoire of models according to the availability of past CBCs for each particular individual (see Supporting Methods S1, also for management of missing values and outliers).

Classification method

We have found that the best-performing classifiers are comprised of ensembles of decision trees. In each tree, the score of an individual is determined through a sequence of binary decisions on the values of single features ( Figure 1 A), while the overall prediction is based on the collected predictions of many such trees, thus avoiding overfitting. We combine 2 methods – the Gradient Boosting Model and random forest ³¹ (RF). The final prediction is selected from the scores generated by the 2 models. The learned model’s parameters consist of the number of decision trees in the ensembles, the structure of each tree, the feature and value queried at the internal nodes of every tree, and the value generated at each external node (see Supporting Methods S1). We used the R implementation of RF and the C library, which is also used in the R implementation of the Gradient Boosting Model. ³²

Validation exclusion and inclusion

Individuals diagnosed with cancer other than CRC were excluded. All other individuals were assigned a single score to avoid the bias of overrepresenting individuals with many blood counts. Individuals diagnosed with CRC were assigned the most recent score within a defined time window prior to CRC diagnosis. To assess the performance of our model, we selected a time window of 3–6 months, and the assigned score was that of the most recent CBC performed in that time window. If no CBC was available within this window, the individual was excluded. For control (cancer-free) individuals, we randomly selected a single CBC for assigning a score. We included only individuals aged 50–75 years for the validation analyses, as this age group reflects current guidelines for CRC screening in Israel and many other countries. ^33,34 Performance on an additional time-window (0–30 days, reflecting the model’s ability to detect cancers at time of diagnosis) is described in Supplementary Data in Supporting Methods S1.

Measuring performance

As our model produces continuous scores, we evaluated both its overall performance and its performance in different clinical scenarios ( Figure 1 B). First, as an overall measure of performance, we used the standard area under the receiver operating characteristic curve (AUC). Second, to assess our ability to identify individuals with the highest probability of having CRC, we considered a model threshold score that corresponds to a false positive rate of 0.5% (a low proportion of CRC-free individuals who are incorrectly identified), and evaluated the odds ratio for risk of harboring CRC. Finally, to examine our ability to identify a significant fraction of the CRC cases, we evaluated the specificity of the model (the proportion of correctly identified CRC-free individuals) at a model score threshold that corresponds to 50% sensitivity (CRC detection rate). We used the standard bootstrapping approach to estimate 95% confidence intervals for all of the above measures (see Supporting Methods S1).

Model calibration

To examine the calibration of our model, we translated the score produced by our model into probabilities. This was required because our model does not produce scores that can be readily interpreted as probabilities. To perform the translation, we performed a simplified version of isotonic calibration ^35,36 on our cross-validation predictions. We divided the range of scores the model produces into 10 segments corresponding to equal numbers of individuals in the training set (cross-validation). For each segment, we evaluated the corresponding expected probability of CRC diagnosis compared to the observed probability in the validation sets. As our study includes both cohort and case-control sets, we had to normalize the overall probability of CRC within the validation sets using the expected incidence rate. ³⁷ We used both Hosmer-Lemeshow ³⁸ and Cox-calibration ^39,40 tests to evaluate the calibration of the model.

Measuring added value

The added value of our model was evaluated using the logarithmic scoring rule ⁴¹ and by comparing our model to a basic model that corresponds to current knowledge and practices. Due to the fact that we use cohort and case-control sets, some normalization of probabilities was required before applying the scoring rule. This was done by adjusting the observed frequencies in the case-control set to estimated frequencies on the whole population from which it was derived using the sampling rate.

Asymptomatic individuals

To identify scores given to asymptomatic individuals in the UK database, we constructed a list of Read codes (a standard clinical terminology system used in general practice in the UK) that correspond to CRC symptoms (see Supplementary Data ) and evaluated the performance of our model only on scores assigned before any of these symptoms were recorded. We ignored symptoms recorded more than 1 year prior to CRC diagnosis, as we assumed that those symptoms did not lead to the diagnosis of CRC.

Contribution of parameters to the model

To obtain insight into the parameters that were most important for generating the predictions, we considered the change in performance after sequentially removing various parameters. For the CBC-related parameters, we applied a method that considered the redundant contribution of the various correlated parameters.

Fecal occult blood test

Fecal occult blood test information was available for the derivation subset of the Israeli dataset. All tests were gFOBT (Hemoccult II SENSA), and each test comprised 3 stool samples. A test with at least 1 positive sample was considered positive. In analyzing the potential added value of the model to fecal occult blood test (FOBT) use in the population, we considered individuals 50–75 years of age for whom gFOBTs or CBCs were available during the years 2008–2009. For comparison, we selected a model score threshold at which the fraction of individuals above it (i.e., the fraction of individuals classified as positive by our model) was equal to the fraction of individuals with a positive gFOBT.

RESULTS

Datasets

The derivation dataset consisted of 606 403 individuals, 466 107 of whom had CBCs (53.6% women, mean age in 2011, 58.7 years). The Israeli validation dataset consisted of 173 251 individuals, 139 205 of whom had CBCs (53.1% women, mean age in 2011, 58.6 years). There were 2437 CRC cases with CBCs before diagnosis in the derivation set, and 698 such cases in the Israeli validation set. Unlike the Israeli cohort, the UK external validation dataset is a case-control set that consisted of 5061 CRC cases and 20 552 individuals without cancer (all with CBCs; 50.8% women, mean age in 2011, 67.4 years). The apparent excessive prevalence of CRC in the UK dataset is due to the way it was derived from the complete THIN database, selecting all available CRC cases but only a random sample of the control population (see Supplemental Appendix for data completeness and additional details). As seen in Table 1 , there are differences in the distribution of the tumor locations between the 2 populations. It is possible that these differences are the result of biases in the missing UK tumor data reported by primary care physicians in the UK dataset. About 50% of the tumor locations are unspecified in the UK data, compared to the more complete Israeli data collected from the mandatory National Cancer Registry, where < 10% of the tumor location is unspecified (see Materials and Methods ).

Table 1:

Characteristics of the Israeli and UK datasets

	Females				Males
	Cancer free a		CRC		Cancer free a		CRC
	Israel b	UK c	Israel b	UK c	Israel b	UK c	Israel b	UK c
No. of individuals	225 399	11 356	1154	2323	198 058	9224	1283	2738
Mean ageyears (stdv)	58 (13)	59 (14)	68 (12)	73 (12)	57 (12)	59 (12)	68 (11)	71 (11)
Tumor location d
Proximal colon (%)			31	16			28	11
Distal colon (%)			35	10			33	11
Rectum (%)			26	23			30	29
Unspecified (%)			8	52			9	48

^a Individuals free of all cancer types.

^b Cohort design.

^c Case control design.

^d Sites of primary colorectal cancers were extracted from the recorded as proximal (C18.0: cecum, C18.1: appendix, C18.2: ascending colon, C.18.3: hepatic flexure, C18.4: transverse colon), distal (C18.5: splenic flexure, C18.6: descending colon, C18.7: sigmoid), and rectal (C19.9: rectosigmoid, C20.9: rectum).

Accuracy of CRC prediction

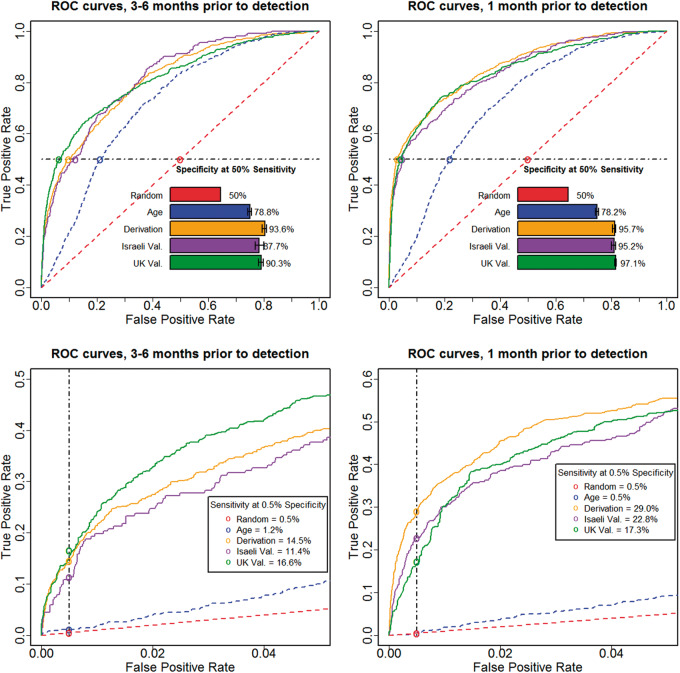
We applied the model to the Israeli validation dataset and considered all CBCs performed 3–6 months before CRC diagnosis. The AUC (measuring the overall performance of the model) was 0.82 ± 0.01, the odds ratio at a false positive rate of 0.5% (measuring the model’s ability to identify individuals with the highest probability of having CRC) was 26 ± 5, and the specificity at 50% sensitivity (a significant fraction of CRC cases detected) was 88 ± 2%. (See Supplementary Data for more performance measures.) As an additional independent validation, we applied our model to an external dataset extracted from the THIN database in the UK. The population in this dataset is different in ethnicity, environmental backgrounds, and health care practices from the original Israeli-based dataset used to develop the model. In this population, fewer blood counts are performed (4 ± 6 CBCs for CRC-free patients having complete follow-up data throughout 7 years, compared to 8 ± 7 CBCs in the Israeli population), many CBCs are partial, and some CBC parameters are not measured (e.g., Red blood cell Distribution Width (RDW); see Supplemental Appendix ). Despite these different characteristics, our model achieved a similar performance (AUC = 0.81, odds ratio = 40, specificity = 94%); Figure 2 shows the overall receiver operating characteristic of the model, as well as the performance of the model in the high score region.

Figure 2:

Performance of the model on unseen independent populations. Shown are ROC curves and other performance measures up to 1 month prior to diagnosis (2 right panels), and 3–6 months prior to diagnosis (2 left panels), for the derivation set cross-validation population (Derivation, yellow), and the externally validated populations of the Israeli dataset (Israeli Val., purple), and of the UK dataset (UK Val., green). Predictions based only on age (blue) and random predictions (red) are also shown for comparison. The 2 upper panels show the full ROC curves and the specificity corresponding to 50% sensitivity, whereas the 2 lower panels show zoomed-in views from the upper panels, focusing on the model behavior at the highest risk scores (at 0.5% false-positive rate).

Performance on asymptomatic individuals

The potential clinical utility of our approach relies on the ability to detect CRC cases earlier than in current practice. We tried to evaluate this by analyzing the detailed medical records available in the UK database and by considering only scores assigned to asymptomatic individuals. Considering CBCs in the 3–6 month time window and the score threshold corresponding to 90% specificity, we found that 67% of the CRC cases in this time window are asymptomatic (386 out of 568) and that sensitivity was unchanged. In addition, we considered low hemoglobin levels (below 12 g/dl for men and 11 g/dl for women), even when there was no recorded clinical diagnosis of anemia. With this additional definition, 45% of the cases had CBCs in the time window that preceded any symptoms. The specificity for detecting 50% of those cases was reduced (to 82%) but was still significantly better than age alone (74%) and thus was of potential clinical value.

Contribution of parameters to the model

The single most important contributing parameter to the performance of the model was age. We compared our model to age alone, and found that our model achieved much better performance in all 3 measures (AUC = 0.81 vs 0.72, odds ratio = 34 vs 2, and specificity = 90% vs 79%). The predictive value of sex alone is lower for CRC – the odds ratio for males as compared to females is 1.15 on the Israeli dataset (compared to 1.4 on the relevant age group, as deduced from Surveillance, Epidemiology, and End Results (SEER) ³⁷ ).

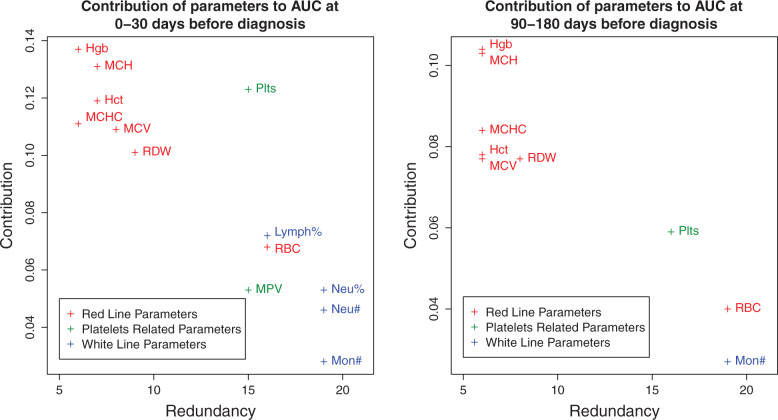
Estimating the importance of the blood-related parameters is complicated by the high correlation between various parameters. When evaluating the importance of a parameter, we addressed both its direct contribution to the performance measure, as well as its redundancy with the other model parameters (i.e., the degree to which its contribution can be replaced by other parameters). We used iterative removal of parameters from the model and performance evaluation by AUC to assign 2 values to each parameter – contribution and redundancy. Considering hemoglobin, e.g., we observe the decrease of AUC between the full model and the model without hemoglobin ( ${\Delta }_0$ ). We then find the parameter that is most closely correlated to hemoglobin viz. hematocrit and remove it from the full model. Now, we evaluate the decrease of AUC between the partial model (without hematocrit) and partial model without hemoglobin ( ${\Delta }_1$ ). We repeat the process until we are left with hemoglobin alone (defining ${\Delta }_2\text{…}\hspace{0.17em}{\Delta }_{19}$ ). The contribution of hemoglobin is defined as the maximal decrease in AUC (max{Δi}), while the redundancy is defined by the number of other parameters we remove until removing hemoglobin gives a significant decrease (e.g., the point where other parameters cannot compensate for its contribution, ${\text{min}}_i\left\{{\Delta }_i>\text{Threshold}\right\}$ ). We repeat the process for all blood count parameters.

The analysis shows that age is followed in importance by various hemoglobin-related parameters, consistent with previous findings in CRC patients. ⁴² See Figure 3 for a 2-dimensional representation of the contribution-redundancy space (see Supplementary Data for the naïve analysis of features’ contributions according to the difference in values between CRC cases and controls).

Figure 3:

Contribution of parameters to our model’s performance. Shown is an evaluation of the contribution of the CBC parameters to the performance of our model. (Specifically, to the AUC measure at the 0–30 day and 90–180 day time windows.) When evaluating the importance of a parameter, we address both its direct contribution to the performance measure as well as its redundancy with the other model parameters (i.e., the degree to which its contribution can be replaced by other parameters). Thus, each parameter is assigned a point in a 2-dimensional space of redundancy (horizontal axis) and direct contribution (vertical axis). To this end, we remove other parameters from the model one by one, ordered by their correlation to the parameter in question. At each step we determine the performance of the submodel with and without the parameter in question and calculate the difference. The redundancy of the parameter is the minimal number of such steps required before the difference is significant (defined by 2 standard deviations as estimated by the bootstrapping process), and the direct contribution is defined by the maximal difference. We show only parameters that achieve significant contribution at some point. We found that the red blood cell line parameters are the main contributors, that platelet-related parameters contribute less and are more redundant with other parameters, and that the white blood cell line parameters contribute mainly at the 0–30 day time window.

CRC detection rate when using our model in addition to FOBT

To assess the potential contribution of our model to the current CRC detection rate in the Israeli dataset, we compared our method’s CRC detection rate to that of gFOBT. The dataset contained 75 822 gFOBT tests for 63 847 individuals, compared to 210 923 individuals with CBCs. The gFOBT positive rate was 5%, and at this working point, our model discovered 48% more CRC cases than gFOBT (252 versus 170). In addition, considering individuals who were identified either by our model or by gFOBT allowed us to increase the number of CRC cases detected by 115% (from 170 to 365).

Investigating the performance of our model

We examined different aspects of the performance of our model. Since some aspects require defining subsets of the population and such subsets resulted in small sample sizes in the validation datasets, we performed the analyses using the larger derivation set.

Calibration of the model

Figure 5 shows the calibration graph of the Israeli and UK validation sets. The model is well calibrated on the Israeli set, with Hosmer-Lemeshow P -value 0.47, and Wald P -value for Cox calibration test 0.08. The UK validation shows slightly lesser calibration, with Hosmer-Lemeshow and Cox calibration tests P -values of 1e-5 and 1e-6, respectively.

Figure 5:

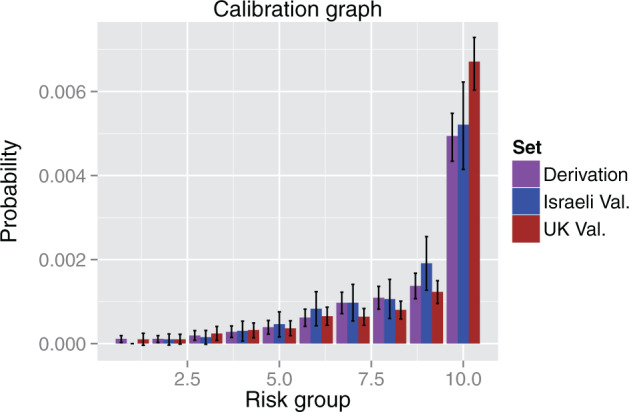
Calibration graph. The graph shows the calibration of the model on the derivation set and the 2 validation sets. The range of scores was divided into 10 deciles that covered equal parts of the population in the derivation set (cross-validation) and the probability of having CRC within 3–6 months was evaluated for each of the deciles on each set. The probabilities on the derivation set are the expected ones, while the probabilities on the validation sets are the observed ones. The probability was normalized according to CRC incidence to account for the fact that the Israeli set is a cohort, while the UK set is case-control. We see that the Israeli validation set is well calibrated, and that the UK set shows good calibration for the 9 lower deciles, but higher CRC probability in the highest decile.

Comparison to anemia guidelines

As discussed above, guidelines of several health care organizations require further evaluation of individuals with unexplained iron deficiency anemia. ²¹ Such guidelines specify hemoglobin levels below 11 g/dl for women and 12 g/dl for men. The specificity for such thresholds for men and women of ages 50–75 is 97.3%. We therefore considered a threshold in our model with the same specificity, and compared the sensitivities of the 2 approaches. Considering blood counts taken 3–6 months before diagnosis, we found that the anemia guideline sensitivity was 20%, while our model’s sensitivity was 30% ( P  < 1e-5).

Added value over current practices

To evaluate the added value of our approach over current practices, we developed a simple linear model that uses age, sex, and an anemia indicator (defined by the guidelines above). We compared the logarithmic scoring rule of this model to our model in the 2 validation sets. We find that on the Israeli validation set, our method score is −0.0071 compared to −0.0074 (AUC 0.82 compared to 0.76) of the simple model, while on the UK validation set, it is −0.0085 compared to −0.0091 (AUC 0.81 compared to 0.76).

Performance of our model on malignancies of other organs

To evaluate the specificity of our model to CRC, we examined the model’s sensitivity to various malignancies. We considered the 3–6 month time window on the derivation set and examined the sensitivity at a false positive rate of 3% (shifted from 0.5% above to allow for reliable results on less common cancers). Figure 6 shows that our model is most sensitive to CRC and stomach cancers, followed by several hematological cancers, and less sensitive to other common cancers. Note that there is a baseline sensitivity to most types of cancers due to the age-dependent incidence. We focus our interest here on CRC due to the much lower incidence of stomach cancer in the study populations.

Figure 6:

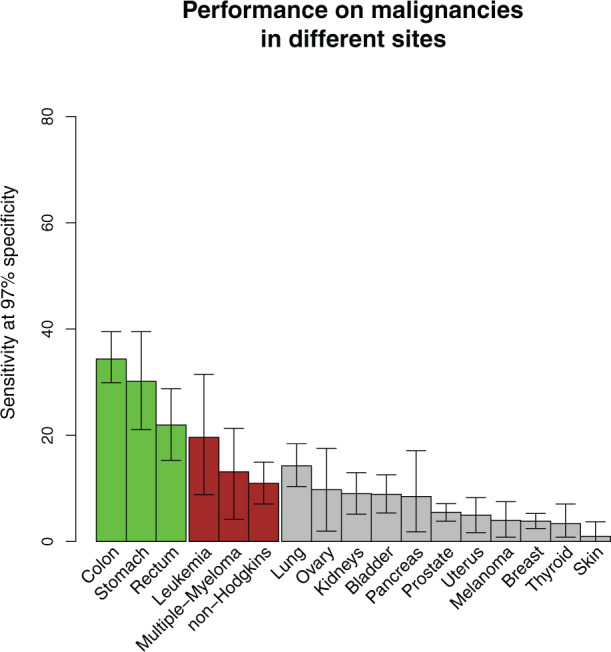
Sensitivity to other cancers. The graph shows the sensitivity of our model at 3% false-positive rate to malignancies of various sites on the derivation set (cross-validation). Green bars signify gastrointestinal cancers, red bars signify hematological cancers, and gray bars signify other cancer types. Only sites that were sufficiently common are shown. The score shows high sensitivity to CRC and stomach cancers (other gastrointestinal tract tumors such as those in the esophagus or small intestine are ignored due to their very low prevalence in the Israeli population), to some types of hematological cancers, and, to a lesser degree, to lung cancer. The residual sensitivity to all malignancies is due to age dependence.

Clinical significance of our model

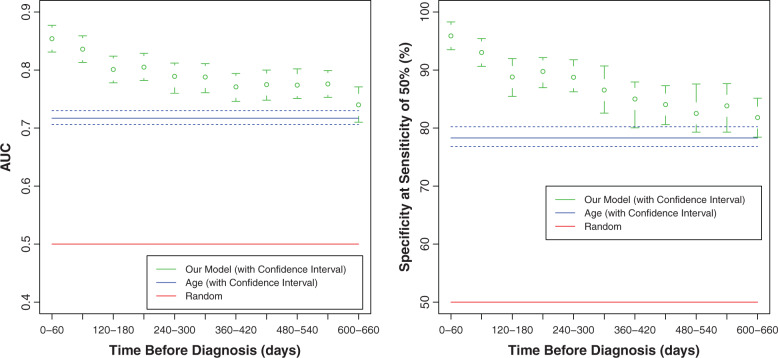
We tested the ability of the model to detect CRC at different time points prior to the CRC diagnosis date. We evaluated its performance when using only CBCs performed in 2-month time windows prior to CRC diagnosis, e.g., using CBCs performed 0–2 months, 2–4 months, etc., before diagnosis. Although performance gradually decreased with time windows at increasing intervals prior to diagnosis, at all time windows it was significantly better than age alone ( Figure 4 ). In particular, considering the 10–12 month time window, which is twice as early as the previously discussed 3–6 month time window, we found AUC = 0.79, odds ratio = 21, and specificity = 86.5%.

Figure 4:

Our model predicts CRC even using CBCs taken 2 years prior to CRC diagnosis. Shown is performance (AUC and specificity corresponding to 50% sensitivity) when using only CBCs taken at 60-day time windows prior to the diagnosis date. Age-only (blue) and random (red) performance are also shown for comparison. Note that our model performs significantly better than age alone, also when CBCs are restricted to those performed 2 years before CRC diagnosis.

Second, as a test of our ability to detect CRC at an early stage, we evaluated the model’s performance on early stage (localized) CRCs comprising 23% of CRC cases. (See Supporting Methods S1 for a description of cancer staging.) Although our performance in this subset was lower than that achieved on all CRC cases, we still found a specificity of 85%, corresponding to a sensitivity of 50%, for CBCs 3–6 months before diagnosis.

Finally, to evaluate the potential of our model to detect malignancies in different parts of the colon and the rectum, we classified the CRC cases in the Israeli derivation set according to their location, and measured the sensitivity of our model at 90% specificity. We found that there were significant differences of performance between different sites (e.g., the specificity for achieving 50% sensitivity to malignancies in the right colon was 96.1%, while for malignancies in the rectum, it was 85.9%), but importantly, performance was significantly better than age alone at all sites ( Table 4 ).

Table 4.

Model performance on malignancies in different sites of the colon

Cancer site	Specificity at 50% sensitivity (95% CI)	Number of cases
Rectum	85.9 (82.2–90.9)	177
Left colon	87.4 (81–91.5)	201
Transverse colon	93.6 (90.4–98.9)	21
Right colon	96.1 (91.3–98.2)	116

DISCUSSION

The growing availability of large health care datasets facilitates the development of analytic tools to help physicians and health management organizations provide better patient care. ⁴³ Such tools can produce actionable recommendations by analyzing real-world clinical data. Here we describe a novel approach to identifying individuals at increased risk of harboring CRC by analyzing their CBCs, thereby potentially enhancing early detection of CRC in primary care.

We have developed a computational model using a large derivation dataset of over 450 000 Israeli individuals and validated it on 2 separate and independent datasets of primary care patients, consisting of over 139 000 Israeli and over 25 500 UK individuals. Our approach applies novel methods both in feature generation (where we use a set of linear models to handle sparse and irregular measurements along time) and in model construction (where we combined 2 tree-based models – RF and Gradient Boosting). We showed that our approach can detect 50% of CRC cases 3–6 months before diagnosis at 88% specificity in the Israeli dataset and 94% specificity in the UK dataset. Although the clinical parameters of the Israeli and UK are different ( Tables 1–3 ), the performance of the model is very similar in both validation sets, indicating that it is robust and applicable to populations from different countries.

Table 2:

CBC characteristics of females in the Israeli and UK datasets

	CRC patients		Cancer-free individuals d
	Israel a	UK b	Israel a	UK b
CBC values, c median (Q1–Q3)
Red Blood Cell Count (RBC)	4.2 (3.9–4.6)	4.2 (3.8–4.5)	4.5 (4.2–4.7)	4.4 (4.2–4.7)
White Blood Cell Count (WBC)	7 (5.8–8.4)	8 (6.6–9.9)	6.6 (5.7–7.7)	6.7 (5.7–8)
Mean Platelet Volume (MPV)	10.6 (10–11.3)	9 (8.1–10)	10.9 (10.3–11.5)	9.3 (8.5–10.3)
Hemoglobin	11.7 (9.6–12.8)	11 (9.4–12.8)	12.9 (12.3–13.6)	13.3 (12.6–13.9)
Hematocrit	36.2 (31.4–39.6)	34.5 (30.3–39.2)	39.4 (37.6–41)	40 (38–41.9)
Mean Corpuscular Volume (MCV)	85 (80–89)	85 (77.5–89.3)	88.7 (85.8–91.3)	90.4 (87.4–93.4)
Mean Corpuscular Hemoglobin (MCH)	27.4 (24.8–29.1)	27.5 (24.4–29.4)	29.2 (28.1–30.2)	30.2 (29–31.3)
Mean Corpuscular Hemoglobin Concentration (MCHC)	31.8 (30.8–32.7)	32.2 (30.9–33.1)	32.9 (32.3–33.4)	33.3 (32.7–33.9)
Red blood cell Distribution Width (RDW)	14.6 (13.7–16)	NA (NA–NA)	13.5 (13.1–14.2)	NA (NA–NA)
Platelets	296 (246.8–366)	362 (284–444)	253 (219–290.7)	274.3 (236.2–315.6)
Eosinophils (#)	0.16 (0.1–0.26)	0.13 (0.1–0.23)	0.15 (0.1–0.22)	0.17 (0.1–0.24)
Eosinophils (%)	2.3 (1.4–3.6)	2.2 (1.7–3)	2.4 (1.7–3.3)	2.3 (1.6–3.5)
Neutrophils (#)	4.1 (3.3–5.3)	5.3 (4.2–7)	3.7 (3.1–4.5)	3.9 (3.2–4.9)
Neutrophils (%)	60 (53.7–66.5)	68.7 (63.1–72.2)	56.5 (51.7–61.2)	58.7 (53.4–64)
Monocytes (#)	0.58 (0.46–0.72)	0.6 (0.5–0.8)	0.5 (0.42–0.59)	0.48 (0.39–0.59)
Monocytes (%)	8.2 (7.1–9.9)	7.9 (6.8–9.9)	7.6 (6.6–8.7)	6.6 (5.1–8)
Basophils (#)	0.03 (0.02–0.04)	0.02 (0–0.09)	0.02 (0.01–0.04)	0.03 (0–0.06)
Basophils (%)	0.4 (0.3–0.6)	0.35 (0.2–1)	0.42 (0.3–0.57)	0.6 (0.4–0.9)
Lymphocytes (#)	1.9 (1.5–2.4)	1.7 (1.3–2.2)	2.1 (1.7–2.5)	2 (1.6–2.4)
Lymphocytes (%)	28.5 (22.9–34)	20.3 (17–26.6)	32.4 (28.1–36.9)	29.5 (24.5–35)

^a Cohort design.

^b Case control design.

^c For calculating the median, Q1 and Q3 quartiles, CBCs were age matched between the Israeli and UK populations. For cancer-free individuals, CBC values were represented by the average values of all available CBCs of the individual. For CRC patients, CBC values were represented by the average values of CBCs available 1 month prior to diagnosis.

^d Individuals free of all cancer types.

Table 3:

CBC characteristics of males in the Israeli and UK datasets

	CRC patients		Cancer-free individuals
	Israel a	UK b	Israel a	UK b
CBC values, c median (Q1–Q3)
Red Blood Cell Count (RBC)	4.6 (4.2–4.9)	4.5 (4–4.8)	4.9 (4.7–5.2)	4.9 (4.6–5.1)
White Blood Cell Count (WBC)	7.5 (6.2–8.7)	7.8 (6.3–9.4)	7.1 (6.1–8.2)	6.8 (5.8–8.1)
Mean Corpuscular Volume (MPV)	10.7 (9.9–11.3)	9 (8.1–10)	10.9 (10.3–11.5)	9.3 (8.5–10.3)
Hemoglobin	12.5 (10.6–14.1)	12.4 (10.1–14.1)	14.7 (14–15.3)	14.9 (14.1–15.5)
Hematocrit	38.9 (34.1–42.7)	38.4 (32.2–42.5)	43.6 (41.8–45.4)	44 (42–46)
Mean Corpuscular Volume (MCV)	86 (80–90)	86 (80.1–91.1)	88.5 (85.9–91.2)	90.9 (88–93.7)
Mean Corpuscular Hemoglobin (MCH)	28.1 (25.1–29.6)	28.3 (25.6–30.5)	29.8 (28.8–30.7)	30.7 (29.7–31.8)
Mean Corpuscular Hemoglobin Concentration (MCHC)	32.4 (31.1–33.3)	32.8 (31.5–33.7)	33.6 (33–34.1)	33.8 (33.2–34.3)
Red blood cell Distribution Width (RDW)	14.4 (13.5–16)	NA (NA–NA)	13.3 (12.9–13.9)	NA (NA–NA)
Platelets	249 (207–318.3)	293 (239.5–370)	224.3 (193.5–258.8)	244 (209.5–283.9)
Eosinophils (#)	0.2 (0.12–0.3)	0.2 (0.1–0.3)	0.19 (0.13–0.27)	0.2 (0.12–0.29)
Eosinophils (%)	2.7 (1.8–4)	2.5 (1.6–4.4)	2.7 (1.9–3.8)	2.8 (2–4.1)
Neutrophils (#)	4.4 (3.6–5.5)	4.9 (3.9–6.5)	4 (3.4–4.9)	4 (3.2–4.9)
Neutrophils (%)	61.6 (54.8–67)	69 (63–73.3)	57.2 (52.5–61.7)	58.4 (53–62.9)
Monocytes (#)	0.65 (0.51–0.81)	0.61 (0.5–0.8)	0.59 (0.5–0.71)	0.53 (0.43–0.67)
Monocytes (%)	8.8 (7.6–10.4)	8 (6.3–10.4)	8.4 (7.4–9.6)	7.5 (6–8.9)
Basophils (#)	0.03 (0.02–0.04)	0.02 (0–0.06)	0.02 (0.02–0.04)	0.03 (0–0.06)
Basophils (%)	0.4 (0.25–0.6)	0.4 (0.1–1)	0.4 (0.29–0.54)	0.6 (0.38–1)
Lymphocytes (#)	1.9 (1.5–2.4)	1.7 (1.3–2.1)	2.1 (1.8–2.6)	2 (1.6–2.4)
Lymphocytes (%)	26.3 (20.8–31.9)	19.4 (16.2–25.6)	30.7 (26.5–35.1)	29.3 (24.6–34.2)

^a Cohort design.

^b Case control design.

^c For calculating the median, Q1 and Q3 quartiles, CBCs were age matched between the Israeli and UK populations. For cancer-free individuals, CBC values were represented by the average values of all available CBCs of the individual. For CRC patients, CBC values were represented by the average values of CBCs available 1 month prior to diagnosis.

^d Individuals free of all cancer types.

Our model was well calibrated when tested on the Israeli validation set. The calibration is less than perfect when considering the UK validation set, due to the many differences in populations and health care practices. The difference in calibration is also reflected in the logarithmic scoring rule, which shows significant added value for our model over current knowledge in both validation sets and a better score (of both models) on the Israeli set.

We examined the specificity of our model to CRC, and showed that it is sensitive mainly to CRC and stomach cancer, with some sensitivity to hematological cancers and (to a lesser degree) to lung cancer. Our model has residual sensitivity for all malignancies, mainly due to the age-dependent incidence and the fact that age is part of our score.

We demonstrated the potential utility of our model for early detection of CRC by showing that it achieved good performance when applied to CRC cases diagnosed at early, localized stages, and also when restricted to CBC data collected about 1 year before diagnosis. The model detected CRCs in asymptomatic (in particular, nonanemic) patients, supporting the likelihood of significant clinical benefit and possible added value over symptom-based tools mentioned above. ¹⁰

When applied to the Israeli dataset, in addition to FOBT (Hemoccult SENSA, a higher sensitivity gFOBT) our model enabled the detection of many more CRC cases (2.1-fold increase). Moreover, we showed that the model can detect CRC throughout the colon with increased performance toward proximal sites. This trend is consistent with previously reported anemia prevalence. ⁴⁴ This feature could enhance noninvasive CRC screening tools (i.e., FOBT/Fecal Immunochemical Test (FIT)), which are less sensitive for detecting right-sided compared to left- sided colon cancer. ⁴⁵

Our data concerning variable specificity of CRC in different colonic locations is consistent with previous reports ⁴⁴ where the prevalence of anemia tends to diminish when malignancies are located distally towards the rectum. FOBT testing, especially when used in combination with flexible sigmoidoscopy, has been shown to be relatively insensitive for the detection of right-sided CRC, ^45,46 thus supporting the potential clinical contributions of our method given regional demographic changes in CRC location, most notably a shift to the right colon, as reported in national screening programs. ⁴⁷

Analyses of the contributing parameters to the model showed the significance of changes in the red blood cell line. This is in agreement with current guidelines according to which iron deficiency anemia warrants further evaluation. We showed that our model is superior in performance to guidelines that consider only hemoglobin level at the time of the test. This is achieved by using additional parameters of the blood counts, trends in their values, and age.

Our study has several limitations. Although CBC data are widely available in Israel, this information may be less accessible in other countries and different health care organizations due to infrequent testing or limited data recording. A counter to this argument is the good performance obtained on the UK validation set, in which blood counts are less frequent than in the Israeli dataset and are often partial. Another limitation of our study is that we validated its results by a retrospective analysis. We partly addressed this by carefully designing our study to be blinded, such that the model was first developed on a derivation set, and only then did we test it on 2 additional independent datasets, including 1 of an unrelated population from a different country. The similar performance achieved on these 2 external datasets provides support for the validity of the model. Nevertheless, a prospective clinical trial would provide a more accurate evaluation of our model’s performance. Finally, we believe that the results derived from the UK database are reliable due to its large size, which compensates for the dataset being incomplete and containing inaccuracies. The ad hoc cancer registry derived for this database is potentially partial, especially before 2007, which we addressed by considering only scores given after January 2007.

To allow for broad applicability, we restricted our model’s input data to CBC, age, and sex. However, incorporation of additional clinical data such as family history, medications, and co-morbidities, when available from medical records, should further enhance its performance. The ability of our model to detect CRC at early stages should be further evaluated, and information such as tumor size, grade, and histology could be incorporated to define more precisely the resolution at which we can detect CRC.

The ability of our model to outperform iron deficiency anemia guidelines, to increase the number of CRC detected cases (when used in addition to FOBT), and to detect CRC at early stages suggests that it could enhance primary care efforts to detect CRC. Our model could be applied in conjunction with current screening approaches, as well as in opportunistic primary care detection. Due to its flexibility, the model can be employed in different clinical situations. One scenario is population-wide detection of individuals at risk of harboring CRC who do not adhere to screening guidelines. Here, we have demonstrated the potential increase of more than 2-fold in CRC detection when applying our model in conjunction with gFOBT (considering individuals with either positive gFOBT or positive scores) to the Israeli dataset. Another potential setting focuses on the highest-scoring patients. This may be particularly useful for some individuals who are currently outside conventional screening guidelines (e.g., younger than age 50 or older than age 75) for whom the model also worked well – see Supplementary Data . Also, in conjunction with symptom-based CRC detection models, ^10,11 our model may enhance early CRC detection in primary care. It could assist physicians in identifying patients with CBC profiles that warrant further clinical evaluation such as referral to a gastroenterologist. In summary, we have described an easy-to-use, inexpensive, and flexible method that could be used to enhance the detection of CRC at an earlier stage.

CONCLUSIONS

We have described a method to enhance detection of CRC at an earlier stage by analyzing age, sex, and CBC data, all commonly available in EMRs. Our ability to validate the method on 2 different populations suggests that it may be applicable to other countries.

Ethics approval

This study was approved by the Maccabi Healthcare Services Institutional Ethics Committee (“Assuta Hospital Helsinki Committee” approval no. 2 010 027) and the THIN Scientific Research Committee (approval 12-053R). The Ethics Committees granted waivers of informed consent since this study involved analyses of retrospective data where all patient information was anonymized and de-identified prior to analysis.

FUNDING

The work was funded by Medial Research.

COMPETING iNTERESTS

Y.K., N.K., and P.A. are employees of Medial Research. BL is a consultant to Medial Research. E.H. was a consultant to Medial Research. All other authors declare that they have no conflicts of interest.

CONTRIBUTORSHIP

Y.K. and N.K. developed the model. I.G. collected the Maccabi Healthcare Services data. Y.K., N.K., P.A., and I.G. analyzed the data. Y.K., N.K., P.A., and B.L. analyzed the model’s performance. N.K., P.A., G.C., and V.S. did the study design. E.H. and B.L. assisted in evaluation of the clinical aspects of the study (data interpretation). Y.K., P.A., and B.L. wrote the manuscript. All authors contributed to the review and revisions of the manuscript. All the authors have seen and approved the final version of the manuscript.