Abstract
Antiretroviral preexposure prophylaxis (PrEP) with once-daily dosing of tenofovir and tenofovir-emtricitabine was shown to be effective for preventing HIV-1 infection in individuals who had HIV-1-seropositive partners (the Partners PrEP Study). We developed a population pharmacokinetic model for tenofovir and investigated the impacts of different dose reporting methods. Dosing information was collected as patient-reported dosing information (PRDI) from 404 subjects (corresponding to 1,280 drug concentration records) from the main trial and electronic monitoring-based adherence data collected from 211 subjects (corresponding to 327 drug concentration records) in an ancillary adherence study. Model development was conducted with NONMEM (7.2), using PRDI with a steady-state assumption or using PRDI replaced with electronic monitoring records where available. A two-compartment model with first-order absorption was the best model in both modeling approaches, with the need for an absorption lag time when electronic monitoring-based dosing records were included in the analysis. Age, body weight, and creatinine clearance were significant covariates on clearance, but only creatinine clearance was retained in the final models per stepwise selection. Sex was not a significant covariate on clearance. Tenofovir population pharmacokinetic parameter estimates and the precisions of the parameters from the two final models were comparable with the point estimates of the parameters, differing from 0% to 35%, and bootstrap confidence intervals widely overlapped. These findings indicate that PRDI was sufficient for population pharmacokinetic model development in this study, with a high level of adherence per multiple measures.
INTRODUCTION
The nucleotide reverse transcriptase inhibitor (NRTI) tenofovir disoproxil fumarate (TDF) has been used in combination with other antiretroviral agents for the treatment of HIV-1 infection. TDF, the oral prodrug formulation of tenofovir, was approved by the U.S. FDA in 2012 for preexposure prophylaxis (PrEP) in a fixed-dose combination with emtricitabine (FTC) to reduce the risk of sexually acquired HIV-1 among people who are at high risk of HIV infection. The Partners PrEP Study, a phase 3 trial that contributed to the approval, demonstrated the efficacy of TDF alone and in combination with FTC in reducing the risk of HIV-1 acquisition in HIV-1-seronegative members of serodiscordant heterosexual couples (1).
Successful HIV-1 prevention depends on individuals' sustained adherence to the medication during periods of risk. Poor drug adherence has been an important challenge in some PrEP trials (2). Tenofovir-containing regimens failed to show efficacy at reducing the risk of acquiring HIV-1 in studies where drug adherence was low as evidenced by undetectable plasma tenofovir concentrations for a large percentage of participants (3, 4). In the Partners PrEP Study, blood samples were drawn during clinic visits to determine drug concentrations in plasma after completion of the study as a measure of drug adherence. In addition, an ancillary study was conducted to determine drug adherence by use of multiple methods, which included counting pills during home visits (announced in the main trial and unannounced in the ancillary study); using electronic monitoring, with the times of pill container openings recorded by a microelectronic circuit (medication event monitoring system [MEMS]) in the cap; and drawing blood samples for measurement of plasma tenofovir concentrations for all subjects in the main trial and a randomly selected subset in the ancillary study (5). Results from the Partners PrEP Study showed that both TDF monotherapy and the combination of TDF and FTC were effective for reducing the risk of HIV-1 acquisition in HIV-1-seronegative partners, and the drug adherence was high, i.e., estimated to be 97% by the pill counts in the main trial and 99.1% and 97.2% by unannounced pill counts (UPC) and use of MEMS, respectively, in the ancillary study.
In addition to providing a measure of adherence, plasma concentrations may provide important information on sources of variability in drug exposure. The study of population pharmacokinetics (PK) by use of nonlinear mixed-effects modeling methodology is suitable for large-scale, sparse sample collection, such as that done in the Partners PrEP Study. However, reliable dosing records and informative pharmacokinetic sampling are important for unbiased pharmacokinetic parameter estimation. Several population pharmacokinetic models for tenofovir have been reported (6 – 16). However, all of them include data from HIV-1-infected subjects or a mix of healthy and HIV-infected subjects (7), except for our recent reports on a population of healthy women (15, 16). In the current study, patient-reported dosing information (PRDI) was collected in the main trial, and electronic adherence measurements were available in the adherence substudy. Our objectives were to develop a population pharmacokinetic model for tenofovir and to investigate the impacts of different types of dosing records on population pharmacokinetic parameters.
MATERIALS AND METHODS
Study design.
The Partners PrEP Study was a multisite, randomized, double-blind, placebo-controlled clinical trial conducted in Kenya and Uganda. A detailed description of the study was published previously (1). Briefly, a total of 4,758 heterosexual couples in which one member was HIV-1 seronegative and the other HIV-1 seropositive were enrolled in the study. The HIV-1-uninfected participants were randomly assigned at a 1:1:1 ratio to receive once-daily oral TDF (300 mg), a combination of FTC (200 mg) and TDF (300 mg), or matching placebo. The subjects were monitored by monthly clinic visits for provision of study medication, HIV-1 testing, and symptom evaluation, for up to 36 months. At each monthly visit, adherence was assessed by a self-report questionnaire and a pill count. Plasma samples were collected on the visits in the first month and every 3 months thereafter. A total of 1,147 HIV-uninfected participants in Uganda with at least 6 months of follow-up remaining in the main trial were enrolled in an ancillary adherence study, the full details of which are described elsewhere (5). In the ancillary study, which involved convenience samples from three study sites with approximately equal distributions among study arms, additional adherence assessment was performed using two validated objective measures: (i) pill counts at unannounced visits (UPC) to the participant's home on a random day monthly for the first 6 months and quarterly thereafter and (ii) electronic adherence measurements using MEMS (WestRock, Richmond, VA) to record the date and time of pill container openings. The MEMS data were downloaded during the monthly clinic visits. Participants found to have UPC adherence of <80% were enrolled in a counseling-based adherence intervention (5). Blood samples were collected during the unannounced home visits at months 6, 12, and 24 to measure systemic levels of study medication. Age, body weight, creatinine clearance (CLCR), and gender information for the subjects were recorded. Tenofovir concentrations in the plasma samples were determined by high-performance liquid chromatography–tandem mass spectrometry (HPLC-MS/MS) as previously reported (17). The lower limit of quantitation (LLOQ) was 0.31 ng/ml.
Modeling strategy and population pharmacokinetic model.
Population pharmacokinetic analysis was conducted within the software NONMEM (version 7.2), with Intel/gfortran compilers interfaced with wings for NONMEM (WFN) or Perl-speaks-NONMEM (PsN) (18, 19). Models were developed using data sets generated under the following three scenarios: (i) tenofovir plasma concentrations with patient-reported dosing information (PRDI) for times of the doses prior to the blood collections, with a steady-state assumption made for the administered doses (PRDI data set); (ii) tenofovir plasma concentrations with time information collected by MEMS, without assumption of the steady state for the MEMS-recorded doses (EMS data set); and (iii) a combined data set, with patient-reported times of the doses prior to the blood collections replaced with MEMS records where available (combined data set). One- and two-compartment models with first-order absorption, with and without a lag time incorporated, were tested using the first-order conditional estimation method with interaction. Inclusion and exclusion of concentrations below the LLOQ (BQL) were tested. When the BQL values were included, the M3 method was applied with the LAPACIAN option as previously reported (20). Pharmacokinetic parameters were assumed to follow a log normal distribution as defined by the following equation: θi = θpop × exp(ηi), where ηi denotes the difference between θi, the parameter for the ith individual, and θpop, the population mean for the parameter, and η values are normally distributed, with a mean of zero and the variance ω2.
Residual error models, including models of additive error, coefficient of variation constant error, and a combination of additive error and coefficient of variation constant error, were tested for description of the residual variability. The interindividual variability for the additive error was also tested as previously reported (21).
Covariate selections.
Sex, age, body weight, and creatinine clearance (estimated by the Cockcroft-Gault equation) were evaluated for their influence on the pharmacokinetic parameters of tenofovir. The covariate model was built using a stepwise forward-addition procedure followed by backward elimination (22). For continuous variables, such as age, creatinine clearance, and body weight, the covariates were centered to the median values for the variable (for age and creatinine clearance) or to a standard value (70 kg for body weight). Models with linear, power, and exponential functions were tested.
Model selection.
R scripts and XPOSE4 were used to generate diagnostic plots (23, 24). Goodness of fit was determined by visualization of scatterplots of predicted versus observed tenofovir plasma concentrations and conditional weighted residuals versus time of postdose and by the distribution of normalized prediction distribution errors (25). The objective function value (OFV) is approximately equal to −2 × log(likelihood) (−2LL), differences in which between two hierarchical models follow a χ2 distribution. A decrease in OFV of >3.84 was considered to be statistically significant (P < 0.05; df = 1) for inclusion of one extra parameter in the model. During the backward elimination step for covariate model development, a more stringent criterion, i.e., an increase in OFV of >10.83 (P < 0.001; df = 1), was utilized to retain a covariate in the model. Selection of the structural PK model and residual error model was based on a global judgment of the model adequacy based on goodness-of-fit plots, successful convergence, biological plausibility, precision of the model parameter estimates, and objective function values.
Model evaluation.
To check the stability of the selected models, nonparametric bootstraps of 1,000 iterations were conducted to estimate 95% confidence intervals for the population parameters. Visual predictive checks with proportions of BQL values predicted by the model were performed as previously described (26) to characterize the model's predictability. Briefly, final models were used to simulate 1,000 data sets with the same study design as that for the original data set. The observed tenofovir plasma concentrations as well as the 5th, 50th, and 95th percentiles (90% prediction intervals) were plotted against the corresponding percentiles for the simulated values. The observed fractions of BQL values were plotted along with 95% prediction intervals for the predicted fractions of BQL values from the simulated data sets. The agreement of distributions between the observations and simulations was inspected visually.
RESULTS
Availability of data and patient demographics.
For the PRDI data set, a total of 1,280 tenofovir plasma concentrations were available from 404 participants in the Partners PrEP Study main trial (3.2 concentrations per participant); 214 of the concentrations (17%) were BQL. For the EMS data set, a total of 327 tenofovir plasma concentrations were available from 211 patients who participated in the ancillary adherence study (1.5 concentrations per participant), and 8% of the concentrations in this data set were BQL. In the combined data set, MEMS records replaced the patient-reported dosing records where available. The median follow-up time for the participants in the ancillary adherence study was 11.3 months. There were no statistically significant differences between the demographics (Table 1) of EMS data set participants and the participants without EMS data in terms of age, sex, and body weight, except that creatinine clearances were significantly different (P < 0.05).
TABLE 1.
Summary of data sets and participant demographics
| Covariate | Value |
||
|---|---|---|---|
| PRDI data set | Combined data set | EMS data set | |
| No. of participants | 404 | 404 | 211 |
| No. of tenofovir concentrations | 1,280 | 1,278 | 327 |
| Age (yr) (mean ± SD) | 35 ± 8 | 35 ± 8 | 36 ± 7 |
| wt (kg) (mean ± SD) | 61 ± 11 | 61 ± 11 | 60 ± 10 |
| CLCR (ml/min) (mean ± SD) | 106 ± 31 | 106 ± 31 | 100 ± 33 |
| Sex (% male) | 55 | 55 | 50 |
Population PK model for tenofovir.
A two-compartment model with first-order absorption was the best pharmacokinetic model to describe the disposition of tenofovir for the PRDI and combined data sets (Fig. 1). The major difference was that inclusion of a lag time (ALAG1) and fixing of the absorption rate constant (Ka) were needed in the model for the combined data set but not for the PRDI data set. The analysis with the EMS data set did not result in a robust and credible model. Rather, the majority of the models were sensitive to initial estimates or results for parameters that were not consistent with the known pharmacokinetics of tenofovir. Accordingly, the EMS data set was not used in further analyses.
FIG 1.
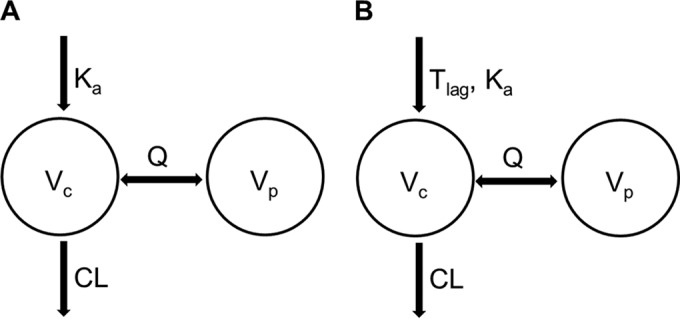
Model structures of tenofovir population pharmacokinetics. (A) Model from analysis using patient-reported dosing data (PRDI data set). (B) Model from analysis using the combined data set, in which patient-reported dosing data were replaced with MEMS data if available (combined data set). CL, Vc, Vp, and Q represent clearance, volume of central compartment, volume of peripheral compartment, and intercompartmental clearance, respectively.
The final model parameters for tenofovir from the PRDI and combined models are shown in Table 2. Except for the peripheral volume of distribution (Vp/F) and Ka, the values of the parameters identified by both models were similar. A combination of proportional and additive error models was the best to describe the residual variability of tenofovir plasma concentrations in both models. Inclusion of interindividual variability (IIV) in the additive error significantly decreased the objective function value. The interindividual variabilities (% coefficient of variation [%CV]) of clearance (CL/F) were similar, with values of 19% and 16%, respectively, for the two models. In addition to the interindividual variability of CL/F and the additive error, which were estimated for both models, replacing patient-reported dosing records with MEMS data in the combined data set supported the estimation of additional interindividual variability for the volume of distribution in the central compartment (V1/F) and Ka. Age, body weight, and creatinine clearance were significant covariates on clearance for both analyses, but only creatinine clearance was retained in the final model, because body weight and age are correlated with creatinine clearance. Inclusion of creatinine clearance decreased the objective function value by 53 and 63 points in the models with the PRDI and combined data sets, respectively.
TABLE 2.
Population pharmacokinetic parameters for tenofovir determined using different dose reporting methodsc
| Parameter | PRDI data |
Combined data |
||||
|---|---|---|---|---|---|---|
| Base model | Final model |
Base model | Final model |
|||
| Meana | Mean (RSE) | Bootstrap median (95% CI) | Mean (SE) | Mean (RSE) | Bootstrap median (95% CI) | |
| NONMEM OFV | 9,965.622 | 9,912.708 | 9,914.648 (9,263.063–10,607.98) | 9,915.521 | 9,852.249 | 9,843.429 (9,177.683–10,457.48) |
| θCL (liters/h) | 55 | 57 (2) | 58 (52–61) | 58 (2) | 61.5 (2) | 62 (57–65) |
| θV1 (liters) | 478 | 393 (14) | 393 (109–653) | 518 (14) | 345 (10) | 345 (211–692) |
| θKa (/h) | 2.21 | 4.7 (77) | 4.7 (1.46–128.15) | 1.5 (fixed) | 1.5 (fixed) | 1.5 (fixed) |
| θQ (liters/h) | 167 | 178 (19) | 178 (90–227) | 187 (17) | 231 (9) | 231 (125–335) |
| θVp (liters) | 667 | 614 (10) | 614 (523–869) | 735 (18) | 830 (10) | 830 (612–1101) |
| θALAG1 (h) | NA | NA | NA | 0.369 (22) | 0.41 (18) | 0.41 (0.30–0.67) |
| θCLCRb | NA | 0.379 (12) | 0.379 (0.286–0.441) | NA | 0.376 (13) | 0.38 (0.27–0.49) |
| IIV on CL | 20 | 16 (9) | 16 (14–17) | 19 (3) | 16 (14) | 16 (13–19) |
| IIV on V1 | NA | NA | NA | 43 (51) | 25 (119) | 25 (22–62) |
| IIV on Ka | NA | NA | NA | 69 (71) | 61 (29) | 61 (44–82) |
| Residual variability | ||||||
| Additive (ng/ml) | 30 | 28 (9) | 28 (22.03–39.57) | 41 (7.29) | 30.2 (8.48) | 30.20 (23.43–41.35) |
| IIV on additive error | 132 | 143 (12) | 143 (109–164) | 93 (14) | 136 (11) | 136 (103–155) |
| Proportional (%CV) | 21 | 21 (7) | 21 (11–25) | 14 (21) | 20 (5) | 20 (12–25) |
The covariance step for the base model with the PRDI data set was not successful, and thus RSE was not estimated.
CL = θCL*(CRCL/120)θCRCL.
SE, standard error; RSE, relative standard error; 95% CI, 95% confidence interval; NA, not applicable.
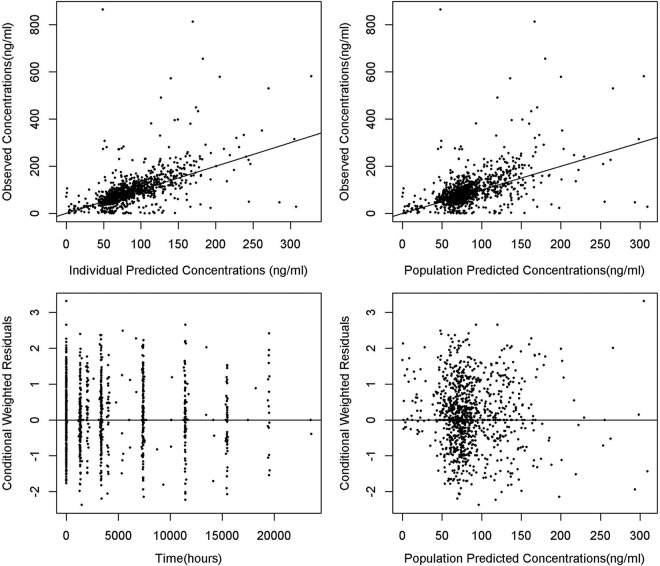
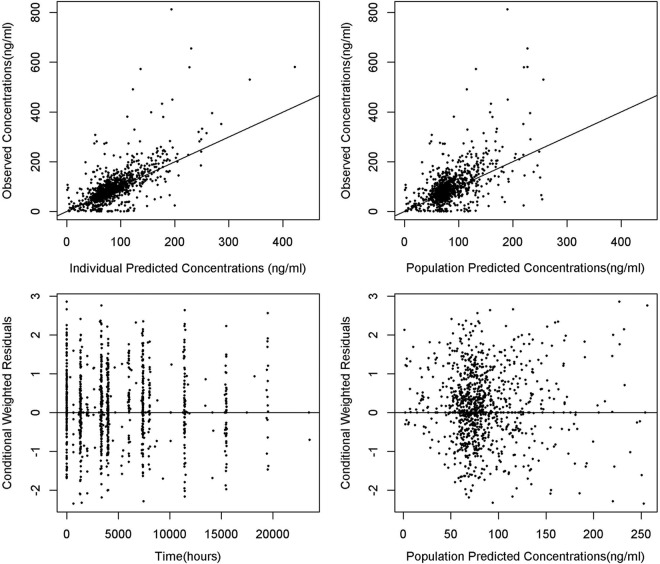
Diagnostic plots for the models based on the PRDI and combined data sets are shown in Fig. 2 and 3, respectively. No major bias was observed in the diagnostic plots.
FIG 2.
Basic goodness-of-fit plots for PRDI model.
FIG 3.
Basic goodness-of-fit plots for combined model.
Stability and predictability of the models.
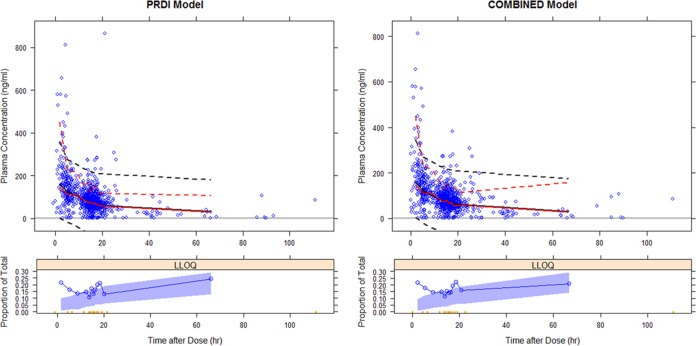
Population pharmacokinetic parameter estimates for the final models for the PRDI and combined data sets were similar in the medians for the parameters estimated during the bootstrap process and fell within the range of the 2.5th to 97.5th percentiles for the bootstrap replicates (Table 2). The median values for the models derived from the PRDI and combined data sets were close, and the 95% confidence intervals largely overlapped for the pharmacokinetic parameters of both models. Visual predictive checks showed that the line of 50th percentiles for simulated tenofovir plasma concentrations obtained using the two final models almost overlapped that for the observed tenofovir concentrations (Fig. 4). Despite underestimations of the concentrations above the maximum concentration of drug in serum (Cmax) that were commonly observed in previously reported studies, approximately 90% of the observed plasma concentrations fell within the range of the 5th to 95th percentiles for the simulated concentrations. The observed BQL fraction was higher than the simulation-based confidence intervals for the 15 hours after dosing.
FIG 4.
Visual predictive checks for PDRI model (left) and combined model (right). Solid red and black lines represent medians for observed and simulated concentrations, respectively. Broken red and black lines represent upper and lower 90% observed and predicted intervals, respectively. The LLOQ panels at bottom represent the proportions of BQL values observed (solid blue lines), with 95% prediction variability shown by the blue shaded areas.
DISCUSSION
We developed a population pharmacokinetic model for tenofovir in a large PrEP trial incorporating both objective and subjective measures of dosing times. Population pharmacokinetics of tenofovir for HIV-infected patients have been described previously by several authors (6 – 16), but none of them used electronic monitoring for adherence. We previously reported population pharmacokinetic models for tenofovir in plasma (15) and for tenofovir in plasma and intracellular tenofovir diphosphate in healthy women (16), with different methods of adherence correction utilizing superposition principles within the model framework. The current study included both men and women and provided an opportunity to test sex as a covariate. No sex effect on total body clearance (CL/F) was observed for tenofovir in this analysis. This is in agreement with a recent pharmacokinetic study of oral TDF in healthy Chinese research participants, in which no significant differences in pharmacokinetic parameters were found between men and women and pharmacokinetic profiles were comparable to those for Western populations (27). The current U.S. FDA label also states that tenofovir pharmacokinetics are similar in male and female subjects. Creatinine clearance was a significant covariate of clearance and is biologically meaningful because tenofovir is a renally cleared drug. The population pharmacokinetic parameters are in general agreement with those in previous reports (6 – 16).
In the current work, no significant improvement was found in the model using electronic adherence measurements as dosing records compared to using patient-reported dosing information alone. However, a clear advantage of electronic adherence measures in population pharmacokinetic model development was shown by Savic et al., as within-individual variability (interoccasion variability) for atazanavir was almost completely explained when dosing was defined by electronic adherence measures (28) compared with patient-recollected dosing information in the ANRS 134-COPHAR 3 trial. We believe that a few important methodological and study design aspects may have led to such different conclusions drawn from the present work versus the previous work. First, the plasma sampling schedule was rich and informative to capture the full temporal pharmacokinetic profile of atazanavir from 35 subjects in the ANRS 134-COPHAR 3 trial. A total of nine plasma concentrations per subject were collected over 6 months, including concentrations determined predose and 1, 2, 3, 4, and 8 h post-clinic-observed dose at week 4 and trough concentrations determined at weeks 8, 16, and 24. In contrast, only one plasma sample per clinic visit was collected in the Partners PrEP Study. More PK sample collections in this large randomized controlled clinical trial were deemed logistically unfeasible. Second, the contributions of pharmacokinetic data with respect to clinic visits were evenly distributed across various clinic visits in the present study, whereas approximately 66% of the total data were captured in one clinic visit (at week 4) in the ANRS 134-COPHAR 3 trial. Third, the Partners PrEP Study had high adherence rates (>90% by pill counts), and thus the additional information provided by MEMS beyond self-reported dosing information might have been small. However, Savic et al. reported almost 100% adherence in the ANRS 134-COPHAR 3 trial, indicating that, with sufficient sample times, the increased precision of MEMS data improves the explanatory value of the model. In the current analysis, only a subset (26%) of plasma concentrations were associated with MEMS records. Thus, a direct comparison of MEMS-only versus PRDI data could not be tested. We did not utilize the “gold standard” approach described by Savic et al., where concentrations are selected and/or excluded based on “reliable dosing history,” defined as concordance (within 3 h) between electronic measurement of dose intake and self-reported dose intake. Such treatment resulted in only <5% of the data being excluded in their case. In contrast, approximately 20% of the data met that exclusion criterion in our EMS data set. We believe that exclusion of data by use of external criteria may potentially exclude important information in the data and thus proceeded with a philosophy of data-driven exploration.
We did not model interoccasion variability in pharmacokinetic parameters because of inherent unidentifiability by study design (i.e., only a single concentration was measured at every quarterly visit). The absorption rate constant was fixed by a local search due to numerical instabilities posed during modeling of the combined data set. The random effect parameter estimates were comparable between the models using electronic and patient-recollected adherence information. However, between-subject variabilities of the central volume and the absorption rate constant provided better model fits in terms of NONMEM objective function values and diagnostic plots in the case of the combined data set. This finding may have been due to the potential loss of information due to resetting of pharmacokinetics when the steady-state option (SS = 1) in NONMEM was executed with the PDRI data set. An interindividual variability parameter for the additive residual error component was retained in both scenarios of analysis, indicating that similar degrees of dosing errors may be present in both cases. Some of the shortcomings of electronic adherence monitoring include participants taking out multiple doses with one opening, opening the device without removing pills, taking pills at a time other than the cap opening time, and not using the device due to stigma or unanticipated travel.
Several BQL values were observed in this study. More than 90% of all BQL values were observed within 24 h after the participant reported dose administration, and approximately 27% occurred within 12 h after the dose administration. The M3 method was applied for appropriate handling of these observations (20). The current model was not able to describe the BQL values that occurred within 12 h postdose (Fig. 3, bottom panels). Several BQL values did not make pharmacokinetic sense based on comparison of an individual's data and dosing history. For instance, a participant had a plasma concentration that was BQL 3.5 h after a dose recorded at a clinic visit, but the same subject had plasma concentrations of 233 and 242 ng/ml at 3.6 and 2.9 h, respectively, in other visits. Another subject had BQL values 2 to 14 h after a dose administration in five of six clinic visits but had a plasma concentration of 178 ng/ml 2.7 h after dosing at the sixth clinic visit. A recent clinical study (HPTN 066) with directly observed dosing of oral tenofovir showed that 24 h postdose plasma concentrations of tenofovir were well above the limit of quantitation, with a median of ∼52 ng/ml (29). Thus, many of the BQL values may represent several potential sources of errors, such as errors in the dosing history obtained from either PRDI or MEMS data, sample mix-up, analytical errors, and administrative errors. A sensitivity analysis was conducted by fitting the final model to the data set, excluding BQL values. Population pharmacokinetic parameters were comparable to those for the data set with BQL values, except for a notable difference in the residual variability. With exclusion of the BQL values, the proportional error (%CV) was reduced to 8 to 9%, from 20 to 21%, and additive error (standard deviation) was reduced to ∼10 ng/ml, from 28 to 30 ng/ml.
In conclusion, our analysis described the population pharmacokinetics of tenofovir in a healthy human population by using both objective and subjective measures of dosing information. Parameter estimates were comparable between both methods of dose description. Creatinine clearance was a significant covariate of tenofovir clearance. We did not identify a clear advantage of EMS data in our model building. However, the adherence level was very high in the Partners PrEP Study, and plasma concentration sampling was very sparse, thus leaving little room for improvement by adding more dose timing accuracy to our model results. In several previous reports with more informative pharmacokinetic sampling, the advantage of adding EMS data was significant in population pharmacokinetic analyses, even with a smaller sample size.
ACKNOWLEDGMENTS
We acknowledge the significant contributions to this research from the research participants themselves, without whom the work would not have been possible. We thank Katherine Thomas (The University of Washington) and the Partners Ancillary Adherence Study Team for their support.
The Partners PrEP Study was funded through a research grant from the Bill & Melinda Gates Foundation (grant OOP47674), and the current analysis was supported by a subaward (grant OOP52516) from the Massachusetts General Hospital to Mercer University and by the Johns Hopkins University Center for AIDS Research (grant 5P30AI094189-04).
Funding Statement
The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.
REFERENCES
- 1.Baeten JM, Donnell D, Ndase P, Mugo NR, Campbell JD, Wangisi J, Tappero JW, Bukusi EA, Cohen CR, Katabira E, Ronald A, Tumwesigye E, Were E, Fife KH, Kiarie J, Farquhar C, John-Stewart G, Kakia A, Odoyo J, Mucunguzi A, Nakku-Joloba E, Twesigye R, Ngure K, Apaka C, Tamooh H, Gabona F, Mujugira A, Panteleeff D, Thomas KK, Kidoguchi L, Krows M, Revall J, Morrison S, Haugen H, Emmanuel-Ogier M, Ondrejcek L, Coombs RW, Frenkel L, Hendrix C, Bumpus NN, Bangsberg D, Haberer JE, Stevens WS, Lingappa JR, Celum C, Partners PrEP Study Team. 2012. Antiretroviral prophylaxis for HIV prevention in heterosexual men and women. N Engl J Med 367:399–410. doi: 10.1056/NEJMoa1108524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.van der Straten A, Van Damme L, Haberer JE, Bangsberg DR. 2012. Unraveling the divergent results of pre-exposure prophylaxis trials for HIV prevention. AIDS 26:F13–F19. doi: 10.1097/QAD.0b013e3283522272. [DOI] [PubMed] [Google Scholar]
- 3.Van Damme L, Corneli A, Ahmed K, Agot K, Lombaard J, Kapiga S, Malahleha M, Owino F, Manongi R, Onyango J, Temu L, Monedi MC, Mak'Oketch P, Makanda M, Reblin I, Makatu SE, Saylor L, Kiernan H, Kirkendale S, Wong C, Grant R, Kashuba A, Nanda K, Mandala J, Fransen K, Deese J, Crucitti T, Mastro TD, Taylor D, FEM-PrEP Study Group. 2012. Preexposure prophylaxis for HIV infection among African women. N Engl J Med 367:411–422. doi: 10.1056/NEJMoa1202614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Marrazzo JM, Ramjee G, Richardson BA, Gomez K, Mgodi N, Nair G, Palanee T, Nakabiito C, van der Straten A, Noguchi L, Hendrix CW, Dai JY, Ganesh S, Mkhize B, Taljaard M, Parikh UM, Piper J, Mâsse B, Grossman C, Rooney J, Schwartz JL, Watts H, Marzinke MA, Hillier SL, McGowan IM, Chirenje ZM, VOICE Study Team. 2015. Tenofovir-based preexposure prophylaxis for HIV infection among African women. N Engl J Med 372:509–518. doi: 10.1056/NEJMoa1402269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Haberer JE, Baeten JM, Campbell J, Wangisi J, Katabira E, Ronald A, Tumwesigye E, Psaros C, Safren SA, Ware NC, Thomas KK, Donnell D, Krows M, Kidoguchi L, Celum C, Bangsberg DR. 2013. Adherence to antiretroviral prophylaxis for HIV prevention: a substudy cohort within a clinical trial of serodiscordant couples in East Africa. PLoS Med 10:e1001511. doi: 10.1371/journal.pmed.1001511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Baheti G, Kiser JJ, Havens PL, Fletcher CV. 2011. Plasma and intracellular population pharmacokinetic analysis of tenofovir in HIV-1-infected patients. Antimicrob Agents Chemother 55:5294–5299. doi: 10.1128/AAC.05317-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Duwal S, Schütte C, von Kleist M. 2012. Pharmacokinetics and pharmacodynamics of the reverse transcriptase inhibitor tenofovir and prophylactic efficacy against HIV-1 infection. PLoS One 7:e40382. doi: 10.1371/journal.pone.0040382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dumond JB, Nicol MR, Kendrick RN, Garonzik SM, Patterson KB, Cohen MS, Forrest A, Kashuba AD. 2012. Pharmacokinetic modelling of efavirenz, atazanavir, lamivudine and tenofovir in the female genital tract of HIV-infected pre-menopausal women. Clin Pharmacokinet 51:809–822. doi: 10.1007/s40262-012-0012-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bouazza N, Urien S, Hirt D, Frange P, Rey E, Benaboud S, Foissac F, Blanche S, Tréluyer JM. 2011. Population pharmacokinetics of tenofovir in HIV-1-infected pediatric patients. J Acquir Immune Defic Syndr 58:283–288. doi: 10.1097/QAI.0b013e3182302ea8. [DOI] [PubMed] [Google Scholar]
- 10.Hirt D, Ekouévi DK, Pruvost A, Urien S, Arrivé E, Blanche S, Avit D, Amani-Bosse C, Nyati M, Legote S, Ek ML, Say L, McIntyre J, Dabis F, Tréluyer JM. 2011. Plasma and intracellular tenofovir pharmacokinetics in the neonate (ANRS 12109 trial, step 2). Antimicrob Agents Chemother 55:2961–2967. doi: 10.1128/AAC.01377-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Benaboud S, Hirt D, Launay O, Pannier E, Firtion G, Rey E, Bouazza N, Foissac F, Chappuy H, Urien S, Tréluyer JM. 2012. Pregnancy-related effects on tenofovir pharmacokinetics: a population study with 186 women. Antimicrob Agents Chemother 56:857–862. doi: 10.1128/AAC.05244-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hirt D, Ekouévi DK, Pruvost A, Urien S, Arrivé E, Blanche S, Avit D, Amani-Bosse C, Nyati M, Legote S, Ek ML, Say L, McIntyre J, Dabis F, Tréluyer JM. 2009. Population pharmacokinetics of tenofovir in HIV-1-infected pregnant women and their neonates (ANRS 12109). Clin Pharmacol Ther 85:182–189. doi: 10.1038/clpt.2008.201. [DOI] [PubMed] [Google Scholar]
- 13.Gagnieu MC, Barkil ME, Livrozet JM, Cotte L, Miailhes P, Boibieux A, Guitton J, Tod M. 2008. Population pharmacokinetics of tenofovir in AIDS patients. J Clin Pharmacol 48:1282–1288. doi: 10.1177/0091270008322908. [DOI] [PubMed] [Google Scholar]
- 14.Jullien V, Tréluyer JM, Rey E, Jaffray P, Krivine A, Moachon L, Lillo-Le Louet A, Lescoat A, Dupin N, Salmon D, Pons G, Urien S. 2005. Population pharmacokinetics of tenofovir in human immunodeficiency virus-infected patients taking highly active antiretroviral therapy. Antimicrob Agents Chemother 49:3361–3366. doi: 10.1128/AAC.49.8.3361-3366.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Burns RN, Hendrix CW, Chaturvedula A. 2015. Population pharmacokinetics of tenofovir and tenofovir-diphosphate in healthy women. J Clin Pharmacol 55:629–638. doi: 10.1002/jcph.461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chaturvedula A, Fossler MJ, Hendrix CW. 2014. Estimation of tenofovir's population pharmacokinetic parameters without reliable dosing histories and application to tracing dosing history using simulation strategies. J Clin Pharmacol 54:150–160. doi: 10.1002/jcph.221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Keller MJ, Madan RP, Torres NM, Fazzari MJ, Cho S, Kalyoussef S, Shust G, Mesquita PM, Louissaint N, Chen J, Cohen HW, Diament EC, Lee AC, Soto-Torres L, Hendrix CW, Herold BCA. 2011. Randomized trial to assess anti-HIV activity in female genital tract secretions and soluble mucosal immunity following application of 1% tenofovir gel. PLoS One 6:e16475. doi: 10.1371/journal.pone.0016475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Parke J, Holford NH, Charles BG. 1999. A procedure for generating bootstrap samples for the validation of nonlinear mixed-effects population models. Comput Methods Programs Biomed 59:19–29. doi: 10.1016/S0169-2607(98)00098-4. [DOI] [PubMed] [Google Scholar]
- 19.Lindbom L, Ribbing J, Jonsson EN. 2004. Perl-speaks-NONMEM (PsN)—a Perl module for NONMEM related programming. Comput Methods Programs Biomed 75:85–94. doi: 10.1016/j.cmpb.2003.11.003. [DOI] [PubMed] [Google Scholar]
- 20.Ahn JE, Karlsson MO, Dunne A, Ludden TM. 2008. Likelihood based approaches to handling data below the quantification limit using NONMEM VI. J Pharmacokinet Pharmacodyn 35:401–421. doi: 10.1007/s10928-008-9094-4. [DOI] [PubMed] [Google Scholar]
- 21.Karlsson MO, Jonsson EN, Wiltse CG, Wade JR. 1998. Assumption testing in population pharmacokinetic models illustrated with an analysis of moxonidine data from congestive heart failure patients. J Pharmacokinet Biopharm 26:207–246. doi: 10.1023/A:1020561807903. [DOI] [PubMed] [Google Scholar]
- 22.Wählby U, Jonsson EN, Karlsson MO. 2002. Comparison of stepwise covariate model building strategies in population pharmacokinetic-pharmacodynamic analysis. AAPS Pharm Sci 4:E27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jonsson EN, Karlsson MO. 1999. Xpose—an S-PLUS based population pharmacokinetic/pharmacodynamic model building aid for NONMEM. Comput Methods Programs Biomed 58:51–64. [DOI] [PubMed] [Google Scholar]
- 24.R Core Team. 2015. R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria: https://www.R-project.org/. [Google Scholar]
- 25.Comets E, Brendel K, Mentré F. 2008. Computing normalised prediction distribution errors to evaluate nonlinear mixed-effect models: the npde add-on package for R. Comput Methods Programs Biomed 90:154–166. doi: 10.1016/j.cmpb.2007.12.002. [DOI] [PubMed] [Google Scholar]
- 26.Bergstrand M, Hooker AC, Karlsson MO. 2009. Visual predictive checks for censored and categorical data, abstr 1604. Abstr Annu Meet Popul Approach Group Eur, St Petersburg, Russia. [Google Scholar]
- 27.Hu CY, Liu YM, Liu Y, Chen Q, Wang W, Wu K, Dong J, Li J, Jia JY, Lu C, Sun SX, Yu C, Li X. 2013. Pharmacokinetics and tolerability of tenofovir disoproxil fumarate 300 mg once daily: an open-label, single- and multiple-dose study in healthy Chinese subjects. Clin Ther 35:1884–1889. doi: 10.1016/j.clinthera.2013.09.020. [DOI] [PubMed] [Google Scholar]
- 28.Savic RM, Barrail-Tran A, Duval X, Nembot G, Panhard X, Descamps D, Verstuyft C, Vrijens B, Taburet AM, Goujard C, Mentré F, ANRS 134-COPHAR 3 Study Group. 2012. Effect of adherence as measured by MEMS, ritonavir boosting, and CYP3A5 genotype on atazanavir pharmacokinetics in treatment-naive HIV-infected patients. Clin Pharmacol Ther 92:575–583. doi: 10.1038/clpt.2012.137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hendrix CW, Andrade A, Bumpus NN, Kashuba AD, Marzinke MA, Moore A, Anderson PL, Bushman LR, Fuchs EJ, Wiggins I, Radebaugh C, Prince HA, Bakshi RP, Wang R, Richardson P, Shieh E, McKinstry L, Li X, Donnell D, Elharrar V, Mayer KH, Patterson KB. 2016. Dose frequency ranging pharmacokinetic study of tenofovir-emtricitabine after directly observed dosing in healthy volunteers to establish adherence benchmarks (HPTN 066). AIDS Res Hum Retroviruses 32:32–43. doi: 10.1089/aid.2015.0182. [DOI] [PMC free article] [PubMed] [Google Scholar]