Waves of Cdk1 activity in S-phase synchronize the cell cycle in Drosophila embryos

Summary

Embryos of most metazoans undergo rapid and synchronous cell cycles following fertilization. While diffusion is too slow for synchronization of mitosis across large spatial scales, waves of Cdk1 activity represent a possible process of synchronization. However, the mechanisms regulating Cdk1 waves during embryonic development remain poorly understood. Using biosensors of Cdk1 and Chk1 activities, we dissect the regulation of Cdk1 waves in the Drosophila syncytial blastoderm. We show that Cdk1 waves are not controlled by the mitotic switch but by a double negative feedback between Cdk1 and Chk1. Using mathematical modeling and surgical ligations we demonstrate a fundamental distinction between S-phase Cdk1 waves, which propagate as active trigger waves in an excitable medium, and mitotic Cdk1 waves, which propagate as passive phase waves. Our findings show that in Drosophila embryos, Cdk1 positive feedback serves primarily to ensure the rapid onset of mitosis, while wave propagation is regulated by S-phase events.

eTOC Blurb

Deneke et al. investigate the mechanisms ensuring rapid and synchronous nuclear divisions in Drosophila embryos, demonstrate that waves of Cdk1 activity synchronize the cell cycle and are regulated by double negative feedback between Cdk1 and Chk1 in S-phase. S-phase Cdk1 waves trigger propagation of passive mitotic Cdk1 phase waves.

Introduction

Early development in most metazoans is characterized by remarkably fast and coordinated cell cycles (O'Farrell et al., 2004). This early cell cycle program is thought to be under strong selective pressure for organisms that lay eggs externally, as eggs depend entirely on the maternal nutrients deposited within them (Farrell and O'Farrell, 2014). In such systems, mothers lay large eggs which store sufficient nutrients for embryonic development, and embryos rapidly amplify their DNA content prior to activation of zygotic gene expression at the maternal-to-zygotic transition (O'Farrell, 2015). This is achieved through exceptionally rapid and synchronous cleavage divisions. Synchronization appears to be necessary in order to ensure that a precise developmental program is executed in a timely manner throughout the entire embryo during morphogenesis.

After fertilization, the Drosophila embryo undergoes 13 synchronous rounds of S-phase and mitosis (Rabinowitz, 1941), which take place in a multi-nucleated syncytium. The first 9 cell cycles are extremely rapid, lasting about 8–9 minutes (Edgar et al., 1994; Farrell and O'Farrell, 2014; Foe and Alberts, 1983). The remaining 4 cell cycles get gradually longer (Edgar et al., 1994; Farrell and O'Farrell, 2014; Foe and Alberts, 1983). This lengthening of the cell cycles is accounted by longer S-phase, as mitosis has a stereotypical duration of about 4 minutes (Farrell and O'Farrell, 2014), and by the activation of the DNA replication checkpoint (Farrell and O'Farrell, 2014; Fogarty et al., 1997; Sibon et al., 1997), which is likely triggered by the increase in DNA content of the embryo. The main effector of the DNA replication checkpoint is Chk1, which regulates the cell cycle by inhibiting Cdk1 activity (Morgan, 2007). This is accomplished in part by the activation of Wee1 by Chk1 (Lee et al., 2001), which is required for the low activity of Cdk1 observed in interphases of cell cycles 12 and 13 (Fasulo et al., 2012; Price et al., 2000; Royou et al., 2008; Stumpff et al., 2004). However, the contribution of these and other regulatory mechanisms to the synchronization of the early cell cycles remains unclear.

How spatial coordination is achieved during development across hundreds of microns remains largely uncharacterized. The Drosophila embryo provides a good model to study the synchronization of biological events during development. It is about 500 μm long and 150 μm wide (Foe and Alberts, 1983), and, despite its large size, the embryo follows a precisely timed program. Diffusion within the large cytoplasm is too slow to account for long-distance synchrony. Assuming a diffusion coefficient of about 10μm²/s (which would be expected for a typical protein), it would take several hours for a protein to diffuse across the embryo, a timescale which is clearly incompatible with the synchronization of the Drosophila cell cycle, which happens on timescales of tens of seconds. Chemical waves provide a much more rapid mechanism of communication between and across cells and have been observed in many species. There are two classes of chemical waves: trigger waves and phase waves. Trigger waves in reaction kinetics systems are generated by the coupling of catalytic loops with diffusion, which can spread biochemical activity much faster than simple diffusion (Gelens et al., 2014; Tyson and Keener, 1988). Dimensional analysis indicates that the speed of a trigger wave is determined by Luther’s formula: v~(Dk)^1/2, where D indicates the diffusion coefficient and k is the relevant kinetic rate (Tyson and Keener, 1988). Systematic analysis of the reaction-diffusion system responsible for the generation of the wave is required to deduce the relevant rate k (van Saarloos, 1998). Conversely, phase waves are passive and do not involve any spatial coupling or diffusion (Winfree, 2001). They arise as a purely kinematic mechanism, which reflects spatially non-uniform timing mechanisms. For example, a set of identical oscillators with a spatially non-uniform initial phase would generate a wave, even in the absence of any diffusion or coupling among the oscillators (Winfree, 2001). For this reason, phase waves are often referred to as pseudo-waves. Physical barriers provide the standard experimental tool to distinguish between trigger and phase waves. While the propagation of a trigger wave is hindered by a barrier, phase waves would move undisturbed through the barrier.

Recent in vitro experiments suggest that propagation of chemical waves of Cdk1 activity synchronize cell cycles in the Xenopus extract system (Chang and Ferrell, 2013). Indeed, interlinked positive feedback loops involving Wee1 and Cdc25 (Morgan, 2007) provide a bistable Cdk1 network capable of transmitting chemical waves. However, in Drosophila the speed of the mitotic waves slows down from cell cycle 10 to cell cycle 13 (Idema et al., 2013), without a concomitant slowing of mitosis (Farrell and O'Farrell, 2014; Foe and Alberts, 1983). The mitotic waves in this system were instead suggested to stem from excitable mechanical waves (Idema et al., 2013). Collectively, these observations indicate that the physical and molecular mechanisms responsible for cell cycle synchronization in vivo remain to be elucidated.

Here we address the mechanisms driving synchronization of cell cycles 10–13 of the early Drosophila embryo. By making use of biosensors for Cdk1 and Chk1 activity, we directly document chemical waves and test the relationship between chemical and mitotic waves. We found that in cell cycles 12 and 13 the slowdown of Cdk1 waves is not explained by a slower activation of the mitotic switch but rather by the activation of the S-phase DNA replication checkpoint, which controls Cdk1 through the Chk1/Wee1 pathway. Mathematical modeling captured the speed of the waves and predicted a fundamental distinction between S-phase Cdk1 waves, which propagate as active trigger waves in an excitable medium, and mitotic Cdk1 waves, which propagate as passive phase waves that reflect the delays set by the trigger waves. Confirming that prediction, we show that physical barriers interrupt propagation of S-phase but not of mitotic waves. Our findings demonstrate that in Drosophila embryos, Cdk1/Wee1/Cdc25 positive feedbacks serve primarily to ensure a rapid activation of Cdk1. Conversely, the S-phase activity of Cdk1 and its regulation by Chk1 is responsible for triggering and regulating the speed of the mitotic wave.

Results

Visualization and quantification of Cdk1 and mitotic waves

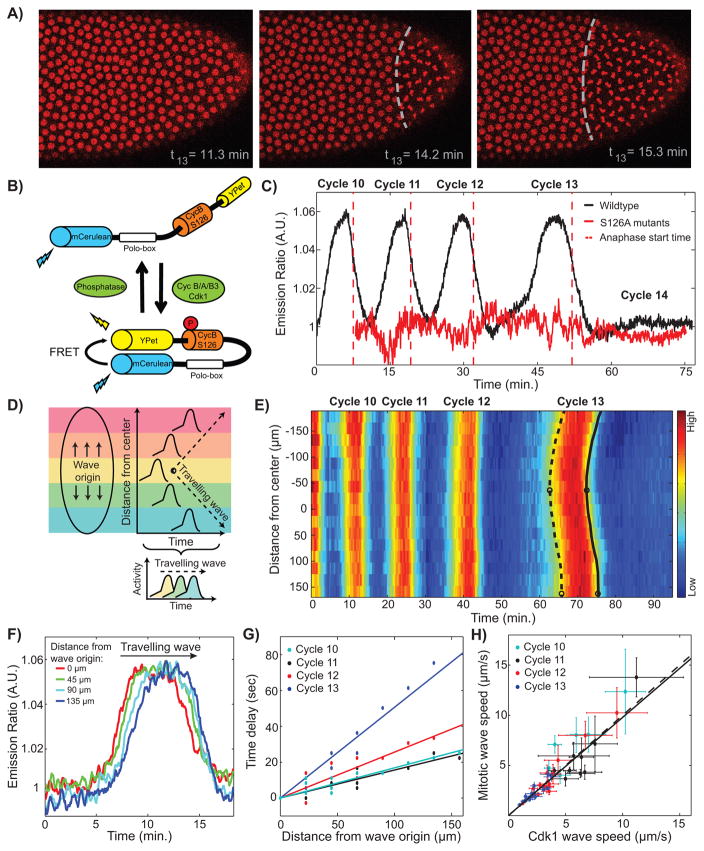
Mitotic waves spread across the embryo, as revealed by confocal microscopy of embryos with tagged histones (Figure 1A and Movie S1). In agreement with previous results (Idema et al., 2013), the wave of mitotic entry and the wave of mitotic exit are strongly correlated in space and time, with a consistent delay of 4 minutes between prophase and anaphase. This observation implies that the physical properties (e.g. speeds) of the two waves are essentially identical and hereafter we will refer to them as mitotic waves interchangeably. Surgical ligation experiments, which separate the embryo into two compartments (Newman and Schubiger, 1980; Sander, 1971), demonstrate that physical barriers block mitotic waves, indicating active wave propagation (Movie S2). These confocal-imaging observations confirm classical observations by Edgar et al. (Edgar et al., 1986). To unravel the regulatory mechanisms that control mitotic waves, we used a FRET-based biosensor for the activity of Cdk1 (Figure 1B) (Gavet and Pines, 2010). The Cdk1 FRET signal showed clear oscillations corresponding to cell cycle progression (Figure 1C), and RNAi experiments indicated that the Cdk1 sensor responds to CycA-, CycB-, and CycB3-Cdk1 complexes in this system (Figure S1B–C). Imaging at high spatial and temporal (2 s) resolution allowed us to obtain a precise spatiotemporal map of Cdk1 activity (Figures 1D–1E). Analysis of the dynamics of Cdk1 activity in different regions along the anterior-posterior axis of the embryo revealed the propagation of waves of Cdk1 activity (Figure 1F). Measuring the time required for the waveform to travel a given distance, we found that waves propagate through the embryo at roughly constant speed (Figure 1G, Figure S1H). Moreover, the speeds of Cdk1 waves and mitotic waves are strongly correlated, suggesting that Cdk1 activity drives the mitotic waves (Figure 1H).

Figure 1. Cdk1 waves drive mitotic waves.

(A) Time lapse series depicting the propagation of a mitotic wave in an embryo with RFP-tagged histones. (B) Schematic view of the Cdk1 FRET biosensor composed of two fluorophores, YPet and mCerulean, which are linked by a Cdk1 phosphorylation site from cyclin B1 (S126) and the polo box domain of Plk1. Upon phosphorylation of the Cdk1-specific phosphorylation site, the sensor undergoes a conformational change that results in increased FRET efficiency. (C) Emission ratio of FRET sensor averaged across one embryo shows clear oscillations of Cdk1 activity, which increases upon mitotic entry and remains low during early interphase 14, when the levels of active Cdk1 are uniformly low. Red line, S126A mutant; red dotted line, average anaphase entry time. (D) Cdk1 traveling waves can be visualized by plotting the activity profiles as a function of space and time. First, images are divided into different regions along the anterior-posterior axis of the embryo (colored boxes). Activity profiles for each region are then calculated and plotted as a function of time and space, which allows for the visualization of the wave front (dotted line). (E) Heat-map of Cdk1 activity over time and along the anterior-posterior (AP)-axis of an embryo. White circles indicate wave origins at cycle 13, dotted line indicates the mitotic entry front and the black line indicates the anaphase wave front. (F) Cdk1 activity profiles for different positions along the AP-axis of an embryo in cell cycle 13. (G) The speed of the wave is estimated by computing the time elapsed for the wave to travel a given distance along the embryo: the inverse slope of a linear fit yields the speed. (H) Mitotic wave speed as a function of Cdk1 wave speed. Dotted line, identity line; solid line, best-fit curve. Scale-bars, 10μm. Error bars, 95% confidence interval (CI); a.u., arbitrary units. See also Figure S1 and Movies S1 and S2.

Cdk1 activity during S-phase is predictive of mitotic and Cdk1 wave speed at cycles 12 and 13

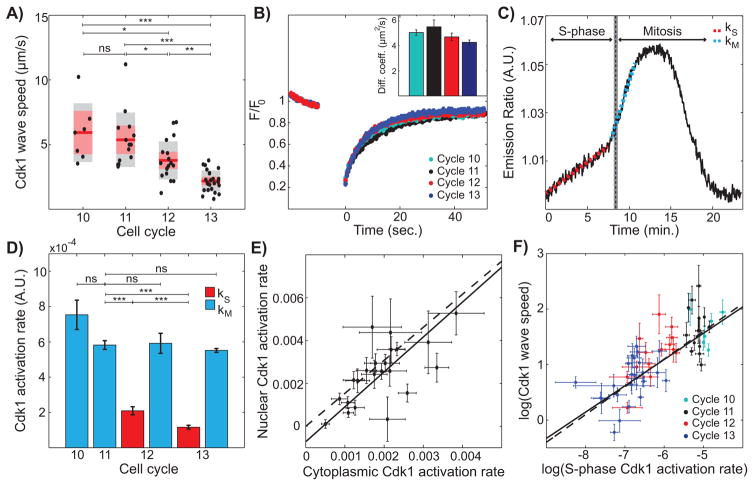
Mitotic waves decrease in speed as developmental cycles progress (Idema et al., 2013). Cdk1 waves also slow down from cycle 10 to 13 (Figure 2A). Dimensional analysis predicts that the velocity v of a chemical wave follows Luther’s formula, $v\approx \sqrt{Dk}$, where D is the diffusion coefficient and k is the relevant reaction rate (Luther, 1906). This suggests that, for chemical waves to slow down with the cycles, the reactions that control wave propagation and/or the diffusion of key factors should decrease. FRAP experiments showed that Cdk1 diffusion does not change significantly in cycles 10–13 (Figure 2B). Conversely, Cdk1 activation is biphasic during late cycles, with a slow rise (rate k_S) followed by a fast activation (rate k_M) during mitotic entry (Figure 2C). Using the disappearance of tagged PCNA foci as a readout for completion of DNA replication (Shermoen et al., 2010) (Figure S2), we determined that the inflection point of the biphasic Cdk1 activation slightly precedes the time of completion of S-phase. This result indicates that the slow rise at rate k_S reflects the activation of Cdk1 during S-phase. The rate of Cdk1 activation upon mitotic entry (k_M) remains constant during cycles 10–13 (Figure 2D, blue bars). This is consistent with the observation that the duration of mitosis is roughly constant during these cell cycles (Farrell and O'Farrell, 2014; Foe and Alberts, 1983), which was interpreted in (Idema et al., 2013) as evidence against chemical waves and in favor of mechanical waves. However, chemical rates significantly decrease during S-phase, i.e. k_S diminishes at cycles 12 and 13 (Figure 2D, red bars) both in the cytoplasm and in nuclei (Figure 2E). These data suggest that the rate k_S of Cdk1 activation in S-phase controls the slowing of the Cdk1 chemical waves as $v\approx \sqrt{D{k}_{\mathrm{S}}}$, which was indeed confirmed in Figure 2F.

Figure 2. Cdk1 activity during S-phase is predictive of mitotic and Cdk1 wave speed.

(A) Cdk1 wave speed as a function of developmental cycles. Red line, mean; gray box, 95% CI; red box, 1 standard deviation (SD). (B) Normalized fluorescence intensity profile of YFP-tagged Cdk1 before and after photobleaching. Inset, calculated diffusion coefficient per cell cycle. Error bars, standard error of the mean (s.e.m.) (C) Emission ratio of Cdk1 sensor for cycle 13 displays biphasic behavior. Red dotted line corresponds to Cdk1 activation rate during S-phase (k_S) and blue dotted line corresponds to Cdk1 activation rate during mitosis (k_M). Completion of S-phase was determined through the disappearance of RFP-tagged PCNA foci, see Supplemental Information for details. (D) Average Cdk1 activation rate per cell cycle. Red bars, S-phase Cdk1 activation rate (k_S); blue bars, mitotic Cdk1 activation rate (k_M). Error bars, s.e.m. (E) Nuclear and cytoplasmic Cdk1 activities were calculated by segmenting nuclei with an intensity threshold and averaging intensity inside and outside nuclear mask, respectively. Dotted line, line with a slope given by the ratio of nuclear Cdk1 levels to cytoplasmic Cdk1 levels, measured using embryos expressing Cdk1-YFP; solid line, best-fit curve. Error bars, 95% CI. (F) Log-log plot of Cdk1 speed versus S-phase Cdk1 activation rate. Solid line, best-fit curve; dotted line, Luther’s formula. Error bars, 95% CI. For all graphs, *, p<0.05; **, p<0.001; ***, p<0.0001; ns, not significant. See also Figure S2.

The speed of Cdk1 waves is regulated by the Chk1/Wee1 pathway and by DNA content

Our results argue that the velocity of mitotic and Cdk1 waves is controlled by Cdk1 activation during S-phase. To test this model, we looked for genetic perturbations that specifically alter the rate of activation of Cdk1 in S and M phases. We first analyzed mutants of the main effector kinases of the DNA replication checkpoint, Chk1 and Chk2. We used chk1 chk2 mutants, instead of chk1 mutants, as chk1 mutants undergo a Chk2-dependent developmental arrest which makes the analysis of the last syncytial cycles difficult (Takada et al., 2007). In chk1 chk2 mutants these developmental defects are greatly ameliorated (Takada et al., 2007). Embryos mutant for chk1 and chk2 fail to slow Cdk1 activation in S-phase, resulting in premature mitotic entry and the completion of two extra syncytial cycles (Figure 3A and Movie S3) (Fogarty et al., 1997; Sibon et al., 1997). Notably, chk1 chk2 embryos do not display biphasic Cdk1 activation (Figures 3A, 3C), and wave propagation does not slow during cycles 10–13 (Figure 3E). A similar behavior was observed in embryos mutant for wee1 (Figures 3B, 3D–3E) (Price et al., 2000), a downstream effector of Chk1 (Farrell and O'Farrell, 2014; Morgan, 2007). These findings suggest that the increase in DNA content during the developmental cycles activates the DNA replication checkpoint to slow Cdk1 activation and thereby reduce the speed of the waves. To test this idea, we modified the DNA content of the embryos using compound chromosomes (Merrill et al., 1988). As predicted, k_S (the rate of Cdk1 activation in S-phase) is inversely proportional to DNA content, and cell cycle duration increases with DNA amount (Figure 3F).

Figure 3. Cdk1 waves are dependent on the Chk1/Wee1 pathway and on DNA content.

(A-B) Emission ratio of Cdk1 sensor for wildtype embryos (black line), chk1 chk2 embryos (A, green line), and wee1 embryos (B, red line). (C-D) Average Cdk1 activation rate per cell cycle for wildtype (black), chk1 chk2 (C, green) embryos, and wee1 embryos (D, red). Error bars, s.e.m. (E) Log-log plot of Cdk1 speed versus S-phase Cdk1 activation rate for wildtype (black), chk1 chk2 (green), and wee1 (red) embryos. Error bars, 95% CI. (F) S-phase Cdk1 activation rate as a function of DNA content. Inset, cell cycle period, marked from anaphase start time of one cycle to the next, as a function of DNA content. 100% indicates the DNA content of wild type embryos at cycle 13. Error bars, s.e.m. For all graphs, ***, p<0.0001; ns, not significant.

A Cdk1/Chk1 double negative feedback controls Cdk1 waves

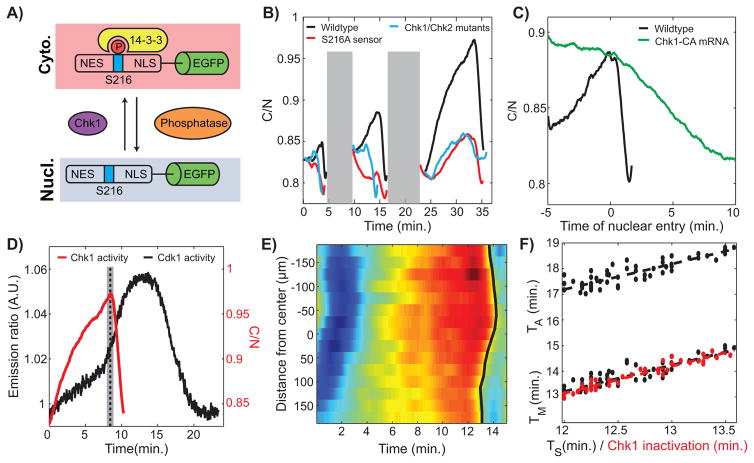
To gain quantitative insights on the dynamics of Chk1, we engineered a localization sensor that responds primarily to its activity during cell cycles 12 and 13. We fused a peptide from human Cdc25C (amino acids 183-251), which contains an NLS, NES and a Chk1 phosphorylation site (Serine 216) to EGFP (Figure 4A). Phosphorylation of S216 triggers the binding of 14-3-3, which masks the NLS downstream of Serine 216 decreasing the nuclear import rate (Perry and Kornbluth, 2007). An NES sequence upstream of Serine 216 mediates nuclear export (Perry and Kornbluth, 2007). We found that cytoplasmic-to-nuclear ratio (C/N) of the sensor increases from cycle 11 to cycle 13 (Figure 4B), which is consistent with an increase of Chk1 activity. To determine whether the sensor responds primarily to Chk1 activity at cycles 12 and 13, we compared its localization dynamics to that of a sensor in which Serine 216 was mutated to Alanine (S216A). We also quantified the localization dynamics of the sensor in chk1 chk2 mutants as well as under various genetic perturbations, which reduce or slightly increase the activity of Chk1 (Figure 4B and Figure S3A). Collectively, our experiments indicate that the increase in the nuclear exclusion of the sensor observed in cycles 12 and 13 is mainly dependent on Chk1 activity. The sensor undergoes a rapid nuclear import at the onset of mitosis, which precedes nuclear envelope breakdown by about one minute (Figure S3B). To confirm that this rapid nuclear import reflects a rapid inactivation of Chk1 at completion of S-phase, we forced embryos to enter mitosis in the presence of high Chk1 activity, established through injection of mRNA encoding for a constitutively active Chk1 mutant (Chk1-CA) (Wang et al., 2012). The sensor enters nuclei very slowly at the onset of mitosis (Figure 4C), consistent with a role of Chk1 in slowing down the rate of import of the sensor. Expression of Chk1-CA results in longer cell cycles (about 30 min compared to 12 min for cycle 12) with a significant contribution to cell cycle lengthening from a longer mitosis (Figure S3C). This is in agreement with the notion that inactivation of Chk1 is required for rapid mitosis. Based on all these observations, we conclude that the rapid import of the Cdc25^183-251-EGFP sensor reflects the rapid inactivation of Chk1 at the onset of mitosis.

Figure 4. A Cdk1/Chk1 double negative feedback controls Cdk1 waves.

(A) Schematic view of Chk1 localization sensor. The cytoplasmic to nuclear ratio provides a readout of Chk1 activity. (B) Cytoplasmic to nuclear intensity ratio of the Chk1 sensor in wild type (black), mutant sensor (S216A; red line), and chk1 chk2 mutants (blue line) for cycles 11–13. In order to compare cell cycles of similar durations, we used cycle 15 (instead of cycle 13) for chk1 chk2 mutants. Gray shaded box represents mitosis, when the absence of nuclear envelope precludes a reliable measure of the C/N ratio. (C) C/N ratio for a cycle 12 wild type and an embryo injected with Chk1-CA mRNA. (D) Average Cdk1 and Chk1 activities at cycle 13 measured in two different embryos. Dotted line, completion of S-phase. (E) Heat-map of Chk1 activity over time and along the anterior-posterior (AP)-axis of an embryo. Black line, Chk1 inactivation wave front. (F) Time of entry into mitosis (T_M) and anaphase start time (T_A) as a function of the time of completion of S-phase (T_S) (black line) and Chk1 inactivation (red line). Slopes: 1.0±0.1. See also Figure S3 and Movie S3.

Using the biosensor described above, we established that the activity of Chk1 increased at cycles 12 and 13 relative to cycle 11 (Figure 4B). Chk1 activity plummets about one minute prior to nuclear envelope breakdown (Figure 4B and Figure S3B), indicating that Chk1 inactivation coincides with the abrupt activation of Cdk1 (Figure 4D). In fact, Chk1 inactivation propagates in a wave-like manner synchronized with the wave of Cdk1 activity (Figures 4E–4F), arguing that Cdk1 triggers Chk1 inactivation, consistent with previous results (Yuan et al., 2012). Completion of S-phase coincides with the time of Chk1 inactivation and propagates in the same wave-like pattern (Figure 4F: the wave of completion of S-phase precedes the waves of mitotic entry and mitotic exit by about 1 and 5 minutes, respectively). These observations suggest that Cdk1 negatively regulates Chk1 through its ability to promote completion of S-phase (Farrell et al., 2012), removing the DNA replication checkpoint stimulus. We also found that the nuclear levels of Chk1 start decreasing about a minute prior to mitosis (see Figure S3B), a process which might contribute to the reversal of the DNA replication checkpoint. We propose that a double-negative feedback between Cdk1 and Chk1 is the molecular mechanism that initiates the spreading of the Cdk1 waves at cycle 12 and 13 and controls their physical properties.

Mitotic switch ensures rapid activation of Cdk1 during mitosis but does not regulate S-phase Cdk1 activation rate

Previous studies implicated positive feedback among Cdk1, Cdc25 and Wee1 as providing the bistability necessary for propagation of mitotic waves in Xenopus (Chang and Ferrell, 2013; Novak and Tyson, 1993). Positive feedback is due to Cdk1-mediated phosphorylation of Wee1 and Cdc25. To test the role of this regulation in Drosophila embryos, we generated feedback-deficient embryos that lack the relevant phosphorylation sites. Wee1-9A and Twine-3A (Twine and String are the two Cdc25 phosphatases in Drosophila embryos) have all of the putative Cdk1 sites mutated to nonphosphorylatable residues (Di Talia and Wieschaus, 2012; Harvey et al., 2011; Pomerening et al., 2005). We focused on Twine because String is degraded earlier than Twine, which makes Twine the major phosphatase that controls cell cycle 13 (Di Talia et al., 2013; Farrell and O'Farrell, 2013). Embryos mutant for endogenous wee1 and twine (but expressing Wee1-9A and Twine-3A) lack the Cdk1/Wee1/Cdc25 feedback at cycle 13. We found that the rate of Cdk1 activation during mitotic entry is reduced 2–3 fold at cycle 13 (Figures 5A–5B and Figure S4), confirming that the positive feedback in the mitotic switch is required for the abrupt activation of Cdk1 in mitosis. Conversely, the activation of Cdk1 during S-phase is unaffected and remained smaller than the mitotic activation rate. Notably, Cdk1 waves still propagate, although with a speed slower than wild-type (Figure 5C and Movie S4). We conclude that the positive feedback through Wee1/Cdc25 phosphorylation is required for the invariant mitotic activation rate of Cdk1, which in turn ensures that the speed of the wave is not altered by changes in mitotic rates but is controlled by the rate of Cdk1 activation in S-phase. We observe that embryos in which only one of the two feedbacks is abrogated show intermediate phenotypes and demonstrate that the double negative feedback between Cdk1 and Wee1 plays a stronger role than the feedback between Cdk1 and Twine (Figure S4).

Figure 5. Mitotic switch ensures rapid activation of Cdk1 during mitosis but does not regulate S-phase Cdk1 activation rate.

(A) Emission ratio of Cdk1 sensor for wildtype embryos (black line) and twine-3A wee1-9A embryos (red line). (B) Average Cdk1 activation rate per cell cycle for wildtype (black) and twine-3A wee1-9A (red) embryos. Error bars, s.e.m., ***, p<0.0001; ns, not significant. (C) Log-log plot of Cdk1 speed versus S-phase Cdk1 activation rate for wildtype (black) and twine-3A wee1-9A (red) embryos. Error bars, 95% CI. Inset, Cdk1 wave speed of wildtype (black) and twine-3A wee1-9A (red) embryos at cycle 13. Error bars, s.e.m. See also Figure S4 and Movie S4.

A mathematical model of Chk1 and Cdk1 activities captures the physical properties of Cdk1 waves

To gain further insight into the nature of the mitotic waves, we built a mathematical model for Cdk1 dynamics (see Experimental Procedures and Supplemental Information). Bistability coupled with diffusion provides the classical mechanism that triggers chemical waves (Tyson and Keener, 1988; van Saarloos, 1998). This can be understood intuitively as follows. When a region of the embryo transitions from a low state of Cdk1 activity to a high state, diffusion of active Cdk1 can initiate a similar transition in a neighboring region, which can then spread to another region and thereby generates a traveling wave. Mathematically, the bistable nature of a model is elucidated using phase-plane analysis (Strogatz, 2000). By plotting the time derivative of active Cdk1 (da/dt) as a function of its concentration (a) (top panel in Fig. 6A), one can readily visualize the rate of change of a (the arrows pointing to the right reflect increasing a and those to the left reflect decreasing a). The points where the time derivative vanishes are defined as fixed points. The changes in concentration (“flows”) either point towards these points (stable fixed points, full circles) or away from them (unstable fixed points, open circles). A bistable system is characterized by two stable fixed points (and an unstable one in between), as shown in Figure 6A. Therefore, in the presence of bistability, a deterministic dynamical system will evolve toward one of the two fixed points, depending on its current status.

Figure 6. A mathematical model of Cdk1 activity captures the scaling of the speed with S-phase activity.

(A) Top: phase plane diagram depicting stable fixed points (filled circles) and unstable fixed points (open circles). Bottom: schematic view of the Cdk1 network. (B) Cdk1 (solid line) and Chk1 (dotted line) activity profiles for cycles 10–13, as obtained from the mathematical model described in the main text and Supplemental Information. (C) Phase plane analysis for different time points in cycle 11 (left) and 13 (right). The open circles denote unstable fixed points and filled circle denote stable fixed points. Notice that for both cycles bistability is observed transiently and for early time points, plots extend beyond cyclin-Cdk1 concentration. (D) Log-log plot of Cdk1 speed versus S-phase Cdk1 activation rate for experimental data (black) and simulated data (red). (E) Log-log plot of Cdk1 speed versus S-phase Cdk1 activation rate for simulations of the wild type (black) and simulations of the twe^3A wee1^9A mutants (purple). (F) Plot of the effective bistable potential appearing in the model (calculated at the time when Cdk1 transitions from the low to the high state). Arrows indicate the kinetic barrier. All error bars, 95% CI. See also Figure S5.

In our mathematical model, Chk1 inhibits Cdk1 by modulating the activities of Wee1 and Cdc25 (bottom panel in Fig. 6A). As in previous work (Chang and Ferrell, 2013), the effects of Wee1 and Cdc25 were implicitly incorporated by using nonlinear feedback terms (see Experimental Procedures). Conversely, Cdk1 regulates the time of Chk1 downregulation (likely via the control of S-phase completion, Figure 6A) and we explicitly included the dynamics of Chk1 to account for the differences that we observed among developmental cycles 10–13. Our model reproduces the Cdk1 dynamics observed in the different cycles by simply assuming different initial levels of Chk1 activity in each cycle (Figure 6B). The first slope observed in Figure 6B for late cycles corresponds to a ramp-up phase where Chk1 inhibits the activity of Cdk1. Once the level of Chk1 drops, its restraint on Cdk1 is removed and the stereotypic fast growth of Cdk1 activity follows (second slope in Figure 6B). The drop in Chk1 is rather abrupt as the reaction-diffusion model features transient bistability, i.e. the system displays two stable states, one with low Cdk1 activity and one with high activity (Figure 6C). Bistability in Cdk1 regulation coupled to diffusion ensures that the spreading of Cdk1 in the model is indeed wave-like (see Supplemental Information). The corresponding velocities reproduce the experimentally observed scaling of the speed as a function of the S-phase rate of increase of Cdk1 activity (Figure 6D). Our mathematical model also reproduces the behavior of the feedback-defective mutants, i.e. reduced rate of activation of Cdk1 in mitosis and Cdk1 waves still present but of reduced speed (Figure S5F–G and Figure 6E).

To obtain an intuitive understanding of why the speed of Cdk1 waves decreases as Chk1 activity increases, we use an idea from the physics of phase transitions (van Saarloos, 1998), where similar wave-like propagation is observed, for example, in the solidification of supercooled liquids (van Saarloos, 1998). In these systems, bistability is depicted by a free energy function that has two local minima which represent a stable and a metastable state (e.g. solid and liquid). A supercooled liquid is trapped in the metastable (liquid) state, until a fluctuation overcomes the energy barrier that separates the metastable from the stable state. The height of the kinetic barrier that must be overcome for the initiation and spreading of the waves is a key element in setting the speed of the wave (van Saarloos, 1998). In our model, this barrier becomes higher in later developmental cycles (Figure 6F, see Supplemental Information for details on how to derive an effective energy function for our mathematical model), as Chk1 activity increases and stabilizes the low state of activity of Cdk1. In summary, a simple mathematical model including a double negative feedback between Chk1 and Cdk1 and the Cdk1/Wee1/Cdc25 feedbacks captures and explains the physical properties of the Cdk1 waves.

S-phase waves are generated by an active mechanism, while anaphase waves are a kinematic and passive process

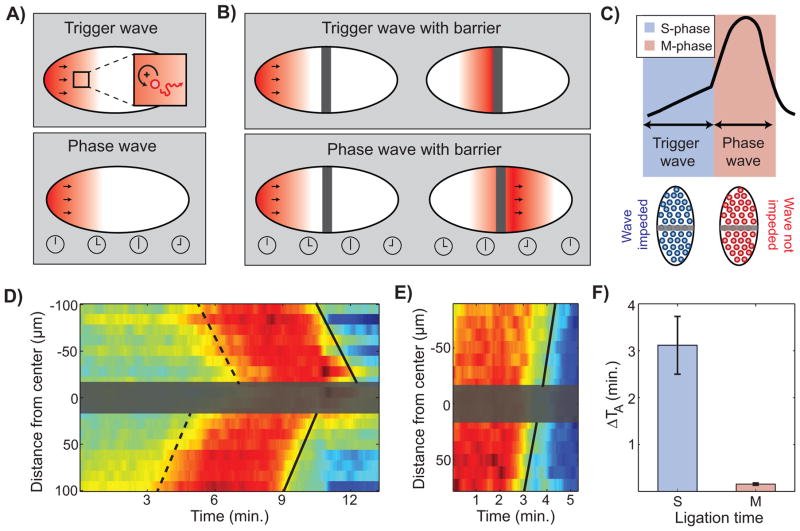
Nuclear cycles are completed by mitotic exit events, which are initiated by a decline in Cdk1 activity (Figure 1). Positive feedback mechanisms sharpening the metaphase-anaphase transition (Holt et al., 2008; Ishihara et al., 2014; López-Avilés et al., 2009) raise the possibility that, like the S-phase Cdk1 waves, the anaphase waves also propagate as chemical trigger waves. If that were the case, then any slowing of anaphase waves in successive cycles should be accompanied by changes in the Cdk1-inactivation reactions. However, we found that the rate of Cdk1 inactivation is invariant (Figure S6), yet anaphase waves display the same slowing observed for completion of S-phase and mitotic entry in different cycles (Figure 4F). The previous observations and the analysis of our mathematical model suggest that S-phase Cdk1 waves are trigger waves, while anaphase waves are phase waves. Trigger waves involve the catalytic production of a propagating species and its diffusion into neighboring regions (Figure 7A). Conversely, phase waves are kinematic, and just reflect pre-defined delays (Figure 7A). In our case, delays are those set by the Cdk1 waves in the S-phase, which explains the strong correlation of velocities in Figure 1H.

Figure 7. Mitotic waves are kinematic phase waves.

(A) Schematic of the difference between trigger waves and phase waves. Trigger waves involve the transport or diffusion (red line) of material from one neighboring region to another, and depend on positive feedback loops (black circular arrow), which ensure the rapid production of the diffusing species. Phase waves are kinematic phase waves that reflect a delay in timing between neighboring regions (bottom panel). (B) The difference between a trigger wave and a phase wave becomes evident when an impermeable barrier is introduced. A trigger wave is blocked when a barrier is present (top panel), whereas a phase wave is unaffected (bottom panel). (C) Schematic of our prediction that synchronization of mitosis should be disrupted if an impermeable barrier is introduced during S-phase (prior to the S-phase Cdk1 trigger wave) and be unaffected if a barrier is introduced during M-phase. (D-E) Heat-map of Cdk1 activity through time and across the anterior-posterior (AP)-axis of an embryo ligated during S-phase (D) or M-phase (E), respectively. Gray box, ligation barrier; dotted line, prophase wave front; solid line, anaphase wave front. The continuity in (E) of the lines on the two sides of the barrier demonstrates that mitotic waves are indeed phase waves. (F) Anaphase delay (computed as the difference in anaphase time on the two sides of the barrier) caused by the introduction of a barrier in S-phase or M-phase. Error bars, s.e.m. See also Figure S6 and Movies S5 and S6.

The different nature of trigger and phase waves is highlighted by placing a physical barrier along the path of the wave. The barrier is expected to impede the propagation of a trigger wave, but not of a phase wave (Figures 7B–7C). We modified the design of a micromanipulator for surgical ligations of embryos (Newman and Schubiger, 1980; Sander, 1971) in order to be able to introduce a barrier with a temporal resolution of about 1 minute in embryos expressing the Cdk1 sensor and His2Av-mRFP. To test whether our predictions were correct, we used this setup to introduce a barrier between two regions of the embryo either during S-phase (to block Cdk1 waves) or M-phase (to test whether or not anaphase waves would be blocked). When the barrier was introduced during interphase, the two sides of the embryo became asynchronous (Figure 7D and Movie S5). Conversely, when the barrier was introduced at the onset of mitosis, the anaphase wave travelled unperturbed through the barrier (Figures 7E–7F and Movie S6). These observations confirm our predictions and demonstrate that the wave of anaphase is indeed a kinematic wave (phase wave), which reflects the delays set by the trigger chemical wave that synchronizes the S-phase.

Discussion

Cell cycle synchronization through chemical waves of Cdk1 activity

The large size of embryos poses a major challenge for biological processes that need to be rapidly coordinated across the entire cell. While diffusion takes too long to transfer information across large embryos, chemical waves provide a physical mechanism that is poised to be much more rapid. Here, we have focused on how such waves synchronize the four cell cycles prior to the maternal-to-zygotic transition of the syncytial Drosophila embryo. Using surgical ligations, we have confirmed classical observations that physical uncoupling of two regions of the embryo can introduce a delay of several minutes in the time when embryos reach the maternal-to-zygotic transition at cell cycle 14 (Edgar et al., 1986). During cell cycle 14, Drosophila embryos first undergo cellularization, a specialized form of cytokinesis enclosing nuclei in individual cells, and then begin gastrulation. Gastrulation requires an exquisite degree of spatiotemporal coordination of cellular dynamics. We propose that mitotic waves during the syncytial cell cycles are necessary to ensure that all the cells in the embryo enter cycle 14 at about the same time, enabling proper coordination of gastrulation.

We have shown that cell cycles 10–13 in Drosophila embryos are synchronized by waves of Cdk1 activity. These waves were first proposed as a mechanism for the synchronization of mitosis in the Xenopus egg extract system (Chang and Ferrell, 2013), but we provide the first direct evidence for such waves using a FRET-based biosensor of Cdk1 activity (Gavet and Pines, 2010). In contrast to the proposed role of the mitotic switch in Xenopus, in Drosophila embryos we found that the Cdk1 waves of cell cycles 12 and 13 propagate based on S-phase (and not M-phase) Cdk1 regulation. In fact, mitotic waves are not the result of an active mechanism, but simply a consequence of earlier differences in the timing of DNA replication. As a consequence, the speed of the Cdk1 and mitotic waves is controlled by the activity of Cdk1 during S-phase and is sensitive to the activity of the DNA replication checkpoint. We point out that, consistently with previous observations (Foe and Alberts, 1983), the slowdown of mitotic waves during Drosophila development is not accompanied by a slowdown in the duration of mitotic processes (which likely depend on the mitotic rate of activation of Cdk1). This observation was previously taken as evidence that the mechanism generating the mitotic waves could be of a mechanical nature, reflecting the decrease in inter-nuclear distance that occurs as nuclei proliferate (Idema et al., 2013). Our results have provided a different explanation for the slowdown of mitotic trigger waves, based on the reduced chemical rates of Cdk1 activation during the S-phase (Edgar et al., 1986; Farrell and O'Farrell, 2014; Price et al., 2000; Stumpff et al., 2004) which is consistent with a role for Cdk1 waves in the synchronization of the cell cycle. Furthermore, the observation that mutants, such as wee1, that specifically affect Cdk1 activity (Morgan, 2007; Price et al., 2000), alter the speed of mitotic waves in a quantitatively predictive manner argues against the existence of a mechanical signal upstream of Cdk1 activity that triggers the mitotic waves.

By visualizing and quantifying the dynamics of Cdk1 and Chk1 waves, we have unraveled the molecular and physical mechanisms of collective synchronization of the cell cycle. Cdk1 activity propagates through the large embryo as a trigger wave during S-phase, followed by a phase wave of mitotic events. Trigger waves are dependent on diffusion and feedback loops. We determined that the S-phase activity of Cdk1 and its interaction with the checkpoint effector kinase Chk1 is the primary positive feedback responsible for triggering and regulating the speed of the mitotic wave. Using a novel biosensor which responds primarily to Chk1 during the late syncytial cycles, we have shown that Chk1 activity decreases abruptly at completion of S-phase. Similar conclusions were reached by Yuan et al. who analyzed cell cycle dynamics upon cyclin knockdowns (Yuan et al., 2012). While the mechanisms triggering the decrease of Chk1 activity at completion of S-phase remain unclear, it is likely that mechanisms similar to the ones elucidated in mammalian cells might be at play (Zhang and Hunter, 2014). Once DNA replication is completed, Chk1 cannot be phosphorylated and activated by DNA damage. If the phosphatase(s) deactivating Chk1 is active at the end of S-phase, the checkpoint could be reversed very rapidly. Other mechanisms, e.g. the degradation of the DNA replication checkpoint factor Claspin and nuclear exclusion of Chk1, could also contribute significantly to the rapid reversal of the DNA replication checkpoint (Zhang and Hunter, 2014).

The Cdk1 positive feedback through direct phosphorylation of Wee1 and Cdc25 does not control the activity of Cdk1 in S-phase, but is important to ensure a stereotypically rapid activation of Cdk1 upon entry into mitosis. This is at variance with the observations in Xenopus egg extract, where the positive feedbacks involved in the mitotic switch directly control wave propagation (Chang and Ferrell, 2013). We suggest that the mechanisms of cell cycle control are plastic and allow different levels of regulation.

Quantitative analysis of chemical waves during embryonic development

Dissecting the physical properties of the Cdk1 and mitotic waves required accurate measurements of Cdk1 activity with high spatiotemporal resolution. Such precise measurements gave us the possibility to quantitatively test ideas for the initiation and the spreading of the Cdk1 waves. Our mathematical model is not meant to reproduce all features of the cell cycle dynamics: for instance, it does include different Cyclin-Cdk1 complexes, which are likely to have different affinities for S-phase and M-phase targets (Loog and Morgan, 2005), and the downregulation of Chk1 by Cdk1 is likely to be a multi-layered process (Zhang and Hunter, 2014). The model was introduced to illustrate the minimal features that can account for the stringent constraints imposed by the rapid synchronization of cell cycles during Drosophila embryonic development, and can generate predictions to be tested experimentally. We propose that this interplay between precise dynamical measurements of pathways’ activity and modeling is a useful method to reveal important principles of spatiotemporal coordination of embryonic development.

Chemical waves have been described in a variety of biological systems and can be classified as trigger and phase waves (Winfree, 2001). While phase waves originate from kinematic mechanisms and just reflects pre-existing gradients in the underlying timing of events, trigger waves are generated by active mechanisms and require the propagation of physical information. The coupling of bistability and diffusion represents the classical mechanism for the generation of trigger waves and in fact such waves are observed in both biological and physical systems (e.g. supercooled liquids) (Tyson and Keener, 1988; van Saarloos, 1998). The initiation and spreading of Cdk1 waves can be described as follows. Cdk1 dynamics is governed by a bistable potential, which evolves over time in such way that the energy barrier between the low and high state of Cdk1 activity decreases (see Figure S5). When the barrier becomes similar to the noise levels in the regulation of Cdk1, a fluctuation triggers the transition from the low to the high state of Cdk1 activity in a region and the perturbation propagates across the embryo. This observation implies that the transition point (and therefore the speed of the propagating wave) is influenced by noise. Figure 6F shows that the “energy barrier” (or to the changes in concentration) that must be overcome for the activation of Cdk1 increases as a function of Chk1 activity, which provides an intuition for the slowdown of Cdk1 waves during development.

Bistability is a property of many signaling pathways, including several ones that undergo cell-to-cell communication through diffusion. Since the coupling of diffusion and bistability can generate chemical waves, it is likely that such waves generally emerge as an important feature for the coordination of cellular processes across large spatial scales. Our analysis demonstrates that biphasic regulation of Cdk1 activity uncouples the speed of Cdk1 waves from the regulation of mitotic Cdk1 activation. In principle, such uncoupling could allow biological systems to achieve an independent control of the speed of chemical waves and the rapidity of execution of cellular transitions. Whether this signaling feature is used for synchronization of cellular processes in large tissue remains to be established.

Experimental Procedures

Plasmids

Plasmids were constructed using either standard ligation or Gibson assembly (NEB). The Cdk1-FRET sensor, the Chk1 sensor (human Cdc25C aa 183-251, fused to EGFP) and the Chk1-TagRFP-T construct were all cloned in plasmid pBabr containing the maternal Tubulin promoter and the spaghetti squash 3’ UTR (gift of Yu-Chiun Wang and Eric Wieschaus, Princeton University). The PCNA-TagRFP-T plasmid was generated by substituting the EGFP sequence with Tag-RFP-T sequence from a PCNA-EGFP plasmid (gift of Shelby Blythe and Eric Wieschaus, Princeton University). The twine^3A construct was generated starting from a rescue construct (Alphey et al., 1992) for twine (isolated from a Pacman BAC plasmid (CH322-159O07) by BamHI digestion) cloned in pBabr. A twine fragment in which the 3 putative Cdk1 sites (SP/TP) were mutated (AP) was synthesized (IDT) and cloned into the twine rescue construct. To generate the wee1^9A construct, we first generated a plasmid containing just the twine promoter and the twine 3’UTR from the twine rescue construct. The wee1^9A sequence (Di Talia and Wieschaus, 2012) was then inserted. Transgenic flies were generated by site directed integration of plasmids on various sites on the 2^nd and 3^rd chromosomes (attp40, VK1, attP2, VK5, VK33).

Stocks

Stocks were generated using standard methods. A list of stock used in this study is available in the Supplemental Experimental Procedures. To generate embryos with different DNA content we used homo compound chromosomes: C(2)EN and C(3)EN, in which both copies of chromosome 2 and 3 are fused together respectively. Analysis of cell cycle timing reveals two classes of embryos: embryos with shorter cell cycles than wild type (1 copy of chromosome 2 or 3) and embryos with longer cell cycle (3 copies of chromosome 2 or 3). To confirm that the cell cycle timing in fact correlates with chromosome copy number, we performed high resolution imaging of His2Av-mRFP, which allows the visualization of the longer C(2)EN and C(3)EN chromosomes (Martins et al., 2013). The results were confirmed by analyzing embryos from crosses with a C(2)EN stock (BDSC #2974), which only gives embryos with one copy of chromosome 2 (Martins et al., 2013).

Microscopy

Imaging experiments were performed with an upright Leica SP8 confocal microscope, a 20X/0.75 numerical aperture oil-immersion objective, an argon ion laser, and a 561-nm diode laser. For embryos expressing His2Av-RFP and Cdk1-FRET we acquired images (800x300 pixels) with a frame rate of 1/2.89s. For embryos expressing the Chk1 sensor, as well as embryos expressing the tagged Chk1 proteins, images were acquired with a frame rate of about 1/2s. For embryo expressing His2Av-GFP and PCNA-TagRFP-T, images were collected with a frame rate of about 1/0.7s.

FRAP experiments

The diffusion constants of Cdk1 and Chk1 were estimated by performing Fluorescence Recovery After Photobleaching (FRAP) experiments. Circular areas of 15 μm radius were bleached and the recovery of the fluorescence signal was acquired with a resolution of about 100 ms. Diffusion coefficients were estimated using an approach previously described (Brown et al., 1999).

Validation and characterization of Cdk1 FRET sensor

To validate the Cdk1 FRET sensor and to establish which cyclin-Cdk1 complexes phosphorylate the sensor in living Drosophila embryos, we performed single and pairwise knockdown of cyclins using double-strand RNA (dsRNA) injections. Knockdown of all three mitotic cyclins (CycA, CycB and CycB3) results in a low and constant FRET ratio, indicating that the oscillation in the emission ratio of the sensor is in fact due to changes in Cdk1 activity (Figure S1B). Furthermore, knockdown of Cyclin B or of any pair of cyclins still showed oscillations in the emission ratio of the sensor, supporting the idea that the sensor responds to all mitotic cyclins-Cdk1 complexes (Figures S1B-S1C). The efficiency of the knockdowns was determined by the observed cell cycle lengthening which is consistent with previous reports (McCleland et al., 2009).

Data and image analysis

Cdk1 FRET curves were computed by taking the fluorescence intensity ratio of YFP signal over CFP signal averaged over the entire embryo or over vertical slices of a width of 22.4 μm. S-phase Cdk1 activation rates were computed by fitting a straight line through the first 2–3 minutes of Cdk1 activity increase. M-phase Cdk1 activation rates were computed in a similar manner, fitting a straight line through a time interval of 2–3 minutes after Cdk1 inflection point. To estimate nuclear and cytoplasmic Cdk1 activities, nuclei were segmented with custom-made MATLAB software. Cytoplasmic activity was calculated by inverting nuclear masks. Completion of S-phase was interpreted to be the time at which PCNA foci disappeared. This time was estimated from changes in the coefficient of variation of PCNA-TagRFP intensity signal in each nucleus (Figure S2). The cytoplasmic to nuclear ratio of the Chk1 sensor was estimated by measuring nuclear signals from segmenting nuclei and cytoplasmic signals from rings 2 pixels-wide at 2 pixels-distance from the nuclear border (generated through dilation of the nuclear masks).

Computational method to calculate Cdk1 and mitotic wave speeds

To measure the speed of Cdk1 and mitotic waves, we developed a computational method that extracts the speed based on delays in Cdk1 activity or mitotic events at different regions of the embryo. In the Supplemental Information we demonstrate that the Cdk1 and mitotic waves are well approximated by one dimensional waves spreading along the anterior-posterior (AP) axis. Therefore, we start by dividing the embryo in 20 regions across that axis (Figure S1D). We then estimate the activity of Cdk1 and the geometrical properties (aspect ratio) of nuclei for each region separately (Figure 1 and Figure S1E-F). To estimate the delays of each region relative to the region where the Cdk1 wave originated, we computed correlation coefficients comparing the dynamics of Cdk1 or of the morphological changes of nuclei in a given region to the ones in the region where the wave originated (Figure S1G). The time-dependence of this correlation was examined by temporally shifting the data sets relative to each other. The delay was estimated as the time shift that gave the maximum correlation of the two dynamics (Figure S1G). Using a linear fit of the delay as a function of the distance from the wave center (Figure 1G), we extracted the speed as the inverse slope of such fit.

Embryo manipulations

Embryos were collected on apple juice agar plates after 0–2 hours at 25°C. Following collection, embryos were dechorionated with 50% bleach for 1 minute and rinsed with water. For injections, embryos were aligned on agar plates using a metal probe and transferred to cover slips lined with double-sided tape, desiccated for 7–9 minutes and then covered with 700 Halocarbon oil (Sigma Aldrich). Double-stranded RNA was injected at a concentration of 0.5 mg/ml. For permanent embryo ligations, a dull razor blade was lowered onto desiccated embryos aligned on double-sided tape with a micromanipulation apparatus previously described (Sander, 1971). After 10 minutes, the blade was removed and the slide was transferred to the microscope for imaging. For ligations performed during imaging, we used a modified micromanipulation apparatus, which allowed us to raise a dull razor blade onto accurately staged embryos glued to a glass slide.

Production of dsRNA

Double-stranded RNA (dsRNA) was synthesized by in vitro transcription of a DNA template containing the T7 promoter sequence on both ends. Amplicons for each cyclin from the Drosophila RNAi Screening Center (DRSC) (Cyclin A: DRSC 11123, Cyclin B: DRSC 04605, Cyclin B3: DRSC 16618) were PCR-amplified using Herculase II Fusion DNA polymerase. Amplified DNA templates were in vitro transcribed (Ambion Megascript Kit) and diluted to a final concentration of 1mg/ml.

Mathematical model

We developed a mathematical model of the network shown in Figure 6A. As in (Chang and Ferrell, 2013), the feedback between Cdk1 and Cdc25 is described by an activating sigmoidal function, while the feedback between Cdk1 and Wee1 is described by an inhibiting one. To capture the dynamics of Cdk1 at cycles 10–13, we include a second equation that describes the activity of Chk1 and its regulation of Cdk1 activity through modulation of the activities of Cdc25 (inhibition) and Wee1 (activation). We also use another Hill function in the dynamics of Chk1 to model its rapid inactivation triggered by Cdk1 activity. The dynamics of the different cell cycles is obtained simply by setting the initial activity of Chk1 at different values (no other parameter of the model is changed).

We also include diffusion and noise in our model. All the specified assumptions yield the following partial-differential stochastic equations (see Supplemental Information for further details and Table S1 for the values of all the parameters that appear in the model):

$$\begin{array}{lll}\frac{\partial f}{\partial t}\hfill & =\hfill & D_{\mathit{Chk}1}\frac{{\partial }^{2}f}{\partial x^2}-\frac{a^{\sigma }}{K_{\mathit{Chk}1}^{\sigma }+a^{\sigma }}{r}_{0}f+{\xi }_f(x,t)\hfill \\ \frac{\partial a}{\partial t}\hfill & =\hfill & D_{\mathit{Cdk}1}\frac{{\partial }^{2}a}{\partial x^2}+\alpha +r_{+}(a,f)(c(x,t)-a)-r_{-}(a,f)a+{\xi }_c(x,t)+{\xi }_r(x,t)\hfill \\ \frac{\partial c}{\partial t}\hfill & =\hfill & D_{\mathit{Cdk}1}\frac{{\partial }^{2}c}{\partial x^2}+\alpha +{\xi }_c(x,t)\hfill \end{array}$$ (1)

Here, the field a(x,t) denotes the amount of active Cdk1, the field f(x,t) describes the activity of Chk1 and the field c(x,t) describe the total amount of cyclin-Cdk complex. Our model can be taken one-dimensional (waves propagation along the anterior-posterior axis) for reasons discussed in the Supplemental Information, so the space variable x has a single component. As mentioned above, the inhibition of Cdk1 activity by Cdc25 and its activation by Wee1 are effectively taken into account via two Hills functions.

$$\begin{array}{lll}{r}_{+}(a,f)\hfill & =\hfill & \left(c_0+c_1\frac{a^{\nu }}{K_{\mathit{Cdc}25}^{\nu }+a^{\nu }}\right)(f_{\mathit{max}}-f)\hfill \\ r_{-}(a,f)\hfill & =\hfill & \left(w_0+w_1\frac{K_{\mathit{Wee}1}^{\mu }}{K_{\mathit{Wee}1}^{\mu }+a^{\mu }}\right)f\hfill \end{array}$$

The two expressions above are similar to those in (Chang and Ferrell, 2013), except for the dependence on f, which is crucial for capturing the cell cycle remodeling of Cdk1 activity during development. The Cdc25 function includes a term (f_max-f) that decreases with Chk1 activity (inhibition of Cdc25 by Chk1), while the Wee1 function includes a term proportional to f (activation of Wee1 by Chk1).

Numerical simulations of the mathematical model

The partial differential equations of the model (see Supplemental Information for details) were simulated using the xmds2 package (Collecutt and Drummond, 2001) (www.xmds.org).

Research Highlights.

• Mitotic waves are controlled by S-phase waves of Cdk1 activity in Drosophila embryos

• A double negative feedback between Cdk1 and Chk1 controls the Cdk1 waves

• A mathematical model can capture the physical properties of the waves

• S-phase waves are trigger waves, while mitotic waves are a purely kinematic process