Abstract.
Active shape models (ASMs) have been widely used for extracting human anatomies in medical images given their capability for shape regularization of topology preservation. However, sensitivity to model initialization and local correspondence search often undermines their performances, especially around highly variable contexts in computed-tomography (CT) and magnetic resonance (MR) images. In this study, we propose an augmented ASM (AASM) by integrating the multiatlas label fusion (MALF) and level set (LS) techniques into the traditional ASM framework. Using AASM, landmark updates are optimized globally via a region-based LS evolution applied on the probability map generated from MALF. This augmentation effectively extends the searching range of correspondent landmarks while reducing sensitivity to the image contexts and improves the segmentation robustness. We propose the AASM framework as a two-dimensional segmentation technique targeting structures with one axis of regularity. We apply AASM approach to abdomen CT and spinal cord (SC) MR segmentation challenges. On 20 CT scans, the AASM segmentation of the whole abdominal wall enables the subcutaneous/visceral fat measurement, with high correlation to the measurement derived from manual segmentation. On 28 3T MR scans, AASM yields better performances than other state-of-the-art approaches in segmenting white/gray matter in SC.
Keywords: abdomen, active shape model, multiatlas label fusion, level set, spinal cord
1. Introduction
Segmentation of human anatomical structures is challenging in medical images due to their physiological and pathological variations in shape and appearance, the complicated surrounding context, and the image artifacts. Active shape models (ASM1), also known as statistical shape models,2 provide a reasonable approach to characterize the variations in human anatomy, and thus have been widely used in the medical image community.3–5 Given training datasets and their representation of the shape (usually landmarks), statistical models can be established for the structure of interest to characterize (1) the modes of its shape variations and (2) the local appearances around its shape boundary to drive the segmentation on other images.
However, as a model-based approach, ASM may present catastrophic segmentation failures if configured inappropriately. Since the shape updates of ASM focus only on local context, ASM segmentation can be sensitive to the model initialization and/or fall into local minimum when given a large search range for the updates and thus undermines its performance. This problem can get worse in a common segmentation procedure of clinical acquired medical scans, e.g., computed-tomography (CT) and magnetic resonance (MR) images given their highly variable contexts. We posit that integrating traditional ASM with global optimization can improve its robustness to those challenging problems.
There have been efforts to combine ASM with level set (LS) techniques, where shapes are implicitly represented by signed distance function (SDF), and the statistical models build on SDF using principle component analysis (PCA) are used to regularize the LS evolution.6–8 Region-based LS builds its speed function on global information, where the Chan–Vese (CV) algorithm9 is most commonly used to evolve the SDF by minimizing the variance both inside and outside the zero LS. Tsai et al.7 augmented the CV algorithm with two additional terms in the speed function that penalized the deviance from pretrained shape model to segment the left ventricle and prostate on MR. Despite its success in shape constraint, this approach was not built for accurate structural segmentation since no local appearance searching from traditional ASM was deployed to capture the boundaries of structures. In addition, it is difficult to design an LS speed function to handle more variable contexts, e.g., secondary structures located within and around the structure of interest.
The multiatlas label fusion (MALF) technique10,11 recently has become popular for its robustness. Given the capabilities of the state-of-the-art registration tools to roughly match two images regardless of the underlying contextual complexity, MALF leverages canonical atlases (training images associated with labeled masks) for target segmentation by image registration, and statistical label fusion. MALF, by design, provides not only the hard (categorical) segmentation, but also soft (probabilistic) estimation. Xu et al.12 integrated MALF with shape constraints to improve spleen segmentation on CT by probabilistic combination; however, it was sensitive to the alignment between the MALF estimate and the shape model.
Here, we propose a two-dimensional (2-D) augmented ASM (AASM) by integrating MALF and LS into the traditional ASM framework. Three-dimensional (3-D) consistency is achieved by post hoc regularization. Briefly using the AASM approach, the landmark updates are optimized globally via a region-based LS evolution applied on the probability map generated from MALF. This augmentation effectively extends the searching range of correspondent landmarks while reducing sensitivity to the image contexts, and thus improves the robustness of the segmentation. In the following sections, we present our proposed algorithm and validate its efficacy on a toy example and two different clinical datasets. This work is an extension of a previous SPIE conference paper.13
2. Theory
2.1. Problem Definition
Consider a collection of training datasets (also called atlases in the context of MALF) including the raw images and their associated labels , where is the number of voxels in each image, and represents the label for the background and the structure of interest, respectively (only considering binary cases for simplicity). Based on each training label, the shape of the structure is characterized by a set of landmarks. The landmark coordinates are collected in a shape vector for each training dataset as . Correspondences of these landmarks across all training datasets are required. For a target image , the goal is to provide a set of landmarks that represents the shape of the estimated segmentation .
2.2. Active Shape Model and Shape Regularization
The mean , covariance of the shape vectors of the training datasets are computed, where
| (1) |
Using PCA, the eigenvectors with its associated eigenvalues are collected. Typically, eigenvectors correspondent to the largest eigenvalues were retained to keep a proportion of the total variance such that , where . Within this eigensystem, any set of landmarks can be approximated (often called shape projection) by
| (2) |
where is a -dimensional vector given by
| (3) |
where can be considered as shape model parameters and its values are usually constrained within the range of when fitting the model to a set of landmarks so that the fitted shape is regularized by the model.
2.3. Local Appearance Model and Active Shape Search
The intensity profiles along the normal directions of each landmark are collected to build a local appearance model to suggest the locations of landmark updates when fitting the model to an image structure. For each landmark in the -th training image, a profile of pixels is sampled with samples on each side of the landmark. Following Ref. 14, the profile is collected as the first derivative of the intensity and normalized by the sum of absolute values along the profile, indicated as . Assuming multivariate Gaussian distribution of the profiles among all training data, a statistical model is built for each landmark
| (4) |
where and represent the mean and covariance, respectively. This is also called the Mahalanobis distance that measures the fitness of a newly sampled profile to the model. Given a search range of pixels () on each side of the landmark along the normal direction, the best match is considered with the minimum value among possible positions.
2.4. Multiatlas Label Fusion and Probability Map Generation
A pair-wise image registration is performed between each atlas and the target image to generate a transformation that maximizes a similarity metric SM between the two images
| (5) |
This transformation is propagated on both the atlas image and label, where
| (6) |
A label fusion procedure LF is then used on the registered atlases to generate a label-wise probabilistic estimation on the target
| (7) |
where the registered labels are combined on a voxel (or pixel) basis and typically weighted by the similarities between the registered images and the target image. The probability map of the structure of interest can then be derived by normalizing
| (8) |
where and represent the background and foreground probability, respectively. We note that we leave some abstract notions (e.g., , SM, and LF) in the description of MALF above given its sophisticated process and the large number of variants in implementation.
2.5. Level Set Evolution with Chan–Vese Algorithm
In the LS context, the evolving surface is represented as the zero LS of a higher dimensional function and propagates implicitly through its temporal evolution (speed function) with a time step . is defined as SDF, i.e., SDF with negative/positive distance values inside/outside with regard to the evolving surface, respectively. The CV algorithm evolves the SDF by minimizing the variances of the underlying image both inside and outside the evolving surface. Given in {} and in {}, the temporal evolution of CV can be written as
| (9) |
where is the Dirac delta function, represents the curvature of SDF, and are considered as the evolution coefficient and smoothness factor, respectively.
2.6. Augmented Active Shape Search
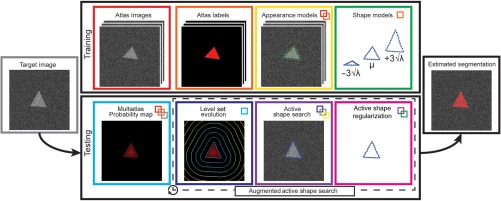
Given (1) trained ASM, (2) trained local appearance model, and (3) probability map generated from MALF, an augmented active shape search procedure is performed in each iteration of the shape updates (Fig. 1).
Fig. 1.
Flowchart of the proposed AASM approach. Shape models and local appearance models are constructed based on the atlas images and labels during the training stage. When testing on a target image to yield an estimated segmentation, an iterative process is performed. During each iteration, region-based LS is used to evolve on the probabilistic map generated by MALF to augment the traditional active shape search by global optimization, followed by the active shape regularization on the segmentation. Note that the borders of blocks are colored in distinctive colors. The small colored boxes within a block represent its prerequisite blocks in corresponding colors. For example, multiatlas probability map requires (1) atlas images, (2) atlas labels, and (3) target image.
Let () be the current landmark position and be the current zero LS. First, LS evolution using Eq. (9) is performed by assigning for iterations and the zero LS moves to . Then, the zero-crossing point along the normal direction of () on is collected as () and considered as the landmark position after LS evolution. Along (), the gradient intensity profiles are sampled, then the active shape search suggests an updated position at () with its correspondent profile . The newly searched positions for all landmarks are then projected to the model space by Eq. (3). After constraining each model parameter, where , the landmark positions are then regularized by Eq. (2) and used as the initialization of LS evolution for the next iteration. Note that is a small number since the LS evolution here is used to suggest a globally optimal landmark movement as opposed to provide the final segmentation.
2.7. Optional Variants
The baseline pipeline can be optionally modified as follows to tailor for specific applications.
A multilevel scheme can be applied to the local appearance model, the LS evolution, and the active shape search. Typical downsample ratio is for the -th level; the landmark updates performed on this level are with a multiplication of in the original image size, which effectively enlarges the search range.
An optional mask can be used so that the evolution will only be affected by the masked region of interest (ROI), where the computation of the averages are modified as in { and } and .
The landmark positions can be normalized by a transformation before deriving landmark positions from the evolved LS
| (10) |
where () and () represent the centroid and the range along each dimension of the region within the zero LS, () and () represent the correspondent measurements for the current landmarks. With normalization, the landmark derivation from LS can be more robust to large shape updates.
Nonzero LS can also be considered as the surface to collect the updated landmarks after LS evolution to adjust the desirable intermediate segmentation in terms of .
3. Methods and Results
3.1. Toy Example
We defined a simulated observation consisting of three triangles in small, medium, and large sizes on a image. We used the medium-sized triangle as the target of interest sandwiched by the other two triangles to increase its segmentation difficulty [see Fig. 2(a)]. An equilateral triangle centered in the image was created as a shape template, where the radius of its circumscribed circle was 20 voxels. A 2-D affine transformation model with a rotational (), two translational (), and two scaling components () was constructed as
| (11) |
All components were drawn from Gaussian distributions to generate randomized observations. Specifically, deg, voxels, voxels, , and . , the base scale, was assigned as 1, 2, and 3 for the small, medium, and large triangles, respectively. The voxel-wise intensities over the small and large triangles were drawn from while those over the background and the medium triangle were from . The datasets of our toy example include 100 randomly generated observations.
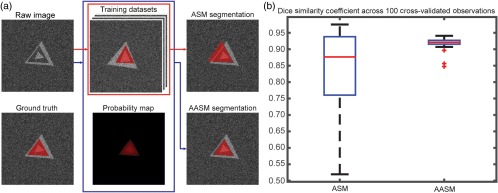
Fig. 2.
Results of a toy example. (a) Qualitative comparison between ASM and AASM segmentation on an individual observation. (b) Quantitative comparison between ASM and AASM segmentation in DSC across 100 cross-validated observations.
A leave-one-out cross-validation scheme was used to validate the segmentation results of ASM and AASM. For each target observation, 99 other observations were used as training datasets. For each training data, 33 landmarks were evenly sampled on each side of the triangle (99 in total around the triangle). The ASM was trained with 98% of the total variances while the local appearance model was trained at two levels with an intensity gradient profile of three pixels collected along each side the normal directions of each landmark (seven pixels in total) at each level. During testing, both ASM and AASM were initialized by the mean model shape at the center of the image. In each iteration of the landmark update, the local search range was six pixels along each side of the normal direction. The shape updates were regularized within standard derivations of the eigenvalues over 100 iterations at two levels. For enabling AASM, a probability map was simulated by smoothing the ground truth by applying a Gaussian kernel with a standard deviation of five voxels. Five iterations of LS evolution were performed based on the simulated probability map with the time step, evolution coefficient, and smoothness factor set as 0.01, 100,000, and 0.00001, respectively, during each iteration of landmark update. The landmark positions were normalized based on the region within zero LS before determining the landmark movement based on the LS evolution.
Given the global optimization from the probability map, AASM was able to capture the correct boundary of the target shape, i.e., the medium triangle. Outlier segmentations in ASM were corrected in AASM based the Dice similarity coefficient (DSC) performances across 100 observations.
3.2. Abdominal Wall
3.2.1. Data
Under institutional review board (IRB) supervision, abdominal CT data on 250 cancer patients were acquired clinically in anonymous form. These patients represent part of an overall effort to evaluate abdominal wall hernia disease in the cancer resection population. About 40 patients were randomly selected, where we used 20 as training datasets and the other 20 for testing purposes. The field of views (FOV) of the selected 40 scans range from to , with various resolutions ( to ). Various numbers (78 to 236) of axial slices with same in-plane dimension () were found.
All 40 scans were labeled using the medical image-processing and visualization (MIPAV15) software by an experienced undergraduate based on our previously published labeling protocol.16 Following Ref. 17, essential biomarkers, i.e., xiphoid process (XP), pubic symphysis (PS), and umbilicus (UB), were identified, and the abdominal walls were delineated on axial slices spaced every 5 cm with some amendments (contour closure required here). About 177 and 184 axial slices were obtained with the whole abdominal wall labeled for the training and testing datasets, respectively. Here, we characterize the whole abdominal wall structure as enclosed by the outer and inner surface, bounded by XP and PS.17 This definition covers thoracic, abdominal, and pelvic regions, and includes not only the musculature, but also the kidneys, aorta, inferior vena cava, lungs, and some related bony structures to make the inner and outer boundaries anatomically reasonable.
3.2.2. Implementation
Here, we employed AASM to segment the whole abdominal wall on 184 testing slices.
Preprocessing
Given the large variations of appearance in the abdominal wall and its surrounding anatomical structures along the cranial–caudal direction, the proposed slice-wise segmentation was trained and tested on five exclusive classes given the position of the axial slices with respect to XP, PS, and UB. These three biomarkers were acquired from manual labeling for the training sets while estimated using random forest for the testing sets. We used 10 random scans from the training data to characterize the centroid coordinates of the biomarkers with long-range feature boxes following Ref. 18 and yielded the estimated biomarkers positions on the testing data with a mean distance error of 14.43 mm. Four bounding positions were empirically defined among the vertical position of the three biomarkers to evenly distribute the available training data (25, 35, 50, 31, 36 slices for each class, ordered from bottom to top). Given a target testing volume, each axial slice between the estimated positions of XP and PS was extracted and assigned a class based on the estimated bounding positions. In this experiment, we only tested on the 184 slices with manual labels.
All slices (training and testing) were centered in the image after body extraction and background removal to reduce variations. A body mask can be obtained by separating the background with -means clustering, and then filling holes in the largest remaining connected component. A margin of 50 pixels was padded to each side of the slices in case the body was in contact with the original slice boundary, which made the slice size .
Training
On each training slice, landmarks were collected along the outer and inner wall contours using marching squares.19 The horizontal and vertical middle lines of the slice were used to divide each closed contour into four consistent segments across all slices assuming all patients were facing toward the same direction in the scan. About 53 correspondent landmarks were then acquired on each of the segments via linear interpolation (212 for each of outer and inner wall). Each set of the landmarks was first centered to the origin and then sets of landmarks from the same class were used to construct one ASM covering 98% of the total variances. The local appearance model was trained at three levels; at each level, an intensity gradient profile of five pixels was collected along each side the normal directions of each landmark (11 pixels in total).
Testing
For each testing slice, all training slices from the same class were considered as atlases and nonrigidly registered to it using NiftyReg.20 The registered atlases were combined by joint label fusion21 to yield a probabilistic estimation of the abdominal wall. Default parameters were used for both. Within each iteration of landmark update, a region-based LS evolution with five iterations using CV algorithm was used to drive the landmark movement based on the global probabilistic estimation. The time step, evolution coefficient, and smoothness factor were set to 0.01, 100,000, and 0.1, respectively. The local search range for the landmark update was eight pixels along each side of the normal direction. The shape updates were regularized within ±3 standard derivations of the eigenvalues. We allowed 100 iterations for three levels of shape updates.
Customized configuration
In this study, a two-phase scheme was used to improve the robustness of whole abdominal wall segmentation. The proposed approach was first applied to only the outer wall. Initialized by the position of the outer-wall segmentation, our approach was then applied to the combination of the outer and inner wall, while the outer-wall landmark positions were fixed during the second-phase shape updates. ASM and local appearance model were thus trained on (1) outer wall and (2) outer and inner wall. The LS evolution for the second-phase only considered the region within the outer-wall segmentation obtained in the first phase.
Fat measurement
Following Ref. 22, the fat tissue was obtained by using a two-stage fuzzy c-means (FCM). For each slice, the subcutaneous fat was considered as outside the outer surface of the abdominal wall, while the visceral fat as inside the inner surface.
3.2.3. Results
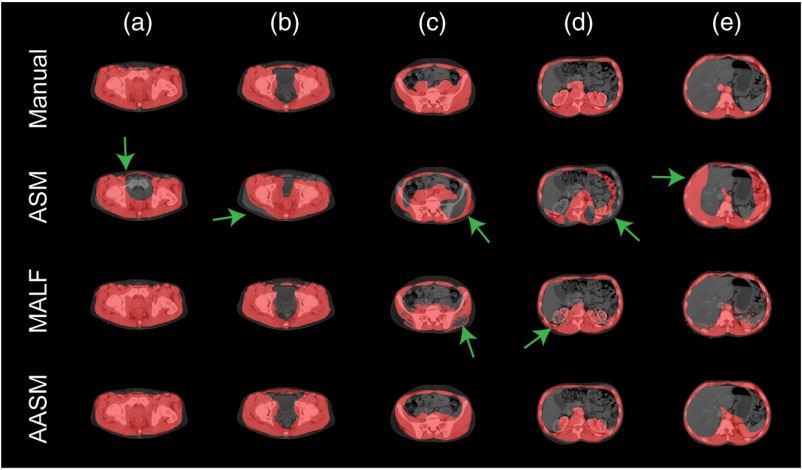
The segmentation results were validated against the manual labels on 184 testing slices using DSC, mean surface distance (MSD), and Hausdorff distance (HD) with comparison to results using ASM and MALF individually. Approximately, a slice-wise registration took around 50 s. On average, an MALF process took around 30 min for the registrations and 2 min for label fusion. On top of MALF, the iterative ASM-LS optimization took around 1 min. Qualitatively, ASM was sensitive to initialization and could be trapped into local minimum. MALF captured the majority of the abdominal muscles well; however, it had speckles and holes in the segmentations or leaked into the abdominal cavity, where structures with similar intensities to muscles were present. AASM presented the most robust result, except that the posterior inner wall surface was sometimes overly smoothed due to the shape regularization (Fig. 3). Quantitatively, large decreases in HD were observed when using AASM without undermining the DSC performance (Table 1). More importantly, the nature of ASM kept the topology of the abdominal wall and enabled the compartmental fat measurement; MALF failed to do so even though it presented the best DSC performance. The absolute differences in subcutaneous and visceral measure using our augmented ASM against the measurement using manual labels were largely reduced comparing to traditional ASM (Table 2). In terms of the Pearson’s correlation coefficient and R-squared value between the estimated and manual measurement of subcutaneous fat, visceral fat, and the ratio of visceral to subcutaneous fat, AASM demonstrated consistent superiority over ASM (Table 2).
Fig. 3.
Qualitative comparison of ASM, MALF, and AASM segmentation of abdominal wall. (a)–(e) Slices in five exclusive classes on one subject. The green arrows indicate segmentation outliers including speckles, holes, oversegmentation, and label leaking problems.
Table 1.
Abdominal wall segmentation metrics.
| Method | DSC | MSD (mm) | HD (mm) |
|---|---|---|---|
| ASM | |||
| MALF | |||
| AASM |
Table 2.
Abdominal fat measurement errors.
| Method | () | () | ||||||
|---|---|---|---|---|---|---|---|---|
| ASM | 0.92 | 0.80 | 0.69 | 0.85 | 0.64 | 0.47 | ||
| AASM | 0.94 | 0.96 | 0.87 | 0.88 | 0.93 | 0.76 |
Note that indicates the absolute difference between the area derived from the manual label and the estimated segmentation, represents the Pearson’s correlation coefficient, and is the R-square value of a linear regression. The subscripts , and represent subcutaneous fat, visceral fat, and the ratio of visceral fat to subcutaneous fat, respectively.
3.3. Spinal Cord
3.3.1. Data
With IRB approval, two batches of MR volumes of cervical spinal cord (SC) were acquired as training and testing datasets. The training datasets consisted of 67 scans of healthy controls, each approximately covering an FOV of with 30 axial slices at a nominal resolution of . The testing datasets included 28 scans, each approximately covering an FOV of with 10 to 14 axial slices at a nominal resolution of , reconstructed to an in-plane resolution of . Both datasets were acquired axially on a 3T Philips Achieva scanner (Philips Medical Systems, Best, The Netherlands), where T2*-weighted volumes were obtained using a high-resolution multiecho gradient echo (mFFE) sequence to provide good contrast between the white matter (WM) and gray matter (GM).23 All scans generally covered the region from the second to fifth cervical vertebrae, and the center of the image volume was aligned to the space between the third and fourth cervical vertebrae. The in-plane dimensions for axial slices ranged from to . About 17 of the 28 testing subjects were diagnosed with multiple sclerosis (MS). Local and diffuse inflammatory lesions were presented for MS patients throughout the cervical cord WM with similar appearance to GM in mFFE images.24
The “gold standard” manual labels were constructed on both datasets. For each slice, two labels, i.e., WM and GM., were considered: The labeling process was performed using MIPAV15 by an experienced rater on a collection of 1538 slices with reasonable contrast (not all slices due to image artifacts) in the training datasets, while using FSLView25 by another experienced rater on all 364 slices in the testing datasets; both raters were familiar with MR images of the cervical SC.
3.3.2. Implementation
Here, we integrated AASM into the slice-wise SC segmentation framework in Ref. 26 with some essential modification.
Preprocessing
A common ROI with the size of was created using the 1538 coregistered training slices given the extent of the manual SC labels. All testing slices were transferred into this space before the segmentation.
A volume-wise initialization was first performed using 2-D convolution. Consider the average image of the testing volume along the cranial–caudal axis as , the average image of all cropped training image slices as , and a matrix with all entry values as 1/25; the highest response point of was identified as the approximate centroid of SC for the testing volume, and considered as the starting point for the following slice-wise registration.
The slice-wise registration followed Ref. 26. Briefly, an active appearance model was created using the cropped training images to capture the modes of variations of the SC appearance within the ROI. A target slice was projected to the low-dimensional model space. It was then registered using a model-specific cost function given the differences in intensities and model parameters between the current estimate and the closest cropped training images. The registration searched at five levels (coarse to fine) over the three degrees of freedom (DoF), i.e., two translational ( and along - and -axes, respectively) and one rotational component (). At each level, the registration was optimized using line search on each DoF, followed by Nelder–Mead simplex method on all DoFs.
After registration, 30 cropped training images closest to the target image in the model space were selected. These images were used as the target-specific training sets for building ASM, as well as the atlases for MALF in the following process. Note that, given our proposed surface-based approach, we converted the segmentation problem of WM and GM as to extract the surface of the whole SC and GM.
Training
Using marching squares, landmarks along the contours of manually labeled SC and GM were extracted. The correspondent landmarks of SC were acquired using the same way as the abdominal wall (212 in total). For GM, six key points along were first identified (two as the tips of the posterior horn and four as the valley points on the left, right, anterior, and posterior side), each of the six segments in between were then evenly resampled with 32 landmarks (192 in total). ASMs covering 99% of the total variances and local appearance models using intensity gradient profiles of two pixels (five pixels in total) were built for both structures.
Testing
For each target slice, an MALF process similar to that of the abdominal wall segmentation above was performed. The probability map of GM was generated by normalizing the GM label probability, while that of SC was normalized to the sum of WM and GM label probability. For both structures, 10 iterations of LS evolution were performed within masked regions (larger than zero probability) to drive the landmark updates toward the LS. The time step, evolution coefficient, and smoothness factor were set to 0.01, 10,000, and 0.0001, respectively. The active shape searching range was three pixels along each side of the normal direction. The shape updates were constrained within and standard derivations of the eigenvalues for SC and GM, respectively, over 100 iterations at a single level.
After the SC and GM were segmented, WM was derived as the region by excluding GM from SC. The WM and GM labels were then transferred back to the original target space.
3.3.3. Results
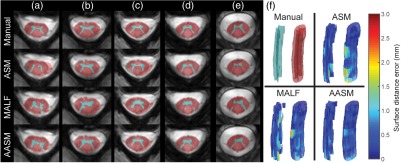
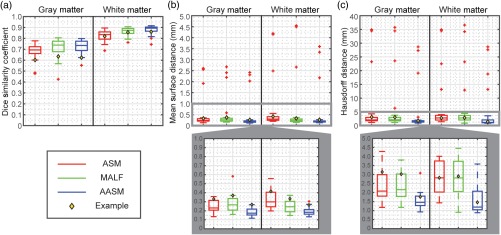
The segmentation results were validated against the manual labels on the 28 testing volumes using DSC, MSD, and HD with comparison to results using ASM and MALF individually. MALF failed to preserve the GM shape. ASM could fall into local minimums and generated outliers that did not match with the underlying structures. AASM captured the shape of WM and GM more robustly even with the presence of lesions [Figs. 4(a)–4(e)], and yielded WM and GM surfaces smoothly along the whole volume with less surface distance error [Fig. 4(f)]. Quantitatively across 28 subjects, AASM significantly ( in cases using single-tail -tests) increased the mean DSC value by 0.01, decreased the mean MSD by 0.11 mm, and decreased the mean HD by 1.43 mm compared to the best case of ASM and MALF (Fig. 5).
Fig. 4.
Qualitative comparison of ASM (1st column, red), MALF (2nd column, green), and AASM (3rd column, blue) segmentation of SC. (a)–(e) Slices at five different locations (from bottom to top) on one subject. (f) 3-D surface renderings of the segmented GM (left) and WM (right) colored in the surface distance error toward the corresponding manual segmentations.
Fig. 5.
Quantitative comparison of ASM, MALF, and AASM segmentation of SC in terms of DSC, MSD, and HD. Note that additional zoomed-in boxplots are generated for MSD and HD to compare the results in a limited range. The yellow diamond marks indicate the subject demonstrated in Fig. 4.
4. Discussion and Conclusion
In this study, we proposed an automatic framework (AASM) that coherently integrates three modern image segmentation techniques including ASM, MALF, and LS. Great synergies were found within this framework, where (1) ASM and MALF used the same training datasets to generate statistical models and probabilistic atlases, respectively, (2) LS, using the CV speed function, can be directly applied to the probability map generated from MALF, and (3) the region-based LS evolution extends the range of correspondent landmark search of ASM. Using AASM, challenging segmentation problems can benefit from the shape regularization and topology preservation of ASM, contextual robustness of MALF, and global optimization of region-based LS. On 20 abdominal CT scans, we presented the first automatic segmentation approach to extract the outer and inner surfaces of the whole abdominal wall covering thoracic, abdominal, and pelvic regions, and thus enabled subcutaneous and visceral fat measurement with high correlation to the measurement derived from manual segmentation. On 28 3T MR scans of cervical SC, we demonstrated robust WM and GM segmentation with the presence of MS lesions. It is worth to note that with minor postprocessing (3-D smoothing), our SC segmentation approach improved the start-of-the-art method26 by 25% in DSC on the same datasets.
Our proposed AASM framework was inspired from experiments on abdominal wall segmentation using ASM and MALF individually. While both presented some promising results, neither was ideal to address the challenging problem. With a strong desire to combine the unique benefits from these two methods and our previous experience,27 we introduced LS to make the surface-based (ASM) and the pixel-based (MALF) approaches compatible in one segmentation framework (AASM), and observed substantially improved performances. The integration of the three components is generic; we see huge opportunities to adapt the proposed method to other anatomical structures in 2-D medical images, whose complexity cannot be easily handled by ASM, MALF, or LS individually.
There have been other successful efforts to address the initialization and local minima issues of the standard ASM, especially with cardiac datasets. Ecabert et al.28 used a shape-constrained deformable model for full heart segmentation. The model was initialized by generalized Hough transform, rigid alignment, and a subsequent multiaffine transformation, while the shape updates were driven by energy terms combining prior shape knowledge and local image characteristics, and could be further refined with feature learning for identifying optimal feature functions for local profile search.29 Zheng et al.30 used marginal space learning and steerable features to localize four heart chambers by determining the translation, orientation, and scale sequentially of the chamber bounding boxes, and deployed learning-based boundary delineation for nonrigid shape refinement. Compared to these methods, our framework can handle more complicated tasks, e.g., whole abdominal walls containing multiple types of tissues, SCs with pathological appearances, and irregular shapes. Our MALF component provides a robust and precise localization in the form of a probability map instead of a mean shape or a bounding box to drive the ASM updates. On the other hand, our ASM local search component can be upgraded using the learning-based approaches from these methods to further improve the performances.
AASM has many parameters to configure as it combines three image segmentation techniques. While universally ideal configuration can be hardly found, robustness can be achieved for individual applications with empirical parameter settings, especially the balance between the length of local search range and the number of LS evolution. For example, the LS evolution should dominate the shape updates if the local contexts around the structure are ambiguous (see the SC application), while the active shape search is preferred if the local appearances are uniquely identifiable (see the abdominal wall application). In any case, the structural shapes are properly regularized within the proposed framework.
The proposed AASM approach uses 2-D image processing followed by 3-D regularization to take advantage of spatial similiarity of structures with long-axis regularity. The target applications, the spinal column and the abdomen, exhibit strong regularity of structure with axially oriented imaging. Other medical imaging contexts, such as imaging of the extremities, spinal column, pelvis, and thorax, may also meet these conditions. In these situations, the ASM and MALF can be trained with sample size proportional to the number of slices (rather than the number of subjects if a strictly 3-D approach was used). Extension of the AASM approach to a fully 3-D is nontrivial from both a practical perspective (e.g., runtime issues, sufficient training) and from a theoretical perspective (e.g., correspondence issues). Investigation of using MALF and LS to extend the range of ASM search within a 3-D context is a fascinating area of future work. Yet such effort lies beyond the focus of this manuscript, which is on the AASM as a practical method that provides robust segmentation for the abdomen and SC.
On both clinical datasets, the larger variations were observed over the secondary structures than the structure of interest, i.e., the abdominal wall and SC, along the cranial–caudal direction. In addition, slices at different locations presented various shapes, appearances, and contexts. Therefore, we performed slice-wise AASM segmentation by using target-specific statistical shape and appearance models to capture the desirable variations. The target-specific selection of the training datasets has a substantial impact on ASM and MALF and thus, the overall performance of AASM.
For the abdominal wall, a rough spatial division along the cranial–caudal axis was used to include enough training slices to prevent overfitting given that each subject was labeled only on axial slices spaced every 5cm. This can be improved if we have the axial slices labeled more densely (see the training data manifold in the SC datasets). Investigation in the classification system for clustering similar datasets can be beneficial for further improvement. The 2-D abdominal registrations are challenging given the complicated anatomies around the abdominal wall. Thus, we did not see a clear path to use registration to obtain the exact landmark correspondence. Manual identification would be ideal, however impractical for the time cost. We instead performed interpolation on the four segments of the derived abdominal wall contours by assuming consistent body orientations, and the appearance variations along each segment within one subject is no larger than those across subject. There are some underfitting issues especially around the posterior part of the inner wall; some feature-based landmark detection can be helpful to improve the correspondence identification.31,32
The large computation cost of MALF mainly comes from image-based registrations. Correspondence detection should be investigated for (1) less computational demanding feature-based registrations, and (2) more anatomically relevant landmark distributions. In addition, classifier-based appearance model can be performed in place of the Gaussian-based model to improve the local search. Another perspective of future work can focus on multiregion segmentation, where hierarchical ASM5 and multichannel LS33 can be integrated.
Acknowledgments
This research was supported by the National Institutes of Health (NIH) 1R03EB012461, NIH 2R01EB006136, NIH R01EB006193, ViSE/VICTR VR3029, NIH UL1 RR024975-01, NIH UL1 TR000445-06, NIH P30 CA068485, NIH 1R21NS087465-01, NIH 1R01EY023240-01A1, and NMSS RG-1501-02840. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.
Biographies
Zhoubing Xu received his BS degree in biomedical engineering from Shanghai Jiao Tong University, Shanghai, China, in 2011. Since then, he has been a PhD candidate of electrical engineering at Vanderbilt University, Nashville, Tennessee, USA, where he is a member of the Medical-Image Analysis and Statistical Interpretation Laboratory. His research concentrates on translating the state-of-the-art segmentation approaches, e.g., multiatlas segmentation, to work for the highly variable abdomen anatomy, and provide quantitative assessment for large-scale clinical trials.
Benjamin N. Conrad received his BS degree in pregraduate psychology from Middle Tennessee State University in 2012. In 2013, he joined the Vanderbilt University Institute of Imaging Science as a research assistant, where he worked on a variety of neuroimaging projects looking at the functional and structural properties of both brain and spinal cord in healthy and diseased populations, including multiple sclerosis and epilepsy. Currently, he is pursuing his PhD in cognitive and systems neuroscience from Vanderbilt University.
Rebeccah B. Baucom received her BS degree in mathematics from Texas A&M University in 2005 and attended medical school at the University of Texas Southwestern Medical Center, Dallas, Texas, USA, in 2009. She began residency training in general surgery at Vanderbilt University Medical Center in 2009 and pursued a research fellowship from 2012 to 2015. Her research focuses primarily on health services research in general surgery, primarily related to incisional hernias and colorectal surgery.
Seth A. Smith received his BS degree in physics and his BS degree in mathematics from Virginia Tech in 2001. He then completed his PhD in molecular biophysics from Johns Hopkins University. Since 2009, he has been a faculty member at the Vanderbilt University Institute of Imaging Science, where he is currently the director of the Center for Human Imaging and an associate professor. His research focuses on the development of MRI methods to assess tissue damages.
Benjamin K. Poulose received his MD degree from Johns Hopkins University School of Medicine in 1999, his MPH degree from Vanderbilt University School of Medicine in 2005, and his BS degree from the University of North Carolina, Chapel Hill, in 2014. He is an associate professor of surgery at Vanderbilt University Medical Center. He works in a busy surgical practice in an academic setting that is committed to excellence in patient care, research, and teaching. He is actively involved with the Americas Hernia Society.
Bennett A. Landman received his BS and ME degrees in electrical engineering and computer science from Massachusetts Institute of Technology in 2001 and 2002, respectively. After graduation, he worked before returning for a doctorate in biomedical engineering from Johns Hopkins University School of Medicine in 2008. Since 2010, he has been with the Faculty of the Electrical Engineering and Computer Science Department, Vanderbilt University, where he is currently an assistant professor. His research concentrates on applying image-processing technologies to leverage large-scale imaging studies.
References
- 1.Cootes T. F., et al. , “Active shape models—their training and application,” Comput. Vision Image Understanding 61(1), 38–59 (1995). 10.1006/cviu.1995.1004 [DOI] [Google Scholar]
- 2.Heimann T., Meinzer H.-P., “Statistical shape models for 3D medical image segmentation: a review,” Med. Image Anal. 13(4), 543–563 (2009). 10.1016/j.media.2009.05.004 [DOI] [PubMed] [Google Scholar]
- 3.Patenaude B., et al. , “A Bayesian model of shape and appearance for subcortical brain segmentation,” NeuroImage 56(3), 907–922 (2011). 10.1016/j.neuroimage.2011.02.046 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Heimann T., Wolf I., Meinzer H.-P., “Active shape models for a fully automated 3D segmentation of the liver—an evaluation on clinical data,” in Medical Image Computing and Computer-Assisted Intervention (MICCAI’06), pp. 41–48, Springer; (2006). [DOI] [PubMed] [Google Scholar]
- 5.Okada T., et al. , “Abdominal multi-organ segmentation from CT images using conditional shape-location and unsupervised intensity priors,” Med. Image Anal. 26(1), 1–18 (2015). 10.1016/j.media.2015.06.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Leventon M. E., Grimson W. E. L., Faugeras O., “Statistical shape influence in geodesic active contours,” Proc. IEEE Conf. on Computer Vision and Pattern Recognition, pp. 316–323 (2000). 10.1109/CVPR.2000.855835 [DOI] [Google Scholar]
- 7.Tsai A., et al. , “A shape-based approach to the segmentation of medical imagery using level sets,” IEEE Trans. Med. Imaging 22(2), 137–154 (2003). 10.1109/TMI.2002.808355 [DOI] [PubMed] [Google Scholar]
- 8.Pohl K. M., et al. , “Logarithm odds maps for shape representation,” in Medical Image Computing and Computer-Assisted Intervention (MICCAI’06), pp. 955–963, Springer; (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chan T. F., Vese L., “Active contours without edges,” IEEE Trans. Image Process. 10(2), 266–277 (2001). 10.1109/83.902291 [DOI] [PubMed] [Google Scholar]
- 10.Rohlfing T., et al. , “Evaluation of atlas selection strategies for atlas-based image segmentation with application to confocal microscopy images of bee brains,” NeuroImage 21(4), 1428–1442 (2004). 10.1016/j.neuroimage.2003.11.010 [DOI] [PubMed] [Google Scholar]
- 11.Iglesias J. E., Sabuncu M. R., “Multi-atlas segmentation of biomedical images: a survey,” Med. Image Anal. 24(1), 205–219 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Xu Z., et al. , “Shape-constrained multi-atlas segmentation of spleen in CT,” Proc. SPIE 9034, 903446 (2014). 10.1117/12.2043079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Xu Z., et al. , “Whole abdominal wall segmentation using augmented active shape models (AASM) with multi-atlas label fusion and level set,” Proc. SPIE 9784, 97840U (2016). 10.1117/12.2216841 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cootes T., Baldock E., Graham J., “An introduction to active shape models,” in Image Processing and Analysis, pp. 223–248 (2000). [Google Scholar]
- 15.McAuliffe M. J., et al. , “Medical image processing, analysis and visualization in clinical research,” in Proc. 14th IEEE Symp. on Computer-Based Medical Systems, 2001. CBMS 2001, pp. 381–386, Oxford University Press, United Kingdom: (2001). 10.1109/CBMS.2001.941749 [DOI] [Google Scholar]
- 16.Allen W. M., et al. , “Quantitative anatomical labeling of the anterior abdominal wall,” Proc. SPIE 8673, 867312 (2013). 10.1117/12.2007071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xu Z., et al. , “Quantitative CT imaging of ventral hernias: preliminary validation of an anatomical labeling protocol,” PLoS One 10(10), e0141671 (2015). 10.1371/journal.pone.0141671 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Criminisi A., et al. , “Regression forests for efficient anatomy detection and localization in computed tomography scans,” Med. Image Anal. 17(8), 1293–1303 (2013). 10.1016/j.media.2013.01.001 [DOI] [PubMed] [Google Scholar]
- 19.Maple C., “Geometric design and space planning using the marching squares and marching cube algorithms,” in Proc. 2003 Int. Conf. on Geometric Modeling and Graphics, pp. 90–95 (2003). 10.1109/GMAG.2003.1219671 [DOI] [Google Scholar]
- 20.Modat M., et al. , “Fast free-form deformation using graphics processing units,” Comput. Meth. Programs Biomed. 98(3), 278–284 (2010). 10.1016/j.cmpb.2009.09.002 [DOI] [PubMed] [Google Scholar]
- 21.Wang H., et al. , “Multi-atlas segmentation with joint label fusion,” IEEE Trans. Pattern Anal. Mach. Intell. 35(3), 611–623 (2013). 10.1109/TPAMI.2012.143 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yao J., Sussman D. L., Summers R. M., “Fully automated adipose tissue measurement on abdominal CT,” Proc. SPIE 7965, 79651Z (2011). 10.1117/12.878063 [DOI] [Google Scholar]
- 23.Wheeler-Kingshott C., et al. , “The current state-of-the-art of spinal cord imaging: applications,” NeuroImage 84, 1082–1093 (2014). 10.1016/j.neuroimage.2013.07.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lycklama G., et al. , “Spinal-cord MRI in multiple sclerosis,” Lancet Neurol. 2(9), 555–562 (2003). 10.1016/S1474-4422(03)00504-0 [DOI] [PubMed] [Google Scholar]
- 25.Smith S. M., et al. , “Advances in functional and structural MR image analysis and implementation as FSL,” NeuroImage 23, S208–S219 (2004). 10.1016/j.neuroimage.2004.07.051 [DOI] [PubMed] [Google Scholar]
- 26.Asman A. J., et al. , “Groupwise multi-atlas segmentation of the spinal cord’s internal structure,” Med. Image Anal. 18(3), 460–471 (2014). 10.1016/j.media.2014.01.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Xu Z., et al. , “Texture analysis improves level set segmentation of the anterior abdominal wall,” Med. Phys. 40(12), 121901 (2013). 10.1118/1.4828791 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ecabert O., Peters J., Weese J., “Modeling shape variability for full heart segmentation in cardiac computed-tomography images,” Proc. SPIE 6144, 61443R (2006). 10.1117/12.652105 [DOI] [Google Scholar]
- 29.Peters J., Ecabert O., Weese J., “Feature optimization via simulated search for model-based heart segmentation,” Int. Congr. Ser. 1281, 33–38 (2005). 10.1016/j.ics.2005.03.023 [DOI] [Google Scholar]
- 30.Zheng Y., et al. , “Four-chamber heart modeling and automatic segmentation for 3-D cardiac CT volumes using marginal space learning and steerable features,” IEEE Trans. Med. Imaging 27(11), 1668–1681 (2008). 10.1109/TMI.2008.2004421 [DOI] [PubMed] [Google Scholar]
- 31.Shen D., Herskovits E. H., Davatzikos C., “An adaptive-focus statistical shape model for segmentation and shape modeling of 3-D brain structures,” IEEE Trans. Med. Imaging 20(4), 257–270 (2001). 10.1109/42.921475 [DOI] [PubMed] [Google Scholar]
- 32.Rueckert D., Frangi A. F., Schnabel J. A., “Automatic construction of 3-D statistical deformation models of the brain using nonrigid registration,” IEEE Trans. Med. Imaging 22(8), 1014–1025 (2003). 10.1109/TMI.2003.815865 [DOI] [PubMed] [Google Scholar]
- 33.Brox T., Weickert J., “Level set based image segmentation with multiple regions,” in Pattern Recognition, pp. 415–423, Springer; (2004). [Google Scholar]