The Competing Mechanisms of Phosphate Monoester Dianion Hydrolysis

Abstract

Despite the numerous experimental and theoretical studies on phosphate monoester hydrolysis, significant questions remain concerning the mechanistic details of these biologically critical reactions. In the present work we construct a linear free energy relationship for phosphate monoester hydrolysis to explore the effect of modulating leaving group pK_a on the competition between solvent- and substrate-assisted pathways for the hydrolysis of these compounds. Through detailed comparative electronic-structure studies of methyl phosphate and a series of substituted aryl phosphate monoesters, we demonstrate that the preferred mechanism is dependent on the nature of the leaving group. For good leaving groups, a strong preference is observed for a more dissociative solvent-assisted pathway. However, the energy difference between the two pathways gradually reduces as the leaving group pK_a increases and creates mechanistic ambiguity for reactions involving relatively poor alkoxy leaving groups. Our calculations show that the transition-state structures vary smoothly across the range of pK_as studied and that the pathways remain discrete mechanistic alternatives. Therefore, while not impossible, a biological catalyst would have to surmount a significantly higher activation barrier to facilitate a substrate-assisted pathway than for the solvent-assisted pathway when phosphate is bonded to good leaving groups. For poor leaving groups, this intrinsic preference disappears.

Introduction

Phosphoryl transfer is one of the most broadly occurring reactions in biology, playing a central role in cellular signaling, protein synthesis, and energy production, among other life processes.^1,2 The biological hydrolysis of phosphate esters is, in turn, facilitated by a diverse group of enzymes, which utilize a variety of chemical strategies to accelerate these reactions.³⁻⁷ From a conceptual point of view, the uncatalyzed hydrolysis of a phosphate ester should be straightforward, as it only involves a nucleophilic displacement reaction to yield inorganic phosphate and the corresponding alcohol. However, these esters are among the slowest reacting biologically relevant functional groups,^8,9 making the enzymes that facilitate these reactions some of the most proficient catalysts known to date. Following from this, despite the considerable body of experimental and theoretical data accumulated over the past decades (for reviews, see, e.g., refs (5 and 7) and references cited therein), just how these reactions proceed in solution and the corresponding enzyme-catalyzed processes remain controversial, with proposals of multiple mechanisms for the same reaction^5,7 (Figure 1) and the suggestion that these transfer reactions may display considerable plasticity in their character.¹⁰

Figure 1.

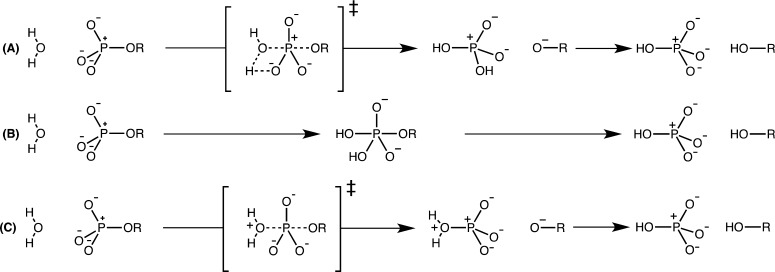
Hypothetical pathways for the hydrolysis of phosphate monoester dianions considered in this work. (A) A concerted pathway with substrate-assisted nucleophilic attack, in which the attacking water molecule is deprotonated by the substrate at some point along the reaction coordinate. (B) A stepwise pathway in which proton transfer from the nucleophile to the substrate is concerted with nucleophilic attack, leading to a pentacoordinate intermediate that breaks down with concerted proton transfer to the leaving group. (C) A concerted pathway with solvent-assisted nucleophilic attack, in which there is no proton transfer from the nucleophile in the rate-limiting step. This figure was adapted from ref (23).

For example, in the case of phosphate monoester dianions with good leaving groups, experimental evaluation of kinetic isotope effects (KIE),¹¹ linear free energy relationships (LFER),^12,13 and entropic effects¹² have been interpreted in terms of a reaction proceeding through a concerted pathway with a dissociative transition state (TS), i.e., a TS that has little bonding to the nucleophile and leaving group, in contrast to the more associative TSs expected for the hydrolysis of phosphate di- and triesters (see discussion in, e.g., ref (5)). On the other hand, computational studies have suggested two viable concerted pathways with TS that are either dissociative or associative in nature, depending on the pK_a of the leaving group.¹⁴⁻¹⁷ These pathways can be viewed as extremes on a relatively flat potential surface, where the TS structure changes extensively as the nature of the leaving group is changed, or competing processes, where the TS structures for each pathway are similar regardless of the leaving group (and there is a large energetic penalty if the structure is distorted).^18,19 Finally, it has been suggested that the qualitative interpretation of traditional experimental markers such as LFER,^15,20,21 activation entropies,¹⁷ and KIE¹⁵ can be ambiguous, with different pathways potentially giving rise to similar experimental observables.²⁰

Of the range of experimental approaches that can be used to distinguish different pathways, LFER have proven to be particularly useful for probing the bonding patterns and charge distributions of the TSs across a series of homologous substituted compounds.²² Specifically, by examining the effect of adding electron-donating or -withdrawing groups to the leaving group of a reactant on the corresponding reaction rate, LFER measure the sensitivity of the reaction to charge changes at the position of bond cleavage during the reaction. The steeper the correlation between the rate constant and the pK_a of the leaving group (or, more formally, the equilibrium constant of the reaction for a fundamental step), the more advanced bond cleavage is likely to be at the TS, provided that the variations in structure are sufficiently far from the reaction center to avoid changes caused by steric effects and that the total electronic changes are not so large as to cause a large variation in TS structure.²⁴

There exist several LFER for phosphoryl and related group transfer reactions in the literature;⁵ however, most of the experimental data used to analyze LFER for phosphoryl transfer reactions have been obtained using good leaving groups. For example, Kirby et al.¹³ examined the LFER for the cleavage of both phosphate ester mono- and dianions at 39 °C. In doing so, they obtained a steep leaving group dependence with a Brønsted coefficient (β_lg) of −1.23 for phosphate monoester dianions using leaving groups with pK_as <7.2 (β_lg = −1.26 if the value for phenol from Lad et al.⁸ is also included) and very little leaving group dependence (β_lg = −0.27) for phosphate monoester monoanions (the insensitivity to the leaving group allowed these data to include substrates with relatively poor leaving groups, such as methyl phosphate). They also observed a small (but systematic) deviation from the original straight line for ortho-substituents, with o-nitro groups being hydrolyzed more quickly and o-chloro substituents being hydrolyzed more slowly than would have been expected from the original relationship. The high sensitivity of the rate of hydrolysis of the dianions to leaving group pK_a was interpreted as resulting from a loose TS with extensive bond cleavage to the leaving group, which is corroborated by the KIE studies of Hengge and co-workers.¹¹

As ref (13) considered only good leaving groups, Lad and co-workers⁸ later extended the range of compounds studied to also include phenyl phosphate (pK_a = 10) and alkoxy phosphates as leaving groups. The corresponding thermodynamic parameters for phenyl phosphate, i.e., an enthalpy of activation of 38 ± 2 kcal·mol^–1 and slightly positive activation entropy of 7 ± 2 cal·mol^–1·K^–1, were interpreted as evidence that the reaction proceeds via a loose TS as proposed for other aryl phosphate dianions (although the complications with inferring mechanism from activation entropies have been discussed below). Using an Arrhenius plot to extrapolate the observed rate constants to 39 °C gives an estimated rate constant of 1 × 10^–12 s^–1, which is in good agreement with the LFER prediction of the previous data (Figure 2). Similarly, measuring the hydrolysis of methyl and neopentyl phosphate at high temperature led to an estimated rate constant for the hydrolysis of alkoxy phosphate dianions of 2 × 10^–17 s^–1 at 39 °C.⁸ Unlike the other data, this datum involves the specific acid-catalyzed reaction of the phosphate dianion and so represents an upper limit for the spontaneous reaction (see discussion below). The LFER predicts a value of 5 × 10^–19 s^–1 at 39 °C for methoxide as a leaving group, which is consistent with this observation and provides the current experimental estimate for the reactivity of a phosphate dianion with an alkoxy leaving group.

Figure 2.

Observed β_lg for the spontaneous hydrolysis of phosphate dianions: benzoyl phosphates (gray, data from ref (25)); monoaryl phosphates with no ortho substituents (black); monoaryl phosphates with 2-nitro groups (red); monoaryl phosphates with 2-chloro groups (blue). Data from ref (13) at 39 °C except for phenyl phosphate, where the value was extrapolated from measurements at higher temperature, as reported in ref (8)). The green circle is for methyl phosphate in 1 M KOH, where the value was extrapolated from measurements at higher temperature as reported in ref (8). The data used to create this figure are given in Table S1.

We have recently performed a detailed study of the mechanisms of phosphate monoester hydrolysis in aqueous solution, considering the competition between a solvent-assisted pathway with a loose TS and a substrate-assisted reaction pathway with a more compact TS, comparing their energetics and using calculated KIEs as a tool to discriminate between different pathways.²³ Experimental evidence that we did not consider in detail in this work was the leaving group dependence of the hydrolysis of these compounds, as we only considered the two extremes of a very good and a very poor leaving group. It has been suggested, from extensive density functional theory (DFT) calculations of the energy landscapes for the hydrolysis of a range of phosphate monoester dianions, that the choice of reaction mechanism is dependent on the pK_a of the leaving group,^15,16 whereby the better the leaving group, the more dissociative the TS. However, a limitation of the study in ref (15) is that it only considered the pathways directly observed on the calculated 3D energy landscapes (defined in terms of bond making and bond breaking coordinates and the associated energy changes). While this provides some insight into potential choices of mechanism, examining only the calculated 3D energy landscapes can miss the preferred reaction pathways^23,26,27 when more complex reaction coordinates are involved, e.g., with multiple bonds being formed and broken simultaneously.

The purpose of this work is to complete the mechanistic picture for aryl phosphate monoester hydrolysis by examining this central piece of experimental evidence, namely, the LFER for the hydrolysis of these compounds, to explore how the leaving group affects both the solvent- and substrate-assisted pathways for the hydrolysis of phosphate monoester dianions. This, in turn, leads to greater insights into the likely competition between these processes for compounds with different structures. We have analyzed the energetics for each of the two pathways by DFT calculations using the M06-2X²⁸ and ωB97X-D²⁹ functionals. Our results show that while there is a clear preference for a dissociative, solvent-assisted pathway for the hydrolysis of compounds with good leaving groups, this gradually diminishes such that a crossover to a more associative, substrate-assisted pathway becomes increasingly plausible with poorer leaving groups. We discuss the implications of this observation for understanding the mechanisms of enzyme-catalyzed phosphoryl transfer reactions.

Materials and Methods

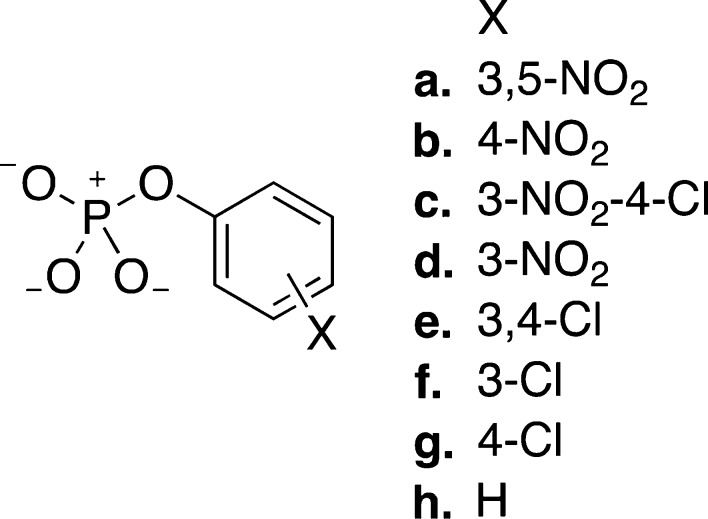
The different reaction pathways analyzed in this study are schematically presented in Figure 1. In our recent work²³ we obtained TSs for 4-nitrophenyl hydrolysis through both solvent- and substrate-assisted pathways, in the presence of eight water molecules, optimized at the M06-2X/6-31+G(d) level of theory. These structures were used as starting points to obtain TSs for the hydrolysis of all other compounds shown in Figure 3, by perturbing the initial TS through replacement of the substituent and reoptimizing the resulting structures using the 6-31+G(d) basis set with either the M06-2X²⁸ (Tables S2–S3) or the ωB97X-D functionals²⁹ (Tables S4–S5). Both are dispersion corrected functionals and have been successfully applied to the study of a wide range of mechanistic questions.³⁰⁻³²

Figure 3.

Aryl phosphate monoester dianions examined in this work. These were selected to give a wide range of pK_a values, ensuring hydrogen is in the ortho positions to avoid direct interactions between the reaction center and the substituents.

Solvation was accounted for by using a mixed explicit/implicit solvent model, comprising of eight explicit water molecules (not including the nucleophilic water molecule) and the solvent model density (SMD) implicit model,³³ as in our recent work.²³ We note that when using only a limited number of explicit water molecules, the calculated energetics are strongly dependent on the precise positioning of the water molecules, as different stabilizing interactions will be created based on where they are placed. However, we demonstrated in ref (23) that once a sufficient number of explicit water molecules are added, this problem is mitigated as potential interaction partners become saturated with explicit hydrogen-bonding interactions, and the calculations become less sensitive to the precise number of water molecules included in the model. We found that for simple phosphate monoester dianions, eight explicit water molecules provided a good compromise between the computational cost and reliability of the calculations. In particular, the results we obtained for methyl phosphate hydrolysis with eight water molecules included in the calculation (in addition to the nucleophile) where very similar to those obtained by Schlitter³⁴ using full explicit solvation, increasing our confidence in the reliability of the model. Water molecules were added to the system symmetrically (alternately adding one to the leaving group or the nucleophile side of the central PO₃ group at the TS) to avoid overstabilizing one side of the reacting system compared to the other.

Finally, the resulting TS were characterized by frequency calculations, as well as by following the intrinsic reaction coordinate (IRC)^35,36 to minima in both directions, followed by unconstrained geometry optimizations at the same level of theory. In all cases, the optimization was performed using an ultrafine numerical integration grid and tight optimization criteria (as implemented in Gaussian 09),³⁷ with the exception of a few stationary points, mainly in the product states, where it was impossible to obtain a convergent structure with tight optimization criteria. Additional single point frequency calculations were performed on the key stationary points using the larger 6-311+G(d,p) basis set and a scaling factor of 0.970 by analogy to related basis sets,³⁸ in order to correct for zero-point energies and entropies and obtain the final free energies for these reactions. Finally, in all cases we compared the energetics of the final optimized reactant states obtained from following the IRC for each pathway, and the lowest energy of these was used as a reference state for both pathways as this is closer to the global minimum on the energy surface and allows us to compare both TSs relative to the same reference state (see ref (23)). All electronic-structure calculations presented in this work have been performed using the Gaussian 09 simulation package (revision D.01).³⁷

Results and Discussion

Leaving Group Effects and the Competition Between Substrate- and Solvent-Assisted Mechanisms

Figure 1 provides an overview of the different possible mechanisms for phosphate monoester hydrolysis, which could be very close in energy, as suggested in refs (14, 15, 17, 23, and 34). To assess how changing the leaving group affects the competition between substrate- and solvent-assisted pathways, we examined the hydrolysis of a series of aryl phosphate monoesters with eight different leaving groups (Figure 3), spanning a pK_a range from 6.7 to 10, as well as the hydrolysis of methyl phosphate. In each case, two potential pathways were studied: a substrate-assisted mechanism, in which nucleophilic attack occurs in either a concerted or stepwise fashion and is coupled with proton transfer from the attacking water molecule to one of the nonbridging oxygens of the phosphate, and a solvent-assisted mechanism, in which the nucleophile is not deprotonated in the rate-limiting TS but is stabilized by the solvent (see also Figure 1 for details).

A comparison of the calculated energetics of the two different pathways obtained at the SMD-M06-2X/6-311+G(d,p)//SMD-M06-2X/6-31+G(d) and SMD-ωB97X-D/6-311+G(d,p)//SMD-ωB97X-D/6-31+G(d) levels of theory are illustrated in Figure 4, with the corresponding data shown in Table 1. All calculations were performed with eight explicit water molecules in order to solvate the reacting fragments appropriately, as discussed in our previous work.²³ Additionally, our reference state for both mechanisms is the reactant complex with the lowest absolute energy obtained from following the IRC on the two different pathways, to allow for direct comparison between the two pathways from the same reference state. The absolute energetics of each species is also provided as Supporting Information for comparison.

Figure 4.

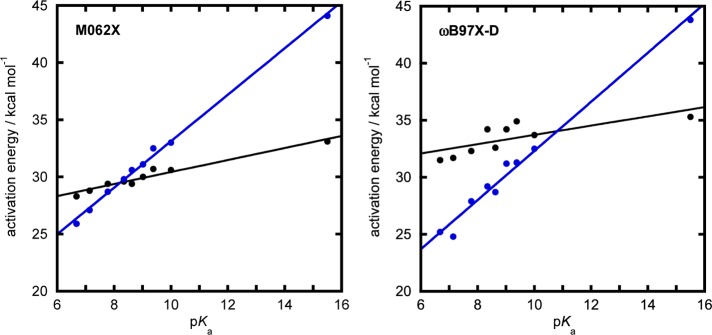
Calculated activation energies for the addition of water to the aryl phosphate dianions shown in Figure 3 as well as to the methyl phosphate dianion via either a solvent (blue solid circles) or substrate-assisted (black solid circles) pathway. The energies were obtained at the (left) SMD-M06-2X/6-311+G(d,p)//SMD-M06-2X/6-31+G(d) and (right) SMD-ωB97X-D/6-311+G(d,p)//SMD-ωB97X-D/6-31+G(d) levels of theory, respectively, with the corresponding numerical values presented in Table 1.

Table 1. Energetics for the Spontaneous Hydrolysis of the Aryl Phosphate Monoesters Shown in Figure 3, through Either Substrate- Or Solvent-Assisted Pathways^a.

systems		substrate-assisted pathway				solvent-assisted pathway
		M06-2X		ωB97X-D		M06-2X	ωB97X-D
	pKa	ΔGstep1⧧	ΔGstep2⧧	ΔGstep1⧧	ΔGstep2⧧	ΔG⧧	ΔG⧧
3,5-NO2	6.68	28.3	–	31.5	–	25.9	25.2
4-NO2	7.14	28.8	–	31.7	–	27.1	24.8
3-NO2, 4-Cl	7.78	29.4	25.7	32.3	–	28.7	27.9
3-NO2	8.35	29.6	26.7	34.2	–	29.8	29.2
3,4-Cl	8.63	29.4	26.1	32.6	–	30.6	28.7
3-Cl	9.02	30.0	27.6	34.2	31.1	31.1	31.2
4-Cl	9.38	30.7	29.0	34.9	30.8	32.5	31.3
H	10.0	30.6	29.4	33.7	30.7	33.0	32.5
methyl	15.5	33.1	35.6	35.3	40.1	44.1	43.8

^aIn the case of the substrate-assisted pathway, ΔG_step1^⧧ and ΔG_step2 correspond to the activation free energies of the addition and elimination steps, respectively. In cases where the energy of the elimination step is represented as “–”, the reaction proceeds through a concerted pathway with a single TS. In the case of the solvent-assisted pathway, the reaction also proceeds through a single TS throughout, the activation free energy of which is represented by ΔG^⧧. Frequency calculations were performed at 312 K. A more detailed energy decomposition for each pathway is presented in Tables S2–S5. All energies are presented in kcal·mol^–1 at the SMD-M06-2X/6-311+G(d,p)//SMD-M06-2X/6-31+G(d) and SMD-ωB97X-D/6-311+G(d,p)//SMD-ωB97X-D/6-31+G(d) level of theory relative to the lowest-energy reactant state for the two pathways.

The trends in these data show that the mechanistic preference between the two pathways changes across the series, with the solvent-assisted pathway being preferred for the best leaving groups and the substrate-assisted pathway being preferred for poor leaving groups. For both functionals, the calculated change in energy across the series for the solvent-assisted pathway is substantial, with the energetics increasing by about 7 kcal·mol^–1 upon moving from the best to the poorest leaving group in the series of aryl phosphates. In contrast, the calculated energetics of the substrate-assisted pathway are more constant and do not change by more than 2 kcal·mol^–1 across the series. Both functionals give a similar set of absolute values for the solvent-assisted pathway, but give significantly different values for the substrate-assisted pathway (by almost 6 kcal mol^–1). This leads to quite different predictions for where the crossover between the two pathways will occur. For the M06-2X functional, this occurs at pK_a of 8.4 (i.e., at the 3-nitrophenyl leaving group), but for the ωB97X-D functional one would expect a crossover between the two pathways at a pK_a ∼ 11. Overall, both sets of calculations provide a consistent picture of the trends in reactivity with changing leaving group for both pathways, but provide different predictions of their relative importance.

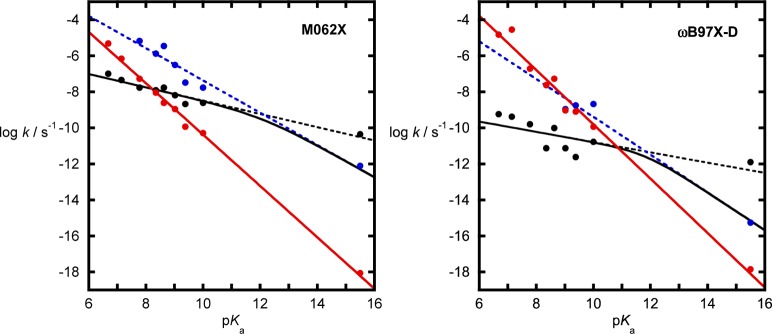
These data can also be expressed as Brønsted plots for the hydrolyses of these compounds to allow comparison with the experimental data (Figure 5). In the case of the solvent-assisted pathway, a steep linear correlation is obtained with β_lg values of −1.42 ± 0.03 (M06-2X) and −1.51 ± 0.07 (ωB97X-D), as would be expected from a TS with extensive cleavage to the leaving group and is in good agreement with that obtained experimentally (β_lg value of −1.26 ± 0.07).^8,39 For the substrate-assisted pathway, an intermediate forms for compounds with pK_a <7.5 (M06-2X) or 9.0 (ωB97X-D); for compounds with lower pK_as, the intermediate becomes a shoulder on the potential energy curve, and the reaction is concerted but dominated by bond formation to the nucleophile, i.e., the TS is similar to the formation of the intermediate when the reaction is stepwise. The steepness of the correlation depends on which step is rate limiting. When this is bond formation, β_lg values of −0.37 (M06-2X) and −0.28 (ωB97X-D) are obtained; when the second step is rate limiting, β_lg values of −0.89 (M06-2X) and −1.05 (ωB97X-D) are obtained. These are combined in Figure 5 to show the predicted values of the observed rate constant for each compound. The point at which the rate-limiting step changes differs slightly depending on functional (12.1 for M06-2X and 11.8 for ωB97X-D, respectively), which is well before the nucleophile and leaving group have similar leaving group abilities. This may be due to the fact that the proton that is transferred from the nucleophilic water to the nonbridging oxygen is still in position to make the nucleophile behave as a much better leaving group through intramolecular general acid catalysis. For example, our data (Tables S2–S5) show that the status of any intermediates appears to be marginal, with even rotation of the P–OH group being potentially too slow to intervene in the reaction. It has been argued that a substrate-assisted pathway involving an additional water molecule that acts as a bridge between the nucleophile and the nonbridging oxygens of the phosphate has a lower energy than direct proton transfer from the nucleophile.^40,41 However, in our previous work, the presence of intervening water molecules to facilitate proton transfer did not enhance proton transfer between bridging and nonbridging positions.²³ In addition, the nonlinear Brønsted plot may have similarities to the behavior of RNA models under basic conditions, which are also nonlinear, but where the dianionic intermediate is believed to have marginal stability and only partitions between substrate and product. In that case, the break in the plot is much closer to the pK_a of the incoming nucleophile, but no proton transfers are involved.⁴²

Figure 5.

Brønsted plots for the spontaneous hydrolysis of the aryl phosphate monoesters shown in Figure 3 and for methyl phosphate. For the substrate-assisted pathway, steps 1 (black) and 2 (blue) are plotted individually (dotted lines), and combined to show the predicted overall rate constant (solid black line). The solvent-assisted pathway is shown with a linear least-square fit (red). Energy calculations were performed at 312 K at the SMD-M06-2X/6-311+G(d,p)//SMD-M06-2X/6-31+G(d) and SMD-ωB97X-D/6-311+G(d,p)//SMD-ωB97X-D/6-31+G(d) levels of theory. Rate constants were obtained from the calculated activation free energies, using TS theory.

The similarities in both the trends and the energetics for the solvent-assisted pathway obtained using two different functionals and the good agreement with the experimental data suggest that this is a sufficient explanation of the observed data for the spontaneous hydrolysis of aryl phosphate dianions, although it does not preclude a contribution or near contribution from the substrate-assisted pathway. Our previous work strongly suggests that the 4-nitrophenyl phosphate dianion reacts primarily through the solvent-assisted pathway due to the KIE that has been measured and calculated for this compound. The substrate-assisted pathway also shows a consistent trend for both functionals, but there is a much weaker dependence of the activation energy on the pK_a of the aryloxide leaving group when the reaction is dominated by nucleophilic attack (and a weaker dependence when leaving group departure is rate limiting). As the correlations between the energy and pK_a for the two pathways are significantly different, this leads to the conclusion that there will be some leaving groups where the two pathways have a similar energy barrier, and, after this point, there will be a change in the dominant mechanistic pathway for the reaction from solvent- to substrate-assisted. However, the absolute activation energies of the substrate-assisted pathway do appear to be sensitive to the functional, and this means that the predicted crossover point differs for the two sets of calculations. To try and refine where the crossover may occur, we also consider the kinetic and thermodynamic experimental data that exists.

Thermodynamically, Guthrie has measured parameters for a series of phosphorane species, leading to estimates of the likely relative stabilities of the key intermediates for the two pathways.⁴³ For a fully dissociative pathway involving the formation of metaphosphate, the free energy of the equilibrium, where an ethoxy anion is fully dissociated from the dianion of ethyl phosphate, is 37 ± 3 kcal·mol^–1. This figure was derived from kinetic data for phosphate monoesters with good leaving groups by assuming the formation of metaphosphate followed by rate-limiting attack of water, which was estimated to have a rate constant of 10^–9 s^–1. This corresponds to an additional barrier of ∼5.4 kcal·mol^–1, leading to an overall barrier ∼42 kcal·mol^–1 for forming the initial product on the solvent-assisted pathway, which is in very good agreement with our calculated values for the solvent-assisted pathway. We note that our calculations do not predict the formation of a formal metaphosphate intermediate, in keeping with the conclusions from additional experiments involving stereochemical probes;⁴⁴⁻⁴⁶ the difference in the two analyses is whether there is any bonding to the leaving group in the TS (see below). Guthrie also combined thermochemical data for ethoxy phosphoranes with estimated pK_as to calculate the enthalpy of addition of water to ethyl phosphate dianion,⁴³ and the value is 33 ± 4 kcal·mol^–1, which is in very good agreement with the calculated energy for the formation of the intermediate formed in the substrate-assisted pathway. Thus, for the methoxy leaving group, the thermodynamics suggest that both pathways involve species that have comparable stabilities. For these poor leaving groups, the difference between the two pathways depends on the intrinsic barrier for the reactions, which has been assumed to be more substantial for phosphorane formation due to the movement of more heavy atoms. Our calculations suggest that there is not a large intrinsic barrier to the decomposition of the marginally stable dianionic phosphorane, which is why this pathway appears to be competitive with the solvent-assisted pathway for these leaving groups. This may be because the initially formed intermediate has a phosphoryl proton (received from the nucleophile) poised to allow intramolecular general acid catalysis of the departure of the leaving group in a process similar to that suggested for the reactions of phosphate monoester monoanions.

As noted above, the dianion of phenyl phosphate appears to have a rate constant that is consistent with the experimental LFER obtained for lower pK_a leaving groups and to be accounted for by the solvent-assisted pathway. Thus, the substrate-assisted pathway does not appear to be dominant for this compound, although it could be similar energetically. The data for phosphate monoester dianions with much poorer leaving groups (methanol or neopentyl alcohol) are even sparser. The data revealed this even in 1 M KOH, the dominant reaction involves specific acid catalysis, which is kinetically equivalent to the reaction of the very small amount of monoester monoanion present. Extrapolating these data to 100 °C agrees very well with predictions from the pH rate profile for methyl phosphate at this temperature (Figure 6A). In this figure, the circle is the datum extrapolated from high temperature in 1 M KOH. The limiting values at high pH (dotted lines) are the estimates of the dianion reaction from the LFER, assuming a similar entropy of activation to the phenyl phosphate dianion. These data show that the spontaneous reaction is even slower over the range these data were measured. Similarly, extrapolating the data for the reaction of the monoanion to 39 °C and combining this with the second pK_a for methyl phosphate also agree with predicted rate constant derived from the data measured in 1 M KOH at high temperature.

Figure 6.

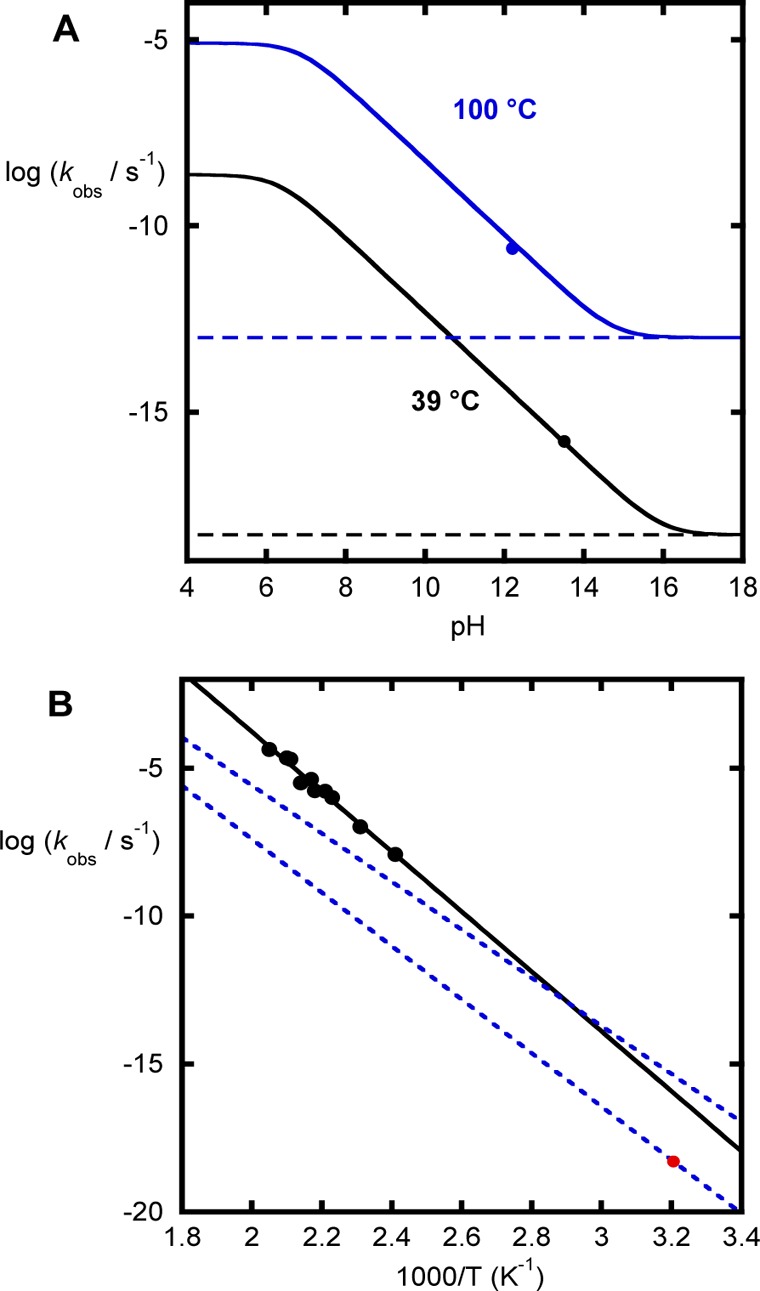
(A) pH dependence of methyl phosphate hydrolysis. The black line (39 °C) was obtained by using the data reported for the hydrolysis of the monoanion at 100 °C and the reported activation parameters and a value of 6.3 for the second pK_a of methyl phosphate. The blue line was obtained from the data reported for the hydrolysis of the monoanion at 100 °C, and the circle is the datum extrapolated from high temperature in 1 M KOH. (B) Temperature dependence of methyl phosphate hydrolysis. The black circles and line are the experimental data reported for methyl phosphate in 1 M KOH. The red point is the predicted rate constant for the solvent-assisted mechanism according to the Brønsted plot at 39 °C. The blue dashed lines illustrate the predictions for a potential substrate-assisted mechanisms with the entropy of activation fixed at −12 eu. For the corresponding temperature dependence, see Figure S1.

Adding the rate constant for the spontaneous reaction of the dianion predicted by the Brønsted plot at 39 °C shows that this reaction is expected to be about 300-fold lower than that derived from the Arrhenius plot of the reaction in 1 M KOH. This means that a mechanistic change is only expected when the pH is >16 and indicates that the spontaneous reaction of the dianion is invisible over the usual pH range at this temperature. The observed value for the enthalpy of activation for this reaction (44.7 kcal·mol^–1) is very similar to the value we have calculated for the solvent-assisted reaction 44 kcal·mol^–1), slightly higher than derived from Guthrie’s data⁴³ (above; 42 kcal·mol^–1) and slightly lower than the value obtained (46 kcal·mol^–1) by combining the value from the Brønsted plot at 39 °C with the measured entropy of activation for phenyl phosphate.⁸ Using any of these estimates that the difference between the two pathways will remain about 2 orders of magnitude at any temperature where experiments can be carried out and the direct observation of the solvent-assisted pathway is not possible.

The experimental data from high temperature measurements and the Brønsted plot have been the basis of the best estimate for the spontaneous hydrolysis of the methyl phosphate dianion and provide a lower limit for the reactivity for the spontaneous hydrolysis of the methyl phosphate dianion. However, as shown in Figure 6B, it is possible that a slower reaction at higher temperature with a lower enthalpy of activation could become the dominant reaction at ambient temperature. Such a reaction would be invisible to extrapolations from the Arrhenius (as the reaction of a different ionic species is dominant) and Brønsted analyses (which predicts the rate constant for the solvent-assisted pathway). Thus, the experimental data available do not rule out a transition to a substrate-assisted pathway for leaving groups with higher pK_a than phenol. Figure 6B illustrates some limiting cases for methyl phosphate hydrolysis, assuming that a 10% or lower contribution to the observed rate constant for the last experimental data point would not be detectable in an Arrhenus plot (i.e., no detectable deviation from linearity in the data; it is likely that a greater contribution would also be undetectable). In this figure, the upper line is for a reaction that contributes 10% of the observed rate constant for the experimental data point at the lowest temperature and has an enthalpy of activation of 36.5 kcal·mol⁻¹, which predicts a rate constant of 4 × 10⁻¹⁶ s⁻¹ at 39 °C (∼1000 fold greater than predicted by the Brønsted plot). The lower line is for a reaction with the same rate constant at 39 °C as the solvent-assisted reaction predicted by the Brønsted plot, but an enthalpy of activation of 40.7 kcal·mol⁻¹. This lower line would contribute <0.1% of the experimentally observed rate constant at the lowest temperature.

These limiting cases show that an alternative reaction pathway with an enthalpy of activation between 36.5 and 40.7 kcal·mol^–1 has a rate constant at least as large as that predicted by the Brønsted plot at 39 °C, but is experimentally invisible under any accessible conditions or practical timescales. These estimates are based on an entropy of activation of −12 eu, as a plausible value for the addition of solvent to the phosphate dianion. We note that intepreting and predicting the entropy of activation is difficult, as this measurement includes changes in both the reacting system the solvent environment, and so this value is merely a conventional approximation for a reaction between a substrate and the solvent. If the entropy of activation is closer to zero, then the enthalpy of activation would need to be closer to the experimental value for an alternative reaction to be both dominant at lower temperature and undetectable at higher temperature. We also note that the experimental data for methyl phosphate at high pH indicate that it is an acid catalyzed reaction between the dianion and acid and has an observed entropy of activation of +6 eu and that 4-nitrophenyl sulfate undergoes a solvent-assisted, dissociative reaction with solvent, and has an entropy of activation of −18.5 eu. Thus, this parameter should be considered with caution and preferably in conjunction with other observables for diagnosing mechanisms.

Interestingly, the intermediate formed is similar to that obtained from hydroxide addition to a phosphate diester (where the equatorial proton is replaced by an alkyl group, see Figure S2 for the Brønsted plot of the second-order rate constant for hydroxide-promoted hydrolysis of phosphate diesters). The comparison between spontaneous reaction of a dianion and hydroxide attack at the monoanion presents some difficulties as it involves the use of model reactions and the attendant assumptions to be made.^47,48 Using dimethyl phosphate as a model compound for the reaction of hydroxide with methylphosphate monoanion and calculating the fraction of methyl phosphate in the correct ionic form to react by, this mechanism reaction predicts that the overall reaction (∼3 × 10^–20 s^–1) is slightly slower than for the solvent-assisted pathway predicted by the LFER extrapolation (∼5 × 10^–19 s^–1). This assumes that the ionic form as a pair of stable species is on the reaction pathway and that their reaction is similar to the equivalent reaction of a diester. If proton transfer only occurs within the reactant complex (i.e., general base catalysis by the substrate of addition by water), then this assumption is not necessarily applicable and the barrier for the addition may be lower that that obtained from this extrapolation.

The relative merits of the two pathways have also been considered by Vigroux et al.,¹⁶ who studied the substrate-assisted pathway for a series of aryl and alkyl phosphate monoester dianions using computational methods and compared them with the experimental LFER. The authors concluded that while this pathway was unlikely to apply to aryl phosphates, it was feasible for the hydrolysis of alkyl phosphate esters. They predicted a crossover at pK_a = 13 based on comparison between their calculated alkyl compounds and the available experimental data for aryl compounds, which was assumed to proceed by a dissociative pathway (but was not explicitly modeled). The substrate-assisted mechanism proceeded through concerted pathways and was sensitive to the positioning of the proton on the monoester. In this and previous work, these authors suggested that although an alkyl group was a reasonable substitute for a proton on the nonbridging phosphoryl oxygen, the protonated species was slightly more reactive.

Overall, based on this analysis, the available experimental data suggest that mechanistic ambiguity is plausible for phosphate monoester dianions with poor leaving groups, although the energetic preference for the solvent-assisted pathway is likely to be strongly preferred for substrates with very good leaving groups.

Corresponding Transition-State Geometries

As a final note, Figures 7 and S3 show comparison of changes in P–O bond orders and geometries at the TS to the incoming nucleophile (P–O_nuc) and departing leaving group (P–O_lg) upon changing the pK_a of the leaving group. From these figures, it can be seen that changing the nature of the leaving group has little effect on the TS structure for either pathway across the series (apart from becoming slightly tighter with poorer leaving groups) and with either functional. Using M06-2X, the substrate-assisted process becomes stepwise at a pK_a of 7.78, but with ωB97X-D, an intermediate only forms when the leaving group pK_a is 9.02. In both cases, nucleophilic attack remains rate-limiting as the barrier to subsequent elimination of the leaving group is very low. In contrast, for the solvent-assisted pathway, the process is always concerted. As can be seen from Figure 7, upon moving from good to poor leaving groups, there is a small increase in the P–O_nuc bond order and a very small decrease in the P–O_lg bond order at the TS, such that the overall bonding in the TS does not change much across the series. Therefore, despite the uncertainities about the crossover point between the substrate- and solvent-assisted pathways, the energetic trends presented in Figure 4 are in good qualitative agreement with the rate-limiting TS structures obtained for each pathway: the solvent-assisted mechanism involves greater bond cleavage to the leaving group than the substrate-assisted mechanism, and so a corresponding greater sensitivity to the leaving group is observed.

Figure 7.

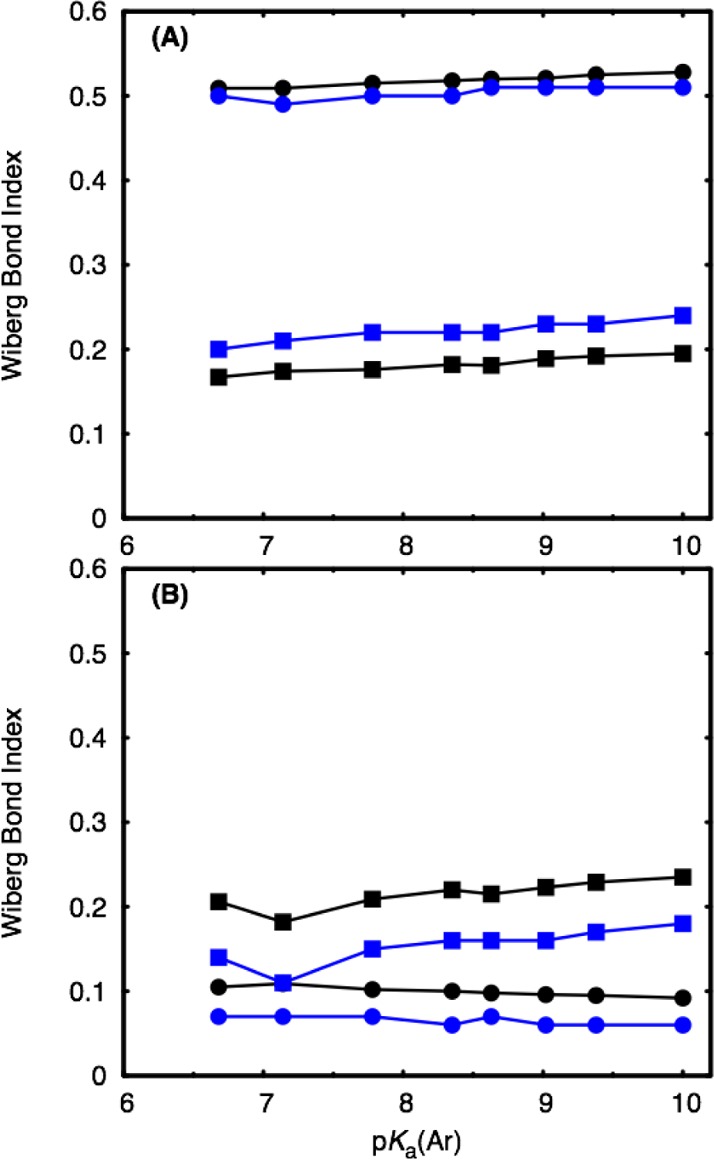
Calculated Wiberg bond indexes to the incoming nucleophile (P–O_nuc, solid squares) and departing leaving group (P–O_lg, solid circles) at the TS of the rate-limiting step for the (A) substrate- and (B) solvent-assisted hydrolysis of the compounds shown in Figure 3 at the SMD-M06-2X/6-311+G(d,p)//SMD-M06-2X/6-31+G(d) (black) and SMD-ωB97X-D/6-311+G(d,p)//SMD-ωB97X-D/6-31+G(d) (blue) levels of theory. For the corresponding numerical values see Table S6. The corresponding distances are presented in Figure S4 and Table S7.

Overview and Conclusions

In this study, we have explored leaving group effects on the competition between solvent- and substrate-assisted mechanisms for phosphate monoester dianion hydrolysis. As well as being a valuable mechanistic probe, these effects are important to understand, given the wide variety of leaving groups that are found in natural phosphates. We demonstrate that the mechanistic choice between the two pathways is dependent on the nature of the leaving group, with good leaving groups preferring a more dissociative solvent-assisted TS. However, moving to poorer leaving groups gradually reduces the energy difference between the two pathways and will ultimately lead to a preference for the substrate-assisted pathway, with the crossover point likely to occur for simple alcohol leaving groups.

There have been extensive computational studies of the uncatalyzed hydrolysis of phosphate monoesters with poor leaving groups,^14,16,34 but very few of the corresponding uncatalyzed hydrolysis of phosphate monoesters with good leaving groups.^23,49 In accurately reproducing the LFER for phosphate monoester hydrolysis, we demonstrate how the competition between the possible pathways varies with the leaving group. A detailed analysis of the available experimental data suggests that the competition between the two pathways is plausible for simple alcohols but also demonstrates that direct kinetic characterization of these reactions is not accessible due to competing processes and experimental limitations on measuring extremely slow reactions.

The possibility of such competition between two pathways has implications for our understanding of enzyme-catalyzed phosphoryl transfer reactions, that is, while the relevant enzymes would have to overcome a larger energy barrier to facilitate the hydrolysis of a phosphate monoester with a good leaving group (such as for instance GTP or ATP) through a substrate-assisted pathway, such a pathway would be viable for enzymes that catalyze the hydrolysis of phosphate esters with poor leaving groups (such as serine/threonine or possibly even tyrosine phosphatases), and such a mechanistic possibility needs to be seriously considered. Irrespective of the preferred pathway in aqueous solution, it is of course feasible that this preference could be changed in the nonhomogenous environment of an enzyme active site or a synthetic catalyst, provided that the intrinsic energy difference between the two pathways is sufficiently small.

Furthermore, we note that if an enzyme has evolved to catalyze phosphate hydrolysis with a poor leaving group, this could reasonably occur through either pathway, presumably with different local interactions. When presented with a substrate with a better leaving groups, both sets of interactions would lead to faster turnover of this substrate, although the associative pathway would reduce the rate less if the same amount of TS stabilization is achieved. In contrast, if an enzyme has evolved to stabilize the dissociative reaction of a monoester with a good leaving group, the transition to a poor leaving group would have a higher penalty. Finally, if an enzyme has evolved to stabilize the more compact dianionic TSs apparently favored in the alkaline hydrolysis of phosphate diesters,^5,7 it may be feasible to transfer sufficient activity toward phosphate monoester dianion hydrolysis through a substrate-assisted pathway to provide an evolutionary beneficial function. This is reflected by/in line with the high promiscuous phosphomonoesterase activities observed in a number of promiscuous phosphodiesterases,⁵⁰⁻⁵² suggesting that these enzymes can hydrolyze phosphate monoester hydrolysis through compact substrate-assisted TSs that are similar in geometry and charge distribution to those of the reactions of their diester counterparts. In contrast, an active site that has evolved to accommodate a loose solvent-assisted pathway for phosphate monoester hydrolysis is not well equipped to facilitate reactions that require tighter TSs (with different charge distributions) such as either substrate-assisted phosphomonoesterase activity or phosphodiesterase activity. This is again reflected in the fact that the discrimination between phophomono- and diesterase activity is much larger when the enzyme is a native phosphomonoesterase^53,54 than when it is a phosphodiesterase.

In summary, our calculations demonstrate that catalyzing the hydrolysis of phosphate monoester dianions with good leaving groups is far more energetically demanding for an associative pathway than for a dissociative one. However, the energy difference between the two pathways decreases as the leaving group pK_a increases, leading to mechanistic ambiguity in the case of poor leaving groups. This creates different mechanistic possibilities for the reactions of alkyl phosphates and their corresponding enzyme-catalyzed reactions, as both pathways are apparently plausible. Finally, detailed analysis of the existing experimental data defines what is and can be known from experimentation: direct kinetic characterization of these reactions is not accessible, and so computational approaches are central to understanding these reactions.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.6b06277.

• Summaries of relevant experimental data from the literature to further support our computational conclusions. Energy breakdown for the different mechanisms studied in this work. Key distances, absolute energies in Hartrees and Cartesian coordinates of key stationary points (PDF)

Author Present Address

^§ Chemistry Research Laboratory, University of Oxford, 12 Mansfield Road, Oxford, OX1 3TA, United Kingdom, and Physical and Theoretical Chemistry Laboratory, University of Oxford, South Parks Road, Oxford OX1 3QZ, United Kingdom.

The authors declare no competing financial interest.