Taming the beast: extracting generalizable knowledge from computational models of cognition

Abstract

Generalizing knowledge from experimental data requires constructing theories capable of explaining observations and extending beyond them. Computational modeling offers formal quantitative methods for generating and testing theories of cognition and neural processing. These techniques can be used to extract general principles from specific experimental measurements, but introduce dangers inherent to theory: model-based analyses are conditioned on a set of fixed assumptions that impact the interpretations of experimental data. When these conditions are not met, model-based results can be misleading or biased. Recent work in computational modeling has highlighted the implications of this problem and developed new methods for minimizing its negative impact. Here we discuss the issues that arise when data is interpreted through models and strategies for avoiding misinterpretation of data through model fitting.

Behavioral and physiological data in systems and cognitive neuroscience are generally collected in reduced environments and constrained experimental conditions, often designed to be diagnostic of competing theories. The generalization of knowledge from simple experiments is crucial to advance our broader understanding of brain and behavior. However, interpreting data according to existing theories causes our knowledge to be conditioned on the quality of said theories and the assumptions thereof. In many cases these conditions are met and theory can drive scientific progress by reducing a dazzling array of neuroscientific data into simpler terms, yielding falsifiable predictions. In other cases a general overarching theory can lead to wasted resources and, at worst, can even impede scientific progress.

Both the advantages and potential dangers of theory are amplified for computational theories, which provide extremely explicit predictions under a specific set of assumptions. Such theories offer an advantage over more abstract ones in that they make predictions about behavior or neurophysiology that are testable, falsifiable, and comparable across models. They do so by formalizing the fundamental definition of the model and linking it to experimental data through a set of assumptions (e.g., the particular form of the behavioral or neural likelihood distribution, conditional independencies in choice behavior, parameter stationarity, etc.). These assumptions can affect how we interpret evidence for or against a model, how we explain differences in the behavior of individuals or how we ascribe functional roles to biological systems based on physiological measurements. Here we examine the theoretical and practical consequences of these assumptions, paying special attention to the factors that determine whether a given assumption will give rise to spurious interpretations of experimental data. In particular, we highlight and evaluate methods used to minimize the impact of modeling assumptions on interpretations of experimental results.

What can go wrong?

While we appreciate that assumptions implicit in experimental designs are critical for data interpretation, and that inappropriate model selection or fitting techniques can produce misleading results, here we focus specifically on issues that can arise when computational models are appropriately and quantitatively linked to meaningful empirical data [1–4]. Under such conditions, quantitative model fitting offers at least three key advantages: 1) competing models can be compared and ranked according to their abilities to fit empirical data, 2) differences across individuals or task conditions can be assessed according to model parameter estimates, providing potential mechanisms giving rise to those differences, and 3) neural computation can be evaluated by comparing physiological measurements to latent model variables. In this section we discuss recent work that highlights how each of these potential advantages can be negated by unmet assumptions.

The impact of modeling assumptions on the arbitration of competing models was recently highlighted in a factorial comparison of visual working memory models [5]. The study decomposed working memory into three distinct processes (item limitation, precision attribution, and feature binding) to construct a large model-set through exhaustive combination of possible computational instantiations of each process. The model set contained archetypical models such as competing “slots” and “resource” models of working memory capacity limitations, but also contained novel combinations that had never been previously tested. This combinatorial model set was fit to data from ten previously published studies that had come to different conclusions regarding the nature of capacity limitations (roughly half had concluded in favor of discrete slots [6,7], whereas the other half had concluded in favor of continuous resource limitation[8,9]). Despite the fact that the original studies had arrived at contradictory conclusions, rank ordered fits from the combinatorial model set were remarkably consistent across datasets. The contradictory conclusions of the original studies were possible because each study compared only a small subset of models by making fixed assumptions (that differed across study) regarding untested model processes, allowing essentially the same data to be used to support competing and mutually exclusive psychological theories.

Similar issues can arise when estimating parameters within a single model. Computational modeling provides a powerful framework for inferring individual differences in latent parameters governing behavior, such as the learning rate used to incorporate new information in supervised or reinforcement learning tasks [10–13]. However, fairly subtle aspects of model specification can have major effects on this estimation process. One recent computational study showed that the common and seemingly innocuous assumption that learning rate is fixed over time can have drastic consequences on interpretations of behavioral differences: failure to model adjustments in learning rate led to the spurious conclusion that faster learners were best fit by lower learning rates [14,15]. This is to say that, in at least in some extreme cases, naïve reliance on parameter fits can give rise to an interpretation that is exactly opposite to the truth. A similar phenomenon has been noted in computational studies of reinforcement learning and working memory contributions to behavioral learning: failure to appropriately model the working memory process can lead to spurious identification of deficits in the reinforcement learning system [16,17].

The impact that inappropriate assumptions can have on model selection and parameter estimation in turn corrupts the latent variables that are used to test theories of neural computation. Without valid computational targets, analysis of physiological measurements such as fMRI BOLD or EEG are more likely to yield null results, or worse, provide misleading information regarding the computational origins of behavior [18,19]. Or, more simply put, if we do not have a clear understanding of the computations that govern behavior, what hope do we have of discovering the neural instantiations of those computations?

Avoiding the pitfalls

So how can computational models be used to generalize knowledge across cognitive tasks, contexts and species without falling prey to the risks described above? A prominent notion in statistics is that robust inference can be achieved through iteration of steps comprised of model estimation and model criticism [20]. In formal terms, the estimation step involves estimating parameters that allow for the best description of behavior given a candidate model, and the criticism step involves estimating the probability of all possible datasets that could have been observed given that model parameterization [20,21]. This type of criticism is referred to as predictive checking and allows the modeler to ask whether the empirical data that were observed were “typical” for a given model. If the observed data are atypical for the fit model, then model revisions are necessary.

In practice, researchers are generally focused on particular meaningful features of the data motivated by the experimental design, and the typicality of data is often assessed through analyses designed to probe these key features. Specifically, parameters are estimated through model fitting and then parameterized models are used to simulate data that are subjected to the same descriptive analyses originally applied to the empirical data (e.g., a learning study might be concerned with learning curves and/or asymptotic accuracy in one condition compared to another). This approach depends critically on the precision with which behavior can be characterized through these descriptive analyses: the more precisely a behavior of interest can be quantified through a descriptive analysis, the more diagnostic it will be of model sufficiency [15]. In some cases, ability of simulated data to reproduce basic properties of the original dataset (e.g., conditional accuracy and reaction time) can provide rich information regarding why a given model fits the data better than other candidates [16,22]. In other cases, the failure to adequately describe these key features, or some aspect of them, can reveal an inappropriate assumption or a missing component of the empirical data (see figure 1). For example, distributional analyses of response times can reveal when a model captures empirical data and where it may miss (e.g., the tail or leading edge of the distribution and how they do or don’t differ between task conditions); [23,24], patterns that can be revealed via posterior predictive checks [25,26]. In reward learning tasks, sequential choice behavior can be described as a linear function of outcome and reward history, which allows validation of (or reveals deviations from) the specific patterns of data expected by basic reinforcement learning models [27,28]. This type of analysis was recently extended to directly test a model of how rewards can be misattributed in lesioned monkeys, in a manner that was relatively insensitive to modeling assumptions [29].

Figure 1. Predictive checking can reveal model insufficiency and guide model improvement.

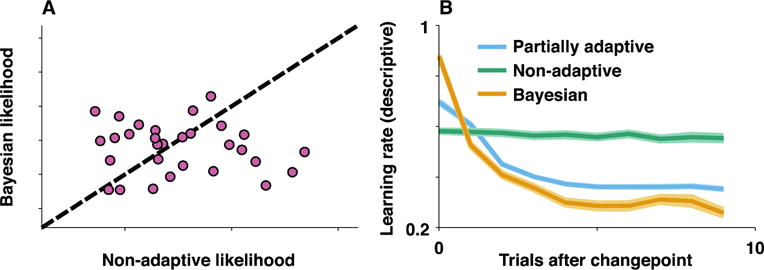
Behavioral data were simulated for 30 subjects in dynamic inference task using an error-driven learning rule that adapts learning rates in accordance with subject behavior (eg. learning rates were adapted in accordance with principles of normative learning, but less so than would be prescribed by an optimal inference algorithm) [14]. Simulated data was fit using two separate models: 1) a Bayesian model assuming rational inference with 2 free parameters (hazard rate, update variability) and 2) a fixed learning rate error-driven learning model with 2 free parameters (learning rate, update variability). A) Both models provide a reasonable fit to the data in terms of likelihood and neither model is systematically preferred across simulated subjects. B) Simulated data from partially adaptive model shows a characteristic decay in learning rate after task change-points (dark/light blue indicate mean/SEM across simulated subjects). To facilitate predictive checking, data was simulated from Bayesian and fixed learning rate models using maximum likelihood parameter values for each simulated subject. Descriptive analyses were used to separately estimate learning rates for subsets of trials according to how recently the outcome contingencies of the simulated task underwent a fundamental change [54]. Simulated data from Bayesian (yellow) and fixed learning rate (green) models over- and under-estimate learning rate dynamics respectively and thus both fail the predictive checking procedure. In this case the failed predictive check not only reveals model insufficiency, but also sheds light on how the models could be improved (eg. through parametric modulation of learning rate dynamics).

A related strategy for evaluating model sufficiency is through diagnostic techniques based on predicted likelihood functions. There is a rich statistical literature on the problems that can arise when residuals are not distributed according to the expected likelihood function [30]. Cognitive computational models can fall prey to similar issues; non-uniformity or heteroscedasticity of residuals can inflate some measures of goodness-of-fit and give undue influence to particular data points leading to increased variance or even bias in parameter estimates [31,32]. In some cases, differences in the model-predicted and actual likelihood functions can be observed directly by computing residuals and systematic mismatches between the two can be corrected through changes to the existing model [33]. The appropriate likelihood function is particularly important if one considers the possibility that some small proportion of trials are generated by alternative processes other than the model in question. For example, in value-based decision making, the commonly used softmax choice function assumes that choices are increasingly noisy when the differences between alternative choice values are small, and more deterministic when these value differences grow. There is ample evidence for this type of choice function [34], as opposed to alternative epsilon-greedy choice functions in which the level of choice stochasticity is uniform across value differences. But several studies have shown that choice likelihood can deviate substantially from either of these functions (for example as a result of just a few choices driven by a different process altogether, such as attentional lapses), and the failure to take into account this irreducible noise can over- or under-emphasize particular data points and potentially bias results (see figure 2) [17,35–37].

Figure 2. Likelihood function determines which data points are most influential for model fitting. A).

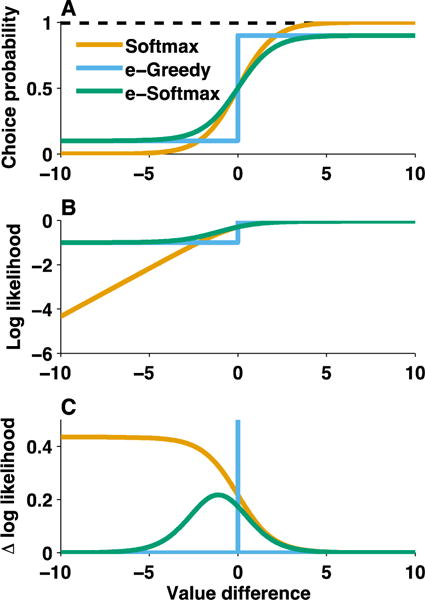
Probability of a rightward choice (ordinate) was computed analytically for an agent performing a two alternative choice task across a range of value differences (abscissa) using three different likelihood functions. While each likelihood function dictates a higher probability of choosing the higher value option, the exact shapes of the functions differ. Softmax (β=1) action selection dictates a sigmoid choice probability function with asymptotes of 0 and 1 for negative and positive value differences respectively (this function assumes increasingly deterministic choice as value differences are large enough). In contrast, epsilon-greedy (e=0.2) action selection dictates a step function with asymptotes at 0.1 and 0.9 (this function assumes exploitation of higher value options with some noise but with no difference in the degree of exploitation as a function of value differences). E-softmax (β=1, e=0.2) is a mixture of these two functions, assuming softmax value-based action selection but with some irreducible noise; it has a sigmoid shape and asymptotes at 0.1 and 0.9. B) Model fitting typically involves maximizing log-likelihood of the data for a given model. Considering the log likelihood of a rightward choice for different levels of value difference provides an indicator of the trials that matter most for this process. For the softmax function, unpredicted rightward responses (large negative value difference) are severely penalized in terms of log likelihood, and hence likelihood maximization will adjust model parameters to increase value differences for rightward choices. In contrast, differences in the log likelihood of expected responses (e.g. positive value differences) are deemphasized such that it is difficult to see the difference between asymptotic log likelihoods of softmax [log(1)] and e-greedy [log(1-e)] functions. C) Depending on the assumed likelihood function, some rightward shifts will be more influential. The impact of a rightward shift on log likelihood, or the derivative of the log likelihood function, is plotted at each value difference for each likelihood function. The likelihood functions differ dramatically in sensitivity to different value differences: 1) softmax gives most credit to improvements in value difference of the most unlikely outcomes, 2) e-greedy only cares about the ones near zero (indifference) and 3) e-softmax cares most about pushing slightly negative value-differences toward (or above) zero. A key takeaway is that choosing a likelihood function has fairly strong statistical implications on the types of errors that will have the greatest effects on model selection and parameter estimation.

So if a model can simulate the key descriptive findings and links computational variables to experimental data through a suitable likelihood function can concerns regarding untested assumptions be set aside? Not necessarily. While these are important criteria for evaluating inferences drawn from a computational theory, they are not typically exclusive to a single model. Thus the question always remains: could the data be better explained through a different set of mechanisms under a different set of assumptions? While this problem is endemic to all of science and not just computational models, one approach to answering this question is to explicitly validate the robustness of model-based findings across a broad range of assumptions. Typically, such validations are conducted using parameters that were originally fixed for simplicity without strong a priori rationale [31,38]. A related strategy for assessing the impact of faulty assumptions is to simulate data from models that make a range of assumptions and attempt to recover information from these models with a separate set of models containing mismatched assumptions. In some cases this strategy has revealed problems, such as with the interpretability of softmax temperature in learning models [15], but in other cases it has highlighted the robustness of specific model-based strategies, such as in the estimation of fMRI prediction error signals using reinforcement learning models under certain conditions [39].

An alternative to explicitly testing the assumptions through which data are linked to a model is to derive and test axioms that should hold irrespective of assumptions [40]. Just as Euclidean geometry postulates that all triangles should have interior angles that sum to 180 degrees, the equations defining a computational model can often be rearranged to identify sets of equalities or inequalities that the entire class of models must obey. One notable example of this strategy comes from economics, where choice consistency, which was established as a fundamental prediction of utility maximization theory, was pivotal for both the falsification of the theory and the subsequent development of better behavioral models [41–43]. Recently, the same approach has been used to test the suitability of reward prediction error models for description of fMRI, electrophysiology, and voltammetry signals [44–47]. While axioms are not mathematically tractable for all models, the basic approach can be followed by identifying testable predictions or boundary conditions through model simulation [48,49]. On its face, the axiomatic approach seems to differ from those discussed above in philosophy: quantitative model fitting promotes inductive reasoning based on reverse inference across a fixed model space, whereas the axiomatic approach lends itself to rejection and revision of failed explanations.

However, this characterization of standard modeling approaches in cognitive science is missing the concept of criticism. Fitting assumptive computational models allows us to induce knowledge regarding the general structure of our world based on specific examples, but rigorous criticism ensures that the knowledge we gain in this way will generalize outside of our model set and experimental space [20,21,50]. Falsification of specific model predictions guides model revisions that make theories more robust and reduces the likelihood of misleading interpretations of experimental results. Through this lens axiomatic methods can be considered as a specific form of criticism tailored to the core assertions of a computational model. It has been noted that the process of careful model criticism can be thought of as obeying an epistemological theory of hypothetico-deductivism, whereby information is gained through rejecting unlikely models, as opposed to through producing support for more likely ones [51].

While we essentially agree with this perspective, we believe that well specified computational theories and the models that instantiate them provide the best of both worlds in terms of philosophy of science: 1) the ability to induce general knowledge from specific data points within a constrained modeling space [52] and 2) the ability to test, reject, and improve upon existing models through a deductive hypothesis testing approach [53]. A balance of these two approaches should allow steady scientific progress through inductive reasoning kept in check by a commitment to falsification of invalid or inappropriate assumptions.

HIGHLIGHTS.

• Computational models extract general principles from specific data.

• However, such principles are conditional on modeling assumptions.

• Faulty assumptions can bias findings and mislead data interpretation.

• The modeler’s toolkit includes several techniques to avoid this pitfall.

• These techniques are critical to broadly interpret computational findings.

Box 1.

Computational model

A mathematical description of the processes giving rise to behavioral or physiological phenomena that in many cases reflects a tractable, concrete instantiation of a cognitive theory.

Model assumptions

The complete set of transformations through which a computational model generates behavioral or physiological data. This includes both fundamental assumptions, which are critical predictions of the overarching cognitive theory, as well as structural assumptions such as about the distributional form, conditional dependency, or stationarity of variables. While structural assumptions are not generally central to the cognitive theory, they nevertheless have important implications for the testing of cognitive theories using computational models.

Parameter

A quantity of the computational model that is allowed to take a range of values to achieve a range of different behaviors and account for individual differences without requiring an entirely different model. For example, one could think about the volume knob on a radio as controlling a parameter that defines the amplitude of sound waves.

Model fitting

The process of adjusting model parameters to values that maximize some utility function, often log likelihood of the observed data.

Model selection

The process of determining which model within a set provides the best description of the data.

Likelihood function

The function used to directly map internal representations (such as the reward value of possible actions in decision making) onto a probability distribution over observed data (the chosen actions).

Latent variable

An element of a computational model that is internally regulated (ie. does not require external selection or adjustment) to allow for different modes of model behavior. For example, action values are adjusted over time in reinforcement learning models to allow for adaptation to changes in action outcome contingency.

Predictive checking

The practice of simulating data from computational models using parameter values fit to empirical data in order to determine which aspects of empirical data the model can or cannot account for.