Removing Orientation-Induced Localization Biases in Single-Molecule Microscopy Using a Broadband Metasurface Mask

Abstract

Nanoscale localization of single molecules is a crucial function in several advanced microscopy techniques, including single-molecule tracking and wide-field super-resolution imaging ¹. To date, a central consideration of such techniques is how to optimize the precision of molecular localization. However, as these methods continue to push toward the nanometre size scale, an increasingly important concern is the localization accuracy. In particular, single fluorescent molecules emit with an anisotropic radiation pattern of an oscillating electric dipole, which can cause significant localization biases using common estimators ^2-5. Here we present the theory and experimental demonstration of a solution to this problem based on azimuthal filtering in the Fourier plane of the microscope. We do so using a high efficiency dielectric metasurface polarization/phase device composed of nanoposts with sub-wavelength spacing ⁶. The method is demonstrated both on fluorophores embedded in a polymer matrix, and in dL5 protein complexes that bind Malachite green ^{7, 8}.

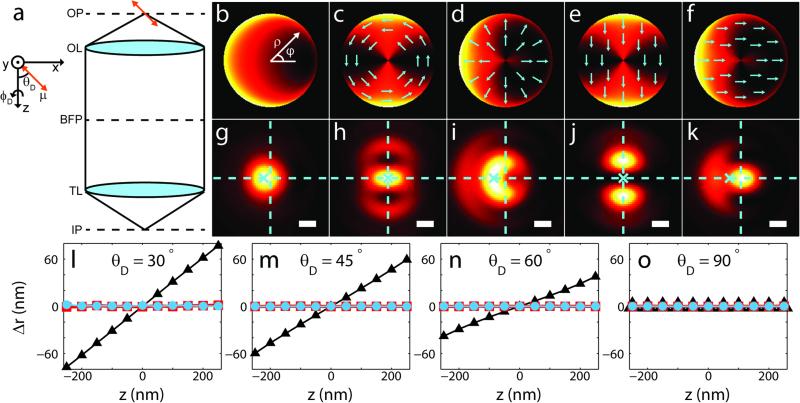
High-precision (~10-nm) molecular localization typically relies on estimators that assume isotropy of the collected fluorescence about the true position of the emitter, such as fitting the image to a two-dimensional Gaussian function¹. However, molecules radiate via their transition electric dipole moments (μ) and so produce the characteristic anisotropic radiation distribution of an oscillating electric dipole⁹. Thus the shape of the image appearing in a microscope is highly dependent on the orientation of the molecule relative to the microscope optics¹⁰. Fig. 1a shows a simplified microscope schematic. The dipole emitter's orientation is defined by two angles (Fig. 1a): the polar angle θ_D made between μ and ẑ (optical axis), and the azimuthal angle ϕ_D about ẑ. Throughout this letter we consider the distribution of light in both the microscope's image and Fourier planes, the latter of which is located at the back focal plane (BFP) of the objective. The anisotropic intensity distribution at the BFP for an example dipole with orientation (θ_D = 45°,ϕ_D = 0°) is shown in Fig. 1b. This asymmetric illumination of the BFP gives rise to an asymmetric image (Fig. 1g). The centroid of the image and the true underlying molecular position in Fig. 1g are offset by 70 nm, revealing an orientation-induced localization bias that has been highlighted in previous studies^{2, 3, 5, 11}. Clearly such poor accuracy in molecular localization must be considered when reporting ~10-nm localization precision.

Figure 1. Concept.

a, Microscope schematic: object plane (OP), objective lens (OL), back focal plane (BFP), tube lens (TL), and image plane (IP). b, Simulated intensity at BFP for molecule with (θ_D = 45°, ϕ_D = 0°). BFP coordinates (ρ, φ). c, Azimuthally-polarized component of the light in b. Heatmap depicts light intensity, blue arrows show polarization basis. d, Radially-polarized component of the light in b. e, Same intensity distribution as in c, but polarization axis rotated to −y. f, Same intensity distribution as in d, but polarization axis rotated to x. g-k, High-resolution image resulting from same example molecule, with z_D = 250 nm and each panel corresponding to the BFP case directly above. Dashed crosshairs mark molecule position, “x” marks image centroid. Scale bars = 200 nm. l-o, Simulated localization bias Δr at various θ_D for standard PSF (black triangles), phi-PSF (red squares), and y-phi-PSF (blue circles).

Ensuring sufficient rotational mobility of each molecular dipole label is one way to avoid this mislocalization^{5, 12}. However, the degree of rotational freedom depends on the labeling scheme and warrants careful characterization. In addition, the rotational freedom may be purposely restricted for certain applications such as biological motor tracking^{13, 14}.

For the case of a rotationally fixed dipole emitter, one approach is to use a sophisticated image model that takes orientation into account^{15, 16}, or to directly estimate the bias and correct it computationally^{11, 17}. Such techniques have been shown to work in principle, but they are limited by the need to accurately model the imaging system, are computationally expensive, or require relatively high signal-to-noise. A more direct removal of the bias is desirable.

A recent theoretical study found that an azimuthal polarization filter located at the BFP would provide such a bias removal¹⁸ (details in Supplementary Information). Radially polarized light contains contributions from a basis dipole oriented along z, as well as ones along x and y. This superposition induces the asymmetry. By contrast, the azimuthally polarized portion contains only contributions from the x and y basis dipoles. The (inversion-) symmetric intensity distribution of the azimuthally polarized component of the light for the same example orientation is shown in Fig. 1c. The corresponding point spread function (“phi-PSF”) is also symmetric, and the localization bias is completely expunged (Fig. 1h). The rejected radially polarized light carries the entirety of the asymmetry producing the bias (Fig. 1d, i).

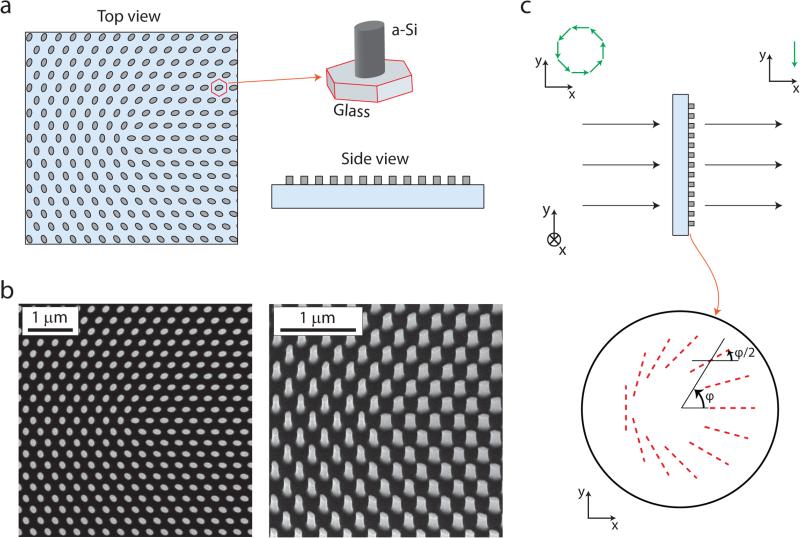
We report the first (to our knowledge) experimental demonstration of single-molecule localization bias removal via azimuthal filtering. Segmented polarizers are often used in laser science to produce azimuthally polarized beams¹⁹, but the inherent macroscopic approximation of the filter pattern is not ideal for photon-limited single-molecule imaging. Other more sophisticated schemes (e.g. using two spatial light modulators and appropriate wave plates²⁰) could work, but generally require additional optics to compensate for an incurred spiral phase modulation¹⁹. Instead, we designed and employed a mask based on a novel type of high-efficiency dielectric metasurface that provides complete control of phase/polarization with subwavelength spatial resolution⁶. The metasurface consists of an array of amorphous silicon nanoposts with elliptical cross sections arranged on a hexagonal lattice with subwavelength period (Fig. 2a-b). The nanoposts act as short elliptical-cross-section waveguides with strong birefringence. They behave as uncoupled scatterers and can locally modify both polarization and phase of transmitted light to any desired form⁶.

Figure 2. Details of mask.

a, Schematic drawings of a metasurface y-phi mask composed of an array of a-Si nanoposts on a glass substrate. The elliptical-cross-section nanoposts behave as uncoupled birefringent scatterers with principal axis orientation along the ellipse diameters. b, Scanning electron micrographs of the top view (left), and tilted view (right) of a fabricated metasurface y-phi mask. c, Schematic illustration of a y-phi mask which converts azimuthally polarized light to y-polarized light. The mask locally functions as a half-wave plate whose principal axis orientation (shown by red dashed lines) gradually varies across the mask.

For this application, a specific nanopost array was designed to rotate the local polarization of the light at the BFP such that radially (ρ; see coordinate definitions in Fig. 1b) polarized light is converted to x and azimuthally (ϕ) polarized light is converted to –y (Fig. 2c) with high experimental efficiency of 86.5% (Supplementary Information). We refer to the mask as the “y-phi” (as in “WiFi”) mask. To effectively remove ρ-polarized light we can place the y-phi mask at the BFP followed by a y-oriented linear polarizer. In the Fourier plane this produces light that resembles Fig. 1e—the intensity distribution is the same as in Fig. 1c, but the polarization has been rotated. The resulting y-phi-PSF (Fig. 1j) is symmetric, but inequivalent to the phi-PSF (Fig. 1h). Instead, the additional polarization rotation renders the light concentrated into two bright lobes, with a line of symmetry along the direction ϕ_D. The response of the y-phi-PSF as a function of (θ_D,ϕ_D, z_D), where z_D is the z position of the dipole emitter, is shown in Supplementary Fig. 1. The y-phi mask acts correspondingly on radially polarized light (Fig. 1f, k).

We simulated noisy images to compare the behavior of the phi-, y-phi-, and standard PSFs. Fig. 1l-o depicts the localization biases resulting from simple Gaussian-based estimators of the images. As expected, the standard PSF shows large position biases when θ_D < 90° and |z_D| > 0, resulting in an apparent lateral shift of the molecule as z_D is varied; the phi-PSF and y-phi-PSF both completely remove this bias.

While the phi-PSF removes localization bias, it worsens the localization precision relative to that of the standard PSF, largely due to the fact that the azimuthal polarization filter reduces the number of detected signal photons¹⁸ (Supplementary Fig. 2). Surprisingly, both simulated Gaussian fitting and the computed Cramer-Rao lower bound (CRLB) ^{21, 22} show that the y-phi-PSF recovers much of this precision, despite the fact that the number of detected photons is the same between the phi-PSF and y-phi-PSF (Supplementary Fig. 3). Evidently, splitting the light into two lobes (Fig. 1j) is more than offset by the suppression of the side lobes of the phi-PSF (Fig. 1h). Furthermore, the lobes of the y-phi-PSF rotate as a function of ϕ_D, yielding precise estimations of ϕ_D (Supplementary Fig. 3).

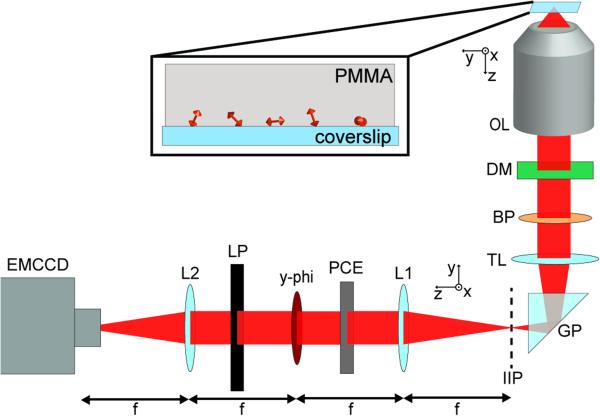
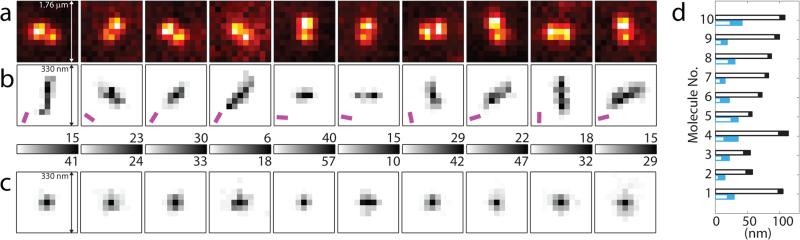
Figure 3 sketches the setup used for experimental demonstration. Our first sample consisted of DCDHF-A-6 fluorophores²³ immobilized in a thin layer of PMMA polymer (Fig. 3 inset). Each field-of-view was imaged continuously as the objective was scanned in z from −200 nm to 200 nm. Fig. 4a shows in-focus y-phi-PSF images of ten example molecules. The various orientations of the y-phi-PSF indicate the different underlying ϕ_D values. Each molecule was also imaged with the y-phi mask and polarizer removed: Fig. 4b shows two-dimensional histograms of the lateral positions estimated using the standard PSF as the objective was scanned in z. Due to the z-dependent localization bias, each of these molecules appears to shift in the direction of the estimated ϕ_D, yielding severely elongated localization clusters. By contrast, Fig. 4c depicts the analogous localization histograms obtained with the y-phi mask and polarizer in place. The bias removal results in localization clusters that are dramatically more symmetric and concentrated. Fig. 4d depicts the distance between the apparent lateral positions at either end of the depth range for both PSFs. We see improvement as large as a factor of ~7 (from 80 ± 2 nm to 11 ± 4 nm) such that the bias disappears into the photon-limited localization precision. Supplementary Fig. 4 shows similar results for 15 additional example molecules.

Figure 3. Experimental setup.

(Inset) Sample consisting of dyes spun in layer of PMMA. Fluorescence collected with the objective lens (OL), filtered through dichroic mirror (DM) and bandpass (BP). Within the body of the commercial inverted microscope the tube lens (TL) focuses the collected light onto the intermediate image plane (IIP). Between the TL and the IIP there is a reflecting glass prism (GP). A 4f optical processing unit consisting of two lenses (L1, L2) was built outside the microscope. The y-phi mask was placed at the conjugate Fourier plane. A linear polarizer (LP) was placed immediately after the y-phi mask in order to pass only y-polarized light. A phase compensating element (PCE) had to be placed before the y-phi mask in order to compensate for the reflection from the GP and birefringence of the DM (see Supplementary Information). Images were recorded on an EMCCD camera.

Figure 4. Experimental results.

a, Experimental images of ten in-focus example molecules with different orientations, as obtained using the y-phi mask (pixel size = 160 nm). Images are averages of ten 300-ms exposures. b 2D histograms of (x, y) localizations of each molecule over z scan from −200 to 200 nm (bin size = 20 nm), as obtained with the standard PSF (i.e. y-phi mask and linear polarizer removed). c, Localization histograms obtained with y-phi mask and linear polarizer in place. Numbers above and below color bars indicate max number of localizations per bin in b, c, respectively. Mean ϕ_D estimated from y-phi-PSF marked in b by magenta bars. d, Mean distance between (x, y) localizations determined at each edge of z scan, from first scan of each molecule. Black = standard PSF, blue = y-phi-PSF. Filled portions give uncertainty range (± S. E. M.).

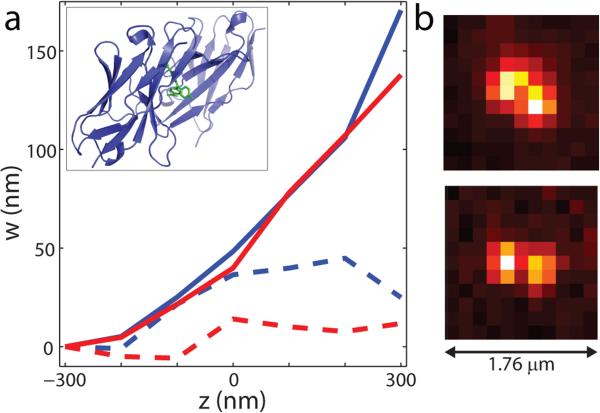
As a final biological demonstration of our method we imaged dL5, a Fluorogen Activating Protein consisting of a tandem dimer of antibody variable light chain domains that binds malachite green (MG) (Fig.5a inset)^{7, 8}. This protein is a recently developed genetically directed label for use in cells. Since the fluorogen is bound strongly, the orientation of the emission dipole is restrained relative to the protein, and thus would thus benefit from azimuthal filtering in localization microscopy. The dL5 complexes were cast on a poly-L-lysine layer on a glass coverslip and the same basic imaging procedure was repeated. Fig. 5a shows successful removal of localization bias in the lateral direction w along the estimated in-plane orientation for two such dL5 complexes (raw images in Fig. 5b).

Figure 5. Biological demonstration.

a, Dipole-induced lateral shift of dL5 complexes 1 (blue) and 2 (red) along the direction of estimated in-plane orientation w = xcosϕ_D + ysinϕ_D. Estimates of ϕ_D were 34 ± 4° and 9 ± 2° (± standard deviation) for dL5 complexes 1 and 2, respectively. Solid lines show shift with standard PSF, dashed lines show results from y-phi-PSF. Data depict the average of two scans for each dL5 complex. (Inset) structure of dL5 Fluorogen Activating Protein showing the tandem dimer variable light chain domains (purple) and bound Malachite green (green)⁷. b, Y-phi-PSF images of dL5 complexes 1 (top) and 2 (bottom).

We have experimentally demonstrated an all-optical, direct removal of the orientation-induced lateral mislocalization of single molecules based on azimuthal polarization filtering in the microscope's Fourier plane. The y-phi mask is compatible with typical wide-field microscopes since the parts can be added to the exterior. In many biological samples fluorophore labels will display intermediate rotational mobility. This is compatible with our scheme since the method ensures an inversion-symmetric image for all degrees of floppiness. Only the estimator needs to be adjusted. We reserve a more thorough investigation of rotational mobility for future work.

One constraint is that the silicon absorbs toward the visible range, requiring redder fluorophores. Ongoing work should lift this limitation. We hope this work inspires future collaborations between the metamaterials and single-molecule communities: while Fourier-plane engineering with more conventional optics has already proven extremely valuable in single-molecule imaging²⁴, the exquisite control provided by metasurfaces will lead to even more dramatic advances in the future.

Methods

Simulations

Simulated distributions of light at the BFP were produced by propagating dipole emission fields using the appropriate Green's tensor^{24, 25}. The mathematical formalism, including symmetry considerations for the current application, is provided in the Supplementary Information. We assumed a numerical aperture of 1.4 and emission wavelength of 686 nm, consistent with the peak emission of DCDHF-A-6²³. Fig. 1 and Supplementary Fig. 3 assume the indices of refraction of both the sample and imaging medium are matched to that of immersion oil (n = 1.518). In addition, Supplementary Fig. 5 considers an emitter placed in water 1 μm above a water-glass interface (e. g. as in a cell imaging measurement), while Supplementary Fig. 6 corresponds to the molecule embedded at the bottom of a 30-nm layer of PMMA, as in our first demonstration. To simulate the action of the y-phi mask we effectively multiplied the field computed at the BFP by the spatially-varying Jones matrix J:

$$\mathbf{J}=\left[\begin{array}{cc}\hfill \cos \phi \hfill & \hfill \sin \phi \hfill \\ \hfill \sin \phi \hfill & \hfill -\cos \phi \hfill \end{array}\right]$$

Simulated images were produced by taking the appropriately scaled Fourier transform of the field at the BFP (details in Supplementary Information), with 100x magnification. High-resolution images (20-nm sampling) were first produced then binned into pixels of side length 160 nm to match the conditions of our imaging setup. For simulated data we realized 10⁴ noisy images for each data point. We assumed Poisson noise with photon numbers and background as stated in Fig. 3. Mean signal photons were scaled as necessary for polarization, relative detection efficiency (e.g. ~0.7, 0.8, and 0.9 for θ_D = 30°, 45°, and 60°, resp.), and relative pumping efficiency sin²θ_D (assuming a collimated, circularly polarized source). We fit each noisy image to a Gaussian-based estimator using the MATLAB function “lsqnonlin”.

CRLB calculations

CRLB data is presented in Supplementary Figs. 3, 5, and 6. To compute the CRLB of σ_r and σ_ϕD we assumed Poisson noise and constructed the Fisher Information (FI) matrix as outlined in previous work²². The square roots of the diagonal elements of the FI matrix give the CRLB for each parameter. To compute σ_r we constructed a 2×2 FI matrix with parameters (x, y); to compute σ_ϕD the FI matrix was 3×3 with parameters (x, y, ϕ_D). This distinction was made because we noted that σ_r actually worsens when ϕ_D is included because off-diagonal elements appear in the FI matrix, representing a propensity to confuse the estimated parameters. We chose to report the CRLB of σ_r in this way since typical position estimators of the standard PSF don't fit ϕ_D.

Mask design and fabrication

Post height, lattice constant, and ellipse diameters were used as design parameters for optimization of the metasurface y-phi mask shown in Fig. 2a. For each set of the design parameters, transmission coefficients t_y and t_x were computed for the uniform array shown in Supplementary Fig. 7a using the rigorous coupled wave analysis (RCWA) technique with a freely available software package²⁶. These transmission coefficients were computed at 8 wavelengths: 650 nm to 720 nm, in steps of 10 nm. Wavelength dependence of the refractive index and extinction coefficient of amorphous silicon (a-Si) was considered in these simulations. The a-Si refractive index and extinction coefficient values used in the simulations were measured using a variable angle spectroscopic ellipsometer, and are shown in Supplementary Fig. 7b. For each design, the φ-to-y conversion efficiency (η) was obtained at each wavelength using the simulated transmission coefficients t_y and t_x. A weighted average of the conversion efficiency values was used for comparison of different metasurfaces with different design parameters. The conversion efficiency values were weighted by the relative power density emitted from the fluorescent dye at each wavelength. The emission spectrum of DCDHF-A-6 was approximated by a Gaussian function centered at 686 nm and with 60 nm full width at half maximum bandwidth. Using this approach, optimum values of 365 nm, and 325 nm were found for the post height and lattice constant, respectively. Supplementary Fig. 7c shows the average conversion efficiency values for an array with the optimum lattice constant and post height as a function of the elliptical post diameters. Diameters of D_x = 180 nm, and D_y = 110 nm (indicated by a black dot in Supplementary Fig. 7c) were selected to reduce the sensitivity to fabrication induced errors in the diameters of the elliptical posts, and to achieve an average conversion efficiency of 88%. The simulated conversion efficiency of the optimized metasurface mask as a function of wavelength is presented in Supplementary Fig. 7d.

A metasurface y-phi mask with a diameter of 4.2 mm was fabricated on a 500-μm-thick fused silica substrate using standard nanofabrication techniques. First, a 365-nm-thick layer of hydrogenated a-Si was deposited on the substrate using a 5% mixture of silane in argon at 200° C through the plasma enhanced chemical vapor deposition technique. Then,a ~300-nm-thick positive electron beam resist (ZEP 520-A, Zeon Chemicals) was spin-coated on the a-Si layer and was baked at 180° C for 3 min. To avoid static charging effects during electron beam lithography, a ~60-nm-thick layer of a water-soluble charge dissipative conductive polymer (aquaSave, Mitsubishi Rayon) was spin-coated on the resist and baked at 70° C for 5 min. After writing the nanopost pattern on the resist using electron beam lithography, the charge dissipative polymer was dissolved in water, and the resist was developed by immersing the sample in a solvent (ZED-N50, Zeon chemicals) for 3 min followed by 30 sec rinse in methyl isobutyl ketone. The pattern was subsequently transferred through a lift-off process to a 70-nm-thick layer of aluminum oxide which was evaporated on the resist after its development. The patterned aluminum oxide layer was used as a hard mask for inductively coupled plasma reactive ion etching of the a-Si layer in a mixture of SF₆ and C₄F₈ gases. Finally, the aluminum oxide mask was removed in a 1:1 mixture of ammonium hydroxide and hydrogen peroxide at 80° C. Scanning electron microscope images of the top and tilted views of the final device are shown in Fig. 2b.

Additional characterization of the y-phi mask is described in the Supplementary Information and Supplementary Fig. 8.

Experimental

DCDHF-A-6 was dissolved in 1% poly(methyl methacrylate) in toluene to a final concentration of ~2 nM. The solution was spin-coated on ozone-etched glass coverslips, then samples were mounted on an inverted Olympus IX71 microscope and pumped with a 561-nm laser (CrystaLaser) in epi-illumination mode (peak intensity ~125-400 W/cm²) after reflection from a 561 dichroic beam splitter (Semrock). Fluorescence was collected through an oil immersion objective (Olympus UPlan-SApo 100×/1.40) and passed through a 675/50 band-pass emission filter (Chroma Technology). The 4f system of Fig. 3 consisted of two achromatic doublet lenses (Edmund Optics, 50mm Dia. × 150mm FL, VIS-NIR Coated). The linear polarizer (Newport 20LP-VIS-B) was placed just after the y-phi-mask. A broadband λ/2 wave plate (B. Halle 500-900 nm achr. L) was placed just before the mask to act as a phase compensating element (PCE in Fig. 3) in order to partially offset the phase incurred from reflection off the glass prism within the Olympus IX71 plus the birefringence of the dichroic (see Supplementary Information). Images were recorded on an EMCCD camera (Andor iXon+) operating with EM gain either 100 or 300, at 3.33-Hz frame rate.

Each field-of-view (FOV) was imaged with the y-phi mask and linear polarizer in place while scanning the objective in z using a piezo (Mad City Labs C-Focus) from −300 nm to +300 nm (only the center 400 nm was analyzed) in 100-nm steps, with 10 camera acquisitions/step. The linear polarizer and y-phi mask were then removed and a z scan was taken of the FOV in clear aperture. Finally, a set of defocused (~1 μm toward the air) images was recorded (Supplementary Fig. 9) to check for consistency in lobe orientation. The whole procedure was repeated 5 more times per FOV. Data were analyzed using custom MATLAB software. Molecules were hand-selected. Background was estimated from a nearby region of the image and subtracted. Mean signal and background levels for the molecules depicted in Fig. 4 are given in Supplementary Table 1. A small amount of asymmetry was noted in the intensity of the lobes of the y-phi mask, which may be a result of small residual aberrations (e. g. coma) in the imaging system²⁷ (Supplementary Fig. 10 and accompanying text), or from imperfections in the mask itself. Future applications may require further correction of these residual aberrations.

In order to visualize single dL5-MG complexes, we prepared recombinant dL5 protein using a pET21A expression vector in Rosetta gami II DE3 cells (Novagen). Protein expression and purification was performed as per a previous reported protocol.⁸ This protein stock was diluted in PBS (pH 7.4) and supplemented with MG-ester such that the final concentration of dL5 and MG in the solution were 10nM and 100pM, respectively. 50 μL of this solution was incubated on etched glass coverslips (FisherFinest, #1.5, 22×22 mm) that were coated with 0.01% (w/v) Poly-L-Lysine. After a 15 minute incubation, the solution was washed twice using PBS and dried for 2 hours at room temperature.

Imaging experiments with the dL5 samples were conducted the same manner as for DCDHF-A-6, with minor differences. The spectrum of the labeled protein required a 647-nm laser pump (Coherent OBIS), which required a different dichroic beamsplitter (Semrock Di01-R405/488/561/635). This dichroic induced a different relative phase lag between x and y polarizations, so to compensate a second long-pass dichroic (Semrock FF650-Di01) was added to the emission path in addition to the λ/2 wave plate from the DCDHF-A-6 measurement. The fluorescence was passed through a 650 long-pass filter (Omega Optical) and a 700/75 band-pass filter (Chroma Technology). We noted a larger lobe asymmetry in these experiments than in the DCDHF-A-6 experiments, which may have resulted from a combination of the facts that the mask was not optimized for the dL5 emission spectrum, and that the different optical elements produced stronger aberrations. These issues can be improved upon in future applications. Because the bound MG are inherently less bright and stable than DCDHF-A-6, we binned image acquisitions into 3.9-s effective exposures to obtain sufficient signal-to-noise with either the standard or y-phi imaging configurations.