Abstract
Premise of the study:
Root biomass is an important trait often disregarded in woody perennial selection due to the challenge and expense of accurately and efficiently measuring large populations. In this study, we aim to develop a simple method that can predict root dry weight within a diverse shrub willow (Salix) breeding population representing species hybrids and their parents using root electrical capacitance (REC).
Methods:
The REC method was tested on plants started from cuttings and grown in pots with potting mix in the greenhouse for 11 wk to assess the relationship of REC with 24 biomass traits and its usefulness in allometric models for root and stem dry biomass.
Results:
Strong linear and positive correlations were found between REC and root dry biomass (r = 0.88). The total proportion of variance of root and stem dry biomass explained by predictors in multiple regression was 85% and 69%, respectively. The relative importance of predictor variables in allometric models was dominated by the contribution of REC.
Discussion:
This work provides an efficient and nondestructive technique to indirectly quantify root biomass of genetically diverse shrub willow progeny, which has great promise for selection of genotypes with varying root biomass and for the accurate estimation of belowground carbon sequestration.
Keywords: bioenergy, biomass, breeding, phenotype, selection, short-rotation coppice
The measurement of belowground traits of woody perennials has been the subject of renewed interest in recent years, because root biomass and architecture are critical for drought tolerance and for long-term carbon sequestration (Ericsson et al., 1996). Measurement of root biomass is a tremendously difficult and painstaking task in woody perennial breeding programs, as it requires careful washing, filtering, drying, and weighing fine root tissues, and thus is often avoided. For decades, electrical capacitance has been used to estimate the aboveground biomass of herbaceous perennials (Currie et al., 1987) and forest plantations (Lekas et al., 1990), but few root electrical capacitance (REC) studies have focused on clonal woody perennial plants as a model for predicting root biomass. Previous work on the estimation of root biomass using the REC method has primarily focused on hydroponically grown seedlings (Rajkai et al., 2005; Repo et al., 2005; Cao et al., 2011; Dietrich et al., 2012; Cseresnyés et al., 2013; Kormanek and Tomasz, 2015) or a limited number of genotypes (Whitlow et al., 1992; Pitre et al., 2010).
Dalton (1995) provided the first and most widely accepted conceptual model for using electrical capacitance as an in situ measurement for assessing root development. Electrical capacitance is measured in farads (F) and is considered the ability of a body (i.e., plant root tissue) to store an electrical charge, such that when charged with one coulomb (C) of energy, there is a potential difference of one volt (V), where F = C/V. His method assumes that root capacitance is equivalent to a parallel resistance-capacitance circuit formed by the interface between soil and water and the root surface; or simply, that roots are equivalent to cylindrical capacitors where the epidermis and xylem are external and internal electrodes, respectively. Capacitance is formed by the polarization and relaxation of root membranes, which promotes fluctuations in amplitude and phase of the AC signal (Repo et al., 2000). This root–soil interface exhibits a capacitance proportional to the size of the membranes.
What exactly REC measures is debatable. Using hydroponically grown barley seedlings, Dietrich et al. (2012) argued that capacitance is linearly correlated with the sum of root cross-sectional areas at the solution surface and inversely related to the distance between the plant electrode and the solution surface. Likewise, the capacitance of barley is not determined by actual root biomass but by the cross-sectional area of roots at the solution surface (Dietrich et al., 2013). The distinction between this model and Dalton’s is that Dalton generalized roots to be cylindrical capacitors acting in parallel, whereas Dietrich argued that the capacitances of tissues along an unbranched root can be considered to be connected in series and the entire root system, in parallel. Although Repo et al. (2005) found a strong linear relationship between the cross-sectional area and the resistance of the stem, there was no difference in the relationship between resistance and cross-sectional area with or without the roots attached. Ellis et al. (2013) found little evidence that capacitance alone could be related to root mass, but these measurements could be used together with approximations of average root tissue fresh density to estimate coarse root length.
Dietrich et al. (2012) provides good evidence to modify the conceptual framework of Dalton’s original model, yet all analyses were based on fresh root mass of a hydroponically grown herbaceous annual. Compared to dry mass, wet mass can be extremely variable and heavily dependent on environmental factors (Lam et al., 2008) and is not an ideal estimate of root biomass for shrub willow. Furthermore, the compositional differences and developmental stage between seedling and mature, fully developed root systems cannot be ignored.
Here, we simply assume the Dalton model using a diverse breeding population of shrub willow (Salix; Salicaceae), with no assumptions concerning root morphology or architecture. Shrub willow has been bred as an energy crop in Europe since the early 1970s with the goal of producing fast-growing bioenergy feedstock cultivars that are high-yielding, genetically diverse, pest and disease resistant, and able to grow on marginal land without competing with food crops (Karp et al., 2011; Smart and Cameron, 2012). Shrub willow are dioecious riparian species commonly found near riverbanks and streambeds and are well adapted to the hypoxic conditions of wetlands (Kuzovkina et al., 2008). More than 350 species have been described in Salix L. (Argus, 2005; Lauron-Moreau et al., 2015) and have tremendous ecological amplitude, found within marginal and riparian habitats from the arctic plains to the subtropics (Kuzovkina et al., 2008). As the challenge to meet global energy objectives increases (Kriegler et al., 2014) along with global temperatures (Walther et al., 2002; Whiteman et al., 2013), the demand for low-input renewable bioproducts (Rose et al., 2014) gives shrub willow great potential as a competitive bioenergy feedstock for biomass production and conversion to biofuels to offset fossil fuel usage (Bonosi et al., 2013).
Our main objectives of this study were: (1) to investigate the relationship between electrical capacitance and root dry weight in diverse shrub willow families, (2) to contrast REC of parent genotypes and their hybrid progeny, (3) to study the relationship between REC and above- and belowground biomass traits, and (4) to evaluate the relative importance of REC in allometric models for the prediction of root and stem dry weight.
MATERIALS AND METHODS
Plant material
Parent genotypes and randomly chosen progeny of Salix purpurea L. (2n = 2x = 38), S. miyabeana Seemen (2n = 4x = 76), and S. viminalis L. (2n = 2x = 38) species crosses were grown from stem cuttings (20 cm) in 12-L plastic pots with peat moss–based potting mix (Fafard, Agawam, Massachusetts, USA) to evaluate growth traits under greenhouse conditions over an 11-wk period. Families consisted of 12 progeny individuals and their parents from diploid intraspecific S. purpurea F1 and F2 crosses, two reciprocal diploid interspecific crosses (S. purpurea × S. viminalis), three triploid interspecific crosses (S. purpurea × S. miyabeana, S. miyabeana × S. viminalis, and S. viminalis × S. miyabeana), and an intraspecific tetraploid cross of S. miyabeana for a total of 104 genotypes (Table 1). One exception is that one of the parents of the S. miyabeana family (SX64, male parent of 425) was not included. Plot was defined as a single cutting planted in a pot; pots were arranged in a randomized complete block design with four replicate blocks. Two blocks were located on benches in one greenhouse with the other two blocks in an adjacent greenhouse set for identical growing conditions. Supplemental greenhouse lighting was provided on a 14-h day:10-h night regimen with maximum daytime temperature of 26°C and a nighttime temperature of 18°C. Beyond weekly applications of beneficial insects and mites for pest management, no pesticides were required, as there were no symptoms of biotic or abiotic stress on any plant material throughout the length of the study. Liquid fertilizer (Peter’s 15-16-17 Peat-Lite Special; Scotts Miracle-Gro Company, Marysville, Ohio, USA) was applied weekly after week 4 according to manufacturer recommendations. The age of plants and the frequency of trait measurements is depicted in Table 2.
Table 1.
Description of family, pedigree, and generation in intraspecific and interspecific crosses of shrub willow (Salix; Salicaceae).
| Family ID | Female parent | Male parent | Pedigree | Fn | Ploidy |
| 082 | 94006 | 94001 | S. purpurea × S. purpurea | F1 | 2x |
| 317 | ‘Wolcott’ | ‘Fish Creek’ | S. purpurea × S. purpurea | F2 | 2x |
| 407 | 94006 | ‘Jorr’ | S. purpurea × S. viminalis | F1 | 2x |
| 421 | 07-MBG-5027 | 94001 | S. viminalis × S. purpurea | F1 | 2x |
| 415 | 94006 | 01-200-003 | S. purpurea × S. miyabeana | F1 | 3x |
| 423 | 07-MBG-5027 | 01-200-003 | S. viminalis × S. miyabeana | F1 | 3x |
| 430 | 01-200-006 | ‘Jorr’ | S. miyabeana × S. viminalis | F1 | 3x |
| 425 | 01-200-006 | SX64 | S. miyabeana × S. miyabeana | F1 | 4x |
Table 2.
List of biomass-related variables including their descriptions and units.
| Trait abbreviation | Description | Units | Measured (WAP) |
| Aboveground | |||
| SDW | Stem dry weight | g plant−1 | 11 |
| SSL | Sum stem length | cm | 2–11 |
| MSL | Mean stem length | cm | 2–11 |
| MXL | Maximum stem length | cm | 2–11 |
| MSA | Mean stem area | cm2 | 11 |
| SSA | Sum stem area | cm2 | 11 |
| RGR | Relative growth rate | cm d−1 | 3–11 |
| PSN | Primary stem number | # | 11 |
| ASN | Axial stem number | # | 5, 10 |
| LDW | Leaf dry weight | g plant−1 | 11 |
| SPD | SPAD | SPAD units | 2, 4, 10, 11 |
| PHE | Vegetative phenology | 0→5 | 2–3 |
| MSD | Mean stem diameter | cm | 11 |
| SSD | Sum stem diameter | cm | 11 |
| LFA | Leaf area | cm2 | 11 |
| SLA | Specific leaf area | cm2 g−1 | 10 |
| LMA | Leaf mass per area | g cm−2 | 10 |
| Belowground | |||
| REC | Root electrical capacitance | nF | 11 |
| RDW | Root dry weight | g plant−1 | 11 |
| CDIA | Cutting diameter | cm | 11 |
| CDW | Cutting dry weight | g plant−1 | 11 |
| RDIA | Mean root diameter | cm | 11 |
| PRN | Primary root number | # | 11 |
| SRN | Secondary root number | # | 11 |
| TRN | Total root number | # | 11 |
Note: WAP = weeks after planting.
Root electrical capacitance
Root electrical capacitance was measured using a DCM3 digital capacitance meter (UEi Test Instruments, Beaverton, Oregon, USA) with conductance ranges of 200 pF to 20 mF, and a ±1% reading and digital accuracy below 2000 μF. Custom-designed electrodes were attached to the capacitance meter as follows: the positive lead wire was connected to a 10-gauge (0.27 × 20 cm) solid copper wire, while the negative lead was connected to a 7.5 × 1.0 cm copper-plated gator clip. The copper wire attached to the positive lead of the capacitance meter was inserted 15 cm into the potting mix approximately 10 cm from the cutting, and the negative lead was clamped to the cutting 2 cm above the surface of the potting mix. Root electrical capacitance was measured approximately 2 h after pots were completely saturated with reverse-osmosis water immediately after harvesting aboveground biomass. To minimize within-plot variation, four readings were taken equidistant to the cutting and then averaged for each pot. The appropriate experimental nominal capacitance was determined to be 200 nF or 20 μF (if REC >200 nF) at 820 and 82 Hz test frequencies, respectively.
Aboveground biomass traits
Starting approximately 7 d after planting, the vegetative phenology stage (PHE) of each plot was scored 7, 9, 11, 13, and 15 d after planting (DAP). Vegetative phenology was scored as six stages described as: stage (0) dormant axillary buds are tightly closed and covered by bud scales, (1) axillary buds begin to swell and change color, (2) generative buds burst with visible leaves, (3) leaves emerge and begin to unfold, (4) unfolded leaves begin expanding, and (5) at least two leaves are fully expanded.
Primary stems were defined as those emerging from dormant axillary buds and ≥6 cm in length. Secondary stems were defined as emerging from axillary buds on the primary stem from current-season growth (sylleptic) and were counted as the total number of secondary branches within each plot with a vegetative phenology stage ≥3. The length of all stems ≥6 cm per plant was measured from the base of the primary stems at the original cutting surface to the distal shoot tip (the inner-whorl of the leaf primordia). Starting in the second week of the study until its termination, all primary stems were measured within each plot once a week over a period of nine weeks.
Mean stem length (MSL) per plant was the mean of individual stem lengths, and sum of stem length (SSL) was the sum of all primary stems measured for a plant. The diameter of each primary stem within a plot was measured at the base in the final week of the study using a digital caliper. The stem diameters were used to calculate mean stem area (MSA) for all of the stems on a plant, and all stem areas were summed to determine sum of stem area per plant (SSA). Only primary stems >20 cm in length were used to calculate stem traits. Stem and leaf biomass were harvested separately from each plot, dried in an oven to constant weight at 65°C, and weighed to determine stem dry weight (SDW) and leaf dry weight (LDW).
Leaf area (LFA) was determined using a portable leaf area meter (model no. CI-203; CID Bio-Science, Camas, Washington, USA). A representative leaf from each plot was scanned, then excised, dried to constant weight at 65°C, and weighed to obtain leaf dry weight. Petioles were excluded from leaf area and dry weight measurements. Specific leaf area (SLA) was calculated as the ratio of the total leaf area and dry weight as well as its inverse, leaf mass per area (LMA). As an indirect measurement of leaf chlorophyll and nitrogen content, leaves were measured using a SPAD 502 Chlorophyll Meter (Spectrum Technologies, Aurora, Illinois, USA). Four fully expanded leaves from the upper 25% of the canopy were measured and averaged for each plant at weeks 2, 4, 6, and 10.
Belowground biomass traits
Root biomass was harvested from a subset of 20 pots (2–3 unique individuals per family) that were selected from the 416 pots as representing a distribution of capacitance readings, ranging from 70.5 nF (clone 13X-425-110) to 283.8 nF (clone 13X-430-033). To assure the retrieval of fine root hairs, potting mix was washed from roots by first soaking root balls in water for 12 h without their pots, then rinsing them by hand repeatedly, and decanting into 2.4-mm and 1.0-mm aluminum test sieves. Root samples were considered appropriate for dry weight analysis when root biomass was visually free of debris. Root biomass and cuttings were separately dried in an oven and weighed to obtain root dry weight (RDW) and cutting dry weight (CDW). The base diameter and number of each primary root as well as the average distance between secondary root primordia of primary roots were measured using an Absolute Digimatic digital caliper (model no. CD-6″CSX; Mitutoyo USA, Aurora, Illinois, USA).
Statistical analysis
All statistical analyses were performed in the statistical computing environment, R 3.2.2 (R Development Core Team, 2011). Traits (Table 2) were tested for paired associations (α = 0.05) with REC using the cor.test function. To determine the best transformation of REC for the response variables, the Box-Cox procedure was used. Only SDW and LDW were found to be log-linear (λ∼0) to REC; consequently, a log transformation of REC was performed in linear and multiple regressions for these traits. When significant differences were observed, Tukey’s studentized range test was used for family mean comparisons and significant differences.
Variance components were estimated using lmer in the package lme4 (Bates et al., 2015) using the restricted maximum likelihood (REML) method. To analyze the effects of male, female, and male × female interactions, the following linear mixed model was used:
where, is the observed value, is the overall mean, is the effect of block i, is the effect of the male parent j, is the effect of the female parent k, is the interaction effect between male and female parent jk (i.e., family), is the effect of clone l within family, and is the random error. All effects except were considered random.
The general combining ability (GCA) or the effects of parents was extracted from this model to provide the relative phenotypic contributions of the male parent () and female parent () to family progeny. The deviation of progeny trait values relative to their parents (midparent heterosis [MPH]) was calculated for each family as ((F1 progeny – midparent)/midparent) × 100. Family 425 was removed from MPH calculations because the male parent was not present.
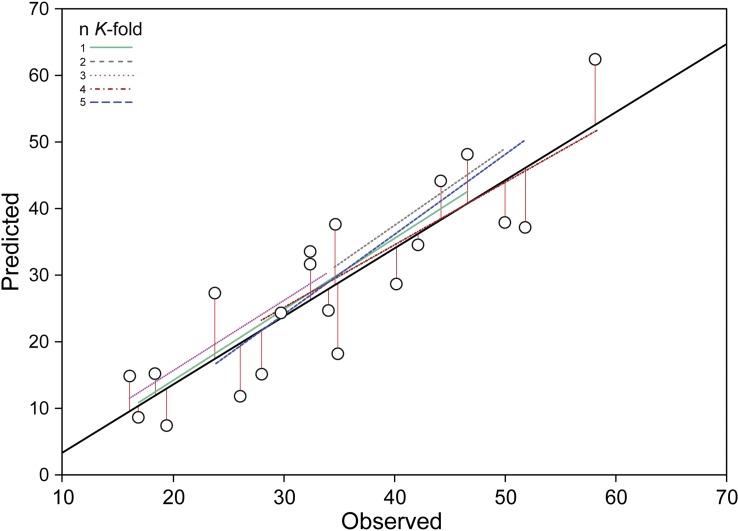
Initial estimates of the predictive accuracy of RDW using REC (adjusted R2 = 0.77, P = 0.001) were cross-validated via K-fold (k = 5) and leave-one-out (N − 1) methods (R2 = 0.71, RMSE = 5.1) using the least-square estimates of model coefficients as well as the root mean squared error (RMSE) to determine the prediction loss of the model in the package cvTools (Alfons, 2012). To evaluate the total variance explained by each predictor variable in multiple linear regression analyses, Lindeman, Merenda, and Gold (LMG; Lindeman et al., 1980), First and Last, Genizi (Genizi, 1993), and Pratt (Pratt, 1987) metrics were used to order predictors and decompose R2 in the relaimpo (Relative Importance for Linear Regression) package (Grömping, 2006). To assess which regressors are different in terms of relative importance, confidence intervals (CIs) were calculated using 1000 bootstrapped replicates (Bonferonni CI = 95%). Pratt and LMG indices were used to partition the additive properties of R2, calculated as the sum of their individual importance irrespective of the correlation among predictor variables. Correlations of above- and belowground biomass-related traits with REC and SDW were performed to rank predictors in multiple regression models. To avoid any potential issues with collinearity in downstream analysis, repeated trait measurements were reduced to a single representative measurement based on the proportion of model variance it explained. For instance, the third of five phenology measurements (12 DAP) and the sixth of nine stem length and stem number measurements (48 DAP) were chosen because they had the strongest correlation with REC and/or SDW.
Important predictors of RDW were selected from a total of 15 cutting and root traits from 20 individuals selected along the distribution of REC readings using stepwise regression (step Akaike Information Criterion [AIC], direction = both) of the linear model fit. Variable selection for SDW was conducted using common relative importance indexing methods. Confidence intervals for each model were produced using 1000 bootstrap replicates at a 95% level of significance. The LMG method is the most commonly used metric in multiple regression. With regard to ranking predictors based on their relative importance, Genizi and Pratt CIs were equivalent to the LMG method. Outcomes from the Genizi predictor ranking method were excluded, as both predictor importance and contributions were nearly identical to the LMG method. The Pratt index was selected to order predictor relative importance in multiple regression analyses because it explains the total variance as the sum of predictor R2.
RESULTS
Family variation in REC and biomass production
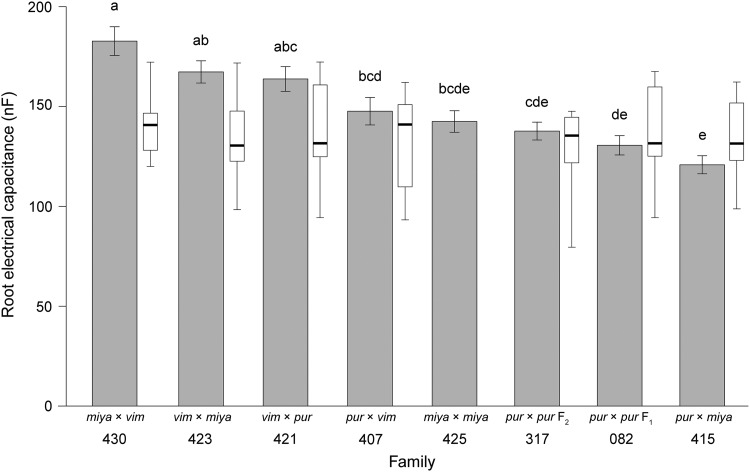
The means of REC significantly differed by up to 34% among the eight full-sib families (Fig. 1, Appendix S1 (20KB, docx) ). The triploid family 430 (S. miyabeana × S. viminalis) displayed the greatest REC means (182.8 nF), while the triploid family 415 (S. purpurea × S. miyabeana) has the lowest REC with a mean of 120.8 nF (Fig. 1, Appendix S1 (20KB, docx) ). The effect of clone within family accounted for a majority of the variance of REC. In addition, the effect of the female parent was almost twice that of the male parent. Combinations of parents with high GCA values should theoretically produce progeny with high absolute trait values. In absolute terms, the S. purpurea female clone 94006 had the greatest GCA of all parents. Of the families analyzed, MPH for REC was observed in the families 421, 423, and 430 but not in families 082 (F1 S. purpurea × S. purpurea), 317 (F2 S. purpurea × S. purpurea), 415 (S. purpurea × S. miyabeana), and 407 (S. purpurea × S. viminalis) (Fig. 1). Because one of the parents of family 425 was not included, heterosis was not calculated for that family. The female and male S. viminalis (07-MBG-5027 and ‘Jorr’) and the female S. miyabeana (01-200-006) parent clones had the greatest GCA of family parents (Appendix S2 (58.3KB, docx) ) contributing to progeny REC. Midparent heterosis for REC was the most dramatic for interspecific crosses of these parents, i.e., families 430 (t = 4.09, P < 0.001) (01-200-006 × ‘Jorr’), 423 (t = 3.56, P = 0.003) (07-MBG-5027 × 01-200-003), and 421 (t = 2.59, P = 0.02) (07-MBG-5027 × 94,001) (Appendix S1 (20KB, docx) ).
Fig. 1.
Root electrical capacitance (REC) family means and errors (±SE) of four replicates as well as their respective Tukey’s honest significant difference (HSD) at a 95% level of confidence. Outlined box plots to the right of bars represent the corresponding midparent value (±SD) for the parents of each family. Midparent means within box plots are denoted by bold horizontal lines. The male parent of family 425 was not present in this trial, thus the midparent box plot of family 425 is not shown. The species pedigree of each family is abbreviated above family identifiers, where pur = Salix purpurea, vim = S. viminalis, and miya = S. miyabeana. The direction of the cross is designated as female parent × male parent species.
Model selection and predictor comparison
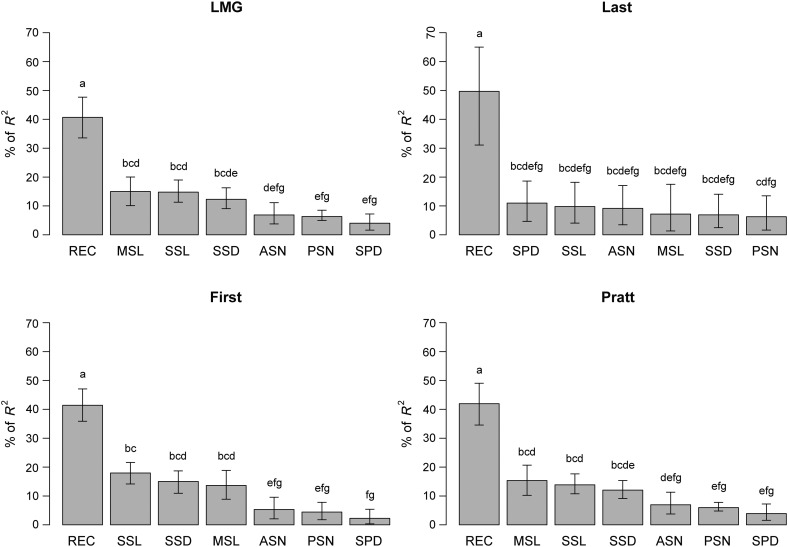
For all traits analyzed, significant REC correlation coefficients (P < 0.05) ranged from 0.11 (SPAD) to 0.88 (RDW). The REC trait was positively correlated with many above- and belowground biomass traits (Table 2, Fig. 2). Aboveground traits that most strongly correlate with REC were SDW, LDW, SSL, and MSA (Table 3). Belowground traits that most strongly correlated with REC were RDW, CDW, and CDIA (Table 3). Owing to the significant contribution of REC and SRN predictor variables, the reduced model, RDW ∼ REC + CDIA + PRN + SRN, explains a substantial portion of the variation in RDW (multiple R2 = 0.85, P < 0.001) (Appendix S3 (64.3KB, docx) ). Relative importance metrics for SDW predictor variables did not vary greatly among model orderings (i.e., rank); in contrast to within-trait R2 and bootstrapped CIs (boot = 1000, Bonferonni CI = 95%), the magnitude of the difference in variation explained in the predictors did vary significantly (Fig. 3). The proportion of variance that could be explained using the seven predictors in the final allometric model, SDW ∼ REC + SSL + MSL + SSD + ASN + PSN + SPD, was 68.5% (Appendix S4 (116.2KB, docx) ). A large proportion of the variance is explained by the relative individual contributions of REC (R2 = 0.42), SSL (R2 = 0.14), and MSL (R2 = 0.15). When REC is not included as a predictor variable in multiple regression, only 55.9% of the variation in SDW could be explained by the remaining variables—a difference of 12.6%. In each model index, REC was found to be significantly different compared to all other predictor variables and explained the greatest proportion of variance in each model index.
Fig. 2.
Linear regression and K-fold cross-validation scatter plot of observed root dry weight biomass (RDW) predicted by root electrical capacitance (REC). The linear regression is y = 0.21x – 6.91 (R2 = 0.77). Vertical red lines perpendicular to the regression line (solid black) represent the residual of the model fit, and colored lines represent K-fold sampling.
Table 3.
Pearson correlation coefficients, their confidence intervals, and significance of above- and belowground traits with root electrical capacitance (REC) and root dry weight (RDW). See Table 2 for trait definitions.
| REC | RDW | |||||
| Trait | r | CI | P value | r | CI | P value |
| Aboveground | ||||||
| SDW | 0.72 | 0.66–0.75 | <0.001 | 0.52 | 0.29–0.75 | 0.019 |
| LDW | 0.56 | 0.49–0.62 | <0.001 | 0.78 | 0.51–0.91 | <0.001 |
| SSL | 0.53 | 0.45–0.59 | <0.001 | 0.59 | 0.22–0.82 | 0.005 |
| MSL | 0.37 | 0.28–0.45 | <0.001 | 0.69 | 0.35–0.86 | <0.001 |
| MXL | 0.44 | 0.35–0.31 | <0.001 | 0.78 | 0.52–0.91 | <0.001 |
| RGR | 0.42 | 0.33–0.49 | <0.001 | 0.33 | 0.27–0.44 | 0.005 |
| MSA | 0.23 | 0.14–0.32 | <0.001 | 0.31 | — | 0.178 |
| SSA | 0.39 | 0.31–0.46 | <0.001 | 0.20 | — | 0.406 |
| LFA | 0.09 | — | 0.092 | 0.32 | — | 0.159 |
| PSN | 0.22 | 0.13–0.31 | <0.001 | 0.23 | — | 0.310 |
| ASN | 0.19 | 0.10–0.28 | <0.001 | 0.64 | 0.29–0.85 | 0.002 |
| SPD | −0.11 | 0.01–0.20 | <0.001 | −0.34 | — | 0.139 |
| PHE | 0.38 | 0.29–0.46 | <0.001 | 0.58 | 0.18–0.81 | 0.007 |
| MSD | 0.13 | 0.03–0.22 | <0.001 | 0.33 | — | 0.148 |
| SSD | 0.39 | 0.31–0.47 | 0.0091 | 0.19 | — | 0.414 |
| SLA | −0.23 | 0.13–0.31 | <0.001 | −0.56 | 0.15–0.80 | 0.010 |
| LMA | 0.24 | 0.20–0.30 | <0.001 | 0.59 | 0.13–0.79 | 0.007 |
| Belowground | ||||||
| REC | 0.88 | 0.71–0.95 | <0.001 | |||
| RDW | 0.88 | 0.71–0.95 | <0.001 | |||
| CDIA | 0.65 | 0.30–0.85 | 0.001 | 0.67 | 0.33–0.86 | 0.001 |
| CDW | 0.67 | 0.33–0.86 | <0.001 | 0.70 | 0.37–0.84 | <0.001 |
| RDIA | 0.20 | 0.27–0.59 | 0.002 | 0.05 | — | 0.982 |
| PRN | 0.64 | 0.29–0.84 | 0.016 | 0.50 | 0.08–0.77 | 0.023 |
| TRN | 0.59 | 0.20–0.81 | 0.041 | 0.53 | 0.12–0.79 | 0.005 |
| SRN | 0.34 | 0.12–0.67 | 0.006 | 0.45 | 0.03–0.74 | 0.041 |
Fig. 3.
Relative importance predictor index metrics for total stem dry weight biomass (SDW). Bar plots of each model index describe the variance explained as a percentage R2 (summed to 100%). For each predictor, confidence intervals (CIs) were produced using 1000 bootstrap replicates at a 95% level of significance. Low percentages of total R2 or CIs approaching zero describe unimportant variable contributions (e.g., SPD, “First” index method).
DISCUSSION
There are a number of key traits that could be selected in shrub willow breeding programs if a rapid method for phenotyping root traits was available, including rate of rooting establishment, ability to compete with weeds, drought tolerance, and total carbon sequestration ability (Pacaldo et al., 2013). The partitioning of photoassimilate from foliage to stem and root biomass is largely dependent upon a complex network of photosynthetic and transport processes (Dickson, 1989; Ericsson et al., 1996), as well as other morphological and environmental factors (Samuelson and Kelly, 1996). Rather than assume that the root:shoot ratio is constant among segregating progeny, it is likely there are genotypic differences in the accumulation of root biomass in proportion to aboveground biomass. While it is true that the quantitative nature of REC does not offer direct insight into root morphology or architecture, the specific morphologically based variances in REC need not be known if it is still a good predictor of RDW.
Increased vigor can be observed in intraspecific crosses of shrub willow, but the effect is generally more dramatic in the progeny of interspecific crosses (Serapiglia et al., 2014), especially in triploid progeny derived from the hybridization of tetraploid and diploid parents (Serapiglia et al., 2015; Fabio et al., 2016). Likewise, we show that the interspecific families 421, 423, and 430 had significantly higher means for REC compared to their respective midparent values (Fig. 1, Appendix S1 (20KB, docx) ). For instance, the interspecific diploid family 421 is the result of a wide cross between parent species S. viminalis (sect. Viminella Ser.) and S. purpurea (sect. Helix Dumort.), whereas the interspecific triploid families 430 and 423 were derived from parents of contrasting ploidy-level as well as membership within sect. Helix, which may explain higher levels of midparent heterosis for this trait within these families. Neither the F1 or F2 intraspecific S. purpurea families displayed significant MPH for REC and were among the lowest performing families in this study.
We find that REC is highly correlated with RDW among all progeny and parent genotypes in this study, comparable to previous correlations found for one cultivar of shrub willow (S. viminalis × S. schwerinii E. L. Wolf ‘Olof’) (Pitre et al., 2010) and hybrid poplar (Populus deltoides W. Bartram ex Marshall × P. nigra L.) (Preston et al., 2004). Correlations of aboveground biomass traits with REC were similar to those of RDW, but the power to detect significant associations was weaker for RDW as a result of small sample size. Working with four commercial shrub willow cultivars, Cunniff et al. (2015) demonstrated LFA to have the strongest correlation with RDW (R2 = 0.49) compared with other aboveground traits in a field setting. Besides the strong correlation of RDW with REC, RDW had strong linear and positive correlations with LDW and LMA, and a strong negative correlation with SLA (Table 3). Species with high LMA tend to have high leaf and root longevity (Ryser, 1996), which more efficiently conserve acquired nutrients and carbon, thereby providing a competitive advantage for species with high LMA in nutrient-poor soils (Poorter et al., 2009). In this study, LFA was weakly correlated with RDW (R2 = 0.32, P = 0.16) and only significantly correlated with REC (R2 = 0.40, P = 0.005) in the diploid family 407 (S. purpurea × S. viminalis). The weak relationship between LFA and RDW can potentially be explained by high genotypic variances in carbon partitioning in leaves (Weraduwage et al., 2015) or a relatively small sample size.
Both REC and RDW strongly correlate to SDW. Early prediction of harvestable biomass yield is extremely important for the selection of high-performance woody perennial crops like shrub willow. If RDW contributes a substantial portion of SDW variance, it is exemplified by the REC technique. In all multiple regression model orderings, REC has shown to be the best predictor of SDW among all traits attributing to each model. Although LDW was strongly correlated with SDW (R2 = 0.81, P < 0.001), it was excluded as a predictor variable in multiple regression analyses because it is a destructive measurement and not manageable to collect leaf biomass in a field setting. As far as we know, this is the first attempt using REC as a predictor variable in allometric models for yield.
Estimation of root biomass relative growth rates may be modeled from multitemporal data with minimal effort. The root system of shrub willow typically resides in the upper 20–30 cm of the soil and fine roots in the upper 10 cm (Pacaldo et al., 2013), which may find worthy implementation of REC as a long-term indicator of root development in research field trials. It may be that the proximal morphology of adventitious roots from the cutting surface may provide the best explanation for the strong and positive correlation of REC with RDW. For the reason that shrub willow does not produce a large tap root from a cutting, it is possible that the proximity of the capacitance meter lead in the soil and the proximal root system provides a strong signal to the extent that a majority of the variance of root biomass can be explained by REC. However, comparisons of both seedlings and cuttings of shrub willow families must be conducted to determine if there are significant differences associated with root morphology impacting the prediction of RDW with REC. The effect of aboveground biomass on REC should be considered while conducting REC on a large-scale field study, and curves must be recalibrated accordingly. For the reason that aboveground biomass was harvested prior to taking REC measurements in this study, any confounding factors that may have been introduced into analyses were avoided. For instance, the difficulty of maintaining equivalent moisture content across genotypes is relative to the transpiration rate of respective genotypes, which were extremely diverse. Because the moisture content needed to be stable across plots, as noted in Dalton (1995), REC was measured after aboveground biomass was harvested, ensuring minimal water loss from pots over time. In the application of REC to the measurement of a large-scale field experiment, one would also need to measure moisture content adjacent to each REC measurement to use as a covariate in order to account for error associated with local variation in soil moisture content.
In addition to estimating RDW, there is also potential to investigate the relationship of REC with the occurrence and distribution of ectomycorrhizal and arbuscular mycorrhizal populations among short-rotation plantations and natural stands of shrub willow (Dhillion, 1994; Cseresnyés et al., 2013). Repo et al. (2016) implemented a PC-based method using electrical impedance spectra to assess the hardiness of mycorrhizal and nonmycorrhizal roots of Scots pine seedlings. Although there were no significant differences due to mycorrhizal treatments, Repo et al. (2016) found differences between treatment temperatures. Whether the accumulation of mycorrhizae is genotype-specific or impacts REC (Cseresnyés et al., 2016) in Salix spp. has not yet been characterized. It would be worthwhile to measure REC and sample mycorrhizae concurrently in a field setting to analyze the effects of altered environmental conditions on root growth and biomass yield.
The REC method provides an efficient, reproducible, and nondestructive alternative to more traditional “shovel-omics” techniques. However, the efficiency of REC must still be improved and the equipment itself scaled up to withstand heterogeneous soil profiles and thick stems on stools with multiple stems of mature plants in the field. For instance, Ellis et al. (2013) used the electrical capacitance 4T method (resistor and capacitor in series) as an indicator of root length in Pinus L., Eucalyptus L’Hér., and Corymbia K. D. Hill & L. A. S. Johnson forest tree plantations, resolving capacitance somewhat related to root mass within species but a poor indicator of diameter at breast height, root mass, or root length across species, age, or sites. In this study, we selected a relatively small sample size for validation of REC and RDW because of the rigor and time expense associated with carefully washing and retrieving fine and coarse roots from mature root masses in a short period of time. Only a few days after harvesting stem and leaf biomass from pots, new shoots began to emerge from their stools. Moreover, washing root samples over a one- or two-week period could introduce unwanted error into statistical analyses, thereby impacting the relationship between REC collected at harvest and RDW, as well as correlations with morphological and physiological traits collected at the termination of the study. Technological improvements in field-based root phenotyping (Rautenbach et al., 2013; Meister et al., 2014) will hopefully allow for high-throughput quantification of root architecture and biomass at a reasonable efficiency and cost.
Compared to annual crops, it is likely that the electrical capacitances of perennial shrub willows will change over time as a result of root suberization, repeated coppicing, and seasonal variation of biotic and abiotic stressors. As implied, future work must be accomplished to determine if the strong relationship between REC and biomass-related traits on second- and third-year growth are equally as strong as in the first year. It is likely that over multiple coppice cycles, environment will play an important role in determining the genotypic stability of this trait in shrub willow. Nevertheless, the strength of REC prediction estimates of above- and belowground dry biomass is sufficient to conclude that it is not only valuable but is adaptable across Salix species, ploidy level, and hybrid pedigree.
Supplementary Material
LITERATURE CITED
- Alfons A. 2012. cvTools: Cross-validation tools for regression models. Comprehensive R Archive Network. Website https://CRAN.R-project.org/package=cvTools [accessed 11 July 2016].
- Argus G. W. 2005. Guide to the identification of the genus Salix (willow) in New England and New York. Delta Institute of Natural History, Bowdoin, Maine, USA. [Google Scholar]
- Bates D., Mächler M., Bolker B., Walker S. 2015. lme4: Mixed-effects modeling with R. Fitting linear mixed-effects models using lme4. Journal of Statistical Software 67: 1–48. [Google Scholar]
- Bonosi L., Ghelardini L., Weih M. 2013. Towards making willows potential bio-resources in the South: Northern Salix hybrids can cope with warm and dry climate when irrigated. Biomass and Bioenergy 51: 136–144. [Google Scholar]
- Cao Y., Repo T., Silvennoinen R., Lehto T., Pelkonen P. 2011. Analysis of the willow root system by electrical impedance spectroscopy. Journal of Experimental Botany 62: 351–358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cseresnyés I., Takács T., Végh K. R., Anton A., Rajkai K. 2013. Electrical impedance and capacitance method: A new approach for detection of functional aspects of arbuscular mycorrhizal colonization in maize. European Journal of Soil Biology 54: 25–31. [Google Scholar]
- Cseresnyés I., Rajkai K., Takács T. 2016. Indirect monitoring of root activity in soybean cultivars under contrasting moisture regimes by measuring electrical capacitance. Acta Physiologiae Plantarum 38: 121. [Google Scholar]
- Cunniff J., Purdy S. J., Barraclough T. J. P., Castle M., Maddison A. L., Jones L. E., Shield I. F., et al. 2015. High yielding biomass genotypes of willow (Salix spp.) show differences in below ground biomass allocation. Biomass and Bioenergy 80: 114–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Currie P. O., Hilken T. O., White R. S. 1987. Evaluation of a single probe capacitance meter for estimating herbage yield. Journal of Range Management 40: 537–541. [Google Scholar]
- Dalton F. N. 1995. In-situ root extent measurements by electrical capacitance methods. Plant and Soil 173: 157–165. [Google Scholar]
- Dhillion S. S. 1994. Ectomycorrhizae, arbuscular mycorrhizae and Rhizoctonia sp. of alpine and boreal Salix spp. in Norway. Arctic and Alpine Research 26: 304–307. [Google Scholar]
- Dickson R. E. 1989. Carbon and nitrogen allocation in trees. Annals of Forest Science 46: 631s–647s. [Google Scholar]
- Dietrich R. C., Bengough A. G., Jones H. G., White P. J. 2012. A new physical interpretation of plant root capacitance. Journal of Experimental Botany 63: 6149–6159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dietrich R. C., Bengough A. G., Jones H. G., White P. J. 2013. Can root electrical capacitance be used to predict root mass in soil? Annals of Botany 112: 457–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellis T. W., Murray W., Paul K., Kavalieris L., Brophy J., Williams C., Maass M. 2013. Electrical capacitance as a rapid and non-invasive indicator of root length. Tree Physiology 33: 3–17. [DOI] [PubMed] [Google Scholar]
- Ericsson T., Rytter L., Vapaavuori E. 1996. Physiology of carbon allocation in trees. Biomass and Bioenergy 11: 115–127. [Google Scholar]
- Fabio E. S., Volk T. A., Miller R. O., Serapiglia M. J., Gauch H. G., Van Rees K. C. J., Hangs R. D., et al. 2016. Genotype × environment interaction analysis of North American shrub willow yield trials confirms superior performance of triploid hybrids. GCB Bioenergy 10.1111/gcbb.12344. [Google Scholar]
- Genizi A. 1993. Decomposition of R2 in multiple regression with correlated regressors. Statistica Sinica 3: 407–420. [Google Scholar]
- Grömping U. 2006. Relative importance for linear regression in R: The package relaimpo. Journal of Statistical Software 17: 1–27. [Google Scholar]
- Karp A., Hanley S. J., Trybush S. O., Macalpine W., Pei M., Shield I. 2011. Genetic improvement of willow for bioenergy and biofuels. Journal of Integrative Plant Biology 53: 151–165. [DOI] [PubMed] [Google Scholar]
- Kormanek M., Tomasz G. 2015. Modification of the tree root electrical capacitance method under laboratory conditions. Tree Physiology 36: 121–127. [DOI] [PubMed] [Google Scholar]
- Kriegler E., Weyant J. P., Blanford G. J., Krey V., Clarke L., Edmonds J., Fawcett A., et al. 2014. The role of technology for achieving climate policy objectives: Overview of the EMF 27 study on global technology and climate policy strategies. Climatic Change 123: 353–367. [Google Scholar]
- Kuzovkina Y. A., Romero M. A., Charles J., Hurst S., McIvor I., Karp A., Trybush S., et al. 2008. Salix: Botany and global horticulture. Horticultural Reviews 34: 447–489. [Google Scholar]
- Lam P. S., Sokhansanj S., Bi X., Lim C. J., Naimi L. J., Hoque M., Mani S., et al. 2008. Bulk density of wet and dry wheat straw and switchgrass particles. Applied Engineering in Agriculture 24: 351–358. [Google Scholar]
- Lauron-Moreau A., Pitre F. E., Argus G. W., Labrecque M., Brouillet L. 2015. Phylogenetic relationships of American willows (Salix L., Salicaceae). PLoS ONE 10: e0138963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lekas T. M., MacDougall G. R., MacLean D. A., Thompson R. G. 1990. Seasonal trends and effects of temperature and rainfall on stem electrical capacitance of spruce and fir trees. Canadian Journal of Forest Research 20: 970–977. [Google Scholar]
- Lindeman R. H., Merenda P. F., Gold R. Z. 1980. Introduction to bivariate and multivariate analysis, 119. Longman Higher Education, Glenview, Illinois, USA. [Google Scholar]
- Meister R., Rajani M. S., Ruzicka D., Schachtman D. P. 2014. Challenges of modifying root traits in crops for agriculture. Trends in Plant Science 19: 779–788. [DOI] [PubMed] [Google Scholar]
- Pacaldo R. S., Volk T. A., Briggs R. D. 2013. No significant differences in soil organic carbon contents along a chronosequence of shrub willow biomass crop fields. Biomass and Bioenergy 58: 136–142. [Google Scholar]
- Pitre F. E., Brereton N. J. B., Audoire S., Richter G. M., Shield I., Karp A. 2010. Estimating root biomass in Salix viminalis × Salix schwerinii cultivar ‘Olof’ using the electrical capacitance method. Plant Biosystems 144: 479–483. [Google Scholar]
- Poorter H., Niinemets U., Poorter L., Wright I. J., Villar R. 2009. Causes and consequences of variation in leaf mass per area (LMA): A meta-analysis. New Phytologist 182: 565–588. [DOI] [PubMed] [Google Scholar]
- Pratt J. W. 1987. Dividing the indivisible: Using simple symmetry to partition variance explained. In T. Pukkila and S. Puntanen [eds.], Proceedings of the second international conference in statistics, 245–260. University of Tampere, Tampere, Finland [Google Scholar]
- Preston G. M., McBride R. A., Bryan J., Candido M. 2004. Estimating root mass in young hybrid poplar trees using the electrical capacitance method. Agroforestry Systems 60: 305–309. [Google Scholar]
- R Development Core Team 2011. R: A language and environment for statistical computing. R foundation for statistical computing, 1–409. Vienna, Austria. Website https://www.R-project.org/ [accessed 11 July 2016].
- Rajkai K., Égh K. R. V., Nacsa T. 2005. Electrical capacitance of roots in relation to plant electrodes, measuring frequency and root media. Acta Agronomica Hungarica 53: 197–210. [Google Scholar]
- Rautenbach C., Mudde R. F., Yang X., Melaaen M. C., Halvoresen B. M. 2013. A comparative study between electrical capacitance tomography and time-resolved X-ray tomography. Flow Measurement and Instrumentation 30: 34–44. [Google Scholar]
- Repo T., Zhang G., Ryyppö A., Rikala R. 2000. The electrical impedance spectroscopy of Scots pine (Pinus sylvestris L.) shoots in relation to cold acclimation. Journal of Experimental Botany 51: 2095–2107. [DOI] [PubMed] [Google Scholar]
- Repo T., Laukkanen J., Silvennoinen R. 2005. Measurement of the tree root growth using electrical impedance spectroscopy. Silva Fennica 39: 159–166. [Google Scholar]
- Repo T., Korhonen A., Lehto T., Silvennoinen R. 2016. Assessment of frost damage in mycorrhizal and non-mycorrhizal roots of Scots pine seedlings using classification analysis of their electrical impedance spectra. Trees (Berlin) 30: 483–495. [Google Scholar]
- Rose S. K., Kriegler E., Bibas R., Calvin K., Popp A., van Vuuren D. P., Weyant J. 2014. Bioenergy in energy transformation and climate management. Climatic Change 123: 477–493. [Google Scholar]
- Ryser P. 1996. The importance of tissue density for growth and life span of leaves and roots: A comparison of five ecologically contrasting grasses. Functional Ecology 10: 717–723. [Google Scholar]
- Samuelson L. J., Kelly J. M. 1996. Carbon partitioning and allocation in northern red oak seedlings and mature trees in response to ozone. Tree Physiology 16: 853–858. [DOI] [PubMed] [Google Scholar]
- Serapiglia M. J., Gouker F. E., Smart L. B. 2014. Early selection of novel triploid hybrids of shrub willow with improved biomass yield relative to diploids. BMC Plant Biology 14: 74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serapiglia M. J., Gouker F. E., Hart J. F., Unda F., Mansfield S. D., Stipanovic A. J., Smart L. B. 2015. Ploidy level affects important biomass traits of novel shrub willow (Salix) hybrids. BioEnergy Research 8: 259–269. [Google Scholar]
- Smart L. B., Cameron K. D. 2012. Shrub willow. In C. Kole, S. Joshi S., and D. Shonnard [eds.], Handbook of bioenergy crop plants, 687–708. Taylor and Francis Group, Boca Raton, Florida, USA. [Google Scholar]
- Walther G. R., Post E., Convey P., Menzel A., Parmesean C., Beebee T. J. C., Fromentin J. M., et al. 2002. Ecological responses to recent climate change. Nature 416: 389–395. [DOI] [PubMed] [Google Scholar]
- Weraduwage S. M., Chen J., Anozie F. C., Morales A., Weise S. E., Sharkey T. D. 2015. The relationship between leaf area growth and biomass accumulation in Arabidopsis thaliana. Frontiers in Plant Science 6: 167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whiteman G., Hope C., Wadhams P. 2013. Vast costs of Arctic change. Nature 499: 401–403. [DOI] [PubMed] [Google Scholar]
- Whitlow T. H., Bassuk N. L., Ranney T. G., Reichert D. L. 1992. An improved method for using electrolyte leakage to assess membrane competence in plant tissues. Plant Physiology 98: 198–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.