Strong Genetic Overlap Between Executive Functions and Intelligence

Abstract

Executive functions (EFs) are cognitive processes that control, monitor, and coordinate more basic cognitive processes. EFs play instrumental roles in models of complex reasoning, learning, and decision-making, and individual differences in EFs have been consistently linked with individual differences in intelligence. By middle childhood, genetic factors account for a moderate proportion of the variance in intelligence, and these effects increase in magnitude through adolescence. Genetic influences on EFs are very high, even in middle childhood, but the extent to which these genetic influences overlap with those on intelligence is unclear. We examined genetic and environmental overlap between EFs and intelligence in a racially and socioeconomically diverse sample of 811 twins ages 7-15 years (M = 10.91, SD = 1.74) from the Texas Twin Project. A general EF factor representing variance common to inhibition, switching, working memory, and updating domains accounted for substantial proportions of variance in intelligence, primarily via a genetic pathway. General EF continued to have a strong, genetically-mediated association with intelligence even after controlling for processing speed. Residual variation in general intelligence was influenced only by shared and nonshared environmental factors, and there remained no genetic variance in general intelligence that was unique of EF. Genetic variance independent of EF did remain, however, in a more specific perceptual reasoning ability. These results provide evidence that genetic influences on general intelligence are highly overlapping with those on EF.

Childhood intelligence is an important, early marker of lifelong socioeconomic and health gradients, ranging from educational attainment, income, and occupational success to mental health, physical health, and longevity (e.g., Deary, 2008; Deary, Weiss, & Batty, 2010; Koenen et al., 2009; Schmidt & Hunter, 1998). Much of the variation in intelligence is associated with genetic differences between people. Behavioral genetic studies, capitalizing on differences in genetic similarity across family members, find that genetic factors account for approximately 50% of population-level variation in intelligence by the end of the first decade of life. This proportion increases to approximately 70% by late adolescence (Haworth et al., 2010; Tucker-Drob, Briley, & Harden, 2013) and remains similarly high throughout much of adulthood (Bouchard & McGue, 1981; Pedersen, Plomin, Nesselroade, & McLearn, 1992). Beginning around age 10, genetic influences on intelligence become highly stable across time, indicating that increasing heritability from middle childhood through adolescence results from amplification of the effects of the same genes that influenced intelligence earlier in the lifespan (Briley & Tucker-Drob, 2013; Tucker-Drob & Briley, 2014). Molecular genetic studies that capitalize on measured genetic similarity across unrelated individuals find somewhat lower – but still developmentally stable – genetic influences on intelligence by the end of the first decade of life (Davies et al., 2011; Deary et al., 2012; Trzaskowski et al, 2014). Finally, large-scale genome-wide association studies (GWAS) recently have begun to identify specific genetic polymorphisms associated with intelligence (Rietveld et al., 2014), although most of the genes influencing intelligence remain unidentified.

Together, these findings reinforce a longstanding interest in identifying simpler cognitive processes that are hypothesized to lie intermediate along the pathway from genotype to intelligence, that are manifest by middle childhood, and that statistically mediate – in full or in part – genetic influences on intelligence. Early attempts to partition individual differences in intelligence into more basic cognitive components focused on very simple indices of reaction time and information processing speed (Deary, Spinath, & Bates, 2006; Jensen, 1980; Jensen, 1998; Neubauer, 1997). Researchers reasoned that such “elementary cognitive processes” were dependent upon very basic properties of the human nervous system. Measures of elementary cognitive processes were expected to either be unaffected by acquired knowledge or only depend on forms of knowledge that were overlearned to the point of being universal across individuals. Thus, it was assumed such measures would be very minimally affected by environmental variation, that is, highly heritable. Moreover, because it was thought that the aggregation of these elementary cognitive processes composed the building blocks of complex thought (Kail & Salthouse, 1994; Jensen, 1980), it was assumed that performance on simple cognitive tasks would correlate strongly with intelligence and statistically mediate genetic influences on intelligence.

Counter to expectations, empirical correlations between elementary cognitive tasks and intelligence tended to be modest (r ≈ 0.2; Smith & Stanley, 1983; Neubauer, 1997), with larger convergent validity coefficients obtained only when the elementary tasks increased in complexity (Jensen, 2006). Studies of elementary cognitive processes seldom used genetically informative samples, and the few behavior genetic studies that were conducted reported heritabilities no stronger than those obtained for more complex abilities (Luciano et al., 2001; Luciano et al., 2004; Posthuma, Mulder, Boomsma, & De Geus, 2002; Rijsdijk, Vernon, & Boomsma, 1998). Furthermore, multivariate analyses indicated that, while genetic influences on elementary cognitive tasks were partially shared with intelligence, each process was also substantially influenced by unique genetic factors (Luciano et al., 2001; Petrill, Luo, Thompson, & Detterman, 1996; Spinath & Borkenau, 2000). Persistent difficulty establishing empirical support for a cognitive architecture of intelligence based upon elementary cognitive processes ultimately resulted in a call for the identification of less elementary, more mechanistically complex cognitive correlates of intelligence (Deary, 2002).

More recently, researchers have turned toward a suite of effortful, supervisory processes known as executive functions (EFs) to more fully account for variation in intelligence. EFs are conceptualized as cognitive processes that coordinate, monitor, maintain, and manipulate more basic processes to give rise to higher-order reasoning, learning, and goal-directed behavior (Alvarez & Emory, 2006; Diamond, 2006; Miller & Cohen, 2001; Zelazo & Müller, 2002). EFs constitute a range of related but separable skills, including inhibition of learned or prepotent responses, maintenance and manipulation of incoming information, and changing of response patterns based on new rules or information. Converging evidence points to a stable, multidimensional organization for EF: Individual differences in EFs are attributable to variance specific to individual task performance, variance common to tasks via domain-specific factors (e.g., switching, inhibition, working memory, and updating), and variance shared across domains via a general EF factor (Engelhardt, Briley, Mann, Harden, & Tucker-Drob, 2015; Miyake et al., 2000).

EFs feature prominently in formal cognitive models of reasoning, learning, and decision-making (Anderson, 2001; Carpenter, Just, & Shell, 1990; Kieras & Meyer, 1997; Meyer & Kieras, 1997) and have received considerable attention as hypothesized intermediate mechanisms through which basic biological factors affect these complex outcomes (Kane & Engle, 2002). An especially active line of empirical research has investigated the neural bases of EFs. Converging evidence from functional and structural neuroimaging studies of healthy samples of individuals, along with lesion mapping from patient samples, points to a complex network of connected brain regions encompassing both the prefrontal cortex and parietal lobes as subserving executive processes (Alvarez & Emory, 2006; Carpenter, Just, & Reichle, 2000; Collette, Hogge, Salmon, & Van der Linden, 2006; Nowrangi, Lyketsos, Rao, & Munro, 2014; Power & Petersen, 2013). Compared to researchers in neuroscience, behavioral geneticists have paid less attention to EFs. The small body of genetic research on EF, however, has found that it is remarkably heritable. In studies of early adulthood (Friedman et al., 2008) and middle childhood (Engelhardt et al., 2015), a common EF factor representing shared variance among EF domains was found to be nearly 100% heritable. Longitudinal investigations of adult EF performance (Friedman et al., 2015) revealed high stability across a 6-year period of emerging adulthood. Moreover, longitudinal twin models indicated that stability was primarily attributable to genetic factors. Together, these findings position EF as a strong candidate intermediate phenotype that might share large proportions of genetic variance in intelligence. There is very little work, however, examining the extent to which genetic influences on EF and intelligence indeed overlap.

Many empirical studies of EF as a source of variance in intelligence have restricted their scope to working memory measures of EF. Early interest in phenotypic overlap between working memory and intelligence led to the suggestion that working memory capacity was nearly indistinguishable from fluid intelligence (e.g., Engle et al., 1999; Engle, 2002; Kyllonen & Christal, 1990), an ability that is itself statistically – and potentially mechanistically – central to general intelligence (Gustafsson, 1984; Marshalek, Lohman, & Snow, 1983; Tucker-Drob & Salthouse, 2009). Under prominent views originating from these lines of research, working memory tasks are thought to tap a latent executive attention capacity that is itself fundamental to higher-order cognition, particularly abstract reasoning (Blair, 2006; Kane & Engle, 2002). More recent work has found working memory and intelligence to be strongly overlapping, but not equivalent (Ackerman et al., 2005; Conway et al., 2003). Less attention has been paid to how a diverse system of EFs – including individual domains such as switching and inhibition, as well as a general factor common to multiple EF domains – correlate with intelligence, although there have been some reports of overlap between intelligence and inhibitory control (Dempster, 1991; Salthouse, Atkinson, & Berish, 2003), switching (Salthouse, Fristoe, McGuthry, & Hambrick, 1998), and a general factor of EFs (Friedman et al., 2008). Theoretical accounts for this overlapping variance describe executive functions as general-purpose processes that coordinate complex cognitive functions (Miyake & Friedman, 2000), with other accounts emphasizing fluid intelligence as itself reflecting a highly general capacity for controlled and effortful processing (Deary, 2000; Salthouse, Pink, & Tucker-Drob, 2008).

Behavioral genetic work testing the extents to which EFs relate to intelligence via genetic and environmental mechanisms has been rare. Much of the small body of the research on EF-intelligence associations has tended to rely on single measures of EF, rather than latent EF factors (see, e.g., Lee et al., 2012; Polderman et al., 2006; Polderman et al., 2009). One of the few exceptions is a study by Friedman et al. (2008), who reported that genetic variance in full scale IQ correlated with genetic variance in general EF at r = .57. However, we are aware of no other behavioral genetic research on overlap between intelligence and a general EF factor derived from a diverse multivariate battery, and it is therefore unclear how representative this single estimate will be once a larger body of research accumulates. Indeed, it is possible that the Friedman et al. (2008) findings represent a conservative estimate of shared genetic influence because IQ and EF were assessed a year apart, at participant ages 16 and 17 years, respectively.

The current study tests for genetic and environmental overlap between EF and intelligence in a sample of 3^rd- through 8^th-grade children (approximately ages 8 to 14 years in the U.S.). While genetic influences on general EF already approach 100% in this age group (Engelhardt et al., 2015), those operating on intelligence have yet to reach their maximum; however, meta-analytic evidence indicates that increases in the heritability of intelligence from this period forward results from magnification of genes already expressed (Briley & Tucker-Drob, 2013; Tucker-Drob & Briley, 2014). Meanwhile, the neurobiological foundations of EFs and intelligence are in the midst of a relatively protracted period of morphological and connection-based maturation (e.g., Douand et al., 2014; Jung & Haier, 2007; Power, 2012). Thus, this period of middle childhood represents an important transition point at which cognitive abilities and their neurobiological bases continue to progress along a trajectory of positive growth while individual differences become canalized and amplified. Remarkably, previous investigations of associations between executive functions and intelligence during this period have been limited, both in absolute number and in the scope of the measures employed. In the present study, we investigate an array of EFs, each measured with multiple indicators, allowing us to partition EF variation into test-specific, domain-specific, and general factors. In order to test the possibility that detected overlaps in EF and intelligence are simply due to shared dependence on processing speed, itself a strong correlation of intelligence (Salthouse, 1996), we also test whether these associations are robust to controls for a latent speed factor.

Method

Participants

Families were recruited from public school rosters as part of the Texas Twin Project (Harden, Tucker-Drob, & Tackett, 2013). The current sample consisted of 811 children in grades three to eight (age range 7.80 - 15.25 years; M = 10.91; SD = 1.75), 51.2% of whom were female. 61.4% were non-Hispanic White, 18.4% were Hispanic, 6.9% were African American, 3.0% were Asian, 1.2% were of another race/ethnicity, and 9.1% reported multiple races or ethnicities. Thirty-five percent of the participating families reported having received needs-based public assistance such as food stamps. We report data for 431 pairs: 380 twin pairs and 51 pairwise combinations from 17 triplet sets.

Zygosity

All opposite-sex pairs were classified as dizygotic (DZ). The zygosity of same-sex pairs was assessed by a latent class analysis of experimenters’ and parents’ ratings of physical similarity and how frequently the pairs are mistaken for one another. Latent class analysis of such ratings to assess zygosity has been reported to be over 99% accurate, as compared to classifications employing genotyping (Heath et al., 2003). The sample consisted of 141 (32.7%) monozygotic (MZ) pairs, 147 (34.1%) same-sex dizygotic pairs, and 143 (33.2%) opposite-sex dizygotic pairs.

Measures

Data collection for the current project has been ongoing for approximately three years. As EF tasks are well known for poor levels of reliability relative to psychometric measures of cognitive-ability measures (Miyake et al., 2000), we placed a great deal of emphasis on selecting tasks that have been reported to have strong psychometric properties in child samples (Engelhardt et al., 2015). Three of the twelve EF tasks (Stop Signal, 2-Back, Plus-Minus) were administered to participants during approximately the first two years of data collection only. During the third year of data collection, these tasks were replaced by new tasks that were amenable for use in an MRI scanner; data for the three new tasks were not analyzed for the current report. The remaining nine EF tasks were collected across all years of data collection. We describe all measures below (also see Table 1). More comprehensive task descriptions can be found in Engelhardt et al. (2015).

Table 1.

Descriptive Statistics for Executive Function, Intelligence, and Processing Speed Tasks

Domain/Task	Dependent Variable	n	M	SD	Skewness	Kurtosis	Reliability Estimate (α)
Inhibition
Animal Stroop	Mean RT cost for incongruent conditions relative to congruent and neutral conditions	809	229.83ms	221.94	−2.92 (.09)	19.29 (.17)	.84a
Mickey	Mean RT cost for incongruent trials relative to congruent and neutral trials	747	23.03ms	55.19	−.33 (.09)	2.88 (.18)	.36b
Stop Signal Auditory	Mean RT cost for go trials relative to stop signal delay (time between arrow and stop signal presentation)	521	326.25ms	80.63	−.48 (.11)	1.87 (.24)	.40b
Switching
Trail Making	Mean RT cost for alternating conditions relative to simple conditions	807	1285.12ms	1031.00	−.16 (.09)	1.35 (.17)	.87a
Local-Global	Mean RT cost for alternating conditions relative to simple conditions	795	1424.95ms	765.66	−.04 (.09)	4.83 (.17)	.73a
Plus-Minus	Mean RT cost for alternating conditions relative to simple conditions	584	672.15ms	1199.62	−1.72 (.10)	8.71 (.20)	.69a
Working Memory
Digit Span Backward	Total number of trials correctly recalled	810	7.02	1.82	.38 (.09)	.58 (.09)	.59c
Symmetry Span	Total number of visually presented squares correctly recalled	802	20.30	8.75	−.15 (.09)	−.36 (.17)	.78c
Listening Recall	Total number of auditorily presented letters correctly recalled	799	23.44	7.96	.12 (.09)	−.43 (.17)	.78c
Updating
Keeping Track	Total number of verbally presented words correctly recalled	796	6.65	2.36	−.11 (.09)	−.47 (.17)	.52c
Running Memory for  Letters	Total number of visually presented letters correctly recalled	786	18.90	8.29	−.05 (.09)	−.69 (.17)	.75c
2-Back	Total number of hits (correct matches) minus false alarms (non-matches indicated)	599	2.62	8.09	.11 (.10)	−.21 (.20)	.84b
Intelligence
Block Design	Points awarded for recreating block designs	807	27.01	13.16	.38 (.09)	−.55 (.17)	.83c
Matrix Reasoning	Number of items correctly identified as following spatial pattern	807	18.15	4.64	−.94 (.09)	.85 (.17)	.87c
Vocabulary	Points awarded for defining words	807	29.67	6.88	−.35 (.09)	−.35 (.17)	.86c
Similarities	Points awarded for determining similarities between two concepts	807	24.30	5.73	−.23 (.09)	.54 (.17)	.82c
Full Scale IQ		804	103.65	14.14	.19 (.09)	.00 (.17)	.94d
Processing Speed
Letter Comparison	Total number of pairs of letter strings identified as matches or rejected as mismatches	809	27.52	7.26	.63 (.09)	.55 (.17)	.85b
Pattern Comparison	Total number of pairs of symbols identified as matches or rejected as mismatches	810	14.06	5.00	.21 (.09)	.33 (.17)	.84b
Symbol Search	Total number of symbols identified as matches or rejected as mismatches	808	24.58	7.03	−.03 (.09)	.01 (.17)	.79d

Note. RT = reaction time. Standard errors for skewness and kurtosis are presented in parentheses.

^aReliability estimates were calculated based on difference scores formed by subtracting reaction time on non-switch (or non-inhibit) blocks from reaction time on switch (or inhibit) blocks, for each possible pair of switch (inhibit) and non-switch (non-inhibit) blocks.

^bReliability estimates were calculated across blocks.

^cReliability estimates were calculated across trials.

^dShort-term test-retest stability for FSIQ and Symbol Search came from WASI-II and WISC-IV technical manuals, respectively.

EFs

We selected twelve tasks to measure individual differences in the following EF domains: inhibition, switching, working memory, and updating.

Inhibition refers to the ability to stop oneself from executing a prepotent or practiced behavior. The tasks selected to assess inhibition were Animal Stroop (Wright, Waterman, Prescott, & Murdoch-Eaton, 2003), Stop Signal (Logan, Schachar, & Tannock, 1997; Verbruggen, Logan, & Stevens, 2008), and Mickey (an anti-saccade paradigm; Lee & Bull, 2013). An inhibition cost was calculated for Stroop and Mickey by comparing reaction times for inhibit and non-inhibit trials. The dependent variable of interest for Stop Signal was stop signal reaction time (SSRT), an estimate of how quickly one can inhibit a prepotent motor response when cued to stop.

Switching involves shifting one’s attention to different stimulus features or task rules. This domain was measured with the Trail Making (Salthouse, 2011), Local-Global (Miyake et al., 2000), and Plus-Minus (Miyake et al., 2000) tasks. The switch tasks compare low-demand, non-switch performance (e.g., connecting letters alphabetically in Trail Making) to high-demand, switch performance (e.g., connecting letters and numbers in an alternating fashion). Switch costs were calculated to represent longer reaction times for switch relative to non-switch conditions.

Working memory refers to simultaneous processing and storage of information. We selected Digit Span Backward (Wechsler, 2003), Symmetry Span (Kane et al., 2004), and Listening Recall (Daneman & Carpenter, 1980) to assess working memory. The latter two tasks involve storing and manipulating spatial and verbal information, respectively. The number of items correctly recalled served as the dependent variable for all working memory tasks.

Updating involves monitoring incoming stimuli and replacing old information with new, more relevant information. The tasks selected to measure updating were 2-Back (an N-Back paradigm comprised of all 2-back trials; Jaeggi et al., 2010), Keeping Track (Miyake et al., 2000), and Running Memory for Letters (Broadway & Engle, 2010), each of which requires participants to recall the most recent x number of stimuli in an ongoing set. The number of items correctly recalled served as the dependent variable for Keeping Track and Running Memory for Letters. The outcome of interest for 2-Back was the number of correctly identified matches minus incorrectly identified non-matches.

Intelligence

The Wechsler Abbreviate Scale of Intelligence (WASI-II; Wechsler, 2011) was administered to assess general intelligence. The WASI-II consists of four tests (Vocabulary and Similarities subtests assess verbal comprehension [crystallized intelligence]; Block Design and Matrix Reasoning subtests assess perceptual reasoning [fluid intelligence]) that, when age-standardized (based on published norms from a nationally representative reference sample) and combined, form a full scale intelligence quotient (IQ) that reliably approximates full scale IQ indexed from a more extensive intelligence test battery (correlation between full-scale IQ measured by the WASI-II and the Wechsler Intelligence Scale for Children-IV: r = .86; Wechsler, 2003). The average FSIQ of participants in our sample was 103.65, with a standard deviation of 14.14. FSIQ scores are normed to have a mean of 100 and standard deviation of 15 in the general U.S. population. Thus, our sample was closely representative of children in the general U.S. population both in terms of average ability and range of ability. FSIQ was uncorrelated with age (r = .03, p = .64), indicating that our sample is equally representative of ability in the general U.S. population across the age range sampled.

Processing Speed

Processing speed was measured with three tasks: Letter Comparison (Salthouse & Babcock, 1991), Pattern Comparison (Salthouse & Babcock, 1991), and Symbol Search (Wechsler, 2003). These timed tasks require participants to assess similarities across lexical- or symbol-based sets of stimuli as quickly as possible while maintaining near perfect accuracy.

Analyses

Structural equation models, which allow the simultaneous estimation of statistical associations involving both observed and latent variables, were fit with Mplus Version 7.11 (Muthén & Muthén, 2012). To account for missing data, Mplus takes a full-information maximum likelihood approach, which uses all available data to compute parameter estimates. All analyses implemented the Complex Survey option in Mplus to correct for the non-independence of observations that arises when including data from individuals within the same family. As triplet sets contribute three pairwise combinations of siblings to the dataset, behavioral genetic analyses employed the Weighting function to down-weight data from triplet pairs by 50%.

Prior to examining interrelations between our outcomes of interest, we fit separate confirmatory factor models for EF, general intelligence, and processing speed. Path analyses were constructed to investigate the contributions of EF and processing speed to the intelligence measures. All phenotypic and biometric models were applied to scores residualized for sex. When estimating models involving the general intelligence factor, we regressed the individual WASI-II test scores (Block Design, Matrix Reasoning, Vocabulary, Similarities) onto age to account for age differences in WASI-II test scores in a manner most closely resembling how FSIQ composites are created (in which individual test scores are first age-standardized prior to being combined). When estimating models involving EF and Speed factors, we chose a parsimonious approach in which we controlled for age at the level of the first order EF factors (Inhibition, Switching, Working Memory, Updating) and the Speed factor, rather than at the level of the individual tasks. We have previously reported that both factor loadings and intercepts of the individual EF measures are measurement invariant across age groups (Engelhardt et al., 2015). We report loadings of the individual intelligence tests and the first-order EF factors on their respective superordinate factors standardized relative to total variance (i.e., semipartial with respect to age).

To examine genetic and environmental influences on the outcomes, we fit a series of behavioral genetic models. These models decompose variance in a given outcome into additive genetic (A), shared environmental (C), and non-shared environmental (E) factors. Influences attributable to A serve to make genetically more similar individuals more alike on the phenotype under investigation, those attributable to C serve to make individuals raised in the same household more similar on the phenotype irrespective of their genetic relatedness, and those attributable to E serve to differentiate individuals on the phenotype even when raised together and perfectly matched on genotype. Model fit for both the phenotypic and behavioral genetic analyses was assessed by the chi-square test, the root-mean-square error of approximation (RMSEA), the comparative fit index (CFI), and the Akaike information criterion (AIC). To compare fit across models, we computed scaled chi-square difference statistics (Satorra & Benter, 2010).

Results

Scores for timed EF tasks were converted to reaction time metrics prior to computing switch costs and inhibition costs. Switch and inhibition costs were then multiplied by −1 so that higher scores represented better task performance. To correct for positive skew, we log transformed Trail Making and Local-Global scores, and square root transformed 2-Back and Listening Recall scores. Plus-Minus scores greater than 3 SD from the mean were Winsorized to the next least extreme value. Adhering to the Stop Signal exclusion protocol set by Congdon et al. (2010), we first computed Stop Signal Reaction Time (SSRT) for blocks consisting of 64 trials each. Block-level scores were omitted on the basis of consistent stop failures, misidentification of arrow direction, failure to respond to go trials, and low SSRTs. Remaining block scores were averaged to create a final SSRT measure.

Descriptive Statistics

Sample sizes, descriptive statistics and reliability estimates for all tasks can be found in Table 1. As is typical for the literature, reliability estimates for EF indices were occasionally somewhat lower than is standard for psychometric measures. This likely stems, in part, from the fact that EF indices are often calculated from difference scores between executive and nonexecutive conditions, leading to the compounding of measurement error (Cronbach & Furby, 1970). Consistent with this inference, we have previously reported high reliabilities for the individual task conditions upon which difference scores are based (Engelhardt et al., 2015).

Correlations among age, sex, and scores on the individual tasks are presented in Table 2. Age was significantly correlated with performance on all tasks aside from Full Scale IQ, which is computed using standard scores relative to a nationally representative aged-matched norming sample. Visual inspection of scatterplots and loess curves of age effects on the individual measures indicated that age effects were predominantly linear. Estimated quadratic age trends were trivial and inconsistent across tasks. Correlations between task performance and sex were inconsistent, with only 4 of the 20 tasks correlating significantly with sex. All models reported below were conducted using scores residualized for sex.

Table 2.

Correlation Matrix of Task Performance, Age, and Sex

Variable	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1. Stroop
2. Mickey	.09*
3. Stop Signal	.04	.13**
4. Trail Making	.23***	.14***	.09
5. Plus-Minus	.27***	.06	.03	.21***
6. Local-Global	.27***	.14***	.06	.42***	.24***
7. Digit Span  Back	.18***	.12***	.11*	.38***	.16***	.27***
8. Symmetry  Span	.26***	.16***	.06	.40***	.22***	.37***	.32***
9. Listening  Recall	.29***	.20***	.05	.45***	.27***	.41***	.42***	.53***
10. Running  Memory	.25***	.15***	.09	.45***	.23***	.39***	.44***	.46***	.60***
11. Keep Track	.22***	.12**	.09	.41***	.17***	.29***	.34***	.38***	.47***	.48***
12. 2-Back	.23***	.15***	.15***	.38***	.16**	.35***	.33***	.39***	.47***	.55***	.42***
13. Block  Design	.23***	.18***	.12**	.46***	.16***	.36***	.35***	.51***	.47***	.47***	.42***	.36***
14. Matrix  Reasoning	.20***	.14***	.11*	.43***	.14**	.33***	.36***	.38***	.44***	.49***	.45***	.42***	.57***
15. Vocabulary	.27***	.19***	.10*	.44***	.22***	.37***	.34***	.45***	.56***	.56***	.45***	.50***	.50***	.53***
16. Similarities	.25***	.17***	.10*	.45***	.21***	.37***	.32***	.43***	.51***	.50***	.41***	.43***	.50***	.45***	.74***
17. Full Scale IQ	.12**	.09*	.06	.36***	.10*	.22***	.29***	.30***	.37***	.45***	.41***	.36***	.63***	.69***	.67***	.66***
18. Pattern  Comparison	.27***	.19***	.08	.41***	.18***	.38***	.27***	.42***	.44***	.40***	.32***	.35***	.41***	.37***	.48***	.44***	.23***
19. Letter  Comparison	.28***	.18***	.03	.42***	.23***	.41***	.33***	.46***	.44***	.38***	.28***	.32***	.40***	.30***	.45***	.44***	.18***	.69***
20. Symbol  Search	.33***	.21***	.15***	.45***	.25***	.45***	.33***	.50***	.50***	.47***	.41***	.37***	.52***	.39***	.48***	.48***	.27***	.60***	.58***
21. Age	.34***	.25***	.14**	.43***	.25***	.44***	.31***	.52***	.54***	.44***	.37***	.38***	.48***	.37***	.53***	.51***	.02	.58***	.61***	.62***
22. Sex	−.08	.09**	−.02	−.01	−.03	−.03	.00	.14***	−.05	−.03	−.07	−.08*	.11**	.03	−.07	.00	.02	−.05	.00	−.05

Note. Zero-order Pearson correlation coefficients. All task scores are standardized. Positive correlations with sex represent better performance by males.

^*p ≤ .05,

^**p ≤ .01,

^***p ≤ .001

Phenotypic Models

Table 3 presents the standardized loadings from the confirmatory factor models. Based on our prior investigation of the structure of EF in a subset of 505 individuals from the current sample (Engelhardt et al., 2015), we first specified a hierarchical model in which each task loaded onto one of four first-order EF factors (Inhibition, Switching, Working Memory, or Updating), and each first-order factor loaded onto a latent general factor of EF (Common EF). The factor loadings of individual EF tasks onto the first-order factors were all significant at p < .05 (M_lambda = .55). The factor loadings of the first-order EF factors onto Common EF were significant at p < .001 (M_lambda = .62). As shown in Table 4, this model fit the data well (χ²(58) = 91.12, p = .0036, RMSEA = .03, CFI = .99). Moreover, the full four-factor model fit significantly better than reduced models in which two or more of the first-order EF factors were collapsed (p’s < .01). Given the low reliability of Stop Signal performance (α = .40) and its poor loading onto the Inhibition factor (λ = .16), we examined whether excluding the Stop Signal variable from the four-factor CFA would change the pattern of parameter estimates appreciably. In this model, which fit the data well (χ²(47) = 75.74, p = .005, RMSEA = .03, CFI = .99), the factor loadings of the remaining inhibition tasks did not change dramatically (Stroop λ = .37 and Mickey λ = .25, compared to .40 and .27, respectively, in the original model), nor did the loading of the Inhibition factor onto Common EF (λ = .47, compared to .43 in the original model).

Table 3.

Standardized Factor Loadings and Age Relations from Phenotypic Models of EF, g, and Speed

	Latent Factor
Indicator	In	Sw	WM	Up	Common EF	g	Speed
Hierarchical Factor Model of EF
Stroop	.40*** [.27, .53]
Mickey	.27*** [.15, .39]
Stop Signal	.16** [.04, .28]
Trail Making		.67*** [.61, .74]
Plus-Minus		.35*** [.25, .46]
Local-Global		.62*** [.55, .69]
Digit Span Back			.53*** [.47, .59]
Symmetry Span			.68*** [.63, .73]
Listening Recall			.78*** [.74, .83]
Running Memory				.79*** [.75, .83]
Keep Track				.63*** [.58, .68]
2-Back				.67*** [.60, .73]
Inhibition factor					.43*** [.24, .62]
Switching factor					.58*** [.49, .67]
Working Memory  factor					.70*** [.62, .78]
Updating factor					.77*** [.70, .85]
Factor Model of g a
Block Design						.49* [.11, .86]
Matrix Reasoning						.60** [.20, 1.00]
Vocabulary						.56* [.15, .98]
Similarities						.48*** [.19, .77]
Factor Model of Processing Speed
Pattern Comparison							.81*** [.77, .85]
Letter Comparison							.82*** [.78, .86]
Symbol Search							.75*** [.69, .80]
Age Relations
Age effect	.89*** [.61, 1.17]	.67*** [.61, .74]	.70*** [.64, .76]	.57*** [.49, .65]			.75*** [.71, .79]

Note. Standardized loadings of individual tasks onto higher-order factors, standardized loadings of first-order EF factors onto a Common EF factor, and standardized regression coefficients of first-order EF factors and the latent Speed factor onto age. 95% confidence intervals are reported in brackets. Manifest variables were residualized for sex prior to model fitting. The effect of age is controlled for at the level of the individual intelligence tests, the first-order EF factors, and the Speed factor. Loadings of the individual intelligence tests and the first-order EF factors on their respective superordinate factors are standardized with respect to total factor variances (including age-related variance). EF = Executive Function, g = general intelligence, In = Inhibition, Sw = Switching, WM = Working Memory, Up = Updating.

^aThe residual correlation between Block Design and Matrix Reasoning was .20 (p = .52). The residual correlation between Vocabulary and Similarities was .45 (p < .05).

^*p ≤ .05,

^**p ≤ .01,

^***p ≤ .001

Table 4.

Model Fit Statistics for Alternative Confirmatory Factor Models of EFs

	Model fit							Model fit vs. full model
Model	χ 2	χ2 scaling factor	df	p	RMSEA	CFI	AIC	χ2 diff	df	p
Four factors (full  model): In, Sw,  WM, Up	91.12	1.06	58	.0036	.03	.99	22561.99
Three factors:  In, Sw, WM-Up	117.28	1.05	60	.0000	.03	.98	22585.09	26.16	2	4.25e-7
Three factors:  In-Sw, WM, Up	103.07	1.05	60	.0005	.03	.98	22570.33	11.95	2	1.78e-3
Two factors:  In-Sw, WM-Up	130.79	1.05	63	.0000	.04	.97	22593.77	39.67	5	1.55e-7
One factor: Common EF	166.23	1.06	65	.0000	.04	.96	22628.57	75.11	7	7.57e-13

Note: In = Inhibition; Sw = Switching; WM = Working Memory; Up = Updating; RMSEA = root-mean-square error of approximation; CFI = comparative fit index; AIC = Akaike information criterion.

In the model of intelligence, all four WASI-II test scores were specified to load onto a latent general intelligence factor (i.e., a g factor), and correlated residuals were specified between Block Design and Matrix Reasoning, as well as between Vocabulary and Similarities. Loadings of the individual cognitive tasks onto the g factor were moderate (M_lambda = .53; p’s < .05). The model of processing speed specified a single common factor representing variance common to the three processing speed tasks. In this model, loadings of the tasks onto the latent Speed factor were high (M_lambda = .79; p’s < .001).

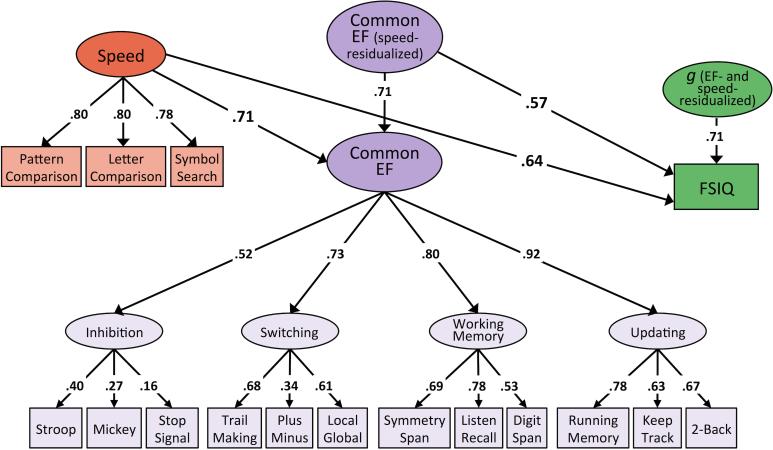
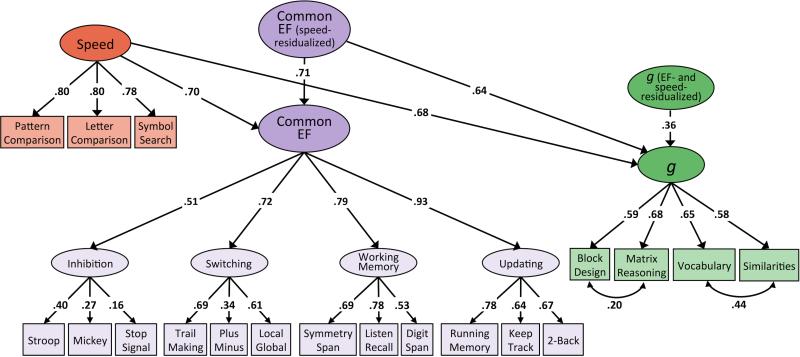
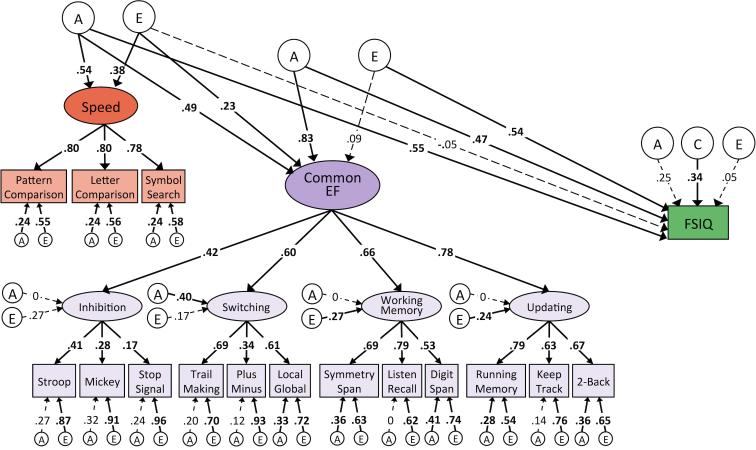
Correlations among the higher-order variables (Switching, Working Memory, Updating, Common EF, g, FSIQ, and Speed) were all significant at p < .001, with the exception of those involving the Inhibition factor, which were large yet not statistically significant (see Table 5). Notably, the Common EF factor correlated with FSIQ at .71 and with g at .91. To more directly assess the relationship between EF and intelligence, we fit a model in which the indices of intelligence were regressed onto a Common EF factor residualized for the effects of speed (see Figures 1a and 1b). After extracting the variance in Common EF that was unique of Speed, EF continued to be a strong predictor of both FSIQ (β = .57, p < .001) and g (β = .64, p < .001). Fifty percent of the variance in FSIQ remained unique of Speed and EF, and 13% of variance in g was explained by neither EF nor Speed. Residual variances for these analyses are reported in supplementary materials.

Table 5.

Correlations Among EF, g, and Speed Factors

Latent Variable	1	2	3	4	5	6	7
1. Inhibition
2. Switching	.99
3. Working Memory	.90	.77***
4. Updating	.84	.74***	.93***
5. Common EF	–	–	–	–
6. Full Scale IQ	.64	.59***	.64***	.69***	.71***
7. g	.82	.76***	.83***	.89***	.91***	–
8. Speed	.78	.63***	.54***	.44***	.55***	.41***	.53***

Note. Pearson correlation coefficients, semipartial with respect to age. Manifest variables were residualized for sex prior to model fitting. The effect of age is controlled for in models at the level of the individual intelligence tests, the first-order EF factors, and the Speed factor. Correlations with Common EF were modeled separately from correlations with first-order EF factors because correlations among the first-order EF factors are statistically redundant with factor loadings onto a latent variable. Because Full Scale IQ and g are constructed from the same tasks, correlations with each measure of intelligence were also estimated in separate models.

^*p ≤ .05,

^**p ≤ .01,

^***p ≤ .001

Figure 1.

Phenotypic models of FSIQ and g regressed onto Speed and Speed-residualized EF.

Note. Path diagrams for relationships between speed, executive function (EF) unique of speed, and measures of intelligence unique of speed and EF. Figure 1a depicts these relationships with respect to Full Scale IQ (FSIQ), while Figure 1b depicts them with respect to the latent g factor. Numbers on arrows represent standardized regression coefficients and factor loadings. All parameters are standardized and have been residualized for sex. The effect of age is controlled for at the level of the individual WASI-II tests, the first-order EF factors, and the Speed factor. Relations between Speed, Common EF, and intelligence are standardized relative to total factor variance, as are loadings of WASI-II tests onto g and of Inhibition, Switching, Working Memory, and Updating onto Common EF. Fit statistics for model depicted in Figure 1a: χ²(107) = 229.37, p < .001, RMSEA = .038, CFI = .97. Fit statistics for model depicted in Figure 1b: χ²(151) = 318.64, p < .001, RMSEA = .037, CFI = .97. Solid paths and bolded estimates indicate significance at p ≤ .01.

We were interested in whether these findings substantively differed when storage-plus-processing measures of working memory were excluded, but updating measures remained, such that the structure would more closely resemble the Miyake & Friedman (2000) three-factor structure. This was a potential concern because the inclusion of working memory measures and updating measures (such that Working Memory and Updating tasks composed six out of twelve EF measures) may have shifted the centroid of the EF construct hyperspace toward a Working Memory/Updating region that may be more strongly related to intelligence and away from a more diffuse central executive region that may be only moderately related to intelligence (for a general explication of the effect of indicator choice on factor identification, see Little, Lindenberger, and Nesselroade, 1999). The results of this analysis were very similar to those of the full model in which Working Memory tasks were included. Specifically, after extracting the variance in Common EF that was unique of Speed, EF continued to be a strong predictor of g (β = .68, p < .001), and only 5% of the variance in g was unique of both Speed and EF.

We next tested an alternative model in which speed and the domain-specific EFs served as indicators (rather than predictors) of g. Factor loadings of these additional indicators onto g were all significant at p < .001 (Inhibition λ = .36, Switching λ = .61, Working Memory λ = .66, Updating λ = .78, Speed λ = .36). Nevertheless, there was a significant decrement in model fit relative to the model in which g was regressed onto the Speed factor and the speed-residualized Common EF factor (χ²_diff(4) = 13.18, p = .002). Thus, in our behavioral genetic analyses, we proceeded with the original parameterization of the relationship between these factors.

Behavioral Genetic Models

Correlations between monozygotic (MZ) twins were greater than those between dizygotic (DZ) twins for 19 of the 20 manifest variables (see Table 6), indicating some degree of genetic influence on the measured outcomes. The confirmatory factor models from the phenotypic analyses served as the basis for our initial behavioral genetic models. We first estimated A, C, and E contributions to individual differences in EF, intelligence, and speed separately. For each set of variables, we assessed genetic and environmental influences on the highest-order factor, as well as residual genetic and environmental influences on the lower-order factors (in the case of EF) and individual tasks. Standardized parameter estimates are shown in Table 7.

Table 6.

Univariate Task Twin Correlations

Task	MZ	DZ
Stroop	0.33	0.09
Mickey	0.18	0.12
Stop Signal	−0.04	0.23
Trail Making	0.57	0.24
Plus-Minus	0.41	−0.08
Local-Global	0.46	0.31
Digit Span Back	0.47	0.23
Symmetry Span	0.50	0.42
Listening Recall	0.52	0.43
Running Memory	0.70	0.43
Keep Track	0.40	0.25
2-Back	0.54	0.30
Block Design	0.78	0.50
Matrix Reasoning	0.47	0.41
Vocabulary	0.69	0.58
Similarities	0.62	0.54
FSIQ	0.72	0.43
Pattern Comparison	0.57	0.50
Letter Comparison	0.57	0.50
Symbol Search	0.33	0.09

Note. Pearson correlation coefficients for cross-twin, within-task performance on measures of EF, speed, and intelligence. Variables were residualized for age and sex prior to analysis.

Table 7.

Standardized Parameter Estimates from Behavioral Genetic Analyses of EF, Intelligence, and Speed

	Models with shared environmental effects included			Model with shared environmental effects omitted
Variance component	a	c	e	a	e
Behavioral Genetic Model of EF
Common EF	.97*** [.80, 1.13]	.10 [−1.24, 1.44]	.24* [.04, .45]	.97*** [.92, 1.02]	.24* [.05, .43]
Inhibition-specific	.00 [.00, .00]	.00 [.00, .00]	.31 [−.56, 1.18]	.00 [.00, .00]	.28 [−.71, 1.27]
Switching-specific	.42*** [.23, .62]	.00 [.00, .00]	.20 [−.22, .63]	.42*** [.23, .62]	.20 [−.22, .63]
Working Memory-  specific	.00 [.00, .00]	.00 [.00, .00]	.27*** [.13, .40]	.00 [.00, .00]	.27*** [.13, .40]
Updating-specific	.00 [.00, .00]	.00 [.00, .00]	.19* [.01, .37]	.00 [.00, .00]	.19* [.01, .37]
Stroop-specific	.27 [−.16, .70]	.00 [.00, .00]	.87*** [.72, 1.02]	.27 [−.16, .70]	.88*** [.73, 1.02]
Mickey-specific	.21 [−.94, 1.35]	.21 [−.64, 1.06]	.91*** [.82, 1.01]	.32* [.07, .57]	.91*** [.81, 1.00]
Stop Signal-specific	.00 [.00, .00]	.31** [.12, .50]	.94*** [.87, 1.00]	.24 [−.07, .56]	.96*** [.87, 1.04]
Trail Making-specific	.22 [−.04, .48]	.00 [.00, .00]	.70*** [.61, .79]	.22 [−.04, .48]	.70*** [.61, .79]
Plus-Minus-specific	.08 [−1.64, 1.79]	.00 [.00, .00]	.93*** [.79, 1.08]	.07 [−1.72, 1.87]	.93*** [.78, 1.08]
Local-Global-specific	.33*** [.16, .50]	.00 [.00, .00]	.72*** [.64, .80]	.33*** [.16, .50]	.72*** [.64, .80]
Digit Span Back-  specific	.35 [−.08, .78]	.19 [−.37, .75]	.75 [.66, .83]	.41*** [.28, .54]	.74*** [.66, .82]
Symmetry Span-  specific	.34* [.03, .64]	.13 [−.47, .73]	.64*** [.57, .71]	.37*** [.26, .46]	.64*** [.57, .70]
Listening Recall-  specific	.00 [.00, .00]	.00 [.00, .00]	.61*** [.56, .66]	.00 [.00, .00]	.61*** [.56, .66]
Running Memory-  specific	.25*** [.10, .40]	.00 [.00, .00]	.55*** [.48, .62]	.25*** [.10, .40]	.55*** [.48, .62]
Keep Track-specific	.14 [−.20, .48]	.00 [.00, .00]	.77*** [.69, .84]	.14 [−.19, .48]	.77*** [.69, .84]
2-Back-specific	.38*** [.23, .52]	.00 [.00, .00]	.64*** [.55, .74]	.38*** [.23, .52]	.64*** [.55, .74]
Behavioral Genetic Model of Full Scale IQ
FSIQ	.74*** [.55, .92]	.40** [.14, .66]	.55*** [.46, .64]	.85*** [.79, .90]	.53*** [.45, .61]
Behavioral Genetic Model of g a
g	.88*** [.63, 1.12]	.34 [−.17, .87]	.34** [.13, .54]	.95*** [.88, 1.01]	.32*** [.13, .52]
Block Design-specific	.60*** [.51, .70]	.03 [−.13, .18]	.47*** [.39, .54]	.53*** [.41, .66]	.46*** [.38, .54]
Matrix Reasoning-  specific	.28*** [.14, .42]	.26*** [.10, .41]	.66*** [.60, .73]	.16 [−.02, .33]	.65*** [.57, .74]
Vocabulary-specific	.12 [−.13, .19]	.27* [.02, .52]	.49*** [.42, .56]	.45*** [.34, .56]	.49*** [.43, .56]
Similarities-specific	.19 [−.07, .46]	.29* [.05, .53]	.57*** [.50, .64]	.47*** [.36, .57]	.57*** [.51, .63]
Behavioral Genetic Model of Speed
Speed	.53*** [.44, .62]	.00 [.00, .00]	.39*** [.28, .50]	.53*** [.44, .62]	.39*** [.28, .50]
Pattern Comparison-  specific	.15 [−.46, .76]	.14 [−1.24, 1.51]	.55*** [.35, .74]	.22** [.07, .37]	.54*** [.46, .62]
Letter Comparison-  specific	.05 [−.03, .12]	.56** [.18, .93]	.15 [−1.29, 1.58]	.19* [.03, .35]	.54*** [.47, .62]
Symbol Search-  specific	.09* [.02, .16]	.66*** [.60, .72]	.02 [−.67, .71]	.29*** [.16, .42]	.60*** [.51, .68]

Note. Standardized regression coefficients for separate behavioral genetic analyses of EF, speed, and intelligence. 95% confidence intervals are reported in brackets. Manifest variables were residualized for sex prior to model fitting. The effect of age is controlled for at the level of the individual intelligence tests, the first-order EF factors, and the Speed factor. Loadings of the individual intelligence tests and the first-order EF factors on their respective superordinate factors are standardized with respect to total factor variance. EF = executive function, a = additive genetics, c = shared environment, e = non-shared environment, g = general intelligence.

^aResidual ACE correlations for Block Design and Matrix Reasoning: r_A = 1.00 (p < .001), r_C = 1.00 (p < .001), r_E = .03 (p = .71). Residual AE correlations for Block Design and Matrix Reasoning: r_A = .97 (p < .001), r_E = .08 (p = .42). Residual ACE correlations for Vocabulary and Similarities: r_A = 1.00 (p < .001), r_C = 1.00 (p < .001), r_E = .27 (p < .001). Residual AE correlations for Vocabulary and Similarities: r_A = .77 (p < .001), r_E = .27 (p < .001).

^*p ≤ .05,

^**p ≤ .01,

^***p ≤ .001

With regard to the Common EF factor, the a coefficient representing additive genetic influences was .97 (p < .001), the c coefficient representing shared environmental influences was .10 (p = .88), and the e coefficient representing non-shared environmental influences was .24 (p < .05). Thus, the heritability of Common EF was estimated at 94% (i.e., a^{2 =} .97²). Of the first-order EF domains, only Switching exhibited significant genetic influence above and beyond that of Common EF (a = .42, p < .001). Working Memory and Updating exhibited significant non-shared environmental influences independent of Common EF (Working Memory e = .38, p < .001; Updating e = .19, p < .05). We observed significant (p < .05) residual A influences operating on four of the tasks, significant C influences operating on one of the tasks, and significant E influences operating on all EF tasks.

Full Scale IQ was moderately heritable (a = .74, p < .001; a² = 55%) with significant contributions coming from environmental factors (c = .40, p < .01; e = .55, p < .001). The behavioral genetic decomposition of g indicated higher genetic contributions (a = .88, p < .001; a² = 77%) and somewhat lower environmental contributions (c = .34, p = .20; e = .34, p < .01) than did the decomposition of FSIQ. Residual genetic variance was observed for Block Design (a = .60, p < .001) and Matrix Reasoning (a = .28, p < .001). Shared environmental variance independent of g was found for Similarities (c = .29, p < .05) and Matrix Reasoning (a = .26, p < .001), and all four WASI-II tasks exhibited significant residual non-shared environmental variance (p’s < .01). With respect to Speed, genetic (a = .53, p < .001) and non-shared environmental (e = .39, p < .001) influences predominated, with no observable effect of the shared environment. Unique genetic and shared environmental factors operating on Symbol Search were significant, as were residual non-shared environmental factors contributing to Pattern Comparison (p’s < .05).

We next fit separate AE models for EF, intelligence, and processing speed (see final two columns in Table 7). The resulting estimates for EF and speed were consistent with those of the ACE models: significant genetic contributions to the higher-order EF and Speed factors and a small number of indicators, combined with significant non-shared environment contributions to the common factors and the majority of indicators. Nested model comparisons indicated that the fits of AE and ACE models of EF were not significantly different from one another (p = .95), meaning that the omission of the c parameters did not significantly decrease model fit. The same was the case for a nested comparison of the AE and ACE models of speed (p = .37). Dropping the c parameters from the behavioral genetic model of g resulted in inflation of the a coefficients corresponding to the g factor and three of the four tasks. A nested model comparison indicated that the AE model of g fit significantly worse than the ACE model of g (p = .006), indicating a decrement in model fit with the omission of shared environment factors. Based on the results of these model comparisons, we proceeded with AE models of EF and speed and ACE models of FSIQ and g for the remaining analyses.

In an alternative parameterization of the genetic architecture of EFs, we specified an AE bifactor model in which all 12 tasks loaded directly onto Common EF, in addition to their respective first-order EFs. The pattern of genetic and environmental contributions to EFs in this model was extremely similar to that of the original hierarchical model. Additive genetic influences on Common EF – a latent factor defined as shared variance across all tasks – were estimated at .98 (p < .001; a² = 96%), and unique environmental contributions were estimated at .22 (p < .05). Significant genetic influences not accounted for by the common factor operated only on Switching (a = .52, p < .001), while significant environmental factors independent of Common EF operated only on Working Memory (e = .39, p < .001). Estimates of task-specific genetic and environmental influences were also similar to those for the hierarchical AE model (see Supplementary Figure 1).

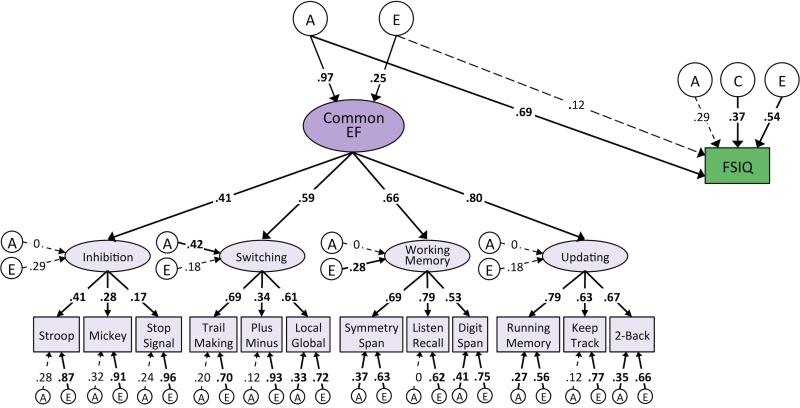
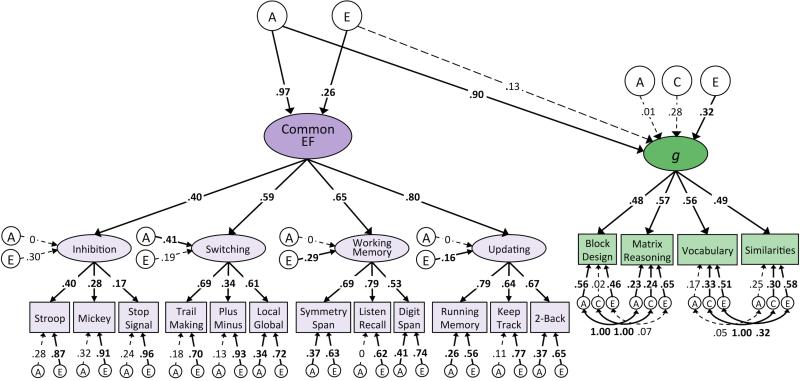
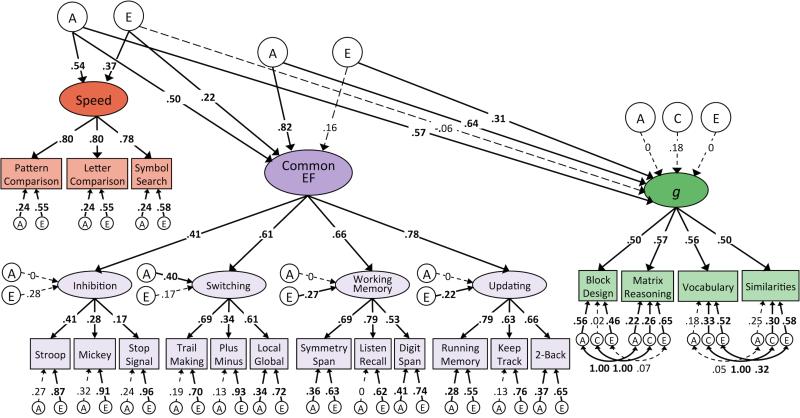
After characterizing the genetic and environmental structures of the three sets of variables separately, we combined them to examine whether overlapping genetic and/or environmental factors contribute to the observed relations between EF, intelligence, and processing speed. First, we fit a model of EF and intelligence in which we regressed the measures of intelligence onto the A and E factors of the higher order Common EF factor from the hierarchical model of EF (see Figures 2a and 2b). Genetic influences on Common EF explained just under half of the variance in FSIQ (β = .69, p < .001), and the genetic correlation between EF and FSIQ was high (r_A = .92, p < .001). Conversely, non-shared environment contributions to Common EF had a negligible effect on FSIQ (β = .12, p = .24), which corresponds to a correlation of .22 (p = .22) between the E factors for EF and FSIQ. Environmental influences unique to FSIQ remained high (c = .37, p = .001; e = .54, p < .001). The finding of overlapping genetic influences was even more pronounced when we operationalized intelligence using the g factor: Genetic influences on Common EF explained 80% of the variance in g (β = .90, p < .001). Moreover, the genetic correlation between EF and g was 1.00 (p < .001), meaning that after incorporating genetic factors for EF into the behavioral genetic model for g, there were negligible residual genetic influences on g (a = .01, p = .98). As with FSIQ, the non-shared environment important for EF did not significantly predict g (β = .13, p = .29), and environmental influences unique to g were evident (c = .28, p < .05; e = .32, p < .001). The non-shared environment correlation between EF and g was .38 (p = .22). Importantly, however, there was some indication of unique genetic influences on individual WASI-II measures that were unique of g and EF.

Figure 2.

Behavioral genetic models of FSIQ and g regressed onto EF.

Note. Bivariate Cholesky decomposition for additive genetic (A), shared environmental (C), and non-shared environmental (E) contributions to executive function (EF) and measures of intelligence. Figure 2a depicts these relationships with respect to Full Scale IQ (FSIQ), while Figure 2b depicts them with respect to the latent g factor. Numbers on arrows represent standardized regression coefficients and factor loadings. All parameters are standardized and have been residualized for sex. The effect of age is controlled for at the level of the individual WASI-II tests, the first-order EF factors, and the Speed factor. Relations between Speed, Common EF, and intelligence are standardized relative to total factor variance, as are loadings of WASI-II tests onto g and of Inhibition, Switching, Working Memory, and Updating onto Common EF. Fit statistics for model depicted in Figure 2a: χ²(738) = 1046.54, p < .001, RMSEA = .044, CFI = .91. Fit statistics for model depicted in Figure 2b: χ²(1089) = 1492.15, p < .001, RMSEA = .041, CFI = .93. Solid paths and bolded estimates indicate significance at p ≤ .01.

To examine the extent to which individual EFs accounted for genetic and environmental variance in intelligence, we also fit bivariate Cholesky models in which g was regressed onto the A and E factors for, separately, Inhibition, Switching, Working Memory, and Updating. The results of these analyses, including residual ACE influences on g, are shown in Table 8. Genetic influences operating on each of the first-order EFs significantly contributed to g (M_beta = .89, p’s < .001), as did non-shared environment influences operating on Inhibition (β = .32, p < .01). Interestingly, genetic influences on Inhibition were appreciable but not significant (a = .22, p = .08), although they significantly related to g. This may be the result of lower power to detect effects involving the Inhibition factor, as its factor loadings tended to be very low. Across these models, genetic influences on g unique of EF were not significant. That either genetic variance common to all four EFs or genetic variance in each EF domain could account for nearly the entirety of genetic variance in intelligence likely results from the fact that nearly all of the genetic variance in each EF domain was shared with all the other domains.

Table 8.

Standardized Parameter Estimates for Bivariate Cholesky Models of Individual EFs and g

EF entered as upstream variable	AE factors operating on EFs		Regression coefficient for g onto AE factors of EF		Residual ACE factors operating on g
	a	e	β a	β e	a	c	e
Inhibition	.22 [−.03, .47]	.45* [.04, .86]	.91*** [.69, 1.13]	.32** [.12, .53]	.00 [.00, .01]	.27 [−.37, .90]	.01 [−.44, .45]
Switching	.72*** [.60, .85]	.19 [−.24, .62]	.77*** [.61, .92]	.04 [−.37, .45]	.42 [−.06, .89]	.36 [−.02, .74]	.33 [.14, .53]
Working Memory	.57*** [.47, .67]	.43*** [.30, .55]	.95*** [.82, 1.08]	.08 [−.06, .23]	.00 [.00, .00]	.11 [−.78, 1.00]	.29** [.08, .50]
Updating	.76*** [.69, .83]	.28*** [.13, .43]	.94*** [.87, 1.01]	.04 [−.21, .28]	.00 [.00, .00]	.01 [−.31, .32]	.34*** [.16, .51]

Note. Standardized regression coefficients for separate Cholesky decompositions modeling relationships between g and the AE factors of Inhibition, Switching, Working Memory, and Updating. 95% confidence intervals are reported in brackets. Manifest variables were residualized for sex prior to model fitting. The effect of age is controlled for at the level of the individual WASI-II tests and the EF factors. Relations between each EF and g are partial with respect to age. EF = executive function, a = additive genetics, c = shared environment, e = non-shared environment, g = general intelligence.

^*p ≤ .05,

^**p ≤ .01,

^***p ≤ .001

In order to test the possibility that overlapping genetic influences on EF and intelligence were simply due to processing speed, we next fit a multivariate model in which Common EF was regressed on the A and E factors for Speed, and intelligence was regressed on the A and E factors for both Speed and Common EF. These results are depicted in Figure 3. Genetic and non-shared environmental influences on Speed also contributed significantly to Common EF ability (β = .49, p < .001 for a; β = .23, p < .001 for e). The E factor for Common EF significantly contributed to FSIQ (β = .54, p < .001) but did not appreciably contribute to Common EF itself after extracting variance unique of Speed (e = .07, p = .10). The E factor of Speed did not appreciably contribute to FSIQ (β = −.05, p = .44). Genetic variation in Speed accounted for 30% of the variance in FSIQ (β = .55, p < .001). Genetic variation in Common EF unique of genetic influences on Speed accounted for an additional 22% of the variance in FSIQ (β = .47, p < .001). Residual genetic influences on FSIQ were not significant after accounting for genetic influences mediated by Speed and EF (a = .25, p = .24). Results were very similar when intelligence was measured by the latent g factor. Genetic influences on Speed explained 46% of the variance in g (β = .68, p < .001). The Speed-unique genetic factors for Common EF explained 41% of the variance in g (β = .66, p < .001). No genetic influences unique to g remained after accounting for genetic contributions to Speed and EF (β = .00, p = .73). The E factor for EF impacted general intelligence (β = .31, p < .01) but did not appreciably contribute to Common EF itself after controlling for genetic contributions of Speed (e = .16, p = .07). The E factor for Speed did not impact general intelligence (β = −.06, p = .41). There was some indication of unique genetic influences on the individual WASI-II measures that were unique of g, EF, and Speed.

Figure 3.

Behavioral genetic models of FSIQ and g regressed onto Speed and Speed-residualized EF.

Note. Multivariate Cholesky decomposition for additive genetic (A), shared environmental (C), and non-shared environmental (E) contributions to executive function (EF), measures of intelligence, and speed. Figure 3a depicts these relationships with respect to Full Scale IQ (FSIQ), while Figure 3b depicts them with respect to the latent g factor. Numbers on arrows represent standardized regression coefficients and factor loadings. All parameters are standardized and have been residualized for sex. The effect of age is controlled for at the level of the individual WASI-II tests, the first-order EF factors, and the Speed factor. Relations between Speed, Common EF, and intelligence are standardized relative to total factor variance, as are loadings of WASI-II tests onto g and of Inhibition, Switching, Working Memory, and Updating onto Common EF. Fit statistics for model depicted in Figure 3a: χ²(1098) = 1606.64, p < .001, RMSEA = .046, CFI = .91. Fit statistics for model depicted in Figure 3b: χ²(1521) = 2167.13, p < .001, RMSEA = .044, CFI = .91. Solid paths and bolded estimates indicate significance at p ≤ .01.

To examine the extent to which EFs account for genetic and environmental variance in more specific components of intelligence, we also fit bivariate Cholesky models in which WASI-II Verbal Comprehension Index (VCI, a composite of age-standardized Vocabulary and Similarities scores) and WASI-II Perceptual Reasoning Index (PRI, a composite of age-standardized Block Design and Matrix Reasoning scores) were regressed onto the A and E factors for, separately, Common EF, Inhibition, Switching, Working Memory, and Updating. The results of these analyses, including residual ACE influences on the PRI and VCI composites, are shown in Table 9. Genetic influences operating on Common EF, as well as those acting on each of the first-order EFs, significantly contributed to variance in PRI (M_beta = .59, p’s < .001) and VCI (M_beta = .61, p’s < .001). Variance in PRI was also attributable to non-shared environmental factors for Common EF (β = .31, p < .05). Consistent with the decompositions of g reported above, residual genetic influences on VCI (i.e., those unique of EF) were not significant in any model. Conversely, we observed genetic influences on PRI that were unique of those for Common EF (a = .49, p < .01), Switching (a = .48, p < .01), and Updating (a = .51, p < .001). These results indicate that EFs capture all of the genetic variance in verbal comprehension and all of the variance that is shared between the verbal comprehension and perceptual reasoning measures (i.e., general intelligence), but they do not capture all of the genetic variance in perceptual reasoning.

Table 9.

Standardized Parameter Estimates for Bivariate Cholesky Decompositions of EFs, Perceptual Reasoning, and Verbal Comprehension

EF entered as upstream variable	AE factors operating on EFs		Regression coefficient for composite onto AE factors of EF		Residual ACE factors operating on composite
	a	e	β a	β e	a	c	e
Cholesky Decompositions of EFs and PRI
Common EF	.97*** [.92, 1.02]	.25** [.06, .43]	.54*** [.46, .63]	.31* [.06, .55]	.49** [.19, .80]	.28 [−.09, .65]	.54*** [.38, .69]
Inhibition	.20 [−.08, .48]	.45 [−.13, 1.02]	.71*** [.45, .96]	.21 [−.23, .66]	.00 [.00, .01]	.34 [−.01, .70]	.58*** [.38, .78]
Switching	.73*** [.61, .85]	.17 [−.32, .66]	.49*** [.36, .63]	.23 [−.47, .92]	.48** [.15, .82]	.37* [.08, .66]	.58*** [.31, .85]
Working Memory	.55*** [.43, .67]	.45*** [.31, .58]	.64*** [.50, .78]	.11 [−.03, .24]	.29 [−.37, .95]	.35* [.03, .68]	.61*** [.49, .73]
Updating	.77*** [.69, .85]	.27** [.10, .44]	.55*** [.45, .65]	.19 [−.03, .40]	.51*** [.21, .82]	.22 [−.28, .72]	.59*** [.47, .71]
Cholesky Decompositions of EFs and VCI
Common EF	.97*** [.92, 1.01]	.25** [.06, .43]	.62*** [.55, .70]	.09 [−.14, .31]	.00 [.00, .00]	.46*** [.38, .54]	.63*** [.55, .70]
Inhibition	.23 [−.05, .50]	.44 [−.15, 1.02]	.64*** [.45, .83]	.22 [−.25, .69]	.00 [.00, .00]	.44*** [.21, .67]	.59*** [.40, .77]
Switching	.72*** [.59, .84]	.18 [−.29, .65]	.48*** [.34, .63]	−.02 [−.42, .45]	.36 [−.01, .73]	.48*** [.34, .63]	.64*** [.57, .70]
Working Memory	.57*** [.47, .67]	.43*** [.30, .55]	.65*** [.54, .75]	.01 [−.12, .14]	.00 [.00, .00]	.44*** [.30, .57]	.62*** [.57, .68]
Updating	.77*** [.70, .85]	.25** [.08, .42]	.67*** [.59, .75]	−.17 [−.07, .41]	.00 [.00, .00]	.40*** [.29, .51]	.60*** [.50, .70]

Note. Standardized regression coefficients for separate Cholesky decompositions modeling relationships between WASI-II composites and the AE factors of Common EF, Inhibition, Switching, Working Memory, and Updating. 95% confidence intervals are reported in brackets. Manifest variables were residualized for sex prior to model fitting. The effect of age is controlled for at the level of the composites and the first order EF factors. Relations between each EF and WASI-II composites are partial with respect to age. EF = executive function, a = additive genetics, c = shared environment, e = non-shared environment, PRI = WASI-II Perceptual Reasoning Index, VCI = WASI-II Verbal Comprehension Index.

^*p ≤ .05,

^**p ≤ .01,

^***p ≤ .001

Sensitivity Analyses

We were interested in probing the sensitivity of our key finding of high genetic overlap between general EF and intelligence by testing alternative modeling choices. First, we examined whether the results substantively differed when the bifactor model of EF described earlier was included in the Cholesky decomposition of g on EF. Results of this analysis revealed high genetic overlap between g and Common EF (β = .89, p < .001). Consistent with estimates from the hierarchical EF model, genetic (a = .11, p = .90) and shared environmental (c = .26, p = .36) influences unique to g were not significant. In contrast to results from the hierarchical model of EF, we found that residual non-shared environmental influences continued to significantly contribute to variance in g in the bifactor model (e = .33, p < .01).

We next fit a multivariate behavioral genetic model in which the WASI-II tasks, first-order EF factors, and the Speed factor served as indicators of a higher-order g factor. Parameter estimates for the ACE components of this analysis can be found in Supplementary Table 3. The results of this analysis revealed a highly heritable g factor (a = .96, p < .001; a² = 92%) that was only minimally influenced by environmental factors (c = .17, p = .64; e = .24, p < .01). Switching and Speed exhibited genetic influence independent of g (Switching a = .39, p < .001; Speed a = .42, p < .001). Of the latent indicators of g, Working Memory, Updating, and Speed were influenced by non-shared environment influences unique of general intelligence (Working Memory e = .29, p < .001; Updating e = .25, p < .001; Speed e = .36, p < .001).

Finally, we tested whether our key finding of strong genetic overlap between EFs and intelligence would hold after omitting storage-only measures of working memory, so as to closely approximate the three-factor structure established by Miyake and Friedman (2000). The results of this analysis indicated that, even in the absence of working memory storage measures, genetic influences on Common EF that were not attributable to Speed explained 46% of the variance in g (β = .68, p < .001). As in the full model, no genetic influences unique to g remained after accounting for genetic contributions to Speed and EF (β = .00, p = .71).

Discussion

There has been widespread and longstanding interest in identifying fundamental cognitive processes that account for genetic variation in higher-order mental abilities, but very few studies have capitalized on genetically informative research designs. The goal of the current study was to test EF as a source of variance underlying genetic influences on intelligence in a cross-sectional child sample. Results indicated that genetic influences on broad executive functioning ability – as indexed by a latent factor capturing common variance across four specific EF domains – account for a large proportion of phenotypic variance and all of the genetic variance in childhood intelligence. Importantly, there exists substantial shared genetic variance between general EF and intelligence that is independent of variation that both variables share with processing speed. Results did indicate, however, that EFs strongly, but do not fully, capture genetic variation in a more specific perceptual reasoning index.

Previous studies have reported strong links between various EF domains and individual differences in intelligence across the lifespan (Ackerman et al., 2005; Blair, 2006; Brydges, Reid, Fox, & Anderson, 2012; Conway et al., 2003; Engle, 2002; Kyllonen & Christal, 1990; Salthouse et al., 2003; Salthouse, 2005), but fewer studies have examined relations in the context of the multidimensional hierarchical model of EF. Importantly, constructing latent EF variables from multiple indicators enabled us to isolate variance in each EF domain of interest from task-specific (and potentially non-executive) variance. Other studies that have used latent variable approaches to examine EF-intelligence relations (e.g., Engle, Tuholski, Laughlin, & Conway, 1999; Polderman et al., 2009; Salthouse et al., 2003; Schmiedek, Hildebrandt, Lövdén, Wilhelm, & Lindenberger, 2009) have reported stronger and more consistent relations than those implementing single measures (e.g., Jaeggi et al., 2010; Kane, Conway, Miura, & Colflesh, 2007; Salthouse, 2005).

The current report of a strong, genetically-mediated relationship between latent EFs and intelligence in childhood is similar to the pattern of results reported for a young adult sample that also employed a latent variable approach to modeling EFs (Friedman et al., 2008). However, our results and those of Friedman et al. (2008) do differ somewhat in terms of the specific magnitude of genetic correlation between general EF and intelligence. Friedman et al. (2008) report the association between EF and FSIQ at r_A = .57, whereas the current estimate of this association was r_A = .92 (95% CIs: .73, 1.11). One possible reason for this difference could be the different age ranges of the two samples. However, the difference could also stem from other causes, some of which we were able to probe. First, we did not specify a cognitive architecture of EF identical to Friedman et al.’s, in that we included measures of both storage (working memory) and storage-plus-processing (updating). To more directly compare our results with those of Friedman et al. (2008), we conducted a sensitivity analysis that excluded the Working Memory latent variable. The EF-intelligence association in this sensitivity analysis remained very strong, indicating that it was not driven by our original EF structure being more heavily weighted toward working memory. A second difference between the two studies is that the loadings of the inhibition measures on the Inhibition factor were somewhat stronger in the Friedman et al. study than in the current study. It is possible that the paradigms commonly accepted as tapping “inhibition” in fact represent a rather heterogeneous, weakly overlapping set of processes, particularly in developmental samples (for a review, see Lee et al., 2013). Nevertheless, the primary results of our study held after removing the weakest-loading Inhibition indicator (Stop Signal) from the model, suggesting that our Inhibition factor does not unduly bias either the phenotypic or the genetic relations among the remaining variables. Finally, it is possible that while the point estimates from our study and that of Friedman et al. (2008) differ somewhat in magnitude, they both reflect a similar population effect size. In other words, the point estimates may potentially differ simply because of sampling variability.

In statistically mediating genetic effects on intelligence, EFs meet a primary criterion for what others have termed endophenotypes (Cannon & Keller, 2006; Gottesman & Gould, 2003; Meyer-Lindenberg & Weinberger, 2006). Endophenotypes are conceptualized as intermediaries between the genome and a more environmentally-influenced phenotype. One major criterion for a variable to be considered an endophenotype is that genetic factors that contribute to its variance should also account for substantial genetic variance in the phenotype of interest. Endophenotypes may share genetic variation with phenotypes because of causal mediation, in that they occupy an intermediate position along the causal chain between genotype and phenotype. However, they may also share genetic variation with phenotypes because they simply index the same genetic liability for that phenotype without playing causal roles per se (Kendler & Neale, 2010; Solovieff, Cotsapas, Lee, Purcell, & Smoller, 2013). Indeed, it is even possible that the direction of causality is from the purported phenotype (in this case, intelligence) to the purported endophenotype (EF). Although a large theoretical and computational literature in cognitive psychology operates on the assumption that EFs are causal to intelligence, we were not able to directly test this hypothesis in the current study. Nevertheless, the finding that EFs and intelligence share substantial genetic variance is of high theoretical and practical importance regardless of the causal basis of this association. For instance, although researchers who document genetic associations between EFs and other outcomes, such as academic achievement or psychopathology, may be tempted to interpret these associations in terms of the very specific regulatory processes that happen to have been tapped by the EF measures that were administered in a particular study, our results suggest that such findings may be manifestations of genetic etiology shared with a much broader set of cognitive abilities.

The finding that the genes that are relevant to EF are highly overlapping with those that impact intelligence held true regardless of whether intelligence was formally modeled as a latent factor or simply indexed by FSIQ (a composite measure). However, intelligence as indexed by a latent variable was much more highly heritable than intelligence as indexed by FSIQ. Importantly, the heritability of FSIQ in the current sample (mean age = 11 years) was 55%, exactly the same estimate reported by Haworth et al. (2010) for composite measures (oftentimes FSIQ) of intelligence in a meta-analytic sample of N = 4,934 pairs of twins (mean age = 12 years, labeled the “adolescence” age group by those authors) from four different countries.¹ Additionally, shared and nonshared environmentalities of FSIQ were, respectively, 16% and 30% in our sample, compared to 18% and 27% in Haworth et al. (2010). Thus, the higher heritability estimate of 77% that we obtained for g does not appear to be attributable to differences between the current sample and existing samples, but is attributable to the latent variable modeling strategy. Indeed, studies that have formally modeled g as a latent variable have also reported very high heritability estimates (Cheung, Harden, & Tucker-Drob, 2015; Panizzon et al., 2014; Petrill, 1997). In formal latent variable models, environmental influences predominantly act on more specific ability domains measured by individual tests (Petrill, 1997). This distinction has potentially interesting implications for research on age trends in the heritability of intelligence. For example, are developmental increases in the heritability of intelligence – which primarily have been identified in studies of composite measures of intelligence – driven by age-related changes in the overall magnitude of genetic influence on cognitive abilities per se, or simply by age-related increases in genetic covariation among cognitive ability domains? How do such trends compare to the age trends in the genetics of EFs and their covariation with intelligence? Investigations of developmental transformations in the genetic and environmental influences of intelligence that model age trends in both domain-general and domain-specific components of test score variation (cf. Cheung et al., 2015) are needed in order to discern these possibilities.

The finding that EFs share all of their genetic variance with general intelligence and verbal comprehension but only some of their genetic variance with perceptual reasoning may appear initially to be somewhat of a puzzle. Because both EFs and perceptual reasoning reflect highly abstract forms of cognitive mechanics (Baltes, 1987), whereas verbal comprehension reflects a culturally contextualized form of acquired knowledge, one might expect EFs to share more genetic variance with perceptual reasoning than with verbal comprehension. One possible explanation for this finding is that EFs more fully index motivational and self-regulatory skills important for learning and knowledge acquisition (Tucker-Drob, Briley, Engelhardt, Mann, & Harden, in press) than does perceptual reasoning. Thus, greater shared genetic variance between EFs and verbal comprehension than between EFs and perceptual reasoning may reflect a stronger role for EFs than for perceptual reasoning in intellectual investment processes (Cattell, 1987; Tucker-Drob & Harden, in press).

The very high heritability of EF and its strong phenotypic and genetic covariation with intelligence raises the question of whether strong genetic influences are universal across individuals. One intriguing hypothesis that has existed in the literature for some time is that genetic influences on intelligence (and, by implication, possibly EFs as well) differ as a systematic function of childhood socioeconomic status, with genetic influences being suppressed under conditions of greater socioeconomic adversity (Scarr-Salapatek, 1971). This is an important hypothesis with potentially widespread implications for science and policy. A recent meta-analysis of such Gene × Socioeconomic Status interaction research indicated support for the Scarr-Salapatek (1971) hypothesis in US samples, but not in samples from Western Europe and Australia (Tucker-Drob & Bates, 2016). Importantly, however, Tucker-Drob and Bates (2016) conducted a power analysis based on the meta-analytic effect sizes, which indicated that sample sizes of at least 3,300 twin pairs are required to obtain acceptable power to detect a Gene × Socioeconomic Status interaction. We have therefore chosen not to examine this hypothesis in the current data. The question of whether genetic influences on EF and its covariation with intelligence vary systematically with family socioeconomic status thus remains an open question.

The finding of strong phenotypic overlap and nearly perfect genetic overlap between EF and intelligence has important implications for the intersection of two traditionally distinct fields of study: genetics and neuroscience. Intelligence is a highly studied phenotype not only in behavioral genetics (e.g., twin studies) but also in molecular genetic association studies (e.g., GWAS). Recently, researchers in genetics have made strides in identifying the molecular-genetic foundations of intelligence (e.g., Davies et al., 2015; Rietveld, 2014), but the genetics of EFs are far less studied. The reverse occurs in neuroscience, in that the neural foundations of EFs are much more highly studied than those of intelligence. Researching the genetics of the neural foundations of both intelligence and EFs might benefit from an integration of findings across fields. For instance, polygenic scores derived from large-scale GWA studies of intelligence might be used in smaller neuroimaging studies of EF. Our results suggest that such approaches might be quite fruitful.

In conclusion, we found that the genetic factors underlying individual differences in childhood EFs also account for significant proportions of variance in concurrently measured intelligence, measured both in latent and manifest space. These findings provide a foundation for future investigations into the psychological and physiological processes that link genetic variation to individual differences in complex, socially meaningful traits such as intelligence. These results may also serve as a springboard for future studies of age- and socioeconomic-based differences in the heritability of cognitive processes, including EFs and intelligence. Together, the results of this study further our understanding of the psychological functions hypothesized to support broad mental capacities that are relevant across time and settings.