SUSCEPTIBILITY-BASED TIME-RESOLVED WHOLE-ORGAN AND REGIONAL TISSUE OXIMETRY

Abstract

The magnetism of hemoglobin – being paramagnetic in its deoxy and diamagnetic in its oxy state – offers unique opportunities to probe oxygen metabolism in blood and tissues. The magnetic susceptibility χ of blood scales linearly with blood oxygen saturation, which can be obtained by measuring the magnetic field ΔB of the intravascular MR signal relative to tissue. In contrast to χ the induced field ΔB is non-local. Therefore, to obtain the intravascular susceptibility Δχ relative to adjoining tissue from the measured ΔB demands solution of an inverse problem. Fortunately, for ellipsoidal structures, to which a straight, cylindrically shaped blood vessel segment conforms, the solution is trivial. The article reviews the principle of MR susceptometry-based blood oximetry. It then discusses applications for quantification of whole-brain oxygen extraction – typically on the basis of a measurement in the superior sagittal sinus – and, in conjunction with total cerebral blood flow, the cerebral metabolic rate of oxygen (CMRO₂). By simultaneously measuring flow and venous oxygen saturation (SvO₂) a temporal resolution of a few seconds can be achieved, allowing the study of the response to nonsteady-state challenges such as volitional apnea. Extensions to regional measurements in smaller cerebral veins are also possible, as well as voxelwise quantification of venous blood saturation in cerebral veins accomplished by quantitative susceptibility mapping (QSM) techniques. Applications of susceptometry-based oximetry to studies of metabolic and degenerative disorders of the brain are reviewed. Lastly, the technique is shown to be applicable to other organ systems such as the extremities using SvO₂ as a dynamic tracer to monitor the kinetics of the microvascular response to induced ischemia.

1. Background and Introduction

1.1. Motivation: Quantifying Oxygen Consumption as a Measure of Energy Requirements

All living cells require energy to sustain their function. In mammalian systems, energy is produced by oxidation of nutrients after they are broken down into smaller molecules (usually glucose or fatty acids). In aerobic metabolism the typical end product of this process is carbon dioxide, which is released in the lungs and exhaled while oxygen is inhaled from the air and taken up by hemoglobin in red cells. Knowledge of the metabolic rate of oxygen (MRO₂) provides us with a direct measure of energy consumption. MRO₂ is therefore a key physiologic parameter. In organs such as muscle of the peripheral skeleton or the heart, MRO₂ varies widely as a function of the work-load, ranging from about 1 to 50 ml O₂ /100g/ min for resting and contracting muscle, respectively. In contrast, brain, i.e. cerebral MRO₂ (typically referred to as CMRO₂) remains on the order of 3 ml (~130 μmol) O₂ /100g /min regardless of the functional demand of different brain activities. Even during light sleep there is only a minor reduction in CMRO₂ (1), and only during deep sleep (2) and particularly during anesthesia (3), is energy demand substantially lower.

CMRO₂ can be obtained from a measurement of the arteriovenous oxygen difference, AV O₂ = SaO₂ − SvO₂, where SaO₂ and SvO₂ are the arterial and venous hemoglobin oxygen saturations, respectively, and blood flow (rate), BF, to or from the organ of interest, expressed in ml blood/100g tissue/min, via Fick’s Law, as:

$${\mathit{CMRO}}_2=C_a·{\mathit{AVO}}_2·BF$$ [1]

where C_a is a constant expressing the blood’s oxygen carrying capacity (836μmol O₂/100ml blood at hematocrit of 0.42). There has been much recent interest to quantify CMRO₂ via image-based methods. The ability to noninvasively map oxygen utilization by the brain would provide new insight into brain physiology and enable evaluation of pathology-induced disruption of normal brain metabolism in disorders such as Alzheimer’s disease, multiple sclerosis and cancer.

Much of prior research on image-based CMRO₂ mapping has been conducted by positron emission tomography (PET), achieved by quantifying H₂¹⁵O after inhaling¹⁵O₂, and measuring blood flow rate based on injection of H₂¹⁵O used as a blood flow tracer (4). The method has since been refined and streamlined, and has provided unique information on the brain’s response to external stimuli (5). Although PET is widely regarded the gold standard for CMRO₂ mapping, it has several limitations. First, it is highly invasive, requiring both arterial and venous punctures, as well as exposure to radiation. The complexity and cost of the protocol, and the need for an on-site cyclotron to produce the ¹⁵O tracers, have so far confined PET-based CMRO₂ mapping to very few sites possessing these capabilities.

While some work has shown that ¹⁷O, the only NMR active nucleus among the three oxygen isotopes, can serve as a tracer analogous to ¹⁵O in PET, the high cost of isotopically enriched ¹⁷O, and the complexity of the set-up, make it all but impractical in humans (6). In contrast, methods that exploit the paramagnetism of deoxyhemoglobin as a source of contrast in MRI have significantly advanced the field during recent years.

Even though quantification of CMRO₂ (and for that matter MRO₂ in general), demands knowledge of both SvO₂ and CBF, obtaining SvO₂ is the far greater problem. MRI-based methods for quantification of SvO₂ can be broadly categorized based on the MR contrast methods employed: T₂ (7,8), T₂* (BOLD) (9), T₂’ (10), and susceptibility-based approaches (11). Most of the former approaches involve complex models relating their respective relaxation rates to blood deoxyhemoglobin concentration. In distinction, susceptibility based methods rely on a simple linear relationship between blood deoxyhemoglobin concentration and blood magnetic susceptibility. Susceptibility-based methods have other distinct advantages, including the possibility of high temporal resolution for application to dynamic quantification of SvO₂. In keeping with the scope of this Special Issue of the Journal, this article focuses on susceptibility-based methods only.

1.2. Volume Magnetic Susceptibility of Whole Blood

Hemoglobin, ubiquitous in vertebrates, is arguably the most thoroughly studied metalloprotein. It is the fundamental carrier of oxygen, enabling its transport by the blood from the lungs to organs for energy production. A key physical property on which virtually all magnetic resonance methods rely for gaining quantitative insight into oxygen metabolism is hemoglobin’s magnetism, first studied systematically by Pauling and Coryell in 1936 (12). In its deoxy state all but two of the six d-electrons of Fe²⁺ in each of the four heme moieties occupy separate orbitals, thereby resulting in an electron spin S=2, making deoxyhemoglobin paramagnetic. In contrast, in the oxy state, the slightly increased ligand field splitting between the two pairs of d-orbitals make spin pairing energetically more favorably, resulting in zero net spin, thus making oxyhemoglobin (HbO₂) diamagnetic.

Thulborn et al. (13) studied the oxygenation dependence of T₂ relaxation of blood and showed the transverse relaxation rate (1/T₂) to scale linearly with deoxyhemoglobin (dHb) concentration, and demonstrated the effect to be caused by diffusion of water molecules in the locally inhomogeneous fields set up by the different intra- and extracellular magnetic environments. Further, the authors estimated the volume susceptibility difference between fully deoxygenated and fully oxygenated whole blood (Δχ - χ_do − χ_oxy) by measuring the difference in the water NMR resonance frequency between the two states. The measurement was performed on a blood sample in a cylindrical tube oriented parallel to the static field of a 270 MHz spectrometer, yielding a value of 0.2ppm (cgs). A decade later, Weisskoff and Kiihne (14) measured the susceptibility of deoxygenated blood by field mapping with an asymmetric spin-echo EPI sequence, on a similar cylindrical sample positioned perpendicular to the main field (1.5 T). The value reported in this work (Δχ= 0.18ppm, cgs) was of the same order as that in (13) and served as a basis for subsequent work (see, for example, (15)). In separate work, Ogawa et al measured the NMR difference frequency Δv of the water resonance at v_o = 360 MHz in a concentric tube arrangement parallel to the static field, with the inner tube containing deoxygenated blood at 35% hematocrit (Hct), and water in the annulus (16). In this arrangement the relative frequency shift is related to the susceptibility difference Δχ as Δv/v_o = (4π/3)Δχ from which the authors obtained value of 1 × 10⁻⁶. When extrapolated to 100% Hct, this value corresponds to Δx_do = 2.86 × 10⁻⁷, cgs and is in remarkable agreement with values reported much later.

Nevertheless, uncertainties in the value of Δχ remained, which prompted Spees et al to reexamine the problem (17). Invoking Wiedemann’s law, the susceptibility of a mixture can be calculated as the volume-fraction weighted mean of its constituents (18). Together with the magnetic moment of Fe²⁺ in deoxyhemoglobin (12), they obtained for the susceptibility difference between completely deoxygenated and completely oxygenated erythrocytes, Δx_do = 0.264 ppm (we shall henceforth use the subscript “0” to indicate the susceptibility difference between fully deoxygenated and fully deoxygenated red cells at 100% Hct). The authors corroborated this value experimentally in two different ways, first by measuring the NMR resonance frequency in a cylindrical tube containing blood oxygenated to various levels, both with the tube parallel and perpendicular to the B₀ field. The frequency difference between these two configurations is given as:

$${\nu }_{\Vert }-{\nu }_{\perp }=2\pi ·\mathrm{\Delta }{\chi }_{do}·\mathit{Hct}·(1-Y)·{\nu }_0+2\pi ({\chi }_{\mathit{oxy}}-{\chi }_{\mathit{air}})$$ [2]

where v₀ is the spectrometer frequency and Y the oxygen saturation, the remaining symbols are self-explanatory. From Eq. 2 one recognizes that at a given hematocrit the slope of Δv versus Hct(1-Y) yields Δχ independent of the susceptibility of air. The value obtained in this manner, 0.27±0.03 ppm, agrees well with their prediction based on the known magnetic moment of Fe²⁺ in deoxyhemoglobin. The second experiment based on SQUID magnetometry yielded Δx_do = 0.27±0.02 ppm, again in excellent agreement with the NMR results.

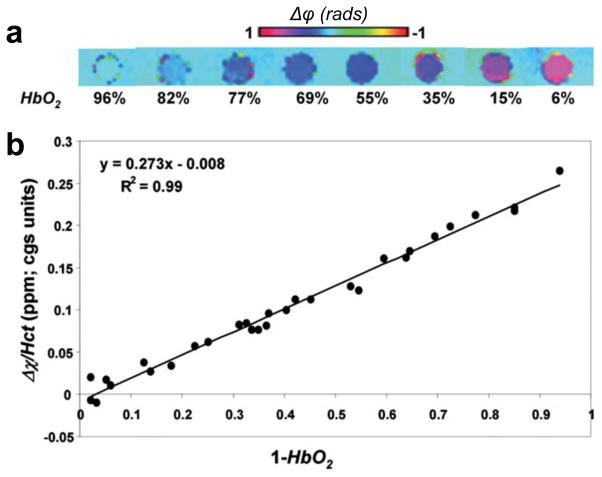
More recently, Jain et al. further corroborated these results, using field mapping techniques (19). HbO₂ saturation was quantified for a range of oxygen saturation levels by field-mapping on freshly drawn human blood from seven donors. The experimental arrangement involved sample tubes of length to diameter ratio ~10 (satisfies the long cylinder approximation), parallel to the main field and immersed in distilled water. The resulting data were compared with results from blood gas analysis. Figure 1 shows field maps for a range of oxygen saturation values along with a plot of MRI-derived Hct-weighted susceptibilities measured relative to water. From these images, Δx_do was computed as the slope of the linear relation:

$$\frac{\mathrm{\Delta }\chi }{\mathit{Hct}}=\mathrm{\Delta }{\chi }_{do}(1-Y)+\mathrm{\Delta }{\chi }_{\mathit{oxy}}$$ [3]

Figure 1.

a) Representative phase difference images of cylindrical sample tubes containing blood oxygenated to various HbO₂ levels, oriented parallel to the B₀ field and immersed in distilled water. b) Susceptibility difference (Δχ) between blood and surrounding water normalized to individual Hct level plotted against the level of deoxygenation. The slope of the regression line represents the susceptibility difference between fully oxygenated and deoxygenated blood (Δχ_do) and intercept Δχ_oxy represents the susceptibility difference between fully oxygenated blood and water (from (19), with permission.

Regression analysis yielded (0.273 ± 0.006) and −0.008 ± 0.003 ppm (cgs) respectively, for Δx_do and Δx_oxy, in excellent agreement with the work by Spees et al (17).

2. Quantitative Imaging Approaches

2.1. Fundamentals of Susceptometry-Based Oximetry

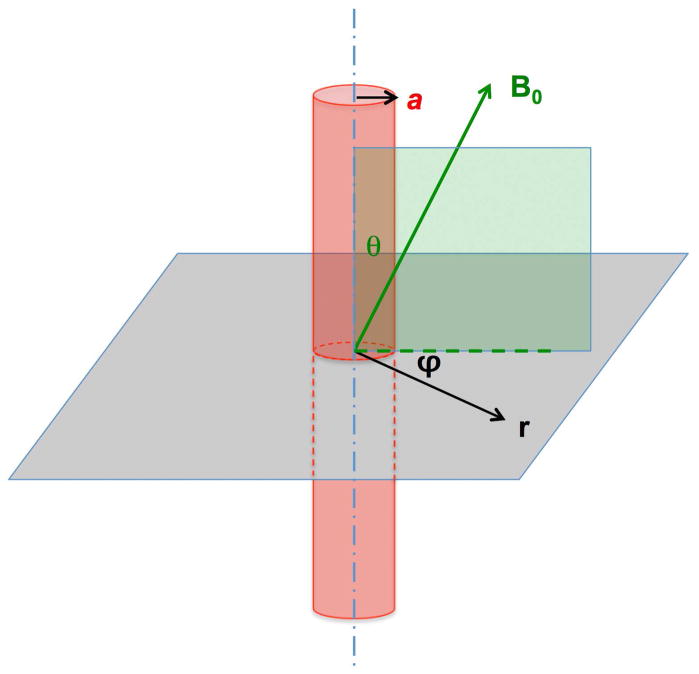
Susceptometry-based methods for quantifying blood oxygen saturation in blood vessels has its foundation in the special behavior of ellipsoidally shaped magnetized objects (see, for instance, Schenck (20)). While for all other irregularly shaped objects numerical methods are needed (21), the induced field inside an ellipsoid is homogeneous and the field outside can be calculated analytically. Of particular interest in this context is the rotational ellipsoid with an aspect ratio (long /short axis)→ ∞ based on the notion that a blood vessel resembles a long cylinder. In this case, the following simple relationship holds between the z-component, ΔB_int of the induced field, relative to the field distant from the cylinder:

$$\mathrm{\Delta }{B}_{\mathit{int}}=\frac{\mathrm{\Delta }\chi }{2}\left({\mathit{cos}}^2\theta -\frac{1}{3}\right)B_0$$ [4]

In Eq. 4 (which includes the Lorentz sphere correction), Δχ is the difference in susceptibility between the two compartments, and θ is the angle of the cylinder axis with respect to the applied field B₀. The relative field outside the vessel is homogeneous as long as its axis is parallel to B₀. More generally, ΔB_ext obeys the following relationship (20):

$$\mathrm{\Delta }{B}_{\mathit{ext}}=\left(\frac{\mathrm{\Delta }\chi }{2}{\mathit{sin}}^2\theta ·\frac{a^2}{r^2}·cos2\phi \right)B_0$$ [5]

In Eq. 5, a is the vessel radius, r is the distance perpendicular to the vessel axis, and φ is the azimuthal angle. The geometric parameters in Eqs. 4 and 5 are defined in Figure 2.

Figure 2.

Relationship between applied field, B₀, vessel orientation and angles θ and φ in Eqs. 4 and 5.

The induced field ΔB_int inside the vessel can be obtained by measuring the phase difference between the intra- and extravascular signal as long as the inhomogeneity outside the vessel is negligible, i.e. if ΔB_ext ≈ 0 can be assumed. Eq. 5 suggests that for small angles, i.e. θ < 20⁰ (sin² θ ~ 01), ΔB_ext falls off quickly with a/r, decreasing to <1% five cylinder (i.e. vessel) radii away from the vessel axis. Further, because of the sinusoidal dependence on the azimuthal angle φ, ΔB_ext averages to zero within a circular tissue reference region.

The local field offset ΔB is obtained from the phase difference between two successive echoes as:

$$\mathrm{\Delta }\phi (x,y)=\gamma ·\mathrm{\Delta }B·\mathrm{\Delta }TE$$ [6]

where Δψ(x,y) is the inter-echo phase difference at pixel location (x,y), and ΔTE is the inter-echo time.

Combining Eqs. 3, 4 and 6 yields for the venous blood oxygen saturation SvO₂:

$${\mathit{SvO}}_2=1-\frac{2\mid \mathrm{\Delta }{\phi }_{ie}\mid }{\gamma B_0·\mathrm{\Delta }TE·\mathrm{\Delta }{\chi }_{do}·\mathit{Hct}({cos}^2\theta -1/3)}+\frac{\mathrm{\Delta }{\chi }_{\mathit{oxy}}}{\mathrm{\Delta }{\chi }_{do}}$$ [7]

We note that Eq. 7 assumes that ΔB_ext ≈ 0. Here, Δφ_ie = Δφ_intra − Δφ_extra represents the intra- to extravascular inter-echo phase difference. Vessel orientation is determined from axial images while hematocrit is obtained from a blood draw.

The initial work toward quantification of whole-brain SvO₂ was conducted in the internal jugular veins (22). However, this location turns out to be difficult in practice due to the large induced fields resulting from the air spaces in the neck. It is for this reason that most subsequent whole-brain susceptometry was performed in the superior sagittal sinus (SSS).

2.2. Sources of Systematic Error and Correction Methods

Deviations of Blood Vessel from Cylindrical Geometry

Blood vessels – in particular veins – rarely conform to the straight cylinder model. They exhibit curvature, branching and tapering, and veins, by virtue of much lower blood pressure, often do not have circular cross section. A case in point is the SSS, which has triangular cross-section, conforming to the small space in the longitudinal fissure immediately adjacent to the skull. Langham et al computed the error in SvO₂ analytically for a long, straight elliptical cylinder (a shape most typically found for the veins of the lower extremities) as a function of eccentricity $\epsilon =\frac{a}{a+b}-\frac{1}{2}$ where a and b are the long and short axes of the cylinder (23). They found for a vessel tilt angle of 20º and eccentricity ∈ = 0.2 the error did not exceed ±2% SvO₂ from typical nominal values. The problem was also addressed numerically by Li et al (24) using a voxel-based perturbation method (25). They found that at typical SvO₂ levels of 65%, the absolute error in %HbO₂ estimated via a closed-form cylinder approximation was <3 %HbO₂ averaged over three locations in the three veins studied (SSS, jugular and femoral vein) and did not exceed 5% for vessel tilt angles <30º at any one location. Finally, the error was also evaluated experimentally in phantoms containing gadolinium-doped water range of susceptibility values encountered in venous blood (11). The authors found that for a long triangular prism (mimicking the SSS) the mean difference between the susceptibility values did not exceed 2.6% from those measured in circular cross-section tubes, which would correspond to an average absolute difference of 0.8% SvO₂ at hematocrit of 0.42 and SvO₂ of 65%. As shown in (23), the cross-sectional geometry has little or no effect if the vessel tilt angle is small. The data thus suggest the infinite cylinder model to be remarkably accurate for SvO₂ quantification.

Large-Scale Magnetic Field Gradients

Perhaps the main source of error in MR susceptometry is static field inhomogeneity caused by susceptibility mismatch at the interface between the tissue and the surrounding air (Δχ~9 ppm). High-pass filtering (see for example, (26)) is commonly implemented to reduce the effect of the static field inhomogeneity characterized by low spatial-frequency modulations on field maps. However, high-pass filtering implemented in k-space indiscriminately affects the phase to be quantified in a manner dependent on filter size. Therefore, the high-pass filter cannot separate static or background field inhomogeneity from the field offset relative to the susceptibility difference between intravascular blood and surrounding tissue.

The effects of field inhomogeneity are significantly reduced by fitting the phase difference image Δφ(x,y) to a second-order polynomial to estimate the macroscopic or low spatial-frequency field variation as:

$$\mathrm{\Delta }\phi (\mathrm{x},\mathrm{y})\approx c_o+c_{1}x+c_{2}y+c_{3}xy+c_4{x}^2+c_5{y}^2$$ [8]

Here, x and y are coordinates in the 2D image plane, and coefficients c_i are determined through a weighted least-squares fit. The key step before fitting the field inhomogeneity to second-order polynomial of Eq. 8 is weighting the phase difference image by the corresponding magnitude image after masking out the vessels and suppressing the background (27).

The adverse effect of indiscriminate high-pass filtering on the measured hemoglobin saturation levels was investigated in (27). The results demonstrate that the venous saturation measurement is critically dependent on filter size, which is typically determined subjectively to achieve a desired level of uniformity in phase images. Further, after a critical filter size (n>10) images become visually indistinguishable. It should be noted that the “critical” size is dataset-dependent and the extent to which the images are visually distinguishable depends on the window level.

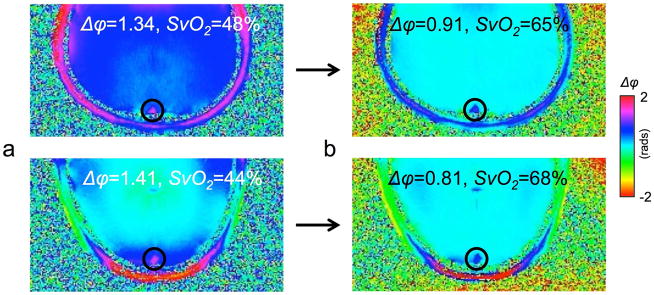
Figure 3 shows the effect of polynomial background field correction in two subjects for the determination of SvO₂ in the SSS.

Figure 3.

Effect of polynomial fitting on phase maps for two subjects: a) before, b) after fitting. Not only do phase maps become visually more homogeneous but the extracted intra- to extravascular phase difference for the SSS yield plausible values for SvO₂ between 60 and 70%.

2.3. Quantitative Susceptibility Mapping (QSM) for Regional and Voxelwise Oximetry

Mapping OEF along veins

Instead of relying on a vessel model, recent advances in susceptibility imaging allow for SvO₂ to be quantified more generally in veins of arbitrary orientation and geometry by means of quantitative susceptibility mapping (QSM). The method is discussed in greater detail in other articles of this Special Issue of NMR in Biomedicine. In brief, QSM takes a measured local field, ΔB, and aims to recover the underlying susceptibility distribution, Δχ, that gives rise to the induced field (28,29). The reconstructed Δχ map reflects the susceptibility effect of deoxyhemoglobin (dHb) in the venous tree. Intravenous susceptibility, and the corresponding oxygen saturation, can then be mapped along all resolved cerebral veins. QSM requires solution of the following inverse problem in Fourier space:

$$\mathcal{F}(\mathrm{\Delta }B)=\mathcal{F}(\mathrm{\Delta }\chi )·(\frac{1}{3}-\frac{k_z^2}{k^2})$$ [9]

where ℱ is the Fourier operator, $D=\frac{1}{3}-\frac{k_z^2}{k^2}$ is the dipole kernel, and k is the magnitude of the k-space vector (30). Unfortunately, this inversion is fraught with difficulties because of the singularities that occur for D near the magic angle (54.7°). Accurate quantification of OEF in veins thus requires careful selection of the QSM algorithm and parameters for narrow vessel structures.

Various QSM algorithms have been used in initial studies to assess venous oxygenation. Haacke et al (31) mapped susceptibility in vessels through use of thresholded k-division, which restricts the minimum value of D to avoid division by zero during QSM reconstruction (32). From this study, the relative susceptibility values in large veins draining deep gray matter corresponding to SvO₂ ranging from 66.1% – 79.3%. During caffeine ingestion, QSM values in veins also showed expected signal increases, corresponding to increased dHb content (i.e. lower SvO₂). Although thresholded k-division successfully removed dipolar field patterns around vessels perpendicular to the main field, streaking artifacts occurred in the QSM image volume that remain to be addressed in future work.

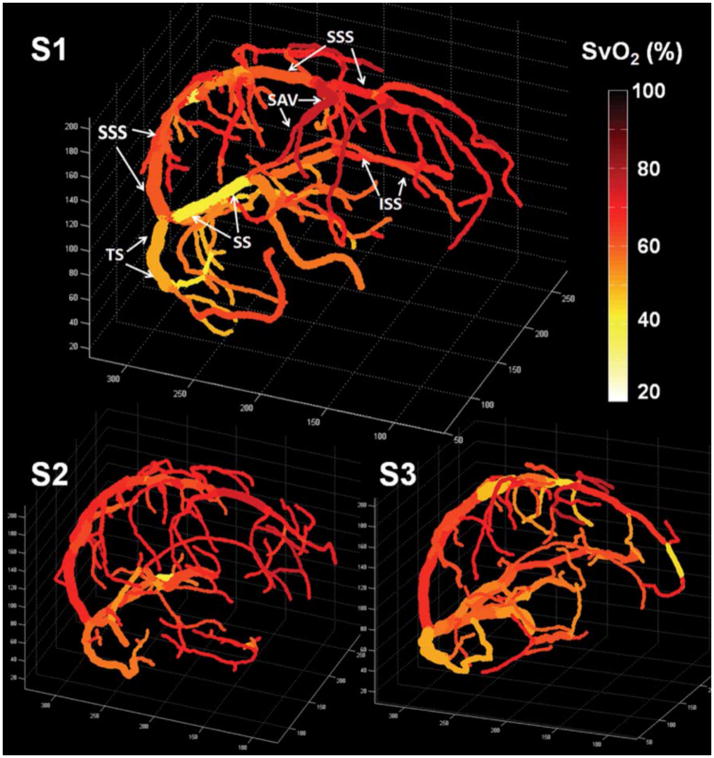
Other QSM studies used regularization to incorporate prior knowledge about the underlying susceptibility, to solve the dipole inversion. Fan et al. measured susceptibility in veins through use of L1-regularization (33), which gives a QSM map that tends to be piecewise constant within anatomical tissue boundaries (34). Figure 4 shows SvO₂ maps superimposed on venograms from healthy volunteers based on L1-regularized QSM maps; mean baseline SvO₂ values from QSM ranged from 61.8 – 66.7% across subjects. This QSM approach also revealed expected increases in SvO₂ in pial veins during breathing of mild levels of CO₂, which is known to globally increase SvO₂ in the brain (35). Xu et al used a different, non-linear regularization approach (36) to create QSM maps with more sophisticated correction for flow artifacts in veins (37). This work yielded a similar mean SvO₂ of 72.2% ± 4% in cerebral pial veins across subjects.

Figure 4.

Quantitative oxygenation venograms display baseline SvO₂ (%) along each vein in three healthy volunteers. In the first subject, major veins in the brain are identified, including the superior sagittal sinus (SSS), inferior sagittal sinus (ISS), straight sinus (SS), transverse sinus (TS), and superior anastomic vein (SAV). (Reproduced from (34), with permission).

The above studies suggest QSM as a promising approach to map baseline SvO₂ along the venous tree. While physiologically plausible, some caution should be exercised in comparing the SvO₂ values in these limited studies (Table 1) because the methods used for background field removal and QSM reconstruction differ. For instance, the regularization methods likely smooth and underestimate vessel susceptibility, and are sensitive to the regularization parameters chosen as part of the QSM reconstruction.

Table 1.

Comparison of quantitative susceptibility mapping (QSM) studies to map oxygenation.

Study	QSM technique	Veins analyzed	SvO2 values (%)
Haacke et al. (31)	Thresholded k-division	Large veins (8mm – 16mm diameter), e.g. vein of Galen and thalamostriate veins	66.1 – 79.4 (calculated)
Fan et al. (34)	Regularization with L1-penalty	Large sinuses e.g. sagittal sinus, transverse sinus, straight sinus	47.7 – 67.6
		Pial veins e.g. superior anastomic vein	70.2 – 75.3
Xu et al. (37)	Nonlinear dipole inversion	Pial veins	72.2 ± 4 (mean)
Zhang et al. (41)	Regularization with L1-penalty	Tissue voxels	66.1 ± 10 (mean gray matter)

Mapping of tissue OEF in response to exogenous challenges

Recent work has investigated the potential of frequency mapping and QSM for obtaining quantitative information on changes in tissue oxygenation in response to functional activation. The recognition that functional dHb-dependent effects are more pronounced on MRI phase than magnitude images (38), prompted two groups to use QSM time series to probe tissue oxygenation changes during motor and visual tasks at 7 Tesla (39); and during finger-tapping task at 3 Tesla (40). These functional QSM studies offer a quantitative way to map tissue BOLD changes without geometric dipole contaminations, but focus on functional responses instead of baseline oxygenation. More work is needed to understand the different sensitivity and activation patterns of functional QSM relative to magnitude-based approaches.

To map baseline oxygenation in tissue, Zhang et al proposed a method that requires collection of QSM images and perfusion data in two isometabolic brain states, chosen to be pre- and post caffeine ingestion (41). The caffeine challenge globally alters SvO₂ in the tissue but is assumed not to change oxygen metabolism. The authors created SvO₂ maps at 3 mm isotropic resolution and observed a decrease in SvO₂ from 66.1% ± 10% (before caffeine) to 45.5% ± 13% (after caffeine) across gray matter. While promising, this method to map tissue SvO₂ requires use of a challenge (e.g. caffeine vasoconstriction) and separate perfusion imaging in both brain states, which may be difficult to implement in clinical settings.

Potential sources of error in susceptibility maps

Most of the reported SvO₂ values from QSM (Table 1) are higher than ¹⁵O PET measurements ranging from 58% to 64% (42–44). Partial volume artifacts likely lead to underestimation of susceptibility in narrow veins and overestimation of SvO₂ from QSM, especially in pial veins. This consideration naturally restricts the smallest vein diameter that can be used for local SvO₂ measurement, and has motivated careful work on susceptibility measurements in narrow cylinder structures (45,46). Improved spatial resolution (0.4-mm isotropic) achievable at ultra-high field has the potential to expand the method to smaller veins (47). These smaller veins may better indicate local brain function. Recent work further suggests joint use of magnitude and phase images to simultaneously estimate partial volume fraction and SvO₂, so as to minimize partial volume effects in parallel vessels (48).

Residual flow artifacts, especially in large veins, may also contribute to SvO₂ overestimation from QSM maps. These flow artifacts occur due to moving spins in veins through an inhomogeneous magnetic field gradient and persist even in spite of the use of velocity compensation. Xu et al showed that second-order flow artifacts may overestimate baseline SvO₂ at 3 Tesla in pial veins (37). Vessels near the periphery of the brain such as the sagittal sinus are especially challenging for QSM because of background field removal during preprocessing. Current field removal methods (49,50) require delineation of a brain mask and may provide incorrect results at the brain boundary. For this reason, QSM methods often mask out much of the brain periphery such that reliable SvO₂ values are not available in many of the draining sinuses and pial vessels near the cortical surface. Extensions to these methods have been proposed to recover field map information near the brain edges (51).

Additional technical confounds with QSM include variations in SvO₂ due to vessel orientation. The QSM reconstruction theoretically removes angle-dependent effects of the dipole kernel, such that SvO₂ values are consistent across all vessel angles. However, data from veins oriented near the magic angle is more heavily undersampled, such that QSM algorithms often fail to recover the complete susceptibility information for these vessel segments. As a result, while favorably oriented (e.g. parallel) vessels experience minimal SvO₂ bias, vessels tilted near the magic angle exhibit up to 10% SvO₂ underestimation from QSM maps (34). Future technical developments to segment cerebral veins directly from gradient echo scans (52) can help to visualize the vascular anatomy. This structural information could offer new priors to improve modeling and QSM reconstruction and achieve consistent SvO₂ values across vessel orientations.

3. Integration of Susceptometry and CBF Measurement for Whole-Brain CMRO₂ Quantification

3.1. Bi-Level Methods

Quantifying CMRO₂ requires knowledge of both SvO₂ and blood flow rate (see Eq. 1). In the brain, quantification of global SvO₂ has to be accompanied by a measurement of total cerebral blood flow (tCBF). Typically, the latter is measured by phase-contrast MRI of the major arterial conduits – internal carotid and vertebral arteries – which can be assessed via a single axial imaging slice selected distal to the carotid bifurcation. In this manner, a spatial map of blood flow velocity is obtained that, when averaged spatially across the four main feeding arteries, yields total blood flow rate. Since CMRO₂ represents the oxygen consumption per minute, normalized to 100 ml of tissue, CBF has to be normalized accordingly in mL/min/100g, which requires knowledge of brain mass, easily obtained from a separate 3D T₁-MPRAGE acquisition.

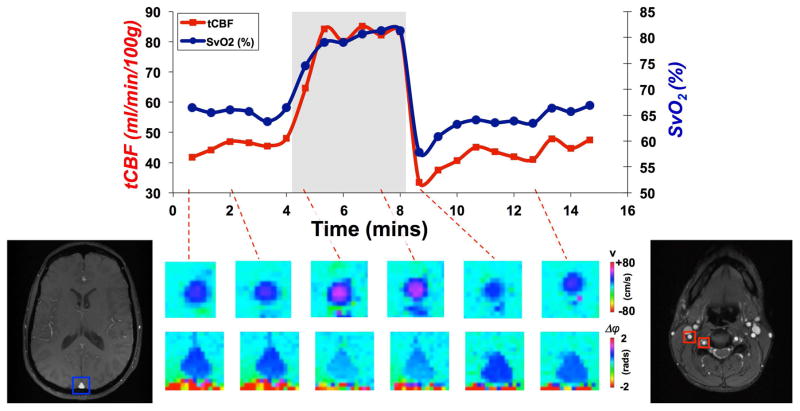
Ideally, both quantities (SvO₂ and tCBF) are measured simultaneously, which is complicated by the different measurement locations (i.e. superior sagittal sinus in the head for SvO₂, feeding arteries in the neck for tCBF). Jain et al conceived a method to achieve measurement at the SSS and neck in an interleaved fashion with a 4-cycle gradient-recalled echo sequence toggling alternately between the two locations (11). In this manner flow rates are obtained in the arteries of the neck and SvO₂ in the SSS. The method, subsequently termed OxFlow, achieves a temporal resolution of 30 seconds and has been shown to be able to yield whole-brain CMRO₂ both at baseline and during hypercapnia (53) (Figure 5).

Figure 5.

OxFlow derived time-course at rest and during hypercapnia yielding tCBF and SvO₂ simultaneously. Bottom images display velocity in the right internal carotid artery and phase difference in the SSS at select temporal locations (modified, from (53)).

A more recent implementation of the OxFlow, referred to as fast OxFlow (F-OxFlow) provided significantly improved temporal resolution (8s versus 30s), achieved with only three instead of the four interleaves, by sampling a dual-echo in one interleave and compacting the pulse sequence (54). While the three-interleave version causes a slight mismatch in the steady state between the phase-contrast sequence interleaves, this did not cause a significant bias in the data in the baseline values of CMRO₂, measured in 10 healthy subjects (123±14 versus 124±12 μmol O₂/100g/min). The authors also provided evidence that the method is able to capture the response to a breath-hold stimulus.

3.2. Single-Vessel OxFlow for High-Speed CMRO₂ Measurement

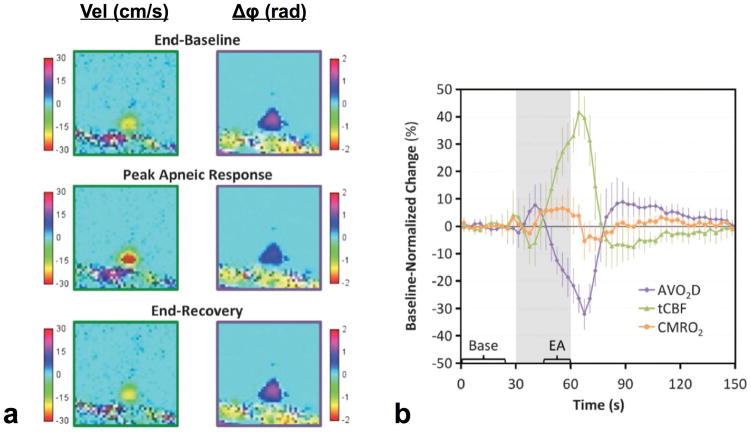
To improve the temporal resolution of CBF and SvO₂ measurements phase and velocity mapping can be performed at the same site, e.g. at the SSS, as shown by Rodgers et al (55). In this manner a temporal resolution of three seconds was achieved via a combination of view-sharing (56) and SSS estimation of tCBF. However, since the SSS drains only about half the brain (essentially the cortex), a prior calibration scan by means of the full bi-level OxFlow sequence is required to obtain the subject’s SSS blood flow (SSSBF) to tCBF ratio before starting a time series of measurements in response to a stimulus. The ratio is subsequently used to convert dynamically measured SSSBF to tCBF. In a related study in 10 subjects a mean SSSBF:tCBF ratio of 0.48±0.03 was found (57). The method was applied in a study of the response to volitional apnea (breath-hold) where high temporal resolution is required due to the transient nature of the stimulus. Figure 6 shows parametric images of CBF and phase representative of three temporal periods, along with the fractional changes in arteriovenous difference (AVO₂ = SaO₂ – SvO₂), tCBF and CMRO₂. Subject-averaged maximum changes in tCBF and AVO₂ were 43.5±9.4% and 32.1±5.7%, respectively, resulting in a small (6.0±3.5%) but statistically significant (p<0.0005) increase in average end-apneic CMRO₂. The results suggest apnea – a mixed hypercapnic and hypoxia stimulus -- to be slightly pro-metabolic, with increased CMRO₂ to a breath-hold challenge in healthy individuals. This is consistent with previous data showing hypercapnia to be isometabolic (53,58) and hypoxia to be slightly prometabolic (59). Increased CMRO₂ during breath-hold may reflect a physiologic mechanism to buffer the brain’s energy supply in anticipation of prolonged oxygen supply.

Figure 6.

Effect of volitional apnea on brain vascular-metabolic parameters: a) Expanded parametric maps of flow velocity and phase difference Δφ (for SvO₂ measurement) obtained with a single-site OxFlow sequence acquiring data at the same anatomic site (SSS) at 3s temporal resolution, showing enhanced flow and increased SvO₂ (manifested by reduced phase difference) during apnea. b) Fractional changes in parameter values normalized to average baseline. Error bars indicate ±1 SD, gray area the apnea period. Values in time-course plot were averaged across the three repeated blocks of the paradigm. Bracketed sections ‘Base’ and ‘EA’ indicate the data used for computing average baseline values and end-apnea values (reproduced from (55), with permission).

3.3. Regional Approaches for CMRO₂ Measurement

Just as QSM reconstruction has enabled mapping of oxygenation, regional maps of CMRO₂ can, in principle, be created through combination of phase-based SvO₂ quantification with CBF mapping by arterial spin labeling MRI (see, for instance, (60)). However, generating parametric images of tissue SvO₂ in absolute physiologic units on the basis of phase mapping has proven difficult.

An alternative approach toward regional CMRO₂ quantification is based on intravascular QSM yielding SvO₂ (34,37). Here, SvO₂ from gray matter veins are combined with local CBF in a region of interest drawn around the spatial location of the vessel (61). Fan et al reported mean gray matter CMRO₂ of 158 ± 18 μmol/100g/min in healthy volunteers with this approach, and observed elevated CMRO₂ in the occipital lobe in good agreement with PET data. One limitation with this approach is that the physiological tissue region drained by each vein is not well characterized, especially in cases of pathology. To define the appropriate ASL tissue ROI for a given vein for which SvO₂ is quantified, imaging of the pertinent venous territory would be required, for example by the spin-labeling MRI approach proposed by Wong et al (62). Furthermore, while regional CMRO₂ imaging would be useful to monitor local disturbances in oxygen metabolism, these approaches require longer scan time, especially for volumetric QSM. Thus, scan-time considerations limit the temporal resolution of regional relative to global approaches, and motivate faster gradient echo imaging to make the technique clinically practical (63).

4. Clinical Applications of Susceptibility-Based Oximetry to the Brain

4.1. Brain Oxygenation Measurement in the Fetal and Neonatal Brain

Adequate oxygen metabolism is critical to early development of the brain. From the third trimester until several months after birth, the brain energy source shifts from anaerobic glycolysis to more-efficient aerobic metabolism to meet increasing energy demands as brain structures mature. Disruption of oxygen supply to the fetus can lead to hypoxic ischemic injury, and result in postnatal developmental delays and deficits. For this reason, the ability of MRI to noninvasively probe brain oxygenation and predict ischemia at gestational ages earlier than 36 weeks is important (see for instance, (64)). Fetal imaging of oxygenation is challenging due to fetal motion, maternal breathing, and necessarily large field of views that lead to long scan times. Nonetheless, Dai et al used 1.5 T susceptibility-weighted imaging (SWI) to examine 167 veins in fetuses of 42 pregnant women, and were able to identify the veins of Galen and internal cerebral veins on the SWI scans (65). A separate study in five fetuses (mean gestational age of 33.7 weeks) measured SvO₂ in utero from susceptome-try-based oximetry in the SSS; yielding a mean value across fetuses of 66% ± 9% (66).

In neonates, congenital heart disease (CHD) comprises various anatomical abnormalities of the heart that changes cerebral hemodynamics and metabolism. These infants need to undergo reparative surgery within the first few days of life. A recent study by Jain et al measured tCBF and global CMRO₂ in 32 neonates with congenital heart disease before surgery (67). This study encountered unique challenges due to the small size of carotid and vertebral arteries in neonates. Therefore, both flow and phase-based SvO₂ were measured in the SSS, taking into account that this vein drains only 45% of total brain blood flow (see also (55), discussed earlier). The authors performed CMRO₂ measurements at rest and during hypercapnia to determine whether neurovascular reactivity was affected by disease. While the CO₂ reactivity in these patients remained intact, baseline CBF (9.7 ml/100g/min) and CMRO₂ (23μmol O₂/100g/min) were strikingly low. The data suggest that neonates with severe CHD to have brain physiology similar to that of premature infants, and that low baseline CMRO₂ could be predictive of eventual white matter damage affecting cognitive function.

4.2. Obstructive Sleep Apnea

Obstructive sleep apnea (OSA) is characterized by structural and functional failure of the upper airways to remain patent during sleep, leading to periodic slowing or stopping of breathing. OSA is associated with numerous cerebrovascular and neurologic comorbidities, including impaired cognitive function and cerebral lesions characteristic of hypoxic damage. However, work described previously (55) suggests that CMRO₂ is maintained, or even increased slightly, in the normal apneic response. In recent work, Rodgers et al hypothesized that patients with OSA may not have a normal response to apnea, allowing hypoxic brain damage to occur during nocturnal OSA events, and potentially leading to further impairment in cerebrovascular autoregulation. To investigate this hypothesis, the authors applied a fast, single-slice OxFlow technique described previously to quantify CMRO₂ during a breath-hold paradigm in 11 patients with OSA and 10 subjects examined for sleep disorders but without a diagnosis of OSA (68). Interestingly, while patients with OSA did not show a statistically significant difference in CBF response, they displayed reduced baseline CMRO₂ and a reduced CMRO₂ response to the breath-hold challenge. Baseline CMRO₂ was 117 ± 38 μmol/100g/min in patients with OSA compared to 152 ± 30 μmol/100g/min in the control group of patients without OSA; CMRO₂ decreased by 10.9 ± 9% in patients during volitional apnea compared to 4.0 ± 6% in controls (68). These findings were interpreted as suggesting impaired vascular regulation and a resulting inability to maintain CMRO₂ during apnea in OSA. While more work is needed to investigate this potential mechanism of hypoxic brain damage in OSA, this study shows that OxFlow provides fast and robust quantitative CMRO₂ measurement capable of detecting both baseline and dynamic differences in brain metabolism in patient populations.

4.3. Cerebrovascular-Metabolic Disorders and Injury

Even short-term loss of oxygen supply can have devastating physiological and functional consequences in many cerebrovascular disorders, most strikingly in acute stroke. While SWI has been able to visualize hemorrhage and microbleeds in stroke, perhaps the most exciting prospect is to use susceptibility information quantify oxygenation and thus assess tissue viability (69,70). High oxygen extraction fraction (OEF = (SaO₂ − SvO₂)/SaO₂ ≈ AvO₂) has been shown to identify salvageable tissue (i.e., the penumbra) in the brain and guide therapy for stroke patients.

A review of 43 publications and 1145 patients found that low T₂* signal in veins near the infarct, indicative of elevated dHb content (and thus increased OEF), was common in 81% of SWI scans from stroke patients (71). The susceptibility-weighted magnitude signal allows assessment of signal intensity and caliber of specific veins; sufficient SWI resolution could be even achieved to study pediatric stroke (72). Recent studies have transitioned to quantify SvO₂ on high-pass filtered phase images. Li et al examined the change in signal phase in 10 veins each from 10 stroke patients at three time points following onset of stroke (< 24 hours, 2–3 weeks, and 2 months) (73). The results suggested that increased SvO₂ over time corresponded to better patient outcomes during the follow-up period. Another study went further to directly reconstruct susceptibility maps from 3D gradient echo phase scans in stroke patients. In asymmetrically prominent veins, i.e. dilated veins on the ischemic hemisphere, Xia et al found lower SvO₂ by 16% – 44% relative to the normal-appearing hemisphere (74). Phase-based oximetry thus has the potential to noninvasively assess OEF by MRI and, combined with perfusion studies, may provide valuable information about tissue viability for imaging-based stratification of stroke patients for treatment.

Phase-derived SvO₂ may also provide an earlier biomarker to monitor neurodegenerative diseases, conceivably before the occurrence of structural damage (e.g. lesions and atrophy) in patients. Fan et al applied cylinder-based oximetry to quantify OEF in ~10 cortical veins on high-resolution 7 Tesla phase images (0.33 x 0.33 x 1.0mm³) of patients with various stages of MS (75). Patients showed a 3.4% OEF reduction in gray matter relative to age-matched healthy volunteers (P = 0.0025) that was not different across brain regions. Furthermore, cortical OEF was an independent predictor of patients’ cognitive ability in in terms of processing speed, independent of white and gray matter lesions typical of MS tissue damage. Lastly, regional SvO₂ mapping may have potential to follow patients longitudinally during treatment.

Vascular injury is a frequent aspect of traumatic brain injury (TBI), and likely contributes to the pathogenesis of TBI and subsequent chronic disability (76). Recent human investigations in TBI patients probed the potential of SWI to assess oxygenation-dependent changes in cerebral veins. In 12 patients with mild TBI, one study observed small decreases in venous susceptibility, suggesting increased SvO₂ in the left thalamostriate and right basal vein of Rosenthal (P = 0.04) (77). However, these findings did not correlate with symptoms on neuropsychological testing. Using more advanced quantitative SWI approaches Liu et al studied 23 TBI patients and reported relative susceptibility values in deep veins and small hemorrhages. They found mean susceptibility of deep veins and hemorrhagic lesions of 435 – 206 ppb and 108 – 56 ppb (SI), respectively (78).

5. MRI Oximetry of the Extremities

5.1. Temporally-resolved SvO₂ as a Dynamic Tracer

The oxygen consumption rate of skeletal muscle can increase by as much as 50-fold during heavy exercise relative to the resting state. The primary mechanism to accommodate greater oxygen demand is hyperemia, i.e. a transient increase in blood flow rate, since storage of oxygen in the form of myoglobin is limited. During hyperemia the blood flow in the conduit artery is markedly increased through reduction of microvascular resistance. The resulting increase in shear rate to the endothelium after cuff release leads to vasodilation of the conduit artery, typically induced by nitric oxide release (79).

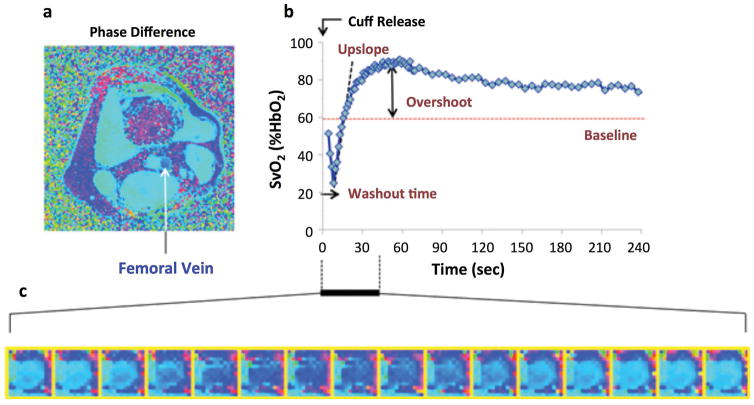
MR susceptometry-based oximetry offers an opportunity to evaluate vascular dysfunction in the lower extremities by monitoring SvO₂ in the femoral vein in response to a physiological challenge such as cuff-induced ischemia. Vascular dysfunction is well known to occur in peripheral artery disease (PAD) as well as in early, presymptomatic atherosclerosis, for instance, caused by cigarette smoking. Following disruption of the inflow of oxygenated blood via occlusion of a major supplying artery such as the femoral or popliteal artery with a blood pressure cuff, the tissue oxygen store will gradually deplete, and the desaturated capillary blood can serve as an endogenous tracer. Upon restoration of flow via cuff release gradual replacement of the oxygen-depleted blood in the capillary bed can be monitored by mapping oxygen saturation in the femoral vein. From the time-course of SvO₂ vascular reactivity can be expressed in terms of three parameters (80): washout time, upslope and overshoot (Figure 7). Washout time and upslope provide quantitative information on the washout rate of oxygen-depleted blood from the tissue as well as the rate at which tissue is resaturated. The overshoot may reflect the magnitude of hyperemia since tissue has reduced time to extract O₂, a time consuming process driven by diffusion. Thus, the rise in SvO₂ above baseline is expected in the event of more pronounced hyperemia. Conversely, impaired flow in patients with PAD leads to prolonged O₂ extraction time, thereby contributing to reduced upslope and overshoot. The principle of the method has been described in Sections 2.1 and 2.2, optimized for temporal resolution to accurately map the SvO₂ versus time curve (80). A phase difference image is then computed between two successive echoes of equal polarity (to minimize off-resonance errors). In distinction to applications in the brain the pulse sequence includes spectrally selective fat saturation to reduce contamination from fat near the muscle and first-moment nulling along the slice (i.e. blood flow) direction and flow is temporally resolved via projection velocimetry.

Figure 7.

Quantification of reactive hyperemia with dynamic oximetry: a) Cross-sectional phase difference image of the thigh, 10 cm below the inferior boundary of the pressure cuff; b) post-ischemia femoral vein SvO₂ time course; c) zoomed phase images showing relative phase of venous blood during period indicated. Darker blue represents lower saturation levels. Parameterization of time-course data in panel b yields quantitative metrics: washout time, upslope and overshoot (from Langham et al, JCMR 2015, with permission).

5.2. Dynamic Oximetry in Patients with Peripheral Arterial Disease

One of the most common disorders of the peripheral vasculature is PAD, in which atherosclerosis causes narrowing of the major arteries supplying the lower extremities (iliac, femoral, popliteal and the runoff arteries). The initial diagnosis of patients with PAD is made on the basis of the ankle-brachial index (ABI, ratio of blood pressure at the ankle and radius). A low ABI is a strong indicator of the presence of PAD but a normal ABI does not rule out risk due to relatively high false negative rates (81). Thus, a direct physiological measurement would be desirable for more accurate clinical assessment.

Dynamic oximetry is able of capturing reduced capacity of the peripheral vascular system to respond to a challenge such as cuff-induced ischemia. In a recent study involving three cohorts (Table 2): patients with PAD, older healthy controls (OHC) and young healthy subjects (YH), highly significant differences in oximetric parameters were observed between OHC and PAD. Further, the upslope and overshoot parameters were sensitive to age as shown in Table 2. A subsequent study found that washout time was not only related to PAD disease presence, but was also significantly correlated with patients’ ABI as a clinical measure of disease severity (82).

Table 2.

Average (standard error) of parameters of dynamic oximetry (89).

Groups	N	ABI	Age (years)	Washout (s)	Upslope (%HbO2/s)	Overshoot (%HbO2)
OHC	43	1.12 (0.09)	61 (7.6)	16.9 (1.1)	1.3 (0.08)*	14 (1.2)*
PAD	38	0.69 (0.15)	64.6 (7.7)	28.6 (1.2)**	0.60 (0.1)**	8 (1.4)**
YH	19	1.1 (0.12)	34.3 (7.5)	15 (1.7)	1.88 (0.13)	19 (1.9)

^{* and **}correspond to statistically significant mean difference between OHC and YH, and between OHC and PAD, respectively.

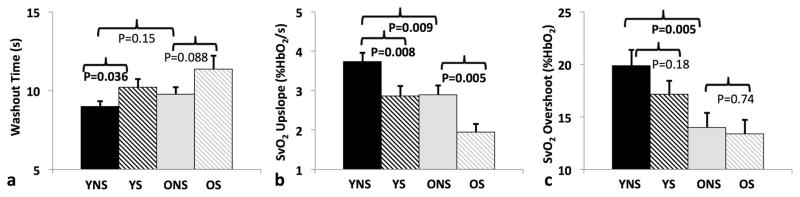
Another recent study applying dynamic oximetry focused on the effect of cigarette smoking in asymptomatic subjects (83). Cigarette smoking is a well-known cause of vascular dysfunction, characterized by a reduction in the bioavailability of nitric oxide (NO), leading to impaired endothelium-dependent vasodilation (84). The study enrolled a total of 169 subjects divided into four groups: young healthy non-smokers (YNS: N = 45, mean age = 30.2 ± 0.7 years, age range: 26–40 years), age-matched young smokers (YS: N = 39, mean age = 32.1 ± 0.7), older healthy non-smokers (ONS: N = 45, mean age = 57.8 ± 0.6 years, age range: 51–65 years), and age-matched older smokers (OS: N = 40, age = 56.3 ± 0.6). All study participants were free of symptomatic CVD as a means to test the method’s ability of detecting early, preclinical manifestations of endothelial dysfunction. Figure 8 summarizes the differences in the oximetric parameters between the four cohorts. The results are consistent with the notion of age- and smoking-related impaired microvascular reactivity. Importantly, for all functional and parameters evaluated the effects of smoking and age were independent of one another.

Figure 8.

Inter-group comparisons of dynamic oximetric parameters. Data suggest prolonged washout time in smokers (a), reduced rate of resaturation (upslope) in both smokers and older subjects (b), and similarly, lower overshoot (c). Significant p-values (P < 0.05) are highlighted in bold (from reference (83), with permission).

5.3. Quantification of Skeletal MRO₂ in Response to Exercise

Maximal pulmonary oxygen uptake (VO₂max), defined in terms of the Fick principle as left ventricular (end-diastolic volume – end-systolic volume) × heart rate × arteriovenous oxygen difference, is the gold standard measure of an individual’s cardiorespiratory capacity (85). Decreased VO₂max is a hallmark of heart failure associated with decreased exercise tolerance (86). Isolation of large muscle VO₂ during an exercise paradigm may provide additional insight into the mechanisms that contribute to decreased exercise tolerance in those at risk for or with heart failure. With this goal in mind, Mathewson et al (87) demonstrated feasibility of estimating peak exercise VO₂ and the recovery time constant of VO₂ associated with post-exercise (off-kinetics) in healthy males after a period of knee extensor exercise, which targeted the quadriceps femoris muscles. Quantification of SvO₂ and blood flow velocity in proximal superficial femoral vein was performed sequentially with dynamic oximetry and 1D MR velocimetry (88). Each measure took 2.4 s, resulting in effective temporal resolution of 4.8 s. The mean baseline and peak exercise VO₂ was 0.68 and 9.6 ml O₂/ 100g/ min, respectively. Lastly, Thompson et al. found statistically significant (p<0.05) correlation between quadriceps muscle mass and peak VO₂.

Concluding Remarks

This review was not meant to be comprehensive, and techniques not directly relying on a susceptibility measurement, including qBOLD (10), calibrated BOLD (9) and T₂-based blood oximetry (e.g. TRUST (8)), have deliberately been omitted, to adhere to the intended scope of this Special Issue of the journal. MRI oximetry exploiting hemoglobin magnetism for assessing oxygen metabolism is still in its infancy. An exception is global CMRO₂, which can now be measured reliably by means of susceptometry via quantification of venous oxygen saturation in a large draining vein, in conjunction with measurement of cerebral blood flow. The simple inversion procedure to extract intravascular magnetic susceptibility, based on the analytical solution for ellipsoids, is also applicable to smaller veins, but the method suffers from inadequate knowledge of the tissue volume drained. QSM has been used with some success for regional mapping of oxygenation in the venous tree and, in at least one instance, to estimate baseline CMRO₂. Expected advances of current approaches toward voxelwise CMRO₂ mapping techniques would provide additional insight into neurocognitive disorders and facilitate monitoring of the response to therapeutic intervention. Lastly, applications to other organ systems, including skeletal tissues, are emerging.