Reducing the dosimetric impact of positional errors in field junctions for craniospinal irradiation using VMAT

Abstract

Aim

To improve treatment plan robustness with respect to small shifts in patient position during the VMAT treatment by ensuring a linear ramp-like dose profile in treatment field overlap regions.

Background

Craniospinal irradiation (CSI) is considered technically challenging because the target size exceeds the maximal field size, which necessitates using abutted or overlapping treatment fields. Volumetric modulated arc therapy (VMAT) is increasingly being examined for CSI, as it offers both better dose homogeneity and better dose conformance while also offering a possibility to create field junctions which are more robust towards small shifts in patient position during the treatment.

Materials and methods

A VMAT treatment plan with three isocenters was made for a test case patient. Three groups of overlapping arc field pairs were used; one for the cranial and two for the spinal part. In order to assure a ramp-like dose profile in the field overlap region, the upper spinal part was optimised first, with dose prescription explicitly enforcing a ramp-like dose profile. The cranial and lower spinal part were done afterwards, taking into account the dose contribution of the upper spinal fields.

Results

Using simple geometrical reasoning, we demonstrated that hot- and cold spots which arise from small displacement of one treatment field relative to the other treatment field can be reduced by taking two precautions: (a) widening the field overlap region, and (b) reducing the field gradient across the overlap region. The function with the smallest maximal gradient is a linear ramp. We present a treatment planning technique which yields the desired dose profile of the two contributing fields, and minimises dosimetric dependence on minor positional errors in patient set-up.

1. Background and aim

Craniospinal irradiation is a technically challenging task. The length of the planning target volume (PTV) exceeds the maximal size of a treatment field, thus requiring some method of combining treatment fields to treat the whole target. While the standard set-up for craniospinal irradiation is still based on the set-up described by Van Dyk almost 40 years ago,¹ other modalities such as intensity modulated radiation therapy (IMRT),2, 3, 4, 5, 6, 7 volumetric modulated arc therapy (VMAT),8, 9, 10, 11 tomotherapy,12, 13 and proton therapy¹⁴ are increasingly being examined as a possibility for cranio-spinal irradiation.

The studies seem to agree that both IMRT and VMAT treatment planning offer both a more conformal and a more homogeneous dose coverage of the target and better sparing of some organs at risk (e.g., thyroid gland) with respect to the traditional 3D CRT approach, while at the same time they raise concern about the increased dose to other organs at risk, in particular lungs and kidneys.

A particular problem in the craniospinal irradiation are the field junctions. Set-up inaccuracies of a few millimeters in the cranio-caudal direction can result in large over- or underdosing. In conventional set-up, moving the treatment field junction after a given dose, usually every 9 Gy, has been adopted both for reducing dose inhomogeneity and to minimise over- or underdosing which can occur due to systematic errors; the technique is known as “feathering”.¹⁵ Studies using IMRT employ a variety of field-junction techniques: “hybrid” junction,² “jagged-junction”,4, 5 and field overlap⁷ techniques, while studies using VMAT use almost exclusively the field overlap technique,8, 10 relying on the optimiser algorithm to arrive at a smooth field overlap junction.

In the present study, we focus exclusively on the field junction area. We show that a wider field junction can result in a smaller dosimetric impact of a given positional error. We also demonstrate that, left to itself, the dose optimiser algorithm may not arrive at a dose profile which is the most robust towards small positional errors in patient set-up. Finally, we present a treatment planning procedure which reduces the dosimetric impact of positional errors.

2. Materials and methods

2.1. Idealised field junction

We start by showing that in two overlapping treatment fields, a linear ramp is the dose profile which yields hot- and cold spots of the smallest magnitude when one field is displaced by a small amount with respect to the other. Denoting dose contributions of the two treatment fields by f(x) and g(x), where f(x) + g(x) = 1, with f(x) = 0 and g(x) = 1 for x ≤ 0 and f(x) = 1 and g(x) = 0 for x ≥ L, we are interested in the deviation of the sum of both contributions from unity, with one field being displaced by Δx:

$$1-(f(x)+g(x+\mathrm{\Delta }x))=f(x+\mathrm{\Delta }x)-f(x).$$

When the displacement Δx is small, we may expand the above difference in a Taylor series and, retaining only the linear term in Δx, we obtain:

$$1-(f(x)+g(x+\mathrm{\Delta }x))\approx f^{\prime }(x)\mathrm{\Delta }x.$$

Thus, at a given shift Δx, dose deviation is proportional to the dose gradient f′(x). Of all the functions raising from 0 to 1 over the distance L, the linear function has the smallest maximal gradient.

Another quantity of interest would be the average deviation of the dose from unity across the field junction:

$$\begin{array}{ccc}\frac{1}{L}{\int }_0^{L-\mathrm{\Delta }x}\left[1-(f(x)+g(x+\mathrm{\Delta }x))\right]\mathrm{d}x\hfill & \approx \hfill & \frac{\mathrm{\Delta }x}{L}{\int }_0^L{f}^{\prime }(x)\mathrm{d}x\hfill \\ \hfill & =\hfill & \frac{\mathrm{\Delta }x}{L}.\hfill \end{array}$$

Thus, for small displacements, when Δx ≪ L holds and terms in Δx/L higher than linear can be neglected, the shape of dose profile only affects the magnitude of hot- and cold spots, but not the average dose deviation.

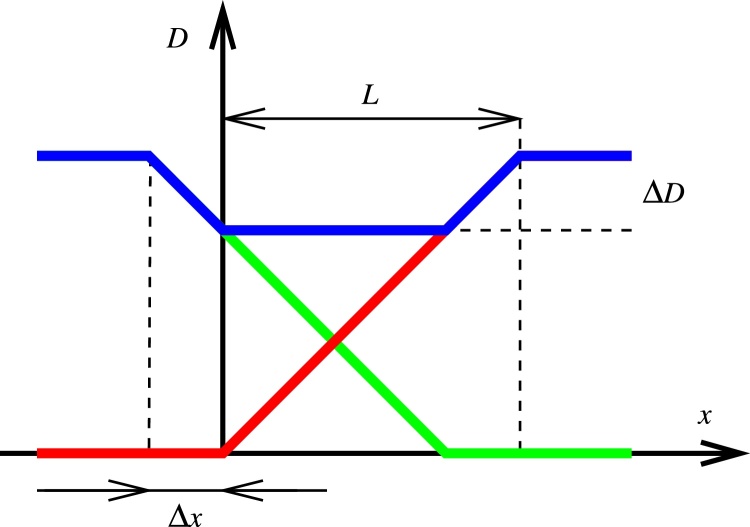
Fig. 1 shows the dose profile across a field junction in which f(x) and g(x) are represented by linear ramps, one of them shifted with respect to the other. The contributions of the two overlapping groups of fields (with VMAT, a group of fields is usually a pair of arc fields; with IMRT it is usually 5–7 fields) – f(x) and g(x) – are shown in red and green, respectively, and the total dose shown in blue. In this simplified example, we arrive at the same expression for dose deviation ΔD:

$$\mathrm{\Delta }D=100\%\times \frac{\mathrm{\Delta }x}{L}.$$

As an illustration, a 5 mm positional shift is expected to result in a 5% dose difference across a 10 cm field junction. The ratio 100 %/L is the dose gradient.

Fig. 1.

Dose profile across an idealised field junction in which the individual field contributions are shown in red and green, respectively, and the total dose shown in blue. A positional shift Δx of one dose contribution with respect to the other results in a dose difference of ΔD.

2.2. Patient and target selection

An adolescent female patient (18 yo) was selected as a test case. The patient had undergone CT simulation in supine position with the head and shoulders immobilised in a thermoplastic mask and the arms resting comfortably at the patient's sides. PTV encompassed the whole brain and spinal cord down to S2 vertebra, resulting in a total length of 75.9 cm. The prescribed dose to this target was 30.6 Gy in 17 fractions.

2.3. Treatment planning

Treatment planning was done on Eclipse 10.0 treatment planning system, with Varian Unique Performance equipped with Millenium MLC 120 and Exact IGRT couch as the target treatment machine (Varian Medical Systems, Palo Alto, CA, USA). The treatment plans were generated using Progressive Resolution Optimiser algorithm PRO3,¹⁶ and the dose was computed with the Analytical Anisotropic algorithm (AAA) using 2.5 mm calculation grid resolution.

To cover the whole PTV, 3 isocenters in the cranial, upper spinal (Th3) and lower spinal (L2) region were chosen, with 23 cm separating the cranial and the upper spinal isocenters, and 26 cm separating both spinal isocenters. To simplify patient positioning, the coordinates of the three isocenters only differed in the cranio-caudal direction. The field set-up used by center C in ref. 8 was adopted, with two partial arcs used at each isocenter, avoiding irradiation from the anterior position by omitting the sector 310–50°, and the collimator rotated to 10° and 350°, respectively.

Dose optimisation was performed in two steps. The treatment plan for the upper spinal region was made in the first step. Within the upper spinal region, a central region (PTVt; 14.4 cm) was defined with a homogeneous dose prescription, surrounded by two 10.8 cm transitional regions (Fig. 2). Each of the transitional regions was further divided into 9 subregions, each extending 1.2 cm in the cranio-caudal direction. The dose prescription in each subregion gradually increased from the periphery towards the center; i.e. to both outermost subregions (labelled as 1 in Fig. 2) a dose of 0–3.4 Gy was prescribed, to the adjacent regions (2) a dose of 3.4–6.8 Gy was prescribed, and so on, up to the innermost subregions (9), to which a dose of 27.2–30.6 Gy was prescribed.

Fig. 2.

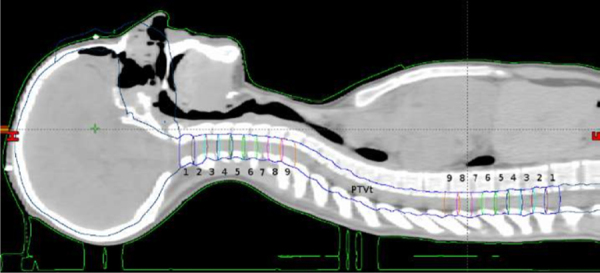
Sagittal view showing the auxiliary structures used for treatment planning.

After the treatment plan for the upper spinal region had been optimised, the treatment plans covering the cranial and lower spinal regions were made, taking into account the dose distribution for the upper spinal region, and filling up the dose to the prescribed value.

2.4. Positional error simulation

A positional error in the cranio-caudal direction was simulated by taking an already optimised plan and making two modifications to it: the isocenter position for the cranial pair of treatment fields was moved 5 mm in the cranial direction, and the isocenter position for the lower spinal pair of fields was moved 5 mm in the caudal direction. The dose was recalculated while keeping the same monitor unit count. In a complementary simulation, the isocenter position for the cranial pair of treatment fields was moved 5 mm in the caudal direction, and the isocenter position for the lower spinal pair of fields was moved 5 mm in the cranial direction. The same procedure was repeated for the positional shifts of ±1, ±3, ±7, and ±10 mm.

2.5. Treatment plan verification

The treatment plan was verified using film dosimetry (Gafchromic EBT3; Ashland, Wayne, NJ, USA). A radiochromic film was mounted into the slot for film dosimetry in the IBA MultiCube phantom (IBA Dosimetry, Schwarzenbruck, Germany), with the phantom turned onto its side so that the film lied in the sagittal plane. Irradiated films were later analysed using a web application for radiochromic film dosimetry (Radiochromic.com, v2.2; https://radiochromic.com/),¹⁷ using a correction for scanner response variability.¹⁸

3. Results

3.1. Dose profiles

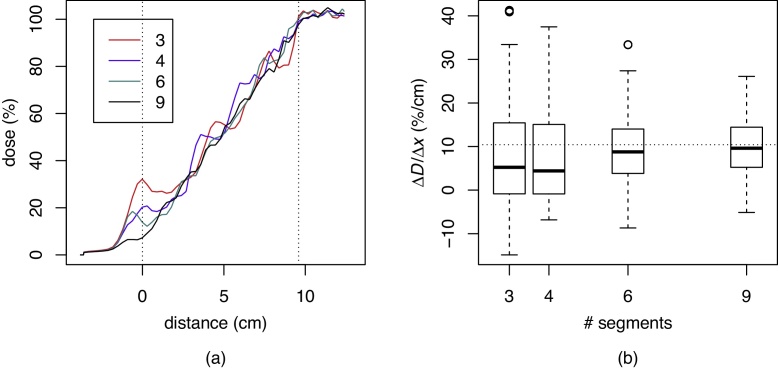
In order to determine the minimum number of segments needed to obtain a smooth linear ramp dose profile in the transition region, we ran a separate experiment. In the dose optimisation step for the treatment field for the upper spinal region, the transitional region (17 CT slices, separated 6 mm apart, total length 96 mm) was divided into either 3, 4, 6, or 9 segments. Fig. 3a shows the dose profile contributed by the upper spinal fields to the spinal–spinal junction. Fig. 3b shows the distribution of dose gradient along the transitional region for the above mentioned segmentations, presented as box plots. A linear ramp has a uniform slope of 100%/96 mm, or 10.4%/cm. One can see that increasing the number of segments leads to a dose profile closer to the desired linear ramp.

Fig. 3.

The calculated dose profile in the transitional region after optimisation in the case of dividing the transitional region into 3, 4, 6, or 9 segments (a). Distribution of dose gradient within the transitional region in the case of dividing the transitional region into 3, 4, 6, or 9 segments. The horizontal line corresponds to a uniform gradient (b).

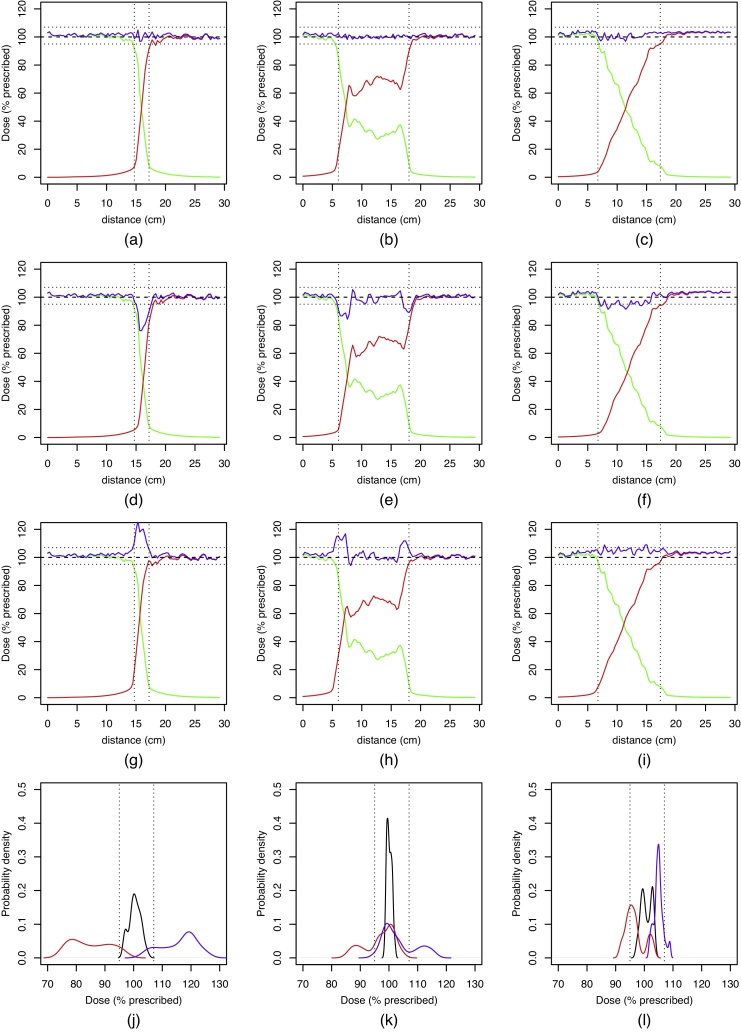
For different treatment plans, Fig. 4a–l show a dose profile along a line between the same two points in the patient's body, encompassing the spinal–spinal junction. The contribution of the two upper spinal arc fields (clockwise and counter-clockwise summed up) is shown in green, the contribution of the two lower spinal fields is shown in red, and the total dose in blue. Dose profiles in Fig. 4a and b have both been obtained by using the progressive resolution optimiser PRO3 on two overlapping pairs of VMAT fields, the only difference being that in Fig. 4a, the overlap region is narrow (2.5 cm), while in Fig. 4b, it is wide (12.0 cm). Fig. 4c shows the dose profile along a linear ramp junction (10.4 cm) described in the previous section.

Fig. 4.

Dose profile across the field junction region in the spinal–spinal junction for a narrow junction (a), wide junction (b) and linear ramp junction (c). The dose contribution of the upper spinal field is shown as green, and the contribution of the lower spinal field as red. Figures (d–f) show the simulated effect of a −5 mm shift (apart in the cranio-caudal direction), and figures (g–i) show the effect of a +5 mm shift (towards each other). Figures (j–l) show the dose distribution in the field junction region; no positional shift (black), −5 mm shift (red), +5 mm shift (blue). Vertical lines in (a–i) show the extent of the field overlap region. Horizontal lines in (a–i) and vertical lines in (j–l) denote 95% and 107% of the prescribed dose, respectively.

By comparing Fig. 4a and b, it is clear that simply widening the junction does not result in a significantly smaller dose gradient of either upper or lower spinal field contribution. Instead, the dose optimiser algorithm produces a fairly constant total dose across the junction using non-monotonous upper or lower spinal field contributions, each of them still having areas of steep dose gradient. Fig. 4c, however, shows that the treatment planning technique presented in the previous section results in a dose profile which is close to the ideal (Fig. 1).

Fig. 4d–f show the behaviour of the field junctions shown in Fig. 4a–c in a simulated case in which the distance between the isocenters of the upper and lower spinal fields has been increased by 5 mm. As expected, a large drop in the total dose is observed in the regions where the upper and lower spinal fields have a high dose gradient. In a similar manner, Fig. 4g–i show the behaviour of the field junctions shown in Fig. 4a–c in a simulated case in which the distance between the isocenters of the upper and lower spinal fields has been decreased by 5 mm. Again, a large rise in the total dose is observed in the regions of high dose gradient.

Fig. 4j–l show the dose distribution along the dose profile line in the junction area for the field junctions shown in Fig. 4a–c. Black lines correspond to no positional shift, red lines to the distance between the isocenters increased by 5 mm, and blue lines to the distance between the isocenters decreased by 5 mm. While a 5 mm shift of one of the fields with respect to the other can result in a ±30% change in dose in the case of a narrow junction, this value drops to ±15% in the case of a wide junction, and down to ±10% in the case of a linear ramp junction. Note this coincides fairly well with the previous estimates for an idealised field junction: as the original treatment plan aimed to cover the target with 95–105% of the prescribed dose, a 5 mm positional shift over a 10 cm junction is expected to pull the dose up or down by another 5%, depending on the direction of the shift.

Counting merely the percentage of points staying within the [95%, 107%] dose range after a ±5 mm shift is performed, the linear ramp dose profile does not offer a significant improvement over other dose profiles at comparable junction widths. A narrow junction clearly shows the worst results, with only 10% and 13% points staying within the prescribed dose range after the distance between the isocenters increased or decreased by 5 mm, respectively. With a wide junction, these values climb up to 73% and 71%, respectively, while in the case of a linear ramp junction, they are 68% and 91%. Thus, while overall a linear ramp junction performs slightly better, we do not consider this difference as important as the magnitude by which the dose departs from the prescribed range.

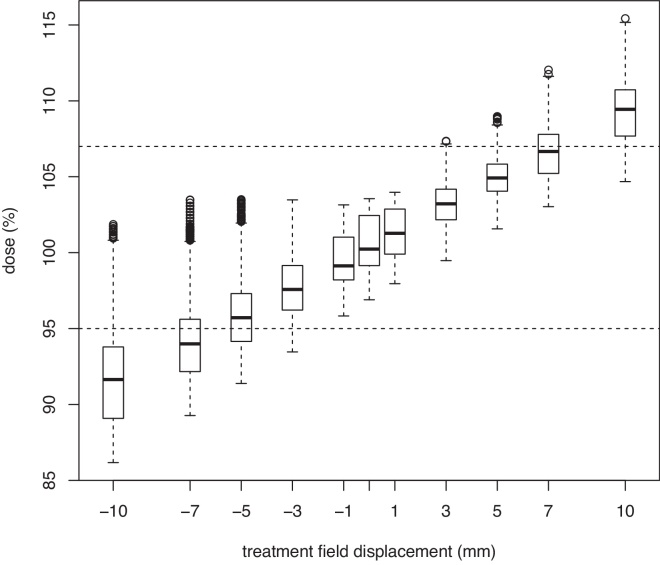
For a linear ramp junction, the sensitivity of the dose coverage within the transitional area to the magnitude of positional shift has been assessed (Fig. 5). In this experiment, after dose optimisation, the isocenter of the lower spinal treatment field pair was shifted ±1–±10 mm in the cranial or caudal direction, and the dose was recalculated. Dose distribution within the transitional area of the spinal–spinal junction is shown as a box plot. One can see that a positional shift up to ±3 mm generally leads to dose distributions which are within the [95%, 107%] range, which is considered acceptable,¹⁹ while larger positional shifts, even though they may still yield an acceptable dose distribution in some circumstances, are generally considered unacceptable.

Fig. 5.

Dose distribution along the dose profile within the transitional region of the spinal–spinal junction for different values of positional shift of the lower spinal treatment field pair. Horizontal lines denote 95% and 107% of the prescribed dose, respectively.

3.2. Dosimetric influence of arm movement

Using the whole arc except the sector [300°, 50°] for irradiation means irradiating through the patient's arms. While this has been done with suitable immobilisation,²⁰ it is generally not advised, because of the dosimetric inaccuracies induced by a non-deliberate change in the patient's arms position. In a separate simulated experiment, we estimated the effect of a complete omission of the patient's arms: after optimising the treatment plan, the same treatment plan was recalculated on another structure set, identical to the original one with the exception of the patient's arms being excluded from the calculation volume. As expected this produced a slightly higher dose at the same MU value, with D_50% for the spinal PTV rising from 101.3% of the prescribed dose to 103.1% of the prescribed dose. Similarly, D_98% rose from 94.8% to 96.8% of the prescribed dose, and D_2% rose from 104.2% to 107.5% of the prescribed dose. This is the extreme case; we can expect that a minor change in position would induce a dosimetric error smaller than this worst-case scenario. The relatively low impact of arm displacement is consistent with a relatively low dose received by the patient's arms; even though no special restrictions to the dose in the arms were used, the maximal dose to both humeri stayed at around 10% of the dose prescribed to PTV.

3.3. Treatment plan verification

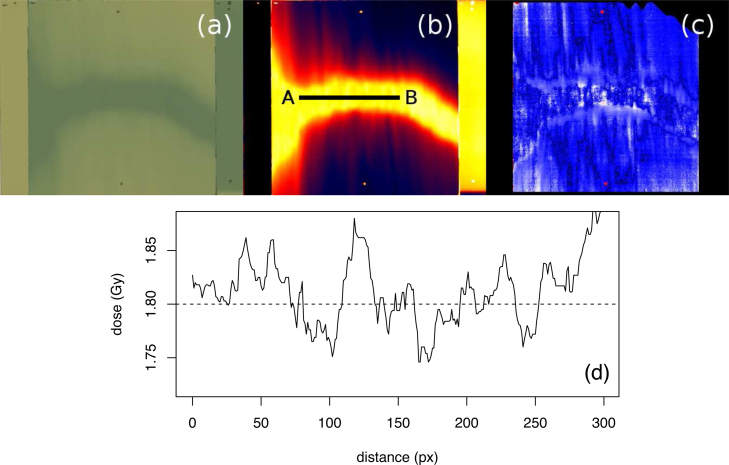
Fig. 6 shows the results of treatment plan verification using film dosimetry; the irradiated film scan (Fig. 6a), the calculated dose (Fig. 6b), the gamma index analysis (Fig. 6c) of the match between the dose obtained with the radiochromic film and the dose plane exported from the treatment planning system, and the dose profile across the field overlap region (Fig. 6d). For gamma index analysis,²¹ 3% dose tolerance and 3 mm positional tolerance was used along with a threshold value set at 10% of D_max and global normalization, resulting in the average γ value of 0.16 and 99.7% points passing γ < 1 criterion. Points with γ < 1 are shown in blue, and points with γ > 1 are shown in red.

Fig. 6.

QA verification of the cranio-spinal field junction; (a) irradiated radiochromic film with two vertical stripes containing a non-irradiated film and a film exposed to 1.8 Gy, (b) dose calculated from the radiochromic film readout, (c) gamma index analysis of the match between the dose obtained with the radiochromic film and the dose plane exported from the treatment planning system, (d) dose profile along the line A–B.

4. Discussion

4.1. Prone vs. supine patient position

While the original set-up for craniospinal irradiation¹ employed a prone patient position, there are numerous studies advocating the supine patient position.22, 23, 24, 25 After judging the advantages and the disadvantages of both set-ups, we decided to employ it as well. The obvious advantage of the prone position – easier visualisation of treatment field junctions – became less important with the advancement of image-guided radiotherapy, which made the supine position a viable alternative, allowing for greater patient comfort and easier access for the paediatric patients requiring anaesthesia.

4.2. Dose profile in field overlap area

While the studies treating the craniospinal axis using IMRT often paid special attention to achieving a desired dose profile in the field junction area (e.g., staircase,4, 5), the studies using VMAT usually seem to rely on the dose optimiser to obtain a suitable dose profile. As we have shown earlier, this often results in non-monotonous dose profiles.

However, a recent study²⁶ dealing with the robustness of treatment plans with respect to positional shifts of the patient claims that the authors specifically aimed for a sigmoidal dose profile in the field overlap region. In another study on localization errors¹¹ the authors propose a staircase dose profile in order to minimize such errors. An interesting feature of this study is that the authors actually arrived at a linear ramp profile when the junction region was too narrow to support staircase dose profile (Fig. 4a in ref. 11), but brushed it off as a mere curiosity without realising that it gives even better results than the technique they propose. Using a linear ramp instead of a staircase dose profile, we predict the ±10% spikes observed by Myers et al. (Fig. 3b and d in ref. 11), which correspond to a ±5 mm shift applied to a 116 mm overlap region, would drop down to ∼5%.

4.3. Maximal vs. average positional errors

Earlier studies27, 26 have proven that the position shifts in the cranio-caudal direction result in greater dosimetric changes than the shifts in the other two directions. Consequently, we limited our study to the cranio-caudal direction. A comparison of the dosimetric changes reported in 27, 26 to the ones reported here is difficult for two reasons: (a) we examined local effects (hot- and cold spots) rather than their influence on the volume–dose histogram, and (b) we evaluated the dosimetric impact of the maximal shift, i.e., ±5 mm, while the authors in 27, 26 chose three random values from the [−5 mm, +5 mm] range and used their mean and standard deviation. Assuming that the samples are distributed uniformly, the mean of several uniform distribution is a rectangular mean distribution, sometimes called Bates distribution. For 3 uniformly distributed samples taken from the [−5 mm, +5 mm], the expected mean and standard deviation is 0 ± 1.67 mm. It can be argued that this approach better reflects the reality of a clinical department; however we have deliberately chosen more direct observables which allow for easier analysis. A 21% increase of the maximum dose reported in 26 is however close to the expected value of 25% for a 5 mm shift in the cranio-caudal direction applied to a 20 mm overlap region.

4.4. Quality assurance of medical accelerators

Craniospinal irradiation, in particular when performed in its conventional set-up, is a technique which leaves little margin for errors. As its requirements are close to the tolerance levels specified in the quality assurance (QA) recommendations for medical accelerators, it is important to consider the relevant parameters. The conventional set-up relies on the jaw position for half-beam block and the treatment couch position; tolerance levels for them are 1 mm and 2 mm, respectively, both are checked monthly.²⁸

With image-guided techniques, assuring that the imaging system isocenter coincides with the treatment isocenter is of prime importance. The suggested tolerance levels here are 1.5–2 mm, checked monthly.29, 30 The inaccuracies introduced by mis-alignment result in systematic errors which do not cancel out by day-to-day variations.

5. Conclusions

Using an idealised schematic field junction with partial field overlap, we have shown that hot- and cold spots which arise from small displacement of one treatment field relative to the other treatment field can be reduced by taking two precautions: (a) widening the field overlap region, and (b) reducing the field gradient across the overlap region. The function with the smallest maximal gradient is a linear ramp, and we presented a treatment planning technique for craniospinal irradiation which yields the desired dose profile of the two contributing fields, and minimises dosimetric dependence on minor positional errors in patient set-up. The treatment planning technique was developed using VMAT, but can be equally well applied to every IMRT-derived technique.

Conflict of interest statement

The authors of the manuscript “Reducing the dosimetric impact of positional errors in field junctions for craniospinal irradiation using VMAT” declare no conflict of interests with regard to this manuscript.

Financial disclosure statement

Primož Peterlin acknowledges the financial support from the Slovenian Research Agency through research grants P3-0307 and P1-0389. The other two authors of the manuscript “Reducing the dosimetric impact of positional errors in field junctions for craniospinal irradiation using VMAT” have no financial disclosure to declare.