Determination of boundaries between ranges of high and low gradient of beam profile

Abstract

Aim

This work addresses the problem of treatment planning system commissioning by introducing a new method of determination of boundaries between high and low gradient in beam profile.

Background

The commissioning of a treatment planning system is a very important task in the radiation therapy. One of the main goals of this task is to compare two field profiles: measured and calculated. Applying points of 80% and 120% of nominal field size can lead to the incorrect determination of boundaries, especially for small field sizes.

Materials and methods

The method that is based on the beam profile gradient allows for proper assignment of boundaries between high and low gradient regions even for small fields. TRS 430 recommendations for commissioning were used.

Results

The described method allows a separation between high and low gradient, because it directly uses the value of the gradient of a profile. For small fields, the boundaries determined by the new method allow a commissioning of a treatment planning system according to the TRS 430, while the point of 80% of nominal field size is already in the high gradient region.

Conclusions

The method of determining the boundaries by using the beam profile gradient can be extremely helpful during the commissioning of the treatment planning system for Intensity Modulated Radiation Therapy or for other techniques which require very small field sizes.

1. Background

A number of official publications,1, 2 papers3, 4, 5, 6, 7, 8 and verification audits9, 10, 11 confirm that the commissioning of the treatment planning system (TPS) is very important in radiation therapy. On the one hand, this task requires at least a basic control of TPS, and on the other hand, performing the verification of measurements involves consideration and preparation. The measurements for modeling have to be performed with high precision and accuracy as well. Unfortunately, very often, the TPS does not contain any useful tool for the verification purpose. Even if the tool exists, it is either very simple and the data (for example, dose profile as numbers in a text file) need to be processed in external software or it turns out to be very complex in use.

This article presents our experiences with TPS commissioning. In particular, we describe our method, tools and results of comparing beam profiles generated in TPS with the ones from measurements. The method we used to design boundaries between regions of low and high gradient is based on the real value of the profile gradient. For each profile, the gradient is numerically determined and its given value is the boundary between regions of low and high gradient. Another method based on field size (for example 80 and 120% of the field size) fails in small fields. As we show below, it is because small field profiles practically do not contain the plateau in the middle part of the profile. Applying recommended tolerances to these fields, leads to large errors. The proposed method allows such errors to be avoided.

2. Aim

The aim of the study is developing a method to determine areas of large and small gradient dose rate in the beam profile. Further, the aim is to use the developed method to verify the calculations of the planning system.

3. Materials and methods

The Elekta linac with 160 leaves MLC has been recently installed in the Opole Oncology Center. Our two older machines have different collimators with only 80 leaves. All linacs installed in the Opole Oncology Center have three photon energies – 4, 6, and 18 MV. All profile measurements, both for modeling purposes and for verification, were performed using a full scattering 3D water phantom. Two completely separate collections of profiles were performed. We used two ionization chambers CC13 by Wellhofer, recommended by the producer of TPS.¹² The first chamber was designated as the field detector, the second as the reference detector for all measurements. For commissioning purposes, for each photon energy we measured two profiles with at least 8 cm margins, which were averaged at the end. Both sets of measurements were collected with a constant resolution of 1.2 mm.

The TPS recommendations for data collecting for the modeling purposes were as below: for cross plane and in plane four field sizes: 5 cm × 5 cm, 10 cm × 10 cm, 15 cm × 15 cm and 20 cm × 20 cm at four depths: 1.5, 5, 10 and 20 cm. In addition to that, so-called star profiles and diagonal profiles were collected for maximal field (40 cm × 40 cm) at 10 cm depth. Star profiles were measured in 10° increments from 0° to 180°. We chose SSD = 90 cm for all measurements.

For the TPS verification, the following set of symmetric open fields was chosen (all sizes are in cm in isocenter): 5 × 5, 10 × 10, 30 × 30, 20 × 5, 5 × 20 and for wedged fields: 10 × 10, 20 × 5 and 5 × 20. In addition, a few asymmetric open fields were checked: half-beams 5 × 10 and 2 × 10 and one fourth of the 10 × 10 field – 5 × 5. All of the above measurements were executed for the surface – source distance equals to 90 cm. We also checked different distances between source and water surface: 75, 100 and 109 cm. All profiles were done at four different depths: depth of the maximum dose rate for given energy, 5, 10 and 20 cm. We collected data along major axes – cross plane and in plane.

Once the models of photon beams were obtained, the Oncentra External Beam 4.3 TPS by Nucletron¹³ was verified. The plans with appropriate beams were made for the set of measurements described above. For the profile comparison, we used recommendations from Ref. 1 The Oncentra TPS allows exporting a dose distribution as a single column of numeric values. In such a form, the data can be further processed in a spreadsheet. However, navigation in this type of data is rather unintuitive, especially when a dense dose grid and a large phantom are used.

In the process of verification, we used dedicated software packages which use the DICOM dose files originating from TPS. The DICOM standard we used is described in detail on the website.¹⁴ First, the measured profiles were averaged and smoothed. After that, each profile was normalized to 100% in the axis for the open fields and to 100% in the point of maximal dose rate for the wedged fields. A significant speedup in the verification process was possible due to the fact that the initial preparation was done simultaneously for a large number of profiles. Data from TPS was generated with a cuboid dose grid (2 mm resolution). Contrary to the measured profiles – the calculated profiles did not require smoothing. The differences between profiles were calculated with 1 mm resolution using the following formula from Ref. 1:

$$\delta =100\times \frac{D_{calc}-D_{meas}}{D_{\mathrm{meas,point}}}$$ (1)

where δ is the difference (in %); D_calc is the calculated dose in a given point; D_meas is the measured dose in a given point; D_meas,point is the measured dose on the central axis for open on-axis beams and in the point of maximum dose for off-axis beams and wedged beams.

The process of comparison was multistage. In the first stage, we calculated differences in beam sizes for open fields (distances between 50% intensity for the profile normalized to 100% in the axis of beam). This allowed to both evaluate the positioning of the jaws and determine real field sizes obtained from TPS. The differences in beam sizes were not calculated for wedged beams.

In the next stage, the field sizes were centered and renormalized. The software used in the centering process determined 50% of profile intensity (normalized to 100% in the beam axis) and defined distances of these points from the beam axis. At first, each beam profile was centered by shifting every point in the direction of the x-axis to get a symmetrical profile with respect to that axis (but not necessarily with the nominal field size). Next, all profiles were renormalized – the software found the ratio of the nominal field size to the value obtained after centering. The x-coordinate of each point was multiplied by the ratio described above, while the value of the function remained unchanged. These procedures were applied to both the profiles from TPS and from the measurements.

Centering and renormalization were necessary because some profile comparisons from our determination of the boundary between high and low gradient of the beam profile were unacceptable (differences in the field sizes were too large).

Accuracy of the above procedures was checked experimentally using a water phantom and the following field sizes: 9.8 × 9.8 and 10.2 × 10.2 (all sizes are in cm in the isocenter). These values were taken from two sources: the declaration of linac's maker¹⁵ and Polish recommendations.¹⁶ Quantitative comparison of the profiles (after centering and renormalization) confirmed that in the selected boundaries our method does not give any measurable errors.

For the determination of the profile gradient the calculated data was used. Profiles which came from TPS were smoother in comparison to the measured profiles. The gradient was numerically determined. In general, the data for a single profile contains two columns of numbers: coordinate of distance from beam axis and value of the dose. The x-coordinate has an increasing pattern. The gradient was numerically determined. The algorithm was as described below. The first set of points was taken. Software provides gradient computation on the base of several points: two, three, four or more. To our calculation, three points were taken into account. The software determines the equation of the straight line for the first set (these points can be referred to as 1–3). The tangent value was the gradient for the second point. Next, the slope was determined for points 2–4 and the gradient value was calculated for point 3. The procedure was repeated for all sets of points.

Only a small part of the software was used for comparison purposes. Its plausible application is much wider. Apart from the above described tools the software contains tens of other tools which help in many medical physicist's daily tasks. For example, one component is used in the Opole Oncology Center as the second monitor units calculator for plan checking, the other allows for designation of all desired photon and electron parameters of profiles and PDDs. Software also allows the importing of measured data from the most popular automatic 3D phantoms and the importing of calculated data from treatment planning systems in DICOM format. The next feature is the possibility for preparing the measured data for export to a few popular treatment planning systems. The software has been constantly developing since 1990.

4. Results

Comparison between measured and calculated profiles as part of the verification process of the TPS requires high accuracy. It turned out that for the small field sizes part of the profile lying between 80% was already in the high gradient and that caused large error values between compared profiles for the low gradient. We decided to compute the boundary between gradients in a different way – by using their own values. All other compared dosimetric parameters were in agreement and were within the tolerance.

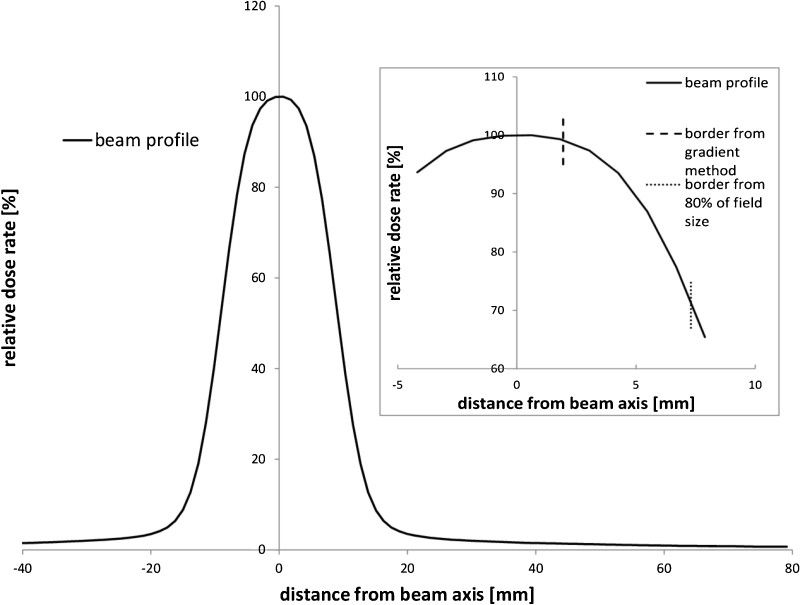
In the original divisions into a high and low gradient, we used points whose arguments had 80 and 120% of nominal field size and the high gradient was between these two values (distance based approach¹⁷). Our comparisons showed that obtained error values for small field sizes (5 cm, and 2 cm) exceeded the tolerance¹ for all photon energies. Further analysis demonstrated that the boundaries between gradients were the source of this problem. In our opinion, the original method of determining the boundary was failing, because for small field sizes the shape of a profile is becoming similar to the Gaussian curve. The example of a small field profile is showed in the main frame of Fig. 1. The near-axis part of the profile practically does not contain the flat section, as is characteristic of larger fields. The source of the problem is presented on the inset of Fig. 1. This is the zoom of the peak part of the small field profile. Dotted vertical line is a gradient boundary obtained using a distance based approach (80% of the field size). A dashed vertical line was determined by our method taking the given value of the beam profile gradient as the border value. Applying recommended tolerances of low gradient for parts of the profile containing high gradient values could lead to large errors.

Fig. 1.

The plot of the smaller side of field 2 cm × 10 cm for 4 MV photon beam for SSD = 90 cm and for the depth of a maximum dose rate. Inset: the peak part of the profile with marked borders derived by using the gradient value of 0.5%/mm (dashed line) and by using 80% of the field size (dotted line).

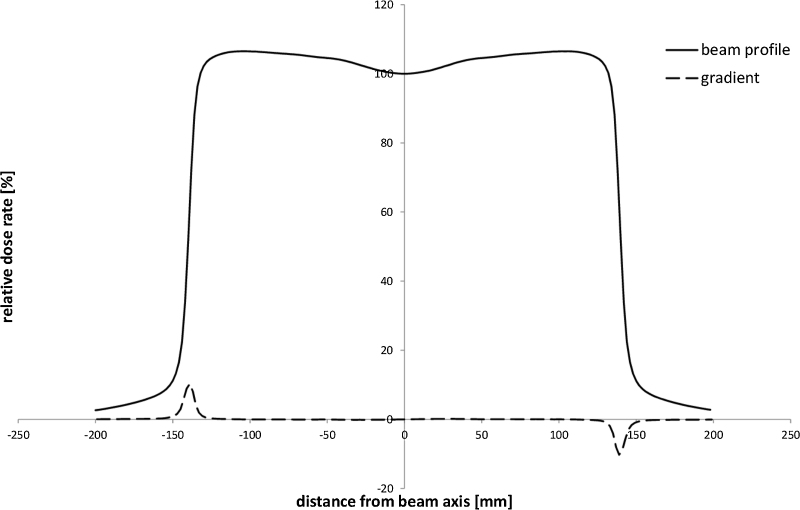
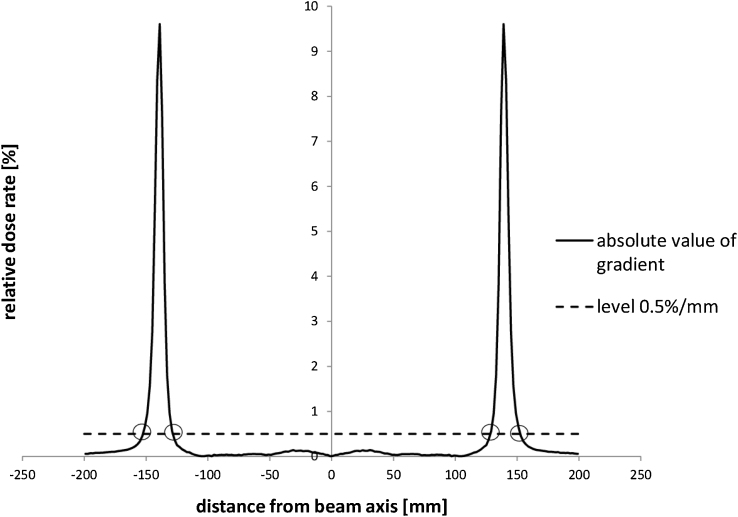
After checking hundreds of profiles, we found the one with the largest gradient in the near-axis region. The plot in Fig. 2 was deliberately chosen, because of the dose gradient inside the 80% region was the largest (near to beam axis) among all the profiles. Solid line presents a profile collected for 18 MV photon beam on the maximum dose depth for SSD = 90 cm. A numerically calculated profile gradient is plotted by a dashed line. The spatial resolution of the numerical calculation was 1.0 mm. We were interested in finding the highest gradient value near the beam axis. For the boundary between gradient ranges the slightly higher value was taken. Next, the boundary value was used for automatic designation of ranges of high and low gradient for all fields. The main idea is presented in Fig. 3. The chart shows the absolute value of gradient (solid line) and the dose gradient level of 0.5%/mm (dashed line) for gradient taken from Fig. 2. Four intersection points in this plot separate five regions of different gradients. For all open fields, the value of 0.5%/mm was chosen as a boundary between high and low dose regions. For wedged fields, due to the relatively high value of dose gradient in the middle of the beam and the way these fields were normalized, we used the value of 1.0%/mm. Such designation of the gradient boundaries allowed a correct application of recommended tolerances for real regions of low or high gradient. Using the gradient method, we obtained comparisons, in which uncertainties were smaller than recommended tolerances, including results for small fields. The TPS verification was positive and the Oncentra External Beam 4.3 was approved for clinical use.

Fig. 2.

The beam profile of 30 cm × 30 cm field for 18 MV, SSD = 90 cm and at the depth of maximum dose rate (solid line). It is the profile with the highest dose rate gradient in the region near the beam axis among all measured beams. Dashed line shows the gradient of the beam profile.

Fig. 3.

The plot of absolute value of the gradient from Fig. 2. Solid line shows the absolute value of the gradient. Dashed line represents the dose gradient level of 0.5%/mm. Four intersection points are used as bounds between ranges of high and low gradient of beam profile.

5. Conclusions

Modern radiation therapy uses smaller and smaller field sizes. It is caused by both the treated volumes which are sometimes subcentimeter scale (for example stereotactic radiosurgery) and the way of treatment delivery. In a highly advanced IMRT volumetric technique the whole treatment arch contains hundreds of segments. The shapes of the segments are precisely calculated by TPS and a single segment is often very small or very narrow. The problem of proper measurements and careful commissioning for small fields is absolutely vital.

There are a few problems with small fields in applications in radiation therapy. According to Ref. 18 the most important of them are: lack of electron equilibrium, partial blocking of the beam source and availability of small detectors. For modeling the physical parameters of small fields, the Monte Carlo method was also used,¹⁹ but for now it is not the routine way due to the lack of ready-made tools (software) and very time-consuming computations. In Ref. 20 comparison of measured beam penumbra in function of detector size is shown. The proposal for the profiles part of the article¹⁹ is that the smaller detector the better. In our case, we used 0.125 cm³ chamber, which gives penumbra twice larger than the diamond detector. Similar problems can occur during the verification procedure, especially when measurements for modeling would have been done with a different detector type than the verification set. In our case, all data was collected with the same measurement set. We assumed, that if our measurements done by 0.125 cm³ chamber were in agreement with the calculated profiles, the verified dosimetric model could be used in treatment.

A similar method of gradient determination was described in Ref. 17, but the boundaries were taken from the inflection points of profiles. The method from Ref. 17 retrieves boundary points that (compared to our method) are placed already in the range of higher values of dose gradient. It is possible that the method using the inflection point determines different gradient values than the boundaries for different beams. Our method is based on the real value of the dose profile gradient and the boundary has always the same value.

The presented method has proven to be very convenient and fast. The software used almost automatically centered and renormalized profiles, found the boundaries between high and low dose gradients and determined all desired parameters. The method of determining the boundaries can be extremely helpful during the commissioning of the TPS for Intensity Modulated Radiation Therapy or for other techniques which require very small field sizes. Even for small fields, where the shape of a profile is becoming similar to the Gaussian curve, the proposed method allows a proper assignment of boundaries between high and low gradient regions.

Conflict of interest

None declared.

Financial disclosure

None declared.