Costs of Clock-Environment Misalignment in Individual Cyanobacterial Cells

Abstract

Circadian rhythms are endogenously generated daily oscillations in physiology that are found in all kingdoms of life. Experimental studies have shown that the fitness of Synechococcus elongatus, a photosynthetic microorganism, is severely affected in non-24-h environments. However, it has been difficult to study the effects of clock-environment mismatch on cellular physiology because such measurements require a precise determination of both clock state and growth rate in the same cell. Here, we designed a microscopy platform that allows us to expose cyanobacterial cells to pulses of light and dark while quantitatively measuring their growth, division rate, and circadian clock state over many days. Our measurements reveal that decreased fitness can result from a catastrophic growth arrest caused by unexpected darkness in a small subset of cells with incorrect clock times corresponding to the subjective morning. We find that the clock generates rhythms in the instantaneous growth rate of the cell, and that the time of darkness vulnerability coincides with the time of most rapid growth. Thus, the clock mediates a fundamental trade-off between growth and starvation tolerance in cycling environments. By measuring the response of the circadian rhythm to dark pulses of varying lengths, we constrain a mathematical model of a population’s fitness under arbitrary light/dark schedules. This model predicts that the circadian clock is only advantageous in highly regular cycling environments with frequencies sufficiently close to the natural frequency of the clock.

Introduction

Synechococcus elongatus PCC 7942 (S. elongatus) is a photosynthetic, unicellular cyanobacterium that has been extensively used as a model system for the study of circadian rhythms (1, 2). Each cell contains a remarkably precise oscillator based on the kai genes (3). KaiA, KaiB, and KaiC work together to generate near-24-h rhythms in phosphorylation of the core clock protein KaiC, forming a biochemical oscillator that can be reconstituted in vitro (4, 5). In the cell, rhythmic changes in KaiC signal through histidine kinases to exert genome-wide control of transcription (6, 7, 8) and metabolism (9, 10).

Much is known about the behavior of this system under conditions of constant illumination, where it is easiest to observe robust cell-autonomous oscillations (11, 12, 13, 14, 15). However, under constant conditions, S. elongatus can grow robustly even without a functioning clock (13, 16), which led us to suspect that we could reveal the importance of the clock by monitoring the physiology of cells under conditions that fluctuate between light and dark. Landmark work by the Johnson lab established that fitness defects occur in fluctuating environments with schedules that do not match the circadian clock period, but the underlying mechanisms for these effects are still unclear (1, 16). Because environmental challenges may reveal heterogeneous behavior in a population, we designed a microscopy system that allowed us to quantitatively measure the clock state, growth rate, and cell division in individual cyanobacterial cells over several days in an environment that fluctuated between light and dark (Fig. 1; Movie S1 in the Supporting Material). Using these single-cell measurements, we then developed a phenomenological model in which the growth rate and the probability of surviving the night are determined by the current clock state, which is itself updated after each light-dark transition. This model provides a framework for calculating the impact on organismal fitness from a circadian clock driven by an arbitrary fluctuating environment.

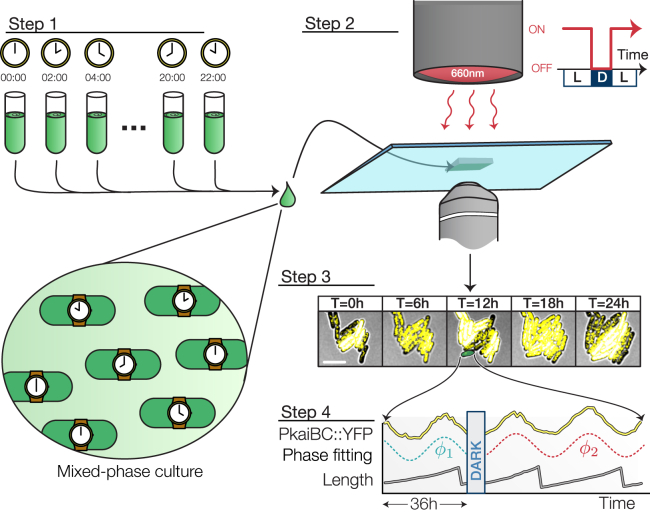
Figure 1.

Experimental setup. Twelve populations were entrained under staggered 12 h:12 h L/D regimes and combined into a single experiment. A multiplexed measurement of phase shift or growth rate modulation was achieved by exposing the mixed-phase population to a single pulse of darkness (scale bar, 5 μm). Fluorescence and brightfield micrographs recorded every hour were used to extract every cell’s physiological parameters (e.g., length and clock reporter). To see this figure in color, go online.

Materials and Methods

Cyanobacterial strains

The clock phase was tracked using the yfp-ssrA reporter strain wild-type (WT)/JRCS35 (MRC1006), which carries a PkaiBC::eyfp-ssrA fluorescence reporter. The JRCS35 plasmid integrated PkaiBC::eyfp-ssrA into NS2 (neutral site 2) with a kanamycin resistance cassette (12). To create the ΔkaiBC strain (MRC1009), the WT/JRCS35 strain was transformed with plasmid MR0091, replacing the endogenous kaiBC locus (from the kaiB start codon to ∼200 bp upstream of the kaiC stop codon) with a gentamicin resistance cassette. The KaiBC overexpression strain (MRC1010) was created by transforming the WT/JRCS35 strain with plasmid MR0095, integrating kaiBC under control of the isopropyl β-D-1-thiogalactopyranoside (IPTG)-inducible trc promoter into neutral site 1 (NS1).

Culture conditions

For all experiments, cyanobacterial strains were grown in BG11 liquid medium supplemented with 20 mM HEPES (pH 8.0) at 30°C. To create the mixed-phase population, 200 μL of a cell culture grown under continuous illumination (LL) of 75 μmol photons m⁻²s⁻¹ was pipetted into each well of a black (opaque) 96-well plate. For experiments that included either kaiBC-null or kaiBC-overexpression strains, the strains and WT cells were grown in separate wells within the same plate to expose them to the same culture and illumination conditions. For the kaiBC-overexpression experiment, the medium was supplemented with IPTG at a final concentration of 1 mM within the plate. A custom-made Arduino-driven LED array was used to illuminate each well (Arduino, http://www.arduino.cc). Each output pin of the Arduino supplied 23 mA of current to eight red LEDs, and each pin corresponded to one column of the 96-well plate. The Arduino was programmed to generate 2 days of symmetric light/dark (LD) conditions (light conditions: 10 μmol photons m⁻²s⁻¹ (23 mA); dark conditions: 0 mA) preceded by at least 12 h of continuous light conditions so that each population was subjected to two entrainment cycles. Light levels were maintained at ∼10 μmol photons m⁻²s⁻¹ for an additional 24 h before cells were collected for microscopy. All culture wells of the entrained 96-well plate were collected and combined in a single test tube. The distribution of phases produced by this protocol is broad, but is not precisely uniform (Fig. S1). The deviations from a uniform distribution might be caused by differential growth of the wells subjected to differently phased cycles, or mild phase shifts caused by transferring the cultures to the microscope.

For experiments that included kaiBC-null or kaiBC-overexpression strains, the cells were combined in equal proportions as determined by OD750 measurements after entrainment. This provided a mixed population of WT and mutant cells within a single experiment, as shown in Movies S3 and S4.

Time-lapse microscopy

The mixed-phase culture was diluted to an OD750 of 0.1 using BG11 medium and 1 μL of the cell solution was pipetted onto a glass-bottom six-well plate (MatTek, Ashland, MA). A small (1 mm × 1 mm × 0.5 mm) pad of BG11 + 2% low-melting-point agarose (LMPA) was placed atop the cell suspension. Then, 10 mL of liquid BG11 + 2% LMPA that had been cooled to 37°C was poured inside the well to cover the LMPA pad. For the kaiBC-overexpression experiment, the BG-11/agar mixture was supplemented with IPTG at a final concentration of 1 mM before it was poured into the well. Once the LMPA solidified, the six-well plate was moved to a motorized microscope held at 30 C (IX71; Olympus, Center Valley, PA) and fluorescence and brightfield images were recorded every 60 min.

Control of the microscope was carried out using μManager (17). Every 60 min, a motorized microscope stage (Prior, Rockland, MA) visited 24 preassigned locations containing at least 10 cells, and brightfield (exposure: 100 ms), chlorophyll (exposure: 200 ms; excitation: 501 nm; emission: 590 nm), and YFP fluorescence (exposure: 2 s; excitation: 501 nm; emission: 550 nm) micrographs were then recorded using an EMCCD camera (Luca; Andor, Belfast, UK).

The SimpleAutofocus routine provided by the μManager suite used the chlorophyll autofluorescence of the population to identify the focal plane before each set of micrographs was recorded. A collimated LED light (wavelength: 625 nm; Thorlabs, Newton, NJ) was used to illuminate the cells throughout the experiment and a microcontroller (Arduino) controlled the output level of the LED light (light conditions: ∼10 μmol photons m⁻²s⁻¹ (23 mA); dark conditions: 0 mA).

Single-cell analysis and phase information extraction

The outline of every cell in the brightfield image was traced using a watershed algorithm and the physiological properties of each cell (length and YFP fluorescence intensity) were recorded. The CellTracker image-processing (18) suite was then used to reconstruct the lineage history of each cell, assigning an age to each pole and computing the instantaneous elongation rate.

The complete lineage of every cell present at the onset of the dark pulse was reconstituted and the YFP signal of each lineage was then subjected to a Fourier transform. The (complex) factor multiplying the 24 h frequency component (henceforth called c₂₄) was computed using the last 36 h of data prior to the dark pulse. The phase of the cell before the dark pulse (called φ₁ in the main text) was found by extracting the angle of c₂₄ using the arctan2 branching function, i.e., φ = arctan2(imag(c₂₄), real(c₂₄)).

To find the phase of the clock after the dark pulse (φ₂), the YFP intensity of the old-pole lineage (i.e., the lineage that inherited the oldest pole after each division) was extracted and the phase information was found by computing the angle of the c₂₄ factor of the YFP signal. After the dark pulse, only the first 36 h of data were considered (to ensure that c₂₄ existed). Non-oscillatory cells (such as the ΔkaiBC and kaiBC-overexpression strains) were identified by monitoring intensity traces that varied by <30% over the duration of the experiment.

Since the production and maturation rate of YFP proteins have a finite timescale that is determined, among other factors, by the growth rate of the cells, the clock phases we report are shifted by 4 h relative to the extracted peak YFP phase to bring them more closely in line with the estimated peak transcriptional activity. This value is similar to other values reported in the literature (12).

Growth arrest probability

We identified arrested cells by tracking the cumulative increase in the total length of the cell after the dark pulse. If the total length of a cell and its progeny increased by <33% after 24 h, the cell was scored as arrested. Because of the altered morphology of the kaiBC-overexpression strain, we used an alternative test for these cells: if the relative elongation rate was <1%/h over the 4 h after the dark pulse, the cell was scored as arrested.

Elongation rate measurements

The elongation rate was computed from six experimental replicates of mixed-phase populations grown under constant light conditions. Cells were grown for a total of 36 h under constant light conditions and the last 12 h (T = 24–36 h) were used to compute the elongation rate. The instantaneous elongation rate was found by computing the relative increase in cell size between two consecutive frames. Specifically,

$$g=\frac{l_{t+1}-l_t}{l_t}\sim \frac{d\mathit{log}\left(l\right)}{dt}$$

The growth rate g(t) was then binned according to the cell’s circadian phase and averaged over a 1-h window. A three-point moving average was used to smooth the data used to derive the phenomenological model (see Fig. 3 B).

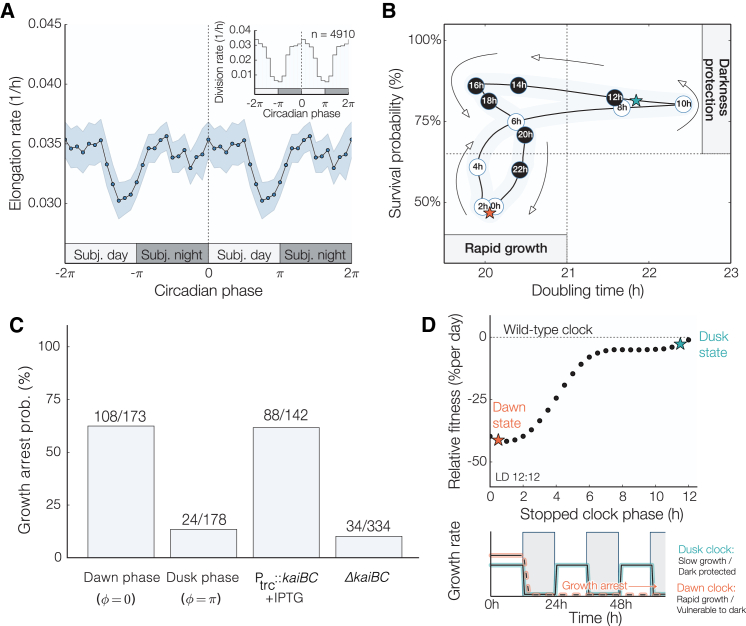
Figure 3.

Clock-dependent fitness trade-offs. (A) Elongation rate measurements (mean ± 3 × SEM) for cells grown under constant light conditions display a transient decrease at subjective dusk. Inset: clock-dependent division rates computed from 4910 individual division events. Elongation and division rate measurements are double plotted to illustrate their periodicity. (B) Phenomenological model of the time evolution of the circadian fitness trade-off. The subjective circadian time is inscribed inside each data point to show how a cell’s phenotype cycles between rapid growth and a starvation-protected state. The properties of the dusk and dawn phenotypes are marked with cyan and orange stars, respectively. (C) Growth arrest probabilities for WT and kaiBC mutant cells after an 18-h pulse of darkness. (D) Comparison between a clock that stopped at dusk (cyan) and one that stopped at dawn (orange). Since no fixed daytime strategy exhibits superior fitness at all times, the performance of stopped-clock daytime strategies is lower compared with that of a circadian phenotype under circadian (12 h:12 h LD) environments. Although growth-arrest and elongation rates were measured for all circadian times, physiological states corresponding to subjective night (circadian times between 12 and 24 h) were excluded from this analysis because they are unattainable during the night in cycling 12 h:12 h LD conditions. Bottom: cells in a dusk-like phenotypic state grow more slowly but are protected against the dark. Cells in a dawn-like phenotypic state grow more rapidly but are vulnerable to darkness. See also Fig. S2. To see this figure in color, go online.

Robustness and phase resetting

The resetting index and the D5 phase shift (Fig. S3 B) were extracted from 5-h and 9-h phase-shift experiments (see Fig. 4, E and G). Graphically, the D5 phase-shift index measures how much the phase of a cell subjected to a 5h dark pulse deviates from an unperturbed cell, a quantity that is measured as the vertical distance between φ₂ and the φ₁ = φ₂ dashed blue line in Fig. 4 E. The resetting index, on the other hand, measures how similar a phase shift is to a complete reset by the 12h dark pulse, quantified as the distance between individual data points and the φ₂ = π dashed red line in Fig. 4 G. The data were binned over a 1-h window and noise was smoothed out using a three-point moving average.

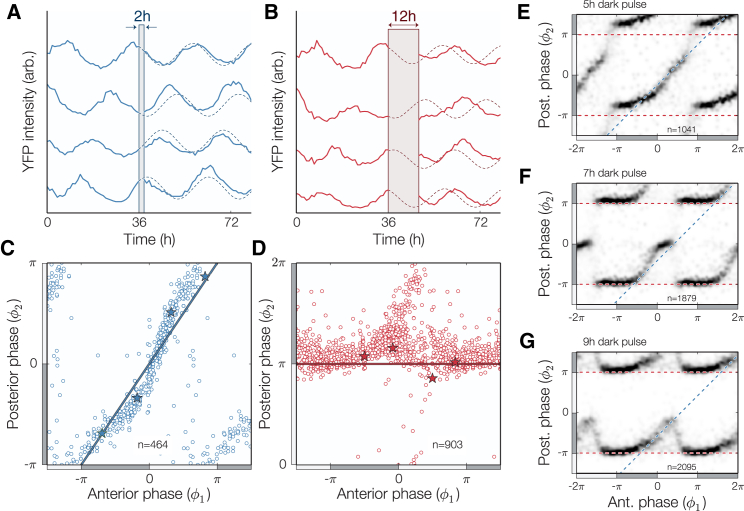
Figure 4.

Single-cell clock response to dark-pulse perturbations. (A and B) Individual traces (P_kaiBC::eyfp-ssrA) show phase shifts caused by weak (2-h dark pulse) and strong (12-h dark pulse) perturbations. (C and D) Phase resetting of individual cells grown under constant light conditions for 36 h before being subjected to a 2-h (blue) or 12-h (red) pulse of darkness, with specific examples from panels (A) and (B) highlighted (^∗). Two distinct resetting behaviors are observed: a robust response (blue line in C) or a full phase reset (red line in D). (E–G) Density plot showing the phase response to 5-h, 7-h, and 9-h dark pulses, with resetting that switches between no response and full reset (blue and red dashed lines, respectively). Cells were grown under constant light conditions for 36 h before each dark pulse. In all panels, the location of subjective day (night) is marked with a light (dark) gray bar. See also Fig. S3. To see this figure in color, go online.

Fitness advantage measurement

To measure the performance of various clock periods under a sustained 12 h:12 h LD schedule, it was necessary to compute 1) the probability μ that a cell would enter a state of growth arrest after the 12-h dark pulse, and 2) the number of cell doublings that happened during the 12 h of light. We determined μ by using f_12h^P to find the phase of the cell at nightfall, to identify the survival probability at that phase according to Fig. 2 D (that is, we assumed for the sake of simplicity that growth arrest occurred at the same rate for 12 h and 18 h nights). We determined the number of cell doublings per day by first using f_12h^P to identify the phase at the beginning of the day. We then advanced this phase variable through the light portion of the day to compute the average elongation rate $\overline{g}$. The historical fitness (19) was used to quantify the fitness of the population at a given period. The historical fitness differs from conventional fitness measurements in that it considers the cumulative (or integrated) number of doublings of a single cell over its complete life history. Consequently, the historical fitness of a population will contain two factors: ${\left(1-\mu \right)}^{\lfloor T/2\rfloor }$, which accounts for the fraction of the population that enters a state of growth arrest during the dark pulse, and $e^{\overline{g}T/2}$, which tracks the number of cell doublings that happen under light conditions.

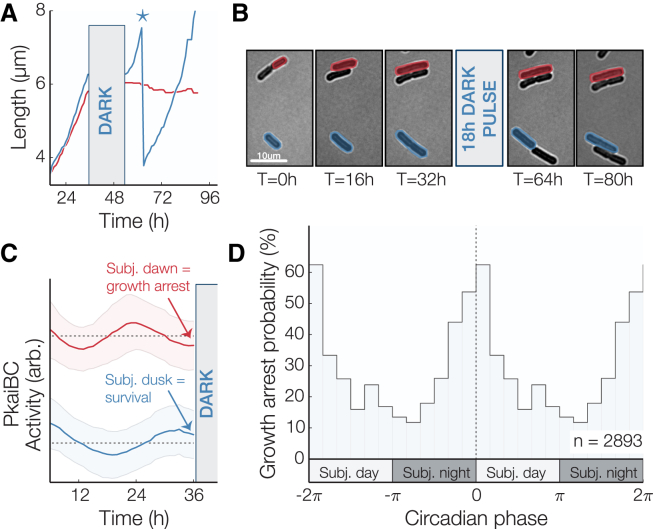
Figure 2.

Clock-dependent growth arrest after unexpected darkness. (A) Individual growth curves showing survival (blue) and growth arrest (red) of two neighboring cells (^∗ indicates cell division). (B) Example of cells that entered a state of arrested growth after an 18-h pulse of darkness. Cells remained dormant after >36 h in constant light. (C) Average ± SD of the predarkness clock reporter signal for surviving (blue) and arrested (red) populations. An arbitrary vertical shift has been added to the surviving/arrested subpopulations to assist in comparison. (D) Phase-dependent probability of growth arrest for cells grown under constant light conditions for 36 h before being subjected to an 18-h pulse of darkness (n = 2983). The maximal growth arrest probability occurs when a dark pulse falls near subjective dawn (transition between subjective night and day). The growth arrest probability is double plotted to illustrate its periodicity. See also Fig. S1. To see this figure in color, go online.

The historical fitness for a simulation that lasted for a time T for a given clock period P was given by the product of these two factors:

$$H_P={\left(1-\mu \right)}^{\lfloor \frac{T}{2}\rfloor }{e}^{\frac{\overline{g}T}{2}}$$

for a simulation that lasted for a time T for a given clock period P. The values of H_P were plotted relative to H_24h.

Results and Discussion

A subset of cells with misaligned clocks do not survive the night

Some photosynthetic organisms that rely exclusively on light for growth are known to halt DNA synthesis and enter a dormant state (20), or even die (21), in the absence of light. Since control of gene expression in the dark and consumption of energy metabolites are both under active control of the circadian clock in cyanobacteria (9, 10, 22), we hypothesized that unanticipated nightfall at clock times when energy reserves are low and metabolic rates are high could have deleterious effects. To test this hypothesis, we exposed a mixed-phase population (Fig. S1) to a period of darkness corresponding to a long night (18 h). Surprisingly, we found that a subset of cells experienced a catastrophic growth arrest after the simulated night: growth of these cells ceased and did not resume even after 36 h of subsequent light exposure (Fig. 2, A and B; Movie S2). Importantly, this effect required prolonged darkness—we did not observe arrested cells after 5-h dark pulses.

To determine whether the ability to tolerate darkness-induced starvation is influenced by the circadian clock, we assigned a clock time to each cell by measuring rhythms in a fluorescent reporter of clock gene expression before the dark pulse. We found that the fraction of cells that failed to resume growth was strongly enriched for cells with clock states corresponding to the early day, when nightfall is not anticipated. Indeed, the probability of dark-induced growth arrest oscillated with clock time, reaching a minimum at subjective dusk when nightfall is expected to occur (Fig. 2, C and D). Thus, the ability of individual S. elongatus cells to tolerate prolonged starvation is clock dependent, with cells displaying enhanced starvation tolerance when the onset of darkness coincides with subjective dusk.

The clock allows rapid growth early in the day

In many microbes, stress tolerance is generally anticorrelated with growth rate (23). A classic example is the bacterial stringent response to amino acid starvation: mutants that cannot mount the stringent response can grow faster than the WT as nutrients are being depleted, but these mutants cannot survive conditions of prolonged starvation (24, 25). We therefore asked whether the rhythmic dark tolerance we observed in cyanobacteria is similarly linked to a change in growth rate during the circadian cycle.

By tracking morphological changes in single cells, we assigned an instantaneous growth rate to each cell and identified cell-division events. We found that subjective dusk, the time when starvation resistance is highest, is also a time of slowed biomass incorporation (Fig. 3 A). This time of slowed growth approximately coincides with the previously reported (26, 27) clock-controlled inhibition of cell division (Fig. 3 A, inset). This reduction in cell growth and division is anticorrelated in time with the vulnerability of cells to darkness, suggesting the existence of a fundamental trade-off between the capacity for rapid growth and active division, and the ability to tolerate starvation (Fig. 3 B). Interestingly, cells early in the subjective night (i.e., circadian time between 14 and 18 h) were able to both grow rapidly and survive prolonged darkness. This indicates that darkness protection is not caused entirely by the instantaneous growth rate. One possible explanation for this is that a key determinant of darkness protection is not slow growth per se, but the accumulation of starvation-tolerance factors that are produced at subjective dusk in anticipation of a prolonged darkness that transiently persists in the cell after rapid growth resumes. A possible molecular mechanism for this effect involves glycogen storage: glycogen has been shown to accumulate during the portion of the cycle in which we find slowed growth (10), potentially protecting the cell against starvation. This is in accord with the general phenomenon of phenotypic memory (28), in which previous adaptations are retained to confer an adaptive phenotype after the source of stress or stimulus has been removed.

To determine whether these changes in dark tolerance are indeed caused by signaling from the circadian clock, we repeated these experiments using cells with the kaiBC genes either deleted or overexpressed under the control of an IPTG-inducible promoter. Based on previous studies, we expected deletion of kaiBC to result in arrhythmic high expression of dusk-expressed genes and elevated glycogen levels, mimicking a dusk-like state (3, 10). Conversely, we expected overexpression of kaiBC to cause arrhythmia while repressing dusk genes (29).

Consistent with the expectation that their physiology would be dusk-like, we found that the kaiBC-null cells failed to efficiently undergo cytokinesis, and some cells exhibited filamentous growth under the microscope (Movie S3). Further, the kaiBC-null mutant was quite dark tolerant and showed a slightly lower elongation rate, but a much higher survival rate, independently of the timing of darkness (Figs. 3 C and S2). In contrast, kaiBC overexpression made the cells highly vulnerable to a light-dark transition, and the majority of these cells did not survive our dark-pulse treatment (Fig. 3 C). When cells were grown on the microscope, kaiBC overexpression led to some cell death before the dark pulse, and it also led to a surprising morphological defect: the cytoplasm appeared to expand at a rate that was not properly balanced by elongation, causing the cells to lose their rod-like shape (Movie S4).

We used these growth and survival data to calculate the expected fitness for a simulated population of cells with a constant growth rate and constant dark tolerance, according to the inverse relationship we observed for the WT. This calculation predicted that oscillating growth would outperform all fixed daytime growth strategies in 12 h:12 h LD cycles (Fig. 3 D). Recent theoretical work suggested that organisms typically optimize evolutionary trade-offs by adopting a compromise phenotype that interpolates between archetypes that represent the extreme demands on the system (30). Our findings represent a dynamical version of this phenomenon in which cyanobacteria are able to achieve higher fitness by cycling between incompatible states of growth and starvation protection.

The response of single cells to dark pulses is nearly all-or-none

Having characterized the impact of a pulse of prolonged darkness on clock-dependent growth, we sought to determine how the clock state in single cells is reset by pulses of darkness, so that we could build a model describing how cyanobacterial cells grow in arbitrary fluctuating environments. External cues, such as dark pulses, cause the cell to reset its phase in an attempt to bring the clock into alignment with the environment (31, 32). This phenomenon has been studied using bulk cultures of cyanobacteria (10, 33, 34), but such population-wide measurements may mask important features such as loss of coherence and amplitude attenuation because they are based on signals that represent the average of oscillations coming from many independent cells.

We thus exposed populations of hundreds of cells in a spectrum of clock states to dark pulses of varying lengths and determined the clock phase both before (φ₁) and after (φ₂) the dark pulse. When the dark pulse was brief (2 h), cells at all clock times were largely resistant to the perturbation and we observed only small phase changes (Fig. 4, A and C). In contrast, long dark pulses corresponding to the length of the night (12 h) were capable of effecting a nearly full reset, such that most cells were synchronized to the onset of darkness (Fig. 4, B and D).

Surprisingly, dark pulses of intermediate length produced a discontinuous combination of these responses. When the clock time was far from subjective dusk, the response of the system to a dark pulse was very small (Fig. 4, E–G, data near the blue 1:1 lines). In a critical range of clock times, however, the response changed abruptly so that the system strongly synchronized to the onset of darkness. The range of times when this nearly complete reset occurred grew as the dark pulse became longer (Fig. 4, E–G, data near the φ₂ = π red lines). Biochemical studies of the Kai proteins have correlated changes in metabolite levels (such as the ATP/ADP ratio) during the night with the ability of the circadian clock to reset its phase (31, 35). The change in resetting behavior we observed here for intermediate-length dark pulses may be caused in part by a timescale associated with depletion of key metabolites in the cell.

This abrupt change from insensitivity to strong sensitivity as the clock time progresses may represent an optimal strategy for dealing with unexpected fluctuations in the environment, as it could enable cells to ignore short dark pulses at times of day when they are unlikely (Fig. S3 B). This behavior would be difficult to detect without high-resolution, single-cell measurements because averaging over many cells with slightly different phases would tend to blur out the true sharpness of the response (Fig. S3 C).

Mathematical model of fitness in fluctuating environments

We combined our measurements of clock-dependent growth and darkness-induced growth arrest (Fig. 5 A) with darkness-induced clock resetting to build a mathematical model (36) of cyanobacteria growing under arbitrary schedules of light and dark. We first asked how successfully the circadian clock could synchronize to a 24-h day (12 h:12 h LD) if the clock period were altered. In particular, the phase-resetting information obtained in Fig. 4, E–G, was used to generate the mapping for different clock periods. The relationship between φ_i and φ_i+1 was given by the recurrence relation φ_i+1 = f_n^P(φ_i), where the map f_n^P(φ_i) describes the phase at dusk after a dark pulse of duration n subjected to a clock of period P. To determine the precise shape of f_n^P(φ_i), we interpolated the phase-resetting curves by assuming that the effect of a dark pulse of the phase would scale with the period of the clock (for instance, a 5-h dark pulse would have the same effect on a 24-h clock that a 10-h dark pulse would have on a 48-h clock). We used the shift between the phase before (φ_i) and after (φ_i+1) to construct an expression for f_n^P that would accurately capture the features of the 5-h, 7-h, 9-h, and 12-h dark pulse measurements. In particular, we used the “after” expression to model f_n^P:

$$f_n^P\left({\varphi }_{\mathit{i}}\right)=\{\begin{array}{ll}\pi \hfill & \text{if}\frac{6\pi \left(n-9\right)}{P}<{\varphi }_1<\frac{\pi }{\mathit{2}}\text{or}{\varphi }_1>\frac{6\pi \left(n-1\right)}{P}\hfill \\ {\varphi }_{\mathit{i}}-\frac{6\pi \left(n-1\right)}{P}+A·\mathit{sin}\left({\varphi }_{\mathit{i}}-\frac{6\pi \left(n-1\right)}{P}\right)\hfill & \text{otherwise}\hfill \end{array},$$

where A is given by min(n/P, π/4). Plots of this function for various dark pulse lengths are shown in Fig. S4.

Figure 5.

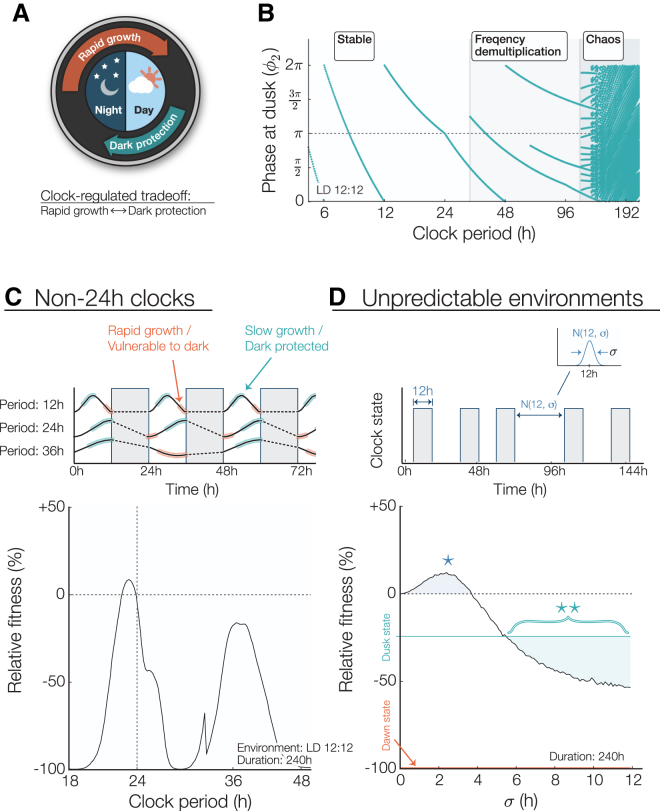
Mathematical model of clock-regulated growth under noisy and period-mismatched schedules. (A) Circadian trade-off between rapid growth and stress protection. Each phenotype occupies a specific region of the circadian cycle. (B) Map showing phase entrainment, or lack thereof, under 12 h:12 h LD for different clock periods. Standard conditions would result in a phase at dusk equal to π. Clock periods longer than 40 h result in faulty phase tracking caused by frequency demultiplication, and those longer than 100 h lead to chaos. (C) Top: effect of a noncircadian clock period. The 24-h clock is stable and accurate under 12 h:12 h LD environments: a 12-h clock is robustly entrained but is unable to accurately anticipate nightfall, whereas the entrainment of a 36-h clock is unstable and leads to an incorrect nightfall prediction 50% of the time. Bottom: the historical fitness H_P of clock mutants with a period P subjected to a 12 h:12 h LD circadian environment for 240 h is compared with the historical fitness H_24h of a 24-h clock (relative fitness = $H_P/H_{24h}$). The fitness advantage is greatest when the clock and the environment are in constructive resonance (i.e., 24-h and 36-h clocks, which leads to a correct nightfall prediction 100% and 50% of the time, respectively) and lowest when they are in destructive resonance (i.e., 18-h, 30-h, and 48-h clocks, which results in nightfall occurring during the subjective morning). (D) Top: fitness under 12-h nights but variable day lengths. Day durations are normally distributed with a 12-h average and a variance σ. Bottom: the presence of a low level of noise in the day-length distribution increases fitness for WT clocks (region highlighted with an ^∗). As the day length becomes more unpredictable (σ > 5 h), an always-protected dusk state is more beneficial than a circadian phenotype (^∗∗ region). Fitness is the average of 10,000 simulations. To see this figure in color, go online.

Using this expression for f_n^P, we interpolated from our measured dark-pulse response data to find a stable recurrence relation corresponding to clock entrainment by plotting the value(s) of φ_i that converged for i ≫ 1 for a 12-h dark pulse each clock period (Fig. 5 B). When the clock period is <40 h, the model predicts that the clock will stably entrain to the environment, but a period mismatch will result in an entrained phase that is generally incorrect (i.e., subjective dusk does not fall near actual nightfall). For longer periods, the oscillator entrains to subharmonics of the environmental period, and for still longer periods, chaotic dynamics can occur.

Next, to investigate how circadian misalignment would affect the long-term fitness of a population of cells in the model, we used the growth and survival functions measured in Figs. 1 and 2 to extract the fitness of a single cell under a given light/dark regime. By assuming that growth occurs only under light conditions and the growth arrest probability is dependent on the phase at the onset of darkness, we calculated the growth and survival of cells with a range of clock periods and found that the model predicts that the long-term fitness is highest when the clock period is near 24 h. This result indicates that the measured effects on growth and darkness tolerance may constitute sufficient selective pressures to explain the precision of the circadian clock. However, when the clock period is far from 24 h, large fitness costs can occur because the clock synchronizes inappropriately and consequently the morning clock state occurs at nightfall every day (Fig. 5 C). These model results show trends similar to those previously revealed in competition experiments by the Johnson lab (1, 16): a long-period (30 h) clock mutant is severely disadvantaged relative to the WT in 12 h:12 h LD cycles, and a short-period (23 h) mutant is more mildly affected. Our model calculation shows an asymmetry in fitness as a function of the clock period, such that periods slightly shorter than 24 h outperform longer periods. This follows from an asymmetry in the fitness cost associated with the window of protection against nightfall. If the clock period is slightly short, the protected window arrives early and the cost is unnecessarily slow growth. However, if the clock period is long, the window of protection is delayed, causing the much more severe cost of cell death.

How does the circadian rhythm optimize the fitness of a cell? In our model, cells must grow slowly near nightfall to avoid the possibility of metabolic catastrophe when darkness falls. The clock enforces this growth slowdown late in the day while still allowing cells to grow rapidly in the morning. This suggests that the advantages conferred by a circadian clock are a result of a finely tuned match with the temporal structure in the environment. Such a strategy might become detrimental in unnatural conditions where the environment cycles irregularly between light and dark. To test this hypothesis, we simulated cyanobacteria growing in days with random variation by selecting the duration of each light period from a normal distribution with a mean of 12 h. The model predicts that when the variability in the light/dark schedule exceeds σ = 5 h, cells that employ an arrhythmic, slow-growing strategy similar to deletion of the kaiBC genes will become more successful than the WT (Fig. 5 C). Surprisingly, our model predicts that WT cells may grow faster and achieve a higher fitness in the presence of some timing variability (Fig. 5 C, σ < 3.75 h) in the duration of the day.

Conclusions

Despite the ubiquity of circadian clocks, it has remained challenging to pinpoint the benefits of a rhythmic physiology (37). Our ability to detect the costs and benefits of clock function at the single-cell level provides a framework to address this issue. We found that considerable fitness penalties result from the failure of cells to correctly predict the withdrawal of energy associated with nightfall. We thus conclude that a major function of the cyanobacterial circadian clock is to provide a safeguard against darkness-induced starvation, giving the cell permission to grow rapidly early in the day.

A possible explanation for the failure of a subset of cells to survive the night is that these cells were unable to properly manage their energy consumption over the length of the night. An analysis of microarray expression data for S. elongatus (8) provides some mechanistic insight into the origin of clock-dependent starvation tolerance (Table S1). Expression of genes involved in photosynthesis and the biosynthesis of essential compounds peaks at clock times corresponding to the early morning, suggesting that the clock tunes metabolism to allow rapid growth early in the day. On the other hand, genes involved in DNA replication, DNA repair, and metabolism under nutrient limitation peak late in the day, suggesting a clock-dependent activation of mechanisms that enable cells to tolerate nightfall. Furthermore, we previously found that the clock controls the storage and consumption of energy-storage metabolites, with reserves of glycogen being lowest near the beginning of the day (10). Coupled with the gene-expression data, our results suggest that proper temporal regulation of energy storage and circadian regulation of growth and division in anticipation of dusk may play a critical role in allowing a cell to survive the night.

These results suggest an alternative to the hypothesis that circadian rhythms evolved primarily as a means to anticipate and avoid light-induced photodamage, i.e., a flight-from-light scenario. If our experimental conditions approximate the challenges faced by the ancient ancestors of modern cyanobacteria, the daily threat posed by an extended time of resource limitation during the night may have been a major selective pressure on primordial clock systems. Thus, a key function of the circadian clock would be to orchestrate physiology during the day to prepare for the coming night, i.e., a prepare-for-night scenario. We note that our microscopy growth conditions may well intensify the stresses associated with darkness relative to growth in flasks, allowing us to observe growth defects after a single LD cycle, whereas liquid-culture studies require many days before measurable effects emerge (1, 16).

Our dark-pulse experiments show that the circadian clock has robustness properties that allow it to track the 24-h cycle in the environment even in the face of random fluctuations. The flip side of this robustness is a remarkable fragility in environments that fail to have a 24-h periodicity. Although such environments are unlikely to occur in nature, the poor performance of clocks in these conditions may be relevant to other organisms that display a clock control of cellular divisions (38, 39), and to the irregular work schedules and patterns of light exposure that are typical of modern society.

Author Contributions

G.L. and M.J.R. designed the study and wrote the manuscript. G.L. and J.C. carried out the experiments. G.L. analyzed the data.

Editor: Reka Albert.

Supporting Material

Movie S1. Single-Cell Microscopy and Mixed-Phase Experiments

Time-lapse images showing WT cells in multiple phases growing in the same field of view. Production of yellow fluorescent proteins is under the control of the PkaiBC clock-dependent promoter.

Movie S2. Dormancy after Prolonged Darkness

Movie showing WT cells being subjected to an 18-h pulse of darkness. White arrows indicate which cells entered a state of arrested growth.

Movie S3. Response of ΔkaiBC Mutants to an 18-h Dark Pulse

Movie showing a mixture of WT and ΔkaiBC cells being subjected to an 18-h pulse of darkness. A larger fraction of ΔkaiBC cells display filamentous morphology compared with WT cells. ΔkaiBC cells at the beginning of the movie are indicated by red arrows.

Movie S4. Response of kaiBC-Overexpression Mutants to an 18-h Dark Pulse

Movie showing a mixture of WT and kaiBC-overexpression cells being subjected to an 18-h pulse of darkness. kaiBC-overexpression cells display an abnormal rounded morphology compared with WT cells. P_trc::kaiBC cells at the beginning of the movie are indicated by blue arrows.