Diffusion Tensor Analysis by Two-Dimensional Pair Correlation of Fluorescence Fluctuations in Cells

Abstract

In a living cell, the movement of biomolecules is highly regulated by the cellular organization into subcompartments that impose barriers to diffusion, can locally break the spatial isotropy, and ultimately guide these molecules to their targets. Despite the pivotal role of these processes, experimental tools to fully probe the complex connectivity (and accessibility) of the cell interior with adequate spatiotemporal resolution are still lacking. Here, we show how the heterogeneity of molecular dynamics and the location of barriers to molecular motion can be mapped in live cells by exploiting a two-dimensional (2D) extension of the pair correlation function (pCF) analysis. Starting from a time series of images collected for the same field of view, the resulting 2D pCF is calculated in the proximity of each point for each time delay and allows us to probe the spatial distribution of the molecules that started from a given pixel. This 2D pCF yields an accurate description of the preferential diffusive routes. Furthermore, we combine this analysis with the image-derived mean-square displacement approach and gain information on the average nanoscopic molecular displacements in different directions. Through these quantities, we build a fluorescence-fluctuation-based diffusion tensor that contains information on speed and directionality of the local dynamical processes. Contrary to classical fluorescence correlation spectroscopy and related methods, this combined approach can distinguish between isotropic and anisotropic local diffusion. We argue that the measurement of this iMSD tensor will contribute to advance our understanding of the role played by the intracellular environment in the regulation of molecular diffusion at the nanoscale.

Introduction

Biomolecule dynamics at the subcellular level is a master regulator of cell function and fate. In fact, in the highly compartmentalized 3D cell environment, signaling processes are regulated by the precise spatiotemporal control of molecular diffusion and/or flow (1, 2). Communication and transmission of biochemical signals depend on the complex interplay between the spatiotemporal pattern of molecule-specific interactions (3, 4) and the physical structure of the cellular components that confine and can actually locally guide molecular motion (5, 6). As a result, there is much interest in acquiring detailed knowledge of the mechanisms driving molecule dynamics at the nanoscale (7). Unfortunately, we lack experimental approaches that can probe these phenomena with the required spatiotemporal resolution within cells. Single-particle tracking (SPT) approaches could in principle provide an answer (8, 9, 10). Indeed, the trajectories of single molecules represent the ideal quantitative description of molecular motion in space and time (e.g., by means of the derived mean-square displacement (MSD)). Unfortunately, the applicability of SPT-based approaches to the cell environment is hampered by several limitations, including 1) the need to produce, purify, and label single molecules with suitably high signal/noise marker particles (e.g., gold nanoparticles or semiconductor quantum dots); 2) steric-hindrance effects introduced by the label (it was shown that single-molecule measurements can also be performed with small organic fluorescent tags or fluorescent proteins (11, 12), but at the expense of the observation times accessible); and 3) the large number of trajectories needed to satisfy statistical requirements.

In this context, fluorescence correlation spectroscopy (FCS) (13, 14, 15) is emerging as a valid alternative actually capable of providing information on single-molecule dynamics without dwelling on any of them individually. As a consequence, this technique is usable with relatively dimly fluorescent and densely labeled molecules, as is the case for genetically encoded fluorescent proteins expressed in living cells. Importantly, FCS yields very good statistics in a fairly limited observation time. In fact, several different FCS-based approaches showed the possibility of measuring the same quantities accessible by SPT (e.g., the MSD) with no need to extract the individual molecule trajectories. Molecular displacements were calculated directly from the FCS curve (16) or measured by gradually increasing ((17, 18)) or decreasing (by stimulated emission depletion (3)) the observation spot. Unfortunately, these single-point (or “local”) approaches are not sensitive to the directionality of motion; in other words, they fail to detect “where” the molecules are going. In this context, spatiotemporal image correlation spectroscopy (STICS) represents an interesting alternative, since it is in principle sensitive to the directionality of motion, e.g., in the case of fluxes (19). Moreover, STICS can be used to measure the molecular MSD in the case of diffusion (20, 21, 22) and can be applied to small regions of interest (ROIs) to map molecular dynamics (23). Unfortunately, the minimal size of the ROI to be analyzed must be significantly larger than the optical resolution to properly sample particle displacements and avoid underestimating particle motion. Consequently, the information on molecular dynamics is averaged over microns, and any local dynamic heterogeneity is lost. An FCS-based strategy that is highly sensitive to the presence of barriers to diffusion is the pair-correlation-function (pCF) approach (24). By spatiotemporal cross correlation of the fluorescence fluctuations between pairs of points acquired along a chosen line scan, the pair-correlation algorithm is able to map the accessibility of the cellular landscape and its role in determining the diffusive routes adopted by molecules (25, 26, 27, 28, 29, 30, 31, 32). This limitation to line-scan acquisitions implies, however, that the direction along which motion can be studied is predetermined by the chosen scanning pattern.

In this work, we extend the pCF approach to two-dimensional (2D) image analysis by calculating the spatiotemporal correlation function (named hereafter 2D pCF) at each point (pixel) of a 2D image. This process does not require extensive space averaging and can be applied to submicrometric ROIs. Rather than the usual average spatiotemporal correlation function of the acquired 2D image, we calculate the pCF for each point against the entire image and obtain a 2D-pCF. This correlation function contains the complete information on the dynamics of molecules that contributed to the fluorescence intensity fluctuations recorded at the selected point. To quantitatively extract and present this information, we adopt the image-derived MSD (iMSD) approach within this 2D pCF (20, 21).

By selected in silico experiments, we demonstrate that the present 2D pCF/iMSD combined analysis yields a quantitative description of the dynamics at each pixel. Moreover, we demonstrate that this measurement can be performed in a direction-dependent fashion and that it yields the “average trajectory” of the molecules that crossed the selected point. Finally, we apply this approach to two exemplary biological cases. First, we analyze a submicrometer sample in which diffusion is confined by cell shape by measuring the iMSD of green fluorescent proteins (GFPs) diffusing in the cytoplasm of Escherichia coli. Second, by applying this approach to H-Ras-GFP, an exemplary lipid-anchored protein of the inner leaflet of the plasma membrane, we show the highly anisotropic nature of molecular motion at the nanoscale in the proximity of large protein clusters, for the case of focal adhesion complexes.

We believe that this approach further extends the capability of correlation spectroscopy methods and provides, to our knowledge, a useful new tool for the characterization of the spatiotemporal dynamics of molecules in living cells.

Materials and Methods

Fluorescence microscopy

Fluorescence measurements were carried out with a Leica AF6000 fluorescence microscope (Leica Microsystems, Wetzlar, Germany) in total internal reflection fluorescence (TIRF) mode, with a penetration depth of the evanescent wave of <100 nm, for Chinese hamster ovary (CHO) plasma membrane imaging and in epifluorescence illumination mode for E. Coli imaging. Images were acquired by illuminating the sample with a 488 nm laser, using a 100× (NA 1.47) oil-immersion objective to collect fluorescence and a cooled EM-CCD Andor 897 Ultra (Andor Technology, Belfast, United Kingdom). To reach 100 nm of pixel size, an additional 1.6× lens was used and to reduce the illuminated field on the camera, an Optomask (Andor Technology) was used. Each cell was followed for at least 60 s, with a sampling rate of 500–1150 fps depending on the sample (at least 5.0 × 10⁴ frames in total).

Cell culture and treatments

CHO-K1 cells (CCL-61, ATCC, Manassas, VA) were grown in Dulbecco’s modified Eagle’s medium nutrient mixture F-12 supplemented with 10% v/v fetal bovine serum and maintained at 37°C and 5% CO₂. Plasmid encoding for GFP-tagged H-Ras was provided by Addgene (plasmid 18662) and previously published by Yasuda et al. (33). Plasmid encoding for red fluorescent protein (RFP)-tagged vinculin was purchased from Evrogen (Moscow, Russia). Cells were transiently transfected using Lipofectamine (Invitrogen, Carlsbad, CA) according to the manufacturer’s protocol.

E. coli recombinant strain expressing EGFP

E. coli expressing the EGFP protein was obtained by the transformation of bacterial cells with the plasmid pBSU101 kindly provided by Prof. Barbara Spellerberg using the protocol described by Aymanns et al. (34). Briefly, E. coli DH5a (Invitrogen) cells were transformed by electroporation with a Gene-Pulser Electroporator System (Bio-Rad, Hercules, CA) after the generation of electrocompetent cells through repeated washing in 10% glycerol. Recombinant E. coli cells were selected on Luria broth agar plates supplemented with 125 mg/mL of spectinomycin.

Data analysis

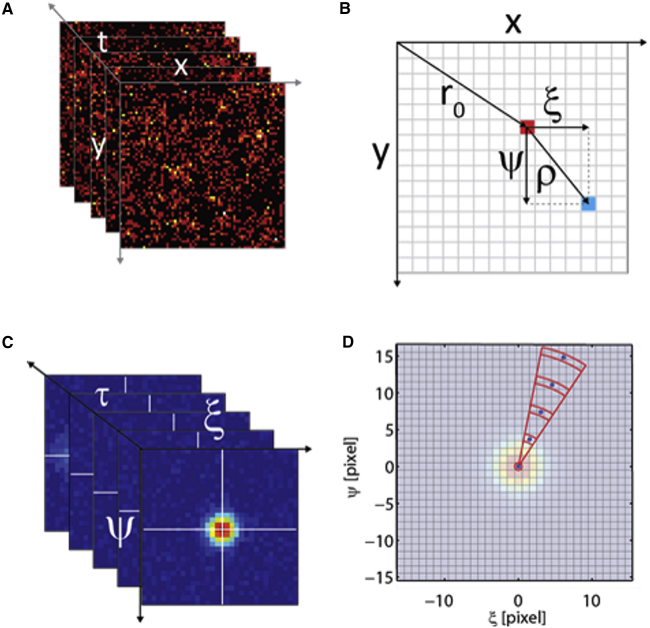
To calculate the 2D pCF associated with point r₀ = (x₀,y₀) of the acquired image series (I(r,t); Fig. 1 A), the fluorescence intensity measured at r₀ as a function of time is cross correlated with the intensity measured in all other points (pixels) of the image whose position ρ = (ξ,ψ) is given relative to r₀ (Fig. 1 B) according to

$$G\left(\mathbf{\rho },\tau ,{\mathbf{r}}_0\right)=\frac{{\langle \delta I\left({\mathbf{r}}_0,t\right)\delta I\left({\mathbf{r}}_0+\mathbf{\rho },t+\tau \right)\rangle }_t}{{\langle I\left({\mathbf{r}}_0,t\right)\rangle }_t{\langle I\left({\mathbf{r}}_0+\mathbf{\rho },t\right)\rangle }_t},$$ (1)

where ${\langle \dots \rangle }_t$ indicates time averaging and $\delta I\left({\mathbf{r}}_0,t\right)=I\left({\mathbf{r}}_0,t\right)-{\langle I\left({\mathbf{r}}_0,t\right)\rangle }_t$. The 2D pCF is a 3D matrix (ξ, ψ, and τ) that is shown in Fig. 1 C as a set of correlation images at different time delays, τ. For very short time delays (τ →0), the 2D pCF is well represented by a 2D Gaussian distribution representing the instrumental point spread function (PSF) (see Eq. S2 in the Supporting Material).

Figure 1.

Calculation and sampling of the 2D pCF. (A) An image sequence, I(r,t), is acquired by camera-based fluorescence microscopy. (B) A starting point for the analysis, r₀ = (x₀, y₀), is selected (red pixel) and the 2D pCF is calculated by cross correlation to all the other image pixels. Each pixel (e.g., light blue pixel) is identified with reference to r₀ by the 2D vector ρ = (ξ, ψ). (C) The resulting 2D pCF is a 3D matrix. (D) A portion of the polar grid used to sample the measured 2D pCF. Each polar region yields one single averaged value associated with the blue sampling point. To see this figure in color, go online.

To perform the required calculations, the image series recorded were loaded and processed within Matlab R14 (The MathWorks, Natick, MA) taking advantage of the Bio-Formats library (35) and a custom code, respectively. Before calculating the correlation function, image series were filtered by a moving-average algorithm to avoid correlation due to slow collective sample motion (24). Furthermore, to reduce the noise, the G(r₀;ρ,τ) value at each ρ was set to the average of the values obtained at that ρ in the 2D pCFs associated with r₀ and with its eight next neighbors (i.e., we averaged the values calculated in correspondence to nine r₀ points on a 3 × 3 square region). Finally, to reduce the size of the 3D matrices without compromising resolution, we sampled the 2D pCF on a polar grid (ρ_i, ${\theta }_i$) (with ${\theta }_i$ taking only values 0, ±π/8, …, ±7π/8, π, and ρ_i taking a value of 0–16 pixels, where the pixel size is 0.1 μm) and set the value at each point to the weighted average of the values of the corresponding polar quadrant (see Fig. 1 D). As weighting functions, we chose Gaussian functions both in ρ (i.e., $\propto \text{exp}\left(-{\left(\rho -{\rho }_i\right)}^2\right)$) and in θ ($\propto \text{exp}\left(-2{\left(\theta -{\theta }_i/\left(\pi /8\right)\right)}^2\right)$ with |θ| < π).

Following previous methods (20, 21), we then extracted the iMSD corresponding to each sampled direction, ${\theta }_i$, by fitting the $G\left({\mathbf{r}}_0;{\rho }_i,{\theta }_i,\tau \right)$ values at the sampled ρ_i with

$$g\left({\mathbf{r}}_0;\tau \right)\text{exp}\left(-\frac{{\rho }^2}{\text{iMSD}\left({\mathbf{r}}_0;{\theta }_i,\tau \right)}\right),$$ (2)

where $g\left({\mathbf{r}}_0;\tau \right)$ and $\text{iMSD}\left({\mathbf{r}}_0;{\theta }_i,\tau \right)$ are the fitting parameters at each time delay. Finally, an effective diffusion tensor, $D^{\ast }\left({\mathbf{r}}_0;{\theta }_i\right),$ was calculated by fitting the $\text{iMSD}\left({\mathbf{r}}_0;{\theta }_i,\tau \right)$ behavior for small τ: $\text{iMSD}\left({\mathbf{r}}_0;{\theta }_i,\tau \right)=4D^{\ast }\left({\mathbf{r}}_0;{\theta }_i\right)\tau$. Here, we choose for the simulated experiments and for the experiments in the eukaryotic cell τ < 0.1 s to compare the resulting diffusivity values with recent SPT experiments (9, 36, 37), whereas for the prokaryotic cell, we measured the diffusion tensor for τ < 5 × 10⁻² s.

Finally, to quantify the diffusion-tensor anisotropy, we approximated $D^{\ast }\left({\mathbf{r}}_0;{\theta }_i\right)$ with an ellipse and determined its principal axes, $D_{\max }^{\ast }\left({\mathbf{r}}_0\right)$ and $D_{\text{min}}^{\ast }\left({\mathbf{r}}_0\right)$, by diagonalization, similar to what is done in magnetic resonance diffusion tensor imaging (38). The diffusion anisotropy at point ${\mathbf{r}}_0$ was then defined as

$$\Phi \left({\mathbf{r}}_0\right)=\frac{D_{\max }^{\ast }\left({\mathbf{r}}_0\right)-D_{\text{min}}^{\ast }\left({\mathbf{r}}_0\right)}{D_{\max }^{\ast }\left({\mathbf{r}}_0\right)+D_{\text{min}}^{\ast }\left({\mathbf{r}}_0\right)}.$$ (3)

In the following, we shall also discuss the average effective diffusivity for a specific point, r₀ $\left(D_{\text{avg}}^{\ast }\left({\mathbf{r}}_0\right)\right)$, obtained by averaging $D^{\ast }\left({\mathbf{r}}_0;{\theta }_i\right)$ over all (or subsets of) θ_i values.

Simulated experiments

Simulated experiments were performed by MatLab R14 (The MathWorks) as previously described (20). Each x and y coordinate was changed separately by adding a random number drawn from a normal distribution with zero mean, and standard deviation $\sigma =\sqrt{2D{\Delta }_t}$, where D is the diffusion coefficient, and Δ_t is the time interval between consecutive simulated steps. To simulate anisotropic diffusion, we simulated two parallel barriers. The barriers are simulated as infinitely thin and impermeable: a molecule that tries to cross them remains at its position. The molecule-position matrix was convoluted with a Gaussian filter to simulate the experimental diffraction-limited acquisition, and a Poissonian-weighted random number generator was used to simulate the photon-detection process. Circular boundary conditions for both molecule movement and convolution were applied. In all cases, a density of 10 molecules/μm² was randomly seeded in a square matrix of 64 × 64 pixels (0.1 μm/pixel). The simulated acquisitions were 5 × 10⁴ frames long, with a time step of 1 ms/frame; the instrumental PSF was set to 300 nm. To measure the local MSD of a selected point, we calculated the weighted average over the MSD of all simulated molecules using the number of photons of each molecule collected at the selected point as the weight. As a consequence, molecules that never contribute to the fluorescence collected at the selected point do not contribute to the local MSD.

Results

Theoretically expected 2D pCF for characteristic dynamical processes

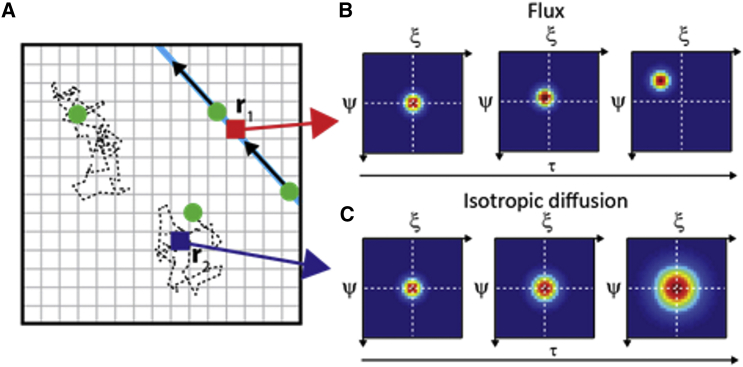
To present the expected time evolution of the 2D pCF, three representative cases of particle motion are shown: 1) molecular flow (by directed active transport); 2) isotropic diffusion; and 3) diffusion in the presence of barriers. The quantitative modeling of these is presented in the Supporting Material. In case 1, all molecules move in the same direction (Fig. 2 A, black arrows): as shown in Fig. 2 B, for increasing τ, the 2D-pCF peak shifts in the direction of molecular motion without broadening. In this case, the characteristic velocity of molecules can be measured by tracking the position of the 2D-pCF peak (see Eq. S4). In case 2, molecules are randomly diffusing off the selected point: the correlation function spreads uniformly in all directions (Fig. 2 C). The waist of the 2D pCF can be fitted with Eq. S6 to estimate molecular diffusivity.

Figure 2.

2D pCF in the case of flux (by directed active transport) and isotropic diffusion. (A) ROI in which molecules are either dragged by active motion or isotropically diffuse. (B and C) Expected 2D pCF associated with a point from a region characterized by active motion (r₁, red pixel, $\left|\mathbf{v}\left({\mathbf{r}}_2\right)\right|$ = 5 μm/s) or isotropic diffusion (r₂, dark blue pixel, $D_{\text{avg}}^{\ast }\left({\mathbf{r}}_2\right)$ = 1 μm² s⁻¹), respectively. 2D-pCF plots shown in (B) and (C) correspond to τ = 1, 20, and 100 ms. To see this figure in color, go online.

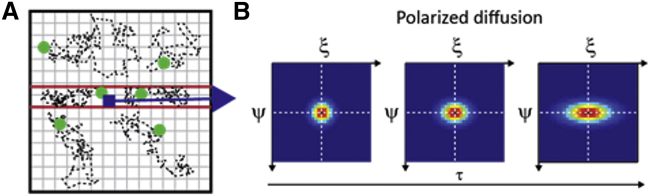
In the first two cases, the correlation function can be well approximated by a simple Gaussian function (Eqs. S4 and S6, respectively). This is not true in case 3, where barriers to molecular motion are present and molecules are constrained to diffuse along specific directions (Fig. 3 A). As a consequence, in tightly confined regions, the spreading of the correlation function with time is highly anisotropic (Fig. 3 B) and cannot be described by a simple Gaussian function. It can be fitted, however, with a Gaussian function whose variance is direction dependent. Such a fit (see Eq. 2) yields a direction-dependent iMSD value.

Figure 3.

2D-pCF analysis unveils the directionality of molecular diffusion. (A) Molecules diffusing in the presence of barriers (red lines). (B) 2D-pCF behavior relative to the position indicated by the dark blue pixel in (A). The time evolution of the correlation peak deforms as a result of motion being suppressed in certain directions: ($D^{\ast }\left({\mathbf{r}}_0;0\right)=D^{\ast }\left({\mathbf{r}}_0;\pi \right)$ = 1 μm² s⁻¹, $D^{\ast }\left({\mathbf{r}}_0;\pm \raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)$ = 0). Plots shown correspond to τ = 1, 20, and 100 ms. To see this figure in color, go online.

Quantitative description of molecular dynamics by 2D pCF: probing the diffusion tensor

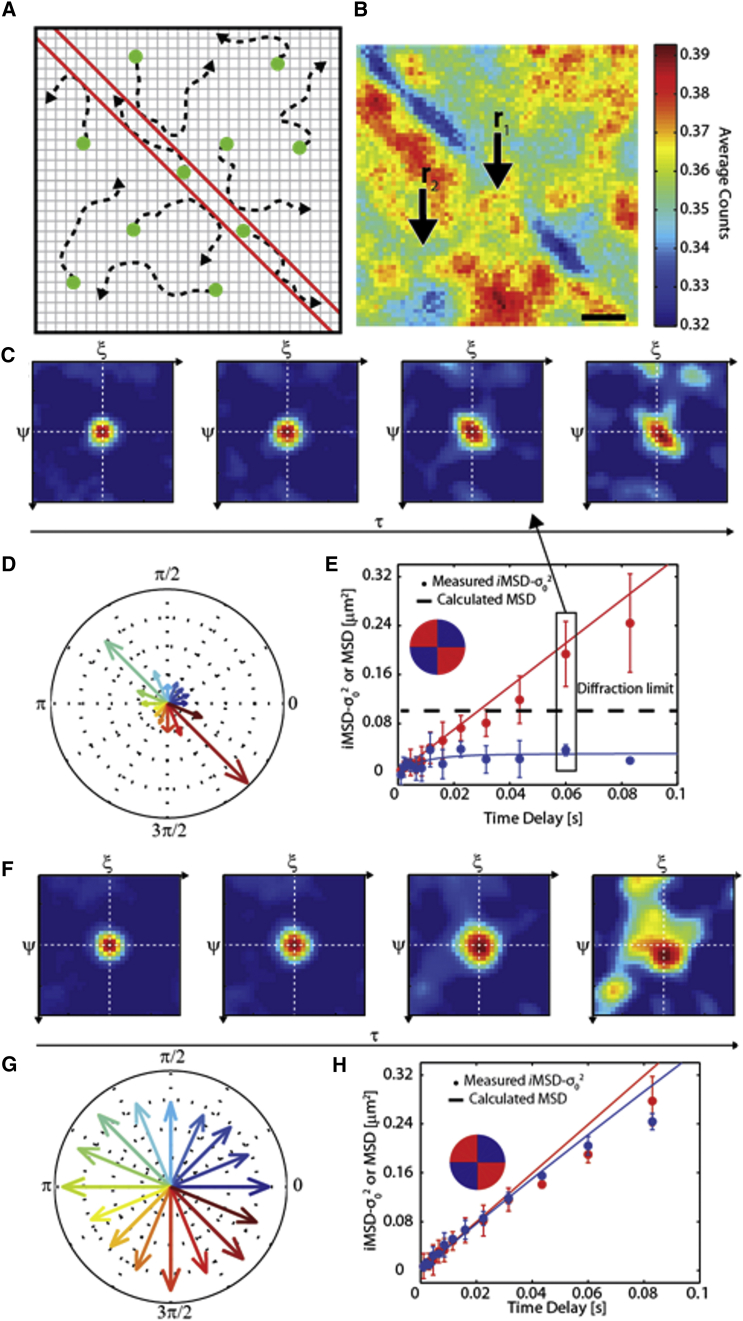
The last case of constrained diffusion is particularly interesting and will be discussed in some detail. We simulated a 2D physical channel with infinitely thin barriers that is able to confine the motion in a given direction. Molecules can freely diffuse (and we imposed D = 1 μm² s⁻¹) at every point of the simulated space (both within and off the channel), but they cannot cross the channel walls (placed at a distance of 300 nm) (Fig. 4 A). Representative trajectories of molecules diffusing within (or off) the channel are reported in Fig. S1. Despite the marked difference of individual trajectories, the position of the channel walls cannot be identified by inspection of the fluorescence image (see Fig. 4 B; note that the image is scaled (see scale bar on the right)). This can be seen also in the specific example of Fig. 4 B: some weak fluorescence spots appear in the simulated image in the proximity of the barriers, but they are quite similar to darker spots that appear far from the channel as a result of local fluctuations, such as the spot in the lower left corner.

Figure 4.

The iMSD tensor reveals the local anisotropy of molecular diffusion. (A) Scheme of the simulated system: molecules can freely diffuse without crossing the two barriers (red lines) that form a channel. (B) Average fluorescence intensity obtained for the simulated experiment. The color scale represents the average counts per pixel per frame. Two representative points, r₁ and r₂, are chosen, the former at the center of the channel and the latter far from the barriers. (C) Time evolution of the 2D pCF associated with r₁: plots shown correspond to τ = 1, 12, 60, and 160 ms. The 2D pCF evolves into a markedly anisotropic shape (i.e., polarized in the direction of the channel). (D) Diffusion-tensor-measured values in the sampled directions (see text). (E) The iMSD(r₁;ρ,τ) measured by fitting to Eq. 2 at selected τ values (solid circles) is compared with its theoretical behavior as calculated from the simulated trajectories (solid lines). Two directions are considered, parallel (red) and perpendicular (blue) to the channel. Below 10 ms, the dynamics in the two directions is similar; above this timescale, the effect of the barriers clearly appears, and the MSD in the direction perpendicular to the barriers saturates. Please note that for two dimensions, the actual MSD coincides with iMSD – σ₀². (F) Time evolution of the 2D pCF associated with r₂. The plots shown correspond to τ = 1, 12, 60, and 160 ms. The 2D pCF shows a round-shaped correlation that expands in time, indicating free diffusion. (G) Diffusion tensor values in the sampled directions. (H) iMSD(r₂;ρ,τ) traces in the directions parallel and perpendicular to the barriers are superimposable. To see this figure in color, go online.

On the contrary, if we calculate the 2D pCF starting from a point within the channel (the point indicated by the arrow labeled ${\mathbf{r}}_1$ in Fig. 4 B), it is immediately apparent that the correlation spreads out in time only along the channel direction (Fig. 4 C). At the same time, consistent with the absence of directed active transport, the correlation peak does not shift and remains at the center of the correlation space. In this case, as mentioned above, the shape of the overall correlation function is not well represented by a 2D isotropic Gaussian function.

The 2D pCF must be sampled for specific directions (see Materials and Methods) and the corresponding iMSD calculated thanks to Eq. 2. Fig. 4 D shows the average iMSDs measured in the directions parallel and perpendicular to the simulated channel (Fig. 4 E, red and blue polar quadrants and points) as a function of the time delay. Although for short time delays the two iMSDs overlap, for longer time delays they can be easily distinguished. Indeed, in the direction parallel to the channel, the iMSD grows linearly in time over the measured time delays (i.e., no barriers to diffusion are present); by contrast, in the direction perpendicular to the channel, the iMSD saturates, indicating that the motion is obstructed by the impenetrable channel walls. To verify that the measured iMSD faithfully represents the actual MSD of the molecules, we quantitatively compared the iMSD measured as previously described with the MSD calculated from the trajectories of the simulated molecules, selecting only those that contributed to the fluorescence intensity recorded in the selected point (see Materials and Methods for a detailed definition of the local MSD). In Fig. 4 E, the straight line represents the iMSD measured from simulated trajectories, whereas solid circles represent the iMSD measured from the 2D pCF. The good overlap between these two quantities demonstrates that the measured iMSD tensor faithfully describes the actual MSD. Using this approach, we can estimate the mobility in different directions and obtain the diffusion tensor for the selected point. By means of the diffusion tensor, anisotropic diffusivity within the channel (Fig. 4 E) can be distinguished from the isotropic diffusivity present off the channel (Fig. 4, F–H; data are relative to the point marked by the arrow labeled ${\mathbf{r}}_2$ in Fig. 4 B). In the case of a linear iMSD tensor, the apparent diffusivity could be measured in principle by fitting only the first two experimental points. Since the iMSD can be rather noisy, however, we opted for using at least 12 points, as shown in Fig. 4, D and G.

Mapping the regions of anisotropic motion with the diffusion tensor approach

The approach presented here also makes it possible to identify regions where diffusion is free or constrained. As illustrated in the Data Analysis section we shall make use of parameter Φ(r₀) (see Eq. 3) as an index of diffusion anisotropy. Φ(r₀) values ≫0 indicate anisotropic diffusion at r₀ (i.e., points where obstacles or barriers hinder diffusion): when this occurs, the direction corresponding to $D_{\max }^{\ast }\left({\mathbf{r}}_0\right)$ yields the preferred direction of motion locally imposed by the microenvironment anisotropy. In the remainder of this section, we show that by inspection of the 2D pCF it is possible to map regions where molecule diffusion is constrained or guided by local anisotropies.

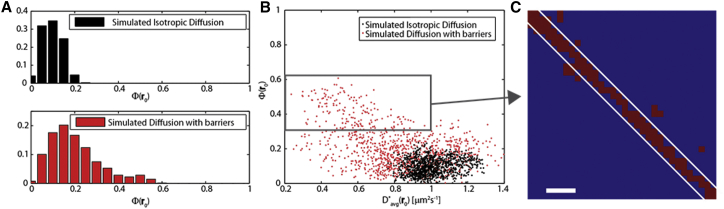
Let us compare two of the simulated cases: free diffusion and diffusion in the presence of barriers (whose position is, in principle, not known). We calculate Φ(r₀) values at all r₀ points according to the procedure detailed in Data Analysis and plot in the histogram of Fig. 5 A the frequency of these values (free diffusion in the upper plot and constrained diffusion in the lower plot). Note that since in the Brownian-motion case, no anisotropy is expected, the observed distribution of Φ(r₀) values is determined by the impact of the limited observation time and the measurement protocol. In our case, the measured distribution peaked around 0.1, and Φ(r₀) never exceeds 0.3. On the other hand, in the presence of the impenetrable barriers, we can see a significantly wider and more skewed distribution for the diffusion anisotropy values that reaches values up to 0.6, corresponding to a $D_{\max }^{\ast }\left({\mathbf{r}}_0\right)/D_{\text{min}}^{\ast }\left({\mathbf{r}}_0\right)$ ratio of ∼4. Note that the distribution in Fig. 5 A, lower, includes all points r₀, both close to and far from the barriers, but still is qualitatively different from the isotropic case. We can readily identify the location of constrained diffusivity by plotting the measured Φ(r₀)-$D_{\text{avg}}^{\ast }\left({\mathbf{r}}_0\right)$ pairs at each r₀ (again keeping the two cases for comparison; see the scatter plot in Fig. 5 B (black dots, free diffusion; red dots, diffusion in the presence of barriers). In the case of isotropic diffusion, the measured $D_{\text{avg}}^{\ast }\left({\mathbf{r}}_0\right)$ recovers the imposed value (1 μm² s⁻¹) in the presence of barriers by finding an apparent reduced value (together with an increased anisotropy parameter value). Finally, by taking advantage of the simulated results regarding isotropic diffusion (where no Φ(r₀) >0.3 was measured), we can select a threshold value of Φ(r₀) > 0.3 and highlight the corresponding r₀ points in the (x,y) plane (Fig. 5 C, red squares). This protocol yields the physical position of the barriers in the sample under study and correctly recovers the simulated system (Fig. 5 C, white lines).

Figure 5.

Identification of the regions of constrained diffusion. (A) Distribution of measured Φ(r₀) values for the case of isotropic diffusion (upper) and constrained diffusion (lower) presented in Fig. 4. (B) Scatter plot of the measured Φ(r₀), $D_{\text{avg}}^{\ast }\left({\mathbf{r}}_0\right)$ pairs for the case of isotropic diffusion (blue dots) and diffusion with barriers (red dots). The presence of barriers leads to a more dispersed distribution characterized by lower $D_{\text{avg}}^{\ast }\left({\mathbf{r}}_0\right)$ and higher Φ(r₀) values. (C) The points corresponding to the Φ(r₀), $D_{\text{avg}}^{\ast }\left({\mathbf{r}}_0\right)$ pairs in the boxed region in (B) are highlighted in red and identify the region of constrained diffusion. The position of the barriers is readily deduced, thus demonstrating that the diffusion tensor is able to unveil the localization of anisotropic diffusion areas. Scale bar, 500 nm. To see this figure in color, go online.

Biological applications

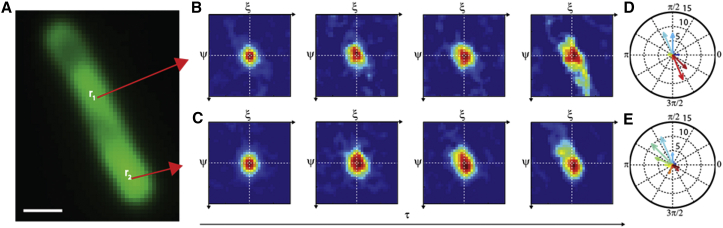
To confirm the ability of the approach presented here to reveal anisotropic diffusion in an actual experiment, we measured GFP diffusion in the cytoplasm of E. coli. The oblong shape of this bacterium naturally confines GFP diffusion within a channel-like structure (on average 500 nm wide and a few microns long). As a consequence, we can expect a significant reshaping of the 2D pCF for longer delays. A representative fluorescence image of an E. coli cell expressing GFP is presented in Fig. 6 A. Fig. 6, B and C, represents the 2D pCF calculated for two representative points chosen along the major axis of a bacterial cell. As expected, although for short time delays (Fig. 6, B and C, left) the calculated 2D pCF still appears round-shaped, for longer time delays (Fig. 6, B and C, right), the correlation function starts to elongate in the direction of the cell major axis owing to the physical confinement imposed by the cell walls. This effect becomes increasingly pronounced for larger time delays (e.g., 50 ms, Fig. 6, B and C, right), and the calculated diffusion tensor (Fig. 6, D and E) consistently appears markedly polarized along the cell major axis. Importantly, the quantitative analysis of the diffusion tensor yields $D^{\ast }\left({\mathbf{r}}_0;5\pi /8\right)=8\pm {2\text{μm}}^2{\text{s}}^{-1},$ consistent with previously published estimates of GFP diffusivity based on fluorescence recovery after photobleaching along the same direction (39). These results confirm that the proposed approach can reveal anisotropic diffusion in a biological environment and demonstrate its compatibility with the use of GFP as a label.

Figure 6.

2D-pCF analysis of GFP in a submicrometric confined environment. (A) Fluorescence image of a GFP expressed in an E. coli cell. Scale bar, 1 μm. (B and C) The 2D pCF measured at two representative points in the cell. Plots shown correspond to τ = 0.87, 2.6, 7, and 50 ms. (D and E) The polarization of the diffusion tensor measured at the two points highlights the presence of anisotropic diffusion. To see this figure in color, go online.

H-Ras presents different dynamical properties in apparently identical membrane regions

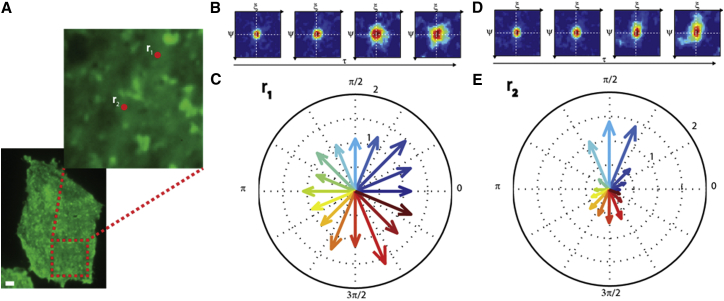
To further illustrate the potential of the presented approach, we used 2D-pCF analysis to study the dynamics of a protein diffusing on the plasma membrane of eukaryotic cells. We selected a GFP-tagged variant of H-Ras, a lipid-anchored protein of the plasma-membrane inner leaflet. It acts as a key regulator in the signal transduction activated by growth-factor-related transmembrane receptors and controls cell growth (40). A representative TIRF microscope image of the basal membrane of a CHO-K1 cell transiently transfected with H-Ras-GFP is shown in Fig. 7 A (lower). A smaller region is also shown in Fig. 7 A that was selected to perform high-speed time-lag imaging (1.6 ms). By selecting a first point (r₁) and calculating the 2D pCF, we can see that the maximum of the correlation function does not change position in time (indicating the absence of a net molecular flux) and that the 2D-pCF peak displays a waist that is roughly circular (Fig. 7 B). Fig. 7 C shows the measured diffusion-tensor values at different θ_i and yields free diffusion with $D_{\text{avg}}^{\ast }\left({\mathit{r}}_1\right)$ ≈ 1.2 μm²s⁻¹. This implies isotropic H-Ras-GFP diffusion at the selected point. If we repeat this analysis at another point, r₂ (∼1 μm from r₁), a different behavior is observed. In fact, although the absence of directed active flow is confirmed (the maximum of the correlation function does not change position in time), the 2D pCF spreads out in space rather anisotropically. Fig. 7 E shows the diffusion tensor values for several θ values and clearly indicates a preferential anisotropic diffusion roughly in the vertical direction with $D_{\text{min}}^{\ast }\left({\mathbf{r}}_2\right)$ = 0.2 μm² s⁻¹ and $D_{\max }^{\ast }\left({\mathbf{r}}_2\right)=1{.1\text{μm}}^2{\text{s}}^{-1}$. Please note that this information would be hidden in a classical FCS measurement (both single-point and STICS based). Fig. S2 shows FCS curves calculated at the two selected points; they overlap and yield a diffusion coefficient of ∼1.1 μm² s⁻¹ in both cases.

Figure 7.

H-Ras-GFP diffusion on the plasma membrane. (A) Fluorescence image of H-Ras-GFP expressed in a CHO-K1 cell recorded at the plasma membrane by TIRF microscopy. The red box and the zoom show a typical acquisition region. Scale bar, 2 μm. (B) 2D-pCF time evolution at point r₁. The plots shown correspond to τ = 2, 12, 50, and 90 ms. (C) Diffusion tensor measured at point r₁, showing isotropic properties within experimental error. (D) 2D-pCF time evolution at point r₂. The plot shown corresponds to the same timescales as in (B). (E) Diffusion tensor measured at r₂ showing marked anisotropy. To see this figure in color, go online.

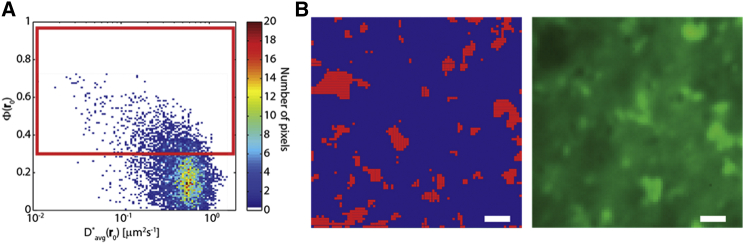
We can further investigate this inhomogeneity by applying the protocol described with the simulated experiments to identify the regions of H-Ras-GFP anisotropic diffusion on the plasma membrane. Fig. 8 A is the scatter plot of the Φ(r₀)-$D_{\text{avg}}^{\ast }\left({\mathbf{r}}_0\right)$ pairs extracted from the measured 2D pCF at all r₀ points studied. Note that high $D_{\text{avg}}^{\ast }\left({\mathbf{r}}_0\right)$ values typically correspond to lower anisotropy values, whereas low $D_{\text{avg}}^{\ast }\left({\mathbf{r}}_0\right)$ values correspond to high anisotropy values, consistent with the presence of “guided” diffusion at the nanoscale. By selecting, as before, all points r₀ where Φ(r₀) > 0.3, we identify several micrometer-sized patches on the plasma membrane (Fig. 8 B, left). These are the regions where our analysis shows that H-Ras-GFP undergoes constrained diffusion. Note that they do not correlate with the fluorescence intensity distribution (Fig. 8 B, right). This may be somewhat surprising, as one might expect an accumulation of the protein in the regions close to barriers, particularly if characterized by a lower $D_{\text{avg}}^{\ast }\left({\mathbf{r}}_0\right)$. However, as shown in the simulated measurements, in the absence of specific binding interactions, the iMSD measured in the direction of a channel is comparable to the iMSD measured outside the channel, and in fact, we did not observe any significant accumulation of fluorescence in the proximity of the barriers (Fig. 5 B).

Figure 8.

Diffusion of H-Ras-GFP is obstructed and highly anisotropic. (A) Scatter plot of Φ(r₀), $D_{\text{avg}}^{\ast }\left({\mathbf{r}}_0\right)$ pairs obtained in the experiment described in Fig. 7. The color indicates the number of pixels in the respective 2D bin (see scale bar at right). The red box encloses the region of the histogram where Φ(r₀) > 0.3. (B) Pixels corresponding to the pairs within the red box in (A) are plotted in red to highlight their position in the (x,y) plane (left); the average fluorescence intensity from the same area is also shown (right; same image as in Fig. 7A; scale bar, 1 μm). To see this figure in color, go online.

Regions of anisotropic H-Ras-GFP motion correlate with vinculin localization

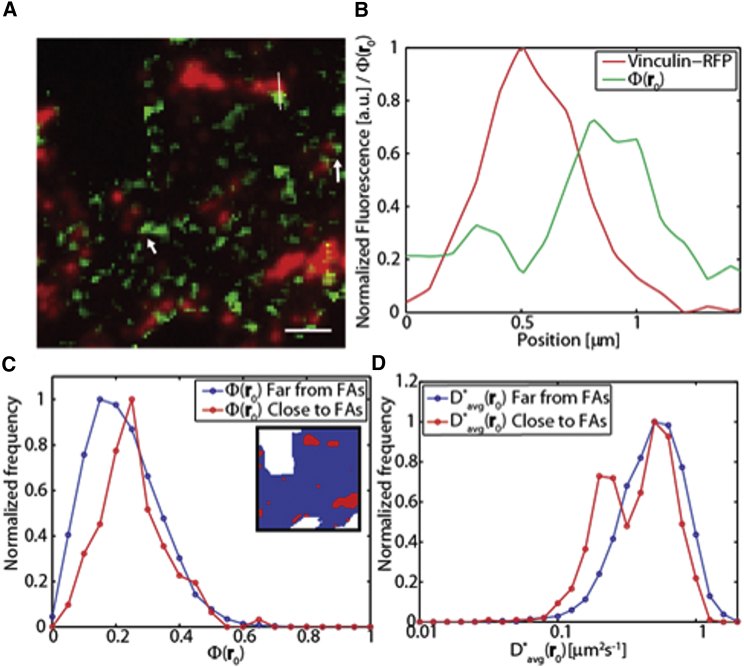
Recent findings show that plasma-membrane functionality in eukaryotic cells is regulated by the cytoskeleton components (e.g., F-actin and microtubules), which act as structurally organized barriers that locally guide the diffusion of selected molecular components (e.g., the transmembrane scavenger receptors CD36 (41, 42) and LOX-1 (43)). Moreover, it was recently shown that focal adhesions (FAs), a cluster of proteins linked to the cytoskeleton and mediating cell-extracellular matrix interaction (44), act as partially permeable barriers for mobile membrane components (37), including, in particular, lipid-anchored GTPases (36). Thus, even in the absence of direct interactions with intrinsically polarized components of cellular architecture like the cytoskeleton, one can expect to observe constrained diffusion on the plasma membrane in proximity to physical obstacles to motion, such as the protein clusters involved in FAs. To verify whether the observed regions of H-Ras-GFP diffusion anisotropy are in the proximity of FAs, we cotransfected H-Ras-GFP and a genetically encoded label of functional FAs, vinculin-RFP (hereafter, Vin-RFP) (45, 46). A representative TIRF image of Vin-RFP (red) overlapped with diffusion anisotropy of H-Ras-GFP (green) is presented in Fig. 9 A. Many of the regions characterized by high diffusion anisotropy are in close proximity to a Vin-RFP spot. Fig. 9 B shows in particular the profile of Vin-RFP fluorescence and Φ(r₀) along the white segment in Fig. 9 A. Close to the FA, Φ(r₀) can reach values up to 0.7, indicating highly anisotropic diffusion. To verify the statistical significance of this behavior, we measured the spatial cross-correlation function between Vin-RFP fluorescence and Φ(r₀) in the whole region. As reported in Fig. S4 A, a positive cross correlation was found. Notably, it is shifted a few hundred nanometers off the center of the correlation space (Fig. S4). Such a shift closely matches the one observed between the fluorescence profiles of Vin-RFP and Φ(r₀) reported in Fig. 9 B. Moreover, we compared the distribution of Φ(r₀) measured in regions of high and low Vin-RFP fluorescence (Fig. 9 C, inset). As shown in Fig. 9 C, the regions close to FAs are characterized by a different distribution of Φ(r₀) that is, specifically, significantly shifted to larger diffusion anisotropy values (p = 0.001 according to the Mann-Whitney U test). Please note that in the FA regions, we also observed a reduced diffusivity of H-Ras-GFP with respect to the surroundings, as shown in Fig. 9 C. In particular, very close to the adhesions, we observe a bimodal distribution of H-Ras-GFP diffusivity (Fig. 9 D) that displays a second peak around 0.2 μm² s⁻¹, consistent with previous observations (36, 37).

Figure 9.

Focal adhesions and H-Ras diffusion anisotropy regions. (A) Superimposition of Vin-RFP fluorescence signal (red) and the Φ(r0) value map relative to H-Ras-GFP (green). The scale of red signal is saturated to enhance the visualization of isolated adhesions. The nonsaturated image is shown in Fig. S3. Scale bar, 2 μm. (B) Vin-RFP fluorescence intensity profile and Φ(r0) values along the white segment in (A). (C) Comparison of Φ(r0) distribution in (red) and off (blue) the regions of high Vin-RFP fluorescence. In the inset, we report the selected regions in the corresponding color. (D) Distribution measured in the two regions shown in the inset of (C). To see this figure in color, go online.

Discussion

Here, by extending the pCF analysis from a pair of points to many points in space and combining this with the quantitative measurement of molecular displacements (via the iMSD approach), we demonstrate that we can probe the characteristic diffusion tensor and gain information on the spatial constraints influencing molecular motion.

Notably, the diffusion tensor can be measured 1) without molecular-localization algorithms, 2) with no influence from the photophysics of the label, and 3) in a superresolved fashion. We wish to stress that all this is achieved by using a commercial microscope. Concerning point 1, unlike with SPT, here we do not measure all single-molecule trajectories, but only the average spatiotemporal distribution of the molecules that are crossing a selected point, extracting what we define as an “average trajectory”. Since it is based on fluctuation analysis, this approach does not require localization of the molecules and can be applied to dim and dense labels, such as fluorescent proteins under transfection conditions. In addition, since the average dynamics of many molecules is measured simultaneously at each point, molecular diffusion can be quantitatively probed on a large (micrometric) scale. Concerning point 2, it should be kept in mind that fluorophore blinking is a major limitation for trajectory relinking in a typical SPT measurement (47, 48). Also, FCS-based approaches are in principle affected by the photophysics of the fluorophore (49), which is typically on a timescale similar to the diffusion of the molecule (50). However, fluorophore photophysics (e.g., blinking and bleaching) is a pure temporal phenomenon and, consequently, acts only on the amplitude (pure temporal part) of the 2D pCF. More explicitly, when a fluorophore turns off, it will stop contributing to the correlation function; however, since the turning off can occur at any position in space, it will reflect a homogenous lowering of the correlation amplitude that does not alter the spatial shape of the 2D pCF. As a consequence, blinking and bleaching do not affect the width of the correlation function used in the iMSD approach to measure particle displacement (20, 23). Concerning point 3, we should like to stress that the diffusion tensor measured here corresponds to average molecular displacements well below the diffraction limit. The possibility of superresolution of molecular diffusion by FCS is the object of intense debate in the field of correlation spectroscopy (51, 52). As already pointed out by Krichevsky and colleagues (52), the correlation function loses half its amplitude when molecules move a distance comparable with the characteristic size of the observation area (i.e., the optical resolution). However, it is clear that the precision in the measurement of the correlation function can be high enough to appreciate a loss in the correlation amplitude much smaller than half of its maximum: in other words, a molecular displacement below the optical resolution can be potentially detected. By exploiting STICS and STICS-related techniques, it was shown that the resolution in the measurement of molecular displacement depends on the accuracy in measurement of the correlation function “position” (in the case of molecular flux (19)) or “width” (in the case of molecular diffusion (20, 21, 22)). In this context, it must be kept in mind that pixel size will influence the overall resolution in the measurement of the particle displacement by introducing a further uncertainty in the localization of the collected photons (53). Just as importantly, a compromise on pixel size is required to allow oversampling of the PSF while limiting the noise in the overall 2D-pCF correlation function. In our experience, a good compromise is reached at characteristic lengths around 100–150 nm. It is worth noting that by applying the iMSD approach to the 2D-pCF analysis, molecular displacements can be superresolved, highlighting a further potentiality of the pCF approach, to date often assumed to be limited by the optical resolution (24, 32). In fact, in the classical pCF approach, the molecular transit time between the two selected points is quantified by the position of a maximum of correlation that appears only for those pairs of points at a distance greater than the optical resolution of the measurement. Here, we measure the particle displacement by the decay of the spatial correlation at a fixed time delay, so that the maximum resolution (given a sufficient signal/noise ratio of the measurement) is fixed by the particle displacement between two consecutive frames.

Finally, we remark that this approach is compatible with multicolor imaging (e.g., to detect how association or dissociation between different molecules contributes to the regulation of molecular diffusion), fluorescence lifetime imaging microscopy and fluorescence resonance energy transfer to detect molecular flow upon protein activation (22, 54), superresolution microscopy (STED) to further increase spatial resolution (32), and single-plane illumination microscopy (SPIM) to carry out such a 2D-pCF analysis deep in the 3D intracellular environment (55).

Author Contributions

C.D.R. performed the research, analyzed data, and wrote the article; F.C. analyzed data and wrote the article; M.D.L. prepared transfected bacterial cells and wrote the article; F.B. designed the research, analyzed data, and wrote the article; E.G. designed the research, analyzed data, and wrote the article.

Editor: Katharina Gaus.

Supporting Citations

References (56, 57) appear in the Supporting Material.