Direct Observation of the Intrinsic Backbone Torsional Mobility of Disordered Proteins

Abstract

The fundamental backbone dynamics of unfolded proteins arising due to intrinsic ϕ-ψ dihedral angle fluctuations dictate the course of protein folding, binding, assembly, and function. These internal fluctuations are also critical for protein misfolding associated with a range of human diseases. However, direct observation and unambiguous assignment of this inherent dynamics in chemically denatured proteins is extremely challenging due to various experimental limitations. To directly map the backbone torsional mobility in the ϕ-ψ dihedral angle space, we used a model intrinsically disordered protein, namely, α-synuclein, that adopts an expanded state under native conditions. We took advantage of nonoccurrence of tryptophan in α-synuclein and created a number of single-tryptophan variants encompassing the entire polypeptide chain. We then utilized highly sensitive picosecond time-resolved fluorescence depolarization measurements that allowed us to discern the site-specific torsional relaxation at a low protein concentration under physiological conditions. For all the locations, the depolarization kinetics exhibited two well-separated rotational-correlation-time components. The shorter, subnanosecond component arises due to the local mobility of the indole side chain, whereas the longer rotational-correlation-time component (1.37 ± 0.15 ns), independent of global tumbling, represents a characteristic timescale for short-range conformational exchange in the ϕ-ψ dihedral space. This correlation time represents an intrinsic timescale for torsional relaxation and is independent of position, which is expected for an extended polypeptide chain having little or no propensity to form persistent structures. We were also able to capture this intrinsic timescale at the N-terminal unstructured domain of the prion protein. Our estimated timescale of the segmental mobility is similar to that of unfolded proteins studied by nuclear magnetic resonance in conjunction with molecular dynamics simulations. Our results have broader implications for a diverse range of functionally and pathologically important intrinsically disordered proteins and disordered regions.

Introduction

The dynamic description of disordered proteins, which comprise an ensemble of heterogeneous and rapidly interconvertible structures, is immensely useful in the mechanistic understanding of protein folding, binding-coupled folding, assembly, misfolding, and aggregation. The dynamical processes in proteins can occur at a wide range of timescales ranging between picoseconds and milliseconds that may involve local motion of side chains, backbone segmental dynamics involving torsional fluctuations, short-range conformational fluctuations, long-range correlated dynamics, global rotational dynamics, collective domain motions, etc. (1, 2, 3). Among these processes, the backbone segmental mobility in the Ramachandran ϕ-ψ conformational space constitutes the intrinsic dynamical feature that dictates the course of folding, assembly, and function (4, 5). To characterize the site-specific segmental dynamics, the proteins must be unfolded in a high concentration of chemical denaturants such as urea or guanidine hydrochloride (6). However, several extraneous factors pose a bottleneck in the accurate estimation of inherent segmental dynamics in the denaturant-unfolded proteins. These factors may include binding of denaturant molecules to the polypeptide backbone, resulting in an apparent increase in the polypeptide chain dimension and modifications in both bulk- and microviscosities around the polypeptide chain. Denaturant molecules are known to bind to the polypeptide chains and alter the chain dynamics (7, 8). Therefore, in the denatured state, the backbone dynamics is expected to be significantly dampened, and hence, the measured timescale of the mobility is likely to be overestimated. To circumvent this problem, we have chosen a natively unfolded, or intrinsically disordered protein (IDP), to monitor the residue-specific segmental mobility under native physiological conditions.

IDPs belong to the emerging class of proteins that do not undergo autonomous folding into a well-defined 3D structure and are associated with a number of functions and diseases (9, 10, 11, 12, 13). The astonishing conformational plasticity of IDPs allows them to sample a wide range of structural ensembles under the native (physiological) condition due to the presence of (independent) large-amplitude internal backbone dynamics. Therefore, IDPs are well-suited to study the short-range backbone segmental mobility under native conditions. For our studies, we have used a model IDP, namely human α-synuclein, which has been extensively characterized as an extended IDP in the monomeric form under physiological conditions (14, 15, 16, 17, 18, 19, 20, 21, 22, 23). α-synuclein, a 140-residue presynaptic protein, adopts an ensemble of disordered states that have some propensity to exhibit long-range interactions (17, 18, 19, 20), and it is implicated in the etiology of Parkinson’s disease in its aggregated form (15). An IDP such as α-synuclein, comprising predominantly an ensemble of expanded coils, is largely devoid of stable local interactions, and therefore, we envisioned that the observed chain dynamics can be unambiguously attributed to the large-scale segmental mobility arising due to backbone torsional fluctuations. In this work, we have performed residue-specific fluorescence depolarization studies using picosecond time-resolved fluorescence anisotropy measurements to discern the side-chain and backbone dynamics. We first describe the dynamic characteristics of a model (globular) protein, namely, β₂-microglobulin in its folded- and unfolded forms. We then characterize the intrinsic backbone torsional mobility of a natively disordered state of α-synuclein in a site-specific manner. Finally, we show that this inherent backbone dynamics is also present in an intrinsically disordered segment of a folded protein, such as the prion protein.

Materials and Methods

Mutagenesis, protein expression, purification, and sample preparation

Human α-synuclein cloned in pT7-7 plasmid and transformed into Escherichia coli BL21(DE3) was used for protein expression. A single tryptophan (Trp) was introduced at 10 different residue positions (F4W, A27W, Y39W, A56W, A69W, A78W, A90W, A107W, A124W, and A140W) using the site-directed mutagenesis kit QuikChange, purchased from Stratagene (San Diego, CA). The recombinantly expressed protein was expressed, purified, and characterized using the protocol described previously (24). Protein solutions prepared in Dulbecco’s phosphate buffer saline (2.67 mM KCl, 1.47 mM KH₂PO₄, 138 mM NaCl, and 8.06 mM Na₂HPO₄; pH 7.4). Before every experiment, all the protein solutions were filtered through a 50 kDa AMICON filter to remove oligomers, if any, and then concentrated using a 3 kDa AMICON filter (Millipore, Billerica, MA). The stock of proteins was diluted to get a final concentration of 25 μM. A recombinant human prion protein (PrP 90-231) gene cloned in pQE-30 was expressed in E. coli strain SG13009(pREP4) and purified using the protocol described previously (25). The protein samples were prepared in 5 mM phosphate buffer, pH 7.2. A single Trp mutant of human β₂-microglobulin was created using overlap extension polymerase chain reaction. The construct (W60F) was transformed into BL21 (DE3) pLysS E. coli strain. Protein purification was carried out using Q-Sepharose resin followed by gel filtration chromatography.

Time-resolved fluorescence anisotropy measurements

Picosecond time-resolved fluorescence anisotropy decay measurements were carried out using a Ti:sapphire laser coupled to a time-correlated single-photon-counting setup as described in our previous publications (26). The laser wavelength of 885 nm frequency tripled (third harmonic output) to obtain an excitation wavelength of 295 nm. The instrument response function was collected using a dilute colloidal suspension and was estimated to be ∼40 ps. The Trp fluorescence emission was collected using a microchannel plate photomultiplier (model 2809u; Hamamatsu, Hamamatsu City, Japan). The fluorescence intensity decays (I (t)) were collected at the magic angle (54.7°) at 350 nm with a bandpass of 10 nm. The photon counts at the peaks were at least 10,000. The intensity decays were deconvoluted with respect to the instrument response function and were analyzed using the equation

$$I\left(t\right)=\sum _i{\alpha }_i{e}^{-t/{\tau }_i},$$ (1)

where ${\alpha }_i$ and ${\tau }_i$ represent the contributions and lifetime, respectively, of the different lifetime components and were used in the anisotropy decay analysis.

For fluorescence depolarization measurements, fluorescence was collected at 0° (I_|| (t)) and 90° (I_⊥(t)) with respect to the excitation polarization. I_||(t) was always corrected using the G-factor that was independently obtained using the free Trp analog N-acetyl-L-tryptophanamide (NATA) in water (Fig. S1 in the Supporting Material). The anisotropy decays were analyzed by globally fitting I_||(t) and I_⊥(t) using

$$I\Vert \left(t\right)=\frac{I\left(t\right)\left[1+2r\left(t\right)\right]}{3},$$ (2)

$$I\perp \left(t\right)=\frac{I\left(t\right)\left[1-\mathit{r}\left(t\right)\right]}{3}.$$ (3)

The time-resolved anisotropy decays (r(t)) can be described by a biexponential decay law that accounts for the fast and slow rotational correlation time components as given below.

$$r\left(t\right)=r_0\left[{\beta }_{\text{fast}}\text{exp}\left(-t\text{/}{\varphi }_{\text{fast}}\right)+{\beta }_{\text{slow}}\text{exp}\left(-t\text{/}{\varphi }_{\text{slow}}\right)\right],$$ (4)

where r₀ represents the initial anisotropy of a Trp, and ϕ_fast and ϕ_slow represent the fast and slow rotational correlation times, respectively, with β_fast and β_slow as their corresponding amplitudes. r₀ was estimated using NATA in glycerol and found to be 0.200 ± 0.005, which is close to the previously reported r₀ value for Trp (27) (Fig. S1). In the anisotropy decay analysis program, an r₀ value of 0.200 ± 0.005 was used. To get an initial estimate of all the anisotropy decay parameters, the analyses were performed by floating all the parameters. Subsequently, to assess the robustness of the recovered rotational correlation times, one rotational correlation time was fixed at different values, whereas the other parameters were floated. In each case, the goodness of fit was assessed by reduced χ² values, randomness of residuals, and autocorrelation analysis (see Figs. S3–S7 for representative data analysis, Table S1 for recovered parameters, and Table S2 for mean rotational correlation times with errors).

Dynamic-light-scattering measurements

The samples were prepared and filtered as described in the sample preparation section. The dynamic-light-scattering (DLS) measurements were carried out on a Zetasizer Nano ZS90 instrument (Malvern Instruments, Malvern, United Kingdom).

Results and Discussion

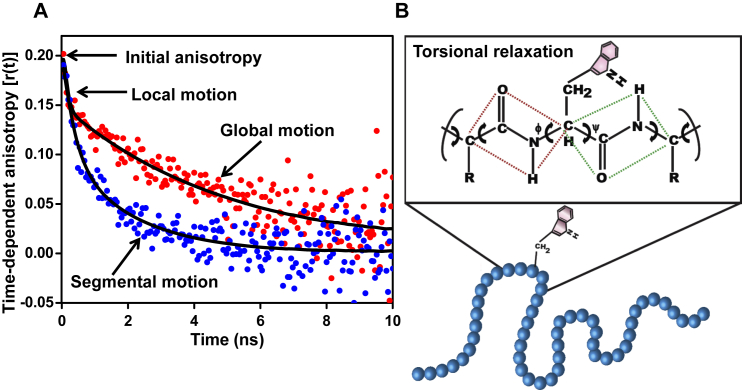
As a prelude, we first describe the characterization of the dynamic signatures of a (folded) globular protein in both the native and the denatured forms. To capture the dynamic characteristics at a high temporal resolution, we utilized picosecond time-resolved fluorescence depolarization measurements that offer some unique capabilities: 1) the high-time-resolution allows one to discern the chain dynamics down to picoseconds; 2) the autonomous dynamics of specific segments containing the probe can be determined in a site-specific manner without the influence of the entire protein; and 3) the high sensitivity of fluorescence is well-suited for studying the dynamics of the monomeric form of an aggregation-prone protein at low micromolar concentrations. The measurement of depolarization kinetics of Trp offers a powerful mean to delineate the different modes of rotational relaxation in proteins on the timescale of fluorescence decays (28, 29, 30, 31, 32). In these depolarization measurements, Trp is excited using polarized picosecond laser pulses, and the emission decays are collected at parallel and perpendicular polarizations. These intensity decays are globally analyzed to extract the different modes of dynamics in the range of picoseconds to nanoseconds (see Materials and Methods). The constructed time-resolved fluorescence anisotropy decay curves represent the depolarization kinetics and depict the randomization of the transition dipoles from an initial value to zero owing to the rotational relaxation of Trp due to local, segmental, and/or global protein motion. For instance, a folded globular protein containing a Trp, such as β₂-microglobulin, typically exhibits biexponential depolarization kinetics (Fig. 1) that can be described using a well-known “wobbling-in-a-cone” model (33, 34). The early subnanosecond (ϕ_fast ≤ 0.2 ns) component represents the local rotational motion of the Trp side chain, whereas the longer component (ϕ_slow = ∼5 ns) indicates the global tumbling of the entire protein that is related to the hydrodynamic radius (R_h = ∼2 nm) by the Stokes-Einstein relationship (Eq. 5),

$${\varphi }_{\text{slow}}=\frac{\frac{4}{3}\pi R_{\text{h}}^3\eta }{k_{\text{B}}\text{T}},$$ (5)

where η is the viscosity, k_B is the Boltzmann constant, and T is the absolute temperature.

Figure 1.

(A) Time-resolved fluorescence anisotropy decays of a single-Trp variant of β₂-microglobulin (Trp-95) in the native state (red solid circles), indicating local and global motions, and in the denatured state (4 M guanidine hydrochloride) (blue solid circles), indicating the segmental motion of the unfolded state. The black solid lines are anisotropy decay fits. For details of data acquisition and analysis, see Materials and Methods. See Fig. S1 for anisotropy decay of a free fluorophore in water and in a glycerol-water mixture. (B) Schematic of backbone torsional mobility of an unfolded polypeptide chain in the ϕ-ψ dihedral space. To see this figure in color, go online.

Upon unfolding using a high concentration of guanidine hydrochloride, the longer rotational correlation time decreased to ∼3 ns despite an increase in the overall hydrodynamic volume of the protein (Fig. 1 A). This correlation time, with the bulk viscosity correction, is in agreement with a previous report (26) and may correspond to the backbone segmental mobility, which is independent of the global rotational tumbling (Fig. 1 B). However, as discussed earlier, the recovered correlation time cannot be used to quantify the segmental mobility in the denaturant-induced disordered state due to the change in the microviscosity and the binding of denaturant to the polypeptide chain. Therefore, we next measured the fluorescence depolarization kinetics of natively unfolded α-synuclein to eliminate the extraneous factors. In addition, an expanded coil, such as α-synuclein, is devoid of any stable intrachain interactions, and therefore, we conjectured that the observed polypeptide chain dynamics could be unambiguously attributed to the backbone torsional fluctuations. Before embarking on the depolarization measurements, we carried out DLS experiments on α-synuclein to obtain its hydrodynamic size and an estimate of the rotational correlation time. Our DLS data revealed that the hydrodynamic radius (R_h) of α-synuclein is ∼3 nm (Fig. S2), which is in accordance with a previous report (35). Therefore, according to Eq. 5, the rotational correlation time of the entire protein molecule was estimated to be ∼25 ns.

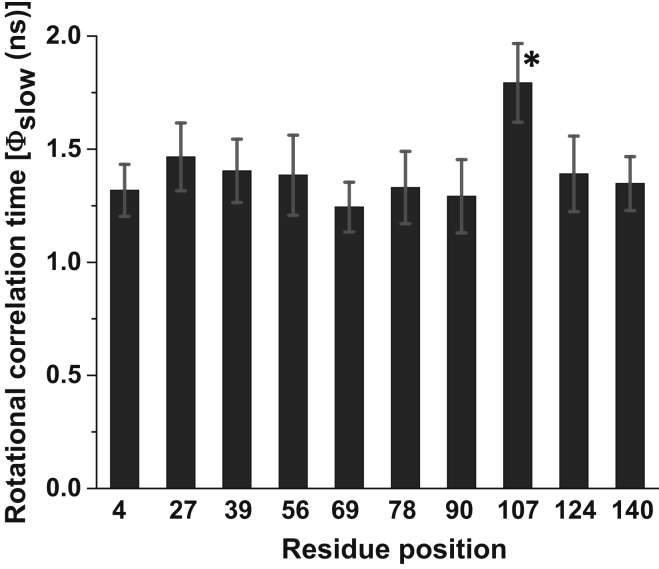
Since α-synuclein is devoid of Trp, we utilized site-directed mutagenesis to incorporate single Trps at various residue positions over the entire polypeptide chain from the N- to the C-terminal ends (Fig. 2) and confirmed that the mutations did not affect the conformational characteristics of α-synuclein (24). These single Trp variants enabled us to monitor the time-resolved fluorescence depolarization, which provided dynamical insights into the disordered polypeptide chain of α-synuclein at the residue-specific level. For all nine different locations (residues 4, 27, 39, 56, 69, 78, 90, 124, and 140), analysis of the time-resolved anisotropy decays exhibited two well-separated rotational correlation time components (Fig. 3 and Eq. 4). The fast, subnanosecond component (ϕ_fast = ∼0.2 ns) reveals the local rotational mobility of Trp, resulting in ∼50% depolarization of the initial anisotropy, and, as anticipated, the C-terminal residue (Trp-140) exhibited the end effect and showed much higher amplitude (∼70%) of the local mobility. The remaining part of the depolarization kinetics is contributed by a longer nanosecond component (ϕ_slow) of 1.37 ± 0.15 ns (Fig. 4), which is over an order of magnitude faster than the global correlation time estimated from our DLS results (∼25 ns) and hence cannot represent the global tumbling of the entire protein. Therefore, such a short rotational timescale indicated that the large-amplitude backbone segmental fluctuations in the disordered state are sufficient to completely depolarize the Trp transition dipoles.

Figure 2.

(A) Amino acid sequence of α-synuclein. Underscored residues indicate sites of single-Trp mutations, and the asterisk indicates a pre-proline residue at position 107 (see text). (B) One of the NMR structures (18) of expanded α-synuclein taken from the protein ensemble database (http://pedb.vib.be; PeDB: 9AAC; conformation no. 147) and generated using PyMOL (Version 1.8, Schrödinger, LLC, New York). Single Trp mutation positions are shown in yellow. To see this figure in color, go online.

Figure 3.

Representative time-resolved fluorescence anisotropy decays of single-Trp mutants of α-synuclein. (A) Trp-39. (B) Trp-78. (C) Trp-140. The insets show the global fitting of parallel (I_||(t)) and perpendicular (I_⊥(t)) intensity components. (D) Trp-107. The inset shows the overlay of the decay fits for Trp-78 and Trp-107 in the log scale, indicating a slower decay for Trp-107. The fits are indicated by black solid lines. See Materials and Methods for data acquisition and analysis and Table S1 for the mean fluorescence lifetime and the typical parameters associated with the decay analysis. See Figs. S3–S6 for the global fitting of parallel and perpendicular intensity decays, residual plots, and the autocorrelation analysis. A representative plot of rotational correlation time (ϕ_slow) and goodness of fit (χ²), indicating the robustness of the recovered rotational correlation times, is shown in Fig. S7. To see this figure in color, go online.

Figure 4.

Longer rotational correlation times (ϕ_slow) for different residue positions. The standard deviations were estimated from independent experiments and analyses. The asterisk indicates a slower correlation time for the pre-proline residue Trp-107. See Table S2 for the mean rotational correlation times with errors.

If the depolarization of Trp anisotropy is solely governed by the torsional mobility, one would expect a dampened relaxation time at a pre-proline residue, since proline comprises a pyrrolidine ring with a fixed ϕ of −60° and imparts significant restriction on the ψ dihedral angle rotation of the preceding carbon atom (C^α−C=O) (36). To test this hypothesis, we used another single Trp variant, previously created by us (24), at residue 107, which is located just before Pro-108 (Fig. 2 A). Indeed, this pre-proline residue exhibited restrained backbone mobility with a rotational correlation time of ∼1.8 ns (Fig. 3 D), suggestive of limited conformational accessibility in the Ramachandran ϕ-ψ dihedral angle space. Taken together, a characteristic timescale of ϕ_slow = ∼1.4 ns indicates that the rotational correlation time is independent of the overall rotational tumbling and residue position, except for a pre-proline residue (Fig. 4). The constancy in ϕ_slow along the polypeptide chain provides evidence in favor of the rapidly fluctuating ensemble of disordered states devoid of any significant local structure. In contrast to extended disordered proteins, the fluorescence depolarization kinetics of either folded proteins or collapsed globules, demonstrating small-amplitude backbone segmental mobility, can be satisfactorily explained by the rotational tumbling of the entire molecule, since the backbone dynamics does not significantly contribute to depolarization (26). Therefore, our observation is also consistent with the hypothesis that an extended polypeptide chain possesses a large-amplitude backbone flexibility that is independent of tumbling.

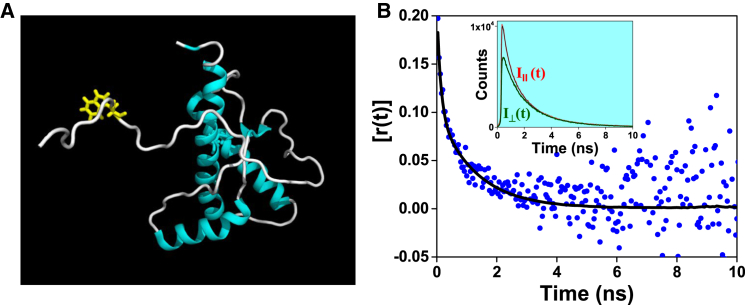
To demonstrate the power of fluorescence depolarization to capture the characteristic backbone dihedral fluctuations in the intrinsically disordered regions of globular proteins, we chose the human prion protein (PrP 90-231) containing an N-terminal unstructured segment juxtaposed with a predominantly helical globular domain. PrP, which is associated with (deadly) transmissible neurodegenerative diseases, switches to an amyloid state in vitro and contains a single Trp at residue position 99 encompassing the flexible disordered domain between residues 90 and 125 (Fig. 5 A) (25, 37, 38, 39). The time-resolved fluorescence anisotropy measurements revealed the presence of ϕ_slow = ∼1.3 ns, demonstrating the existence of intrinsic backbone dynamics in a disordered segment of a folded protein (Fig. 5 B). We point out that Trp-99 did not experience the presence of the folded domain, which is 26 residues away. Therefore, we suggest that the internal backbone dynamics will allow us to characterize a wide range of IDPs and will distinguish the flexible segments in intrinsically disordered regions of multidomain proteins.

Figure 5.

(A) The NMR structure of human PrP (90–231) ((39) PDB: 2LSB) generated using PyMOL (Version 1.8, Schrödinger, LLC, New York). The single (intrinsic) Trp located at the 99th position of the N-terminal unstructured region is shown in yellow. (B) Time-resolved fluorescence anisotropy decay of PrP. The inset shows the global fitting of I_||(t) and I_⊥(t). To see this figure in color, go online.

The backbone segmental motion in proteins arises due to several rotatable C^α-N and C^α-C bonds on both sides of a residue, which is manifested in ϕ_slow. Although the single-bond rotations occur on the picosecond timescale, the rotations around C^α-N and C^α-C bonds are hindered due to steric clashes, and therefore, the complete loss in the correlation observed by fluorescence depolarization requires torsional relaxation in the ϕ-ψ dihedral angle space over several residues on both sides. In other words, the torsional mobility in the ϕ-ψ dihedral angle space that is essential to completely randomize the transition dipole is felt over a short peptide length over which the correlation of direction is lost. Beyond a certain length, the fluorescence depolarization kinetics will be insensitive to the torsional relaxation. Therefore, the observed rotational relaxation time is linked to the persistence length of the polypeptide chain, in which the orientations of the segments are correlated. For disordered polypeptides in the excluded-volume limit, the local length scale spans nearly seven residues in which the correlated sequence-specific effects are manifested (40, 41). In fact, our recovered correlation time (∼1.4 ns) is in close agreement with the estimated reorientation timescale (1.3–1.6 ns) of 14-residue statistical (Kuhn’s) segments of α-synuclein (42). In addition, our data corroborate the previous results obtained from molecular dynamics (MD) simulations that characterized the local dihedral angle fluctuations of flexible loops and unfolded proteins (34, 43). In fact, the results from MD and NMR also indicated the presence of a timescale ranging between 1.3 and 1.4 ns that corresponds to the short-range dihedral angle fluctuations in the unfolded state (43). We do not rule out the presence of a small fraction of long-range and global conformational dynamics that are not detected due to the limited time window offered by the short fluorescence lifetime of Trp (∼2 ns). Nevertheless, our picosecond time-resolved fluorescence depolarization quantifies the short-range torsional dynamics, whereas the previous NMR relaxation measurements detected the long-range correlated dynamics on a slower timescale (5–8 ns) (42). Thus, fluorescence depolarization and NMR relaxation measurements complement each other and can be coupled to construct a comprehensive backbone dynamical map of disordered proteins.

Conclusions

In summary, we have carried out sensitive and site-specific time-resolved depolarization measurements to discern local conformational hopping in the ϕ-ψ space. Our findings provide an experimental underpinning for the existing results obtained using MD simulations. Fluorescence depolarization measurements allowed us to access a timescale that is not easily obtainable in other relaxation measurements. In addition, since fluorescence emission is highly sensitive, one can use much lower protein concentrations to study a predominantly monomeric form, minimizing the effect of aggregation. This approach can also be utilized at the single-molecule level by using much brighter fluorophores. The use of long-lifetime fluorescent probes will further improve the characterization of a wide range of dynamical events. Site-specific backbone segmental mobility will be highly sensitive to the local and global structural transitions, the coil−to−globule transition, the presence of chimeric structural components, and “composition-to-conformation” relationships in IDPs (44, 45). Furthermore, the torsional mobility will be a powerful readout to monitor disorder-to-order transitions during amyloid aggregation of IDPs and unordered peptides (46, 47, 48). In addition, recent all-atom MD simulations have revealed that the hops in the dihedral angle space provide the dominant mechanism of internal friction (49, 50). We envision that the experimental quantification of short-range segmental mobility will allow us to decipher the contribution of internal friction in IDPs and in the disordered regions of proteins.

Author Contributions

S.M. conceived and designed research; N.J., D.N., K.B., V.D., and M.B. performed research; N.J., D.N., V.D., S.A., M.B., and S.M. analyzed data; and M.B. and S.M. wrote the article.

Editor: Elizabeth Rhoades.