Abstract
Medication adherence is thought to be the principal clinical predictor of positive clinical outcomes, not only for serious mental illnesses such as schizophrenia, bipolar disorder, or depression, but also for physical conditions such as diabetes. Consequently, research on medication often looks not only at medication condition (e.g., placebo, standard medication, investigative medication), but also at adherence in taking those medications within each medication condition. The percentage (or proportion) scale is one of the more frequently employed and easily interpretable measures. Patients can be 0% adherent, 100% adherent, or somewhere in between. For simplicity, many reported adherence analyses dichotomize or trichotomize the adherence predictor when estimating its effect on outcomes of interest. However, the methodological literature shows that the practice of categorizing continuously distributed predictors reduces statistical power at best and, at worst, can severely bias parameter estimates. This can result in inflated Type I errors (false positive acceptance of null adherence effects) or Type II errors (false negative rejection of true adherence effects). We extend the methodological literature on categorization to the construct of adherence. The measurement scale of adherence leads to a diverse family of potential distributions including uniform, n-shaped, u-shaped (i.e., bimodal), positively skewed, and negatively skewed. Using a simulation study, we generated negative, null, and positive “true” effects of adherence on simulated continuous and binary outcomes. We then estimated the adherence effect with and without categorizing the adherence variable. We show how parameter estimates and standard errors can be severely biased when categorizing adherence. The categorization of adherence is shown to cause null effects to become positive or negative depending on the distribution of the simulated adherence variable, inflating Type I errors. When the adherence effect was significantly different from zero, categorization can render the effect null, inflating Type II errors. We recommend that adherence be measured continuously and analyzed without categorization when using it as a predictor in regression models.
Keywords: adherence, measurement, serious mental illness, general medicine, health behavior
INTRODUCTION
Adherence to prescribed medication regimens is thought to improve clinical outcomes and reduce the need for costly interventions, including hospitalizations, which are sometimes necessary to stabilize conditions exacerbated due to outpatient medication nonadherence (Sokol et al., 2005). Clinical and cost benefits of adherence have been identified for a variety of mental health (Davis et al., 2003; Ascher-Svanum et al., 2010) and physical (Hepke et al., 2004; Wood et al., 2003; Simpson et al., 2006; Ho et al., 2009) conditions across both individual studies and meta-analytic work. However, there may be reasons to reconsider such findings, principally related to the impact of categorizing continuous measures of adherence when they are modeled as independent variables. Specifically, the International Society of Pharmacoeconomics and Outcomes Research (ISPOR) recommends that any categorization of adherence data should be both clinically justified and subjected to a statistical sensitivity analysis (Peterson et al., 2007), although this appears to be rare in practice. Of concern, prior methodological research has illustrated that categorizing normally distributed predictors reduces statistical power at best and, at worst, can severely bias parameter estimates (MacCallum et al., 2002). Biased estimates of the effects of adherence, if they are present, have implications for policy, clinical care, decision models, and efficacy and effectiveness trials. For example, it is estimated that if adherence could be increased by as little as 20%, annual Medicaid rehospitalization savings would approach $7.5 million (Sun et al., 2007); however, it is unclear if these estimates are accurate in light of biases that may result from categorizing medication adherence. In the current study, we attempt to expand on ISPOR recommendations by quantifying the biases resulting from categorizing adherence data via a simulation study.
Measuring Adherence
The medication adherence literature reveals that there are multiple ways to measure adherence to a prescribed regimen, that some sort of categorization is undertaken frequently, and that many categorization thresholds are employed. This variability suggests that adherence researchers as a whole are struggling to define adherence in some categorical way, identifying the adherent from the nonadherent.
The measurement of adherence falls into three broad categories: self-report, pill count, and derivation via administrative data. Self-report measures can be simple, such as a binary indicator of adherence to the prescribed regimen on a “regular” basis (Svarstad et al., 2001) or some other threshold (e.g., possessing medication 80% of the days under study) (Olfson et al., 2014; Swartz et al., 1998a; Knapp et al., 2004; Swanson et al., 2007; Swartz et al., 1998b). Some studies develop scales to measure medication adherence (e.g., Yen et al., 2005), including the Brief Adherence Rating Scale, for example (cf., Byerly et al., 2008). Others ask respondents the number of days they adhered to their medication over a given time frame and compute the percentage adherent (e.g., Maggiolo et al., 2007). Semistructured interviews capturing the percentage of doses taken have also been used to estimate adherence (Hommel et al., 2008).
Pill counts or counts of missed doses allow researchers to determine percent compliance by dividing the number of pills taken by the number prescribed. This approach has been used in psychiatric research (Swanson et al., 2008), antiretroviral therapy (Ballif et al., 2009), and cardiovascular disease (Wei et al., 2008). Alternatively, some studies simply record whether any medication was taken, as done in research on malaria treatment (Onyebuchi et al., 2014). Medication event monitoring systems, which record the number of times, in addition to the day and time, the bottle was opened have also been used in cancer research (Ibrahim et al., 2011; Ferguson et al., 2005) and psychiatric research (Byerly et al., 2005; Remington et al., 2007; Nakonezny et al., 2008).
Medical claims or medical possession data are used frequently to construct measures of adherence on a continuous percentage scale. One such example is the medication possession ratio (MPR), which is based on the total days of supply with the denominator being a refill interval, and can take values ranging from 0% to more than 100%. The MPR has been used in studies of antipsychotics (Van Dorn et al., 2013; Weiden et al., 2004; Valenstein et al., 2006; Ivanova et al., 2012; Gilmer et al., 2004; Valenstein et al., 2002), hormone therapy (Hsieh et al., 2014; Hershman et al., 2011), respiratory therapy (Vestbo et al., 2009), or for multiple health conditions (Sokol et al., 2005; Roebuck et al., 2011). Another measure used increasingly with medical claims data is the proportion of days covered (PDC), which is frequently used in diabetes research (Nichols et al., 2015; Buysman et al., 2015; Juarez et al., 2013). PDC values range between 0 and 1 and are based on the total days all drugs were available divided by the days in the follow-up period. As with MPR, the PDC can be multiplied by 100 to transform it to a percentage scale. Measures like MPR or PDC can be computed from medical records, as done for injection antipsychotic adherence (Acosta et al., 2014).
Categorizing Adherence
When categorizing adherence based on adherence measured on a percentage scale, the choice of cut values often appears to be arbitrary and lacking scientific justification (Peterson et al., 2007). However, increasingly, studies are using an 80% threshold (Van Dorn et al., 2013; Acosta et al., 2014; Valenstein et al., 2006; Ivanova et al., 2012; Nichols et al., 2015; Buysman et al., 2015; Hommel et al., 2008; Wei et al., 2008; Juarez et al., 2013; Vestbo et al., 2009; Hershman et al., 2011; Roebuck et al., 2011; Valenstein et al., 2002). Other binary cuts are also used, including 70% (Weiden et al., 2004) or 85% (Ibrahim et al., 2011).
Other studies cut adherence into three or more categories. Trichotomization has been used with cuts at 50% and 80% (Nichols et al., 2015; Gilmer et al., 2004). Other studies move beyond three levels, including, for example, categories representing extremely low (< 55%), low (55%–75%), intermediate (76%–95%), and high (> 95%) levels of adherence, which have been used for AIDS studies (Maggiolo et al., 2007). Categories of 1%–19%, 20%–39%, 40%–59%, 60%–79%, and 80%–100% have been used in hospitalization and antiviral therapy studies (Sokol et al., 2005; Yasuda et al., 2004). Other studies have used cut points for adherence representing never/almost never (0%–25% of the time), sometimes (26%–50% of the time), usually (51%–75% of the time), and always/almost always (76%–100% of the time; Elbogen et al., 2005).
Summary of Adherence Measurement and Categorization
In summary, measurement of adherence is often on a proportion scale from 0 to 1, or percentage scale from 0% to 100%, although many other approaches are used. Frequently, however, the original scaling of the adherence independent variable is categorized, and often it appears, without clinical justification (Peterson et al., 2007). Although a categorized independent variable may be interpreted more intuitively in a regression model (but see below for how adherence effects can be interpreted incorrectly), including the specification of interaction effects, the risk of potential biased results would suggest that the practice of categorizing adherence, when used as an independent variable, should be limited and implemented only when clinically or empirically justified. As note previously, two of the most common categorizations are dichotomization at 80% and trichotomization at 50% and 80%, and we use these conventions in the current study.
The variability in the reported studies suggests that the implicit goal is to cut the continuum of adherence into the adherent and nonadherent, although little empirical work has been done to justify cutting the continuum of adherence. Such efforts are found lacking in the literature, but if they are to be carried out, they will be philosophically challenging and methodologically demanding (Lubke & Tueller, 2010; Lubke & Miller, 2015; Asmundson et al., 2012; Lilienfeld, 2014). In addition, and as noted previously, the methodological literature has shown that categorizing continuous variables without strong justification likely results in reduced statistical power and increased bias in parameter estimates (MacCallum et al., 2002; Fedoro et al., 2009; DeCoster et al., 2009; Shentu & Xie, 2010).
THE COUNTERINTUITIVE INTERPRETATION OF PARAMETER ESTIMATES WHEN CATEGORIZING ADHERENCE
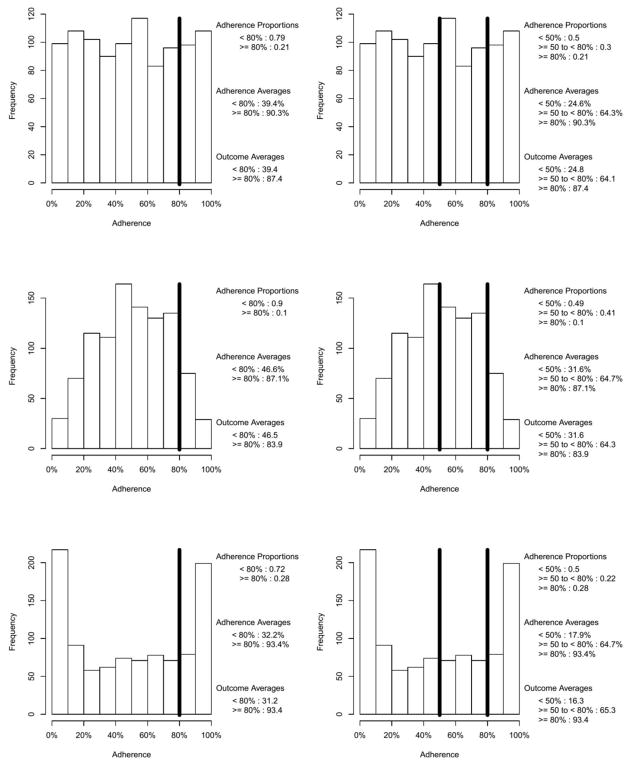
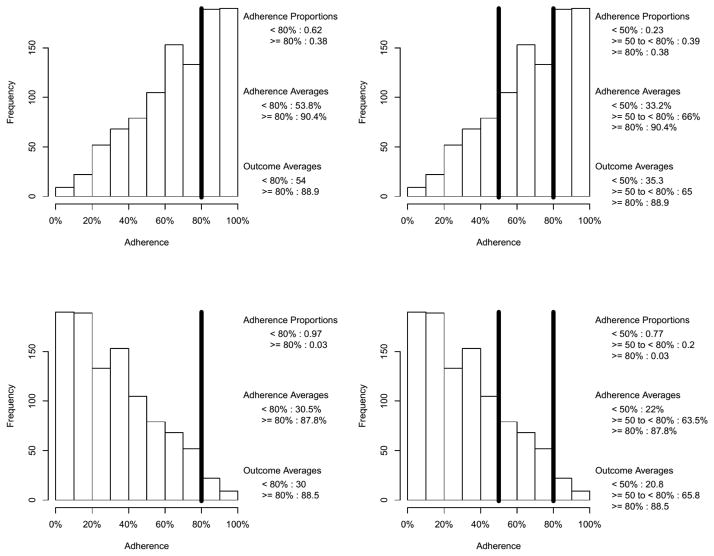
In this section, we illustrate how an adherence threshold of, say, 80%, can be easily misunderstood. At first glance, one might think the effect of adherence dichotomized at 80% on some outcome can be interpreted as the effect of being 80% adherent or higher; this is an imprecise and potentially misleading conclusion. To see why, consider the situation where a one-unit increase in adherence (measured continuously on the percentage scale) is associated with a one-unit increase in some outcome (i.e., B1 = 1). Further consider five different potential adherence distributions, uniform, n-shaped, and u-shaped (see Figure 1a) and negatively skewed and positively skewed (see Figure 1b). As noted previously, adherence research rarely reports the distribution of adherence. We have observed u-shaped and negatively skewed adherence distributions in prior studies of antipsychotic (Swanson et al., 2006) and statin medications (Pringle et al., 2014). Using the equation = B1 * adherence + ε, a population true parameter of B1 = 1, an effect size R2 = .5, and normally distributed simulated error terms, we simulated the adherence distributions of Figures 1a and 1b and constructed normally distributed outcome variables for 1,000 participants yielding five data sets, one for each adherence distribution. Three models were fit to the data set for each of the five adherence distributions, first with the continuous adherence predictor shown in Figures 1a and 1b, second with the adherence predictor dichotomized at 80% (see the left columns of Figures 1a and 1b), and third with the adherence predictor trichotomized at 50% and 80% (see the right columns of Figures 1a and 1b). The estimated parameters and R2 values are given in Table 1.
Figure 1.
Figure 1a. Illustrative Uniform, n-shaped, and u-shaped Continuous Adherence Distributions With a Binary Cut at 80% (left column) and Tertiary Cuts at 50% and 80% (right column)
Figure 1b. Illustrative Negatively and Positively Skewed Continuous Adherence distributions With a Binary Cut at 80% (left column) and Tertiary Cuts at 50% and 80% (right column)
Table 1.
| Shape of Uncategorized Adherence Distribution | Parameter Estimates (True Value B = 1)
|
R2 Estimates (True Value R2 = .5)
|
|||||
|---|---|---|---|---|---|---|---|
| Uncategorized Adherence on the 0%–100% Scale | Binary Adherence Cut at 80% | Tertiary Cut
|
Uncategorized Adherence on the 0%–100% Scale | Binary Adherence Cut at 80% | Tertiary Adherence Cut at 50% & 80% | ||
| < 50% vs. 50% to < 80% | 50% to 80% vs. ≥ 80% | ||||||
| Uniform | 0.97 | 48.0 | 39.3 | 62.6 | 0.48 | 0.23 | 0.40 |
| u-shaped | 0.98 | 37.4 | 32.7 | 52.2 | 0.49 | 0.13 | 0.37 |
| n-shaped | 1.02 | 62.2 | 49.0 | 77.1 | 0.50 | 0.31 | 0.45 |
| Negative skew | 1.01 | 31.0 | 29.2 | 53.2 | 0.50 | 0.32 | 0.42 |
| Positive skew | 0.99 | 58.0 | 43.4 | 63.1 | 0.49 | 0.03 | 0.30 |
The first thing to notice in Table 1 is that if, in fact, one were estimating the effect of being at least 80% compliant, the parameter estimates under both binary and tertiary categorizations are highly variable across the shapes of the uncategorized adherence distribution. The second is that the correct population values of B1 = 1 and R2 = .5 are recaptured when using the continuous adherence predictors. Third, when using the categorized adherence predictors, the estimated R2 values are all attenuated, ranging from slightly attenuated to the extreme being near zero (R2 = .03 for the binary cut of the positively skewed uncategorized adherence distribution). Finally, the parameter estimates for the effect of dichotomized and trichotomized adherence on the outcome appear at first glance to be extremely overestimated. Specifically, the parameter estimates for uncategorized adherence are near the population value of B1 = 1 while the categorized estimates are over an order of magnitude larger, ranging from 29.2 to 77.1.
To understand what these large parameter estimates with a categorized adherence predictor actually represent, consider the following: The average of the outcome within each adherence category, which is given in the lower legend of each panel in Figures 1a and 1b, can be used to calculate the mean difference between categorizations. These values allow one to see the relationships between these mean differences (which is what is being tested in a t-test) and the regression parameter estimates in Table 1.
This is illustrated using the first row of Figure 1a, the uniform adherence distribution. For the binary categorization, the simulated data produce a mean difference of 87.4−39.4 = 48.0. Note that 48.0 is the parameter estimate for the uniform distribution with the binary cut shown in Table 1. Hence, B1 = 48.0 is not the effect of being more than 80% adherent relative to the effect of being less than 80% adherent. Rather, it is the difference of an average outcome of 39.4 (i.e., the mean level of the outcome for all those with adherence < 80%) and an average outcome of 87.4 (i.e., the mean level of the outcome for all those with adherence ≥ 80%). Analogously (and noting that the lowest group is the reference category), 64.1−24.8 = 39.3 and 87.4−24.8 = 62.6, where 39.3 and 62.6 appear in the first line of Table 1 under the tertiary cut column. Hence, B1 = 39.3 is the effect of moving from an average outcome of 24.8% (i.e., the mean level of the outcome for all those with adherence < 50%) to 64.1 (i.e., the mean level of the outcome for all those with adherence ≥ 50% to < 80%) and B1 = 62.6 is the effect of moving from an average adherence of 24.8 to 87.4 (i.e., the mean level of the outcome for all those with adherence ≤ 80%).
The illustration of this section shows that one cannot interpret categorized adherence scores as being, for example, the effect of being at least 80% adherent on any given outcome. Rather, the effect must be interpreted as difference between the average outcome in one adherence category and the average outcome in the reference adherence category. Although this corrected interpretation may enlighten prior and future adherence research, the primary utility of this illustration is pedagogical and has two major limitations. First, for a single sample, this interpretation is most apparent under ideal conditions, for example, when [i] the outcome is continuous, [ii] the effect size is large (R2 ≥ .5), [iii] the sample size is large (n ≥ 1,000), and [iv] under bivariate linear regression (or under multiple linear regression with uncorrelated predictors). Second, the categorized effect might not be directly comparable from study to study unless the distribution of adherence is the same between studies. The distribution of adherence is rarely reported, regardless of whether adherence data are categorized. This potentially challenges any meta-analytic work using categorized adherence predictors, cautions future meta-analytic work, and suggests that adherence researchers should start providing the histogram for adherence.
Although this illustration is useful for understanding some of the issues that arise when categorizing adherence, it relies on a single simulated data set. As such, it is unable to provide information on Type I error rates (false positive acceptance of null adherence effects) or Type II error rates (false negative rejection of true adherence effects) or biases in estimated effect sizes. We conducted a simulation study to provide insight into these issues.
METHODOLOGY
The current work employs simulation methods to study the effects of categorizing adherence data when it is assumed that adherence is a predictor of some positive health outcome. A simulation study allows the researcher to create data with known conditions so that performance of a statistical method can be examined, allowing one to better understand the properties of the statistical method being applied. Simulation studies are used to mimic the processes wanting to be studied while controlling parts of the process (e.g., setting the effect size or types of adherence categorization) and allowing other parts to be random (e.g., simulating random residuals with a known variance). Each facet of the process that is being studied is called a factor in the simulation study, and each factor can have two or more levels. Using the parlance of ANOVA, all factors are typically crossed with all other factors, yielding a full factorial simulation design. Thousands of data sets are simulated within each cell of the factorial design, and results are aggregated within each cell to avoid drawing conclusions that might stem from sampling fluctuations of a single simulated data set. The factors examined for this study are detailed in the next section. In the current work, we mimic the process of estimating the effect of adherence after categorizing adherence measured on the percent scale at 80% or at 50% and 80%, two categorizations used frequently in adherence research as shown previously.
Simulation Study Design
Data were simulated from a simple bivariate linear regression model, y = B1 * adherence + ε. The residual variance ε was distributed normally with a variance selected as a function of B1 to achieve the desired effect size R2. The simulation factors, including the distribution of the adherence predictor, were as follows:
Distribution of adherence: Using a beta distribution, which ranges from 0 to 1, adherence was simulated according to the following shapes: uniform, n-shaped, u-shaped, negatively skewed, and positively skewed. To put scores on the percentage scale, adherence was multiplied by 100.
Categorization of adherence: For each simulated data set, we estimated the bivariate regression model when adherence was uncategorized, when it was dichotomized at 80%, and when it was trichotomized at 50% and 80%.
Effect size: We examined effect sizes of R2 = 0 (which allowed us to examine Type I error rates), and R2 = .1, .25, .5 (which allowed us to examine Type II error rates under a range of effect sizes).
Sample size: We examined sample sizes of 200, 500, and 1,000.
Distribution of y: The outcome variable y was either continuous as described previously, or binary with prevalences of either .9, .25, or .5 (or, analogously by inversion, .1, .75, and .5). For binary outcome variable conditions, bivariate logistic regression models were fit to the simulated data, and McFadden’s R2 (McFadden, 1974; Menard, 2000) is used as the effect size estimate.
These factors combined to yield a simulation study with 5 (adherence distribution) × 3 (adherence (non)categorization) × 5 (effect size) × 3 (sample size) × 4 (outcome distribution) = 900 conditions. For each condition, 5,000 data sets were simulated, yielding a total of 900 × 5,000 = 4.5 million analyses. From each analysis, the following results were saved: the estimate of R2, the estimate(s)* of B1, a binary indicator of whether a Type I error was made (for conditions where R2 = 0), and a binary indicator of whether a Type II error was made (for conditions where R2 > 0).
Data simulation and analysis of each simulated data set using linear or logistic regression was done in R 3.2.0 (R Core Team, 2015). When evaluating p-values, alpha (the Type I error rate) was set to .05.
RESULTS
In the sections that follow, we present the Type I/Type II error rate and bias of R2 results from the simulation study. As illustrated in the section on the counterintuitive interpretation of parameter estimates when dichotomizing adherence, the effect of adherence B1 on the outcome y has a different meaning from the uncategorized adherence to the categorized adherence conditions. Hence, we do not summarize results for the estimates of B1.
Type I and Type II Error Rates
The results for Type I and Type II error rates are summarized in Table 2. The empty cells (designated NA) in Table 2 follow a pattern. Type I errors (false positive conclusions that adherence is related to an outcome) are only defined when the true effect size is null (i.e., the simulation conditions where R2 = 0). Analogously, Type II errors (false negative conclusions that adherence is not related to an outcome) are only defined when the true effect size is not null (i.e., the simulation conditions where R2 > 0). Table 2 is stratified in columns by how adherence was treated in the analysis, whether it was left continuous, dichotomized, or trichotomized. Within each cell, the proportion of simulated data sets is given when a Type I and Type II error was made. This proportion is called the Type I (or Type II) error rate for the simulation study.
Table 2.
Type I and Type II Error Rates
| Simulation Factor | Type I Error Rate
|
Type II Error Rate
|
||||
|---|---|---|---|---|---|---|
| Uncategorized Adherence on the 0%–100% Scale | Binary Adherence Cut at 80% | Tertiary Adherence Cut at 50% and 80% | Uncategorized Adherence on the 0%–100% Scale | Binary Adherence Cut at 80% | Tertiary Adherence Cut at 50% and 80% | |
| R2 | ||||||
| 0.00 | 0.05 | 0.04 | 0.09 | NA | NA | NA |
| 0.05 | NA | NA | NA | 0.13 | 0.42 | 0.20 |
| 0.10 | NA | NA | NA | 0.03 | 0.27 | 0.09 |
| 0.25 | NA | NA | NA | 0.00 | 0.21 | 0.04 |
| 0.50 | NA | NA | NA | 0.00 | 0.38 | 0.09 |
| Distribution of the simulated outcome Y | ||||||
| Normal | 0.05 | 0.05 | 0.09 | 0.01 | 0.07 | 0.02 |
| Binary with 0.10/0.9 split | 0.05 | 0.04 | 0.07 | 0.09 | 0.65 | 0.27 |
| Binary with 0.25/0.75 split | 0.05 | 0.04 | 0.09 | 0.04 | 0.36 | 0.08 |
| Binary with 0.50/0.50 split | 0.05 | 0.05 | 0.09 | 0.03 | 0.19 | 0.05 |
| Simulated sample size | ||||||
| n = 200 | 0.05 | 0.04 | 0.08 | 0.11 | 0.51 | 0.24 |
| n = 500 | 0.05 | 0.04 | 0.09 | 0.01 | 0.29 | 0.06 |
| n = 1000 | 0.05 | 0.05 | 0.09 | 0.00 | 0.17 | 0.02 |
| Shape of uncategorized adherence distribution | ||||||
| Uniform | 0.05 | 0.05 | 0.09 | 0.04 | 0.25 | 0.09 |
| u-shaped | 0.05 | 0.04 | 0.09 | 0.04 | 0.41 | 0.09 |
| n-shaped | 0.05 | 0.05 | 0.09 | 0.04 | 0.17 | 0.08 |
| Negative skew | 0.05 | 0.05 | 0.08 | 0.04 | 0.14 | 0.05 |
| Positive skew | 0.05 | 0.04 | 0.08 | 0.05 | 0.63 | 0.21 |
Note. NA indicates cells that are not define for a given type of error. Specifically, Type I errors are defined when the true effect is null (R2 = 0), and Type II errors are defined when the true effect is non-null (R2 > 0).
For Type I error, using the uncategorized adherence variable as the predictor yielded the Type I error rate specified a priori, i.e., alpha = .05. When adherence was dichotomized, the Type I error rate was attenuated in some conditions. When adherence was trichotomized, the Type I error rate was inflated, meaning researchers will falsely conclude that adherence was related to the outcome up to nearly twice as often as expected with an alpha of .05.
Categorizing adherence was even more problematic for Type II errors. These effects are interpreted relative to the ideal situation where researchers did not categorize adherence. Here, Type II error rates follow patterns expected from the literature on statistical power, where power is 1 minus the Type II error rate. Larger effect sizes have lower Type II error rates. Binary outcomes (Y) have higher Type II error rates than continuous outcomes. Within binary outcomes, having higher variance (i.e., being closer to a .50/.50 cut) yields lower Type II error rates. Larger sample sizes have lower Type II error rates. The distribution of uncategorized adherence has essentially no impact on the Type II error rate relative to any other distribution of uncategorized adherence.
Although most of these patterns hold for categorized adherence, the Type II error rates range from mildly to highly inflated relative to using uncategorized adherence. This reflects the known property that categorization will in general reduce statistical power (MacCallum et al., 2002). The exception to the pattern described in the prior paragraph is the effect of the adherence distribution. The effect of the adherence distribution is especially large when dichotomizing adherence. Type II error rates exceeded .5 in several conditions such as low variance of binary outcomes, small sample size, or positively skewed adherence distribution. This makes conceptual sense—dichotomizing discards the maximum amount of information while still having a nonzero variance. The trichotomized classifications are not as severely affected as dichotomized results. However, this observation should not be taken as justification for trichotomizing instead of dichotomizing. In addition to the warnings and limitations discussed in the section on the counterintuitive interpretation of parameter estimates, Type II error rates can still be highly inflated relative to estimating models using uncategorized adherence.
Bias in Effect Size Estimates
The bias of R2 is the average of the differences between the R2 estimates and the true values of R2 from which the data were simulated. Table 3 provides the absolute and relative bias for each of simulated values of R2. As with the results in Table 2, categorizing adherence almost always yields greater bias than when fitting models with uncategorized adherence. Dichotomizing yields greater bias than trichotomizing. Bias is also almost always negative, indicating that the magnitude of the effect of adherence on the outcome will almost always be underestimated. The relative bias indicates what percentage of the true effect size was recovered on average. For example, when adherence was not categorized and the outcome variable (y) was continuous, there was no bias (i.e., relative bias = 1). When trichotomizing adherence, the estimated effect sizes were 82% to 100% of the true R2, while dichotomizing only estimated 44% to 50% of the true effect size on average. Also observe that the larger the effect size, the larger the bias in general. This is simply due to larger effects having a larger starting point from which to be biased.
Table 3.
Bias of R2 Estimates
| Distribution of the Simulated Outcome Y | R2 | Absolute Bias of R2 Estimates
|
Relative Bias of R2 Estimates
|
||||
|---|---|---|---|---|---|---|---|
| Uncategorized Adherence on the 0%–100% Scale | Binary Adherence Cut at 80% | Tertiary Adherence Cut at 50% and 80% | Uncategorized Adherence on the 0%–100% Scale | Binary Adherence Cut at 80% | Tertiary Adherence Cut at 50% and 80% | ||
| Continuous | 0.00 | 0.00 | 0.00 | 0.01 | NA | NA | NA |
| 0.05 | 0.00 | −0.03 | 0.00 | 1.00 | 0.40 | 1.00 | |
| 0.10 | 0.00 | −0.05 | −0.01 | 1.00 | 0.50 | 0.90 | |
| 0.25 | 0.00 | −0.14 | −0.04 | 1.00 | 0.44 | 0.84 | |
| 0.50 | 0.00 | −0.28 | −0.09 | 1.00 | 0.44 | 0.82 | |
|
| |||||||
| Binary with 0.10/0.9 split | 0.00 | 0.00 | 0.00 | 0.01 | NA | NA | NA |
| 0.05 | −0.02 | −0.03 | −0.02 | 0.60 | 0.40 | 0.60 | |
| 0.10 | −0.04 | −0.08 | −0.05 | 0.60 | 0.20 | 0.50 | |
| 0.25 | −0.11 | −0.20 | −0.14 | 0.56 | 0.20 | 0.44 | |
| 0.50 | −0.23 | −0.43 | −0.31 | 0.54 | 0.14 | 0.38 | |
|
| |||||||
| Binary with 0.25/0.75 split | 0.00 | 0.00 | 0.00 | 0.00 | NA | NA | NA |
| 0.05 | −0.02 | −0.04 | −0.03 | 0.60 | 0.20 | 0.40 | |
| 0.10 | −0.05 | −0.08 | −0.06 | 0.50 | 0.20 | 0.40 | |
| 0.25 | −0.11 | −0.20 | −0.14 | 0.56 | 0.20 | 0.44 | |
| 0.50 | −0.20 | −0.40 | −0.28 | 0.60 | 0.20 | 0.44 | |
|
| |||||||
| Binary with 0.50/0.50 split | 0.00 | 0.00 | 0.00 | 0.00 | NA | NA | NA |
| 0.05 | −0.02 | −0.04 | −0.03 | 0.60 | 0.20 | 0.40 | |
| 0.10 | −0.05 | −0.08 | −0.06 | 0.50 | 0.20 | 0.40 | |
| 0.25 | −0.12 | −0.19 | −0.14 | 0.52 | 0.24 | 0.44 | |
| 0.50 | −0.19 | −0.37 | −0.25 | 0.62 | 0.26 | 0.50 | |
Note. Absolute bias is the average of the differences between estimated R2 and the true value of R2. Relative bias is the average of the ratio of estimated R2 to true R2 (e.g., if estimated effect size is .2 and the true effect size is .5, .2/.5 = .4, or, the estimate is only 40% of the true value). Also note that rows average over adherence distribution and sample size, as these had relatively small effects on bias. For the binary outcome conditions, logistic regression was used and McFadden’s R2 was calculated. NA indicates relative bias that was not computable due to division by zero.
DISCUSSION
Across health conditions, including serious mental illnesses and physical health conditions like diabetes, HIV, and cardiovascular disease, adherence to prescribed pharmacological medication regimens are often the primary evidence-based or guideline-recommended interventions available. However, for many health conditions, when evaluating the effects of medication adherence on subsequent health states, researchers sometimes analyze a categorized version of the original continuous adherence variable. Moreover, the cut points used to categorize adherence appear to be selected without strong empirical or clinical justifications, and even when prior research cautions against categorizing continuous variables because it reduces statistical power and can increase bias (Peterson et al., 2007; MacCallum et al. 2002). We investigated, through a simulation study, the effects of categorizing a continuous adherence variable under multiple conditions, including categorizing adherence at 80% or at 50% and 80%, two categorizations used frequently in adherence research. The results of the simulation provide concrete examples of the negative impact of categorizing adherence, which is often measured on a proportion or percentage scale. The primary implications for future adherence research are first, to measure adherence continuously and second, to estimate the effects of adherence on outcomes without categorizing it.
The results of the current study also have implications for interpreting prior adherence research. First, reported estimates of the effects of adherence are prone to misinterpretation. As noted previously, interpretations of categorized adherence that compare, for example, being adherent less than 80% of the time to being adherent 80% or more of the time, are likely to be incorrect. Instead, the interpretation is correctly based on moving from the average adherence in one group to the average adherence in another group. In addition, within each category of categorized adherence there is variation around the mean-level of adherence. When adherence is categorized, this variation is discarded, which was shown in the simulation study to reduce statistical power. Moreover, this practice treats patients with more or less adherence than the mean level in the categorization as the same. It is unclear how this artificial reduction of heterogeneity in adherence might impact clinical or economic outcome research.
Next, correcting the interpretation of the effects of categorized adherence will not alleviate the reduced statistical power and increased bias in estimated effect sizes shown via a simulation study. That is, although it would be an improvement to see the effects of adherence interpreted correctly in future research, results from the current simulation study show that the outcomes reported from any individual study may be biased to such an extent that they are incorrect, for example, in identifying a significant effect when the true effect is null, or at least misstating the true magnitude of the adherence effect. Still, a correct interpretation of biased or incorrect results does not satisfactorily address the issue brought on by categorizing adherence in the first place.
Third, the distribution of adherence when measured on a continuous scale greatly impacts the interpretation of categorized adherence effects. Consequently, meta-analyses focusing on parameter estimates for effects of categorized adherence on outcomes will not yield comparable estimates unless the distribution of adherence when measured on a continuous scale is the same across studies. Unfortunately, these distributions are not typically reported in adherence research. Fourth, even though meta-analyses of effect sizes such as R2 might still be valid, the estimated effect sizes when categorizing adherences will be underestimated. Fifth, while increasing sample sizes does improve power relative to lower sample size, larger sample size alone is insufficient to ameliorate the negative consequences of categorizing adherence relative to analyses when a continuous measure of adherence is not categorized. Sixth, although trichotomization theoretically throws away less information than does dichotomization (as evidenced by trichotomization having lower Type II error raters than did dichotomization), trichotomization had higher Type I error rates than did dichotomization. Finally, the simulation study showed that categorizing adherence can dramatically decrease statistical power, giving researchers less of what they want when endeavoring to estimate the effect of adherence on important outcomes.
Although the results of this study are primarily cautionary, the recommendations to measure adherence on a continuous scale and not categorize it prior to estimating its effects on outcomes represent a first step in improving the measurement and modeling of adherence. We limited our investigation to the situation in which adherence was an independent variable. In standard regression models, one does not make distributional assumptions about the independent variable. Further investigation is required to develop guidelines on how to model adherence as a dependent variable. This will be required when adherence is treated as a cross-sectional outcome (e.g., when estimating the effect of predictors of adherence such as affordability, access, or concurrent routine, nonpharmacologic interventions), when adherence is treated as a mediator (e.g., when estimating the effect of something thought to be related to both adherence and some primary health outcome), or when adherence is treated as an longitudinal outcome (e.g., when estimating how changes in adherence impact changes in health outcomes).
Another limitation of this work was the assumption of a linear relationship between adherence and the simulated outcome variable. If achieving some cut at adherence such as 80% had a truly meaningful impact on health outcomes, this might be detectable via an inflection point in a nonlinear relationship between adherence and a health outcome. Although standard methods for examining nonlinear relationships are illustrated in regression textbooks (e.g., adding quadratic or higher order polynomial terms for adherence), these do not appear to be routinely practiced among adherence researchers. Although a topic for future research, another situation in which categorization may be justified is in extremely separated u-shaped distributions. Unless situations like this are observed to occur in practice, we advise against approaches that are inherently categorical (i.e., binary self-report measures) when possible. Our work is also limited to the two categorizations used herein. In theory, having more categories than three may yield results less deleterious than dichotomization or trichotomization, but additional research is required to assess this posibility.
In summary, the results of this work have immediate implications for adherence research across both physical and mental health conditions. Correctly estimating the effects of adherence will help yield more effective treatments, substantial cost savings, and improved quality of life for patients.
Acknowledgments
This study was supported by National Institute of Mental Health (1R03MH103477-01A1).
Footnotes
In the conditions trichotomizing adherence, two dummy variables were created with < 50% adherence serving as the reference category. Hence, the model had two parameters to estimate.
Conflicts of Interest Stephen Tueller, Pascal Deboeck, and Richard Van Dorn have no relevant conflicts of interest to disclose.
Compliance with Ethical Standards
Human and animal rights and Informed Consent All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards. Informed consent was obtained from all patients for being included in the study.
Contributor Information
Stephen J. Tueller, Email: stueller@rti.org, RTI International
Pascal R. Deboeck, Email: pascal@ku.edu, University of Kansas
Richard A. Van Dorn, Email: rvandorn@rti.org, RTI International
References
- Acosta FJ, Ramallo-Fariña Y, Siris SG. Should full adherence be a necessary goal in schizophrenia? Full versus non-full adherence to antipsychotic treatment. Comprehensive Psychiatry. 2014;55(1):33–39. doi: 10.1016/j.comppsych.2013.09.005. [DOI] [PubMed] [Google Scholar]
- Ascher-Svanum H, Zhu B, Faries DE, Salkever D, Slade EP, Peng X, Conley RR. The cost of relapse and the predictors of relapse in the treatment of schizophrenia. BMC Psychiatry. 2010;10(1):2. doi: 10.1186/1471-244X-10-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asmundson GJ, Taylor S, Carleton RN, Weeks JW, Hadjstavropoulos HD. Should health anxiety be carved at the joint? A look at the health anxiety construct using factor mixture modeling in a non-clinical sample. Journal of Anxiety Disorders. 2012;26(1):246–251. doi: 10.1016/j.janxdis.2011.11.009. [DOI] [PubMed] [Google Scholar]
- Ballif M, Ledergerber B, Battegay M, Cavassini M, Bernasconi E, Schmid P … Swiss H. I. V. Cohort Study. Impact of previous virological treatment failures and adherence on the outcome of antiretroviral therapy in 2007. PLoS One. 2009;4(12):e8275. doi: 10.1371/journal.pone.0008275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buysman EK, Liu F, Hammer M, Langer J. Impact of medication adherence and persistence on clinical and economic outcomes in patients with type 2 diabetes treated with liraglutide: a retrospective cohort study. Advances in Therapy. 2015;32(4):341–355. doi: 10.1007/s12325-015-0199-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byerly M, Fisher R, Whatley K, Holland R, Varghese F, Carmody T, … Rush AJ. A comparison of electronic monitoring vs. clinician rating of antipsychotic adherence in outpatients with schizophrenia. Psychiatry Research. 2005;133(2):129–133. doi: 10.1016/j.psychres.2004.11.002. [DOI] [PubMed] [Google Scholar]
- Byerly MJ, Nakonezny PA, Rush AJ. The Brief Adherence Rating Scale (BARS) validated against electronic monitoring in assessing the antipsychotic medication adherence of outpatients with schizophrenia and schizoaffective disorder. Schizophrenia Research. 2008;100(1):60–69. doi: 10.1016/j.schres.2007.12.470. [DOI] [PubMed] [Google Scholar]
- Davis JM, Chen N, Glick ID. A meta-analysis of the efficacy of second-generation antipsychotics. Archives of General Psychiatry. 2003;60(6):553–564. doi: 10.1001/archpsyc.60.6.553. [DOI] [PubMed] [Google Scholar]
- DeCoster J, Iselin AMR, Gallucci M. A conceptual and empirical examination of justifications for dichotomization. Psychological Methods. 2009;14(4):349. doi: 10.1037/a0016956. [DOI] [PubMed] [Google Scholar]
- Elbogen EB, Swanson JW, Swartz MS, Van Dorn R. Medication nonadherence and substance abuse in psychotic disorders: impact of depressive symptoms and social stability. The Journal of Nervous and Mental Disease. 2005;193(10):673–679. doi: 10.1097/01.nmd.0000180742.51075.70. [DOI] [PubMed] [Google Scholar]
- Fedorov V, Mannino F, Zhang R. Consequences of dichotomization. Pharmaceutical Statistics. 2009;8(1):50–61. doi: 10.1002/pst.331. [DOI] [PubMed] [Google Scholar]
- Ferguson NM, Donnelly CA, Hooper J, Ghani AC, Fraser C, Bartley LM, … Anderson RM. Adherence to antiretroviral therapy and its impact on clinical outcome in HIV-infected patients. Journal of The Royal Society Interface. 2005;2(4):349–363. doi: 10.1098/rsif.2005.0037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmer TP, Dolder CR, Lacro JP, Folsom DP, Lindamer L, Garcia P, Jeste DV. Adherence to treatment with antipsychotic medication and health care costs among Medicaid beneficiaries with schizophrenia. American Journal of Psychiatry. 2004;161(4):692–699. doi: 10.1176/appi.ajp.161.4.692. [DOI] [PubMed] [Google Scholar]
- Hepke KL, Martus MT, Share DA. Costs and utilization associated with pharmaceutical adherence in a diabetic population. The American Journal of Managed Care. 2004;10(2 Pt 2):144–151. [PubMed] [Google Scholar]
- Hershman DL, Shao T, Kushi LH, Buono D, Tsai WY, Fehrenbacher L, … Neugut AI. Early discontinuation and non-adherence to adjuvant hormonal therapy are associated with increased mortality in women with breast cancer. Breast Cancer Research and Treatment. 2011;126(2):529–537. doi: 10.1007/s10549-010-1132-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho PM, Bryson CL, Rumsfeld JS. Medication adherence: its importance in cardiovascular outcomes. Circulation. 2009;119(23):3028–3035. doi: 10.1161/CIRCULATIONAHA.108.768986. [DOI] [PubMed] [Google Scholar]
- Hommel KA, Davis CM, Baldassano RN. Medication adherence and quality of life in pediatric inflammatory bowel disease. Journal of Pediatric Psychology. 2008;33(8):867–874. doi: 10.1093/jpepsy/jsn022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsieh KP, Chen LC, Cheung KL, Chang CS, Yang YH. Interruption and non-adherence to long-term adjuvant hormone therapy is associated with adverse survival outcome of breast cancer women—an Asian population-based study. PLoS One. 2014;9(2):e87027. doi: 10.1371/journal.pone.0087027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ibrahim AR, Eliasson L, Apperley JF, Milojkovic D, Bua M, Szydlo R, … Marin D. Poor adherence is the main reason for loss of CCyR and imatinib failure for chronic myeloid leukemia patients on long-term therapy. Blood. 2011;117(14):3733–3736. doi: 10.1182/blood-2010-10-309807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanova JI, Bergman RE, Birnbaum HG, Phillips AL, Stewart M, Meletiche DM. Impact of medication adherence to disease-modifying drugs on severe relapse, and direct and indirect costs among employees with multiple sclerosis in the US. Journal of Medical Economics. 2012;15(3):601–609. doi: 10.3111/13696998.2012.667027. [DOI] [PubMed] [Google Scholar]
- Juarez DT, Tan C, Davis J, Mau M. Factors affecting sustained medication adherence and its impact on healthcare utilization in patients with diabetes. Journal of Pharmaceutical Health Services Research. 2013;4(2):89–94. doi: 10.1111/jphs.12016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knapp M, King D, Pugner K, Lapuerta P. Non-adherence to antipsychotic medication regimens: associations with resource use and costs. The British Journal of Psychiatry. 2004;184(6):509–516. doi: 10.1192/bjp.184.6.509. [DOI] [PubMed] [Google Scholar]
- Lilienfeld SO. DSM-5: Centripetal Scientific and Centrifugal Antiscientific Forces. Clinical Psychology: Science and Practice. 2014;21(3):269–279. [Google Scholar]
- Lubke GH, Miller PJ. Does nature have joints worth carving? A discussion of taxometrics, model-based clustering and latent variable mixture modeling. Psychological Medicine. 2015;45(04):705–715. doi: 10.1017/S003329171400169X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lubke G, Tueller S. Latent class detection and class assignment: A comparison of the MAXEIG taxometric procedure and factor mixture modeling approaches. Structural Equation Modeling. 2010;17(4):605–628. doi: 10.1080/10705511.2010.510050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacCallum RC, Zhang S, Preacher KJ, Rucker DD. On the practice of dichotomization of quantitative variables. Psychological Methods. 2002;7(1):19. doi: 10.1037/1082-989x.7.1.19. [DOI] [PubMed] [Google Scholar]
- Maggiolo F, Airoldi M, Kleinloog HD, Callegaro A, Ravasio V, Arici C, … Suter F. Effect of adherence to HAART on virologic outcome and on the selection of resistance-conferring mutations in NNRTI-or PI-treated patients. HIV Clinical Trials. 2007;8(5):282–292. doi: 10.1310/hct0805-282. [DOI] [PubMed] [Google Scholar]
- McFadden D. Conditional logit analysis of qualitative choice behavior. In: Zarembka P, editor. Frontiers in Econometrics. New York, NY: Academic Press; 1974. pp. 105–142. [Google Scholar]
- Menard S. Coefficients of determination for multiple logistic regression analysis. The American Statistician. 2000;54:17–24. [Google Scholar]
- Nakonezny PA, Byerly MJ, Rush AJ. Electronic monitoring of antipsychotic medication adherence in outpatients with schizophrenia or schizoaffective disorder: an empirical evaluation of its reliability and predictive validity. Psychiatry Research. 2008;157(1):259–263. doi: 10.1016/j.psychres.2007.05.001. [DOI] [PubMed] [Google Scholar]
- Nichols GA, Rosales AG, Kimes TM, Tunceli K, Kurtyka K, Mavros P, Steiner JF. Impact on glycated haemoglobin of a biological response-based measure of medication adherence. Diabetes, Obesity and Metabolism. 2015;17(9):843–848. doi: 10.1111/dom.12476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olfson M, Mechanic D, Hansell S, Boyer CA, Walkup J, Weiden PJ. Predicting medication noncompliance after hospital discharge among patients with schizophrenia. Psychiatric Services. 2014;51(2):216–222. doi: 10.1176/appi.ps.51.2.216. [DOI] [PubMed] [Google Scholar]
- Onyebuchi AK, Lawani LO, Iyoke CA, Onoh CR, Okeke NE. Adherence to intermittent preventive treatment for malaria with sulphadoxine-pyrimethamine and outcome of pregnancy among parturients in South East Nigeria. Patient Preference and Adherence. 2014;8:447–452. doi: 10.2147/PPA.S61448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterson AM, Nau DP, Cramer JA, Benner J, Gwadry-Sridhar F, Nichol M. A checklist for medication compliance and persistence studies using retrospective databases. Value in Health. 2007;10(1):3–12. doi: 10.1111/j.1524-4733.2006.00139.x. [DOI] [PubMed] [Google Scholar]
- Pringle JL, Boyer A, Conklin MH, McCullough JW, Aldridge A. The Pennsylvania Project: pharmacist intervention improved medication adherence and reduced health care costs. Health Affairs. 2014;33(8):1444–1452. doi: 10.1377/hlthaff.2013.1398. [DOI] [PubMed] [Google Scholar]
- R Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2015. http://www.R-project.org/ [Google Scholar]
- Remington G, Kwon J, Collins A, Laporte D, Mann S, Christensen B. The use of electronic monitoring (MEMS®) to evaluate antipsychotic compliance in outpatients with schizophrenia. Schizophrenia Research. 2007;90(1):229–237. doi: 10.1016/j.schres.2006.11.015. [DOI] [PubMed] [Google Scholar]
- Roebuck MC, Liberman JN, Gemmill-Toyama M, Brennan TA. Medication adherence leads to lower health care use and costs despite increased drug spending. Health Affairs. 2011;30(1):91–99. doi: 10.1377/hlthaff.2009.1087. [DOI] [PubMed] [Google Scholar]
- Shentu Y, Xie M. A note on dichotomization of continuous response variable in the presence of contamination and model misspecification. Statistics in Medicine. 2010;29(21):2200–2214. doi: 10.1002/sim.3966. [DOI] [PubMed] [Google Scholar]
- Simpson SH, Eurich DT, Majumdar SR, Padwal RS, Tsuyuki RT, Varney J, Johnson JA. A meta-analysis of the association between adherence to drug therapy and mortality. British Medical Journal. 2006;333(7557):15. doi: 10.1136/bmj.38875.675486.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokol MC, McGuigan KA, Verbrugge RR, Epstein RS. Impact of medication adherence on hospitalization risk and healthcare cost. Medical Care. 2005;43(6):521–530. doi: 10.1097/01.mlr.0000163641.86870.af. [DOI] [PubMed] [Google Scholar]
- Sun SX, Liu GG, Christensen DB, Fu AZ. Review and analysis of hospitalization costs associated with antipsychotic nonadherence in the treatment of schizophrenia in the United States. Current Medical Research and Opinion. 2007;23(10):2305–2312. doi: 10.1185/030079907X226050. [DOI] [PubMed] [Google Scholar]
- Svarstad B, Shireman T, Sweeney J. Using drug claims data to assess the relationship of medication adherence with hospitalization and costs. Psychiatr Serv. 2001;52:805–811. doi: 10.1176/appi.ps.52.6.805. [DOI] [PubMed] [Google Scholar]
- Swanson JW, Swartz MS, Van Dorn RA, Volavka J, Monahan J, Stroup TS, … Lieberman JA. Comparison of antipsychotic medication effects on reducing violence in people with schizophrenia. The British Journal of Psychiatry. 2008;193(1):37–43. doi: 10.1192/bjp.bp.107.042630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swanson J, Van Dorn RA, Swartz MS. Effectiveness of atypical antipsychotics for substance use in schizophrenia patients. Schizophrenia Research. 2007;94(1):114–118. doi: 10.1016/j.schres.2007.05.007. [DOI] [PubMed] [Google Scholar]
- Swanson JW, Swartz MS, Van Dorn RA, Elbogen EB, Wagner HR, Rosenheck RA, … Lieberman JA. A national study of violent behavior in persons with schizophrenia. Archives of General Psychiatry. 2006;63(5):490–499. doi: 10.1001/archpsyc.63.5.490. [DOI] [PubMed] [Google Scholar]
- Swartz MS, Swanson JW, Hiday VA, Borum R, Wagner HR, Burns BJ. Violence and severe mental illness: the effects of substance abuse and nonadherence to medication. American Journal of Psychiatry. 1998a;155(2):226–231. doi: 10.1176/ajp.155.2.226. [DOI] [PubMed] [Google Scholar]
- Swartz MS, Swanson JW, Hiday VA, Borum R, Wagner R, Burns BJ. Taking the wrong drugs: the role of substance abuse and medication noncompliance in violence among severely mentally ill individuals. Social Psychiatry and Psychiatric Epidemiology. 1998b;33(1):S75–S80. doi: 10.1007/s001270050213. [DOI] [PubMed] [Google Scholar]
- Valenstein M, Copeland LA, Blow FC, McCarthy JF, Zeber JE, Gillon L, … Stavenger T. Pharmacy data identify poorly adherent patients with schizophrenia at increased risk for admission. Medical Care. 2002;40(8):630–639. doi: 10.1097/00005650-200208000-00002. [DOI] [PubMed] [Google Scholar]
- Valenstein M, Ganoczy D, McCarthy JF, Myra KH, Lee TA, Blow FC. Antipsychotic adherence over time among patients receiving treatment for schizophrenia: a retrospective review. The Journal of Clinical Psychiatry. 2006;67(10):1542–1550. doi: 10.4088/jcp.v67n1008. [DOI] [PubMed] [Google Scholar]
- Van Dorn RA, Desmarais SL, Petrila J, Haynes D, Singh JP. Effects of outpatient treatment on risk of arrest of adults with serious mental illness and associated costs. Psychiatric Services. 2013;64(9):856–862. doi: 10.1176/appi.ps.201200406. [DOI] [PubMed] [Google Scholar]
- Vestbo J, Anderson JA, Calverley PM, Celli B, Ferguson GT, Jenkins C, … Jones PW. Adherence to inhaled therapy, mortality and hospital admission in COPD. Thorax. 2009;64(11):939–943. doi: 10.1136/thx.2009.113662. [DOI] [PubMed] [Google Scholar]
- Wei L, Fahey T, MacDonald TM. Adherence to statin or aspirin or both in patients with established cardiovascular disease: exploring healthy behaviour vs. drug effects and 10-year follow-up of outcome. British Journal of Clinical Pharmacology. 2008;66(1):110–116. doi: 10.1111/j.1365-2125.2008.03212.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiden PJ, Kozma C, Grogg A, Locklear J. Partial compliance and risk of rehospitalization among California Medicaid patients with schizophrenia. Psychiatric Services. 2004;55(8):886–891. doi: 10.1176/appi.ps.55.8.886. [DOI] [PubMed] [Google Scholar]
- Wood E, Hogg RS, Yip B, Harrigan PR, O’Shaughnessy MV, Montaner JS. Effect of medication adherence on survival of HIV-infected adults who start highly active antiretroviral therapy when the CD4+ cell count is 0.200 to 0.350× 109 cells/L. Annals of Internal Medicine. 2003;139(10):810–816. doi: 10.7326/0003-4819-139-10-200311180-00008. [DOI] [PubMed] [Google Scholar]
- Yasuda JM, Miller C, Currier JS, Forthal DN, Kemper CA, Beall GN … California Collaborative Treatment Group. The correlation between plasma concentrations of protease inhibitors, medication adherence and virological outcome in HIV-infected patients. Antiviral Therapy. 2004;9(5):753–762. [PubMed] [Google Scholar]
- Yen CF, Chen CS, Ko CH, Yeh ML, Yang SJ, Yen JY, … Wu CC. Relationships between insight and medication adherence in outpatients with schizophrenia and bipolar disorder: prospective study. Psychiatry and Clinical Neurosciences. 2005;59(4):403–409. doi: 10.1111/j.1440-1819.2005.01392.x. [DOI] [PubMed] [Google Scholar]