MR Fingerprinting Using The Quick Echo Splitting NMR Imaging Technique

Abstract

Purpose

The purpose of the study is to develop a quantitative method for the relaxation properties with a reduced radio frequency (RF) power deposition by combining Magnetic Resonance Fingerprinting (MRF) technique with Quick Echo Splitting NMR Imaging Technique (QUEST).

Methods

A QUEST-based MRF sequence was implemented to acquire high order echoes by increasing the gaps between RF pulses. Bloch simulations were used to calculate a dictionary containing the range of physically plausible signal evolutions using a range of T₁ and T₂ values based on the pulse sequence. MRF-QUEST was evaluated by comparing to the results of spin-echo methods. The SAR of QUEST-MRF was compared to the clinically available methods.

Results

MRF-QUEST quantifies the relaxation properties with good accuracy at the estimated head Specific Absorption Rate (SAR) of 0.03 W/kg. T₁ and T₂ values estimated by MRF-QUEST are in good agreement with the traditional methods.

Conclusion

The combination of the MRF and the QUEST provides an accurate quantification of T₁ and T₂ simultaneously with reduced RF power deposition. The resulting lower SAR may provide a new acquisition strategy for MRF when RF energy deposition is problematic.

Introduction

Magnetic resonance imaging has proven to be an important diagnostic tool in clinical medicine (1–3). The diagnostic information in MR images is typically based on the intensity differences between different tissues. Because the MRI signal is modulated by multiple contrast mechanisms, such as proton density, proton relaxation properties, and water free diffusion, it is difficult to link these signal intensity variations in one contrast-weighted image to the physiological or pathological state of the tissue. For confirmation of a diagnosis, multiple images with different contrasts, such as T₁-weighted and T₂-weighted images, are acquired in one session. Images with different contrasts are generated by adjusting sequence parameters, such as flip angle of RF pulse, echo time, and repetition time, in such a way that one contrast dominates the image at a time. With a handful of acquisition parameters to tweak, it can be challenging to obtain the same results, such as image contrast and signal-to-noise ratio, at different sites, or even at the same site at different times. More importantly, contrast-weighted images are qualitative; the hyper or hypo intensity of a certain tissue does not necessarily indicate the disease stage. This could hinder diagnosis and prevent some early disease diagnosis opportunities (1,4,5).

In contrast to qualitative imaging, the quantitative tissue properties, such as T₁ and T₂ can directly reflect changes at the cellular level. Quantitative imaging has shown its potential in the early detection of diseases (6). In addition, the usage of quantitative imaging methods could simplify the clinic routine and facilitate comparison of results. For these reasons, quantitative MRI has long been a goal in MR research. Multiple methods have been proposed to quantify T₁ (7–9), T₂ (10–13), or both simultaneously (14–17). In addition, a wide range of contrast-weighted images can be generated if needed from high quality T₁ and T₂ maps.

Magnetic Resonance Fingerprinting (MRF) (18) is a recently introduced novel concept in quantitative imaging. In contrast to conventional MRI which acquires the steady-state signal with a set of fixed flip angles at a constant repetition time, MRF acquires the transient state signal that is sensitive to relaxation properties, by using variable flip angles and repetition times. After acquisition, a pattern recognition algorithm is utilized to match the acquired signal to the best entry in a dictionary of possible signal evolutions calculated using Bloch simulations to quantify multiple tissue properties simultaneously. A previous study has demonstrated that an inversion-recovery balanced steady state free precession (IR-bSSFP) based MRF allowed accurate and efficient measurement of T₁, T₂, proton density, and off-resonance, but this is just one of the infinite possibilities for sequence design, since the pattern recognition process can accommodate any signal evolutions of MRF acquisition. The data for the MRF time course can be obtained using nearly any variable acquisition parameters. Thus one can purposely design an acquisition with different desired properties. Here we investigate an acquisition method with extremely low RF energy deposition to quantify the relaxation times.

In general, RF energy deposition during MRI scans is well-regulated and monitored to ensure no ill-effects (19). However, the presence of an implantable medical device (IMD), such as a deep brain stimulator (DBS), can cause a high concentration of the local RF power deposition, which can lead to temperature increases in the surrounding tissue of over 45 °C that could cause irreversible thermal lesion (20). It is difficult to predict this temperature increase due to variations in the length, dimension, shape and location of the devices in the body (21). Thus MR imaging for the patient with an IMD has more stringent constraints in RF power deposition. For example, the patient implanted with a DBS device is recommended to have MR scans with the head SAR smaller than 0.1 W/kg in a 1.5 T magnet with a transmit-receive head array (22). This constrains the image contrast to be proton-density weighted which would only provide limited diagnostic information. Furthermore, imaging at 3 T and higher field scanners requires more power deposition compared to the lower field, which could cause problematic RF heating even in a normal patient. Even though it is well-known contrast for soft tissues, the current available methods in MRI have difficulty to provide different contrast-weighted images with an extremely low RF power deposition, such as smaller than 0.1 W/kg, within a clinically accepted acquisition time. Thus conventional MRI has a clear trade-off between the contrast of the images and the RF power deposition that can be achieved in a clinically acceptable time.

To design a method that can generate diagnostic information while keeping the minimal RF energy deposition would be beneficial. In this work, we combined the concept of MRF with QUEST to simultaneously quantify standard tissue properties, namely T₁, T₂, and proton density, with reduced RF power deposition. With the quantitative maps, different contrast-weighted images can be generated on demand. The Quick Echo Splitting NMR technique (QUEST) (23,24) was proposed to acquire the maximum number of signals with the minimum number of RF pulses. QUEST can be used to generate and acquire high order echoes by employing an aperiodic stop-experiment approach after each RF pulse. With extended delays between RF pulses, each coherence pathway is refocused to form an echo. Each high order echo has its unique relaxation signature, which would help MRF quantify the relaxation properties. It uses very low RF power to acquire data, which could provide a new acquisition strategy when the RF energy absorption is problematic, such as at ultra high fields or for patients with implanted metal devices.

Methods

Pulse Sequence

The original QUEST consisted of four RF pulses applied at geometrically increasing time spacing. A series of equidistant echoes were acquired after applying a central 180° pulse (23,24). The spacings between RF pulses determine the number of echoes that can be refocused within each period (25). For example, Figure 1 shows two phase graphs that have different time spacings between RF pulses. The spacings between the RF pulses of the phase graph shown in Figure 1a increase according to 3ⁿ⁻¹τ, where n is the index of RF pulses, and τ is the delay between the first two RF pulses. In this case, (3ⁿ⁻¹ – 1)/2 echoes can be generated after the n^th pulse. This represents the most optimized RF spacing in term of the number of achievable echoes to the number of RF pulses because each high order coherence pathway forms the echo individually, however, the magnetization level in many of these echoes is very low. As an alternative, Figure 1b shows a phase graph of four RF pulses that has the spacing increment as 2ⁿ⁻¹τ. In this case, 2ⁿ⁻¹-1 pathways will be refocused to form echoes after the n^th pulse. This is the preferred sequence structure for the work shown here.

Figure 1.

Phase graphs with aperiodic RF gaps. The gaps after RF pulses increase in a) 3ⁿ⁻¹τ, b) 2ⁿ⁻¹τ, where n is the number of RF pulse, and τ is the delay between first two RF pulses. Solid dots represent FIDs right immediately following the RF pulses. The open circles represent possible achievable echoes by refocusing the high coherence pathways.

In the study, in addition to the echoes that are generated after the last RF pulse as the original QUEST, our method also acquires FIDs and echoes after each RF pulse. Obviously, the number of FIDs is equal to the number of applied RF pulses. The number of echoes is the summation of echoes of all RF pulses. For example, three RF pulse scheme in Figure 1a generates 3 FIDs and 5 echoes, and the scheme with 4 RF pulses in Figure 1b generates 4 FIDs and 11 echoes.

Figure 2a shows a pulse sequence diagram of the 4-RF pulse QUEST sequence. The ratio of the time spacings between RF pulses to the spacing of the first two RF pulses is 1, 2, 4 and 8 corresponding to the phase graph shown in Figure 1b in order to increase the number of echoes with high signal levels. Dephasing between each coherence pathway is achieved by an unbalanced slice selection gradient. In the MRF-QUEST sequence, the high order echoes are encoded into different temporal frames. To fully resolve the relaxation effects, the four RF pulse QUEST block was repeated 15 times after an adiabatic inversion pulse as shown in Figure 2b. For a proof-of-concept, the flip angles were randomly selected from 1 to 60° as shown in Figure 2c. The gap between the first two RF pulses (i.e., minimal echo spacing) of each QUEST block was varied randomly between 10 to 13 ms as shown in Figure 2d. No additional delays were added between the QUEST blocks.

Figure 2.

a) The QUEST pulse sequence diagram corresponding to the phase graph in Fig. 1b. The unbalanced slice-selective gradient is used to create phase difference between high order echoes. The MRF-QUEST sequence repeating QUEST for 15 times after an adiabatic inversion pulse (TI of 20.64 ms) is shown in (b). The total time of (b) is 2.6 seconds. A 3-second delay is added after (b) to allow the magnetization to return to equilibrium. A total of 60 RF pulses were utilized to acquire 225 echoes. The flip angles were pseudorandomly selected from 1 to 60° shown in (c). The minimal echo spacing of each QUEST block was varied randomly between 10 to 13 ms shown in (d).

In this study, a variable density spiral trajectory with zero and first gradient moment compensation (26,27) was used. The spiral trajectory was designed to cover a field-of-view of 300 × 300 mm² with a 256 × 256 matrix size. It requires 12 interleaves to sample the inner 25 × 25 points fully, and 48 interleaves to sample the entire 256 × 256 matrix fully. As described previously, one adiabatic inversion pulse (TI of 20.64 ms) with 60 pulses were used for one spiral interleaf. The spiral interleaf rotated 7.5° from one frame to the next so that each frame has different undersampling artifacts. To cover the kspace, twelve rotating spiral arms were acquired to fully sample the inner kspace. The acquisition time for one spiral arm was 2.6 seconds. A 3-second delay was added between each acquisition of one spiral arm to allow the magnetization to return to equilibrium. The total acquisition time for one slice was 67 seconds.

Dictionary and Pattern Recognition

The Bloch simulation calculates the signal time course of the entire executed sequence for each T₁ and T₂ combination. Because of the unbalanced gradient in the MRF-QUEST sequence, the simulation of signal evolutions for the dictionary calculation cannot treat a voxel as a single isochromat as in previous work (18). In this study, since the spiral trajectory was designed with the zero and first moments compensation, and the unbalanced gradient moment was only along the slice selective direction, each voxel was treated as 200 isochromats (or spins) evenly distributed along the slice selective direction. The slice profile of a hanning-filtered sinc RF pulse (2000 microseconds duration with a time bandwidth product of 8), and the dephasing of the unbalanced gradient moment were calculated with 10 microseconds per time point. Each isochromat has different signal amplitude and phase due to its location along the slice. Each dictionary entry was then the summation of the signals of 200 isochromats.

A dictionary containing a total of 4,800 combinations of T₁ and T₂ was calculated with Bloch simulations, using a range of T₁ values (10 ms ~ 90 ms with an increment of 10 ms; 100 ms ~ 1000 ms with an increment of 20 ms; 1000 ms ~ 2000 ms with an increment of 40 ms; 2000 ms ~ 3000 ms with an increment of 100 ms; and 3000 ms ~ 5000 ms with an increment of 200 ms) and T₂ values (2 ms ~ 8 ms with an increment of 2 ms; 10 ms ~ 100 ms with an increment of 5 ms; 100 ms ~ 300 ms with an increment of 10 ms; and 300 ms ~ 500 ms with an increment of 50 ms), that covers the physiological range of T₁ and T₂ values (18). The calculation time for this dictionary was about 18 minutes in Matlab 2015a (The MathWorks, Natick, MA) in a workstation with Intel Xeon 2.4 GHz CPU (Intel Corporation, Santa Clara, CA).

Similar to the pattern recognition in the original MRF paper (18), the calculated dictionary was normalized to make each entry have the same sum-squared magnitude. The complex inner products between the measured time course of each pixel denoted as x and all entries of the normalized dictionary d_j (1 ≤ j ≤ n) were calculated. n is the number element of the dictionary. The entry in the dictionary d_ℓ was choosen to satisfy

$$d_{\ell }=arg{max}_{d_j}\left|d_j{x}^{\ast }\right|$$ [1]

where * represents the conjugate transpose of the vector. The T₁ and T₂ values of this dictionary entry were then used to represent the relaxation times in the voxel. The proton density was calculated as the scaling factor between the measured signal and the matched signal evolution from the dictionary.

Phantom and In vivo experiments

All studies were performed on a Siemens Magnetom Skyra 3 T scanner (Siemens AG Medical Solutions, Erlangen, Germany). To evaluate the performance of MRF-QUEST, a phantom study was performed to compare the results to traditional spin echo methods. A phantom of 10 cylindrical tubes with varying concentration of gadolinium and agarose was scanned. An inversion recovery spin-echo sequence (5 TIs of 250 ms, 500 ms, 1000 ms, 1500 ms and 2500 ms) and a multiple single-echo spin echo sequence (10 echoes with TEs from 7.5 ms to 600 ms with a TR of 10 seconds) were used to quantify T₁ and T₂ values, respectively. T₁ and T₂ values were calculated by pixel-by-pixel three-parameter nonlinear least squares fitting. The MRF-QUEST sequence was performed with the acquisition parameters shown in Figure 2. For the phantom experiment, MRF-QUEST and spin echo methods have the same spatial resolution of 1.2 × 1.2 mm² and the slice thickness of 5 mm.

The efficiency of the proposed method for estimation of T₁ and T₂ values was calculated by a bootstrapped Monte Carlo method (28). A normal acquisition and a separate noise measurement with no RF pulses applied were acquired on phantom. Fifty “pseudo multiple replicas” were created by repeatedly adding randomly resampled noise into the raw data. T₁ and T₂ values were estimated from each replica respectively. The means and standard deviations of T₁ and T₂ along the fifty repetitions were calculated from 100 voxels in each tube of the phantom. The efficiency of T₁ and T₂ estimation is defined as

$$\mathrm{\Gamma }=\frac{T_n}{{\sigma }_{T_n}\sqrt{T_{\mathit{acq}}}}$$ [2]

where T_n (n = 1 or 2) is the mean value of T₁ or T₂, σ_Tn is the standard deviation of T₁ or T₂. T_acq is the acquisition time (14). The efficiency of the proposed method was compared to the efficiency of the FISP based MRF method with the acquisition parameters reported in (29).

To examine the effect of the dictionary resolution on the estimation of T₁ and T₂ values in the MRF-QUEST method, the “pseudo multiple replicas” were matched against two dictionaries with different step sizes for T₁ and T₂. One dictionary has the step size of 20 ms for T₁, and 10 ms for T₂; the other has the step size of 10 ms for T₁ and 5 ms for T₂. Both dictionaries have the same range of T₁ from 100 ms to 2000 ms, T₂ from 10 ms to 200 ms, which covers the T₁ and T₂ values of the phantom. The means and standard deviations of T₁ and T₂ along the fifty repetitions were calculated from 100 voxels in each tube.

In vivo human brain data using MRF-QUEST were performed in 5 healthy volunteers after informed consent with the same parameters as the phantom study. One of the volunteers was scanned with an inversion recovery spin echo (6 TIs of 21 ms, 200 ms, 500 ms, 1500 ms, 3000 ms and 4500 ms) with TR of 8000 ms for the reference T₁ values, and a multiple single-echo spin echo (5 TEs of 12 ms, 22 ms, 42 ms, 62 ms and 102 ms) with TR of 5000 ms for the reference T₂ values. In order to reduce the total scan time, the spatial resolution for the spin echo acquisitions was 2.4 × 2.4 × 5 mm³, and all scans were acquired with 6/8 partial fourier acquisition. The total acquisition time was 60 minutes and 48 seconds for acquiring the reference T₁ and 31 minutes and 40 seconds for the reference T₂. T₁ and T₂ values were calculated by the nonlinear least squares fitting on the magnitude of the images. Different regions of interest in white matter (WM) and gray matter (GM) were drawn to compare the results of MRF-QUEST to the T₁ and T₂ values of the spin echo methods.

MRF-QUEST data from both phantom and human were reconstructed using non-uniform Fourier transform (NUFFT) (30). Images of mutiple coils were combined using the adaptive coil combination method (31). The quantitative maps were generated by matching the reconstucted images with the pre-calculated dictionary. The template matching for one slice with 256 × 256 matrix size was about 12 seconds using the same workstation to caculate the dictionary.

The head specific absorption rate (SAR) during a brain scan of a normal volunteer (150 lbs body weight) was reported with a body coil for transmission, and a 12-channel head array for receive. The proposed method was compared to T₁-weighted 3D FLASH with TR of 11 ms and FA of 20°, T₂-weighted 2D TSE with TR of 4500 ms, 20 slices, and refocusing FA of 150°, and FISP-based MRF method. The FOV was 300 mm, and the spatial resolution was 1.2 × 1.2 × 5 mm³ for all methods. The acquisition time was 2 minutes 40 seconds for 3D FLASH and 2 minutes 30 seconds for 2D TSE.

Results

Figure 3 shows an example of the signal evolution from MRF-QUEST in a phantom with a T₁ value of 881 ms and a T₂ value of 59 ms (as measured by the spin echo methods). The acquired signal is shown in solid black, and the matched MRF dictionary entry is shown as a dotted red line. The measured T₁ and T₂ values from MRF-QUEST are 870 ms and 60 ms, respectively.

Figure 3.

An example of the signal evolution from MRF-QUEST in a phantom with T₁ of 881 ms and a T₂ value of 59 ms as measured by the spin echo methods. The acquired signal is in solid black, and the matched dictionary entry is in dotted red line. The calculated T₁ value equal to 870 ms, and T₂ value of 60 ms from MRF-QUEST method.

Figure 4a shows the T₁, T₂, and proton density maps of all the phantom tubes acquired by MRF-QUEST. Figure 4b shows the correlation curve of T₁ values from MRF-QUEST to T₁ from inversion recovery spin echo method. Figure 4c shows the correlation curve of T₂ values from MRF-QUEST to T₂ of the multiple single spin echo method. The correlation curves show that both T₁ and T₂ values estimated simultaneously by the proposed method are in good agreement with the standard spin echo methods.

Figure 4.

a) T₁, T₂, and proton density maps generated with MRF-QUEST in a phantom containing vials with materials of different relaxation times. The correlations of b) T₁ values and c) T₂ values from MRF-QUEST to the spin echo methods. The efficiencies of MRF-QUEST at different d) T₁ and e) T₂ values are compared to the results generated from FISP-based MRF method.

Figure 4d shows the efficiency of MRF-QUEST compared to the efficiency of MRF-FISP at different T₁ and T₂ values. MRF-FISP acquisition time was 13 seconds for 1000 frames as reported in (29). The efficiencies in quantification of T₁ and T₂ values of the proposed method are lower compared to the ones of FISP based MRF method due to the longer acquisition time. However, MRF-QUEST still achieves high precision in T₁ and T₂ estimation. For example, for a T₁ value of 881 ms, it achieves a precision of ± 4.9 ms (or 0.56%); and for T₂ value of 60 ms, it achieves a precision of ± 2.0 ms (or 3.36%).

Figure 5a shows the comparison between the mean T₁ retrieved from the dictionary with 20 ms step size and the values from the dictionary with 10 ms step size. Figure 5b compares the mean T₂ retrieved from the dictionary with 10 ms step size with the values from the dictionary with 5 ms step size. The standard deviations of the estimations are plotted in Figure 5c and 5d, respectively. It can be seen that the mean values stay same with the different dictionary resolutions. However, the standard deviations reduce with the finer step size for both T₁ and T₂.

Figure 5.

The effects of dictionary resolution on the estimations of T₁ and T₂ values. a) The comparison between the mean T₁ retrieved from the dictionary with 20 ms step size and the values from the dictionary with 10 ms step size. b) The comparison between the mean T₂ retrieved from the dictionary with 10 ms step size with the values from the dictionary with 5 ms step size. The standard deviations of the c) T₁ and d) T₂ estimations retrieved from the dictionaries with different resolutions.

Figure 6 shows the representative T₁, T_2, and proton density maps of the in vivo human brain from the proposed MRF-QUEST method. The average T₁ value of 5 normal volunteers is 786 ± 48 ms in WM and 1278 ± 98 ms in GM; the average T₂ value is 52 ± 8 ms in WM and 66 ± 11 ms in GM, which are in the range of reported values in the previous literature (33). The proton density map shows a smooth variation across the FOV because it is the scaling factor between the measured signal and the matched signal evolution from the dictionary, which in this case will also be affected by the coil sensitivity.

Figure 6.

a) T₁, b) T_2, and c) proton density maps from MRF-QUEST in one in vivo human brain study.

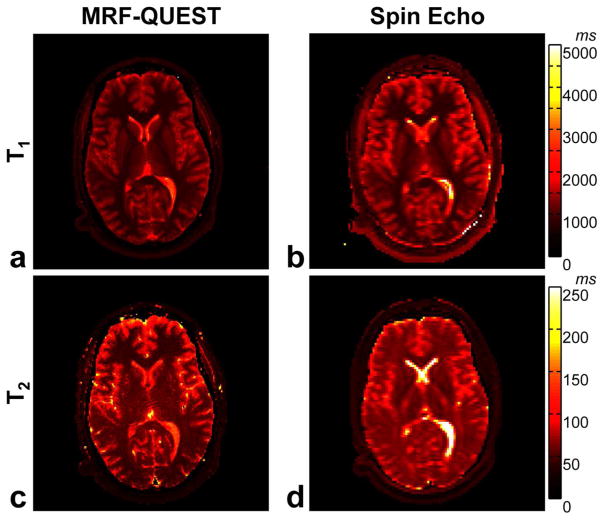
Figure 7 shows T₁ and T₂ maps from MRF-QUEST method compared to the maps from standard spin echo methods in one of the volunteers. Table 1 lists T₁ and T₂ values of the selected regions in WM and GM from MRF-QUEST compared to the results from the standard spin echo methods. In vivo results show that T₁ from the proposed method is in a good agreement with the results of inversion recovery spin echo. A good agreement is also observed in T₂ values in GM between MRF-QUEST and multiple single-echo spin echo method. T₂ estimation in WM is slightly lower in MRF-QUEST compared to the results of single-echo spin echo method.

Figure 7.

a) T₁ and b) T₂ maps from MRF-QUEST are compared to c) T₁ and d) T₂ maps from the standard spin echo methods in one representative volunteer.

Table 1.

T₁ and T₂ values derived from MRF-QUEST compared to T₁ of inversion-recovery spin echo and T₂ of multiple single-echo spin echo in region of white matter, gray matter and cerebrospinal fluid (CSF) in one representative volunteer.

		T1 (ms)		T2 (ms)
		MRF-QUEST	IR-SE	MRF-QUEST Single-SE
		White Matter	Frontal WM	809 ± 24	834 ± 26	44 ± 4	61 ± 3
	Corpus Callosum	744 ± 14	797 ± 38	48 ± 4	54 ± 6
	Occipital WM	777 ± 45	822 ± 19	55 ± 6	66 ± 2
Gray Matter	Caudate Nucleus Head	1240 ± 27	1342 ± 25	68 ± 7	65 ± 3
	Thalamus	1008 ± 33	1062 ± 33	64 ± 5	59 ± 3
	Occipital GM	1493 ± 50	1516 ± 31	71 ± 6	74 ± 4
CSF		2000~3800	2400~5000	115~160	285~650

With these quantitative maps in hand, Figure 8 shows T₁-weighted and T₂-weighted images that generated according to Eq. 1.

Figure 8.

a) T₁-weighted image generated according to Eq. 3. with TR of 350 ms and TE of 2.5 ms and b) acquired T₁-weighted image by GRE with same TR and TE. c) T₂- weighted image, with TR of 5800 ms and TE of 96 ms and d) acquired T₂-weighted image by TSE with same TR and TE.

$$I=M_0·\left(1-e^{-TR/T_1}\right)·e^{-TE/T_2}$$ [3]

Values of TR = 350 ms and TE = 2.5 ms were used for generating a T₁-weighted image, and TR = 5800 ms and TE = 96 ms were used for generating a T₂-weighted image. For comparison, T₁-weighted image was acquired with TR of 350 ms, TE of 2.5 ms and flip angle of 60° by a FLASH sequence; T₂-weighted image was acquired with TR of 5800 ms and TE of 96 ms by a TSE sequence.

With reduced number of RF pulses, and the low amplitude of these pulses, MRF-QUEST can acquire data with extremely low RF energy. The head SAR of MRF-QUEST, 3D FLASH, 2D TSE and 2D MRF-FISP estimated at the scanner are reported in Table 2.

Table 2.

Comparison of the head-only SAR of MRF-QUEST, GRE, MRF-FISP and TSE sequences at 3 T. Refer to the text for detailed sequence parameters.

	MRF-QUEST	GRE	MRF-FISP	TSE
SAR (W/kg)	0.03	0.1	0.2	0.3

Discussion

This work introduces a method for relaxation time measurement that combines the MRF framework with the concept of acquisition of high order echoes with QUEST. The proposed method benefits from the synergistic combination of MRF and QUEST. MRF imposes no requirements of signal shape, which allows high order echoes to be used in the acquisition. With a small number of RF pulses, QUEST generates the maximum achievable number of echoes. Aside from the adiabatic pulse for inversion recovery at the beginning of the pulse sequence, all flip angles are smaller than 60°. With the extended spacings between RF pulses, it leads to a quantitative acquisition with very low RF power deposition, which should promote the application of MRF in the ultra-high fields such as 7 T or above where the SAR limitation could be a problem.

Because of its unbalanced gradient scheme, each voxel cannot be treated as a single isochromat in Bloch simulations. In the current implementation, the slice-selective gradient is unbalanced, and the spiral readout is balanced with zero and first moments compensation. However, other schemes could also be implemented. For example, an unbalanced spiral waveform can also be implemented in MRF-QUEST with the penalty of a more complex dictionary calculation in order to account for the dephasing caused by the gradient. The relative advantages of this kind of approach will depend on the exact application where the sequence is used. In general this will give the user the option to choose the direction of unbalanced gradient in order to avoid the unbalanced gradient moment to be along the physiological motion direction, or flexibility to extend the proposed method to a 3D acquisition. In this study, the unbalanced gradient is only along the slice-selective direction. While it simplifies the dictionary computation, the results of the current implementation could be affected by the sensitivity to the motion. On the one hand, the noticeable effect is the underestimated T₁ and T₂ values in the cerebrospinal fluid (CSF) along the slice-selective direction due to the pulsation, and on the other hand because of the fully balanced spiral gradient, the signal of the in-plane blood vessels don’t get spoiled as the conventional spin echo sequence. This leads to the slightly different contrast in the synthesized T₂-weighted image compared with the acquired one. Imperfect slice profiles have been known to affect quantitative results (34). In this study, the effective flip angle due to the change of the slice profile is a non-linear function of the flip angle increment, and thus it cumulatively affects the amplitude of the high order echoes. The dictionary calculation used here intrinsically takes into account the slice profile correction. While Bloch simulations were used in this study, an extended phase graph (EPG) method can also be used to calculate the possible signal evolutions for creating the dictionary. In order for EPG to achieve the slice profile correction, it would also need multiple isochromats along the slice to calculate the signal (10), and thus the relative gain in computational speed is minimal at this point. Severe B₁+ inhomogeneity could also affect the accuracy of the flip angle across FOV, especially in a larger FOV, more complicated coil setup or are acquired in a higher field. However, in these cases, there is no requirement for a homogeneous B₁+, only that the B₁+ is known. Some early studies, which either included B₁+ into the dictionary (35) or added an extra measurement of B₁+ (36), show the potential to further improve the quantification accuracy by taking these factors into account.

The phantom measurement shows a good correlation between the MRF-QUEST and the standard spin echo methods. In vivo T₁ values of GM and WM, and T₂ values of GM from MRF-QUEST also agree with the results of the spin echo methods. However, T₂ of WM of the proposed method is underestimated compared to T₂ derived from spin echo measurements. While the exact factors that causes lower T₂ estimation need to be further investigated, it could possible be the more complex tissue microstructure in WM than GM and phantom, which leads to a broad spectrum of T₂ values (37). Magnetization transfer (MT) could also affect the quantification, especially in variable multiple flip angle methods (38,39). While the effect of MT is more apparent when using high power RF pulses with a short repetition time (40), the exact effect of MT, especially on high order echoes needs to be further investigated.

As noted in prior studies, the choice of dictionary resolution is arbitrary and can be set by the user based on their expected precision levels. The dictionary used in MRF method can always be expanded to cover a wider range or a finer step size of T₁ and T₂ for different applications. In this study, we showed that the accuracy of the T₁ and T₂ estimations were not affected by the different dictionary resolutions, but that the standard deviations of the estimated T₁ and T₂ values were reduced with the finer dictionary step size. This quantization effect is consistent with previous study reported in the supplementary information (18). In this study we used one of the most straightforward template matching methods possible. Other studies (41,42) have shown that the dictionaries in MRF are highly compressible, and thus one can achieve a high precision without sacrificing computation time. Thus the dictionary precision could likely be set to be arbitrarily high in future studies.

The goal of this study was to design a quantitative method with reduced RF power deposition. This work demonstrates that a QUEST-based sequence can be used in combination with the MRF framework to achieve this goal. This work also suggests that the MRF concept has its potential to be applied to different pulse sequence structures besides the steady-state free precession sequence structures. The proposed MRF-QUEST method achieves quantitative measurements of relaxation times with only 0.03 W/kg. While there is a trade-off between the SAR value and the acquisition time of a pulse sequence, the lower SAR value presented by MRF-QUEST cannot be simply achieved by elongating the repetition time in SSFP-based MRF sequence without effects on the quantitative results or prohibitively long scan times. Especially in balanced SSFP method, a longer TR could also lead to unacceptable banding artifacts due to the inhomogeneous field. However, MRF-QUEST does not achieve the near 50 times acceleration shown in the SSFP-based MRF methods. Due to the extended RF spacing, the signal evolution of the proposed method in this study could not be driven to vary smoothly as the signal of SSFP-based MRF, which makes the undersampling artifacts potentially more problematic. For a proof-of-concept, the sequence parameters (flip angles and echo spacing) used in the current study were pseudorandomly generated. Further optimization to choose the acquisition parameters (number of RF pulse, echo spacing and flip angles) to achieve more signal for high order echoes (24) or using a genetic algorithm to minimize the error in the quantification (43) has the potential to improve the efficiency of the acquisition. Also, further acceleration is potentially achievable with existing parallel imaging methods (44,45).

Conclusion

In summary, an alternative pulse sequence based on QUEST was demonstrated for MRF. It was shown that T₁ and T₂ were quantified by MRF-QUEST method with good accuracy and significantly reduced SAR compared with conventional methods. The quantitative T₁ and T₂ maps could also be used to generate synthetic images in SAR-critical applications.